An efficient Bayesian approach for Gaussian Bayesian network structure learning

Abstract

This article proposes a Bayesian computing algorithm to infer Gaussian directed acyclic graphs (DAG’s). It has the ability of escaping local modes and maintaining adequate computing speed compared to existing methods. Simulations demonstrated that the proposed algorithm has low false positives and false negatives in comparison to an algorithm applied to DAG’s. We applied the algorithm to an epigenetic data set to infer DAG’s for smokers and non-smokers.

1. Introduction

There is an increasing attention on learning Directed Acyclic Graphs (DAG’s), or Bayesian networks, which have an appealing property of encoding conditional independence relations by graphs explicitly. By definition, a graph is a DAG if all the links (edges) are directed, but there are no directed loops (circles). Conditional independence means each variable in the graph is conditionally independent of its non-descendants given its parent set. Two DAG’s are Markov equivalent if they represent the same set of conditional independence. To characterize the class of DAG’s with the same set of conditional independence, a partially directed acyclic graph (CPDAG) is introduced, which may be with both directed links and undirected links. One can refer to Andersson et al. (1997); Chickering (2002) for details. It still remains a challenge for inferring Bayesian networks due to network complexity and the existence of multiple local maximums. A number of algorithms are devoted to estimate Bayesian networks, including greedy local search (Heckerman and Chickering, 1995), Optimal Reinsertion search (Moore and keen Wong, 2003), Max-Min Hill-Climbing (Tsamardinos et al., 2006), genetic algorithm (Larranaga et al., 1996; Lee et al., 2010), dynamic programming (Eaton, 2007), branch-and-bound algorithm (de Campos et al., 2011), Markov Chain Monte Carlo (MCMC) approaches (Madigan et al., 1995, 1996; Giudici and Green, 1999; Friedman and Koller, 2003; Ellis and Wong, 2008; Zhou, 2011; Han et al., 2014). The PC algorithm, proposed by Spirtes et al. (2000) becomes very popular to infer DAG’s by detecting the conditional independence, then orienting the links as long as there are no directed circles in the resulting network. It is worthy noting that the PC algorithm finds completed partially directed acyclic graphs, not single DAGs. Subsequently related work include Kalisch et al. (2007); Kalisch and Bhlmann (2008); Harris and Drton (2013).

Among these, Friedman and Koller (2003) made an important improvement in inferring Bayesian networks by introducing graph order MCMC and previous work include Bouckaert (1994). Assuming the order is known, Shojaie and Michailidis (2010) proposed an efficient penalized likelihood method for estimation of adjacent matrix of directed graphs; Altomare et al. (2013) proposed an objective method for DAG inference. Even with order MCMC, it is sill difficult to capture the underlying distributions because of the common problem of multiple local maximums, as experimentally demonstrated by Ellis and Wong (2008). To improve sampling efficiency, Ellis and Wong (2008) suggests the use of advanced sampling technique-single queue Equi-Energy sampler, a variant of the Equi-Energy sampler proposed by Kou et al. (2006) to obtain more reliable posterior samples.

However, most efforts, although stated applicable to continuous variables, focus on discrete networks in which each node is a categorical variable such as in the work by Ellis and Wong (2008); Liang and Zhang (2009); Zhou (2011); Balov (2013), and among others. In biomedical studies, to utilize these methods, continuous variables have to be transformed into discrete variables. This discretization manipulation may induce the risk of losing some meaningful information, for instance the dependence relationships among variables. Furthermore, some data sets are continuous in nature and discretizing them may practically be meaningless. In this work, these limitations motivate us to investigate the structure of Bayesian networks from continuous data.

Section 2 presents the model, including an introduction to Bayesian network, priors and posteriors for parameters. The posterior computing, e.g., the proposed algorithm, is given in section 3. Simulation studies and a real data application are included in section 4. It ends with summary and discussion in section 5.

2. The Model

Bayesian network is a directed acyclic graph which can be characterized by two components, a set of nodes X (random variables), and a collection of directed links, E. Throughout we assume there are n nodes, X = {X₁,X₂,··· ,X_n}, in the network, and the data are fully observed without any missing values. The joint distribution of X satisfies, by Markov property

$$P(\mathit{X})={\displaystyle \prod _{i=1}^{n}P}\left(X_i|Pa\left(X_i\right)\right),$$

where Pa(X_i) ⊂ X \{X_i} is the parent set of X_i. We assume each X_i is a Gaussian random variable with its mean as a function of its parents, i.e., $X_i={\beta }_{i0}+{\displaystyle \sum _{j:X_j\in Pa\left(X_i\right)}{\beta }_{ij}}{X}_j+{ϵ}_i,$ i = 1,2,··· ,n. Parameters β_ij are coefficients and _i is assumed to be Gaussian random noise with mean 0 and variance ${\sigma }_i^2$ . We have

$$X_i|Pa\left(X_i\right)~N({\mu }_{X_i},{\sigma }_i^2),$$

where ${\mu }_{X_i}={\beta }_{i0}+{\displaystyle \sum _{j:X_j\in Pa\left(X_i\right)}{\beta }_{ij}}{X}_j.$ Let θ_i be the set of parameters associated with node X_i, i.e., θ_i = {β_i0,β_i1,β_i2,···, ${\beta }_{{iT}_i},{\sigma }_i^2$} and all parameters for the network are denoted by $\mathit{\theta }={\bigcup }_{i=1}^n{\mathit{\theta }}_i$ , where T_i = |Pa(X_i)|, the number of parents for node X_i. In the following, we assume T_i ≤ 4, i.e., the maximum number of parents is no more than 4. The assumption of boundness on the number of parents is quite common and unavoidable in Bayesian network structure learning since graphs with overwhelmingly large number of links are usually preferred, resulting in over-fitting problem (Ellis and Wong, 2008; Zhou, 2011; Fu and Zhou, 2013).

Suppose there are M independent observations for each variable in the network, x_ih, i = 1,2,··· ,n; h = 1,2,··· ,M. Let $\mathbb{X}$ = {x_ih, i = 1, 2,··· ,n; h = 1, 2,··· , M}. Given the graph $\mathcal{G}$ and the parameter associated with this graph, ${\mathit{\theta }}^{\mathcal{G}}$(${\mathit{\theta }}^{\mathcal{G}}$ has the same definition as θ but is specific to graph $\mathcal{G}$), we have

$$P(\mathbb{X}|\mathcal{G},{\mathit{\theta }}^{\mathcal{G}})={\displaystyle \prod _{h=1}^M{\displaystyle \prod _{i=1}^{n}P}}\left(x_{ih}|Pa\left(x_{ih}\right),{\mathit{\theta }}_i^{\mathcal{G}}\right).$$

Prior distributions

To infer the parameter ${\mathit{\theta }}^{\mathcal{G}}$, we use the fully Bayesian approach. We choose inverse gamma for the prior distribution of ${\sigma }_i^2$, i.e., ${\sigma }_i^2|{\delta }_i$, ψ_i ∼ Inv − Gamma(δ_i,ψ_i), with δ_i, ψ_i known and set the conditional priors for 𝜷_i = (β_i0,β_i1,β_i2,··· ,β_iTi)^T to be of the form 𝜷_i| ∼ $MVN(0,{\sigma }_i^2{({\mathit{X}}_i^{\mathit{P}{\mathit{a}}^T}{\mathit{X}}_i^{Pa})}^{-1})$, where “MV N” denotes multivariate normal distribution, ${\mathit{X}}_{\mathit{i}}^{\mathit{P}\mathit{a}}$ is an M × (T_i + 1) matrix and represents the observational data for the parents of node X_i. This prior allows us to obtain the posterior in closed form in (1).

The prior distribution over structures is commonly chosen to be uniform distribution (Heckerman, 1999; Friedman and Koller, 2003), and the sparse network is usually preferred. In our approach, similar to Ellis and Wong (2008), we consider structure priors as a function of the number of links as $P(\mathcal{G})\propto {\gamma }^{{\displaystyle {\sum }_{i=1}^n|P{a}^{\mathcal{G}}\left(X_i\right)|}},$ for some 0 < γ < 1.

Posterior distributions

The joint posterior distribution of $\left({\mathit{\theta }}^{\mathcal{G}},\mathcal{G}\right)$ is

$$P\left({\mathit{\theta }}^G,\mathcal{G}|\mathbb{X}\right)\propto P\left({\mathit{\theta }}^{\mathcal{G}},\mathcal{G}\right)\times P(\mathbb{X}|{\mathit{\theta }}^{\mathcal{G}},\mathcal{G})$$

By integrating out the parameters, the marginal posterior distribution of $\mathcal{G}$ is

$$P(\mathcal{G}|\mathbb{X})\propto {\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\pi }^{\frac{T_i+1}{2}}{|{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}|}^{-\frac{1}{2}}\times \frac{\mathrm{\Gamma }\left(\frac{M}{2}+{\delta }_i\right)}{{\left\{{\psi }_i-\frac{1}{4}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+\frac{1}{2}{\mathit{X}}_i^T{\mathit{X}}_i\right\}}^{\frac{M}{2}+{\delta }_i}}],$$ (1)

where ${\mathit{X}}_i^{Pa}$ is an M × (T_i + 1) matrix with the hth row $\left(1,x_{h1}^{(i)},\cdots ,x_{h{T}_i}^{(i)}\right)$, h= 1,2,⋯,M, X_i = (x_i1,x_i2,⋯,x_iM)^T, i = 1,2,⋯,n, an M × 1 observation vector for node X_i, and ${\mathit{\eta }}_i={\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i$ . The derivation is given in Appendix. When X_i has no parent, i.e. $|T_i|=0,{\mathit{X}}_i^{Pa}={(1,1,\cdots ,1)}^T$, X_i = (x_i1,x_i2,··· ,x_iM)^T . Thus

$$P\left(X_i;Pa\left(X_i\right)=\varnothing \right)=\sqrt{\frac{\pi }{M}}\frac{\mathrm{\Gamma }\left(\frac{M}{2}+{\delta }_i\right)}{[{\psi }_i-\frac{{\left({\displaystyle {\sum }_{h=1}^M{x}_{ih}}\right)}^2}{4M}+\frac{1}{2}{\displaystyle {\sum }_{h=1}^M{x}_{ih}{}^2}{]}^{\frac{M}{2}+{\delta }_i}}.$$

3. Posterior Computing

3.1. Adjusted Single Queue Equi-Energy sampler (ASQEE)

Many algorithms for network structure inference are available, as described in Section 1. Learning Bayesian networks is known to be NP hard (Chickering et al., 2004) and it poses great challenge on many traditional learning algorithms using MCMC on individual network structures (Madigan et al., 1995, 1996; Giudici and Green, 1999; Grzegorczyk and Husmeier, 2008). Another difficulty in network inference stems from the non-regular posterior distribution of the networks of interest. Friedman and Koller (2003) made a substantial improvement by focusing on graph orders (i.e., treating graph ordering as a random variable), rather than on individual network structures, to build a Markov chain since the space of orders is experimentally verified to be much smaller and more regular than the space of structures. In stead of inferring graphs using (1), we follow the idea of Friedman and Koller (2003) to estimate the orders and construct the graphs based on inferred linked edges.

Given a directed acyclic graph, there exist at least one total ordering, $\mathcal{O}$ (an ordering of n variables, X₁,X₂,··· ,X_n), in which X_i proceeds X_j if X_i ∈ Pa(X_j). On the other hand, if X_i proceeds X_j in order $\mathcal{O}$, directed links from X_j to X_i are prohibited in all of its consistent graphs, imposing an restriction on network structures. One advantage of graph orders is that it is not necessary to perform acyclicity checking, which is commonly required when updating individual network by edge addition, deletion or reversal. In Friedman and Koller (2003), a Markov chain on graph orders $\mathcal{O}$ and its posterior probability is obtained using all consistent graphs,

$$P(\mathcal{O}|\mathbb{X})\propto P(\mathcal{O})\times {\displaystyle \sum _{\mathcal{G}:{\mathcal{G}}^O}P}(\mathbb{X}|\mathcal{G},\mathcal{O})P(\mathcal{G}|\mathcal{O}),$$

where ${\mathcal{G}}^{\mathcal{O}}$ are all consistent graphs with order $\mathcal{O}$. However, the enumeration of all consistent graphs becomes practically intractable for large networks. Instead of sampling all consistent graphs, Ellis and Wong (2008) suggested sampling a number of distinct consistent graphs such that

$${\displaystyle \sum _{i=1}^{k}P}\left({\mathcal{G}}_i|\mathcal{O}\right)>1-ϵ,$$

where ϵ is a pre-specified small positive number, ${\mathcal{G}}_i$, i = 1,2,··· ,k are distinct consistent graphs. However, $P\left({\mathcal{G}}_i|\mathcal{O}\right)$ is usually known up to a normalization constant, and calculation of the exact probability is practically impossible. To bypass this difficulty, given an order, we propose to sample a number of consistent graphs and only use the one with highest probability.

Even with smaller space of orders, the problem of local maximum is still severe. To avoid being trapped at local maximums when drawing posterior samples of $\mathcal{O}$, we propose to use the Single-Queue Equi-Energy sampling (SQEE) proposed by Ellis and Wong (2008), a variant of the Equi-Energy (EE) sampler (Kou et al., 2006). The EE sampling proceeds as follows. The first step is to define a sequence of temperatures 1 = T₁ < T₂ < ··· < T_W , where W is the number of chains. Then a sequence of energy levels are introduced, i.e., H₁ < H₂ < ··· < H_W where $H_1\le \underset{x}{{\displaystyle min}}H(x),H_W\le \infty$ . Based on these energy levels, the tempered distributions are defined as ${\pi }_l(x)=exp\left(\frac{-max\left\{H(x),H_l\right\}}{T_l}\right)l=1,2,\cdots ,W,$ which is the target distribution of lth chain and the energy rings are constructed as D_l = {x|H(x) ∈ [H_l,H_l+1), l = 1, 2,··· , W}. By definition, the larger the value of l, the more flatten distribution the lth chain gets, enhancing the ability of the chain jumping across different modes. Specifically, when l = 1, π₁(x) is the target distribution and π₁(x) = exp(−H(x)). This illustrates the relation between energy function and the distribution. That is H(x) = −log(π₁(x)) = −log(P(O)). One can refer to Kou et al. (2006) for detailed discussions. The SQEE sampler is the same as the EE sampler, except for the sampling of orders at each chain. The construction of the l-th chain in the EE sampler is only based on the (l + 1)-th chain. The SQEE sampler, on the other hand, uses information from any of previous higher order chains, l + 1, l + 2, ··· ,W, which makes a better communications between different chains.

Due to the use of a single graph in the SQEE sampler for a given order, we name the sampler as the adjusted single queue equi-energy sampler (ASQEE). Admittedly, the use of only one representative graph with highest posterior probability may result in bias in calculating the posterior probability of an order. However, it significantly reduces the computing difficulty in Ellis and Wong (2008). Our simulations discussed later indicate that this approximation is applicable and produces reasonably good result.

3.2. Ordering proposal

As discussed in earlier sections, graph ordering is a random variable. Order proposal plays a crucial role in building the Markov chain. We still follow the “cylindrical shift” operation (Ellis and Wong, 2008). To improve the convergence of Markov chain, the number of nodes to be flipped in proposing orders is adjusted in a dynamic way for each single chain. Specifically, the number of flipping nodes decreases as the number of iterations grows. That is, at the beginning of MCMC, we expect the chain to move fast from the current stage, while when the MCMC reaches a relatively stable state, then we expect it to move forward slowly. This will help the MCMC chain reach a more reliable stationary distribution quickly. Metropolis-Hastings (Hastings, 1970) algorithms is applied to determine whether the newly proposed ordering will be accepted or not, which is the standard local Metropolis-Hastings move. Thus the graph order is random and to be updated in the MCMC. The detailed algorithm is presented in Algorithm 1.

3.3. Performance Evaluation

Our interest is on directed links of the network, e.g., the link X_i → X_j, and the associated posterior probabilities. Given a collection of a number of order samplers, ${\mathcal{O}}_1,{\mathcal{O}}_2,\cdots ,{\mathcal{O}}_K$ the posterior probability of a directed link f can be calculated

$$\begin{gathered} P(f|\mathbb{X})={\displaystyle \sum _{k}P}\left(f,{\mathcal{O}}_k|\mathbb{X}\right) \\ ={\displaystyle \sum _{k}P}\left({\mathcal{O}}_k|\mathbb{X}\right)\times P(f|{\mathcal{O}}_k,\mathbb{X}) \\ ={\displaystyle \sum _k[P\left({\mathcal{O}}_k|\mathbb{X}\right)\times {\displaystyle \sum _{i}P}(f|{\mathcal{G}}_i^{{\mathcal{O}}_k}{\mathcal{O}}_k,\mathbb{X})P({\mathcal{G}}_i^{{\mathcal{O}}_k}|{\mathcal{O}}_k,\mathbb{X})]}, \end{gathered}$$ (2)

where ${\mathcal{G}}_i^{{\mathcal{O}}_k}$ are consistent graphs sampled for order ${\mathcal{O}}_k$. By using (2), for a set of links of interest, the posterior probabilities can be calculated. Given a threshold, a positive number between 0 and 1, a set of directed edges could be collected with posterior probability greater than the threshold. Further more, false positives and false negatives can be obtained as well for different threshold for the purpose of comparing between different methods in Bayesian network inferences.

Algorithm 1.

Adjusted Single Queue Equi-Energy algorithm (ASQEE)

Assign $X_1^{(W)}$ an initial ordering, set ${\widehat{D}}_l=\varnothing ,l=1,2,\cdots ,W.$

For n = 1,2,···

For l = W,W − 1,··· ,1

1: if n > (W − l)(B + N) (B is the burn in period) then

2:     do

3:     if l = W or if ${\widehat{D}}_{I\left(X_{n-1}^{(i)}\right)}\ne$ ∅ then

4:         Perform local M-H move to update $X_{n-1}^{(l)}$ by $X_n^{(l)}$ with target distribution πl

5:     else if l < W AND if ${\widehat{D}}_{I\left(X_{n-1}^{(l)}\right)}\ne$ ∅ then

6:         Generate μ ∼ U(0,1)

7:         if μ > pee then

8:             Perform local M-H move to update $X_{n-1}^{(l)}$ by $X_n^{(l)}$ with target distribution πl

9:         else if $\mu ⩽p_{ee}$ then

10:             Uniformly pick a state y from ${\widehat{D}}_{I\left(X_{n-1}^{(l)}\right)}({\widehat{D}}_{I\left(X_{n-1}^{(l)}\right)}$ is the union of all previ-ous energy rings with similar energy level) and $X_n^{(l)}\leftarrow y$ with probability $min\left(1,\frac{{\pi }_l(y)Q\left(y;X_{n-1}^{(l)}\right)}{{\pi }_l\left(X_{n-1}^{(l)}\right)Q\left(X_{n-1}^{(l)};y\right)}\right)(Q(.,.)$ is the transition kernel function; $X_n^{(l)}\leftarrow X_{n-1}^{(l)}$ with the remaining probability

11:         end if

12:     end if

13:     if n > (W − l)(B + N) + B then

14:         ${\widehat{D}}_{I\left(X_n^{(l)}\right)}\leftarrow {\widehat{D}}_{I\left(X_n^{(l)}\right)}+\left\{X_n^{(l)}\right\}$

15:     end if

16: end if

In simulations, $P\left({\mathcal{O}}_k|\mathbb{X}\right)$ is estimated using its relative frequency over all sampled orders after burn in. Similarly, we estimated $P\left(f,{\mathcal{G}}_i^{{\mathcal{O}}_k}|{\mathcal{O}}_k,\mathbb{X}\right)$ by using the relative frequency of related consistent graphs over all sampled consistent graphs of the order.

4. Numerical Studies

4.1. Simulated Experiments

Simulation scenarios

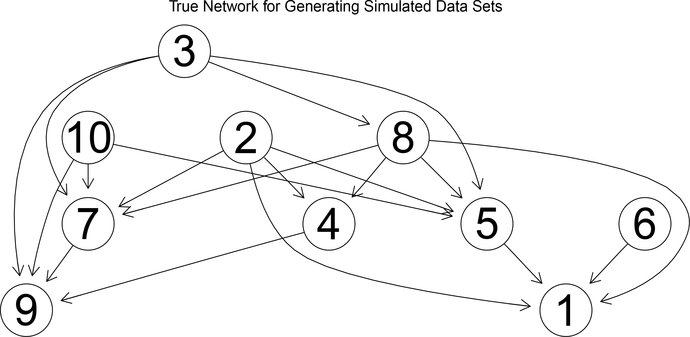
In this section, networks with 10 nodes are considered. An order of these 10 nodes is generated via random rearrangement of r₁,r₂,··· ,r₁₀ with r_i ∈ {1,2,··· ,10}, i.e., ${\mathcal{O}}^{*}$: r₁,r₂,··· ,r₁₀,r_i ∈ {1,2,··· ,10}. Generation of a consistent graph proceeds in the following way, similar to Ellis and Wong (2008). For each node r_i, select the number of its parents, n_i, between 0 and min{(i − 1), R}, R is the maximum parents allowed, then assign n_i parents to node r_i chosen from i − 1 proceeding nodes. The nodes and the parents of each node consist of the whole network structure. The network structure used to simulated data sets is presented in Fig 1. Given this order and network structure, multiple data sets are generated with the following parameters: ${ϵ}_i~N\left(0,{\sigma }_i^2\right);{\beta }_{\mathit{i}}~MVN\left({\mu }_{{\beta }_i},{\mathbf{\Sigma }}_{{\beta }_i}\right);{\mu }_{{\beta }_i}~MVN(\mu ,\mathbf{\Sigma })$, where μ is a (T_i +1)×1 vector with all entries being 2, Σ, and ${\Sigma }_{{\beta }_i}$ are both diagonal matrix with all elements being 0.1. To evaluate the effect of sample size, we set M = 100, 500, 1000. The impact of variance of the inference of network is also considered; σ_i is considered at two levels, σ_i = 0.5, 1.0.

Figure 1:

True network structure used for generating simulated data sets

To the best of our knowledge, FK algorithm (Friedman and Koller, 2003) is the only order based sampling approach which can make a fair comparison with the proposed ASQEE. Another Bayesian approach by Altomare et al. (2013) focuses on the situation with the order known, which is different from our case. Both FK and ASQEE are tested on generated data sets. To implement FK, an initial order is randomly generated and the total number of iterations is set at 20,000 with the first 10,000 as the burn-in period. To reduce the autocorrelations within the chain, order samples are collected every 200 iterations after burn-in. Thus 50 order samples are collected in the final analysis. To make the result from ASQEE comparable to that from FK, the top 50 order samples from ASQEE in terms of posterior probability are used to make the final inference.

Result

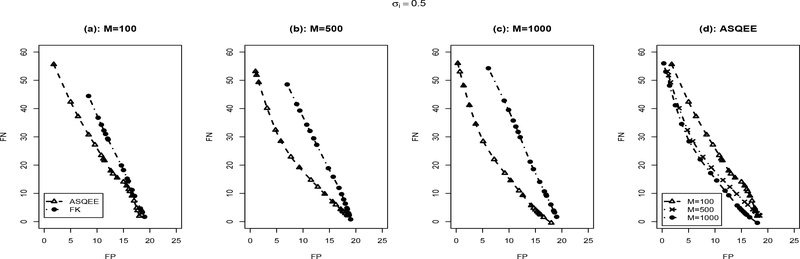
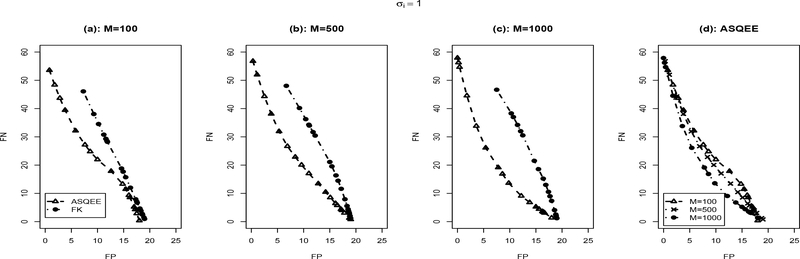
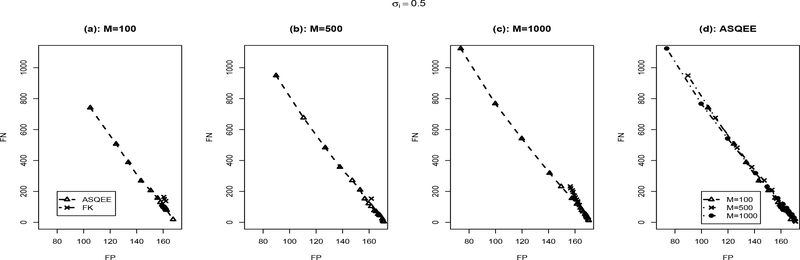
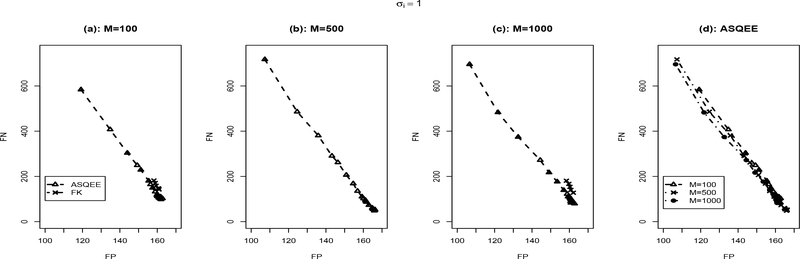
We applied both the ASQEE and FK algorithm on 10 simulated data sets generated following each of the simulation scenarios. The averaged number of false positive and false negatives with different parameter settings is reported in Figures 2, 3, respectively. For the ASQEE approach, at a given level of noise, increasing sample size will result in better inference as indicated by smaller number of false positives and false negatives (Figures 2(d) and 3(d)). Higher level in noise seemed to weaken the quality of the inferences, but they are improved as the sample size gets larger. However, for the FK method, in general, it has higher false positives and false negatives. This may be due to its weak ability of escaping local modes. Overall, regardless of the sample size and the level of noise, ASQEE performs better than FK in terms of the averaged number of false positives and false negatives in both scenarios (Figures 2(a)-(c) and Figures 3(a)-(c)).

Figure 2:

Comparison between ASQEE and FK ((a), (b), (c)) and sample size effect of ASQEE ((d)) in terms of average number of false positives and false negatives across 10 randomly generated data sets with σ_i = 0.5, M = 100, 500, 1000.

Figure 3:

Comparison between ASQEE and FK ((a), (b), (c)) and sample size effect of ASQEE ((d)) in terms of average number of false positives and false negatives across 10 randomly generated data sets with σ_i = 1.0, M = 100, 500, 1000.

The findings are as expected. ASQEE has a better ability of escaping local maximum traps but the FK does not. Our simulations also indicate that using all consistent graphs result in a smaller bias compared to using one single consistent graph in calculating the posterior probability of an order. For small networks (n < 10) where enumerating all consistent graphs is possible, it is still recommended to use as many consistent graphs as possible. However, for large networks (n ≥ 10), selecting one consistent graph with highest posterior probability using M-H is likely to be a good choice.

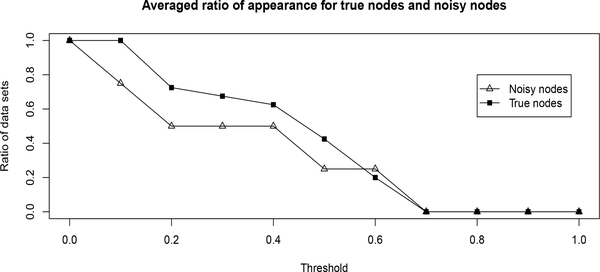
To further test the better ability of the proposed method in identifying true links, we simulated data sets based the graph in Figure 1, but added two additional noisy nodes generated from normal distribution with mean 0 and variance 0.25. These two nodes are isolated, i.e., without any links to the true graph or between each other. For the purpose of demonstration, we focus on the case where M = 100,σ_i = 0.5. Small sample size (M = 100) is considered since when sample size is large, the impact of noisy nodes is expected to be reduced. Given a threshold within interval (0,1), a set of directed links are collected with the posterior probability higher than the cutoff. Based on the collection of directed links, a node is said to be present if it is in the collection. Then we calculated the relative frequency of each node in the collection across 10 randomly generated data sets. The averages of relative frequency are displayed in Figure 4 for the true nodes and noisy nodes respectively. Consistent low frequencies indicate the the method is robust with respect to noisy nodes.

Figure 4:

Averaged ratio of appearance for both true nodes and noisy nodes across 10 randomly generated data sets with M = 100,σ_i = 0.5.

Large Network Inference

The above simulations are based on networks with 10 nodes. We further applied the ASQEE to networks with 50 nodes to assess its ability in dealing with larger networks. The simulation procedure follows the same way as previously stated except that we included four times more nodes in the networks. The averaged numbers of false positives and false negatives of ASQEE and FK are graphically presented in Figure 5 and Figure 6. The FK approach never reached high false positives and never reached low false positives either. On the other hand, the proposed approach (ASQEE) gives a much longer span on possible false positives and false negatives compared to the FK approach, emphasizing the weak ability of FK escaping local modes as noted earlier. Among comparable false positives and false negatives (the lower right corner of each plot in Figures 5 and 6), apparently, our approach overall outperforms FK by observing lower false positives and false negatives.

Figure 5:

Comparison between ASQEE and FK ((a), (b), (c)) and sample size effect of ASQEE ((d)) in terms of average number of false positives and false negatives across 10 randomly generated data sets with σ_i = 0.5, M = 100, 500, 1000 for larger network with 50 nodes.

Figure 6:

Comparison between ASQEE and FK ((a), (b), (c)) and sample size effect of ASQEE ((d)) in terms of average number of false positives and false negatives across 10 randomly generated data sets with σ_i = 1.0, M = 100, 500, 1000 for larger network with 50 nodes.

Moreover, the computing time of FK is much longer than that of ASQEE. This is as expected, since the number of networks is growing exponentially as the number of nodes becomes larger and the FK approach estimates exact posterior probabilities instead of highest posterior probability as in the proposed method. Compared to the performance when dealing with smaller networks with 10 nodes, both ASQEE and FK do not perform equally well when working with larger networks, indicating a great need of developing inference algorithms for large networks.

4.2. An Application to A DNA Methylation Data Set

To illustrate the proposed method, we apply it to a set of 26 CpG sites in 10 genes which are related to maternal smoking (Joubert et al., 2012) and aim to explore the connections among them using networks. The relevant information for all 26 CpG sites are given in Table 1. DNA methylation data of 245 girls measured at age 18 is used in the analysis. These 245 subjects are a random sample from the Isle of Wight birth cohort (Arshad and Hide, 1992). Among these 245 girls, 48 were exposed to maternal smoking during pregnancy.

Table 1:

Relevant information on 26 CpG sites. Chr denotes the chromosome location.

Chr	Gene	CpG	CpG Index in the inferred network
1	GFI1	cg10399789	10
1	GFI1	cg09662411	8
1	GFI1	cg06338710	7
1	GFI1	cg18146737	18
1	GFI1	cg12876356	15
1	GFI1	cg18316974	19
1	GFI1	cg09935388	9
1	GFI1	cg14179389	16
5	AHRR	cg23067299	25
5	AHRR	cg03991871	2
5	AHRR	cg05575921	6
5	AHRR	cg21161138	22
6	HLA-DPB2	cg11715943	11
7	MYO1G	cg19089201	21
7	MYO1G	cg22132788	23
7	MYO1G	cg04180046	3
7	MYO1G	cg12803068	14
7	ENSG00000225718	cg04598670	4
7	CNTNAP2	cg25949550	26
8	EXT1	cg03346806	1
14	TTC7B	cg18655025	20
15	CYP1A1	cg05549655	5
15	CYP1A1	cg22549041	24
15	CYP1A1	cg11924019	12
15	CYP1A1	cg18092474	17
21	RUNX1	cg12477880	13

To apply the proposed algorithm to the methylation data set, logit transformation is applied to transform the methylation data in the interval (0,1) to the whole real line domain. The multivariate assumption of the logit-transformed DNA methylation data was satisfied based on Shapiro-Wilk normality tests. We applied the ASQEE algorithm to the data of 197 subjects not exposed and to the 48 exposed subjects. Five chains are run sequentially from high order to low, each with the total number of 3000 iterations and the first 2700 iterations are treated as burn in. Order samples are collected for final analysis. Given an order, Metropolis Hastings algorithm is applied to sample a number of consistent graphs and the one with highest posterior probability is used to construct the pool of directed links, each with its posterior probability estimated by the frequency of the graph sampled in MCMC after convergence.

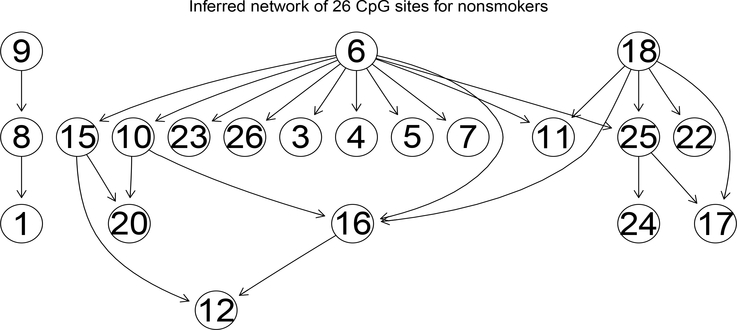
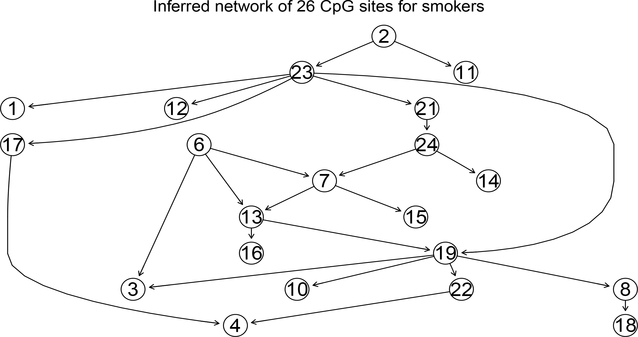
With different cutoffs on posterior probability, a varying number of directed links are obtained. So the choice of cutoffs becomes crucial in building the finally inferred network. We follow the rule that a cutoff should be chosen such that the resulting network is of moderate size (“moderate size” means most of the nodes appearing and the number of links is approximately two or three times of the number of nodes) and captures the important information on the connections between genes. The finally inferred graph is then built upon the selected directed links. The result networks for nonsmokers and smokers are presented in Figures 7 and 8, respectively, inferred based on similar thresholds.

Figure 7:

This inferred network is for 197 girls exposed to mother smoking during pregnancy with cutoff 0.25. CpG sites indices are given in Table 1.

Figure 8:

This inferred network is for girls of 48 mothers who smoked during pregnancy with cutoff 0.3. CpG sites indices are given in Table 1.

The network inferred for the non-smokers (Figure 7) indicates a strong regulatory path from cg 05575921 (CpG index number 6; Table 1 ) in AHRR gene to CpG sites in genes GFI1, MYO1G, CNTNAP2, ENSG00000225718, CYP1A1, and HLA-DPB2. This is consistent with a recent finding on the AHRR gene related to its potential as a biomarker for smoking (Philibert et al., 2013). The dominance of cg 05575921 does not change in the network for smokers for cg 06338710 (index number 7) in gene GFI1 and cg 04180046 (index number 3) in gene MYO1G. Although the direct control of cg05575921 to some CpG sites in the network for non-smokers disappeared in the network for smokers (Figure 8), indirect connection is still observed for most CpG sites shown in Figure 7. For instance, the regulatory function of cg05575921 to CpG sites cg10399789 (index number 10) and cg 12876356 (index number 15) in gene GFI1 and cg 04598670 (index number 4) in gene ENSG00000225718. We postulate that maternal smoking is likely to impose stronger dependence between CpG sites compared to subjects not exposed to maternal smoking. The size of the network for subjects exposed to maternal smoking is larger than that for non-exposed subjects. We do not expect this difference in network size is caused by sample size difference (197 v.s. 48). Random samples of size 48 chosen from the 197 non-smoking exposed girls resulted in networks with even smaller sizes, supporting the postulation of weaker dependence between CpG sites among non-smokers compared to smokers.

5. Summary and Discussion

In this paper, we propose a Bayesian computational algorithm to infer directed links or networks among variables of interest, together with posterior probability. This algorithm is based on a more advanced sampler, Equi-Energy sampler. Moreover, graph orders, of which the space is much smaller than space of networks are employed to build the Markov chain. The proposed algorithm has a better ability of escaping local traps and is expected to obtain more regular posterior distributions compared to existing FK algorithm.

It performs consistently well in terms of smaller number of false positives and false negatives, as seen in simulations. Furthermore, the proposed method has the potential to exclude noisy nodes which should not be in the network. This finding provides informative assistance in the interpretation of the estimated graphs using real data, in that some nodes are shown in the network for non-smokers, but absent in the network for smokers. One potential limitation of the EE or SQEE is the computing efficiency. Although the proposed ASQEE improved the computing efficiency by use of one graph with a high probability, there is still a need to further reduce the computing time, and this is our ongoing work.

6. Appendix-Derivation of the marginal posterior of $\mathcal{G}$

The joint posterior of ${\mathit{\theta }}^{\mathcal{G}}$, $\mathcal{G}$ is, up to a normalizing constant,

$$\begin{gathered} P\left({\mathit{\theta }}^{\mathcal{G}},\mathcal{G}|\mathbb{X}\right)\propto P\left({\mathit{\theta }}^{\mathcal{G}},\mathcal{G}\right)\times P(\mathbb{X}|{\mathit{\theta }}^{\mathcal{G}},\mathcal{G}) \\ ={\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[\frac{{\psi }_i^{{\delta }_i}}{\mathrm{\Gamma }\left({\delta }_i\right)}{\left({\sigma }_i^2\right)}^{-{\delta }_i-1}{e}^{-\frac{{\psi }_i}{{\sigma }_l^2}}{\left(2\pi {\sigma }_i^2\right)}^{-\frac{n_i+1}{2}}{|{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}|}^{-\frac{1}{2}}exp\{-\frac{{\beta }_i^T{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}{\beta }_i}{2{\sigma }_i^2}\} \\ \times {\displaystyle \prod _{h=1}^M{\displaystyle \prod }_{i=1}^n}[\frac{1}{\sqrt{2\pi {\sigma }_i^2}}exp\{-\frac{{\left(x_{ih}-{\beta }_i^T{x}_i^{Pa}\right)}^2}{2{\sigma }_i^2}\}] \\ \propto {\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\left({\sigma }_i^2\right)}^{-\frac{M}{2}}exp\{-\frac{1}{2{\sigma }_i^2}{\left({\mathit{X}}_i-{\mathit{X}}_i^{Pa}{\beta }_i\right)}^T\left({\mathit{X}}_i-{\mathit{X}}_i^{Pa}{\beta }_i\right)\} \\ \times {\left({\sigma }_i^2\right)}^{-\frac{T_i+1}{2}}exp\{-\frac{{\beta }_i^T\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right){\beta }_i}{2{\sigma }_i^2}\}\times {\left({\sigma }_i^2\right)}^{-{\delta }_i-1}exp\{-\frac{{\psi }_i}{{\sigma }_i^2}\}] \\ ={\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\left({\sigma }_i^2\right)}^{-\frac{T_i+1}{2}}exp\{-\frac{2{\beta }_i^T\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right){\beta }_i+{\mathit{X}}_i^T{\mathit{X}}_i^{-}{\mathit{X}}_i^T{\mathit{X}}_i^{Pa}{\beta }_i-{\beta }_i^T{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i}{2{\sigma }_i^2}\} \\ \times {\left({\sigma }_i^2\right)}^{-\left(\frac{M}{2}+{\delta }_i\right)-1}exp\{-\frac{{\psi }_i}{{\sigma }_i^2}\}] \\ ={\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\left({\sigma }_i^2\right)}^{-\frac{T_i+1}{2}}exp\{-\frac{{\left({\beta }_i-\frac{1}{2}{\mathit{\eta }}_{{}_i}\right)}^T\left[2{\mathit{X}}_{{}_i}^{P{a}^T}{\mathit{X}}_{{}_i}^{Pa}\right]\left({\beta }_{{}_i}-\frac{1}{2}{\mathit{\eta }}_{{}_i}\right)}{2{\sigma }_i^2}\} \\ \times {\left({\sigma }_i^2\right)}^{-\left(\frac{M}{2}+{\delta }_i\right)-1}exp\{-\frac{2{\psi }_i-\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+{\mathit{X}}_i^T{\mathit{X}}_i}{2{\sigma }_i^2}\}] \end{gathered}$$ (3)

where ${\mathit{\eta }}_i={\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i$ . The last equality is because

$$\begin{gathered} 2{\beta }_{\mathit{i}}^T\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right){\beta }_i+{\mathit{X}}_i^T{\mathit{X}}_i-{\mathit{X}}_i^T{\mathit{X}}_i^{Pa}{\beta }_i-{\beta }_i^T{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i \\ ={\left[{\beta }_{\mathit{i}}-\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right]}^T\left[2{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right]\left[{\beta }_i-\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right] \\ -\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right)}^{-1}{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i+{\mathit{X}}_i^T{\mathit{X}}_i \\ ={\left({\beta }_i-\frac{1}{2}{\mathit{\eta }}_i\right)}^T\left[2{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right]\left({\beta }_i-\frac{1}{2}{\mathit{\eta }}_i\right)-\frac{1}{2}{\left({\mathit{X}}_i^{\mathbf{P}{\mathbf{a}}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+{\mathit{X}}_i^T{\mathit{X}}_i \end{gathered}$$

By integrating out ${\sigma }_i^2$, 𝛽_i, we get the marginal posterior distribution of $\mathcal{G}$,

$$\begin{gathered} P(\mathcal{G}|\mathbb{X})\propto {\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}{\displaystyle \underset{{\sigma }_i^2}{\int }{\displaystyle \underset{{\beta }_i}{\int }\left[{\left({\sigma }_i^2\right)}^{-\frac{T_i+1}{2}}exp\{-\frac{{\left({\beta }_i-\frac{1}{2}{\mathit{\eta }}_i\right)}^T\left[2{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}\right]\left({\beta }_i-\frac{1}{2}{\mathit{\eta }}_i\right)}{2{\sigma }_i^2}\right]}} \\ \times {\left({\sigma }_i^2\right)}^{-\left(\frac{M}{2}+{\delta }_i\right)-1}exp\{-\frac{2{\psi }_i-\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+{\mathit{X}}_i^T{\mathit{X}}_i}{2{\sigma }_i^2}\}] \\ ={\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\pi }^{\frac{T_{i+1}}{2}}{|{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}|}^{-\frac{1}{2}}{\displaystyle \underset{{\sigma }_i^2}{\int }{\left({\sigma }_i^2\right)}^{-\left(\frac{M}{2}+{\delta }_i\right)-1}}exp\{-\frac{2{\psi }_i-\frac{1}{2}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+{\mathit{X}}_i^T{\mathit{X}}_i}{2{\sigma }_i^2}\} \\ ={\displaystyle \prod _{i=1}^n{\gamma }^{T_i}}[{\pi }^{\frac{T_{i+1}}{2}}{|{\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i^{Pa}|}^{-\frac{1}{2}}\times \frac{\mathrm{\Gamma }\left(\frac{M}{2}+{\delta }_i\right)}{{\left\{{\psi }_i-\frac{1}{4}{\left({\mathit{X}}_i^{P{a}^T}{\mathit{X}}_i\right)}^T{\mathit{\eta }}_i+\frac{1}{2}{\mathit{X}}_i^T{\mathit{X}}_i\right\}}^{\frac{M}{2}+{\delta }_i}}]\square \end{gathered}$$ (4)