The single cell transcriptional landscape of mammalian organogenesis

Junyue Cao; Malte Spielmann; Xiaojie Qiu; Xingfan Huang; Daniel M Ibrahim; Andrew J Hill; Fan Zhang; Stefan Mundlos; Lena Christiansen; Frank J Steemers; Cole Trapnell; Jay Shendure

doi:10.1038/s41586-019-0969-x

. Author manuscript; available in PMC: 2019 Aug 20.

Published in final edited form as: Nature. 2019 Feb 20;566(7745):496–502. doi: 10.1038/s41586-019-0969-x

The single cell transcriptional landscape of mammalian organogenesis

Junyue Cao ^1,^2,^†, Malte Spielmann ^1,^†, Xiaojie Qiu ^1,², Xingfan Huang ^1,³, Daniel M Ibrahim ^4,⁵, Andrew J Hill ¹, Fan Zhang ⁶, Stefan Mundlos ^4,⁵, Lena Christiansen ⁶, Frank J Steemers ⁶, Cole Trapnell ^1,^7,^*, Jay Shendure ^1,^7,^8,^*

PMCID: PMC6434952 NIHMSID: NIHMS1518381 PMID: 30787437

Abstract

Mammalian organogenesis is an astonishing process. Within a short window of time, the cells of the three germ layers transform into an embryo that includes most major internal and external organs. Here we set out to investigate the transcriptional dynamics of mouse organogenesis at single cell resolution. With sci-RNA-seq3, we profiled ~2 million cells, derived from 61 embryos staged between 9.5 and 13.5 days of gestation, in a single experiment. The resulting ‘mouse organogenesis cell atlas’ (MOCA) provides a global view of developmental processes during this critical window. We identify hundreds of cell types and 56 trajectories, many of which are detected only because of the depth of cellular coverage, and collectively define thousands of corresponding marker genes. With Monocle 3, we explore the dynamics of gene expression within cell types and trajectories over time, including focused analyses of the apical ectodermal ridge, limb mesenchyme and skeletal muscle.

Main

Most studies of mammalian organogenesis rely on model organisms, and in particular, the mouse. Mice develop quickly, with just 21 days between fertilization and birth. The implantation of the blastocyst (E4.0) is followed by gastrulation and the formation of germ layers (E6.5-E7.5)^1,2. At the early-somite stages, the embryo transits from gastrulation to early organogenesis, forming the neural plate and heart tube (E8.0–E8.5). In the ensuing days (E9.5-E13.5), the embryo expands from hundreds-of-thousands to over ten million cells, and concurrently develops nearly all major organ systems. Unsurprisingly, these four days have been intensively studied. Indeed, most genes underlying major developmental defects can be studied in this window^3,4.

The transcriptional profiling of single cells (scRNA-seq) represents a promising avenue for obtaining a global view of developmental processes^5–7. For example, scRNA-seq recently revealed remarkable heterogeneity in neurons and myocardiocytes during mouse development^8,9. However, although two scRNA-seq atlases of mouse were recently released^10,11, they are mostly restricted to adult organs, and do not attempt to characterize the emergence and dynamics of cell types during development.

Single cell RNA-seq of 2 million cells

Single cell combinatorial indexing (‘sci-’) is a methodological framework involving split-pool barcoding of cells or nuclei^12–19. We previously developed sci-RNA-seq and applied it to generate 50-fold shotgun coverage of the cellular content of L2 stage Caenorhabditis elegans¹⁷. A conceptually identical method was recently termed Split-Seq²⁰. To increase the throughput, we explored >1,000 experimental conditions (Extended Data Fig. 1ab; Methods). The major improvements of the resulting method, sci-RNA-seq3, include: (i) Nuclei are extracted directly from fresh tissues without enzymatic treatment, then fixed and stored. (ii) For the third level of indexing¹⁷, we switched from Tn5 tagmentation to hairpin ligation. (iii) Individual enzymatic reactions were optimized. (iv) FACS sorting was replaced by dilution, and sonication and filtration steps added to minimize aggregation. Even without automation, sci-RNA-seq3 library preparation can be completed through the intensive effort of a single individual in one week at a cost of less than $0.01 per cell.

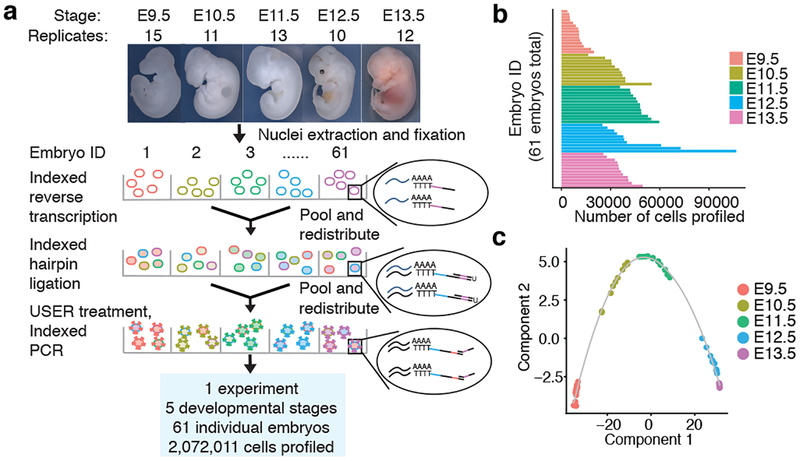
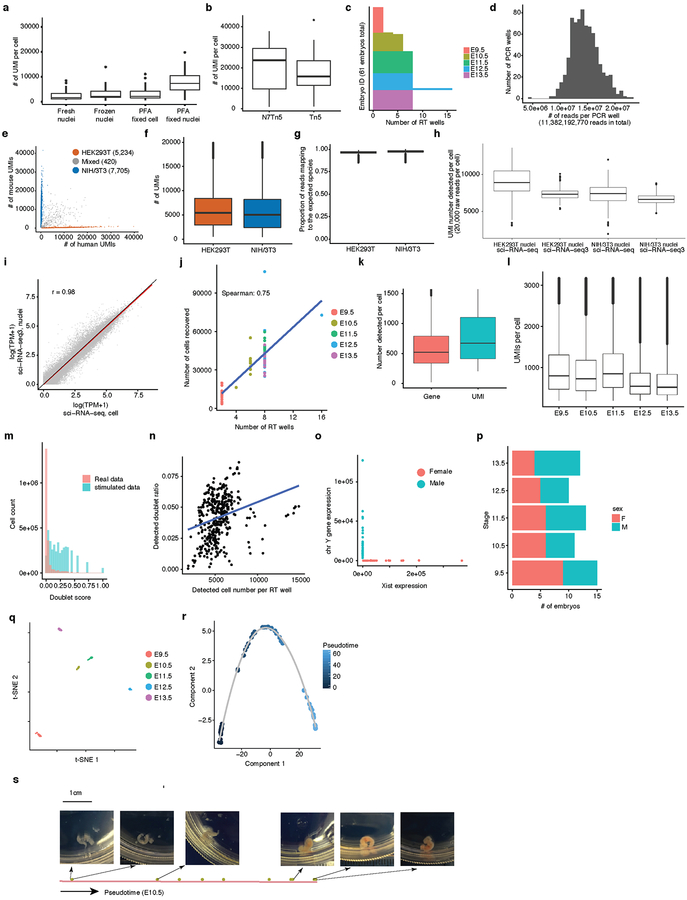
We collected 61 C57BL/6 mouse embryos at E9.5, E10.5, E11.5, E12.5 or E13.5, and snap froze them in liquid nitrogen. Nuclei from each embryo were isolated and deposited to different wells, such that the first index identified the originating embryo of any given cell. As a control, we spiked a mixture of human HEK293T and mouse NIH/3T3 nuclei into two wells. The resulting sci-RNA-seq3 library was sequenced in a single Illumina NovaSeq run, yielding 11 billion reads (Fig. 1a; Extended Data Fig. 1cd).

From one experiment, we recovered 2,058,652 cells from mouse embryos and 13,359 cells from HEK293T or NIH/3T3 cells (UMI (unique molecular identifier) count ≥ 200). Transcriptomes from human/mouse control wells were overwhelmingly species-coherent (3% collisions), with performance similar to previous experiments¹⁷ (Extended Data Fig. 1e–i). A limitation is that only ~7% of cells entering the experiment were ultimately profiled, with losses largely consequent to filtration steps intended to remove aggregates of nuclei.

We profiled a median of 35,272 cells per embryo (Fig. 1b; Extended Data Fig. 1j). Despite shallow sequencing (~5,000 raw reads per cell; 46% duplicate rate), we recovered a median of 671 UMIs (519 genes) per cell (Extended Data Fig. 1k). 3.7-fold deeper sequencing of a subset of wells nearly doubled complexity (to a median of 1,142 UMIs per cell; 87% duplicate rate). As we are profiling RNA in nuclei, 59% of UMIs per cell strand-specifically mapped to introns, and 25% to exons. Our profiles may thus primarily reflect nascent transcription, temporally offset but also predictive²¹ of the cellular transcriptome. Later stage embryos exhibited somewhat reduced UMI counts, possibly reflecting decreasing nuclear mRNA content (Extended Data Fig. 1l). We used Scrublet²² to detect 4.3% likely doublet cells, corresponding to a doublet estimate of 10.3% including both within- and between-cluster doublets (Extended Data Fig. 1mn).

Based on our rough estimates of the number of cells per embryo at each timepoint (Methods), our ‘shotgun cellular coverage’ of the mouse embryo is 0.8× at E9.5 (200K cells/embryo; 152K profiled across all replicates), 0.3× at E10.5 (1.1M cells/embryo; 378K profiled), 0.2× at E11.5 (2.6M cells/embryo; 616K profiled), 0.08× at E12.5 (6M cells/embryo; 475K profiled), and 0.03× at E13.5 (13M cells/embryo; 437K profiled). Thus, although we are not yet oversampling¹⁷, our depth of profiling is equivalent to 3–80% of the cellular content of an individual mouse embryo.

Embryos were readily identified as male (n = 31) or female (n = 30) (Extended Data Fig. 1op). Applying t-stochastic neighbor embedding (t-SNE) to “pseudo-bulk” profiles (aggregating the transcriptomes of each embryo’s cells) resulted in five tightly clustered groups corresponding to developmental stages (Extended Data Fig. 1q). We also ordered the mouse embryos along a pseudotime trajectory²³ (Fig. 1c). Two prominent gaps (E9.5-E10.5 and E11.5-E12.5) suggest particularly dramatic changes during these windows (Extended Data Fig. 1rs). In these pseudo-bulk profiles, 12,236 genes were differentially expressed across developmental stages (Supplementary Table 1).

Identification of cell types and subtypes

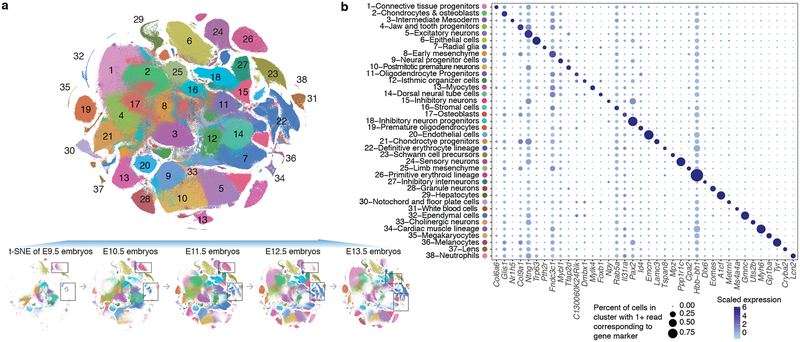
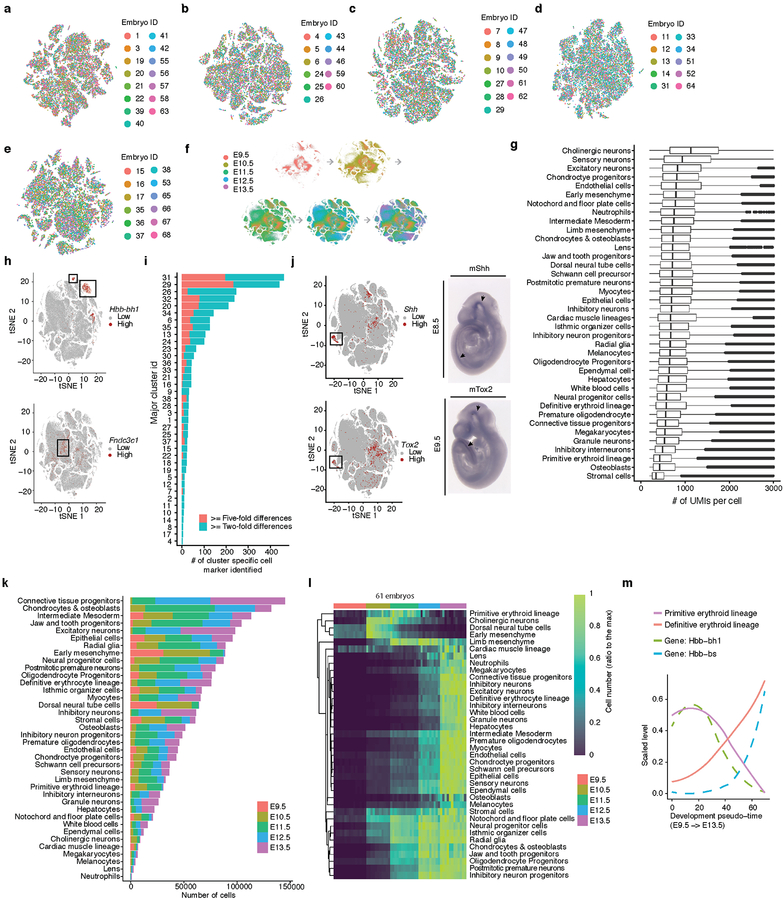
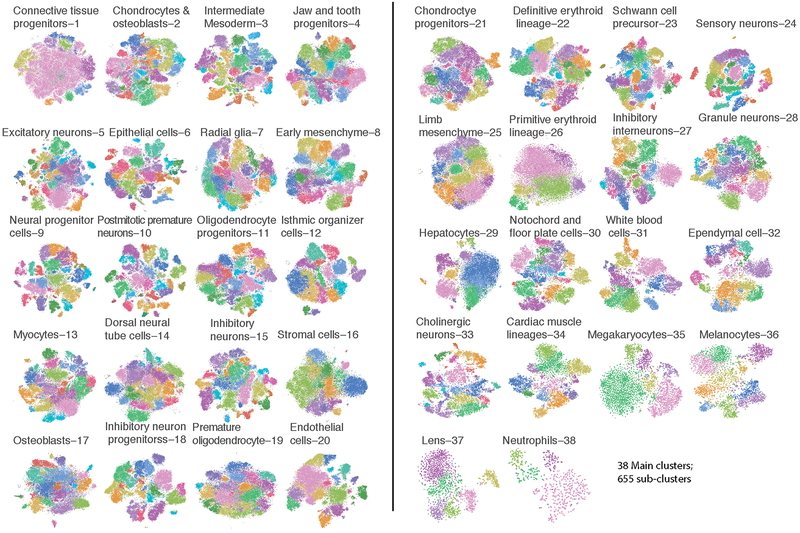
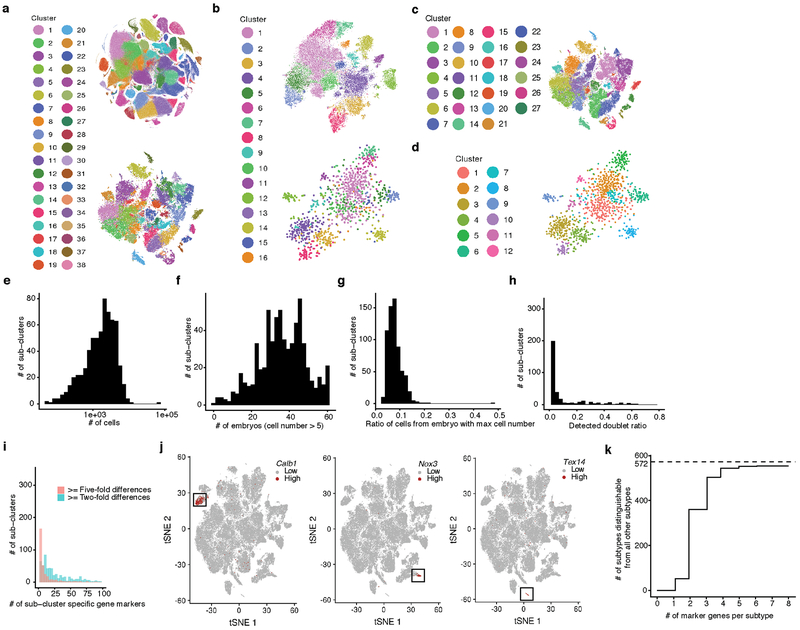
We subjected the 2,058,652 single cell transcriptomes to Louvain clustering and t-SNE visualization (Fig. 2a). Reassuringly, cells from replicate embryos of the same developmental stage were similarly distributed, whereas cells from different stages were not (Extended Data Figs. 2a–f). Based on genes specific to each of 40 clusters, we manually annotated cell types (Supplementary Table 2). Merging two clusters both corresponding to the definitive erythroid lineage and discarding a putative doublet cluster (detected doublet rate of 52%) yielded 38 major cell types (Fig. 2b; Extended Data Fig. 2g).

In general, highly specific marker genes made the annotation of these major cell types straightforward (Fig. 2b; Supplementary Table 3). For example, cluster 6 (epithelial cells) specifically expressed Epcam and Trp63^{24, 25}, while cluster 29 (hepatocytes) specifically expressed Afp and Alb¹⁰. Smaller clusters were readily annotated as well. For example, cluster 36 (melanocytes) specifically expressed Tyr and Trpm1^26,27, while cluster 37 (lens) specifically expressed Cryba2. Some markers, although observed in a substantial proportion of cells in many clusters, were much more highly expressed in one cluster (e.g. Hbb-bh1 in primitive erythroid cells). For clusters corresponding to the embryonic mesenchyme and connective tissue, annotation was more challenging because fewer markers are known (e.g. Fndc3c1 in early mesenchyme; Extended Data Fig. 2h)

17,789 of 26,183 genes (68%) were differentially expressed across the major cell types (5% FDR; Supplementary Table 4). Amongst these, we identified 2,863 cell type-specific marker genes (mean 75; those with >2-fold expression difference between first and second ranked cell type; a cutoff of >5-fold yielded 932 marker genes; Extended Data Fig. 2i). The vast majority of these markers are novel. For example, we detect the highest expression of sonic hedgehog (Shh)²⁸ in the notochord (cluster 30), together with Ntn1, Slit1, and Spon1, all known to be expressed in the cells of the notochord and floor plate during development^29–31. However, Tox2, Stxbp6, Schip1, Frmd4b, not previously been described as markers of the notochord, were also markers of cluster 30. Whole-mount in situ hybridization (WISH) of Shh (known) and Tox2 (novel) confirmed both genes are expressed in notochord at E10.5 (Extended Data Fig. 2j).

We observed marked changes in the proportions of cell types during organogenesis. While most major cell types proliferated exponentially, a few were transient and disappeared by E13.5 (Extended Data Fig. 2kl). For example, at E9.5, we detect cells corresponding to the primitive erythroid lineage, originating from the yolk sack (cluster 26; marked by Hbb−bh1). However, the definitive erythroid lineage, originating from the fetal liver (cluster 22; marked by Hbb−bs), progressively displaces it to become the exclusive red cell lineage by E13.5 (Fig. 2a; Extended Data Fig. 2m).

The 38 major cell types are represented by a median of 47,073 cells, the largest containing 144,648 cells (connective tissue progenitors), and the smallest only 1,000 cells (neutrophils). As additional heterogeneity was readily apparent, we adopted an iterative strategy, repeating Louvain clustering on each major cell type. After subclusters dominated by a few embryos were removed and highly similar subclusters merged (Methods), 655 subclusters were identified (Extended Data Fig. 3). As an operational definition specific to this manuscript, we refer to the 38 major clusters as cell types, and the 655 subclusters as subtypes. Notably, our sensitivity to detect cell types and subtypes in this study was dependent on the large number of cells profiled (Extended Data Fig. 4a–d). The 655 subtypes consist of a median of 1,869 cells, and range from 51 (a subtype of notochord) to 65,894 (a subtype of connective tissue progenitors) cells (Extended Data Fig. 4e–g).

We annotated 13% of subtypes as likely artifacts (>10% of cells in these subtypes are predicted doublets; Extended Data Fig. 4h). For the remaining 572 subtypes, we identified a median of 20 subtype-specific markers (>2-fold expression difference between first and second ranked cell subtypes of the corresponding major cell type; Extended Data Fig. 4ij). Furthermore, most subtypes can be distinguished from all 571 other non-doublet subtypes based on marker gene sets and >4-fold expression differences (63% with 2 markers, 95% with 4 markers; Methods; Extended Data Fig. 4k; Supplementary Table 5).

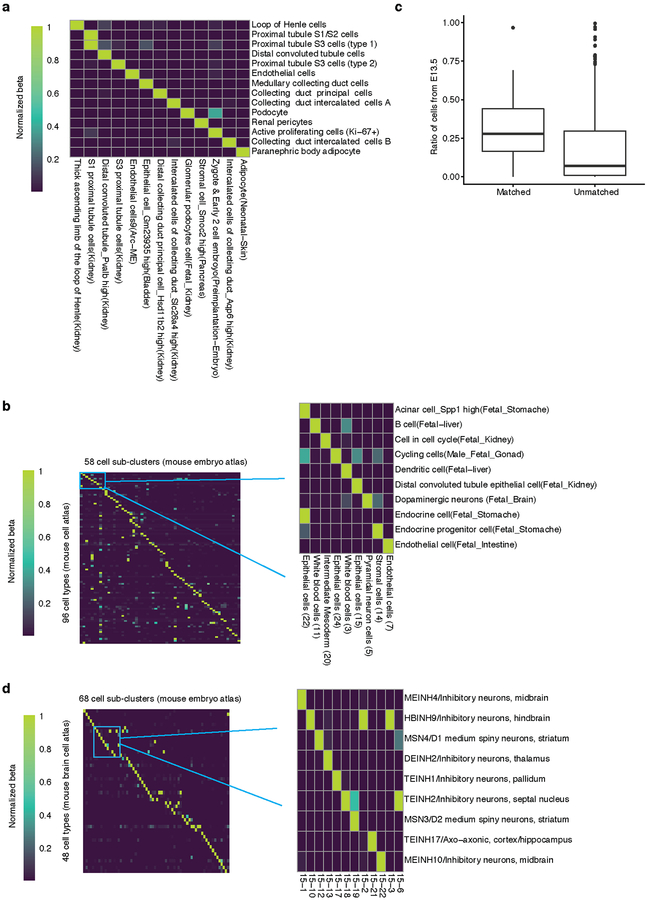
As there are presently no comparable single cell atlases of E9.5-E13.5, we compared MOCA subtypes to 130 fetal cell types (E14.5) of a recent mouse cell atlas (MCA)¹⁰. With a new inter-study cross-matching method, we matched 96 MCA cell types to 58 MOCA subtypes (Methods; Extended Data Fig. 5a–c; Supplementary Table 5). As expected, MOCA subtypes that failed to match MCA cell types tended to derive from earlier stages (e.g. neural tube) or were rare (e.g. lens), while MCA cell types that failed MOCA subtypes were mostly tissue-specific immune or epithelial cells, potentially because they emerge after E13.5. Nonetheless, the atlases unquestionably inform one another, as the MCA’s anatomical resolution is useful for localizing MOCA subtypes, while MOCA’s developmental focus informs the embryonic origin of MCA cell types (Extended Data Fig. 5b). As an example of the former, a subcluster of endocrine epithelial cells in MOCA mapped to both the acinar and endocrine cells of the fetal stomach in the MCA. As an example of the latter, “cells in cell cycle” in the MCA’s fetal kidney mapped to a subtype of intermediate mesoderm in MOCA, plausibly corresponding to progenitors of the kidney. A similar analysis matched 48 cell types annotated in a recent mouse brain atlas (BCA)³² to 68 MOCA subtypes with high specificity (Extended Data Fig. 5d).

Characterization of the apical ectodermal ridge

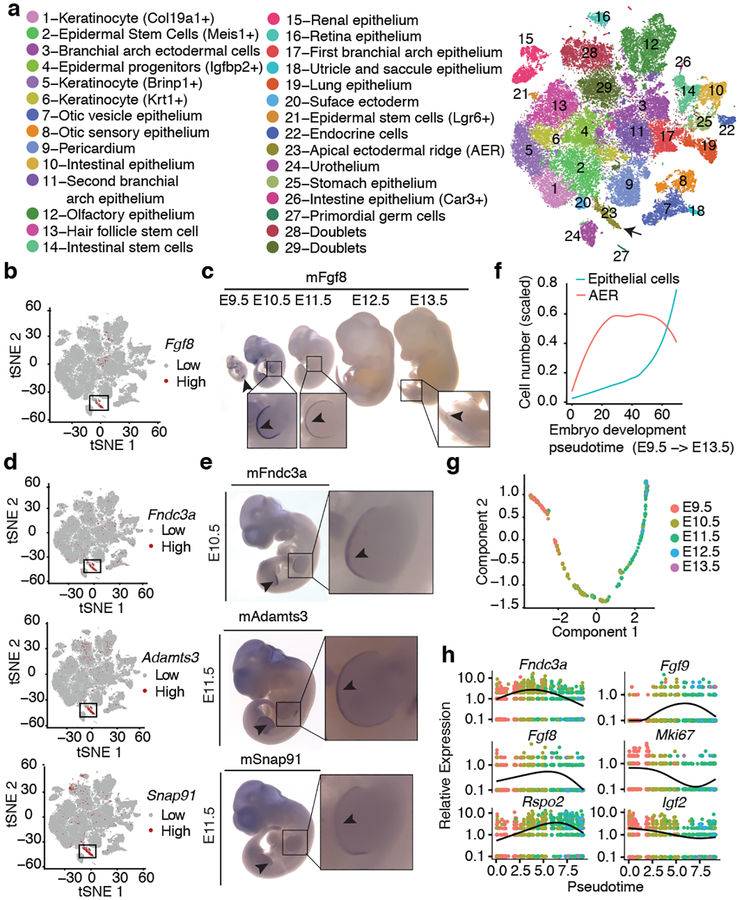
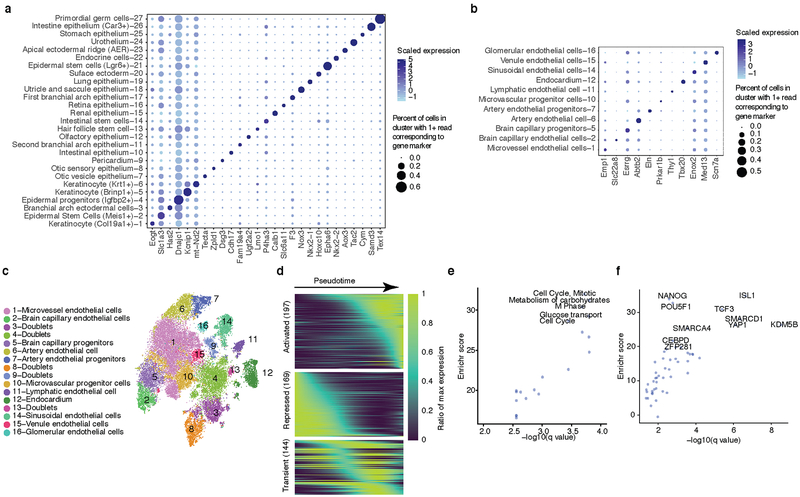
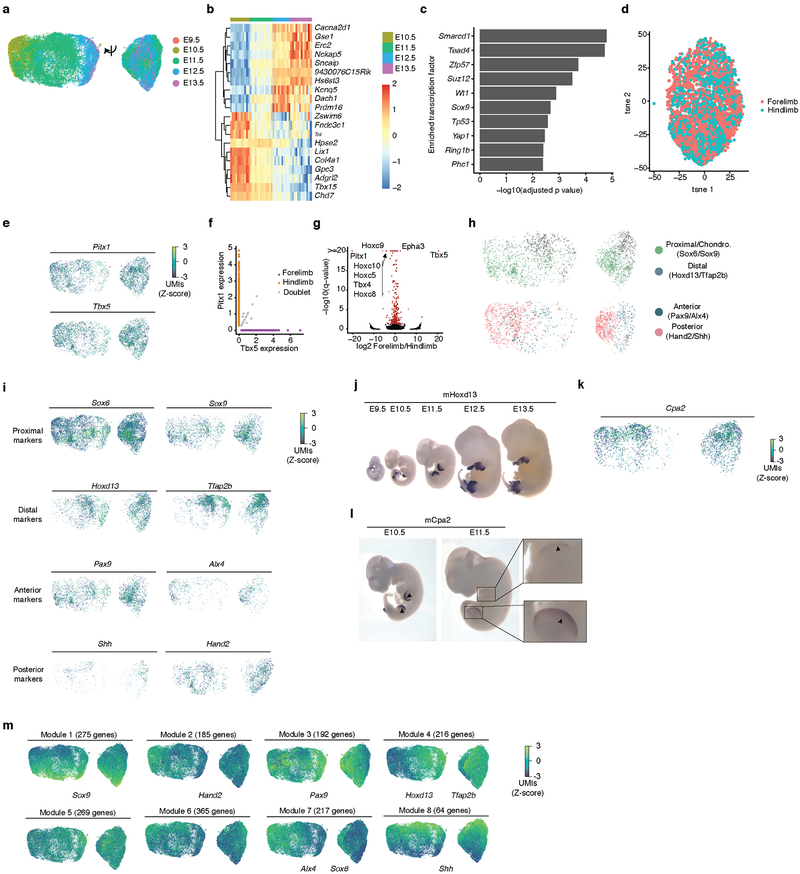
We annotated all subtypes of epithelium and endothelium (clusters 6 and 20, respectively; Fig. 3a; Extended Data Fig. 6a–c; Supplementary Table 2). For example, epithelial subtype 6.8 was marked by Oc90, exclusively expressed in the epithelium of the otic vesicle³³; epithelial subtype 6.23 by Fgf8, Msx2. and Rspo2, known markers of the apical ectodermal ridge (AER)³⁴; and endothelial subtype 20.12 by Tbx20 and Tmem108, specific to endocardial cells and cardiac valve endothelium^35,36.

To investigate a subtype in more detail, we focused on the AER, a highly specialized epithelium involved in digit development³⁷. In addition to known markers for AER, subtype 6.23 (1,237 cells; 0.06% of MOCA) was distinguished by expression of Fndc3a, Adamts3, Slc16a10, Snap91, and Pou6f2. WISH of Fgf8 (known), Fndc3a, Adamts3, and Snap91 (all novel) confirmed expression specific to the most distal tip of the limb bud representing the AER at E10.5 or E11.5 (Fig. 3b–e).

We next examined the dynamics of AER proliferation and gene expression. Although detected at all timepoints and nearly all embryos, the estimated number of AER cells per embryo peaks between E10.5 and E11.5 (Fig. 3f), consistent with a previous report³⁸ and our validations (Fig. 3c). We performed pseudotemporal ordering of AER cells, yielding a simple early-to-late trajectory and 710 differentially expressed genes (5% FDR; Fig. 3gh; Extended Data Fig. 6d; Supplementary Table 6). For example, Fgf8, Fgf9³⁹ and Rspo2³⁴ are preceded in their activation dynamics by Fndc3a. Genes whose expression significantly decreased include Mki67 and Igf2, which have roles in promoting cellular proliferation^40,41. Pathway-level analyses also showed the downregulation of proliferative programs in this window (Extended Data Fig. 6ef).

Reconstructing developmental trajectories

We next sought to investigate the developmental trajectories that cell types traverse during mammalian organogenesis. Most contemporary algorithms for trajectory reconstruction assume a continuous manifold (whereas our data begin at E9.5, and therefore are missing at least some ancestral states) and do not allow for convergence of cell fates (whereas some cell types are known to derive from multiple transcriptionally distinct lineages). To overcome these limitations while also enabling scaling to millions of cells, we developed a new version of Monocle⁴². Monocle 3 first projects cells onto a low-dimensional space encoding transcriptional state using UMAP⁴³. It then groups mutually similar cells using the Louvain community detection algorithm, and merges adjacent groups into ‘supergroups’⁴⁴. Finally, it resolves the paths or trajectories that individual cells can take during development, identifying the locations of branches and convergences within each supergroup.

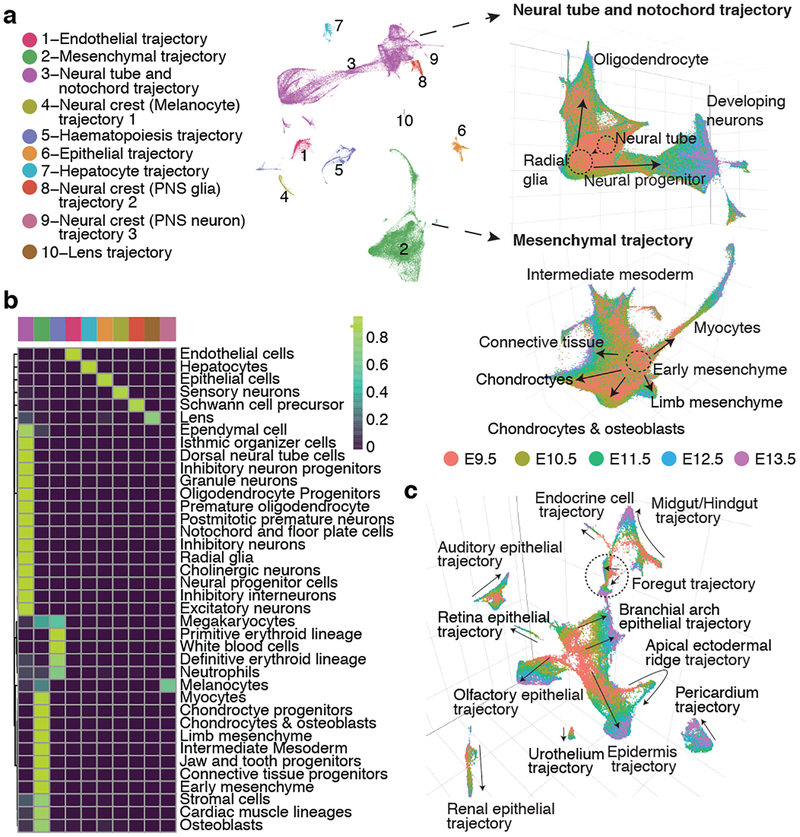
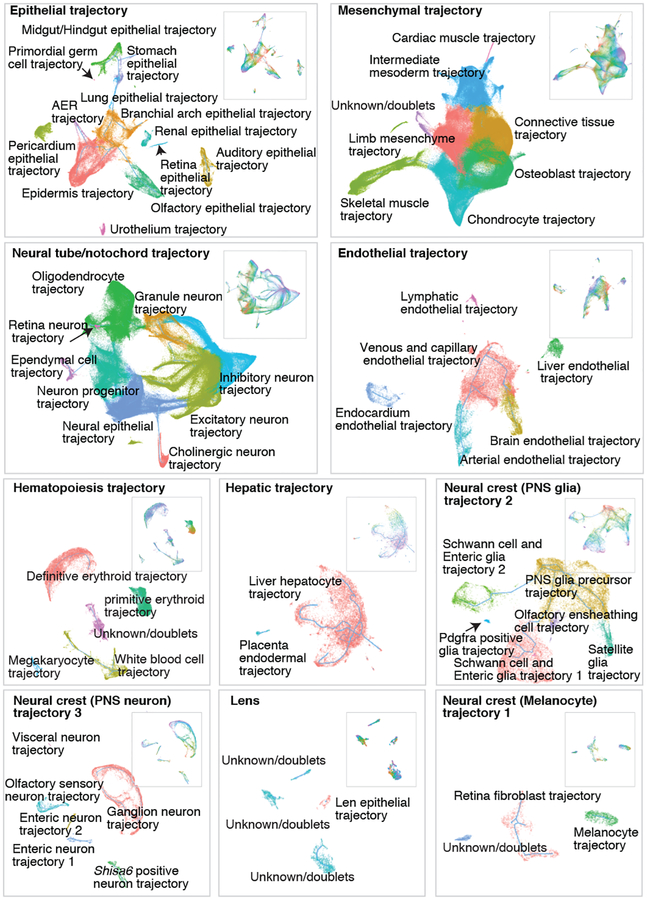
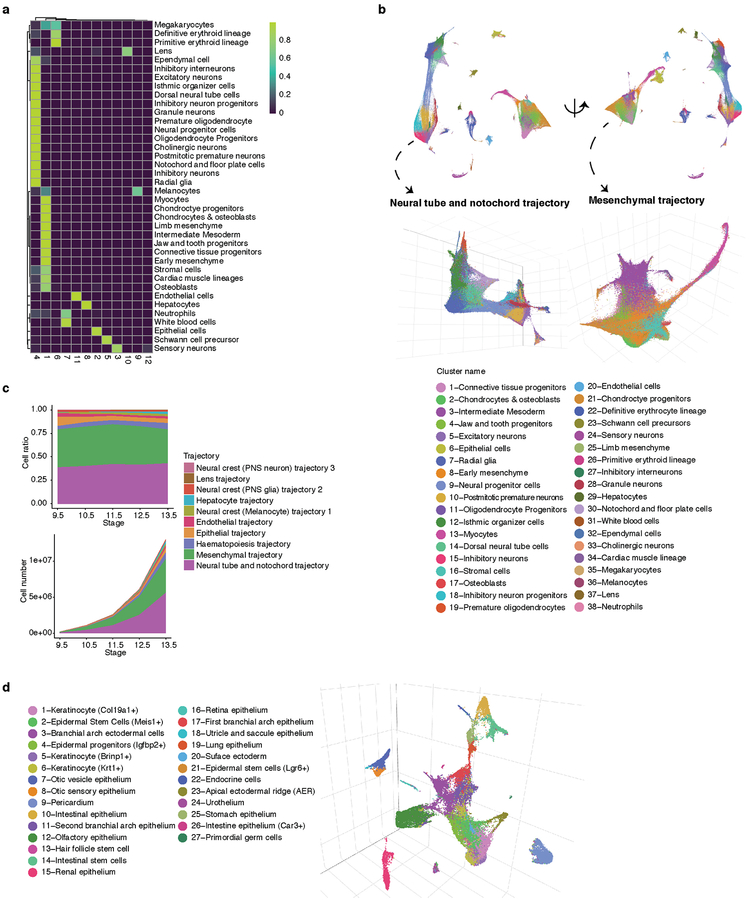
Subsequent to a focused application of Monocle 3 to cells corresponding to the limb bud mesenchyme (Supplementary Note 1; Extended Data Fig. 7; Supplementary Tables 7–9), we applied it to identify major developmental trajectories across the entire dataset. Monocle 3 organized 1,524,792 high-quality cells (UMI > 400) into twelve groups. We merged two groups corresponding to sensory neurons, and another two corresponding to blood cells. Nearly all of the 38 major cell types fall almost exclusively in one of the ten resulting trajectories (Fig. 4a–b; Extended Data Fig. 8ab). The two most complex structures are the neural tube/notochord trajectory, which includes the notochord, neural tube, progenitor and developing neuronal and glial cell types, and the mesenchymal trajectory, which includes all mesenchymal and muscle cell types. There are three neural crest trajectories, corresponding to sensory neurons, Schwann cell precursors and melanocytes. The hematopoietic trajectory includes megakaryocytes, erythrocytes and white blood cells, while the remaining four trajectories (endothelial, epithelial, hepatic, lens) each correspond to a single major cell type (Fig. 4b). The discontinuity between these ten major trajectories likely reflects the lack of representation of some intermediate or ancestral states, consequent to our study beginning at E9.5. Although the estimated number of cells per embryo in each trajectory increases exponentially, their proportions remain relatively stable, with the exception of hepatocytes, which markedly increase their contribution from 0.3% at E9.5 to 2.8% at E13.5 (Extended Data Fig. 8c).

Fig. 4. — (a) UMAP 3D visualization of our overall dataset; left: views from one direction; bottom: zoomed view of neural tube/notochord (top) and mesenchymal (bottom) trajectories, colored by development stage. PNS: peripheral nervous system. (b) Heatmap showing the proportion of cells from each of the 38 major cell types (rows) assigned to each of the 10 major trajectories (columns; color key in left panel of a). (c) UMAP 3D visualization of epithelial subtrajectories colored by development stage (color key in right panel of a).

Unlike t-SNE, UMAP places related cell types near one another. For example, cell types found at later developmental timepoints such as inhibitory neurons are connected to early CNS precursors (radial glia) by a ‘bridge’ of neural progenitor cells; however, the same radial glial cells project in a different direction towards increasingly mature oligodendrocytes (Fig. 4a, left). Similarly, early mesenchymal cells radiate from a defined region into myocytes, limb mesenchyme, chondrocytes/osteoblasts and connective tissues (Fig. 4a, right).

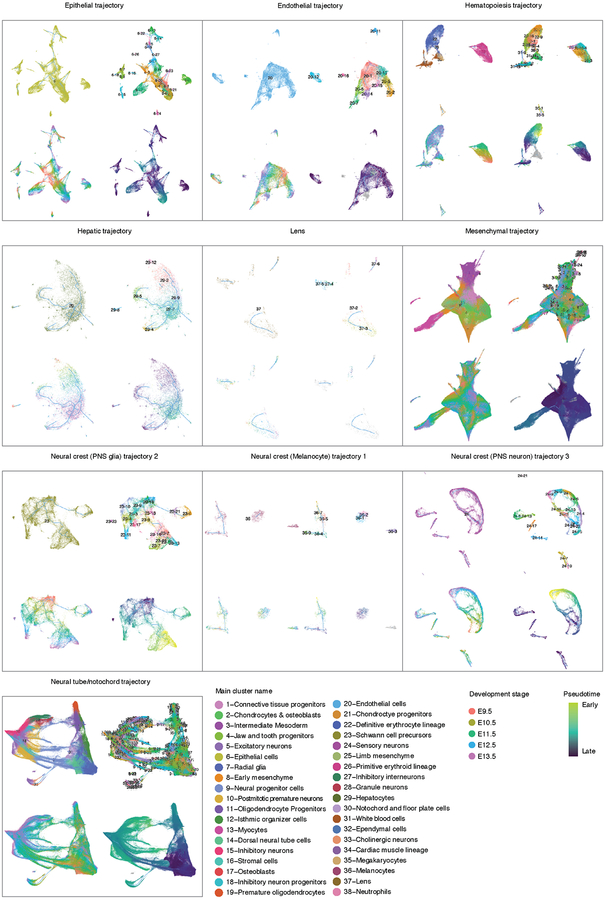
After removing 12% of cells corresponding to doublet-annotated cells and/or subclusters, we iteratively reanalyzed the ten major trajectories (Fig. 5; Extended Data Fig. 9). For example, the epithelial trajectory breaks into several discontinuous subtrajectories, each emanating from a focal concentration of E9.5-derived cells and projecting in one or more directions, through cells corresponding to progressively later timepoints (Fig. 4c; Extended Data Fig. 8d). Notably, the AER subtrajectory projects out of surface ectoderm and then back into epidermis, consistent with its transitory nature.

Fig. 5. — After removing doublet-annotated cells and subclusters, we iteratively reanalyzed each of the ten major trajectories. Colored by subtrajectory name (main plots) or developmental stage (insets; colors as in Fig. 4c). Edges in the principal graphs that define trajectories reported by Monocle 3 are shown as light blue line segments.

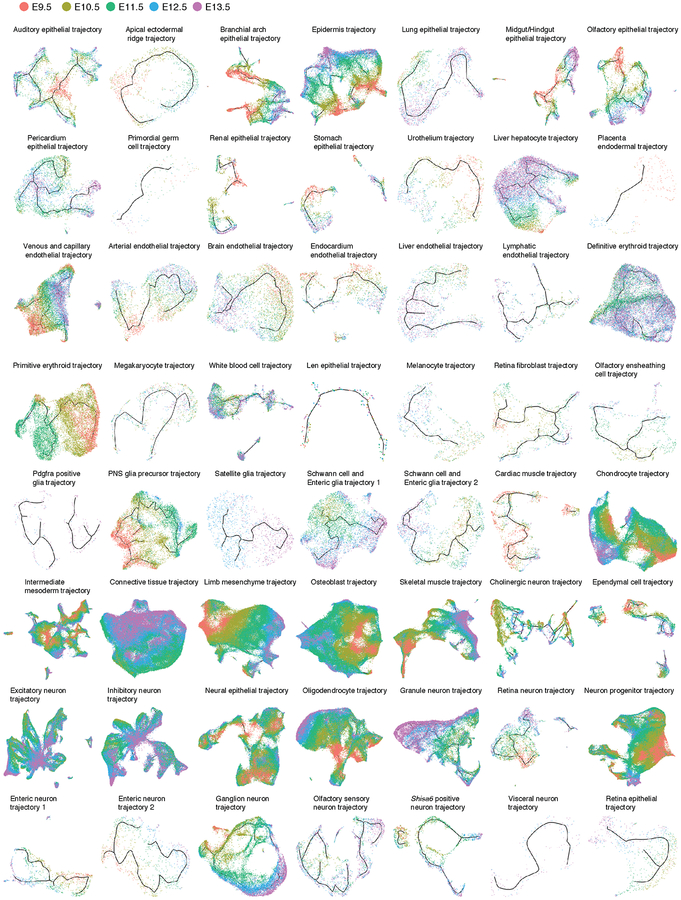
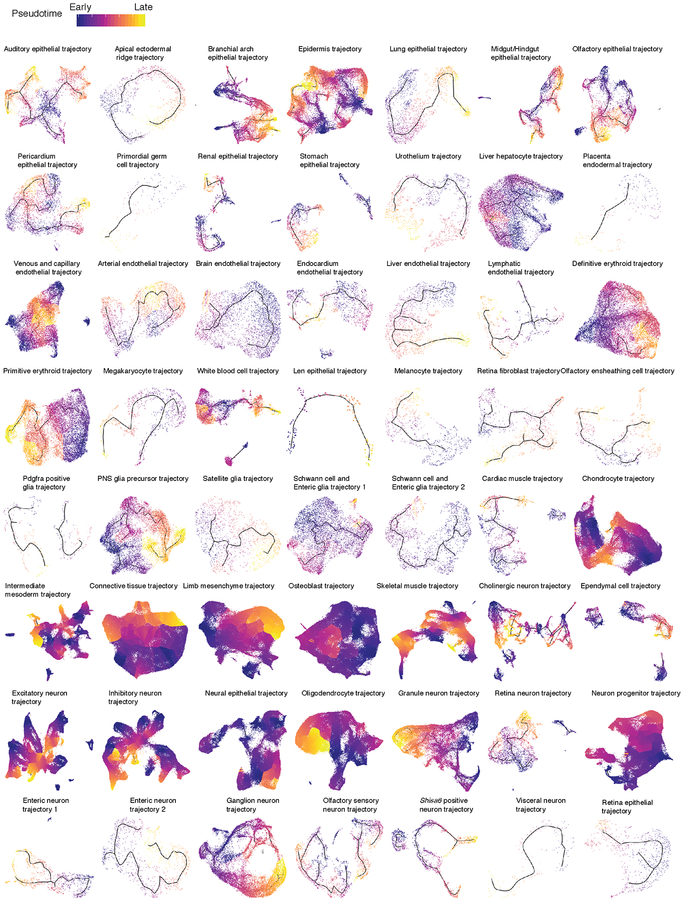
We mapped the 572 subtypes defined by t-SNE and Louvain clustering to the developmental subtrajectories defined by Monocle 3 (Extended Data Fig. 9). The vast majority of subtypes mapped to a single subtrajectory, often as temporally restricted subsets (Supplementary Table 5). We annotated the subtrajectories on the basis of marker genes of subtypes mapping to them. The resulting 56 developmental subtrajectories span all major systems including the CNS, PNS, respiratory, digestive, cardiovascular, immune, lymphatic, urinary, endocrine, integumentary, skeletal, muscular and reproductive systems (Fig. 5; Extended Data Fig. 10).

In some cases, we observe a single, simple linear trajectory. However, we also observe many examples of branching trajectories, as well as of cell types that appear to be generated via multiple parallel paths. As an example of the latter, both CNS excitatory and inhibitory neurons appear to develop through multiple, convergent trajectories, possibly due to the maturation in multiple anatomical locations. Other subtrajectories exhibited even more complex features, including multiple starting and ending points within a continuous structure (e.g. intermediate mesoderm trajectory).

Although Monocle 3 did not have access to these labels, the subtrajectories are highly consistent with developmental time (i.e. cells ordered from E9.5 to E13.5, Extended Data Fig. 9–10). To orient subtrajectories, we identified one or several starting points as focal concentrations of E9.5 cells, and then computed developmental pseudotime for cells present along various paths (Extended Data Fig. 11; Methods). We also annotated each subtype according to the subtrajectory to which it maps, as well as its relative temporal position within that subtrajectory (e.g. subtype 6.14 = “auditory epithelial trajectory.1-of-3”) (Supplementary Table 5). These representations provide a starting point for more detailed explorations of the 572 subtypes and 56 subtrajectories.

Reconstructing skeletal myogenesis

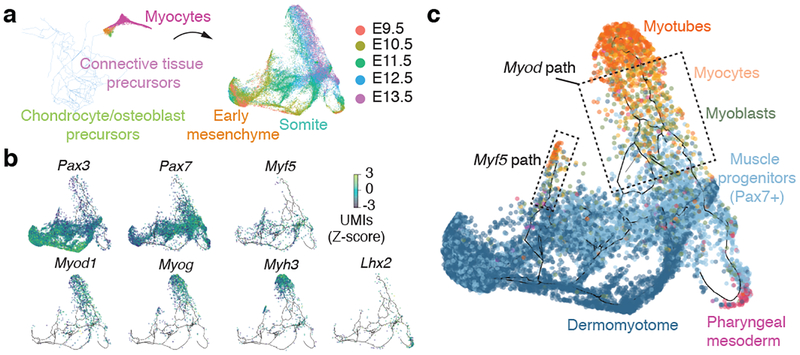
To investigate a developmental process in greater detail, we focused on developing muscle, which is comprised of distinct mesodermal lineages that form prior to E9.5⁴⁵. We hypothesized that the myogenic trajectory would feature multiple entry points that feed cells into a common path corresponding to activation of the core gene expression program shared by myotubes.

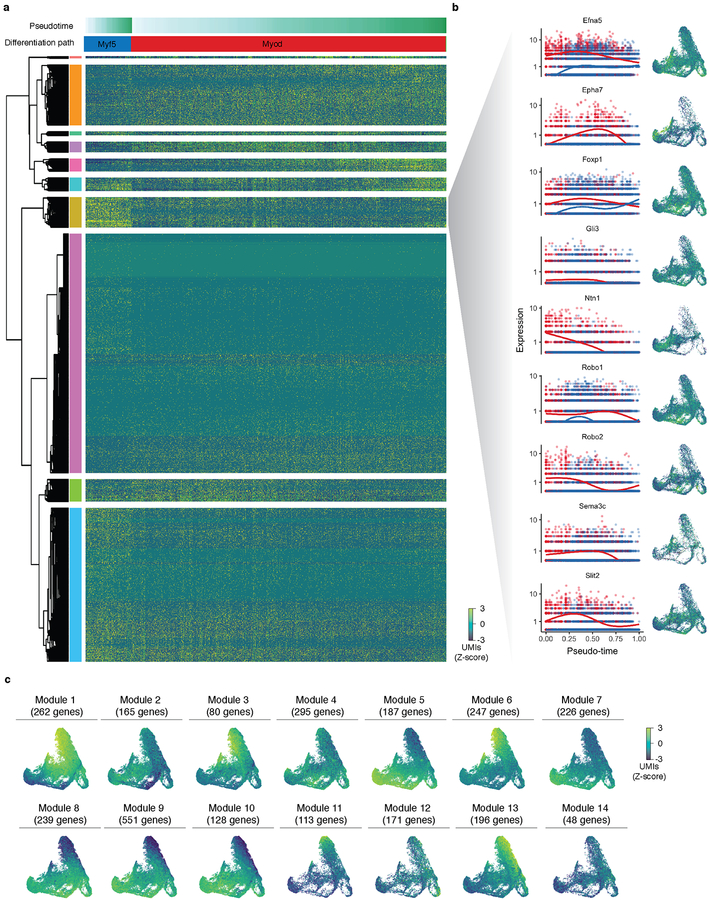
To test this, we in silico isolated myocytes and their putative ‘ancestral’ cells from the mesenchyme trajectory (Fig. 6a; Methods). Next, we used Monocle 3 to construct a myogenesis-specific trajectory, which featured multiple focal concentrations of E9.5 cells, with cells from later stages distributed over several paths radiating outward (Fig. 6a). Pax3 and Pax7, which mark skeletal muscle progenitors, were expressed over a broad swath of the principal graph (Fig. 6b). Cells expressing Myf5 co-localized with a subset of Pax7+ cells, consistent with the role of Myf5 in embryonic myogenesis⁴⁶. From this region of the trajectory, two parallel linear segments emanated, on which cells expressed either Myf5 or Myod. Both paths terminate with cells expressing Myog or Myh3, markers of myocytes and myotubes, respectively. The cells on the Myf5+ path, largely from early time points, also expressed higher levels of genes in the Robo/Slit signaling pathway, which has been implicated in driving “pioneer myoblasts” to form embryonic myofibers⁴⁷ (Extended Data Fig. 12). An additional path traversed by cells from E9.5, which expressed Lhx2, Tbx1, and Pitx2 but very low levels of Pax3, feeds into the trajectory just upstream of the Myf5 and Myod1 segments, and possibly corresponds to pharyngeal mesoderm⁴⁵. Overall, the trajectory is consistent with the view that different mesodermal lineages use distinct factors to converge on a core program of muscle genes (Fig. 6c). Globally, we detected 2,908 genes expressed in a trajectory-dependent manner (FDR < 0.05 and Moran’s I > 0.01) that grouped into 14 distinct patterns (Extended Data Fig. 12; Supplementary Table 10).

Discussion

Here, to obtain a global view of mammalian organogenesis, we profiled the transcriptomes of ~2 million cells from mouse embryos spanning E9.5 to E13.5. In the resulting atlas (MOCA), we identify over 500 subtypes of cells and 56 developmental subtrajectories, each distinguished by multiple marker genes and collectively spanning essentially every organ system. With sci-RNA-seq3, we introduce a technical framework for individual labs to generate datasets corresponding to millions of single cells. With Monocle 3, we introduce a computational framework for trajectory inference that operates at this same scale. These data constitute a potentially foundational resource for the mammalian developmental biology field. MOCA and the underlying data are made freely available, together with a website to facilitate their further exploration (http://atlas.gs.washington.edu/mouse-rna/).

MOCA has limitations. First, although not sequenced to saturation, the cell-by-gene matrix is sparse. Nonetheless, our results support the view that cell types are readily distinguishable despite hundreds rather than thousands of UMIs per cell⁴⁸. Of course, the tradeoff between breadth and depth depends on one’s goals. As an example supporting the ‘many cells, few UMIs per cell’ approach, consider primordial germ cells, which were readily identifiable despite their rarity (subtypes 16.13 and 6.27, which sum to 269/2,058,652 cells or 0.01% of MOCA). Nonetheless, despite its unprecedented depth, our study does not exceed 1-fold coverage of the mouse embryo at any timepoint, and it is possible that we are missing extremely rare cell types.

Second, although we are reasonably confident in our annotations, they should be regarded as preliminary. Mid-gestational mouse development has not previously been extensively studied at single cell resolution, and many published markers have limited specificity. Furthermore, because we studied disaggregated whole embryos, the assignment of anatomical specificity is challenging. We anticipate that the comprehensive annotation of MOCA will benefit from community input and domain expertise, and to that end created an interactive wiki (http://atlas.gs.washington.edu/mouse-rna/). Inevitably, however, additional experiments (e.g. in situ analyses of marker genes) will be necessary to resolve ambiguities. Importantly for future atlasing efforts, we found the annotation of temporally-resolved developmental trajectories to be much more straightforward than that of cell types.

A long-standing dream, perhaps at last within sight from a technical perspective, is a comprehensive, spatiotemporally-resolved molecular atlas of mammalian development at single cell resolution. To this end, the mouse has several advantages, including its small size, the accessibility of early developmental timepoints, an inbred genetic background, and genetic manipulability. It also seems likely that ‘whole organism’ profiling of small mammals will be essential for identifying the inevitable gaps in any efforts to generate a comprehensive atlas of human cell types.

Single cell atlases of the development of wild-type mice may also represent an important step towards understanding pleiotropic developmental disorders at the organismal scale, and for detailed investigations of subtle roles for genes and regulatory sequences in development. For example, many knockouts of both coding and conserved regulatory sequences do not show any abnormalities with conventional phenotyping⁴⁹. We anticipate that ‘whole organism’ sc-RNA-seq will empower reverse genetics, e.g. potentially enabling the discovery of subtle defects in the molecular programs or the relative proportions of specific cell types⁵⁰.

METHODS

Data reporting

No statistical methods were used to predetermine sample size. Embryos used in experiment were randomized before sample preparation. Investigators were blinded to group allocation during data collection and analysis: embryo collection and sci-RNA-seq3 analysis were performed by two different researchers.

Embryo dissection

The C57BL/6 mice were obtained from The Jackson Laboratory (Bar Harbor, ME) and plug matings were set up. Noon on the day of the vaginal plug was considered as embryonic day (E) 0.5. Dissections were done as previously described⁵² and all embryos were immediately snap frozen in liquid nitrogen. Embryos were collected from at least three independent litters per development stage. All animal procedures were in accordance with institutional, state, and government regulations and approved by the Office of Animal Welfare (OAW) under the IACUC protocol 4378–01.

Whole-mount in situ hybridization

The mRNA expression in E9.5-E13.5 mouse embryos was assessed by whole mount in situ hybridisation (WISH) using a digoxigenin-labeled antisense riboprobe transcribed from a cloned gene specific probes (PCR DIG Probe Synthesis Kit, Roche). Whole embryos were fixed overnight in 4% PFA/PBS. The embryos were washed in PBST (0.1% Tween), and dehydrated stepwise in 25%, 50% and 75% methanol/PBST and finally stored at −20°C in 100% methanol. The WISH protocol was as follows: Day 1) Embryos were rehydrated on ice in reverse methanol/PBST steps, washed in PBST, bleached in 6% H₂O₂/PBST for 1 hour and washed in PBST. Embryos were then treated in 10 μg/ml Proteinase K/PBST for 3 minutes, incubated in glycine/PBST, washed in PBST and finally re-fixed for 20 minutes with 4% PFA/PBS, 0.2% glutaraldehyde and 0.1% Tween 20. After further washing steps with PBST, embryos were incubated at 68°C in L1 buffer (50% deionised formamide, 5× SSC, 1% SDS, 0.1% Tween 20 in DEPC; pH 4.5) for 10 minutes. Next, embryos were incubated for 2 hours at 68°C in hybridisation buffer 1 (L1 with 0.1% tRNA and 0.05% heparin). Afterwards, embryos were incubated o.n. at 68°C in hybridisation buffer 2 (hybridisation buffer 1 with 0.1% tRNA and 0.05% heparin and 1:500 DIG probe). Day 2) Removal of unbound probe was done through a series of washing steps 3×30 minutes each at 68°C: L1, L2 (50% deionised formamide, 2× SSC pH 4.5, 0.1% Tween 20 in DEPC; pH 4.5) and L3 (2× SSC pH 4.5, 0.1% Tween 20 in DEPC; pH 4.5). Subsequently, embryos were treated for 1 hour with RNase solution (0.1 M NaCl, 0.01 M Tris pH 7.5, 0.2% Tween 20, 100 μg/ml RNase A in H₂O), followed by washing in TBST 1 (140mM NaCl, 2.7mM KCl, 25mM Tris-HCl, 1% Tween 20; pH 7.5). Next, embryos were blocked for 2 hours at RT in blocking solution (TBST 1 with 2% calf-serum and 0.2% BSA), followed by incubation at 4°C o.n. in blocking solution containing 1:5000 Anti-Digoxigenin-AP (catalog number: Roche-11093274910). Day 3) Removal of unbound antibody was done through a series of washing steps 8× 30 min at RT with TBST 2 (TBST with 0.1% Tween 20, and 0.05% levamisole/tetramisole) and left o.n. at 4°C. Day 4) Staining of the embryos was initiated by washing at RT with alkaline phosphatate buffer (0.02 M NaCl, 0.05 M MgCl₂, 0.1% Tween 20, 0.1 M Tris-HCl, and 0.05% levamisole/tetramisole in H₂O) 3× 20 minutes, followed by staining with BM Purple AP Substrate (Roche). The stained embryos were imaged using a Zeiss Discovery V.12 microscope and Leica DFC420 digital camera.

Mammalian cell culture

All mammalian cells were cultured at 37°C with 5% CO2, and were maintained in high glucose DMEM (Gibco cat. no. 11965) for HEK293T (from ATCC) and NIH/3T3 (a gift from T. Reh’s lab at the University of Washington) cells, both supplemented with 10% FBS and 1× Pen/Strep (Gibco cat. no. 15140122; 100U/ml penicillin, 100 μg/ml streptomycin). Cells were trypsinized with 0.25% typsin-EDTA (Gibco cat. no. 25200–056) and split 1:10 three times a week.

Mouse embryo nuclei extraction and fixation

Mouse embryos from different development stages were processed together to reduce batch effects. Each mouse embryo was minced into small pieces by blade in 1 mL ice-cold cell lysis buffer (10 mM Tris-HCl, pH 7.4, 10 mM NaCl, 3 mM MgCl2 and 0.1% IGEPAL CA-630 from⁵³, modified to also include 1% SUPERase In and 1% BSA) and transferred to the top of a 40 μm cell strainer (Falcon). Tissues were homogenized with the rubber tip of a syringe plunger (5 ml, BD) in 4 ml cell lysis buffer. The filtered nuclei were then transferred to a new 15 ml tube (Falcon) and pelleted by centrifuge at 500×g for 5 min and washed once with 1 ml cell lysis buffer. The nuclei were fixed in 4 ml ice cold 4% paraformaldehyde (EMS) for 15 min on ice. After fixation, the nuclei were washed twice in 1 ml nuclei wash buffer (cell lysis buffer without IGEPAL), and re-suspended in 500 μl nuclei wash buffer. The samples were split to two tubes with 250 μl in each tube and flash frozen in liquid nitrogen. We estimated the nuclei extraction efficiency based on the extracted nuclei number vs. expected total nuclei number in each embryo. The estimated nuclei extraction efficiency ranged from 60% to 85%.

As a quality control, HEK293T and NIH/3T3 cells were trypsinized, spun down at 300×g for 5 min (4°C) and washed once in 1× PBS. Equal numbers of HEK293T and NIH/3T3 cells were combined and lysed using 1 mL ice-cold cell lysis buffer followed by the same fixation and storage conditions as used for the mouse embryos.

Mouse embryo cell counts

3–5 embryos per developmental stage were microdissected in PBS at room temperature. Each mouse embryo was minced into small pieces by blade and a single cell suspension was obtained by incubating the tissue in 4 ml Trypsin-EDTA 0.05% (Gibco) at 37°C for 10 min vortexing every other minute. The cells of each embryo were diluted in 4 ml medium and transferred to the top of a 40μ m cell strainer (Falcon). Cell numbers was then determined by counting cells using a hemocytometer.

sci-RNA-seq3 library preparation and sequencing

Thawed nuclei were permeabilized with 0.2% TritonX-100 (in nuclei wash buffer) for 3 min on ice, and briefly sonicated (Diagenode, 12 sec on low power mode) to reduce nuclei clumping. The nuclei were then washed once with nuclei wash buffer and filtered through 1 ml Flowmi cell strainer (Flowmi). Filtered nuclei were spun down at 500×g for 5 min and resuspended in nuclei wash buffer.

Nuclei from each mouse embryo were then distributed into several individual wells in four 96-well plates. The links between well id and mouse embryo were recorded for downstream data processing. For each well, 80,000 nuclei (16 μL) were mixed with 8 μl of 25 μM anchored oligo-dT primer (5′-/5Phos/CAGAGCNNNNNNNN[10bp barcode]TTTTTTTTTTTTTTTTTTTTTTTTTTTTTT-3′, where “N” is any base; IDT) and 2 μL 10 mM dNTP mix (Thermo), denatured at 55°C for 5 min and immediately placed on ice. 14 μL of first-strand reaction mix, containing 8 μL 5× Superscript IV First-Strand Buffer (Invitrogen), 2 μl 100 mM DTT (Invitrogen), 2 μl SuperScript IV reverse transcriptase (200 U/μl, Invitrogen), 2 μL RNaseOUT Recombinant Ribonuclease Inhibitor (Invitrogen), was then added to each well. Reverse transcription was carried out by incubating plates by gradient temperature (4°C 2 minutes, 10°C 2 minutes, 20°C 2 minutes, 30°C 2 minutes, 40°C 2 minutes, 50°C 2 minutes and 55°C 10 minutes).

After ligation reaction, 60 μL nuclei dilution buffer (10 mM Tris-HCl, pH 7.4, 10 mM NaCl, 3 mM MgCl2 and 1% BSA) was added into each well. Nuclei from all wells were pooled together and spun down at 500×g for 10 min. Nuclei were then resuspended in nuclei wash buffer and redistributed into another four 96-well plates with each well including 4 μL T4 ligation buffer (NEB), 2 μL T4 DNA ligase (NEB), 4 μL Betaine solution (5M, Sigma-Aldrich), 6 μL nuclei in nuclei wash buffer, 8μL barcoded ligation adaptor (100 uM, 5’-GCTCTG[9 bp or 10 bp barcode A]/dideoxyU/ACGACGCTCTTCCGATCT[reverse complement of barcode A]-3’) and 16 μL 40% PEG 8000 (Sigma-Aldrich). The ligation reaction was done at 16°C for 3 hours.

After RT reaction, 60 μL nuclei dilution buffer (10 mM Tris-HCl, pH 7.4, 10 mM NaCl, 3 mM MgCl2 and 1% BSA) was added into each well. Nuclei from all wells were pooled together and spun down at 600×g for 10min. Nuclei were washed once with nuclei wash buffer and filtered with 1 ml Flowmi cell strainer (Flowmi) twice, counted and redistributed into eight 96-well plates with each well including 2,500 nuclei in 5 μL nuclei wash buffer and 5 μL elution buffer (Qiagen). 1.33 μl mRNA Second Strand Synthesis buffer (NEB) and 0.66 μl mRNA Second Strand Synthesis enzyme (NEB) were then added to each well, and second strand synthesis was carried out at 16°C for 180 min.

For tagmentation, each well was mixed with 11 μL Nextera TD buffer (Illumina) and 1 μL i7 only TDE1 enyzme (62.5 nM, Illumina), and then incubated at 55°C for 5 min to carry out tagmentation. The reaction was then stopped by adding 24 μL DNA binding buffer (Zymo) per well and incubating at room temperature for 5 min. Each well was then purified using 1.5× AMPure XP beads (Beckman Coulter). In the elution step, each well was added with 8 μL nuclease free water, 1 μL 10× USER buffer (NEB), 1 μL USER enzyme (NEB) and incubated at 37°C for 15 min. Another 6.5 μL elution buffer was added into each well. The AMPure XP beads were removed by magnetic stand and the elution product was transferred into a new 96-well plate.

For PCR amplification, each well (16 μL product) was mixed with 2 μL of 10 μM indexed P5 primer (5′-AATGATACGGCGACCACCGAGATCTACAC[i5]ACACTCTTTCCCTACACGACGCTCTTCCGATCT-3′; IDT), 2 μL of 10 μM P7 primer (5′-CAAGCAGAAGACGGCATACGAGAT[i7]GTCTCGTGGGCTCGG-3′, IDT), and 20 μL NEBNext High-Fidelity 2× PCR Master Mix (NEB). Amplification was carried out using the following program: 72°C for 5 min, 98°C for 30 sec, 12–14 cycles of (98°C for 10 sec, 66°C for 30 sec, 72°C for 1 min) and a final 72°C for 5 min.

Of note, for a single experiment, we have 384 barcodes introduced at the reverse transcription step, 384 barcodes introduced by hairpin ligation and 768 barcodes introduced by PCR. This corresponds to 384 * 384 * 768 = ~113 million possible combinations.

After PCR, samples were pooled and purified using 0.8 volumes of AMPure XP beads. Library concentrations were determined by Qubit (Invitrogen) and the libraries were visualized by electrophoresis on a 6% TBE-PAGE gel. All libraries were sequenced on one NovaSeq platform (Illumina) (Read 1: 34 cycles, Read 2: 52 cycles, Index 1: 10 cycles, Index 2: 10 cycles).

Processing of sequencing reads

Base calls were converted to fastq format using Illumina’s bcl2fastq/v2.16 and demultiplexed based on PCR i5 and i7 barcodes using maximum likelihood demultiplexing package deML⁵⁴ with default settings. Downstream sequence processing and single cell digital expression matrix generation were similar to sci-RNA-seq¹⁷ except that RT index was combined with hairpin adaptor index, and thus the mapped reads were split into constituent cellular indices by demultiplexing reads using both the RT index and ligation index (ED < 2, including insertions and deletions). Briefly, demultiplexed reads were filtered based on RT index and ligation index (ED < 2, including insertions and deletions) and adaptor clipped using trim_galore/v0.4.1 with default settings. Trimmed reads were mapped to the mouse reference genome (mm10) for mouse embryo nuclei, or a chimeric reference genome of human hg19 and mouse mm10 for HEK293T and NIH/3T3 mixed nuclei, using STAR/v 2.5.2b⁵⁵ with default settings and gene annotations (GENCODE V19 for human; GENCODE VM11 for mouse). Uniquely mapping reads were extracted, and duplicates were removed using the unique molecular identifier (UMI) sequence, reverse transcription (RT) index, hairpin ligation adaptor index and read 2 end-coordinate (i.e. reads with identical UMI, RT index, ligation adaptor index and tagmentation site were considered duplicates). Finally, mapped reads were split into constituent cellular indices by further demultiplexing reads using the RT index and ligation hairpin (ED < 2, including insertions and deletions). For mixed-species experiment, the percentage of uniquely mapping reads for genomes of each species was calculated. Cells with over 85% of UMIs assigned to one species were regarded as species-specific cells, with the remaining cells classified as mixed cells or “collisions”. To generate digital expression matrices, we calculated the number of strand-specific UMIs for each cell mapping to the exonic and intronic regions of each gene with python/v2.7.13 HTseq package⁵⁶. For multi-mapped reads, reads were assigned to the closest gene, except in cases where another intersected gene fell within 100 bp to the end of the closest gene, in which case the read was discarded. For most analyses we included both expected-strand intronic and exonic UMIs in per-gene single-cell expression matrices.

Because of the marked increase in processing time that it would entail, we note that we did not perform a UMI error correction step. However, to confirm that our failure to do so would not inflate UMI counts, we compared results with vs. without UMI error correction (edit distance of 1) for a subset of wells. Compared with skipping UMI error correction, 99.4% of reads remain after UMI error correction, which indicated to us that the error correction step only has minor impact on the estimated UMI counts per cell (less than 1%). This is likely due to the high quality of sequencing data that we obtained on the NovaSeq, the low number of PCR amplification steps, and the low duplication rate. We emphasize that groups implementing sci-RNA-seq3 should either perform UMI error correction or a similar data quality check.

Whole mouse embryo analysis

After the single cell gene count matrix was generated, each cell was assigned to its original mouse embryo based on the RT barcode. Reads mapping to each embryo were aggregated to generate “bulk RNA-seq” for each embryo. For sex separation of embryos, we counted reads mapping to a female-specific non-coding RNA (Xist) or chrY genes (except Erdr1 which is in both chrX and chrY). Embryos were readily separated into females (more reads mapping to Xist than chrY genes) and males (more reads mapping to chrY genes than Xist).

Pseudotemporal ordering of whole mouse embryos was done by Monocle 2⁵⁷. Briefly, an aggregated gene expression matrix was constructed as described above. Differentially expressed genes across different development conditions were identified with differentialGeneTest function of Monocle 2⁵⁷. The top 2,000 genes with the lowest q value were used to construct the pseudotime trajectory using Monocle 2⁵⁷. Each embryo was assigned a pseudotime value based on its position along the trajectory.

Cell clustering, t-SNE visualization and marker gene identification

A digital gene expression matrix was constructed from the raw sequencing data as described above. Cells with fewer than 200 UMIs or over 3,172 UMIs (two standard deviation above the mean UMI count) were discarded. Downstream analysis were performed with Monocle2/v2.6.0⁵⁷ and python package scanpy/v1.0⁵⁸. Briefly, gene count mapping to sex chromosomes were removed before clustering and dimensionality reduction. Preprocessing steps were similar to the approach used by ref⁵⁹. Briefly, genes with no count were filtered out and each cell was normalized by the total UMI count per cell. The top 2,000 genes with the highest variance were selected and the digital gene expression matrix was renormalized after gene filtering. The data was log transformed after adding a pseudocount, and scaled to unit variance and zero mean. The dimensionality of the data was reduced by PCA (30 components) first and then with t-SNE, followed by Louvain clustering performed on the 30 principal components (resolution=1.5). For Louvain clustering, we first fitted the top 30 PCs to compute a neighborhood graph of observations with local neighborhood number of 15 by scanpy.api.pp.neighbors function in scanpy/v1.0⁶⁰. We then cluster the cells into sub-groups using the Louvain algorithm implemented as scanpy.api.tl.louvain function⁶⁰. For tSNE visualization, we directly fit the PCA matrix into scanpy.api.tl.tsne function⁶⁰ with perplexity of 30. 40 clusters were identified. We then sampled 1,000 cells from each cluster and differentially expressed genes across different clusters were identified with differentialGeneTest function of Monocle 2/v2.6.0⁵⁷. Genes specific to each cluster were identified similar as previously described⁶¹. Clusters were assigned to known cell types based on cluster-specific markers (Supplementary Table 3). One cluster had abnormally high UMI counts but no strongly cluster-specific genes, suggesting that it may be a technical artifact of cell doublets and therefore was removed. This was confirmed upon analysis for doublets with Scrublet (see next paragraph). Another two clusters both appeared to correspond to the definitive erythroid lineage and were merged. Consensus expression profiles for each cell type were constructed as previously described⁶¹. Differentially expressed genes across cell types were identified with the differentialGeneTest() function of Monocle 2/v2.6.0⁶². To identify cell type-specific gene markers, we selected genes that were differentially expressed across different cell types (FDR of 5%, likelihood ratio test) and also with a >2-fold expression difference between first and second ranked cell types.

For the detection of potential doublet cells, we first split the dataset of ~2 million cells into four equally sized subsets, and then applied the scrublet/v0.1 pipeline⁶³ to each subset with parameters (min_count = 3, min_cells = 3, vscore_percentile = 85, n_pc = 30, expected_doublet_rate = 0.06, sim_doublet_ratio = 2, n_neighbors = 30, scaling_method = ‘log’) for doublet score calculation. Cells with doublet score over 0.25 are annotated as detected doublets. We detected 4.3% potential doublet cells in the whole data set, which corresponds to an overall estimated doublet rate of 10.3% (including both within- and between-cluster doublets). The aforementioned major cluster with abnormally high UMI counts but no strongly cluster-specific genes (see last paragraph) had a high detected doublet proportion (52%), confirming it as a doublet-related artifact. For detection of doublet derived subclusters, we redid the above analysis on the whole dataset after removing the doublet-derived main cluster. Subclusters with detected doublet proportion of >10% were annotated as doublet derived subclusters.

For subcluster identification, we selected high quality cells (UMI > 400) in each major cell type and applied PCA, t-SNE, Louvain clustering similarly to the major cluster analysis. Subclusters were filtered out if most cells (>50%) of the cluster derived from a single embryo. Highly similar subclusters were merged if their aggregated transcriptomes were highly correlated (Pearson correlation coefficient > 0.95) and the two clusters were close with each other in t-SNE space. Genes differentially expressed across subclusters were identified for each major cell type as described above. Subclusters with a detected doublet ratio (by Scrublet) over 10% are annotated as doublet-derived subclusters.

To identify a distinguishing set of gene markers for each of the 572 subclusters (those of the 655 with detected doublet cell ratio <= 10%), we used the following algorithm: 1) We selected genes detected in at least 5% of cells in the target subcluster; 2) From these, we identified genes with a >4-fold greater expression in the target cluster than all 571 other subclusters; 3) If there was no such gene, the algorithm tried to identify a gene (“marker A”) such that subclusters with low expression of marker A (less than 25% of its expression in the target cluster) are readily distinguished from the target cluster based on this difference, and are therefore removed from the comparison set. Gene marker A is selected to maximize the number of subclusters removed from the comparison set. 4) To identify markers that separate the target cluster from the remaining subclusters, we repeat steps 2–3 until a marker with a >4-fold expression difference between the target cluster and all remaining subclusters is identified. The set of markers identified through this heuristic is sufficient to distinguish the target subcluster from all 571 other non-doublet subclusters on the basis of >4-fold expression differences.

For identifying correlated cell types between two cell atlas datasets, we first aggregate the cell type specific UMI counts, normalized by the total count, multiplied by 100,000, and log transformed after adding a pseudo-count. We then applied non-negative least squares (NNLS) regression to predict the gene expression of target cell type (T_a) in dataset A with the gene expression of all cell types (M_b) in dataset B:

T_{a} = β_{0 a} + β_{1 a} M_{b}

where T_a and M_b represent filtered gene expression for target cell type from data set A and all cell types from data set B, respectively. To improve accuracy and specificity, we selected cell type-specific genes for each target cell type by: 1) ranking genes based on the expression fold-change between the target cell type vs. the median expression across all cell types, and then selecting the top 200 genes. 2) ranking genes based on the expression fold-change between the target cell type vs. the cell type with maximum expression among all other cell types, and then selecting the top 200 genes. 3) Merge the gene lists from step (1) and (2). β_1a is the correlation coefficient computed by NNLS regression.

Similarly, we then switch the order of datasets A and B, and predict the gene expression of target cell type (T_b) in dataset B with the gene expression of all cell types (M_a) in dataset A:

T_{b} = β_{0 b} + β_{1 b} M_{a}

Thus, each cell type a in dataset A and each cell type b in dataset B are linked by two correlation coefficients from the above analysis: β_ab for predicting cell type a using b, and β_ba for predicting cell type b using a. We combine the two values by:

β = 2 * (β_{a b} + 0.01) * (β_{b a} + 0.01)

and find β reflects the matching of cell types between two data sets with high specificity (Extended Data Fig. 5a). For each cell type in dataset A, all cell types in dataset B are ranked by β and the top cell type (with β > 0.01) is identified as the matched cell type. For validation, we first applied cell type correlation analysis to independently generated and annotated analyses of the adult mouse kidney (sci-RNA-seq component of sci-CAR¹⁹ vs. Microwell-seq¹⁰). We subsequently compared cell subclusters from this study (with detected doublet cell ratio <= 10%) to fetus-related cell types (those with annotations including the term “fetus”) from the Microwell-seq-based Mouse Cell Atlas (MCA)¹⁰. A similar comparison was performed against cell types annotated in a recent mouse brain atlas (BCA)³².

For estimation of the number of cells of each cell type (or cell subtype), we first calculated the proportion of each cell type in individual embryos, and then multiplied the proportion by the estimated total cell number for each embryo (E9.5: 200,000, E10.5: 1,100,000; E11.5: 2,600,000; E12.5: 6,100,000; E13.5: 13,000,000).

Assuming that ~100 cells are required to detect a cell type and that the cell type in question is only present at one timepoint, we note that the power of this study would be limited to detecting cell types whose ‘population size’ per embryo is >125 cells at E9.5, >333 cells at E10.5, >500 cells at E11.5, >1,250 cells at E12.5, or >3,400 cells at E13.5. However, our power may be greater than that for cell types that are present across timepoints. For example, the primordial germ cell subcluster 16.13, which includes just 88 of 2,058,652 cells in the dataset, is contributed to by cells from all five timepoints.

AER and limb mesenchyme pseudo-time analysis

Pseudotemporal ordering of AER cells, forelimb or hindlimb was done with Monocle 2⁵⁷. Briefly, differentially expressed genes across five development stages were identified with the differentialGeneTest function of Monocle 2⁵⁷. The top 500 genes with the lowest q value were used to construct the pseudotime trajectory using Monocle 2⁵⁷, with UMI count per cell as a covariate in the tree construction. Each cell was assigned a pseudotime value based on its position along the trajectory. Smoothed gene marker expression change along pseudotime were generated by plot_genes_in_pseudotim function in Monocle 2⁵⁷. Cells in the trajectory were grouped in the same method as a previous study⁶⁴. Briefly, cells were grouped first at similar positions in pseudotime by k-means clustering along the pseudotime axis (k = 10). These clusters were subdivided into groups containing at least 50 and no more than 100 cells. We then aggregated the transcriptome profiles of cells within each group. The gene expression along pseudotime was calculated in the same approach as a previous study⁶⁴. Briefly, genes passing significant test (FDR of 5%) across different treatment conditions were selected and a natural spline was used to fit the gene expression along pseudotime, with mean_number_genes included as a covariate. The gene expression for each gene was subtracted by the lowest expression and then divided by the highest expression. Genes with max expression within the early 20% of pseudotime were labeled as repressed genes. Genes with max expression in the last 20% of pseudotime were labeled as activated genes. Other genes were labeled as transient genes. Enriched reactome terms (Reactome_2016) and transcription factors (ChEA_2016) were identified using EnrichR/v1.0 package⁶⁵.

Trajectory inference with Monocle 3

The Monocle 3 workflow consists of 3 core steps to organize cells into potentially discontinuous trajectories, followed by optional statistical tests to find genes that vary in expression over those trajectories. Monocle 3 also includes visualization tools to help explore trajectories in three dimensions.

Dimensionality reduction with Uniform Manifold Approximation and Projection (UMAP)

Monocle 3 first projects the data into a low-dimensional space, which facilitates learning a principal graph that describes how cells transit between transcriptomic states. Monocle 3 does so with UMAP/v0.3.2, a recently proposed algorithm based on Riemannian geometry and algebraic topology to perform dimension reduction and data visualization⁶⁶. Its visualization quality is competitive with the popular t-SNE (t-stochastic neighbor embedding) method used widely in single-cell transcriptomics. However, where t-SNE mainly aims to place highly similar cells in the same regions of a low-dimensional space, UMAP also preserves longer-range distance relationships. The UMAP algorithm itself is also more efficient (the algorithm complexity of UMAP is O(N) vs. O(Nlog(N)) for t-SNE). Briefly, UMAP first constructs a topological representation of the high dimensional data with local manifold approximations and patches together their local fuzzy simplicial set representations. UMAP then optimizes the lower dimension embedding, minimizing the cross-entropy between the low dimensional representation and the high dimensional one.

The computational efficiency of UMAP dramatically accelerated the analysis of the mouse embryo data. We found that UMAP finished processing two million cells dataset in around 3 CPU hours while t-SNE took more than 64 CPU hours. A few implementation details lead to the effectiveness of UMAP. Two major steps are involved in both the UMAP and t-SNE algorithms: first, the preprocessing step before UMAP is similar to Monocle 2. Briefly, genes expressed in fewer than 10 cells (or fewer than 5 cells in datasets with fewer than 1,000 cells) were filtered out. The digital gene count matrix was first normalized by cell specific size factor estimated by “estimateSizeFactors” function in Monocle 3, log transformed after adding a pseudocount, and then scaled to unit variance and zero mean. The top 5,000 most highly dispersed genes (2,000 genes for datasets with fewer than 5,000 cells, 300 genes for datasets with fewer than 1,000 cells) were selected. The matrix was then projected into 50 top PCs (30 top PCs for trajectory analysis of the ten supergroups, 10 top PCs for data sets with fewer than 5,000 cells, 5 top PCs for data sets with fewer than 1,000 cells) by partial SVD. Thus an intermediate structure from the high dimension space (here, we used the top 50 principal components constructed from the 5,000 most highly dispersed genes) is built and then a low dimensional embedding is found to represent the intermediate structure. For the second step, both methods used stochastic grid descent approach with differing loss functions to embed the data into low dimension space. While t-SNE needs a loss function for global normalization, UMAP uses a different objective function that avoids that need. This step essentially enables UMAP to scale linearly with the number of data samples.

Dimensionality reduction was implemented with the reduceDimension() function in Monocle 3. This function calls the UMAP/v0.3.2 python implementation (https://github.com/lmcinnes/umap) from Leland McInnes and John Healy through the reticulate/v1.10 package (https://cran.r-project.org/web/packages/reticulate/index.html). To process all the cells together, we set UMAP parameters as follows: (n_neighbors = 50, min_dist = 0.01, cosine distance metric). To more finely resolve subtrajectories, we adjusted these as such: (n_neighbors = 15, min_dist = 0.1, cosine distance metric).

Partitioning cells into discontinuous trajectories

Recently, Wolf and colleagues proposed the idea to organize single-cell transcriptome data into a “partitioned approximate graph abstraction” (PAGA) that relates clusters of cells that might be developmentally related to one another. Briefly, their algorithm constructs a k-nearest neighbor graph on cells and then identifies “communities” of cell via the Louvain method, similar to previous methods for analyzing CyTOF or single-cell RNA-seq data⁶⁷. PAGA then constructs a graph in which the vertices are Louvain communities. Two vertices are linked with an edge in the PAGA graph when the cells in the respective communities are neighbors in the kNN graph more frequently than would be expected under a simple binomial model⁶⁸. Similar methods were also recently developed and applied in analyzing zebrafish and xenopus cell atlas datasets^5,6.

Monocle 3 draws from these ideas, first constructing a kNN graph (k=20) on cells in the UMAP space, then grouping them into Louvain communities, and testing each pair of communities for a significant number of links between their respective cells. Those communities that have more links than expected under the null hypothesis of spurious linkage (FDR < 1%) remain connected in the PAGA graph, and those links that fail this test are severed. The resulting PAGA graph will have one or more components, each of which is passed to the next step (learning the principal graph) as a separate group of cells that will be organized in a trajectory. The PAGA algorithm essentially stops at this stage, presenting the PAGA graph as a kind of coarse-grained trajectory in each community reflects a different state cells can adopt as they develop. In contrast, as described in the next section, Monocle 3 uses the PAGA graph to constrain the space of principal graphs that can form the final trajectory. That is, Monocle 3 uses the coarse-grained PAGA graph to learn a fine-grained trajectory.

Monocle 3’s implementation of the above procedures (in the partitionCells() function) scales to millions of cells. Briefly, it uses the clustering_louvain function from the igraph package to perform community detection. Next, the core PAGA calculations from Wolf et al. are computed via a series of sparse matrix operations. Let X be a (sparse) matrix representing the community membership of the cells. Each column of X represents a Louvain community and each row of X corresponds to a particular cell. X_ij = 1 if cell i belongs to Louvain community j, otherwise 0. We can further obtain the adjacency matrix A of the kNN graph used to perform the louvain clustering where A_ij = 1 if cell i connects to j in the kNN graph. Then the connection matrix M between each cluster is calculated as,

M = X^{T} A X

Once M is constructed, we can then follow Supplemental Note 3.1 from ref.⁶⁸ to calculate the significance of the connection between each louvain clustering and consider any clusters with p-value larger than 0.05 by default as not disconnected.

Learning the principal graph

Monocle 3 learns a principal graph (via the learnGraph() function) that resides in the same low-dimensional space as the data to represent the possible paths cells can take as they develop. Monocle uses a principal graph embedding procedure that is based on the SimplePPT algorithm^69,70, with several key enhancements that accelerate graph embedding, support large datasets, allow for loops, and smooth the graph to eliminate noisy branches.

The first enhancement is that Monocle 3 learns the principal graph in the (by default, 3 dimensional) UMAP space using a fast reduced-representation approach to avoid dealing directly with many thousands of cells. It first selects a set of “landmark” cells using by first running the kmeans() clustering algorithm in R with k equal to the value of the “ncenter” argument, which can be passed to learnGraph() by the user. The landmark cells are then selected by first mapping each cell to its nearest kmeans point, and then selecting the cell for each kmeans point with the highest local density. By default, Monocle 3 uses a data-dependent policy for adjusting ncenter automatically⁶². Here, unless otherwise specified, we override the default policy and use ncenter = 2000 in the analyses of the embryo data. Monocle 3 will then learn a principal graph within these landmarks cells rather than the full dataset to accelerate the optimization. Running time and fine detail in the trajectory will depend on the number principal graph nodes; more nodes generally results in a more accurate tree but at increased running time.

The second enhancement is a procedure to smooth and refine the principal graph to exclude small branches. In order to capture smaller fine details of a trajectory such as complex branching architecture, SimplePPT requires that the principal graph contain hundreds or even thousands of principal graph nodes. Consequently, the principal tree reported by SimplePPT often contains very small branches to which a very small percentage of cells project. Although SimplePPT does provide tuning parameters that control graph smoothness to a certain extent, we have found that a simple heuristic pruning procedure is effective and easier for users to understand how to control. The procedure operates via a depth-first visitation of the graph nodes in the principal tree. At nodes with degree ≤ 2, no action is taken. For nodes with degree > 2, the diameter path for each subtree rooted at a neighbor not yet visited in the search is computed. If the path is less than a user-specified length (by default, 10 principal tree nodes), the whole subtree is pruned.

The third major enhancement is that Monocle 3 can learn principal graphs with loops instead of requiring that the trajectory be a tree. This is achieved by augmenting the principal tree reported by SimplePPT with additional edges meant to close loops in the trajectory. The algorithm considers adding an edge between two leaf nodes a and b in the principal graph if the pair meet several criteria. The first criteria is that the geodesic distance between a and b along the principal tree should be at least a certain minimum distance (by default, ⅓ of the tree’s diameter path). That is, when the nodes are close in (euclidean) UMAP space, but distant in the graph, they ought to be linked. The second criteria is that they shouldn’t be linked if doing so would create an especially long edge. By default, a and b cannot not be farther apart in UMAP space than the longest edge in the principal tree. The third criteria is based on the same test of connectivity used when partitioning the cells: consider leaf nodes a and b, which serve as proxies between two clusters of cells (those for which a and b are their nearest k-medioid). If cells near a have an unexpectedly high number of cells near b amongst their k nearest neighbors (p < 0.05 by default), then learnGraph() will link a and b in the principal graph, provided the other two criteria discussed above are also met.

For analysis of the ten major trajectories, we used ncenter = 5,000 for neural tube/notochord trajectory, and ncenter = 2,000 for epithelial and mesenchymal trajectories. For the other supergroups, we used ncenter = (number of cells) / 25 and minimal_branch_len = 20. For analysis of the 56 subtrajectories, we mostly used ncenter = (number of cells in the trajectory) / 30 [2,000 maximum], and minimal_branch_len = 20. Each subtrajectory was manually checked and the parameters (ncenter and minimal_branch_len) for about a quarter of these were adjusted, mostly to further prune branches such that the principal graph follows cell transition path from early to late development stages.

The principal graph offers users a means of selecting subsets of cells that lead to particular lineages for further analysis. For example, to isolate cells leading to the myocyte fate, we first quantified the fraction of cells at each principal graph node that were classified as myocytes (cluster 13). From all ‘majority myocyte’ nodes, we then used the principal graph’s edges to expand this set of nodes into wider ‘neighborhood’ of cells.

Computing pseudotimes

In order to calculate cell-wise pseudotime, we developed a projection strategy which is applicable to datasets with millions of cells. This strategy works by constructing a graph ψ on all cells using the principal graph as a guide, and then computing each cell’s pseudotime as its geodesic distance back to one or more user-selected “root” nodes in the trajectory. In more detail, we first map each cell to its nearest principal point based on euclidean distance in the UMAP space. Then, for each principal graph edge, retrieve all the cells that map to its endpoints a and b. Next, orthogonally project each cells to the nearest point on the principal graph edge as previously described⁷¹, so that each cell c_i can be ordered along the edge according to its projection p(c_i). Without loss of generality, suppose this order is a < p(c_i) < p(c_j) < b. We then add edges (a, c_i) and (c_j, b) to ψ. If c_i and c_j are in the same louvain component or connected louvain components (as determined during partitionCells), we also add (c_i, c_j) to ψ. Given ψ and a set of user-specified principal graph nodes, we can then assign pseudotime values to all cells. Monocle provides several ways to specify these nodes, either by name (i.e. programmatically) or interactively. Each cell’s pseudotime is taken as the geodesic distance along ψ to the closest of these root nodes.

For root node selection of the mesenchymal and neural tube/notochord trajectories, we first assigned each principal point to a subcluster with the maximum cell proportion. We then selected the subcluster with the earliest average developmental stage, and use the earliest principal point assigned to this sub-cluster as the root state for pseudotime computation. For the other major trajectories, we assigned root nodes to the earliest principal point in each subtrajectory (except in neural crest trajectory 2, where we assigned the root node to the earliest principal points in PNS glia precursor cell trajectory and Pdgfra-positive glia trajectory). Some cells from complex trajectories (mesenchymal trajectory, neural tube/notochord trajectory, epithelial trajectory and endothelial trajectory) show outlier pseudotime values (more than 3 standard deviation higher than the mean values). These extreme values are clipped to the max value after excluding the outliers. For root node selection of the 56 cell type specific trajectories, we first computed the average development stage for each principal point. As the root state features the earliest development stage, we compared the average development stage of each node and its k-nearest neighbors (k = 10). We then manually checked each trajectory and selected root nodes from principal points with earlier development stage than all its nearby neighbours.

Identifying genes with complex trajectory-dependent expression

In order to identify genes that vary in expression over a developmental trajectory, we borrow a statistical test commonly used in analyzing spatial data. Moran’s I statistic is a measure of multi-directional and multi-dimensional spatial autocorrelation. The statistic encodes spatial relationships between data-points via a nearest neighbor graph, making it particularly well suited for analyzing large single-cell RNA-seq datasets.

Moran’s I test⁷² is defined as:

I = \frac{N}{W} \frac{\sum_{i} \sum_{j} w_{i j} (x_{i} - \bar{x}) (x_{j} - \bar{x})}{\sum_{i} {(x_{i} - \bar{x})}^{2}}

where N is the number of cells indexed by i and j; x is the expression value of gene of interest; ${\bar{x}}_{i}$ ( ${\bar{x}}_{j}$ ) is the mean of the gene expression for cell i’s (or j’s) nearest neighbors; w_ij is a matrix of weights defined by a nearest neighbor graph with zero on the diagonal (i.e., w_ii = 0) and w_ij = 1/k_i where k_i is the number of nearest neighbors; and W is the sum of all w_ij.

To identify the nearest neighbors used for creating the weight matrix W, we first build a k (default to be 25) nearest neighbor graph (kNN) for all cells in the UMAP space. We also project each cell to its nearest node in the principal graph. Then we remove all edges from the kNN graph that connect cells that project onto principal graph nodes do not share an edge.

In Monocle 3, we implemented the principalGraphTest() function to identify correlated genes on the complex trajectory embedded in the manifold which relies on modified versions of routines from spdep package for performing the Moran’s I test.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this paper.

Code Availability

Scripts for processing sci-RNA-seq3 sequencing were written in python and R with code available at https://github.com/JunyueC/sci-RNA-seq3_pipeline. Trajectory analysis was done with Monocle 3 with setup instructions and tutorial available at http://cole-trapnell-lab.github.io/monocle-release/monocle3/.

Data Availability

sci-RNA-seq3 protocol and all data are made freely available, including through a cell type wiki to facilitate their ongoing annotation by the research community (http://atlas.gs.washington.edu/mouse-rna/). The data generated by this study can be downloaded in raw and processed forms from the NCBI Gene Expression Omnibus (GSE119945).

Extended Data

Extended Data Fig. 3. — As cell type heterogeneity was readily apparent within many of the 38 clusters shown in Fig. 2a, we adopted an iterative strategy, repeating Louvain clustering on each main cell type to identify subclusters. After subclusters dominated by one or two embryos were removed and highly similar subclusters merged, a total of 655 subclusters (also termed ‘subtypes’ to distinguish them from the 38 major cell types identified by the initial clustering). Cell number n for each cell type is listed in Supplementary Table 3.

Extended Data Fig. 4. — (a) t-SNE visualization of all cells (top plot, n = 2,026,641) and downsampled subset of high-quality cells (bottom plot, n = 50,000, UMI > 400), colored by Louvain cluster IDs from Fig. 2a. (b) t-SNE visualization of all endothelial cells (top plot, n = 35,878) and those from the downsampled subset (bottom plot, n = 1,173), colored by Louvain cluster ID computed based on the 35,878 endothelial cells. (**c-d**) t-SNE visualization of the downsampled subset of 50,000 cells (c), and 1,173 endothelial cells (d), colored by Louvain cluster ID computed based on sampled cells only. The number of clusters and subclusters identified with the same parameters drops from 38 (a, bottom plot) to 27 (c) and 16 (b, bottom plot) to 12 (c), respectively. (e) Histogram showing the distribution of subclusters with respect to cell number (median 1,869; range 51–65,894). (f) Histogram showing the distribution of subclusters with respect to the number of contributing embryos (>5 cells to qualify as a contributor). (g) Histogram showing the distribution of subclusters with respect to the ratio of cells derived from the most highly contributing embryo. (h) Histogram showing the distribution of subclusters with respect to the ratio of doublet cells detected by Scrublet. (i) Histogram showing the distribution of subclusters with respect to the number of marker genes (at least 2-fold (blue) or 5-fold (red) higher expression when compared with the second highest expressing cell subtype within the same main cluster; 5% FDR). 644 of 655 sub-clusters (98%) have at least one such gene marker with a 2-fold difference, and 441 of 655 (67%) have at least one such marker with a 5-fold difference. (j) t-SNE visualization of subcluster specific marker expression (as example, cell number n = 74,651): *Calb1* (left), *Nox3* (middle) and *Tex14* (right) are gene markers for three endothelial subclusters. “High” indicates cells with UMI count for *Calb1* > 0, *Nox3* > 0, *Tex14* >1. (k) Cumulative histogram showing how many subtypes (out of a total of 572 non-doublet-artifact subtypes) can be distinguished from all other subtypes on the basis of one or several markers and >4-fold expression differences (see also Methods, Supplementary Table 5).

Extended Data Fig. 5. — (a) Cell type correlation analysis (Methods) matched cell types between independently generated and annotated analyses of the adult mouse kidney (sci-RNA-seq component of sci-CAR¹⁹ (rows) vs. Microwell-seq¹⁰ (columns)). All cell types identified by sci-RNA-seq are shown, but we only show Microwell-seq cell types that are top matches for 1+ sci-RNA-seq cell types. Colors correspond to beta values, normalized by the maximum beta value per row. (b) Left: We compared our subtypes against 130 fetal cell types annotated in the MCA¹⁰ with cell type correlation analysis, matching 96 MCA-defined cell types (rows) to 58 subtypes in our mouse embryo atlas (columns). Colors correspond to beta values, normalized by the maximum beta value per row. All MCA cell types with maximum beta of matched cell type > 0.01 are shown (rows; n = 96), as are mouse embryo atlas cell types that are top matches for 1+ displayed MCA cell types (columns; n = 58). Right: zoom-in to a subset of matches shown on the left. Cell types annotations are from MCA (rows) or our study (columns; major cell type annotation and sub-cluster id). (c) Box plot showing the ratio of cells from E13.5 for subclusters with (sub-cluster number n = 58) vs. without (sub-cluster number n = 514) a matched cell type in the MCA. Thick horizontal lines, medians; upper and lower box edges, first and third quartiles, respectively; whiskers, 1.5 times the interquartile range; circles, outliers. (d) Left: We compared our subtypes against 265 cell types annotated by a recent mouse brain cell atlas (BCA)³² with cell type correlation analysis, matching 48 BCA-defined cell types (rows) to 68 subtypes in our data (columns). Colors correspond to beta values, normalized by the maximum beta value per row. All mouse embryo cell types with maximum beta of matched cell type > 0.01 are shown (column; n = 68), as are BCA cell types that are top matches for 1+ displayed mouse embryo cell types (rows; n = 48). Right: zoom-in to a subset of matches shown on the left. Cell types annotations are from BCA (rows) or our study (columns; major cell cluster and sub-cluster id).

Extended Data Fig. 6. — (**a-b**) Dot plot showing expression of one selected marker gene per epithelial (a) or endothelial (b) subtype. Doublet-derived subclusters (2/29 epithelial subtypes and 5/16 endothelial subtypes) are excluded from these plots, but are still shown in Fig. 3a and panel c, respectively. The size of the dot encodes the percentage of cells within a cell type, and its color encodes the average expression level. (c) t-SNE visualization and marker-based annotation of endothelial cell subtypes (n = 35,878). (d) Heatmap showing smoothed pseudotime-dependent differential gene expression (169 genes at FDR of 1%) in AER cells, generated by a spline fitting with generalized linear model (assuming gene expression following the negative binomial distribution) and scaled as a percent of maximum gene expression. Each row indicates a different gene, and these are split into subsets that are activated (top), repressed (middle) or exhibit transient dynamics (bottom) between E9.5 and E13.5. (**e-f**) Plots showing the −log10 transformed q value and Enrichr based combined score of enriched Reactome terms (e) and transcription factors (f) for genes whose expression significantly decreases in AER development. The top enriched pathway terms (Reactome2016) for significantly decreasing genes include cell cycle progression (Mitotic Cell Cycle, qval = 0.0002, one-sided Fisher exact test with multiple comparisons adjusted) and glucose metabolism (Metabolism of carbohydrates, qval = 0.0002, one-sided Fisher exact test with multiple comparisons adjusted). The top enriched TFs with targets from decreasing genes include pluripotent factors such as *Isl1* (qval < 1e-5), *Pou5f1* (qval = 0.002, one-sided Fisher exact test with multiple comparisons adjusted) and *Nanog* (qval = 0.003, one-sided Fisher exact test with multiple comparisons adjusted).

Extended Data Fig. 7. — (a) UMAP 3D visualization of limb mesenchymal cells colored by development stage (cell number n = 26,559, left and right represent views from two directions). (b) Heatmap showing top differentially expressed genes between different developmental stages for limb mesenchyme cells. (c) Bar plot showing the −log10 transformed adjusted p value (one-sided Fisher exact test with multiple comparisons adjusted) of enriched transcription factors for significantly up-regulated genes during limb mesenchyme development. (d) t-SNE visualization of limb mesenchyme cells colored by forelimb (Tbx5 +, cell number n = 2,085) and hindlimb (Pitx1+, cell number n = 1,885). Cells with no expression or both expression in Tbx5 and Pitx1 are not shown. (**e, h, i, k**) Each panel illustrates a different marker gene. Colors indicate UMI counts that have been scaled for library size, log-transformed, and then mapped to Z-scores to enable comparison between genes. Cells with no expression of a given marker are excluded to prevent overplotting. (e) Hindlimb marker *Pitx1* and forelimb marker *Tbx5*. (f) Scatter plot showing the normalized expression of *Pitx1* and Tbx5 in limb mesenchyme cells. Only cells in which *Pitx1* and/or *Tbx5* detected were shown. (g) Volcano plot showing the differentially expressed genes (FDR of 5%, one-sided likelihood ratio test with multiple comparisons adjusted, colored by red) between forelimb (cell number n = 2,085) and hindlimb (cell number n = 1,885). Top differentially expressed genes are labeled. X axis: log2 transformed fold change between forelimb and hindlimb for each gene. Y axis: −log10 transformed qval from differential gene expression test. (h) Same visualization as panel e, colored by normalized gene expression of proximal/chondrocyte (*Sox6, Sox9*), distal (*Hoxd13*, *Tfap2b*), anterior (*Pax9*, *Alx4*), or posterior (*Hand2*, *Shh*) markers. Only cells with the gene marker expressed are plotted. (i) Same visualization as panel e. First row: proximal limb markers *Sox6* (which also marks chondrocytes) and *Sox9*. Second row: distal limb markers *Hoxd13* and *Tfap2b*. Third row: Anterior limb markers⁵¹ *Pax9* and *Alx4*. Fourth row: posterior limb markers *Shh* and *Hand2*. (j) *In situ* hybridization images of *Hoxd13* in E9.5 to E13.5 embryos, n = 5. (k) Same visualization as panels e, colored by normalized gene expression of *Cpa2*. Only cells with positive UMI counts are shown. Values are log10-transformed, standardized UMI counts. Its expression pattern within this trajectory led us to predict that *Cpa2* is a distal marker of the developing limb mesenchyme, like *Hoxd13*. (l) *In situ* hybridization images of *Cpa2* in E10.5 and E11.5 embryos, n = 5. Arrow: site of gene expression. (m) Modules of spatially restricted genes in the limbs. A total of 1,783 genes were clustered via hierarchical clustering. The dendrogram was cut into 8 modules using the cutree function in R, and the aggregate expression of genes in each module was computed. Colors indicate aggregate UMI counts for each module that have been scaled for library size, log-transformed, and then mapped to Z-scores to enable comparison between modules. Cells with no expression of a given module are excluded to prevent overplotting.

Extended Data Fig. 8. — (a) Heatmap showing the proportion of cells from each of the 38 major cell types assigned to each of the twelve PAGA algorithm-identified groups. We merged two groups corresponding to sensory neurons (12 & 3), and another two groups corresponding to blood cells (6 & 7), as each pair was closely located in UMAP space upon visual inspection, yielding the ten supergroups shown in a similar heatmap in Fig. 4b. (b) Same as Fig. 4a, but with colors corresponding to the 38 major cell clusters. (c) Area plot showing the estimated proportion (top) and estimated absolute number (bottom) of cells per embryo derived from each of the ten major cell trajectories from E9.5 to E13.5. Although the estimated number of cells per embryo in each of these supergroups increases exponentially, their proportions remain relatively stable, with the exception of hepatocytes which expand their contribution by nearly ten-fold during this developmental window (from 0.3% at E9.5 to 2.8% at E13.5). (d) UMAP 3D visualization of epithelial subtrajectories (as in Fig. 4c), colored as per the epithelial subtypes shown in Fig. 3a.

Extended Data Fig. 9. — We iteratively reanalyzed each of the ten major trajectories, nearly all of which further resolved into multiple subtrajectories. The ten major cell trajectories are visualized with UMAP (as in Fig. 5) but colored: as per the 38 major cell clusters (top left), sub-cluster id (top right), developmental stage (bottom left) and pseudotime (bottom right). The lines correspond to the principal graph learned by Monocle 3. These images are also available at http://atlas.gs.washington.edu/mouse-rna/3dplot/ as manipulatable 3D renderings.

Extended Data Fig. 10. — We further iteratively reanalyzed and visualized with UMAP each of the 56 subtrajectories. Although Monocle 3 did not have access to these labels, the subtrajectories are highly consistent with developmental time (*i.e*. cells ordered from E9.5 to E13.5). The lines correspond to the principal graph learned by Monocle 3.

Extended Data Fig. 11. — To orient each subtrajectory (same projections as Extended Data Fig. 10), we identified one or several starting points as focal concentrations of E9.5 cells, and then computed developmental pseudotime for cells present along various paths. The lines correspond to the principal graph learned by Monocle 3.

Extended Data Fig. 12. — (a) Genes that are differentially expressed between the Myf5 path and the Myod path highlighted in Fig. 6. Cells along each path were compared via Monocle’s differentialGeneTest function. Pseudotimes along each path were scaled from 0 to 100 independently. The “full model” formula was “~path * sm.ns(Pseudotime, df=3)”, while the “reduced model” was “~sm.ns(Pseudotime, df=3)”. Differentially expressed genes (FDR < 1%, one-sided likelihood ratio test with multiple comparisons adjusted) were clustered via Ward’s method and visualized as a heatmap via the pheatmap package. (b) Pseudotemporal kinetics for selected genes involved in Robo/Slit signaling. Red indicates cells on the Myod path, while blue corresponds to the Myf5 path. Next to the expression curves for each are shown the standardized expression scores for each gene on the original myogenic trajectory. Only cells with detectable expression are rendered to prevent overplotting. (c) Modules of genes differentially expressed over the myogenic trajectory. A total of 2,908 genes were clustered via hierarchical clustering. The dendrogram was cut into 14 modules using the cutree function in R, and the aggregate expression of genes in each module was computed. Colors indicate aggregate UMI counts for each module that have been scaled for library size, log-transformed, and then mapped to Z-scores to enable comparison between modules. Cells with no expression of a given module are excluded to prevent overplotting.

Supplementary Material

Reporting_summary

NIHMS1518381-supplement-Reporting_summary.pdf^{(1.3MB, pdf)}

SI Guide

NIHMS1518381-supplement-SI_Guide.docx^{(16.1KB, docx)}

Supplement note 1

NIHMS1518381-supplement-Supplement_note_1.pdf^{(108KB, pdf)}

Supplementary tables S1 to S11

NIHMS1518381-supplement-Supplementary_tables_S1_to_S11.xlsx^{(19MB, xlsx)}

Acknowledgements

We thank members of the Shendure and Trapnell labs, especially D. Cusanovich, R. Daza, G. Findlay, A. McKenna, H. Pliner and V. Ramani, as well as L. McInnes, D. Beier, N. Ahituv and S. Tapscott, for helpful discussions and feedback. We also thank R. Hunter, and R. Rualo in the Transgenic Resources Program of University of Washington and N. Brieske and A. Stiege at the Max Planck Institute for Molecular Genetics for their exceptional assistance. We thank S. Geuer for the Fndc3a probe. M.S. was supported by a grant from the Deutsche Forschungsgemeinschaft (SP1532/2–1). This work was funded by the Paul G. Allen Frontiers Group (Allen Discovery Center grant to J.S. and C.T.), grants from the NIH (DP1HG007811 and R01HG006283 to J.S.; DP2 HD088158 to C.T.), the W. M. Keck Foundation (to C.T. and J.S.). J.S. is an Investigator of the Howard Hughes Medical Institute.

Footnotes

Supplementary Information is available in the online version of the paper.

REFERENCES

1.Kojima Y, Tam OH & Tam PPL Timing of developmental events in the early mouse embryo. Semin. Cell Dev. Biol 34, 65–75 (2014). [DOI] [PubMed] [Google Scholar]
2.Tam PPL & Loebel DAF Gene function in mouse embryogenesis: get set for gastrulation. Nat. Rev. Genet 8, 368–381 (2007). [DOI] [PubMed] [Google Scholar]
3.Dickinson ME et al. High-throughput discovery of novel developmental phenotypes. Nature 537, 508–514 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Meehan TF et al. Disease model discovery from 3,328 gene knockouts by The International Mouse Phenotyping Consortium. Nat. Genet 49, 1231–1238 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Wagner DE et al. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Briggs JA et al. The dynamics of gene expression in vertebrate embryogenesis at single-cell resolution. Science 360, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Farrell JA et al. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science 360, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Mayer C et al. Developmental diversification of cortical inhibitory interneurons. Nature 555, 457–462 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Lescroart F et al. Defining the earliest step of cardiovascular lineage segregation by single-cell RNA-seq. Science (2018). doi: 10.1126/science.aao4174 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Han X et al. Mapping the Mouse Cell Atlas by Microwell-Seq. Cell 172, 1091–1107.e17 (2018). [DOI] [PubMed] [Google Scholar]
11.The Tabula Muris Consortium, Quake SR, Wyss-Coray T & Darmanis S Transcriptomic characterization of 20 organs and tissues from mouse at single cell resolution creates a Tabula Muris (2017). doi: 10.1101/237446 [DOI] [Google Scholar]
12.Amini S et al. Haplotype-resolved whole-genome sequencing by contiguity-preserving transposition and combinatorial indexing. Nat. Genet 46, 1343–1349 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Adey A et al. In vitro, long-range sequence information for de novo genome assembly via transposase contiguity. Genome Res 24, 2041–2049 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Cusanovich DA et al. Multiplex single cell profiling of chromatin accessibility by combinatorial cellular indexing. Science 348, 910–914 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Vitak SA et al. Sequencing thousands of single-cell genomes with combinatorial indexing. Nat. Methods 14, 302–308 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Ramani V et al. Massively multiplex single-cell Hi-C. Nat. Methods 14, 263–266 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Cao J et al. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 357, 661–667 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Mulqueen RM et al. Scalable and efficient single-cell DNA methylation sequencing by combinatorial indexing (2017). doi: 10.1101/157230 [DOI] [Google Scholar]
19.Cao J et al. Joint profiling of chromatin accessibility and gene expression in thousands of single cells. Science 361, 1380–1385 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Rosenberg AB et al. Single-cell profiling of the developing mouse brain and spinal cord with split-pool barcoding. Science (2018). doi: 10.1126/science.aam8999 [DOI] [PMC free article] [PubMed] [Google Scholar]
21.La Manno G et al. RNA velocity of single cells. Nature 560, 494–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Wolock SL, Lopez R & Klein AM Scrublet: computational identification of cell doublets in single-cell transcriptomic data (2018). doi: 10.1101/357368 [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Qiu X et al. Reversed graph embedding resolves complex single-cell developmental trajectories (2017). doi: 10.1101/110668 [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Yang A et al. p63 is essential for regenerative proliferation in limb, craniofacial and epithelial development. Nature 398, 714–718 (1999). [DOI] [PubMed] [Google Scholar]
25.McQualter JL, Yuen K, Williams B & Bertoncello I Evidence of an epithelial stem/progenitor cell hierarchy in the adult mouse lung. Proc. Natl. Acad. Sci. U. S. A 107, 1414–1419 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Cichorek M, Wachulska M, Stasiewicz A & Tymińska A Skin melanocytes: biology and development. Advances in Dermatology and Allergology 1, 30–41 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Tomihari M, Hwang S-H, Chung J-S, Cruz PD Jr. & Ariizumi K Gpnmb is a melanosome-associated glycoprotein that contributes to melanocyte/keratinocyte adhesion in a RGD-dependent fashion. Exp. Dermatol 18, 586–595 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Varjosalo M & Taipale J Hedgehog: functions and mechanisms. Genes Dev 22, 2454–2472 (2008). [DOI] [PubMed] [Google Scholar]
29.Strähle U, Lam CS, Ertzer R & Rastegar S Vertebrate floor-plate specification: variations on common themes. Trends Genet 20, 155–162 (2004). [DOI] [PubMed] [Google Scholar]
30.Holmes GP et al. Distinct but overlapping expression patterns of two vertebrate slit homologs implies functional roles in CNS development and organogenesis. Mech. Dev 79, 57–72 (1998). [DOI] [PubMed] [Google Scholar]
31.Akle V et al. F-spondin/spon1b expression patterns in developing and adult zebrafish. PLoS One 7, e37593 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Zeisel A et al. Molecular Architecture of the Mouse Nervous System. Cell 174, 999–1014.e22 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Hartman BH, Durruthy-Durruthy R, Laske RD, Losorelli S & Heller S Identification and characterization of mouse otic sensory lineage genes. Front. Cell. Neurosci 9, 79 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Szenker-Ravi E et al. RSPO2 inhibition of RNF43 and ZNRF3 governs limb development independently of LGR4/5/6. Nature 557, 564–569 (2018). [DOI] [PubMed] [Google Scholar]
35.Cai X et al. Tbx20 acts upstream of Wnt signaling to regulate endocardial cushion formation and valve remodeling during mouse cardiogenesis. Development 140, 3176–3187 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Miller RA, Christoforou N, Pevsner J, McCallion AS & Gearhart JD Efficient array-based identification of novel cardiac genes through differentiation of mouse ESCs. PLoS One 3, e2176 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Petit F, Sears KE & Ahituv N Limb development: a paradigm of gene regulation. Nat. Rev. Genet 18, 245–258 (2017). [DOI] [PubMed] [Google Scholar]
38.Guo Q, Loomis C & Joyner AL Fate map of mouse ventral limb ectoderm and the apical ectodermal ridge. Dev. Biol 264, 166–178 (2003). [DOI] [PubMed] [Google Scholar]
39.Lewandoski M,E et al. Fgf8 signalling from the AER is essential for normal limb development. - PubMed - NCBI Available at: https://www.ncbi.nlm.nih.gov/pubmed/11101846. (Accessed: 22nd April 2018) [DOI] [PubMed]
40.Gerdes J, Schwab U, Lemke H & Stein H Production of a mouse monoclonal antibody reactive with a human nuclear antigen associated with cell proliferation. Int. J. Cancer 31, 13–20 (1983). [DOI] [PubMed] [Google Scholar]
41.Bergman D, Halje M, Nordin M & Engström W Insulin-like growth factor 2 in development and disease: a mini-review. Gerontology 59, 240–249 (2013). [DOI] [PubMed] [Google Scholar]
42.Trapnell C et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol 32, 381–386 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
43.McInnes L & Healy J UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction (2018). [Google Scholar]
44.Alexander Wolf F. et al. Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. bioRxiv 208819 (2017). doi: 10.1101/208819 [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Braun T & Gautel M Transcriptional mechanisms regulating skeletal muscle differentiation, growth and homeostasis. Nat. Rev. Mol. Cell Biol 12, 349–361 (2011). [DOI] [PubMed] [Google Scholar]
46.Comai G, Sambasivan R, Gopalakrishnan S & Tajbakhsh S Variations in the efficiency of lineage marking and ablation confound distinctions between myogenic cell populations. Dev. Cell 31, 654–667 (2014). [DOI] [PubMed] [Google Scholar]
47.Halperin-Barlev O & Kalcheim C Sclerotome-derived Slit1 drives directional migration and differentiation of Robo2-expressing pioneer myoblasts. Development 138, 2935–2945 (2011). [DOI] [PubMed] [Google Scholar]
48.Heimberg G, Bhatnagar R, El-Samad H & Thomson M Low Dimensionality in Gene Expression Data Enables the Accurate Extraction of Transcriptional Programs from Shallow Sequencing. Cell Syst 2, 239–250 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Osterwalder M et al. Enhancer redundancy provides phenotypic robustness in mammalian development. Nature 554, 239–243 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Dickel DE et al. Ultraconserved Enhancers Are Required for Normal Development. Cell 172, 491–499.e15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

Methods References

51.Li D et al. Formation of proximal and anterior limb skeleton requires early function of Irx3 and Irx5 and is negatively regulated by Shh signaling. Dev. Cell 29, 233–240 (2014). [DOI] [PubMed] [Google Scholar]
52.Kraft K et al. Deletions, Inversions, Duplications: Engineering of Structural Variants using CRISPR/Cas in Mice. Cell Rep (2015). doi: 10.1016/j.celrep.2015.01.016 [DOI] [PubMed] [Google Scholar]
53.Buenrostro JD, Giresi PG, Zaba LC, Chang HY & Greenleaf WJ Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, DNA-binding proteins and nucleosome position. Nat. Methods 10, 1213–1218 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Renaud G, Stenzel U, Maricic T, Wiebe V & Kelso J deML: robust demultiplexing of Illumina sequences using a likelihood-based approach. Bioinformatics 31, 770–772 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Dobin A et al. STAR: ultrafast universal RNA-seq aligner. Bioinformatics 29, 15–21 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Anders S, Pyl PT & Huber W HTSeq--a Python framework to work with high-throughput sequencing data. Bioinformatics btu638 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Qiu X et al. Reversed graph embedding resolves complex single-cell developmental trajectories (2017). doi: 10.1101/110668 [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Wolf FA, Angerer P & Theis FJ SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19, 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Zheng GXY et al. Massively parallel digital transcriptional profiling of single cells. Nat. Commun 8, 14049 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Wolf FA, Angerer P & Theis FJ SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19, 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Cao J et al. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 357, 661–667 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Qiu X et al. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 14, 979–982 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Wolock SL, Lopez R & Klein AM Scrublet: computational identification of cell doublets in single-cell transcriptomic data (2018). doi: 10.1101/357368 [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Pliner H et al. Chromatin accessibility dynamics of myogenesis at single cell resolution (2017). doi: 10.1101/155473 [DOI] [Google Scholar]
65.Kuleshov MV et al. Enrichr: a comprehensive gene set enrichment analysis web server 2016 update. Nucleic Acids Res 44, W90–7 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
66.McInnes L & Healy J UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction (2018). [Google Scholar]
67.Levine JH et al. Data-Driven Phenotypic Dissection of AML Reveals Progenitor-like Cells that Correlate with Prognosis. Cell 162, 184–197 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
68.Wolf FA et al. Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells (2017). doi: 10.1101/208819 [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Mao Q, Wang L, Tsang I & Sun Y Principal Graph and Structure Learning Based on Reversed Graph Embedding. IEEE Trans. Pattern Anal. Mach. Intell (2016). doi: 10.1109/TPAMI.2016.2635657 [DOI] [PMC free article] [PubMed] [Google Scholar]
70.Mao Q, Yang L, Wang L, Goodison S & Sun Y SimplePPT: A Simple Principal Tree Algorithm in Proceedings of the 2015 SIAM International Conference on Data Mining 792–800 [Google Scholar]
71.Qiu X et al. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 14, 979–982 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
72.Moran PAP Notes on continuous stochastic phenomena. Biometrika 37, 17–23 (1950). [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Reporting_summary

NIHMS1518381-supplement-Reporting_summary.pdf^{(1.3MB, pdf)}

SI Guide

NIHMS1518381-supplement-SI_Guide.docx^{(16.1KB, docx)}

Supplement note 1

NIHMS1518381-supplement-Supplement_note_1.pdf^{(108KB, pdf)}

Supplementary tables S1 to S11

NIHMS1518381-supplement-Supplementary_tables_S1_to_S11.xlsx^{(19MB, xlsx)}

Data Availability Statement

[R1] 1.Kojima Y, Tam OH & Tam PPL Timing of developmental events in the early mouse embryo. Semin. Cell Dev. Biol 34, 65–75 (2014). [DOI] [PubMed] [Google Scholar]

[R2] 2.Tam PPL & Loebel DAF Gene function in mouse embryogenesis: get set for gastrulation. Nat. Rev. Genet 8, 368–381 (2007). [DOI] [PubMed] [Google Scholar]

[R3] 3.Dickinson ME et al. High-throughput discovery of novel developmental phenotypes. Nature 537, 508–514 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.Meehan TF et al. Disease model discovery from 3,328 gene knockouts by The International Mouse Phenotyping Consortium. Nat. Genet 49, 1231–1238 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.Wagner DE et al. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] 6.Briggs JA et al. The dynamics of gene expression in vertebrate embryogenesis at single-cell resolution. Science 360, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.Farrell JA et al. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science 360, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] 8.Mayer C et al. Developmental diversification of cortical inhibitory interneurons. Nature 555, 457–462 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] 9.Lescroart F et al. Defining the earliest step of cardiovascular lineage segregation by single-cell RNA-seq. Science (2018). doi: 10.1126/science.aao4174 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Han X et al. Mapping the Mouse Cell Atlas by Microwell-Seq. Cell 172, 1091–1107.e17 (2018). [DOI] [PubMed] [Google Scholar]

[R11] 11.The Tabula Muris Consortium, Quake SR, Wyss-Coray T & Darmanis S Transcriptomic characterization of 20 organs and tissues from mouse at single cell resolution creates a Tabula Muris (2017). doi: 10.1101/237446 [DOI] [Google Scholar]

[R12] 12.Amini S et al. Haplotype-resolved whole-genome sequencing by contiguity-preserving transposition and combinatorial indexing. Nat. Genet 46, 1343–1349 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.Adey A et al. In vitro, long-range sequence information for de novo genome assembly via transposase contiguity. Genome Res 24, 2041–2049 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.Cusanovich DA et al. Multiplex single cell profiling of chromatin accessibility by combinatorial cellular indexing. Science 348, 910–914 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] 15.Vitak SA et al. Sequencing thousands of single-cell genomes with combinatorial indexing. Nat. Methods 14, 302–308 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] 16.Ramani V et al. Massively multiplex single-cell Hi-C. Nat. Methods 14, 263–266 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] 17.Cao J et al. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 357, 661–667 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.Mulqueen RM et al. Scalable and efficient single-cell DNA methylation sequencing by combinatorial indexing (2017). doi: 10.1101/157230 [DOI] [Google Scholar]

[R19] 19.Cao J et al. Joint profiling of chromatin accessibility and gene expression in thousands of single cells. Science 361, 1380–1385 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Rosenberg AB et al. Single-cell profiling of the developing mouse brain and spinal cord with split-pool barcoding. Science (2018). doi: 10.1126/science.aam8999 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] 21.La Manno G et al. RNA velocity of single cells. Nature 560, 494–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] 22.Wolock SL, Lopez R & Klein AM Scrublet: computational identification of cell doublets in single-cell transcriptomic data (2018). doi: 10.1101/357368 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] 23.Qiu X et al. Reversed graph embedding resolves complex single-cell developmental trajectories (2017). doi: 10.1101/110668 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] 24.Yang A et al. p63 is essential for regenerative proliferation in limb, craniofacial and epithelial development. Nature 398, 714–718 (1999). [DOI] [PubMed] [Google Scholar]

[R25] 25.McQualter JL, Yuen K, Williams B & Bertoncello I Evidence of an epithelial stem/progenitor cell hierarchy in the adult mouse lung. Proc. Natl. Acad. Sci. U. S. A 107, 1414–1419 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] 26.Cichorek M, Wachulska M, Stasiewicz A & Tymińska A Skin melanocytes: biology and development. Advances in Dermatology and Allergology 1, 30–41 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] 27.Tomihari M, Hwang S-H, Chung J-S, Cruz PD Jr. & Ariizumi K Gpnmb is a melanosome-associated glycoprotein that contributes to melanocyte/keratinocyte adhesion in a RGD-dependent fashion. Exp. Dermatol 18, 586–595 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.Varjosalo M & Taipale J Hedgehog: functions and mechanisms. Genes Dev 22, 2454–2472 (2008). [DOI] [PubMed] [Google Scholar]

[R29] 29.Strähle U, Lam CS, Ertzer R & Rastegar S Vertebrate floor-plate specification: variations on common themes. Trends Genet 20, 155–162 (2004). [DOI] [PubMed] [Google Scholar]

[R30] 30.Holmes GP et al. Distinct but overlapping expression patterns of two vertebrate slit homologs implies functional roles in CNS development and organogenesis. Mech. Dev 79, 57–72 (1998). [DOI] [PubMed] [Google Scholar]

[R31] 31.Akle V et al. F-spondin/spon1b expression patterns in developing and adult zebrafish. PLoS One 7, e37593 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.Zeisel A et al. Molecular Architecture of the Mouse Nervous System. Cell 174, 999–1014.e22 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.Hartman BH, Durruthy-Durruthy R, Laske RD, Losorelli S & Heller S Identification and characterization of mouse otic sensory lineage genes. Front. Cell. Neurosci 9, 79 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] 34.Szenker-Ravi E et al. RSPO2 inhibition of RNF43 and ZNRF3 governs limb development independently of LGR4/5/6. Nature 557, 564–569 (2018). [DOI] [PubMed] [Google Scholar]

[R35] 35.Cai X et al. Tbx20 acts upstream of Wnt signaling to regulate endocardial cushion formation and valve remodeling during mouse cardiogenesis. Development 140, 3176–3187 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Miller RA, Christoforou N, Pevsner J, McCallion AS & Gearhart JD Efficient array-based identification of novel cardiac genes through differentiation of mouse ESCs. PLoS One 3, e2176 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] 37.Petit F, Sears KE & Ahituv N Limb development: a paradigm of gene regulation. Nat. Rev. Genet 18, 245–258 (2017). [DOI] [PubMed] [Google Scholar]

[R38] 38.Guo Q, Loomis C & Joyner AL Fate map of mouse ventral limb ectoderm and the apical ectodermal ridge. Dev. Biol 264, 166–178 (2003). [DOI] [PubMed] [Google Scholar]

[R39] 39.Lewandoski M,E et al. Fgf8 signalling from the AER is essential for normal limb development. - PubMed - NCBI Available at: https://www.ncbi.nlm.nih.gov/pubmed/11101846. (Accessed: 22nd April 2018) [DOI] [PubMed]

[R40] 40.Gerdes J, Schwab U, Lemke H & Stein H Production of a mouse monoclonal antibody reactive with a human nuclear antigen associated with cell proliferation. Int. J. Cancer 31, 13–20 (1983). [DOI] [PubMed] [Google Scholar]

[R41] 41.Bergman D, Halje M, Nordin M & Engström W Insulin-like growth factor 2 in development and disease: a mini-review. Gerontology 59, 240–249 (2013). [DOI] [PubMed] [Google Scholar]

[R42] 42.Trapnell C et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol 32, 381–386 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] 43.McInnes L & Healy J UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction (2018). [Google Scholar]

[R44] 44.Alexander Wolf F. et al. Graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. bioRxiv 208819 (2017). doi: 10.1101/208819 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] 45.Braun T & Gautel M Transcriptional mechanisms regulating skeletal muscle differentiation, growth and homeostasis. Nat. Rev. Mol. Cell Biol 12, 349–361 (2011). [DOI] [PubMed] [Google Scholar]

[R46] 46.Comai G, Sambasivan R, Gopalakrishnan S & Tajbakhsh S Variations in the efficiency of lineage marking and ablation confound distinctions between myogenic cell populations. Dev. Cell 31, 654–667 (2014). [DOI] [PubMed] [Google Scholar]

[R47] 47.Halperin-Barlev O & Kalcheim C Sclerotome-derived Slit1 drives directional migration and differentiation of Robo2-expressing pioneer myoblasts. Development 138, 2935–2945 (2011). [DOI] [PubMed] [Google Scholar]

[R48] 48.Heimberg G, Bhatnagar R, El-Samad H & Thomson M Low Dimensionality in Gene Expression Data Enables the Accurate Extraction of Transcriptional Programs from Shallow Sequencing. Cell Syst 2, 239–250 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.Osterwalder M et al. Enhancer redundancy provides phenotypic robustness in mammalian development. Nature 554, 239–243 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] 50.Dickel DE et al. Ultraconserved Enhancers Are Required for Normal Development. Cell 172, 491–499.e15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

The single cell transcriptional landscape of mammalian organogenesis

Junyue Cao

Malte Spielmann

Xiaojie Qiu

Xingfan Huang

Daniel M Ibrahim

Andrew J Hill

Fan Zhang

Stefan Mundlos

Lena Christiansen

Frank J Steemers

Cole Trapnell

Jay Shendure

Abstract

Main

Single cell RNA-seq of 2 million cells

Fig. 1. sci-RNA-seq3 enables profiling of 2,072,011 cells from 61 mouse embryos across 5 developmental stages in a single experiment.

Identification of cell types and subtypes

Fig. 2. Identifying the major cell types of mouse organogenesis.

Characterization of the apical ectodermal ridge

Fig. 3. Identification and characterization of epithelial cell subtypes and the limb apical ectodermal ridge (AER).

Reconstructing developmental trajectories

Fig. 4. Characterization of ten major developmental trajectories present during mouse organogenesis.

Fig. 5. UMAP visualization of individual major trajectories.

Reconstructing skeletal myogenesis

Fig. 6. Resolving cellular trajectories in myogenesis.

Discussion

METHODS

Data reporting

Embryo dissection

Whole-mount in situ hybridization

Mammalian cell culture

Mouse embryo nuclei extraction and fixation

Mouse embryo cell counts

sci-RNA-seq3 library preparation and sequencing

Processing of sequencing reads

Whole mouse embryo analysis

Cell clustering, t-SNE visualization and marker gene identification

AER and limb mesenchyme pseudo-time analysis

Trajectory inference with Monocle 3

Dimensionality reduction with Uniform Manifold Approximation and Projection (UMAP)

Partitioning cells into discontinuous trajectories

Learning the principal graph

Computing pseudotimes

Identifying genes with complex trajectory-dependent expression

Reporting summary

Code Availability

Data Availability

Extended Data

Extended Data Fig. 1. Performance and QC-related analyses for sci-RNA-seq3.

Extended Data Fig. 2. Identifying the major cell types and cell composition dynamics during mouse organogenesis.

Extended Data Fig. 3. Louvain clustering and t-SNE visualization of subclusters of the each of 38 major cell types.

Extended Data Fig. 4. Analysis of cell subtypes during mouse organogenesis.

Extended Data Fig. 5. Cell type correlation analysis between single cell mouse atlases.

Extended Data Fig. 6. Analysis of mouse epithelium, endothelium and limb apical ectodermal ridge cells.

Extended Data Fig. 7. Characterizing cellular trajectories during limb mesenchyme differentiation.

Extended Data Fig. 8. Characterization of ten major developmental trajectories present during mouse organogenesis.

Extended Data Fig. 9. UMAP visualization of the ten major cell trajectories.

Extended Data Fig. 10. UMAP visualization of the 56 subtrajectories, colored by development stage.

Extended Data Fig. 11. UMAP visualization of the 56 subtrajectories, colored by inferred pseudotime.

Extended Data Fig. 12. Gene dynamics in the myogenic trajectory.

Supplementary Material

Acknowledgements

Footnotes

REFERENCES

Methods References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases