Abstract
Objective:
High breast density is a risk factor for breast cancer. The aim of this study was to develop a deep convolutional neural network (dCNN) for the automatic classification of breast density based on the mammographic appearance of the tissue according to the American College of Radiology Breast Imaging Reporting and Data System (ACR BI-RADS) Atlas.
Methods:
In this study, 20,578 mammography single views from 5221 different patients (58.3 ± 11.5 years) were downloaded from the picture archiving and communications system of our institution and automatically sorted according to the ACR density (a-d) provided by the corresponding radiological reports. A dCNN with 11 convolutional layers and 3 fully connected layers was trained and validated on an augmented dataset. The model was finally tested on two different datasets against: i) the radiological reports and ii) the consensus decision of two human readers. None of the test datasets was part of the dataset used for the training and validation of the algorithm.
Results:
The optimal number of epochs was 91 for medio-lateral oblique (MLO) projections and 94 for cranio-caudal projections (CC), respectively. Accuracy for MLO projections obtained on the validation dataset was 90.9% (CC: 90.1%). Tested on the first test dataset of mammographies (850 MLO and 880 CC), the algorithm showed an accordance with the corresponding radiological reports of 71.7% for MLO and of 71.0% for CC. The agreement with the radiological reports improved in the differentiation between dense and fatty breast for both projections (MLO = 88.6% and CC = 89.9%). In the second test dataset of 200 mammographies, a good accordance was found between the consensus decision of the two readers on both, the MLO-model (92.2%) and the right craniocaudal-model (87.4%). In the differentiation between fatty (ACR A/B) and dense breasts (ACR C/D), the agreement reached 99% for the MLO and 96% for the CC projections, respectively.
Conclusions:
The dCNN allows for accurate classification of breast density based on the ACR BI-RADS system. The proposed technique may allow accurate, standardized, and observer independent breast density evaluation of mammographies.
Advances in knowledge:
Standardized classification of mammographies by a dCNN could lead to a reduction of falsely classified breast densities, thereby allowing for a more accurate breast cancer risk assessment for the individual patient and a more reliable decision, whether additional ultrasound is recommended.
Introduction
Breast cancer is the most frequently diagnosed cancer among females with an incidence of 12.3% in the normal population1,2 and it is the second most common cause of cancer death in females.3 Epidemiological studies have shown that females with extremely dense breast tissue present a two- to six-fold increased risk of developing breast cancer.4 Due to different X-ray absorption properties, fibroglandular breast tissue, comprised of glandular tissues, fibrous tissues, and stroma cells, appears opaque on a mammography as compared to the lucent fatty tissue. The mammographic density (MD) or breast density, i. e. the measure of the relative amount of fibroglandular parenchyma and fat tissue in the breast based on the mammographic appearance of the fibroglandular parenchyma, provides an objective assessment of the relative amount of glandular tissue in the breast, which is otherwise not inferable from a physical examination.5 Studies performed during the last decades have shown that the MD reflects changes in breast density due to aging and menopausal transition.4,6 Moreover, lifestyle risk factors (such as body mass index, alcohol intake, or breastfeeding) can have an effect on MD.7
Besides its relevance in the assessment of the individual risk of developing breast cancer, the MD also represents an important parameter in the planning of systematic mammography screening programs. Scientific studies have shown that the sensitivity of screening mammographies strongly depends on the MD. While for low density breast a sensitivity of 87% is reported, for dense breast tissue a dramatic drop of the sensitivity to 63% has been observed.8 Patients with dense breast may require additional imaging, such as tomosynthesis, ultrasound or breast MR to increase the cancer detection chances.9
In mammography screening, reports are typically formulated according to the American College of Radiology Breast Imaging-Reporting and Data System (ACR BI-RADS) catalog last updated in November 2015. In ACR BI-RADS, breast density is classified into four subcategories: A (“almost entirely fatty”), B (“scattered areas of fibroglandular density”), C (“heterogeneously dense breasts, which may obscure small masses”), and D (“extremely dense breasts, which lowers the sensitivity of mammography”). In spite of this cataloging, the classification of the MD suffers from a poor inter reader and intra reader reproducibility.10
In this investigation, we evaluated whether a deep convolutional neural network (dCNN) trained with approximately 20,000 mammography projections, labeled with an ACR MD score obtained from the corresponding report, allows for accurate, objective, and standardized MD classification.
Methods and materials
Database search
The local ethics committee “Kantonale Ethikkommission Zürich” approved this retrospective study and waived the need for informed consent (Approval Number: 2016–00064). All reports from mammography patients of the years 2012 and 2013 were indexed to an anonymous ID and the study date. The corresponding mammographies were downloaded and indexed to the previously assigned ID and the respective study date. Overall, 20,578 diagnostic mammography views from 5,221 unique patients (including 153 patients with a one-sided mastectomy) with a mean age of 58.3 ± 11.5 years were linked to the ACR BI-RADS density from the corresponding radiological report using a home-written text searching MATLAB script (Release 2013b, MathWorks, Natick, MA). To avoid over representation of ACR densities B and C, the original dataset made of 20,578 views was reduced to 12,932 views.
Data preparation
All computations were performed on a consumer-grade desktop computer equipped with an Intel i7-7700 CPU with 16 GB random access memory and an NVIDIA 1080 GTX graphics processing unit with 8 GB graphics random access memory. The computer was running Ubuntu Linux 16.04 with Tensorflow 1.0.1 and Keras 2.0.4. All images were resized from their initial dimensions of 3072 × 2816 pixels to 351 × 280 pixels. To increase the number of mammographies, all projections were reoriented to the right-sided position for analysis, and all computations were performed with right-side projections [medio-lateral oblique (MLO): n = 6470; cranio-caudal (CC): n = 6462] . Data augmentation was further performed with the ImageDataGenerator of Keras expanding the dataset to achieve an equal distribution of breast densities for the training and the validation phase (Table 1). Digitally generated images were computed performing random vertical and horizontal shifts, and image shearing transformations.
Table 1.
Number of mammographies used for training/validation of the dCNN
| ACR A | ACR B | ACR C | ACRD | |
| RMLO | 1,565 | 2,158 | 1,635 | 1,112 |
| RMLO augmented | 6,579 | 5,720 | 4,786 | 5,329 |
| RCC | 1,561 | 2,150 | 1,641 | 1,110 |
| RCC augmented | 6,696 | 5,759 | 4,667 | 5,317 |
ACR, American College of Radiology; dCNN, deep convolutional neural network;RMLO, right medial-lateral oblique; RCC, right cranicaudal;
The resulting dataset was randomly shuffled and stratified with respect to the density classes, and then split into a 70% partition for the training and a 30% partition for the validation of the model. Prior to the density estimation each mammographic view was classified according to its orientation (MLO or CC) and side (right or left).
The performance of the algorithm was tested on two different test datasets. The first test dataset was referenced to the radiological reports of our institution and consisted of 850 MLO (882 CC) projections composed of 167(201) ACR A, 347 (308) ACR B, 260 (249) ACR C, and 76 (124) ACR D densities. The second test dataset was made by 200 images (100 MLO and 100 CC projections) previously excluded from training or validation of the algorithm. The subset contained an equal distribution of breast density classes (each with 50 images) taken from the radiological reports. Classes were presented to the readers and the dCNN in a random order. The dCNN-based MD classifications for the subset were compared to the consensus decision made by two experienced radiologists with over 5 years experience in mammographic imaging and 1500 mammographic cases read per year.
dCNN architecture
A dCNN model was employed in this study for classification of an input mammography projection into four categories. In order to find a good compromise between memory usage of the graphical processor unit and validation accuracy, and to prevent overfitting, different network architectures regarding the number of layers, number of filters, dropout rate and number of epochs, were systematically evaluated to avoid overfitting. The final convolutional network consisted of 13 convolutional layers followed by max-pooling for reduction of the dimensionality of the feature maps and 4 dense layers with a final fully connected softmax layer as depicted in Figure 1. The number of applied filters amounted 32, which were randomly initialized using the glorot_uniform method. The convolution layers were zero-padded; Nesterov momentum11 and dropout with a rate of 50% were used to improve the performance of the model and to prevent overfitting. Batch size was set to 40, and maximum number of epochs for training was 120. The weights with the best performance on the validation set were saved and used for evaluation on the test dataset. After complete training of the model, density classification was assigned to each image of the test dataset based on the highest probability assigned to the four categories A to D (keras predict_proba function).
Figure 1.
Schematic representation of the applied dCNN. dCNN, deep convolutional neural network.
Human readout
All images in the test set were presented in the same random order to two radiologists (Reader 1: MM; Reader 2: NB), who were blinded to the clinical information as well as to the study design. Each reader rated the images individually according to the ACR BI-RADS catalog. After the individual evaluation of each image, all images rated differently by Reader 1 and Reader 2 were again classified by both readers in consensus. The classification results derived by the consensus decision of both readers served as ground truth for the evaluation of the classification accuracy of the dCNN and of the initial classification of each reader.
Statistical analyses
Statistical analysis was performed using the SPSS software package (SPSS v. 23, IBM Corp., Armonk, NY). The metrics of the confusion matrices were quantified to assess the overall performances of the dCNN and of each reader as compared to the consensus decision.12 Inter rater reliabilities of the MD classifications between the dCNN, both readers, and the ground truth were assessed by calculating Cohen’s kappa (κ) coefficients with quadratic weights evaluated according to Landis and Koch.13,14 The diagnostic performance of the dCNN compared to the human readout was assessed by conducting a receiver operating characteristics (ROC) analysis. For this, the multiple classification problem of the test dataset into four density categories (i.e. A, B, C, and D) was translated into four binary classification problems (i.e. A vs all; B vs all; C vs all; D vs all). For each binary classification sensitivity and specificity of each human reader and of the dCNN were computed. Diagnostic accuracies were expressed as the area under the curves (AUC) (ROC curves) and compared with DeLong’s non-parametric test.15 All tests were two-tailed and p-values < 0.05 were considered indicative of significant differences.
Results
Training and validation
In total 12,932 mammography views were successfully linked to the ACR BI-RADS density from the corresponding radiological report. After image pre-processing and data augmentation a balanced training and validation dataset subdivided into four classes composed of n = 22,414 MLO projections and n = 22,439 CC projections was available.
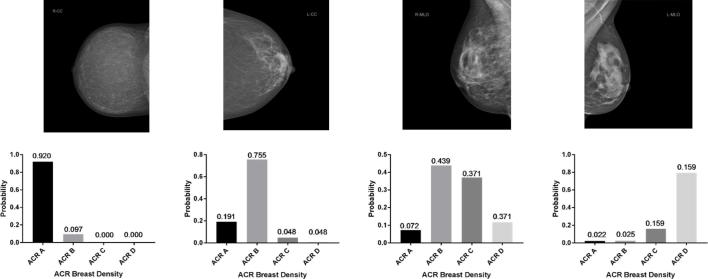
The model computations for the MLO and CC projections were completed in 20.3 and 21.6 h, respectively. For both models, initially accuracy was higher on the validation dataset compared to the training dataset (Figure 2), which may be attributed to the relatively small batch size, whereas validation after each cycle is performed with the complete validation set. For the MLO model, accuracy on the validation set was 90.9% (CC: 90.1%) after 91 (CC: 94) epochs. At about 90–95 epochs, accuracy on the validation set gradually reached saturation. Afterwards, the network started to overfit on the training data. Typical examples of the evaluation on three mammography projections unknown to the models are depicted in Figure 3.
Figure 2.
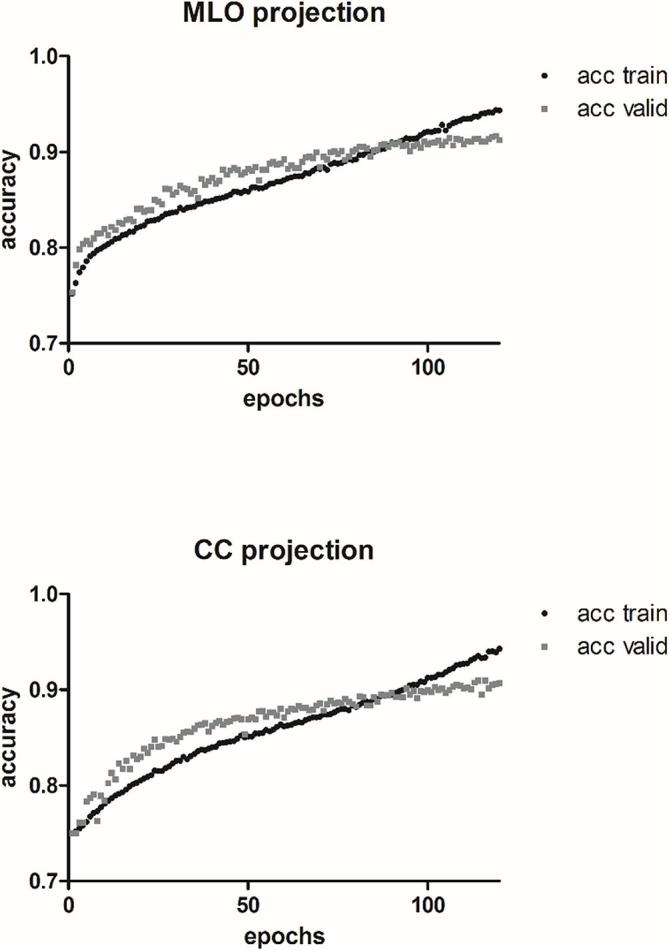
Accuracy curves for the training and validation datasets for both projections. CC, cranio-caudal; MLO, medio-lateral oblique.
Figure 3.
Examples of mammography evaluations using the dCNN. dCNN, deep convolutional neural network.
Test datasets: radiological report as ground truth
In the test dataset referenced to the radiological reports, an accordance of 71.7% was obtained for 850 MLO projections. Comparable results were found for the 882 CC projections (accordance of 71.0%). Evaluating the accordance for the distinction between fatty (ACR A and B) and dense (ACR C and D) breast tissue, an accordance of 88.6% was reached for MLO projections, and of 89.9% for CC projections. The corresponding confusion matrices are shown for both projections and for 4/2 class discrimination in Tables 2 and 3, respectively.
Table 2.
Normalized confusion matrix of the “real-world” test dataset for the dCNN, considering the radiological reports as ground truth
| Reference:radiological report | PREDICTED | ||||||||
| RMLO projections | RCC projections | ||||||||
| ACR A | ACR B | ACR C | ACR D | ACR A | ACR B | ACR C | ACR D | ||
| GROUND TRUTH | ACR A | 86.8 | 18.2 | 1.5 | 0.0 | 84.6 | 20.8 | 1.6 | 0.0 |
| ACR B | 12.6 | 68.6 | 17.7 | 0.0 | 8.5 | 64.3 | 10.0 | 0.0 | |
| ACR C | 0.6 | 11.5 | 63.5 | 18.4 | 5.5 | 10.4 | 60.2 | 12.9 | |
| ACR D | 0.0 | 1.7 | 17.3 | 81.6 | 1.5 | 4.5 | 28.1 | 87.1 | |
ACR, American College of Radiology; dCNN, deep convolutional neural network; RCC, right craniocaudal;
Table 3.
Normalized confusion matrix of the “real-world” test dataset for the dCNN, with the radiological reports underlying as ground truth, applying the two-class discrimination fatty vs dense
| Reference: radiological report | PREDICTED | ||||
| RMLO projections | RCC projections | ||||
| Fatty | Dense | Fatty | Dense | ||
| GROUND TRUTH | Fatty | 90.3% | 9.7% | 93.9% | 6.1% |
| Dense | 14.1% | 85.9% | 14.9% | 85.1% | |
dCNN, deep convolutional neural network;RCC, right craniocaudal;
Test dataset: consensus of two experienced radiologists as ground truth
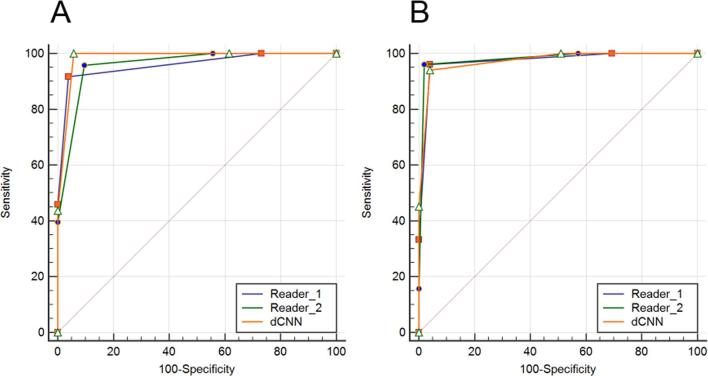
As compared to the consensus decision of the two experienced radiologists for the subset of the test dataset, the dCNN achieved an overall classification accuracy of 92.2% for the MLO and 87.4% for the right craniocaudal projections (Table 4). In the distinction between fatty (ACR A and B) and dense (ACR C and D) breast tissue, an overall classification accuracy of 99% was observed for MLO projections, and of 96% for CC projections. The corresponding confusion matrices are shown for both projections and 4/2 class discrimination in Table 5 . For the MLO projections, the ROC analyses measured an AUC of 0.96 [95% CI: (0.90–0.99)] for Reader 1 and for Reader 2, while for the dCNN the AUC was 0.98 [95% CI: (0.93–0.99)] (Figure 4A, Table 6). For the CC projections, the AUC amounted to 0.97 [95% CI: (0.92–0.99)] for Reader 1, to 0.98 [95% CI: (0.93–0.99)] for Reader 2, and to 0.97 [95% CI: (0.92–0.99)] for the dCNN (Figure 4B, Table 6). For both projections, no significant differences in the diagnostic accuracy were found between the two readers and the dCNN (p = 0.16–0.99).
Table 4.
Normalized confusion matrix for the “real-world” dataset with the consensus decision of the two readers as ground truth, applying the four classes of the ACR density definition
| Reference:consensus decision | PREDICTED | ||||||||
| RMLO projections | RCC projections | ||||||||
| ACR A | ACR B | ACR C | ACR D | ACR A | ACR B | ACR C | ACR D | ||
|
GROUND TRUTH |
ACR A | 73.7(89.5%)[89.5%] | 26.3(10.5%)[10.5%] | 0.0%(0.0%)[0.0%] | 0.0%(0.0%)[0.0%] | 79.0%(100.0%) [94.7% ] | 21.1%(0.0%)[5.3%] | 0.0%(0.0%)[0.0%] | 0.0%(0.0%)[0.0%] |
| ACR B | 0.0%(18.2%)[9.1%] | 93.9%(66.7%)[87.9%] | 6.1%(15.2%)[3.0%] | 0.0%(0.0%)[0.0%] | 0.0% (6.9%) [20.7%] | 93.1%(93.1%)[79.3%] | 6.9%(0.0%)[0.0%] | 0.0%(0.0%)[0.0%] | |
| ACR C | 0.0%(0.0%)[0.0%] | 16.0%(8.0%)[0.0%] | 80.0%(84.0%)[100.0%] | 4.0%(8.0%)[0.0%] | 0.0% (0.0%) [0.0%] | 8.1%(5.4%)[2.7%] | 83.8%(94.6%)[75.7%] | 8.1%(0.0%)[21.6%] | |
| ACR D | 0.0%(0.0%)[0.0%] | 0.0%(0.0%)[0.0%] | 8.7%(26.1%)[8.7%] | 91.3%(73.9%)[91.3%] | 0.0% (0.0%) [0.0%] | 0.0%(0.0%)[0.0%] | 6.7%(46.7%)[0.0%] | 93.3%(53.3%)[100.0%] | |
ACR, American College of Radiology ; dCNN, deep convolutional neural network;RCC, right craniocaudal;
Reader 1, no brackets; Reader 2, round brackets ( ); the dCNN, square brackets [ ].
Table 5.
Normalized confusion matrix for the “real-world” data with the consensus decision of the two readers as ground truth, applying the two-class discrimination fatty vs dense
| Reference: consensus decision | PREDICTED | ||||
| RMLO projections | RCC projections | ||||
| Fatty | Dense | Fatty | Dense | ||
| ACTUAL | Fatty | 96.2% (90.4%) [98.1%] |
3.9% (9.6%) [1.9%] |
95.8% (100.0%) [100.0%] |
4.2% (0.0%) [0.0%] |
| Dense | 8.3% (4.2%) [0.0%] |
91.7% (95.8%) [100.0%] |
5.8% (3.9%) [1.9%] |
94.2% (96.2%) [98.1%] |
|
dCNN, deep convolutional neural network;RCC, right craniocaudal;
Reader 1 (no brackets), Reader 2 (round brackets), and the dCNN (square brackets)
Figure 4.
ROC Curves. ROC, receiver operating characteristics.
Table 6.
ROC analyses for the “real-world” dataset with the consensus decision of the two readers underlying as ground truth
| RMLO n = 100 | RCC n = 100 | |||||||||
| AUC [%] (95% CI) | Specificity [%] | Sensitivity [%] | PPV [%] | NPV [%] | AUC [%] (95% CI) | Specificity [%] | Sensitivity [%] | PPV [%] | NPV [%] | |
| Reader 1 | 0.96 a (0.90–0.99) | 91.7 | 96.2 | 92.6 | 95.7 | 97.3 (0.91–0.99) | 94.2 | 95.8 | 93.9 | 96.1 |
| Reader 2 | 0.96 a (0.90–0.99) | 95.8 | 90.4 | 95.9 | 90.2 | 98.0 (0.93–0.99) | 96.2 | 100.0 | 96.0 | 100.0 |
| dCNN | 0.98 a (0.93–0.99) | 100.0 | 98.1 | 100.0 | 98.0 | 97.4 (0.92–0.99) | 98.1 | 100.0 | 98.0 | 100.0 |
AUC, Area under the curves; dCNN, deep convolutional neural network; NPV, negative predictive value; PPV, positive predictive value; ROC, receiver operating characteristics;RCC, right craniocaudal;
p < 0.005.
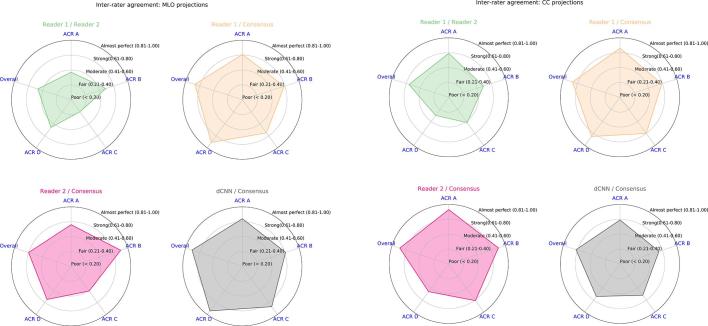
For the MLO projections the agreement between each individual reader and the dCNN compared to the consensus decision ranged between “strong” {ACR B: dCNN/Consensus [κ: 0.75 (95% CI: 0.60–0.92)]} and “almost perfect” {ACR A: Reader 2/Consensus [κ: 0.93 (95% CI: 0.85–1.00)]}. Regarding the agreement for the classification of all ACR MD scores, both Reader 1 and the dCNN achieved “almost perfect”, whereas for Reader 2 “strong” agreement was measured [κ: 0.80 (95% CI: 0.73–0.88)]. (Figure 5A; Table 7).
Figure 5.
Evaluated Inter rater agreement.
Table 7.
Inter rater agreement for the MLO projections for both readers and the dCNN compared to each other and to the consensus decision
| RMLO Projections | ACR A | ACR B | ACR C | ACR D | Overall | |||||
| κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | |
| Reader 1/Reader 2 | 0.57 (0.37–0.77) |
Moderate | 0.69 (0.55–0.85) |
Strong | 0.40 (0.22–0.60) |
Fair | 0.66 (0.48–0.85) |
Strong | 0.67 (0.58–0.76) |
Strong |
| Reader 1/Consensus | 0.81 (0.66–0.97) |
Almost perfect | 0.79 (0.66–0.92) |
Almost perfect | 0.75 (0.61–0.91) |
Strong | 0.91 (0.82–1.00) |
Almost perfect | 0.87 (0.81–0.93) |
Almost perfect |
| Reader 2/Consensus | 0.76 (0.60–0.91) |
Strong | 0.90 (0.80–0.99) |
Almost perfect | 0.61 (0.47–0.80) |
Strong | 0.75 (0.60–0.92) |
Strong | 0.80 (0.73–0.88) |
Strong |
| dCNN/Consensus | 0.84 (0.70–0.97) |
Almost perfect | 0.81 (0.69–0.93) |
Strong | 0.87 (0.77–0.98) |
Almost perfect | 0.94 (0.86–1.00) |
Almost perfect | 0.91 (0.86–0.96) |
Almost perfect |
ACR, American College of Radiology; dCNN, deep convolutional neural network; MLO, medio-lateral oblique;
For the CC projections the agreement between Reader 1, Reader 2, and the dCNN compared to the consensus decision as ground truth ranged between “strong” {ACR D: Reader 2/Consensus [κ: 0.66 (95% CI: 0.43–0.89)]} and “almost perfect” {ACR A: Reader 2/Consensus [κ: 0.93 (95% CI: 0.85–1.00)]}. The inter rater agreement between both human readers ranged between “moderate” [κ: 0.5 (95% CI: 0.26–0.75)] for ACR D and “strong” for ACR A scored images [κ: 0.79 (95% CI: 0.64–0.95)]. With respect to the overall classification for both readers as well as the dCNN measured “almost perfect” agreement was measured, with κ ranging from 0.82 (dCNN) to 0.89 (Reader 2) (Figure 5B; Table 8).
Table 8.
Inter rater agreement for the CC projections for both readers and the dCNN compared to each other and to the consensus decision
| ACR A | ACR B | ACR C | ACR D | Overall | ||||||
| RCC Projections | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement | κ (95% CI) |
Agreement |
| Reader 1/Reader 2 | 0.79 (0.64–0.95) |
Strong | 0.69 (0.55–0.85) |
Strong | 0.62 (0.46–0.78) |
Strong | 0.50 (0.26–0.75) |
Moderate | 0.76 (0.68–0.85) |
Strong |
| Reader 1/Consensus | 0.86 0.72–0.99) |
Almost perfect | 0.79 (0.66–0.92) |
Almost perfect | 0.80 (0.68–0.93) |
Almost perfect | 0.85 (0.70–0.99) |
Almost perfect | 0.87 (0.81–0.94) |
Almost perfect |
| Reader 2/Consensus | 0.93 (0.85–1.00) |
Almost perfect | 0.90 (0.80–0.99) |
Almost perfect | 0.81 (0.69–0.93) |
Almost perfect | 0.66 (0.43–0.89) |
Strong | 0.89 (0.83–0.95) |
Almost perfect |
| dCNN/Consensus | 0.79 (0.65–0.94) |
Strong | 0.75 (0.61–0.89) |
Strong | 0.72 (0.58–0.87) |
Strong | 0.74 (0.58–0.90) |
Strong | 0.82 (0.75–0.89) |
Almost perfect |
ACR, American College of Radiology ; CC, cranio-caudal; dCNN, deep convolutional neural network;RCC, right craniocaudal;
Discussion
In the present study, we propose an automatic approach for determination of mammographic breast density according to the ACR BI-RADS catalog using a machine learning algorithm based on a deep convolutional neural network. The dCNN was trained with over 20,000 mammographies, which were successfully linked to the ACR BI-RADS density from the corresponding radiological report. For the implemented dCNN, an optimal number of 90–95 epochs was determined, reaching an average validation accuracy of 91%. In a real-world situation with mammographies acquired in our institution between November and December 2011, an accordance between radiological report and prediction of 71% was reached. A notably better accordance of 89–90% was found for the clinical relevant distinction between fatty and dense MD.
In the clinical routine, MD is qualitatively rated according to the ACR BI-RADS catalog on the basis of the radiologist’s subjective perception. Numerous studies demonstrated that breast density classification using the ACR four-category scale is observer-dependent with reported inter reader agreement ranging between 0.43 and 0.89.16–19 Intra reader comparability showed that experienced radiologists more robustly reproduce breast density assessments as compared to radiologists not routinely reading mammographies.20,21 Therefore, the accuracy of the trained dCNN presented in this study is in accordance with the expectations due to the inter reader variability of the real-world dataset labeling constituted by the radiological reports. Moreover, an average accuracy of 91% achieved by our dCNN can probably not be further improved, as the classification error was part of the provided training dataset and can be described as a systematic bias, which is forward-propagated to the learning routine of the dCNN. To overcome the problem of the intrinsically high inter reader variability in the assessment of the MD of the radiological reports, two experienced radiologists were requested to classify a second “real-world” test dataset. As compared to the consensus of the two experienced radiologists, the dCNN showed an excellent performance (MLO: 92.2%; CC: 87.4%). The robustness of the dCNN especially in the clinical relevant distinction between fatty and dense breast was confirmed with high accuracy (MLO: 99%; CC: 96%). Our results showed that while the dCNN performance is high for both projections, the two human readers have a slightly better agreement to the consensus for the CC projections as compared to the MLO (Table 6). The proposed dCNN provides an observer-independent, objective, and robust evaluation of MD. The training of the algorithm with the collective “wisdom” of the local institution database resulted in robust performances, which suggest that the algorithm may eliminate intra and inter reader variability.
The definition of a correct ground truth for the MD assessment is not a trivial issue. In this study, the performances of the dCNN were compared to the radiological reports of our institution and to the consensus of two experienced radiologists. Alternative methods for MD quantification have been proposed in the scientific literature. Those methods rely on the quantification of the percentage of the segmented areas of highest density on the mammographic image. Segmentation can be performed manually or be based on interactive thresholding.22 The first method is time consuming, labor intensive, and does not cover regions with inhomogeneous fibroglandular tissue, which can lead to significant inaccuracies. The second method relies on a semi-automated technique, where the observer interactively applies thresholding values on the mammography for assessment of fibroglandular tissue pixels. The amount of breast tissue is then calculated by dividing the semi-automated segmented area of fibroglandular tissue by the area of the entire breast. This approach is less time consuming but constitutes a semi-subjective method due to the required user input. Both methods did not find a use in the clinical routine also because they do not provide an equivalent for the broadly accepted ACR-based classification.10,23,24 A further drawback of those methods is that they provide an overall percentage of breast tissue, which may not reflect high-density parenchymal patterns in local areas of the breast.
In accordance to our results, Mohamed et al also recently showed that a dCNN algorithm can discriminate between categories B and C with an accuracy of 94% as compared to the radiological reports of the local institution. Classification accuracy was reported to increase up to 98%, when excluding image data of poorer quality.25 In our study a four-class classification was kept to comply the ACR BI-RADS classification. The algorithm was trained with data, whose quality reflects the clinical standard of our institution.
A main peculiarity of the algorithm is that the applied dCNN emulates the clinical workflow in decision making and can thus easily be integrated in the clinical routine for MD assessment according to the ACR BI-RADS catalog. The implementation of the proposed dCNN into the clinical workflow may reduce the subjectivity in the breast density classification leading to a reduction of falsely classified breast densities. Additionally, it may help standardization of decisions for follow-up diagnostic ultrasound simultaneously reducing morbidities and overall costs. Moreover, an objective evaluation of MD via artificial intelligence will allow for a more accurate calculation of the breast cancer risk in the individual patient and for large screening cohorts.26 Lastly, the proposed dCNN could serve as a quality control tool retrospectively applied to large numbers of mammographies. The obtained data could be used to characterize a screening cohort or to assess variability in breast density assessment between different centers.
Conclusion
In conclusion, we applied a dCNN trained on over 20,000 mammography projections, which allowed for accurate, standardized, and observer-independent classification of breast density according to the ACR BI-RADS catalog. The implementation of dCNN into the clinical workflow may help improving the diagnostic accuracy and reliability of mammographic breast density assessment in the clinical routine.
Footnotes
The authors Alexander Ciritsis and Cristina Rossi contributed equally to the work.
Contributor Information
Alexander Ciritsis, Email: alexander.ciritsis@usz.ch.
Cristina Rossi, Email: cristina.rossi@usz.ch.
Ilaria Vittoria De Martini, Email: ilaria.demartin@usz.ch.
Matthias Eberhard, Email: matthias.eberhard@usz.ch.
Magda Marcon, Email: magda.marcon@usz.ch.
Anton S. Becker, Email: anton.becker@usz.ch.
Nicole Berger, Email: nicole.berger@usz.ch.
Andreas Boss, Email: andreas.boss@usz.ch.
REFERENCES
- 1. Advani P, Moreno-Aspitia A. Current strategies for the prevention of breast cancer. Breast Cancer 2014; 6: 59–71. doi: 10.2147/BCTT.S39114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lee J, Nishikawa RM. Automated mammographic breast density estimation using a fully convolutional network. Med Phys 2018; 45: 1178–90. doi: 10.1002/mp.12763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kamangar F, Dores GM, Anderson WF. Patterns of cancer incidence, mortality, and prevalence across five continents: defining priorities to reduce cancer disparities in different geographic regions of the world. J Clin Oncol 2006; 24: 2137–50. doi: 10.1200/JCO.2005.05.2308 [DOI] [PubMed] [Google Scholar]
- 4. Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, et al. . Mammographic density and the risk and detection of breast cancer. N Engl J Med 2007; 356: 227–36. doi: 10.1056/NEJMoa062790 [DOI] [PubMed] [Google Scholar]
- 5. Lam PB, Vacek PM, Geller BM, Muss HB. The association of increased weight, body mass index, and tissue density with the risk of breast carcinoma in Vermont. Cancer 2000; 89: 369–75. doi: [DOI] [PubMed] [Google Scholar]
- 6. Burton A, Maskarinec G, Perez-Gomez B, Vachon C, Miao H, Lajous M, et al. . Mammographic density and ageing: a collaborative pooled analysis of cross-sectional data from 22 countries worldwide. PLoS Med 2017; 14: e1002335. doi: 10.1371/journal.pmed.1002335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Rice MS, Bertrand KA, Lajous M, Tamimi RM, Torres G, López-Ridaura R, et al. . Reproductive and lifestyle risk factors and mammographic density in Mexican women. Ann Epidemiol 2015; 25: 868–73. doi: 10.1016/j.annepidem.2015.08.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Boyd NF. Mammographic density and risk of breast cancer. Am Soc Clin Oncol Educ Book 2013; 33: e57–e62. doi: 10.1200/EdBook_AM.2013.33.e57 [DOI] [PubMed] [Google Scholar]
- 9. Berg WA, Blume JD, Cormack JB, Mendelson EB, Lehrer D, Böhm-Vélez M, et al. . Combined screening with ultrasound and mammography vs mammography alone in women at elevated risk of breast cancer. JAMA 2008; 299: 2151–63. doi: 10.1001/jama.299.18.2151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Melnikow J, Fenton JJ, Whitlock EP, Miglioretti DL, Weyrich MS, Thompson JH, et al. . Supplemental screening for breast cancer in women with dense breasts: a systematic review for the U.S. preventive services task force. Ann Intern Med 2016; 164: 268–78. doi: 10.7326/M15-1789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Nesterov Y. A method of solving a convex programming problem with convergence rate O (1/k2). Soviet Mathematics Doklady 1983; 27: 372–6. [Google Scholar]
- 12. Beleites C, Neugebauer U, Bocklitz T, Krafft C, Popp J. Sample size planning for classification models. Anal Chim Acta 2013; 760: 25–33. doi: 10.1016/j.aca.2012.11.007 [DOI] [PubMed] [Google Scholar]
- 13. Cohen J. Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit. Psychol Bull 1968; 70: 213–20. doi: 10.1037/h0026256 [DOI] [PubMed] [Google Scholar]
- 14. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics 1977; 33: 159–74. doi: 10.2307/2529310 [DOI] [PubMed] [Google Scholar]
- 15. DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988; 44: 837–45. doi: 10.2307/2531595 [DOI] [PubMed] [Google Scholar]
- 16. Ekpo EU, Ujong UP, Mello-Thoms C, McEntee MF. Assessment of interradiologist agreement regarding mammographic breast density classification using the fifth edition of the BI-RADS atlas. AJR Am J Roentgenol 2016; 206: 1119–23. doi: 10.2214/AJR.15.15049 [DOI] [PubMed] [Google Scholar]
- 17. Winkel RR, von Euler-Chelpin M, Nielsen M, Diao P, Nielsen MB, Uldall WY, et al. . Inter-observer agreement according to three methods of evaluating mammographic density and parenchymal pattern in a case control study: impact on relative risk of breast cancer. BMC Cancer 2015; 15: 274. doi: 10.1186/s12885-015-1256-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ciatto S, Bernardi D, Calabrese M, Durando M, Gentilini MA, Mariscotti G, et al. . A first evaluation of breast radiological density assessment by QUANTRA software as compared to visual classification. Breast 2012; 21: 503–6. doi: 10.1016/j.breast.2012.01.005 [DOI] [PubMed] [Google Scholar]
- 19. Berg WA, Campassi C, Langenberg P, Sexton MJ, Reporting BI. Breast Imaging Reporting and Data System: inter- and intraobserver variability in feature analysis and final assessment. AJR Am J Roentgenol 2000; 174: 1769–77. doi: 10.2214/ajr.174.6.1741769 [DOI] [PubMed] [Google Scholar]
- 20. Gard CC, Aiello Bowles EJ, Miglioretti DL, Taplin SH, Rutter CM. Misclassification of breast imaging reporting and data system (BI-RADS) mammographic density and implications for breast density reporting legislation. Breast J 2015; 21: 481–9. doi: 10.1111/tbj.12443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Lobbes MB, Cleutjens JP, Lima Passos V, Frotscher C, Lahaye MJ, Keymeulen KB, et al. . Density is in the eye of the beholder: visual versus semi-automated assessment of breast density on standard mammograms. Insights Imaging 2012; 3: 91–9. doi: 10.1007/s13244-011-0139-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kang E, Lee EJ, Jang M, Kim SM, Kim Y, Chun M, et al. . Reliability of computer-assisted breast density estimation: comparison of interactive thresholding, semiautomated, and fully automated methods. AJR Am J Roentgenol 2016; 207: 126–34. doi: 10.2214/AJR.15.15469 [DOI] [PubMed] [Google Scholar]
- 23. Harvey JA, Bovbjerg VE. Quantitative assessment of mammographic breast density: relationship with breast cancer risk. Radiology 2004; 230: 29–41. doi: 10.1148/radiol.2301020870 [DOI] [PubMed] [Google Scholar]
- 24. Kolb TM, Lichy J, Newhouse JH. Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: an analysis of 27,825 patient evaluations. Radiology 2002; 225: 165–75. doi: 10.1148/radiol.2251011667 [DOI] [PubMed] [Google Scholar]
- 25. Mohamed AA, Berg WA, Peng H, Luo Y, Jankowitz RC, Wu S. A deep learning method for classifying mammographic breast density categories. Med Phys 2018; 45: 314–21. doi: 10.1002/mp.12683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Mandelblatt JS, Stout NK, Schechter CB, van den Broek JJ, Miglioretti DL, Krapcho M, et al. . Collaborative modeling of the benefits and harms associated with different U.S. breast cancer screening strategies. Ann Intern Med 2016; 164: 215–25. doi: 10.7326/M15-1536 [DOI] [PMC free article] [PubMed] [Google Scholar]