Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2017 Dec 1;7(10):661–670. doi: 10.1089/brain.2017.0512

Data-Driven Topological Filtering Based on Orthogonal Minimal Spanning Trees: Application to Multigroup Magnetoencephalography Resting-State Connectivity

Stavros I Dimitriadis 1,,2,,3,,4,,5,✉, Marios Antonakakis 6, Panagiotis Simos 7,,8, Jack M Fletcher 9, Andrew C Papanicolaou 10,,11
PMCID: PMC6435350  PMID: 28891322

Abstract

In the present study, a novel data-driven topological filtering technique is introduced to derive the backbone of functional brain networks relying on orthogonal minimal spanning trees (OMSTs). The method aims to identify the essential functional connections to ensure optimal information flow via the objective criterion of global efficiency minus the cost of surviving connections. The OMST technique was applied to multichannel, resting-state neuromagnetic recordings from four groups of participants: healthy adults (n = 50), adults who have suffered mild traumatic brain injury (n = 30), typically developing children (n = 27), and reading-disabled children (n = 25). Weighted interactions between network nodes (sensors) were computed using an integrated approach of dominant intrinsic coupling modes based on two alternative metrics (symbolic mutual information and phase lag index), resulting in excellent discrimination of individual cases according to their group membership. Classification results using OMST-derived functional networks were clearly superior to results using either relative power spectrum features or functional networks derived through the conventional minimal spanning tree algorithm.

Keywords: : brain networks, network topology, optimization of information flow, resting state, topological filtering

Introduction

Neuronal populations generate oscillatory electrical activity as a result of complex neurophysiological processes taking place within individual neurons and across neuronal populations (Buzsáki, 2006; Buzsáki and Draguhn, 2004; Llinas, 2014). Such firing patterns can give rise to synchronized input to other cortical areas, supporting the interaction of a given assembly with more distant neuronal assemblies at the prominent oscillating frequency of the source population (Shew et al., 2009). It has been proposed that this cross-frequency coupling (CFC) promotes accurate timing between different oscillatory rhythms and dynamic control of distributed functional networks (Buzsáki, 2006; Canolty and Knight, 2010; Varela et al., 2001). Magnetoencephalography (MEG) is uniquely suited to address functional connectivity based on CFC because it possesses adequate temporal resolution to describe the real-time dynamics of fine-grained interactions between neuronal populations. There is rapidly accumulating experimental evidence supporting the role of CFC in cognition (Buzsáki and Watson, 2012; Canolty and Knight, 2010; Dimitriadis et al., 2015a, 2015c, 2016a, 2016b, 2016c, 2016d; Jirsa and Müller, 2013) and as a marker of neurophysiological dysfunction in developmental disorders such as reading disability (Dimitriadis et al., 2016b).

Neuronal interactions at the basic brain rhythms (Buzsáki, 2006) can be quantified through a variety of connectivity estimators, each featuring distinct advantages and limitations (Bastos and Schoffelen, 2016). The application of any type of connectivity estimator to a multichannel recording set leads to a fully connected graph containing a large proportion of potentially spurious connections. Identifying such spurious interactions requires statistical filtering (Aru et al., 2015). The most common approach toward this goal is through surrogate analysis that permits calculation of p-values associated with each interaction, which are then thresholded using an adaptive criterion, such as false discovery rate, to control for type I error.

Following statistical filtering, surviving interactions typically need to undergo spatial (topological) filtering to derive a network structure that contains only the essential interactions between nodes and is consequently more likely to be meaningful from a neuroscience perspective (Bullmore and Bassett, 2011; Van Wijk et al., 2010). Existing topological filtering approaches rely on largely arbitrary criteria, such as absolute weight threshold (e.g., >0.5), upper density limits (e.g., keeping the strongest 10% of connections), and mean graph degree (e.g., retaining connections so that the mean degree value is kept >5; Dimitriadis et al., 2010). A recent study explored the caveats of applying proportional thresholding on fMRI resting-state brain networks from clinical populations (van den Heuvel et al., 2017). The aforementioned observations highlight the need for data-driven topological filtering techniques. In principle, the latter may possess greater sensitivity to network features to serve as connectomic biomarkers for disorders such as Alzheimer's disease, schizophrenia, autism, and reading disability. Data-driven techniques are also crucial to ensure compatibility of results across laboratories and/or scanner types where absolute threshold criteria are not applicable (Abraham et al., 2017; Dansereau et al., 2017).

An increasingly popular, assumption-free method for identifying the essential set of connections within a fully connected graph is based on minimal spanning trees (MSTs) (Meier et al., 2015; Tewarie et al., 2015). More specifically, the MST connects all the N nodes in a graph through N−1 connections by minimizing the total cost of information flow and without introducing cycles. The method addresses crucial limitations of existing topological filtering schemes, which rely on absolute threshold or density and, additionally, preserves the connectedness of the brain network. However, the conventional MST approach typically results in trees with only N−1 links, which for large graphs are too sparse to allow reliable discrimination between two (Antonakakis et al., 2016; Dimitriadis et al., 2015c) or more groups (Khazaee et al., 2016). To address this problem, the orthogonal MST (OMST) approach was introduced (Dimitriadis et al., 2017) by utilizing alternative algorithms to construct the MST of a weighted graph (Kruskal, 1956; Prim, 1957). The OMST method preserves the main advantage of MST (i.e., assumption-free, data-driven approach that maintains network connectedness) and further ensures a denser and, potentially, more meaningful network. It is implemented by sampling connections over multiple rounds of MST to identify the subset of functional interactions that would ensure optimal information flow (indexed by network global efficiency [GE]) while minimizing the cost incurred by preserved functional connections. OMST has been used in pattern recognition and computer vision task as a reranking method (Fotopoulou et al., 2014). The superior performance of this topological filtering approach over several conventional filtering schemes has recently been demonstrated using large EEG and fMRI databases (Dimitriadis et al., 2017).

In the present work, we demonstrate the advantages of OMST as a topological filtering approach for sensor-level, resting-state neuromagnetic recordings. At the temporal scale characteristic of CFC, source localization (and related arbitrary choices of algorithms and anatomic templates) may introduce significant distortions to the source-level (reconstructed) signals. This added layer of complexity, although in principle desirable to enhance the anatomic relevance of results, would likely have confounded the primary goal of the study.

In addition to using OMST, a novel feature of the present work involves use of mutual information derived from symbolized time series (symbolic mutual information [SMI]) to quantify the strength of coupling between MEG sensors both within- and between-predefined frequency bands (i.e., CFC) (Robinson and Mandell, 2015). In this approach, neuromagnetic signals are first transformed into symbolic sequences consisting of a finite set of substrings (Janson et al., 2004). Signal complexity was assessed by the degree of repeatability of substring sequences over time using the symbolization procedure described in Dimitriadis et al. (2016a). The theoretical advantage of SMI lies in its capacity to represent each pair of time series as a set of two symbolic sequences utilizing a common set of symbols. SMI is a weighted connectivity estimator that describes interactions between any two signals in the form of the strength of linear and nonlinear functional associations (King et al., 2013; Robinson and Mandell, 2015). Being less susceptible to artifacts, SMI was chosen to handle MEG data from young children in the current study. Moreover, SMI was favored over delay transfer entropy, which may be more appropriate for source-level data (Roux et al., 2013). A more conventional connectivity estimator (phase lag index [PLI]) was also used to derive functional connectivity graphs (FCGs), which were submitted to the OMST-based topological filtering in a separate analysis.

Briefly, the analysis pipeline adopted in the present study involves the use of surrogate data sets to perform statistical filtering of functional connections, resulting in integrated functional brain networks featuring the dominant types of sensor interactions for each participant (Engel et al., 2013; Dimitriadis et al., 2016b). Such sparse networks were obtained independently for SMI and PLI and were subsequently filtered, topologically, using OMST. The sensitivity of this procedure to differences in resting-state brain connectivity attributed to participant age, presence of reading disability, and history of acute brain insult (mild traumatic brain injury [mTBI]) was assessed on a large data set consisting of four subgroups of participants: healthy adults (n = 50), adults who have suffered mTBI (n = 30), typically developing children (n = 27), and reading-disabled (RD) children (n = 25).

Materials and Methods

Participants

For the demonstration of the proposed algorithm, we used resting-state neuromagnetic recordings from four groups: healthy adults (n = 50; 31 women, aged: 33.5 ± 9.32 years with 15.4 ± 3.3 years of formal education), adults who had suffered mTBI (n = 30; 13 women, aged: 32.3 ± 9.9 years with 15.1 ± 2.9 years of formal education), typically developing children (n = 27; 15 girls, aged: 10.45 ± 2.6 years), and RD children (n = 25; 14 girls, aged: 11.05 ± 2.42 years). Resting-state data were collected as part of ongoing projects at the Magnetoencephalography Laboratory, University of Texas Health Science Center-Houston. Detailed information on participant characteristics can be found elsewhere (Antonakakis et al., 2016; Dimitriadis et al., 2013, 2015, 2016b).

Preprocessing

The MEG data underwent artifact reduction using MATLAB (The MathWorks, Inc., Natick, MA) and Fieldtrip (Oostenveld et al., 2011). Independent component analysis was used to separate cerebral from noncerebral activity using the extended infomax algorithm as implemented in EEGLAB (Delorme and Makeig, 2004). The data were whitened and reduced in dimensionality using principal component analysis with a threshold set to 95% of the total variance (Delorme and Makeig, 2004; Escudero et al., 2011). Kurtosis, Rényi entropy, and skewness values of each independent component were used to identify and remove ocular and cardiac artifacts. A given component was considered an artifact if, after normalization to zero mean and unit variance, more than 20% of its values were greater/lower than two SDs from the mean (Antonakakis et al., 2015, 2016; Dimitriadis et al., 2013, 2015b, 2015c; Escudero et al., 2011). To further ensure that independent components meeting the aforementioned criterion were indeed artifactual, we examined their time course and morphology (characteristic for cardiac and myogenic artifacts). In addition, source localization was performed using linearly constrained minimum variance beamformers (van Veen et al., 1997) to ensure that source locations at the magnetic field peak of each artifact were outside the brain.

Subsequently, the reconstructed axial gradiometer recordings were transformed into planar gradiometer field approximations using the sincos method implemented in Fieldtrip (Oostenveld et al., 2011). The data were finally bandpass-filtered in the following frequency ranges using a third-order Butterworth filter (in zero-phase mode): 0.5–4, 4–8, 8–10, 10–13, 13–15, 15–19, 20–29, and 30–45 Hz corresponding to δ, θ, α1, α2, β1, β2, β3, and γ bands.

Integrated FCGs

The strength of intra- and inter-frequency coupling for each pair of sensors was indexed by the undirected, weighted SMI (King et al., 2013; Robinson and Mandell, 2015). Initially, each pair of time series was transformed into two symbolic sequences utilizing a common set of symbols using the Neural Gas algorithm, which was first adapted to handle time series pairs (see the Common Symbolization Approach for Pairs of Magnetoencephalography Time Series section in Supplementary Data; Supplementary Data are available online at www.liebertpub.com/brain). Our group has demonstrated the utility and relative advantages of the Neural Gas algorithm in identifying dynamic functional graphs and introduced the notion of functional connectivity microstates (Dimitriadis et al., 2013). In addition, we have used the Neural Gas algorithm to symbolize pairs of time series and then estimate delay symbolic transfer entropy (Dimitriadis et al., 2016a). We have further demonstrated that the Neural Gas algorithm produced more stable results, which were proven more robust to various types of noise, compared to ordinal pattern analysis, a frequently used alternative method to symbolize time series.

SMI is defined as:

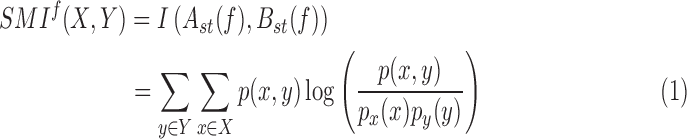graphic file with name eq1.gif

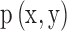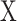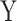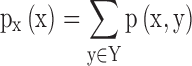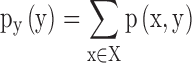where X = Ast and Y = Bst are the two symbolic sequences, Inline graphic is the joint probability distribution function of Inline graphic and Inline graphic, and Inline graphic and Inline graphic are the marginal probability distribution functions of X and Y, respectively. SMI values range between 0 and 1, with 0 denoting no functional coupling and 1 indicating perfect functional coupling over the entire recording period. This procedure resulted in a single FCG per participant, frequency band (8), and pair of frequency bands (28) consisting of SMI values.

Individual FCGs were submitted to statistical filtering using surrogate data to determine the dominant intrinsic coupling mode (DICM) for each pair of symbolic sequences (sensors). Ten thousand surrogate data sets were created by shuffling the symbolic sequence of the second MEG time series (Bst) in each pair (Ast, Bst) and re-estimated the SMI values. The concept of DICM is closely linked to the notion that although the specific frequencies and strengths of interactions between sensors may vary during the resting-state recording for a given participant, each sensor pair displays a typical (i.e., more temporally stable) mode of interaction, which can be identified via application of a conservative statistical criterion using surrogate data (Dimitriadis, 2016; Dimitriadis et al., 2016b, 2016d). In the present work, a p-value was assigned to each pair of symbolic sequences (same-frequency/between-sensor, cross-frequency/between-sensor, and cross-frequency/within-sensor pairs) reflecting the proportion of permutations that yielded surrogate SMI values higher than the observed SMI values. This procedure produced a three-dimensional (3D) tensor of p-values for each participant of size 36 × 248 × 248. Significant DICM(s) for each pair of symbolic sequences were determined by applying a Bonferroni-adjusted p < 0.01/36 = 0.00028 to control for family-wise Type I error. When more than one frequency or frequency pairs exceeded this threshold, the one associated with the lowest p-value was retained. This procedure resulted in two two-dimensional (2D) matrices for each participant of size 248 × 248: one containing the highest/statistically significant SMI values and the second the identity of the corresponding frequency or frequency pair (e.g., 1 for δ, 2 for θ, …, 8 for γ, 9 for δ-θ, …, 15 for δ-γ,…, 36 for β3-γ).

For comparison, FCGs were also constructed using a conventional connectivity metric, PLI (Stam et al., 2007), which is considered to be less susceptive to volume conduction (see the Dominant Coupling Modes Based on the Phase Lag Index section in Supplementary Data).

Topological filtering of FCGs using OMST

A crucial difference of the OMST algorithm from the conventional MST method is that the latter tends to preserve the weakest connections under the constraint of minimizing overall cost of connecting all the nodes in the graph. To address this limitation, FCGs were first inverted to emphasize the strongest connections corresponding to higher SMI values.

The proposed OMST algorithm was applied to the statistically thresholded FCGs, independently for each participant, as follows (Dimitriadis et al., 2017):

(1) The MSTs were extracted by iteratively applying Kruskal's algorithm on the inverted weighted FCGs containing the DICM for each pair of sensors.

(2) After extracting the first MST, which connects all the N sensors through N−1 edges, the N−1 edges were substituted with “Inf” in the original network to avoid capturing the same edges and also to maintain orthogonality with the next MST. Then, a second MST was estimated that connects all of the N sensors with minimal total distance, satisfying the constraint that it is orthogonal (i.e., does not share common edges) with the first MST. Next, the N−1 connections of the second MST were substituted with zeros and a third MST was estimated that connected the sensors with the minimal total weight, subject to the constraint that it is orthogonal to the previous two constructed MSTs (first and second). In general, an mth-MST is orthogonal to all the previous (m−1)th MSTs, having exactly m(N−1) edges.

(3) Connections were aggregated across OMSTs (including the first) to optimize the function of GE minus Cost over Cost as described in more detail in (5) below. For instance, this step can aggregate 3 × (N−1) edges from the first three OMSTs plus the fourth OMST.

(4) For each added connection to the aggregated network, the objective function of global cost efficiency = GE-Cost was estimated, where Cost denotes the ratio of the total weight of the selected edges, over multiple iterations of OMST, divided by the total strength of the original fully weighted graph. The values of this formula range within the limits of an economical small-world network for healthy control participants (Bassett and Bullmore, 2006). The network that is considered functionally optimal is the one associated with the maximum value of the following quality formula:

graphic file with name eq7.gif

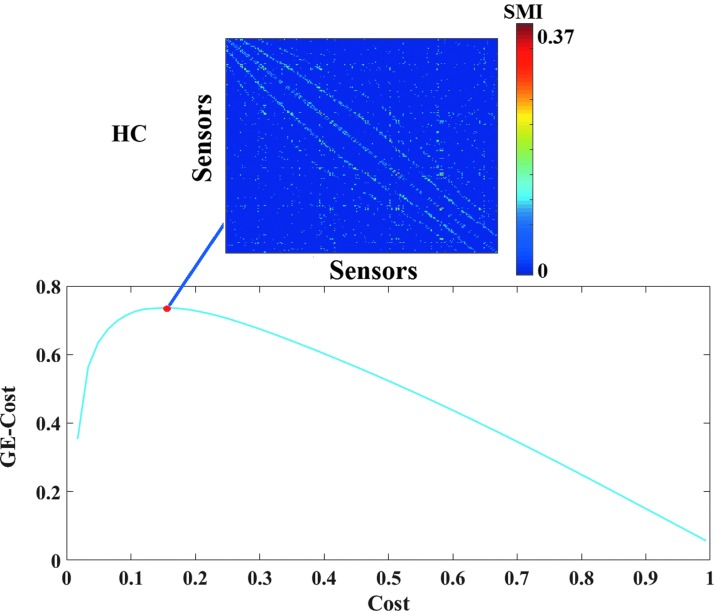
(5) Topological filtering on the subject-specific FCGs featuring the DICMs entailed retaining those sensor interactions that optimized the function of GE minus Cost over Cost. A sample plot of this function from a typical reader, obtained after running exhaustive OMSTs until all observed weights were tested, is shown in Figure 1. The maximum of this (always) positive curve reflects the optimization of the proposed OMST algorithm. In the example of Figure 1, the GE-Cost versus Cost function was optimized after 11 OMSTs leading to a selection of 2689 connections—a mere 8.9% of the total number of connections that were initially retained following statistical filtering.

FIG. 1.

FIG. 1.

Open in a new tab

Optimization of the function of GE minus Cost over Cost over multiple OMST runs in data from a typical reader. The red circle denotes the peak of the computed curve, while the resulting topologically filtered FCGs are shown in the inset. FCGs, functional connectivity graphs; GE, global efficiency; HC, typically developing children; SMI, symbolic mutual information. Color images available online at www.liebertpub.com/brain

Person-specific graph metrics of topologically filtered FCGs

Subject-specific, OMST-filtered FCGs were characterized using the following network metrics: GE, eccentricity, radius, and diameter. GE is the average inverse shortest path length in the network and is perhaps the most informative estimator of the integration of information flow within a network. Eccentricity is defined as the maximum shortest path length between a given sensor and any other sensor, whereas the radius and diameter correspond to the average and maximum eccentricity values across all sensors, respectively. Graph metrics selected for the present study represent the most widely used across imaging modalities and research questions (Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Stam, 2014; Telesford et al., 2011). Pairwise group comparisons on each network metric were performed using the Wilcoxon-rank sum test (evaluated at a conservative p < 0.0001).

Graph diffusion distance: a metric of group differences on network structure

To assess group differences in the OMST-filtered FCGs at the single-case level, we computed the graph diffusion distance (GDD) metric (Fouss et al., 2012; Hammond et al., 2013). The graph Laplacian operator of each subject-specific FCG was defined as L = D−FCG, where D is a diagonal degree matrix related to FCG. This method entails modeling hypothetical patterns of information flow among sensors based on each observed (static) FCG. The diffusion process on the person-specific FCG was allowed for a set time t; the quantity that underwent diffusion at each time point is represented by the time-varying vector 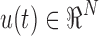Inline graphic. Thus, for a pair of sensors i and j, the quantity FCGij (ui(t)−uj(t)) represents the hypothetical flow of information from i to j via the edges that connect them (both directly and indirectly). Summing all these hypothetical interactions for each sensor leads to 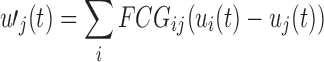Inline graphic, which can be written as follows:

graphic file with name eq10.gif

where L is the graph Laplacian of FCG. At time t = 0, Equation (2) has the analytic solution: 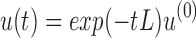Inline graphic Here exp(−tL) is an N × N matrix function of t, known as the Laplacian exponential diffusion kernel (Fouss et al., 2012), and u(0) = ej, where 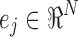Inline graphic is the unit vector with all zeros except in the jth component. Running the diffusion process through time t produced the diffusion pattern exp(−tL)ej corresponding to the jth column of exp(−tL).

Next, a metric of dissimilarity between every possible pair of person-specific diffusion-kernelized FCGs (FCG1, FCG2) was computed in the form of the graph diffusion distance dgdd(t). The higher the value of dgdd(t) between two graphs, the more distinct is their network topology as well as the corresponding, hypothetical information flow. The columns of the Laplacian exponential kernels, exp(−tL1) and exp(−tL2), describe distinct diffusion patterns, centered at two corresponding sensors within each FCG. The dgdd(t) function is searching for a diffusion time t that maximizes the Frobenius norm of the sum of squared differences between these patterns, summed over all sensors, and is computed as follows:

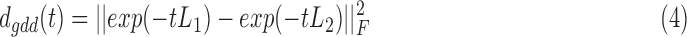graphic file with name eq13.gif

where 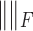Inline graphic is the Frobenius norm.

Given the spectral decomposition L = VΛV (V defines the eigenvectors and Λ the eigenvalues), the Laplacian exponential can be estimated via the following:

graphic file with name eq15.gif

where for Λ, exp(−tΛ) is diagonal to the ith entry given by 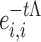Inline graphic. We computed dgdd(FCG1,FCG2) by first diagonalizing L1 and L2 and then applying Equations (3) and (4) to estimate dgdd(t) for each time point t of the diffusion process. In this manner, a single dissimilarity value was computed for each pair of participants based on their corresponding FCGs.

Group differences on relative spectral power

Relative power (RP) in each frequency band was examined as a lower level feature that could account for group differences in FCGs. Initially, statistical filtering was applied to the RP values obtained for each of 8 frequency bands (Fr) and 248 sensors (S) by first computing Laplacian scores (LSFr_S). The null distribution for each of the 1984 features was obtained through bootstrapping by randomizing the group identity labels assigned to each feature for 10,000 times and estimating the corresponding Laplacian scores. Next, we assessed deviations of the Laplacian score of each feature from the null distribution 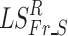Inline graphic and assigned a (one-sided) p-value as the percentage of observed 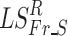Inline graphic exceeding the original estimated LSFr_S (evaluated at a Bonferroni-corrected p < 0.05/(8 × 248)).

Group separation and classification

A k-nearest neighbor classifier was used to assess the accuracy of assigning cases to each of the four study groups based on either the GDD metric derived from the OMST-filtered FCGs or the statistically filtered RP metrics. Results were obtained for two classification schemes to permit direct comparison with those obtained using the proposed OSMT-GDD scheme: (1) contrasting groups in a pairwise manner and (2) multigroup classification.

Finally, GDD values were projected to a common 3D space using multidimensional scaling, as a means of visualizing the level of similarity of individual cases (Borg and Groenen, 2005). The multidimensional scaling algorithm aims to place each case in N-dimensional space by preserving between-case distances. Each case was then assigned coordinates on each of a predetermined set of N dimensions (N = 3 in the present work).

Results

Group characteristics on topologically filtered FCGs

Typically achieving students showed higher eccentricity and radius values, as well as smaller diameter values than adult typical readers (Fig. 2). Moreover, RD children showed lower GE and higher eccentricity, radius, and diameter values than age-matched typical readers. Participants with a history of mTBI displayed higher diameter and lower eccentricity and higher GE and diameter values than healthy adults.

FIG. 2.

FIG. 2.

Open in a new tab

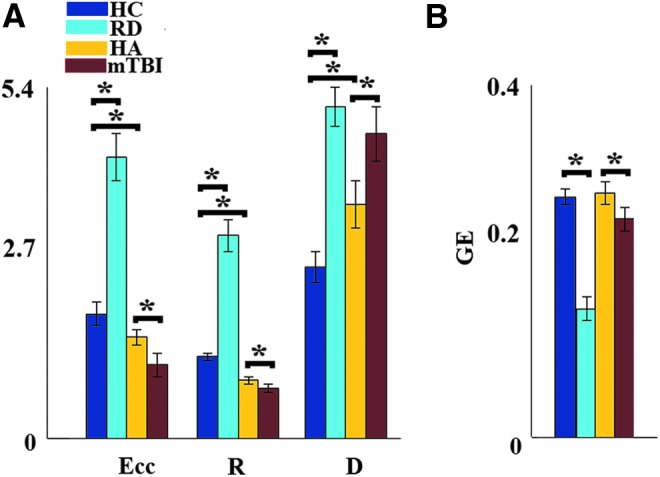
Group-averaged network metrics (Eccentricity, Radius, and Diameter in [A]; Global Efficiency in [B]) of the topologically filtered FCGs characterizing magnetoencephalography resting-state data. Brackets indicate significant pairwise group differences (*Wilcoxon rank sum test p < 0.0001). D, diameter; Ecc, eccentricity; GE, global efficiency; HA, healthy adults; HC, typically developing (healthy) children; mTBI, mild traumatic brain injury patients; R, radius; RD, reading-disabled children. Color images available online at www.liebertpub.com/brain

The reliability of OMST-derived network metrics was further assessed through split-half analyses, through which GE, eccentricity, radius, and diameter values were recomputed for each age- and gender-matched split-half sections of the four study groups. As shown in Supplementary Figure S2, average network metrics were very similar between split-half subgroups (p > 0.15 in all cases).

Group differences on OMST-derived network features

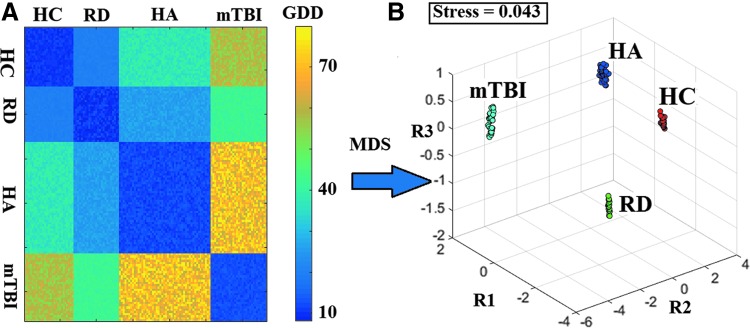
Applying dgdd(t) in a pairwise manner on subject-specific FCGs based on SMI across the 132 participants produced the dissimilarity matrix displayed in Figure 3A. The clear group separation was visualized by projecting individual GDD values onto a common 3D space following dimensionality reduction using multidimensional scaling (Fig. 3B). Classification accuracy reached 100% for both the pairwise and multigroup contrasts. As displayed in Supplementary Figure S1, similar results were obtained for the OMST-derived PLI-based FCGs.

FIG. 3.

FIG. 3.

Open in a new tab

Topological filtering of GDD values using OMST. (A) Dissimilarity matrix of subject-specific FCGs (N = 132) based on the GDD metric. (B) MDS was applied to the dissimilarity matrix of GDD values, which were rescaled and projected in a common three-dimensional space. Stress indicates the % loss of information due to the dimensionality reduction process via the MDS algorithm. GDD, graph diffusion distance; HA, healthy adults; HC, typically developing (healthy) children; MDS, multidimensional scaling; mTBI, mild traumatic brain injury patients; R1, R2, and R3 indicate the three predetermined dimensions used to plot participant cases through MDS; RD, reading-disabled children. Color images available online at www.liebertpub.com/brain

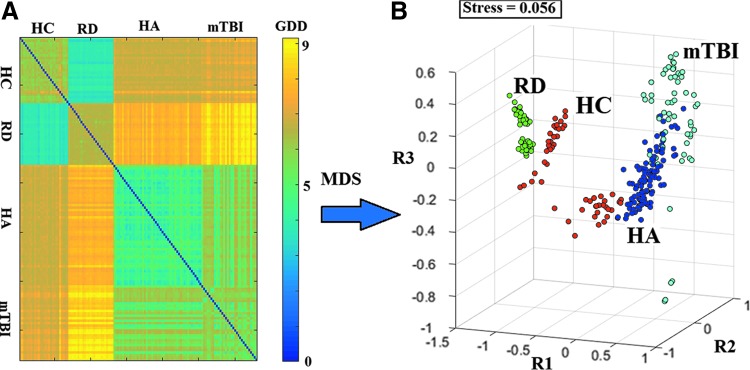
For comparison, we computed a dissimilarity matrix of Laplacian kernels using FCGs, which were subsequently topologically filtered through conventional MST (Tewarie et al., 2015). Results of multidimensional scaling displayed in Figure 4 reveal poor separation of individual cases especially among the healthy adult, mTBI, and typically achieving children. Classification accuracy did not exceed 45% for either the pairwise or the multigroup contrast.

FIG. 4.

FIG. 4.

Open in a new tab

Topological filtering of GDD values using conventional Minimal Spanning Tree. Dissimilarity matrix (A) and MDS results (B) for subject-specific FCGs (N = 132). All conventions are similar to those in Figure 3. Color images available online at www.liebertpub.com/brain

To further ensure that discrimination between healthy adults and adults with a history of mTBI was not confounded by differences in gender ratio between the two groups, the entire analysis was replicated on gender-matched subsets of the two groups (n = 44 and n = 28, respectively). Results presented in the OMST-Based Differences Between Age- and Gender-Matched Healthy Adults and mTBI Patients section of the Supplementary Data confirmed the superiority of topological filtering using OMST compared with conventional MST in deriving FCGs that clearly distinguish between the two clinical groups (see Figure S3).

Group differences on RP

Statistical filtering of RP features derived a total of 14 features that were used for contrasting nonimpaired and reading-disabled readers resulting in an average of 67.3% correct classification (Supplementary Table S1). Discrimination accuracy between nonimpaired readers (children) and healthy young adults averaged 62.3% using a total of 49 features. Similarly, discrimination accuracy between mTBI subjects and healthy young adults averaged 68.1% using a total of 11 features. Finally, the multigroup discrimination accuracy did not exceed 53.3% using a total of 48 features.

Group-specific dominant coupling modes

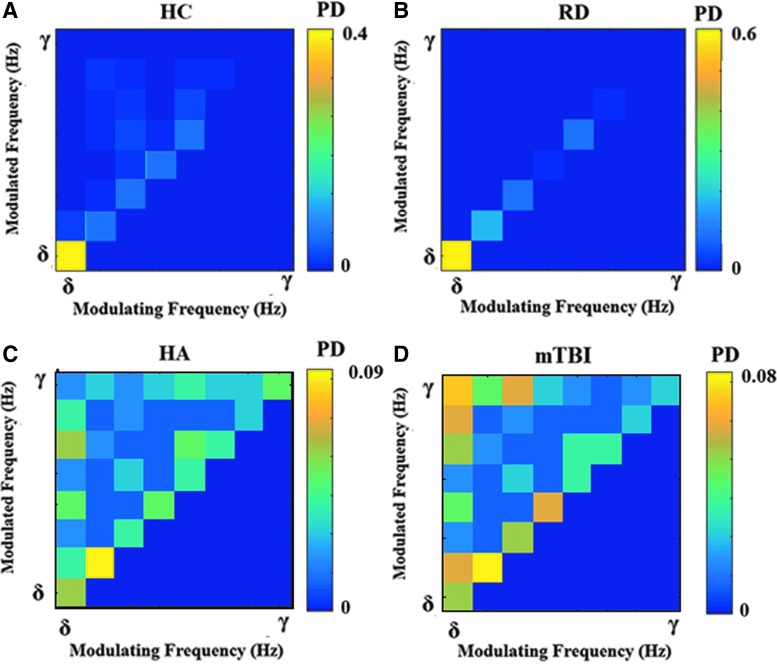
Characteristic dominant coupling modes, based on SMI, for each group of participants are displayed in the comodulograms of Figure 5. Each 2D matrix tabulates the probability distribution of functional connections associated with intrafrequency (diagonal cells) or interfrequency coupling (cells above the diagonal). A notable finding is the higher proportion of significant CFC modes among typically achieving students (12% compared with only 5% in the RD group). Conversely, the latter group showed slightly higher within-frequency DICMs in the θ, α1, and β1 bands compared to nonimpaired readers. Interestingly, both groups showed prominent DICMs in the δ band (Fig. 5A vs. B).

FIG. 5.

FIG. 5.

Open in a new tab

Group-averaged empirical probability distributions of dominant intrinsic coupling modes. Within-frequency coupling is shown in diagonal cells, whereas cross-frequency interactions are shown in the off-diagonal cells. HC, typically developing (healthy) children. (A); RD, reading-disabled children (B); HA, healthy adults (C); mTBI, mild traumatic brain injury patients (D). Color images available online at www.liebertpub.com/brain

Moreover, the comodulograms of both adult groups were characterized by substantially higher relative contributions of cross-frequency DICMs compared to groups of younger participants (with over 40% of DICMs representing cross-frequency interactions). Compared to healthy adults, participants with a history of mTBI displayed (1) prominent modulation of all higher frequency oscillations by δ frequencies and (2) more prominent within-frequency DICMs in the α1 and α2 bands.

Discussion

Topological filtering using OMST

The OMST algorithm was introduced in the present work as a convenient, data-driven, and computationally efficient method to perform topological filtering of a dense functional brain network. This method was introduced previously by our group to help identify the essential connections within a given network in a manner that optimizes information flow between every element (node) of the network while maintaining the functional/metabolic cost of connections at a minimum. Results from classification analyses on sensor-level MEG data from 132 participants confirmed the prediction that network metrics obtained from OMST-filtered networks would be sensitive to age- and diagnostic-group categories. Moreover, the superiority of OMST over the conventional MST approach, which is often too sparse to capture the most significant connections of a network, was unquestionable (100% vs. 45% classification accuracy in the multigroup analyses). The high classification accuracy based on the topologically filtered sensor networks via OMST underlines the effectiveness of this method to capture the most essential pathways of information flow within a given functional brain network. Robust group discrimination results were demonstrated for FCGs derived from two complementary types of interdependency metrics: within- and cross-frequency coupling (Dimitriadis, 2016; Dimitriadis et al., 2015a, 2016a, 2016b, 2016c, 2016d), as well as the PLI, which is considered to be less susceptible to volume conduction effects (Stam et al., 2007).

In the current application example, static sensor-level networks were analyzed, although the OMST method may be suitable for a variety of features (including dynamic metrics of MEG resting-state data, and also network metrics derived from task-related MEG recordings; Dimitriadis et al., 2017). The OMST method was supplemented by estimation of the diffusion distance metric (GDD), bearing distinct advantages over traditional approaches used to derive person-specific FCGs, which rely on either unstructured data or vectors. In contrast, the diffusion distance metric was designed to identify systematic individual differences in functional brain networks, associated with distinct patterns of modeled information flow (Dimitriadis et al., 2015b). The GDD metric substituted Euclidean distance in a k-nearest neighbor classifier as a more appropriate distance metric that respects the 2D format of the FCG.

Developmental and clinical correlates of OMST-derived functional networks

Although the present findings were based on sensor-level data, limiting their anatomic interpretability, the fact that we used planar-gradiometer neuromagnetic data to estimate patterns of within- and cross-frequency modes permits tentative conclusions regarding certain apparent features of underlying brain networks at rest. At a global network level, participants with a history of developmental (RD) or acute brain damage (mTBI) demonstrated lower GE and higher diameter indices compared to typically achieving students and healthy adults, respectively (Fig. 2) (Antonakakis et al., 2016; Dimitriadis et al., 2013, 2016b, 2015c). This finding is consistent with less efficient information flow during rest (at least at the sensor level) in both clinical groups compared to their age-matched typical/healthy counterparts. Compared to both student groups, adult comodulograms were also characterized by substantially higher proportions of cross-frequency interactions (40% and 45%, for young adults and mTBI patients, respectively). This finding is in accordance with the proposed trend toward more complex communication modes between remotely located neuronal assemblies with development (Basar and Duzgun, 2016; Buzsáki and Watson, 2012; Deco et al., 2017; Stamoulis et al., 2015). Interestingly, students who experienced severe reading difficulties in the present study were even less likely to display CFC modes at rest (5% of the total DICMs compared to 12% among age-matched typical readers).

Moreover, history of mTBI was associated with a higher proportion of cross-frequency interactions involving δ modulating oscillators, in agreement with a recent report of abnormalities in functional brain networks in δ frequencies in mTBI (Dunkley et al., 2015).

Limitations and future directions

The present study has several noteworthy limitations. First, static networks were analyzed, although the OMST method is suitable for a variety of features (including dynamic metrics of MEG resting-state data, and also network metrics derived from task-related MEG recordings). Second, connectivity patterns reflecting CFC were explored at the sensor level. At this temporal scale, source localization (and related arbitrary choices of algorithms and anatomic templates) may introduce significant distortions to the source-level (reconstructed) signals. This added layer of complexity, although in principle desirable for enhancing the anatomic relevance of results, would very likely have confounded the primary goal of the study, namely to assess the capacity of OMST as a data-driven technique to derive sufficiently sparse graphs, which could, in turn, reliably differentiate between age- and clinical diagnosis groups of participants. Third, the presently applied OMST did not take into account the actual anatomic distance between sensors. Especially when applied to source-level data, this feature may enhance the sensitivity of the technique to explore functional cortical networks and can be aided by DTI-tractography data. Finally, independent assessment of the performance of the proposed algorithms and analysis pipeline on a new sample that includes both healthy participants and clinical groups is paramount to establish their generalizability.

Conclusions

Orthogonal spanning trees are a promising method to identify important features (connections) of densely interconnected functional networks as represented by both conventional (PLI) and novel connectivity metrics (SMI). Integrating OMST-based network analyses with the notion of dominant coupling modes can offer complementary information regarding functional changes in the resting connectivity during the course of human development and also in relation to both developmental disorders and acute brain insults.

Supplementary Material

Supplemental data
Supp_Data.pdf (320.6KB, pdf)

Acknowledgments

This research was supported, in part, by grant P50 HD052117 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NICHD or the National Institutes of Health. S.I.D. was supported, in part, by MRC grant MR/K004360/1 (Behavioural and Neurophysiological Effects of Schizophrenia Risk Genes: A Multi-locus, Pathway Based Approach) and by a MARIE-CURIE COFUND EU-UK FELLOWSHIP.

Notes

The MATLAB code to implement OMST and the analysis pipeline described in this work is accessible at researchgate (https://www.researchgate.net/profile/Stavros_Dimitriadis), personal website (http://users.auth.gr/∼stdimitr/software.html), and github (https://github.com/stdimitr/multi-group-analysis-OMST-GDD).

Author Disclosure Statement

No competing financial interests exist.

References

  1. Abraham A, Milham M, Di Martino A, Craddock RC, Samaras D, Thirion B, Varoquaux G. 2017. Deriving reproducible biomarkers from multi-site resting-state data: an autism-based example. Neuroimage 147:736–745 [DOI] [PubMed] [Google Scholar]
  2. Antonakakis M, Dimitriadis SI, Zervakis M, Micheloyannis S, Rezaie R, Babajani-Feremi A, et al. . 2016. Altered cross-frequency coupling in resting-state MEG after mild traumatic brain injury. Int J Psychophysiol 102:1–11 [DOI] [PubMed] [Google Scholar]
  3. Antonakakis M, Dimitriadis SI, Zervakis M, Rezaie R, Babajani-Feremi A, Micheloyannis S, et al. . 2015. Comparison of Brain Network Models Using Cross-Frequency Coupling and Attack Strategies. In Proceedings of the 37th Annual International Conference of IEEE EMBS, Milan, Italy, pp. 7426–7429 [DOI] [PubMed] [Google Scholar]
  4. Aru J, Priesemann V, Wibral M, Lana L, Pipa G, Singer W, Vicente R. 2015. Untangling cross-frequency coupling in neuroscience. Curr Opin Neurobiol 31:51–61 [DOI] [PubMed] [Google Scholar]
  5. Basar E, Duzgun A. 2016. The CLAIR model: extension of Brodmann areas based on brain oscillations and connectivity. Int J Psychophysiol 103:185–198 [DOI] [PubMed] [Google Scholar]
  6. Bassett DS, Bullmore E. 2006. Small-world brain networks. Neuroscientist 12:512–523 [DOI] [PubMed] [Google Scholar]
  7. Bastos AM, Schoffelen JM. 2016. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front Syst Neurosci 9:175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Borg I, Groenen P. 2005. Modern Multidimensional Scaling: Theory and Applications, 2nd ed. New York: Springer-Verlag; pp. 207–212 [Google Scholar]
  9. Bullmore ET, Bassett DS. 2011. Brain graphs: graphical models of the human brain connectome. Annu Rev Clin Psychol 7:113–140 [DOI] [PubMed] [Google Scholar]
  10. Bullmore ET, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198 [DOI] [PubMed] [Google Scholar]
  11. Buzsáki G. 2006. Rhythms of the Brain. New York, NY: Oxford University Press [Google Scholar]
  12. Buzsáki G, Draguhn A. 2004. Neuronal oscillations in cortical networks. Science 304:1926–1929 [DOI] [PubMed] [Google Scholar]
  13. Buzsáki G, Watson BO. 2012. Brain rhythms and neural syntax: implications for efficient coding of cognitive content and neuropsychiatric disease. Dialogues Clin Neurosci 14:345–367 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Canolty RT, Knight RT. 2010. The functional role of cross-frequency coupling. Trends Cogn Sci 14:506–515 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dansereau C, Benhajali Y, Risterucci C, Pich EM, Orban P, Arnold D, Bellec P. 2017. Statistical power and prediction accuracy in multisite resting-state fMRI connectivity. Neuroimage 149:220–232 [DOI] [PubMed] [Google Scholar]
  16. Deco G, Cabral J, Woolrich M, Stevner AB, van Hartevelt TJ, Kringelbach M. 2017. Single or multi-frequency generators in on-going brain activity: a mechanistic whole-brain model of empirical MEG data. Neuroimage 152:538–550 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Delorme A, Makeig S. 2004. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods 134:9–21 [DOI] [PubMed] [Google Scholar]
  18. Dimitriadis S, Sun Y, Laskaris N, Thakor N, Bezerianos A. 2016a. Revealing cross-frequency causal interactions during a mental arithmetic task through symbolic transfer entropy: a novel vector-quantization approach. IEEE Trans Neural Syst Rehabil Eng 24:1017–1028 [DOI] [PubMed] [Google Scholar]
  19. Dimitriadis SI. 2016. Combining Intra and Inter-Frequency Dominant Coupling Modes into a single Dynamic Functional Connectivity Graph: Dynome, Dyconnectomics and Oscillopathies. 20th International Conference on Biomagnetism, Seoul, Korea [Google Scholar]
  20. Dimitriadis SI, Laskaris NA, Bitzidou MP, Tarnanas I, Tsolaki MN. 2015a. A novel biomarker of amnestic MCI based on dynamic cross-frequency coupling patterns during cognitive brain responses. Front Neurosci 9:350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Dimitriadis SI, Laskaris NA, Simos PG, Fletcher JM, Papanicolaou AC. 2016b. Greater repertoire and temporal variability of cross-frequency coupling (CFC) modes in resting-state neuromagnetic recordings among children with reading difficulties. Front Hum Neurosci 10:163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dimitriadis SI, Laskaris NA, Simos PG, Micheloyannis S, Fletcher JM, Rezaie R, Papanicolaou AC. 2013. Altered temporal correlations in resting-state connectivity fluctuations in children with reading difficulties detected via MEG. NeuroImage 83:307–31 [DOI] [PubMed] [Google Scholar]
  23. Dimitriadis SI, Laskaris NA, Tsirka V, Vourkas M, Micheloyannis S, Fotopoulos S. 2010. Tracking brain dynamics via time-dependent network analysis. J Neurosci Methods 193:145–155 [DOI] [PubMed] [Google Scholar]
  24. Dimitriadis SI, Sallis C, Tarnanas I, Linden DE. 2017. topological filtering of dynamic functional brain networks unfolds informative chronnectomics: a novel data-driven thresholding scheme based on orthogonal minimal spanning trees (OMSTs). Front Neuroinform 11:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Dimitriadis SI, Sun Y, Kwok K, Laskaris NA, Thakor N, Bezerianos A. 2015b. Cognitive workload assessment based on the tensorial treatment of EEG estimates of cross-frequency phase interactions. Ann Biomed Eng 43:977–89 [DOI] [PubMed] [Google Scholar]
  26. Dimitriadis SI, Sun Y, Thakor NV, Bezerianos A. 2016c. Causal interactions between frontalθ–parieto-occipitalα2 predict performance on a mental arithmetic task. Front Hum Neurosci 10:454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dimitriadis SI, Tarnanas I, Wiederholdg M, Wiederholdh B, Tsolaki M, Fleish E. 2016d. Mnemonic strategy training of the elderly at risk for dementia enhances integration of information processing via cross-frequency coupling. Alzheimers Dement 2:241–249 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Dimitriadis SI, Zouridakis G, Rezaie R, Babajani-Feremi A, Papanicolaou AC. 2015c. Functional connectivity changes detected with magnetoencephalography after mild traumatic brain injury. Neuroimage Clin 9:519–531 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Dunkley BT, Da Costa L, Bethune A, Jetly R, Pang EW, Taylor MJ, Doesburg SM. 2015. Low-frequency connectivity is associated with mild traumatic brain injury. Neuroimage Clin 7:611–621 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Engel AK. 2013. Intrinsic coupling modes: multiscale interactions in ongoing brain activity. Neuron 80:867–886 [DOI] [PubMed] [Google Scholar]
  31. Escudero J, Hornero R, Abásolo D, Fernández A. 2011. Quantitative evaluation of artifact removal in real magnetoencephalogram signals with blind source separation. Ann Biomed Eng 39:2274–2286 [DOI] [PubMed] [Google Scholar]
  32. Fotopoulou F, Economou G. 2014. Graph Based Re-ranking Method with Application to Handwritten Digits. 14th International Conference on Frontiers in Handwriting Recognition (ICFHR), Herakleion, Greece DOI: 10.1109/ICFHR.2014.131 [DOI] [Google Scholar]
  33. Fouss F, Francoisse K, Yen L, Pirotte A, Saerens M. 2012. An experimental investigation of kernels on graphs for collaborative recommendation and semisupervised classification. Neural Netw 31:53–72 [DOI] [PubMed] [Google Scholar]
  34. Hammond D, Gur Y, Johnson C. 2013. Graph Diffusion Distance: A Difference Measure for Weighted Graphs Based on the Graph Laplacian Exponential Kernel. In Proceedings of IEEE GlobalSIP, Austin, TX, p. 419 [Google Scholar]
  35. Janson S, Lonardi S, Szpankowski W. 2004. On average sequence complexity. Theor Comput Sci 326:213–227 [Google Scholar]
  36. Jirsa V, Müller V. 2013. Cross-frequency coupling in real and virtual brain networks. Front Comput Neurosci 7:78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Khazaee A, Ata Ebrahimzadeh A, Babajani-Feremi A. 2016. Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI. Behav Brain Res 322:339–350 [DOI] [PubMed] [Google Scholar]
  38. King JR, Sitt JD, Faugeras F, Rohaut B, El Karoui I, Cohen L, et al. . 2013. Information sharing in the brain indexes consciousness in noncommunicative patients. Curr Biol 23:1914–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kruskal JB. 1956. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc Am Math Soc 7:48–50 [Google Scholar]
  40. Llinas RR. 2014. Intrinsic electrical properties of mammalian neurons and CNS function: a historical perspective. Front Cell Neurosci. 8:320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Meier J, Tewarie P, Van Mieghem PF. 2015. The union of shortest path trees of functional brain networks. Brain Connect 5:575–81 [DOI] [PubMed] [Google Scholar]
  42. Oostenveld R, Fries P, Maris E, Schoffelen 2011. FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011:e156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Prim RC. 1957. Shortest connection networks and some generalizations. Bell Syst Tech J 36: 1389–1401 [Google Scholar]
  44. Robinson SE, Mandell AJ. 2015. Mutual information in a MEG complexity measure suggests regional hyper-connectivity in schizophrenic probands. Neuropsychopharmacology 40:251–252 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Roux F, Wibral M, Singer W, Aru J, Uhlhaas PJ. 2013. The phase of thalamic alpha activity modulates cortical gamma-band activity: evidence from resting-state MEG recordings. J Neurosci 33:17827–17835 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Rubinov M, Sporns O. 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52:1059–1069 [DOI] [PubMed] [Google Scholar]
  47. Shew WL, Yang H, Petermann T, Roy R, Plenz D. 2009. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J Neurosci 29:15595–15600 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Stam CJ. 2014. Modern network science of neurological disorders. Nat Rev Neurosci 15:683–695 [DOI] [PubMed] [Google Scholar]
  49. Stam CJ, Nolte G, Daffertshofer A. 2007. Phase lag index: assessment of functional connectivity from multichannel EEG and MEG with diminished bias from common sources. Hum Brain Mapp 28:1178–1193 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Stamoulis C, Vanderwert RE, Zeanah CH, Fox NA, Nelson CA. 2015. Early psychosocial neglect adversely impacts developmental trajectories of brain oscillations and their interactions. J Cogn Neurosci 27:2512–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Telesford Q, Simpson SL, Burdette JH, Hayasaka S, laurienti PJ. 2011. The brain as a complex system: using network science as a tool for understanding the brain. Brain Connect 1:295–308 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Tewarie P, van Dellen E, Hillebrand A, Stam CJ. 2015. The minimum spanning tree: an unbiased method for brain network analysis. Neuroimage 104:177–88 [DOI] [PubMed] [Google Scholar]
  53. van den Heuvel MP, de Lange SC, Zalesky A, Seguin C, Yeo BT, Schmidt R. 2017. Proportional thresholding in resting-state fMRI functional connectivity networks and consequences for patient-control connectome studies: issues and recommendations. Neuroimage 152:437–449 [DOI] [PubMed] [Google Scholar]
  54. Van Veen BD, van Drongelen W, Yuchtman M, Suzuki A. 1997. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans Biomed Eng 44:867–880 [DOI] [PubMed] [Google Scholar]
  55. Van Wijk BC, Stam CJ, Daffertshofer A. 2010. Comparing brain networks of different size and connectivity density using graph theory. PLoS One 5:e13701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Varela F, Lachaux JP, Rodriguez E, Martinerie J. 2001. The brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci 2:229–239 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Data.pdf (320.6KB, pdf)

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES