Dependence of the Magnetic Resonance Signal on the Magnetic Susceptibility of Blood Studied with Models Based on Real Microvascular Networks

Abstract

PURPOSE:

The primary goal of this study was to estimate the value of β, the exponent in the power law relating changes of the transverse relaxation rate and intra-extravascular local magnetic susceptibility differences as $\mathrm{\Delta }{R}_2{}^{*}\propto {\left(\mathrm{\Delta }\chi \right)}^{\beta }$. The secondary objective was to evaluate any differences that might exist in the value of β obtained using a deoxyhemoglobin-weighted $\mathrm{\Delta }\chi$ distribution versus a constant $\mathrm{\Delta }\chi$ distribution assumed in earlier computations. The third objective was to estimate the value of β relevant for methods based on susceptibility contrast agents with a concentration of $\mathrm{\Delta }\chi$ higher than that used for BOLD fMRI calculations.

METHODS:

Our recently developed model of real microvascular anatomical networks is utilized to extend the original simplified Monte-Carlo simulations to compute $\beta$ from first principles.

RESULTS:

Our results show that $\beta =1$ for most BOLD fMRI measurements of real vascular networks as opposed to earlier predictions of $\beta =1.5$ using uniform $\mathrm{\Delta }\chi$ distributions. For perfusion or functional MRI methods based on contrast agents, which generate larger values for $\mathrm{\Delta }\chi$, $\beta =1$ for $B_0\le 9.4\text{T}$, while at 14 T $\beta$ can drop below 1 and the variation across subjects is large, which indicates that a lower concentration of contrast agent with a lower value of $\mathrm{\Delta }\chi$ is desired for experiments at high $B_0$.

CONCLUSION:

These results improve our understanding of the relationship between R₂* and the underlying microvascular properties. The findings will help to infer the cerebral metabolic rate of oxygen (CMRO₂) and cerebral blood volume (CBV) from BOLD and perfusion MRI respectively.

Introduction

The transverse relaxation rate, $R_2{}^{*}$ of the MR signal is related to the dephasing rate of protons within an imaging voxel, which is sensitive to magnetic susceptibility-induced changes in the local magnetic field, $\mathrm{\Delta }B$. One way to alter the magnetic susceptibility is to use exogenous agents such as gadolinium-based contrast agents (GBCAs), delivered as a bolus injection as in the dynamic susceptibility contrast (DSC) technique, or blood-pool contrast agents such as ultrasmall superparamagnetic iron oxide (USPIO) agents that have long plasma half-lives (1–4). The increase of the transverse relaxation rate $\mathrm{\Delta }{R}_2{}^{*}$ in response to contrast agent injection is a measure of cerebral blood volume (CBV) since $\mathrm{\Delta }{R}_2{}^{*}\propto \text{CBV}\cdot \mathrm{\Delta }{\chi }^{\beta }$ (5), where $\mathrm{\Delta }\chi$ is the magnetic susceptibility difference between blood and tissue and $\beta$ is a parameter in the power law model of the susceptibility effect. In many cases, $\beta$ is assumed to be 1 and the relation is simplified as $\mathrm{\Delta }{R}_2{}^{*}\propto CBV\cdot \mathrm{\Delta }\chi$.

Deoxyhemoglobin is another agent that can alter local magnetic susceptibility, because it is paramagnetic and its presence decreases the MR signal (6,7). This endogenous agent provides a link between the MR signal and neuronal activity (8–11). The blood oxygenation level-dependent (BOLD) signal is a complicated function of several underlying physiological variables including cerebral blood flow (CBF), cerebral metabolic rate of oxygen (CMRO₂) and CBV. The Davis model of calibrated fMRI describes the BOLD signal change during activation as $\delta BOLD=M\left(1-rCMR{O}_2^{\beta }\cdot rCB{F}^{\alpha -\beta }\right)$, where rCBF and rCMRO₂ are the relative changes in CBF and CMRO₂ normalized by their baseline values (12). Here, M is a normalization factor that can be obtained from hypercapnia or hyperoxia calibration techniques, and α is the exponent in the flow-volume relation rCBV = rCBF^α (12–15). The parameter $\beta$ in the original Davis model has the same physiological meaning as in the susceptibility effect, i.e., $\mathrm{\Delta }{R}_2{}^{*}\propto \mathrm{\Delta }{\chi }^{\beta }$. With these parameters identified, the Davis model provides a method to obtain rCMRO₂ during neuronal activation from a combination of BOLD measurements and CBF measurements, with the latter typically acquired using arterial spin labelling (16,17).

The value of the parameter $\beta$ was originally estimated using Monte-Carlo simulations of proton diffusion through random distributions of infinite cylinders, and the resulting value was found to be 1.5 at $B_0=1.5\text{T}$ (5). The main source that gives rise to a non-linear susceptibility effect $\beta \ne 1$, is extra-vascular proton diffusion. For large vessels such as veins, proton diffusion can be ignored and the static dephasing calculations give $\beta =1$, while for small vessels where diffusion is prominent, $\beta =2$ (11,18,19). It is important to note that the motional narrowing effect of diffusion around small vessels leads to the same amount of deoxyhemoglobin having a weaker effect on the BOLD signal compared to larger veins (20). In addition, the cylinders models (5) are simplified versions of a real vascular network where the more complicated structures, such as vessel curvature and bifurcations, found in anatomical vascular networks, are not considered and the size distribution of vessels are not necessarily modeled. More importantly, unlike exogenous contrast agents, the concentration of deoxyhemoglobin is not uniform throughout the vascular network, and instead there is a gradient of deoxyhemoglobin concentration from the arterial side to the venous side of the vascular network. Thus the value of $\beta$, particularly in the Davis model for fMRI, needs a more comprehensive investigation.

In vivo experiments in humans have found that $\beta =1$ in calibrated BOLD experiments at 1.5, 3, and 7 T (21), consistent with recent multi-compartment vascular modeling studies that suggest $\beta =1$ at 3 T (22,23). These vascular modeling studies estimated β and α indirectly by treating them as free parameters of the Davis model in simulations of the BOLD signals. However, these studies have abandoned the physiological meanings of the parameters and did not explicitly determine β through relating ΔR₂* directly to Δχ. In the present study, we obtain the value of β from first-principles by performing calculations using real microvascular networks, obtained using in vivo two-photon measurements in the cerebral cortex of mice, for both deoxyhemoglobin-weighted and uniform Δχ distributions with the concentration range relevant for BOLD fMRI. We find that the value of β decreases with magnetic field strength $B_0$. At lower field strengths, β depends on the details of the vasculature and can vary across subjects and regions for a uniform distribution of Δχ. However, β=1 for most BOLD fMRI measurements at $B_0\ge 3T$ where Δχ is weighted by deoxyhemoglobin concentration, which is a more realistic assumption for the BOLD signals. Setting β=1 greatly simplifies macroscopic models such as the Davis model (12). In addition, the value of β has also been computed with a uniform distribution of Δχ at a higher concentration relevant for perfusion or functional imaging based on contrast agents. For imaging based on contrast agents, $\beta =1$ for $B_0\le 9.4T$, while at 14 T $\beta$ drops below 1 and the variation across subjects is large, which indicates that a lower concentration of $\mathrm{\Delta }\chi$ is desired for experiments at high $B_0$.

Methods

Microvascular network and Vascular Anatomical Network (VAN) modeling

The microvascular networks used here were obtained using in vivo 2-photon imaging of the cerebral cortex of C57BL/6 mice and published in previous studies (23,24). We used six unique microvascular networks obtained from six different mice. The VAN model was then applied to these vascular networks. The VAN model is a bottom-up model that computes blood flow and oxygenation distributions within microscopic vasculature and the resulting MR signal (23,24). The steady-state oxygen distribution is obtained by solving the advection-diffusion equation until it reaches equilibrium (25,26). After the deoxyhemoglobin distribution is computed from the oxygen distribution, the MR signal $S\left(t\right)$ can be obtained from Monte-Carlo simulations of proton diffusion through inhomogeneous magnetic fields.

The magnetic field experienced by a proton is the sum of the magnetic field perturbations produced by all of the vessels in the VAN, each with a magnetic susceptibility $\text{Δ}\chi$. We model BOLD in which case $\text{Δ}\chi$ is given by the deoxyhemoglobin content of each vessel, compared to a constant $\text{Δ}\chi$ distrubution across vessels. The magnetic field inhomogeneity $\text{Δ}B\left(\overrightarrow{x}\right)$ is computed by convolving $\mathrm{\Delta }\chi$ with the magnetic field induced by a unit cube $\text{Δ}{B}_{cube}=\frac{\left(\frac{2}{\pi }\right)a^3}{r^3}\left(3co{s}^2\theta -1\right)B_0$, where $a$ is the grid size (1 μm) and r and $\theta$ are polar coordinates. The phase accumulation of the nth proton is $\text{Δ}{\varphi }_n\left(t\right)=\text{γΔ}{B}_n\left(t\right)\text{Δ}t$, with $\gamma =2.675\times {10}^5$ rad/T/ms=$2.675\times {10}^8$ rad/T/s being the gyromagnetic ratio and $\text{Δ}{B}_n\left(t\right)$ is the local magnetic field perturbation experienced by the nth proton at time t. The initial positions of $1\times {10}^7$ protons within the VAN voxel are random and drawn from a uniform distribution. The diffusion coefficient of protons is set to be $1\times {10}^{-5}$ cm²/s=$1\times {10}^{-9}$ m²/s (23,27), and protons are not allowed to diffuse across the vessel wall. The time step for Monte-Carlo simulations is dt=0.2 ms=$2\times {10}^{-4}$ $\text{s}$ and the echo time TE=30 ms =$3\times {10}^{-2}$ $\text{s}$. A smaller time step of $dt=0.01ms$ is used for large $B_0\ge 9.4T$ and $\mathrm{\Delta }\chi ~1-10\times {10}^6$ as explained in Supporting Information S3. The MR signal at each time step is $S\left(t\right)=Re\left\{\frac{1}{N}\sum _{n=1}^N{e}^{{\varphi }_n\left(t\right)}\right\}$, where the intravascular contribution is ${\varphi }_{n,intra}\left(t\right)=\sum _{k=1}^{t/dt}-T_{2,vessel}^{*}\left(x\left(k\right)\right)$ and the extravascular contribution is ${\varphi }_{n,intra}\left(t\right)=\sum _{k=1}^{t/dt}\text{iΔ}{\varphi }_n\left(t\right)-T_{2,tissue}\left(x\left(k\right)\right)$ The values of of the intrisic $T_{2,vessel}^{*}$ and $T_{2,tissue}$ depend on field strength and blood oxygenation and are obtained experimentally (28). See a more detailed explanation of the simulations in (23,24). In the present study, we only simulate the baseline state and gradient-echo signals to study the susceptibility effect on the reversible transverse relaxation rate $R_2{}^{\text{*}}$. Spin-echo signals and changes driven by functional activation including dynamic vessel dilations and metabolic rate variations can also be modeled if needed using the same framework, which are not examined in this study (23).

The transverse relaxation rate and its relation to magnetic susceptibility change For gradient echo imaging, the MR signal at echo time TE is approximated as

$$S(TE)=exp(-R_2{}^{*}\cdot TE).$$ (1)

The transverse relaxation rate $R_2{}^{*}$ is obtained via

$$R_2{}^{*}=-\text{ln}(S(TE))/TE.$$ (2)

Since $\mathrm{\Delta }{R}_2{}^{*}\propto {\left(\mathrm{\Delta }\chi \right)}^{\beta }$,

$$\text{ln}\mathrm{\Delta }{R}_2{}^{*}=\beta \text{ln}\mathrm{\Delta }\chi +\text{constant}.$$ (3)

We obtain $\beta$ from fitting the $ln\mathrm{\Delta }{R}_2{}^{*}$ versus $ln\mathrm{\Delta }\chi$ curve with varying $\mathrm{\Delta }\chi$. To obtain β relevant for BOLD MRI, we compute $R_2{}^{*}$ for gradient-echo signals in two different ways. The first uses a constant $\mathrm{\Delta }\chi$ across all vessels, with a value ranging from $2\times {10}^{-7}$ to $12\times {10}^{-7}$, which is of the same order as the $\mathrm{\Delta }\chi$ concentration induced by deoxyhemoglobin in BOLD measurement and is referred to as the uniform Δχ distribution. This is similar to how β has been previously computed using infinite cylinders (5,29). In the second method, to account for the influence of the non-uniform deoxyhemoglobin concentration across the vascular tree on the BOLD signal, the magnetic susceptibility inside vessels is weighted microscopically as

$$\mathrm{\Delta }\chi \left(\overrightarrow{r}\right)=\text{Δ}\chi Hct\left(1-S{O}_2\left(\overrightarrow{r}\right)\right),$$ (4)

where $S{O}_2$ is the oxygen saturation obtained from the oxygen advection-diffusion modeling and Hct is the hematocrit, which is assumed to be 0.3 in capillaries and 0.4 in arteries and veins (22). This β calculation is referred to as the deoxyhemoglobin-weighted Δχ distribution. In this case, $\text{Δ}\chi$ is modulated from $2\times {10}^{-6}$ to $4\times {10}^{-6}$ and β is similarly obtained from the slope of the $\text{ln}\mathrm{\Delta }R{2}^{*}$ vs. $\text{Δ}\chi$ curve. For reference, $\text{Δ}\chi$ is typically $4\pi \cdot 0.264\times {10}^{-6}=3.32\times {10}^{-6}$, which is the susceptibility difference between fully oxygenated and fully deoxygenated red blood cells (30). An example of $\mathrm{\Delta }R{2}^{*}$ versus for the uniform Δχ distribution at 1.5 T for one vascular network, shown in Fig. 1a, is shown in Fig. 1b. Unless stated otherwise, $TE=30\text{ms}$ is used to fix the length of proton diffusion during the simulated MR experiment. We are not exploring the non-exponential decay of $S\left(t\right)$ at early times in the current study and we term $R_2{}^{*}$ the apparent transverse relaxation rate (30), the attenuation of the signal at TE relative to that at TE=0. If not stated otherwise, the orientation of the static magnetic field $B_0$ is in the $z$ direction, perpendicular to the surface of the cerebral cortex.

Figure 1.

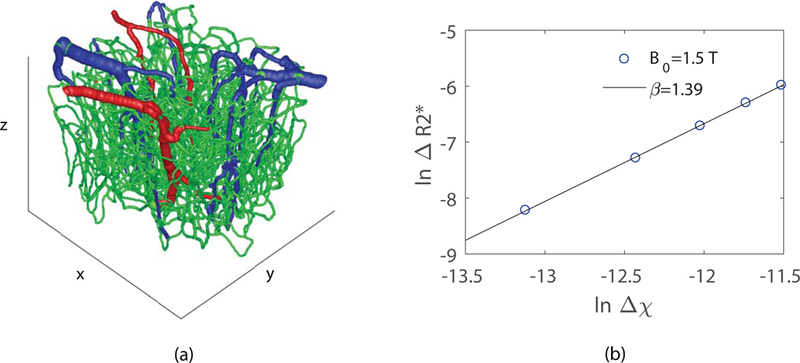
(a) Example of a graphed vascular network obtained from two-photon microscopy measurements (blue: veins; red: arteries; green: capillaries). (b) $\text{ln}\mathrm{\Delta }R{2}^{*}$ as a function of $\text{ln}\mathrm{\Delta }\chi$ for the vascular network in (a) at $B_0=1.5\text{T}$. The value of $\beta$ is obtained from the slope of the linear fit, which is $1.39$ in this example. Here $\mathrm{\Delta }\chi$ distribution is uniform within the BOLD range of $2\times {10}^{-7}$ to $12\times {10}^{-7}$.

One final $\text{Δ}\chi$ range is used to examine the influence of contrast agents on β. A higher concentration of $\text{Δ}\chi$ ranging from $1\times {10}^{-6}$ to $10\times {10}^{-6}$ corresponding to vascular Gd-DTPA concentrations of 3.6 to 36 mM (5), which covers most of the $\mathrm{\Delta }\chi$ range for contrast-enhanced perfusion imaging and is referred to as the contrast agent (CA) range, is also used to compute $\beta$, where Δχ was again set to a constant value across all vessels. This computation is referred to as the contrast-enhanced Δχ distribution.

Monte-Carlo simulations with the random cylinders model

To explore the effect of different size vessels on β at different field strengths $B_0$, we performed Monte-Carlo simulations of proton diffusion within and around randomly distributed magnetic cylinders similar to the original simulations by Boxerman and colleagues (5) but with the size of the cylinders fixed in one configuration instead of using a distribution of sizes. The static magnetic field is $B_0\widehat{z}$. The magnetic field at a point (a,b,c) in space induced by a single, infinitely long cylinder is (31)

$$\mathrm{\Delta }B(x,y,z)/B_0=\{\begin{array}{c}\frac{1}{2}\mathrm{\Delta }\chi {(R/r)}^2\cos 2\phi {\sin }^2\theta ,r\ge R\\ \left(\frac{1}{6}\right)\mathrm{\Delta }\chi \left(3{\cos }^2\theta -1\right),r<R.\end{array}$$ (5)

Here $\theta$ is the angle between the cylinder and $\widehat{z}$, $r$ is the distance of a spatial point from the cylinder axis, $\phi$ is the angle between projections in a plane orthogonal to the cylinder axis of $B_0\widehat{z}$ and a line connecting the point and the cylinder axis. The radius of cylinders $R$ is fixed for a single simulation while the positions and orientations of the cylinders are random. A new configuration is generated for each cylinder size $R$ from 1 to 5 $\text{μm}=(1-5)\times {10}^{-6}$ $\text{m}$ and each considered 5 different $B_0$ to obtain the size dependence of β at different field strengths. These cylinders and protons are contained in a box of size $L=600\text{μm}=6\times {10}^{-4}$ m in x, y and z dimensions in order to match the dimensions of the simulated voxel used in the VAN simulations. We continue to add cylinders to the box until $N\pi R^{2}L/L^3$ is larger than 2%, where $N$ is the total number of cylinders. We have also computed the results for $\frac{N\pi R^{2}L}{L^3}~4\%$ to see the effect of cylinder densities. $\text{Δ}\chi$ distribution is uniform with the CA range from $1\times {10}^{-6}$ to $10\times {10}^{-6}$. The BOLD range of $\text{Δ}\chi$ from $2\times {10}^{-7}$ to $12\times {10}^{-7}$ is also used as a comparison. Proton diffusion was simulated to derive the MR signal following the same procedure as described above for the VAN modeling. $R{2}^{*}$ and β are obtained from Eq. (2) and Eq. (3) respectively. SI units are used throughout this report.

Results

Results of the BOLD-relevant $\beta$ obtained from our six unique VANs for both uniform $\text{Δ}\chi$ distribution, which was used in earlier simulations with random cylinder models (5), and deoxyhemoglobin-weighted $\text{Δ}\chi$ distribution are shown in Fig. 2a and Fig. 2b, respectively.

Figure 2.

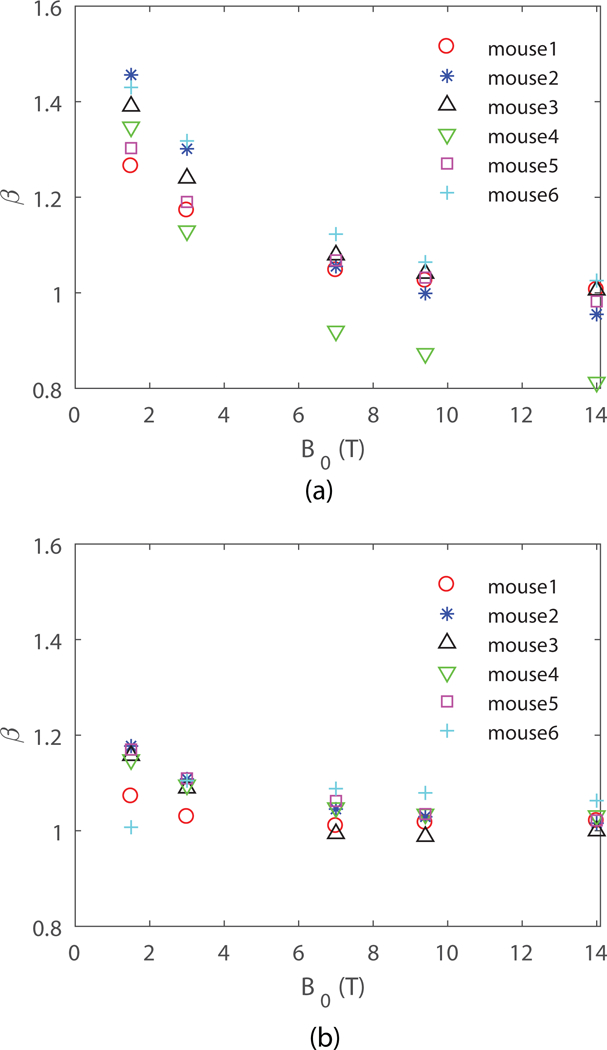
$\beta$ obtained from VAN modeling for (a) uniform $\mathrm{\Delta }\chi$ distribution, and (b) deoxyhemoglobin-weighted $\mathrm{\Delta }\chi$ distribution. $B_0$ is perpendicular to the surface of the cortex.

We see that the value of $\beta$ is generally between 1 and 2, because a real vascular network is a mixture of large (producing $\beta =1$) and small (producing $\beta =2$) vessels. We also see that $\beta$ can vary between the different vascular networks likely because of differences in the size distribution of the vessels. The value of $\beta$ obtained from the deoxyhemoglobin-weighted distribution is closer to the large vessel size limit of $\beta =1$, since in this case the venules that are larger in size maintain higher deoxyhemoglobin concentrations, and thus exert more influence on the diffusing protons than the generally smaller arterioles and capillaries. In both cases, $\beta$ decreases with increasing $B_0$, which shows that the diffusion effect on $\beta$ around small vessels is less important at higher fields. This indicates that $\beta$ is expected to be more uniform across subjects and regions at higher magnetic field strengths.

The impact of the orientation of $B_0$ relative to the cortical surface normal axis on BOLD signals has been shown in (24) to have up to a 40% effect on BOLD signal amplitude. This effect is due to the fact that the orientations of the vessels are not random and the spatial distribution is not uniform (32). Here we investigate whether the orientation of $B_0$ has an effect on the value of $\beta$. Fig. 3a, b show the average $\beta$ from the six VANs for $B_0$ transverse and perpendicular to the surface of the cerebral cortex with both uniform and deoxyhomoglobin-weighted $\mathrm{\Delta }\chi$ distribution. The difference between $\beta$ obtained at the two orientations is less than 5% at 1.5 T and decreases with increasing $B_0$, which shows that the susceptibility effect depends less on the $B_0$ orientation at higher fields. This further suggests a more spatially uniform $\beta$ map at higher magnetic field strengths.

Figure 3.

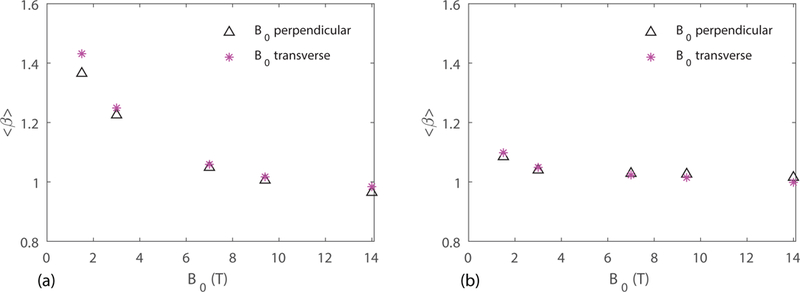
Mean value of $\beta$ obtained from six VANs for $B_0$ transverse and perpendicular to the surface of the cerebral cortex with (a) uniform $\mathrm{\Delta }\chi$ distribution, and (b) deoxyhemoglobin-weighted $\mathrm{\Delta }\chi$ distribution.

In all of the above results, we have fixed the value of $TE=30ms$ to fix the proton diffusion length. In practice, TE is chosen to match tissue $T{2}^{*}$, which varies with $B_0$. The question arises as to whether the value of $\beta$ changes with $TE$. In the ideal case, where $S(t)$ decays truly exponentially, the apparent $R{2}^{*}$ obtained from $lnS(TE)/TE$ and $\beta$ will not change. Fig. 4 shows the mean value of $\beta$ obtained from our six VANs for TE = 15 and 30 ms with uniform and deoxyhomoglobin-weighted $\mathrm{\Delta }\chi$ distribution. The values of $\beta$ are slightly different for different TEs due to the non-exponential decay of $S(t)$ at small $t$ (30), exhibiting a small increase for shorter TE with uniform $\mathrm{\Delta }\chi$ distribution and negligible dependence on TE for deoxyhemoglobin-weighted $\mathrm{\Delta }\chi$ distribution.

Figure 4.

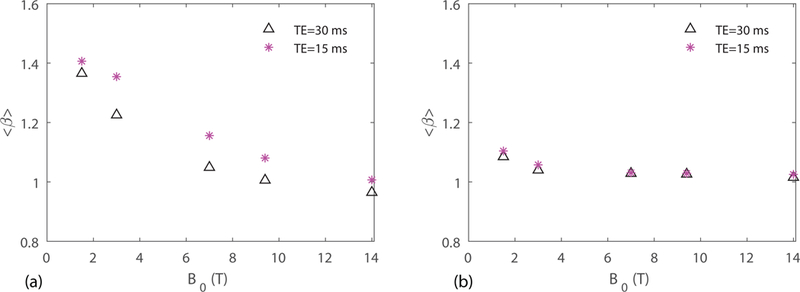
Mean value of $\beta$ obtained from six VANs for TE = 15 and 30 ms with (a) uniform $\mathrm{\Delta }\chi$ distribution, and (b) deoxyhemoglobin-weighted $\mathrm{\Delta }\chi$ distribution.

For perfusion or functional imaging based on intravascular contrast agents, the concentration of $\mathrm{\Delta }\chi$ can be an order of magnitude higher than the range relevant for BOLD fMRI. Since the induced magnetic field inhomogeneity is proprotional to $\mathrm{\Delta }\chi \cdot B_0$, increasing $\mathrm{\Delta }\chi$ has a similar effect as increasing $B_0$ that acts to decrease $\beta$. The values for $\beta$ computed for the CA range of $\mathrm{\Delta }\chi$ from $1\times {10}^{-6}$ to $10\times 6^{-6}$ with a uniform distribution is shown in Fig. 5a. We see that $\beta \approx 1$ for $B_0\le 9.4$ T, which is smaller than the values computed in Fig. 2a with the BOLD fMRI range of $\mathrm{\Delta }\chi$, as expected. However, for $B_0=14T$, $\beta$ drops below 1 and the variations across subjects is large. This indicates that at $14T$, a few large vessels dominate and the value of $\beta$ is no longer between the theoretical predictions of 1 and 2 made under the assumption of a random distribution of vessels. This indicates that at $14T$, a lower concentration of $\mathrm{\Delta }\chi$ is desired. In Fig. 5b, $\beta$ obtained from a lower concentration of $\mathrm{\Delta }\chi$ from $1\times {10}^{-6}$ to $3\times 6^{-6}$, which is relevant for many DSC studies (33), is shown, where $\beta \approx 1$ at all field strengths. The time step in the Monte-Carlo simulations for $B_0=9.4$, $14\text{T}$ is 0.01 ms instead of 0.2 ms as in other simulations.

Figure 5.

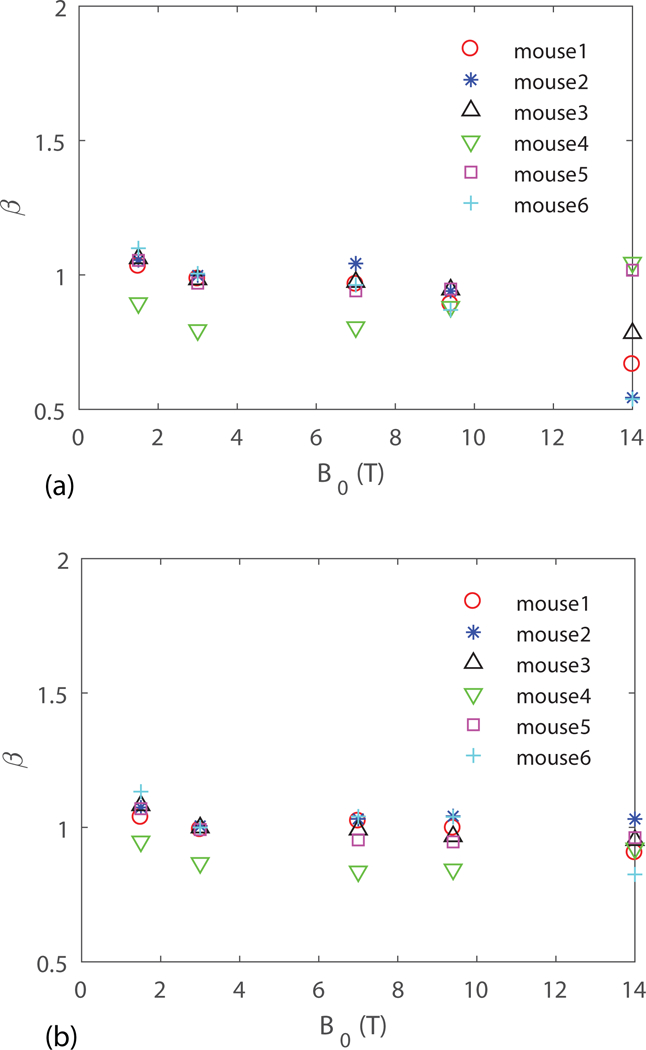
$\beta$ obtained from six VANs for uniform $\mathrm{\Delta }\chi$ distribution within for perfusion or functional imaging based on susceptibility contrast agents (a) from $1\times {10}^{-6}$ to $10\times {10}^{-6}$ and (b) from $1\times {10}^{-6}$ to $3\times {10}^{-6}$.

To help understand the behavior of $\beta$ decreasing with increasing $B_0$, we explored the dependence of $\beta$ on vessel radius and magnetic field strength $B_0$ with Monte-Carlo simulations using a random cylinder model as described in the methods section. The value of $\beta$ is obtained for various radii $R$ of randomly distributed cylinders at different magnetic field strengths, with each value calculated by averaging over four random cylinder configurations. Fig. 6a and Fig. 6b are the results for protons freely moving across vessel walls and no proton exchange across vessels walls respectively. We see that vessel wall permeability has a negligible impact on $\beta$. The critical value of $R$ where $\beta$ deviates from 1 is smaller at higher fields, which indicates that the small vessels act more like large vessel at higher fields, thus $\beta$ is closer to the large vessel limit of $\beta =1$. Fig. 6c shows the results for a cylinder volume fraction of 4% (as opposed to 2% in the other simulations). These can be compared with simulations in the strict static dephasing regime as shown in Fig. 6d where protons are not moving and the value of $\beta$ is about 1, which further confirms that proton diffusion is the main cause of a non-linear susceptibility effect ($\beta \ne 1$). For a typical capillary radius of $3\text{μm}$, $\beta =1$ for 7 T and above. This ensures that $\beta =1$ for imaging regions composed only of capillaries at 7 T and above for high-resolution fMRI. For a range of $\text{Δ}\chi$ similar to that encountered in BOLD fMRI as shown in Fig. 6e, $\beta$ is significantly higher for capillaries compared to the results obtained for a range of $\text{Δ}\chi$ mimicking that found when using a contrast agent as in Fig. 6a. Thus assuming a uniform distribution of $\text{Δ}\chi$ overestimates $\beta$ for BOLD fMRI measurements since the small capillaries with large $\beta$ are weighted the same way as large veins.

Figure 6.

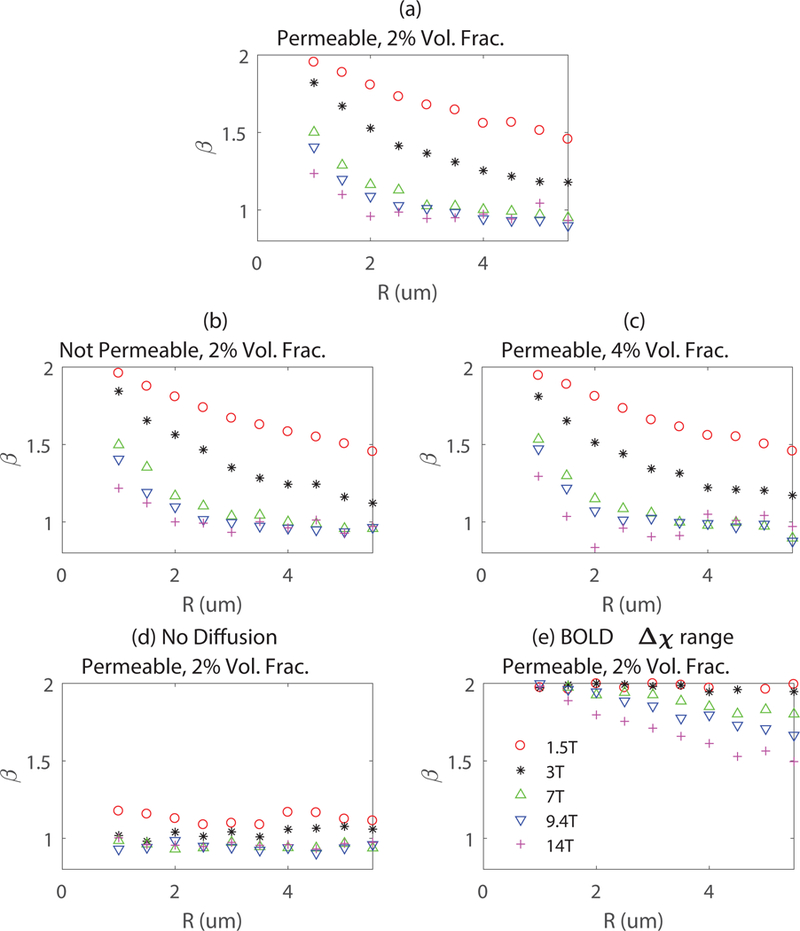
The susceptibility effect parameter $\beta$ obtained for various vessel diameters corresponding to capillaries at different field strengths for (a) Monte-Carlo simulations with freely diffusing protons (2% volume fraction); (b) Monte-Carlo simulations with no proton exchange between intra- and extravascular spaces (2% volume fraction); (c) Monte-Carlo simulations with a cylinder volume fraction of 4% instead of 2%; (d) Static dephasing with protons not moving (2% volume fraction). (e) for BOLD $\mathrm{\Delta }\chi$ range.

Discussion

The parameter $\beta$, the exponent in a power law relationship between the change in transverse relaxation rate $\mathrm{\Delta }{R}_2{}^{*}$ and changes in the magnetic susceptibility of blood $\text{Δ}\chi$ is important in two physiological imaging contexts: 1) Guiding quantitative physiological interpretation of BOLD to help estimate CMRO₂; and 2) Quantifying CBV or perfusion by modeling the signal from an intravascular contrast agent. An important difference between these two applications is that for the BOLD effect the blood susceptibility is altered non-uniformly, weighted by deoxyhemoglobin with the largest changes in the venous vessels, while injected contrast agents change the susceptibility of blood uniformly and the concentration of $\text{Δ}\chi$ is usually higher compared to the range relevant for BOLD fMRI. Here we report the first study of the behavior of $\beta$ at different magnetic field strengths and concentrations of $\text{Δ}\chi$ based on numerical simulations using realistic vascular anatomical models derived from detailed imaging in mice.

Results from both VAN modeling using real micro-vascular networks and Monte-Carlo simulations using randomly orientated infinite cylinders show that proton diffusion effects are less relevant at higher fields for the susceptibility effect, reflected in our finding that $\beta$ decreases towards a value of 1.0 as the field increases. A value of $\beta$ greater than 1.0 occurs when there is some degree of motional narrowing due to diffusing protons sampling a range of the distorted fields around a vessel. In the limit of very fast diffusion, so that each proton samples all of the field offsets within the diffusion length, $\beta =2.0$. Although the extent of proton diffusion is independent of the field strength, the volume of significantly distorted magnetic field around a vessel does increase with the field strength. The observed behavior is implied in the definition of the motional narrowing regime where diffusion is important, that is $\frac{R^2\delta \omega }{D}\ll 1$ as given in earlier studies (5,18). Here D is the proton diffusion coefficient, $\delta \omega \propto B_0$ is in units of angular frequencies and $R$ is the radius of cylinders. This relation can be recast as $B_0{R}^2\ll constant$, thus increasing $B_0$ requires a smaller $R$ for the condition to be satisfied. At higher field strength, the critical vessel radius where $\beta$ deviates from 1 is smaller, which is consistent with the results shown in Fig. 2. The second effect of motional narrowing is that because each proton is sampling a range of field offsets, the net signal decay is reduced compared to what it would have been without diffusion. This is illustrated in Fig. 7, showing that the decay is faster around larger vessels and at higher fields because there is less motional narrowing. Note that both large and small vessels produce faster decay at higher fields, as expected, but the changes in the proportions between the larger and smaller vessels are different, reflecting the reduction of motional narrowing at higher fields.

Figure 7.

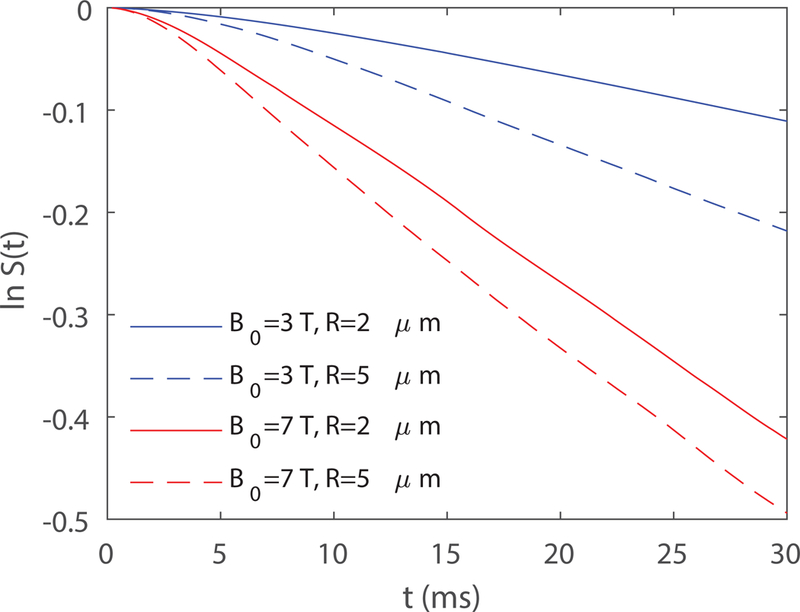
Example of ln S(t) obtained from Monte-Carlo simulations of random cylinders as in Fig. 3a for different $B_0$ and $R$. Here $\text{Δ}\chi =1.2\times {10}^{-6}$ is the same for the four curves.

Although the theoretically predicted value of $\beta$ is between 1 and 2, we see in Fig. 2a that there is one animal (mouse 4) where $\beta$ drops below 1. There are also several $\beta <1$ values in Fig. 5a. This is probably because the voxel size is limited and a single vessel dominates, where the random network predictions of $\beta$ varying between 1 for static dephasing and 2 for motional narrowing no longer holds. Recent experiments have also found $\beta$ to be 0.8 in rodent brain (34), which could also be related to ordered, as opposed to random, network structure. This behavior of $\beta$ may be more prominent for high-resolution fMRI studies in which the dominant effect of single vessels on the MRI signal becomes more likely.

For BOLD fMRI studies, the value of $\beta$ appears in the Davis model (12,35) and is used to compute CMRO₂ changes, but the spatial non-uniformity of $\mathrm{\Delta }\chi$ was not fully addressed in the original studies. This complexity makes the measurement of $\beta$ in the Davis model challenging. The value of $\beta$ was obtained from fitting the macroscopic Davis model in ref. (23). Treating $\beta$ as a free fitting parameter is simple to implement but it no longer maintain its physiological meaning as the parameter that governs the susceptibility effect and the three parameters M, $\alpha$ and $\beta$ are correlated. In VAN modeling, we are able to compute the oxygen distribution within microvascular networks, which provides the microscopic distributions of deoxyhemoglobin concentrations. This enables us to compute the physiological parameter $\beta$ relevant for the Davis model from first-principles. Compared to the uniform $\mathrm{\Delta }\chi$ results, deoxyhemoglobin-weighted results show that $\beta$ is closer to the large vessel limit, since the vessels that contain the most deoxyhemoglobin are large venules. As can be seen in Fig. 2b, $\beta \approx 1.1$ for $B_0=1.5T$ and at $B_0=3T$ and above, $\beta =1$, as opposed to the early calculations of $\beta =1.5$ at 1.5 T (12) and $\beta =1.5$ at 3 T (36).

The study of the field strength dependence on the susceptibility effect provides guidance for CBV measurements in imaging based on contrast agents. One assumption for these techniques is that $\mathrm{\Delta }{R}_2{}^{*}\propto CBV$, and thus the map of an $R_2{}^{*}$ increase after injection of a contrast agent provides a map of $CBV$ (1–4). However, a hidden assumption here is that $\beta$ is uniform since $\mathrm{\Delta }R{2}^{*}\propto CBV*{(\mathrm{\Delta }\chi )}^{\beta }$ and this relation is not accurate if $\beta$ varies within regions. To obtain a more accurate measurement of CBV, a map of $\beta$ or a sense of how $\beta$ changes within different regions is desired to correct estimates of CBV. We have shown in Fig. 5a that for a uniform distribution of $\mathrm{\Delta }\chi$ within the CA range, $\beta \approx 1$ except at $B_0=14T$. This indicates that a lower concentration of $\mathrm{\Delta }\chi$ is desired for $B_0=14$ $T$ as shown in Fig. 5b.

Conclusions

We have analyzed the susceptibility effect on the transverse relaxation rate using realistic micro-vascular anatomical networks and modeling of the oxygen advection and diffusion through the network. Both the uniform and the deoxyhemoglobin-weighted distribution of $\mathrm{\Delta }\chi$ were studied. We show that the parameter $\beta$, which governs the dependence of the transverse relaxation rate on the magnetic susceptibility shift, is closer to the large vessel limit of $\beta =1$ at higher magnetic field strength. For BOLD fMRI, with a realistic anatomy and distribution of hemoglobin saturation, our results indicate that $\beta =1$ for 3 T and above, greatly simplifying macroscopic models such as the Davis model (12). For perfusion and functional imaging techniques based on contrast agents, $\beta =1$ for 9.4 T and below in general. Our work provides insights on the fundamental question of the impact of proton diffusion on MR signals at different field strengths as well as practical applications for CBV measurements with contrast agents and rCMRO₂ measurements with BOLD fMRI.

Supplementary Material

Supp info

Supporting Information Figure S1. (a) The distribution of vessel sizes from the six networks of mouse vasculature measured in vivo. (b) β obtained from the random cylinder model with the vessel size distribution in (a) for both BOLD (2 × 10⁻⁷) to 12 × 10⁻⁷) and CA range (1 × 10⁻⁶) to 10 × 10⁻⁶) of Δχ concentration. (c) The value of β as a function of Δχ concentration in SI units.

Supporting Information Figure S2. (a) The vasculature (blue: veins; red: arteries; green:capillaries) with starting pial artery and vein (branching order = 0) indicated in the figure. (b) Distribution of SO₂ computed in the model as a function of branching orders staring from the pial artery and vein. (c) Δχ concentration in different branching orders. (d) The corresponding vessel diameter in different branching orders.

Supporting Information Figure S3. The value of β obtained for a mouse vascular for different dt values in the Monte-Carlo simulations for (a) the BOLD range of Δχ range (2 × 10⁻⁷) to 12 × 10⁻⁷) and (b) contrast agent range of Δx (1 × 10⁻⁶) to 10 × 10⁻⁶).