Abstract
With 300,000,000 riders annually, roller coasters are a popular recreational activity. Although the number of roller coaster injuries is relatively low, the precise effect of roller coaster rides on our brains remains unknown. Here we present the quantitative characterization of brain displacements and deformations during roller coaster rides. For two healthy adult male subjects, we recorded head accelerations during three representative rides, and, for comparison, during running and soccer headers. From the recordings, we simulated brain displacements and deformations using rigid body dynamics and finite element analyses. Our findings show that despite having lower linear accelerations than sports head impacts, roller coasters may lead to brain displacements and strains comparable to mild soccer headers. The peak change in angular velocity on the rides was 9.9 rad/sec, which was higher than the 5.6 rad/sec in soccer headers with ball velocities reaching 7 m/sec. Maximum brain surface displacements of 4.0 mm and maximum principal strains of 7.6% were higher than in running and similar to soccer headers, but below the reported average concussion strain. Brain strain rates during roller coaster rides were similar to those in running, and lower than those in soccer headers. Strikingly, on the same ride and at a similar position, the two subjects experienced significantly different head kinematics and brain deformation. These results indicate that head motion and brain deformation during roller coaster rides are highly sensitive to individual subjects. Although our study suggests that roller coaster rides do not present an immediate risk of acute brain injury, their long-term effects require further longitudinal study.
Keywords: : brain modeling, head kinematics, traumatic brain injury, wearable sensors
Introduction
An estimated 300,000,000 people ride roller coasters annually at American amusement parks.1 The accelerations experienced on roller coaster rides contribute to their thrilling nature; however, the effect of these accelerations on the brain is largely unknown. Previously, there have been several case studies reporting serious brain injuries attributed to roller coasters,1–3 including seven cases of subdural hematoma,4–10 two cases of subarachnoid hemorrhage,11,12 and multiple cases of concussion.1,13,14 These types of brain injuries have been extensively studied and are thought to be mostly caused by excessive mechanical deformations of the bridging veins causing subdural hematoma,15 of aneurysms causing subarachnoid hemorrhage,12,16 and of the parenchymal brain tissue itself causing concussion.17 Given that most of these patients did not have known pre-existing brain conditions, and that some of these patients specifically denied direct head trauma during the ride, these clinical reports raise a concern of brain injury risks in roller coaster rides.
Brain injury risks are traditionally quantified by head/skull kinematics, and two previous studies have measured head kinematics during roller coaster rides.18,19 One study estimated peak angular head acceleration of <500 rad/sec2 by measuring seat linear accelerations, neglecting neck motion, and assuming that the head pivots stiffly about the base of the skull.19 This assumption likely underestimated head rotation, as it could not account for whiplash from neck motion. Another study used a bite bar to measure head motions during roller coaster rides directly, and reported up to 10g linear acceleration and 10 rad/sec angular velocity.18 This study also calculated the head injury criterion, a linear acceleration-based criterion, and found it to be less than that of an 18 mph car crash. However, the brain injury criterion was originally developed to identify severe brain injuries such as skull fractures, and has not been validated for mild brain injuries such as concussions.17
A major limitation of skull acceleration-based metrics such as the brain injury criterion is that they do not capture brain displacements or deformations and, therefore, may not accurately predict the mechanisms associated with brain trauma. Brain strains could explain the mechanism of diffuse axonal injury and serve as a predictor for concussions or chronic traumatic encephalopathy,17,20–23 and brain displacements may help to explain damage to blood vessels. To estimate brain displacements and deformations, several groups used skull kinematics as inputs for a variety of model-based approaches.20,24–27 Rigid body brain models, validated against in vivo and cadaveric human brain motion imaging data, provide valuable insight into the displacement of the brain relative to the skull and can be used to simulate long-duration events.28 Finite element brain models allow the brain to deform,21,29,30 permitting the quantification of strain patterns within the brain30,31 and thus the identification of local regions at risk for brain tissue damage.32–35 However, finite element brain models are computationally expensive and can only be used to simulate short (e.g., <100 ms) durations (R2-1). Because of these computational limitations, we can use the coarser, but more computationally efficient, rigid body model to simulate long-duration events and identify time periods that are likely to yield large brain strains for simulation in finite elements.
To better understand the risk of brain injury during roller coaster rides, we estimated brain displacements and strains using the previously described model-based approaches. We collected head kinematics from roller coaster rides, and, for comparison, from everyday activities such as running and from mild soccer headers. For each activity, we simulated brain displacements over an entire activity using rigid body simulations. Using a finite element brain model, we also simulated brain deformation over short time windows when the most amount of brain displacements were observed from the rigid body model. We compared the head kinematics as well as brain displacements and strains in each activity. Based on these comparisons, our study could indicate a low—but previously unidentified—risk of brain injury during roller coaster rides.
Methods
Two healthy male human subjects wore instrumented mouthguards36–38 during roller coaster rides, running, and soccer headers to measure head kinematics during these activities. We then used the measured head kinematics to drive a rigid body model28 and a finite element model32 to estimate the displacement and strain experienced by the brain.
Subjects
Two healthy male human subjects were recruited for this pilot study. At the time of the study, Subject A was 26 years old, with a height of 167 cm, weight of 65.8 kg, neck length of 12.5 cm, neck circumference of 37cm, and head circumference of 59 cm. Subject B was also 26 years old, with a height of 175 cm, weight of 59.0 kg, neck length of 12.5 cm, neck circumference of 35 cm, and head circumference of 57.5 cm. Neck length was measured from the C7 spinous process to the tragus of the ear, neck circumference was measured perpendicular to the long axis of the neck above the thyroid cartilage, and head circumference was measured passing through the superciliary ridge and the opisthocranion.39
Measuring head kinematics
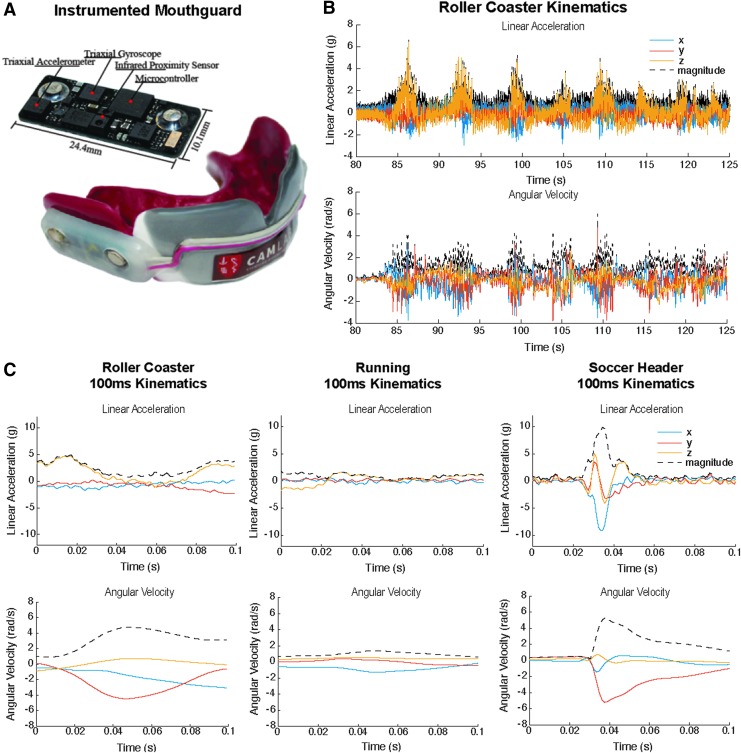
We used our previously validated instrumented mouthguard36–38 (Fig. 1A) to measure head kinematics during roller coaster rides, running, and soccer headers. We custom designed the instrumented mouthguard to fit tightly to the upper dentition of each human subject. This provided tight coupling of the sensors to the skull through the maxilla compared with other sensors mounted on either headgear or the skin. We equipped the instrumented mouthguard with a triaxial accelerometer (H3LIS331DL) and a triaxial gyroscope (ITG3500A) to measure the linear acceleration and angular velocity of the head at 1000 Hz for the entire duration of each activity.
FIG. 1.
Use of instrumented mouthguards to record head kinematics during roller coaster rides. (A) Mouthguard, (B) linear acceleration of the head during the entire duration of a roller coaster ride, and (C) comparison of roller coaster accelerations with running and soccer heading.
Measured activities
Each subject participated in three roller coaster rides at a local amusement park. The roller coaster data collection was a research practicum that did not fall under the purview of the institutional review board (IRB), given the fact that roller coaster rides are a common recreational activity, and the pilot nature of the study. One subject also participated in mild soccer header impacts, which was approved under Stanford IRB #26620. Both subjects wore the instrumented mouthguard to measure head kinematics. Subjects sat side by side during roller coaster rides, which were among the most thrilling rides at the amusement park and had advertised g forces up to 4.5g. Additionally, both subjects performed a 3 min run at an ∼9 min mile pace, which was selected as a representative everyday activity that was considered safe for the brain. The soccer headers represented mild sports head impacts and were delivered using a ball launcher (Soccer Tutor, Burbank, CA) with a ball speed of 7.0 m/sec, which is the average speed for headers in youth.37
Kinematics post-processing
We transformed the raw head linear acceleration and angular velocity kinematics from the mouthguard into a head-fixed anatomical frame and projected to the head's center of gravity, with x in the posterior-anterior direction, y in the right-left direction, and z in the inferior-superior direction. We filtered the linear acceleration signals using a fourth order Butterworth low pass filter with a CFC180 300 Hz cutoff frequency and filtered the angular velocity signals using a fourth order Butterworth low pass filter with a 184 Hz cutoff frequency according to the device's bandwidth. The linear acceleration and angular velocity filters have been shown to be sufficient for measuring impacts in American football,38,40 which likely have higher frequency content than head motions observed during roller coaster rides. We obtained the angular accelerations by differentiating the angular velocity signals using a five point stencil.17 We computed peak linear acceleration magnitude, peak change in angular velocity, and peak angular acceleration magnitude for each roller coaster ride and each activity.
Rigid body simulation of brain displacements
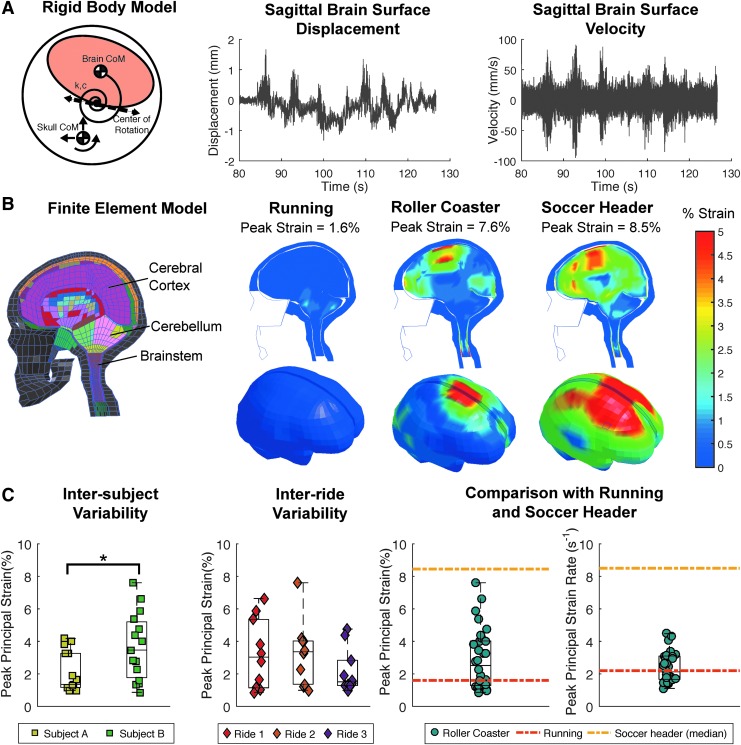
To estimate brain displacements throughout the entire time course of these activities, we performed a rigid body simulation of brain motion within the skull. We modeled the gross motion of the brain using a rigid body representation of the brain–skull interaction with dynamic elements representing the connective tissue.28 We used a previously developed sagittal plane rigid body brain model developed based on in vivo MRI images of mild head impacts and validated against cadaver impacts.26 Because the rigid body model had only been rigorously validated in the sagittal plane, we only used sagittal plane kinematics to drive the rigid body simulation. Because our sagittal plane simulation does not include out-of-plane kinematics, it only provides a surrogate measure to estimate the temporal evolution of the brain displacement with respect to the skull to identify the most critical 100 ms window for the finite element simulation. Using input kinematics from the roller coaster rides, running, and the soccer header activities, we calculated the maximum brain displacement and peak brain velocity at the superior boundary between the brain and skull over the entire time course of the activities. To probe the sensitivity of the maximum brain displacements with respect to varying brain stiffness and varying brain mass, we performed additional rigid body simulation with 80% and 120% of the initial stiffness and of the initial mass for all three rides.
Finite element simulation of brain strains
To estimate local brain deformations, we performed finite element simulations using the KTH brain model.32 The KTH brain model includes an anatomically detailed discretization of the scalp, the skull, the brain, the meninges, the cerebrospinal fluid, 11 pairs of the largest parasagittal bridging veins, and a simple neck with the extension of the spinal cord and the dura mater, with 7128 hexahedral elements in the brain. We used the linear accelerations and angular velocities from the three roller coaster rides, running, and soccer headers as input to the simulation and predicted the deformation field across the brain using the finite element software LS-DYNA (Livermore Software Technology Corporation, Livermore, CA). Because three-dimensional finite element simulations require substantial computational cost and the finite element brain model is not validated for long-duration simulations, we restricted our simulations to selected 100 ms intervals from each activity. For the roller coaster rides and for the running activities, we selected five 100 ms windows that included the largest brain displacements as predicted by the rigid body model. For the soccer header activity, we programmed the mouthguards to only record impact kinematics over a 100 ms period during the head impact. Once the simulations were completed, we processed the results using LS PrePost (Livermore Software Technology Corporation, Livermore, CA). As indicators for brain injury incidence in contact sports, we computed the peak maximum principal Green–Lagrange strains and strain rates from each simulation.17,21 In addition, we extracted the engineering strains in the bridging veins and compared them against reported values for bridging vein failure.41 To probe the sensitivity of the maximum brain strains with respect to varying brain stiffness and varying simulation window size, we performed additional finite element simulation with 80% and 120% of the initial stiffness and 140 ms and 180 ms simulation windows by adding 20 ms and 40 ms at the beginning and end of each simulation for all three rides.
Results
Head kinematics during activities
Figure 1B shows the linear acceleration and angular velocity recording during the ride with the highest kinematics for Subject A. Figure 1C shows selected 100 ms traces of roller coaster kinematics, running, and an average soccer header that were used for finite element simulation. Comparing kinematics from all activities and both subjects, we found that during roller coaster rides, the maximum linear acceleration magnitude was 8.0g, the maximum change in angular velocity magnitude was 9.9 rad/sec, and the maximum angular acceleration magnitude was 290 rad/sec2. During running, the maximum linear acceleration magnitude was 3.6g, the maximum change in angular velocity magnitude was 3.7 rad/sec, and the maximum angular acceleration magnitude was 161 rad/sec2. Finally, during a mild soccer header, the maximum linear acceleration magnitude was 11.6g, the maximum change in angular velocity magnitude was 5.0 rad/sec, and the maximum angular acceleration magnitude was 1100 rad/sec2. Although the maximum angular velocity change in the roller coaster exceeded the maximum angular velocity change in soccer headers, the angular acceleration and linear acceleration magnitudes in roller coaster were lower, indicating a difference in motion duration between the two activities.
To better quantify how roller coaster kinematics and running kinematics compare with mild sports impacts, we identified the number of instances in which roller coaster or running kinematics exceeded our average soccer header kinematics. Over the 14 mild soccer headers administered, the average linear acceleration was magnitude 9.4g, the average angular velocity was magnitude 4.8 rad/sec, and the average angular acceleration magnitude was 847 rad/sec2. Our mild soccer header average linear acceleration is in agreement with the previously reported 10g average on the field.42 For Subject A, roller coaster angular velocity exceeded average soccer header angular velocity just once during ride 2. For Subject B, roller coaster angular velocity exceeded average soccer header angular velocity a total of 21 times over all three rides, with the majority (17) of instances occurring during ride 2. These data suggest there exists inter-subject and inter-ride variability. Summary statistics broken down by subject and by ride are presented in Figure S1 and Table S1 (see online supplementary material at http://www.liebertpub.com). Briefly, the ride with the highest kinematics (ride 2) had up to 50% greater kinematics than the ride with the lowest kinematics (ride 3). In addition, Subject B had up to 50% greater kinematics than Subject A in all activities. Roller coaster linear acceleration and angular acceleration magnitudes did not exceed average soccer header values for either subject. In addition, neither subjects' running kinematics exceeded average soccer header kinematics.
Simulated brain displacements
We estimated brain displacements over the time course of our activities using a rigid body simulation, assuming that the brain acts like a rigid body within the skull. The peak brain surface displacement was highest during the mild soccer headers, with magnitudes of 4.2 mm. For both subjects, roller coaster brain surface displacements were highest for ride 2, with 3.6 mm and 4.0 mm, and lowest for ride 3, with 2.1 mm and 2.0 mm. Rides 1 and 3 were also the rides with the highest and lowest change in angular velocity. For both subjects, the brain surface displacements were lowest in running, with 0.68 mm and 1.5 mm. Similar trends were observed for the brain surface velocity. Figure 2A illustrates representative time histories of the brain surface displacement and velocities from ride 3 for Subject A. The simulated brain displacements were sensitive to the brain model stiffness and mass: decreasing/increasing the stiffness by 20% increased/decreased the maximum displacement by ∼20%; decreasing/increasing the mass by 20% decreased/increased the maximum displacement by ∼20%.
FIG. 2.
Use of rigid body dynamics and finite element modeling to estimate brain displacements and deformations. (A) Rigid body model and results, (B) finite element model and results, (C) comparison of brain deformations across subjects, rides, and activities.
Simulated brain strains
We calculated brain strains with the KTH finite element model using selected 100 ms windows from the roller coaster rides, running, and soccer headers based on maximum displacement as predicted by the rigid body model. Because these 100 ms windows were chosen based on results from the rigid body model, the 100 ms windows were primarily sagittal motions. This also allows for comparison against the primarily sagittal mild soccer headers. Figure 2B compares the strain profiles across the brain for all three activities. Our simulations show that the highest peak strain from roller coaster rides is greater than strains in running, but comparable with those from soccer headers. However, a larger region of the brain experienced strains >5% in the soccer header than in the roller coaster simulation.
Figure 2C illustrates the inter-subject and inter-ride variability of the simulated peak principal strains and strain rates. We observed a significant variation in the peak strains between the two subjects, and notable differences across the three rides. Subject A experienced smaller brain strains in roller coaster rides than did Subject B (p < 0.05, unpaired t test). The maximum principal strain among all rides was 7.6%, recorded for Subject B during ride 2 (Fig. 2C). Of the three different rides, the average peak brain strains were highest during ride 2 and lowest during ride 3. The average peak strains during ride 2 were 60% larger than those during ride 3. The majority of the roller coaster simulations predicted strains <5.0%, and most of the roller coaster simulations stayed within the 1.0–2.0% strain regime, suggesting that the strains remained low during most of the ride. The simulated brain strains were sensitive to the brain model stiffness and simulation window: decreasing/increasing the stiffness by a factor two increased/decreased the maximum strain approximately by a factor of two; increasing the simulation window from 100 ms to 140 ms and 180 ms decreased the strains during rides 1 and 3, but increased the strains during ride 2. When compared with other activities, roller coaster peak strains were higher than strains during running, but at or below the level of a soccer header. The peak strain rates during roller coaster rides were comparable with the strain rates observed during running, and both were markedly lower than those observed in mild sports impacts. Peak strains during roller coaster rides were primarily located at the cortical surface around the posterior part of the frontal lobe near the midsagittal plane, which agrees with the location of peak displacements in the rigid body model. Finally, peak engineering strains in the bridging veins remained <1.0% for all simulated roller coaster time windows.
Discussion
In this study, we present the first-ever estimated brain displacements and brain deformations from riding roller coaster rides simulated using measured head kinematics. We recorded linear acceleration and angular velocity kinematics of two subjects equipped with a custom-designed instrumented mouthguard during three selected rides, and used the recordings to quantify brain displacements and strains using rigid body dynamics and finite element analysis. For comparison, we performed the same analysis for everyday activities and mild sports impacts. Our preliminary finding is that during all rides, the average brain displacements and strain levels remain lower than those in mild sports head impacts and likely present low risk of acute brain injuries. However, the peak brain displacements and strains during these rides are higher than in everyday activities and comparable with mild sports impacts.
Overall, our recorded peak linear accelerations and angular velocities during roller coaster rides are similar to those previously reported in the literature.18 With a maximum linear acceleration of 8.0g, the recorded linear accelerations are twice as high as the advertised g force level of 4.5g,1 indicating that roller coaster seat kinematics may underestimate the head motion experienced. The maximum angular acceleration of 290 rad/sec2 is much smaller than the one previously reported.18 The discrepancy in angular accelerations may be the result of a difference in instrumentation. In the previous study, subjects were instrumented with a bite bar wherein the accelerometers and gyroscopes were located at the end of a tab that extended outside of the mouth. A previous mouthguard validation study has suggested that such tabs can overpredict kinematics as a result of the tab resonating as a cantilever beam.43 Our instrumentation with sensors located directly inside the mouthguard do not exhibit cantilever resonance by placing sensors closer, and therefore more rigidly affixed, to the upper dentition.37,38
The kinematics observed between the two subjects differed during the roller coaster rides. This is evidenced by the fact that Subject B experienced head angular velocities exceeding average mild soccer header impacts 21 times over all three rides, whereas Subject A experienced large head angular velocities only once in ride 2. Discrepancy in the kinematics may be the result of a number of factors, including seating position and subject anatomy. We controlled for seating position by having our two subjects sit side by side on each of the three rides. In terms of anatomy, Subject A had greater mass, and larger neck and head circumference. This may indicate a slightly stronger neck, which would better stabilize the head, resulting in lower roller coaster kinematics.
To assess the relative risk of roller coaster kinematic events, we performed a direct comparison with mild soccer headers, which may have a non-negligible injury risk, and running, which we assume to be a safe activity. Our measurements show that linear accelerations during roller coaster rides lie between those of mild soccer headers and running. We observe a similar trend for the angular accelerations; however, the angular velocities during roller coaster rides are similar—if not slightly higher—than the angular velocities during mild soccer headers. Head angular velocity has been reported to correlate better with brain strain than linear head kinematics.20,32 Therefore, even though the roller coaster linear and angular accelerations are lower than mild soccer headers, indicating low injury risks in line with previous findings, the higher angular velocity in the rides may be causing higher than expected amounts of brain deformation.
To quantify the effects of the head kinematics on the brain, we calculated brain displacements using our measured skull kinematics. Our simulations revealed brain surface displacements of up to 4.0 mm with respect to the skull, and brain velocities of up to ∼10 cm/sec. These values lie within the range of previous studies that had reported brain displacements on the order of 2.0–3.0 mm in response to mild 2.0 cm head drops with no injury to the brain.44 However, our rigid body model was initially developed and validated only in the sagittal plane. As such, it does not include out-of-plane kinematics and only provides a surrogate measure to estimate the temporal evolution of the overall displacement. The maximum three-dimensional displacement across the entire brain could potentially be significantly larger. For bridging veins with an average length of 6.0 mm and an orientation along the anterior-posterior direction, our maximum sagittal brain surface displacements of 4.0 mm would translate into stretches up to 1.67, which is close to or even beyond the critical bridging vein failure stretch of 1.50.
The rigid body analysis allowed us to coarsely assess the effect of head kinematics on the brain over the time course of an entire event, which cannot be achieved using more refined finite element models. To obtain a more detailed view of brain deformations, we calculated brain strains using three-dimensional finite element simulations of substantial brain displacement events, and compared the resulting maximum principal strains and strain rates across different activities. Our results show that although peak brain strains remain <5.0% in most simulated roller coaster events, the peak strains do reach levels comparable with those resulting from mild sports impacts during soccer headers, and exceed the strains experienced during normal activities, including running. Our peak strains during roller coaster rides of 7.6% are smaller than injury thresholds for concussion reported in the literature: recent finite element analyses using the same model have shown that football players who sustained concussions experienced strain levels of 30%.32 A recent injury criterion developed using another finite element brain model suggests that there is a 25% chance of mild traumatic brain injury (TBI) at strain levels of 14%.45 Controlled ex vivo experiments on white matter tissue report functional and structural injury thresholds at strain levels of 18% and 21%.22 Although previous research shows that more severe injuries are typically associated with strain concentrations in deeper regions of the brain,17 our simulations predict localized peak strains during roller coaster rides near the cortical surface. Neither of our subjects experienced acute concussion symptoms. Even though roller coaster strains are likely subconcussive, repeated subconcussive impacts have been linked with cumulative brain damage and subsequent long-term neurodegeneration.46–48
To quantify the effect of large linear and angular velocities on brain deformation rates, we calculated the strain rate, because rate effects have been shown to correlate with the risk of concussion.32,49 Strain rates during roller coaster rides were closer to those during running, and both were lower than those during mild sports impacts. Although similar changes in angular velocity magnitudes were observed in roller coaster rides compared with mild sports impacts, the angular acceleration magnitudes were much lower, indicating more gradual change in angular velocity, which may help explain the lower strain rates during roller coaster rides. Recent axon injury models suggest that strain rates play a critical role in diffuse axonal injury and that axonal damage is more likely when axons are stretched faster.49–51 The moderate strain rates observed during roller coaster rides suggest that strain rates are unlikely to trigger acute brain tissue damage; however, their long-term effects—especially when occurring often and repetitively over long periods of time—remain unclear, and likely require further longitudinal study.
Rigid body and finite element simulations provide a promising starting point to explore mechanisms for roller coaster induced subdural hematomas.6,8–10 Our rigid body simulations estimate roller coaster brain surface displacement on the order of 2.0–4.0mm, which may lead to stretching of the bridging veins between the brain and skull.41 Although the rigid body model does not represent the bridging veins as individual substructures, we can estimate the maximum stretch within the sagittal plane: If bridging veins were oriented along the anterior-posterior direction and had an average length of 6.0 mm, they would experience stretches up to 1.67, which is close to or even beyond the critical bridging vein failure stretch of 1.50. Our finite element simulations provide more detail and show significant peak strains near the superior surface of the brain. Although our finite element model includes 11 pairs of the largest parasagittal bridging veins,32 their structural and material properties have not yet been validated with experimental measurements. Another potential limitation is that the KTH brain model represents the brain through its convex hull only.26 Representing the brain with its complex surface geometry with individual gyri and sulci30 might help increase the accuracy of the model. Further development of a model validated for estimating displacements at the brain–skull boundary is necessary to accurately model the impact of brain displacements and strains on the bridging veins as a mechanism for subdural hematomas.
Although our study provides valuable insight into the interplay of brain kinematics, displacement, and strain, it has a few limitations that need to be addressed in future studies. First, although our rigid body simulations efficiently provide an initial insight into the effects of elevated head kinematics, they are currently limited to sagittal in-plane effects. It has been shown that brain strains are more sensitive to axial and coronal angular rotations,52 which our methodology does not capture because of the sagittal-plane rigid body model. However, we believe that the results from the sagittal plane model and finite element simulations may represent a lower bound on the true peak brain strains and strain rates observed in roller coaster rides. In addition, we found the rigid body simulations to be useful in identifying time windows of extreme kinematic events. Second, although our rigid body simulations cover the entire roller coaster ride of ∼3 min, we limit each finite element simulation to a 100 ms simulation window because of its high computational cost. We selected this length because the model had previously been validated with 100 ms duration impacts.26 Third, we adopted resting state initial conditions, although the simulation windows were located in the middle of the ride. Table S2 highlights the sensitivity of the simulated peak strains with respect to the simulation window (see online supplementary material at http://www.liebertpub.com). When the simulation is increased from 100 ms to 140 ms and 180 ms, the peak strains either increase or decrease depending on the overall velocity and acceleration profile. This shows that although current finite element brain simulations often assume zero initial conditions at the beginning of impacts, future studies are needed to quantify the sensitivity of brain strains to different initial conditions. Finally, finite element modeling of the brain is still an active area of research. Multiple models have been developed, and comparisons of such models do not show one-to-one correspondence in their predictions of brain deformations because of differences in model characteristics such as mesh size, material properties, and geometry.53 As a result, in our study, we mainly made comparisons of the brain deformation measures with published injury threshold levels developed using the same model. Further, additional development of the model may help further increase accuracy through investigations of the effects of incorporating anisotropy, vasculature, and more complex geometry such as sulci and gyri.54–56 Tables S2 and S3 highlight the sensitivity of maximum brain displacements and strains with respect to varying brain stiffness and mass for three different rides (see online supplementary material at http://www.liebertpub.com). Our sensitivity studies suggest that, in our low impact regime, brain displacements and strains vary approximately linearly with variations in stiffness and mass. The original finite element model was parameterized and validated for more severe impacts with linear acceleration >20g and angular accelerations >20 rad/sec, whereas most of the roller coaster acceleration events had less severe kinematics. More studies are needed to ensure that our model parameters are insensitive to the longer duration and reduced magnitude of roller coaster acceleration events.
Our study represents the first thorough analysis of the effect of brain dynamics during roller coaster rides on the displacement and deformations inside the brain, with the ultimate goal of characterizing the risk of injury and comparing it with that of contact sports. Our results suggest that the brain experiences surface displacements and local strains comparable with those observed in mild sports impacts. Although we only piloted the analysis for two study subjects and three representative rides, peak principal strains and strain rates displayed a notable inter-subject and inter-ride variability. Although our two study subjects were of the same gender and age and of a similar height, and performed the same three rides, their brain kinematics and brain strains were statistically significant with differences of up to 63%. This suggests that injury susceptibility can vary greatly on an individual basis; testing rides on multiple subjects could more rigorously ensure safety. The limiting of g forces alone might be an insufficient design criterion for roller coaster rides. Further studies will be needed to more comprehensively estimate brain dynamics across different roller coaster rides and across a more diverse population of roller coaster enthusiasts.
Supplementary Material
Acknowledgments
We thank Dr. Svein Kleiven for providing the KTH brain model, which was used to compute brain deformations. This work was mainly supported by the Stanford Bio-X Graduate Research Fellowship Program, the Stanford Child Health Research Institute, Lucile Packard Foundation for Children's Health, Stanford CTSA (UL1 TR001085), and the Natural Sciences and Engineering Research Council of Canada.
Author Disclosure Statement
There was no significant financial support for this work that could have influenced its outcome. L.C.W., C.K., K.L., and D.B.C. are developing the Stanford Mouthguard as a research device to study mild TBI, and the findings of this study may help inform sensor design. L.C.W., C.K., and D.B.C. are also co-inventors on Stanford-owned patents related to instrumented mouthguard design, which are not directly related to this work.
References
- 1.Braksiek R.J., and Roberts D.J. (2002). Amusement park injuries and deaths. Ann. Emerg. Med. 39, 65–72 [DOI] [PubMed] [Google Scholar]
- 2.Levenson M.S., Product U. S. C. & Commission S. (2002). Amusement ride-related injuries and deaths in the United States: 2002 Update. Consumer Product Safety Commission, Bethesda, MD [Google Scholar]
- 3.Pelletier A.R., and Gilchrist J. (2005). Roller coaster related fatalities, United States, 1994–2004. Inj. Prev. 11, 309–312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bo-Abbas Y., and Bolton C.F. (1995). Roller-coaster headache. N. Engl. J. Med. 332, 1585. [DOI] [PubMed] [Google Scholar]
- 5.Fernandes C.M., and Daya M.R. (1994). A roller coaster headache: case report. J. Trauma 37, 1007–1010 [PubMed] [Google Scholar]
- 6.Fukutake T., Mine S., Yamakami I., Yamaura A., and Hattori T. (2000). Roller coaster headache and subdural hematoma. Neurology 54, 264. [DOI] [PubMed] [Google Scholar]
- 7.Roldan-Valadez E., Facha M.T., Martinez-Lopez M., and Herrera-Mora P. (2006). Subdural hematoma in a teenager related to roller-coaster ride. Eur. J. Paediatr. Neurol. 10, 194–196 [DOI] [PubMed] [Google Scholar]
- 8.Scranton R.A., Evans R.W., and Baskin D.S. (2016). A motion simulator ride associated with headache and subdural hematoma: first case report. Headache 56, 372–378 [DOI] [PubMed] [Google Scholar]
- 9.Snyder R.W., Sridharan S.T., and Pagnanelli D.M. (1997). Subdural hematoma following roller coaster ride while anticoagulated. Am. J. Med. 102, 488–489 [DOI] [PubMed] [Google Scholar]
- 10.Williams K.A., Kouloumberis P., and Engelhard H.H. (2009). Subacute subdural hematoma in a 45-year-old woman with no significant past medical history after a roller coaster ride. Am. J. Emerg. Med. 27, 517..e5-6. [DOI] [PubMed] [Google Scholar]
- 11.Nencini P., Basile A.M., Sarti C., and Inzitari D. (2000). Cerebral hemorrhage following a roller coaster ride. JAMA 284, 832–833 [DOI] [PubMed] [Google Scholar]
- 12.Senegor M. (1991). Traumatic pericallosal aneurysm in a patient with no major trauma. Case report. J. Neurosurg. 75, 475–477 [DOI] [PubMed] [Google Scholar]
- 13.Olympia R.P., Brady J., Rupp V., and Lansenderfer C. (2011). Emergency department visits from a local amusement park. J. Emerg. Med. 41, 14–20 [DOI] [PubMed] [Google Scholar]
- 14.Thompson M.C., Chounthirath T., Xiang H., Smith G.A. (2013). US pediatric injuries involving amusement rides, 1990–2010. Clin. Pediatr. (Phila) 52, 433–440 [DOI] [PubMed] [Google Scholar]
- 15.Gennarelli T.A., Thibault L.E. (1982). Biomechanics of acute subdural hematoma. J. Trauma 22, 680–686 [DOI] [PubMed] [Google Scholar]
- 16.Suarez J.I., Tarr R.W., and Selman W.R. (2011). Aneurysmal subarachnoid hemorrhage. N. Engl. J. Med. 18, 388–396 [DOI] [PubMed] [Google Scholar]
- 17.Hernandez F., Wu L.C., Yip M.C., Laksari K., Hoffman A.R., Lopez J.R., Grant G.A., Kleiven S., and Camarillo D.B. (2015). Six degree-of-freedom measurements of human mild traumatic brain injury. Ann. Biomed. Eng. 43, 1918–1934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pfister B.J., Chickola L., and Smith D.H. (2009). Head motions while riding roller coasters: implications for brain injury. Am. J. Forensic Med. Pathol. 30, 339–445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Smith D.H., and Meaney D.F. (2002). Roller coasters, g forces, and brain trauma: on the wrong track? J. Neurotrauma 19, 1117–1120 [DOI] [PubMed] [Google Scholar]
- 20.Ji S., Zhao W., Li Z., and McAllister T.W. (2014). Head impact accelerations for brain strain-related responses in contact sports: a model-based investigation. Biomech. Model. Mechanobiol. 13, 1121–1136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goriely A., Budday S., and Kuhl E., (2015). Neuromechanics: From neurons to brain. In Advances in Applied Mechanics, pp. 78–139 [Google Scholar]
- 22.Bain A.C., Raghupathi R., and Meaney D.F. (2001). Dynamic stretch correlates to both morphological abnormalities and electrophysiological impairment in a model of traumatic axonal injury. J. Neurotrauma 18, 499–511 [DOI] [PubMed] [Google Scholar]
- 23.Sullivan S., Eucker S.A., Gabrieli D., Bradfield C., Coats B., Maltese M.R., Lee J., Smith C., and Margulies S.S. (2015). White matter tract-oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities. Biomech. Model. Mechanobiol. 14, 877–896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Low , Tah C., and Stalnaker R.L. (1987). A lumped parameter approach to simulate the rotational head motion. Proceedings of the International Research Council of the Biomechanics of Injury Conference, Vol. 15 Int. Res. Counc. Biomechs. of Injury [Google Scholar]
- 25.Willinger R., Taleb L., and Kopp C.M. (1995). Modal and temporal analysis of head mathematical models. J. Neurotrauma 12, 743–754 [DOI] [PubMed] [Google Scholar]
- 26.Kleiven S., and Hardy W.N. (2002). Correlation of an FE model of the human head with local brain motion–consequences for injury prediction. Stapp Car Crash J. 46, 123–144 [DOI] [PubMed] [Google Scholar]
- 27.Takhounts E.G., Eppinger R.H., Campbell J.Q., Tannous R.E., Power E.D., and Shook L.S. (2003). On the development of the SIMon finite element head model. Stapp Car Crash J. 47, 107–133 [DOI] [PubMed] [Google Scholar]
- 28.Laksari K., Wu L. C., Kurt M., Kuo C., and Camarillo D.C. (2015). Resonance of human brain under head acceleration. J. R. Soc. Interface 12, 20150331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rooij , de R., and Kuhl E. (2015). Constitutive modeling of brain tissue: current perspectives. Appl. Mech. Rev. 68, 1–33 [Google Scholar]
- 30.Weickenmeier J., Butler C.A.M., Young P.G., Goriely A., and Kuhl E. (2017). The mechanics of decompressive craniectomy: personalized simulations. Comput. Methods Appl. Mech. Eng. 314, 180–195 [Google Scholar]
- 31.Cloots R.J.H., van Dommelen J.A.W., Kleiven S., and Geers M.G.D. (2012). Multi-scale mechanics of traumatic brain injury: predicting axonal strains from head loads. Biomech. Model. Mechanobiol. 12, 137–150 [DOI] [PubMed] [Google Scholar]
- 32.Kleiven S. (2007). Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp Car Crash J. 51, 81–114 [DOI] [PubMed] [Google Scholar]
- 33.Marjoux D., Baumgartner D., Deck C., and Willinger R. (2008). Head injury prediction capability of the HIC, HIP, SIMon and ULP criteria. Accid. Anal. Prev. 40, 1135–1148 [DOI] [PubMed] [Google Scholar]
- 34.Giordano C., Cloots R.J.H., van Dommelen J.A.W., and Kleiven S. (2014). The influence of anisotropy on brain injury prediction. J. Biomech. 47, 1052–1059 [DOI] [PubMed] [Google Scholar]
- 35.Goriely A., Geers M.G., Holzapfel G.A., Jayamohan J., Jérusalem A., Sivaloganathan S., Squier W., van Dommelen J.A., Waters S., and Kuhl E. (2015). Mechanics of the brain: perspectives, challenges, and opportunities. Biomech. Model. Mechanobiol. 14, 931–965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu L.C., Zarnescu L., Nangia V., Cam B., and Camarillo D.B. (2014). A head impact detection system using SVM classification and proximity sensing in an instrumented mouthguard. IEEE Trans. Biomed. Eng. 61, 2659–2668 [DOI] [PubMed] [Google Scholar]
- 37.Wu L.C., Nangia V., Bui K., Hammoor B., Kurt M., Hernandez F., Kuo C., and Camarillo D.B.(2015). In vivo evaluation of wearable head impact sensors. Ann. Biomed. Eng. 44, 1234–1245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kuo C., Wu L.C., Hammoor B.T., Luck J.F., Cutcliffe H.C., Lynall R.C., Kait J.R., Campbell K.R., Mihalik J.P., Bass C.R., and Camarillo D.B. (2016). Effect of the mandible on mouthguard measurements of head kinematics. J. Biomech. 49, 1845–1853 [DOI] [PubMed] [Google Scholar]
- 39.Vasavada A.N., Danaraj J., and Siegmund G.P. (2008). Head and neck anthropometry, vertebral geometry and neck strength in height-matched men and women. J. Biomech. 41, 114–121 [DOI] [PubMed] [Google Scholar]
- 40.Wu L.C.Laksari K., Kuo C., Luck J.F., Kleiven S., 'Dale' Bass C.R., and Camarillo D.B. (2016). Bandwidth and sample rate requirements for wearable head impact sensors. J. Biomech.49, 2918–2924 [DOI] [PubMed] [Google Scholar]
- 41.Famaey N., Cui Z.Y., Musigazi G.U., Ivens J., Depreitere B., Verbeken E., and Vander Sloten J. (2015). Structural and mechanical characterisation of bridging veins: a review. J. Mech. Behav. Biomed. Mater. 41, 222–240 [DOI] [PubMed] [Google Scholar]
- 42.Naunheim R.S., Bayly P.V., Standeven J., Neubauer J.S., Lewis L.M., and Genin G.M. (2003). Linear and angular head accelerations during heading of a soccer ball. Med. Sci. Sports Exerc. 35, 1406–1412 [DOI] [PubMed] [Google Scholar]
- 43.Camarillo D.B., Shull P.B., Mattson J., Shultz R., and Garza D. (2013). An instrumented mouthguard for measuring linear and angular head impact kinematics in american football. Ann. Biomed. Eng. 41, 1939–1949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Feng Y., Abney T.M., Okamoto R.J., Pless R.B., Genin G.M., and Bayly P.V. (2010). Relative brain displacement and deformation during constrained mild frontal head impact. J. R. Soc. Interface 7, 1677–1688 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang L., Yang K.H., and King A.I. (2004). A proposed injury threshold for mild traumatic brain injury. J. Biomech. Eng. 126, 226–236 [DOI] [PubMed] [Google Scholar]
- 46.Matser J.T., Kessels A.G., Jordan B.D., Lezak M.D., and Troost J. (1998). Chronic traumatic brain injury in professional soccer players. Neurology 51, 791–796 [DOI] [PubMed] [Google Scholar]
- 47.Koerte I.K., Kaufmann D., Hartl E., Bouix S., Pasternal O., Kubiki M., Rouschen A., Li D.K., Dadachanji S.B., Taunton J.A., and Forwell L.A. (2012). A prospective study of physician-observed concussion during a varsity university hockey season: white matter integrity in ice hockey players. Part 3 of 4. Neurosurg. Focus 33, E3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Talavage T.M.Nauman E.A., Breedlove E.L., Yoruk U., Dye A.E., Morigaki K.E., Feuer H., and Leverenz L.J. (2010). Functionally-detected cognitive impairment in high school football players without clinically-diagnosed concussion. J. Neurotrauma 31, 327–338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tang-Schomer M.D., Patel A.R., Baas P.W., and Smith D.H. (2010). Mechanical breaking of microtubules in axons during dynamic stretch injury underlies delayed elasticity, microtubule disassembly, and axon degeneration. FASEB J. 24, 1401–1410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ahmadzadeh H., Smith D.H., and Shenoy V.B. (2014). Viscoelasticity of tau proteins leads to strain rate-dependent breaking of microtubules during axonal stretch injury: Predictions from a mathematical model. Biophys. J. 106, 1123–1133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Van Den Bedem H., and Kuhl E. (2015). Tau-ism: the yin and yang of microtubule sliding, detachment, and rupture. Biophys. J. 109, 2215–2217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhao W., Ford J.C., Flashman L.A., McAllister T.W., and Ji S. (2016). White matter injury susceptibility via fiber strain evaluation using whole-brain tractography. J. Neurotrauma 33, 1834–1847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ji S., Ghadyani H., Bolander R.P., Beckwith J.G., Ford J.C., McAllister T.W., Flashman L.A., Paulsen K.D., Ernstrom K., Jain S., Raman R., Zhang L., and Greenwald R.M. (2014). Parametric comparisons of intracranial mechanical responses from three validated finite element models of the human head. Ann. Biomed. Eng. 42, 11–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cloots R.J.H., van Dommelen J.A W., Kleiven S., and Geers M.G.D. (2013). Multi-scale mechanics of traumatic brain injury: predicting axonal strains from head loads. Biomech. Model. Mechanobiol. 12, 137–150 [DOI] [PubMed] [Google Scholar]
- 55.Giordano C., Cloots R.J.H., van Dommelen J.A.W., and Kleiven S. (2014). The influence of anisotropy on brain injury prediction. J. Biomech. 47, 1052–1059 [DOI] [PubMed] [Google Scholar]
- 56.Ho J., and Kleiven S. (2009). Can sulci protect the brain from traumatic injury? J. Biomech. 42, 2074–2080 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.