The role of annealing and fragmentation in human tau aggregation dynamics

Abstract

Alzheimer's disease pathogenesis is associated with the conversion of monomeric tau protein into filamentous aggregates. Because both toxicity and prion-like spread of pathogenic tau depend in part on aggregate size, the processes that underlie filament formation and size distribution are of special importance. Here, using a combination of biophysical and computational approaches, we investigated the fibrillation dynamics of the human tau isoform 2N4R. We found that tau filaments engage in a previously uncharacterized secondary process involving end-to-end annealing and that rationalization of empirical aggregation data composed of total protomer concentrations and fibril length distributions requires inclusion of this process along with filament fragmentation. We noted that annealing of 2N4R tau filaments is robust, with an intrinsic association rate constant of a magnitude similar to that mediating monomer addition and consistent with diffusion-mediated protein–protein interactions in the absence of long-range attractive forces. In contrast, secondary nucleation on the surface of tau filaments did not detectably contribute to tau aggregation dynamics. These results indicate that tau filament ends engage in a range of homotypic interactions involving monomers, oligomers, and filaments. They further indicate that, in the case of tau protein, fibril annealing and fragmentation along with primary nucleation and elongation are the major processes controlling filament size distribution.

Introduction

Tau aggregation is a defining event in the pathogenesis of tauopathic neurodegenerative disorders such as Alzheimer's disease. It is an established marker for differential disease diagnosis and staging (1), a surrogate marker for neurodegeneration (2, 3), a potential vector for disease propagation (4, 5), and a source of toxicity in biological models (6). For these reasons, the mechanisms through which tau misfolds and aggregates are of central importance for understanding disease pathogenesis. In vitro, the primary pathway to filamentous cross-β-sheet aggregates leverages a nucleation–elongation mechanism (7) where the rate-limiting nucleation event corresponds to dimerization (8, 9) and the efficient elongation phase corresponds to addition of monomers to the ends of growing polymers (8, 9) (Fig. 1). A pathway involving isodesmic assembly of small aggregates constitutes an alternative route to these stable structures (9–12). As observed with other aggregating proteins (13–15), secondary events such as filament fragmentation (also known as “breakage” or “fracture”) can increase apparent overall tau aggregation rate by increasing the number of filament ends available for elongation (16, 17). Secondary nucleation has been predicted to be especially important for creating small, highly diffusible aggregates associated with toxicity (18). Together with filament fragmentation, this secondary process may seed aggregation and foster spread of misfolding through the nervous system (19). Each of these alternative or secondary processes increases filament number and therefore tends to decrease average filament length (15, 20). However, in the case of tau protein aggregates, intracellular filaments within the neurofibrillary lesions of Alzheimer's disease can exceed micrometers in length (21). Moreover, synthetic tau aggregates prepared in vitro also achieve stable length distributions extending to long lengths even under aggregation conditions that are claimed to be isodesmic (9, 22). The length distributions observed in situ and in vitro suggest the existence of a distinct, previously uncharacterized secondary process that opposes filament fragmentation by promoting increases in average filament length. A candidate for this interaction is end-to-end annealing, which has been observed in linear assemblies of cytoskeletal protein, including tubulin (23), actin (24, 25), intermediate filament proteins (26), and septins (27). In the case of actin, end-to-end annealing is highly favorable and strongly dependent on length (i.e. annealing efficiency decreases as filaments lengthen (28)). In fact, it is not possible to rationalize F-actin filament length distribution without incorporating both annealing and fragmentation terms into its nucleation-dependent assembly mechanism (25). In the case of vimentin, an intermediate filament protein, modeling studies have shown that end-to-end annealing is obligatory for rationalizing the appearance of long filaments (26). Because β-sheet edges are especially interaction-prone (29), the ends of filamentous cross-β-sheet tau aggregates may be subject to annealing interactions as well.

Figure 1.

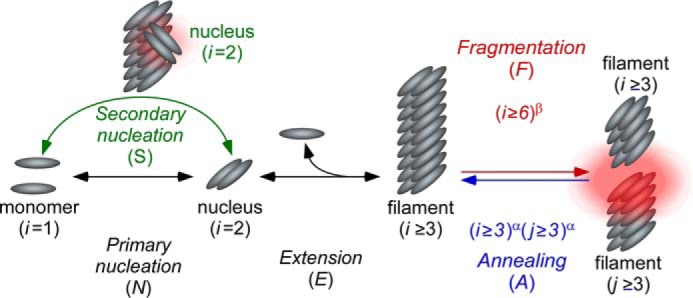
Tau aggregation models. In vitro aggregation of 2N4R tau was modeled as beginning with aggregation-competent monomer generated by the presence of an inducer. Primary processes include the formation of a dimer, which corresponds to filament nucleation (N) and its elongation (E) to form filaments through endwise addition of monomers. Secondary processes include secondary nucleation (S), filament fragmentation (F), and filament annealing (A). See text for details.

Here, we test this hypothesis with special emphasis on secondary processes that influence tau aggregate size distribution. The results indicate that tau filament ends can anneal and that their propensity to engage in such homotypic interactions is length-dependent. We propose that interactions at tau filament ends are candidate mediators of size-dependent phenomena reported in biological models.

Results

Tau filaments anneal in vitro

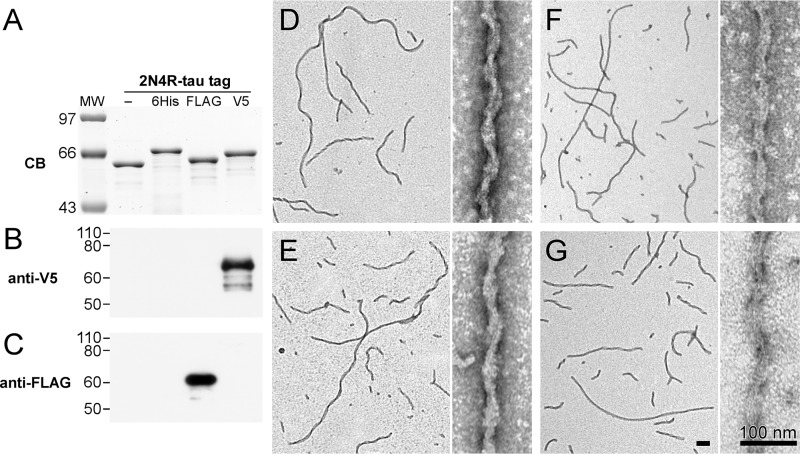
To enable selective detection of tau filament populations, two recombinant human 2N4R tau constructs containing N-terminal V5 or FLAG epitopes were engineered. Full-length 2N4R was used as the tau isoform for both constructs because it aggregates efficiently at near physiological conditions of ionic strength, pH, and sulfhydryl reducing conditions (30). On the basis of immunoblot analysis, tagged proteins strongly and selectively bound their cognate anti-V5 and anti-FLAG antibodies (Fig. 2). To test their aggregation propensity, these proteins along with full-length N-terminally His₆-tagged (6His-2N4R) and nontagged 2N4R tau were incubated in the presence of Geranine G after which time the products were subjected to transmission EM (TEM)² imaging. Geranine G was used as the anionic aggregation inducer because of its ability to drive aggregation of submicromolar full-length 2N4R tau into filaments having mass-per-unit length similar to authentic brain-derived filaments under near-physiological buffer conditions and submicromolar tau concentrations (8, 30, 31). The resulting TEM micrographs showed that the presence of an N-terminal tag did not affect aggregation propensity or ∼80-nm filament axial periodicity relative to nontagged 2N4R tau, regardless of whether the tag was composed of His₆, V5, or FLAG (Fig. 2). In contrast, only filaments prepared from V5- or FLAG-tagged 2N4R monomers bound cognate anti-V5 and anti-FLAG antibodies (Fig. 3). Extensive decoration of filaments with these antibodies obscured filament morphology but preserved observation of length and, in conjunction with 12- or 5-nm gold–conjugated secondary antibodies, provided clear evidence for the presence of V5- or FLAG-tagged 2N4R tau protomers, respectively (Fig. 3).

Figure 2.

N-terminal tau fusion constructs display similar aggregation propensity and aggregate morphology. Recombinant 2N4R tau and N-terminal fusion constructs 6His-2N4R, FLAG-2N4R, and V5–2N4R were expressed in Escherichia coli, purified, and subjected to SDS-PAGE (500 ng) or immunoblot (10 ng) analyses. A, representative SDS-PAGE migration pattern visualized by Coomassie Blue stain. The presence of epitope tags changes protein migration on SDS-PAGE proportionate to the size of the tag. B and C, immunoblots probed with polyclonal anti-V5 (B) and monoclonal anti-FLAG (C), respectively. Antibody labelings were specific for their cognate epitopes. Recombinant 2N4R tau (D) and N-terminal fusion constructs FLAG-2N4R (E), 6His-2N4R (F), and V5–2N4R (G) were induced to aggregate in the presence of Geranine G inducer and incubated under aggregation conditions for 24 h at 37 °C. Samples were adsorbed onto grids and imaged by TEM. All three N-terminal fusion constructs aggregated with similar efficiency and produced filaments of similar morphology as nonfusion 2N4R tau. All scale bars, 100 nm.

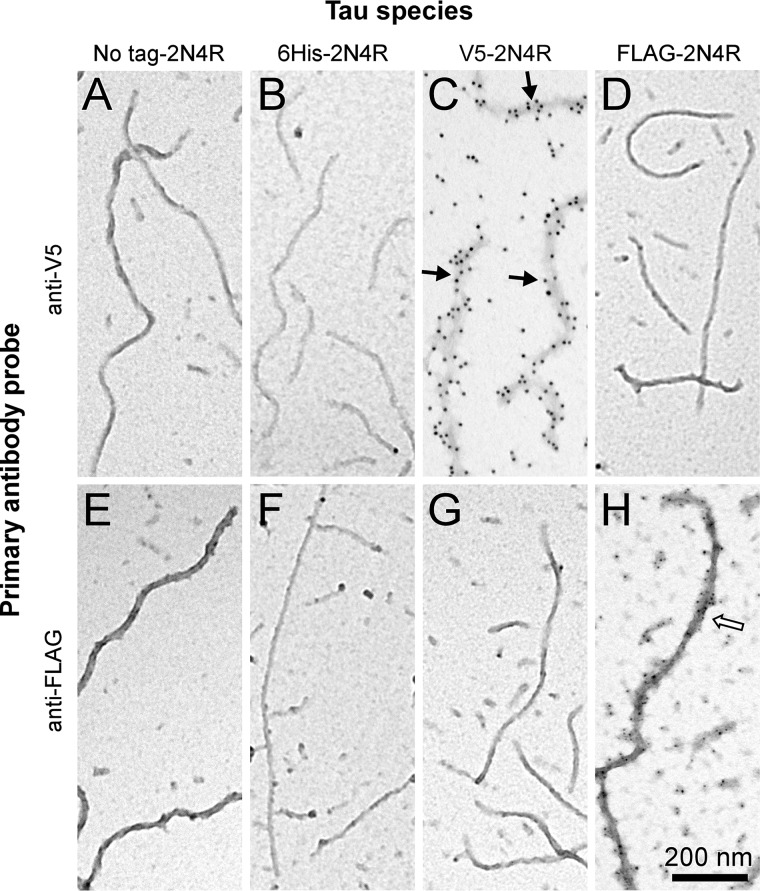
Figure 3.

Control labelings with immunogold. Recombinant 2N4R tau and N-terminal fusion constructs 6His-2N4R, V5–2N4R, and FLAG-2N4R were induced to aggregate in the presence of Geranine G inducer for 24 h at 37 °C. Samples were then adsorbed onto carbon-coated TEM grids and subjected to immunogold labeling using anti-V5 primary/12-nm gold–conjugated secondary antibodies (A–D) and anti-FLAG primary/5-nm gold-conjugated secondary antibodies (E–H). Gold labelings using anti-V5 (black arrows) and anti-FLAG (white arrow) antibodies were specific for filaments containing their cognate epitope.

To test for tau filament annealing, separate populations of V5- and FLAG-tagged 2N4R filaments were prepared by incubating protein monomers in the presence of Geranine G beyond aggregation plateau (≥16 h (8, 30)) and then mixing them together and incubating for additional time (0–24 h) before subjecting products to immunogold labeling with anti-V5/12-nm gold or anti-FLAG/5-nm gold beads followed by TEM imaging. Immediately after mixing, most fibrils were labeled exclusively with 5- or 12-nm gold beads, reflecting the presence of aggregates composed entirely of one construct or the other in the mixture (Fig. 4, A and B). However, after 24-h incubation, double labeling with anti-V5/12-nm gold and anti-FLAG/5-nm gold revealed the presence of fibrils with extended alternate segments of 12- or 5-nm gold, consistent with end-to-end annealing of the two populations (Fig. 4, C–F). In contrast, filaments prepared from equal concentrations of V5- and FLAG-tagged 2N4R monomers stained uniformly with anti-V5/12-nm gold and anti-FLAG/5-nm gold with no sign of alternating segments of 12- or 5-nm gold after 48-h incubation (Fig. 4G). These data indicate that extended alternate staining segments did not arise from selective propagation of tagged monomers at filament ends.

Figure 4.

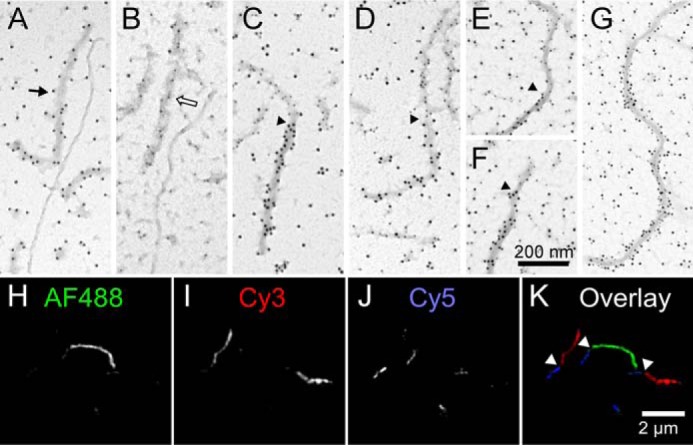
Direct visualization of tau filament annealing. A–F, synthetic filaments composed of V5–2N4R or FLAG-2N4R tau proteins were prepared separately in the presence of aggregation inducer Geranine G (1 μm tau incubated for 16 h at 37 °C), then mixed together, and incubated for an additional 0–24 h. A and B, when mixtures incubated for 0 h were subjected to immunogold labeling using either anti-V5 (A) or anti-FLAG (B) primary antibodies, only homogeneous labeling of single filaments was observed on TEM imaging. Black arrow, V5/12-nm gold immunoreactivity; hollow arrow, FLAG/5-nm gold immunoreactivity. C–F, in contrast, mixtures incubated for 24 h prior to immunogold labeling with both anti-V5 and anti-FLAG antibodies identified filaments containing extended regions of both gold labels, consistent with filament annealing. Arrowheads mark junctions between anti-FLAG and anti-V5 immunoreactivities in annealed filaments. G, synthetic filaments prepared from a mixture of V5–2N4R and FLAG-2N4R tau monomers (0.5 μm each; incubated for 48 h at 37 °C) were subjected to immunogold labeling with both anti-V5 and anti-FLAG primary antibodies. Only homogeneous labeling of filaments was observed, indicating that neither V5- nor FLAG-tagged 2N4R tau was selectively propagated over extended incubation conditions. H–K, synthetic filaments composed of 2N4R tau covalently conjugated to Alexa Fluor 488 (AF488), Cy3, or Cy5 were prepared separately in the presence of aggregation inducer octadecyl sulfate (1.5 μm tau incubated for 5 h at 37 °C), then mixed together, and incubated for an additional 24 h prior to fluorescence microscopy imaging. K, overlay composed of three channels (H–J) where white arrows mark junctions between annealed filaments.

The annealing experiment was then repeated using filaments prepared from recombinant 2N4R tau covalently labeled with Alexa Fluor 488, Cy3, or Cy5 as substrate; octadecyl sulfate as an alternative to Geranine G aggregation inducer (32); and fluorescence microscopy as detection method. When filaments composed of each labeled tau were mixed and incubated for 24 h, super-resolution fluorescence microscopy recorded the presence of fibrils with extended segments of Alexa Fluor 488, Cy3, or Cy5 fluorescence, again consistent with end-to-end annealing among the three filament populations (Fig. 4, H–K). Together, these imaging experiments provide direct evidence for tau filament annealing.

Empirical estimation of the annealing rate constant for tau filament annealing

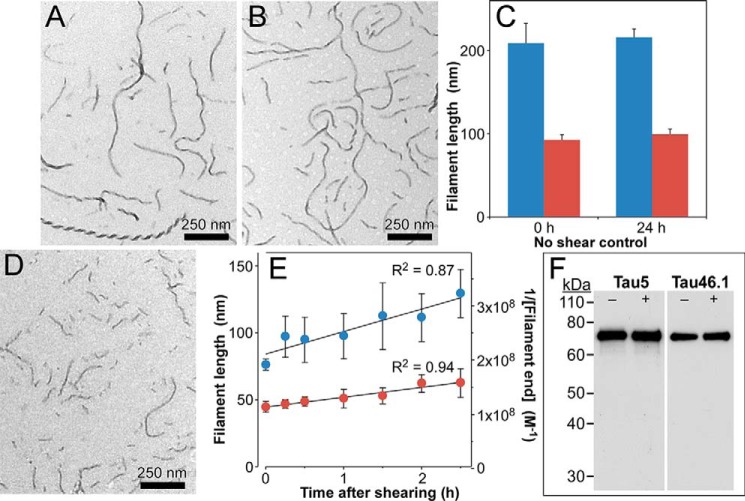
Because annealing rate depends on the concentration of filament ends (33), annealing kinetics are sensitive to acute perturbation of plateau filament length distributions (e.g. by shearing). This approach has been used to estimate annealing rates of actin filaments (24). When tau filaments composed of His₆-tau prepared in the presence of Geranine G for 24 h were incubated for an additional 0–24 h, both median and average length remained constant, consistent with the population attaining aggregation plateau (Fig. 5, A–C). However, when this filament population was sheared to transiently increase the concentration of filament ends (by decreasing filament lengths) prior to the 24-h extended incubation (Fig. 5D), a time-dependent increase in both mean and median filament lengths was observed (Fig. 5E, left axis). The His₆-tau protein remained intact throughout shearing and extended incubation periods (Fig. 5F), indicating that the increase did not result from generation of amyloidogenic truncation products (34, 35). Because filament lengths are inversely proportional to filament concentration at aggregation plateau, length data could be converted into reciprocal filament concentration units (Fig. 5E, right axis). On the basis of regression analysis, the correlation between reciprocal filament end concentration and time was positive and linear throughout the time series (Fig. 5E), in conformance with the integrated rate law for a second-order homotypic association. Under these conditions, the slope of the correlation approximates the rate constant for the process (36). Assuming that end-to-end annealing was the principal process responsible for initial velocity yielded preliminary estimates of apparent association rate constant ranging from 10³ to 10⁴ m⁻¹ s⁻¹ for this sheared filament population (Fig. 5E). These data demonstrate that 2N4R tau annealing rates are robust and measurable.

Figure 5.

Annealing time course approximates second-order kinetics. Synthetic filaments prepared from 6His-2N4R tau protein (1 μm) incubated for 24 h at 37 °C were subjected to TEM either immediately (A) or after extending incubation for an additional 24 h at 37 °C (B). C, quantification of filament length distributions (triplicate determination) revealed no significant differences between the two populations with respect to mean (blue) or median (red) lengths, indicating that aggregation processes had plateaued under these conditions. D, in contrast, shearing of 6His-2N4R filaments aggregated to plateau yielded an artificially shortened length distribution. E, sheared filaments incubated an additional 24 h at 37 °C resulted in time-dependent changes in length distribution as reflected in the mean (blue) and median (red) lengths of the filament populations (triplicate determination; left axis). Error bars represent S.D. Mean and median lengths were converted into concentrations of filament ends assuming a critical concentration of 200 nm (8) and two active ends per filament (plotted as reciprocals on the right axis). Linear regression analysis (solid lines) yielded slopes of 4.9 × 10³ and 1.1 × 10⁴ m⁻¹ s⁻¹ for the reciprocal mean and median filament concentration time series, respectively. F, 6His-2N4R filaments prepared with (+) or without (−) shearing as in A and B above were subjected to immunoblot analysis using antibodies Tau5 (2N4R epitope Ser²¹⁰–Arg²³⁰) and Tau46.1 (2N4R epitope Leu⁴²⁸–Leu⁴⁴¹) Error bars represent S.D. Immunoreactivity for both epitopes was retained, indicating that the extended aggregation and shearing process did not induce amyloidogenic fragmentation of tau protein.

Mathematical model of tau fibrillation

To rigorously quantify the contribution of annealing and other secondary processes to tau aggregation kinetics, 2N4R tau aggregation time series were fit by an equilibrium nucleation–elongation scheme (8, 37) modified to include secondary events, including secondary nucleation, fragmentation, and end-to-end annealing (Fig. 1). The nucleation component of the primary pathway was constrained to a cluster size of 2 on the basis of previous rate measurements (8). Therefore, the smallest stable filament corresponded to a trimer, which also is reported to be the minimal size for spontaneous propagation among cells in biological models (5). The elongation phase was assumed to proceed by adding or losing one monomer at a time from filament ends and to be governed by rate constants that were insensitive to filament length (38, 39). Elongation also was constrained by experimental estimation of rate constants k_e− and k_e+ (8, 30) and the assumption that both filament ends participated equally in this process. The expressions describing the primary nucleation–elongation pathway were extended to model filaments up to n = 900 protomers in length (Fig. S1, black font).

Secondary nucleation (“S”) was added to this model assuming it was governed by distinct nucleation association (k_n2+) and dissociation (k_n2−) rate constants but was mediated by the same cluster size as primary nucleation (40, 41), here a dimer. It also was assumed that secondary nuclei detached immediately from fibrils to join primary nuclei in forming a single bulk population (Fig. 1, green arrow). As a result, secondary nucleation terms were added only to the rate equations for tau monomers and dimers (Fig. S1, green font). It also was assumed that the secondary nucleation rate was proportional to filament concentration c_i once lengths met a specific threshold (i ≥ 10, corresponding to ≥2 nm in length, or approximately the length of a fully extended ³⁰⁶VQIVYK³¹¹ nucleating sequence motif (42)).

Filament fragmentation (“F”) was modeled as a first-order process governed by rate constant k_fr and filament concentration c_i. The model requires that all products of fragmentation be filamentous (i.e. at least three protomers in length), and so i must be ≥6 before being susceptible to fragmentation (Fig. 1, red arrow). As a result, fragmentation terms appear in the rate equations for all aggregates ≥3 protomers in length (Fig. S1, red font). In theory, the fragmentation rate for stiff rods depends on both filament length (i) and location of the breakage point (33). Therefore, fragmentation terms included power exponent β to capture length dependence of the fragmentation rate (Fig. S1, red font). Additionally, β was constrained to range from 0 to 4, its theoretical maximum (33). However, the model made the simplifying assumption that the probability of fragmentation was identical between all protomers of each filament (25, 43).

Finally, end-to-end annealing (“A”) was modeled as a second-order process governed by rate constant k_an and the concentrations of filaments of length i and j (i.e. c_i and c_j) (Fig. 1, blue arrow). Like fragmentation, annealing involves only filaments, and so it acts only when i and j are ≥3.

As a result, fragmentation terms appear in the rate equations for all aggregates ≥3 protomers in length (Fig. S1, blue font). In theory, the annealing rate should vary inversely with reactant lengths i and j, with magnitude dependent on the steric requirements of the annealing interaction (33). Therefore, the model included power exponent α to capture the dependence of annealing on both reactant lengths. When i = j, the power dependence of annealing rate on length is 2α. Therefore, 2α was constrained to range from 0 to 2, its theoretical maximum (33).

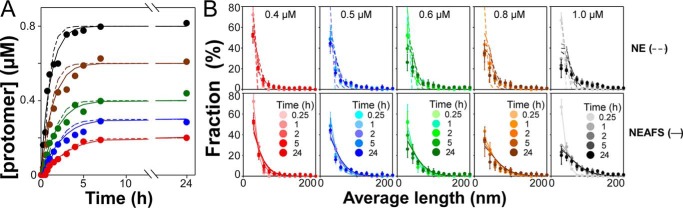
Combination of the primary and all three secondary processes created a full model termed “NEAFS.” It and the simplest model containing only the primary nucleation–elongation (NE) steps were then fit to aggregation time series collected at different bulk 2N4R tau concentrations (0.4, 0.5, 0.6, 0.8, and 1.0 μm) in the presence of Geranine G aggregation inducer using quantitative TEM imaging (44). These assay conditions were used because they allowed quantification of 2N4R fibrillation in terms of both total filamentous protomer concentration (Fig. 6A) and relative filament length distribution (Fig. 6B) at times through fibrillation plateau. The resulting time series were fit by simultaneously minimizing the root square error between observed and modeled evolution of total protomer concentration and filament length distribution. On visual inspection, the simple NE model approximated the evolution of total protomer concentration (Fig. 6A) but not of length distribution at any time point at any bulk tau concentration (Fig. 6B). Specifically, this model was unable to recapitulate the skew toward longer lengths in observed length distributions (Fig. 6B). In contrast, the full NEAFS model more accurately captured protomer concentrations and length distributions at all tau concentrations and time points (Fig. 6, A and B). These results indicate that accurate description of 2N4R tau aggregation kinetics requires inclusion of secondary processes.

Figure 6.

Fits of models to protomer concentration and length distribution time series. Full-length recombinant 2N4R tau (0.4 μm, red; 0.5 μm, blue; 0.6 μm, green; 0.8 μm, brown; 1 μm, black) incubated (37 °C) in the presence of Geranine G (100 μm) inducer was assayed for fibrillation as a function of time (up to 24 h) in terms of protomer concentration (A) and length distribution (B) using TEM methods. Each point represents the average of triplicate determination, and dashed and solid lines represent fits to data points by the NE and NEAFS mathematical models, respectively. Error bars represent S.D.

Model evaluation

To clarify the relative contribution of each secondary process to tau aggregation dynamics, the NEAFS model was subjected to global sensitivity analysis (GSA). GSA quantifies how changes in model input values affect model output, defined here as goodness of fit to the observed protomer concentration and length distribution time series at 1 μm bulk tau concentration. This condition was analyzed because it populated length bins even at the earliest time points (Fig. 6B). The resulting sensitivity indices for each kinetic parameter represent the fraction of output variance resulting from changes in parameter value on a normalized scale of 0 to 1. The first-order index (S_i) represents model variance explained by the variability of each parameter individually, whereas the total sensitivity index (S_Ti) includes additional impact arising through interactions among parameters. GSA revealed that the quality of fit of the NEAFS model to protomer concentration was strongly sensitive to primary processes (i.e. parameters associated with nucleation and extension) but only weakly sensitive to secondary processes aside from annealing (Fig. 7A). These results were consistent with secondary processes having limited impact on aggregation rate (relative to primary processes) and no effect on aggregation plateau (15). Moreover, differences between S_Ti and S_i were small (Fig. 7A), indicating that the quality of the NEAFS fits were driven directly by individual parameters rather than by interactions among them. In contrast, the quality of fit of the NEAFS model to length distribution data were far more sensitive to secondary processes and to interactions among them (Fig. 7B). With respect to modeling methods, these results indicate that protomer concentration and length distribution data provide complementary information. With respect to tau aggregation dynamics, the calculated sensitivity indices (Fig. 7, A and B) predict that annealing and fragmentation, but not secondary nucleation, are the major secondary processes under in vitro 2N4R aggregation conditions.

Figure 7.

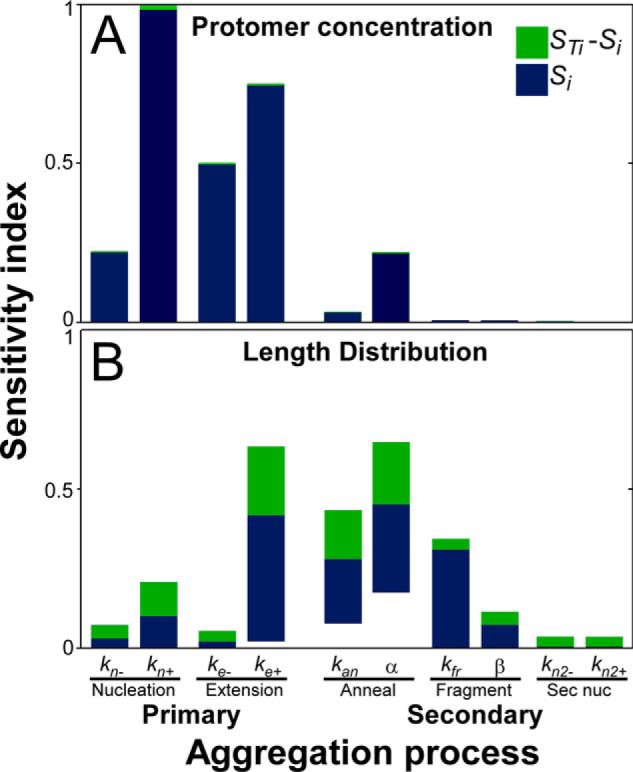
Global sensitivity analysis of the NEAFS model. Main (S_i) and total sensitivity (S_Ti) indices were calculated for the NEAFS model fit to the 1 μm starting tau concentration data set. Indices describe the sensitivity of model output in the forms of protomer concentration (A) or length distribution (B) to changes in NEAFS input parameters. Higher-order interactions were then calculated as S_Ti − S_i and plotted along with S_i to identify sources of sensitivity. Each bar represents the maximum and minimum sensitivity indices for each parameter across all time points (A) or all length bins at all time points (B). Sec nuc, secondary nucleation.

To test this hypothesis, various combinations of the primary and each of the three secondary processes were prepared to yield six additional mathematical models composed of nucleation–elongation steps with either one (NEA, NEF, and NES) or two (NEAS, NEFS, and NEAF) secondary processes. Fits of all models to protomer concentration (Fig. S2) and length distribution (Fig. S3) time series were then compared visually with those for NE and NEAFS. Consistent with GSA, protomer concentrations were only weakly sensitive to inclusion of secondary processes. In fact, models encoding combinations of any two or more secondary processes fit protomer concentration data similarly well (Fig. S2), perhaps reflecting the positive impact of adding free parameters to modeling output. However, only inclusion of both annealing and fragmentation processes could simultaneously capture length distribution (Fig. S3). These data confirmed that parameters associated with secondary nucleation were unessential for the fit and that the simplest model capable of rationalizing both total protomer concentration and filament length distribution time series was NEAF.

All rate constants calculated from the final NEAF model are summarized in Table 1. The intrinsic rate constant for 2N4R tau filament annealing (k_an) was estimated as 4.9 × 10⁴ m⁻¹ s⁻¹, confirming that annealing is a secondary process involved in 2N4R tau aggregation kinetics. We conclude that 2N4R tau filament ends are active, that they can efficiently engage in homotypic interactions (i.e. with tau monomers, oligomers, and filaments), and that their engagement in secondary processes takes the form of an equilibrium with filament fragmentation.

Table 1.

NEAF model parameters

Symbol	Description	Units	Values
kn+	Nucleation association rate constant	m−1 s−1	84
kn−	Nucleation dissociation rate constant	s−1	0.82
ke+	Elongation association rate constant for monomer addition to both ends	m−1 s−1	5.0 × 104
ke−	Elongation dissociation rate constant for monomer subtraction from both ends	s−1	1.0 × 10−2
kan	Annealing rate constant (for trimers)	m−1 s−1	4.9 × 104
kfr	Fragmentation rate constant (hexamer)	s−1	2.3 × 10−5
2α	Annealing power exponent for length dependence	None	−0.70
β	Fragmentation power exponent for length dependence	None	0.50

Discussion

These results are significant in two respects. First, they clarify the individual contributions of secondary pathways to tau aggregation dynamics. We found that end-to-end annealing is a relatively efficient interaction at short filament lengths, with its intrinsic rate constant (k_an) being of similar magnitude to that for monomer elongation (k_e+) (Table 1). Although our estimate for k_an is orders of magnitude slower than that reported for F-actin annealing (25), the value is typical of diffusion-mediated protein–protein interactions in the absence of long-range attractive forces (45). As tau filaments lengthen, however, the annealing rate changed by the power exponent 2α = −0.70 (Table 1). The negative sign of 2α indicates that annealing efficiency decreased with increasing length (as predicted by theory (33)), whereas its magnitude suggests either that the steric requirements for annealing were low (as reported for F-actin (46)) or that filament diffusion rates were limited by aggregate flexibility. Indeed, the estimated value of 2α approximates the power exponent for length-dependent flexible linear polymer diffusion (−0.588 (47)), consistent with the persistence length of synthetic 2N4R filaments being far lower than for actin (48).

We also found that tau fibrillation dynamics are governed by fragmentation. The intrinsic rate constant for 2N4R tau filament fragmentation (k_fr) estimated here was orders of magnitude slower than for monomer dissociation (k_e−; Table 1), consistent with the breakage of additional noncovalent bonds. However, it was faster than the constants reported for cytoskeletal assemblies such as actin (25) or for tau over weeks under oxidizing conditions (49) and more similar in magnitude to the fast rate constants estimated for prion fragmentation (49, 50). k_fr was length-dependent with power exponent β = 0.50 (Table 1). The positive sign of β indicates that fragmentation efficiency increased with increasing length (as predicted by theory (33)), whereas its magnitude was substantially lower than reported for rigid amyloid or cytoskeletal aggregates (25, 51). These data again are consistent with the flexible nature of synthetic 2N4R tau filaments.

Together, fragmentation and annealing rate constants create an equilibrium at filament ends (K_eq) that influences the size distribution of tau aggregates in a population. Tau aggregate size distribution is further controlled by power exponents β and 2α, which act together to render K_eq length-dependent. For example, K_eq was subnanomolar and strongly supportive of annealing when 2N4R tau filaments were short, whereas it became less favorable as filaments lengthened (Fig. 8). Post-translational modifications that rigidify tau protein (such as phosphorylation (52, 53)) and thereby increase filament persistence length are predicted to raise power exponents β and 2α still higher (33). Increases in power exponents would be predicted to sharpen the length dependence of K_eq (Fig. 8) to favor fragmentation, a process that in authentic prions is associated with propagation efficiency (19). This may reflect an additional mechanism through which tau post-translational modification can affect neurofibrillary lesion formation.

Figure 8.

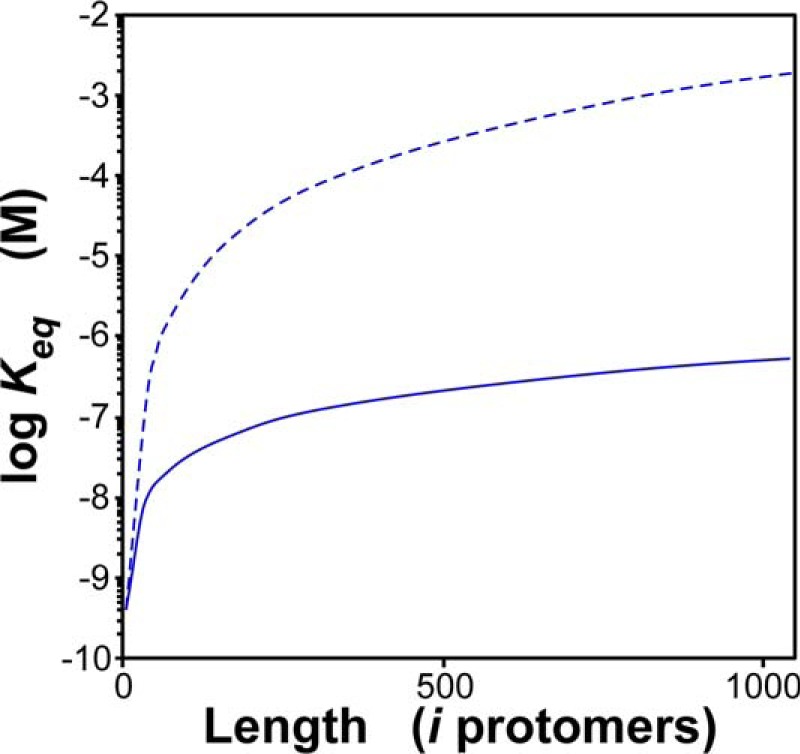
Tau filament annealing/fragmentation equilibrium is length-dependent. The solid line represents the equilibrium constant for annealing/fragmentation (K_eq) calculated from k_an, 2α, k_fr, and β values (Table 1) as a function of tau filament length, and the dashed line corresponds to K_eq calculated under identical conditions except that 2α and β were doubled to −1.4 and 1.0, respectively.

Our modeling results predict that annealing and fragmentation are the major secondary processes governing tau aggregate size, which in model systems varies inversely with biological activity (54, 55). In contrast, kinetic modeling of other cross-β-sheet aggregate–forming proteins has implicated secondary nucleation as the principal process playing this role (18). The discrepancy likely stems from the unique structure of tau filaments, which differ from other aggregates in being surrounded by a “fuzzy coat.” This structure, which has been detected on synthetic 2N4R tau filaments (56) as well as authentic brain-derived filaments (57), arises from the intrinsically disordered regions of tau protomers that extend away from the cross-β-sheet aggregate core (58). The fuzzy coat limits access of tau filament surfaces to macromolecules (56), including the tau monomers necessary to support secondary nucleation. Our kinetic modeling results were consistent with these reported observations.

Second, the results also have implications for aggregation methodology. Protomer concentration time series, whether captured by thioflavin dye fluorescence (59), centrifugation (60), TEM imaging (herein), or other method, are sensitive primarily to the primary aggregation processes of nucleation and elongation. In contrast, here it was found that length distribution data are especially sensitive to secondary processes and therefore provide information that complements protomer concentration data. The two together efficiently restrict parameter space even under conditions where the number of free parameters is high.

In summary, these data identify tau filament ends as mediating a range of homotypic interactions that include monomers and other tau aggregates. Indeed, it has been argued that exposed β-sheet ends are fraught with danger and, as a result, are blocked to lessen risk of interaction (29). Reports of tau aggregate interactions with α-synuclein (61) suggest that tau filaments engage in heterotypic interactions as well. It will be important to investigate whether interactions occurring at tau filament ends also can directly contribute to aggregate toxicity.

Experimental procedures

Tau preparations

Recombinant human tau proteins were expressed and purified as described previously (62). Preparations included isoform 2N4R (63) and 2N4R fused to N-terminal tags containing polyhistidine (6His-2N4R (62)), FLAG tag (FLAG-2N4R; i.e. MDYKDDDDK-2N4R), and V5 tag (V5–2N4R; i.e. MGKPIPNPLLGLDST-2N4R). Expression plasmids for FLAG-2N4R and V5–2N4R were built by inserting synthetic DNA sequence into the NcoI-NdeI sites of vector pT7c-htau40 (62). Fluorophore-labeled monomeric tau was prepared from 2N4R tau and Alexa Fluor 488–, Cy3-, or Cy5-maleimide as described previously (64).

Immunoblot analysis

Tau proteins were fractionated by SDS-PAGE (8% acrylamide) and subjected to immunoblotting on polyvinylidene difluoride membranes as described previously (65) using rabbit polyclonal anti-V5 antibody (Bethyl Laboratories, A190-120A) and mouse monoclonal antibodies anti-FLAG (Agilent, 200471), Tau5 (2N4R epitope Ser²¹⁰–Arg²³⁰ (62, 66)), and Tau46.1 (2N4R epitope Leu⁴²⁸–Leu⁴⁴¹ (62, 67)) as primary antibodies. Immunoreactivity was detected by the enhanced chemiluminescence Western blot analysis system (GE Healthcare) and captured on film. Molecular weight was estimated relative to prestained markers (Thermo Fisher, LC5800).

Tau aggregation

Recombinant human tau preparations were incubated (37 °C without agitation unless stated otherwise) in assembly buffer (10 mm HEPES, pH 7.4, 100 mm NaCl, 5 mm DTT) for up to 24 h in the presence of fibrillation inducers Geranine G (100 μm; TCI America (44)) or octadecyl sulfate (60 μm; Lancaster Synthesis (68)). Aggregation products were then either analyzed immediately, sheared, or mixed and further incubated in the presence of additional 5 mm DTT. Shearing was completed by passing aggregation products through a 28-gauge syringe needle four times. Total tau protomer concentration in filaments and relative filament length distributions were estimated as described previously (44).

Transmission electron microscopy

For length measurements, reaction aliquots (50-μl final volume) were treated with 2% glutaraldehyde (final concentration), mounted on Formvar/carbon-coated grids (Electron Microscopy Sciences), and negatively stained with 2% uranyl acetate as described previously (44). Random fields were viewed with a Tecnai G2 Spirit BioTWIN transmission electron microscope (FEI Co.) operated at 80 kV and 23,000–49,000× magnification. Filament lengths were estimated as described previously (44).

For immunogold labeling experiments (44), reaction products were adsorbed directly onto grids and then incubated with rabbit polyclonal anti-V5 antibody (Bethyl Laboratories) and/or mouse monoclonal anti-FLAG (Agilent) for 4 h at 4 °C. After washing with 1% BSA in PBS, grids were incubated with 12-nm gold–conjugated goat anti-rabbit IgG (heavy + light) EM grade (Jackson ImmunoResearch Laboratories) and/or 5-nm gold–conjugated goat anti-mouse IgG (Sigma-Aldrich). Samples were then stained with 2% uranyl acetate for 1 min and viewed by TEM as described above.

3D structured illumination microscopy

Super-resolution 3D structured illumination microscopy images were captured on a DeltaVision OMX-SR system (GE Healthcare) equipped with a 60×/1.42 numerical aperture oil immersion objective. Tau filaments labeled with Alexa Fluor 488, Cy3, or Cy5 were excited with 488, 568, or 640 nm laser light, respectively, with resulting fluorescence captured with a dedicated complementary metal-oxide semiconductor (CMOS) camera for each line. Image stacks (1.25 μm) were acquired with a z-distance of 0.125 μm and computationally reconstructed to generate super-resolution optical serial sections. Images were reconstructed with Softwork software package version 6.5.2 (GE Healthcare). Subsequent image processing was performed using ImageJ software.

Mathematical modeling

Systems of ordinary differential equations derived from aggregation model NEAFS (Fig. S1) were scripted in MATLAB (2016b, The MathWorks) and converted to C code using MATLAB Coder. To systematically eliminate secondary processes from the overall model, rate constants governing annealing (k_an), fragmentation (k_fr), or secondary nucleation (k_n2+ and k_n2−) were set to 0. Numerical solutions were generated using ODE15s, a MATLAB function that implements the variable order method for solving stiff ordinary differential equations (69). The models were fit to recombinant 2N4R aggregation data consisting of total protomer concentration developed over 24 h at 0.4, 0.5, 0.6, 0.8, and 1 μm bulk tau levels and filament length distributions at every time point (8). Parameters were allowed to vary except k_e+ and k_e−, which were constrained within 2-fold of their experimentally estimated values (8). Fitting yielded systematically calculated parameter sets that minimized the root square error for both time series and length distributions at each bulk tau concentration.

Main (S_i) and total (S_Ti) sensitivity indices were calculated using the extended Fourier amplitude sensitivity test (eFAST) (70) and either the quality of fits (i.e. root square error) to protomer concentration or length distribution time series as model output. Parameter space corresponding to best-fit parameters ±15% variation was searched using random phase shift resampling (n = 15 shifts) to ensure stability of the estimates (71). For two-dimensional data (i.e. protomer concentration versus time), sensitivity indices were calculated for each time point and expressed as a range, whereas for three-dimensional data (i.e. length distribution versus time) each time point represents the average sensitivity index across all length bins. All mathematical simulations and analyses were scripted and performed in MATLAB.

Author contributions

C. J. H., R. B., and J. K. conceptualization; C. J. H. and J. K. resources; C. J. H. and R. B. formal analysis; C. J. H. and J. K. supervision; C. J. H. and J. K. funding acquisition; C. J. H. and R. B. writing-original draft; C. J. H. and J. K. project administration; C. J. H., R. B., and J. K. writing-review and editing; R. B. and J. K. methodology.