Voltage-induced long-range coherent electron transfer through organic molecules

Significance

Charge transfer through organic molecules is extensively studied theoretically and experimentally owing to its importance in basic biological processes. Long-distance electron transport through such molecules, which are typically insulating, is commonly attributed to thermally activated hopping. We introduce an additional mechanism that supports electron transfer across appreciable distances, even at zero temperature. It originates from the electric potential that is either internally created or externally applied before charge flows. The electronic wavefunctions are dramatically changed by this potential, allowing them to efficiently mediate current. This mechanism can explain recent experiments where electron transfer shows only a weak temperature dependence. Our result is an important contribution to the long-standing challenge of developing a comprehensive theory for charge transfer through organic molecules.

Abstract

Biological structures rely on kinetically tuned charge transfer reactions for energy conversion, biocatalysis, and signaling as well as for oxidative damage repair. Unlike man-made electrical circuitry, which uses metals and semiconductors to direct current flow, charge transfer in living systems proceeds via biomolecules that are nominally insulating. Long-distance charge transport, which is observed routinely in nucleic acids, peptides, and proteins, is believed to arise from a sequence of thermally activated hopping steps. However, a growing number of experiments find limited temperature dependence for electron transfer over tens of nanometers. To account for these observations, we propose a temperature-independent mechanism based on the electric potential difference that builds up along the molecule as a precursor of electron transfer. Specifically, the voltage changes the nature of the electronic states away from being sharply localized so that efficient resonant tunneling across long distances becomes possible without thermal assistance. This mechanism is general and is expected to be operative in molecules where the electronic states densely fill a wide energy window (on the scale of electronvolts) above or below the gap between the highest-occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). We show that this effect can explain the temperature-independent charge transport through DNA and the strongly voltage-dependent currents that are measured through organic semiconductors and peptides.

Nonadiabatic charge transfer through organic molecules is commonly described as a two-stage process (1). First, electronic energies of the reductant (donor) and oxidant (acceptor) become degenerate as a result of polarization fluctuations of the molecule and the surrounding medium. Second, charge is transmitted between the donor and the acceptor. As a result, the charge transfer rate is proportional to the product of the probabilities of these two events (1–3). For localized donor and acceptor states, the thermally activated energy matching usually dominates the charge transfer rate and is often well described by the Marcus formula (1). This reorganization energy shrinks as the donor and acceptor states become more delocalized: for example, in very large chromophores or in metal–molecule–metal junctions. There, the charge transfer rate is instead limited by the electron transmission probability. Consequently, electron transmission characteristics are directly accessible through transport experiments.

To describe the second part of the charge transfer process, which is the focus of this work, the molecule is often treated as a bridge connecting donor and acceptor (4, 5). Such models have helped identify two important mechanisms for electron transmission through short and long organic molecules (this is reviewed in ref. 6). At short distances ($\lesssim 2-3\text{nm}$) and large energy separation between the bridge orbitals and the donor/acceptor ($>1\text{eV}$), the dominant electron transport mechanism is quantum tunneling (7–10). Thus, the transport probability decays exponentially with the donor-acceptor distance. At longer distances, charge transfer proceeds by thermally activated (incoherent) single-step or multistep hopping.

This study considers the influence of an applied electric field on bridge-mediated charge transfer. For simplicity, we first examine a bridge where each site $n$ hosts a single orbital of energy ${\epsilon }_n$ (Fig. 1A). The corresponding Hamiltonian is

$$H=-\sum _{n=1}^{N-1}{t}_n\left(c_{n+1}^{†}{c}_n+c_n^{†}{c}_{n+1}\right)+\sum _{n=1}^N{\epsilon }_n{c}_n^{†}{c}_n+\sum _{n=1}^N{\mathcal{V}}_n{c}_n^{†}{c}_n.$$ [1]

Here, $c_n^{†}$ ($c_n$) creates (annihilates) an electron on site $n$ of a bridge with length $L=N{d}_0$, where $d_0$ is the intersite distance. The first term in Eq. 1 describes the coupling $t_n$ between neighboring orbitals. The second term accounts for the energy ${\epsilon }_n$ of each orbital. The final term describes the local energy shift due to the electric field ${\mathcal{E}}_n=\left({\mathcal{V}}_{n+1}-{\mathcal{V}}_n\right)/e{d}_0$, where $eV\equiv {\mathcal{V}}_L-{\mathcal{V}}_0$ is the electrostatic potential energy drop along the molecule.

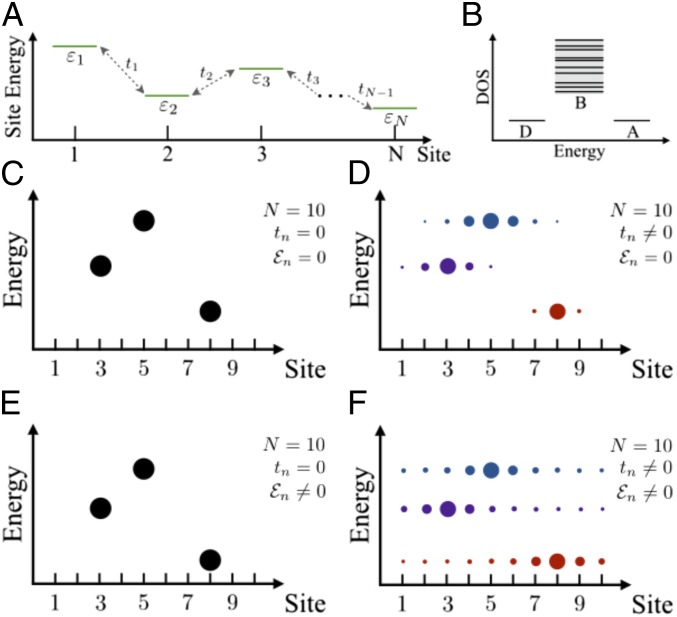
Fig. 1.

Schematic illustrations of the Hamiltonian introduced in Eq. 1, which describes a molecular bridge, and of the corresponding DOS are shown in A and B, respectively. Without an applied electric field (${\mathcal{E}}_n=0$) and for vanishing intersite couplings ($t_n=0$), each electronic state is localized on a single site (C). When $t_n\ne 0$, neighboring orbitals mix, but the system’s eigenstates are localized with an energy-dependent localization length (D). In the presence of an applied electric field (${\mathcal{E}}_n\ne 0$), the electronic eigenstates are localized when $t_n=0$ (E) but acquire power-law tails when $t_n\ne 0$ (F). The sizes of the circles in C–F indicate the probability amplitude on each site, and in each panel we illustrate only part of the eigenstates (3 out of 10).

While our main goal is to examine the effect of the applied field on the bridge-mediated transport, we begin by summarizing the existing paradigm for bridge-mediated transport at ${\mathcal{V}}_n=0$ (Fig. 1 C and D). The density of electronic states (DOS) in the molecule, corresponding to the Hamiltonian in Eq. 1, depends on both ${\epsilon }_n$ and $t_n$ and extends over a finite energy window (Fig. 1B). For example, if all $t_n=t$ and all ${\epsilon }_n=\epsilon$, a single band of extended states forms with energies between $\epsilon -2t$ and $\epsilon +2t$ (SI Appendix). An incoming electron with energy $E$ in this window is transmitted with a probability of order unity. In this case, the electron transport is only sensitive to the couplings between electrodes and bridge. An incoming electron with energy outside of the band can either tunnel through the molecule or hop incoherently from the donor to the bridge and then to the acceptor.

A periodic bridge model without disorder in nearest neighbor couplings or site energies rarely describes well real organic molecules. Even for nearly periodic chemical structures (e.g., DNA with a single repeating base pair or conducting organic polymers), the surrounding environment, the nuclear degrees of freedom, and thermal fluctuations create disorder in the orbital energies ${\epsilon }_n$ and the intersite couplings $t_n$ of the bridge (11). Since these fluctuations are slow compared with the electron traversal time, each electron transferring through the molecule experiences different ${\epsilon }_n$ and $t_n$ (12). It is, therefore, convenient to separate the uniform and random contributions to the site energies and nearest neighbor couplings by writing them as ${\epsilon }_n=\epsilon +U_{\text{dis}}\left(n\right)$ and $t_n=t+{\tau }_{\text{dis}}\left(n\right)$, where $U_{\text{dis}}\left(n\right)$ and ${\tau }_{\text{dis}}\left(n\right)$ average to zero over space ($n$).

Measuring the dc current through these molecules amounts to averaging over the thermally accessible disorder that is available to the molecule. This randomness localizes the states in the bridge (Fig. 1D), and the electron transmission probability at zero temperature drops exponentially with distance even within the band energy $\epsilon -2t\lesssim E\lesssim \epsilon +2t$ (SI Appendix). At high temperatures, a power-law decay of the transmission with distance is established by a mechanism of sequential thermally activated hopping (13, 14). When the contacts and bridge host electronic states that are close in energy, extended delocalization via flickering resonance is important at intermediate molecular lengths (11). This process is activated, as is multistep hopping, with a characteristic temperature dependence that is determined by the free energy offsets of the participating bridge sites and the reorganization energies for moving the electron charge. Models based on (combinations of) tunneling, hopping, and flickering resonance can successfully explain a sizable portion of the experimental data.

Growing numbers of systems involving biological molecules and/or $\pi$-conjugated constructs are not well described by the existing theoretical frameworks. Specifically, these structures exhibit temperature-independent electron transport over distances exceeding $3\text{nm}$ (6, 15–19). At these distances, however, tunneling and flickering resonances become very small, and the only available mechanism for charge transfer is via thermally activated hopping. This emerging body of experimental observations suggests that an alternative mechanism may control long-range electron transmission. Our work is motivated by the additional observation that temperature-independent electron transport is strongly voltage dependent. For example, in the 10-nm-wide organic semiconductor films measured in ref. 15, the current doubles as temperature is changed from 100 to 250 K but grows by four orders of magnitude as the applied voltage is increased from 1 to $2\hspace{0.17em}\text{V}$. A detailed summary of these experiments is presented in SI Appendix.

Our analysis of how applied electric fields affect charge transport through bridges is based on a theory that was established for amorphous semiconductors (20–26). We find that, although the electric field only weakly affects the orbitals at each site, it changes the spatial structure of the electronic eigenstates in the bridge from decaying exponentially with distance to power law (Fig. 1 E and F). The corresponding transmission probability for an electron with energy $\epsilon -2t\lesssim E\lesssim \epsilon +2t$ decays with the molecular length as a power law, even at 0 K. We show that this transport mechanism becomes particularly important when electronic states of the bridge have energies that are within a few hundred millielectronvolts of the electrodes’ Fermi energies. Thus, the model described here applies to the temperature-independent, voltage-sensitive electron transport reported in refs. 15, 16, and 18. We first demonstrate the effect of an applied electric field on the bridge model of Eq. 1. Then, we construct a tight-binding model for transport through DNA, and we show the dependence of its transport properties on the applied voltage.

Electrostatic effects on charge transport in organic systems have been discussed in the past. For example, applying an electric potential can reduce the energy barriers for tunneling or hopping without significantly perturbing the electronic states of the bridge (27–29). Moreover, thermal hopping assisted by an electric field was observed in organic semiconductors (30–33), and field effects were used to explain the fast charge separation observed in photovoltaic cells (34–36). These electrostatic effects do not account for the qualitative change in the bridge’s electronic states discussed here.

Model

We now analyze the influence of an applied electric field on electron transport through a bridge described by Eq. 1. Here and throughout the paper, $U_{\text{dis}}\left(n\right)$ is drawn randomly from a uniform distribution of uncorrelated site energies in the domain $\left[-W,W\right]$ (a Gaussian distribution yields similar results). For the purpose of illustration, we take the intersite couplings to be uniform (nonrandom), ${\tau }_{\text{dis}}\left(n\right)=0$, and $W=t$. Our numerical calculations use the methods of refs. 21 and 37 (more details are in SI Appendix). The averaging over different disorder realizations mimics the effect of low-frequency vibrational modes on the system’s energetics. In all calculations, the averaging was performed for at least 500 realizations until convergence was reached. We set $E=0$ to be the lowest-energy eigenvalue of the band of bridge states without disorder and electric field (i.e., $\epsilon =2t>0$). We first examine the case of a linear electrical potential drop along the molecule (i.e., ${\mathcal{V}}_n=-e\mathcal{E}{d}_{0}n$), where $\mathcal{E}$ is the uniform electric field. In SI Appendix, we show that other choices of the potential behave qualitatively the same.

Without an external electric field ($\mathcal{E}=0$) but with $U_{\text{dis}}\ne 0$, eigenstates of Eq. 1 with energies $0<E<4t$ are localized near particular bridge sites and decay with distance as $\mathrm{\Psi }\left(n\right)\sim e^{-n{d}_0/{\ell }_{\text{loc}}\left(E\right)}$. The electronic states are smeared over a (small) number of neighboring sites. Near the bottom of the band, $E\ll 2t$, the energy dependence of the localization length is ${\ell }_{\text{loc}}\left(E\right)\sim \left(t{d}_0^{2}E\right)/\mathrm{\Sigma }$, where $\mathrm{\Sigma }\propto W^2{d}_0$ is defined through the spatial correlations of the disorder potential $d_0{N}^{-1}{\sum }_{p=1}^N{U}_{\text{dis}}\left(n+p\right)U_{\text{dis}}\left(m+p\right)=\mathrm{\Sigma }{\delta }_{n,m}$ (38). The linear dependence of ${\ell }_{\text{loc}}$ on $E$ is characteristic for disordered systems where (Anderson) localization arises from interference effects and is not sensitive to the physical origins of the disorder (39). The exponential decay of the wavefunctions and the zero-temperature electron transmission probability through the bridge are illustrated in Fig. 2 A and B.

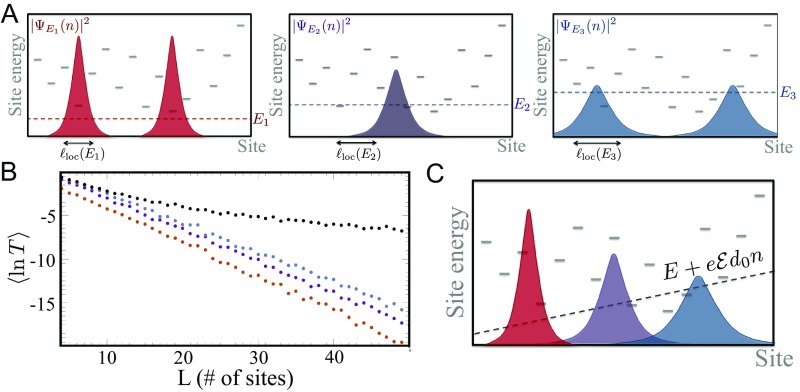
Fig. 2.

A schematically illustrates typical electronic probability densities in a one-dimensional disordered bridge (gray lines denote onsite energies). The three probability densities are at energies $E_1=0.01t$ (red), $E_2=0.05t$ (purple), and $E_3=0.09t$ (blue). All wavefunctions decay exponentially with the distance, but their localization lengths grow with energy. B illustrates the length dependence of the transmission probability $T$ calculated for these energies; specifically, we plot the disorder-averaged logarithm of $T$. At all three energies $E_1$ (red), $E_2$ (purple), and $E_3$ (blue), the transmission decays exponentially with system size. By contrast, the transmission probability (at energy $E=0.05t$) decays with $L$ as a power law in the presence of an electric field ($e\mathcal{E}{d}_0=0.03t$), as is also demonstrated by the logarithmic plot in Inset. The origin of this dramatic change is illustrated in C. The electric field shifts the wavefunctions, previously at $E_1$, $E_2$, and $E_3$, closer in energy. This allows them to hybridize, resulting in a power-law decay of the wavefunctions as discussed in the text.

Transmission Probability in the Presence of an Electric Potential

When the electric field $\mathcal{E}$ is nonzero, the electronic eigenstates of the bridge no longer decay exponentially with distance at all energies. At low energies, near the bottom of the band, the electronic states instead assume a power-law form $\mathrm{\Psi }\left(n\right)\sim n^{-\alpha \left(\mathcal{E}\right)}$, where $\alpha \left(\mathcal{E}\right)\propto 1/\mathcal{E}$. This quasidelocalization arises from two key effects of the external electric field on the electronic structure. First, the energy of each unperturbed ($\mathcal{E}=0$) localized eigenstate acquires a position-dependent energy shift: $E\left(n\right)=E\left(0\right)+e\mathcal{E}{d}_{0}n$ (Fig. 2C), and therefore, states with very different localization lengths can become close in energy. Second, the electric field mixes these near-resonant energy levels to create quasidelocalized states. The resulting wavefunctions can be approximated by replacing the localization length ${\ell }_{\text{loc}}\left(E\right)$ by ${\ell }_{\text{loc}}\left(E\left(n\right)\right)\sim t{d}_0^2\left(E\left(0\right)+e\mathcal{E}{d}_{0}n\right)/\mathrm{\Sigma }$. Averaging ${\ell }_{\text{loc}}\left(E\left(n\right)\right)$ over space gives (23)

$$\begin{array}{ll}\hfill \mathrm{\Psi }\left(n\right)& \sim \exp \left[-\sum _{m=1}^n\frac{d_0}{{\ell }_{\text{loc}}\left(E\left(m\right)\right)}\right]\sim \exp \left[-\frac{\mathrm{\Sigma }}{t{d}_0}\sum _{m=1}^n\frac{1}{E+e\mathcal{E}{d}_{0}m}\right]\hfill \\ \hfill & \hspace{1em}\underset{n\gg E/e\left|\mathcal{E}\right|d_0}{\to }{\left(\frac{E}{e\mathcal{E}{d}_{0}n}\right)}^{\frac{\mathrm{\Sigma }}{t{d}_0^{2}e\mathcal{E}}}\hfill \end{array}$$ [2]

for $\mathcal{E}>0$. The presence of these quasidelocalized states produces a transmission probability $T\sim {\left|\mathrm{\Psi }\left(L\right)\right|}^2$ that agrees well with the numerical results of Fig. 2B for $N>10$. This description sets bounds on the electric field magnitudes that can enhance electron transport. The electronic states arising from the Hamiltonian of Eq. 1 are concentrated mainly in the energy window $0<E<4t$. As the localization length grows for $E<2t$ but decreases for $E>2t$ (SI Appendix, Fig. S1), enhancement of the transmission by the electric field occurs when $e\mathcal{E}L<2t$. We show below that the corresponding electric field energies are comparable with the molecular ionization energy.

Voltage Dependence of Transmission and Current

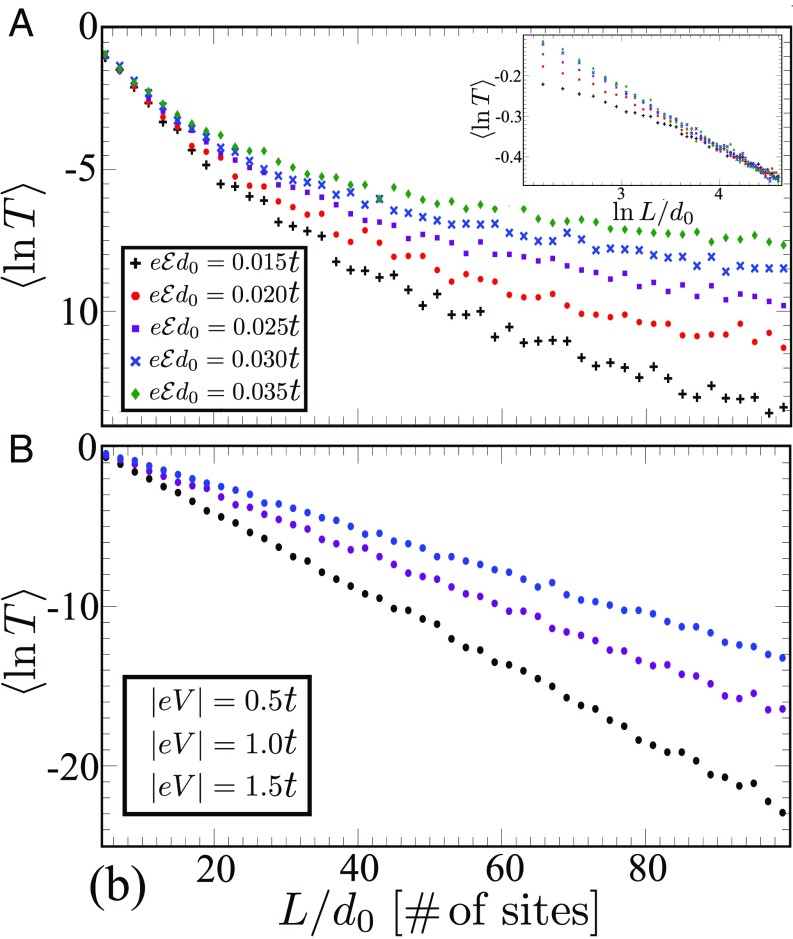
Fig. 3 shows calculations of the transmission probability for electrons with energy $0.05t$ as a function of the bridge length for different $\mathcal{E}$ (Fig. 3A) and different $V$ (Fig. 3B). Our analysis of the wavefunctions (Eq. 2) indicates that the transmission probability at large $L$ is $\ln \left(T\right)\sim \alpha \ln L$, where $\alpha \sim 1/\mathcal{E}$. This large $L$ behavior agrees with the numerical calculation for $T\left(E,L\right)$ in Fig. 3A (21): it arises because many states of different localization lengths are mixed by the electric field at long distances. At short distances, only a small number of states contributes to the transport, and the calculated transmission drops exponentially with length.

Fig. 3.

The logarithm of the transmission probability at $E=0.05t$ averaged over disorder is plotted vs. length for different electric fields (A) and voltages (B). At large $L$, the transmission probabilities as a function of the electric field collapse to a single curve (A, Inset) when the scaling $⟨\ln T⟩e\mathcal{E}{d}_0+g\left(e\mathcal{E}{d}_0\right)$ is applied; here, $g\left(e\mathcal{E}{d}_0\right)$ is a nonuniversal function of the electric field. This scaling supports the prediction that $T\propto L^{-\alpha }$ with $\alpha \propto 1/\mathcal{E}$. For a fixed voltage, the electric field decreases with $L$ and results in an exponential decay of the transmission with length.

The steady-state current’s length dependence in many experiments is measured as a function of voltage $V$ rather than electric field. For fixed $V$, Eq. 2 indicates that the transmission probability decays exponentially with distance

$$T\left(E,L\right)\sim {\left|\mathrm{\Psi }\left(L\right)\right|}^2\underset{eV\gg E}{\to }\exp \left[-2\frac{\mathrm{\Sigma }L}{t{d}_0^2\left|eV\right|}\ln \left(\frac{\left|eV\right|}{E}\right)\right],$$ [3]

and the characteristic decay length is $t{d}_0^2\left|eV\right|/\mathrm{\Sigma }\ln \left(\left|eV\right|/E\right)$, which exceeds ${\ell }_{\text{loc}}\left(E\right)=t{d}_0^{2}E/\mathrm{\Sigma }$ (Fig. 3B). Thus, for fixed $V$, the transmission depends exponentially on $L$ and has a voltage-dependent $\beta$ parameter. Indeed, a voltage dependence of this kind is reported in ref. 16. The transmission curves in Fig. 3 are reminiscent of the length dependence of the current/electron transfer rate that was measured for nucleic acids (40, 41). Importantly, our mechanism of transport is temperature independent and supports long-distance electron transport even at zero temperature. At higher temperatures, thermally assisted mechanisms enhance transmission probabilities and can eventually become dominant.

The voltage drop along the molecule need not be linear as we assumed above. Screening effects, even when weak, modify the potential energy along the molecule. Nevertheless, the conclusions do not change qualitatively as long as the local electric field ${\mathcal{E}}_n=\left({\mathcal{V}}_{n+1}-{\mathcal{V}}_n\right)/e{d}_0$ is nonzero over a length larger than ${\ell }_{\text{loc}}\left(E\right)$. In this case, sufficient number of states are mixed by the electric field, and the wavefunctions remain quasiextended $\mathrm{\Psi }\left(n\right)>n^{-\alpha \left(\mathcal{E}\right)}$, where $\alpha \left(\mathcal{E}\right)<\alpha \left({\mathcal{E}}_{\text{min}}\right)$ with ${\mathcal{E}}_{\text{min}}=\underset{n}{min}\left[{\mathcal{V}}_{n+{\ell }_{\text{loc}\left(E\right)}}-{\mathcal{V}}_n\right]/e{\ell }_{\text{loc}}$. Therefore, although the transmission coefficient decreases as screening effects grow, it is still enhanced as long as the electric field does not vanish inside the molecule (SI Appendix). The change in transmission probability caused by screening highlights the role of polarizability in the electric field-induced transport mechanism. For highly polarizable molecules, we expect the field-induced mechanism not to be particularly relevant. When the polarizability is temperature dependent (e.g., through vibrational modes), the electron transmission inherits a temperature dependence through the electric field ${\mathcal{E}}_n\to {\mathcal{E}}_n\left(T\right)$.

We have focused so far on the transmission probability of an injected electron or hole at a given energy inside the band ($0<E<4t$) under the influence of an applied voltage. This is most relevant for photoinduced electron transfer experiments. In molecular junction measurements, however, electrons are injected over a range of energies. The electric current flowing through a molecule that is bridging the electrodes can be readily computed from the transmission probability via the Landauer formula (42, 43), $I=-e/h\int dET\left(E,L\right)\left[f_{\mathcal{T}}\left(E-{\mu }_R\right)-f_{\mathcal{T}}\left(E-{\mu }_L\right)\right]$. Here, $f_{\mathcal{T}}$ is the Fermi distribution function at temperature $\mathcal{T}$, and ${\mu }_L$ (${\mu }_R$) is the chemical potential of the left (right) lead. The voltage serves two purposes: (i) it creates an electric field inside the molecule, and (ii) it injects electrons with energy between ${\mu }_R$ and ${\mu }_L$. To find the current, we calculate the transmission probability as a function of energy for a given voltage and substitute it into the zero-temperature Landauer formula:

$$I=\frac{e}{h}{\int }_{{\mu }_R}^{{\mu }_R+eV}dE\hspace{0.17em}T\left(E,L\right).$$ [4]

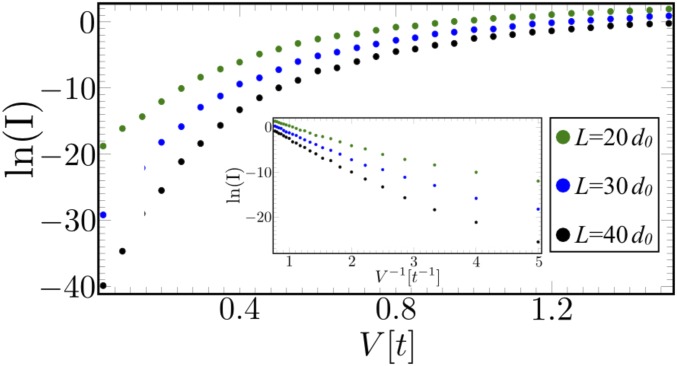
This calculation requires knowledge of the difference between the Fermi energy of the contacts and the bridge orbitals as well as of the screened electric potential inside the molecule (which can substantially differ from the external potential). In Fig. 4, we show the current as a function of voltage for molecules of different lengths, assuming no screening. The chemical potential at the right lead is taken to be $-0.5t$ (i.e., well below the lowest-energy states of the bridge with $U_{\text{dis}}=0$ and $V=0$). Since the main contribution to the current is from electrons injected at energies near ${\mu }_R+eV$, the characteristic decay length of the current is proportional to $V^{-1}$.

Fig. 4.

The current as a function of voltage for molecules of various lengths. The chemical potential in the right lead is fixed to be $-0.5t$, while it changes with the voltage ${\mu }_L={\mu }_R+eV$ in the left lead. Inset shows that the current grows exponentially with the voltage as $\ln \left(I\right)\sim V^{-1}$.

We note that the current–voltage characteristics in Fig. 4 resemble the data in refs. 15, 16, and 18, where electron transport was measured through layers of oligothiophene, bis-thienyl benzene oligomers, and homopeptides, respectively. The former two found that the scaling $\ln \left(I\right)\propto V^{1/2}$ fits the experimental data better than $\ln \left(I\right)\propto V^{-1}$. We show in SI Appendix that such scaling corresponds to a partially screened electric potential. Specifically, a power-law decay of the potential given by ${\mathcal{V}}_n={\mathcal{V}}_0{\left[{\left(n{d}_0/\lambda \right)}^2+1\right]}^{-1}$, where $\lambda$ is the screening length, reproduces the scaling seen in experiment. Since some degree of screening is expected in any molecule, we discuss its general effect in SI Appendix. In addition, we provide a comprehensive comparison with the experimental findings (15, 16, 18).

Applying the Model to Nucleic Acids

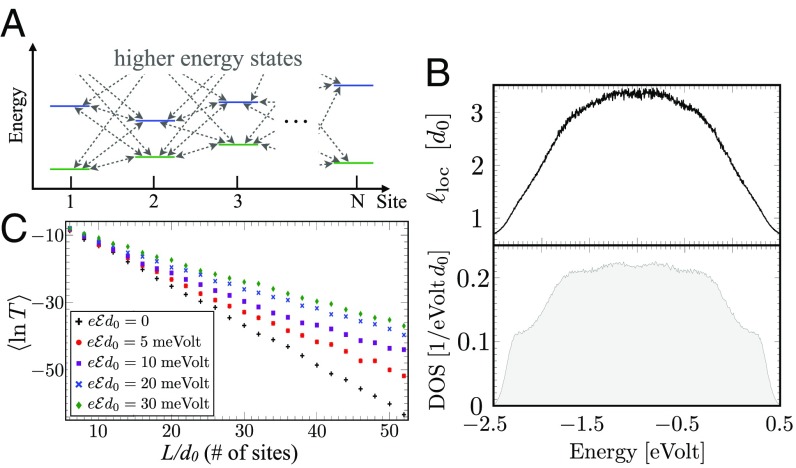
To connect our model to specific molecular charge transport studies, we consider the example of electron transmission through DNA. Charge current through DNA is most often mediated by the flow of holes (44), and the most relevant bridge band comprises superpositions of nucleic acid base pair HOMOs. Of the four bases [guanine (G), adenine (A), cytosine (C), and thymine (T)], G has the highest-energy HOMO, and hole transport is expected to occur through it (45, 46). Therefore, we first examine a nucleic acid duplex composed only of G–C base pairs, which we model using the Hamiltonian of Eq. 1 with $U_{\text{dis}}={\mathcal{V}}_n=0$. The typical HOMO-LUMO gap size is several electronvolts (47). The average coupling between neighboring G–C base pairs is $t\approx 100\hspace{0.17em}\text{meV}$ (44), and the fluctuations in the site energies $U_{\text{dis}}\left(n\right)$ are predicted to have an SD of 300–500 meV (11, 48). In our approximation of uniformly distributed disorder, $U_{\text{dis}}\left(n\right)\in \left[-W,W\right]$ with $W=300$–500 meV or equivalently, $W=3t$–$5t$. While the disorder is somewhat stronger than in the previous sections, we expect our previous results to hold qualitatively provided that we can neglect any additional bands formed by other nucleobase orbitals. This is valid if mixing of states within the same band is stronger than with states from different bands (i.e., when the voltage is smaller than both the bandwidth and the energy difference between the bands).

In experiments on DNA, large voltages are frequently used, and a single orbital per site would not be sufficient to capture the transport properties correctly. Consequently, we amend our model to include lower-energy orbitals below the G’s HOMO. These orbitals can originate from the purines and pyrimidines (49) as well as the backbone (50). The extended model Hamiltonian is

$$\begin{array}{ll}\hfill H& =-\sum _{n=1}^{N-1}\sum _{i,j=0}^{\infty }{t}_{i,j}\left(n\right)\left(c_{i,n+1}^{†}{c}_{j,n}+c_{j,n}^{†}{c}_{i,n+1}\right)\hfill \\ \hfill & \hspace{1em}+\sum _{n=1}^N\sum _{i=0}^{\infty }\left[{\epsilon }_i+U_{\text{dis}}^i\left(n\right)\right]c_{i,n}^{†}{c}_{i,n}+\sum _{n=1}^N\sum _{i=0}^{\infty }{\mathcal{V}}_n{c}_{i,n}^{†}{c}_{i,n}.\hfill \end{array}$$ [5]

The typical energy-level spacing $\mathrm{\Delta }{\epsilon }_{i+1}{=\epsilon }_i-{\epsilon }_{i+1}$ is in the range 300–600 meV (49, 50), which is comparable with $3t-6t$, and the DOS is nearly continuous (51). Although the HOMO energies ${\epsilon }_i$ are not spaced uniformly, our calculations are not very sensitive to the exact values of $\mathrm{\Delta }{\epsilon }_i$. Hence, we take $\mathrm{\Delta }{\epsilon }_i=400\hspace{0.17em}\text{meV}$ for all $i$ in our simulations. Because disorder in the couplings produces the same effect as increasing the site energy disorder in the single-orbital model (Eq. 1), unequal couplings do not strongly alter the previous results. By contrast, the possibility of mixing different orbitals can be important for the model of Eq. 5. Quantum chemical calculations find that the electronic coupling terms $t_{i,j}\left(n\right)$ in the most common double-helix DNA structure (known as B-DNA) vary from 10 to 200 meV (44). Following these estimates, we take $t_{i,j}\left(n\right)$ to be uniformly distributed in $\left[\mathrm{0,200}\text{meV}\right]$ for $i=j$ and in $\left[-200\text{meV},200\text{meV}\right]$ for $i\ne j$.

Fig. 5A illustrates the model Hamiltonian of Eq. 5. Fig. 5B shows the corresponding DOS as well as the energy-dependent localization length when the first five HOMO levels on each site are included $\left(i=0,\dots 4\right)$ and the disorder potential $U_{\text{dis}}\left(n\right)$ is uniformly distributed in $\left[-400\text{meV},400\text{meV}\right]$. Despite the different parameters, the continuous window with a nonzero DOS and the growth of the localization length as the energy is lowered (increased) near the top (bottom) of the band are features that are shared by the simpler model of Eq. 1. It is not surprising that the effect of an applied electric field on the transmission (Fig. 5C) is similar to that of Fig. 3. We, therefore, expect the electronic states to change from exponential localization to power-law decay in the presence of an external voltage in DNA composed of G–C base pairs as for the simplified model of Eq. 1. Moderate changes to the parameters used to calculate the transmission probabilities in Fig. 5C (SI Appendix) yield only small quantitative changes.

Fig. 5.

The DOS, the energy-dependent localization length (${\ell }_{\text{loc}}$), and the transmission for a duplex DNA composed of G–C base pairs. A illustrates the model Hamiltonian in Eq. 5. The parameters used for the calculation are all described below Eq. 5. B shows the DOS and ${\ell }_{\text{loc}}\left(E\right)$ for a chain with only the first five HOMO states in each site. The localization length grows with increasing electron or hole energy. Correspondingly, the transmission probability of a hole injected at energy $E=100$ meV decays exponentially with length in the absence of an electric field (C). The length dependence of the probability changes to a power law when an electric field is applied, as in the single-orbital case (Fig. 2).

Finally, we address the influence of an applied electric field on transport through DNA molecules that include both A–T and G–C base pairs. In principle, each DNA sequence should be modeled by a bridge, where the energy levels on each site correspond to the first several HOMOs of A–T or G–C. In practice, the energies of the HOMOs of the A–T and G–C base pairs are in similar energy windows. Moreover, the energy differences between HOMOs are a few hundreds of millielectronvolts (45), similar to the onsite energy dispersion caused by disorder. Thus, the inclusion of A–T base pairs can be studied using the Hamiltonian in Eq. 5 by moderately increasing the level of disorder ($W$). In addition, the coupling between neighboring sites is enhanced, and the parameters $t_{i,j}\left(n\right)$ are distributed over a wider energy window (52). Such a treatment is consistent with the observation that electron transmission through DNA oligomers exhibits an approximately exponential dependence on the number of A–T base pairs (53, 54) and is nearly independent of the number of G–C base pairs (54). From the arguments given above, it follows that DNA molecules of arbitrary sequence should display qualitatively the same dependence of the transport probabilities on the external electric potential. In particular, the results derived for the Hamiltonian of Eq. 1 also apply for DNA.

Conclusions

We presented a mechanism that produces temperature-independent charge transport induced by an electric field. This effect provides a simple explanation for the experimental observations of temperature-independent but voltage-dependent long-range electron currents through organic films (15, 16) and DNA oligomers (17), which are otherwise difficult to explain. For molecules with a large screening length, our model provides testable predictions for the length and voltage dependence of the steady-state current. It is crucial that the electronic states in the molecule or film through which charge transfer occurs (e.g., the first few occupied high-energy orbitals in DNA) are localized as a result of strong energy fluctuations between different sites, which can consist of single atoms or nucleobases in the case of DNA. These states should also have significant coupling to neighboring sites so that the DOS is nearly continuous over a large energy window (on the order of electronvolt or more). If there are extended electronic states, such as low-lying Rydberg excitations with energies close to the HOMO or LUMO energies, these can facilitate efficient charge transport that is insensitive to the mechanism discussed here. Moreover, in organic molecules with a continuous DOS over a very narrow energy window, application of a voltage that exceeds this window mixes states that are more localized. We, therefore, predict a nonmonotonous dependence of the current on voltage. As discussed above and shown explicitly in SI Appendix, our model can predict the scaling of the current with voltage for an arbitrary electric field profile inside the molecule. The latter can be deduced from the measurable molecular polarizability. Thus, performing independent measurements of polarizability and current in relevant organic systems would provide a concrete test of our model.

In systems where transport is mediated by bridge states that are energetically distant from the electrodes’ Fermi energies by several electronvolts, the main effect of the voltage on the current would be to lower the gap, and our mechanism would only play a supporting role. By contrast, it becomes important if the transferred charges are excited to energies near or inside the band of bridge states: for example, by absorbing photons. Moreover, we wish to emphasize that previous studies of electric field-induced quasidelocalization considered solid-state systems, where the conduction band is populated by a large number of electrons for which energy loss due to joule heating (collisions with phonons) is significant and the electric field effect on transport is masked. By contrast, the small number of electrons in organic molecules and the relatively low energy loss to vibrations may make them ideal systems for realizing and studying this mechanism.