Abstract
Single-cell expression profiling (scRNA-seq) is a rich resource of cellular heterogeneity. While profiling every sample under study would be advantageous, it is time-consuming and costly. Here we introduce Cell Population Mapping (CPM), a deconvolution algorithm in which the composition of cell types and states is inferred from the bulk transcriptome using reference scRNA-seq profiles ('scBio' CRAN R-package). Analysis of individual variations in lungs of influenza virus-infected mice, using CPM, revealed that the relationship between cell abundance and clinical symptoms is a cell-state-specific property that varies gradually along the continuum of cell-activation states. The gradual change was confirmed in subsequent experiments and was further explained by a mathematical model in which clinical outcomes relate to cell-state dynamics along the activation process. Our results demonstrate the power of CPM in reconstructing the continuous spectrum of cell states within heterogeneous tissues.
Introduction
Single-cell RNA sequencing (scRNA-seq) provides a powerful approach to understanding the composition of different cell identities within a complex tissue, including discrete cell types, cell states that arise transiently during the progression of time-dependent processes, and continuous dynamic transitions within the space of possible cell states1,2. The frequency of cell types and cell states may vary between genetically distinct individuals, environments, chemical perturbations, or disease states. To investigate this variation at high resolution, it is possible to generate scRNA-seq profiles for each sample of interest and then use it to evaluate the frequency of the different cell types and states3–5. However, such studies are costly and time-consuming, and have therefore been performed only on a limited scale.
An alternative strategy would be to construct a comprehensive collection of reference scRNA-seq profiles representing various cell types and cell states. Deconvolution algorithms can then utilize those reference profiles to computationally predict the abundance of different cell types and states within a given sample, based on only the bulk expression data from that sample2,6–8. This strategy should in principle avoid the scaling issues associated with multiple scRNA-seq experiments, but in practice, using a large number of reference profiles typically results in reduced prediction accuracy9. A standard solution is to cluster the single-cell reference profiles into a relatively small number of cell-groups reference profiles10–12. However, while this clustering-based approach may provide a rough quantification of discrete cell types and states, the continuous cell-state space remains sparse and fragmented. Therefore, there is a substantial need for a deconvolution methodology that can exploit the rich spectrum of single-cell reference profiles.
Here we propose the Cell Population Mapping (CPM) method, which provides an advantageous alternative to existing deconvolution approaches, particularly in providing a fine-resolution mapping. Similarly to recent studies10–12, CPM constructs its reference collection from scRNA-seq profiles derived from one or a few relevant samples, and then exploits this collection to infer cell composition within additional, bulk-profiled samples. However, instead of focusing on quantifying a few dozens of discrete cell subtypes, CPM analyses thousands of single-cell profiles scattered across the wide landscape of cell states. Using synthetic data, we demonstrate that deconvolution with CPM significantly improves the quantification of both gradual and abrupt changes in cell abundance over the continuous space of cell types and states. Furthermore, by analyzing complex changes in lung tissues, across influenza virus-infected mice of various genetic backgrounds, we demonstrated the effectiveness of CPM in probing phenotypic diversity in large cohorts.
Results
Overview of CPM
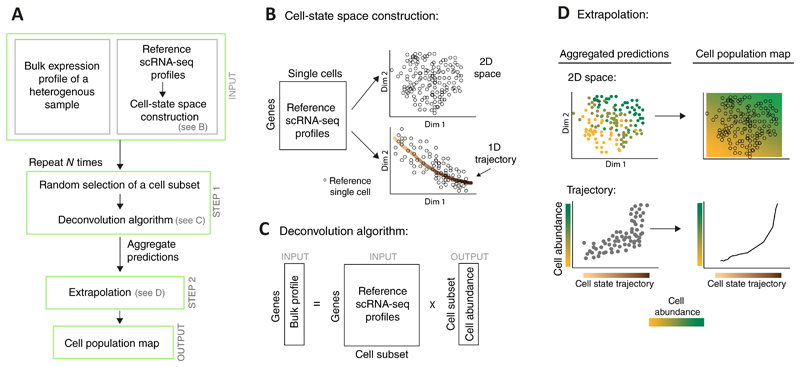
We developed CPM, a method based on computational deconvolution for identifying a cell population map from bulk gene expression data of a heterogeneous sample. In our framework, the cell population map is the abundance of cells over a cell-state space. Whereas the biological definition of a cell type refers to the core characteristics of a cell, a cell state can be thought of as the current phenotype in which a given cell type can be found (e.g., various proliferation, activation and differentiation states)1. The cell-state space specifies each cell state as a point in a multi-dimensional space; as cells undergo changes from one state to another, they travel through the space along a trajectory between these two states13. Unlike existing computational methods that are focused on reconstruction of the cell-state space from scRNA-seq data1, CPM takes as its input the previously-reconstructed cell state space of a certain scRNA-seq data, and then relies on this input to infer the abundance of each point in this space within a given bulk cell population.
Formally, CPM relies on two input types (Fig. 1A): first, a bulk expression profile of the heterogeneous cell population, and second, scRNA-seq profiles of individual single cells derived from one or a few representative samples ('reference data'). We assume that the cell-state space of the reference cells is given as input and that the particular position of each reference single cell within this space is known. The cell-state space is typically obtained by dimension-reduction (such as t-SNE14) that capture the essence of gene-regulation variation among the reference single cells (exemplified in Fig. 1B top). It is also possible to use a well-defined trajectory within this space as an alternative "one-dimensional space"; such trajectory can explicitly describe the progression of cells through a biological process (exemplified in Fig. 1B bottom).
Figure 1. Overview of the CPM algorithm.
A flowchart of the CPM pipeline (A) with illustrations of specific steps (B-D). The prior (reference) knowledge consists of single-cell RNA-seq profiles (derived from one or a few individuals) together with their associated cell-state space structure (A, top); such space may be constructed either through dimension reduction (e.g., a two-dimensional space in B, top) or through further identification of a well-defined cell trajectory (e.g., a "one-dimensional space" in B, bottom). Given a bulk expression profile of a complex tissue, CPM utilizes a deconvolution approach to infer the quantity of each reference cell (A middle, C) and then extrapolates these predictions over the entire cell-state space, thereby providing the output 'cell population map' (A bottom, D). To avoid simultaneous deconvolution with a very large number of reference profiles, deconvolution is applied N times on subsets of the reference profiles, and the inferred quantities are then aggregated.
CPM consists of two steps (Fig. 1A and Online Methods): (i) Applying a deconvolution approach [here, support vector regression (SVR) approach], which combines the bulk profile of a complex tissue with a collection of reference scRNA-seq profiles to infer the composition of cells within the complex tissue input. The output of this step is the abundance of cells at the sub-region of each reference single cell. Such prediction poses two substantial challenges: first, an accuracy problem in deconvolving a very large number of reference profiles (typically, the analysis may involve thousands of single cells15), and secondly, a potential bias owing to the non-uniform distribution of reference cells over the cell-state space. To address these challenges, CPM applies deconvolution using a relatively small subset of reference profiles, which are obtained by an unbiased random sampling to ensure that every region in the cell space has an equal chance of being sampled (Fig. 1C). The sampling and deconvolution procedures are repeated N times (here, N = 1,500), and the results are aggregated and averaged into a single inferred abundance for each reference single cell. (ii) From the inferred cell abundance in each particular reference coordinate, CPM extrapolates the cell abundance in any other cell-state coordinate (Fig. 1D). In this extrapolation it is assumed that the shape of the cell distribution over the cell-state space is continuous and smooth. We refer to this smoothed continuous output as the 'cell population map'. Notably, CPM may use input bulk data either as a relative profile (i.e., response between two samples) or as an absolute (single-sample) profile, thereby predicting relative or absolute cell-state abundance, respectively.
Performance analysis
We used a simulation framework to measure the ability of CPM to predict the cell population map at fine resolution. The simulation was based on a collection of 1860 reference scRNA-seq profiles16 taken from murine lungs during influenza virus infection and encompassing nine major immune and non-immune cell types: fibroblasts, epithelial cells, blood and lymphatic endothelial cells, T cells, B cells, NK cells, granulocytes, and cells of the mononuclear phagocyte system (MPS), encompassing monocytes (MO), macrophages (MΦs) and dendritic cells. In this reference dataset, one well-characterized trajectory is the gradual transition of cell states (within each cell type) from resting (naive)-like cells into active cells that respond to the influenza virus infection16. Synthetic bulk profiles of a complex tissue were created by mixing these single-cell profiles according to predetermined biologically-relevant functions over the cell-state space, introducing noise in the expression of genes and in the coordinates of single cells (denoted 'expression noise' and 'cell space noise', respectively). The quality of this strategy is demonstrated in Supplementary Fig. 1A and further discussed in Supplementary Note 1. CPM was compared to three alternative deconvolution methods - DCQ17, Cibersort18 and standard SVR19 - whose reference collection was the "averaged" profiles of single-cell groups (the larger the number of such single-cell groups, the higher the 'granularity' analyzed by the alternative methods; Online Methods). The 'accuracy' of predictions was evaluated by comparing the ground-truth cell abundance to the predicted abundance of each reference single cell.
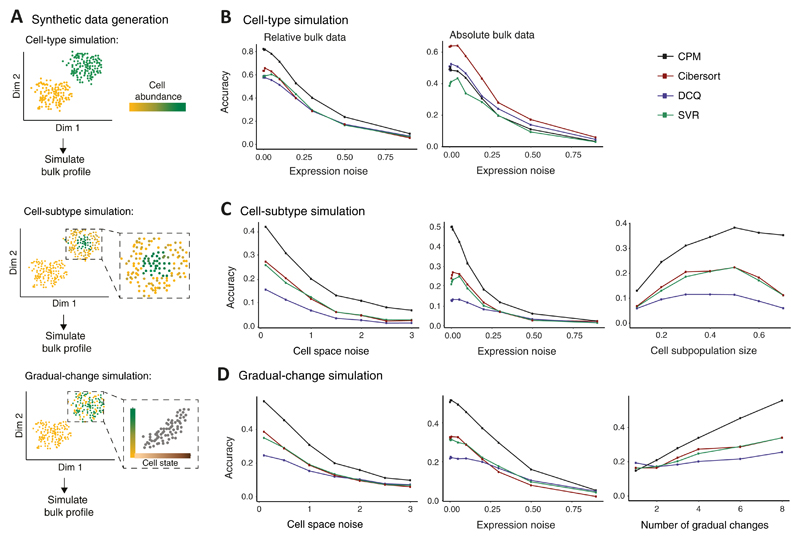
To analyze performance, we focused on three fundamental types of simulations: (i) The 'cell-type simulation', in which cell abundance varies from one cell type to another, but within each cell type, the abundance is uniformly distributed over the cell-state space; (ii) the 'cell-subtype simulation', consisting of a modified abundance of a subpopulation of cell states within selected cell types; and (iii) the 'gradual-change simulation', representing continuous alterations of cell abundance along the trajectory of cell activation states (within selected cell types) (Fig. 2A). Overall, whereas the cell-type simulation is focused on inter-cell-type variation, the cell-subtype and gradual-change simulations are focused on intra-cell-type variation, which arises from differences among cell states within the same cell type.
Figure 2. Performance assessed via synthetic data.
(A) Synthetic data were generated either by changes of cell percentage in discrete cell types ('cell-type simulation', top); by changes of cell percentage in cell subtypes, within cell types ('cell-subtype simulation', middle); or by gradual changes in cell percentage along a trajectory of cell states ('gradual-change simulation', bottom). Illustration and abbreviation are as in Fig. 1. (B−D) Accuracy of inferring cell abundance for the three simulation types: cell-type simulation (B), cell-subtype simulation (C), and the gradual-change simulation (D). Accuracy (y axis) is defined as the Pearson correlation coefficient between predicted and true cell abundance and is shown across varying data parameters (x axis) for alternative deconvolution methods (colour coded). Results are shown for bulk relative profiles (B left, C and D) or absolute profiles (B right). The alternative methods were applied with a reference dataset that was generated using granularity of 4 cell groups.
Consistent with previous observations, changes in discrete cell types were accurately modelled by the alternative deconvolution methods (Fig. 2B, Supplementary Fig. 1B). However, in the case of intra-cell-type changes in the composition of cell states (the 'cell-subtype' and 'gradual-change' simulations), CPM showed consistent improvement in prediction accuracy compared to existing deconvolution methods (relative bulk data: Fig. 2CD and Supplementary Fig. 2AB; absolute bulk data: Supplementary Fig. 3AB) within a reasonable running time (Supplementary Fig. 2CD). Unsurprisingly, CPM was able to capture the continuous nature of the input tissue, unlike the alternative deconvolution methods that could provide only a discrete approximation with lower accuracy (Supplementary Figs. 2E, 3C). Furthermore, CPM outperformed the existing methods in its ability to handle a high cell-state complexity and in its 'scalability' to a large number of reference profiles (Supplementary Fig. 2FG, detailed in Supplementary Note 1). Quantitatively similar results were also observed for varying parameter settings (Supplementary Fig. 4), using different cell-state space solutions (Supplementary Fig. 5A), and for regions of different local density within the cell-state space (Supplementary Fig. 5BC). Of note, CPM may lose power with lower sequencing depth (Supplementary Fig. 6, discussed in Supplementary Note 1).
Relationships between infection symptoms and cell abundance are a cell-state-specific property
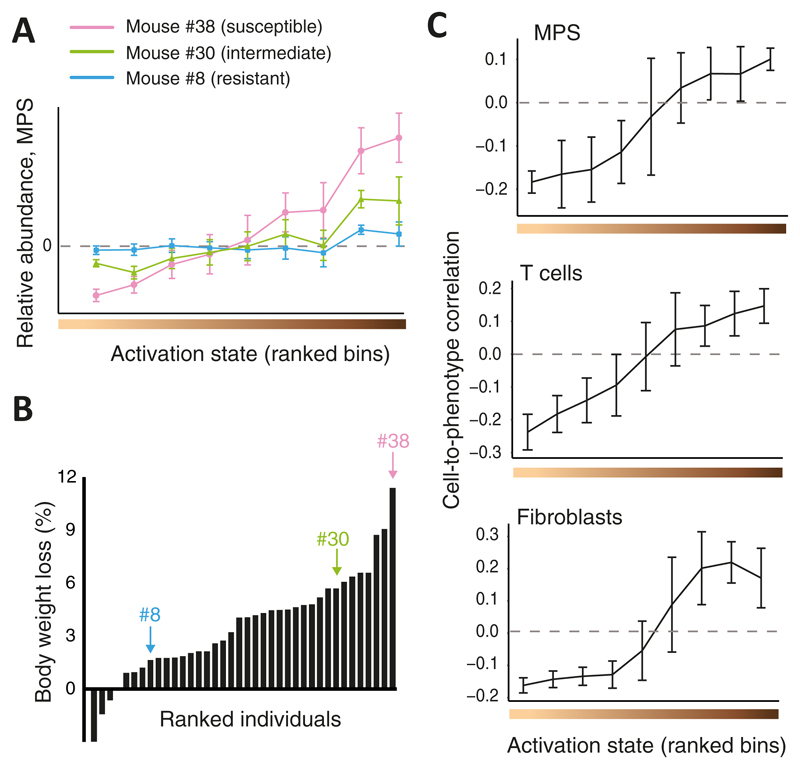
We applied CPM to investigate in-vivo influenza virus infection across the Collaborative Cross (CC) recombinant inbred strains20, a panel of mouse lines designed to mimic the phenotypic and genotypic diversity seen in human populations. To this end, we generated bulk transcriptional expression profiles derived from lung tissues of 38 infected and 34 phosphate-buffered saline (PBS)-treated control mice (typically one or two individuals of each CC strain; Supplementary Table 1, Online Methods). We transformed absolute bulk profiles into relative bulk profiles using a common control profile as the normalizer, and then applied CPM to each of these bulk profiles using the abovementioned single-cell measurements of the same experimental setting (lung tissues from influenza virus-infected mice16) as the reference data. As the cell-state space, CPM utilized the continuous sequence of cell-activation states that were previously defined for each of the nine immune and non-immune cell types in this reference dataset16. Altogether, CPM calculated a relative cell population map consisting of relative cell abundance in each cell state for each individual mouse. We found that CPM predictions varied considerably between individuals (see examples in Fig. 3A) and that this variation was robust across the N deconvolution repeats (Supplementary Fig. 7A).
Figure 3. Cellular heterogeneity during in-vivo influenza virus infection, reconstructed by CPM.
(A) Shown are CPM-inferred relative MPS abundance values (y axis), averaged over cells from each activation state bin (bins were ranked with increasing activation states from left to right; x axis), for three representative infected individuals (colour coded). n=103 cells; error bars, standard deviation. (B) Percentages of measured body weight loss (y axis) of 38 infected individuals, ranked by disease severity (x axis). Marked individuals are the three shown in A. (C) Cell-to-phenotype Pearson correlation coefficients across the 38 infected CC mice (y axis), averaged by activation state bins (x axis), presented for MPS cells (top, 103 cells), T cells (middle, 378 cells) and fibroblasts (bottom, 375 cells). Error bars, standard deviations.
While the inferred cell population maps demonstrated substantial variation, the extent to which these cell-state changes relate to the clinical outcome of disease remained unclear. To elucidate this point, we monitored one of the main clinical symptoms of murine infection, namely the body weight loss (measured at 2 days post-infection (p.i.); Fig. 3B), and calculated the correlation (across individuals) between this outcome and the inferred relative abundance of each reference cell (denoted the 'cell-to-phenotype correlation'). By splitting the reference cells into consecutive activation-state intervals (within each cell type) we could assess the variation in cell-to-phenotype correlations over the activation trajectory (illustrated in Supplementary Fig.7B). Intriguingly, cell-to-phenotype correlations across infected mice clearly manifested a gradual increase over the trajectory of cell-activation states, ranging from negative correlations at the lower (naive-like) range toward positive correlations at the upper (activated) range (mainly in T cells, MPS and fibroblasts, Fig. 3C). In fact, no particular threshold could be found that splits the activation-state trajectory into two discrete groups in which cell-to-phenotype correlations did not gradually change. Similar conclusions about the gradual change in cell-to-phenotype correlations were obtained using a second public dataset of influenza virus infection21 and using additional computational analyses (Supplementary Note 1, Supplementary Fig. 7C-H). As expected, the use of unrelated (uninfected) reference datasets and alternative deconvolution methods did not yield the same conclusions (Supplementary Note 1, Supplementary Fig. 7IJ). Taken together, these findings highlight the advantage of a CPM model that is based on a continuous space of cell states, and further emphasize the importance of using reference and bulk data derived from a similar experimental setting.
Experimental validation of predictions
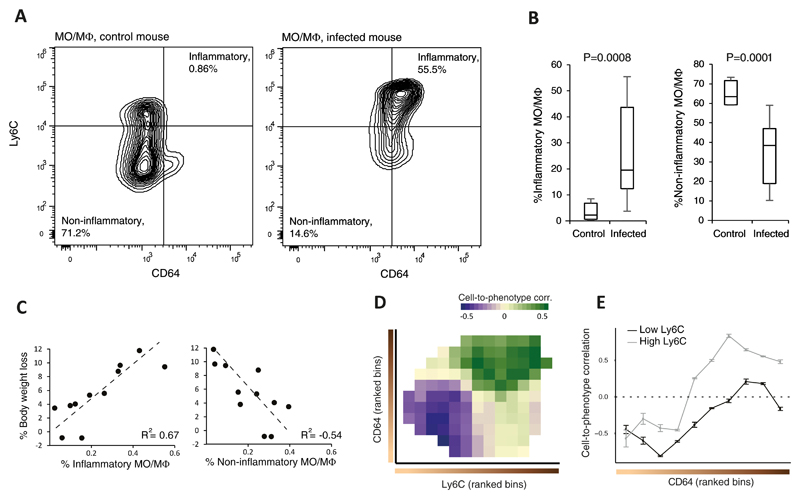
To test for the presence of a gradual change in cell-to-phenotype relationships as predicted by CPM, we performed flow cytometry analyses of lung cells from influenza-infected CC mice at 2 days p.i. We focused on MO/MΦ cell types, which constitute a major fraction of the total MPS population. To determine the activation states of MO/MΦs we used flow cytometry with two established cell-activation markers, CD64 and Ly6C22. The use of these markers enabled us to quantify the distribution of cells over a trajectory of activation states ranging from non-inflammatory (CD64lowLy6Clow) to inflammatory (CD64highLy6Chigh) MO/MΦs. As expected, the fraction of inflammatory MO/MΦs was higher in infected mice than in PBS-treated controls (Fig. 4AB; Supplementary Table 1). Encouraged by this observation we then used the flow cytometry measurements to calculate cell-to-phenotype correlation, i.e., the correlation between the clinical readout (weight loss at 2 days p.i.) and the MO/MΦ cell fractions enumerated by flow cytometry across infected individuals. The correlation analysis yielded several lines of evidence that validated the reconstruction by CPM: (i) inflammatory MO/MΦs showed a positive cell-to-phenotype correlation (r2 = 0.67, Fig. 4C left); (ii) non-inflammatory MO/MΦs had a negative cell-to-phenotype correlation (r2=−0.54, Fig. 4C right); (iii) cell-to-phenotype correlations increased with each of the two separate activation markers (Fig. 4D); and (iv) flow cytometry analysis confirmed a gradual increase in correlation values over the CD64-cell-state continuum for both Ly6Chigh and Ly6Clow cell states (Fig. 4E). The lack of cell-to-phenotype correlation obtained when we used the total MO/MΦs count (r2=0.1, Supplementary Fig. 8A) further validated the contention that cell-to-phenotype relationships depend on particular cell-activation states, thus accentuating the importance of fine-resolution deconvolution mapping. Whereas the observed association between activated-inflammatory MO/MΦs and severe physiological responses (Fig. 4C left) has been previously reported23–25, the opposite trend of naive MO/MΦs (Fig. 4C right) and the continuous transition between negative and positive correlations over the activation process (Fig. 4E) have not been previously described.
Figure 4. Confirmation of gradual changes in relationships of cells to physiology over a trajectory of cell-activation states.
Flow cytometry analyses of lung-derived MO/MΦs, stained for CD64 and Ly6C activation markers; cell percentages were calculated relative to the entire population of lung MO/MΦs. (A) Shown are representative analyses of control (left) and infected (right) animals (CC line 5001A). Statistics for the remaining individuals is shown in B. (B) Box plots showing the percentages of inflammatory MO/MΦs (CD64+Ly6C+; left) and non-inflammatory MO/MΦs (CD64-Ly6C- ;right) in 11 infected and 5 control CC animals. Boxes represent the 25th, 50th and 75th percentiles; whiskers show maxima and minima. P-values are indicated, one-sided t-test. (C) Shown are percentages of body weight loss of infected individual mice (y axis) as a function of their percentage of inflammatory (left) and non-inflammatory (right) MO/MΦs (x axis). (D) Shown are cell-to-phenotype correlation coefficients (calculated across the infected mice), binned and ranked according to the levels of the activation markers (CD64, y axis; Ly6C, x axis) and colour-coded in each bin. (E) Cross sections of the 2-dimensional map in D. Data are mean ± stdev across n=100 bootstrapped samples.
Inferring dynamics with a Markov model
Given that the CPM-reconstructed map yielded accurate predictions for MPS cells, we next investigated the temporal dynamics over the activation trajectory for these cells. Our results showed that the association between cell abundance and weight loss varies in a gradual manner along the MPS-activation process (Figs. 3C, 4E), but that the total MPS counts did not correlate with the body weight loss (Supplementary Fig. 8A). A parsimonious explanation for this observation is that the phenotypic diversity is associated with inter-individual variation in temporal dynamics along the activation process; for example, inter-individual variation in onset times, or in cell-state progression rates. Like scRNA-seq data26, the CPM-reconstructed data provided valuable information that allowed such temporal dynamics to be computationally reconstructed. For instance, we focused here on cell-state progression, and since its underlying mechanism is a stochastic process, we assumed a Markov process of naive-to-activation transitions between consecutive cell states (Supplementary Fig. 8B, Online Methods). We used this model to predict the probability of transition ('transition rate') between sequential states in each individual mouse (see examples in Supplementary Fig. 8C). With the assumption that the activation-onset time in all individuals is the same, comparison of the inferred transition rates might reveal complex transition-rate-to-phenotype relationships (Supplementary Fig. 8D). By calculating transition rates based on CPM predictions, we found that weight loss is indeed positively correlated with transition rates over a wide range of the MPS activation axis (at its early and intermediate parts; Supplementary Fig. 8E). These CPM-predicted transition rates closely matched the rates calculated from flow cytometry measurements (Supplementary Fig. 8EF). Overall, this theoretical approach suggests a mechanistic model of in-vivo influenza-outcome diversity and demonstrates a general strategy for uncovering inter-individual variation in temporal dynamics.
Discussion
Now that the ability to generate scRNA-seq data of multiple experiments exists, it should become possible to gain a detailed understanding of variations in cellular heterogeneity that correlate with clinical and molecular factors3. However, such analyses will continue to pose substantial challenges: generation of scRNA-seq measurements across multiple experiments is time-consuming, costly and requires expertise in single-cell technologies. In addition, fine-resolution deconvolution using a large repertoire of cell states is not readily available due to a trade-off between tissue-complexity and scalability (Supplementary Fig. 2F). CPM tackles this challenge by allowing reconstruction of cellular heterogeneity at fine resolution in many bulk-profiled samples, relying on reference single-cell data from only one or a few representative samples (Fig. 1). Using synthetic data we showed here that although changes in the quantity of a discrete cell population are accurately modelled by existing deconvolution methods (Fig. 2B), CPM outperforms these methods in accurately mapping the continuous spectrum of cell states within discrete cell types (e.g., Fig. 2CD).
We further demonstrated the power of CPM by using complex clinical and genomics data derived from in-vivo infections of genetically-diverse mice. First, CPM successfully recapitulated the previously reported23–25 positive cell-to-phenotype correlations in the high-activation range (Figs. 3C). In addition, CPM revealed previously unreported negative cell-to-phenotype correlations at the low-activation range, as well as gradual changes in the relationships between cellular heterogeneity and in-vivo phenotypes along the trajectory of cell-activation states (Fig. 3C). Experimental validation of MO/MΦ cells supported these gradual changes from negative to positive correlations (Fig. 4C-E), demonstrating that CPM-inferred cell-state-specific quantities can provide valuable information needed for modelling phenotypic diversity in large cohorts.
We believe that CPM is likely to prove useful for additional analysis, such as calculations of cell-state-specific expression within complex tissues27, reconstruction of temporal dynamics of cell-state progression (Supplementary Figure 8), and studying cellular heterogeneity within the massive body of existing bulk genomics data such as TCGA28 and GTeX29. Furthermore, as extensive single-cell catalogues (e.g. the Human Cell Atlas30) are currently constructed, it may soon become possible to analyze cellular heterogeneity in bulk expression data without requiring expertise in single-cell technologies (discussed in Supplementary Note 1).
Online Methods
The CPM algorithm
CPM takes as input both bulk transcriptome and reference data. The input bulk transcriptome is represented in a column vector of expression values across all genes. Bulk expression values can be either the measured expression values in a single heterogeneous tissue or the relative values between two experiments, such as disease vs. healthy heterogeneous tissues. The input reference data consists of scRNA-seq profiles, represented in a matrix of the format Rij where the ij-th entry is the expression levels of gene j in single cell i. A row vector Ri in this matrix is a RNA-seq signature of a certain reference single cell i (referred to as a 'reference profile'). We further assume that the main split of cells into broad cell type categories is known, and that low quality cells were already removed16. Additionally, we assume that each cell type is associated with a pre-determined neighborhood structure, denoted the 'cell-state space' structure. The cell-state space is represented as a set of coordinates where the i-th entry represents the position of reference single cell i within the cell-state space. The cell space should be constructed in a pre-processing step through various single-cell analysis techniques. For instance, it is possible to exploit standard dimension reduction methods that provide cell positions in a low dimensionality space (such as t-SNE or using several principle components14). Alternatively, it is possible to determine the position of cells along a certain trajectory of cell states and utilize this trajectory as a 1-dimensional cell-state space14.
CPM starts with a preprocessing step in which genes carrying many dropout events (here, fraction of zero expression values across single cells > 90%) are filtered. Both the reference profiles and the input bulk profile are then standardized. Next, the algorithm proceeds in two steps: first, infer the level of the reference cells within the complex tissue, and then use this information to predict cell abundance over the entire continuous cell-state space.
Step 1 (deconvolution)
To infer the abundance level of the reference cells in a bulk expression profile, we solve the following linear regression: , where Ri is the expression vector of all genes in reference single cell i, U is the vector of expression levels of all genes in the complex tissue, and βi indicates the unknown abundance of single cell i in the complex tissue. As in Cibersort18, we achieve robustness by solving this regression using linear SVR (the "LiblineaR" R package19) to prevent biases due to outliers. To further improve performance in the presence of a large number of reference profiles, we use a consensus approach, in which the abovementioned SVR inference is repeated N times for N different subsets of the reference profiles (denoted 'reference subsets'), each reference subset consists of Ns profiles. Predicted abundance values of the N runs are then averaged for each individual reference cell.
We apply several improvements that make step 1 more robust and accurate. First, we perform an unbiased random selection of the reference subset (without replacements) so that the selected subset is uniformly distributed over the cell-state space. To address this, each reference cell is sampled by random sampling of a 'pivot point' within the cell-state space using inverse transform sampling and then choosing an arbitrary reference cell in the proximity of this pivot point. A grid was added to the cell-state space so that all reference cells that fall in a certain entry of this grid are defined as the proximity group for a pivot that falls in this entry. The number of grid-entries, calculated on each cell type separately, is the number of reference single cells divided by the cell neighborhood size. N was set to a value in which each reference cell would be selected to an average depth of at least Nr repeats. In particular, given that cells in high-density grid-entries are less likely to be selected, we calculate N based on the highest-density entry by requiring that each cell in this entry would be selected to an average depth of Nr repeats.
The second improvement is that each SVR run is applied on a set of genes that is tailored for a specific reference subset. The basic idea is to select a gene set that offers the best ability to distinguish between the reference profiles. Similarly to Cibersort18, for each gene we compare its expression in different scRNA-seq profiles using one-way ANOVA (the Nd nearest neighbors of each cells are used to calculate the within-group variance component); each gene is then associated with the cell profile in which it attains the highest average expression, and the Ng top ANOVA-score genes associated with each cell profile are selected. In particular, Ng is defined as the number that minimizes the 'condition number' that is calculated with the R 'kappa' function.
Step 2 (extrapolation)
To infer the abundance of a given candidate cell state, CPM averages the predicted abundances of its Nd nearest-neighbor reference cells. This leads to a smoothed cell abundance over the entire cell-state space. We refer to this solution as the 'cell population map'.
Overall, the methodology relies on three parameters: the number of deconvolution repeats (determined by Nr), the reference subset size (Ns) and the cell neighborhood size (Nd). Here we used Nr=5, Ns=50 and Nd=10 as our default setting. The contribution of CPM is further discussed in Supplementary Note 1.
The reference single-cell data
The reference data is a collection of 1860 single cells that were collected from the lungs of a C57BL/6 mouse at 2 days after infection with 4.8x103 pfu (in 40 μl phosphate buffered saline - PBS) of the PR8 influenza virus (published data16 from GEO accession number GSE107947). As previously reported16, this collection already excludes poor-quality cells, and the cells were already partitioned into nine cell-type groups (in total, 92 B cells, 135 blood endothelial cells, 24 epithelial cells, 291 granulocytes (GN), 345 lymphatic endothelial cells, 375 fibroblasts, 103 mononuclear phagocyte system (MPS) cells, 117 natural killers (NK) cells and 378 T cells). Furthermore, it was previously defined, for each of the nine immune and non-immune cell type, the progression of cell states through a trajectory of an antiviral-activation response16. We refer to this continuum as the 'trajectory' of cell activation states. Briefly, the cell-state trajectory was constructed in two steps: first, a group of 101 generic-response genes were defined (consisting of all genes that were upregulated in all nine cell types during influenza infection); next, for each single cell, its average expression level across these generic genes was used as the activation-state trajectory16; in Figs. 3AC, 4DE and Supplementary Figs. 7C-G,I,J, this trajectory was further binned into equal intervals. Unless stated otherwise, this reference single-cell collection, together with its cell type groups and cell-state trajectory, were utilized as input in our analyses. We note that scRNA-seq data from a replicate infected mouse16 was used to corroborate the results (Supplementary Figure 7F).
Synthetic data analysis
Synthetic bulk profiles were generated by mimicking the heterogeneity of cells within a biological complex tissue. Each synthetic bulk profile was generated as a mixture of reference scRNA-seq profiles according to pre-designed fractions of single cells. Our pre-designed fractions of cells represent prevalent realistic scenarios, including changes in the overall level of a certain subpopulation (the cell-type and cell-subtype simulations), as well as changes along cellular trajectories such as cell-state shifts (the gradual-change simulation). We generated both absolute and relative synthetic bulk profiles and in both cases tested the entire range of noise parameter (ranging from an entirely non-informative data to an almost-zero noise). The 'accuracy' was calculated as the Pearson correlation between the actual and predicted fractions of cells. Technical details about synthetic data generation and the accuracy score are available in Supplementary Note 1.
For each synthetic data collection, CPM's performance were compared to alternative state-of-the-art deconvolution algorithms, including (i) the digital cell quantifier (DCQ) algorithm17 that builds on elastic net regression; (ii) Cibersort18 that utilizes a non-iterative linear support vector regression; and (iii) a standard linear SVR. SVR was applied using L2-regularized L2-loss support (primal) vector regression because it provided similar accuracy compared to alternative settings but is faster than the alternatives. SVR was applied with the optimal setting of its C (the "LiblineaR" R package19) and ε=0.001 (all results were maintained with alternative εvalues such as 0.1 and 0.001; Supplementary Fig. 2H). Using SVR and Cibersort, in the case of relative data we retained the negative coefficients, as previously suggested17. For the CPM algorithm, we further tested the effect of modifying the Nr, Ns and Nd parameters. Since the three compared deconvolution methods rely on a relatively small number of input reference profiles, the reference data was constructed by grouping the scRNA-seq profiles. We generally used K-means clustering of the scRNA-seq data16 and then used the averaged profile of each group as a reference profile. Supplementary Note 1 further describes alternative reference-construction methods whose accuracy levels are presented in Supplementary Fig. 4E). Each of the compared methods was analyzed using a variety of K (granularity) values. Finally, we further compared CPM to an alternative approach in which cell composition is evaluated through enrichment of each individual reference profile (an 'enrichment scheme', as previously described31, detailed in Supplementary Note 1).
To validate that the mixture of single cells fully resembles real-data bulk profiles, we generated synthetic bulk expression values as a mixture of scRNA-seq of an uninfected C57BL/6J mouse (2075 cells derived from the lung tissue, partitioned into nine cell types16), using quantities that were previously measured within the lungs of naive C57BL/6J mice (flow cytometry fractions from previous studies22,32). We further measured bulk lung profiles of a naive C57BL/6J mouse (Supplementary Table 1) and found a good match between measured and computationally-synthesized bulk data (Supplementary Fig. 1A), supporting the validity of aggregating single cells into synthetic bulk profiles.
Mice
The present study used female mice aged 7-9 weeks from the Tel-Aviv University (TAU) collection of Collaborative Cross recombinant inbred mice20 and the C57BL/6J strain. The mice were raised at the Animal Facility at the Sackler Faculty of Medicine in TAU. All experimental mice and protocols were approved by the Institutional Animal Care and Use Committee (IACUC) of TAU, approval numbers 04-14-049, which adheres to Israeli guidelines and follows the NIH/USA animal care and use protocols. Mice were housed on hardwood chip bedding under 12h light/dark cycle at 21–23°C. Mice given tap water and standard rodent chow diet ad libitum since their weaning day until the end of the experiment.
In-vivo influenza virus infection
Mouse-adapted PR8 strain, influenza virus A/Puerto Rico/8/34 (A/PR/8/34, H1N1), was persistently grown in hen egg amnion, and its effective titer was quantified. All mice were anesthetized with 7mg/mL Ketamine and 1.4 mg/mL Xylazine at 0.1 ml/10 gr body weight, I.P. Animals were then infected intranasally with PR8 (4.8·103 pfu in 40 μL PBS), whereas mock-treated ('control') animals received only 40 μL of PBS. All mice were monitored daily for percentage of body weight loss and clinical disease manifestations, and sacrificed at 48 hours post treatment. Of note, this experimental setting closely resembles the one of the reference scRNA-seq data16 (e.g., the same gender, time point and virus strain, and a similar age and virus doses).
RNA isolation, library construction and pre-processing
To test CPM on complex tissues, murine lungs were harvested immediately after the time of sacrifice, sliced into small pieces, homogenized using BeadBlaster Microtube Homogenizer (90sec, 4000rpm) in the presence of QIAzol, and used for total RNA extraction using the miRNeasy Mini Kit (Qiagen, CA). Library quality and concentration was measured using a TapeStation System (Agilent Technologies) and a Qubit Fluorometric Quantitation (Life Technologies) as described earlier17. mRNA sequencing libraries were constructed as previously described17. Absolute bulk profiles were generated through reads alignment and transcript quantification as described earlier17 (detailed in Supplementary Note 1). Absolute profiles were transformed into "relative" profiles using a common control profile as the normalizer, where the control profile was pooled from the PBS-treated mice. Relative profiles were calculated using log-transformed infected and control samples. Unless stated otherwise, reported are the results of using relative profiles.
Cell-to-phenotype correlations
CPM was applied on each bulk RNA-seq lung sample by integrating the reference single cell collection (a total running time of ~16 minutes for deconvolution of 72 samples, using six cores of a Dell Latitude E6430 laptop, containing an Intel i7-3740QM CPU). Our analysis builds on the CPM-inferred abundance of each reference single cell in each mouse individual. For each reference cell (associated with a particular cell activation state) we calculated the Pearson correlation coefficient between the predicted abundance of cells at this cell state compared to the in-vivo clinical phenotype at two days post infection over the individual mice (illustrated in Supplementary Fig. 7B). The coefficient is referred to as the 'cell-to-phenotype correlation'. The cell-to-phenotype correlation was calculated using two groups of mice: either the infected or the control (PBS-treated) mice. Cell-to-phenotype correlations were binned into nine equal intervals along the trajectory of cell activation states. Supplementary Note 1 describes several tests that were applied to support the inferred gradual-changes over the cell activation bins.
Fluorescence-activated cell sorting and analysis
To validate the performance of CPM we sorted the population of macrophages from the lungs of various CC mice (Supplementary Table 1). To address this, the lungs were dissociated into single cell suspensions using Miltenyi Biotec lung dissociation kit (130-095-927), according to manufacturer’s instructions. Isolated lung cells were then enriched for CD45+ cells by a positive selection (CD45 microbeads, Miltenyi Biotec, 130-052-301), incubated with blocking solution (5% normal mouse serum, 5% normal rat serum, and 1% anti-Mouse CD16/CD32) for 30 min on ice, and stained with fluorochrome-conjugated antibody for CD11b (M1/70), CD64 (X54-5/7.1), I-A/I-E (M5/114.15.2), Ly6G (1A8), Ly6C (HK1.4), and CD45 (30-F11, Miltenyi Biotec). All antibodies were from Biolegend, unless otherwise mentioned (clone number in parentheses). Data was acquired with a SH800 flow cytometer (Sony Biotechnology) and analyzed with FlowJo v.10 Software. Mononulear phagocyte cells were gated as CD11b+CD45+Ly6G-I-A/I-E+, as previously described22, and the expression levels of Ly6C and CD64 were analyzed.
Inferring dynamics with a Markov model
In this analysis we rely on the assumption that cells along the activation trajectory are partitioned into D equal intervals. The i-th interval represents a discrete cell state i. In addition, we assume that the probability of transition between any two states (per unit time) is constant over time. The 'stochastic matrix' QDxD encodes the probabilities of transitions qij from state i to state j per unit time (referred to as "transition rates"). Assuming that each cell in each state i may remain in the same state or switch into state i+1 (but not to any other cell state), it follows that (i) for each i, qii+qi,i+1=1; and (ii) for each j ∉ {i,i + 1}, qij=0. We further define a row vector F1XD=(f1, f2,…, fD) where fi is the proportion of cells in state i (denoted a 'state proportions vector'). We assume that each cell resides in exactly one of the cell states, and therefore . The state proportions vector before infection and in any time t after infection are F(0) and F(t), respectively. Qt encodes the probability of transitions after t units of time and therefore F(t)= F(0)Qt. Using known state proportions vectors F(0) and F(t) (either CPM-inferred or FACS-measured, in Supplementary Figs. 8E and 8F, respectively), we fit the missing transition rate parameters {qi,i+1 | i = 1,…, D – 1}.
Supplementary Material
Acknowledgments
This work was supported by the European Research Council (637885) (AF, NP-Y, OC, DR, YS and IG-V), and partially supported by the Israeli Centers of Research Excellence (I-CORE) Center No 41/11 (AF, YS), the Broad−Israel Science Foundation (ISF) 1168/14 (DR, NP-Y), ISF 1824/13 (EB), partial fellowships from the Edmond J. Safra Center for Bioinformatics at Tel Aviv University (AF, YS), and a Shulamit Aloni Scholarship (YS). Research in the IG-V lab was supported by an ISF 288/16. IG-V is a Faculty Fellow of the Edmond J. Safra Center for Bioinformatics at Tel Aviv University and an Alon Fellow. We thank Oded Danziger and Hanifa J. Abu-Toamih Atamni (Tel Aviv University, Israel) for help with mouse work, and Shirley Smith for scientific editing.
Footnotes
Code availability
CPM is implemented in the 'scBio' CRAN R package (the CPM function): https://cran.r-project.org/web/packages/scBio/index.html
Data Availability
All RNA-seq data that support the findings of this study have been deposited in the Gene Expression Omnibus (GEO) database, under GEO accession numbers GSE113530 and GSE117975.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Author Contributions
AF, NP-Y, EB and IG-V conceived and designed the study. NP-Y, OC, DR, LV, FI, MM, LM, IA and EB developed experimental protocols and conducted the experiments. AF developed computational methods and performed bioinformatics analysis. YS performed bioinformatic analyses. AF, NP-Y, EB and IG-V wrote the manuscript with input from all authors.
Declaration of Interests
The authors declare no competing interests.
References
- 1.Wagner A, Regev A, Yosef N. Revealing the vectors of cellular identity with single-cell genomics. Nature Biotechnology. 2016;34:1145. doi: 10.1038/nbt.3711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chen X, Teichmann SA, Meyer KB. From Tissues to Cell Types and Back: Single-Cell Gene Expression Analysis of Tissue Architecture. Annual Review of Biomedical Data Science. 2018 doi: 10.1146/annurev-biodatasci-080917-013452. [DOI] [Google Scholar]
- 3.Krieg C, et al. High-dimensional single-cell analysis predicts response to anti-PD-1 immunotherapy. Nature Medicine. 2018;24:144. doi: 10.1038/nm.4466. [DOI] [PubMed] [Google Scholar]
- 4.Shalek AK, Benson M. Single-cell analyses to tailor treatments. Science Translational Medicine. 2017;9 doi: 10.1126/scitranslmed.aan4730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kim K-T, et al. Application of single-cell RNA sequencing in optimizing a combinatorial therapeutic strategy in metastatic renal cell carcinoma. Genome Biology. 2016;17:80. doi: 10.1186/s13059-016-0945-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shen-Orr SS, Gaujoux R. Computational deconvolution: extracting cell type-specific information from heterogeneous samples. Current opinion in immunology. 2013;25:571–578. doi: 10.1016/j.coi.2013.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baron M, et al. A Single-Cell Transcriptomic Map of the Human and Mouse Pancreas Reveals Inter- and Intra-cell Population Structure. Cell Systems. 2016;3:346–360.e344. doi: 10.1016/j.cels.2016.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Frishberg A, Brodt A, Steuerman Y, Gat-Viks I. ImmQuant: a user-friendly tool for inferring immune cell-type composition from gene-expression data. Bioinformatics. 2016;32:3842–3843. doi: 10.1093/bioinformatics/btw535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Avila Cobos F, Vandesompele J, Mestdagh P, De Preter K. Computational deconvolution of transcriptomics data from mixed cell populations. Bioinformatics. 2018;34:1969–1979. doi: 10.1093/bioinformatics/bty019. [DOI] [PubMed] [Google Scholar]
- 10.Puram SV, et al. Single-Cell Transcriptomic Analysis of Primary and Metastatic Tumor Ecosystems in Head and Neck Cancer. Cell. 2017;171:1611–1624.e1624. doi: 10.1016/j.cell.2017.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tirosh I, et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science. 2016;352:189. doi: 10.1126/science.aad0501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schelker M, et al. Estimation of immune cell content in tumour tissue using single-cell RNA-seq data. Nat Commun. 2017;8:2032. doi: 10.1038/s41467-017-02289-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Trapnell C. Defining cell types and states with single-cell genomics. Genome Res. 2015;25:1491–1498. doi: 10.1101/gr.190595.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rostom R, Svensson V, Teichmann Sarah A, Kar G. Computational approaches for interpreting scRNA – seq data. FEBS Letters. 2017;591:2213–2225. doi: 10.1002/1873-3468.12684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Svensson V, Vento-Tormo R, Teichmann SA. Exponential scaling of single-cell RNA-seq in the past decade. Nature Protocols. 2018;13:599. doi: 10.1038/nprot.2017.149. [DOI] [PubMed] [Google Scholar]
- 16.Steuerman Y, et al. Dissection of influenza infection in vivo by single-cell RNA sequencing. Cell Systems. 2018;6:679–691. doi: 10.1016/j.cels.2018.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Altboum Z, et al. Digital cell quantification identifies global immune cell dynamics during influenza infection. Molecular systems biology. 2014;10:720–720. doi: 10.1002/msb.134947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Newman AM, et al. Robust enumeration of cell subsets from tissue expression profiles. Nature Methods. 2015;12:453–457. doi: 10.1038/nmeth.3337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fan R-E, Chang K-W, Hsieh C-J, Wang X-R, Lin C-J. LIBLINEAR: A Library for Large Linear Classification. The Journal of Machine Learning Research. 2008;9:1871–1874. doi: 10.1145/1390681.1442794. [DOI] [Google Scholar]
- 20.Welsh CE, et al. Status and access to the Collaborative Cross population. Mammalian Genome. 2012;23:706–712. doi: 10.1007/s00335-012-9410-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bottomly D, et al. Expression quantitative trait Loci for extreme host response to influenza a in pre-collaborative cross mice. G3 (Bethesda, Md.) 2012;2:213–221. doi: 10.1534/g3.111.001800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yu Y-RA, et al. A Protocol for the Comprehensive Flow Cytometric Analysis of Immune Cells in Normal and Inflamed Murine Non-Lymphoid Tissues. PloS one. 2016;11:e0150606. doi: 10.1371/journal.pone.0150606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ferris MT, et al. Modeling host genetic regulation of influenza pathogenesis in the collaborative cross. PLoS pathogens. 2013;9:e1003196–e1003196. doi: 10.1371/journal.ppat.1003196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dengler L, et al. Cellular changes in blood indicate severe respiratory disease during influenza infections in mice. PloS one. 2014;9:e103149–e103149. doi: 10.1371/journal.pone.0103149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Coates BM, et al. Inflammatory Monocytes Drive Influenza A Virus–Mediated Lung Injury in Juvenile Mice. The Journal of Immunology. 2018;200:2391–2404. doi: 10.4049/jimmunol.1701543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tanay A, Regev A. Scaling single-cell genomics from phenomenology to mechanism. Nature. 2017;541:331. doi: 10.1038/nature21350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shen-Orr SS, et al. Cell type–specific gene expression differences in complex tissues. Nature Methods. 2010;7:287. doi: 10.1038/nmeth.1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hutter C, Zenklusen JC. The Cancer Genome Atlas: Creating Lasting Value beyond Its Data. Cell. 2018;173:283–285. doi: 10.1016/j.cell.2018.03.042. [DOI] [PubMed] [Google Scholar]
- 29.Kaul R. Enhancing GTEx by bridging the gaps between genotype, gene expression, and disease. Nature Genetics. 2017;49:1664–1670. doi: 10.1038/ng.3969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Regev A, et al. The Human Cell Atlas. eLife. 2017;6:e27041. doi: 10.7554/eLife.27041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Aran D, Hu Z, Butte AJ. xCell: digitally portraying the tissue cellular heterogeneity landscape. Genome Biol. 2017;18:220. doi: 10.1186/s13059-017-1349-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Singer BD, et al. Flow-cytometric method for simultaneous analysis of mouse lung epithelial, endothelial, and hematopoietic lineage cells. American Journal of Physiology - Lung Cellular and Molecular Physiology. 2016;310:L796–L801. doi: 10.1152/ajplung.00334.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.