Improved photoacoustic-based oxygen saturation estimation with SNR-regularized local fluence correction

Abstract

As photoacoustic (PA) imaging makes its way into the clinic, accuracy of PA-based metrics becomes increasingly important. To address this need, a method combining finite-element-based local fluence correction (LFC) with signal-to-noise-ratio (SNR) regularization was developed and validated to accurately estimate oxygen saturation (SO₂) in tissue. With data from a Vevo LAZR system, performance of our LFC approach was assessed in ex vivo blood targets (37.6% – 99.6% SO₂) and in vivo rat arteries. Estimation error of absolute SO₂ and change in SO₂ reduced from 10.1% and 6.4%, respectively, without LFC to 2.8% and 2.0%, respectively, with LFC, while accuracy of the LFC method was correlated with the number of wavelengths acquired. This work demonstrates the need for SNR-regularized LFC to accurately quantify SO₂ with PA imaging.

I. Introduction

ASSESSMENT of tissue hypoxia is useful for cancer diagnosis and therapy as tumor growth, malignancy, and therapeutic resistance have been shown to correlate with the presence of hypoxic tumor microenvironments [1]–[4]. Specifically, disease progression and poor treatment response characterized by accelerated tumor growth have been linked to increased levels of hypoxia for solid tumors [5], [6]. Therefore, developing an imaging biomarker that correlates with tumor hypoxia would be beneficial for improving the diagnosis and treatment response for multiple types of cancer [7].

The most direct method to assess tissue hypoxia in vivo is to use fiber-optic fluorescence probes or polarographic electrodes to measure oxygen partial pressure (pO₂), which has been shown to correlate with extracellular hypoxia [8]. Such instruments, however, are limited to invasive point measurements, which can affect tissue physiology and provide only a time-averaged value for a single sampling location [9]. Nuclear medicine imaging methods, such as positron emission tomography or single-photon emission computed tomography, have been used for non-invasively assessing tissue hypoxia [10], [11]. Limited spatiotemporal resolution and a need for exogenous radioactive agents, however, make these modalities far from ideal. Blood-oxygen-level dependent (BOLD) magnetic resonance imaging is a tracer-free method that provides relative measurements of oxygenated (HbO₂) and deoxygenated (HHb) hemoglobin, but its implementation can present quantification challenges due to its dependence on blood volume and magnetic-field inhomogeneities, which can be difficult to characterize [12]. Diffuse optical tomography (DOT) has also shown promise in imaging hemoglobin concentration and oxygenation state, but its poor spatial resolution restricts its ability to image the heterogeneity of intratumoral blood oxygen saturation (SO₂) [13], [14], which is the ratio of HbO₂ to total hemoglobin.

Photoacoustic (PA) imaging is a non-invasive and tracer-free modality that can provide high-contrast data based on ultrasonic (US) imaging of acoustic sources that result from local optical absorption of a scattered laser pulse [15]. Because of its use of US detection rather than optical detection, PA imaging is capable of higher spatial resolution at greater penetration depths than purely optical techniques, such as DOT [13], [14]. Spectroscopic PA (sPA) imaging, which utilizes different laser irradiation wavelengths, can readily estimate relative HbO₂ and HHb concentrations and thus provide PA-based SO₂ estimates [16], [17]. sPA imaging forms the basis of a number of quantitative PA imaging approaches that provide local assessment of photo-absorber (e.g., HbO₂ or HHb) concentration in tissue.

Although SO₂ quantification does not give a direct measurement of tissue hypoxia, it has been shown to correlate with pO₂ of tissue proximal to vasculature and therefore is a promising surrogate biomarker for assessing tissue oxygenation [18]. Given the observed spatial heterogeneity of hypoxia in solid tumors, the improved spatial resolution afforded by PA imaging is critical to ensure that tumor-specific imaging features are not lost through volume averaging, which could mitigate diagnostic sensitivity or reduce precision of local therapy monitoring [19], [20]. In addition, more accurate and high-resolution SO₂ images could help improve our burgeoning understanding of the mechanistic interplay between tumor microenvironment and disease progression or treatment response [21].

Unfortunately, accurate estimation of SO₂ with quantitative PA imaging is not straightforward due its dependence on local fluence and its often poor signal-to-noise ratio (SNR), particularly at depth [17]. Estimation of local fluence distributions requires solving an ill-posed inverse problem with a large number of unknown and heterogeneous tissue properties and a non-unique solution (i.e., absorption-scattering non-uniqueness) [22]. Additionally, sPA data tend to be signal-limited at depth (i.e., > 1 cm) due to the exponential decay of fluence that occurs in turbid tissues. Consequently, utilization of poor-SNR sPA data can result in significant noise bias when estimating SO₂. In fact, noise can be the dominant contribution in large portions of the image – particularly for deeper-lying voxels – and thus lead to erroneous SO₂ quantifications.

There are a number of methods that have been proposed and validated (to varying extents) for the purpose of quantitative PA imaging, which generally involves optical and acoustical inversion problems to obtain estimates of absolute distributions of absorber concentrations [22]. However, in the specific case of SO₂ estimation considered here, only relative absorber concentrations are needed, and thus reconstructed PA image intensity is often assumed to be proportional to initial pressure through a single constant, obviating the need for an acoustical inversion step. Consequently, the primary focus for inversion becomes modeling the effects of spectral coloring through pixel-wise normalization of data by wavelength-dependent fluence, which directly impacts PA image intensity.

If only relative concentrations are needed and local fluence is assumed constant or just proportional to measured laser-pulse energy, then the simplest and most commonplace method for absorber estimation is linear inversion, which is typically straightforward to solve with matrix inversion [23], [24]. If light propagation in the medium is modeled analytically with the radiative transfer equation (RTE), it is possible to implement direct inversion methods [25], [26]. For relatively homogenous [16] or superficial imaging [27] (e.g., PA microscopy), an analytical model for local fluence correction can be used. However, such an approach is often intractable for heterogeneous media, in which case numerical modeling (e.g., Monte Carlo methods [28]–[30] or finite element methods [FEMs] using the diffusion approximation of the RTE [31]) can provide accurate local fluence estimation based on heterogeneous optical properties and an arbitrary photon-source distribution. Modeled optical properties can be based entirely on a priori assumptions (e.g., values from the literature) or on supplemental information from other modalities, such as DOT. Additionally, given the known relationship between a PA image and local optical absorption, it is possible to rewrite the model equations such that an unknown parameter (i.e., absorber concentration) equals a known function of itself, leading to fixed-point [32] or model-based [22] iteration approaches. While a fixed-point approach can converge to a correct solution, a model-based approach relies on minimization of a cost function relating known output to an estimate of this output obtained by a forward calculation with iteratively updated estimates of the unknown parameters. Since these iterative approaches depend on acquired data, which inherently contain noise, regularization in the cost function should be implemented to avoid model over-fitting to noise, which reduces overall accuracy. In addition, such model-based minimization tends to be ill-posed and usually does not provide a unique solution [22]. Approaches based on tissue segmentation [33] and multiple illuminations [34] have been implemented to reduce ill-posedness and to improve the uniqueness of the solution. However, the need for sufficient contrast to implement tissue segmentation and additional hardware to achieve multiple illuminations limits the application of such approaches in practice.

In this work, we developed an SNR-regularized local fluence correction (LFC) approach to obtain improved estimation and visualization of local SO₂ in tissue. Validation of our approach was performed on blood targets in rats postmortem and on in vivo rat arteries. Results from these studies demonstrate that SNR-regularized LFC significantly improves accuracy for estimates of absolute SO₂ and change in SO₂ in ex vivo and in vivo environments.

II. Methods

In brief, we acquired sPA and US imaging data (II.A) on ex vivo (II.D.2) and in vivo (II.D.3) normal Buffalo rats. These imaging data and matched noise acquisitions (II.B) were then processed with the work flow summarized in Fig. 1 to obtain acquisition-specific SNR images and achieve LFC (II.C). Fluence-corrected SO₂ estimates were then compared to gold-standard CO-oximeter measurements and assumed arterial oxygenation levels (i.e., near 100%) for the ex vivo and in vivo models, respectively, to assess overall performance.

Fig. 1.

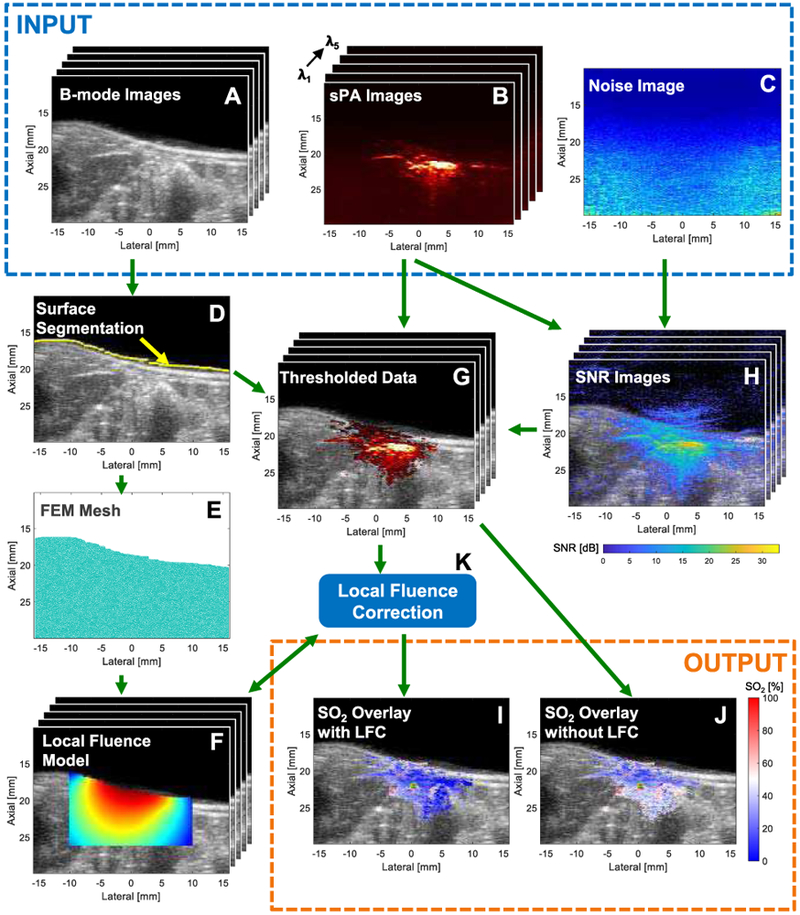
Stacks (i.e., λ₁..λ_N) of co-registered (A) B-mode US images and (B) sPA images for all 5 acquisition wavelengths with corresponding (C) PA noise image. (D) B-mode image showing tissue-surface segmentation (yellow). (E) 2D FEM mesh of ROI and (F) stack of local fluence estimates presented on a log scale. (G) Stack of SNR-thresholded PAUS images, (H) Stack of SNR-US overlays, and (K) LFC procedure. SO₂ overlays (I) with and (J) without LFC.

A. Imaging System

A Vevo 2100-LAZR photoacoustic-ultrasonic (PAUS) imaging system (FUJIFILM VisualSonics Inc., Toronto, Canada) was used to perform three-dimensional (3D) B-mode and PA imaging in all experiments. An LZ-201 transducer array with 256 elements and a nominal 15-MHz center frequency was used with narrow-field (~1 cm) fiber-bundle outputs centered and flanking the posterior/anterior aspects of the US array and tilted such that they concentrate laser output toward the imaging plane. sPA imaging data were acquired at the following wavelengths: 710, 734, 760, 800, and 850 nm (Fig. 1B). These wavelengths were selected to include the local minimum and maximum of the HHb extinction spectrum, the isosbestic point for hemoglobin at 800 nm, as well as the furthest extents of this aforementioned NIR range (e.g., 710 and 850 nm), which provide the greatest contrast between HbO₂ and HHb. Ten imaging frames were averaged to form a single, two-dimensional (2D) PA image at each wavelength. The US transducer was then mechanically translated in the elevation dimension with a 0.27-mm step size to acquire a 3D data set. Conventional delay-and-sum beamforming was utilized for all image reconstruction. Pulse energy was measured for each imaging frame with an energy meter and beam splitter incorporated in the Vevo system; these frame-specific energy values were then used for pulse-to-pulse energy correction of each PA imaging frame and for the SNR analysis detailed in II.D.1. Note that pulse-to-pulse energy correction was applied to all images, even those not undergoing LFC.

B. Establishment of SNR Mask

To estimate the voxel-wise noise level for specific operating parameters (e.g., a particular overall gain, time-gain compensation [TGC], and field of view [FOV]), a hundred frames of PA noise data were acquired in room-temperature water without pulsed laser irradiation (i.e., Q-switch of the laser was disengaged; Fig. 1C). The noise histogram was determined to be log-normal distributed based on the Kolmogorov-Smirnov goodness-of-fit test (p-value=0.8) and on previous results [35]. The mean (μ) and standard deviation (σ) at each pixel were calculated assuming a log-normal distribution of the 100-frame ensemble, and SNR (Fig. 1H) is given by [35]

$${\mathbf{SNR}}^{i,j,\lambda }=10\log \left(\frac{{\mathbf{PA}}^{i,j,\lambda }-{\mu }^{i,j}}{{\sigma }^{i,j}}\right),$$ (1)

where PA is PA image intensity, and μ and σ are the mean and standard deviation, respectively, of matched (i.e., same FOV, TGC, etc.) PA noise data. Note that in all equations, bold indicates an array with elements defined by the superscript (e.g., i = 1,…, m; j = 1,…, n; and λ = λ₁,…, λ_N). The tissue surface for all PA imaging frames was then automatically segmented based on their co-registered B-mode US frame, as is shown in Fig. 1D. These tissue-surface segmentations were used to mask the near-field coupling stand-off (i.e., gel or water) of each PA frame from subsequent analysis and display. Voxel-wise SNR was calculated using Eq. 1 for each PA image. An SNR threshold was then determined based on minimization of a cost function equal to the squared error of SO₂ estimates in known blood samples (described in II.D.2) divided by the number of voxels within the SNR threshold mask. For optimization purposes, SNR thresholds ranging from 5 dB to 13 dB were tested, while the number of wavelengths (i.e., for a given pixel) that were required to exceed that threshold ranged from 2 to 5 wavelengths. The dB-threshold and wavelength-number criterion that resulted in minimization of the cost function was then used to generate SNR masks for all other experiments. Optimizing the SNR threshold and number of wavelengths used is expected to provide a reasonable trade-off between effective imaging depth and overall accuracy, respectively. It is important to note that the number of wavelengths considered for purposes of SNR mask generation is not the same as the number of wavelengths used for SO₂ estimation. With the exception of the experiment investigating the impact of the number of wavelengths used for spectral unmixing, all 5 wavelengths were always used for SO₂ estimation for any pixels included in an SNR mask. This SNR mask was then used to regularize PA data for assessing model optimization (II.C.3) and to determine which voxels to display in PAUS overlay images (Fig. 1G, I, and J). Acquisition-specific TGC arrays were obtained by averaging PA noise acquisitions in the lateral dimension.

C. Local Fluence Correction Model

Empirically determined estimates of tissue-surface fluence (II.C.1) were used as inputs to an FEM-based model of local fluence within the relevant extent of the imaging FOV, as defined by an SNR threshold (II.B). The predicted fluence distribution for each frame was then determined through iterative optimization of the inverse model, described in II.C.3. The flowchart (Fig. 2) summarizes the algorithm used for SO₂ estimation with and without LFC. In both approaches, tissue-surface segmentation and assessment of electronic noise within the FOV are required to generate the SNR mask used for regularization.

Fig. 2.

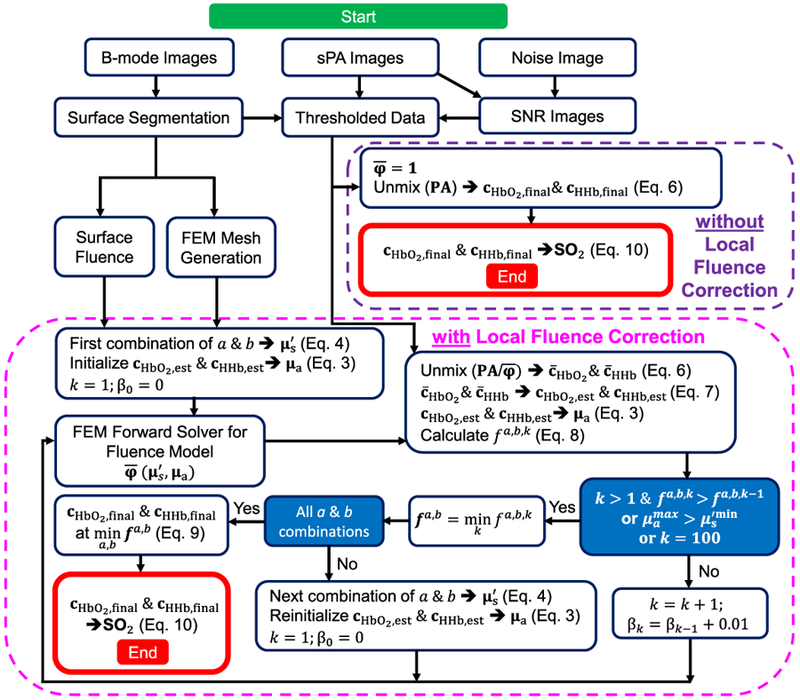
Flowchart of the procedure used to estimate voxel-wise concentrations of HbO₂ and HHb with and without LFC.

1). Tissue-Surface Fluence Estimation:

Frame-specific laser fluence at the tissue-surface interface was measured as input for forward calculations of local fluence. To estimate tissue-surface fluence for arbitrary imaging depths and tissue-surface profiles, a 1-mm-diameter ball bearing embedded on the surface of a gelatin stand-off was raster-scanned at different lateral, axial (i.e., depth), and elevational locations relative to the center of the imaging transducer. To ensure elevational alignment, the maximum average PA signal at 710 nm within an ROI containing the ball bearing was determined through elevation and obtained for each lateral-axial position; these data were used to generate a normalized fluence look-up table for all expected tissue-surface locations, as is shown in Fig. 3A. An example of the normalized fluence profile at an axial position of 18.5 mm is shown in Fig. 3B. Based on the lateral-axial positions of all segmented tissue-surface voxels (II.B), an estimate of normalized tissue-surface laser fluence was obtained and used as a frame-specific input for numerical modeling of fluence, as is described in II.C.3.

Fig. 3.

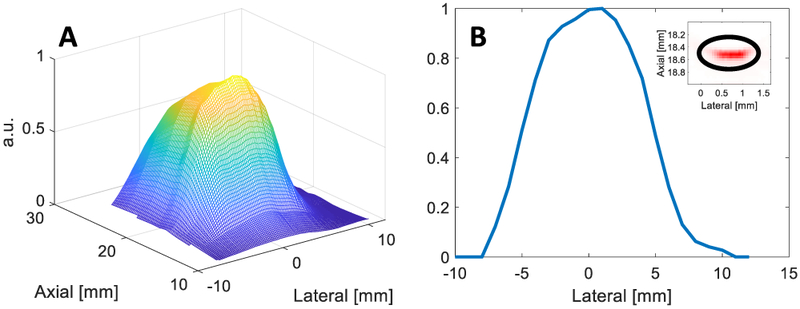
(A) Surface plot of normalized tissue-surface fluence as a function of axial and lateral position. (B) Plot of normalized tissue-surface fluence as function of lateral position at a fixed axial position (18.5 mm) with an inset showing acquired PA image of ball bearing with analysis ROI at 710 nm.

2). Relationship of PA Image to Hemoglobin Concentration and Local Fluence:

PA image intensity is proportional to the initial pressure generated by absorbed laser energy and is given by [36], [37]

$${\mathbf{PA}}^{i,j,\lambda }={\Gamma }^{i,j}{\alpha }^{i,j}{\mu }_{\mathrm{a}}^{i,j,\lambda }{\phi }^{i,j,\lambda },$$ (2)

where Γ [unitless] is the thermal expansion Grüneisen parameter; α [unitless] includes the acoustic response (e.g., frequency-dependent attenuation) of the medium and the US-system response (e.g., TGC); μ_a [mm⁻¹] is the optical absorption coefficient; and φ [J mm⁻²] is local fluence, which is a function of μ_a and the reduced scattering coefficient, ${\mu }_{\mathrm{s}}^{\prime }$. In the near-infrared window, hemoglobin tends to be the dominant absorber in tissue, and therefore the absorption coefficient can be approximated by

$${\mu }_{\mathrm{a}}^{i,j,\lambda }={\mathbf{c}}_{{\mathrm{HbO}}_2}^{i,j}{\epsilon }_{{\mathrm{HbO}}_2}^{\lambda }+{\mathbf{c}}_{\mathrm{HHb}}^{i,j}{\epsilon }_{\mathrm{HHb}}^{\lambda },$$ (3)

where c_HbO2 and c_HHb [M] are concentrations of HbO₂ and HHb, respectively, while ε_HbO2 and ε_HHb [M⁻¹ mm⁻¹] are their molar extinction coefficients, respectively. For the purpose of the modeling presented herein, ${\mu }_{\mathrm{s}}^{\prime }$ is assumed to follow a spatially-invariant, wavelength-dependent power law given by [38]

$${\mu }_{\mathrm{s}}^{{\prime }_{i,j,\lambda ,a,b}}=a{\left(\frac{\lambda }{500(\text{nm})}\right)}^{-b},$$ (4)

where the coefficients a [mm⁻¹] and b [unitless] are assumed to be the same for all voxels in a given imaging frame. This constraint is imposed for regularization and to reduce the illposedness of the inverse problem. Finally, PA image intensity can be expressed as

$${\mathbf{PA}}^{i,j,\lambda }={\Gamma }^{i,j}{\alpha }^{i,j}\left({\mathbf{c}}_{{\mathrm{HbO}}_2}^{i,j}{\epsilon }_{{\mathrm{HbO}}_2}^{\lambda }+{\mathbf{c}}_{\mathrm{HHb}}^{i,j}{\epsilon }_{\mathrm{HHb}}^{\lambda }\right){\overline{\phi }}^{i,j,\lambda ,a,b},$$ (5)

where $\overline{\phi }$ represents the fluence estimated by a numerical model using a, b, c_HbO2, and c_HHb as inputs.

3). Inverse Model and SO₂ Estimation:

We used a two-part inverse model that first uses a fixed-point iteration method to estimate relative voxel-wise hemoglobin concentrations at specific reduced-scattering parameters, a and b, then regularizes the hemoglobin concentrations to estimate μ_a for the next iteration. The regularized hemoglobin concentration estimates are then used in an objective function (Eq. 8) to determine the error between measured PA data and PA estimates. In Eq. 5, the values of Γ and α are unknown; however, since only relative hemoglobin concentrations are to be reconstructed and realizing that α^i,j = α^′i,j TGC^i,j, we can set the values of Γ and α^′ to 1 and estimate TGC from the PA noise image, as described in (II.B). Relative hemoglobin concentrations can then be expressed as

$$\left[\begin{array}{c}\hfill {\overline{\mathbf{c}}}_{{\mathrm{HbO}}_2}^{i,j}\hfill \\ \hfill {\overline{\mathbf{c}}}_{\mathrm{HHb}}^{i,j}\hfill \end{array}\right]=\frac{1}{{\mathbf{TGC}}^{i,j}}{\left[\begin{array}{cc}\hfill {\epsilon }_{{\mathrm{HbO}}_2}^{{\lambda }_1}\hfill & \hfill {\epsilon }_{\mathrm{HHb}}^{{\lambda }_1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\epsilon }_{{\mathrm{HbO}}_2}^{{\lambda }_N}\hfill & \hfill {\epsilon }_{\mathrm{HHb}}^{{\lambda }_N}\hfill \end{array}\right]}^{†}\left[\begin{array}{c}\hfill \frac{{\mathbf{PA}}^{i,j,{\lambda }_1}}{{\overline{\phi }}^{i,j,{\lambda }_1,a,b}}\hfill \\ \hfill ⋮\hfill \\ \hfill \frac{{\mathbf{PA}}^{i,j,{\lambda }_N}}{{\overline{\phi }}^{i,j,{\lambda }_N,a,b}}\hfill \end{array}\right],$$ (6)

where † indicates the Moore-Penrose inverse, and $\overline{c}$ [unitless] indicates a relative concentration. Given that an absolute reduced scattering coefficient is used in the model, relative hemoglobin concentrations were converted to absolute concentrations through regularization by setting the maximum value of the concentrations to an unknown constant value, β [M], such that

$$\left[\begin{array}{c}\hfill {\mathbf{c}}_{{\mathrm{HbO}}_2,\text{est}}^{i,j}\hfill \\ \hfill {\mathbf{c}}_{\mathrm{HHb},\text{est}}^{i,j}\hfill \end{array}\right]=\frac{\beta }{\left(\left[{\overline{\mathbf{c}}}_{{\mathrm{HbO}}_2}^{i,j};{\overline{\mathbf{c}}}_{\mathrm{HHb}}^{i,j}\right]\right)}\left[\begin{array}{c}\hfill {\overline{\mathbf{c}}}_{{\mathrm{HbO}}_2}^{i,j}\hfill \\ \hfill {\overline{\mathbf{c}}}_{\mathrm{HHb}}^{i,j}\hfill \end{array}\right].$$ (7)

For given reduced-scattering coefficient parameters (i.e., a and b), estimated hemoglobin concentrations (i.e., c_HbO2,est and c_HHb,est [M]), and an assumed tissue-surface fluence distribution (II.C.1), the local fluence $\overline{\phi }$ can be calculated numerically using the diffusion approximation of the RTE and the FEM method, which is described in II.C.4.

Eqs. 6 & 7 then transform to a fixed-point iteration method over iteration number, k, by setting ${\overline{\phi }}^{i,j,\lambda ,a,b}\to {\overline{\phi }}^{i,j,\lambda ,a,b,k-1}$; ${\overline{c}}^{i,j}\to {\overline{c}}^{i,j,k}$; ${\mathbf{c}}_{\text{est}}^{i,j}\to {\mathbf{c}}_{\text{est}}^{i,j,k}$; and ${\mathbf{c}}_{\text{est}}^{i,j,k=0}=0$. Because β is unknown, a range of values was tested for each unique combination of a and b to find the best estimate of β, corresponding to the minimum error between the estimated and measured PA image arrays. Numerical experiments indicate the fixed-point iteration is independent of the initial condition and converges approximately in one iteration. Therefore, to estimate the fixed point for an array of beta values, we replace β by β_k and increase β_k at each iteration by steps of 0.01 M starting from β₀ = 0 M. The estimated hemoglobin concentrations that correspond to the previous iteration (i.e., ${\mathbf{c}}_{\text{est}}^{i,j,k-1}$) are then used for estimation of $\overline{\phi }$ in the current iteration.

We define an objective function at iteration k as the l₁-norm (used because of its robustness to noise) of the difference between the measured and estimated PA image arrays within the optimization ROI by

$$f^{a,b,k}=\sum _{i,j}{\Vert {\mathbf{PA}}^{i,j,\lambda }-{\mathbf{TGC}}^{i,j}\times ({\overline{\mathbf{c}}}_{{\mathrm{HbO}}_2}^{i,j,k}{\epsilon }_{{\mathrm{HbO}}_2}^{\lambda }+{\overline{\mathbf{c}}}_{\mathrm{HHb}}^{i,j,k}{\epsilon }_{\mathrm{HHb}}^{\lambda }){\overline{\phi }}^{i,j,\lambda ,a,b,k-1}\Vert }_1.$$ (8)

The iterative calculation of voxel-wise hemoglobin concentrations continues at increasing values of β_k until one of three conditions is achieved: (1) a local minimum of the objective function is reached (i.e., $f_{a,b}^k>f_{a,b}^{k-1}$); (2) the maximum μ_a value exceeds the minimum ${\mu }_{\mathrm{s}}^{\prime }$ value used for fluence estimation; or (3) β_k reaches its maximum value of 1. The values of a and b, ranging from 1 to 2.5 mm⁻¹ and 0.5 to 2.0, respectively, were tested with a step size of 0.5 for each, resulting in 16 unique combinations of a and b. These ranges were based on values found in the literature for the following tissue types: liver tissue, with average values for a and b of 0.9 mm⁻¹ and 0.6, respectively; adipose tissue, with average values of 1.8 mm⁻¹ and 0.7, respectively; and skin tissue, with average values of 4.6 mm⁻¹ and 1.4, respectively [38]. The minimization problem was solved sixteen times in order to consider all combinations of a and b values tested, generating an array of minimum objective function values (i.e., f^a,b). The final estimates for voxel-wise hemoglobin concentrations were considered to be those corresponding to the global minimum of f^a,b, defined as (a*, b*) = arg f^a,b, such that

$$\left[\begin{array}{c}\hfill {\mathbf{c}}_{{\mathrm{HbO}}_2,\text{final}}^{i,j}\hfill \\ \hfill {\mathbf{c}}_{\mathrm{HHb},\text{final}}^{i,j}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathbf{c}}_{{\mathrm{HbO}}_2,\text{est}}^{i,j,a^{\ast },b^{\ast }}\hfill \\ \hfill {\mathbf{c}}_{\mathrm{HHb},\text{est}}^{i,j,a^{\ast },b^{\ast }}\hfill \end{array}\right].$$ (9)

Finally, an image of percent SO₂ was calculated from these final hemoglobin concentrations by

$${\mathbf{SO}}_2^{i,j}=\frac{{\mathbf{c}}_{{\mathrm{HbO}}_2,\text{final}}^{i,j}}{{\mathbf{c}}_{{\mathrm{HbO}}_2,\text{final}}^{i,j}+{\mathbf{c}}_{\mathrm{HHb},\text{final}}^{i,j}}\times 100\%.$$ (10)

4). Specific Modeling and Computational Parameters:

For FEM modeling of the fluence distribution, the segmented tissue surface of a matched B-mode image (Fig. 1D) was used to create a binary mask of the tissue ROI and then used to establish a 2D FEM mesh (Fig. 1E) for each imaging frame using NIRFAST, an open-source software package for modeling NIR light transport in tissue [31], [39]–[43]. The average number of nodes and tetrahedron elements of the 2D FEM mesh for an imaging frame were 6,311 and 12,270, respectively. Estimated normalized laser irradiation (II.C.1) at the proximal FEM surface nodes was used as an input for forward calculations where Robin-type boundary conditions were assumed to estimate local fluence distributions (Fig. 1F) using the diffusion approximation of the RTE and a solver developed in previous work [44], [45]. Calculated local fluence at the FEM mesh nodes was then interpolated to obtain the local fluence, $\overline{\phi }$, at all voxels of the PA image. An imaging frame’s SNR mask (i.e., thresholding of Fig. 1H) was used to define the optimization region in an ROI (defined by the smallest rectangular region aligned with the FOV coordinate axes that completely contains the SNR mask) wherein the objective function in Eq. 8 was minimized; only those voxels then included within the SNR mask were considered in the l₁-norm calculation.

When LFC is not applied, there is no iteration required, and Eq. 6 can be used to obtain c_HbO2,final and c_HHb,final by assuming local fluence is unity (i.e., $\overline{\phi }=1$) for all wavelengths. It then becomes straightforward to estimate SO₂ using Eq. 10. The two-chromophore model assumption (i.e., HbO₂ and HHb) employed for unmixing with and without LFC can then be assessed pixel-wise by relative model error, which is calculated using the l₁-norm from Eq. 8, where $\overline{\phi }=1$ and ${\overline{c}}_{{\mathrm{HbO}}_2}$ and ${\overline{c}}_{\mathrm{HHb}}$ equal c_HbO2,final and c_HHb,final, respectively, for the non-LFC case. This residual is then divided by the summation of the sPA data through wavelength and multiplied by 100 to provide an error percentage. Relative model error is a measure of the goodness-of-fit of a pixel’s PA spectrum to the hemoglobin absorption spectrum associated with the pixel’s estimated SO₂ level. Average computation times required for SO₂ estimation for an imaging frame with and without LFC were 470 and 0.5 seconds, respectively. All simulations were performed using a PC with an Intel Core i5-6300U CPU at 2.4 GHz and 8 GB RAM.

D. Experimental Validation

Our SNR-regularized LFC method was assessed in two recently euthanized (i.e., “ex vivo Rat 1 & 2”; II.D.2) and seven anesthetized (i.e., “in vivo Rat 1-7”; II.D.3) male Buffalo rats. Ex vivo validation was performed on bovine blood samples of known SO₂ introduced in rat liver postmortem, while in vivo validation was performed on intrahepatic arteries in rats during inhalation of 100% oxygen.

1). SNR Mask Validation:

The SNR mask was validated using 6 imaging frames to match the number of frames used for definition of tube ROIs (II.D.2) in ex vivo Rat 2 and in vivo Rat 1. First, imaging data were acquired and SNR masks were established based on the steps described in II.A and II.B, respectively. Based on these data, SO₂ images were generated for each imaging frame (II.C.3), and average SO₂ was calculated for all voxels included in (i.e., “Mask”) and excluded from (i.e., “1-Mask”) the SNR mask with and without LFC applied; an average and standard deviation across all 6 frames of these average SO₂ estimates was then calculated. Two “noise” ROIs (Fig. 4A,C) were then chosen at maximal depth extent and lateral offset to include a region assumed to be only noise. The SO₂ estimate in this region was then compared to SO₂ estimates obtained from the inverse of the energy-meter spectrum (i.e., pulse energy vs. wavelength) used for pulse-to-pulse energy normalization. A two-sample Student’s t-test (α = 0.05) was used to assess statistical significance for all experiments.

Fig. 4.

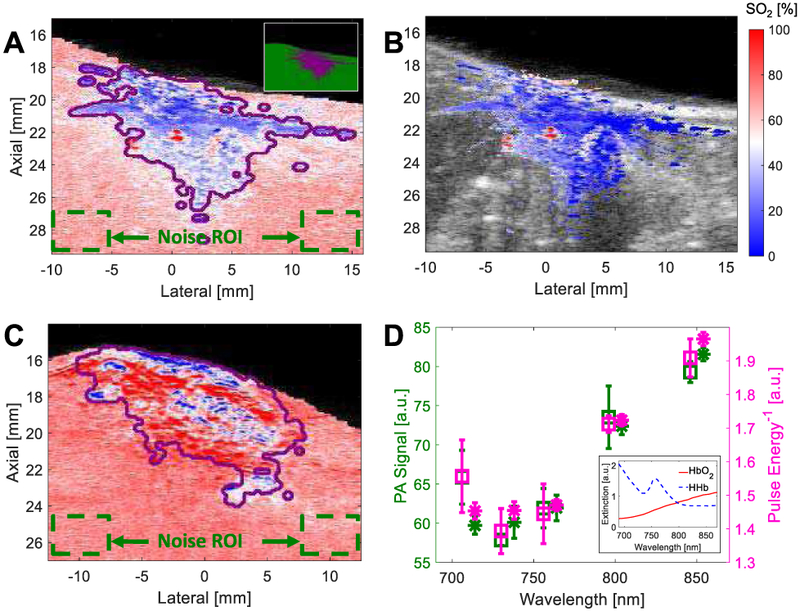
SO₂ image overlays of (A) ex vivo Rat 2 without LFC or SNR masking (but mask outline in purple) with inset offering example of SNR “Mask” (purple) and “1-Mask” (green) regions; (B) ex vivo Rat 2 with LFC and SNR masking; and (C) in vivo Rat 2 without LFC or SNR masking. (D) PA signal for noise ROI and reciprocal of pulse-energy spectrum for ex vivo (squares) and in vivo (asterisks) rats; inset shows extinction spectra of HbO₂ and HHb.

2). Ex Vivo Validation:

Ex vivo Rats 1 & 2 were used for SO₂ estimation validation. Heparinized bovine blood was employed to prepare samples with different SO₂ values, as described in previous work [16], [46]. Briefly, two flasks of blood were used with an inlet in each to allow mixing with pure oxygen or pure nitrogen gas to prepare fully oxygenated or deoxygenated blood, respectively. Using different ratios of oxygenated and deoxygenated blood, samples with varied SO₂ were obtained and measured by a GEM OPL CO-oximeter (Instrumentation Laboratory, Bedford, MA), which has a reported measurement uncertainty of ±1.5%. To create an imaging target, 1-mm-inner-diameter polyethylene (PE) tubes were introduced under US imaging guidance at depths ranging from 2.4 mm to 10 mm into each rat liver. Blood samples were then injected into each PE tube and imaged, as detailed in II.A. Tubes were flushed with deionized water between injections of different SO₂ samples.

3D B-mode data and co-registered SO₂ data were used to manually segment PE tube boundaries. As shown in Fig. 5A-D, four tubes could be fully segmented through elevation (i.e., the US transducer translation direction). Six consecutive elevational frames (i.e., spaced at 0.27 mm) were used to define a unique analysis ROI; analysis was limited to six consecutive frames to ensure intra-frame tube-depth variation remained <0.2 mm. Two of the tubes contained two analysis ROIs, which were located at different elevational positions in the 3D data set. A detailing of the analysis ROIs, their average depth from the tissue surface, and the CO-oximeter-measured SO₂ values for samples imaged in each is provided in Table I.

Fig. 5.

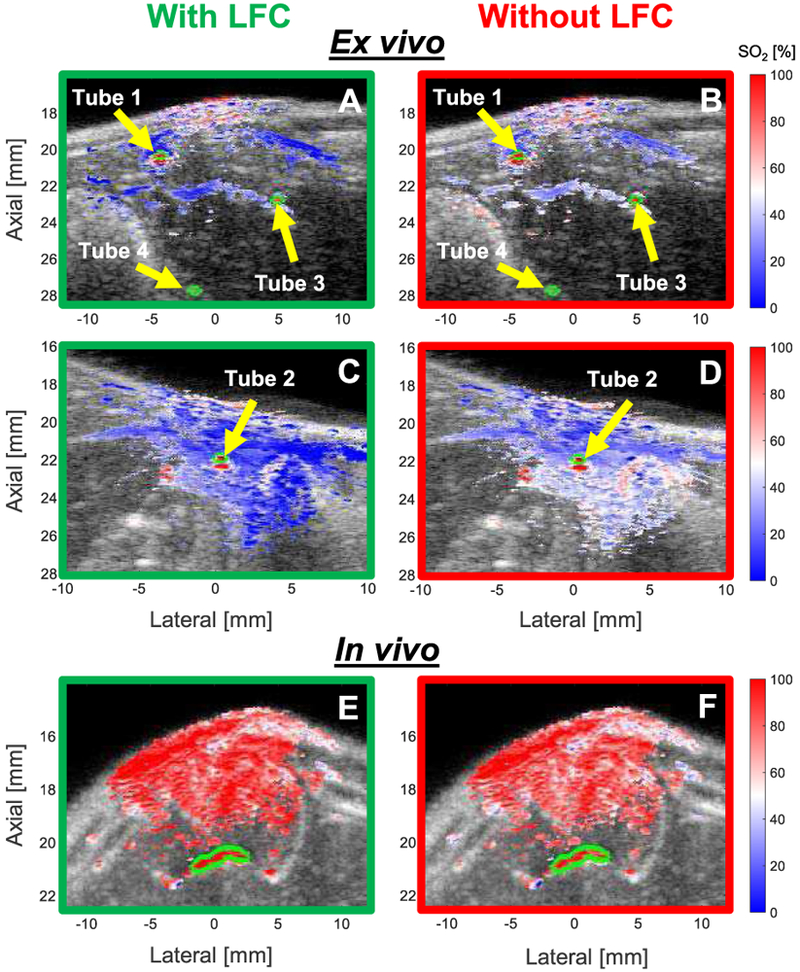
SO₂ image overlays with (green border) and without (red border) LFC in representative frames from: (A – with, B – without) ex vivo Rat 1 (Tubes 1, 3, & 4); (C – with, D – without) ex vivo Rat 2 (Tube 2); and (E – with, F – without) artery (outlined in lime green) in in vivo Rat 10.

TABLE I.

Percent Error of SO₂ Estimation in ex vivo Rats w/ and w/o LFC.

CO-ox SO2 [%]	Tube 1A (2.4 mm)		Tube 1B (2.7 mm)		Tube 3 (5.7 mm)
	With	Without	With	Without	With	Without
98.4	3.5±1.1	0.3±0.9	2.9±2.2	0.9±1.0	9.0±1.6	0.6±0.6
85.5	1.3±1.9	7.3±1.7	2.3±1.5	8.4±1.1	1.4±2.0	10.6±1.2
71.1	0.5±2.2	9.8±1.7	2.6±1.3	11.1±1.1	1.2±2.7	13.0±2.3
59.2	0.6±1.8	10.8±1.1	1.8±1.9	11.7±1.4	1.5±1.7	14.8±2.1
47.0	0.8±2.7	13.9±1.6	2.9±2.5	14.6±1.2	4.2±0.6	19.3±1.2
37.6	2.5±1.8	15.8±0.6	3.2±1.8	15.8±1.1	10.4±2.6	24.5±2.7
Avg.	1.5	9.7	2.6	10.4	4.6	13.8
CO-ox SO2 [%]	Tube 2A (3.0 mm)			Tube 2B (3.1 mm)
	With		Without	With		Without
99.6	0.2±0.8		0.4±0.0	2.3±1.2		0.1±0.2
86.1	0.8±3.1		5.1±2.6	1.3±1.1		8.1±1.1
75.2	2.1±1.2		6.4±1.1	3.6±2.3		10.1±2.5
66.0	3.9±1.1		9.0±1.0	4.3±2.1		11.6±1.6
58.0	0.5±0.7		5.4±1.1	0.7±1.4		9.9±1.1
53.1	2.5±1.0		8.6±1.3	4.3±1.1		13.5±1.1
41.5	4.4±1.8		10.9±1.8	5.4±2.1		15.9±1.6
Avg.	2.1		6.5	3.1		9.9

To analyze the accuracy of SO₂ estimation, PA-estimated SO₂ values, with and without LFC, were compared to matched Co-oximeter measurements. Additionally, to measure the limit of detectability between two different SO₂ values, the change in SO₂ (ΔSO₂) was calculated between two regions of tube located at similar depths (i.e., within 0.3 mm of each other). ΔSO₂ was calculated between two ROIs within the same tube (e.g., Tubes 2A and 2B in Rat 2) or in different tubes (e.g., Tube 1B in Rat 1 and Tube 2A in Rat 2).

As an additional assessment of our SO₂ estimation method, we investigated the impact of the number of wavelengths used for spectral unmixing. Wavelength groups included combinations of 2, 3, 4, and 5 wavelengths; the specific wavelengths used are detailed in Table II. For all wavelength-number combinations, an SNR-thresholding criterion of ≥2 wavelengths and ≥9 dB SNR was used; only those wavelengths used for unmixing were used for SNR thresholding.

TABLE II.

Wavelength Combinations for Investigation of Wavelength-Number Impact on Spectral Unmixing

Number of Wavelengths	2	3	4	5
Group 1	760, 850	760, 800, 850	710, 760, 800, 850	710, 734, 760, 800, 850
Group 2	734, 850	734, 800, 850	734, 760, 800, 850
Group 3	734, 800	710, 734, 800	710, 734, 760, 800
Group 4	710, 800	710, 800, 850	710, 734, 800, 850
Group 5	710, 850	710, 760, 850	710, 734, 760, 850

3). In Vivo Validation:

The abdominal section of in vivo Rats 1-7 was imaged (as described in II.A) during an oxygen challenge (i.e., 100% oxygen inhalation). Acquired sPA data were then used to reconstruct SO₂ imaging frames with and without LFC using the methodology detailed in II.B and II.C. Ten imaging frames (i.e., 3 rats contained 2 analysis frames each) were chosen to be in the liver wherein an artery could be manually segmented based on B-mode and SO₂ data (i.e., regions of uniform uncorrected SO₂ values in excess of 85%) with a high degree of certainty. During imaging, rats were anesthetized using 2% isoflurane and placed on a heating pad to maintain normal body temperature; ECG and respiration-cycle data were monitored to assess animal health. All in vivo imaging was done with approval from MD Anderson Cancer Center’s Institutional Animal Care and Use Committee.

III. Results

A. SNR Mask Selection

Fig. 6A,B shows regions of SNR ≥5, ≥9, and ≥13 dB with criteria of ≥2 and =5 wavelengths, respectively, exceeding this threshold. Increasing the dB-threshold or increasing the number of wavelengths that must be above that threshold predictably decreased the number of voxels included in a thresholded ROI. The number of voxels in the smallest SNR mask (i.e., =5 wavelengths with ≥13 dB SNR) is 13% of the number of voxels of the largest SNR mask (i.e., ≥2 wavelengths with ≥5 dB SNR). Fig. 6C shows the results of the investigation into the impact of the number of wavelengths used for spectral unmixing. The average SO₂-estimation error with increasing number of wavelengths does not change significantly without LFC applied; however, it decreases from 11.2% to 2.8% when using 5 instead of 2 wavelengths with LFC applied.

Fig. 6.

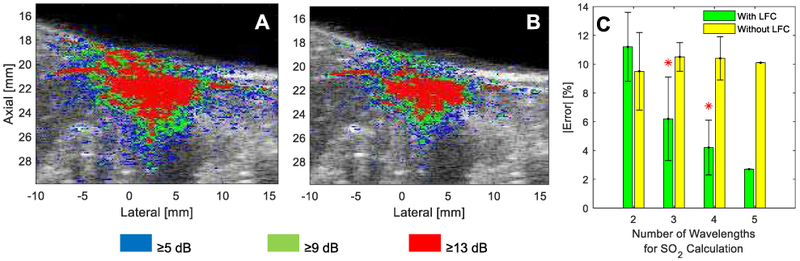
SNR-B-mode overlays showing regions of SNR ≥5 dB, ≥9 dB, and ≥13 dB for (A) ≥2 or (B) =5 wavelengths in a representative imaging frame from ex vivo Rat 2. (C) Comparison of the average SO₂-estimation error with (green) and without (yellow) LFC when SO₂ is calculated with 2, 3, 4, or all 5 wavelengths; an asterisk denotes a significant difference in error compared to the 2-wavelength result.

Fig. 7A shows the square of the average absolute error (i.e., compared to matched CO-oximeter measurements) of estimated SO₂ in the ROIs from the ex vivo experiment in II.D.2 as a function of SNR threshold and number of wavelengths exceeding this threshold. The larger errors in SO₂ estimation obtained at low-SNR thresholds (i.e., <9 dB) are due to contributions from Tube 4, which was the deepest tube analyzed (10-mm depth). The error significantly decreased by increasing the SNR threshold (i.e., ≥9 dB) as this excluded Tube 4 from the SNR mask, and thus error analysis. As Fig. 7B shows, increasing either the SNR threshold or the wavelength number tends to decrease the number of voxels included in the mask. For example, the optimized mask (i.e., ≥2 wavelengths & ≥9 dB SNR) contained only 63% of the pixels contained in the most lenient mask tested (i.e., ≥2 wavelengths & ≥5 dB SNR). Fig. 7C offers a plot of the mask-optimization cost function defined in II.B, which has a minimum at ≥2 wavelengths with an SNR threshold ≥9 dB; unless otherwise noted, these SNR-mask parameters were used for all other results.

Fig. 7.

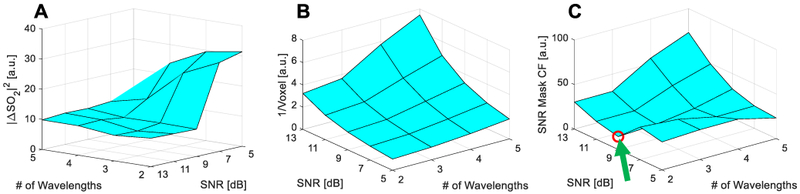
Surface plots of (A) SO₂ estimation error, (B) inverse of total voxel number included in mask, and (C) SNR mask optimization cost function; local minimum denoted with a green arrow and red circle.

B. Assessment of SNR Mask

As is shown in Fig. 4A,C, mean±SD SO₂ estimates across 6 frames of ex vivo and in vivo ROIs within the SNR mask (“Mask”) and without LFC applied are 35.7±1.0% and 67.1±1.3%, respectively, while outside of the mask (“1-Mask”) they are 63.8±1.4% and 72.0±0.4%, respectively. With LFC applied, SO₂ estimates of ex vivo and in vivo ROIs within the mask are 21.6±1.7% and 72.5±0.7%, respectively. Based on unmixing of noise-ROI data (i.e., green dashed boxes in Fig. 4A,C), SO₂ estimates are 69.1±1.5% and 72.5±0.7% for ex vivo and in vivo ROIs, respectively. Based on linear unmixing of the reciprocal of laser-pulse-energy spectra (as are shown in Fig. 4D), SO₂ estimates of 69.8±1.8% and 72.3±0.5% were obtained, which are not statistically different than their matched noise-ROI SO₂ estimates.

C. Ex Vivo and in Vivo Validation

The SO₂ in the tubes in ex vivo Rat 1 and Rat 2 were measured by the CO-oximeter to be 98.4% and 99.6%, respectively, for the representative SO₂ overlay images shown in Fig. 5. Use of LFC results in lower estimates of SO₂ (i.e., bluer image) than when no LFC is applied. Note that application of the SNR mask excluded Tube 4 (10 mm depth) from analysis. The CO-oximeter readings of all tested SO₂ values for tubes in ex vivo Rats 1 and 2 are shown in the first column of Table I. Percent errors for each tube with and without LFC are provided in subsequent table columns. The percent errors with LFC are lower than that without LFC for all tubes and at all tested SO₂ values except for estimates at 98.4% for Tubes 1 and 3 and at 99.6% for tube 2B. With and without LFC, average percent errors tend to increase with depth (e.g., Tube 3 compared to Tubes 1 and 2).

As is shown in Fig. 8A, SO₂ tends to be overestimated (i.e., compared to matched CO-oximeter values) without LFC. The maximum and average percent errors are 24.5% and 10.1%, respectively, without LFC (red traces in Fig. 8A), while these decrease to 10.4% and 2.8%, respectively, with LFC (Fig. 8A, green lines). Fig. 8B shows calculated ΔSO₂ values with and without LFC compared to expected changes based on matched CO-oximeter measurements. Use of LFC provides better accuracy in estimating ΔSO₂ in all cases shown. With LFC, the estimated ΔSO₂ magnitude and direction of change are consistent with CO-oximeter-measured ΔSO₂ values. However, without LFC, six cases show ΔSO₂ estimates with either significantly incorrect magnitude and/or direction when compared to CO-oximeter measurements. The maximum and average errors in estimating ΔSO₂ is reduced from 8.1% and 6.4%, respectively, without LFC to 4.7% and 2.0%, respectively, with LFC. Fig. 8C shows that relative model error (defined in II.C.4) within the SNR “Mask” region is on average lower than that in the “1-Mask” region. Fig. 8D shows the difference between the relative model error before and after LFC; note that relative model error tended to decrease rather uniformly within the “Mask” region following LFC.

Fig. 8.

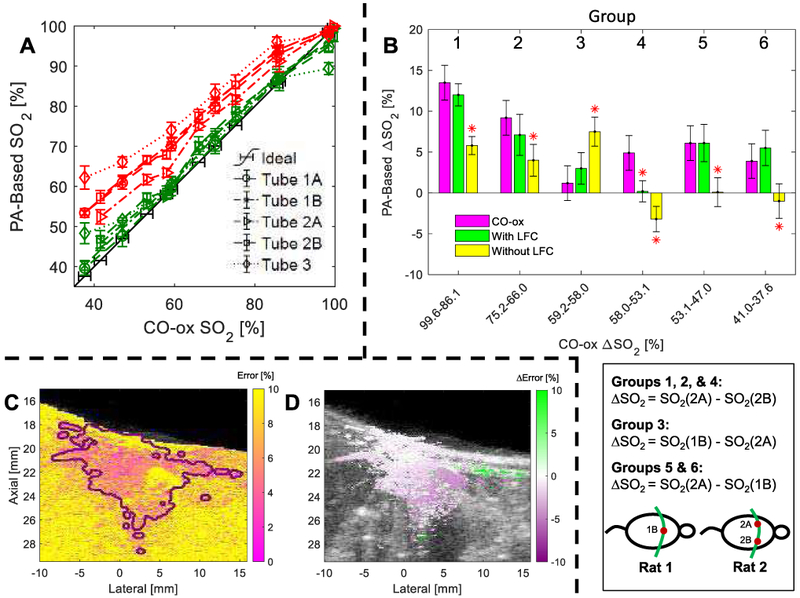
(A) Error-bar plot of PA-based SO₂ estimation vs. CO-oximeter measurements in each tube (denoted by marker type) with (green) and without (red) LFC. (B) Comparison of estimated ΔSO₂ using blood samples of different SO₂ with (green) and without (yellow) LFC compared to CO-oximeter measurements (purple) in different tubes, as depicted in the schematic below the plot. An asterisk denotes a significant difference in ΔSO₂ estimate compared to the matched CO-ox result. Representative example of (C) relative model error and (D) reduction of model error following LFC for ex vivo Rat 2.

In the in vivo study, PA-based SO₂ estimates significantly increased from 92.9±2.9% without LFC to 95.5±1.2% with LFC. The results from all 10 in vivo Rats are summarized in Table III.

TABLE III.

Mean SO₂ Estimates in Arteries w/ and w/o LFC.

ROI	Rat	SO2 [%] With	SO2 [%] Without	Arterial Depth [mm]
1	1	97.5	97.0	1.4
2	2	95.0	88.6	1.9
3	3	96.8	94.3	1.9
4	4	95.9	96.0	2.0
5	5	96.1	93.4	2.0
6	6	94.0	90.2	2.3
7	7	96.4	93.0	3.5
8	1	94.0	95.2	4.4
9	7	94.8	91.9	4.9
10	3	94.4	89.3	5.5
Avg.		95.5±1.2	92.9±2.9

IV. Discussion

In this work, we show that SNR regularization combined with LFC improves PA-based SO₂ estimation accuracy in ex vivo and in vivo tissue environments. The developed LFC model reduces the average SO₂ estimation error from 10.1% to 2.8% in ex vivo tissue, while it increases mean SO₂ estimation from 92.9% to 95.5% in in vivo arteries during an oxygen challenge, when arterial SO₂ is expected to be near 100%. Additionally, the mean error in estimating changes in SO₂ (i.e., ΔSO₂) reduced from 6.4% to 2.0% after application of LFC.

LFC of sPA data improves the accuracy of SO₂ estimates by accounting for the effect of wavelength-dependent optical attenuation, known as spectral coloring [38]. As is shown in Fig. 8A, SO₂ is overestimated when LFC is not applied because scattering – which tends to decrease with increasing wavelength – causes local fluence at longer wavelengths (e.g., 850 nm) to be relatively higher than that at shorter wavelengths (e.g., 710 nm). This results in a redshift of the sPA spectrum, causing it to more closely resemble the monotonically increasing absorption spectrum of HbO₂ and thus yield an artificially high SO₂ estimate [16]. However, given that ${\mathbf{c}}_{\mathrm{HHb},\text{final}}^{i,j}$ in Eq. (10) cannot be negative, such overestimation is bound by a maximum SO₂ estimate of 100%. Such a phenomenon resulted in the abnormally small estimation errors obtained without LFC for samples near 100% SO₂ (i.e., CO-ox SO₂ of 98.4% & 99.6% in Table I). In these specific cases, the SO₂ estimation bound of 100% just happened to nearly coincide with the samples’ CO-oximeter-measured SO₂. Addressing the issue of spectral coloring not only improves accuracy of estimating absolute SO₂, but it also improves the accuracy in assessing relative oxygenation changes (i.e., ΔSO₂). It is often assumed that comparison of similar ROIs (e.g., the same depth in the same tissue type) without LFC permits accurate assessment of relative SO₂ changes, which could be diagnostically useful to track longitudinal variation in disease progression and/or therapy response [15], [47]. In our study, however, an average error of 6.4% was observed in assessing changes in SO₂ for the same or similar ROI without LFC. Unfortunately, this error level is greater than the SO₂ difference reported between control and treatment cohorts in some preclinical studies [48]. Thus, the reduction to 2.0% error achieved through application of our method demonstrates that LFC could be necessary in facilitating successful clinical translation of a robust and diagnostic PA-based assay to measure relative SO₂ changes due to pathology.

Our study also investigated the effect of wavelength number on SO₂ estimation accuracy. To this end, Fig. 6C shows that increasing the number of wavelengths where sPA data are acquired does not significantly change average SO₂ estimation error when LFC is not applied. This is because spectral coloring, which is likely the primary source of this estimation error, persists even with the inclusion of additional wavelengths. On the other hand, a significant error reduction is obtained by increasing the number of wavelengths used for unmixing with LFC. This is likely because the inverse problem is not always well-posed, and therefore increasing the amount of data acquired (for the same unknowns) improves the well-posedness of the solution, which helps with convergence to a stable answer. In future work, the impact of the precise wavelengths selected for analysis on model accuracy will be investigated [49].

In addition to assisting with model convergence, voxel-wise SNR assessment also provides improvement in the accuracy of post-processing analysis. As is shown in Fig. 4A, the average SO₂ estimate outside of the SNR mask (“1-Mask”; 63.5%) is similar to the average estimate in the noise ROI (68.8%), both of which being drastically higher than the average SO₂ obtained in the SNR mask (“Mask”), which presents with a low-SO₂ estimate (35.9% without LFC) that is consistent with ex vivo tissue. Worse yet, the estimated SO₂ in the noise ROI is not significantly different from that estimated by the inverse of the laser-pulse-energy spectrum alone, as is shown in Fig. 4D. Since all sPA data are normalized by the output pulse energy, regions of only noise – such as these most distal noise ROIs – provide a spectrum statistically identical to that of the inverse of pulse energy. In this experiment, “pure” noise presented with an (artifactual) SO₂ estimate of approximately 70%; this is likely near the expected value for noise regions acquired with similar OPO-based PA imaging systems, which tend to have higher pulse energy in the low-NIR range. In the ex vivo example presented herein, the distinction between high/low-SNR and poor-SNR voxels happens to be apparent in the SO₂ image because of the inherent contrast between low-SO₂ estimates for (deoxygenated) ex vivo tissue and the ~70% artifactual estimates for regions that are predominately noise. In an in vivo situation (Fig. 4C), however, high-SNR SO₂ estimates in in vivo tissue can be indistinguishable from poor-SNR regions based on SO₂ alone. Thus, without independent assessment of SNR, one is prone to assigning an analysis ROI that contains a number of voxels with poor SNR, which would introduce a significant bias in the ROI-averaged SO₂ estimate toward the expected value for pure noise (i.e., ~70% SO₂).

Despite achieving significant improvements in the estimation of absolute and relative SO₂, there are limitations in our study that should be addressed in future work. Firstly, although we feel an assumption of spatially invariant scattering is reasonable given the relative homogeneity of the liver, for highly heterogeneous FOVs this assumption might decrease SO₂ estimation accuracy. To address this issue, tissue segmentation based on US contrast could be used to allow for multiple scattering coefficients that would be individually constrained based on a priori knowledge of the assumed tissue types [33]. Secondly, LFC was independently applied to each 2D imaging frame, and out-of-plane variation of optical properties were not considered. Given that a 3D imaging data set was available, it would be possible in the future to simultaneously apply LFC to the entire 3D volume such that out-of-plane absorber distributions impact local fluence estimates, which could improve estimation accuracy of more heterogeneous regions of tissue [22]. Lastly, in an effort to allow for near-realtime (~1 fps) implementation in the future, parallel processing could be implemented [50].

V. Conclusions

This work illustrates the potential of PAUS imaging combined with SNR-regularized LFC in improving the accuracy of estimating absolute SO₂ and relative changes in SO₂ for both ex vivo and in vivo tissue environments. Based on study results presented herein, assessment of voxel-wise SNR for regularization/thresholding purposes appears to be critical, particularly for the purpose of accurate post-processing analysis and display. Additionally, given average reductions in percent error to 2.8% (from 10.1%) and 2.0% (from 6.4%) for absolute and relative SO₂ estimates, respectively, the need for LFC in future clinical endeavors must be carefully considered for achieving robust and accurate quantitative PA imaging.