Abstract
The solubilization of lyophobic compounds in block copolymer micelles has been extensively investigated but remains only partially understood. There is a need to understand the fundamental parameters that determine the spatial distribution of the solubilized compounds within the micelles. Controlling this feature is a key aspect in the design of drug delivery systems with tailored release properties. Using Scheutjens–Fleer self-consistent field (SF-SCF) computations, we found that solubilization is regulated by a complex interplay between enthalpic and entropic contributions and that the spatial distribution can be controlled by the concentration and solubility of the guest compound in the dispersion medium. Upon solubilization, a characteristic change in size and mass of the micelles is predicted. This can be used as a fingerprint to indirectly assess the spatial distribution. Based on these findings, we developed two experimental protocols to control and assess the spatial distribution of lyophobic compounds within block copolymer micelles.
Introduction
Block copolymer micelles are often used to disperse and transport compounds at concentrations exceeding their solubility in the medium. This strategy is widely applied in industrial formulations1 and has great potential for transportation and targeted delivery of drugs in vivo.2−5 Solubilization of guest compounds has been studied extensively during the last few decades. On the basis of spectroscopic studies [UV–visible,6,7 nuclear magnetic resonance (NMR)],8 small-angle scattering experiments (small-angle X-ray scattering9 and small-angle neutron scattering8), and theoretical considerations,10 it has been proposed that the solubilized compound can be located in two regions of the micelles: within the interior of the core and near the core–corona interface. This spatial distribution (or solubilization region) is of key importance as it determines the local environment of the guest molecules. This can dramatically affect, for instance, the release kinetics of the encapsulated compounds in drug delivery systems.11,12 The release of compounds adsorbed at the core–corona interface is typically fast,11 whereas the release of compounds solubilized into the core can be very slow,11 as diffusion throughout the dense desolvated core of the micelle is required prior to release in solution.11 Hence, the ability to control the solubilization region is crucial for the design of drug delivery systems with controlled release properties.
The factors controlling the solubilization region are however only partially understood, as most of the efforts have been made to understand what controls the solubilization efficiency. Some studies13,14 hypothesize that the latter is governed by specific interactions between the guest and the micelle, and semiempirical predictive models have been developed accordingly.14 Although these models provide useful insights into the compatibility between the guest and the micelles, they do not enable accurate quantitative predictions of the encapsulation efficiency and guest distribution.14 In other studies, the solubilization is treated as a partition equilibrium between the solvent and the micelle,15−17 thus considering the latter as a macroscopic phase where there is no distinction between different solubilization regions. Both approaches have another fundamental limitation in common: they do not take into account the change in free energy of the micelle because of the presence of solubilized material. This aspect has been included in the theoretical approach of Nagarajan and co-workers,10,18 but their model does not provide quantitative information about the spatial distribution of the guest compounds within the micelle.
The Scheutjens–Fleer self-consistent field19,20 (SF-SCF) theory is a numerical lattice-based method19 which allows computing the equilibrium properties of self-assembled block copolymer structures in the presence of guest compounds.20−22 The SF-SCF computations are typically very fast (only a few seconds are required to compute the equilibrium properties of a single self-assembled structure); therefore, they are very suitable to systematically study solubilization.
The radial concentration profiles (see Figure 1) generated from the computations describe the spatial arrangement of the components inside and outside the self-assembled structure and can be used to assess the preferred solubilization region, while simultaneously monitoring any change in the micelle structure. Furthermore, the SF-SCF method provides access to important information, such as the number of copolymer chains per micelle at equilibrium (also known as aggregation number, Nagg) and the critical micelle concentration. With the SF-SCF method, we investigate which parameters control the solubilization and local distribution of a model guest compound in diblock copolymer micelles dispersed in a solvent and we identify a signature effect on the micelle equilibrium properties, which will be discussed in detail.
Figure 1.
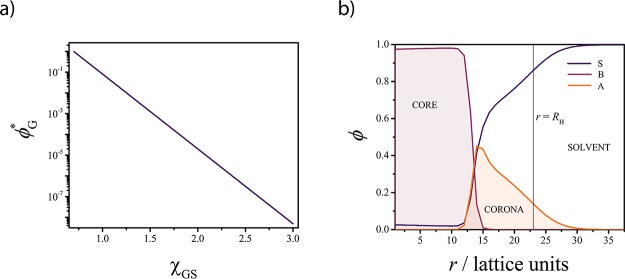
Solubility of guest compound (G) and concentration profile for the model A–B micelle: (a) solubility of G (ϕG*) as a function of χGS (ϕG = 102.52–3.61χGS); (b) SF-SCF concentration profile showing the structure of the A45–B28 micelle in solvent S (χSA = 0.4, χSB = 3, and χAB = 1). The local concentration (ϕ) of each component is plotted as a function of the distance from the center r of the micelle. The vertical black line indicates the hydrodynamic radius RH of the micelle (see the Supporting Information for details).
On the basis of the theoretical findings, we designed a simple experimental protocol where the dominating solubilization region is actively controlled by tuning the guest solubility. To test this methodology, we investigated the solubilization of the solvatochromic dye Nile red (NR) in micelles composed of poly-(ethylene oxide)-block-poly-ε-caprolactone (PEO–PCL). These biocompatible block copolymers are used in biomedical applications and represent suitable candidates for the design and preparation of drug delivery systems.3 The absorption spectrum of NR in the UV–visible range, particularly the wavelength of the absorption maximum λmax, is sensitive to the polarity of the environment.23 Therefore, it is possible to monitor the position of dye within the micelles via UV–visible spectroscopy. As NR is poorly soluble in water (<5 × 10–7 mol·L–1, see the Supporting Information) but well soluble in ethanol, we used mixtures of water and ethanol to tune the NR solubility and control the solubilization region. Further, with the guidance of the SF-SCF theoretical insights, we developed an experimental procedure which we used to determine experimentally the solubilization region of naphthalene (NF), benzophenone (BP), and 2, 2′-bipyridine (BPy) into PEO–PCL micelles. These compounds have been chosen because they are characterized by similar structures but different solubility in water. The procedure uses static light-scattering (SLS) and dynamic light-scattering (DLS) measurements to monitor the variation in the size and mass of the assemblies upon solubilization.
Experimental Section
Materials
Unless differently specified, all the chemicals were obtained from Sigma and the solvents were obtained from Biosolve, the Netherlands.
Synthesis, Purification, and Characterization of PEO–PCL
The diblock copolymer EO45–CL14 (PEO–PCL) has been synthesized and purified using a polymerization procedure and purification method reported previously.24
The number-average molar mass of the synthesized copolymer MnNMR = 3.6 kDa, based on the degree of polymerization, was measured via 1H NMR and carried out on a Varian 400 (400 MHz) spectrometer at 25 °C in deuterated chloroform.
The molar mass dispersity D̵ = Mw/Mn was determined by means of size exclusion chromatography, using Waters GPC equipped with a Waters (model 510) pump and a (model 410) differential refractometer. A set of two mixed bed columns (Mixed-C, Polymer Laboratories, 30 cm, 40 °C) was used and tetrahydrofuran was selected as the eluent. The system was calibrated using narrow molar mass polystyrene standards, ranging from 600 to 7106 Da. A value of D̵ = 1.10 was obtained for the synthesized copolymer.
NR Characterization
UV–vis spectroscopy measurements were performed on a Shimadzu 2700 spectrophotometer. The absorbance (A) spectra of the NR solutions were recorded as a function of the incident light wavelength using a 0.5 nm step size at a medium measurement speed with a 1 nm slit size. The samples and the reference (pure dispersion media) were placed in quartz cuvettes with a path length of 1 cm.
The molar attenuation coefficient of NR was determined in a water–ethanol mixture containing a water volume fraction ϕW = 0.5. To this end, the absorption spectra of solutions with concentrations of 3 × 10–5, 3 × 10–5, 3 × 10–5, and 5 × 10–6 M were recorded in the wavelength range 400 ≤ λ ≤ 800 nm. NR shows a single absorption peak with the maximum at λmax = 576 nm. The absorbance A at λmax was fitted as a function of the dye concentration with a linear regression to obtain the molar attenuation coefficient of NR, εNR = 33 400 l·mol–1·cm–1, according to the Lambert–Beer law (A = εbC, with b = 1 cm the optical path length, and C the molar concentration). The data are plotted in Figure S7 in the Supporting Information. The linear behavior is lost at a higher concentration and the intercept of the fitted line differs significantly from zero. This might indicate the formation of NR dimers or other small, stable aggregates in water–ethanol mixtures.
The solubility of NR in water–ethanol mixtures was determined as a function of the water volume fraction ϕW. An excess of NR was added to different water–ethanol mixtures with 0.5 < ϕW < 0.95 and the mixtures were shaken on a shaking table for 2 h. Centrifugation at 5000 rcf and filtration via a 0.22 μm PTFE syringe filter (VWR) were used to remove the excess insoluble NR before measuring the UV–vis absorbance of the mixtures. The NR solubility CNR* was determined from the value of εNR, approximated as constant in the water–ethanol mixtures (the determination of εNR for high ϕW mixtures is challenging because of the extremely low dye solubility) studied. Under this assumption, CNR is slightly overestimated, as changes in the attenuation coefficients (of the order of a few percent) are known to occur in similar systems with increasing ϕW.25 This, however, is not expected to influence the qualitative interpretation of the data.
Micelle Formation in a 50:50 Water–Ethanol Mixture
A mixture containing 100 mg of PEO–PCL and 2 mL of a ϕW = 0.5 water–ethanol mixture was heated to 60 °C under stirring. At this temperature, the solution becomes optically transparent after a few minutes, indicating the formation of micelle dispersion (see the Supporting Information). The mixtures were subsequently cooled down to 40 °C and half of it (1 mL) was diluted by quickly adding 9 mL of the ϕW = 0.5 water–ethanol mixture at room temperature. The diluted dispersion was analyzed via light scattering to verify the formation of the micelles. The results are reported in the Supporting Information.
Solubilization of NR in PEO–PCL Micelles
A set of six mixtures containing 100 mg of PEO–PCL and 2 mL of 4 × 10–6 M NR solution in ϕW = 0.5 water–ethanol mixtures were heated to 60 °C under stirring. At this temperature after a few minutes, the solution becomes optically transparent, indicating the formation of micelle dispersion (see the Supporting Information). The mixtures were subsequently cooled down to 40 °C and 1 mL of each mixture was quickly transferred into a vial containing 9 mL of solvent mixture at room temperature. The composition of the six mixtures was set in order to obtain final water–ethanol volume fractions of ϕW = 0.5, 0.6, 0.7, 0.8, 0.9, and 0.95, respectively. The final dispersions were analyzed via UV–visible to determine their λmax values. The normalized spectra of the final NR/micelles mixtures are plotted in Figure S6 in the Supporting Information, whereas the λmax values are plotted in Figure 8b.
Figure 8.
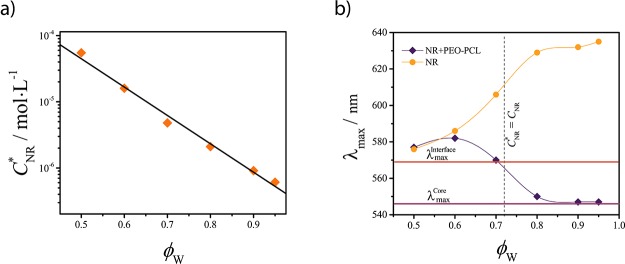
NR solubilization. (a) NR solubility (CNR*) in water–ethanol mixtures as a function of the water volume fraction ϕW. (b) Position of the NR absorption maximum λmax as a function of ϕW in the absence (dots) and presence (diamonds) of the PEO–PCL micelles at a fixed NR concentration CNR = 4 × 10–6 M value. The spline curves are depicted to guide the eye. The vertical dashed line indicates the point where the concentration of NR equals its solubility (CNR = CNR). The horizontal lines correspond to the λmax values of NR into the core (λmaxcore = 546 nm)- and interface (λmax = 569 nm)-mimicking solutions.
Determination of the Solubilization Region of NR
The position of the absorption maximum λmax depends on the polarity of the environment;23 hence, it can be used to distinguish the solubilization region of NR. However, to unambiguously identify such regions, λmax reference values for NR located at the core–corona interface and inside the core of the micelles are needed.
In a previous work,26 we found that the core of PEO–PCL micelles is composed of 95% of PCL and 5% of water, whereas the average composition of the corona was found to be approximately 13% of PEO 87% of water. On the basis of these data, we prepared two solutions which mimic the polarity of the core and the core–corona interface. The core-mimicking solution was prepared by mixing 95% of ε-caprolactone and 5% of water, whereas the interface-mimicking was composed of 50% of ε-caprolactone (Sigma), 15% of PEO (Sigma, Mn = 400 Da), and 35% of deionized water. PEO (400 kDa) has been chosen to reduce the possibility of aggregation of the polymer in solution.27 All the solutions were optically homogeneous (no turbidity was observed because of demixing). The UV–vis absorption spectra of NR dispersed into the core and interface-mimicking solutions (Figure S4 in the Supporting Information) were used as references to determine whether the dye was encapsulated into the core or adsorbed at the core–corona interface of the micelles. To this end, the λmax values obtained from these spectra were compared with that of NR obtained in the different water–ethanol mixtures in the presence of micelles to identify the solubilization region.
Solubilization of NF, BP, and BPy
Micelles of EO45–CL14 in water have been prepared by adding 1 mL of acetone containing 50 mg of the copolymer to 9 mL of distilled water, leading to a final block copolymer concentration of 5 mg·mL–1. The solution was shaken by hand to ensure complete mixing. A similar procedure has been applied to solubilize NF, BP, and BPy into the micelles: two different amounts of encapsulants (4 and 20 mg) have been added in 1 mL of acetone together with 50 mg of the copolymer, followed by quick addition of the solution in 9 mL of deionized water. Each solvent was filtered prior to use with an appropriate 0.22 μm syringe filter. The micelle dispersions were subsequently diluted with deionized water in order to obtain suspensions with various polymer concentrations, which have been analyzed to determine the molar mass and the size of the micelles via light scattering.
SF-SCF Computations and Light-Scattering Analysis
A detailed description of the procedure used for SF-SCF computations and light scattering analysis is reported in the Supporting Information.
Results and Discussion
Solubility of the Guest Compound
Before discussing the SF-SCF results, it is important to establish a connection between the SF-SCF-related quantities and the experimentally measurable ones. The SF-SCF method is based on the Flory–Huggins (FH) theory; therefore, it uses the so-called FH interaction parameters (χ) as a measure of the pair interaction between all the components of the system of interest.28 The components are modeled as sets of connected segments distributed over a lattice.28 According to FH theory, the size of the components (number of connected segments) and their χ parameters determine their miscibility.28 To ease the interpretation of the SF-SCF results, the solubility (ϕG*) of the guest compound (G) (Figure S1 in the Supporting Information) in the solvent (S), in the absence of the copolymer molecules, has been calculated as a function of the interaction parameter χGS (see Figure 1a and the Supporting Information for details). In the following discussion, we will refer to the solubility, expressed as a volume fraction ϕG, instead of χGS.
Self-Assembly of A–B Block Copolymers
The model copolymer used to systematically study the solubilization was an A–B-type diblock copolymer (A45–B28, for which an experimental analog was available) where A is the lyophilic block and B is the lyophobic block (χSA = 0.4, χSB = 3 and χAB = 1). In the absence of the guest compound, the equilibrium SF-SCF computations predict the formation of spherical micelles. These micelles are characterized by an average aggregation number Nagg = 306 and a hydrodynamic radius RH = 23 lattice units (see the Supporting Information for more details). From the radial concentration profiles (Figure 1b), it appears that the blocks are segregated into different domains: a solvent-poor core and a solvent-rich corona (Figure 1b), connected via a 3–4 lattice units wide interface.
Effect of Guest Solubility and Concentration on Solubilization
For understanding how the guest solubility and concentration affect the solubilization of G within the A–B micelles, it is useful to start by neglecting the effect of specific interactions between G and the copolymer blocks. In the SF-SCF computations, such interactions are defined by the two parameters χGA and χGB, which were set to be zero. Under this condition, G and the copolymer interact only via an excluded volume. Unless specified, the average concentration of G in the computational lattice ϕG = 2 × 10–3 and ϕG* is tuned by varying χGS.
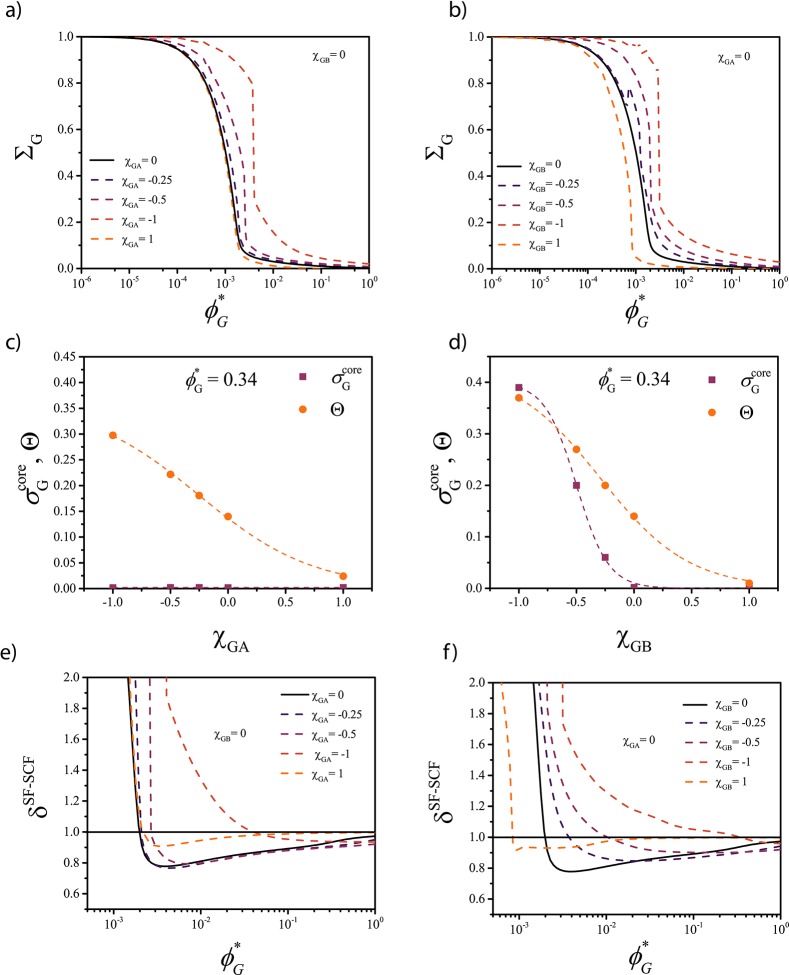
The solubilization efficiency ΣG (Figure 2), defined as the ratio between the number of G molecules solubilized in the micelle and the total number of G molecules in the computational lattice, has been evaluated as a function of the guest solubility ϕG* (see the Supporting Information for details). We find a ΣG transition between the regimes ϕG > ϕG and ϕG* < ϕG, illustrated in the radial concentration profiles in Figure 3. Transferring molecules from the solution and confining them into a micelle is associated with an entropy penalty which (in the absence of attractive interactions) must be overcompensated by a favorable change in the free energy of the micelle. Still, even for athermal interactions and completely soluble G, a portion of the G molecules is already solubilized in the micelle. In fact, for ϕG > ϕG, we observe a small but finite value of ΣG (Figure 2).
Figure 2.
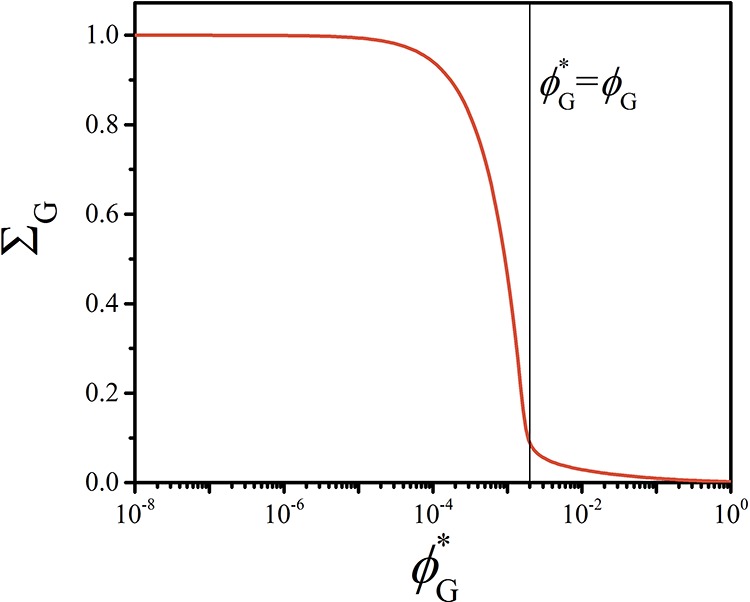
Solubilization efficiency ΣG of the guest compound (G) into the A45–B28 micelles as a function of the G solubility ϕG*.
Figure 3.
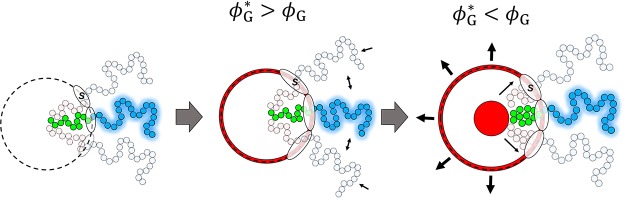
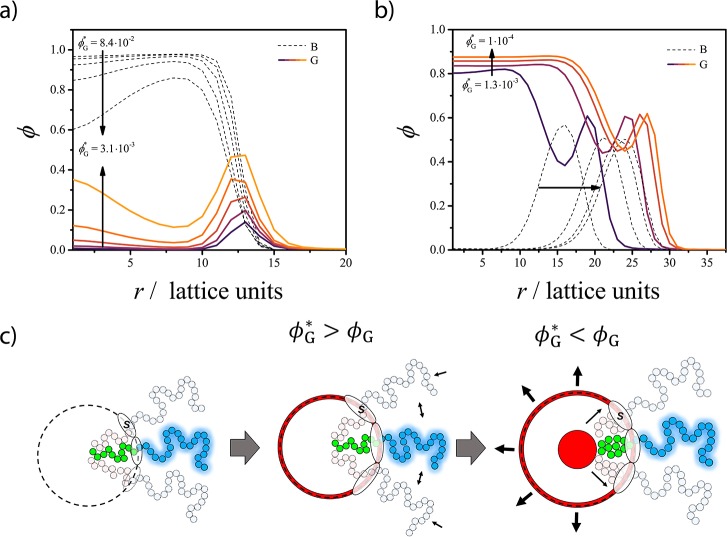
Concentration profiles showing the structure of the A–B micelle upon solubilization of G at (a) ϕG* > ϕG and (b) ϕG < ϕG. The local concentration (ϕ) of the B blocks (dashed curves) and G (continuous curves) are plotted as a function of the distance from the center r of the micelle for different ϕG* values. The A blocks and S are omitted to increase the clarity of the graph. (c) Schematic representation of the structure of the A45–B28 micelle upon solubilization of G in the two regimes as can be derived from the SF-SCF concentration profiles.
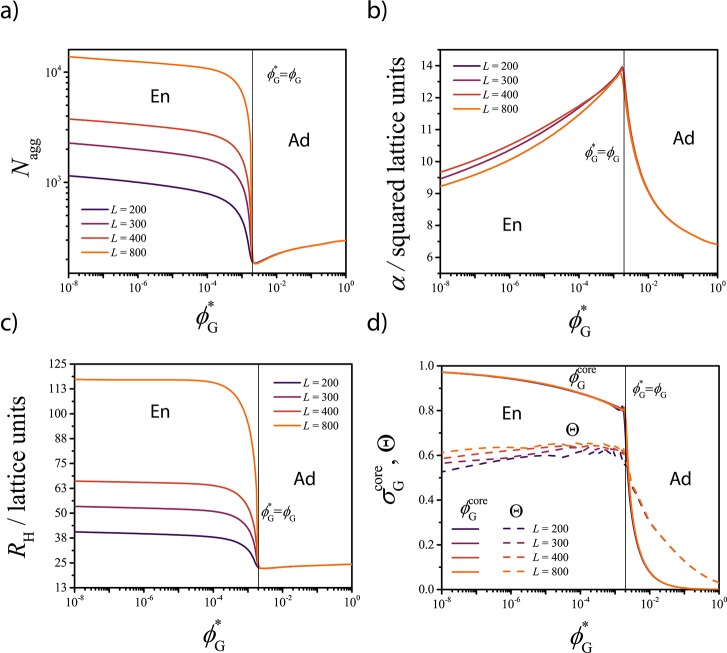
The radial concentration profiles (Figure 3a) show that for ϕG* > ϕG, the solubilized G molecules are mainly adsorbed at the core–corona interface. In Figure 4, the value of Nagg, the surface area α per polymer at the core–corona interface, the micelle hydrodynamic size RH, and the concentration of G into the micelle core σG and at the core–corona interface Θ derived from the SF-SCF computations are presented as a function of ϕG*. The adsorption of G reduces the tension of the core–corona interface,18,29 which leads to a lower effective attraction between the lyophobic chains. This is reflected in the decrease of Nagg and in the increase of the surface area α (α ≈ Nagg–1, see eq S3 in the Supporting Information for details) observed in Figure 4a,b, respectively. A larger α value allows a reduction of chain stretching both in the core and in the corona, with a consequent increase of the configurational entropy (as schematically depicted in Figure 3c).
Figure 4.
SF-SCF results for (a) aggregation number Nagg, (b) surface area occupied by each polymer at the interface between core and corona α, and (c) hydrodynamic radius of the micelle RH as a function of the guest solubility ϕG*. (d) Local volume fraction of G in the center of the core σG (continuous curves) and degree of coverage of the core–corona interface Θ (dashed curves) as a function of ϕG*. Results are plotted for different values of the total number of lattice layers L. The black vertical lines indicate where ϕG = ϕG and separate the adsorption-dominated region (Ad) from the encapsulation-dominated one (En).
In case the guest concentration exceeds the solubility (ϕG* < ϕG), ΣG increases dramatically (Figure 2).
When ϕG* is approximately 10 times smaller than ϕG, the value of ΣG approaches 1 (ΣG = 1 corresponds to a solubilization efficiency of 100%). In this regime, G increasingly accumulates within the core of the micelle, which results in the formation of a G-rich domain, as follows from the concentration profiles in Figure 3b. The values of Nagg and RH increase (Figure 4a,c) with decreasing ϕG, whereas α decreases as more A–B molecules accumulate at the surface of the G-rich droplet. In the encapsulation-dominated regime (ϕG* < ϕG), the value of Nagg and RH strongly depends on the size of the computational lattice L, as shown in Figure 4. This indicates that upon solubilization, the equilibrium characteristics of the assembly depend on the relative amount of guest and copolymer molecules present in the solution (see related discussion in the Supporting Information), similarly to what is observed for emulsions.19,30
The comparison between the local concentration of G inside the lyophobic core (σGcore) and the fraction (Θ) of the core–corona interface covered by G as a function of ϕG (Figure 4d) corroborates that the crossover between adsorption-dominated and encapsulation-dominated regimes is sharp and occurs at ϕG ≈ ϕG*. In the encapsulation-dominated regime, adsorption still takes place, with an interfacial coverage value Θ ≈ 0.6 and almost independent of the guest concentration (Figure 4d).
In another set of computations, the coverage of the core–corona interface Θ has been studied as a function of the overall guest concentration ϕG (thus varying the total number of G molecules in the computational lattice) for three different ϕG* values. The adsorption can be properly described with a Langmuir isotherm for Θ ≪ Θmax, as shown in Figure 5. This finding is in agreement with the experimental observations of Choucair and Eisenberg,6 who studied the solubilization of 2-nitrodiphenylamine in polystyrene-poly(acrylic acid) micelles. The deviation of the SCF data from the Langmuir model (Figure 5) probably results from a competition between adsorption and encapsulation.
Figure 5.
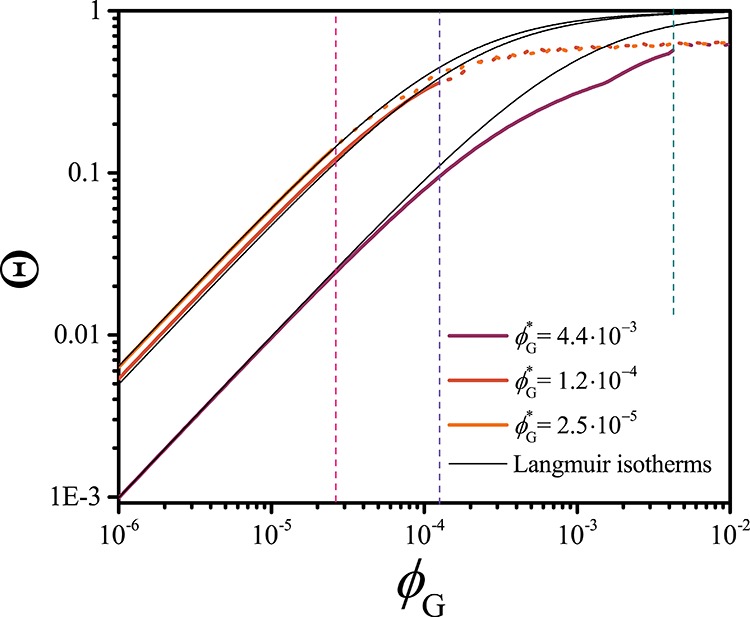
Degree of coverage of the core–corona interface of PEO–PCL micelles upon adsorption of the guest molecule G as a function of the solubility G (ϕG), as obtained from the SF-SCF computations. The results are displayed for three different values of the solubility of G (ϕG*) and are fitted with a Langmuir isotherm (Θ = KadϕG/(1 + KadϕG), where Kad is the adsorption constant) for ϕG < ϕG, corresponding to the conditions where adsorption dominates. The vertical dashed lines indicate the three ϕG = ϕG* values.
We can conclude that in the absence of specific interactions between the guest and the micelles, the guest concentration and solubility govern the preferred solubilization region. At ϕG* > ϕG, the guest molecules adsorb at the core–corona interface in spite of the loss of translational entropy. Adsorption is driven by a reduction of the interfacial tension between the core of the micelle and the solvent. The typical signature of this process is a reduction of the aggregation number of the micelle.
Insoluble compounds, which in the absence of the copolymer molecules would phase-separate, accumulate in the droplets surrounded by the copolymer molecules, forming emulsion-like structures. The typical signature of this process is an increase in the size and the aggregation number of the assemblies, which is a function of the relative concentration between the polymer and the guest.
Effect of Specific Interactions between the Guest and the Micelles
To determine how specific interactions affect solubilization, we performed two sets of computations in which G interacted with the corona (A) or with the core (B) forming blocks, respectively. The specific interactions were introduced by assigning a nonzero value to either χGA or χGB. Both attractive (χGA, χGB = −0.25, −0.5, −1) and repulsive (χGA, χGB = 1) interactions were tested. Illustrative results are plotted in Figure 6.
Figure 6.
Effect of specific interactions between the guest G and (a) corona blocks and (b) core blocks on the solubilization efficiency ΣG of G into the A45–B28 micelles as a function of the G solubility ϕG*. (c,d) Local volume fraction of G in the center of the core σG and degree of coverage of the core–corona interface Θ at ϕG* = 0.34 as a function of (c) χGA and (d) χGB. (e,f) Influence of ϕG on the relative mass of the self-assembled structures δSF-SCF.
Again, two distinct regimes could be identified, characterized by a dramatic difference in encapsulation efficiency. The crossover between the two regimes takes place at ϕG* > ϕG if attraction with one of the blocks (χGA, χGB < 0) is present (see Figure 6a,b) indicating that, not surprisingly, specific attraction allows solubilizing the compounds more efficiently. Interestingly, a strong repulsion with the corona blocks (χGA = 1) seems to have little effect on the solubilization efficiency (Figure 6a), whereas a strong repulsion with the core blocks (χGB = 1, Figure 6b) shifts the position of the transition point toward ϕG < ϕG, as upon solubilization, G is mostly in contact with the core.
Above the transition point (ϕG* > ϕG), the attraction between G and the corona blocks (χGA < 0) enhances the interfacial adsorption (Figure 6c) but does not affect the concentration of G within the core. In contrast, the attraction between G and the core blocks (χGB < 0) enhances both interfacial adsorption and core encapsulation, leading to preferential core encapsulation, even at ϕG ≫ ϕG (Figure 6d).
The ratio between the mass of the self-assembled structures with the solubilized material M over the mass of the bare empty micelles M0 is defined here as δSF-SCF = M/M0 (Figure 6e,f). The SF-SCF computations predict that if the interfacial adsorption dominates, δSF-SCF < 1, whereas if encapsulation is preferred, δSF-SCF > 1 regardless of the way G interacts with the micelles. This quantity is relevant as it can be compared with experimental data.
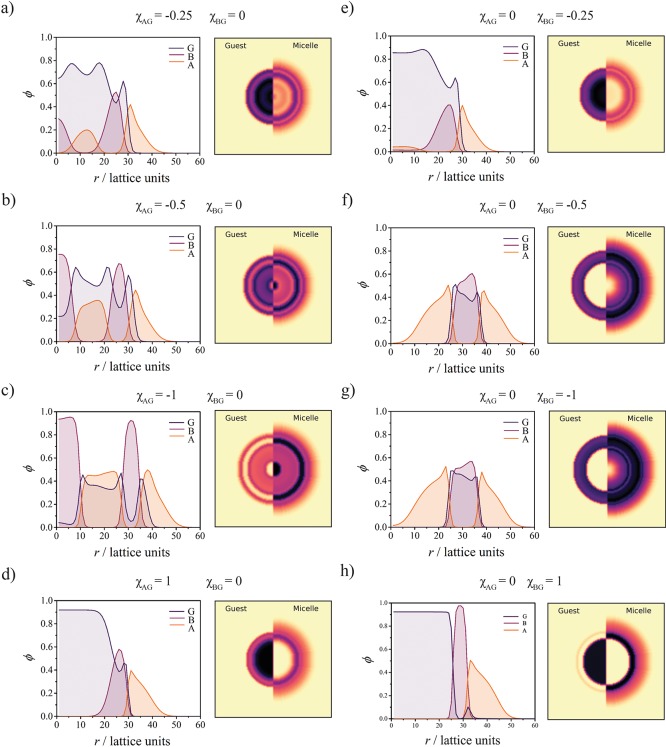
The radial concentration profiles plotted in Figure 7 for ϕG* < ϕG show that the presence of attractive interactions strongly affect the equilibrium morphology of the assemblies. Strikingly, attraction with the corona (Figure 7a–c) leads to the stabilization of multishell “onion-like” structures, where G is mostly dispersed in the A-rich shells. Medium (χGB = −0.5) and strong (χGB = −1) attraction for the core results in a stabilization of bilayer vesicular structures (Figure 7e–g) where G is mostly located into the B-rich region. This morphology is preferred as it allows maximizing the favorable contact between G and B while reducing the stretching of the B chains. In Figure 7d,h, it is shown that a repulsive interaction between G and one of the blocks results in the formation of a G-rich core inside the micelles, similarly to what was observed in the absence of specific interactions with G.
Figure 7.
Radial concentration profiles ϕ(r) and resulting two-dimensional (2D) representations showing the structures of the micelle–guest complex at ϕG* = 9.6 × 10–3 (χGS = 2) and ϕG = 2 × 10–3 for different values of the interaction parameters, indicated at the top of each profile. The 2D representation of the concentration profiles provides the volume fraction of the guest (G) molecules (left) and the volume fraction of the block copolymers. The different panels (a–h) are referred to in the main text (right).
Attraction enhances the uptake of guest molecules by the micelles, while in the presence of repulsion, even if strong (χGA, χGB = 1), solubilization is mostly controlled by lyophobic forces as in the absence of specific interactions. Here, we note that although the SF-SCF computations predict a change in the equilibrium morphology, polymer self-assembly is (usually) controlled by a combination of thermodynamic and kinetic factors.26,31,32 Consequently, the effect of solubilization on the morphology of block copolymer assemblies will be further investigated in a future study.
Active Control of the Dominating Solubilization Region
The SF-SCF computations predict that the preferred solubilization region is influenced by the solubility and concentration of the guest compound. Hence, tuning the solubility of the guest should enable control over the dominating solubilization region. To verify this, we designed an experimental system where PEO–PCL micelles are used to solubilize NR in different water–ethanol mixtures. In such mixtures, the solubility of NR (CNR*) is a function of the water–ethanol ratio, see Figure 8a and the Supporting Information for more details. NR is a solvatochromic dye, that is, its photophysical properties depend on the physical properties of the environment. Specifically, the shift in the position of the absorption maximum λmax in the visible range can be used to probe the polarity of the environment.23 To use this shift for determining the preferred solubilization region of NR, we prepared reference solutions which mimic the polarity of the core and the core–corona interface region. We used the information obtained in previous theoretical and experimental investigations26 to determine the composition of such solutions: the core-mimicking was prepared by mixing 95% of ε-caprolactone and 5% of water, whereas the interface-mimicking was composed of 50% of ε-caprolactone, 15% of PEO, and 35% of deionized water. The λmax values (λmax = 546 nm, λmaxinterface = 569 nm) obtained from the absorption spectra of NR in these solutions are depicted in Figure 8b as horizontal lines (see Figure S4 in the Supporting Information for more details).
Next, UV–vis spectra of NR have been recorded in the different water–ethanol mixtures in the absence of micelles (Figure S5 in the Supporting Information) to monitor the λmax shift as a function of the mixture composition (Figure 8b, dots). Increasing the volume fraction of water ϕW enhances the average polarity of the solvent, resulting in a red shift of the absorption maximum λmax from 576 to 635 nm (Figure 8b).
Subsequently, PEO–PCL micelles were prepared in the different mixtures in the presence of NR to study the solubilization of the dye. A fixed concentration CNR = 4 × 10–6 M was used in all experiments with NR; hence, according to our solubility measurements, the condition CNR* = CNR is achieved at ϕW = 0.72 (Figure 8b, vertical dashed line).
In Figure 8b, it is shown that the λmax value of NR is not affected by the presence of PEO–PCL micelles for ϕW = 0.5. These indicates that the dye is mostly dispersed in solution and does not accumulate inside the micelles. The λmax values follow from the UV–vis spectra of the (PEO–PCL containing) NR solutions reported in Figure S6 in the Supporting Information.
In contrast, for ϕW ≥ 0.6, a gradual blue shift of λmax from 582 to 544 nm is observed, which is opposite to the red shift observed for NR in the absence of micelles (Figure 8b). This indicates that the dye is mainly surrounded by an environment with lower polarity than the solvent; hence, it is preferentially located inside the micelles. When CNR* ≈ CNR, the value λmax ≅ λmax indicates that NR is preferentially located at the core–corona interface. When ϕW increases (hence the solubility further decreases), λmax shifts toward lower wavelengths until the reference plateau value for the core λmaxcore = 546 is reached. Hence, for CNR ≳ CNR (ϕW ≲ 0.72), interfacial adsorption dominates, whereas for CNR* ≲ CNR (ϕW ≳ 0.72), encapsulation in the core takes place, as predicted by the SF-SCF computations. We confirmed experimentally that tuning the solubility of the guest compound allows to actively control the solubilization region.
Determination of the Dominating Solubilization Region
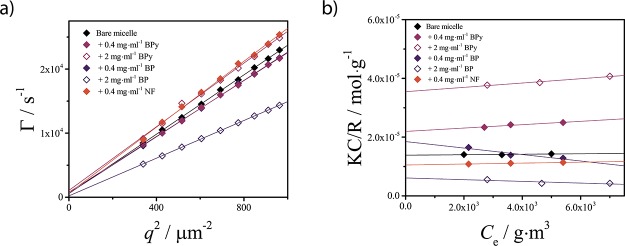
The experimental determination of the preferred solubilization region by electron microscopy or small-angle scattering methods is often not possible because of the low-contrast difference between polymeric micelles and organic guest compounds. However, the SF-SCF results presented here provide a relation between the preferred solubilization region and the hydrodynamic size RH and relative mass of the assemblies δSF-SCF. Consequently, the solubilization region should be indirectly assessable by performing simple static and DLS experiments on the micelles in the presence and absence of the guest. To verify this methodology, we investigated the self-assembly behavior of the PEO–PCL upon solubilization of three compounds, NF, BP, and BPy. It is noted that the structure of these molecules is comparable with the structure of our SF-SCF guest molecule G, see Figure S1 in the Supporting Information. Although not relevant for biomedical applications, these compounds represent an interesting model system, as their chemical structures are (qualitatively) similar to that of many small drugs and are characterized by different water solubility values: CBPy* > CBP > CNF* (see Table S1 in the Supporting Information). Dynamic and static light-scattering properties of the resulting assemblies are plotted in Figure 9. These data have been used to calculate the ratio between the average mass of the micelles M0 with solubilized material over the mass of the bare empty micelles M (see the Supporting Information). This parameter, defined as δexp = M/M0, is the experimental analogue of δSF-SCF. It is expected that if interfacial adsorption dominates, δexp < 1, whereas if encapsulation is preferred, δexp > 1.
Figure 9.
Results of the light-scattering characterizations. (a) Decay rates obtained by fitting the autocorrelation functions at different scattering angles for various samples, as a function of the squared scattering vector q2. (b) Debye plots obtained from the static light-scattering (SLS) measurements at a scattering angle θ = 90 and different sample concentrations.
The obtained values of δexp are reported in Table 1 for the different samples together with the SF-SCF theoretical predictions. The samples studied are bare micelles composed of EO45–CL14 block copolymers and micelles plus either 0.4 or 2 mg·mL–1 of guest molecules. The solubilization of the more soluble BPy results in δBPyexp < 1 values at both concentrations, which are below the BPy solubility CBPy, indicating that interfacial adsorption dominates. The solubilization of BP results in interfacial adsorption at low concentrations (δBPexp < 1), whereas at high concentrations, core encapsulation takes place, as testified by the δBP > 1 value, associated with an increase of the radius of the micelle (see Table 1).
Table 1. Summary of the Features of EO45–CL14 Micelles with and without Solubilized Guest Compounds as Predicted by SF-SCF (Denoted by the SF-SCF Superscript) and Measured Experimentally (Denoted by the exp Superscript).
| sample | a,cδSF-SCF | b,cδexp | aRHSF-SCF/nm | bRHexp/nm |
|---|---|---|---|---|
| bare micelles | 9.2 | 9 | ||
| +0.4 mg·mL–1 BPy | 0.97 | 0.61 | 9.2 | 8 |
| +2 mg·mL–1 BPy | 0.66 | 0.37 | 8.8 | 8 |
| +0.4 mg·mL–1 BP | 0.92 | 0.72 | 9.6 | 9 |
| +2 mg·mL–1 BP | 1.94 | 2.19 | 12.4 | 13 |
| +0.4 mg·mL–1 NF | 1.05 | 1.27 | 10.0 | 9 |
| +2 mg·mL–1 NF | 2.07 | NA | 12.8 | NA |
Value predicted with SF-SCF.
Value obtained from SLS (see the Supporting Information for details).
δ > 1 indicates encapsulation-dominated adsorption and δ < 1 indicates preferential interfacial adsorption.
In contrast, the radius of the micelle remains fairly constant when adsorption at the core–corona interface takes place (δBPexp < 1). These observations are consistent with a guest concentration-dependent transition between the two solubilization regimes.
In the case of NF, Ce > CNF* already at 0.4 mg·mL–1. Hence, the solubilization of NF results in a value of δNF > 1 at the lower concentration. At a high NF concentration, a turbid dispersion containing precipitate was repeatedly observed, and therefore, those sample could not be analyzed. The experimental results are in agreement with the SF-SCF predictions for the solubilization of NF, BP, and BPy into PEO–PCL micelles. A final consideration regards the change in the second virial coefficients of the micelle upon solubilization (the change in the slopes of the Debye plots upon different conditions, Figure 9b). It seems that the presence of solubilized materials affects the way micelles interact, which may be indicative for the type of interaction of the encapsulated compounds with the lyophilic blocks (PEO).
Summary and Conclusions
We have demonstrated theoretically and experimentally that the solubilization locus of the guest compounds inside the block copolymer micelles is mostly determined by the concentration and the solubility of the guest molecules. The presence of attractive interactions between guest and block copolymer molecules enhances the uptake of guests by the micelles and affects the equilibrium morphology of the assemblies. Both experiments and SF-SCF computations reveal that interfacial adsorption is preferred at guest concentrations lower than the solubility, whereas at concentrations that exceed the guest solubility, the core encapsulation dominates. The experimental studies performed with NR show that solvent mixtures can be used to tune the solubility of the guest compound, in order to actively control the solubilization region. The SCF computations predict that encapsulation resembles the formation of a nanoemulsion because a droplet enriched in guest molecules is formed at the center of the micelle core. Each of these two regimes has a characteristic signature on measurable properties of the micelles. Upon adsorption, the mass of the micelles decreases while their size remains rather constant. Upon encapsulation, the mass of the micelles increases, together with their hydrodynamic radius. Hence, the preferred solubilization region, usually difficult to assess via direct methods, can be predicted and experimentally determined by monitoring the change in size and mass of the micelles upon solubilization, for instance, via static and DLS.
Acknowledgments
A.I. thanks Dr. L. Ravotto, G. Gianluca, and the Python community for their efforts in developing free scientific resources. We thank Prof. F. A. M. Leermakers for useful discussions on the SF-SCF calculations, prof. G. de With for critically reading the manuscript, and J. Opdam for support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.9b00180.
SF-SCF computations, light-scattering measurements, and supplementary UV–vis spectra of NR solutions (PDF)
Author Contributions
⊥ A.I. and A.G.G. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Alexandridis P. Amphiphilic Copolymers and Their Applications. Curr. Opin. Colloid Interface Sci. 1996, 1, 490–501. 10.1016/s1359-0294(96)80118-x. [DOI] [Google Scholar]
- Drummond C. J.; Fong C. Surfactant Self-Assembly Objects as Novel Drug Delivery Vehicles. Curr. Opin. Colloid Interface Sci. 2000, 4, 449–456. 10.1016/s1359-0294(00)00020-0. [DOI] [Google Scholar]
- Haag R. Supramolecular Drug-Delivery Systems Based on Polymeric Core – Shell Architectures. Angew. Chem., Int. Ed. 2004, 43, 278–282. 10.1002/anie.200301694. [DOI] [PubMed] [Google Scholar]
- Kim Y.; Dalhaimer P.; Christian D. A.; Discher D. E. Polymeric Worm Micelles as Nano-Carriers for Drug Delivery. Nanotechnology 2005, 16, S484–S491. 10.1088/0957-4484/16/7/024. [DOI] [PubMed] [Google Scholar]
- Batrakova E. V.; Bronich T. K.; Vetro J. A.; Kabanov A. V.. Polymer Micelles as Drug Carriers. In Nanoparticulates as Drug Carriers; Torchilin V. P., Ed.; Imperial College Press: London, 2006; pp 57–95. [Google Scholar]
- Choucair A.; Eisenberg A. Interfacial Solubilization of Model Amphiphilic Molecules in Block Copolymer Micelles. J. Am. Chem. Soc. 2003, 125, 11993–12000. 10.1021/ja036667d. [DOI] [PubMed] [Google Scholar]
- Tang Y.; Liu S. Y.; Armes S. P.; Billingham N. C. Solubilization and Controlled Release of a Hydrophobic Drug Using Novel Micelle-Forming ABC Triblock Copolymers. Biomacromolecules 2003, 4, 1636–1645. 10.1021/bm030026t. [DOI] [PubMed] [Google Scholar]
- Parekh P.; K. Singh K.; Marangoni D. G.; Aswal V. K.; Bahadur P. Solubilization and Location of Phenol and Benzene in a Nonlinear Amphiphilic EO-PO Block Copolymer Micelles:1H NMR and SANS Studies. Colloids Surf., A 2012, 400, 1–9. 10.1016/j.colsurfa.2012.02.029. [DOI] [Google Scholar]
- Akiba I.; Terada N.; Hashida S.; Sakurai K.; Sato T.; Shiraishi K.; Yokoyama M.; Masunaga H.; Ogawa H.; Ito K.; et al. Encapsulation of a Hydrophobic Drug into a Polymer-Micelle Core Explored with Synchrotron SAXS. Langmuir 2010, 26, 7544–7551. 10.1021/la904355p. [DOI] [PubMed] [Google Scholar]
- Nagarajan R.; Chaiko M. A.; Ruckenstein E. Locus of Solubilization of Benzene in Surfactant Micelles. J. Phys. Chem. 1984, 88, 2916–2922. 10.1021/j150657a049. [DOI] [Google Scholar]
- Teng Y.; Morrison M. E.; Munk P.; Webber S. E. Release Kinetics Studies of Aromatic Molecules into Water from Block Polymer Micelles. Macromolecules 1998, 31, 3578–3587. 10.1021/ma971721u. [DOI] [Google Scholar]
- Singla P.; Chabba S.; Mahajan R. K. A systematic physicochemical investigation on solubilization and in vitro release of poorly water soluble oxcarbazepine drug in pluronic micelles. Colloids Surf., A 2016, 504, 479–488. 10.1016/j.colsurfa.2016.05.043. [DOI] [Google Scholar]
- Tian M.; Arca E.; Tuzar Z.; Webber S. E.; Munk P. Light Scattering Study of Solubilization of Organic Molecules by Block Copolymer Micelles in Aqueous Media. J. Polym. Sci., Part B: Polym. Phys. 1995, 33, 1713–1722. 10.1002/polb.1995.090331202. [DOI] [Google Scholar]
- Latere Dwan’Isa D. J.; Rouxhet L.; Préat V.; Brewster M.; Ariën A. Prediction of Drug Solubility in Amphiphilic Di- Block Copolymer Micelles: The Role of Polymer- Drug Compatibility. Pharmazie 2007, 62, 499–504. 10.1691/ph.2007.7.6273. [DOI] [PubMed] [Google Scholar]
- Wille S.; Mokrushina L.; Smirnova I.; Arlt W. Partition Coefficients of Alkyl Parabens and Ibuprofen in Micellar Systems. Chem. Eng. Technol. 2010, 33, 2095–2101. 10.1002/ceat.201000279. [DOI] [Google Scholar]
- Buggert M.; Mokrushina L.; Smirnova I.; Schomäcker R.; Arlt W. Prediction of Equilibrium Partitioning of Nonpolar Organic Solutes in Water- Surfactant Systems by UNIFAC and COSMO-RS Models. Chem. Eng. Technol. 2006, 29, 567–573. 10.1002/ceat.200600015. [DOI] [Google Scholar]
- Wille S.; Mokrushina L.; Schwarze M.; Smirnova I.; Schomäcker R.; Arlt W. Partition Coefficients for Continuous Micellar Reaction Processes. Chem. Eng. Technol. 2011, 34, 1899–1908. 10.1002/ceat.201100359. [DOI] [Google Scholar]
- Nagarajan R.; Ganesh K. Block copolymer self-assembly in selective solvents: theory of solubilization in spherical micelles. Macromolecules 1989, 22, 4312–4325. 10.1021/ma00201a029. [DOI] [Google Scholar]
- Fleer G. J.; Cohen Stuart M. A.; Scheutjens J. M. H. M.; Cosgrove T.; Vincent B.. Polymers at Interfaces; Springer Netherlands, 1993. [Google Scholar]
- Hurter P. N.; Scheutjens J. M. H. M.; Hatton T. A. Molecular modeling of micelle formation and solubilization in block copolymer micelles. 1. A self-consistent mean-field lattice theory. Macromolecules 1993, 26, 5592–5601. 10.1021/ma00073a010. [DOI] [Google Scholar]
- Lebouille J. G. J. L.; Vleugels L. F. W.; Dias A. A.; Leermakers F. A. M.; Cohen Stuart M. A.; Tuinier R. Controlled Block Copolymer Micelle Formation for Encapsulation of Hydrophobic Ingredients. Eur. Phys. J. E 2013, 36, 107. 10.1140/epje/i2013-13107-y. [DOI] [PubMed] [Google Scholar]
- Lebouille J. G. J. L.; Tuinier R.; Vleugels L. F. W.; Cohen Stuart M. A.; Leermakers F. A. M. Self-Consistent Field Predictions for Quenched Spherical Biocompatible Triblock Copolymer Micelles. Soft Matter 2013, 9, 7515–7525. 10.1039/c3sm27829h. [DOI] [Google Scholar]
- Jose J.; Burgess K. Benzophenoxazine-Based Fluorescent Dyes for Labeling Biomolecules. Tetrahedron 2006, 62, 11021–11037. 10.1016/j.tet.2006.08.056. [DOI] [Google Scholar]
- Ianiro A.; Jiménez-Pardo I.; Esteves A. C. C.; Tuinier R. One-Pot, Solvent-Free, Metal-Free Synthesis and UCST-Based Purification of Poly(Ethylene Oxide)/Poly-ε-Caprolactone Block Copolymers. J. Polym. Sci., Part A: Polym. Chem. 2016, 54, 2992–2999. 10.1002/pola.28185. [DOI] [Google Scholar]
- Davis M. M.; Helzer H. B. Titrimetric and Equilibrium Studies Using Indicators Related to Nile Blue A. Anal. Chem. 1966, 38, 451–461. 10.1021/ac60235a020. [DOI] [Google Scholar]
- Ianiro A.; Patterson J.; González García Á.; van Rijt M. M. J.; Hendrix M. M. R. M.; Sommerdijk N. A. J. M.; Voets I. K.; Esteves A. C. C.; Tuinier R. A Roadmap for Poly(Ethylene Oxide)-Block-Poly-ε-Caprolactone Self-Assembly in Water: Prediction, Synthesis, and Characterization. J. Polym. Sci., Part B: Polym. Phys. 2018, 56, 330–339. 10.1002/polb.24545. [DOI] [Google Scholar]
- Linegar K. L.; Adeniran A. E.; Kostko A. F.; Anisimov M. A. Hydrodynamic Radius of Polyethylene Glycol in Solution Obtained by Dynamic Light Scattering. Colloid J. 2010, 72, 279–281. 10.1134/s1061933x10020195. [DOI] [Google Scholar]
- Flory P. J.Principles of Polymer Chemistry; Cornell University Press: Ithaca, United States, 1953. [Google Scholar]
- Nagarajan R.; Ruckenstein E. Theory of surfactant self-assembly: a predictive molecular thermodynamic approach. Langmuir 1991, 7, 2934–2969. 10.1021/la00060a012. [DOI] [Google Scholar]
- Chausson M.; Fluchère A.-S.; Landreau E.; Aguni Y.; Chevalier Y.; Hamaide T.; Abdul-Malak N.; Bonnet I. Block Copolymers of the Type Poly(Caprolactone)-b-Poly(Ethylene Oxide) for the Preparation and Stabilization of Nanoemulsions. Int. J. Pharm. 2008, 362, 153–162. 10.1016/j.ijpharm.2008.06.007. [DOI] [PubMed] [Google Scholar]
- Cui H.; Chen Z.; Zhong S.; Wooley K. L.; Pochan D. J. Block Copolymer Assembly via Kinetic Control. Science 2007, 317, 647–650. 10.1126/science.1141768. [DOI] [PubMed] [Google Scholar]
- Mai Y.; Eisenberg A. Self-Assembly of Block Copolymers. Chem. Soc. Rev. 2012, 41, 5969–5985. 10.1039/c2cs35115c. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.