Solvation Free Energy Calculations with Quantum Mechanics / Molecular Mechanics and Machine Learning Models

Abstract

For exploration of chemical and biological systems, the combined quantum mechanics and molecular mechanics (QM/MM) and machine learning (ML) models have been developed recently to achieve high accuracy and efficiency for molecular dynamics (MD) simulations. Despite its success on reaction free energy calculations, how to identify new configurations on insufficiently sampled regions during MD and how to update the current ML models with the growing database on-the-fly are both very important but still challenging. In this letter, we apply the QM/MM ML method to solvation free energy calculations and address these two challenges. We employ three approaches to detect new data points and introduce the gradient boosting algorithm to reoptimize efficiently the ML model during ML-based MD sampling. The solvation free energy calculations on several typical organic molecules demonstrate that our developed method provides a systematic, robust and efficient way to explore new chemistry using ML-based QM/MM MD simulations.

Graphical Abstract

Introduction

The solvation free energy (SFE) is vital for studying chemical and biological reactions as well as designing drugs.^1–4 Many methods of free energy calculations, such as free energy perturbation,⁵ thermodynamic integration (TI),⁶ umbrella sampling⁷ and λ-dynamics,⁸ have been widely used to calculate SFE from molecular dynamics (MD) simulations.⁹ On one hand, sufficient MD samplings for free energy calculations require an efficient method to calculate the potential energies of the whole system for at least thousands of configurations. On the other hand, an important ingredient to accurately estimate SFE is the appropriate description of potential energy surface (PES). Although empirical models such as molecular mechanical (MM) force fields can predict the SFE of various small organic molecules successfully,^10–14 quantum mechanical (QM) models at the ab initio level are considered to be more general and rigorous. Treating both the solute and solvent molecules using QM method is extremely time-consuming if not impossible. The combined quantum mechanical and molecular mechanical (QM/MM) method, first proposed by Warshel, Karplus and Levitt, considers a tradeoff between accuracy and efficiency for large systems.^15,16 In the framework of QM/MM model, the whole system is divided into a small active site (e.g., the solute) treated at the QM level and a relatively large surrounding part (e.g., the solvents) treated at the MM level. Even though the ab initio QM/MM can achieve high accuracy for PES, it is still computationally demanding in long-time MD simulations.^17–26 Alternatively, the semiempirical QM/MM (SQM/MM) significantly speeds up electronic structure calculations but sometimes sacrifices the accuracy.^27–29

Recently, many kinds of machine learning (ML) techniques such as neural network (NN) representation,^30–32 kernel-based Gaussian approximation potential^33,34 and support vectormachine³⁵ are being increasingly used for accurate interpolation/prediction of PES.^36–39 Inspired by the high-dimensional NN scheme to represent the total potential energy as a sum of atomic energies³² and the Δ-machine learning method to predict the difference between the calculations at two levels,⁴⁰ Shen and Yang developed a novel method to introduce the machine learning methods to QM/MM models, denoted as QM/MM-NN, to achieve the accuracy of high-level ab initio QM/MM with only the computational cost of low-level SQM/MM.^41,42 The highly accurate free energy profiles on aqueous chemical processes such as S_N2 and proton transfer reactions can be obtained from direct QM/MM MD simulations combined with QM/MM-NN.

Although there is a growing trend in molecular simulations based on the ML-predicted PES, how to detect new configurations outside of the domain of training data remains challenging. One choice is based on the boundary of input variables of the current ML model, which may miss many new data points encountered during MD.⁴³ Another way is based on the uncertainty analysis on a machine learning ensemble,^44,45 which may also lead to failure on MD simulations, according to the results of our SFE calculation. Furthermore, in order to explore new regions of the PES, a robust and efficient method to update the current ML model during MD simulations is also an urgent issue. Several adaptive methods have been reported and can be further classified as “microiteration” and “macroiteration” procedures. In the microiteration approach, the ML model was adjusted immediately to mimic the reference when a new conformation was sampled. Despite the success of the related works such as the adaptive ML framework^44,46 and “learn-on-the-fly” technique,^47,48 there are still some challenges that should be addressed. Specially, the reconstruction of ML models is usually frequent and expensive, which hampers the efficiency of ML for exploring diverse configurations. In the macroiteration approach, for example, the adaptive QM/MM-NN proposed by Shen and Yang recently,⁴² the NN construction and MD simulation were performed iteratively. The ML model was unchanged during MD samplings at each iteration cycle and reconstructed using both existing and additional configurations after MD. This approach requires a large number of MD sampling steps before obtaining the final ML model. It may be unavailable for larger systems on which the SQM/MM computational cost becomes considerable. How to explore something new for large systems using ML models, even in the configurational space, is still an open problem without satisfactory solutions.

In this paper, we will address the two aforementioned challenges on the ML-based QM/MM MD for free energy calculations. First, we explore a systematic way for the identification of insufficiently sampled regions during ML-driven MD in order to overcome the limitations on the existing methods based on the boundary of input variables or the uncertainty of machine learning ensembles. Second, we employ the gradient boosting algorithm, which was first reported by Friedman⁴⁹ and followed by classification and regression applications⁵⁰ such as the predictions on elimination half-lives⁵¹ and RNA-protein interactions,⁵² to update the QM/MM ML model effectively when a new configuration is detected. We finally perform SFE calculations on several typical organic molecules to validate our new QM/MM ML approaches.

Methods

For the SFE calculations with QM/MM MD,^53–56 the total potential energy of the system with QM/MM model we use is⁵⁷

$$E_{\text{tot}}=\langle \mathrm{\Psi }|{\widehat{H}}_0+{\lambda }_{\text{ele}}\sum _{i\in \text{MM}}{q}_i{V}_{\text{MM}}({\mathbf{r}}_i)|\mathrm{\Psi }\rangle +E_{\text{QM}/\text{MM}}^{\text{vdw}}({\lambda }_{\text{vdw}})+E_{\text{MM}},$$ (1)

where λ_ele and λ_vdw are two switching parameters varying from 0 to 1 for TI, ${\widehat{H}}_0$ is the Hamiltonian of the QM subsystem, q_i is the point charge of MM atom i, V_MM(r_i) is the electrostatic potential on MM atom i exerted by the QM subsystem, r_i is the position of atom i, and $E_{\text{QM}/\text{MM}}^{\text{vdw}}$ is the soft-core potential that can avoid numerical instability problem in MD simulation when λ_vdw is close to zero (see Simulation Details in SI).⁵⁸ Applying the same MM force field at two levels, the energy difference ΔE between high-level ab initio QM/MM (labeled as H) and low-level SQM/MM (labeled as L) is represented as⁴¹

$$\mathrm{\Delta }E=\langle {\mathrm{\Psi }}^{\text{H}}|{\widehat{H}}_0^{\text{H}}+{\lambda }_{\text{ele}}\sum _{i\in \text{MM}}{q}_i{V}_{\text{MM}}\left({\mathbf{r}}_i\right)|{\mathrm{\Psi }}^{\text{H}}\rangle -\langle {\mathrm{\Psi }}^{\text{L}}|{\widehat{H}}_0^{\text{L}}+{\lambda }_{\text{ele}}\sum _{i\in \text{MM}}{q}_i{V}_{\text{MM}}\left({\mathbf{r}}_i\right)|{\mathrm{\Psi }}^{\text{L}}\rangle .$$ (2)

To properly represent the atomistic environment, two types of descriptors, modified symmetry functions³² and power spectrum,⁵⁹ were employed as the input variables in this work. The same cutoff function⁶⁰ is involved in both input variables as

$$f_{\text{c}}\left(R_{ij}\right)=\{\begin{array}{ll}{\tanh }^3(1-\frac{R_{ij}}{R_{\text{c}}}),\hfill & R_{ij}\le R_{\text{c}}\hfill \\ 0,\hfill & R_{ij}>R_{\text{c}}\hfill \end{array},$$ (3)

where R_ij is the distance between atom i and j, and R_c is the cutoff radius. The interaction is neglected if the distance between two atoms is larger than R_c. Symmetry functions consist of a radial function

$$G_i^{\text{rad}}=\sum _{j\ne i}^N{e}^{-\eta {\left(R_{ij}-R_{\text{s}}\right)}^2}{f}_{\text{c}}\left(R_{ij}\right),$$ (4)

where η and R_s are pre-determined hyperparameters, and an angular function

$$G_i^{\text{ang}}=2^{1-\zeta }\sum _{j,k\ne i}^N{\left(1+\lambda \cos {\theta }_{ijk}\right)}^{\zeta }{e}^{-\eta \left(R_{ij}^2+R_{ik}^2+R_{jk}^2\right)}{f}_{\text{c}}\left(R_{ij}\right)f_{\text{c}}\left(R_{ik}\right)f_{\text{c}}\left(R_{jk}\right),$$ (5)

where ζ and λ are hyperparameters, and θ_ijk is the angle centered at atom i. Since the radial and angular symmetry functions are only dependent on QM geometry, the external electrostatic potential generated by surrounding charges is employed as another input feature to describe the influence of MM subsystem, which is written as⁴²

$$V_i=\sum _{j\in \text{MM}}\frac{{\lambda }_{\text{ele}}{q}_j}{R_{ij}},$$ (6)

where q_j is the point charge on MM atom j. Different from symmetry functions, the input variables of power spectrum are defined as

$$p_{nl}^i=\sum _{m=-l}^l{c}_{nlm}^i*c_{nlm}^i,$$ (7)

where n and l are pre-determined integers, m is an integer varying from −l to l, and $c_{nlm}^i$ is constructed as

$$c_{nlm}^i=\sum _j{e}^{-\alpha {\left(R_{ij}-R_n\right)}^2}{Y}_{lm}\left({\theta }_{ij},{\phi }_{ij}\right){\omega }_j{f}_{\text{c}}\left(R_{ij}\right),$$ (8)

where α and R_n are hyperparameters, Y_lm is the spherical harmonic function to describe the relative positions of i and j using spherical coordinates θ and φ centered at atom i, and ω_j is defined as the nuclear charge Z_j if atom j belongs to the QM subsystem or defined as λ_eleq_j if atom j belongs to the MM subsystem.⁶¹ The original power spectrum⁵⁹ applied orthonormalized high-order polynomials as radial basis functions, but here we change them to equidistant Gaussian functions together with cutoff functions because they are sensitive and cover wide range of distances, which satisfies the requirements mentioned in the original paper.⁵⁹ Note that in the framework of modified symmetry functions, two functions, symmetry functions in Eqs 4 and 5 and external electrostatic potentials in Eq 6, are employed to describe the QM and MM subsystem, respectively; while in the framework of power spectrum, QM and MM subsystems are described with the same function as in Eq 7 with different hyperparameters.

Using modified symmetry functions or power spectrum as input variables, the energy difference ΔE in Eq 2 can be predicted with any ML method such as neural network or Gaussian kernel. Here we use the linear regression model, which has successfully described the energy landscape of metal systems with symmetry functions,^62,63 as

$$\mathrm{\Delta }E=\sum _{j=1}^p{a}_j{x}_j+a_0,$$ (9)

where x_j is the input variables with the total number of p, and a_j is the ML parameters that can be obtained using the component-wise gradient boosting algorithm⁶⁴ combined with the early stopping technique^65,66 (see below for more details). Actually, the initial QM/MM ML model can be constructed with any other training method, not restricted to gradient boosting. The forces acting on atom i can be calculated as

$${\mathbf{F}}_i^{\text{H}}={\mathbf{F}}_i^{\text{L}}-\frac{\partial \mathrm{\Delta }E}{\partial {\mathbf{r}}_i}={\mathbf{F}}_i^{\text{L}}-\sum _{j=1}^p{a}_j\frac{\partial x_j}{\partial {\mathbf{r}}_i},$$ (10)

where atom i belongs to either QM or MM subsystem, and ${\mathbf{F}}_i^{\text{L}}$ is the low-level force calculated with SQM/MM. Using Eq 10, MD evolution can be implemented on the ML-predicted PES. The final SFE through TI is calculated as

$$\mathrm{\Delta }A={\int }_0^1{\langle \frac{\partial E^{\text{H}}}{\partial {\lambda }_{\text{ele}}}\rangle }_{{\lambda }_{\text{ele}}}\text{d}{\lambda }_{\text{ele}}+{\int }_0^1{\langle \frac{\partial E^{\text{H}}}{\partial {\lambda }_{\text{vdw}}}\rangle }_{{\lambda }_{\text{vdw}}}\text{d}{\lambda }_{\text{vdw}},$$ (11)

where the angular bracket denotes an average over the samplings with a fixed λ.

Although many ML predictions are capable of reaching beyond the chemical accuracy,^39,46,67,68 both the energy and forces of some configurations in new regions on PES, where the samples in the existing database are insufficient, are unreliable using the current ML model. A systematic and effective approach to detect such new configurations is necessary. Here we applied three different methods based on the boundary of reference energy, the clustering of data points⁶⁹ and the Gaussian distribution on the density of data space,⁷⁰ respectively. The first method is new to our best knowledge. The second and third are popular clustering algorithms that have been successfully used to solve classification and regression problems.^71–76 For examples, the k-means clustering and Gaussian mixture model have been widely used in molecular simulations, such as enhanced sampling, identifying states, and free energy calculations.^77–82 Here we introduce them to the field of ML-driven MD simulations for real-time detection of new configurations, that is, learn-on-the-fly, because of the insufficiency of the database. The additional computational cost on all methods is small.

The first is denoted as the output-check model (Model 1), which corresponds to the boundary of reference energy. This model is based on the minimum and maximum values of the reference energy in the database. If the predicted value for a configuration is smaller than the minimum or larger than the maximum, the configuration will be identified as a new point and added into the database.

The second is denoted as the k-means clustering model (Model 2), in which the kmeans clustering algorithm is employed to classify the existing data points into k numbers of clusters. The initial centroids are selected by the k-means++,⁸³ and then an iterative procedure is performed to determine optimal clusters.⁶⁹ The database will be extended if the configuration encountered during MD does not belong to any cluster.

The third is denoted as the Gaussian model (Model 3) in which the density of data space is described with multiple Gaussian distributions.⁷⁰ This model is constructed as follows and more details are illustrated in SI. First, the k-th Gaussian distribution is represented with the mean vector μ_k and covariance matrix Σ_k, and the percentage of the k-th Gaussian distribution (denoted as P_k) are initialized using the k-means clustering based on the existing data points. Second, the probability of a configuration x_i in the k-th Gaussian distribution, denoted as P(x_i ∈ k), is expressed as

$$P\left({\mathbf{x}}_i\in k\right)=\frac{P_k\mathrm{Norm}\left({\mathbf{x}}_i|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k\right)}{{\sum }_k{P}_k\mathrm{Norm}\left({\mathbf{x}}_i|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k\right)},$$ (12)

where Norm(x_i|μ_k, σ_k) denotes the k-th Gaussian distribution. The P_k, μ_k and Σ_k are then recalculated based on P(x_i ∈ k) for all existing configurations in the current database, leading to the updated values of P(x_i ∈ k). The iterative procedure is repeated until P_k is unchanged for all Gaussian distributions or the maximum step is reached. Finally, a new configuration x encountered during MD is checked using

$$P(\mathbf{x})=\sum _k{P}_k\mathrm{Norm}\left(\mathbf{x}|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k\right),$$ (13)

and added to the database if P (x) is smaller than the pre-determined threshold.

Once the database is extended during MD simulations on the ML-predicted PES, the ab initio QM/MM potential energy of the additional configuration should be calculated as the reference value, and the current QM/MM ML model should be updated to explore broader regions on PES. Here we applied the component-wise gradient boosting algorithm⁶⁴ for reoptimization. The feature of gradient boosting is to add some weak models (called as the base learner) to the existing ML model to build a stronger model. No matter how complicated the initial ML model is, only the base learner is necessary to be optimized to correct the errors of the existing model. In other words, the choice on base learner for reoptimization is independent of the previous construction, indicating the high efficiency of reoptimization regardless of the complexity of the initial ML model. Generally, the base learner is very simple, e.g., the linear functions in this work, so the computational cost of on-the-fly reconstructions on ML model during ML-driven MD is low. In contrast, frequent reoptimizations on a complicated ML model with either microiteration^44,46–48 or macroiteration⁴² procedure are usually time-consuming. The detailed procedure of the component-wise gradient boosting algorithm used in this work are illustrated in SI.

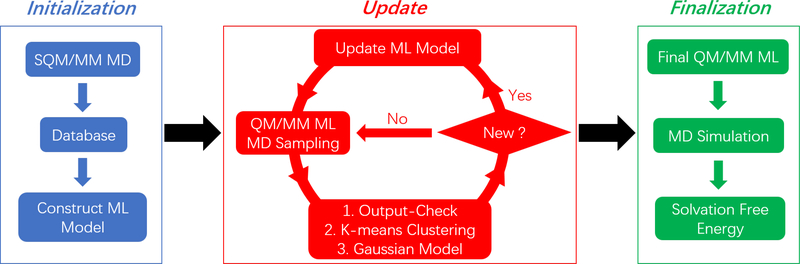
The whole procedure of our method is demonstrated in Figure 1. At the initialization stage, MD simulations with different values of λ_vdw and λ_ele were performed at the SQM/MM level to construct the initial database. The initial models, including the QM/MM ML model, the output-check model, the k-means clustering model and the Gaussian model, were optimized based on the database. In the update stage, the direct QM/MM MD combined with our ML model was implemented. One of the three approaches, that is, the outputcheck model, the k-means clustering model and the Gaussian model, was employed to check the validity of the predictions. If the configuration was identified as a new data point, the potential energy and forces at this step would be calculated using the low-level SQM/MM model. This data point would be added to the ML database unless another configuration within the previous 100 MD steps had been selected. Then the QM/MM ML model would be updated with the gradient boosting technique. At the final stage, MD simulations were performed with the updated QM/MM ML model, and the final properties of interest such as SFE at the approximate ab initio QM/MM level were calculated using Eq 11.

Figure 1.

The flowchart of solvation free energy calculation with ML-based QM/MM MD simulations. The initialization stage contains SQM/MM MD simulation, construction of initial database, and establishment of initial QM/MM ML models. The update stage contains direct QM/MM MD simulations combined with the ML predictions, determination of new configurations encountered during MD, and reconstruction of ML models. The finalization stage contains MD simulation with the final QM/MM ML model and the solvation free energy calculation.

Results and Discussion

Six small organic molecules, acetic acid, acetamide, acetone, benzene, ethanol and methylamine, were investigated to demonstrate our new approach. The self-consistent charge density functional tight binding with second-order formulation and MIO basis (DFTB2/MIO)^84,85 was employed as the low-level SQM model, and the DFT method with the B3LYP hybrid functional^86,87 and the 6–31G(d) basis set was employed as the high-level ab initio QM model. First, we randomly selected about one thousand configurations from low-level QM/MM MD trajectories and assigned them as the training and testing sets to construct the initial QM/MM ML model. Second, we screened the optimal hyperparameters for symmetry functions and power spectrum. For symmetry functions, the R_c, R_s and λ were set as 6 Å, 0 Å and 1.0, respectively. The η and ζ are dependent on elements, which are shown in Table S1. For power spectrum, the R_c is 9 Å, and the n_max, l_max, R_n and α are displayed in Table S2. Note that different n ∈ [1,n_max] and l ∈ [0,l_max] can be chosen for QM and MM subsystems. Finally, the linear regression model was optimized using the component-wise gradient boosting algorithm⁶⁴ combined with the early stopping techniques.^65,66 The reliability of the QM/MM ML model is shown in Table 1. The root mean squared errors (RMSEs) for high-level QM/MM potential energies in all cases are lower than 0.7 kcal/mol. The corresponding Q² values vary from 0.56 to 0.91, most of which are larger than 0.7.

Table 1.

Root Mean Squared Errors (kcal/mol) of Training Set and Testing Set of Symmetry Functions and Power Spectrum with Q² Values (in Parentheses) for Six Molecules.

Molecules	Symmetry Functions		Power Spectrum
	training	testing	training	testing
Acetic acid	0.60	0.57 (0.81)	0.31	0.42 (0.90)
Acetamide	0.57	0.54 (0.66)	0.37	0.49 (0.72)
Acetone	0.44	0.46 (0.56)	0.28	0.34 (0.75)
Benzene	0.32	0.35 (0.82)	0.20	0.26 (0.91)
Ethanol	0.65	0.66 (0.70)	0.36	0.53 (0.80)
Methylamine	0.52	0.51 (0.83)	0.55	0.68 (0.70)

The values of solvation free energies were calculated based on MD samplings using three QM/MM models as DFTB2/MIO/MM, B3LYP/6–31G(d)/MM and the initial QM/MM ML model, that is, the DFTB2/MIO/MM model with ML corrections on the basis of the initial training data. All MD samplings using DFTB2/MIO/MM and B3LYP/6–31G(d)/MM models were repeated by 11 times, respectively, to obtain the values of SFEs with standard deviations (see Table S3). More simulation details can be found in SI. As shown in Table 2, the differences of results between DFTB2/MIO/MM and B3LYP/6–31G(d)/MM are significant, varying from 1.6 to 6.1 kcal/mol. The results with QM/MM ML are very close to the reference in the major part of all testing examples, except the simulations on acetamide, acetone and ethanol with symmetry functions and methylamine with power spectrum. Specially, we terminate MD trajectories for acetamide, acetone and ethanol using symmetry functions once a convergence problem on electronic structure calculations takes place, which indicates that some unphysical configurations are encountered because of the insufficient samples on the present ML database.⁴²

Table 2.

Solvation Free Energies (kcal/mol) from MD Simulations with DFTB2/MIO/MM, B3LYP/6–31G(d)/MM and Initial QM/MM ML Models Using Symmetry Functions and Power Spectrum.

Molecules	DFTB/MM	B3LYP/MM	Initial QM/MM ML
			Symmetry Functions	Power Spectrum
Acetic acid	−5.0	−7.5	−7.0	−7.8
Acetamide	−9.0	−12.1	—a	−11.4
Acetone	−2.3	−4.3	—a	−4.3
Benzene	1.0	−0.6	−1.0	−1.1
Ethanol	−1.0	−4.8	—a	−5.0
Methylamine	0.9	−5.2	−5.3	−43.2

^aMD trajectories are terminated.

To address this issue, we first tried two existing detecting methods, boundary of input variables and uncertainty analysis on a ML ensemble. These methods were first applied to the three cases whose MD trajectories are terminated without updating QM/MM ML models, to validate whether the detecting methods are eligible to select new configurations. With boundary of input variables, MD trajectories of those three cases become normal. However, with uncertainty analysis on a ML ensemble, even though MD trajectories of acetamide and acetone become also normal, the MD trajectory of ethanol is still terminated, since we could find that two ML models have similarly poor predictions on some configurations. Hence, uncertainty analysis on a ML ensemble is not appropriate in this work. Next, the boundary of input variables was applied to all cases and QM/MM ML models were updated on the fly, whose results are displayed in Table S4. All calculated solvation free energies are within the chemical accuracy to the high-level results, except methylamine with power spectrum, which will be explained later. However, even though the percentages of new configurations for symmetry functions are low, the percentages for power spectrum are too high (around 60%), which is unacceptable because such frequent updates, even with gradient boosting, are computationally expensive. Therefore, more effective detecting methods are desirable.

To solve this problem, the QM/MM ML model is updated based on three models, that is, the output-check model, the k-means clustering model and the Gaussian model, respectively. These models for detecting new configurations were also updated every 1, 30 and 50 new data points encountered for output-check, k-means clustering and Gaussian model, respectively. 10 clusters and 10 Gaussian distributions were applied for k-means clustering and Gaussian model, respectively. All MD samplings using QM/MM ML models were repeated by 5 times to obtain average values and standard deviations of SFEs. The results from the updated QM/MM ML models are displayed in Table 3 and Table S3. First, the aforementioned terminated MD trajectories can all be continued using the updated QM/MM ML models. Second, the SFEs calculated with all models are close to the reference values. One exception is the simulations on methylamine with power spectrum. Compared with the results at the ab initio QM/MM level as -5.2 kcal/mol, the final SFE predicted with our updated QM/MM ML models is about -2.5 kcal/mol. However, it is much better than the results of -43.2 kcal/mol using the initial ML database as shown in Table 2. On the other hand, the simulations on methylamine with modified symmetry functions lead to more accurate results, indicating that the errors of power spectrum may result from the higher dimensionality of input variables, which may be more sensitive to small configurational changes and inconsistent with the simple linear regression model. Therefore, for the simplicity ML model, the symmetry functions could be the more appropriate choice as input variables. Finally, in the update stage only the few new configurations are selected by both output-check (≤ 0.4%) and k-means clustering (≤ 2.0%) methods, while the Gaussian model can extract much more new configurations up to 40%. However, only a few cases of the Gaussian model have large percentages and they are much less than those from boundary of input variables. The three models lead to more efficient update, since the number of updating times is the most expensive part for on-the-fly calculations. The accuracy of SFEs using the above three models is similar, so the model extracting lowest percentages of new configurations, that is, output-check model, is suggested among the three models. Since 50 ps of MD simulations are enough in the update stage and the percentages of new configurations are less than 2% for Model 1 and 2 and usually less than 10% for Model 3, the present method appears to be more efficient than the adaptive QM/MM-NN reported by our group recently,⁴² in which 30–50% configurations were observed as new data points using the initial ML model and 150–250 ps of MD samplings were required for reconstructing the NN model. In addition, the update scheme in this work is more efficient than on-the-fly retraining because of the characteristic of gradient boosting.

Table 3.

Solvation Free Energies (kcal/mol) and Percentages of New Configurations Sampled during MD Simulations (in Parentheses) with QM/MM ML Models (Symmetry Functions and Power Spectrum) Updated Using Output-Check (Model 1), k-Means Clustering (Model 2) or Gaussian Model (Model 3) to Detect New Configurations.

Molecules	Symmetry Functions			Power Spectrum
	Model 1	Model 2	Model 3	Model 1	Model 2	Model 3
Acetic acid	−6.8 (0.3%)	−6.7 (1.1%)	−7.0 (20.3%)	−6.9 (0.4%)	−6.8 (1.0%)	−7.3 (6.2%)
Acetamide	−11.4 (0.1%)	−11.3 (1.2%)	−11.6 (16.0%)	−10.9 (0.2%)	−10.9 (0.9%)	−11.7 (3.8%)
Acetone	−3.6 (0.1%)	−3.9 (1.1%)	−3.8 (5.0%)	−3.9 (0.2%)	−3.8 (1.0%)	−3.9 (5.7%)
Benzene	−0.3 (0.2%)	−0.2 (2.0%)	−0.3 (1.8%)	−0.2 (0.3%)	−0.5 (1.6%)	−0.6 (4.4%)
Ethanol	−4.6 (0.1%)	−4.6 (1.3%)	−4.3 (40.0%)	−4.0 (0.4%)	−4.0 (1.0%)	−4.6 (9.8%)
Methylamine	−3.8 (0.4%)	−4.0 (1.7%)	−4.5 (7.2%)	−2.4 (0.4%)	−2.2 (1.3%)	−2.5 (10.2%)

Conclusions

In summary, we developed a novel machine learning method combining with additional models to identify new configurations encountered during MD and the gradient boosting algorithm to update the ML models with an increasing database. The solvation free energies were calculated based on the direct QM/MM MD simulations on the ML-predicted PES. Two types of input features, namely, modified symmetry functions and power spectrum, and three approaches to identify new data points, namely, the output-check model, the k-means clustering model and the Gaussian model, were all implemented and employed. We concluded that the ML methods using linear regression and modified symmetry functions should be updated during MD simulations to achieve robust and accurate results. All three approaches to detect new configurations are reliable, and the output-check model is recommended based on efficiency. The ML models with linear regression fitting and power spectrum meet more challenges, so we suggest modified symmetry functions for the simple ML model. However, power spectrum could be employed for more complex ML model such as neural network and it is more systematically generated. The gradient boosting algorithm makes the procedure to update the QM/MM ML models much more efficient. The present machine learning method for direct QM/MM MD simulations not only achieves the high-level ab initio QM/MM accuracy and low-level SQM/MM efficiency simultaneously, but also provides a systematic, robust and effective way to update ML models on-the-fly. Applying this procedure to various complex ML models such as the high-dimensional neural network and Gaussian kernel should be promising for exploring new chemistry using ML-based simulations.