Abstract
The use of pesticides in agriculture is known to have environmental impacts, namely it leads to underground and spring water contamination. Thus, it turns out that nowadays general‐endeavor towards the sustainability of farmer production requires novel strategies to capture pesticides from water and soils. We propose a methodology based on molecular dynamics simulations to identify polymers that are potentially featured to be applied for pesticide remediation in water and soils. We have employed cymoxanil (CYM), glufosinate ammonium (GLF), imidacloprid (IMI) and mancozeb (MAN) as pesticides, and have tested polymers with different characteristics as removing agents. Specifically, we have investigated oligomers of polypropylene (PP), poly(acrylic acid) protonated (PAAH) and deprotonated (PAA), and chitosan protonated (CTH) and deprotonated (CT). It has been found that all oligomers show a certain degree of selectivity concerning the interaction with the tested pesticides.
Keywords: computational chemistry, molecular dynamics, environmental chemistry, water chemistry, polymers
1. Introduction
The extensive use of pesticides in recent decades, as a result of the need to increase food production, has caused severe damage to soil and water as a consequence of their persistence, bioaccumulation and associated toxicological effects on the environment and human health.1, 2, 3, 4 Thus, the remediation is probably one of the major challenges faced by researchers due to the dynamics between pollutants and medium as well as because some pesticides are persistent pollutants.5 The removal of pesticides from media has been attempted by using different techniques including advanced oxidative processes (AOPs),6, 7, 8, 9, 10 membranes technology,11 soil washing12,13 and the use of adsorbents, such as activated carbon14 or biochar.15 All these techniques have some drawbacks that are essentially related to the high energy cost, the formation of by‐products (as it happens in, e. g., AOPs) and membrane fouling; in turn, activated carbon is cheap and highly efficient as adsorbent for pollutant removal, but its reuse is difficult and expensive. For that reason, in the last years the application of hydrogels as materials for removal pesticides has raised as an alternative to other techniques. Hydrogels can be described as 3D hydrophilic polymers that are able to sorbe significant amounts of water, without dissolving in this solvent. The swelling mechanism of hydrogels,16 dependent on the surrounding media, will allow the removal of pesticides from soils and water by chemical or physical sorption, as well as by trapping the pesticides into the gel matrix. Besides, by employing hydrogels the sorption‐desorption cycles will provide a useful tool to return the pesticides to the soil (by, e. g., diffusion), thus avoiding an excessive application of such pollutants.
In this work, we have studied three different polymers. Two of them are able to form hydrogels either by chemical or physical (e. g., by coacervation17) crosslinking: the chitosan and the poly(acrylic acid) in both neutral and ionic form. These polymers have been chosen because they have shown good performance on the removal of pesticides18, 19, 20 and, in addition, they are cheap and commercially available. The third polymer studied, i. e., the polypropylene, has much better barrier and mechanical properties than the other mentioned polymers, being used alone (e. g., as geomembrane) or forming blends with chitosan and poly(acrylic acid).21, 22, 23
Molecular dynamics (MD) simulations is a powerful tool to investigate a great diversity of phenomena in solution. For instance, we have employed MD simulations to study two enantiomers of ephedrine hydrocloride in solution at different temperatures.24 In turn, Geitner et al.25 have examined nanoparticle‐pesticide adsorptive interactions by using a simplified sub‐class of the MD approach,26 where the potential functions are discretized and the solvent is not explicitly included in the calculation. To achieve significant results, MD calculations require a correct description of the interactions arising among the species inside the simulation box, which has led to the development of force fields that are adequate for the study of an increasing number of chemical systems. Perhaps the most applied force fields are MM3 for organic compounds,27, 28, 29 OPLS‐AA for liquids30,31 (including TIP3P or TIP4P for water32,33), AMBER34 and CHARMM35,36 for biomolecules. In turn, there are several MD packages available in literature, namely, GROMACS,37 LAMMPS,38 AMBER,39,40 CHARMM41,42 and DL_POLY.43 In particular, the open‐source GROMACS code is one of the most employed for MD simulations since it comprises a great variety of tools for the trajectory analysis and it has been designed to have a high CPU and, mainly, GPU computational performance.
We aim with this work to screen the most promising polymers for being employed as materials to remove pesticides from water. We have employed small oligomers of polypropylene, poly(acrylic acid) and chitosan as models for the corresponding polymers. As for the pesticides, we have studied four different species (cf. Figure 1): ammonium glufosinate (GLF), cymoxanil (CYM), imidacloprid (IMI) and mancozeb (MAN). These pesticides are widely used for different crops, as the tomato one, which is quite common in Mediterranean countries. Despite the relevance of these pesticides for the economy, their impact on the biotic cannot be neglected.3,44, 45, 46, 47 The screening strategy proposed in the present study resorts to MD simulations, which allows for a detailed investigation about the main interactions that promote the formation of the oligomer‐pesticide complex. By this methodology we are also able to characterize, when stable, the structure of such complex. In order to discuss the achievements of the work, we organize the paper according to the following plan. In Section 2, we describe the computational methodology employed in the work, including the details concerning the molecular dynamics simulation and the corresponding trajectory analysis. The results are presented and discussed in Section 3 and the main conclusions are gathered in Section 4.
Figure 1.
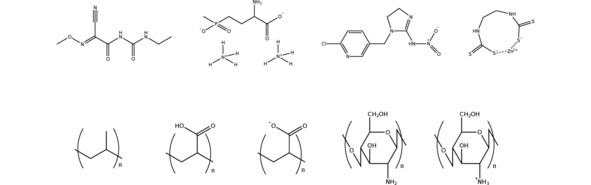
Schematic representation of the pesticides (top) and polymer systems (bottom) employed in this work. From the left to the right, the pesticides are cymoxanil, glufosinate ammonium, imidacloprid and mancozeb, whereas the polymers are polypropylene, poly(acrylic acid) protonated and deprotonated, and chitosan deprotonated and protonated.
2. Methodology
The affinity between pesticides and polymers has been assessed by carrying out molecular dynamics (MD) simulations. We have studied three different polymers [that is, polypropylene, poly(acrylic acid) and chitosan], while four phytopharmaceuticals (cymoxanil, glufosinate‐amonium, imidacloprid and mancozeb) were employed as pesticides. Henceforward, we employ the acronyms CYM, GLF, IMI and MAN for cymoxanil, glufosinate‐amonium, imidacloprid and mancozeb, respectively. In turn, polypropylene is shortly designated as PP. In the case of poly(acrylic acid) and chitosan, we have considered both protonated (designated as PAAH and CTH, respectively) and deprotonated (designated as PAA and CT, respectively) species. Although we did not make any considerations about the relationship between our simulations and “real” systems, qualitatively we may associate the presence of protonated or deprotonated species to different pH regimes in solution. The general 2D structure of the polymers and phytopharmaceuticals studied in this work are shown in Figure 1. In the simulations, three oligomers with 3, 5 and 7 monomers have been selected as models for PP, PAA and PAAH, while 3 monomers have been used for CT and CTH.
2.1. Molecular Dynamics Simulations
All MD calculations have employed the GROMACS program37 and the AMBER force field with GAFF parameters.48 The standard procedure for AMBER force field34,49, 50, 51 has been employed to build the topology of pesticides and polymers: (i) the OpenBabel program52 has been employed to generate the 3D molecular structures; (ii) the 3D geometry is, then, optimized and the partial charges (whose distribution over the atomic sites conforms to the electrostatic field of the molecule) were calculated at the HF/6‐31G* level of theory by using the GAMESS package53 and the RESP fitting protocol, as implemented in the RED program;54 (iii) the AnteChamber PYthon Parser interfacE (ACPYPE) tool55,56 was applied to generate the geometry and topology input files for GROMACS.
To complete the preparation of the system to be studied, pesticide and oligomer molecules are put, apart from each other, in the middle of the cubic simulation‐box. These molecules are, then, solvated with water molecules that are described with the TIP3P model.32 For simulations involving charged oligomers, we also added positive or negative counterions to the cubic box, so that the whole system becomes neutral: was used with PAA, while was employed for CTH. Then, equilibration workflow comprises energy minimization of the whole system followed by two consecutive short simulations of 250 ps (or 1 ns when more than one pesticide is involved) that were performed within the NVT and NPT ensembles, in order to relax to the appropriate temperature and density, respectively. For both NVT and NPT conditions, the temperature has been fixed at 300 K by using the velocity‐rescaling thermostat57,58 with a coupling time of . In addition, the equilibration NPT‐simulation has employed the Parrinello‐Rahman barostat59 to keep the pressure at 1 bar; the corresponding coupling time was .
Once the equilibration stage was completed, the production MD run was carried out, within the above mentioned NVT conditions, for a longer simulation time. Depending on the studied system, we have considered production runs of 100 ns or 200 ns (see below). We note that all dynamics calculations employed periodic boundary conditions and the leapfrog algorithm for the integration of the equations of motion with a time step of 2 fs. Additionally, bond constrains have been imposed through the linear constraint solver (LINKS) scheme60 which is implemented in GROMACS. In turn, the cutoff value of 10 Å has been applied for both Coulombic and van der Waals interactions, while the long‐range electrostatic energy has been evaluated by using the particle mesh Ewald method.61,62
In this study, we have performed simulations involving the combination of each molecule of pesticide with each oligomer; such simulations last for 100 ns. For each of the PP, PAA and PAAH species, we have considered three independent simulations for oligomers with three, five and seven monomers. Since CT and CTH monomers have larger number of atoms and, accordingly, their simulation become computationally more expensive, only oligomers with three units were employed in all calculations. We have also studied mixtures of two pesticides in the presence of an oligomer (PP with 7 monomers or CTH); these MD runs last for 200 ns.
2.2. Trajectory Analysis
The analysis of the MD trajectories has the following targets: (i) representation of the oligomer‐pesticide distance as a function of the simulation time, (ii) calculation of both radial distribution function (RDF) and spatial distribution function (SDF), and (iii) counting the number of hydrogen bonds established between pesticide and oligomer during the simulation. Essentially, SDFs are plots of iso‐surfaces describing a given probability of one molecule to be around the other in the 3D space. Here, the SDFs have been calculated with the TRAVIS program.63 In cases where more than one pesticide is involved, we have also represented the pesticide‐pesticide distance as a function of time, as well as the corresponding RDFs.
3. Results and Discussion
3.1. The Effect of the Oligomer Length
We begin to study the effect of the oligomer length on the ability of either PP or PAAH to closely interact with the pesticides. In both cases, we have run simulations for oligomer chains with three, five and seven monomers, and the main results are shown in Figures 2 and 3 for the four pesticides.
Figure 2.
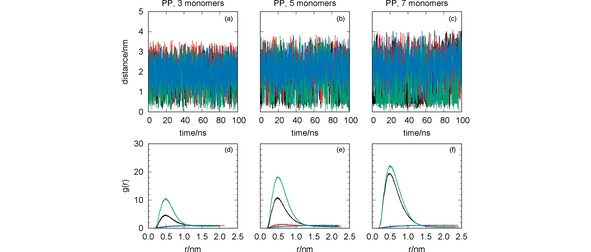
MD simulation of the systems CYM+PP (black lines), GLF+PP (red lines), IMI+PP (green lines) and MAN+PP (blue lines): oligomer‐pesticide distance vs. simulation time [panels (a)–(c)]; radial distribution functions [panels (d)–(f)]. The effect of the oligomer length has been assessed with simulations for PP with three [panels (a) and (d)], five [panels (b) and (e)] and seven [panels (c) and (f)] monomers.
Figure 3.
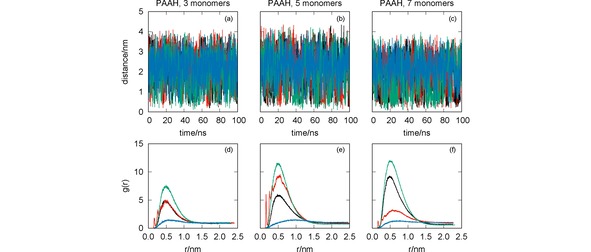
MD simulation of the systems CYM+PAAH (black lines), GLF+PAAH (red lines), IMI+PAAH (green lines) and MAN+PAAH (blue lines): oligomer‐pesticide distance vs. simulation time [panels (a)–(c)]; radial distribution functions [panels (d)–(f)]. The effect of the oligomer length has been assessed with simulations for PAAH with three [panels (a) and (d)], five [panels (b) and (e)] and seven [panels (c) and (f)] monomers.
It is apparent from Figure 2 [panels (a)–(c)] that CYM and IMI are the pesticides approaching closer to the oligomer (<1 nm), while GLF and MAN show average values of the oligomer‐pesticide distance larger than 1.5 nm. This result is independent of the oligomer length, but larger oligomer chains tend to promote the attraction of CYM and IMI. This is particularly visible through the corresponding RDFs displayed in Figure 2 [panels (d)–(f)]. The values of the RDF for both IMI and CYM clearly increase with the length of PP. It is important to emphasize that these pesticides show a non‐spherical shape with several groups that may interact through dispersion forces with the apolar PP longer chain (see Figure 1).
We observe in Figure 3 that the ability of PAAH to interact with the studied pesticides is very sensitive to its length. For the PAAH with three monomers, only the RDF for IMI presents a significant maximum value (even though both CYM and GLF show close distances to the oligomer for some simulation times). As the number of monomers increases, IMI and CYM show an enhancement of the RDF. In contrast, GLF has a peculiar behavior since the corresponding RDF increases for PAAH with 5 monomers, while decreasing for largest oligomer. Conversely, the RDF of MAN suggests a weak interaction with PAAH, independently of the oligomer length.
3.2. PAAH Versus PAA
The appearance of each one of the two forms of the poly(acrylic acid) (PAA or PAAH) depends on environmental conditions, such as the pH of the solution. Because of this, we have performed MD simulations for the pesticides with either PAAH or PAA. We have seen in Subsection 3.1. that the attraction between PAAH and the pesticides depends on the length of the oligomer chain. Now, we want to look at the differences between PAAH and PAA for the longest oligomer chain (i. e., 7 monomers). The results for the protonated and deprotonated oligomer with each pesticide are compared in Figure 4.
Figure 4.
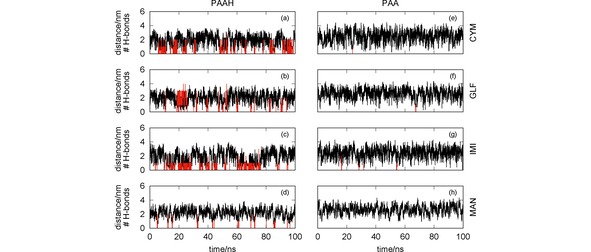
Oligomer‐pesticide distance (black lines) and number of hydrogen bonds (red vertical lines) as a function of the simulation time. The effect of the protonation/deprotonation of the poly(acrylic acid) is assessed by comparing simulations involving PAAH [panels (a)–(d)] and the corresponding ones for PAA [panels (e)–(h)] with the pesticides CYM [panels (a) and (e)], GLF [panels (b) and (f)], IMI [panels (c) and (g)] and MAN [panels (d) and (h)].
It is worth noting in Figure 4 that, as already shown in Figure 3 [panels (c) and (f)], PAAH is able to establish strong interactions with the CYM and IMI, which are mainly due to the formation of hydrogen bonds involving the carbonyl and amine, and nitrite groups of CYM and IMI, respectively. These pesticides are able to establish two (or even three) hydrogen bonds with PAAH along the simulation. It should be also emphasized that GLF can form several (up to 4) H‐bonds with PAAH, though the corresponding RDF does not show a very strong peak for this simulation (see Figure 3). In contrast, PAA is non‐effective to capture the four pesticides, since they become close to each other only for very short time. Although not represented, the corresponding pesticide‐PAA RDFs are quite flat, i. e., do not show a prominent maximum at short distances. In summary, the protonation of the poly(acrylic acid) is essential to establish hydrogen bonds with the pesticides and, hence, to become effective for water remediation.
3.3. Interaction with CT and CTH
As previously mentioned for PAA and PAAH, the presence of the deprotonated (CT) or protonated (CTH) forms of chitosan in water solution is expected to depend on the pH. We should note that chitosan has one amine and two hydroxyl groups per monomer, which allows for the formation of several hydrogen bonds with the pesticides that have very electronegative atoms. In addition, the CTH form is protonated in the amine group, which now carries on positive charge (forming an ammonium group), and hence it is able to interact with negatively charged pesticides. Having in mind these intuitive ideas, we have also performed MD simulations to assess the ability of both CT and CTH to strongly interact with the pesticides.
It is apparent from Figure 5 that, in general, both CT and CTH establish several hydrogen bonds with the pesticides. In particular, the number of hydrogen bonds formed between CTH and GLF is quite impressive, which leads us to conclude that the formation of this complex is essentially assured by H‐bonding. The sole exception to the above mentioned trend arises for the simulation of CT with MAN [panel (d)] where the two species are far apart during most of the time. Indeed, the RDFs presented in Figure 6 clearly show maximum values at , except for the CT+MAN system. Accordingly, Figure 6 showed very high values of the RDF for both MAN and GLF pesticides with CTH, while less prominent peaks arise for IMI and CYM with the same oligomer. In turn, the RDFs displayed in Figure 6 show that CT is more effective than CTH to capture CYM and IMI, but it is non‐effective for GLF and MAN.
Figure 5.
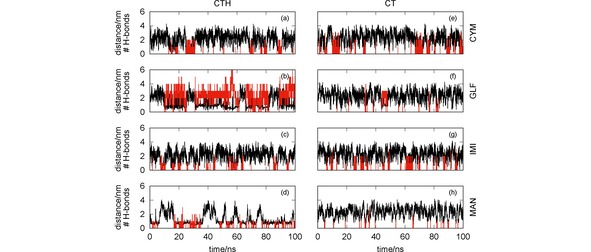
Chitosan‐pesticide distance (black lines) and number of hydrogen bonds (red vertical lines) as a function of the simulation time. The effect of the protonation/deprotonation of the chitosan is assessed by comparing simulations involving CTH [panels (a)–(d)] and the corresponding ones for CT [panels (e)–(h)] with the pesticides CYM [panels (a) and (e)], GLF [panels (b) and (f)], IMI [panels (c) and (g)] and MAN [panels (d) and (h)].
Figure 6.
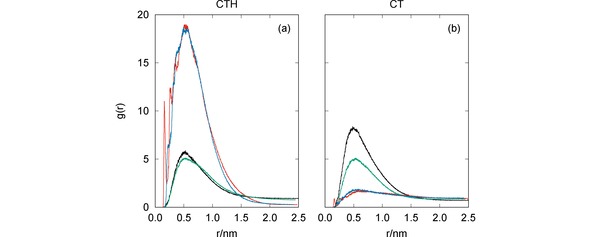
Radial distribution functions for the MD simulations of CTH [panel (a)] or CT [panel (b)] with the pesticides: CYM (black lines), GLF (red lines), IMI (green lines) and MAN (blue lines).
Whereas the hydrogen bonding is closely associated to the formation of pesticide‐CT (or −CTH) complexes that last for more than 1 ns in most of the simulations, other type of interaction appears to be also relevant for capturing MAN by CTH. One may observe in Figure 5(d) that, even though hydrogen bonding may help in the formation of the MAN‐CTH complex, it does not appear to be an imperative driving‐force for such process. Actually, the MAN‐CTH complex may be formed and last for long time intervals without establishing hydrogen bonds. Since MAN and CTH carry on opposite charges, it is expected that Coulomb interactions may develop an important role in the formation of the complex.
In order to identify the main regions of “contact” between oligomer and pesticides, we represent in Figure 7 and Figure 8 the spacial distribution functions (SDFs) for the simulations involving CTH and CT, respectively. It is apparent from Figure 7 that the SDF for both GLF and MAN are very delocalized over the whole oligomer, so that the interaction with the charged ammonium groups would be maximized. In the case of GLF, such delocalization of the SDF is compatible with the formation of several hydrogen bonds [cf. Figure 5]. Nonetheless, it appears from the bottom panel of Figure 7 that the “contact” between GLF and the oligomer occurs mainly from the tail of the GLF chain containing the phosphorous atom. In turn, the maximum probability for the SDF of CTH around MAN arises next to one of the tails of the pesticide that has negative charge and, hence, it is able to interact with the positively charged ammonium groups. We remind that MAN is a symmetric molecule where both tails of the chain show the same atoms. Thus, the fact that the SDF is essentially localized in one of the tails is a consequence of representing only a single MD trajectory.
Figure 7.
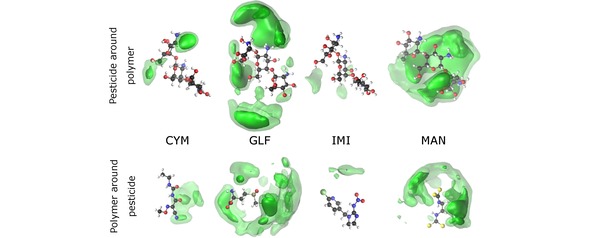
Spatial distribution functions for the MD simulations of CTH with the pesticides CYM, GLF, IMI, and MAN. Top (bottom) plots take as reference the oligomer (corresponding pesticide). The particle density along the dark (light) green iso‐surface is 0.6 nm‐3 (0.3 nm‐3).
Figure 8.
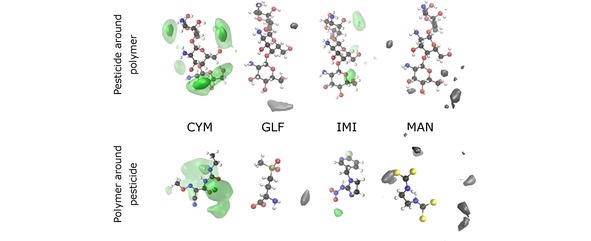
Spatial distribution functions for the MD simulations of CT with the pesticides CYM, GLF, IMI and MAN. Top (bottom) plots take as reference the oligomer (corresponding pesticide). The particle density along the dark (light) green iso‐surface is 0.6 nm‐3 (0.3 nm‐3). Since both GLF and MAN do not significantly bind to CT, the particle densities along the iso‐surfaces (in gray) are very low. For GLF (MAN), the value associated to the gray iso‐surface in the top panel is 0.23 nm‐3 (0.15 nm‐3), while the corresponding one for the bottom panel is 0.11 nm‐3 (0.07 nm‐3).
Concerning CYM and IMI pesticides, Figure 8 shows more localized SDFs, thus, indicating a certain degree of specificity for the intermolecular interactions. In the case of IMI, the interaction occurs essentially between a hydroxyl group of CTH and the nitrate tail of the pesticide chain, which leads to the formation of hydrogen bonds [see also Figure 5(c)]. In turn, the formation of the CYM–CTH complex may be associated to the interaction between the carbonyl groups of CYM and one of the ammonium groups of CTH, in order to establish hydrogen bonds [as also noticed in Figure 5(a)]. It is interesting to observe in Figure 8 that, in contrast, the SDF of CYM with CT shows stronger maxima associated to a hydroxyl group of the oligomer, while it becomes delocalized over the region next to one of the carbonyl groups and the nitrogen atoms of the pesticide. Also the SDF for IMI with CT is more spread over the two molecules than in the case of this pesticide with CTH; nonetheless, the interacting groups are essentially the same in both cases, though the absence of charged ammonium groups (present in CTH) favors the formation of the IMI‐CT complex.
It is worth noting by the gray iso‐surfaces in Figure 8 that the small interaction between GLF and CT comprises some hydrogen bonding involving the hydroxyl groups of the oligomer. However, the SDF is very weak and, hence, no significant probability is observed in Figure 8 around the GLF molecule or the CT oligomer, which is in agreement with the small‐amplitude and broad RDF displayed in Figure 6. In turn, even weaker interactions are expected for MAN with CT, since the gray iso‐surfaces shown in Figure 8 present very low values and are scattered over several regions far from the pesticide and the oligomer structures, which is also compatible with the corresponding RDF in Figure 6(b).
3.4. Mixture of Pesticides in the Presence of Oligomer
We have also studied the effect of having a mixture of two pesticides when interacting with the oligomer. For that, we have selected two oligomers (PP with seven monomers and CTH) which show different type of interactions with the pesticides. The simulations involve PP with a mixture of CYM and IMI, and CTH with GLF and MAN. In both cases, the pesticides are those that form stronger complexes with the corresponding oligomer (see the above discussion).
We represent in Figure 9 the distances between the three main components of the two simulating systems as a function of time, as well as the corresponding RDFs. We observe in Figure 9(a) that the formation of the CYM‐PP complex may be, in general, associated with a close approaching between the CYM and IMI pesticides. The two pesticides tend to form a complex [as shown by the strong peak of the RDF in Figure 9(c)], which favors the association to the oligomer. Because of this, both the CYM‐PP and IMI‐PP complexes last for a longer time than in the simulations involving a single pesticide with the oligomer (cf. Figure 2). As a result, the corresponding RDFs show higher peaks in Figure 9(c), thus indicating a cooperative effect of the two pesticides that increase the ability for being captured by PP. Conversely, we observe in Figure 9 [panels (b) and (d)] that the association between GLF and MAN is very unlikely. This may be rationalized by noting that both pesticides are negatively charged. Actually, it appears to exist a competition of the two pesticides by the oligomer. Since the interaction between GLF and CTH involves a larger number of hydrogen bonds than for MAN (cf. Figure 5), once the former becomes close to the oligomer it stays strongly stucked there and, eventually, may hampers the formation of the MAN‐CTH complex. As we can see by the comparison of the GLF‐CTH and MAN‐CTH RDFs in Figure 9(d) with the corresponding ones in Figure 6(a), such effect leads to increase the ability of CTH to capture GLF while essentially maintaining the interaction of the oligomer with MAN.
Figure 9.
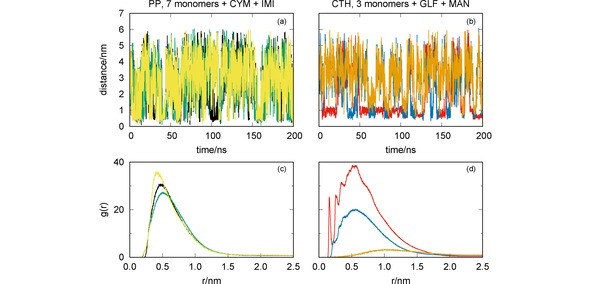
MD simulations of the mixtures of pesticides CYM+IMI with PP (7 monomers) [panels (a) and (c)] and GLF+MAN with CTH [panels (b) and (d)]: oligomer‐pesticide and pesticide‐pesticide distances vs. simulation time [panels (a) and (b)]; radial distribution functions [panels (c) and (d)]. Key for lines: CYM‐IMI (yellow); GLF‐MAN (orange); CYM‐PP (black); IMI‐PP (green); GLF‐CTH (red); MAN‐CTH (blue).
4. Conclusions
The results reported in the previous sections showcase how MD simulations may be applied for screening the ability of several polymers to remove pesticides from water. We believe that the present computational approach based on MD simulations may be a general and powerful methodology to select potentially effective materials and appropriate environmental conditions for cleaning water and soils contaminated with pollutants. It also allows for a detailed rationalization of the intermolecular interactions involved in the removing process, which constitutes an important piece of data to design the “real” material that will act under a given set of environmental conditions.
Concerning the present screening study, the main results show that chitosan (both protonated and deprotonated) is the oligomer that establishes the strongest interactions with the pesticides. Such interactions are mainly due to the formation of hydrogen bonds. In turn, protonated poly(acrylic acid) can also establish hydrogen bonds with cymoxanil, glufosinate‐amonium and imidacloprid, but it is not effective for mancozeb. In addition, deprotonated poly(acrylic acid) is totally non‐effective in establishing interactions with all pesticides. Although not forming hydrogen bonds, polypropylene is able to attract cymoxanil and imidacloprid pesticides. For both polypropylene and protonated poly(acrylic acid), the interactions tend to be stronger as the oligomer chain increases. It is worth noting that the concomitant use of cymoxanil and imidacloprid leads to a synergetic interaction with polypropylene. Finally, it should be emphasized that the present approach constitutes an efficient way to screen for the ability of each polymer to remove pesticides from water, which will be, then, complemented with experimental tests for the most promising instances.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
This project was financed by Portuguese funds through FCT ‐ Fundação para a Ciência e a Tecnologia in the framework of the projects WaterJPI/006/2016 and UID/QUI/00313/2019. F.G.A.E. thanks the grant from the project ERA‐NET “WaterJPI/006/2016” (contract: DPA 17–622). We are grateful for the provision of computational time in the supercomputer resources hosted at Laboratório de Computação Avançada, Universidade de Coimbra.
F. G. A. Estrada, J. M. C. Marques, A. J. M. Valente, ChemistryOpen 2019, 8, 438.
References
- 1. Neuwirthová N., Trojan M., Svobodová M., Vasicková J., Simek Z., Hofman J., Bielská L., Sci. Total Environ. 2019, 646, 1056–1062. [DOI] [PubMed] [Google Scholar]
- 2. Hayat K., Afzal M., Aqueel M. A., Ali S., Khan Q. M., Ashfaq U., Ecotox. Environ. Safe. 2018, 163, 382–390. [DOI] [PubMed] [Google Scholar]
- 3. Ogungbemi A. O., van Gestel C. A. M., Ecotoxicology 2018, 27, 1107–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Li Z., J. Chem. Health Saf. 2018, 25, 28–38. [Google Scholar]
- 5. Rani M., Shanker U., Jassal V., J. Environ. Manage. 2017, 190, 208–222. [DOI] [PubMed] [Google Scholar]
- 6. dos Santos A., Costa G. S., Peralta-Zamora P., Quim. Nova 2017, 40, 327–333. [Google Scholar]
- 7. Huang Y., Yang Y., Wang X., Yuan X., Pi N., Yuan H., Liu X., Ni C., Chem. Eng. J. 2018, 342, 142–154. [Google Scholar]
- 8. Abdennouri M., Baâlala M., Galadi A., El Makhfouk M., Bensitel M., Nohair K., Sadiq M., Boussaoud A., Barka N., Arab. J. Chem. 2016, 9, S313–S318. [Google Scholar]
- 9. Lhomme L., Brosillon S., Wolbert D., Chemosphere 2008, 70, 381–386. [DOI] [PubMed] [Google Scholar]
- 10. Guimaraes B. S., Bernardes A. A., Salcedo G. M., Caldas S. S., Jorge M. B., Bianchini A., Wolke S. I., Primel E. G., J. Braz. Chem. Soc. 2016, 27, 2256–2263. [Google Scholar]
- 11. Plakas K. V., Karabelas A. J., Desalination 2012, 287, 255–265. [Google Scholar]
- 12. Wan J., Wu L., Ye M., Zhang S., Jiang X., Long T., Lin Y., Lu X., Pedosphere 2017, in press, doi: 101016/S1002-0160(17)60328-X. [Google Scholar]
- 13. Ye M., Sun M., Hu F., Kengara F. O., Jiang X., Luo Y., Yang X., Chemosphere 2014, 105, 119–125. [DOI] [PubMed] [Google Scholar]
- 14. Gupta V. K., Gupta B., Rastogi A., Agarwal S., Nayak A., Water Res. 2011, 45, 4047–4055,. [DOI] [PubMed] [Google Scholar]
- 15. Liu Y., Lonappan L., Brar S. K., Yang S., Sci. Total Environ. 2018, 645, 60–70. [DOI] [PubMed] [Google Scholar]
- 16. Zhao S., Environ. Sci. Technol. 2014, 48, 4212–4213. [DOI] [PubMed] [Google Scholar]
- 17. Filho C. M. C., Bueno P. V. A., Matsushita A. F. Y., Rubira A. F., Muniz E. C., Durães L., Murtinho D. M. B., Valente A. J. M., RSC Adv. 2018, 8, 14609–14622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Tiwari A., Bind A., Anal. Chem. Lett. 2014, 4, 267–278. [Google Scholar]
- 19. El-Mohdy H. L. A., Hegazy E. A., El-Nesr E. M., El-Wahab M. A., J. Macromol. Sci. Part A-Pure Appl. Chem. 2012, 49, 814-827. [Google Scholar]
- 20. Ghimici L., Brunchi C.-E., Diaconu A., Cellulose 2016, 23, 3837-3846. [Google Scholar]
- 21. Elsabee M. Z., Abdou E. S., Nagy K. S. A., Eweis M., Carbohydr. Polym. 2008, 71, 187–195. [Google Scholar]
- 22. Husseinsyah S., Amri F., Husin K., Ismail H., J. Vinyl Addit. Technol. 2011, 17, 125–131. [Google Scholar]
- 23. Fasce L. A., Costamagna V., Pettarin V., Strumia M., Frontini P. M., Express Polym. Lett. 2008, 2, 779–790. [Google Scholar]
- 24. Valente A. J. M., Ribeiro A. C. F., Marques J. M. C., Abreu P. E., Lobo V. M. M., Kataky R., J. Chem. Eng. Data 2010, 55, 1145–1152. [Google Scholar]
- 25. Geitner N. K., Zhao W., Ding F., Chen W., Wiesner M. R., Environ. Sci. Technol. 2017, 51, 8396–8404. [DOI] [PubMed] [Google Scholar]
- 26. Proctor E. A., Ding F., Dokholyan N. V., WIREs Comput. Mol. Sci. 2011, 1, 80–92. [Google Scholar]
- 27. Allinger N. L., Yuh Y. H., Lii J. H., J. Am. Chem. Soc. 1989, 111, 8551–8566. [Google Scholar]
- 28. Lii J. H., Allinger N. L., J. Am. Chem. Soc. 1989, 111, 8566–8575. [Google Scholar]
- 29. Lii J. H., Allinger N. L., J. Am. Chem. Soc. 1989, 111, 8576–8582. [Google Scholar]
- 30. Jorgensen W. L., Madura J. D., Swenson C. J., J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar]
- 31. Jorgensen W. L., Maxwell D. S., Tirado-Rives J., J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar]
- 32. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L., J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- 33. Jorgensen W. L., Madura J. D., Mol. Phys. 1985, 56, 1381–1392. [Google Scholar]
- 34. Weiner S. J., Kollman P. A., Nguyen D. T., and Case D. A., J. Comput. Chem. 1986, 7 : 230252. [DOI] [PubMed] [Google Scholar]
- 35. MacKerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., Karplus M., J. Phys. Chem. B 1998, 102, 3586-3616. [DOI] [PubMed] [Google Scholar]
- 36. Mackerell A. D., Feig M., Brooks C. L., J. Comput. Chem. 2004, 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
- 37.GROMACS, M. J. Abraham, D. van der Spoel, E. Lindahl, B. Hess, and the GROMACS development team, 2015.
- 38. Plimpton S., J. Comput. Phys. 1995, 117, 1–19. [Google Scholar]
- 39. Case D. A., Cheatham T. E., Darden T., Gohlke H., Luo R., Merz K. M., Onufriev A., Simmerling C., Wang B., Woods R. J., J. Comput. Chem. 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Salomon-Ferrer R., Case D. A., Walker R. C., WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar]
- 41. Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaminathan S., Karplus M., J. Comput. Chem. 1983, 4, 187–217. [Google Scholar]
- 42. Brooks B. R., Brooks C. L., Mackerell A. D., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., Karplus M., J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Todorov I. T., Smith W., Trachenko K., Dove M. T., J. Mater. Chem. 2006, 16, 1911–1918. [Google Scholar]
- 44. Kwon D., Chung H.-K., Shin W.-S., Park Y.-S., Kwon S.-C., Song J. S., Park B.-G., Mol. Cell. Toxicol. 2018, 14, 105–112. [Google Scholar]
- 45. Carpenter D., Boutin C., Ecotoxicology 2010, 19, 1322–1336. [DOI] [PubMed] [Google Scholar]
- 46.[Anonymous], EFSA J 2008, 6, 1–80.
- 47. Suchail S., Debrauwer L, Belzunces L. P., Pest Manage. Sci. 2004, 60, 291–296. [DOI] [PubMed] [Google Scholar]
- 48. Wang J., Wolf R. M., Caldwell J. W., Kollman P. A., Case D. A., J. Comput. Chem. 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- 49. Cornell W. D., Cieplak P., Bayly C. I., Merz I. R. Gould, Jr. K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., Kollman P. A., J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar]
- 50. Wang J., Cieplak P., Kollman P. A., J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar]
- 51. Weiner S. J., Kollman P. A., Case D. A., Singh U. C., Ghio C., Alagona G., Profeta S., Weiner P., J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar]
- 52. O'Boyle N. M., Banck M., James C. A., Morley C., Vandermeersch T., Hutchison G. R., J. Cheminformatics 2011, 3, 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Schmidt M. W., Baldridge K. K., Boats J. A., Elbert S. T., Gorgon M. S., Jensen J. H., Koseki S., Matsunaga N., Nguyen K. A., Su S., Windus T. L., Dupuis M., J. Montgomery Jr. , J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar]
- 54. Dupradeau F.-Y., Pigache A., Zaffran T., Savineau C., Lelong R., Grivel N., Lelong D., Rosanski W., Cieplak P., Phys. Chem. Chem. Phys. 2010, 12, 7821–7839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Wang J., Wang W., Kollman P. A., Case D. A., J. Mol. Graphics Model. 2006, 25, 247–260. [DOI] [PubMed] [Google Scholar]
- 56. Silva A. W. S., Vranken W. F., BMC Res. Notes 2012, 5, 367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Berendsen H. J. C. in Computer Simulations in Material Science, (Eds.: M. Meyer, V. Pontikis), Kluwer Academic Publishers, Dordrecht, 1991, pp. 139–155. [Google Scholar]
- 58. Bussi G., Donadio D., Parrinello M., J. Chem. Phys. 2007, 126, 014101. [DOI] [PubMed] [Google Scholar]
- 59. Parrinello M., Rahman A., J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar]
- 60. Hess B., Bekker H., Berendsen H. J. C., Fraaije J. G. E. M., J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar]
- 61. Darden T., York D., Pedersen L., J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- 62. Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., Pedersen L. G., J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar]
- 63. Brehm M., Kirchner B., J. Chem. Inf. Model. 2011, 51, 2007–2023. [DOI] [PubMed] [Google Scholar]


