Robust Regression for Optimal Individualized Treatment Rules

Abstract

Because different patients may respond quite differently to the same drug or treatment, there is increasing interest in discovering individualized treatment rules. In particular, there is an emerging need to find optimal individualized treatment rules which would lead to the “best” clinical outcome. In this paper, we propose a new class of loss functions and estimators based on robust regression to estimate the optimal individualized treatment rules. Compared to existing estimation methods in the literature, the new estimators are novel and advantageous in the following aspects: first, they are robust against skewed, heterogeneous, heavy-tailed errors or outliers in data; second, they are robust against a misspecification of the baseline function; third, under some general situations, the new estimator coupled with the pinball loss approximately maximizes the outcome’s conditional quantile instead of the conditional mean, which leads to a more robust optimal individualized treatment rule than traditional mean-based estimators. Consistency and asymptotic normality of the proposed estimators are established. Their empirical performance is demonstrated via extensive simulation studies and an analysis of an AIDS data set.

1 |. INTRODUCTION

Given the same drug or treatment, different patients may respond quite differently. Factors causing individual variability in drug response are multi-fold and complex. This has raised increasing interests of personalized medicine, where customized medicine or treatment is recommended to each individual according to his/her characteristics, including genetic, physiological, demographic, environmental, and other clinical information. The rule that is applied in personalized medicine to match each patient with a target treatment is called the individualized treatment rule. Our goal is to find the “optimal” rule, which if followed by the whole patient population would lead to the “best” clinical outcome of interest.

Q-learning^1,2 and A-learning^3,4 are two main approaches to finding optimal individualized treatment rules based on clinical trials or observational data. Q-learning is based on posing a regression model to estimate the conditional expectation of the outcome at each treatment-decision time point, and then applying a backward recursive procedure to fit the model. A-learning, on the other hand, only requires modeling the contrast function of the treatments at each treatment-decision time point, and it is therefore more flexible and robust to model misspecification of the baseline function. See Schulte et al⁵ for a complete review and comparison of these two methods under various scenarios. Q- and A-learning have good performance when the model is correctly specified but they are sensitive to model misspecification. To overcome this shortcoming, several “direct” methods^6,7 have been proposed, which maximize value functions directly instead of modeling the conditional mean.

Most of the existing estimation methods for optimal individualized treatment rules, including Q-learning and A-learning, belong to mean regression methods as they estimate the optimal estimator by maximizing expected outcomes. In the case of a single decision point, Q-learning is equivalent to the least-squares regression. Least-squares estimates are optimal if the errors are independent and identically distributed normal random variables. However, skewed, heavy-tailed, heteroscedastic errors or outliers of the response are frequently encountered in practice. In such situations, efficiency of the least square estimates is impaired. One extreme example is that when the response takes Cauchy errors, neither Q-learning nor A-learning can consistently estimate the optimal individualized treatment rule. For example, in AIDS Clinical Trials Group Protocol 175 (ACTG175) data,⁸ HIV-infected subjects were randomized to four regimes with equal probabilities, and our objective is to find the optimal individualized treatment rule for each patient based on his/her age, weight, race, gender, and some other baseline measurements. The response, CD4 count post treatment assignment, has skewed heteroscedastic errors, which reduces efficiency of classical Q- and A-learning. Therefore, a method to estimate an optimal individualized treatment rule which is robust against skewed, heavy-tailed, heteroscedastic errors or outliers is highly valuable. To achieve this goal, we propose and investigate a new framework of constructing the optimal individualized treatment rule based on the conditional median or quantiles of responses given covariates rather than based on average effects.

In the following, we first use a simple example to illustrate that a quantile-based treatment rule can be more preferable than mean-based rules. We use higher value of response Y to indicate more favorable outcomes. Figure 1 plots the conditional density values of Y under two treatments, A and B, given a binary covariate X, such as gender: male and female. Under the comparison based on conditional means, A and B are exactly equivalent. However, conditional quantiles provide us more insight. For the male group, the conditional distribution of the response given treatment B is a log-normal and skewed to the right. Therefore, treatment B is less favorable when either 50% or 25% conditional quantiles are considered. For the female group, the conditional distribution of the response given treatment A is a standard normal while a Cauchy distribution given treatment B. Therefore, if we make a comparison based on 25% conditional quantile, treatment A is more favorable.

FIGURE 1.

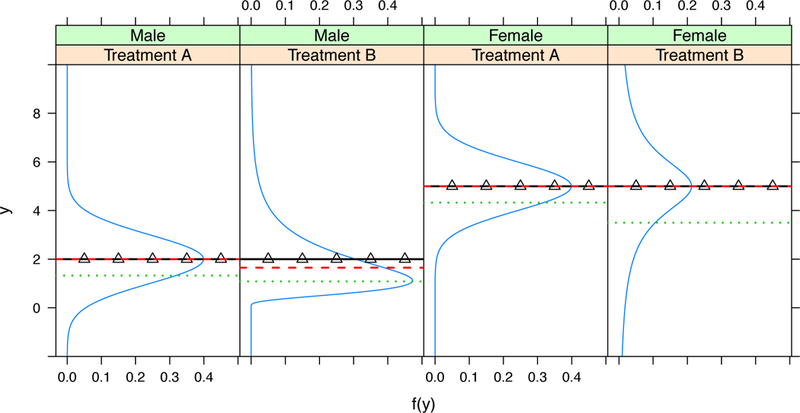
The distribution functions of the response Y, in a randomized clinical trial with two treatments, A and B, for male (two panels on the left) and female (two panels on the right). The solid lines with triangle symbol, dashed line, and dotted lines are the conditional mean, 50% quantile, and 25% quantile functions of Y given the gender and the treatment, respectively.

Optimal individualized treatment rules based on quantiles have been previously studied in Zhang et al,⁹ Linn et al,¹⁰ and Wang et al.¹¹ These papers focus on estimating optimal individualized treatment rules that maximize the marginal quantile of the potential outcome. However, our method is fundamentally different from these works by modeling the conditional quantiles of the response and maximizing the conditional quantile of the potential outcome. Our method is more closely related with standard quantile regression,¹² and it is more favorable in terms of estimation efficiency compared with the direct search methods that maximize the marginal quantile of the potential outcome.

In this paper, we propose a general framework for estimating the optimal individualized treatment rule based on robust regression. Our work focuses on homoscedastic treatment effect cases, i.e. the error term in the considered quantile regression is assumed to be conditionally independent of treatment given covariates. Under such settings, our model can still accommodate heteroscedastic responses; however, the corresponding optimal individualized treatment rules are the same across all quantile levels. Three types of loss-based learning methods will be considered and studied under the new estimation framework : quantile regression, regression based on Huber’s loss, and e-insensitive loss. The proposed methodologies have the following desired features. First, the new treatment rule obtained by maximizing the conditional quantile is suitable for data with skewed, heavytailed errors or outliers. Second, the proposed estimator requires modeling the contrast function only, and is therefore robust against misspecification of the baseline function as in A-learning. Third, empirical results from our comprehensive numerical studies suggest favorable performance of the proposed robust regression estimator over traditional mean-based methods.

The rest of the paper is organized as follows. In Section 2, we introduce the proposed robust estimation procedure for the optimal individualized treatment rule and discuss its connections with and differences from existing methods. In Section 3, we establish asymptotic properties of the proposed estimators, including consistency and asymptotic normality. Simulation studies are conducted to assess the finite sample performance of the proposed estimators in Section 4, followed by its application to the AIDS ACTG175 data in Section 5. Concluding remarks are given in Section 6. All the technical proofs are provided in the Supplementary Appendix A.

2 |. NEW OPTIMAL TREATMENT ESTIMATION FRAMEWORK: ROBUST REGRESSION

2.1 |. Notation and Assumptions

Consider a single stage study with two treatments. For each patient i, i = 1,…,n, the observed data are denoted by (X_i, A_i, Y_i), where $X_i\in \mathcal{X}\subset {ℝ}^p$ denotes the baseline covariates, $A_i\in \mathcal{A}=\{0,1\}$ denotes the treatment assigned to the patient, and Y_i is the real-valued response, which is coded so that higher values indicate more favorable clinical outcomes. Let $Y_i^{*}(a)$ denote the potential outcome that might be observed for individual i had s/he received treatment a. Define the propensity score $\pi (x)=\text{pr}\left(A_i=1|X_i=x\right).$ Following Rubin,¹³ we make the following assumptions: (i) stable unit treatment value assumption: $Y_i=Y_i^{*}(1)A_i+Y_i^{*}(0)\left(1-A_i\right);$ (ii) strong ignorability assumption: $A_i\perp {\left\{Y_i^{*}(a)\right\}}_{a\in \mathcal{A}}|X_i;$ and (iii) positivity assumption: $0<\pi (x)<1,\forall x\in \mathcal{X}.$ We further assume that the the propensity score $\pi (x)$ is either known (usually true in randomized clinical trials) or can be correctly specified and consistently estimated from the data.

2.2 |. New Proposal: Robust Regression

One commonly used mean-based method for estimating optimal individualized treatment rules is Q-learning, which aims to model the Q-function $Q(x,a)\triangleq E\left\{Y_i^{*}(a)|X_i=x\right\}.$ Under assumptions (i)-(ii), one can show that $E\left\{Y_i^{*}(a)|X_i=x\right\}=E\left(Y_i|X_i=x,A_i=a\right)$ and the associated optimal individualized treatment rule is defined as $g_{\mu }^{\text{opt}}(x)=\text{argmax}{}_{a\in \mathcal{A}}Q(x,a)=\text{argmax}{}_{a\in \mathcal{A}}E(Y|X=x,A=a).$ In addition, the value function of a mean-based treatment rule g is defined as $V_{\mu }(g)=E_X[Q\{X,g(X)\}]\text{and}{g}_{\mu }^{\text{opt}}=\text{argmax}{}_g{V}_{\mu }(g).$

In practice, the response variable Y may have a skewed, heavy-tailed, or heteroscedastic distribution. It is well known that the mean-based estimation may fail to provide an efficient and reliable estimator in such situations. This motivates us to develop robust regression techniques for estimating optimal individualized treatment rules. Define the $\tau \text{th}$ conditional quantile of $Y_i^{*}(a)\text{given}{X}_i=x\text{as}{Q}_{\tau }(x,a)\triangleq \inf \left\{y:F_{Y_i^{*}(a)|X_i}(y|x)\ge \tau \right\},\text{where}{F}_{Y_i^{*}(a)|X_i}(y|x)=\text{pr}\left\{Y_i^{*}(a)\le y|X_i=x\right\}.$ Under assumptions (i)-(ii), we have $F_{Y_i^{*}(a)|X_i}(y|x)=F_{Y_i|X_i,A_i}(y|x,a)=\text{pr}\left(Y_i\le y|X_i=x,A_i=a\right).$ Then the conditional quantile-based optimal individualized treatment rule is defined as

$$g_{\tau }^{\text{opt}}(x)={\text{argmax}}_{a\in \mathcal{A}}{Q}_{\tau }(x,a),\tau \in (0,1).$$

For a conditional quantile-based treatment rule g, the value function is defined as $V_{\tau }(g)=E_X\left[Q_{\tau }\{X,g(X)\}\right]$ and $g_{\tau }^{\text{opt}}={\text{argmax}}_g{V}_{\tau }(g).$ It is noted that our defined value function is different from those recently studied in the literature.^9,10,11 Specifically, they considered the marginal cumulative distribution function of the potential outcome, $F_{Y_i^{*}(a)}(y)=\text{pr}\{Y_i^{*}(a)\le \text{y}}.$ The marginal quantile-based value function is defined as ${\tilde{V}}_{\tau }(g)=\inf \left\{y:F_{Y_i^{*}(g)}(y)\ge \tau \right\},\text{where}{F}_{Y_i^{*}(g)}(y)=E_X\left(\text{pr}\left[Y_i^{*}\left\{g\left(X_i\right)\right\}\le y|X_i\right]\right),$ and the optimal individualized treatment rule which maximizes the $\tau \text{th}$ marginal quantile $g_{\tau }^{\text{Opt}-\text{mar}}$ is defined as $g_{\tau }^{\text{opt}-\text{mar}}=\text{argmax}{}_g{\tilde{V}}_{\tau }(g).$ In contrast to the mean-based methods for optimal treatment decision, where the optimal individualized treatment rules are usually the same based on the conditional mean or marginal mean, the maximizers of $V_{\tau }(g)\text{and}{\tilde{V}}_{\tau }(g)$ are generally different in the context of quantile regression. We provide two toy examples in the Supplementary Appendix E to demonstrate the differences and show that the individualized treatment rule that maximizes the marginal quantile may not be the optimal choice for an individual patient. For an individual, the ITR maximizing the conditional quantile may be more desirable comparing with the ITR maximizing the marginal quantile, because an individual only cares how well the ITR does given his/her own X, but doesn’t care how well the ITR does for the whole population. However, the ITR that maximizes the marginal quantile has its own merits. First, the ITR maximizing the marginal quantile can be estimated in a model-free way, for example, as studied in Wang et al¹¹, but the ITR maximizing the conditional quantile usually can not, because it requires a model for the conditional quantile function $Q_{\tau }(x,a).$ In this sense, the ITR maximizing the marginal quantile is more robust to model misspecification. Second, because the estimated value function based on the marginal quantile is a measure for the whole population and nonparametric in nature, it can be used to compare the effectiveness of different ITRs, including the ITR maximizing the conditional quantile.

To connect the conditional quantile-based optimal individualized treatment rule with the mean-based optimal individualized treatment rule, we consider the following model,

$$Y_i=h_0\left(X_i\right)+A_{i}C\left(X_i;{\beta }_0\right)+{ϵ}_i,$$ (1)

where $h_0(\cdot )$ is an unspecified baseline function, $C\left(\cdot ;{\beta }_0\right)$ is the contrast function with a correctly specified parametric form, and ${ϵ}_i$ is the error term which satisfies the conditional independence error assumption ${ϵ}_i\perp A_i|X_i.$ Note that the error term defined in (1) can be very general. For example, we can take ${ϵ}_i={\sum }_{j=1}^K{\sigma }_j\left(X_i\right)e_{ij}$ for some $K\ge 1,$ where ${\sigma }_j{(\cdot )}^{\prime }\text{s}$ are arbitrary positive functions and $e_{ij}\perp \left(A_i,X_i\right)$ for all j = 1,…, K. This class of error representation can be used to model skewness, heavy tailedness, and heteroscedasticity. Under the assumed model and conditional independence error assumptions, we have

$$Q\left(X_i,A_i\right)=h_0\left(X_i\right)+A_{i}C\left(X_i;{\beta }_0\right)+{\mu }_{ϵ}\left(X_i\right);$$

$$Q_{\tau }\left(X_i,A_i\right)=h_0\left(X_i\right)+A_{i}C\left(X_i;{\beta }_0\right)+F_{ϵ}^{-1}\left(X_i;\tau \right),$$

where ${\mu }_{ϵ}\left(X_i\right)\text{and}{F}_e^{-1}\left(X_i;\tau \right)$ denote the conditional mean and the conditional $\tau \text{th}$ quantile of ${ϵ}_i$ given $X_i,$ respectively. Therefore, the mean-based and conditional quantile-based optimal individualized treatment rules are both given by $g_{\mu }^{\text{opt}}(x)=g_{\tau }^{\text{opt}}(x)=g_0^{\text{opt}}(x)=I\left\{C\left(x;{\beta }_0\right)>0\right\}$ for any $\tau \in (0,1).$ Note that model (1) is not a standard quantile regression model since we assume a special error structure. The reason we consider such a model is to make a fair comparison between the mean-based and quantile-based optimal individualized treatment rules because they are the same under the assumed model. In the next Section, we extend some theoretical properties of the proposed estimators to a general quantile regression model.

We propose to estimate $(\beta ,\gamma )$ by minimizing

$$L_n(\beta ,\gamma )=\frac{1}{n}\sum _{i=1}^{n}M\left[Y_i-\phi \left(X_i;\gamma \right)-\left\{A_i-\pi \left(X_i\right)\right\}C\left(X_i;\beta \right)\right],$$ (2)

where $M(\cdot )$ is a nonnegative convex function with the minimum achieved at $0,\text{and}\phi (X;\gamma )$ is a posited parametric function for $h_0(X)+\pi (X)C\left(X;{\beta }_0\right),$ but is not required to be correctly specified, such as a linear function. Denote the minimizer of (2) by $\left({\widehat{\beta }}_M^R,{\widehat{\gamma }}_M^R\right).$ The estimated optimal individualized treatment rule is then ${\widehat{g}}_M^R(x)\triangleq I\left\{C\left(x;{\widehat{\beta }}_M^R\right)>0\right\}.$ In the following, we refer the robust regression with loss function $M(\cdot )$ as RR(M)-learning. In this article, we consider the following three types of loss functions, i.e., the pinball loss

$$M(x)={\rho }_{\tau }(x)\triangleq \{\begin{array}{ll}(\tau -1)x,\hfill & \text{if}x<0\hfill \\ \tau x,\hfill & \text{if}x\ge 0\hfill \end{array}$$

where $0<\tau <1,$ the Huber loss

$$M(x)=H_{\alpha }(x)\triangleq \{\begin{array}{ll}0.5x^2,\hfill & \text{if}\left|x\right|<\alpha \hfill \\ \alpha \left|x\right|-0.5{\alpha }^2,\hfill & \text{if}\left|x\right|\ge \alpha \hfill \end{array}$$

for some $\alpha >0,$ and the $ϵ$-insensitive loss

$$M(x)=J_{ϵ}(x)\triangleq \max (0,|x|-ϵ)$$

for some $ϵ>0.$

The pinball loss is frequently applied to quantile regression, ¹² and the Huber and $ϵ$-insensitive losses are robust against heavy tailed errors or outliers. We will prove in the following section that under model (1) and the conditional independence error assumption, RR(M)-learning methods with these three loss functions all consistently estimate $g_0^{\text{opt}}$ which maximizes both the mean-based value and the conditional quantile-based value. When the conditional independence error assumption is not satisfied, it is hard to characterize the optimal individualized treatment rules obtained by RR(M)-learning with the Huber and $ϵ$-insensitive losses. However, for the RR(M)-learning with the pinball loss, we can prove that the solution approximately maximizes the $\tau \text{th}$ conditional quantile of the potential outcome. A dramatic different feature of pinball loss, Huber loss and $ϵ$-insensitive loss, when compared with the square loss, is that they penalize large deviances linearly instead of quadratically. This property makes them more robust when dealing with responses with non-normal type of errors. In next two sections, we will study theoretical and numerical properties of each of the three estimators.

3 |. ASYMPTOTIC PROPERTIES

For simplicity of presentation, throughout this section we assume that the propensity score π(x) is known, which is usually true in randomized clinical trials. However, the established asymptotic results can be easily extended to the case when the posited model for the propensity score π(x) is correctly specified and consistently estimated from data.

3.1 |. Consistency of Robust Regression: Pinball Loss

We first establish consistency of the robust regression estimator obtained from the pinball loss in the following Theorem.

Theorem 1. Under regularity conditions (C1)-(C8) in the Supplementary Appendix A, ${\widehat{\beta }}_{\rho (\tau )}^R$ converges in probability to ${\beta }_0$ for any $\tau \in (0,1),\text{where}{\widehat{\beta }}_{\rho (\tau )}^R$ is the solution to (2) with $M(x)={\rho }_{\tau }(x).$

Remark 1. The proof of Theorem 1 is given in the Supplementary Appendix A. Theorem 1 does not require the finiteness of E(Y), and therefore it can be applied to the case when ${ϵ}_i$ follows a Cauchy distribution. In addition, the conditional independence error assumption (C2), i.e. ${ϵ}_i\perp A_i|X_i,$ can be tested by various conditional independence tests developed in the literature, for example, see the Reference List.^{14,15,16,17,18} In Section 5, we will demonstrate usefulness of the test by applying the kernel-based conditional independence test (KCI-test).¹⁸ Since the KCI-test does not assume functional forms among variables, it suits our need.

When the conditional independence error assumption does not hold, ${\widehat{\beta }}_{\rho (\tau )}^R$ may no longer be a consistent estimator of ${\beta }_0.$ One intuitive explanation for this is that the error term $ϵ$ may contain extra information with respect to the interaction between A and X. In fact, a general result which can be derived for this case is that, $\left\{{\widehat{\beta }}_{\rho (\tau )}^R,{\widehat{\gamma }}_{\rho (\tau )}^R\right\}$ minimizes a weighed mean-square error loss function with the specification error.^19,20

To do this, we consider a general quantile regression model. Specifically, we assume the conditional $\tau \text{th}$ quantile of Y given A and X is given by $Q_{\tau }(X,A)=h_{0,\tau }(X)+AC\left\{X;{\beta }_0(\tau )\right\},\text{where}{h}_{0,\tau }(x)$ is an unspecified baseline function and $C\left\{X;{\beta }_0(\tau )\right\}$ is the contrast function with respect to the $\tau \text{th}$ quantile. Note that we use ${\beta }_0(\tau )$ instead of ${\beta }_0$ to emphasize that the true $\beta$ may vary with respect to $\tau .$ Define $\widehat{Q}(\beta ,\gamma )=\phi (X;\gamma )+\{A-\pi (X)\}C(X;\beta ).$ Let

$$\{\beta (\tau ),\gamma (\tau )\}=\underset{\beta ,\gamma }{\text{argmin}}E\left[{\rho }_{\tau }\{Y-\widehat{Q}(\beta ,\gamma )\}-{\rho }_{\tau }\left\{Y-\widehat{Q}\left({\beta }^{\prime },{\gamma }^{\prime }\right)\right\}\right],$$ (3)

where $\left({\beta }^{\prime },{\gamma }^{\prime }\right)$ is any fixed point in the parameter space $\mathcal{B}\times \Gamma .$ Define the specification error as ${\Delta }_{\tau }(X,A;\beta ,\gamma )\triangleq \widehat{Q}(\beta ,\gamma )-Q_{\tau }(X,A).$ Moreover, define the quantile-specific residual as ${ϵ}_{\tau }\triangleq Y-Q_{\tau }(X,A)$ with the conditional density function $f_{{ϵ}_{\tau }}(\cdot |X,A).$ Then we have the following approximation theorem.

Theorem 2. Suppose that (i) the conditional density $f_Y(y|X,A)$ exists a.s.; (ii) $E\left\{Q_{\tau }(X,A)\right\}\text{and}E\left\{{\Delta }_{\tau }^2(X,A;\beta ,\gamma )\right\}$ are finite; and (iii) $\{\beta (\tau ),\gamma (\tau )\}$ uniquely solves (3). Then

$$\{\beta (\tau ),\gamma (\tau )\}=\underset{\beta ,\gamma }{\text{argmin}}E\left\{w_{\tau }(X,A;\beta ,\gamma ){\Delta }_{\tau }^2(X,A;\beta ,\gamma )\right\},$$

where

$$w_{\tau }(X,A;\beta ,\gamma )={\int }_0^1(1-u)f_{{ϵ}_r}\left\{u{\Delta }_{\tau }(X,A;\beta ,\gamma )|X,A\right\}du.$$

Remark 2. The proof of Theorem 2 follows that of Theorem 1 in Angrist et al¹⁹ and is thus omitted for brevity. Theorem 2 shows that $\widehat{Q}\{\beta (\tau ),\gamma (\tau )\}$ is a weighted least square approximation to $Q_{\tau }(X,A).$ In other words, $\phi \{X;\gamma (\tau )\}+\{A-\pi (X)\}C\{X;\beta (\tau )\}$ is close to $h_{0,\tau }(X)+AC\left\{X;{\beta }_0(\tau )\right\}.$ Therefore, even though $\beta (\tau )\text{and}{\beta }_0(\tau )$ are not exactly the same, the difference between them is small in general. This coupled with the fact that ${\widehat{\beta }}_{\rho (\tau )}^R$ converges in probability to $\beta (\tau )$ (proved in Theorem 4), leads to the finding that the estimated optimal individualized treatment rule ${\widehat{g}}_{\rho (\tau )}^R(x)\triangleq I\left\{C\left(x;{\widehat{\beta }}_{\rho (\tau )}^R\right)>0\right\}$ maximizes the $\tau \text{th}$ conditional quantile approximately. This observation is justified numerically later in Supplementary Appendix B. When there exists ${\gamma }_0\in \Gamma$ such that $\phi \left(x;{\gamma }_0\right)=h_{0,\tau }(x)+\pi (x)C\left\{x;{\beta }_0(\tau )\right\},\text{we have}\beta (\tau )={\beta }_0(\tau ).$

3.2 |. Consistency of Robust Regression: Other Losses

Under model (1) and the assumption $ϵ\perp A|X,$ similar consistency results can be established for Huber loss and the $ϵ$-insensitive loss, as stated in Theorem 3.

Theorem 3. Under regularity conditions (C1)-(C8) given in the Supplementary Appendix A, we have

• (a)${\widehat{\beta }}_{H(\alpha )}^R$ converges in probability to ${\beta }_0$ for all $\alpha >0,$ where ${\widehat{\beta }}_{H(\alpha )}^R$ is the solution of (2) with $M(x)=H_{\alpha }(x);$
• (b)${\widehat{\beta }}_{J(ϵ)}^R$ converges in probability to ${\beta }_0$ for all $ϵ>0,$ where ${\widehat{\beta }}_{J(ϵ)}^R$ is the solution of (2) with $M(x)=J_{ϵ}(x).$

3.3 |. Asymptotic Normality: Pinball Loss

Without loss of generality, in this section we assume both functions $\phi (X;\gamma )\text{and}C(X;\beta )$ take a linear form: $\phi (X;\gamma )={\tilde{X}}^{\text{T}}\gamma \text{and}C(X;\beta )={\tilde{X}}^{\text{T}}\beta ,\text{where}\tilde{X}={\left(1,X^{\text{T}}\right)}^{\text{T}}.\text{Let}\widehat{\beta }(\tau )={\widehat{\beta }}_{\rho (\tau )}^R\text{and}\widehat{\gamma }(\tau )={\widehat{\gamma }}_{\rho (\tau )}^R.$ Define $W=[A-\pi (x){\tilde{X}}^T,{\tilde{X}}^T{]}^T,\theta (\tau )={\left\{\beta (\tau {)}^T,\gamma (\tau {)}^T\right\}}^T,\hat{\theta }(\tau )={\{\hat{\beta }(\tau {)}^T,\hat{\gamma }(\tau {)}^T\}}^T\text{and}J(\tau )\triangleq E[f_Y\{W^T\theta (\tau )\mid X,A\}W{W}^T]$ Under the following regularity conditions, similar to those assumed in Angrist et al¹⁹ and Lee,²⁰ we establish the asymptotic normality of $\widehat{\theta }(\tau )$ in Theorem 4.

• (B1)$\left\{\left(Y_i,X_i,A_i,{ϵ}_i\right),i=1,\dots ,n\right\}$ are independent and identically distributed random variables;
• (B2)The conditional density function $f_y(y|X=x,A=a)$ exists, and it is bounded and uniformly continuous in y and x;
• (B3)$J(\tau )$ is positive definite for all $\tau \in (0,1),\text{where}\theta (\tau )$ is uniquely defined in (3);
• (B4)$E\left(\Vert X{\Vert }^{2+ϵ}\right)<\infty$ for some $ϵ>0.$

Theorem 4. Suppose regularity conditions (B1)-(B4) hold. Then, we have

1. (Uniform Consistency) ${\underset{}{\sup }}_{\tau }\Vert \widehat{\theta }(\tau )-\theta (\tau )\Vert =o_p(1);$

2. (Asymptotic Normality) $J(\cdot )\sqrt{n}\{\widehat{\theta }(\cdot )-\theta (\cdot )\}$ converges in distribution to a zero mean Gaussian process with covariance function $\Sigma \left(\tau ,{\tau }^{\prime }\right)$ defined as

$$\Sigma \left(\tau ,{\tau }^{\prime }\right)=E\left(\left[\tau -I\left\{Y<W^{\text{T}}\theta (\tau )\right\}\right]\left[{\tau }^{\prime }-I\left\{Y<W^{\text{T}}\theta \left({\tau }^{\prime }\right)\right\}\right]W{W}^{\text{T}}\right).$$

The proof of Theorem 4 is similar to Angrist et al¹⁹ and so omitted here. The asymptotic covariance matrix of $\widehat{\theta }(\tau )$ can be estimated by either a bootstrap procedure²¹ or a nonparametric kernel method.¹⁹ Here, we adopt the bootstrap approach to estimate the asymptotic covariance matrix in Section 5. Under model (1), the results of Theorem 4 can be further simplified, as given in Theorem 5.

Theorem 5. Assume conditions of Theorem 4 hold. Under model (1) with the conditional independence error assumption, we have

1. ${\sup }_{\tau }\Vert \widehat{\beta }(\tau )-{\beta }_0\Vert =o_p(1);$

2. $\sqrt{n}\left\{\widehat{\beta }(\tau )-{\beta }_0\right\}$ converges in distribution to $N\left\{0,J_{11}^{-1}(\tau ){\Sigma }_{11}(\tau ,\tau )J_{11}^{-1}(\tau )\right\},$ where

$$J_{11}(\tau )=E\left[f_{ϵ}\left\{{\tilde{X}}^{\text{T}}\gamma (\tau )-{\phi }_0(X)|X\right\}\pi (X)\{1-\pi (X)\}\tilde{X}{\tilde{X}}^{\text{T}}\right],$$

$${\Sigma }_{11}(\tau ,\tau )=E\left({\left[\tau -I\left\{ϵ<{\tilde{X}}^{\text{T}}\gamma (\tau )-{\phi }_0(X)\right\}\right]}^2\pi (X)\{1-\pi (X)\}\tilde{X}{\tilde{X}}^{\text{T}}\right).$$

Furthermore, we have ${\Sigma }_{11}(\tau ,\tau )\le \left[\min \left\{{\tau }^2,{(1-\tau )}^2\right\}+0.25\right]E\left[\pi (X)\{1-\pi (X)\}\tilde{X}{\tilde{X}}^{\text{T}}\right].$

The proof of Theorem 5 is given in the Supplementary Appendix A. When compared with the mean-based estimator, the established asymptotic distribution of $\widehat{\beta }(\tau )$ yields interesting insights. Specifically, the mean-based estimators ${\widehat{\beta }}_{LS}^A\text{and}{\widehat{\gamma }}_{LS}^A$ are the minimizer of

$$\frac{1}{n}\sum _{i=1}^n{\left[Y_i-\phi \left(X_i;\gamma \right)-\left\{A_i-\pi \left(X_i\right)\right\}C\left(X_i;\beta \right)\right]}^2,$$

and the estimated optimal individualized treatment rule is then ${\widehat{g}}_{LS}^A(x)\triangleq I\left\{C\left(x;{\widehat{\beta }}_{LS}^A\right)>0\right\}.$ We refer to this method as the least square A-learning (lsA-learning). Under model (1) with the conditional independence error assumption $ϵ\perp A|X$ and the assumption that $E(ϵ|X,A)$ exists, or more general the condition $E(Y|X,A)=h_0(X)+AC\left(X,{\beta }_0\right),$ it can be shown that $\left({\widehat{\beta }}_{LS}^A,{\widehat{\gamma }}_{LS}^A\right)$ converges in probability to $\left({\beta }_0,{\gamma }^{*}\right)={\text{argmin}}_{(\beta ,\gamma )}E{[Y-\phi (X;\gamma )-\{A-\pi (X)\}C(X,\beta )]}^2,\text{and}{\widehat{g}}_{LS}^A$ is a consistent estimator of $g_{\mu }^{\text{opt}}.$ The asymptotic normality of ${\widehat{\beta }}_{LS}^A$ is summarized in Theorem 6. Its proof is omitted, and readers are referred to Lu et al.²²

Theorem 6. Under regularity conditions (A1)-(A4) of Lu et al²², we have $\sqrt{n}\left({\widehat{\beta }}_{LS}^A-{\beta }_0\right)$ converges in distribution to $N\left(0,U_{11}^{-1}{\Omega }_{11}{U}_{11}^{-1}\right),\text{where}{U}_{11}=E\left[\pi (X)\{1-\pi (X)\}\tilde{X}{\tilde{X}}^{\text{T}}\right]$ and

$${\Omega }_{11}=E\left[{\left\{h_0(X)+\pi (X)C\left(X;{\beta }_0\right)-\phi \left(X;{\gamma }^{*}\right)+ϵ\right\}}^2\pi (X)\{1-\pi (X)\}\tilde{X}{\tilde{X}}^{\text{T}}\right].$$

Remark 3. When the family of functions $\{\phi (x;\gamma ),\gamma \in \Gamma \}$ cannot well approximate the function $h_0(x)+\pi (x)C\left(x;{\beta }_0\right),$ the term ${\Omega }_{11}$ in the asymptotic variance of ${\widehat{\beta }}_{LS}^A$ may explode, which makes ${\widehat{\beta }}_{LS}^A$ less efficient than $\widehat{\beta }(\tau ).$

In summary, the robust regression with the pinball loss has nice theoretical properties and interpretation even when the conditional independence error assumption does not hold. However, we do not have such good properties for robust regression with Huber and the e-insensitive loss. Therefore we recommend the use of the pinball loss in practice.

4 |. NUMERICAL RESULTS: SIMULATION STUDIES

We consider the following two models with p = 3.

• Model I:

$$Y_i=1+\left(X_{i1}-X_{i2}\right)\left(X_{i1}+X_{i3}\right)+\left\{A_i-\pi \left(X_i\right)\right\}{\beta }_0^T{\tilde{X}}_i+\sigma \left(X_i\right){ϵ}_i,$$

where $X_i={\left(X_{i1},X_{i2},X_{i3}\right)}^{\text{T}}$ are multivariate normal with mean zero, variance one, and $\text{Corr}\left(X_{ij},X_{ik}\right)={0.5}^{|j-k|},{\tilde{X}}_i={\left(1,X_i^{\text{T}}\right)}^{\text{T}}\text{and}{\beta }_0={(0,1,-1,1)}^{\text{T}}.$

• Model II:

$$Y_i={\gamma }_0^{\text{T}}{\tilde{X}}_i+\left\{A_i-\pi \left(X_i\right)\right\}{\beta }_0^{\text{T}}{\tilde{X}}_i+\sigma \left(X_i\right){ϵ}_i,$$

where ${\gamma }_0^{\text{T}}=(0.5,4,1,-3),\text{and}{X}_i,{\tilde{X}}_i\text{and}{\beta }_0$ are the same as Model I.

The propensity score model $\pi (\cdot )$ is assumed known. Here, we consider both the constant case $\pi \left(X_i\right)=0.5$ and the non-constant case $\pi \left(X_i\right)=logit\left(X_{i1}-X_{i2}\right).$ For the non-constant case, it is estimated from the data based on the standard logistic regression. In addition, we consider two different $\sigma \left(X_i\right)$ functions, i.e., the homogeneous case with $\sigma \left(X_i\right)=1,$ and the heterogeneous case with $\sigma \left(X_i\right)=0.5+{\left(X_{i1}-X_{i2}\right)}^2.$ In our implementation, we consider linear functions for both the baseline mean and the contrast function, i.e., $\phi (X;\gamma )={\gamma }^{\text{T}}\tilde{X}\text{and}C(X;\beta )={\beta }^{\text{T}}\tilde{X}.$ We report the results of Model I and II with the constant propensity score in Tables 1 and 2 , respectively. The corresponding results for the non-constant propensity score are reported in Tables 3 and 4 , respectively.

TABLE 1.

Simulation results for Model I with the constant propensity score.

Homogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	1.32 (0.040)	80.7	1.06	2.36 (0.081)	75.7	1.57		58.4	3.75
	p(0.5)	1.44 (0.042)	80.1	1.13	1.73 (0.051)	78.0	1.31	2.69 (0.077)	75.2	1.63
	p(0.25)	1.90 (0.057)	78.3	1.34	1.63 (0.051)	79.0	1.29	5.29 (0.168)	70.4	2.25
	Huber	1.15 (0.034)	81.9	0.93	1.45 (0.044)	79.9	1.13	2.61 (0.072)	74.9	1.66
200	LS	0.68 (0.021)	85.6	0.59	1.10(0.033)	82.0	0.91		58.7	3.70
	p(0.5)	0.73 (0.021)	85.3	0.62	0.78 (0.021)	84.1	0.70	1.23 (0.037)	81.3	0.99
	p(0.25)	0.92 (0.028)	84.0	0.75	0.70 (0.023)	86.0	0.59	2.48 (0.079)	75.7	1.64
	Huber	0.58 (0.017)	86.8	0.50	0.66 (0.018)	85.5	0.58	1.24 (0.035)	80.8	1.03
400	LS	0.33 (0.009)	90.3	0.26	0.56 (0.016)	87.1	0.46		59.2	3.61
	p(0.5)	0.35 (0.010)	90.0	0.29	0.37 (0.010)	89.0	0.34	0.56 (0.016)	87.1	0.48
	p(0.25)	0.43 (0.013)	89.1	0.34	0.33 (0.010)	90.7	0.25	1.16(0.037)	82.9	0.86
	Huber	0.28 (0.008)	91.1	0.22	0.31 (0.009)	90.2	0.27	0.58 (0.017)	86.7	0.49
800	LS	0.17 (0.005)	93.2	0.13	0.26 (0.008)	90.9	0.23		59.4	3.59
	p(0.5)	0.17 (0.005)	93.1	0.13	0.19 (0.005)	92.1	0.17	0.29 (0.009)	90.7	0.24
	p(0.25)	0.22 (0.007)	92.4	0.16	0.18 (0.006)	93.6	0.12	0.59 (0.019)	87.3	0.48
	Huber	0.14 (0.004)	93.8	0.11	0.16 (0.005)	93.1	0.14	0.29 (0.008)	90.5	0.25
Heterogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	3.24 (0.110)	74.7	1.70	8.98 (0.561)	68.6	2.44		56.2	4.05
	p(0.5)	1.70 (0.060)	80.5	1.08	1.80 (0.064)	80.1	1.08	3.45 (0.124)	75.1	1.69
	p(0.25)	2.50 (0.085)	77.4	1.42	2.51 (0.079)	76.8	1.46	9.13(0.341)	67.2	2.66
	Huber	1.70 (0.057)	80.4	1.10	1.87 (0.063)	79.2	1.16	4.27 (0.155)	72.8	1.93
200	LS	1.54 (0.050)	80.6	1.06	4.71 (0.244)	73.4	1.85		55.2	4.17
	p(0.5)	0.78 (0.028)	86.7	0.53	0.90 (0.032)	85.3	0.63	1.49 (0.052)	81.9	0.95
	p(0.25)	1.16(0.039)	83.5	0.81	1.23 (0.039)	82.0	0.91	3.95 (0.150)	73.2	1.90
	Huber	0.77 (0.025)	86.4	0.55	0.94 (0.032)	84.5	0.69	1.94 (0.071)	79.3	1.19
400	LS	0.80 (0.026)	86.0	0.58	2.69 (0.136)	77.8	1.34		54.7	4.26
	p(0.5)	0.39 (0.013)	90.5	0.27	0.44 (0.017)	89.6	0.32	0.71 (0.024)	86.9	0.50
	p(0.25)	0.56 (0.019)	88.8	0.37	0.66 (0.020)	86.9	0.50	1.70 (0.055)	79.6	1.17
	Huber	0.38 (0.012)	90.4	0.27	0.48 (0.017)	88.8	0.36	0.91 (0.029)	84.9	0.65
800	LS	0.41 (0.013)	89.9	0.29	1.35 (0.150)	83.1	0.82		56.5	4.00
	p(0.5)	0.18 (0.006)	93.6	0.12	0.20 (0.007)	92.6	0.16	0.36 (0.013)	91.0	0.25
	p(0.25)	0.28 (0.009)	92.2	0.18	0.31 (0.010)	90.8	0.24	0.89 (0.031)	85.8	0.60
	Huber	0.19 (0.006)	93.3	0.13	0.22 (0.007)	92.1	0.18	0.47 (0.017)	89.2	0.34

LS stands for lsA-learning. P(0.5) stands for robust regression with pinball loss and parameter τ = 0.5. P(0.25) stands for robust regression with pinball loss and parameter τ = 0.25. Huber stands for robust regression with Huber loss, where parameter α is tuned automatically with R function rlm. Column δ_{0 5} is multiplied by 10.

TABLE 2.

Simulation results for Model II with the constant propensity score.

Homogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	0.24 (0.006)	91.1	0.21	1.23 (0.061)	82.4	0.87		58.6	3.73
	P(0.5)	0.36 (0.010)	89.0	0.32	0.39 (0.012)	88.8	0.34	0.80 (0.024)	84.2	0.69
	P(0.25)	0.45 (0.012)	87.8	0.40	0.13 (0.004)	93.4	0.12	2.37 (0.083)	76.0	1.49
	Huber	0.25 (0.007)	90.8	0.22	0.31 (0.010)	90.3	0.26	0.99 (0.029)	82.4	0.84
200	LS	0.11 (0.003)	93.7	0.10	0.52 (0.018)	87.3	0.45		58.7	3.69
	P(0.5)	0.17 (0.005)	92.4	0.16	0.17 (0.005)	92.4	0.15	0.32 (0.009)	89.5	0.30
	P(0.25)	0.20 (0.005)	91.8	0.18	0.06 (0.002)	95.6	0.05	1.03 (0.033)	82.1	0.88
	Huber	0.12 (0.003)	93.6	0.11	0.13 (0.003)	93.5	0.12	0.43 (0.013)	87.9	0.40
400	LS	0.05 (0.001)	95.7	0.05	0.26 (0.008)	90.7	0.23		59.4	3.60
	P(0.5)	0.09 (0.002)	94.5	0.08	0.09 (0.002)	94.5	0.08	0.15 (0.004)	92.8	0.14
	P(0.25)	0.10 (0.002)	94.2	0.09	0.03 (0.001)	96.9	0.02	0.44 (0.012)	87.9	0.39
	Huber	0.06 (0.001)	95.5	0.05	0.06 (0.002)	95.4	0.06	0.21 (0.006)	91.6	0.19
800	LS	0.03 (0.001)	96.9	0.03	0.13 (0.004)	93.5	0.11		59.4	3.58
	P(0.5)	0.04 (0.001)	96.1	0.04	0.04 (0.001)	96.2	0.04	0.07 (0.002)	95.1	0.06
	P(0.25)	0.05 (0.001)	95.8	0.05	0.01 (0.000)	97.9	0.01	0.20 (0.005)	91.5	0.19
	Huber	0.03 (0.001)	96.8	0.03	0.03 (0.001)	96.8	0.03	0.10 (0.002)	94.2	0.09
Heterogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	1.97 (0.072)	79.8	1.13	7.75 (0.514)	70.4	2.22		56.4	4.02
	P(0.5)	0.84 (0.029)	86.1	0.55	1.21 (0.045)	84.3	0.74	1.82 (0.071)	80.5	1.07
	P(0.25)	1.37 (0.049)	82.1	0.90	1.56 (0.051)	80.5	1.04	6.20 (0.261)	69.8	2.25
	Huber	0.84 (0.031)	85.9	0.57	1.33 (0.046)	82.8	0.85	2.69 (0.106)	77.0	1.42
200	LS	0.99 (0.035)	84.7	0.66	4.16 (0.237)	75.2	1.62		55.1	4.19
	P(0.5)	0.41 (0.014)	90.2	0.28	0.58 (0.024)	89.4	0.37	0.79 (0.030)	86.7	0.52
	P(0.25)	0.64 (0.021)	87.4	0.45	0.74 (0.024)	86.1	0.54	2.48 (0.096)	76.9	1.40
	Huber	0.39 (0.013)	90.3	0.27	0.69 (0.027)	87.7	0.45	1.17(0.044)	83.4	0.78
400	LS	0.51 (0.018)	89.0	0.35	2.48 (0.133)	79.3	1.20		54.7	4.25
	P(0.5)	0.20 (0.007)	93.2	0.14	0.29 (0.011)	92.6	0.17	0.32 (0.011)	91.2	0.22
	P(0.25)	0.30 (0.009)	91.3	0.22	0.39 (0.012)	89.9	0.28	0.99 (0.030)	83.0	0.78
	Huber	0.20 (0.007)	93.2	0.14	0.34 (0.012)	91.4	0.22	0.53 (0.016)	88.4	0.37
800	LS	0.25 (0.008)	92.2	0.17	1.25 (0.159)	84.2	0.73		56.4	4.00
	P(0.5)	0.10 (0.004)	95.3	0.07	0.14 (0.006)	94.7	0.09	0.16 (0.006)	93.9	0.11
	P(0.25)	0.14 (0.005)	94.0	0.10	0.18 (0.006)	92.9	0.14	0.49 (0.015)	88.0	0.39
	Huber	0.09 (0.004)	95.3	0.06	0.17 (0.006)	93.9	0.11	0.26 (0.009)	91.8	0.19

LS stands for lsA-learning. P(0.5) stands for robust regression with pinball loss and parameter τ = 0.5. P(0.25) stands for robust regression with pinball loss and parameter τ = 0.25. Huber stands for robust regression with Huber loss, where parameter α is tuned automatically with R function rlm. Column δ_{0 5} is multiplied by 10.

TABLE 3.

Simulation results for Model I with the non-constant propensity scores.

Homogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	1.70 (0.061)	81.9	0.91	2.90 (0.114)	77.6	1.34		59.3	3.61
	P(0.5)	1.90 (0.069)	80.1	1.09	2.13 (0.073)	78.3	1.25	3.54 (0.128)	75.7	1.57
	P(0.25)	2.35 (0.080)	78.2	1.33	1.95 (0.076)	80.4	1.08	8.45 (0.431)	69.8	2.28
	Huber	1.51 (0.053)	82.1	0.89	1.77 (0.065)	80.6	1.02	3.67 (0.127)	75.4	1.60
200	LS	0.77 (0.026)	86.8	0.50	1.35(0.045)	82.2	0.91		59.2	3.63
	P(0.5)	0.88 (0.028)	85.5	0.60	1.00 (0.029)	83.0	0.79	1.54 (0.050)	81.1	1.00
	P(0.25)	1.06 (0.035)	84.5	0.68	0.83 (0.027)	85.9	0.59	3.61 (0.143)	74.7	1.70
	Huber	0.68 (0.022)	87.3	0.46	0.81 (0.025)	85.2	0.62	1.58 (0.052)	80.7	1.03
400	LS	0.39 (0.012)	90.2	0.28	0.65 (0.020)	86.9	0.48		58.0	3.79
	P(0.5)	0.43 (0.013)	89.3	0.32	0.47 (0.014)	88.4	0.38	0.73 (0.022)	86.5	0.51
	P(0.25)	0.53 (0.016)	88.5	0.38	0.41 (0.013)	90.5	0.27	1.50 (0.049)	81.7	0.96
	Huber	0.34 (0.010)	90.6	0.25	0.39(0.012)	89.6	0.30	0.72 (0.022)	86.3	0.53
800	LS	0.18 (0.006)	93.3	0.13	0.32 (0.010)	90.2	0.27		58.3	3.75
	P(0.5)	0.21 (0.007)	92.7	0.15	0.24 (0.007)	91.5	0.20	0.36(0.011)	90.3	0.27
	P(0.25)	0.28 (0.009)	92.4	0.17	0.21 (0.007)	93.4	0.13	0.78 (0.026)	86.9	0.50
	Huber	0.16 (0.005)	93.7	0.11	0.19(0.006)	92.6	0.15	0.37 (0.010)	89.9	0.28
Heterogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	2.84 (0.111)	78.2	1.33	9.96 (0.773)	72.0	2.06		55.2	4.18
	P(0.5)	2.01 (0.082)	80.6	1.09	2.18 (0.080)	79.2	1.21	4.18(0.189)	74.1	1.81
	P(0.25)	2.91 (0.110)	76.7	1.52	3.22 (0.105)	74.2	1.76	10.62 (0.475)	65.3	2.87
	Huber	1.90 (0.074)	80.9	1.06	2.38 (0.090)	78.1	1.32	5.06 (0.230)	71.9	2.04
200	LS	1.46 (0.053)	83.1	0.83	4.47 (0.371)	76.8	1.51		56.3	4.04
	P(0.5)	0.92 (0.033)	86.4	0.55	0.98 (0.035)	85.3	0.64	1.69 (0.065)	81.5	0.98
	P(0.25)	1.35 (0.049)	83.3	0.81	1.47 (0.049)	81.6	0.97	4.73 (0.241)	71.9	2.05
	Huber	0.86 (0.030)	86.6	0.52	1.02 (0.036)	84.7	0.68	2.11 (0.079)	79.3	1.18
400	LS	0.74 (0.029)	87.4	0.47	2.65 (0.402)	81.4	1.04		56.2	4.06
	P(0.5)	0.45 (0.016)	90.2	0.29	0.44 (0.017)	89.5	0.34	0.79 (0.029)	87.2	0.49
	P(0.25)	0.66 (0.025)	88.3	0.41	0.70 (0.023)	86.9	0.50	2.12(0.091)	79.5	1.19
	Huber	0.43 (0.016)	90.2	0.28	0.48 (0.018)	89.0	0.36	1.01 (0.036)	85.0	0.65
800	LS	0.36 (0.013)	90.8	0.25	1.09 (0.066)	85.0	0.69		56.3	4.02
	P(0.5)	0.21 (0.008)	93.2	0.14	0.24 (0.009)	92.3	0.19	0.39 (0.014)	90.5	0.27
	P(0.25)	0.33 (0.013)	91.7	0.21	0.36(0.012)	90.8	0.25	1.01 (0.034)	84.9	0.65
	Huber	0.20 (0.008)	93.2	0.14	0.25 (0.009)	92.1	0.19	0.49 (0.016)	89.1	0.34

LS stands for lsA-learning. P(0.5) stands for robust regression with pinball loss and parameter τ = 0.5. P(0.25) stands for robust regression with pinball loss and parameter τ = 0.25. Huber stands for robust regression with Huber loss, where parameter α is tuned automatically with R function rlm. Column δ_0.5 is multiplied by 10.

TABLE 4.

Simulation results for Model II with non-constant propensity scores.

Homogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	0.36(0.011)	89.8	0.29	1.65 (0.085)	80.8	1.06		58.7	3.69
	P(0.5)	0.57 (0.017)	86.9	0.46	0.61 (0.026)	86.4	0.55	1.31 (0.045)	81.7	0.93
	P(0.25)	0.65 (0.020)	86.2	0.52	0.22 (0.008)	91.7	0.20	4.67 (0.312)	74.7	1.64
	Huber	0.38 (0.012)	89.5	0.30	0.45 (0.018)	88.3	0.40	1.70 (0.060)	79.5	1.14
200	LS	0.16 (0.004)	92.9	0.14	0.74 (0.030)	85.6	0.61		59.1	3.64
	P(0.5)	0.25 (0.007)	91.2	0.21	0.26 (0.008)	90.7	0.24	0.52 (0.017)	87.8	0.41
	P(0.25)	0.30 (0.008)	90.3	0.26	0.09 (0.003)	94.8	0.08	1.69 (0.074)	81.3	0.92
	Huber	0.17 (0.005)	92.8	0.14	0.19 (0.006)	92.2	0.17	0.70 (0.022)	86.2	0.53
400	LS	0.08 (0.002)	95.1	0.06	0.36 (0.013)	89.7	0.30		58.0	3.79
	P(0.5)	0.12 (0.003)	93.8	0.10	0.12 (0.003)	93.8	0.10	0.22 (0.006)	91.6	0.19
	P(0.25)	0.14 (0.004)	93.3	0.12	0.04 (0.001)	96.5	0.03	0.63 (0.021)	86.5	0.49
	Huber	0.08 (0.002)	95.0	0.07	0.09 (0.002)	94.8	0.07	0.30 (0.009)	90.3	0.26
800	LS	0.04 (0.001)	96.5	0.03	0.18 (0.006)	92.3	0.16		58.2	3.76
	P(0.5)	0.06 (0.002)	95.6	0.05	0.06 (0.002)	95.6	0.05	0.10 (0.003)	94.4	0.09
	P(0.25)	0.07 (0.002)	95.3	0.06	0.02 (0.001)	97.5	0.02	0.29 (0.009)	90.6	0.23
	Huber	0.04 (0.001)	96.4	0.03	0.04 (0.001)	96.3	0.04	0.14 (0.004)	93.2	0.12
Heterogeneous Error
		Normal			Log-Normal			Cauchy
n	method	MSE	PCD	δ0.5	MSE	PCD	δ0.5	MSE	PCD	δ0.5
100	LS	1.45 (0.059)	82.9	0.85	8.53 (0.784)	72.4	2.01		54.9	4.22
	P(0.5)	0.94 (0.034)	85.6	0.61	1.29 (0.058)	83.3	0.86	2.27 (0.132)	78.9	1.24
	P(0.25)	1.46 (0.051)	81.5	0.96	1.78 (0.071)	78.2	1.30	7.88 (0.422)	68.1	2.46
	Huber	0.89 (0.034)	86.1	0.57	1.46 (0.067)	81.7	0.99	3.28 (0.157)	75.1	1.65
200	LS	0.84 (0.035)	86.6	0.53	3.85 (0.358)	77.6	1.43		55.9	4.09
	P(0.5)	0.44 (0.016)	90.0	0.29	0.60 (0.024)	89.0	0.39	0.87 (0.034)	86.3	0.56
	P(0.25)	0.69 (0.025)	87.0	0.49	0.75 (0.024)	85.5	0.59	3.08 (0.179)	75.3	1.58
	Huber	0.43 (0.016)	90.3	0.28	0.66 (0.025)	87.7	0.47	1.32 (0.050)	82.4	0.87
400	LS	0.44 (0.020)	90.3	0.28	2.34 (0.393)	82.4	0.95		55.9	4.09
	P(0.5)	0.23 (0.009)	92.9	0.16	0.28 (0.011)	92.5	0.19	0.39 (0.015)	90.8	0.26
	P(0.25)	0.33 (0.011)	91.0	0.23	0.36 (0.012)	90.1	0.27	1.25 (0.048)	82.8	0.82
	Huber	0.22 (0.008)	93.1	0.15	0.31 (0.012)	91.7	0.21	0.60 (0.022)	88.0	0.43
800	LS	0.23 (0.009)	93.0	0.15	0.90 (0.057)	86.2	0.60		56.3	4.03
	P(0.5)	0.11 (0.004)	95.0	0.07	0.14 (0.005)	94.8	0.09	0.18 (0.006)	93.6	0.12
	P(0.25)	0.17 (0.006)	93.7	0.12	0.18 (0.006)	93.0	0.14	0.59 (0.017)	87.3	0.44
	Huber	0.10 (0.004)	95.1	0.07	0.15 (0.006)	94.2	0.11	0.29 (0.010)	91.4	0.21

LS stands for lsA-learning. P(0.5) stands for robust regression with pinball loss and parameter τ = 0.5. P(0.25) stands for robust regression with pinball loss and parameter τ = 0.25. Huber stands for robust regression with Huber loss, where parameter α is tuned automatically with R function rlm. Column δ_0.5 is multiplied by 10.

We make comparisons among four methods: lsA-learning, robust regression with ${\rho }_{0.5}\left(\text{RR}\left({\rho }_{0.5}\right)\right),$ robust regression with ${\rho }_{0.25}\left(\text{RR}\left({\rho }_{0.25}\right)\right),$ and robust regression with Huber loss (RR(H)). The error terms ${ϵ}_i$ are standard independent and identically distribute normal, log-normal or Cauchy distribution, and they are independent with both A and X. It is easy to check that the conditional independence error assumption $ϵ\perp A|X$ is satisfied, and $g_{\mu }^{\text{opt}}=g_{\tau }^{\text{opt}}=I\left\{{\beta }_0^{\text{T}}{\tilde{X}}_i>0\right\}.$ We consider four different sample sizes 100, 200,400 and 800. To evaluate the performance of each method, we compare three groups of criteria: (1) the mean squared error ${\Vert \widehat{\beta }-{\beta }_0\Vert }_2^2(\text{MSE}),$ whichh measures the distance between estimated parameters and the true parameter ${\beta }_0;$ (2) the percentage of making correct decisions (PCD), which are calculated based on a validation set with 10,000 observations. Specifically, we take the formula $100*\left[1-{\sum }_{i=1}^{N_T}\left|I\left\{{\widehat{\beta }}^{\text{T}}{\tilde{X}}_i>0\right\}-I\left\{{\beta }_0^{\text{T}}{\tilde{X}}_i>0\right\}\right|/N_T\right]$ with N_T = 10000; (3) the differences of $V_{\mu }(g)\text{and}{V}_{0.5}(g)$ between the optimal individualized treatment rule and the estimated individualized treatment rule, where ${\delta }_{\mu }=V_{\mu }\left(g_{\mu }^{\text{opt}}\right)-V_{\mu }(\widehat{g})\text{and}{\delta }_{\tau }=V_{\tau }\left(g_{\tau }^{\text{opt}}\right)-V_{\tau }(\widehat{g}),\forall \tau \in (0,1).V_{\mu }(g)\text{and}{V}_{\tau }(g)$ (defined in Section 2.2) are estimated from the validation set as well, and they evaluate the overall performance of a treatment regime g, where the former one focuses on the response’s mean and the latter one focuses on the response’s conditional $\tau \text{th}$ quantile. Under our setting, ${\delta }_{\mu }={\delta }_{0.5}={\delta }_{0.25}$ when they all exists. Thus, only ${\delta }_{0.5}$ is reported. For each scenario, we run 1,000 replications and report the sample average in the tables. We further report the standard errors of MSE to evaluate the variability of the corresponding statistics.

The simulation results with the constant and non-constant propensity scores are similar, so we focus on the result based on constant propensity score. When comparing the performance of the methods under homogeneous and heterogeneous errors, we observe that lsA-learning works much worse under the heterogeneous errors, while all the other methods are generally less affected by the heterogeneity of the errors. When the baseline function is misspecified as in Model I, under the homogeneous normal errors, RR(H) works slightly better than lsA-learning, while $RR\left({\rho }_{0.25}\right)$ works the worst. However, the difference in general is small. For the homogeneous log-normal errors, again RR(H) works the best, while $RR\left({\rho }_{0.5}\right)$ and $RR\left({\rho }_{0.25}\right)$ have similar performance, and lsA-learning works the worst. Under the homogeneous Cauchy errors, $RR\left({\rho }_{0.5}\right)$ works the best and RR(H) has a similar performance. The lsA-learning is no longer consistent, and its MSE explodes. The actual numbers are too large and thus we leave as blank in Tables 1 and 2 . Furthermore, with the Cauchy errors, the PCD of lsA-learning is less than 60% under all scenarios, while other methods’ PCD can be as high as 90%. When the baseline function is correctly specified as in Model II, under homogeneous normal errors, lsA-learning performs the best. However, in this case RR(H) also has a very close performance, and thus makes no difference from a practical point of view to choose between these two methods. The results of Model II under other cases lead to similar conclusions as Model I.

We have also examined the performance of the proposed estimator $\text{RR}\left({\rho }_{\tau }\right)$ with extreme $\tau$ values $(\tau =0.1\text{or}0.9)$ for Model I with the constant propensity score. The results are provided in the Supplementary Appendix C. We find that the $\text{RR}\left({\rho }_{\tau }\right)$ with the extreme $\tau$ value works much worse than that with the $\tau$ value close to 0.5. Thus, we do not recommend using the pinball loss with the extreme $\tau$ value in practice. A reasonable range of $\tau$ may be from 0.2 to 0.8.

The overall conclusion is that, under the conditional independence error assumption, the proposed robust regression method RR(M) is more efficient than mean-based method lsA-learning in the circumstances when observations have skewed, heterogeneous, or heavy-tailed errors. On the other hand, when the error terms indeed follows independent and identically distributed normal distribution, the loss of efficiency of RR(M) is not significant. This is especially true when Huber loss is applied.

In addition, we have done some simulations under the situation that the error term does interacts with the treatment given covariates, and thus the conditional independence error assumption does not hold. The simulation settings and the associated results are provided in Supplementary Appendix B. We find that ${\widehat{g}}_{\rho (\tau )}^R\left(\triangleq I\left\{C\left(x;{\widehat{\beta }}_{\rho (\tau )}^R\right)>0\right\}\right)$ in general approximates the unknown optimal individualized treatment rule $g_{\tau }^{\text{opt}}$ even when the conditional independence error assumption $ϵ\perp A|X$ does not hold.

Last, we have compared our proposed method with the method of Wang et al,¹¹ which maximizes the marginal quantile by directly optimizing an estimate of the marginal quantile-based value function ${\tilde{V}}_{\tau }(g)=\inf \left\{y:F_{Y_i^{*}(g)}(y)\ge \tau \right\},$ and does not require to specify an outcome regression model. We find that, when the conditional independence error assumption is satisfied, both methods target on the same optimal individualized treatment rule, while our robust regression method generally gives better individualized treatment rules than Wang et al’s method in terms of PCD and value, especially when the sample size is relatively large $(n\ge 200).$ This is expected since our robust regression method make more use of the model information. When the conditional independence error assumption is not satisfied, the optimal individualized treatment rules that maximize the conditional quantile and that maximize the marginal quantile are different, and each method maximizes their own target value function. The simulation results and related discussions are provided in the Supplementary Appendix D.

5 |. APPLICATION TO AN AIDS STUDY

We illustrate the proposed robust regression methods to a data set from AIDS Clinical Trials Group Protocol 175 (ACTG175), which has been previously studied by various authors.^23,24,25,22 In the study, 2139 HIV-infected subjects were randomized to four different treatment groups with equal proportions, and the treatment groups are zidovudine (ZDV) monotherapy, ZDV + didanosine (ddI), ZDV + zalcitabine, and ddI monotherapy. Following Lu et al,²² we choose CD4 count (cells/mm³) at 20 ± 5 weeks post-baseline as the primary continuous outcome Y, and include five continuous covariates and seven binary covariates as our covariates. They are: 1. age (years), 2. weight (kg), 3. karnof=Karnofsky score (scale of 0–100), 4. cd40=CD4 count (cells/mm³) at baseline, 5. cd80=CD8 count (cells/mm³) at baseline, 6. hemophilia=hemophilia (0=no, 1=yes), 7. homo-sexuality=homosexual activity (0=no, 1=yes), 8. drugs=history of intravenous drug use (0=no, 1=yes), 9. race (0=white, 1=non-white), 10. gender (0=female, 1=male), 11. Str2= antiretroviral history (0=naive, 1=experienced), and 12. sympton=symptomatic status (0=asymptomatic, 1=symptomatic). For brevity, we only compare the treatment ZDV + didanosine (ddI) (A = 1) and ZDV + zalcitabine (A = 0), and restrict our samples to the subjects receiving these two treatments. Thus, the propensity scores $\pi \left(X_i\right)\equiv 0.5$ in our restricted samples as the patients are assigned into one of two treatments with equal probability.

In our analysis, we assume linear models for both the baseline and the contrast functions. For interpretability, we keep the response Y (the CD4 count) at its original scale, which is also consistent with the way clinicians think about the outcome in practice. ²⁴ We draw the scatter plot of response Y against age, which suggests some skewness and heterogeneity. With some preliminary analysis (fitting a full model with lsA-learning and the proposed robust regression methods, we find that only covariates age, homosexuality, and race may possibly interact with the treatment. So in our final model, only these three covariates are included in the contrast function, while we keep all of the twelve covariates in the baseline function. The estimated coefficients associated with their corresponding standard errors and p-values are given in Table 5 , where the standard errors are estimated with 1,000 bootstrap samples (parametric bootstrap) and p-values are calculated with the normal approximation. Only coefficients included in the contrast function are shown.

Table 5.

Analysis results for the AIDS dataset.

Variable	Least Square			Pinball(0.5)			Pinball(0.25)			Huber
	Est.	SE	PV	Est.	SE	PV	Est.	SE	PV	Est.	SE	PV
intercept	−42.61	32.93	0.196	−33.45	37.32	0.370	−35.77	39.17	0.361	−42.76	31.40	0.173
age	3.13	0.85	0.000	2.62	0.97	0.007	2.46	1.06	0.020	2.80	0.79	0.000
homosexuality	−40.66	16.73	0.015	−33.18	17.68	0.061	−35.38	18.28	0.053	−27.33	15.19	0.072
race	−25.70	17.69	0.146	−33.56	18.12	0.064	−34.21	18.32	0.062	−25.29	16.08	0.116

Est. stands for the estimate; SE stands for the standard error; PV stands for the p-value. All p-values which are significant at level 0.1 are highlighted.

From Table 5 , we make the following observations. First, lsA-learning and robust regression with the pinball loss and the Huber loss have estimates with the same signs for all the covariates. Second, the estimated coefficients are distinguishable across different methods. Third, the covairiate homosexuality is significant under lsA-learning, but not significant in robust regression using either the pinball loss or Huber loss, when the significant level α is set to 0.05.

We further estimate the values $\left(V_{\mu }(\widehat{g})\right)$ for each method by either the inverse probability weighted estimator (IPWE)²⁶ or the augmented inverse probability weighted estimator (AIPWE), ²⁷ where

$${\widehat{V}}_{\mu }^{\text{IPWE}}(\widehat{g})=\frac{{\sum }_{i=1}^{n}I\left\{A_i=\widehat{g}\left(X_i\right)\right\}{Y}_i/p\left(A_i|X_i\right)}{{\sum }_{i=1}^{n}I\left\{A_i=\widehat{g}\left(X_i\right)\right\}/p\left(A_i|X_i\right)},$$

$${\widehat{V}}_{\mu }^{\text{AlPWE}}(\widehat{g})=\frac{1}{n}\sum _{i=1}^n\widehat{E}\left(Y_i|X_i,\widehat{g}\left(X_i\right)\right)+\frac{1}{n}\sum _{i=1}^n\frac{I\left\{A_i=\widehat{g}\left(X_i\right)\right\}}{p\left(A_i|X_i\right)}\left\{Y_i-\widehat{E}\left(Y_i|X_i,A_i\right)\right\},$$

$\widehat{E}\left(Y_i|X_i,A_i\right)=\phi \left(X_i;\widehat{\gamma }\right)+\left\{A_i-p\left(A_i|X_i\right)\right\}C\left(X_i;\widehat{\beta }\right),$ and $p\left(A_i|X_i\right)\equiv \mathrm{0.5.}\text{Both}{\widehat{V}}_{\mu }^{\text{IPWE}}(\widehat{g})\text{and}{\widehat{V}}_{\mu }^{\text{AIPWE}}(\widehat{g})$ are consistent estimator of value $V_{\mu }(\widehat{g}),$ and their asymptotic covariance matrix can also be consistently estimated from the data set.^28,29 The estimates of $V_{\mu }(\widehat{g})$ and their corresponding 95% confidence interval of four methods based on both ipwe and aipwe are given in Table 6 .

TABLE 6.

Results of estimated values and their corresponding 95% confidence interval for the four methods based on IPWE and AIPWE.

Estimator	method	Value	SE	Cl
IPWE	Least Square	405.05	6.72	(391.88,418.22)
	Pinball(0.5)	406.77	6.71	(393.63,419.92)
	Pinball(0.25)	406.07	6.73	(392.87,419.26)
	Huber	407.03	6.71	(393.87,420.18)
AIPWE	Least Square	404.39	6.12	(392.40,416.38)
	Pinball(0.5)	405.93	6.13	(393.92,417.94)
	Pinball(0.25)	403.60	6.62	(390.62,416.58)
	Huber	406.00	6.15	(393.95,418.04)

SE stands for standard error. CI stands for 95% confidence interval.

From Table 6 , robust regression with ${\rho }_{0.5}$ and Huber loss perform slightly better than lsA-learning, while robust regression with p₀₂₅ performs worse than lsA-learning when the values $\left(V_{\mu }(\widehat{g})\right)$ is estimated based on aipwe. We conduct KCI-test to check the conditional independence error assumption $ϵ\perp A|X.\text{For}RR\left({\rho }_{0.5}\right),RR\left({\rho }_{0.25}\right)\text{and}RR(H),$ their p-values for the KCI-test are 0.060,0.002 and 0.083, respectively. The conditional independence error assumption holds at the significance level of 0.05 for $\text{RR}\left({\rho }_{0.5}\right)\text{and RR}(H),$ so the estimated treatment regime can be thought to maximize $V_{\mu }(g).$ On the other hand, this assumption doesn’t hold for $RR\left({\rho }_{0.25}\right)$, since its estimated treatment regime doesn’t maximize $V_{\mu }(g),$ instead it approximately maximizes $V_{0.25}(g).$ This partly explains the relatively bad performance of $\text{RR}\left({\rho }_{0.25}\right)$ in Table 6 . Again, as $\text{RR}\left({\rho }_{0.5}\right)\text{and RR}(H)$ are more robust against heterogeneous, right skewed errors comparing with the least square method, they slightly outperform lsA-learning in term of $V_{\mu }(g).$

6 |. DISCUSSION

In this article, we propose a new general loss-based robust regression framework for estimating the optimal individualized treatment rules. These new methods have the desired property to be robust against skewed, heterogeneous, heavy-tailed errors and outliers. And similar as A-learning, they can produce consistent estimates of the optimal individualized treatment rule even when the baseline function is misspecified. However, the consistency of the proposed methods does require the key conditional independence error assumption $ϵ\perp A|X,$ which is somewhat stronger than the conditions needed for consistency of mean-based estimators. So there are situations when the classical Q- and A-learning are more appropriate to apply. Furthermore, we point out in the article that when the pinball loss ${\rho }_{\tau }$ is chosen and the assumption $ϵ\perp A|X$ doesn’t hold, the estimated treatment regime approximately maximizes the $\tau \text{th}$ conditional quantile and thus maximizes $V_{\tau }(g).$ Generally, the individualized treatment rules that maximize the conditional mean and the conditional quantile can be quite different, especially when the error term has a heavy-tailed distribution and the conditional independence error assumption is not satisfied. In these situations, maximizing the conditional quantile is usually more robust than maximizing the mean, especially when $\tau$ is selected to be close to 0.5.

As for the marginal quantile based optimal treatment rule, e.g. Wang et al¹¹, it is possible that the conditional-quantile based optimal treatment rule is different at different quantile levels, in particular, when the assumption $ϵ\perp A|X$ doesn’t hold. If this is the case, it may be interesting to develop a method to integrate the optimal treatment rules at different quantile levels. For example, we can define an optimal treatment rule to maximize an integrated conditional quantiles, i.e.,

$$g_{\tau }^{\text{opt}}(x)={\text{argmax}}_{a\in \mathcal{A}}{\int }_0^1{Q}_{\tau }(x,a)w(\tau )d\tau ,$$

where $w(\tau )$ is a prespecified deterministic weight function. The empirical and theoretical properties of such an integrated estimator need to be further investigated.

In practice, there are cases when multiple treatment groups need to be compared simultaneously. For brevity, we have limited our discussion to two treatment groups in this article. However, the proposed methods can be readily extended to multiple cases by just replacing equation (2) with the following more complex form,

$$L_n(\beta ,\gamma )=\frac{1}{n}\sum _{i=1}^{n}M\left[Y_i-\phi \left(X_i;\gamma \right)-\sum _{k=1}^{K-1}\left\{I\left(A_i=k\right)-{\pi }_k\left(X_i\right)\right\}{C}_k\left(X_i;{\beta }_k\right)\right],$$

where A = {1,…, K}, K-th treatment is the baseline treatment, ${\pi }_k\left(X_i\right)=\text{pr}\left(A_i=k|X_i\right),\text{and}{C}_k\left(X_i;{\beta }_k\right)$ denotes the contrast function comparing k-th treatment and the baseline treatment. All of the theorems in this paper can be easily extended to this multiple-treatment setting as well.

When the dimension of prognostic variables is high, regularized regression is needed in order to produce parsimonious yet interpretable individualized treatment rules. Essentially this is a variable selection problem in the context of M-estimator, which has been previously studied in Wu and Liu³⁰ and Li et al,³¹ etc. This is an interesting topic that needs further investigation. Another interesting direction is to extend the current method to the multi-stage setting, where sequential decisions are made along the time line.