Mixed graphical models for integrative causal analysis with application to chronic lung disease diagnosis and prognosis

Abstract

Motivation

Integration of data from different modalities is a necessary step for multi-scale data analysis in many fields, including biomedical research and systems biology. Directed graphical models offer an attractive tool for this problem because they can represent both the complex, multivariate probability distributions and the causal pathways influencing the system. Graphical models learned from biomedical data can be used for classification, biomarker selection and functional analysis, while revealing the underlying network structure and thus allowing for arbitrary likelihood queries over the data.

Results

In this paper, we present and test new methods for finding directed graphs over mixed data types (continuous and discrete variables). We used this new algorithm, CausalMGM, to identify variables directly linked to disease diagnosis and progression in various multi-modal datasets, including clinical datasets from chronic obstructive pulmonary disease (COPD). COPD is the third leading cause of death and a major cause of disability and thus determining the factors that cause longitudinal lung function decline is very important. Applied on a COPD dataset, mixed graphical models were able to confirm and extend previously described causal effects and provide new insights on the factors that potentially affect the longitudinal lung function decline of COPD patients.

Availability and implementation

The CausalMGM package is available on http://www.causalmgm.org.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Commonly studied biological and biomedical data are inherently multi-modal: they include both discrete variables (e.g. gender, therapeutic protocol, disease subtype, polymorphisms, mutations) and continuous variables (e.g. drug dose, clinical tests, gene expression, methylation and protein abundance data). The sizes of relevant databases containing these data have become enormous. In many problems, the number of potentially relevant variables and cellular pathways demands the aid of fast, accurate, automated search methods for predicting causal relations. Directed probabilistic graphical models (PGMs) can represent these causal relationships based on the conditional (in)dependencies of the data. In addition, these models fit a joint probability distribution to high-dimensional observations. Causal graphs are represented as directed graphs or collections of directed graphs with identical conditional independencies. The resulting graphs can provide guidance to experimentalists and clinicians and are useful for classification and prediction of clinical outcomes. A number of methods for learning directed graphs have been developed in the past, but they typically assume (for proof of asymptotic correctness) that all variables are of the same distribution type: categorical (multinomial), Gaussian, conditional Gaussian or linear non-Gaussian.

Several groups have developed methods to learn undirected graphs over mixed data types (Chen et al., 2014; Cheng et al., 2013; Fellinghauer et al., 2013; Lee and Hastie, 2013; Tur and Castelo, 2012; Yang et al., 2014); and directed graphs over mixed variables under certain distributional assumptions (Bøttcher, 2001; Romero et al., 2006). One of the popular methods for learning undirected mixed graphical models (MGM) is a pseudolikelihood method (Lee and Hastie, 2013), which we later offered several improvements of (Sedgewick et al., 2016). A major problem of the undirected (i.e. non-causal) graphs, apart from the lack of direction of the represented interactions, is that they are “moralized” graphs; meaning, the parents of a variable are themselves always connected. This can create a large number of false positive edges. In biomedical research, directed causal graphs have been applied to microbiome (Kitsios et al., 2018) genetics of disease (Zhang et al., 2013). However, in the latter case the network learning is restricted in the sense that SNPs can only be parents of other nodes and the comparison is between different models of disease phenotypes and gene expression that are led by the SNPs.

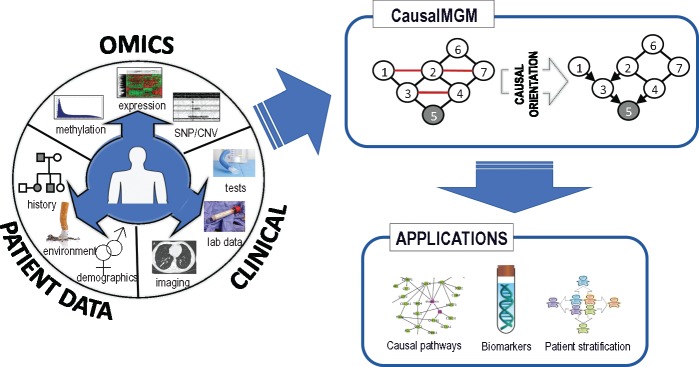
The problem of learning directed graphs over mixed data has been tackled in computer science conferences only recently (Cui et al., 2016; Raghu et al., 2018a). In this paper, we present and test new methods for learning directed MGMs. Figure 1 shows how our approach can be applied to medicine. Patient data are collected from different scales, including molecular (e.g. omics), tissue, organ and individual. They are normalized and passed to CausalMGM framework, which consists of two steps. First, we learn the undirected graph, which we use as a skeleton to perform local directionality determinations with appropriate conditional independence tests we present here. The final learned graph can be used in many applications including identification of causal pathways between the multi-modal variables, biomarker selection and patient stratification.

Fig. 1.

Schematic view of CausalMGM and its applications

We applied CausalMGM on two publicly available datasets consisting of mixtures of multi-modal data (omics, disease). We also applied it on a comprehensive clinical dataset from patients with COPD in order to identify the variables that are causally linked to longitudinal lung function decline. COPD is the third leading cause of death and a major cause of disability and health care costs in the US (Kochanek et al., 2011). COPD cases are traditionally defined using spirometric thresholds of airflow obstruction, i.e. a reduction in the ratio of forced expiratory volume in one second/forced vital capacity (FEV₁/FVC) < 0.7. Progression is defined by longitudinal decline in FEV₁ (2011; Mannino et al., 2007). Currently, there is no good way to predict progression (lung function decline over time) mainly because many of the factors causally linked to it remain unknown. It is expected that causal modeling over well-phenotyped COPD cohorts can help our understanding of the factors that shape COPD progression.

Related work on causal modeling. The problem of learning a sparse undirected graph structure over mixed data has previously attracted some attention (Bøttcher, 2001; Chen et al., 2014; Cheng et al., 2013; Fellinghauer et al., 2013; Lee and Hastie, 2013; Romero et al., 2006; Tur and Castelo, 2011; Yang et al., 2014). The Tur and Castelo method is suitable for studying expression quantitative trait loci (eQTLs), but it does not allow for analysis of downstream discrete clinical variables, because it cannot learn connections between categorical variables. Few proposals suggest a node-wise regression approach for learning networks over a variety of distributions of continuous and discrete variables (Chen et al., 2014; Cheng et al., 2013; Fellinghauer et al., 2013).

The idea of using an undirected method to estimate a superstructure of the true graph, and then restricting the search space of a directed search algorithm to the superstructure has previously been studied for continuous, possibly non-Gaussian data with linear interactions between nodes (Loh and Bühlmann, 2014). Like our proposed method, Loh and Bühlmann first find an undirected graph which serves as an estimate of the moralization of the true graph. The two primary differences between this study and our methods are that Loh and Bühlmann only look at continuous data in their study, and that the directed search is a score-based method while we focus on constraint-based directed search methods here. Another recent method is Copula PC (Cui et al., 2016), which uses a two-step approach. First, it assumes that discrete variables come from continuous latent variables and estimates the latent variables. In the second step, it runs PC (or Rank PC for non-parametric estimation) to find the directed graph. The success of this method depends on how well the continuous-to-discrete approximation works on a given dataset.

2 Materials and methods

2.1 Datasets

We compared CausalMGM to other methods on simulated data (see Supplementary Material) and tested it in three biological and clinical datasets: (i) TCGA breast cancer, (ii) Lung Genomics Resource Consortium (LGRC) and (iii) Pittsburgh Specialized Center of Clinically Oriented Research (SCCOR). The TCGA and LGRC serve as proof-of-principle, showing that CausalMGM can recover known interactions between gene expression and clinical variables. The SCCOR dataset includes only clinical data from 385 COPD patients that had completed the baseline and a 2-year follow up visit, and we used it to identify which factors measured in visit-1 are directly linked to lung function decline, observed two years later. All datasets are described in detail in the Supplementary Material.

2.2 Undirected graph learning

Learning a stable, undirected graph over mixed data is the first step of CausalMGM. For this, we used the method we describe in Sedgewick et al., 2016 (see also, Supplementary Material). In our experiments with synthetic data, we learned MGM graphs across a range of edge sparsity penalties: seven values evenly spaced on the log₂ scale over the range 0$.05\le \mathrm{ }\lambda \le \mathrm{ }0.4$. For the high dimensional data, we added two values to extend this range to $\lambda \le \mathrm{ }0.8$.

2.3 Directed graph search methods

Given an edge scoring method, graph search algorithms are efficient heuristics to search the exponential space of all possible graph configurations. Here we test two popular algorithms, PC-stable and CPC-stable (Colombo and Maathuis, 2014) (description in Supplementary Material). In this paper, we present a likelihood ratio test (LRT) based procedure for conditional independence testing of mixed data types. In addition, instead of starting from a fully connected graph, our method first calculates an undirected graph as in (Sedgewick et al., 2016) and uses it as starting point for PC-stable and CPC-stable. We call these algorithm variants MGM-PCS and MGM-CPCS, respectively.

2.4 Stability selection

Besides our StEPS subsampling procedure for selecting the parameters for stable MGM graphs (Sedgewick et al., 2016), we also tested CPSS (Shah and Samworth, 2013). CPSS is a variation of the Stability Selection (Meinshausen and Bühlmann, 2010) that both loosens the assumptions on the edge selection procedure, and tightens the bounds on the error rate, allowing for a less stringent threshold. Besides the obvious benefit of tighter bounds, the loose assumptions are especially attractive to us, as we would like to be able to substitute a variety of algorithms without worrying about violating the theoretical framework of the method. This method works by learning networks over subsamples of the data and counting how many times a (directed) edge appears. Rather than calculating network instabilities from these empirical edge probabilities, edges are selected by simply thresholding the probabilities. The threshold is calculated from the number of subsamples, the average number of selected edges and the number of variables using Shah and Samworth’s procedure. The user specifies an error control rate where errors are defined as edges that have a lower than random probability of being selected in a given subsample. We ran CPSS in conjunction with MGM-PCS and MGM-CPCS with $\alpha =\mathrm{ }0.05$ and $\lambda =\mathrm{ }0.1$ for the LD dataset and with $\lambda =\mathrm{ }0.2$ for the HD dataset with error rates $q\in \{0.001,\mathrm{ }0.01,\mathrm{ }0.05,\mathrm{ }0.1\}$.

2.5 Edge recovery evaluation

To evaluate network estimation performance, we compare the Markov equivalence classes of the estimated and true networks. Markov equivalence classes represent the variable independence and conditional relationships for an acyclic directed graph by removing the direction from edges that are free to point in either direction without altering the independence relationships in the network. For example, directed graphs $X\mathrm{ }\to Y\to Z$ and $X\mathrm{ }\leftarrow Y\leftarrow Z$ both have the Markov equivalence class $X-Y-Z$ while the graph $X\mathrm{ }\to Y\leftarrow Z$ (v-structure) would remain the same when converted to a Markov equivalence class. Thus, Markov equivalent graphs share the same variables, have the same adjacencies and imply the same independence and conditional independence relations among their variables. We also consider performance on skeleton estimation, (i.e. node adjacencies, without edge orientations).

We use standard classification statistics to evaluate the recovery of the undirected adjacencies from the skeleton of the true graph. Precision, also known as true discovery rate or positive predictive value is the proportion of predicted edges that are found in the true graph. Recall, also known as sensitivity or true positive rate, is the proportion of edges in the true graph that were found in the predicted graph. For direction recovery, we use these same statistics applied to the recovery of only the directed edges in the Markov equivalence class of the true graph. So, in the context of direction recovery, precision is the number of directed edges in the predicted graph that are found in the true graph out of the total number of directed edges in the predicted graph. Bi-directed edges are treated as undirected edges for these statistics because they do not give an indication of which edge direction is more likely.

We use the Matthews correlation coefficient (MCC) (Matthews, 1975) as a measure for overall recovery performance that strikes a balance between precision and recall. The MCC is a formulation of Pearson’s product-moment correlation for two binary variables (i.e. true edge indicators and predicted edge indicators). In addition, we use the structural Hamming distance (SHD) (Tsamardinos et al., 2006) as a combined measure of adjacency and direction recovery. The SHD is the minimum number of edge insertions, deletions and directions changes, where only undirected edges are inserted or deleted, to get from the true Markov equivalence class to the estimated equivalence class.

3 Results

One of the important components of constraint based methods for learning a graph is the edge scoring. This is typically achieved with a hypothesis test for conditional dependence of two variables, X and Y, given a conditioning set of variables, S. The null hypothesis is that X and Y are independent given S, which is denoted by $X\mathrm{ }\perp Y\mathrm{ }|\mathrm{ }S$. By definition, if this null hypothesis is true:

$$P\left(X,\mathrm{ }Y\right|S)=P\left(X|S\right)P(Y\left|S\right)$$

Rearranging, we find:

$$P\left(X\right|S)=\frac{P\left(X,\mathrm{ }Y\right|S)}{P\left(Y\right|S)}=P\left(X|Y,S\right)$$

So, in order to test $X\mathrm{ }\perp Y\mathrm{ }|\mathrm{ }S$, it suffices to test if $P\left(X|S\right)=P\left(X\right|Y,\mathrm{ }S)$ which is done via likelihood ratio test (LRT) of two regressions. This test is known to follow the chi-squared distribution.

$$2\mathrm{l}\mathrm{n}\left(\frac{L\left({\theta }_{\mathrm{X}\mathrm{Y}\mathrm{S}}\right)}{L\left({\theta }_{\mathrm{X}\mathrm{S}}\right)}\right)\sim \left(X^2\left(d_{\mathrm{X}}{d}_{\mathrm{Y}}\right)\right)$$

where $\theta$ represents the regression coefficients to model X given S with and without Y as an additional independent variable. This test is used by PC-stable (Colombo and Maathuis, 2014) but we modify it to accommodate mixed data types. Specifically, we define the degrees of freedom, $d_X$ and $d_Y$, of each variable to be (i) 1 if the variable is continuous and (ii) the number of categories minus 1 if the variable is categorical. Although this description uses regressions with X as the dependent variable, the same reasoning allows us to use Y as the dependent variable instead.

The regressions in this test allow us to formulate this test so that any of the variables can be continuous or categorical. We preform linear or multinomial logistic regressions if the dependent variable is continuous or categorical, respectively. Because of this, if X and Y are of different variable types, we have a choice of whether X or Y should be the independent variable that determines whether we perform logistic or linear regressions. Our own experiments (see Supplementary Material) and observations in previous studies (Chen et al., 2014) suggest that a linear regression will give a more accurate test result than a logistic regression for these continuous-discrete edges. To handle any dependent categorical variables in the regression, we convert each k-level categorical variable to k-1 binary variables.

It is also possible to conduct these tests by regressing Y and S onto X and using a t-test to determine if the regression coefficient of Y is significantly different from 0. In the continuous setting, the t-test and LRT give virtually identical results, but not with discrete or mixed data. If Y is categorical this procedure requires performing a test on each dummy variable associated with Y and then combining them using Fisher’s method. The main advantage of using t-tests over the LRT that it only requires one regression instead of two, so it is significantly faster. The downside is that in our experiments we found that it had less power to detect true edges (Supplementary Fig. S1) and was less robust at low sample sizes, particularly on edges that required a logistic regression. Because of this, we will work exclusively with the LRT based test here.

3.1 Evaluation on simulated data

In order to determine the limitations of the algorithms, we performed experiments using two different dataset sizes and randomly drawn DAG structures. In addition, since optimal parameter setting is a difficult problem that may depend on the needs and goals of the user, we studied a range of possible parameter settings to show the relationship between these settings and edge recovery performance.

3.1.1 Adjacency recovery

Supplementary Figure S2A shows the adjacency recovery performance of PC-stable, MGM-PCS and CPSS on the HD dataset. CPC-stable and MGM-CPCS are not shown because they have the same adjacency predictions as the PC algorithms. Settings of $\lambda$ < 0.2 for the MGM-PCS algorithm are omitted because they extensively overlap with the PC-stable curves. Despite the apparent overlap, these denser MGM structures do cause a slight decrease in the precision of MGM-PCS compared to PC-stable, although this difference is not significant at any of the tested settings. For example, at $\alpha =\mathrm{ }0.05$ and $\lambda =\mathrm{ }0.14$, MGM-PCS has an average precision of 0.739 (standard error of 0.0057) compared to PC-stable which achieves mean precision of 0.744 (standard error is 0.0055). We expect that in the limit of $\lambda \mathrm{ }\to 0$, MGM-PCS becomes equivalent to PC-stable. On the other extreme, the highest settings of lambda result in very sparse initial graphs, which have good precision but poor recall. In general, we see that adding the MGM step increases precision of the PC-stable procedure, at a small cost to recall, depending on the sparsity parameter setting. We see a similar trend in the LD dataset as well (Supplementary Fig. S2B). In addition, all of our algorithms have both lower precision and recall on edges involving discrete variables, which suggests that they are more difficult to learn. These observations differ from the LD setting where we actually achieve the best recall on these dd edges, although still diminished precision compared to cc and cd. In the LD datasets, Copula PC performs very poorly on edges with discrete variables, which could be attributed to its assumption of monotonic relations (which are not always present in categorical data). We note that Copula PC is unable to estimate its correlation matrix in settings where p > n, so it was excluded from the HD results. Finally, these results show that CPSS is a good option for users that want to ensure very high precision in their network estimates, especially in LD datasets and is certainly preferable to using an overly sparse setting of lambda.

3.1.2 Directionality recovery

Next, we evaluated how well each algorithm was able to recover the directions of the edges of the true Markov equivalence class. For these tests, the positive class consists of all estimated directed edges and the negative class is both undirected edges and the absence of an edge. So, an estimated edge is only considered a true positive if it correctly identifies both the existence and the orientation of the edge. Figure 2A shows these results across all of the algorithms. Starting from an (undirected) MGM graph increases direction recovery performance in PC-stable. The main reason for this improvement appears to be the fact that PC-stable alone returns a large number of bidirected edges and only finds a small number of edges with a single direction. Bidirected edges are returned when the v-structure orientation rule in step-2 of PC-stable implies both directions for an edge. We treat these as undirected edges in our statistics. Starting from an MGM graph reduces the number of bidirected edges and increases the number of directed edge predictions. This is evident by the large increase in directed edge recall, but this comes at the price of reduced precision for higher independence test thresholds, $\alpha \in \{0.05,\mathrm{ }0.1\}$.

Fig. 2.

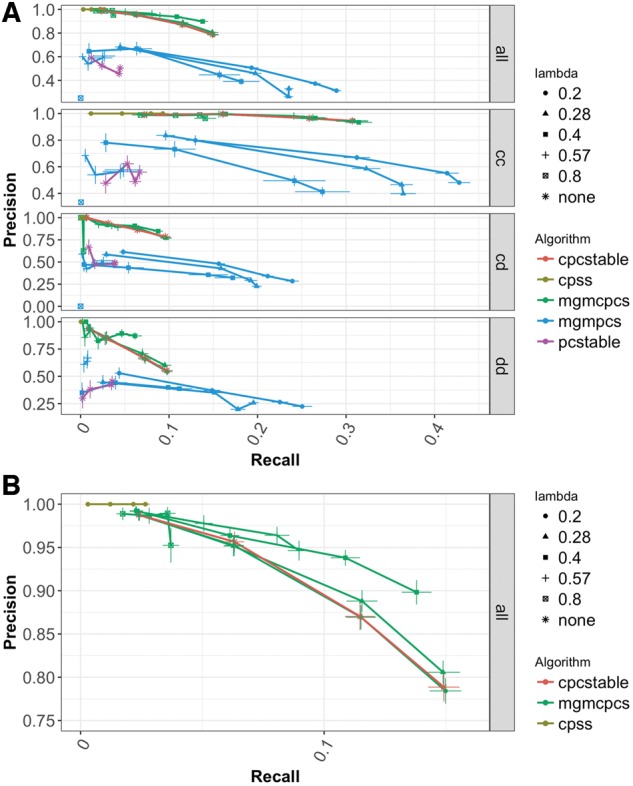
Precision-Recall curves of edge direction recovery on high-dimensional dataset. (A) Full range of algorithms and edge types. (B) Detail view of CPC-stable and MGM-CPC-stable performance averaged over all edge types. Parameter range: 0.2 ≤ λ ≤ 0.8; 0.01 ≤ α ≤ 0.1. Bars correspond to one standard error

Figure 2B gives a detailed view of the direction recovery performance of CPC-stable, MGM-CPCS and CPSS. As with adjacency recovery, we see that as we increase lambda we achieve higher precision at the cost of recall. The reduced recall in $\lambda \in \{0.28,\mathrm{ }0.4\}$ is only slight combined with a significant increase in precision. We can also see that our heuristic for adapting CPSS to directed network recovery is perhaps too conservative as the recall is greatly reduced while precision is near perfect. Indeed, with this set up CPSS predicts the directions of less than 10 edges on average, for the most lenient error rate, $q=\mathrm{ }0.05$, so it does not seem to be a useful option for edge direction predictions.

Overall, direction recovery is difficult in high dimensions and incorporation of prior information can help (Manatakis et al., 2018). While the MGM-PCS method approaches direction recall of 0.3, this is paired with abysmal precision of less than 0.5. CPC-stable and MGM-CPCS give us reasonable precision, but they are able to recall less than 15% of true directed edges. We use a strict heuristic to adapt CPSS to the problem of direction estimation that produces extremely high precision.

3.1.3 Combined measures of network recovery

The Structural Hamming Distance (SHD) is a combined measure of adjacency and direction that gives us an alternative network estimation metric that does not necessitate balancing precision versus recall. Table 1 shows the “best case” performance of the algorithms, where the parameter settings are chosen to maximize the SHD both averaged over all edges and broken down by each edge type. Since SHD is a distance measure, smaller values indicate better performance. By this measure, MGM-PCS and MGM-CPCS both significantly outperform their counterparts on the HD data. We see a similar trend in the LD data (Supplementary Fig. S3), where MGM-PCS performs significantly better than PC-stable, while MGM-CPCS has a slight but non-significant advantage over CPC-stable.

Table 1.

Parameter settings with the best SHD performance by edge type in high-dimensional dataset

Algorithm	α	λ	Edge type	SHD
PC-Stable	0.01	none	all	600.95 (2.25)
(PCS)	0.01	none	cc	130.00 (2.340)
	0.01	none	cd	308.40 (4.20)
	0.001	none	dd	160.45 (3.24)
MGM-PCS	0.01	0.14	all	567.75 (3.34)
	0.05	0.14	cc	108.45 (2.21)
	0.01	0.14	cd	294.70 (3.74)
	0.001	0.1	dd	157.30 (3.28)
CPC-Stable	0.01	none	all	588.10 (2.37)
(CPCS)	0.05	none	cc	111.60 (2.44)
	0.01	none	cd	307.05 (4.18)
	0.01	none	dd	160.80 (2.85)
MGM-CPCS	0.1	0.4	all	564.90 (4.46)
	0.1	0.57	cc	107.05 (2.32)
	0.1	0.4	cd	296.70 (4.17)
	0.1	0.4	dd	157.05 (3.25)

Note: λ and α refer to the parameter threshold values for the undirected graph (skeleton) and the directionality step, respectively. cc, cd, and dd refer to the type of edge (continuous-continuous, cont.-discrete, and discr.-discr.). all refers to the average performance.

Since the best-case performance will be difficult to achieve when the true graph is unknown, especially in this setting where a robust parameter setting scheme is not readily available, we also show SHD performance versus the number of predicted graph edges. These results, presented in Figure 3, show that for parameter settings for MGM-CPCS that produce similar numbers of edge predictions to CPC-stable, the hybrid algorithm can improve SHD performance. Very sparse settings of $\lambda$ result in networks with a large SHD because so many edges are missing compared to the true graph. These too-sparse settings of the MGM are evident from the number of predicted edges, however, so they should be easy for a user to identify.

Fig. 3.

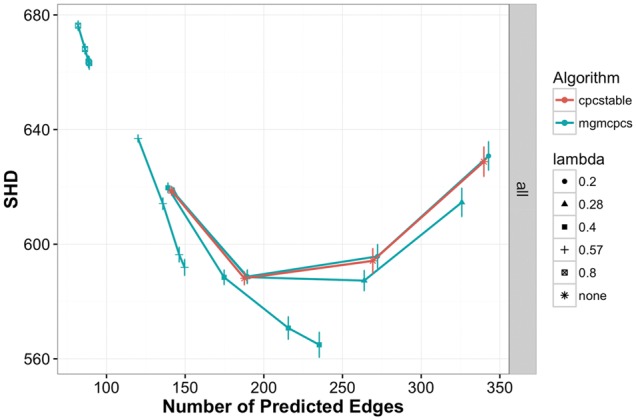
Structural Hamming Distance on high dimensional dataset for CPC-stable and MGM-CPCS. The lower the SHD, the closer the predicted graph is to the true graph. Parameter range: 0.2 ≤ λ ≤ 0.8 and 0.01 ≤ α ≤ 0.1

3.1.4 Run time comparisons

We compared the running times of our algorithms at various parameter settings. In the HD dataset MGM-PCS and MGM-CPCS are significantly faster than PC-stable for sparser settings of $\lambda$, but significantly slower for low values of $\alpha$ and low values of $\lambda$ (Fig. 4). In the LD data (Supplementary Fig. S4), all MGM-based methods are faster than the generic algorithms at all parameter settings and Copula PC is the slowest. We note that our undirected MGM learning method is not parallelized, but the directed learning steps are. A fully parallelized CausalMGM could result in even larger speed improvements. The edge convergence approach we use to learning the undirected MGM is essential to this performance improvement.

Fig. 4.

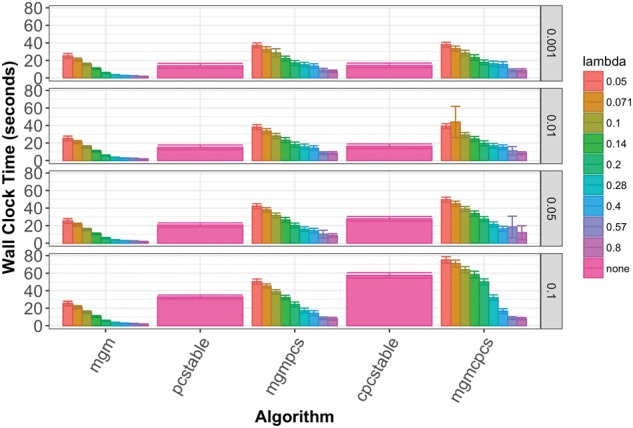
Average running times with 95% confidence interval error bars of search algorithms on high dimensional data. Each row of columns corresponds to a different setting of $\alpha$ and each column corresponds to a different setting of λ. Directed search steps were run in parallel on a 4-core laptop

3.2 Evaluation on real data

3.2.1  Application to breast cancer data (TCGA)

We applied MGM-PCS to gene expression and clinical data from breast cancer patients in TCGA (Cancer Genome Atlas, 2012). For the analysis, we used the 500 genes with the highest variance across samples. We also included the clinical variables for hormone receptor status, node and tumor staging codes and PAM50 subtype. PAM50 is a subtyping scheme that uses gene expression patterns from 50 genes to categorize tumors (Parker et al., 2009), thirteen of which were in the high variance set. We ran MGM-PCS with a sparsity of λ = 0.2 (selected based on stability of edges across subsamples) and the default α = 0.05. The output network (Supplementary Fig. S5) had eight genes connected to the PAM50 variable, three of which were among the 13 included in the analysis (Fisher’s test, P = 1.8e-3).

In addition, we find a number of predicted edges that are supported by biological knowledge. Each clinical variable corresponding to receptor status (ER, PR, HER2; determined through immunohistochemistry) was linked to the gene expression profile of that receptor: progesterone receptor with PGR1, HER2 with ERBB2 and estrogen receptor with ESR1. GATA3 is linked to ESR1, which agrees with (Cimino-Mathews et al., 2013) that found GATA3 to be central in luminal (i.e. estrogen receptor positive) breast cancer. The lymph node stage variable, which indicates degree of lymph node metastasis, in our predicted network was only linked to the expression of E-cadherin gene (CDH1). Hypermethylation and decreased expression of CDH1 has been linked to infiltrating breast cancer (Caldeira et al., 2006).

3.2.2  Application to chronic lung disease -omics and clinical data

As a second test, we applied MGM-PCS to high-variance mRNA expression profiles from the LGRC cohort, which includes clinical data and –omics data from surgical excess tissue specimens of patients with COPD and idiopathic pulmonary fibrosis (IPF). We used a stability-based method, CPSS, to estimate an upper bound for the false discovery rate of our edge predictions. Supplementary Figure S6 shows a subnetwork including all first and second neighbors of eight clinical variables included in the dataset for edges with false positive rate, q < 10%.

We found Gender to be strongly associated with a cluster of Y-chromosome genes, as well as height and weight (Supplementary Fig. S6, bottom right). The spirometry tests FEV₁ and FVC are used by clinicians for making diagnosis (mostly, as their ratio), so it is expected to find them directly linked in this dataset. However, we find that these variables are separated from diagnosis by several mRNA expression variables. Since the diagnosis variable is differential for either COPD or IPF disease, this probably indicates that there is not as much variability in these two measurements with respect to COPD and IPF. We note, however, that one of the key variables that separates the FEV₁ and FVC from diagnosis is the expression of the FREM3 gene, which is an extracellular matrix protein, typically associated with IPF. In this case, FREM3 is also one of the genes that have been linked to COPD susceptibility (Lamontagne et al., 2013). Among the variables directly linked to diagnosis, we note the expression of FIGF and the cigarette smoking history. FIGF (synonym of VEGF), a growth factor, is a key molecule in many fibrotic diseases (Wernig et al., 2017). Smoking history is a known risk factor for both diseases, so it is unexpected that is associated to the diagnosis variable. This is probably because the risk associated to smoking is different in the two diseases: in COPD 25% of the patients have never smoked (Prevention, 2012), while in IPF this percentage is higher (Baumgartner et al., 1997). Our graph shows that cigarette smoking is causally linked to CYP1A1 (cigarette smoking is the parent of CYP1A1). CYP1A1 is upregulated in smokers (Anttila et al., 2001) and it is known to convert polycyclic aromatic hydrocarbons, found in cigarette smoke, into carcinogens (Walsh et al., 2013), which induce lung remodeling similar to that observed in IPF.

3.2.3  Novel baseline factors that are directly linked to longitudinal lung function decline in COPD patients

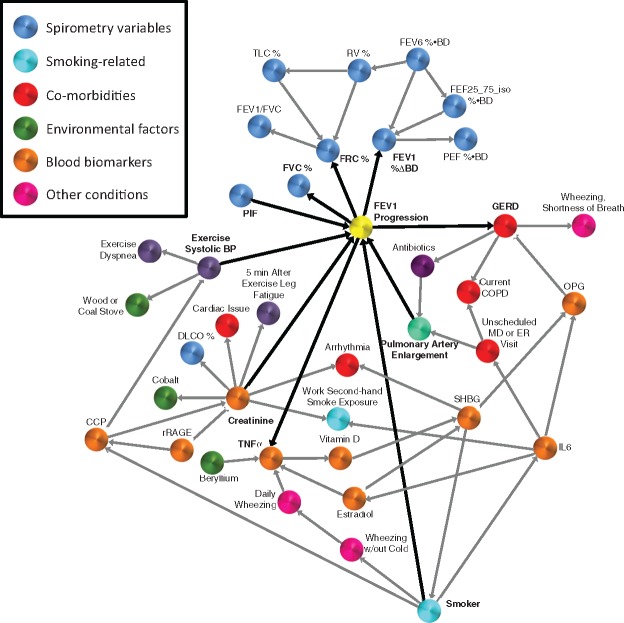
We applied MGM-PCS to the clinical SCCOR dataset to identify the baseline variables that are directly (causally) linked to the 2-yr lung function decline in COPD patients. Given the substantial variation in longitudinal decline in lung function, identification of baseline subject attributes that are connected to disease activity is useful for developing prediction models and offers mechanistic insights and risk factors of progression, which could be used to develop personalized approaches to disease management or treatment. The SCCOR dataset we included 281 variables that recorded a variety of clinical, environmental, psychological and patients’ history data in visit-1 (baseline). We ran MGM-PCS on this dataset and we added a variable measuring the lung function decline between visit-1 and visit-2 (“FEV₁ progression”). The first and second neighbors around this variable are presented in Figure 5. This network offers face validity by identifying variables as direct connectors that are expected to be associated with lung function decline, that being continued tobacco exposure “Smoker” and bronchodilator reversibility “FEV₁%ΔBD”(Anthonisen et al., 2002; Tashkin et al., 1996). Other connectors are novel, more provocative and offer unique perspective. Notably three markers of non-pulmonary co-morbidities are direct connectors to FEV₁ Progression: “Creatinine: (a biomarker of renal dysfunction), “Exercise Systolic BP (Systolic blood pressure at end of 6-min walk exercise) and “GERD” (history of gastroesophageal reflux disease). While each has been previously linked with COPD or its exacerbations (Chandra et al., 2012; Divo et al., 2012; Hersh et al., 2013; Ramos et al., 2014), such a dominant association with lung function decline is not well described. Such associations however are consistent with a systems biology mechanistic model of COPD, whereby activity and interaction in multiple organs rather than a single organ centric approach better defines the potential underlying mechanisms and impact on the patient (Agusti et al., 2011).

Fig. 5.

First and second neighbors of 2-year lung function decline, measured as FEV₁ Progression. The variables that most influence the FEV₁ progression are smoking status, creatinine and TNFα blood levels, pulmonary artery enlargement, history of GERD, systolic BP after exercise and four spirometry variables (% change in FEV₁ before and after bronchodilators, best percent predicted FVC, best percent predicted FRC, and PIF)

Creatinine, for example, is directly connected to FEV₁ decline and is also a hub in our network. The connections within this hub may offer further insights into the mechanistic associations between renal and lung disease. Renal dysfunction and elevated creatinine levels has been associated with pulmonary emphysema severity, which is supported by the direct connection to “DLCO” (Chandra et al., 2012), a marker of parenchymal emphysema or pulmonary vascular dysfunction. Further, recent studies propose a mechanistic link between emphysema and renal dysfunction through RAGE (Chandra et al., 2017; Polverino et al., 2017; Sukkar et al., 2012; Yonchuk et al., 2015), the receptor of which (sRAGE) is a direct connector to Creatinine in our network. The Creatinine hub, is further linked to a number of other important variables and confounders, including the blood biomarker CCP (Clara cell protein) whose association to COPD has been previously reported (Lomas et al., 2008). In fact, the interaction between CCP and RAGE identified in our network provides incentive to explore relationships between these molecular pathways. Other direct links to Creatinine including “Cardiac issue” and “Arrhythmia”, attributes from the subject medical history, may be indicators of a common vascular mechanistic systems link. The Direct link of TNFα, another blood biomarker, with disease progression is of both prognostic and mechanistic interest. TNFα is a representative biomarker for TH1 inflammatory pathways commonly linked with COPD (Hodge et al., 2007). In fact, TNF modulation has been tested as a therapy in COPD, but with mixed results (Rennard et al., 2007).

Another direct connector to FEV₁ progression, “Exercise Systolic BP” may also reflect the vascular/endothelial processes common to pulmonary and systemic processes. The common linkage of CCP between this and the other direct connector, Creatinine is of further interest. We note, though, that the causal direction might be predicted wrongly in these associations. “GERD” the final comorbidity variable as a direct connector to lung function progression is of potential interest in either causal direction, as gastroesophageal reflux has known potential impacts on lung function and lung function decline associated with lung hyperinflation can alter transdiaphragmatic pressure gradients leading to reflux. The direct connection of “Pulmonary Artery Enlargement” with FEV₁ progression is of particular interest given the secondary linkage of this measure with indicators of COPD exacerbation in the past year, that being “Unscheduled MD or ER Visit” and “Antibiotics”. Previously, a high-profile publication connected pulmonary arterial enlargement to COPD (Wells et al., 2012).

Finally, three other pulmonary physiology variables are linked directly to COPD progression: “FRC%” (Functional Residual Capacity), FVC% (forced vital capacity) and PIF (peak inspiratory flow rate). All of these are measures that are directly or indirectly linked to air trapping and lung hyperinflation but are independently measured attributes. To our knowledge, the direct association of these measures with FEV₁ decline has not previously been defined.

These results are significant, not only because this combination of factors can determine and predict COPD progression; but because for the first time we are able to build a causal network of COPD that combines heterogeneous types of information such as measurements of lung function, symptoms, systemic comorbidities and blood biomarkers with environmental exposures such as ongoing tobacco exposure. Other environmental or psychological variables, while not linked to COPD progression directly, were part of the larger network. A variable describing whether the patient has been diagnosed with depression or is on anti-depression medication, for example, was found to be linked to pack years of smoking. The associations found in this network are particularly notable in that they extend previous work describing the important link between non-pulmonary organ comorbidities and lung function impairment, supporting the systems biology paradigm in understanding lung disease activity (Agusti et al., 2011; Divo et al., 2012).

4 Conclusions and future work

We have presented a new, fast method for learning a causal graph over variables of mixed type (continuous and discrete). This work offers a number of new advances. First, it expands our previous work on undirected graphs (Sedgewick et al., 2016) to directed graphs over mixed data; by developing new conditional independence tests. Second, it performs an extensive test of the new set of methods (CausalMGM) to existing state-of-the-art methods in both low- and high-dimensional datasets. Third, its application to three biomedical datasets identifies known and discovers new causal interactions between clinical and other variables.

CausalMGM follows a two-step approach in which a stable, undirected graph is learnt by optimizing conditional-Gaussian pseudo-likelihood over mixed data types. The undirected graph is then used as the skeleton to run local directed graph searches. We have shown that CausalMGM can efficiently reconstruct graphs from simulated data (high- and low-dimensional) with high precision, although recall is more challenging (see also, Raghu et al., 2018b). As expected, recovering edges or directions involving categorical variables was more difficult in high-dimensional settings, but this trend was surprisingly not obvious in the low-dimensional setting. In many cases, our hybrid searches are faster and perform better than the directed search steps by themselves. In the worst case, our hybrid algorithms do no worse than the single algorithms searches and are slightly slower. The search for the undirected graph is O(n²) and the subsequent orientation step is exponential to the number of neighbors for each pair of connected variables; which depends on the sparsity of the undirected graph. CausalMGM algorithms can easily scale to few thousand variables.

Directed MGMs are promising tools for exploratory biomedical research (see results in TCGA breast cancer and LGRC datasets). Our results on the SCCOR clinical data are also significant, because not only we did find a combination of factors that can determine and predict COPD progression, but also for the first time we are able to build a causal network of COPD that combines heterogeneous types of information such as measurements of lung function, symptoms, systemic comorbidities and blood biomarkers with environmental exposures such as ongoing tobacco exposure. Other environmental or psychological variables, while not linked to COPD progression, were part of the larger network. The associations found in this network are particularly notable in that they extend previous work describing the important link between non-pulmonary organ comorbidities and lung function impairment, supporting the systems biology paradigm in understanding lung disease (Agusti et al., 2011).

Funding

This work has been supported by the National Institutes of Health (NIH) under award numbers R01LM012087, P50HL084948, U01HL137159, K23HL126912, U54HG008540, T32EB009403, T32CA082084; and the Commonwealth of Pennsylvania, Department of Health CURE: Commonwealth Universal Research Enhancement Program SAP 4100062224 (FCS). The content is the sole responsibility of the authors and does not necessarily represent the official views of the funding organizations.

Conflict of Interest: none declared.