DeepGSR: an optimized deep-learning structure for the recognition of genomic signals and regions

Abstract

Motivation

Recognition of different genomic signals and regions (GSRs) in DNA is crucial for understanding genome organization, gene regulation, and gene function, which in turn generate better genome and gene annotations. Although many methods have been developed to recognize GSRs, their pure computational identification remains challenging. Moreover, various GSRs usually require a specialized set of features for developing robust recognition models. Recently, deep-learning (DL) methods have been shown to generate more accurate prediction models than ‘shallow’ methods without the need to develop specialized features for the problems in question. Here, we explore the potential use of DL for the recognition of GSRs.

Results

We developed DeepGSR, an optimized DL architecture for the prediction of different types of GSRs. The performance of the DeepGSR structure is evaluated on the recognition of polyadenylation signals (PAS) and translation initiation sites (TIS) of different organisms: human, mouse, bovine and fruit fly. The results show that DeepGSR outperformed the state-of-the-art methods, reducing the classification error rate of the PAS and TIS prediction in the human genome by up to 29% and 86%, respectively. Moreover, the cross-organisms and genome-wide analyses we performed, confirmed the robustness of DeepGSR and provided new insights into the conservation of examined GSRs across species.

Availability and implementation

DeepGSR is implemented in Python using Keras API; it is available as open-source software and can be obtained at https://doi.org/10.5281/zenodo.1117159.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

All eukaryotic organisms share a complex gene structure associated with various control signals (Brown, 2002), as illustrated in Figure 1. Recognition of these genomic signals and regions (GSRs) helps in understanding genome organization, gene regulation, and functions. Additionally, the translation of that knowledge into systems-based applications, combined with genome variations, allows for the association of genes to diseases and facilitates molecular-based medical applications (Dougherty et al., 2009). However, the diverse models proposed for the recognition of specific types of GSRs for different organisms with manually-crafted features bring questions regarding the strengths, weaknesses, and differences of these models. Moreover, different types of GSRs require different sets of features for building efficient recognition models. However, the presence of many types of GSRs in the genomic DNA and the lack of a unified approach to accurately predict them by computational means, make the GSR prediction a challenging problem. Although a considerable number of computational approaches have been published in the past, there is still no available standard procedure or generalized model structure that can be used for the prediction of different types of GSR in various organisms.

Fig. 1.

Hypothetical gene structure and surrounding control signals of eukaryotes

For example, Sharan and Myers (2005) attempted to derive a generalized method to detect signals and their recurrent motifs using a support vector machine for classification. The method is based on probabilistic models for discriminative motifs and their spatial combination. The authors applied their approach for the recognition of core promoters, alternatively spliced exons, and cell-cycle regulated genes and achieved results comparable to other methods.

The prediction of selected GSRs has been addressed separately in previous studies using traditional machine learning techniques, for example (Bajic et al., 2002; Choudhuri, 2014; Jia, 2010; Prohaska et al., 2007; Sonnenburg et al., 2008). On the other hand, gene finding tools implement a set of specialized statistical features to identify different GSRs, such as, introns, coding exons, 5′ and 3′ untranslated regions, among others (Burge, 1997; Hoff et al., 2016; Parra et al., 2000; Reese et al., 2000; Schiex et al., 2001; Stanke et al., 2004). Consequently, the development of many such tools may require a tremendous amount of work. Therefore, an unbiased and generalizable method for the accurate identification of different GSRs would facilitate the development of more accurate gene finding tools and would enable large-scale analyses of different organisms with significantly smaller development efforts. Recently, deep-learning (DL) techniques have been shown to achieve outstanding results in many cases without the need for manually-crafted features (LeCun et al., 2015). As a result, there is a growing number of studies proposing the use of DL techniques with DNA sequences to tackle various computational biology problems (Khurana et al., 2018; Li et al., 2018; Magana-Mora and Bajic, 2017; Veltri et al., 2018; Xiong et al., 2017). A convolutional neural network (CNN) is a suitable DL model for pattern recognition and image classification and exploits spatial correlation/dependencies in the data (Zuo et al., 2015) and has been applied for the prediction of different GSRs. For example, the CNNProm method (Umarov and Solovyev, 2017) for promoter prediction uses a single-dimension CNN to predict promoter regions. The authors derived an independent CNN with customized parameters for each of the five considered organisms and achieved promising results. Alipanahi and colleagues (Alipanahi et al., 2015) proposed the DeepBind method based on a CNN to predict DNA and RNA sequence specificities of the DNA and RNA-binding proteins, as well as for the discovery of new patterns in the sequence. Similarly, another study on the same problem was discussed by Zeng and colleagues (Zeng et al., 2016) achieving comparable results to the study of DNA sequence binding using a large transcription factors dataset. Later, Zhang and colleagues (Zhang et al., 2017) proposed TITER, a DL framework for the prediction of both canonical and non-canonical start codons. TITER framework is based on QTI-seq data, which captures real-time translation initiation events qualitatively and quantitatively. The TITER framework has two approaches for the prediction of translation initiation sites (TIS): one with a prior preference of a TIS codon and the other without such information. Additionally, CNNs have also been applied for the prediction of non-coding functions. In this direction, DeepSEA (Zhou and Troyanskaya, 2015), based on a CNN, predicts the functional effects of the non-coding variants from large-scale chromatin-profiling data. Later, Quang and Xie (2016), developed the DanQ framework, which uses a combination of a CNN and a recurrent neural network for predicting the function of non-coding genes directly from the sequence. Finally, Singh and colleagues (Singh et al., 2016) proposed DeepChrome, the first DL framework for gene expression classification using histone modification data, which outperformed the conventional state-of-the-art methods on 56 different cell types. More applications of DL to problems in bioinformatics and computational biology are reviewed by Min et al. (2016). Even though the previously mentioned studies based on DL models aim at generating data features directly from the sequence, they remain confined to specific tasks and, in many cases, they are tested on a single organism.

Here, we propose a novel DL structure, DeepGSR, for the recognition of different types of GSRs in genomic DNA and explore its potential for the accurate prediction of two such signals. The DL architecture relies on the proper data representation of the GSRs, their genomic neighborhoods, and utilization of the spatial correlation. We evaluated the efficiency of our framework on two types of GSRs, namely, polyadenylation signals (PAS) and TIS signals, in four organisms: Homo sapiens (human), Mus musculus (mouse), Bos taurus (bovine) and Drosophila melanogaster (fruit fly). We conducted genome-wide experiments to assess the performance of DeepGSR using 1) specific models for each organism independently, and 2) cross-organism model testing (i.e., model is developed using data from one organism, and tested on genomic data of different organisms not used for model training). The results demonstrated that DeepGSR outperforms the start-of-the-art results in recognition of both PAS and TIS in the human genome. As such, DeepGSR reduced the classification error rate by more than 29% and 86% for PAS and TIS prediction in human, respectively, and produced an acceptable performance for both genome-wide and cross-organisms experiments, suggesting high conservation of these GSR signals across different species.

2 Materials and methods

Poorly tuned CNN architectures may yield poorer performance than simpler shallow models (Zeng et al., 2016). Therefore, the DeepGSR structure performs a comprehensive and systematic analysis of the CNN architecture, its hyperparameters, and the type of data representation that fit the classification problem in question.

Moreover, DL requires a sufficiently large amount of training data to properly learn an abstract representation of the data under study (Chen and Lin, 2014). Therefore, we first describe the data extraction procedure for PAS and TIS followed by the details of the building, training, and optimization methods for the recognition model based on CNN.

2.1 Datasets

Genomic data extraction is a crucial step in genomic studies and genome analysis. In this study, we extracted PAS and TIS sequences from the genomes of four organisms (human, mouse, bovine, and fruit fly) using the available cDNA data of their respective genomes.

We used cDNA data as a starting point to extract two different types of GSRs related to protein-coding genes, PAS and TIS. The data for the four considered organisms are available online and can be obtained from the National Center for Biotechnology Information (NCBI), University of California Santa Cruz (UCSC) genome browser, Mammalian Gene Collection (MGC), FlyBase, and Ensembl resources (Aken et al., 2016; Gramates et al., 2017; Strausberg et al., 1999; Temple et al., 2009). Then, we mapped the cDNA data back to the genome using Genomic Mapping and Alignment Program (GMAP) (Wu and Watanabe, 2005). Finally, we used bedtools (Quinlan and Hall, 2010) to determine flanking sequences of the considered GSR with 300 nucleotides both upstream and downstream, resulting in a sequence of 600 nucleotides plus the length of the GSR, i.e., 603 and 606 nucleotides for TIS and PAS, respectively. This method can be applied for the extraction of several other types of GSRs, i.e., splice sites, stop codons, etc. The complete workflow for data extraction is depicted in Supplementary Figure S1.

Sequences with false PAS and false TIS (i.e., hexamers and trinucleotides having the same motifs but with no links to the polyadenylation and translation processes, respectively) were selected to be equal in number to the signals determined via cDNA (i.e., positive samples). Moreover, false PAS and false TIS samples were extracted from the chromosome with the closest average of GC-content to the average GC-content of the whole genome. As such, negative data were extracted from chromosomes 21, 13, 28, and X for human, mouse, bovine, and fruit fly, respectively.

Our pipeline extracted in this way 20 933, 18 693, 12 082, and 27 203 true PAS data in total for the 16 PAS motifs; and 28 244, 25 205, 17 558, and 30 283 true TIS data with the ATG signal for human, mouse, bovine, and fruit fly, respectively. Supplementary Table S1 illustrates the comparison between the numbers of all variants of true PAS signals we extracted from the four considered genomes.

The extracted PAS and TIS data for the four organisms provide different insights about the data distribution and the frequency-based ranking of the different motifs. Supplementary Section S1 presents more details about the data extraction procedure and the findings from the extracted data.

2.2 The DeepGSR method

Developing a unified framework with the potential to recognize many different types of GSRs is challenging. We used DL to achieve this objective due to its advantages in generating suitable higher-order features for the problem in question.

In the following subsections, we describe the most relevant aspects to consider for deriving a robust DL model, i.e., selecting the proper data representation, setting the structure of the DL model, and search within the large space of hyperparameters to find the optimal parameter set.

2.2.1 Data representation

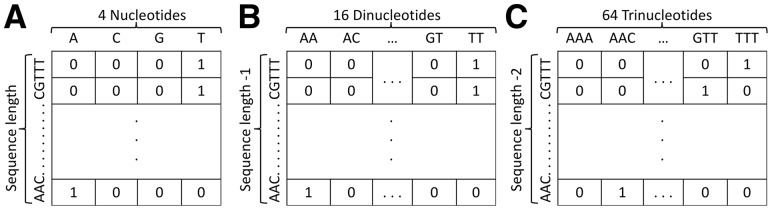
Since DL relies to a considerable degree on a proper representation of the raw data per se, we experimented with multiple data representations and used them to derive a basic CNN structure with fixed parameters. For this, we represent each sequence in a two-dimensional (2D) space that corresponds to mononucleotides (Fig. 2A), dinucleotides (Fig. 2B), and trinucleotides (Fig. 2C), as well as the electron-ion interaction pseudo potential (Nair and Sreenadhan, 2006; Veljković and Lalović, 1973; Veljković and Slavić, 1972), thermodynamic feature (Friedel et al., 2009), and base stacking energy information (Abeel et al., 2008). The results in Supplementary Figures S5 and S6 show a significant correlation between the data representation and the model’s capability to learn directly from data. Notably, the thermodynamic and base stacking data representations completely prevented the network from learning, in which cases the performance accuracy was similar to random predictions. Conversely, the trinucleotide representation achieved the best performance compared to the other representations for both PAS and TIS data (we acknowledge the bias of these two GSRs regarding the coding regions in the upstream region of PAS signals and downstream region in TIS signals). Therefore, DeepGSR uses the trinucleotide data representation as input. The dimensions of the 2 D space for each sequence represented by trinucleotides are (600–2) × 64, where 600 is the length of a DNA sequence with the GSR signal excluded, while 64 corresponds to the trinucleotides sorted in the alphabetic order. For instance, Figure 2C shows a sequence example where the values of one indicate that trinucleotides AAC and TTT are found at the beginning and the end of the sequence, respectively. It is worth noting that the random ordering of the trinucleotides produced comparable results.

Fig. 2.

(A) Mononucleotide data representation. (B) Dinucleotide data representation. (C) Trinucleotide data representation. The best performance was achieved by using the trinucleotide representation

2.2.2 Model structure selection and tuning of model hyperparameters

The CNN has a very complex structure due to the different configurations of stacked layers and tunable hyperparameters, which in turn results in a computationally expensive training of the model. In our implementation of the network, we used Keras (Chollet et al., 2015), a minimalist, highly modular neural networks library, written in Python. We also used Theano library (Al-Rfou et al., 2016; Bastien et al., 2012) as a backend and used GPUs to speed up the network training (Nickolls et al., 2008).

We first defined a general structure of the DeepGSR model consisting of two 2 D convolutional layers as we observed that increasing the number of convolutional layers prevented efficient training, which may be attributed to the vanishing gradient problem (Nielsen, 2015). To introduce the nonlinearity to the system and to tackle the vanishing gradient effect, each of the two convolutional layers is followed by a nonlinear layer with a rectified linear unit (ReLU) as activation function (Glorot et al., 2011), determined according to Equation (1). These convolutional layers are followed by a dropout layer, which is followed by a fully connected layer that functions as a conventional artificial neural network (ANN).

$$f\left(x\right)=\{\begin{array}{c}x, x\ge 0\\ 0, x<0\end{array}$$ (1)

We considered a random search algorithm for selecting the optimized set of hyperparameters (Bergstra and Bengio, 2012) for the dropout layers, fully connected layer, and the first convolutional layer (number and size of filters, optimization methods, initialization methods, batch size, etc.). Due to the large number of possible parameter combinations, the hyperparameters of the second convolutional layer were fixed a priori. Moreover, a single dropout expectation value was tuned during the random search algorithm for both dropout layers. Hundred-random combinations of parameter values were considered, and the best performing model based on the validation set was selected. The hyperparameters search space for the first convolutional and fully connected layers is listed in Table 1, where the parameters in bold indicate the optimized values found. It is important to mention that the number of filters in a convolutional layer is equivalent to the number of features extracted from the data.

Table 1.

DeepGSR parameters

Layer	Parameters	Search space
Conv. layer 1	Number of filters	[20, 50, 100, 150, 200, 250]
	Filter length	[10, 20, 30, 40, 50]
	Filter width	[2, 4, 8, 16, 32, 64]
	Initialization mode	[uniform, lecun_uniform, normal, zero, glorot_normal, glorot_uniform, he_normal, he_uniform]
Conv. layer 2	Number of filters	100
	Filter length	10
	Filter width	8
	Initialization mode	glorot_uniform
Fully connected layer	Activation function	[softmax, softplus, softsign, relu, tanh, sigmoid, hard_sigmoid, linear]
	Number of neurons	[32, 64, 128, 256, 512]
	Initialization mode	glorot_uniform
Learning	Learning batch size	[4, 16, 32, 64, 128]
	Optimizer	[SGD, RMSprop, Adagrad, Adadelta, Adam, Adamax, Nadam]
Regularization	Dropout expectation	[0.05, 0.1, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5]

Note: A single dropout expectation value was tuned for both dropout layers.

Parameters in bold indicate the optimized values found by using a random search algorithm.

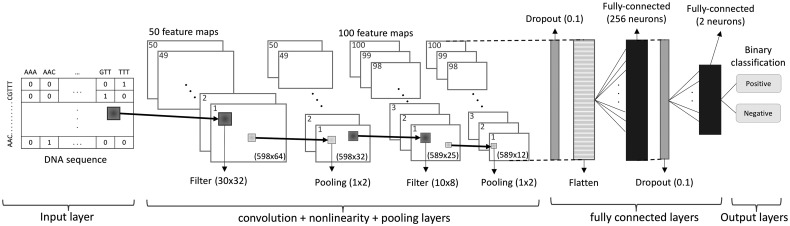
The architecture of DeepGSR is depicted in Figure 3 with details of the selected parameters (from Table 1). The first convolutional layer scans the input with 50 filters of size 30 × 32, a stride of one, and zero padding (to preserve the spatial size of the input layer, 598 × 64). This layer is then followed by a maxpooling layer of size 1 × 2 that selects the best features obtained from the respective filter. The maxpooling layer reduces the spatial dimensions, which lessens both the computation costs and the overfitting of the training data. In our experiments, we observed that the use of average or global pooling negatively affects the results. The combination of the first convolutional and pooling layers may be considered as the global feature extraction block of DeepGSR. The second convolutional layer with 100 filters of size 10 × 8, a stride of one, and no zero padding (producing a reduced output volume with dimensions 589 × 25), extracts 100 more features from the output of the previous layer, representing more specific/local features as they are extracted from a deeper layer of the network (Lu et al., 2017). Similarly, the second convolutional layer is followed by a maxpooling layer of size 1 × 2. To further control the overfitting, the output of the second pooling layer is then followed by a dropout layer (with a dropout expectation of 0.1 selected during the hyperparameters search) that prunes the DeepGSR network during training (by temporarily removing some neurons randomly; Srivastava et al., 2014).

Fig. 3.

The DeepGSR model architecture using 2D-CNN. Each of the two convolutional layers uses ReLU activation function and a maxpooling layer. The input layer is a matrix of size 598 × 64 based on the trinucleotide data representation

After the stacked convolutional layers are used for feature extraction, the output is converted from 3 D (589 × 12 × 100) to 1 D (706, 800) by the flattening layer to make it suitable for a fully-connected layer with 256 hidden neurons, tanh as the nonlinear activation function, and a dropout layer (using the same dropout expectation value as for the first dropout layer). Finally, the fully connected layer is connected to an output classification layer with two output neurons with softmax activation function. These output neurons correspond to the positive (true) and negative (false) target classes (Fig. 3).

It is important to note that although the optimized initialization mode for the first convolutional layer is zero, other initialization modes for this layer achieved competitive results. However, caution has to be made when considering zero initialization. For instance, if the weights for all layers in a network were initialized to zero, all neurons would follow the same gradient during backpropagation, hampering the learning of the CNN. DeepGSR avoids this by using Glorot initialization in the second convolutional and fully connected layers (Glorot and Bengio, 2010).

The 2D-CNN setup has a large number of parameters (∼182 000 000) that need to be tuned during the training, highlighting the need for GPUs to speed up the training process. However, using the same DeepGSR architecture (Fig. 3) but with 1D-CNN and considering the genomic sequences as a text of overlapped trinucleotide words (word embedding) would provide a model with a simpler structure that reduces both the training time and the number of parameters to tune (∼4 000 000). For this, we used the embedding layer in Keras that provides numerical representation for the raw sequence data as a text of overlapped trinucleotide words. The embedding layer takes a matrix of unique words and indices as input, as well as the required embedding dimension. In this setup, we used a grid search algorithm to find the best embedding dimension in the space of 10 to 100 with a step of 10; we found that 20 is the best embedding dimension for DeepGSR.

3 Results

Zeng and colleagues (Zeng et al., 2016) reported that a poorly tuned CNN structure may result in the loss of the functionality and efficiency of the model. However, the number of hyperparameters in CNN makes its tuning a serious challenge. In this study, we performed an extensive and systematic analysis of the multiple hyperparameters combinations and data representation to derive a robust DL structure for the recognition of different GSRs (Section 2). Therefore, the key contribution of our study is the development of DeepGSR, a fixed DL structure with optimized hyperparameters, so that such same structure can be retrained for the recognition of different types of GSRs without making any changes to the originally optimized DL structure. In this study, we trained the DeepGSR structure for the recognition of PAS and TIS signals. We used the human genome data of the most common PAS variant (AATAAA) to select the best data representation, model structure, and set of hyperparameters (Section 2). Since we used the same number of positive and negative samples (balanced data), we report the results based on the accuracy performance measure defined as

$$\text{Accuracy}=\frac{\text{True} \text{predictions}}{\text{All} \text{predictions}}=\frac{\text{tp}+\text{tn}}{\text{tp}+\text{fn}+\text{tn}+\text{fp}}$$ (2)

where tp, tn, fp, and fn denote the number of true positive, true negatives, false positives, and false negatives, respectively. In addition to the accuracy measure, Supplementary Tables S4–S6 show the results using the sensitivity, specificity, and area under the precision recall (AUPR) as performance measures. Additionally, Supplementary Table S7 shows the results of human PAS (AATAAA) and TIS when considering input data with random ordering of trinucleotides.

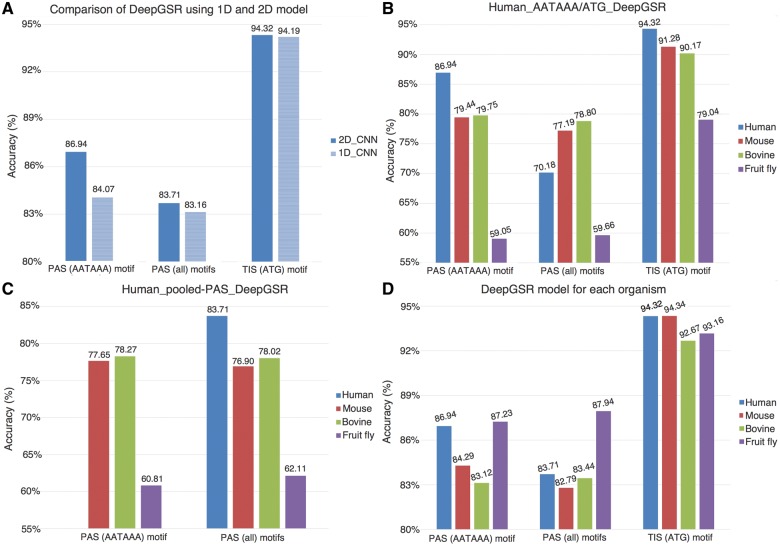
The optimized set of hyperparameters of DeepGSR were determined by using a random search algorithm (Section 2). For all results reported in this section, the optimized structure was trained by using 75% of the data and tested on the remaining 25% of the data. We used the early-stopping technique with a validation set (obtained by selecting randomly 20% of the data from the training set) to stop the training of the network and minimize the overfitting of the model (Prechelt, 1998). Figure 4A shows a comparison between the results obtained by using a 2D-CNN and 1D-CNN with word embedding demonstrating the superiority of the 2 D representation. Therefore, the rest of the reported results are obtained by using the 2 D representation. Nonetheless, we make 1D-CNN model available as it might be suitable for larger scale analyses or for users with limited computational facilities.

Fig. 4.

(A) Performance comparison of DeepGSR using 1D-CNN and 2D-CNN for the recognition of PAS and TIS signals in human genomic DNA. (B) Human_AATAAA_DeepGSR and Human_ATG_DeepGSR were used to test genomes of other organisms (cross-organism tests). For human data only, PAS_all represents all variants except AATAAA + only the testing portion of AATAAA (25%) that was not included in the training. (C) The results on PAS data using Human_pooled-PAS_DeepGSR for predicting PAS in other organisms. (D) The results for PAS and TIS data using DeepGSR organism specific models

3.1 GSR recognition and cross-organism conservation

We conducted cross-organism testing and organism-specific analyses for the recognition of both PAS and TIS in order to assess the performance of the optimized DeepGSR structure. For the cross-organism testing, we derived a DeepGSR model by using the AATAAA PAS variant (human_AATAAA_DeepGSR), and a DeepGSR model trained on human TIS data (human_ATG_DeepGSR). To assess the generalization capabilities of the human_AATAAA_classifier, we tested the model using all PAS variants pooled together, as well as AATAAA variant alone. Moreover, we tested these human-derived models on the genome data of other organisms. Figure 4B shows the results obtained from the model cross-organism testing.

Since the training of DL models requires a sufficiently large training data, it was not possible to derive a model for each PAS variant (as in the case for AATAAA) due to the insufficient number of samples in the less common PAS variants. Therefore, we pooled all PAS variants and trained a classifier, human_pooled-PAS_classifier. Again, we used human PAS data for building the classifier and tested it on data from other genomes for cross-organisms testing. Figure 4C shows the results obtained by the human_pooled-PAS_classifier. In this setup, we obtained similar results as with the human_AATAAA_classifier.

Finally, we conducted organism-specific experiments in which the model was trained and tested on the data from the same genome. We applied this to both PAS and TIS data (Fig. 4D). It is worth mentioning that all results presented in this section are obtained using the same DL structure with the optimized hyperparameters, giving support to a unified framework for GSR recognition.

3.2 Comparison with the state-of-the-art methods

The results in Figure 4D and Supplementary Table S6 show an error rate of 13.06% and 5.68% for the recognition of PAS and TIS in human, respectively. Although our proposed method is free of any GSR-specific or manually crafter features, DeepGSR consistently achieved competitive results for the other considered organisms, and it was able to reduce the error rate of the domain-specific models that were published for the same problems. We compared DeepGSR with Dragon PolyA Spotter (DPS) (Kalkatawi et al., 2013), HMM-SVM (Xie et al., 2013) and Omni-polyA (Magana-Mora et al., 2017) as shown in Table 2 for PAS prediction in the human genome. Table 3 shows the comparison between DeepGSR and TIS-ANN (Haitham et al., 2012; Magana-Mora et al., 2013), iTIS-PseTNC (Chen et al., 2014) and TITER for TIS recognition in the human genome. From the comparison of the results, we observe that DeepGSR models reduced the classification error rate by up to 29% for PAS prediction, and up to 86% for TIS prediction in human compared the state-of-the-art results. The reduction of the error rate was calculated by Equations (3, 4), where x is the method in question, x₁ is a state-of-the-art method and x₂ is DeepGSR.

$$\text{error} \text{rate}(x)=100-\text{Accuracy}(x)$$ (3)

$$\text{relative} \text{error} \text{rate}\left(x_1,x_2\right)=\frac{\left|\text{error} \text{rate}\left(x_1\right)-\text{error} \text{rate}\left(x_2\right)\right|}{\text{error} \text{rate}\left(x_1\right)}$$ (4)

Table 2.

Classification error reduction on the problem of PAS recognition on human

Published models	Published error rate (%)	Reduction of the relative error rate (%)
DeepGSR	13.06	N/A
DPS	16.49	20.80
HMM-SVM	18.59	29.75
Omni-polyA	14.02	6.85
Average	–	19.13

Note: Comparison between the state-of-the-art methods and DeepGSR on the problem of PAS (AATAAA) recognition on the human genome.

Table 3.

Classification error reduction on the problem of TIS recognition on human

Published models	Error rate (%)	Reduction of the relative error rate (%)
DeepGSR	5.68	N/A
TIS-ANN	6.72 (published)	15.48
iTIS-PseTNC	2.08 (published)	−173.08
iTIS-PseTNC	42.32 (tested on DeepGSR data)	86.58
TITER	21.92 (published)	74.09
TITER	18.95 (tested on DeepGSR data)	70.03
Average	—	57.36

Note: Comparison between state-of-the-art methods and DeepGSR on the problem of TIS (ATG) recognition on the human genome.

It is important to note that the published results for the TITER method (TIS predictor) are in terms of the AUROC and AUPR. For a fair comparison, we calculated the classification error reduction achieved by DeepGSR using AUROC measure for TITER, representing a reduction of 47.79% compared to TITER’s published results and 36.82% to TITER’s results on DeepGSR data.

3.3 Performance comparison between manually-crafted features and DL

One important characteristic of DL methods is the ability to automatically extract abstract features from the data. To prove the efficacy of our DL approach presented in DeepGSR, we derived non-GSR-specific manually-crafted features from DNA and compared their performance. The feature generation workflow is shown in Supplementary Figure S7. The manually-crafted features are:

Compositional and statistical properties of nucleotides and polynucleotide sequences.

• Score generated by position probability matrix (PPM) of mono/di/tri nucleotides.

• Electron-ion interaction potential (EIIP) of nucleotides (Veljković and Slavić, 1972).

• Scores generated by position weight matrices (PWM) with and without linear weight function (Equation 5), which assigns different weights to nucleotide positions based on their closeness to the signal under study, i.e., the closer the position the larger the weight.

• GC and AT skew (Lobry, 1996).

• Thermodynamic, structural, and base stacking dinucleotide properties.

• Palindrome sequences.

  $$\text{weight}=2\times \text{position}+1$$ (5)

Each of these features was calculated from four different regions in the sequence to find the sequence region achieving the best classification performance using such feature. These sequence regions are: (i) the whole sequence, (ii) upstream relative to the GSR, (iii) downstream relative to the GSR, and (iv) from windows (overlapped) of different sizes: 10, 20 and 30 base pairs. Supplementary Figure S8 shows the accuracy of an ANN derived by using each of these features individually. Then, we assessed the performance using different feature combinations and selected the top three best performing features and feature combinations. Supplementary Figure S9 shows the accuracy results for these feature combinations. In order to derive a robust model for this comparison, we selected the best performing combination of features and used stacked auto-encoders as an aid to choosing the suitable number of hidden nodes in each layer of a deep ANN.

The results from this comparison (Supplementary Fig. S10) show that the tuned deep ANN derived by using the best performing set of manually-crafted features for PAS human data (AATAAA variant) achieved a maximum accuracy of 81.73%, while DeepGSR achieved 86.94% (representing a reduction of the relative error rate of 28.51%). These results demonstrate that the DL approach is both more reliable and simpler, as features are automatically extracted from the data.

4 Conclusions

In this study, we present DeepGSR, a comprehensive framework based on a DL approach, more specifically CNN, for the recognition of different types of GSR within eukaryotic DNA sequences. The main contribution of this study is the development of a DL structure with optimized hyperparameters. This same structure can be then retrained for different types of GSRs without the need for any further structural optimization. Therefore, DeepGSR provides a fairly general structure for sequence-based recognition of different GSRs, i.e., splice sites, stop codon, etc. On the considered types of GSR, DeepGSR outperformed the state-of-the-art results.

We reported the performance of DeepGSR on the recognition problem of PAS and TIS signals for four different organisms, namely, human, mouse, bovine and fruit fly. We focused on the recognition of PAS and TIS as they are key GSR for understanding certain diseases. For instance, PAS and its surrounding regions may harbor mutations that cause or contribute to different diseases, i.e., thalassaemia, metachromatic leukodystrophy, IPEX and Fabry's disease (Elkon et al., 2013). On the other hand, TIS defines the start of the coding sequence of protein-coding genes. The dysregulation of the translation initiation process may cause various diseases, such as cancer and metabolic disorders (Zhang et al., 2017) while a mutation in TIS may cause inherited disease (Wolf et al., 2011). Thus, accurate determination of such signals in genomic DNA may facilitate studies of such conditions.

We conducted both genome-wide and cross-organism model testing to study the conservation of the GSR across species and the robustness of the DeepGSR model. According to the results with both the TIS and PAS data, the correlation between human, mouse, and bovine appears strong, suggesting high conservation of these signals in mammals, but less than in genomes of more distant eukaryotes (fruit fly). Results also indicate that the 5′UTR, or the start of the gene, appears to be more conserved than the 3′UTR. These observations stem from the very good cross-organisms results of TIS compared to PAS.

Although we applied DeepGSR for the recognition of PAS and TIS, the same approach may be applied for the recognition of splice sites, polyadenylation cleavage sites or stop codons.