False discovery control for penalized variable selections with high-dimensional covariates

Abstract

Modern bio-technologies have produced a vast amount of high-throughput data with the number of predictors much exceeding the sample size. Penalized variable selection has emerged as a powerful and efficient dimension reduction tool. However, control of false discoveries (i.e. inclusion of irrelevant variables) for penalized high-dimensional variable selection presents serious challenges. To effectively control the fraction of false discoveries for penalized variable selections, we propose a false discovery controlling procedure. The proposed method is general and flexible, and can work with a broad class of variable selection algorithms, not only for linear regressions, but also for generalized linear models and survival analysis.

1. Introduction

With the advance of array and sequencing-based technologies, modern transcriptomics studies are capable of simultaneously measuring the expression levels for tens of thousands of genes, providing unprecedented insights into the etiology of many common diseases. By relating gene expression levels to the progression of diseases or other disease phenotypes, previous studies have identified many genes associated with disease-relevant clinical outcomes (Gui and Li, 2005; Shaughnessy et al., 2007).

The standard procedure to perform transcriptomics analysis is to evaluate one gene at a time and examine its relationship with disease-related outcomes. However, this approach often results in low statistical power to identify the disease-associated genes (Sun et al., 2017). Recently, penalized regression methods, such as the Lasso (Tibshirani, 1996) and the elastic net (Zou and Hastie, 2005), have been applied to jointly analyze all predictors to increase the power. These methods are also being applied to genetic association studies and transcriptomics analysis (e.g. Ayers and Cordell (2010); Cho et al. (2010); Wu et al. (2009)). In these applications, the cross-validation procedure is commonly used to select the optimal regularization parameter, which, unfortunately, can not guarantee control of false discoveries.

Controlling for false discovery is important as it is extremely costly to validate false discoveries. In settings for large-scale hypothesis testing, Benjamini and Hochberg’s FDR-controlling procedure (Benjamini and Hochberg, 1995) has been widely adopted. However, for penalized high-dimensional variable selections, little work has been done. A major challenge is that the limiting distribution for the penalized estimators in high-dimensional settings is unknown or difficult to obtain (Bühlmann and van de Geer, 2011). Standard bootstrap or sub-sampling techniques are usually not valid due to the non-continuity of limiting distributions (Efron, 2014). This gap motivates us to propose a novel procedure that improves the performance of variable selection algorithms while providing proper false discovery control. The proposed method is very general and flexible, and can work with a broad class of variable selection algorithms, including the Lasso, the elastic net and iterative sure independent screening (Fan and Lv, 2008), not only for linear regressions, but also for generalized linear models and survival analysis. Using simulations and real data examples, we evaluate our proposed method in combination with the Lasso procedure for variable selection and demonstrate the superior power of our method as compared with previous approaches.

2. Methods

2.1. Notation

Consider a regression model with n independent samples and p predictors. Denote the response vector by $\mathrm{Y}={\left(Y_1,\dots ,Y_n\right)}^T,$ where Y_i is the outcome for the i-th subject. Let $\mathrm{X}={\left[{\mathrm{X}}_1,\dots ,{\mathrm{X}}_n\right]}^T$ be the covariate matrix, where ${\mathrm{X}}_i=\left(X_{i1},\dots ,X_{ip}\right)$ is a p-dimension covariate vector for the i-th subject, 1 ≤ i ≤ n. Let L(β) be a loss function that link X_i to the response Y_i, where β is a p-dimensional vector of regression parameters. Examples of loss functions include the square error loss function for linear regressions, $L(\beta )={\sum }_{i=1}^n{\left(Y_i-{\mathrm{X}}_i^T\beta \right)}^2,$and the negative log-likelihood for logistic regression $L(\beta )=-{\sum }_{i=1}^n\left\{Y_i{\mathrm{X}}_i^T\beta -\log \left(1+\exp \left({\mathrm{X}}_i^T\beta \right)\right)\right\}.$

Our overarching goal is to identify informative variables with non-zero coefficients. Throughout this paper, we use the Lasso (Tibshirani, 1996) as an illustrative example for variable selection, though other variable selection methods could be incorporated as well. The Lasso procedure estimates β via the L₁ penalized optimization

$$\widehat{\beta }=\underset{\beta }{\text{argmin}}\left\{L(\beta )+\lambda \Vert \beta {\Vert }_1\right\},$$

where λ is the regularization parameter that determines the amount of penalization, and $\Vert \beta {\Vert }_1={\sum }_{j=1}^p\left|{\beta }_j\right|$ is the L₁ norm of β. In practice, the regularization parameter is typically determined by K-fold cross-validation (Hastie et al., 2009). For example, split the data into K roughly equal-sized parts. For the kth part, fit the model to the other K – 1 parts, and then calculate the prediction error of the fitted model when predicting the kth part of the data. Repeat for $k=1,\dots ,K$ and λ is chosen to minimize the combined estimates of prediction error. We will show below that this procedure may lead to an excessive number of false discoveries in practical applications.

2.2. False discoveries

We exemplify the issue of false discoveries with simulations based on a real data example (Shaughnessy et al., 2007), which contains a total of 340 patients and 23,052 gene expressions. We simulate continuous outcomes based on real gene expression such that 50 predictors (randomly drawn from the 23,052 predictors) have non-zero effects. The magnitude of the effect size follows a uniform (0.2, 1) distribution. The sign of the effects is randomly selected with equal probability of being positive or negative. The random error for the continuous outcomes is generated from the standard normal distribution. We apply the Lasso (implemented by R package glmnet) with 10-fold cross-validation and randomly repeat the procedure 10,000 times. Figure 1a shows the histogram for the proportion of false discoveries. The cross-validated choices of regularization parameters are data-dependent and the numbers of false discoveries vary substantially. Across all replicates, the algorithm tends to select too many irrelevant variables. In contrast, Figure 1b shows that our proposed procedure (termed PS-Fdr) effectively controls the false discoveries.

Fig. 1:

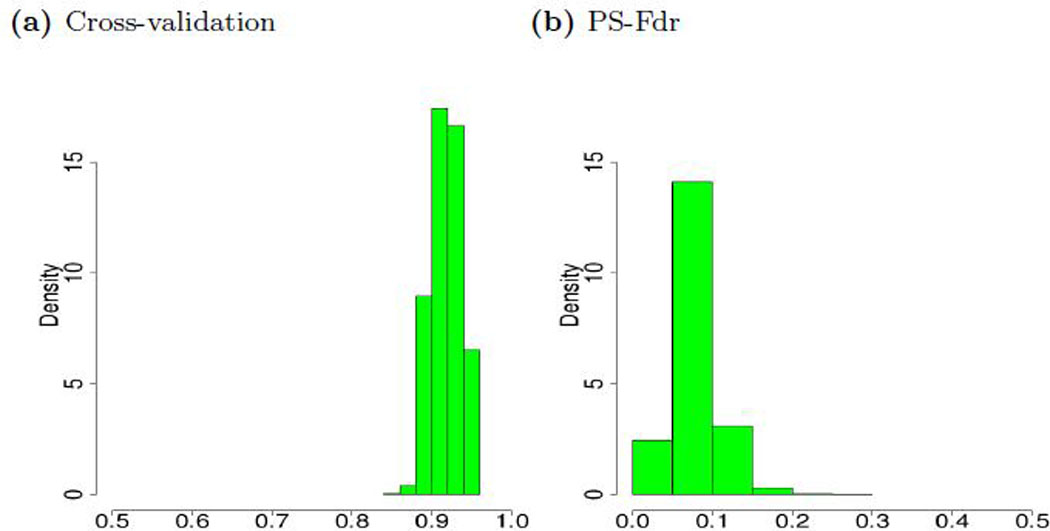
Histograms for the false discovery proportion (FDP). Figure 1a shows the histogram for the proportion of false discoveries for the Lasso with regularization parameters chosen by 10-fold (randomly repeat the procedure 10,000 times). Figure 1b shows the histogram for the proposed PS-Fdr procedure.

2.3. Statistical challenges

In the context of hypothesis testing, classical FDR-controlling procedures act on a set of valid P-values. For penalized variable selection, one major challenge is that the limiting distribution for the penalized estimators is unknown and hence valid P-values are difficult to obtain (Bühlmann and van de Geer, 2011). Even the standard permutation methods are inadequate (Barber and Candês, 2015). For example, although permutation preserves the correlation between the predictors, it involves an extra assumption that the variable selection always follows the same pattern as that under the global null (i.e. no variable is associated with outcomes). In other words, the fact that some of the predictors are non-null does not affect the selection pattern of the null predictors. However, for penalized variable selection, the permuted variables (under the global null so that no permuted variable is associated with outcomes) have much fewer chances of being selected than the non-informative variables in the original samples (where some of the predictors may be non-null). The resulting FDR is under-estimated and the corresponding FDR-controlling procedure tends to select too many irrelevant variables (as shown in Section 3.1 of Barber and Candes (2015)). It is not obvious how to use existing permutation-based techniques to effectively control for false discoveries for penalized variable selections. In the next subsection, we propose a possible approach to this problem. A key ingredient of our proposed method is to construct a valid statistics such that the original predictors and the permuted variables are comparable.

2.4. False discovery controls for penalized variable selections

We consider a variable selection problem with p candidate predictors. We define the predictor j as “null” if it has no association with the outcome variable. Let the random variable FDP represent the false discovery proportion:

$$\text{FDP}=\frac{N_0}{N_{+}}\text{if}{N}_{+}>0,\text{and}\text{FDP}=0\text{if}{N}_{+}=0,$$

where N₀ is the number of falsely selected variables, and N₊ is the total number of selected variables. The false discovery rate in this context is defined as the expectation of FDP, e.g. FDR = E(FDP). Following the notations in Section 2.2 of Efron (2013), we define

$$\text{Fdr}=\frac{e_0}{e_{+}},\text{and}\text{an}\text{estimate}\text{of}\text{Fdr}\text{is}\text{computed}\text{as}\widehat{\text{Fdr}}=\frac{{\widehat{e}}_0}{N_{+}},$$

where e₀ = E(N₀) is the expectation of N₀, e₊ = E(N₊) is the expectation of N₊, and ê₀ is the estimate of e₀. In the context of hypothesis testing, Genovese and Wasserman (2004) showed that

$$\text{FDR}=\text{Fdr}+o(\frac{1}{p}).$$

In this report, we aim to estimate the Fdr for penalized variable selections. A key computational step is then estimating e₀, which we achieve by extending stability selection (Meinshausen et al., 2010) and Significance Analysis of Microarrays (SAM) (Tusher et al., 2001).

We start by implementing stability selection (Meinshausen et al., 2010), which is an effective procedure to rank the importance of predictors. The idea is to identify variables that are included in the model with high probabilities when a variable selection procedure is performed on a random sample of the observations. Specifically, we bootstrap (sample with replacement to form a new sample that is also of size n) multiple (B) times. For each resampled data (e.g. for b=1,..., B), we implement the Lasso and denote the selected index set by

$${\widehat{\mathcal{S}}}^{(b)}=\left\{j=1,\dots ,p:{\widehat{\beta }}_j^{(b)}\ne 0\right\}.$$

The selection frequency is then computed as the empirical probability that each variable is selected

$${\Pi }_j=\frac{1}{B}\sum _{b=1}^{B}I\left(j\in {\widehat{\mathcal{S}}}^{(b)}\right),j=1,\dots ,p.$$

We then order the selection frequencies such that ${\Pi }_{(1)}\le {\Pi }_{(2)}\le \dots \le {\Pi }_{(p)},$ which are effective measures to rank the relative importance of predictors.

As successful as such a procedure is, it also has unresolved issues. For instance, to determine which variables should be selected, a new regularization parameter to be determined is the threshold based on selection frequencies. In practice, it is not obvious how to obtain such a threshold (He et al., 2016), making the selection results difficult to evaluate. To solve this issue, we determine the threshold based on a desired Fdr-controlling level.

To estimate the Fdr, we randomly permute the outcomes M times to decouple the relation between the covariates and the outcomes. On each permuted dataset, say m = 1, …, M, we implement the stability selection procedure and compute the corresponding selection frequencies, denoted by ${\tilde{\Pi }}_j^{(m)},$ $j=1,\dots ,p.$ To avoid under-estimation of e₀, instead of implementing cross-validation to select the number of variables on each permuted sample, we fix the number of selected variables (e.g. the medium number of selected variables using the stability selection procedure on the original sample). We order the selection frequencies such that ${\tilde{\Pi }}_{(1)}^{(m)}\le {\tilde{\Pi }}_{(2)}^{(m)}\le \dots \le {\tilde{\Pi }}_{(p)}^{(m)},$ and then define ${\overline{\Pi }}_{(j)}={\sum }_{m=1}^M{\tilde{\Pi }}_{(j)}^{(m)}/M,$ the permuted counterpart of ${\Pi }_{(j)}.$

To compare original predictors with their permuted counterparts, we compute the normalized statistics, $Z_{(j)}=D\left({\Pi }_{(j)}\right),$${\tilde{Z}}_{(j)}^{(m)}=D\left({\tilde{\Pi }}_{(j)}^{(m)}\right),$ and ${\overline{Z}}_{(j)}=D\left({\overline{\Pi }}_{(j)}\right),$ where for $0\le u\le 1,$ $D(u)=u/(\sqrt{u(1-u)}+\nu ).$ These normalized statistics share the virtue of the original SAM statistics and further tease apart variables by providing larger values for most of the informative variables and smaller values for most of the non-informative ones. To ensure that the denominator of normalized statistics is non-zero, we add a small positive number v (e.g. v = 1/B). The proposed post-selection Fdr-controlling procedure (termed as PS-Fdr) is summarized as follows:

Algorithm (PS-Fdr)

• (1)For a given positive constant Δ, we identify a cutoff for the ordered Z values,

$$Z(\Delta )=\min \left\{Z_{(j)}:j=1,\dots ,p,Z_{(j)}\ge {\overline{Z}}_{(j)}+\Delta \right\}.$$

Note that step (1) is a step-down procedure. For the index $j=1,\dots ,p,$ starting from the left, moving to the right, we find the first $j=j^{*}$ such that the difference between $Z_{\text{(}j\text{)}}$ and its permuted counterpart is above Δ, e.g. $Z_{(j)}-{\overline{Z}}_{(j)}\ge \Delta .$All the indices past this j* have ordered Z values larger than or equal to Z(Δ), and will be selected if Z(Δ) is chosen as the cutoff.

• (2)Count the number of Z values that are above this Z(Δ) cutoff in order to obtain the number of selected variables: $N_{+}(\Delta )={\sum }_{j=1}^{p}I\left(Z_{(j)}\ge Z(\Delta )\right).$
• (3)Count the average number of Z values in the permuted data that are above the Z(Δ) cutoff. This average number serves as an estimate of the expected number of false discoveries

$${\widehat{e}}_0(\Delta )=\sum _{j=1}^p\sum _{m=1}^{M}I\left(\tilde{Z}{}_{(j)}^{(m)}\ge Z(\Delta )\right)/M.$$

• (4)Estimate the false discovery rate by $\widehat{Fdr}(\Delta )={\widehat{e}}_0(\Delta )/N_{+}(\Delta ).$
• (5)Compute $\widehat{Fdr}(\Delta )$ for a range of Δ values, e.g., for each difference ${\Delta }_{(j)}=Z_{(j)}-{\overline{Z}}_{(j)},$ compute the corresponding $\widehat{Fdr}\left({\Delta }_{(j)}\right).$
• (6)For a pre-specified value $q\in (0,1),$ the selected index set is determined by

$${\widehat{\mathcal{S}}}_q=\left\{j:\widehat{Fdr}\left({\Delta }_{(j)}\right)\le q,j=1,\dots ,p\right\}.$$

Remark 1: Such an algorithm ensures that at most q proportion of the selected variables would be false positives. For instance, if q = 0.1 and 10 variables are selected with $\widehat{Fdr}\le q,$ at most 1 of these 10 variables would be a false positive.

Remark 2: One advantage of the proposed method is that it shares the SAM virtue of not requiring the theoretical distribution of the summary statistics; hence it is more flexible for a broad class of regression layouts.

Remark 3: The accuracy of $\widehat{Fdr}$ as an estimate of the false discovery rate depends on the variability of the denominator N₊. As shown in Figure 1a, the numbers of selected variables may vary substantially in practice. This motivates us to compute selection frequencies, which are relatively insensitive to regularization parameters. As shown in Meinshausen et al. (2010), even the magnitudes of selection frequencies vary with different regularization parameters, the relative rankings among predictors are stable.

Remark 4: The proposed $\widehat{Fdr}$ is motivated by the two-groups mixture model discussed in Efron (2008) and Section 2.2 of Efron (2013). In the context of hypothesis testing, $e_0={\pi }_{0}p{F}_0,$where π₀ denotes the unknown proportion of null predictors among all candidate variables, and F₀ is the probability distributions of z-values corresponding to the null predictors. In this paper, we follow the practical strategy of Benjamini and Hochberg (1995) by setting ${\pi }_0=1$ and hence, estimate an upper bound of FDR.

2.5. Related works

To quantify uncertainty of penalized estimators, a familywise error (FWER)-controlling procedure was provided based on multiple sample-splitting (Mein-shausen et al., 2009). This algorithm starts by randomly splitting the original data multiple times. It then selects variables based on the first half of the data, and fits conventional low-dimensional regression and assigns p-values based on the second half of the data. Finally, the adjusted p-values are computed to correct for the multiplicity. Alternatively, the knockoff procedure was recently introduced by Barber and Candês (2015) to construct a set of so-called “knockoff” variables which imitate the correlation structure of the original variables, but are not associated with the response variable. Only those variables that are more associated with the response than their knockoff counterparts are selected. Despite their theoretical advantages, issues such as reduced power may be encountered in finite-sample settings. The results will further worsen for settings with relatively small sample sizes.

3. Simulation

We assess the performance of the proposed PS-Fdr procedure by comparing it with 10-fold cross-validation and the knockoff procedure (Barber and Candês, 2015). These approaches are all based on the Lasso (implemented by the R package glmnet; (Simon et al., 2011)). The PS-Fdr procedure is implemented with B = 50 bootstraps and M = 100 permutations. We also compare our proposed method with the classical Benjamini-Hochberg procedure based on univariate tests (termed Univariate FDR). A control level q = 0.1 is used for the Univariate FDR, the knockoff and the PS-Fdr procedures. For each configuration, a total of 100 independent data are generated.

3.1. n > p

The knockoff procedure proposed by Barber and Candês (2015) was designed for linear regression with sample size greater than the number of predictors. To compare it with the proposed method, we first consider linear regression settings with n > p.

Model A (Linear Regression): Data are generated with n = 550 subjects and p = 500 predictors, which come from a multivariate normal distribution with mean 0 and a unit standard deviation and a block-diagonal covariance structure (5 independent blocks; each with 100 predictors). Within each block the variables follow a first-order autoregressive (AR1) with the auto-correlation parameter 0.6. We generate continuous outcomes such that 20 predictors (randomly drawn from p = 500) are associated with the outcomes. The magnitude of the effect size varies from 0.25 to 0.4. The sign of the effects is randomly selected. The random error for the continuous outcomes follows the standard normal distribution.

Model B (Linear Regression): Data are generated with n = 1, 000 subjects and p = 500 predictors. All other set ups are the same as those in Model A.

Tables 1 and 2 reports five measures: the average number of false discoveries (FD), the average number of false negatives (FN), the average proportion of false discoveries (FDP), the empirical probabilities of informative predictors that are correctly identified as such (Power), and the average number of FD and FN combined (FD+FN). In all settings, the number of falsely chosen variables for the proposed PS-Fdr procedure is well controlled at the desired level. There is clearly a price to pay for controlling the false discoveries, as the cross-validation detects more truly informative variables than other approaches. Although the cross-validation has comparable performance in terms of fewer false negatives and high power, it selects in all cases too many irrelevant variables. The knockoff procedure is considerably less powerful than the proposed method, especially in Model A with relatively small sample size.

Tab. 1:

Summary of simulation results for Model A (n=550 and p=500). FD: numbers of false discoveries; FN: numbers of false negatives; FDP: proportions of false discovery; Power: empirical probabilities to identify informative predictors; FD+FN: FD and FN combined.

|β|	Methods	FD	FN	FDP	Power	FD+FN
0.25	Univariate FDR	14.91	4.15	0.485	0.793	19.06
	Cross-Validation	62.22	0.09	0.758	0.996	62.31
	Knockoff	0.05	18.01	0.025	0.100	18.06
	PS-Fdr	1.83	1.70	0.091	0.915	3.53
0.30	Univariate FDR	19.08	2.92	0.528	0.854	22.00
	Cross-Validation	62.47	0.03	0.758	0.999	62.50
	Knockoff	0.03	17.94	0.014	0.103	17.97
	PS-Fdr	1.83	0.65	0.086	0.968	2.48
0.35	Univariate FDR	22.31	2.27	0.557	0.887	24.58
	Cross-Validation	62.81	0.01	0.759	1.000	62.82
	Knockoff	0.05	17.44	0.019	0.128	17.49
	PS-Fdr	1.91	0.29	0.088	0.986	2.20
0.40	Univariate FDR	24.46	1.98	0.576	0.901	26.44
	Cross-Validation	62.99	0.00	0.759	1.000	62.99
	Knockoff	0.11	16.92	0.034	0.154	17.03
	PS-Fdr	1.85	0.05	0.085	0.998	1.90

Tab. 2:

Summary of simulation results for Model B (n=1,000 and p=500).

|β|	Methods	FD	FN	FDP	Power	FD+FN
0.25	Univariate FDR	35.73	0.72	0.758	0.964	36.45
	Cross-Validation	57.85	0.00	0.743	1.000	57.85
	Knockoff	1.77	4.40	0.102	0.780	6.17
	PS-Fdr	2.14	0.10	0.097	0.995	3.53
0.30	Univariate FDR	41.17	0.63	0.680	0.969	41.80
	Cross-Validation	56.17	0.00	0.737	1.000	56.17
	Knockoff	1.80	1.83	0.090	0.908	3.63
	PS-Fdr	1.57	0.00	0.073	1.000	1.57
0.35	Univariate FDR	45.24	0.58	0.700	0.971	45.82
	Cross-Validation	56.72	0.00	0.739	1.000	56.72
	Knockoff	2.10	0.24	0.096	0.988	2.34
	PS-Fdr	1.72	0.00	0.079	1.000	1.72
0.40	Univariate FDR	48.22	0.53	0.712	0.974	48.75
	Cross-Validation	58.09	0.00	0.744	1.000	58.09
	Knockoff	2.79	0.29	0.124	0.986	3.08
	PS-Fdr	2.15	0.00	0.097	1.000	2.15

3.2. n < p

Model C (Linear Regression): Data are generated with n = 500 subjects and p = 1,000 predictors. The magnitude of the effect size varies from 0.2 to 0.5. All other set ups are similar to those in Model A.

Model D (Logistic Regression): Binary outcomes follow a Bernoulli distribution. The magnitude of the effect size varies from 0.5 to 1.

Model E (Survival Analysis): Death times are generated from the standard exponential distribution. Censoring times are generated from a uniform (0, 3) distribution. The magnitude of the effect size varies from 0.2 to 0.5.

Model F (Linear Regression): To assess the effect of sparsity level, we vary the number of informative variables from 10 to 50. The magnitude of the effect size follows a uniform (0.2, 1) distribution. All other set ups are the same as Model C.

Model G (Logistic Regression): Binary outcomes are generated from a Bernoulli distribution with covariate effects similar to those in Model F.

Model H (Survival Analysis): The death and censoring distribution are similar to Model E. All other set ups are the same as Model F.

As shown in Figures 2 and 3, the proposed method offers a strong advantage over Univariate FDR. In all settings, the proposed method has the highest power while successfully controlling the false discovery proportions.

Fig. 2:

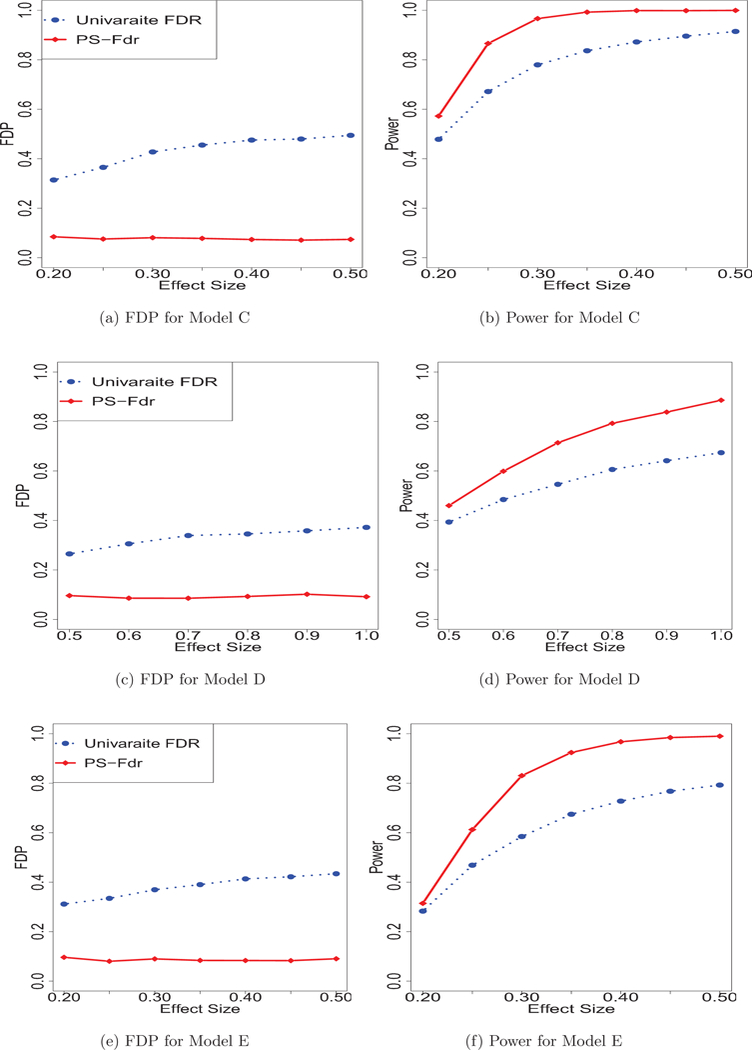
Simulation results for Model C-E. Figure 2 reports two measures: the average proportion of false discoveries (FDP), and the empirical probabilities of informative predictors that are correctly identified as such (Power).

Fig. 3:

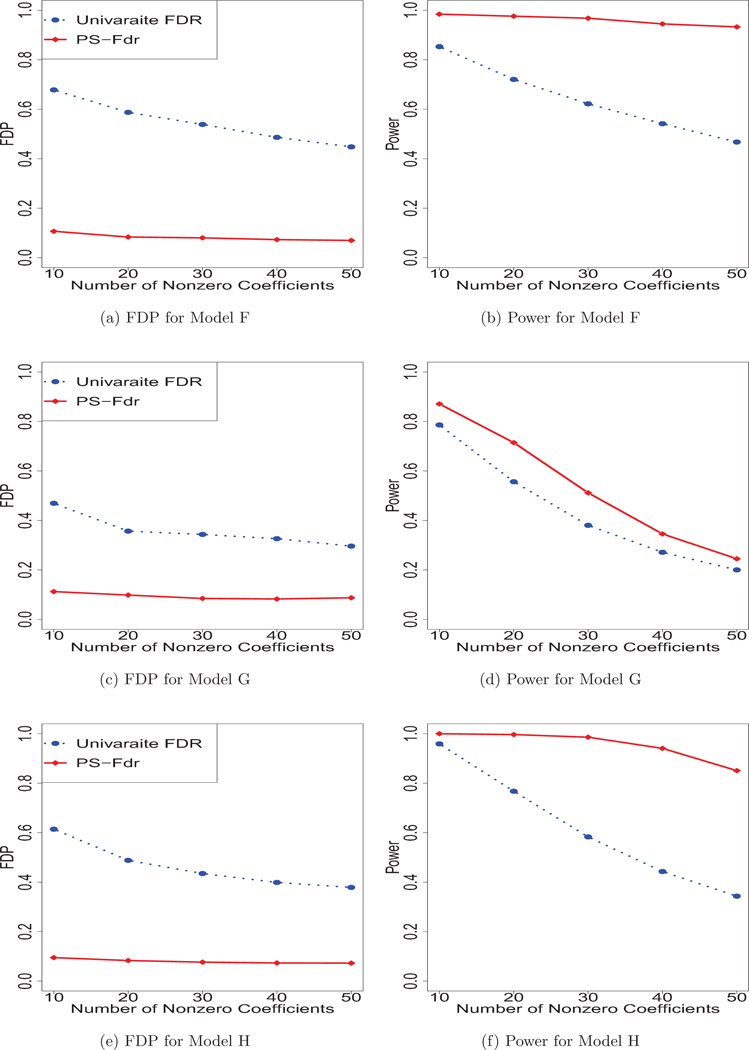
Simulation results for Model F-H. Figure 3 reports two measures: the average proportion of false discoveries (FDP), and the empirical probabilities of informative predictors that are correctly identified as such (Power).

3.3. Performance with various tuning parameters

Figure 4a compares the performance with various choices of regularization parameters. We generate data under Model C with 50 informative variables. For each data configuration, let λ_min and λ_max be the minimum and maximum of the optimal regularization parameters selected by 1,000 replicates of cross-validation. Define

$$\lambda ={\lambda }_{\max }+\gamma \left({\lambda }_{\min }-{\lambda }_{\max }\right).$$

Fig. 4:

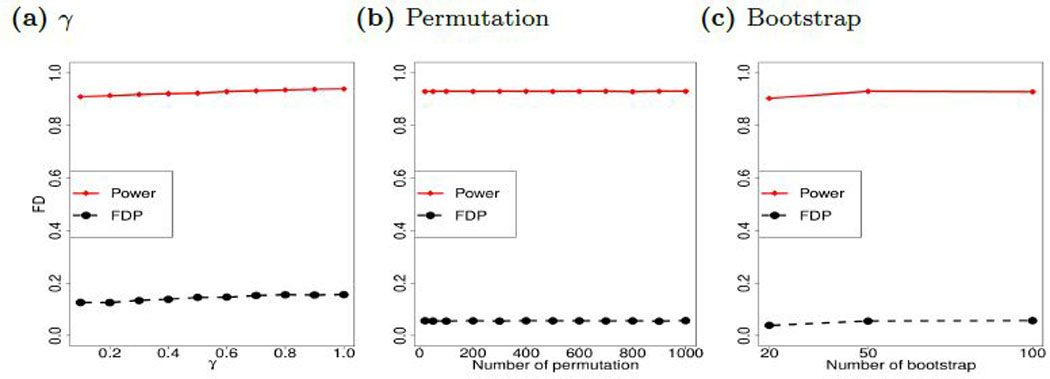
Perturbation with various tuning parameters. (a) Figure 4a compares the performance with various choices of $\lambda :\lambda =\lambda \max +\gamma \left({\lambda }_{\min }-{\lambda }_{\max }\right),\text{where}{\lambda }_{\min }$ and λ_max are the minimum and maximum of regularization parameters selected by 1,000 replicates of cross-validation; (b) Number of permutation; (c) Number of bootstrap.

As we vary γ from 0 to 1 by 0.1, we obtain 11 choices of regularization parameters, which are applied for the proposed method. The results in Figure 4a suggest that the perturbation of regularization parameters has relatively small effects on the proposed PS-Fdr procedure. We also vary the number of permutations or the number of bootstraps to assess the performance of the proposed method. As illustrated in Figures 4b and 4c, the performance of the proposed PS-Fdr procedure is relatively robust to the number of permutations, while 50–100 bootstraps are sufficient for reliable estimations of the Fdr.

4. Real data study

4.1. Multiple myeloma data

We use gene expression and survival outcome from multiple myeloma patients who were recruited into clinical trials UARK 98–026 and UARK 2003–33, which studied total therapy II (TT2) and total therapy III (TT3), respectively. These data are described in Shaughnessy et al. (2007), and can be obtained through the MicroArray Quality Control Consortium II study (Shi et al., 2010), available on GEO (GSE24080). Gene expression profiling was performed using Affymetrix U133Plus2.0 microarrays. Expression values for a total of 23,052 probe sets are used for our analysis. The TT2 arm is used as the training set with 340 subjects and 126 observed deaths. The TT3 arm is used as the validation set with 214 subjects and 55 observed deaths. The overall survival time is calculated from the date of diagnosis to the date of death or the date of the last follow up.

The proposed Fdr procedure is implemented based on the penalized Cox proportional hazards model to identify high-risk genes associated with survival time. The importance of predictors is evaluated by the estimated false discovery rate. We compare the proposed methods with the cross-validation. The cross-validation based Lasso procedure selects 21 predictors. In contrast, no variables are selected by the MS-Split procedure. The proposed Fdr procedure selects 11 variables with the estimated $\widehat{Fdr}\le 0.1,$ which are a subset of variables selected by the Lasso. These results are consistent with those from simulation section. The Lasso tends to select many irrelevant variables. The proposed method selects substantially fewer variables than the Lasso and provides a control for false discoveries.

To assess the selection results, we compute the C-index (i.e. concordance index, an extension of the area under the curve for survival analysis (Uno et al., 2007)) on the validation sample. The set of variables selected by the proposed method achieves a C-index of 0.713, which outperforms the performance of the model based on the classical cross-validation approach (C-index of 0.677).

4.2. Type 2 diabetes data

The second dataset was collected from skeletal muscle samples of Finnish individuals (Scott et al., 2016) as part of the Finland-United States Investigation of NIDDM Genetics (FUSION) project. The data are publicly available in dbGaP with accession code phs001068.v1.p1. The data contains n = 271 individuals and p = 21,735 gene expression measurements.

The proposed PS-Fdr procedure is implemented based on the penalized linear regression to identify genes whose expression level is associated with insulin, a continuous trait related to type II diabetes. In the analysis, we include age, sex and batch labels as covariates following the original study (Scott et al., 2016). The 10-fold cross-validation procedure selects 235 genes. In contrast, no variables are selected by the MS-Split procedure (50 sub-sampling). The proposed PS-Fdr procedure selects one gene with an estimated $\widehat{Fdr}\le 0.1$ and three genes with an estimated $\widehat{Fdr}\le \mathrm{0.2.}$ Finally, we compute the prediction error by a 10-fold cross-validation. The average squared prediction error across 10 partitions for the proposed PS-Fdr (with q = 0.2) and the cross-validation based procedure are 23.27 and 23.92 respectively. Therefore, the proposed method, though selecting substantially fewer variables than the cross-validation based Lasso, maintains similar prediction accuracy.

5. Discussion and Conclusion

Choosing the amount of regularization for penalized variable selection is notoriously difficult for high-dimensional data. Indeed, most existing penalized variable selection algorithms can not guarantee a proper control of false discovery rates. In this report, we propose a false discovery controlling procedure for penalized variable selections in high-dimensional settings. We show that the proposed method, in conjunction with the Lasso, can bring substantial improvements over conventional procedures in terms of false discovery control. Our proposed approach is effective in identifying disease-associated genes while guarding against the inclusion of an excessive number of false discoveries. The proposed method can be integrated with existing variable selection approaches to improve error control for false discoveries.