Jumping dynamics of aquatic animals

Abstract

Jumping out of water is a phenomenon exhibited by a variety of aquatic and semi-aquatic animals. Yet, there is no common groundwork that clarifies the physical constraints required to jump out of water. In this study, we elucidate the physical conditions required for an animal to jump out of water. More than 100 jumps are analysed over five taxonomic groups. By balancing the power produced by animals with drag-induced dissipation, we expect that maximum jumping height, H, scales with body length, L, as H/L ∼ L^−1/3 ∼ Fr², where the Froude number, Fr, is a ratio of inertia to gravity. To identify jumping regimes, simplified experiments are conducted by shooting axisymmetric bodies through the water surface. Here, we see a transition in which partial exits scale as H/L ∼ Fr and complete exits scale as H/L ∼ Fr². A bioinspired robotic flapping mechanism was designed to mimic the fast motion of impulsive jumping animals. When exiting water, the robot carries a large volume of fluid referred to as an entrained mass. A theoretical model is developed to predict the jumping height of various water-exiting bodies, which shows that the mass of the entrained fluid relative to the mass of the body limits the maximum jumping height. We conclude that the lack of entrained fluid allows animals to reach extraordinary heights compared to our water-exiting robots.

1. Introduction

In nature, many animals across five different taxa leap out of water to escape from predators, capture prey, breathe, communicate or even recreationally. It is often used as a survival mechanism, particularly for smaller animals. The copepod (figure 1a), for example, performs the so-called aerial escape mechanism to evade predators [1]. Some fish and frogs (figure 1b) jump out to capture insects on low hanging branches [2,3] or to escape from external stimulii such as motorboats [4]. Many other fish jump to overcome obstacles during migrations [5–7]. Larger animals among a wide range of taxa have also been observed to leap out of water, such as penguins jumping onto ice shelves [8,9], dolphins [10–14], sharks [15] and whales (figure 1c) [16]. Even humans leap partially out of water during various water sports [17,18]. While literature exists for individual animals jumping out of water, there appears to be no common groundwork that clarifies the physical constraints among different animals for leaping out of water.

Figure 1.

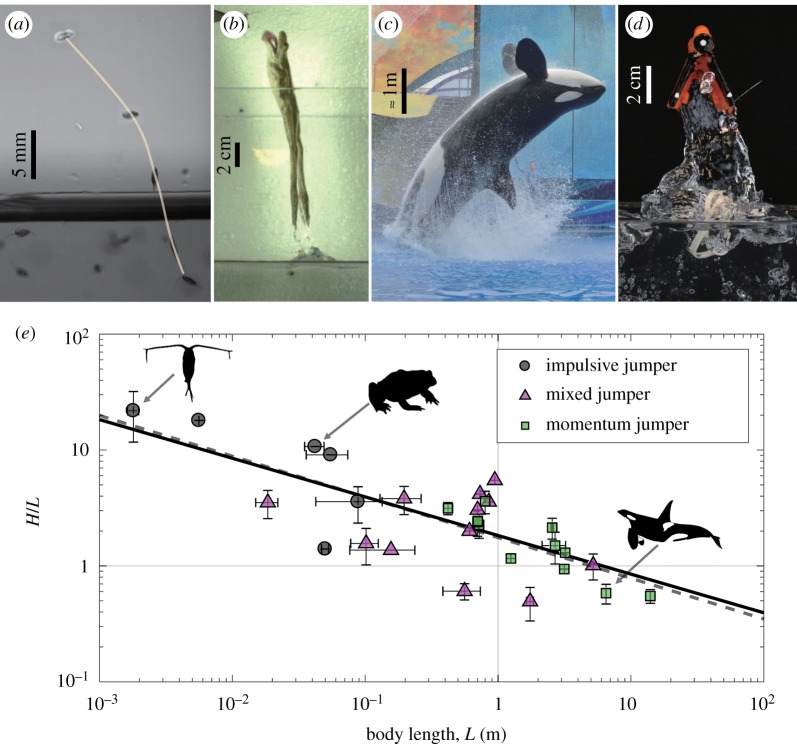
Aquatic animals jumping out of water. (a) Copepod with a thin line tracing its trajectory (H/L ≈ 10, where H is the jump height and L is the body length). Photo courtesy of Brad Gemmell. (b) A frog (H/L ≈ 1.1). (Photo courtesy of Jake Socha and Talia Weiss.) (c) An orca whale (H/L ≈ 0.7). (d) Copepod inspired robot (H/L ≈ 2.6). (e) Normalized jumping height of various animals relative to body length. This follows a slope of H/L ∼ L^−1/3 (solid line), with a line of best fit −0.35 ± 0.12 (dotted lined, r² = 0.57, 95% CI). It is interesting to note that the copepod does not entrain fluid when it completely exits water, whereas the frog, whale and robot entrains fluid. (Online version in colour.)

The mechanics of swimming in animals has been a topic of interest for many years [19–22]. A great deal of work has gone into scaling animal swimming speed. Bainbridge has empirically determined that the swimming speed of steady swimming fish scales with its frequency as f ∼ U/L [23]. Only recently was there a mechanistic rationale for this scaling [24,25]. However, there is a limit to how fast an animal can swim relative to its body size. When incorporating a time scale for which muscles can maintain acceleration, a constraint is placed on the speed of larger animals [26]. The allometry and scaling of swimming animals are well studied, but to the best of our knowledge, few studies have been conducted on the commonality of hydrodynamic forces that govern the leap height for aquatic animals.

Studies have shown that certain species of copepods are able to leap out more than 25 times their own body length [1,27,28]. Here, two dimensionless quantities determine the jumping: Froude number (ratio of inertia to gravity) and Weber number (ratio of inertia to surface tension). By generating a high enough velocity, copepods can break through the water surface [27], which is not a small feat due to their sub-capillary length scale. Looking at animals larger than the capillary length scale, a small fish like the Trinidadian guppy can jump around 3.5 body lengths [7]. A detailed analysis of the archerfish kinematics show they can jump around 2.5 body lengths [29]. While the caudal fin appears to produce the most thrust, this study also showed the importance of the anal, pectoral and dorsal fins during thrust production using particle image velocimetry. It is hypothesized that penguins release air that is trapped under their feathers to reduce drag before exiting the water when they leap onto ice shelves [9]. Presumably, this air layer allows them to reach higher speeds in order for them to leap approximately one body length. Moreover, one study has systematically explored hydrodynamic forces acting on bioinspired bluff bodies exiting water [30]. While jumping out of water has been studied for individual animals, a mechanistic understanding of jumping height relative to body size throughout a range of taxa remains unknown.

In this study, we investigate the hydrodynamic mechanisms and geometry that will allow aquatic and semi-aquatic animals to leap out of water. Animals leaping out of water are first classified into three categories: impulsive jumpers (initially at rest near water surface), momentum jumpers (begin building speed far from water surface) and mixed jumpers (a combination of the other two). By analysing videos of aquatic animals jumping out of water, the jump height per body length was determined to scale as H/L ∼ L^−1/3 (figure 1e), which is mechanistically equivalent to H/L ∼ Fr². To further understand different jumping regimes, axisymmetric bodies are shot through the water surface. Finally, a simple, bioinspired flapping robotic system (figure 1d) was designed to mimic the jumping height to Froude number relationship.

2. Results

2.1. Animal scaling

The animals are divided into three groups based on their kinematics: impulsive jumpers, momentum jumpers and mixed jumpers (electronic supplementary material, figure S1). Impulsive jumpers are characterized by their quick jump, in which they initially start at rest close to the free surface and then flap their appendage with a single stroke. Momentum jumpers first build up momentum, typically far from the water surface, by continuously stroking their appendage, to reach a steady swimming speed prior to exiting the water. A mixed jumper exhibits behaviours from the other two groups, in which jumping occurs near the free surface by using only a few strokes. For example, the archerfish starts from rest near the free surface (similar to an impulsive jumper) but undulates its body several times before exiting the free surface (like a momentum jumper). A simple terrestrial jumping analogy would be that impulsive jumpers are standing jumps, momentum jumpers are a running jump, and mixed jumpers are a running jump with only a few strides taken before the jump. Figure 1e compares the experimental data from animals with our theoretical line of H/L ∼ L^−1/3.

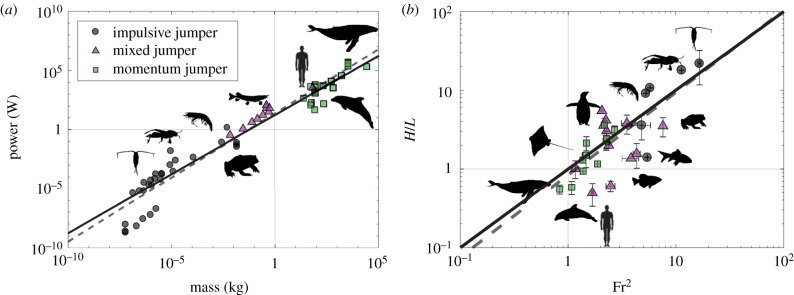
The power produced by some aquatic animals is shown in figure 2a and covers nearly 12 orders of magnitude of animal mass. An approximate power law for the power produced is P ∼ (16.9 W kg⁻¹)M (line of best fit has a power of 1.08 ± 0.07, r² = 0.94, 95% CI). The power data are collected from previous works, either provided directly or calculated as P ≈ M a_max U₀ or P ≈ F U₀, where a_max is the maximum acceleration, U₀ is the maximum (impulsive jumpers) or steady (momentum jumpers) velocity and F is the thrust production (N_copepod = 23, N_cricket = 1, N_frog = 3, N_fish = 10, N_shrimp = 2, N_dolphin = 13, N_whale = 9; see electronic supplementary material, table S1). Considering the power to overcome drag as $P_{\mathrm{drag}}=1/2{\rho }_{\mathrm{w}}{C}_{\mathrm{d}}{U}_0^{3}S$, a balance between power production and drag-induced dissipation is expressed as $kM\simeq 1/2{\rho }_{\mathrm{w}}{C}_{\mathrm{d}}{U}_0^{3}S$, where k is the best fit prefactor 16.9 W kg⁻¹, U₀ is the swimming velocity as defined earlier, ρ_w is the water density, C_d is the drag coefficient and S is the projected area of the animal. We assume an average value of 0.05 for the drag coefficient, which is the case for non-lifting streamlined bodies of revolution [31].

Figure 2.

(a) Relation between power production and animal mass. The dashed line is the best fit with a 1.08 ± 0.07 (r² = 0.94, 95% CI) power law exponent, and the solid line is our 1.00 power law assumption. (b) The normalized jumping height as a function of Froude number. The dashed line is the best fit line with a 1.05 ± 0.35 (r² = 0.57, 95% CI) power law exponent. The solid line is based on our assumption that H/L ∼ Fr², where ${\text{Fr}}^2=U_0^2/(2gL)$ is the ratio of inertia at the time of water exit and gravity. (Online version in colour.)

With the isometric arguments M ≃ ρ_bL³ and S ≃ πL², and assuming a neutrally buoyant animal (ρ_b/ρ_f ≃ 1), we find that U₀ ≃ (2kL/(πC_d))^1/3. This is a useful scaling for calculating the Froude number since we are unable to directly measure the exit velocity of animals jumping out of water. Here, we defined the Froude number, ratio of inertia to gravity, as

$${\text{Fr}}^2=\frac{U_0^2}{2gL},$$ 2.1

which is derived from simple projectile motion, $U_0^2=2gH$ and gives the relationship between jumping height and Froude number as $H/L=U_0^2/2gL={\text{Fr}}^2$. Therefore, the Froude number for animals leaping out of water is scaled as Fr² ≃ (1/2g)(2k/πC_d)^2/3 L^−1/3. This leads to our final solution as

$$\frac{H}{L}\simeq \frac{1}{2g}{\left(\frac{2k}{\pi C_{\mathrm{d}}}\right)}^{2/3}{L}^{-1/3}.$$ 2.2

The above equation is plotted in figure 1e as a solid black line and agrees well with experimental data. In figure 2b, we plot the jumping height of marine animals against Fr², which agrees well with experimental data (best fit slope of 1.05 ± 0.35, r² = 0.57, 95% CI). The animals include amphibians, arthropods, fishes, marine birds and mammals with a body size covering five orders of magnitude (see electronic supplementary material, table S1). Examples of impulsive jumpers are copepods and frogs. Momentum jumpers tend to be larger animals such as penguins, dolphins and whales. Most fish are considered as mixed jumpers, but humans and crocodiles are also included in this category. One may note that as an animal leaps out of water, it carries some volume of water. While the animal scaling neglects any effect of the entrained water, equation (1.2) still matches well with the biological results. This suggests that the entrained water has no influence on the jumping height of aquatic animals, regardless of jumping style. To test this hypothesis, we designed physical experiments with an axisymmetric body and a bioinspired robot. Through these experiments, we are able to deduce that entrained fluid has little effect on animals, therefore allowing them to jump with projectile motion.

2.2. Axisymmetric bodies

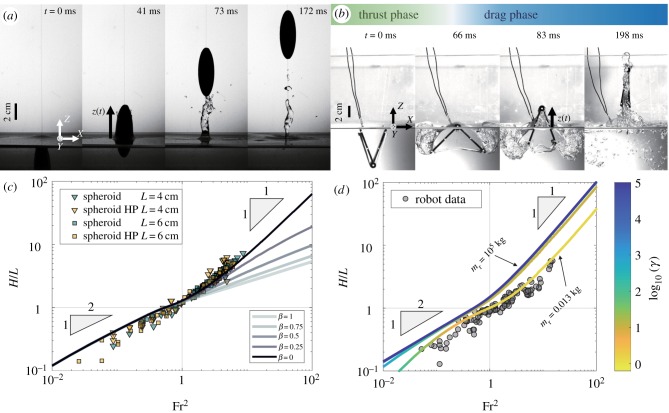
To gain a better understanding of the physics governing animal jump height, axisymmetric bodies were forced out of water using a spring system (see Methods, electronic supplementary material, figure S2). Figure 3a shows a time sequence of a spheroid exiting water. Experimental results of maximum jumping height normalized by major diameter, H/L, versus the Froude number are shown in figure 3b, in which U₀ is the velocity of the body when it reaches the free surface. Two distinct regimes appear. For low Froude numbers Fr < 1, we find that the body jump height scales as H/L ∼ Fr and predominantly performs partial exits. For high Froude numbers Fr > 1, we find that body jump height scales as H/L ∼ Fr² and performs complete exits. This regime has the same scaling as seen in animals.

Figure 3.

(a) Water exit of a prolate spheroid (major diameter is 6 cm, minor diameter is 2 cm, U₀ = 1.72 m s⁻¹). At t = 0 ms, the top of the spheroid reaches the undisturbed free surface line, but creates a deformation at the free surface prior to the exit. Upon exit, a water column is formed, and eventually pinches off. The maximum height of the spheroid is at t = 172 ms. (b) Normalized jumping height (where L is the length of the axisymmetric body and 2R is the diameter) as a function of Froude number for the case of prolate spheroidal bodies. Bodies that are treated with a hydrophobic coating are marked as HP. The solid lines are numerical solutions from the theoretical model testing the influence of the water column. The testing parameter is defined as β = r_w/R, where r_w is the water column radius. (c) Snapshots of the robot leaping out of water. The measured mass of this robot is m_r = 0.013 kg, exiting at a speed of U₀ = 2.7 m s⁻¹. (d) The robot’s normalized jumping height as a function of Froude number in black dots. Numerical results are shown for increasing mass ratio γ = m_r/m_f, where m_r is the robot mass and m_f is the entrained fluid mass. Small body masses are strongly influenced by the mass of the entrained water, and therefore cannot jump as high. A larger body mass would overcome the entrained mass effect. Zoomed in versions of this figure is shown in electronic supplementary material, figure S8. (Online version in colour.)

The growth of the water column begins when the position of the body is at least halfway out, or z(t) > L/2, where z(t) is defined as the vertical position of the top most point of the body. Between L/2 < z(t) < L, there is very little volume of entrained fluid. If the body completely escapes water, we see that the entrained water column grows vertically. In the theoretical model, the entrained water column is modelled as a cylinder with a fixed radius (independent of time). We systematically decrease the radius of the entrained water, compare the results with experiments, and deduce that the contribution of the water column has no effect on the maximum height of water exiting spheroids (figure 3b). The contribution of hydrodynamic forces is discussed in further detail in §2.4.

2.3. Bioinspired robot

A robot inspired by the flapping appendage of the best water-jumping animals (e.g. a copepod or a frog) was built (electronic supplementary material, figure S6). We denote two phases of the robot when it leaps out of water, as depicted in figure 3c: (i) the thrust phase and (ii) the drag phase. During the thrust phase, a rubber band pulls the wings together, which produces an angular velocity that pushes the robot upward. Once the rubber band reaches its original, unstretched length, the elastic energy no longer acts on the wings. This is the beginning of the drag phase, where no propulsive mechanism is present. In this paper, we will focus on the drag phase during water exit.

Experimental results of the robot’s maximum jump height relative to the Froude number are shown in figure 3d. Considering the low Froude number regime, the robot performs partial exits and the normalized maximum jump height scales as H/L ∼ Fr. However, there are subtleties involved in the jumping behaviour for large Fr related to the formation of the entrained water. In comparison to the axisymmetric bodies, the robot entrains far more water while z(t) < L. When z(t) > L, the entrained water generally breaks up, or gets squeezed out, in which case gravity dominates the system. By increasing the exit velocity, less time is spent partially submerged with entrained fluid and more time is spent in a gravity dominated regime. This explains why there is not a sharp transition at Fr = 1. Instead, the numerical solution for the robot (with a measured mass of m_r = 0.013 kg) slowly approaches H/L ∼ Fr². More details are discussed in the theoretical medelling section.

2.4. Theoretical model

When a body exits water, two distinct regimes exist. The first regime occurs while part of the body is still submerged underwater, or z(t) < L. As the body exits further out of water, buoyancy force acting on the submerged portion of the body decreases as $F_{\mathrm{sub}}=({\rho }_{\mathrm{b}}-{\rho }_{\mathrm{w}}){-V}_{\mathrm{sub}}\hspace{0.17em}g$ with time, where ρ_b and ρ_w are the body and water density, respectively, ${-V}_{\mathrm{sub}}$ is the submerged volume and g is the gravity. While buoyancy force decreases, the weight of the body above the water surface increases approximately as F_out ≈ m_b(z/L)g, where m_b is the total body mass. The body will experience additional forces from entrained fluid as $F_{\mathrm{f}}=m_{\mathrm{f}}(z)g+(\mathrm{d}/\mathrm{d}t)(m_{\mathrm{f}}\dot{z})$, where m_f(z) is the mass of the entrained fluid as a function of height, and dots are time derivatives. Finally, there is a drag force acting on the body that is expressed as $F_{\mathrm{d}}=(1/2){\rho }_{\mathrm{w}}{C}_{\mathrm{d}}{A}_{\mathrm{sub}}{\dot{z}}^2$, where C_d is the drag coefficient [32], and A_sub is the projected area of the submerged portion. Therefore, when z(t) < L, the equation of motion may be expressed as

$$(m_{\mathrm{b}}+m_a)\ddot{z}=-F_{\mathrm{out}}-F_{\mathrm{sub}}-F_{\mathrm{f}}-F_{\mathrm{d}},$$ 2.3

where m_a is the added mass acting on the submerged portion of the body [33]. If the body has enough inertia to completely exit the water, z ≥ L, then fluid forces begin to vanish. The weight of the body becomes evenly distributed as F_out = m_bg and F_sub = 0. Effects of drag and added mass become negligible since the resisting fluid is predominantly air. The resulting equation of motion when z(t) ≥ L is

$$m_{\mathrm{b}}\ddot{z}=-F_{\mathrm{out}}-F_{\mathrm{f}}.$$ 2.4

Surface tension effects are neglected because of large Weber numbers, We > 1. Both equations (2.3) and (2.4) are solved numerically using Matlab’s ODE23 function.

We investigate the influence of the entrained fluid after the body has completely exited. Using the axisymmetric bodies, the entrained fluid mass is medelled as a cylinder growing vertically, $m_{\mathrm{f}}(z)={\rho }_{\mathrm{w}}({-V}_{\mathrm{cyl}}(z,r_{\mathrm{w}})-{-V}_s(z,r_{\mathrm{w}}))$, where ${-V}_{\mathrm{cyl}}(z,r_{\mathrm{w}})$ is a cylindrical volume of water growing vertically and ${-V}_s(z,r_{\mathrm{w}})$ is the volume of the solid body that contacts water (see electronic supplementary material, figures S3 and S4). We define the wetted radius (or the entrained water column radius) as r_w = βR, where β is a testing parameter and R is the original radius of the body. By varying β between 0 and 1, we test how much influence the entrained water column mass has on the final jumping height. The entrained fluid only begins to grow when z(t) = L/2. When L/2 < z(t) < L, there is no appreciable difference in solutions between β = 0 and β = 1, which signifies that the growing water column has minimal effect on the jump height. This is because the effective mass of the body (amount of mass that is out of water) is initially higher and grows faster than the mass of the entrained water (see electronic supplementary material, figure S5a). Therefore, we fixed the parameter to β = 1 to remain consistent with later simulations with the robot.

All numerical solutions with Fr < 1 approach H/L ∼ Fr. When z(t) > L, we vary the testing parameter as β = [0, 0.25, 0.5, 0.75, 1]. Decreasing β represents decreasing influence of the entrained water column, revealing solutions that approach H/L ∼ Fr² when Fr > 1 (figure 3b). This means that the entrained water has little to no effect on the overall jumping height of the bodies. Considering the triviality of the entrained fluid, an analytical solution for both regimes can be found when neglecting the entrained fluid as $H/L=\sqrt{{\rho }_{\mathrm{b}}/{\rho }_{\mathrm{w}}}\hspace{0.17em}\text{Fr}$ (Fr < 1) and H/L = Fr² (Fr > 1) (see Methods).

For the bioinspired robot, the entrained fluid mass is geometrically estimated as m_f(z) = (1/2)ρ_w(S₀ W₀/L0)z(t)², where S₀ is the length of opening between the wings (which we assume to be constant), L₀ is the height of the robot and W₀ is the width of the robot (see electronic supplementary material, figures S6 and S7). Different from the axisymmetric bodies, the entrained fluid mass begins to grow as soon as the body leaves water. When z(t) < L, most of the effective mass of the robot mainly comes from the mass of the entrained water between two wings (see electronic supplementary material, figure S5b). Therefore, the entrained fluid plays a significant role on the robot jump height when z(t) < L.

From the axisymmetric bodies, we found that influence of the entrained fluid is not important when the body has completely exited water. This is more apparent in the robotic experiments when the entrained water breaks up during z(t) > L. Therefore, we neglect the growing fluid mass term in equation (2.4), which simply leads to $m_{\mathrm{b}}\ddot{z}=-m_{\mathrm{b}}g$.

Experimental robot data in figure 3d are compared with numerical solutions with changing mass ratio, γ = m_r/m_f, while keeping the geometry constant (L₀ = 6.5 cm, W₀ = 3.5 cm). Each line in the plot signifies different simulated robot masses of m_r = [0.013, 10⁻¹, 10⁰, 10⁵] kg. The measured mass of the robot shown in figure 3c is 0.013 kg, which was used as an input for our model (as shown in figure 3d) and agrees well with our experiments. This solution approaches H/L ∼ Fr² for Fr > 1, but lower by a prefactor difference of about 20 compared to the axisymmetric case. This is due to the strong influence of the entrained water when z(t) < L. By increasing Fr, less time is spent attached to water and more time is spent in the gravity dominated regime.

Increasing the robot mass parameter in the simulation from 10⁻² to 10⁻¹ kg creates a solution that quickly converge to a similar behaviour seen in the axisymmetric bodies, in which H/L ∼ Fr when Fr < 1 and H/L ∼ Fr² when Fr > 1. Very little difference is seen in the curves between robot masses of 10⁰ and 10⁵ kg. On the other hand, lowering the robot mass to m_r = 10⁻⁵ kg shows the lower bound curve in which the entrained fluid effect dominates the system (see electronic supplementary material, figure S8).

Depending on the maximum jump height, H/L, a different ratio of fluid mass is entrained. By increasing Fr², the entrained fluid mass increases, and therefore the mass ratio, γ, is smaller. If the robot leaps more than one body length, z(t) > L, we assume that the entrained fluid no longer affects the trajectory, as evidenced by the axisymmetric bodies. Therefore, γ remains constant past H/L = 1. Larger robot masses are less sensitive to the effects of the entrained water mass, and therefore show higher γ values.

Figure 4.

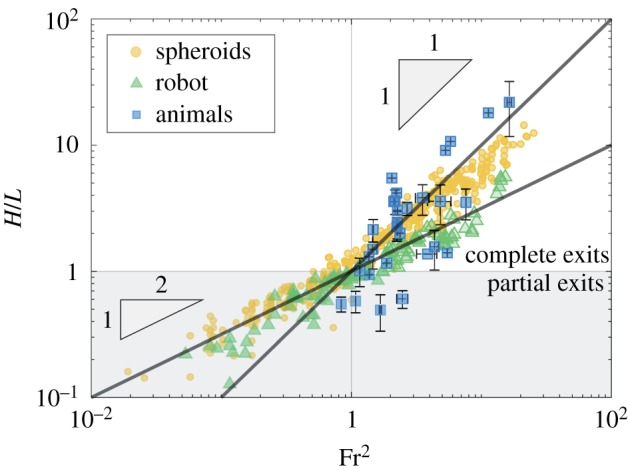
Summary of results including data from animals, all axisymmetric bodies and robot experiments.

3. Discussion

In this paper, we investigated the dynamics of animals leaping out of water. An allometric law for the power produced by aquatic animals was empirically found as P ∼ M. By balancing the power allometry with the power of drag, we find that the jumping height of animals scale as H/L ∼ Fr², i.e. H/L ∼ L^−1/3. This scaling differs from what is known about terrestrial jumpers. Jumping height for terrestrial animals is nearly independent of body size, or H/L ∼ L⁻¹ [34–36]. This means something as small as a flea can leap nearly as high as a human. In the present study, we find that aquatic animals do not follow the same jumping rules as terrestrial animals.

Through simplified experiments in which axisymmetric bodies were shot through the water surface, we find a transition in which the scaling is H/L ∼ Fr for partial jumps (H/L < 1) and H/L ∼ Fr² for complete jumps (H/L > 1). Additionally, a flapping robot was developed to mimic the impulsive jumping behaviour of aquatic animals. By developing a theoretical model, we systematically found that the entrained fluid has no effect on the maximum jumping height when z(t) > L, likely due to the fluid breaking up. However, the entrained fluid just begins to form when z(t) < L and the robot entrains far more water for a longer period of time than the axisymmetric bodies. This creates a delayed transition to the H/L ∼ Fr² scaling for the robot. But by systematically increasing the robot’s mass in the model, we find that effects of the entrained fluid become negligible. Then, only buoyancy dominates the system when H/L < 1 since the bodies are able to jump higher than what projectile motion would predict, and when H/L > 1, the body follows projectile motion. Furthermore, we find that treatments of hydrophobic coatings have no effect on the jumping performance of either the axisymmetric bodies or the robot.

Animals appear to carry an insignificant amount of the entrained fluid based on both qualitative observations and quantitative deduction. Qualitatively, we see that the volume of entrained water is small compared to the volume of the animal. Additionally, most of the entrained water breaks up into a spray of small droplets for larger animals. For smaller animals, close observations show that when copepods or fish leap out of water, little to no fluid is entrained behind them [1,7,28], which suggests that there is no entrained mass effect for small animals. This explains why the copepod’s jumping performance still exceeds that of the robot at a similar Froude number. However, it is worth noting that a relatively large volume of water can sometimes be attached to the copepod after the water column breaks up [28], which may be the cause of significant speed decrements past the interface. Quantitatively, from our physical experiments and modelling, we show that the water column has little effect on axisymmetric bodies, a geometry that is similar to most animals. In the case of the asymmetric robot, we theoretically confirm the importance of the ratio of body mass to entrained water mass. As a result, asymmetric shaped animals that entrain water still jump higher if they have a large enough body mass. Therefore, the main strategy aquatic animals use to jump out of water with projectile motion is to reduce the effect of the entrained fluid.

The above provides design considerations for robotics and vehicles transitioning between the air–water interface. There has been recent developments in systems that can perform both water-entry and -exit tasks, such as the AquaMAV [37,38] and the RoboBee [39]. However, both rely on using jet propulsion mechanisms to propel the body out of water. The robot presented here may inspire future robotic platforms that use a simple energy storage mechanism to leap out of water and the development of environment detection systems. Future works include designing a self-propelling robot inspired by a momentum jumper.

4. Methods

4.1. Animal videos

The jumping height from various animals was acquired either from Youtube (N = 26) or the literature (N = 10) (see electronic supplementary material, table S1). From the videos, jumping height was normalized by the body length. Clips in which the animals jump toward or away from the camera were avoided to minimize kinematic errors and inconsistent scales. Over 100 jumps were analysed spanning a total of 35 different species among arthropods, amphibians, birds, mammals and reptiles.

4.2. Axisymmetric body experiments

A spring mechanism was designed to shoot spheres, spheroids and axisymmetric streamlined bodies through the water surface. However, the object would stray from the straight vertical path or fall over when resting on the spring loader. Therefore, the objects were 3D printed (100% fill) with a small hole through the centre, which allows a thin fishing wire to pass through. This fishing wire acts as a guide so that the object will exit water vertically. For the sphere, the jump height was tested with and without the wire. While the spheres without the wire tended to jump slightly higher, the difference was very small (see electronic supplementary material, figure S10). This is likely to be because the sphere produces large wakes behind it, which makes it oscillate [40,41]. By attaching a wire, some of those oscillations transfer energy to the wire which in turn produces some friction. Simple dropping tests were conducted with and without the string to see the effect of friction on the rate of falling. They all fall close to 9.8 m s⁻², regardless of having a string constraint (see electronic supplementary material, figure S11).

All axisymmetric bodies had a fixed minor diameter of 2 cm. They were forced through the interface at various speeds ranging from 0.1 to 3.2 m s⁻¹. A high speed camera (Edgertronic SC2+ or Photron FastCam Mini) records the trajectory between 1000 and 2000 fps. To test the effect of hydrophobicity on the jumping height, a hydrophobic spray coating (Rust-Oleum NeverWet) was applied. Results for spheres, spheroids and streamlined bodies are shown in electronic supplementary material, figure S9, with respective simulations.

4.3. Simplified analytical solutions

As shown in the main text, bodies that generate enough velocity for complete exits (H/L > 1) follow

$$\frac{H}{L}={\text{Fr}}^2(\text{Fr}>1),$$ 4.1

which is projectile motion simply derived from $\ddot{z}=-g$, where dots are a time derivative and z is the highest position of the object above the undisturbed water surface. This equation neglects effects from the entrained fluid, which we justify in the main text.

However, projectiles that have partial exits (H/L < 1) jump higher than what ballistic motion predicts. This is due to gravity acting on the portion of the body that is out of water. Since the entrained fluid effects are neglected, we model the system as $m_{\mathrm{b}}\ddot{z}=-m_{\mathrm{out}}\hspace{0.17em}g-\mathrm{\Delta }{m}_{\mathrm{sub}}\hspace{0.17em}g$, where m_b ≈ ρ_bR² L is the total mass of the body, m_out ≈ ρ_bR² z(t) is the portion of the mass that escapes water, and Δm_sub ≈ (ρ_b − ρ_w)R² (L − z(t)) is the portion of the mass that remains submerged accounting for buoyancy. Our model is simplified to $\ddot{z}+Az+B=0$, where A = (ρ_w/ρ_b)(g/L) and B = g(1 − ρ_w/ρ_b). The order of magnitude for A and B is 10² s⁻² and 10⁰ m s⁻², respectively. The solution to the second order linear ODE is $z(t)=C_1\cos (\sqrt{A}\hspace{0.17em}t)+C_2\sin (\sqrt{A}\hspace{0.17em}t)-B/A$, where the constants C₁ and C₂ become B/A and $U_0/\sqrt{A}$ based on the initial conditions of z(t = 0) = 0 and $\dot{z}(t=0)=U_0$, respectively. The time to reach the maximum height is τ = A^−1/2tan ⁻¹(ξ), where $\xi =U_0\hspace{0.17em}\sqrt{A}/B$. Finally, the maximum height is calculated for partial jumps to be $H=(C_1+C_2\xi )/\sqrt{{\xi }^2+1}$. An approximation for this solution simply becomes H = C₂, which leads to

$$\frac{H}{L}=\sqrt{\frac{{\rho }_{\mathrm{b}}}{{\rho }_{\mathrm{w}}}}\hspace{0.17em}\text{Fr}(\text{Fr}<1).$$ 4.2

This agrees with our experimental observations in that bodies with partial jumps scale as H/L ∼ Fr as seen in figure 3b and electronic supplementary material, figures S5 and S6.

4.4. Robotic mechanism

To further understand how animals leap out of water in a controlled setting, a simple flapping mechanism was developed. The wings were 3D printed (Makerbot Replicator 5th Gen.) using PLA plastic. This robotic mechanism is composed of a rubber band attached to two wings that freely rotate about a hinge. A thin, stainless steel wire (Malin Co., 0.005 gauge) connects the wings together to keep the system initially stationary. To make the robot jump, a DC power supply (RSR HY5003) produces 24 V to burn the stainless steel wire, which releases the wings. Using a high speed camera (Edgertronic SC2+ or Photron FastCam Mini, 1000 fps), the overall kinematics of the robot was measured. Rubber band tensions ranged from 10 to 150 N m⁻¹. The dimensions of the wings have a fixed thickness of 3 mm and fixed width of 3 cm. The length varied from 3 to 10 cm and the robot mass varied from 6 to 26 g. The lower curve from the numerical simulations shown in figure 3d uses the measured mass of the robot with a wing length of 6.5 cm.

Data accessibility

This article has no additional data.

Authors' contributions

All authors (B.C., J.M., E.V., C.C., H.-Y.K., S.J.) contributed to analysing biological data and developing theory. B.C., E.V., S.J. designed/performed/analysed physical experiments. B.C., H.-Y.K., S.J. designed/performed/analysed robotic experiments.

Competing interests

The authors declare no conflicts of interest.

Funding

This work was partially supported by National Science Foundation EAPSI #1613138 (B.C.) and National Research Foundation of KoreaGrant No. 2018052541 via SNU IAMD (H.-Y.K.).