Tree clusters in savannas result from islands of soil moisture

Significance

Patterns of tree clusters in savannas display well-established characteristics that are explained by exogenous dynamics related to hot spots of soil moisture. These characteristics are related to the probability distribution of the cluster sizes and the fractal dimension of the cluster perimeters, both of which have a narrow range of variation regardless of specific climates. Such characteristics match very well those of the hot spots of high soil moisture when accounting for the impact of fire and herbivores.

Abstract

Tree clusters in savannas are commonly found in sizes that follow power laws with well-established exponents. We show that their size distributions could result from the space–time probabilistic structure of soil moisture, estimated over the range of rainfall observed in semiarid savannas; patterns of soil moisture display islands whose size, for moisture thresholds above the mean, follows power laws. These islands are the regions where trees are expected to exist and they have a fractal structure whose perimeter–area relationship is the same as observed in field data for the clustering of trees. When the impact of fire and herbivores is accounted for, as acting through the perimeter of the tree clusters, the power law of the soil moisture islands is transformed into a power law with the same exponents observed in the tree cluster data.

Among ecosystems, savannas are “not an ecologic middle ground between forests and grasslands, but a system with its own characteristics, including a remarkably stable coexistence of trees and grasses” (ref. 1, p. 361). Savanna ecosystems globally cover near 33 million km² (2) and are highly productive and flammable (3). In semiarid savannas, annual rainfall can be highly seasonal with typically between 250 mm and 750 mm of rain during the growing season (1, 3) with a pronounced interannual rainfall variability, which, combined with the action of fire, has led to interpretations that place savannas as nonstable transitional ecosystems. As the climate becomes drier, the trees become sparser and lower and when moister they grade into woodlands (4). The results presented here explain the spatial structure of their vegetation as stable ecosystems with a matrix of grasses and clusters of trees following a well-defined fractal structure in their sizes and perimeters.

Tree clusters in savannas, as many other patterns in nature, may result from endogenous dynamics or exogenous forces. Small-scale patterns are frequently explained via activation–inhibition Turing-type dynamics, where diffusion or other mechanisms of movement play a key role (5–9). In addition to the existing endogenous dynamics, large-scale patterns frequently involve a response to exogenous forces, for example in the case of stochastic drivers like precipitation, which are filtered through the dominant dynamics controlling the existence of vegetation. This is also the case of many other large-scale patterns like those existing in Antarctic krill (10), where large-scale oceanic dynamics are a key driver. In semiarid savannas, soil moisture is the dominant exogenous variable, resulting from stochastic rainfall events filtered through the space–time soil moisture balance equation. Tree clusters in savannas and their fractal structure likely respond to these exogenous drivers (without denying the existence of endogenous dynamics—e.g., competition between trees and grasses) (11). This makes the study of the probabilistic structure of soil moisture in savannas of crucial interest to explain their observed vegetation patterns. The soil moisture balance equation can be written in a simplified manner (12) as

$$\frac{\partial S\left(\mathbf{u},t\right)}{\partial t}=k{\nabla }_{\mathbf{u}}^{2}S\left(\mathbf{u},t\right)-\mathit{aS}\left(\mathbf{u},t\right)+\mathit{bY}\left(\mathbf{u},t\right),$$

$$\stackrel{\sim }{S}\left(\mathbf{u},t\right)=Z\left(\mathbf{u},t\right)S\left(\mathbf{u},t\right),$$

where all of the terms have been normalized by ${\mathrm{nZ}}_r$ with $\text{n}$ being the soil porosity and $Z_r$ the effective root depth. $S\left(\mathbf{u},t\right)$ is the soil moisture process driven by rainfall at spatial location $\mathbf{u}$ and time $\mathrm{t,}$ $k$ is the diffusion coefficient, $\mathrm{aS}\left(\mathbf{u},t\right)$ is the moisture loss via evapotranspiration and leakage, $\text{b}$ is the normalized infiltration coefficient, and $Y\left(\mathbf{u},t\right)$ is the rainfall process (13) described in SI Appendix. The losses are treated as linear functions of soil moisture as commonly represented for semiarid regions (1). The diffusion term is included for completeness but for realistic values of $k$ it has little importance in the overall dynamics (12, 14). Within a realistic range of small $k$ values, the correlation structure of the $S\left(\mathbf{u},t\right)$ is not affected (12). $S(\mathbf{u},t)$ has a correlation structure with an extremely slow decay fully dominated by the rainfall input which in geographical homogeneous regions may be still of the order of 0.9 at distances of several kilometers (12, 14). The slow decay of the rainfall spatial correlation is well represented by the Cox and Isham (15) model described in SI Appendix. When this model is the sole input, $Y\left(\mathbf{u},t\right),$ in the soil moisture balance equation, it yields $S\left(\mathbf{u},t\right)$ with an unrealistically slow decay in spatial correlation which is fully dominated by the rainfall input for distances of the order of 100 km in regions with homogeneous topography and climate. It is thus necessary to incorporate the crucial impact of fluctuations in topography, soil properties, and vegetation characteristics, which lead to a much faster decay of the soil moisture correlation structure. These fluctuations are modeled via a jitter process (16), $Z\left(\mathbf{u},t\right),$ acting on the space–time soil moisture resulting from the soil moisture balance equation driven solely by rainfall (12). The resulting soil moisture field, $\stackrel{\sim }{S}\left(\mathbf{u},t\right)=Z\left(\mathbf{u},t\right)S\left(\mathbf{u},t\right),$ captures the space–time correlation structure observed in the field (SI Appendix, Fig. S1). The jitter process increases the variance and deflates the correlation structure of $S\left(\mathbf{u},t\right)$ without changing its mean and without allowing negative values of $\stackrel{\sim }{S}\left(\mathbf{u},t\right).$

The parameters of the model are estimated here from soil moisture data via handheld sensors at point locations within three selected footprints of an airborne electronically scanned thinned array radiometer (ESTAR) during the Southern Great Plains 1997 (SGP97) hydrology experiment in Oklahoma (17). The jitter parameters estimated for the Oklahoma site (12) have been used to characterize the jitter in the Kruger site where the unique set of data related to the structure of the special vegetation is available (18). The Kruger site does not have detailed soil moisture data and, moreover, the representation of the impact of very local heterogeneities is likely to be similar in this semiarid/arid region. Rainfall data from the region were used to estimate the parameters of the rainfall model and two different sets of parameters were used for $a$ and $b$ in the soil moisture balance equation (19). The parameter values are listed in Table 1 and their estimation is presented elsewhere (12). The two sets of evapotranspiration parameters $a_i$ $\left(i=1,2\right)$ and infiltration parameters $b_i$ $\left(i=1,2\right)$ were used to represent different plant and soil conditions. Three different rainfall conditions were analyzed. One denoted by average represents the case of the Oklahoma site with 497 mm of growing-season rainfall, and the others correspond to the wet case (746 mm of growing-season rainfall) and the dry case (249 mm of growing-season rainfall).

Table 1.

Parameters of the rainfall model and the soil moisture model

Parameter	Average	Wet	Dry
Rainfall model
$\rho ,$ ${\text{km}}^{-1}$	0.047	0.047	0.047
$\eta ,$ ${\text{d}}^{-1}$	7.12	7.12	7.12
$\lambda ,$ ${\text{km}}^{-2}\cdot {\text{d}}^{-1}$	$8.99\times {10}^{-5}$	$1.17\times {10}^{-4}$	$6.29\times {10}^{-5}$
${\mu }_X,$ $\text{mm}\cdot {\text{d}}^{-1}$	37.74	43.55	26.96
Soil moisture model
$a_1,$ ${\text{d}}^{-1}$	0.014	0.014	0.014
$b_1,$ ${\text{mm}}^{-1}$	0.002	0.002	0.002
$a_2,$ ${\text{d}}^{-1}$	0.025	0.025	0.025
$b_2,$ ${\text{mm}}^{-1}$	0.006	0.006	0.006
$\alpha$	5.84	5.84	5.84
$\beta$	0.755	0.755	0.755
${\sigma }^2$	0.187	0.187	0.187
Mean rainfall during growing season, mm	497.42	746.12	248.71
Mean soil moisture during growing season, case 1	0.195	0.292	0.097
Mean soil moisture during growing season, case 2	0.341	0.511	0.170

The values of parameters in column “average” are estimated from real data (12, 17). The rainfall parameters are changed to what are called the wet and dry cases when the mean growing season rainfall is 50% more or 50% less than the average rainfall case. Two sets of parameters are used to represent different infiltration and evapotranspiration conditions. The parameters of the jitter are considered independent of the rainfall and representative of the local fluctuations in soil, topology, and vegetation in savannas (12).

We can now study via simulation the spatial variability of the soil moisture field by focusing on soil moisture islands. At any given time, soil moisture islands are defined as pixels connected through a shared edge (von Neumann neighborhood) where the soil moisture is above the chosen threshold (see SI Appendix, Fig. S2 for examples). The simulation scheme for the soil moisture field, $\stackrel{\sim }{S}\left(\mathbf{u},t\right)$ is described in SI Appendix.

Of special interest are the islands of soil moisture where trees have a high likelihood of residence. These “islands” are made up of pixels that have average soil moisture above specific thresholds chosen here as 0.2 and 0.3 for $\left(a_1,b_1\right)$ and 0.18 and 0.35 for $\left(a_2,b_2\right).$ These thresholds are average values of soil moisture in sandy soils where savanna trees have good conditions for stable permanency (1). Also, the patterns analyzed refer to ${\stackrel{\sim }{S}}_T,$ which is the average soil moisture, $\stackrel{\sim }{S},$ over each pixel of 10 m $\times$ 10 m during a period of $T=30$ d. For plants the time-averaged soil moisture is more relevant than the instantaneous or daily values. The resulting patterns were very similar for averaging periods of a few days to over 3 mo.

It has been well established that trees in savannas occur in clusters whose areas follow power-law distributions, $P\left(A\ge a\right)\sim a^{-p}$ (20). The $p$ exponent was found to vary in the Kalahari Desert between 0.89 and 1.76 (20) but more recent and precise data in the Kruger National Park region in South Africa found $\text{p}$ to be remarkably consistent around a representative value near 1.78 under different rainfall regimes and soil characteristics (18).

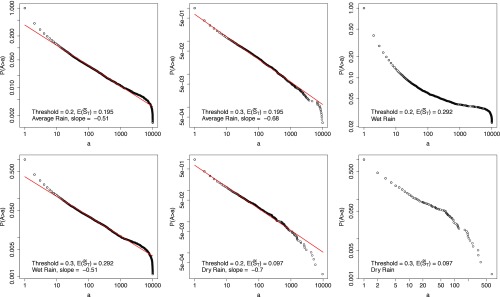
From the simulations of the soil moisture field we find that the islands of connected pixels with average soil moisture above the chosen thresholds closely follow well-defined power laws. Figs. 1 and 2 show $P\left(A\ge a\right)$ for different values of mean growing-season rainfall, different thresholds, and different parameters for losses and infiltration. The power-law distribution fails to describe the size of the islands only when the mean of soil moisture is very small or very large compared with the threshold being used. Thus, when the mean soil moisture is relatively large, as in the wet case with threshold equal to 0.2 (mean soil moisture equal to 0.292), most of the domain is above the threshold and trees will be favored everywhere, signaling the ecosystem is more likely to be a forest rather than a savanna. When the mean of soil moisture is very small and the threshold much higher, as in the dry case with threshold equal to 0.3 (mean soil moisture equal to 0.097), islands of soil moisture are very rare, signaling that trees will rarely cluster in that situation.

Fig. 1.

Distributions of soil moisture islands (case 1). Shown are log–log plots of the $P\left(A\ge a\right)$ distribution for loss and infiltration parameters $a_1=0.014$ $d^{-1}$ and ${\mathbf{b}}_1=0.002$ ${\text{mm}}^{-1}.$ Wet, average, and dry season cases are considered with thresholds 0.2 and 0.3. Here the horizontal axis is the number of pixels, where each pixel is 10 m × 10 m on the 1-km × 1-km field. The number of islands in the last plot (Bottom Right) is much smaller than those in the other plots.

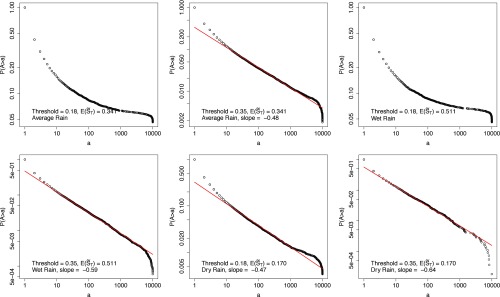
Fig. 2.

Distributions of soil moisture islands (case 2). Shown are log–log plots of the $P\left(A\ge a\right)$ distribution for loss and infiltration parameters $a_2=0.025$ ${\text{d}}^{-1}$ and $b_2=0.006$ ${\text{mm}}^{-1}.$ Wet, average, and dry season cases are considered with thresholds 0.18 and 0.35.

The exponents of the power laws, $P\left(A\ge a\right)\propto a^{-p},$ are in the range from 0.48 to 0.7 with a typical value around 0.51 for a savanna with the assumed average rainfall regime and threshold of 0.2 for tree stable existence. It is interesting that this range of exponents is very similar to that found for Korcak’s law (21–23) which describes the size distribution of ocean islands as a power law with exponent in the range from 0.5 to 0.75, depending on the region of the world.

These fractal properties of the soil moisture field $\stackrel{\sim }{S}\left(\mathbf{u},t\right)$ result from both the correlation structure of the rainfall process, $Y\left(\mathbf{u},t\right),$ and the correlation structure of the jitter process, $Z\left(\mathbf{u},t\right).$ First, the mean of the soil moisture field is totally determined by the rainfall process and the parameters $a$ and $b.$ For a fixed threshold, the soil moisture islands have fractal properties only when the threshold is not too far above or below the mean. As shown in Fig. 2, when the mean of soil moisture is 0.341, the soil moisture islands do not have fractal properties for a threshold of 0.18. This implies the soil moisture mean, which is independent of the jitter process, is a key factor when analyzing the fractal properties of the islands. Besides, according to ref. 12, the spatial correlation function of $\stackrel{\sim }{S}\left(\mathbf{u},t\right),$ denoted by ${\rho }_{\stackrel{\sim }{S}}\left(l,0\right),$ can be expressed as

$${\rho }_{\stackrel{\sim }{S}}\left(l,0\right)=\frac{\left({\sigma }_S^2{\rho }_S\left(l,0\right)+{\mu }_s^2\right){\sigma }_Z^2{\rho }_Z\left(l,0\right)+{\sigma }_S^2{\rho }_S\left(l,0\right)}{\left({\sigma }_S^2+{\mu }_s^2\right){\sigma }_Z^2+{\sigma }_S^2}$$

$$\approx \{\begin{array}{c}\left(1-\gamma \right){\rho }_Z\left(l,0\right)+\gamma ,\text{when}\hspace{0.17em}{\rho }_S\left(l,0\right)\approx 1,\\ \gamma {\rho }_S\left(l,0\right),\hspace{1em}\text{when}\hspace{0.17em}{\rho }_Z\left(l,0\right)\approx 0,\end{array}$$

where ${\rho }_S\left(l,0\right)$ and ${\rho }_Z\left(l,0\right)$ are the spatial correlation functions of the soil moisture field, $S\left(\mathbf{u},t\right),$ driven solely by rainfall and that of the jitter process, $Z\left(\mathbf{u},t\right),$ respectively. The terms ${\sigma }_S^2,$ ${\sigma }_Z^2,$ and ${\mu }_s^2$ are the variances and mean of $S\left(\mathbf{u},t\right)$ and $Z\left(\mathbf{u},t\right),$ and $\gamma ={\sigma }_S^2/\left(\left({\sigma }_S^2+{\mu }_s^2\right){\sigma }_Z^2+{\sigma }_S^2\right)$ is a constant depending on both the rainfall and the jitter. As shown in SI Appendix, Fig. S2 and ref. 13, ${\rho }_S\left(l,0\right)$ and the spatial correlation of the rainfall process are very close to 1 when $l$ is less than 1 km with the parameters estimated in ref. 12. Thus, on a 1-km × 1-km field, the rainfall process, $Y\left(\mathbf{u},t\right),$ and the soil moisture field, $S\left(\mathbf{u},t\right),$ are almost constant for any particular realization, and the shape of the correlation function of $\stackrel{\sim }{S}\left(\mathbf{u},t\right)$ is totally determined by the jitter $Z\left(\mathbf{u},t\right),$ as shown in the above equation and SI Appendix, Fig. S3. However, no matter how fast the correlation function of $Z\left(\mathbf{u},t\right)$ decays for small scales, the correlation of $\stackrel{\sim }{S}\left(\mathbf{u},t\right)$ has a lower bound $\gamma >0$ controlled by both the jitter and the rainfall, and thus it would not die until $l$ becomes much larger. The size of the islands resulting solely from the jitter process exhibits power-law behavior over a limited range of scales but fails to do so at larger scales due to the fast decay of its correlation function (SI Appendix, Fig. S4). As shown in SI Appendix, Fig. S3, the correlation function of $Z\left(\mathbf{u},t\right)$ is already very close to 0 at $l=1$ km. In contrast, the correlation function of the soil moisture has a very heavy tail resulting from the rainfall process, whose spatial correlation function dies only after distances of about 200 km (see refs. 13 and 19 for more details). Therefore, the islands of soil moisture would still have fractal properties at larger scales.

Trees are likely to exist in soil moisture islands whose mean is above an adequate threshold but most certainly they will not occupy the full extent of each island. Fire and herbivores are important factors that will make their occupancy smaller than that of the island. The impact of fire and herbivores will act through the perimeter, $\mathrm{P,}$ of the cluster. Let $A\prime$ denote the area of a tree cluster and $A$ and $P$ denote the area and perimeter of the soil moisture island on which the tree cluster exists. Then one may write

$$A\prime \propto A/P.$$

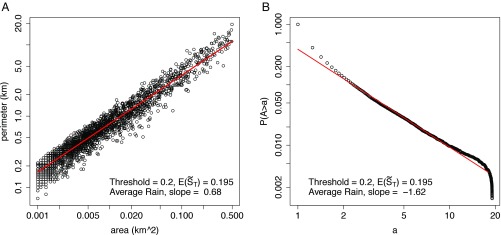
More complicated functional relations could be considered between $A,$ $A\prime ,$ and $P$ but would be quite difficult to justify. For a fractal island Mandelbrot’s area–perimeter equation gives $P\propto A^{D/2},$ where $D$ is the fractal dimension of the perimeter (22). Fig. 3A shows the area–perimeter relationship for a typical case of the cases analyzed before. Other cases are shown in SI Appendix, Fig. S5. An excellent fit is obtained with $D/2=$ 0.68 or fractal dimension 1.36 for the perimeter of the soil moisture islands. This value is very close to the fractal dimension of 1.40 obtained for the perimeters of the tree clusters in the Kruger region with rainfall of 500 mm/y (18). Fig. 3A implies that for this typical case $A\prime \propto A^{1-D/2}=A^{0.32}.$ Fig. 3B shows the distribution of the areas of tree clusters, $A\prime ,$ for the typical case described before obtained from the distribution of $A$ corresponding to soil moisture islands derived via simulations. The plot has a slope of −1.62, very close to the exponent of 1.60 observed for the power laws of tree cluster sizes in the Kruger region for the case of rainfall of 500 mm/y (18).

Fig. 3.

Relationships between area and perimeter of soil moisture islands and the distribution of tree clusters. (A) Perimeter vs. area of soil moisture islands. Here $a_1=0.014$ ${\text{d}}^{-1}$ and $b_1=0.002$ ${\text{mm}}^{-1}$ for the case of average rain and threshold equal to 0.2. It shows that $P\propto A^{D/2}$ with $D=\mathrm{1.36.}$ Plots of perimeter vs. area with different rainfall and thresholds are similar and can be found in SI Appendix, Fig. S5. (B) The distribution function $P\left(A\prime \ge a\right)$ for tree clusters plotted at log–log scale, where $A\prime \propto A^{1-D/2}.$

We infer that the emergence of large-scale spatial patterns of savanna vegetation characterized by clusters of trees in a matrix of grasses with power-law probability distribution of cluster sizes and fractal perimeters of such clusters results from spatial patterns of soil moisture in such ecosystems. The islands of soil moisture above thresholds convenient for tree stable existence display perimeters with the same fractal dimension as that of tree clusters and their sizes follow power laws whose exponents match those found for tree clusters when the impact of fires and herbivores is accounted for. When the rainfall regime is outside the range observed in savannas, the soil moisture spatial structure does not support the above conclusions, reinforcing the understanding that savannas are stable ecosystems and not just transitional unstable states between forests and grasslands. Because of large interannual fluctuations in the rainfall regime, the sizes of tree clusters may be affected but the fractal characteristics in their sizes and perimeters will remain relatively stable. The parameter of the cluster-size power law changes in a relatively small range that reflects changes in the rainfall regime as well as the impact of fire and herbivores.