Computational Neuroscience: Mathematical and Statistical Perspectives

Abstract

Mathematical and statistical models have played important roles in neuroscience, especially by describing the electrical activity of neurons recorded individually, or collectively across large networks. As the field moves forward rapidly, new challenges are emerging. For maximal effectiveness, those working to advance computational neuroscience will need to appreciate and exploit the complementary strengths of mechanistic theory and the statistical paradigm.

1. Introduction

Brain science seeks to understand the myriad functions of the brain in terms of principles that lead from molecular interactions to behavior. Although the complexity of the brain is daunting and the field seems brazenly ambitious, painstaking experimental efforts have made impressive progress. While investigations, being dependent on methods of measurement, have frequently been driven by clever use of the newest technologies, many diverse phenomena have been rendered comprehensible through interpretive analysis, which has often leaned heavily on mathematical and statistical ideas. These ideas are varied, but a central framing of the problem has been to “elucidate the representation and transmission of information in the nervous system” (Perkel and Bullock 1968). In addition, new and improved measurement and storage devices have enabled increasingly detailed recordings, as well as methods of perturbing neural circuits, with many scientists feeling at once excited and overwhelmed by opportunities of learning from the ever-larger and more complex data sets they are collecting. Thus, computational neuroscience has come to encompass not only a program of modeling neural activity and brain function at all levels of detail and abstraction, from sub-cellular biophysics to human behavior, but also advanced methods for analysis of neural data.

In this article we focus on a fundamental component of computational neuroscience, the modeling of neural activity recorded in the form of action potentials (APs), known as spikes, and sequences of them known as spike trains (see Figure 1). In a living organism, each neuron is connected to many others through synapses, with the totality forming a large network. We discuss both mechanistic models formulated with differential equations and statistical models for data analysis, which use probability to describe variation. Mechanistic and statistical approaches are complementary, but their starting points are different, and their models have tended to incorporate different details. Mechanistic models aim to explain the dynamic evolution of neural activity based on hypotheses about the properties governing the dynamics. Statistical models aim to assess major drivers of neural activity by taking account of indeterminate sources of variability labeled as noise. These approaches have evolved separately, but are now being drawn together. For example, neurons can be either excitatory, causing depolarizing responses at downstream (post-synaptic) neurons (i.e., responses that push the voltage toward the firing threshold, as illustrated in Figure 1), or inhibitory, causing hyperpolarizing post-synaptic responses (that push the voltage away from threshold). This detail has been crucial for mechanistic models but, until relatively recently, has been largely ignored in statistical models. On the other hand, during experiments, neural activity changes while an animal reacts to a stimulus or produces a behavior. This kind of non-stationarity has been seen as a fundamental challenge in the statistical work we review here, while mechanistic approaches have tended to emphasize emergent behavior of the system. In current research, as the two perspectives are being combined increasingly often, the distinction has become blurred. Our purpose in this review is to provide a succinct summary of key ideas in both approaches, together with pointers to the literature, while emphasizing their scientific interactions. We introduce the subject with some historical background, and in subsequent sections describe mechanistic and statistical models of the activity of individual neurons and networks of neurons. We also highlight several domains where the two approaches have had fruitful interaction.

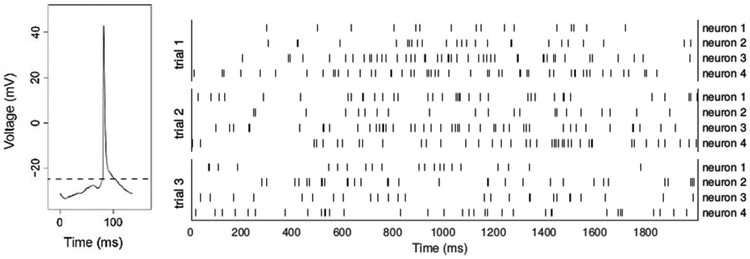
Figure 1.

Action potential and spike trains. The left panel shows the voltage drop recorded across a neuron’s cell membrane. The voltage fluctuates stochastically, but tends to drift upward, and when it rises to a threshold level (dashed line) the neuron fires an action potential, after which it returns to a resting state; the neuron then responds to inputs that will again make its voltage drift upward toward the threshold. This is often modeled as drifting Brownian motion that results from excitatory and inhibitory Poisson process inputs (Tuckwell 1988; Gerstein and Mandelbrot 1964). The right panel shows spike trains recorded from 4 neurons repeatedly across 3 experimental replications, known as trials. The spike times are irregular within trials, and there is substantial variation across trials, and across neurons.

1.1. The brain-as-computer metaphor

The modern notion of computation may be traced to a series of investigations in mathematical logic in the 1930s, including the Turing machine (Turing 1937). Although we now understand logic as a mathematical subject existing separately from human cognitive processes, it was natural to conceptualize the rational aspects of thought in terms of logic (as in Boole’s 1854 Investigation of the Laws of Thought (Boole 1854, p. 1) which “aimed to investigate those operations of the mind by which reasoning is performed”), and this led to the 1943 proposal by Craik that the nervous system could be viewed “as a calculating machine capable of modeling or paralleling external events” (Craik 1943, p. 120) while Mc-Culloch and Pitts provided what they called “A logical calculus of the ideas immanent in nervous activity” (McCulloch and Pitts 1943). In fact, while it was an outgrowth of preliminary investigations by a number of early theorists (Piccinini 2004), the McCulloch and Pitts paper stands as a historical landmark for the origins of artificial intelligence, along with the notion that mind can be explained by neural activity through a formalism that aims to define the brain as a computational device; see Figure 2. In the same year another noteworthy essay, by Norbert Wiener and colleagues, argued that in studying any behavior its purpose must be considered, and this requires recognition of the role of error correction in the form of feedback (Rosenblueth et al. 1943). Soon after, Wiener consolidated these ideas in the term cybernetics (Wiener 1948). Also, in 1948 Claude Shannon published his hugely influential work on information theory which, beyond its technical contributions, solidified information (the reduction of uncertainty) as an abstract quantification of the content being transmitted across communication channels, including those in brains and computers (Shannon and Weaver 1949).

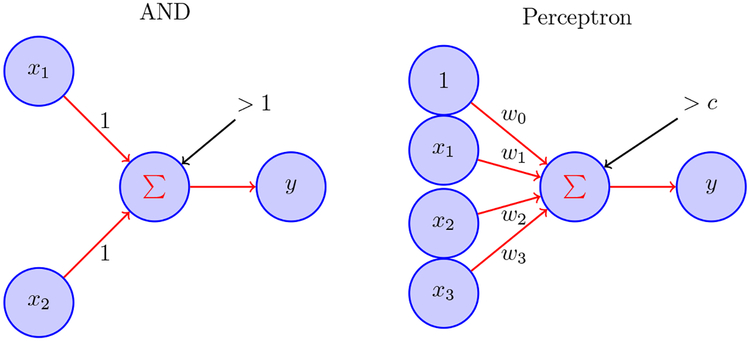
Figure 2.

In the left diagram, McCulloch-Pitts neurons x₁ and x₂ each send binary activity to neuron y using the rule y = 1 if x₁ + x₂ > 1 and y = 0 otherwise; this corresponds to the logical AND operator; other logical operators NOT, OR, NOR may be similarly implemented by thresholding. In the right diagram, the general form of output is based on thresholding linear combinations, i.e., y =1 when ∑w_ix_i >c and y = 0 otherwise. The values w_i are called synaptic weights. However, because networks of perceptrons (and their more modern artificial neural network descendents) are far simpler than networks in the brain, each artificial neuron corresponds conceptually not to an individual neuron in the brain but, instead, to large collections of neurons in the brain.

The first computer program that could do something previously considered exclusively the product of human minds was the Logic Theorist of Newell and Simon (Newell and Simon 1956), which succeeded in proving 38 of the 52 theorems concerning the logical foundations of arithmetic in Chapter 2 of Principia Mathematica (Whitehead and Russell 1912). The program was written in a list-processing language they created (a precursor to LISP), and provided a hierarchical symbol manipulation framework together with various heuristics, which were formulated by analogy with human problem-solving (Gugerty 2006). It was also based on serial processing, as envisioned by Turing and others.

A different kind of computational architecture, developed by Rosenblatt (Rosenblatt 1958), combined the McCulloch-Pitts conception with a learning rule based on ideas articulated by Hebb in 1949 (Hebb 1949), now known as Hebbian learning. Hebb’s rule was, “When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased” (Hebb 1949), that is, the strengths of the synapses connecting the two neurons increase, which is sometimes stated colloquially as, “Neurons that fire together, wire together.” Rosenblatt called his primitive neurons perceptrons, and he created a rudimentary classifier, aimed at imitating biological decision making, from a network of perceptrons, see Figure 2. This was the first artificial neural network that could carry out a non-trivial task.

As the foregoing historical outline indicates, the brain-as-computer metaphor was solidly in place by the end of the 1950s. It rested on a variety of technical specifications of the notions that (1) logical thinking is a form of information processing, (2) information processing is the purpose of computer programs, while, (3) information processing may be implemented by neural systems (explicitly in the case of McCulloch-Pitts model and its descendents, but implicitly otherwise). A crucial recapitulation of the information-processing framework, given later by David Marr (Marr 1982), distinguished three levels of analysis: computation (“What is the goal of the computation, why is it appropriate, and what is the logic of the strategy by which it can be carried out?”), algorithm (“What is the representation for the input and output, and what is the algorithm for the transformation?”), and implementation (“How can the representation and algorithm be realized physically?”). This remains a very useful way to categorize descriptions of brain computation.

1.2. Neurons as electrical circuits

A rather different line of mathematical work, more closely related to neurobiology, had to do with the electrical properties of neurons. So-called “animal electricity” had been observed by Galvani in 1791 (Galvani and Aldini 1792). The idea that the nervous system was made up of individual neurons was put forth by Cajal in 1886, the synaptic basis of communication across neurons was established by Sherrington in 1897 (Sherrington 1897), and the notion that neurons were electrically excitable in a manner similar to a circuit involving capacitors and resistors in parallel was proposed by Hermann in 1905 (Piccolino 1998). In 1907, Lapique gave an explicit solution to the resulting differential equation, in which the key constants could be determined from data, and he compared what is now known as the leaky integrate-and-fire model (LIF) with his own experimental results (Abbott 1999; Brunel and Van Rossum 2007; Lapique 1907). This model, and variants of it, remain in use today (Gerstner et al. 2014), and we return to it in Section 2 (see Figure 3). Then, a series of investigations by Adrian and colleagues established the “all or nothing” nature of the AP, so that increasing a stimulus intensity does not change the voltage profile of an AP but, instead, increases the neural firing rate (Adrian and Zotterman 1926). The conception that stimulus or behavior is related to firing rate has become ubiquitous in neurophysiology. It is often called rate coding, in contrast to temporal coding, which involves the information carried in the precise timing of spikes (Abeles 1982; Shadlen and Movshon 1999; Singer 1999).

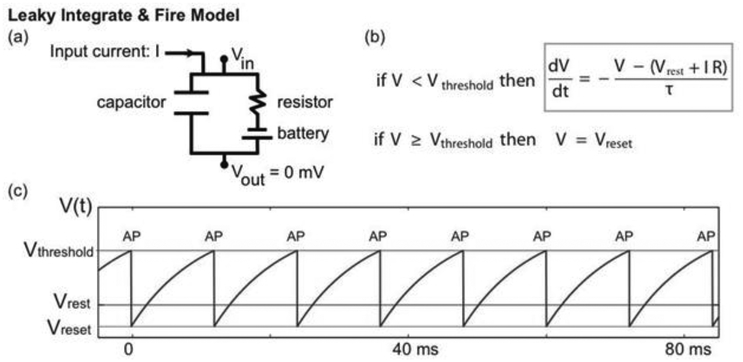
Figure 3.

(a) The LIF model is motivated by an equivalent circuit. The capacitor represents the cell membrane through which ions cannot pass. The resistor represents channels in the membrane (through which ions can pass) and the battery a difference in ion concentration across the membrane. (b) The equivalent circuit motivates the differential equation that describes voltage dynamics (gray box). When the voltage reaches a threshold value (V_threshold), it is reset to a smaller value (V_reset). In this model, the occurrence of a reset indicates an action potential; the rapid voltage dynamics of action potentials are not included in the model. (c) An example trace of the LIF model voltage (blue). When the input current (I) is large enough, the voltage increases until reaching the voltage threshold (red horizontal line), at which time the voltage is set to the reset voltage (green horizontal line). The times of reset are labeled as “AP”, denoting action potential. In the absence of an applied current (I = 0) the voltage approaches a stable equilibrium value (V_rest).

Following these fundamental descriptions, remaining puzzles about the details of action potential generation led to investigations by several neurophysiologists and, ultimately, to one of the great scientific triumphs, the Hodgkin-Huxley model. Published in 1952 (Hodgkin and Huxley 1952), the model consisted of a differential equation for the neural membrane potential (in the squid giant axon) together with three subsidiary differential equations for the dynamic properties of the sodium and potassium ion channels. See Figure 4. This work produced accurate predictions of the time courses of membrane conductances; the form of the action potential; the change in action potential form with varying concentrations of sodium; the number of sodium ions involved in inward flux across the membrane; the speed of action potential propagation; and the voltage curves for sodium and potassium ions (Hille 2001; Hodgkin and Huxley 1952). Thus, by the time the brain-as-computer metaphor had been established, the power of biophysical modeling had also been demonstrated. Over the past 60 years, the Hodgkin-Huxley equations have been refined, but the model’s fundamental formulation has endured, and serves as the basis for many present-day models of single neuron activity; see Section 2.2.

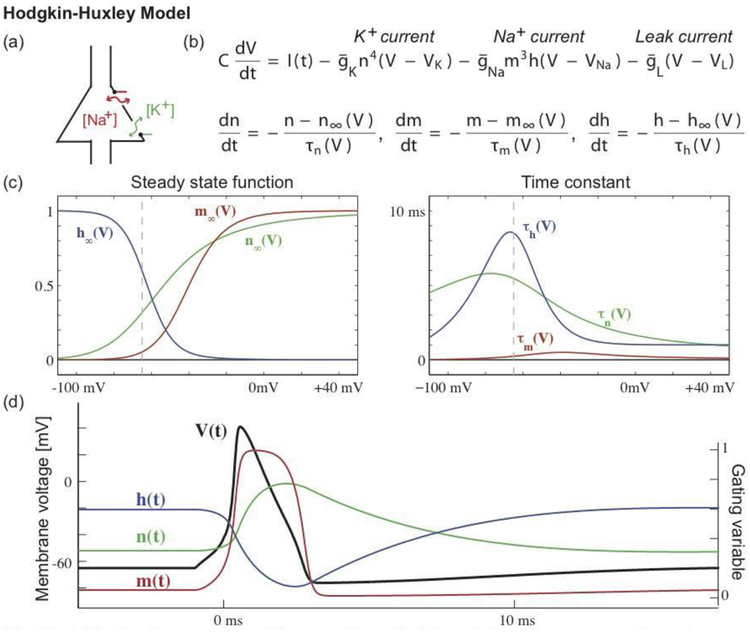
Figure 4.

The Hodgkin-Huxley model provides a mathematical description of a neuron’s voltage dynamics in terms of changes in sodium (Na⁺) and potassium (K⁺) ion concentrations. The cartoon in (a) illustrates a cell body with membrane channels through which (Na⁺) and (K⁺) may pass. The model consists of four coupled nonlinear differential equations (b) that describe the voltage dynamics (V), which vary according to an input current (I), a potassium current, a sodium current, and a leak current. The conductances of the potassium (n) and sodium currents (m, h) vary in time, which controls the flow of sodium and potassium ions through the neural membrane. Each channel’s dynamics depends on (c) a steady state function and a time constant. The steady state functions range from 0 to 1, where 0 indicates that the channel is closed (so that ions cannot pass), and 1 indicates that the channel is open (ions can pass). One might visualize these channels as gates that swing open and closed, allowing ions to pass or impeding their flow; these gates are indicated in green and red in the cartoon (a). The steady state functions depend on the voltage; the vertical dashed line indicates the typical resting voltage value of a neuron. The time constants are less than 10 ms, and smallest for one component of the sodium channel (the sodium activation gate m). (d) During an action potential, the voltage undergoes a rapid depolarization (V increases) and then less rapid hyperpolarization (V decreases), supported by the opening and closing of the membrane channels.

1.3. Receptive fields and tuning curves

In early recordings from the optic nerve of the Limulus (horseshoe crab), Hartline found that shining a light on the eye could drive individual neurons to fire, and that a neuron’s firing rate increased with the intensity of the light (Hartline and Graham 1932). He called the location of the light that drove the neuron to fire the neuron’s receptive field. In primary visual cortex (known as area V1), the first part of cortex to get input from the retina, Hubel and Wiesel showed that bars of light moving across a particular part of the visual field, again labeled the receptive field, could drive a particular neuron to fire and, furthermore, that the orientation of the bar of light was important: many neurons were driven to fire most rapidly when the bar of light moved in one direction, and fired much more slowly when the orientation was rotated 90 degrees away (Hubel and Wiesel 1959). When firing rate is considered as a function of orientation, this function has come to be known as a tuning curve (Dayan and Abbott 2001). More recently, the terms “receptive field” and “tuning curve” have been generalized to refer to non-spatial features that drive neurons to fire. The notion of tuning curves, which could involve many dimensions of tuning simultaneously, widely applied in computational neuroscience.

1.4. Networks

Neuron-like artificial neural networks, advancing beyond perceptron networks, were developed during the 1960s and 1970s, especially in work on associative memory (Amari 1977b), where a memory is stored as a pattern of activity that can be recreated by a stimulus when it provides even a partial match to the pattern. To describe a given activation pattern, Hopfield applied statistical physics tools to introduce an energy function and showed that a simple update rule would decrease the energy so that the network would settle to a pattern-matching “attractor” state (Hopfield 1982). Hopfield’s network model is an example of what statisticians call a two-way interaction model for N binary variables, where the energy function becomes the negative log-likelihood function. Hinton and Sejnowski provided a stochastic mechanism for optimization and the interpretation that a posterior distribution was being maximized, calling their method a Boltzmann machine because the probabilities they used were those of the Boltzmann distribution in statistical mechanics (Hinton and Sejnowski 1983). Geman and Geman then provided a rigorous analysis together with their reformulation in terms of the Gibbs sampler (Geman and Geman 1984). Additional tools from statistical mechanics were used to calculate memory capacity and other properties of memory retrieval (Amit et al. 1987), which created further interest in these models among physicists.

Artificial neural networks gained traction as models of human cognition through a series of developments in the 1980s (Medler 1998), producing the paradigm of parallel distributed processing (PDP). PDP models are multi-layered networks of nodes resembling those of their perceptron precursor, but they are interactive, or recurrent, in the sense that they are not necessarily feed-forward: connections between nodes can go in both directions, and they may have structured inhibition and excitation (Rumelhart et al. 1986). In addition, training (i.e., estimating parameters by minimizing an optimization criterion such as the sum of squared errors across many training examples) is done by a form of gradient descent known as back propagation (because iterations involve steps backward from output errors toward input weights). While the nodes within these networks do not correspond to individual neurons, features of the networks, including back propagation, are usually considered to be biologically plausible. For example, synaptic connections between biological neurons are plastic, and change their strength following rules consistent with theoretical models (e.g., Hebb’s rule). Furthermore, PDP models can reproduce many behavioral phenomena, famously including generation of past tense for English verbs and making childlike errors before settling on correct forms (McClelland and Rumelhart 1981). Currently, there is increased interest in neural network models through deep learning, which we will discuss briefly, below.

Analysis of the overall structure of network connectivity, exemplified in research on social networks (see Fienberg (2012) for historical overview), has received much attention following the 1998 observation that several very different kinds of networks, including the neural connectivity in the worm C. elegans, exhibit “small world” properties of short average path length between nodes, together with substantial clustering of nodes, and that these properties may be described by a relatively simple stochastic model (Watts and Strogatz 1998). This style of network description has since been applied in many contexts involving brain measurement, mainly using structural and functional magnetic resonance imaging (MRI) (Bassett and Bullmore 2016; Bullmore and Sporns 2009), though cautions have been issued regarding the difficulty of interpreting results physiologically (Papo et al. 2016).

1.5. Statistical models

Stochastic considerations have been part of neuroscience since the first descriptions of neural activity, outlined briefly above, due to the statistical mechanics underlying the flow of ions across channels and synapses (Colquhoun and Sakmann 1998; Destexhe et al. 1994). Spontaneous fluctuations in a neuron’s membrane potential are believed to arise from the random opening and closing of ion channels, and this spontaneous variability has been analyzed using a variety of statistical methods (Sigworth 1980). Such analysis provides information about the numbers and properties of the ion channel populations responsible for excitability. Probability has also been used extensively in psychological theories of human behavior for more than 100 years, e.g., Stigler (1986, Ch. 7). Especially popular theories used to account for behavior include Bayesian inference and reinforcement learning, which we will touch on below. A more recent interest is to determine signatures of statistical algorithms in neural function. For example, drifting diffusion to a threshold, which is used with LIF models (Tuckwell 1988), has also been used to describe models of decision making based on neural recordings (Gold and Shadlen 2007). However, these are all examples of ways that statistical models have been used to describe neural activity, which is very different from the role of statistics in data analysis. Before previewing our treatment of data analytic methods, we describe the types of data that are relevant to this article.

1.6. Recording modalities

Efforts to understand the nervous system must consider both anatomy (its constituents and their connectivity) and function (neural activity and its relationship to the apparent goals of an organism). Anatomy does not determine function, but does strongly constrain it. Anatomical methods range from a variety of microscopic methods to static, whole-brain MRI (Fischl et al. 2002). Functional investigations range across spatial and temporal scales, beginning with recordings from ion channels, to action potentials, to local field potentials (LFPs) due to the activity of many thousands of neural synapses. Functional measurements outside the brain (still reflecting electrical activity within it), come from electroencephalography (EEG) (Nunez and Srinivasan 2006) and magnetoencephalography (MEG) (Hämäläinen et al. 1993), as well as indirect methods that measure a physiological or metabolic parameter closely associated with neural activity, including positron emission tomography (PET) (Bailey et al. 2005), functional MRI (fMRI) (Lazar 2008), and near-infrared resonance spectroscopy (NIRS) (Villringer et al. 1993). These functional methods have timescales spanning milliseconds to minutes, and spatial scales ranging from a few cubic millimeters to many cubic centimeters.

While interesting mathematical and statistical problems arise in nearly every kind of neuroscience data, we focus here on neural spiking activity. Spike trains are sometimes recorded from individual neurons in tissue that has been extracted from an animal and maintained over hours in a functioning condition (in vitro). In this setting, the voltage drop across the membrane is nearly deterministic; then, when the neuron is driven with the same current input on each of many repeated trials, the timing of spikes is often replicated precisely across the trials (Mainen and Sejnowski 1995), as seen in portions of the spike trains in Figure 5. Recordings from brains of living animals (in vivo) show substantial irregularity in spike timing, as in Figure 1. These recordings often come from electrodes that have been inserted into brain tissue near, but not on or in, the neuron generating a resulting spike train; that is, they are extracellular recordings. The data could come from one up to dozens, hundreds, or even thousands of electrodes. Because the voltage on each electrode is due to activity of many nearby neurons, with each neuron contributing its own voltage signature repeatedly, there is an interesting statistical clustering problem known as spike sorting (Carlson et al. 2014; Rey et al. 2015), but we will ignore that here. Another important source of activity, recorded from many individual neurons simultaneously, is calcium imaging, in which light is emitted by fluorescent indicators in response to the flow of calcium ions into neurons when they fire (Grienberger and Konnerth 2012). Calcium dynamics, and the nature of the indicator, limit temporal resolution to between tens and several hundred milliseconds. Signals can be collected using one-photon microscopy even from deep in the brain of a behaving animal; two-photon microscopy provides significantly higher spatial resolution but at the cost of limiting recordings to the brain surface. Due to the temporal smoothing, extraction of spiking data from calcium imaging poses its own set of statistical challenges (Pnevmatikakis et al. 2016).

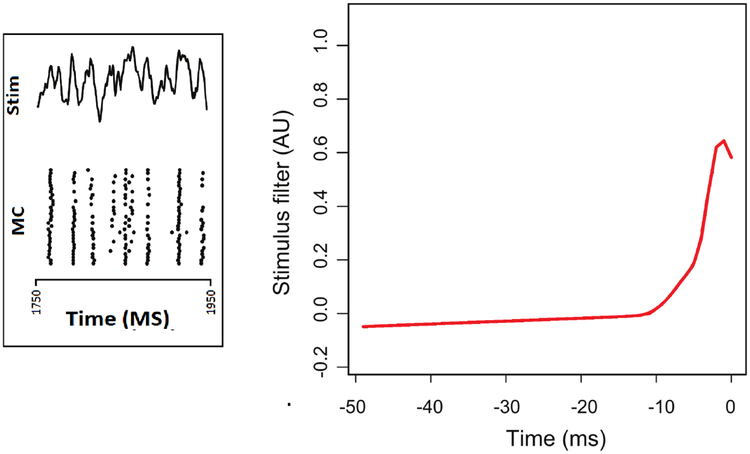
Figure 5.

Left panel displays the current (“Stim,” for stimulus, at the top of the panel) injected into a mitral cell from the olfactory system of a mouse, together with the neural spiking response (MC) across many trials (each row displays the spike train for a particular trial). The response is highly regular across trials, but at some points in time it is somewhat variable. The right panel displays a stimulus filter fitted to the complete set of data using model (3), where the stimulus filter, i.e., the function g₀(s), represents the contribution to the firing rate due to the current I(t − s) at s milliseconds prior to time t. Figure modified from (Wang et al. 2015)

Neural firing rates vary widely, depending on recording site and physiological circumstances, from quiescent (essentially 0 spikes per second) to as many as 200 spikes per second. The output of spike sorting is a sequence of spike times, typically at time resolution of 1 millisecond (the approximate width of an AP). While many analyses are based on spike counts across relatively long time intervals (numbers of spikes that occur in time bins of tens or hundreds of milliseconds), some are based on the more complete precise timing information provided by the spike trains.

In some special cases, mainly in networks recorded in vitro, neurons are densely sampled and it is possible to study the way activity of one neuron directly influences the activity of other neurons (Pillow et al. 2008). However, in most experimental settings to date, a very small proportion of the neurons in the circuit are sampled.

1.7. Data analysis

In experiments involving behaving animals, each experimental condition is typically repeated across many trials. On any two trials, there will be at least slight differences in behavior, neural activity throughout the brain, and contributions from molecular noise, all of which results in considerable variability of spike timing. Thus, a spike train may be regarded as a point process, i.e., a stochastic sequence of event times, with the events being spikes. We discuss point process modeling below, but note here that the data are typically recorded as sparse binary time series in 1 millisecond time bins (1 if spike, 0 if no spike). When spike counts within broader time bins are considered, they may be assumed to form continuous-valued time series, and this is the framework for some of the methods referenced below. It is also possible to apply time series methods directly to the binary data, or smoothed versions of them, but see the caution in Kass et al. (2014, Section 19.3.7). A common aim is to relate an observed pattern of activity to features of the experimental stimulus or behavior. However, in some settings predictive approaches are used, often under the rubric of decoding, in the sense that neural activity is “decoded” to predict the stimulus or behavior. In this case, tools associated with the field of statistical machine learning may be especially useful (Ventura and Todorova 2015). We omit many interesting questions that arise in the course of analyzing biological neural networks, such as the distribution of the post-synaptic potentials that represent synaptic weights (Buzsáki and Mizuseki 2014; Teramae et al. 2012).

Data analysis is performed by scientists with diverse backgrounds. Statistical approaches use frameworks built on probabilistic descriptions of variability, both for inductive reasoning and for analysis of procedures. The resulting foundation for data analysis has been called the statistical paradigm (Kass et al. 2014, Section 1.2).

1.8. Components of the nervous system

When we speak of neurons, or brains, we are indulging in sweeping generalities: properties may depend not only on what is happening to the organism during a study, but also on the component of the nervous system studied, and the type of animal being used. Popular organisms in neuroscience include worms, mollusks, insects, fish, birds, rodents, non-human primates, and, of course, humans. The nervous system of vertebrates comprises the brain, the spinal cord, and the peripheral system. The brain itself includes both the cerebral cortex and sub-cortical areas. Textbooks of neuroscience use varying organizational rubrics, but major topics include the molecular physiology of neurons, sensory systems, the motor system, and systems that support higher-order functions associated with complex and flexible behavior (Kandel et al. 2013; Swanson 2012). Attempts at understanding computational properties of the nervous system have often focused on sensory systems: they are more easily accessed experimentally, controlled inputs to them can be based on naturally occurring inputs, and their response properties are comparatively simple. In addition, much attention has been given to the cerebral cortex, which is involved in higher-order functioning.

2. Single Neurons

Mathematical models typically aim to describe the way a given phenomenon arises from some architectural constraints. Statistical models typically are used to describe what a particular data set can say concerning the phenomenon, including the strength of evidence. We very briefly outline these approaches in the case of single neurons, and then review attempts to bring them together.

2.1. LIF models and their extensions

Originally proposed more than a century ago, the LIF model (Figure 3) continues to serve an important role in neuroscience research (Abbott 1999). Although LIF neurons are deterministic, they often mimic the variation in spike trains of real neurons recorded in vitro, such as those in Figure 5. In the left panel of that figure, the same fluctuating current is applied repeatedly as input to the neuron, and this creates many instances of spike times that are highly precise in the sense of being replicated across trials; some other spike times are less precise. Precise spike times occur when a large slope in the input current leads to wide recruitment of ion channels (Mainen and Sejnowski 1995). Temporal locking of spikes to high frequency inputs also can be seen in LIF models (Goedeke and Diesmann 2008). Many extensions of the original leaky integrate-and-fire model have been developed to capture other features of observed neuronal activity (Gerstner et al. 2014), including more realistic spike initiation through inclusion of a quadratic term, and incorporation of a second dynamical variable to simulate adaptation and to capture more diverse patterns of neuronal spiking and bursting. Even though these models ignore the biophysics of action potential generation (which involve the conductances generated by ion channels, as in the Hodgkin-Huxley model), they are able to capture the nonlinearities present in several biophysical neuronal models (Rotstein 2015). The impact of stochastic effects due to the large number of synaptic inputs delivered to an LIF neuron has also been extensively studied using diffusion processes (Lansky and Ditlevsen 2008).

2.2. Biophysical models

There are many extensions of the Hodgkin and Huxley framework outlined in Figure 4. These include models that capture additional biological features, such as additional ionic currents (Somjen 2004), and aspects of the neuron’s extracellular environment (Wei et al. 2014), both of which introduce new fast and slow timescales to the dynamics. Contributions due to the extensive dendrites (which receive inputs to the neuron) have been simulated in detailed biophysical models (Rall 1962). While increased biological realism necessitates additional mathematical complexity, especially when large populations of neurons are considered, the Hodgkin-Huxley model and its extensions remain fundamental to computational neuroscience research (Markram et al. 2015; Traub et al. 2005).

Simplified mathematical models of single neuron activity have facilitated a dynamical understanding of neural behavior. The Fitzhugh-Nagumo model is a purely phenomenological model, based on geometric and dynamic principles, and not directly on the neuron’s biophysics (Fitzhugh 1960; Nagumo et al. 1962). Because of its low dimensionality, it is amenable to phase-plane analysis using dynamical systems tools (e.g., examining the null-clines, equilibria and trajectories).

An alternative approach is to simplify the equations of a detailed neuronal model in ways that retain a biophysical interpretation (Ermentrout and Terman 2010). For example, by making a steady-state approximation for the fast ionic sodium current activation in the Hodgkin-Huxley model (m in Figure 4), and recasting two of the gating variables (n and h), it is possible to simplify the original Hodgkin-Huxley model to a two-dimensional model, which can be investigated more easily in the phase plane (Gerstner et al. 2014). The development of simplified models is closely interwoven with bifurcation theory and the theory of normal forms within dynamical systems (Izhikevich 2007). One well-studied reduction of the Hodgkin-Huxley equations to a 2-dimensional conductance-based model was developed by John Rinzel (Rinzel 1985). In this case, the geometries of the phenomenological Fitzhugh-Nagumo model and the simplified Rinzel model are qualitatively similar. Yet another approach to dimensionality reduction consists of neglecting the spiking currents (fast sodium and delayed-rectifying potassium) and considering only the currents that are active in the sub-threshold regime (Rotstein et al. 2006). This cannot be done in the original Hodgkin-Huxley model, because the only ionic currents are those that lead to spikes, but it is useful in models that include additional ionic currents in the sub-threshold regime.

2.3. Point process regression models of single neuron activity

Mathematically, the simplest model for an irregular spike train is a homogeneous Poisson process, for which the probability of spiking within a time interval (t, t + Δt], for small Δt, may be written

$$P(\text{ spike in }(t,t+\Delta t])\approx \lambda \Delta t,$$

where λ represents the firing rate of the neuron and where disjoint intervals have independent spiking. This model, however, is often inadequate for many reasons. For one thing, neurons have noticeable refractory periods following a spike, during which the probability of spiking goes to zero (the absolute refractory period) and then gradually increases, often over tens of milliseconds (the relative refractory period). In this sense neurons exhibit memory effects, often called spike history effects. To capture those, and many other physiological effects, more general point processes must be used. We outline the key ideas underlying point process modeling of spike trains.

As we indicated in Section 1.2, a fundamental result in neurophysiology is that neurons respond to a stimulus or contribute to an action by increasing their firing rates. The measured firing rate of a neuron within a time interval would be the number of spikes in the interval divided by the length of the interval (usually in units of seconds, so that the ratio is in spikes per second, abbreviated as Hz, for Hertz). The point process framework centers on the theoretical instantaneous firing rate, which takes the expected value of this ratio and passes to the limit as the length of the time interval goes to zero, giving an intensity function for the process. To accurately model a neuron’s spiking behavior, however, the intensity function typically must itself evolve over time depending on changing inputs and experimental conditions, the recent past spiking behavior of the neuron, the behavior of other neurons, the behavior of local field potentials, etc. It is therefore called a conditional intensity function and may be written in the form

$$\lambda (t|x_t)=\underset{\Delta t\to 0}{\text{lim}}\frac{E\left(N_{(t,t+\Delta t]}|X_t=x_t\right)}{\Delta t}$$

where N_(t,_t+Δt] is the number of spikes in the interval (t,t + Δt] and where the vector X_t includes both the past spiking history H_t prior to time t and also any other quantities that affect the neuron’s current spiking behavior. In some special cases, the conditional intensity will be deterministic, but in general, because X_t is random, the conditional intensity is also random. If X_t includes unobserved random variables, the process is often called doubly stochastic. When the conditional intensity depends on the history H_t, the process is often called self-exciting (though the effects may produce an inhibition of firing rate rather than an excitation). The vector X_t may be high-dimensional. A mathematically tractable special case, where contributions to the intensity due to previous spikes enter additively in terms of a fixed kernel function, is the Hawkes process.

As a matter of interpretation, in sufficiently small time intervals the spike count is either zero or one, so we may replace the expectation with the probability of spiking and get

$$P(\text{spike in }(t,t+\Delta t]|X_t=x_t)\approx \lambda (t|x_t)\Delta t.$$

A statistical model for a spike train involves two things: (1) a simple, universal formula for the probability density of the spike train in terms of the conditional intensity function (which we omit here) and (2) a specification of the way the conditional intensity function depends on variables x_t. An analogous statement is also true for multiple spike trains, possibly involving multiple neurons. Thus, when the data are resolved down to individual spikes, statistical analysis is primarily concerned with modeling the conditional intensity function in a form that can be implemented efficiently and that fits the data adequately well. That is, writing

$$\lambda (t|x_t)=f\left(x_t\right),$$ (1)

the challenge is to identify within the variable x_t all relevant effects, or features, in the terminology of machine learning, and then to find a suitable form for the function f, keeping in mind that, in practice, the dimension of x_t may range from 1 to many millions. This identification of the components of x_t that modulate the neuron’s firing rate is a key step in interpreting the function of a neural system. Details may be found in Kass et al. (2014, Chapter 19), but see Amarasingham et al. (2015) for an important caution about the interpretation of neural firing rate through its representation as a point process intensity function.

A statistically tractable non-Poisson form involves log-additive models, the simplest case being

$$\text{log}\lambda (t|x_t)=\text{log}\lambda (t|H_t)=\text{log}{g}_0(t)+\text{log}{g}_1\left(t-s_{*}(t)\right)$$ (2)

where s_*(t) is the time of the immediately preceding spike, and g₀ and g₁ are functions that may be written in terms of some basis (Kass and Ventura 2001). To include contributions from spikes that are earlier than the immediately preceding one, the term log g₁(t − s_*(t)) is replaced by a sum of terms of the form log g_1j(t − s_j(t)), where s_j(t) is the j-th spike back in time preceding t, and a common simplification is to assume the functions g_1j are all equal to a single function g₁ (Pillow et al. 2008). The resulting probability density function for the set of spike times (which defines the likelihood function) is very similar to that of a Poisson generalized linear model (GLM) and, in fact, GLM software may be used to fit many point process models (Kass et al. 2014, Chapter 19). The use of the word “linear” may be misleading here because highly nonlinear functions may be involved, e.g., in Equation (2), g₀ and g₁ are typically nonlinear. An alternative is to call these point process regression models. Nonetheless, the model in (2) is often said to specify a GLM neuron, as are other point process regression models.

2.4. Point process regression and leaky integrate-and-fire models

Assuming excitatory and inhibitory Poisson process inputs to an LIF neuron, the distribution of waiting times for a threshold crossing, which corresponds to the inter-spike interval (ISI), is found to be inverse Gaussian (Tuckwell 1988) and this distribution often provides a good fit to experimental data when neurons are in steady state, as when they are isolated in vitro and spontaneous activity is examined (Gerstein and Mandelbrot 1964). The inverse Gaussian distribution, within a biologically-reasonable range of coefficient of variations, turns out to be qualitatively very similar to ISI distributions generated by processes given by Equation (2). Furthermore, spike trains generated from LIF models can be fitted well by these GLM-type models (Kass et al. 2014, Section 19.3.4 and references therein).

An additional connection between LIF and GLM neurons comes from considering the response of neurons to injected currents, as illustrated in Figure 5. In this context, the first term in Equation (2) may be rewritten as a convolution with the current I(t) at time t, so that (2) becomes

$$\text{log}\lambda (t|x_t)=\text{log}\lambda (t|H_t,I_t)={\int }_0^{\infty }{g}_0(s)I(t-s)ds+\text{log}{g}_1\left(t-s_{*}(t)\right).$$ (3)

Figure 5 shows the estimate of g₀ that results from fitting this model to data illustrated in that figure. Here, the function g₀ is often called a stimulus filter. On the other hand, following Gerstner et al. (2014, Chapter 6), we may write a generalized version of LIF in integral form,

$$V(t)=V_{\text{rest}}+{\int }_0^{\infty }{g}_0(s)I(t-s)ds+\text{log}{g}_1\left(t-s_{*}(t)\right)$$ (4)

which those authors call a Spike Response Model (SRM). By equating the log conditional intensity to voltage in (4),

$$\text{log}\lambda (t|H_t,I_t)=V(t)-V_{\text{rest}}$$

we thereby get a modified LIF neuron that is also a GLM neuron (Paninski et al. 2009). Thus, both theory and empirical study indicate that GLM and LIF neurons are very similar, and both describe a variety of neural spiking patterns (Weber and Pillow 2016).

It is interesting that these empirically-oriented SRMs, and variants that included an adaptive threshold (Kobayashi et al. 2009), performed better than much more complicated biophysical models in a series of international competitions for reproducing and predicting recorded spike times of biological neurons under varying circumstances (Gerstner and Naud 2009).

2.5. Multidimensional models

The one-dimensional LIF dynamic model in Figure 3b is inadequate when interactions of sub-threshold ion channel dynamics cause a neuron’s behavior to be more complicated than integration of inputs. Neurons can even behave as differentiators and respond only to fluctuations in input. Furthermore, as noted in Sections 1.3 and 2.3, features that drive neural firing can be multidimensional. Multivariate dynamical systems are able to describe the ways that interacting, multivariate effects can bring the system to its firing threshold, as in the Hodgkin-Huxley model (Hong et al. 2007). A number of model variants that aim to account for such multidimensional effects have been compared in predicting experimental data from sensory areas (Aljadeff et al. 2016).

2.6. Statistical challenges in biophysical modeling

Conductance-based biophysical models pose problems of model identifiability and parameter estimation. The original Hodgkin-Huxley equations (Hodgkin and Huxley 1952) contain on the order of two dozen numerical parameters describing the membrane capacitance, maximal conductances for the sodium and potassium ions, kinetics of ion channel activation and inactivation, and the ionic equilibrium potentials (at which the flow of ions due to imbalances of concentration across the cell membrane offsets that due to imbalances of electrical charge). Hodgkin and Huxley arrived at estimates of these parameters through a combination of extensive experimentation, biophysical reasoning, and regression techniques. Others have investigated the experimental information necessary to identify the model (Walch and Eisenberg 2016). In early work, statistical analysis of nonstationary ensemble fluctuations was used to estimate the conductances of individual ion channels (Sigworth 1977). Following the introduction of single-channel recording techniques (Sakmann and Neher 1984), which typically report a binary projection of a multistate underlying Markovian ion channel process, many researchers expanded the theory of aggregated Markov processes to handle inference problems related to identifying the structure of the underlying Markov process and estimating transition rate parameters (Qin et al. 1997).

More recently, parameter estimation challenges in biophysical models have been tackled using a variety of techniques under the rubric of “data assimilation,” where data results are combined with models algorithmically. Data assimilation methods illustrate the interplay of mathematical and statistical approaches in neuroscience. For example, in Meng et al. (2014), the authors describe a state space modeling framework and a sequential Monte Carlo (particle filter) algorithm to estimate the parameters of a membrane current in the Hodgkin-Huxley model neuron. They applied this framework to spiking data recorded from rat layer V cortical neurons, and correctly identified the dynamics of a slow membrane current. Variations on this theme include the use of synchronization manifolds for parameter estimation in experimental neural systems driven by dynamically rich inputs (Meliza et al. 2014), combined statistical and geometric methods (Tien and Guckenheimer 2008), and other state space models (Vavoulis et al. 2012).

3. Networks

3.1. Mechanistic approaches for modeling small networks

While biological neural networks typically involve anywhere from dozens to many millions of neurons, studies of small neural networks involving handfuls of cells have led to remarkably rich insights. We describe three such cases here, and the types of mechanistic models that drive them.

First, neural networks can produce rhythmic patterns of activity. Such rhythms, or oscillations, play clear roles in central pattern generators (CPGs) in which cell groups produce coordinated firing for, e.g., locomotion or breathing (Grillner and Jessell 2009; Marder and Bucher 2001). Small network models have been remarkably successful in describing how such rhythms occur. For example, models involving pairs of cells have revealed how delays in connections among inhibitory cells, or reciprocal interactions between excitatory and inhibitory neurons, can lead to rhythms in the gamma range (30–80 Hz) associated with some aspects of cognitive processing. A general theory, beginning with two-cell models of this type, describes how synaptic and intrinsic cellular dynamics interact to determine when the underlying synchrony will and will not occur (Kopell and Ermentrout 2002). Larger models involving three or more interacting cell types describe the origin of more complex rhythms, such as the triphasic rhythm in the stomatogastric ganglion (for digestion in certain invertebrates). This system in particular has revealed a rich interplay between the intrinsic dynamics in multiple cells and the synapses that connect them (Marder and Bucher 2001). There turn out to be many highly distinct parameter combinations, lying in subsets of parameter space, that all produce the key target rhythm, but do so in very different ways (Prinz et al. 2004). Understanding the origin of this flexibility, and how biological systems take advantage of it to produce robust function, is a topic of ongoing work.

The underlying mechanistic models for rhythmic phenomena are of Hodgkin-Huxley type, involving sodium and potassium channels (Figure 4). For some phenomena, including respiratory and stomatogastric rhythms, additional ion channels that drive bursting in single cells play a key role. Dynamical systems tools for assessing the stability of periodic orbits may then be used to determine what patterns of rhythmic activity will be stably produced by a given network. Specifically, coupled systems of biophysical differential equations can often be reduced to interacting circular variables representing the phase of each neuron (Ermentrout and Terman 2010). Such phase models yield to very elegant stability analyses that can often predict the dynamics of the original biophysical equations.

A second example concerns the origin of collective activity in irregularly spiking neural circuits. To understand the development of correlated spiking in such systems, stochastic differential equation models, or models driven by point process inputs, are typically used. This yields Fokker-Planck or population density equations (Tranchina 2010; Tuck-well 1988) and these can be iterated across multiple layers or neural populations (Doiron et al. 2006; Tranchina 2010). In many cases, such models can be approximated using linear response approaches, yielding analytical solutions and considerable mechanistic insight (De La Rocha et al. 2007; Ostojic and Brunel 2011a). A prominent example comes from the mechanisms of correlated firing in feedforward networks (De La Rocha et al. 2007; Shadlen and Newsome 1998). Here, stochastically firing cells send diverging inputs to multiple neurons downstream. The downstream neurons thereby share some of their input fluctuations, and this, in turn, creates correlated activity that can have rich implications for information transmission (De La Rocha et al. 2007; Doiron et al. 2016; Zylberberg et al. 2016).

A third case of highly influential small circuit modeling concerns neurons in the early visual cortex (early in the sense of being only a few synapses from the retina), which are responsive to visual stimuli (moving bars of light) with specific orientations that fall within their receptive field (see Section 1.3). Neurons having neighboring regions within their receptive field in which a stimulus excites or inhibits activity were called simple cells, and those without this kind of sub-division were complex cells. Hubel and Wiesel famously showed how simple circuit models can account for both the simple and complex cell responses (Hubel and Wiesel 1959). Later work described this through one or several iterated algebraic equations that map input firing rates x_i into outputs y = f(∑_iw_ix_i), where w = (w₁, …, w_N) is a synaptic weight vector.

3.2. Statistical methods for small networks

Point process models for small networks begin with conditional intensity specifications similar to that in Equation (2), and include coupling terms (Kass et al. 2014, Section 19.3.4, and references therein). They have been applied to CPGs described above, in Section 3.1, to reconstruct known circuitry from spiking data (Gerhard et al. 2013). In addition, many of the methods we discuss below, in Section 3.4 on large networks, have also been used with small networks.

3.3. Mechanistic models of large networks across scales and levels of complexity

There is a tremendous variety of mechanistic models of large neural networks. We here describe these in rough order of their complexity and scale.

3.3.1. Binary and firing rate models.

At the simplest level, binary models abstract the activity of each neuron as either active (taking the value 1) or silent (0) in a given time step. As mentioned in the Introduction, despite their simplicity, these models capture fundamental properties of network activity (Renart et al. 2010; van Vreeswijk and Sompolinsky 1996) and explain network functions such as associative memory. The proportion of active neurons at a given time is governed by effective rate equations (Ginzburg and Sompolinsky 1994; Wilson and Cowan 1972). Such firing rate models feature a continuous range of activity states, and often take the form of nonlinear ordinary or stochastic differential equations. Like binary models, these also implement associative memory (Hopfield 1984), but are widely used to describe broader dynamical phenomena in networks, including predictions of oscillations in excitatory-inhibitory networks (Wilson and Cowan 1972), transitions from fixed point to oscillatory to chaotic dynamics in randomly connected neural networks (Bos et al. 2016), amplified selectivity to stimuli, and the formation of line attractors (a set of stable solutions on a line in state space) that gradually store and accumulate input signals (Cain and Shea-Brown 2012).

Firing rate models have been a cornerstone of theoretical neuroscience. Their second order statistics can analytically be matched to more realistic spiking and binary models (Grytskyy et al. 2013; Ostojic and Brunel 2011a). We next describe how trial-varying dynamical fluctuations can emerge in networks of spiking neuron models.

3.3.2. Stochastic spiking activity in networks.

A beautiful body of work summarizes the network state in a population-density approach that describes the evolution of the probability density of states rather than individual neurons (Amit and Brunel 1997). The theory is able to capture refractoriness (Meyer and van Vreeswijk 2002) and adaptation (Deger et al. 2014). Furthermore, although it loses the identity of individual neurons, it can faithfully capture collective activity states, such as oscillations (Brunel 2000). Small synaptic amplitudes and weak correlations further reduce the time-evolution to a Fokker-Planck equation (Brunel 2000; Ostojic et al. 2009). Network states beyond such diffusion approximations include neuronal avalanches, the collective and nearly synchronous firing of a large fraction of cells, often following power-law distributions (Beggs and Plenz 2003). While early work focused on the firing rates of populations, later work clarified how more subtle patterns of correlated spiking develop. In particular, linear fluctuations about a stationary state determine population-averaged measures of correlations (Helias et al. 2013; Ostojic et al. 2009; Tetzlaff et al. 2012; Trousdale et al. 2012).

At an even larger scale, a continuum of coupled population equations at each point in space lead to neuronal field equations (Bressloff 2012). They predict stable “bumps” of activity, as well as traveling waves and spirals (Amari 1977a; Roxin et al. 2006). Intriguingly, when applied as a model of visual cortex and rearranged to reflect spatial layout of the retina, patterns induced in these continuum equations can resemble visual hallucinations (Bressloff et al. 2001).

Analysis has provided insight into the ways that spiking networks can produce irregular spike times like those found in cortical recordings from behaving animals (Shadlen and Newsome 1998), as in Figure 5. Suppose we have a network of N^E excitatory and N^I inhibitory LIF neurons with connections occurring at random according to independent binary (Bernoulli) random variables, i.e., a connection exists when the binary random variable takes the value 1 and does not exist when it is 0. We denote the binary connectivity random variables by ${\kappa }_{ij}^{\alpha \beta }$, where α and β take the values E or I, with ${\kappa }_{ij}^{\alpha \beta }=1$ when the output of neuron j in population β injects current into neuron i in population α. We let J^αβ be the coupling strength (representing synaptic current) from a neuron in population β to a neuron in population α. Thus, the contribution to the current input of a neuron in population α generated at time t by a spike from neuron in population β at time s will be $J^{\alpha \beta }{\kappa }_{ij}^{\alpha \beta }\delta (t-s)$, where δ(t − s) is the Dirac delta function. The behavior of the network can be analyzed by letting N^E → ∞ and N^I → ∞. Based on reasonable simplifying assumptions, the mean M^α and variance V^α of the total current for population α have been derived (Amit and Brunel 1997; Van Vreeswijk and Sompolinsky 1998), and these determine the regularity or irregularity in spiking activity.

We step through three possibilities, under three different conditions on the network, using a modification of the LIF equation found in Figure 3. The set of equations, for all the neurons in the network, includes terms defined by network connectivity and also terms defined by external input fluctuations. Because the connectivity matrix may contain cycles (there may be a path from any neuron back to itself), network connectivity is called recurrent. Let us take the membrane potential of neuron i from population α to be

$${\tau }^{\alpha }\frac{d{V}_i^{\alpha }}{dt}=-V_i^{\alpha }+\underset{\text{ external inputs }}{\underbrace{{\mu }_0^{\alpha }+\sqrt{{\tau }^{\alpha }}{\sigma }_0^{\alpha }{\xi }_i^{\alpha }(t)}}+\underset{\text{ recurrent excitation }}{\underbrace{{\tau }^{\alpha }{J}^{\alpha E}\sum _{j=1}^{N^E}{\kappa }_{ij}^{\alpha E}\delta \left(t-t_{jk}^E\right)}}-\underset{\text{ recurrent inhibition }}{\underbrace{{\tau }^{\alpha }{J}^{\alpha I}\sum _{j=1}^{N^I}{\kappa }_{ij}^{\alpha I}\delta \left(t-t_{jk}^I\right)}}$$ (5)

where $t_{ik}^{\alpha }$ is the k^th spike time from neuron i of population α, τ^α is the membrane dynamics time constant, and the external inputs include both a constant μ₀ and a fluctuating source σ₀ξ(t) where ξ(t) is white noise (independent across neurons). This set of equations is supplemented with the spike reset rule that when $V_i^{\alpha }(t)=V_T$ the voltage resets to V_R < V_T.

The firing rate of the average neuron in population α is ${\lambda }^{\alpha }={\sum }_j{\sum }_k\delta \left(t-t_{jk}^{\alpha }\right)/N^{\alpha }$. For the network to remain stable, we take these firing rates to be bounded, i.e., ${\lambda }^{\alpha }~\mathcal{O}(1)$. Similarly, to assure that the current input to each neuron remains bounded, some assumption must be made about the way coupling strengths J^αβ scale as the number of inputs K increases. Let us take the scaling to be J^αβ = j^αβ/K^γ, with $j^{\alpha \beta }~\mathcal{O}(1)$, as K → ∞, where γ is a scaling exponent. We describe the resulting spiking behavior under scaling conditions γ =1 and γ = 1/2.

If we set γ = 1 then we have J ~ 1/K, so that $JK=j~\mathcal{O}(1)$. In this case we get $M^{\alpha }~\mathcal{O}(1)$ and $V^{\alpha }={\left[{\sigma }_0^{\alpha }\right]}^2+\mathcal{O}(1/\sqrt{K})$. If we further set ${\sigma }_0^{\alpha }=0$, so that all fluctuations must be internal, then V^α vanishes for large K. In such networks, after an initial transient, the neurons synchronize, and each fires with perfect rhythmicity (left part of panel A in Figure 6). This is very different than the irregularity seen in cortical recordings (Figure 3). Therefore, some modification must be made.

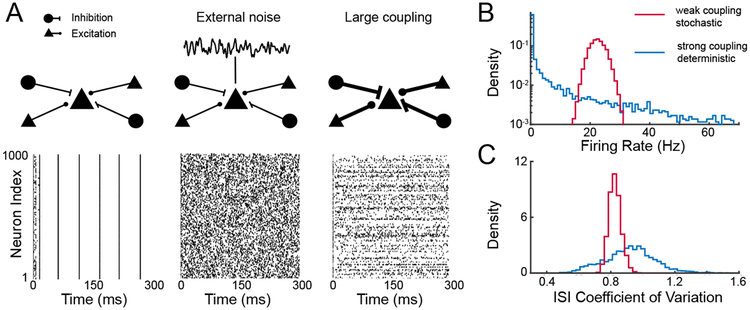
Figure 6.

Panel A displays plots of spike trains from 1000 excitatory neurons in a network having 1000 excitatory and 1000 inhibitory LIF neurons with connections determined from independent Bernoulli random variables having success probability of 0.2; on average K = 200 inputs per neuron with no synaptic dynamics. Each neuron receives a static depolarizing input; in absence of coupling each neuron fires repetitively. Left: Spike trains under weak coupling, current J ∝ K⁻¹. Middle: Spike trains under weak couplng, with additional uncorrelated noise applied to each cell. Right: Spike trains under strong coupling, $J\propto K^{-\frac{1}{2}}$. Panel B shows the distribution of firing rates across cells, and panel C the distribution of interspike interval (ISI) coefficient of variation across cells.

The first route to appropriate spike train irregularity keeps γ = 1 while setting ${\left[{\sigma }_0^{\alpha }\right]}^2~\mathcal{O}(1)$ so that V^α no longer vanishes in the large K limit. Simulations of this network (Figure 6A, middle) maintain realistic rates (Figure 6B, red curve), but also show realistic irregularity (Faisal et al. 2008), as quantified in Figure 6C by the coefficient of variation (CV) of the inter-spike intervals. Treating irregular spiking activity as the consequence of stochastic inputs has a long history (Tuckwell 1988).

The second route does not rely on external input stochasticity, but instead increases the synaptic connection strengths by setting γ = 1/2. As a consequence we get $V^{\alpha }~\mathcal{O}(1)$ even if ${\sigma }_0^{\alpha }=0$ so that variability is internally generated through recurrent interactions (Monteforte and Wolf 2012; Van Vreeswijk and Sompolinsky 1998), but to get $M^{\alpha }~\mathcal{O}(1)$, an additional condition is needed. If the recurrent connectivity is dominated by inhibition, so that the network recurrence results in negative current, the activity dynamically settles into a state in which

$$M^{\alpha }=\sqrt{K}\underset{\mathcal{O}(1/\sqrt{K}):\text{ balance condition }}{\underbrace{\left({\mu }^{\alpha }+j^{\alpha E}{\tau }^{\alpha }{\lambda }^E-j^{\alpha I}{\tau }^{\alpha }{\lambda }^I\right)}}~\mathcal{O}(1),$$ (6)

where ${\mu }_0^{\alpha }$ has been replaced by the constant μ^α using ${\mu }_0^{\alpha }=\sqrt{K}{\mu }^{\alpha }$ so that the mean external input is of order $\mathcal{O}(\sqrt{K})$. The scaling γ = 1/2 now makes the total excitatory and the total inhibitory synaptic inputs individually large, i.e., $\mathcal{O}(\sqrt{K})$, so that the V^α is also large. However, given the balance condition in (6), excitation and inhibition mutually cancel and V^α remains moderate. Simulations of the network with γ = 1/2 and ${\sigma }_0^{\alpha }=0$ shows an asynchronous network dynamic (Figure 6A, right). Further, the firing rates stabilize at low mean levels (Figure 6B, blue curve), while the inter-spike interval CV is large (Figure 6C, blue curve).

These two mechanistic routes to high levels of neural variability differ strikingly in the degree of heterogeneity of the spiking statistics. For the weak coupling with γ = 1 the resulting distribution of firing rates and inter-spike interval CVs are narrow (Figure 6B, C, red curves). At strong coupling with γ = 1/2, however, the spread of firing rates is large: over half of the neurons fire at rates below 1 Hz (Figure 6B, blue curve), in line with observed cortical activity (Roxin et al. 2011). The approximate dynamic balance between excitatory and inhibitory synaptic currents has been confirmed experimentally (Okun and Lampl 2008) and is usually called balanced excitation and inhibition.

3.3.3. Asynchronous dynamics in recurrent networks.

The analysis above focused only on M^α and V^α, ignoring any correlated activity between the currents neurons in the network. The original justification for such asynchronous dynamics in Van Vreeswijk and Sompolinsky (1998) and Amit and Brunel (1997) relied on a sparse wiring assumption, i.e, K/N^α → 0 as N^α → ∞ for α ∈ (E, I). However, more recently it has been shown that the balanced mechanism required to keep firing rates moderate also ensures that network correlations vanish. Balance arises from the dominance of negative feedback which suppresses fluctuations in the population-averaged activity and hence causes small pairwise correlations (Tetzlaff et al. 2012). As a consequence, fluctuations of excitatory and inhibitory synaptic currents are tightly locked so that Equation (6) is satisfied. The excitatory and inhibitory cancellation mechanism therefore extends to pairs of cells and operates even in networks with dense wiring, i.e., $K/N^{\alpha }~\mathcal{O}(1)$ (Hertz 2010; Renart et al. 2010), so that input correlations are much weaker than expected by the number of shared inputs (Shadlen and Newsome 1998; Shea-Brown et al. 2008). This suppression and cancellation of correlations holds in the same way for intrinsically-generated fluctuations that often even dominate the correlation structure (Helias et al. 2014). Recent work has shown that the asynchronous state is more robustly realized in nonrandom networks than normally distributed random networks (Litwin-Kumar and Doiron 2012; Teramae et al. 2012).

There is a large literature on how network connectivity, at the level of mechanistic models, leads to different covariance structures in network activity (Ginzburg and Sompolinsky 1994). Highly local connectivity features scale up to determine global levels of covariance (Doiron et al. 2016; Helias et al. 2013; Trousdale et al. 2012). Moreover, features of that connectivity that point specifically to low-dimensional structures of neural covariability can be isolated (Doiron et al. 2016). An outstanding problem is to create model networks that mimic the low-dimensional covariance structure reported in experiments (see Section 3.4.1).

3.4. Statistical methods for large networks

New recording technologies should make it possible to track the flow of information across very large networks of neurons, but the details of how to do so have not yet been established. One tractable component of the problem (Cohen and Kohn 2011) involves co-variation in spiking activity among many neurons (typically dozens to hundreds), which leads naturally to dimensionality reduction and to graphical representations (where neurons are nodes, and some definition of correlated activity determines edges). However, two fundamental complications affect most experiments. First, co-variation can occur at multiple timescales. A simplification is to consider either spike counts in coarse time bins (20 milliseconds or longer) or spike times with precision in the range of 1–5 milliseconds. We will discuss methods based on spike counts and precise spike timing separately, in the next two subsections. Second, experiments almost always involve some stimuli or behaviors that create evolving conditions within the network. Thus, methods that assume stationarity must be used with care, and analyses that allow for dynamic evolution will likely be useful. Fortunately, many experiments are conducted using multiple exposures to the same stimuli or behavioral cues, which creates a series of putatively independent replications (trials). While the responses across trials are variable, sometimes in systematic ways, the setting of multiple trials often makes tractable the analysis of non-stationary processes.

After reviewing techniques for analyzing co-variation of spike counts and precisely-timed spiking we will also briefly mention three general approaches to understanding network behavior: reinforcement learning, Bayesian inference, and deep learning. Reinforcement learning and Bayesian inference use a decision-theoretic foundation to define optimal actions of the neural system in achieving its goals, which is appealing insofar as evolution may drive organism design toward optimality.

3.4.1. Correlation and dimensionality reduction in spike counts.

Dimensionality reduction methods have been fruitfully applied to study decision-making, learning, motor control, olfaction, working memory, visual attention, audition, rule learning, speech, and other phenomena (Cunningham and Yu 2014). Dimensionality reduction methods that have been used to study neural population activity include principal component analysis, factor analysis, latent dynamical systems, and non-linear methods such as Isomap and locally-linear embedding. Such methods can provide two types of insights. First, the time course of the neural response can vary substantially from one experimental trial to the next, even though the presented stimulus, or the behavior, is identical on each trial. In such settings, it is of interest to examine population activity on individual trials (Churchland et al. 2007). Dimensionality reduction provides a way to summarize the population activity time course on individual experimental trials by leveraging the statistical power across neurons (Yu et al. 2009). One can then study how the latent variables extracted by dimensionality reduction change across time or across experimental conditions. Second, the multivariate statistical structure in the population activity identified by dimensionality reduction may be indicative of the neural mechanisms underlying various brain functions. For example, one study suggested that a subject can imagine moving their arms, while not actually moving them, when neural activity related to motor preparation lies in a space orthogonal to that related to motor execution (Kaufman et al. 2014). Furthermore, the multivariate structure of population activity can help explain why some tasks are easier to learn than others (Sadtler et al. 2014) and how subjects respond differently to the same stimulus in different contexts (Mante et al. 2013).

3.4.2. Correlated spiking activity at precise time scales.

In principle, very large quantities of information could be conveyed through the precise timing of spikes across groups of neurons. The idea that the nervous system might be able to recognize such patterns of precise timing is therefore an intriguing possibility (Abeles 1982; Geman 2006; Singer and Gray 1995). However, it is very difficult to obtain strong experimental evidence in favor of a widespread computational role for precise timing (e.g., an accuracy within 1–5 milliseconds), beyond the influence of the high arrival rate of synaptic impulses when multiple input neurons fire nearly synchronously. Part of the issue is experimental, because precise timing may play an important role only in specialized circumstances, but part is statistical: under plausible point process models, patterns such as nearly synchronous firing will occur by chance, and it may be challenging to define a null model that captures the null concept without producing false positives. For example, when the firing rates of two neurons increase, the number of nearly synchronous spikes will increase even when the spike trains are otherwise independent; thus, a null model with constant firing rates could produce false positives for the null hypothesis of independence. This makes the detection of behaviorally-relevant spike patterns a subtle statistical problem (Grün 2009; Harrison et al. 2013).

A strong indication that precise timing of spikes may be relevant to behavior came from an experiment involving hand movement, during which pairs of neurons in motor cortex fired synchronously (within 5 milliseconds of each other) more often than predicted by an independent Poisson process model and, furthermore, these events, called Unitary Events, clustered around times that were important to task performance (Riehle et al. 1997). While this illustrated the potential role of precisely timed spikes, it also raised the issue of whether other plausible point process null models might lead to different results. Much work has been done to refine this methodology (Albert et al. 2016; Gmn 2009; Torre et al. 2016). Related approaches replace the null assumption of independence with some order of correlation, using marked Poisson processes (Staude et al. 2010).

There is a growing literature on dependent point processes. Some models do not include a specific mechanism for generating precise spike timing, but can still be used as null models for hypothesis tests of precise spike timing. On a coarse time scale, point process regression models as in Equation (1) can incorporate effects of one neuron’s spiking behavior on another (Pillow et al. 2008; Truccolo 2010). On a fine time scale, one may instead consider multivariate binary processes (multiple sequences of 0s and 1s where 1s represent spikes). In the stationary case, a standard statistical tool for analyzing binary data involves loglinear models (Agresti 1996), where the log of the joint probability of any particular pattern is represented as a sum of terms that involve successively higher-order interactions, i.e., terms that determine the probability of spiking within a given time bin for individual neurons, pairs of neurons, triples, etc. Two-way interaction models, also called maximum entropy models, which exclude higher than pairwise interactions, have been used in several studies and in some cases higher-order interactions have been examined (Ohiorhenuan et al. 2010; Santos et al. 2010; Shimazaki et al. 2015), sometimes using information geometry (Nakahara et al. 2006), though large amounts of data may be required to find small but plausibly interesting effects (Kelly and Kass 2012). Extensions to non-stationary processes have also been developed (Shimazaki et al. 2012; Zhou et al. 2015). Dichotomized Gaussian models, which instead produce binary outputs from threshold crossings of a latent multivariate Gaussian random variable, have also been used (Amari et al. 2003; Shimazaki et al. 2015), as have Hawkes processes (Jovanovic et al. 2015). A variety of correlation structures may be accommodated by analyzing cumulants (Staude et al. 2010).

To test hypotheses about precise timing, several authors have suggested procedures akin to permutation tests or nonparametric bootstrap. The idea is to generate re-sampled data, also called pseudo-data or surrogate data, that preserves as many of the features of the original data as possible, but that lacks the feature of interest, such as precise spike timing. A simple case, called dithering or jittering, modifies the precise time of each spike by some random amount within a small interval, thereby preserving all coarse temporal structure and removing all fine temporal structure. Many variations on this theme have been explored (Grün 2009; Harrison et al. 2013; Platkiewicz et al. 2017), and connections have been made with the well-established statistical notion of conditional inference (Harrison et al. 2015).

3.4.3. Reinforcement learning.

Reinforcement learning (RL) grew from attempts to describe mathematically the way organisms learn in order to achieve repeatedly-presented goals. The motivating idea was spelled out in 1911 by Thorndike (Thorndike 1911, p. 244): when a behavioral response in some situation leads to reward (or discomfort) it becomes associated with that reward (or discomfort), so that the behavior becomes a learned response to the situation. While there were important precursors (Bush and Mosteller 1955; Rescorla and Wagner 1972), the basic theory reached maturity with the 1998 publication of the book by Sutton and Barto (Sutton and Barto 1998). Within neuroscience, a key discovery involved the behavior of dopamine neurons in certain tasks: they initially fire in response to a reward but, after learning, fire in response to a stimulus that predicts reward; this was consistent with predictions of RL (Schultz et al. 1997). (Dopamine is a neuromodulator, meaning a substance that, when emitted from the synapses of neurons, modulates the synaptic effects of other neurons; a dopamine neuron is a neuron that emits dopamine; dopamine is known to play an essential role in goal-directed behavior.)

In brief, the mathematical framework is that of a Markov decision process, which is an action-dependent Markov chain (i.e., a stochastic process on a set of states where the probability of transitioning from one state to the next is action-dependent) together with rewards that depend on both state transition and action. When an agent (an abstract entity representing an organism, or some component of its nervous system) reaches stationarity after learning, the current value V_t of an action may be represented in terms of its future-discounted expected reward:

$$V_t=E\left(R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+\cdots \right)$$

$$=E\left(R_t+\gamma V_{t+1}\right)$$

where R_t is the reward at time t. Thus, to drive the agent toward this stationarity condition, the current estimate of value ${\widehat{V}}_t$ should be updated in such a way as to decrease the estimated magnitude of E(R_t + γV_t+1) − V_t, which is known as the reward prediction error (RPE),

$${\delta }_t=\widehat{E}\left(R_t+\gamma V_{t+1}\right)-{\widehat{V}}_t=r_t+\gamma {\widehat{V}}_{t+1}-{\widehat{V}}_t$$

This is also called the temporal difference learning error. RL algorithms accomplish learning by sequentially reducing the magnitude of the RPE. The essential interpretation of Schultz et al. (1997), which remains widely influential, was that dopamine neurons signal RPE.

The RL-based description of the activity of dopamine neurons has been considered one of the great success stories in computational neuroscience, operating at the levels of computation and algorithm in Marr’s framework (see Section 1.1). A wide range of further studies have elaborated the basic framework and taken on topics such as the behavior of other neuromodulators; neuroeconomics; the distinction between model-based learning, where transition probabilities are learned explicitly, and model-free learning; social behavior and decision-making; and the role of time and internal models in learning (Dayan and Nakahara 2017; Schultz 2015).

3.4.4. Bayesian inference.

Although statistical methods based on Bayes’ Theorem now play a major role in statistics, they were, until relatively recently, controversial (McGrayne 2011). In neuroscience, Bayes’ Theorem has been used in many theoretical constructions in part because the brain must combine prior knowledge with current data somehow, and also because evolution may have led to neural network behavior that is, like Bayesian inference (under well specified conditions), optimal, or nearly so. Bayesian inference has played a prominent role in theories of human problem-solving (Anderson 2009), visual perception (Geisler 2011), sensory and motor integration (Körding 2007; Wolpert et al. 2011), and general cortical processing (Griffiths et al. 2012).

3.4.5. Deep learning.

Deep learning (LeCun et al. 2015) is an outgrowth of PDP modeling (see Section 1.4). Two major architectures came out of the 1980’s and 1990’s, convolutional neural networks (CNNs) and long short term memory (LSTM). LSTM (Hochreiter and Schmidhuber 1997) enables neural networks to take as input sequential data of arbitrary length and learn long-term dependencies by incorporating a memory module where information can be added or forgotten according to functions of the current input and state of the system. CNNs, which achieve state of the art results in many image classification tasks, take inspiration from the visual system by incorporating receptive fields and enforcing shift-invariance (physiological visual object recognition being invariant to shifts in location). In deep learning architectures, receptive fields (LeCun et al. 2015) identify a very specific input pattern, or stimulus, in a small spatial region, using convolution to combine inputs. Receptive fields induce sparsity and lead to significant computational savings, which prompted early success with CNNs (LeCun 1989). Shift invariance is achieved through a spatial smoothing operator known as pooling (a weighted average, or often the maximum value, over a local neighborhood of nodes). Because it introduces redundancies, pooling is often combined with downsampling. Many layers, each using convolution and pooling, are stacked to create a deep network, in rough analogy to multiple anatomical layers in the visual system of primates. Although artificial neural networks had largely fallen out of widespread use by the end of the 1990s, faster computers combined with availability of very large repositories of training data, and the innovation of greedy layer-wise training (Bengio et al. 2007) brought large gains in performance and renewed attention, especially when ALEXNET (Krizhevsky et al. 2012) was applied to the ImageNet database (Deng et al. 2009). Rapid innovation has enabled the application of deep learning to a wide variety of problems of increasing size and complexity.

The success of deep learning in reaching near human-level performance on certain highly constrained prediction and classification tasks, particularly in the area of computer vision, has inspired interest in exploring the connections between deep neural networks and the brain. Studies have shown similarities between the internal representations of convolutional neural networks and representations in the primate visual system (Kriegeskorte 2015; Yamins and DiCarlo 2016). Furthermore, the biological phenomenon of hippocampal replay during memory consolidation prompted innovation in artificial intelligence, in part through the incorporation of reinforcement learning (see Section 3.4.3) into deep learning architectures (Mnih et al. 2015). On the other hand, some studies have shown cases in which biological vision and deep networks diverge in performance (Nguyen et al. 2015; Ullman et al. 2016). Even though they are not biologically realistic, deep learning architectures may suggest new scientific hypotheses (Pelillo et al. 2015).

3.5. Connecting mathematical and statistical approaches in large networks

3.5.1. Bridging from dynamical to statistical models of neural spiking.

In Section 2.4 we made an explicit connection between an integrated form of LIF models and GLMs. An alternative is to derive from a mechanistic model, first, an instantaneous intensity by determining mean activity and, second, the variation around the mean. In binary models, the first step leads to a Gaussian integral (Van Vreeswijk and Sompolinsky 1998) and the second to its derivative (Helias et al. 2014; Renart et al. 2010). For spiking models, these steps are conceptually identical, but mathematically more involved. The firing rate follows from the mean first passage time for the membrane voltage to exceed the threshold (Amit and Brunel 1997; Tuckwell 1988). Computing deviations of responses from the mean requires either perturbation theory applied to the Fokker-Planck equation (Richardson 2008) or separation of timescales for slow currents (Moreno-Bote and Parga 2010). These approaches may be united in an elegant framework to produce an equivalent GLM model (Ostojic and Brunel 2011b). Approximating the fluctuations in spiking and binary networks up to linear order, correlations are equivalent to those of linear stochastic differential equations driven by Gaussian noise (Grytskyy et al. 2013). Extensions treat the mechanistic origins of stimulus adaptation in statistical models of neural responses (Famulare and Fairhall 2010).

3.5.2. Multivariate relationships via latent variable models.

An important question is whether mechanistic models can reproduce features of recorded neural activity that go beyond population means and variances. This is especially challenging when, as is usually the case, recorded neurons represent only a very small sample from a vast network. Simple summary statistics, such as the variability of the activity of individual neurons or the correlation between pairs of neurons, can be a helpful first step (Litwin-Kumar and Doiron 2012). A natural next step is to examine summaries based on dimensionality reduction, as in Section 3.4.1, where the same multivariate statistical methods are applied to both the activity produced by the model and to the data. For example, spontaneous activity recorded in the primary visual cortex has been found to be more like activity produced by a spiking network model having clustered connections than that produced by a network with uniform random connectivity (Williamson et al. 2016).

Mechanistic models can also help in characterizing the statistical tools used to study neural population activity by providing ground truth with which to judge performance of statistical methods (Williamson et al. 2016). This includes determination of the amount of data needed in order to identify particular effects. From results outlined in Section 2.4, when LIF models are used these ground truth data sets should be very similar to others generated using GLM neurons (Zaytsev et al. 2015), and it is a topic for future research to take advantage of this relationship.

4. Outlook

In addition to providing readers with an entry into the mathematical and statistical literature in computational neuroscience, we have also tried to highlight places where the two approaches go hand in hand, especially in Sections Section 2.4, Section 2.5, Section 2.6, and 3.5. Another concrete example of this interplay comes from anesthesia, where highly structured oscillations, readily visible in the EEG, change in a systematic way, depending on the dose of a given anesthetic and the molecular targets and neural circuits where the anesthetic acts (Brown et al. 2011). One of the most widely used anesthetics, propofol, acts at multiple sites in the brain to enhance the activity of inhibitory neurons resulting initially in beta oscillations (13 – 25 Hz) followed within seconds by slow-delta oscillations (0.1 – 4 Hz), and then a combination of slow-delta oscillations with alpha oscillations (8 – 12 Hz) when the patient is unconscious. Multitaper spectral time series analysis showed that the alpha oscillations are highly coherent across the front of the scalp, and this was explained by a circuit model using Hodgkin-Huxley neurons (Ching et al. 2010; Cimenser et al. 2011). Because all anesthetics create similar oscillations, the combination of careful statistical analysis and mechanistic modeling may be used to investigate the way other anesthetics create altered brain states.

As this example illustrates, computational neuroscience, like experimental neuroscience, aims to improve knowledge about the functioning of the nervous system. On the one hand, the statistical approach helps by introducing methods to summarize nervous system data. On the other hand, mathematical theory helps by introducing frameworks for describing nervous system behavior. Because both sides of computational neuroscience aim to build understanding from data, they complement each other: mechanistic models refine scientific questions, and can thereby guide development of statistical methods; statistical methods can find important features of data, and can suggest directions for modeling efforts. As the field tackles additional complexity in modeling and data analysis, it will become increasingly important for researchers in computational neuroscience to be cognizant of the essential ideas, tools, and approaches of both domains.

Glossary

Rate coding:

stimulus or behavior changes firing rate

Temporal coding:

stimulus or behavior changes precise timing of spikes

Tuning curve:

the trial-averaged firing considered as a function of one or more variables

Absolute refractory period:

after a neuron fires the sodium channels are unable to open for approximately 1 millisecond

Relative refractory period:

after the hard refractory period a neuron’s probability of firing gradually increases from zero