Cancer Genetic Network Inference Using Gaussian Graphical Models

Abstract

The Cancer Genome Atlas (TCGA) provides a rich resource that can be used to understand how genes interact in cancer cells and has collected RNA-Seq gene expression data for many types of human cancer. However, mining the data to uncover the hidden gene-interaction patterns remains a challenge. Gaussian graphical model (GGM) is often used to learn genetic networks because it defines an undirected graphical structure, revealing the conditional dependences of genes. In this study, we focus on inferring gene interactions in 15 specific types of human cancer using RNA-Seq expression data and GGM with graphical lasso. We take advantage of the corresponding Kyoto Encyclopedia of Genes and Genomes pathway maps to define the subsets of related genes. RNA-Seq expression levels of the subsets of genes in solid cancerous tumor and normal tissues were extracted from TCGA. The gene expression data sets were cleaned and formatted, and the genetic network corresponding to each cancer type was then inferred using GGM with graphical lasso. The inferred networks reveal stable conditional dependences among the genes at the expression level and confirm the essential roles played by the genes that encode proteins involved in the two key signaling pathway phosphoinositide 3-kinase (PI3K)/AKT/mTOR and Ras/Raf/MEK/ERK in human carcinogenesis. These stable dependences elucidate the expression level interactions among the genes that are implicated in many different human cancers. The inferred genetic networks were examined to further identify and characterize a collection of gene interactions that are unique to cancer. The cross-cancer genetic interactions revealed from our study provide another set of knowledge for cancer biologists to propose strong hypotheses, so further biological investigations can be conducted effectively.

Introduction

Cancer is caused by genetic changes that alter normal cell behavior that leads to uncontrolled cell growth. Studying cancer genomics, identifying cancer-causing genes, and learning genetic networks could provide insights into understanding the biology of cancer and developing targeted drug and treatment of cancer.¹ Several studies have reported genome-wide mutational patterns in different types of cancer and identified the potential cancer-causing gene mutations.^2–5 The Cancer Genome Atlas (TCGA) project has generated data sets of the key genomic changes in 33 different types of cancer and gives researchers unprecedented access to the cancer genomic data.^6,7 These data sets, including genomic, transcriptomic, epigenomic, and clinical data, have been made publicly available by TCGA through its data portal. Cross-cancer gene alterations in 21 different cancer types were analyzed and reported.⁸ Despite the advances in cancer genomics, mining the biological significance hidden in the TCGA data sets remains to be a challenge. Many attempts from developing software tools to innovative algorithmic approaches have been made to facilitate the mining process.^9–13

Gaussian graphical model (GGM) as an analytics tool is often used to analyze gene interactions based on gene expression levels.^14–21 For a multivariate random vector having a normal distribution, GGM defines an undirected graph structure through the precision matrix (inverse covariance matrix) which reveals the conditional dependences among variables. A node in the graph represents a variable, and an edge implies the conditional dependence between the two variables incident to the edge. The expression levels of genes are generally considered to be log-normal because their distributions are typically skewed to the right.²² Gaussian graphical model provides an effective approach for learning genetic regulatory networks from log-transformed gene expression profiles. In the networks inferred from gene expression data sets, a node represents an expressed gene, and an edge denotes conditional dependence between the two expressed genes connected by the edge.

To estimate the inverse covariance matrix based on sample observation data, several algorithms have been reported. The underlying idea of the reported approaches is based on the maximum likelihood estimation. The traditional covariance selection with maximum likelihood estimation aims at identifying zero elements in the inverse covariance matrix; the standard algorithm for covariance selections is greedy forward and backward search.^14,15 During greedy forward search, the initial set of edges is empty, and then the edges are iteratively added when the hypothesis testing reaches an indicated level α. The cost of this algorithm is extremely high, making it infeasible to estimate high-dimensional graphs.

An inferred genetic network is expected to be sparse and stable, and it should not change much with different sample data sets. In other words, the estimated inverse covariance matrix should only contain non-zero entries for pairs of genes that are highly related. To ensure the sparsity, the least absolute shrinkage and selection operator (lasso) technique was introduced.¹⁶ Furthermore, several approaches were proposed to obtain sparse high-dimensional graphs using lasso with a penalty on the $L_1-\mathrm{norm}$ of the precision matrix. Neighborhood-selection algorithm learns sparse high-dimensional Gaussian graphs by performing neighborhood selection for each node; it estimates each node separately by fitting linear lasso model.¹⁷ The essence of estimation procedure is equivalent to variable selection for Gaussian linear models. The value of a pair of variables $i$ and $j$ in inverse covariance matrix is estimated to be non-zero if both $p(i|j)$ and $p(j|i)$ are non-zero. To improve the performance of the algorithm and the stability of the estimated network, penalized likelihood methods were proposed, which minimize the negative log-likelihood function with $L_1$ penalty by taking advantage of the efficiency of the maxdet algorithm developed in convex optimization.^18,23 To handle the computational challenge in high dimension, a model-selection method based on block coordinate decent was proposed.¹⁹ This approach converted the inverse covariance matrix finding problem to be a box-constrained quadratic problem that is then solved using interior point algorithm. The proposed method is equivalent to a recursive linear regression with $L_1$ penalty. Based on similar idea, a simple, but more efficient graphical lasso algorithm was proposed.²⁰ This graphical lasso algorithm cycles through the variables, fitting a modified lasso regression to each variable and the individual lasso problems are solved by coordinate descent. Despite all the efforts made to improve the computational performances, graphical lasso is still not efficient enough to be directly used to construct genome-scale networks, which contain tens of thousands genes.

Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway repository is a collection of pathway maps; these pathway maps represent biologists’ knowledge on the molecular interactions, reaction, and relation networks for metabolism, genetic information processing, human diseases, cellular processes, drug development, and so on.²⁴

In this study, we focus on inferring gene interactions in 15 specific types of human cancer using RNA-Seq expression level data and GGM with graphical lasso. We used the subsets of genes outlined in the corresponding KEGG cancer pathways.^24,25 RNA-Seq expression levels of the subsets of genes in solid cancerous tumor and normal tissue were extracted from TCGA. The gene expression data sets were cleaned and formatted; and then the genetic network corresponding to each cancer type was inferred using GGM with graphical lasso. The inferred genetic networks were compared and examined to further identify a collection of cross-cancer gene interactions.

Materials and Methods

To infer genetic networks and identify cross-cancer gene interactions, genes presented in KEGG pathway maps and their RNA-Seq expression levels were extracted from KEGG and TCGA, respectively. We cleaned these data sets and inferred the genetic networks using GGM with graphical lasso. The pipeline for inferring these networks is illustrated in Figure 1 and the details of each step are described below.

Figure 1.

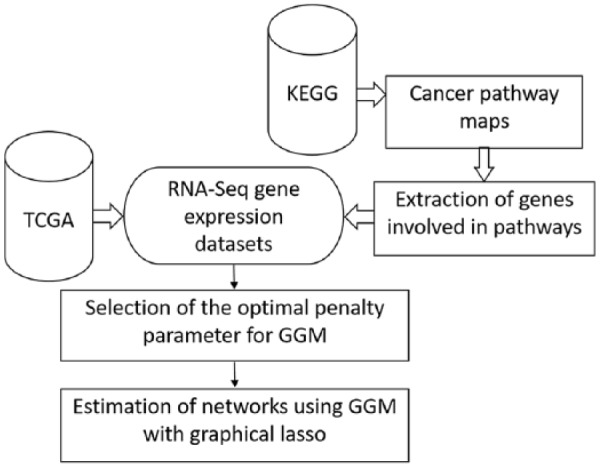
Pipeline of inferring gene-interaction networks.

RNA-Seq gene expression levels in 15 solid cancerous tissues as well as normal tissues were extracted from TCGA⁷ using the R script, TCGA-Assembler version 2.0.5.²⁶ The RNA-Seq data from primary solid tumor and the corresponding normal samples were retrieved. The expression profiles of 20 531 genes were then preprocessed in three steps: (1) removal of 29 putative and retired genes (in the data sets, the IDs of these genes are present, but the symbols are absent); (2) remove the genes whose expression levels are zero across all samples. We note that it is possible that these genes did express but their levels were so low and were not picked up by RNA-Seq technology. There are about 300 such genes for each tissue type; (3) log-transformation of the expression data. We replaced 0 in the data sets by 1 before the transformation.

A total of 13 KEGG cancer pathway maps were downloaded from KEGG pathway repository.²⁵ Genes specific to each pathway were extracted to form the subset of genes for the pathway. The RNA-Seq expression levels in 15 solid cancerous tissues as well as normal tissues of the genes in each subset were extracted from TCGA (data sets not related to any KEGG cancer pathway were not considered).²⁵ Table 1 presents the list of the 15 cancer types/subtypes, their corresponding KEGG pathway IDs, and the number of available TCGA gene expression data sets. The normal gene expression data sets from a specific organ were pooled to form one normal tissue data set for that organ; the pool data sets include one for kidney renal clear cell carcinoma (KIRC) and kidney renal papillary cell carcinoma (KIRP) and one for lung adenocarcinoma (LUAD) and lung squamous cell carcinoma (LUSC). In addition, the normal data sets for brain lower grade glioma (LGG) and skin cutaneous melanoma (SKCM) are not available, and the normal data set for pancreatic adenocarcinoma (PAAD) was not used because the data set with a sample size of three is too small to construct a reliable network. The data sets were then preprocessed and log transformed, resulting in 15 RNA-Seq expression data sets from solid cancerous tissues and 10 data sets from normal tissues.

Table 1.

The 15 cancer types and their KEGG and TCGA IDs as well as the number of TCGA data sets.

Cancer type	KEGG ID	KEGG cancer type	TCGA cancer type	TCGA sample size
				Cancer	Normal
BLCA	hsa05219	Bladder cancer	Bladder urothelial carcinoma	408	19
BRCA	hsa05224	Breast cancer	Breast invasive carcinoma	1094	112
COAD	hsa05210	Colorectal cancer	Colon adenocarcinoma	284	40
KIRC	hsa05211	Renal cell carcinoma	Kidney renal clear cell carcinoma	533	72
KIRP	hsa05211	Renal cell carcinoma	Kidney renal papillary cell carcinoma	290	32
LGG	hsa05214	Glioma	Brain lower grade glioma	515	0
LIHC	hsa05225	Hepatocellular carcinoma	Liver hepatocellular carcinoma	371	50
LUAD	hsa05223	Non-small-cell lung cancer	Lung adenocarcinoma	515	59
LUSC	hsa05223	Non-small-cell lung cancer	Lung squamous cell carcinoma	502	50
PAAD	hsa05212	Pancreatic cancer	Pancreatic adenocarcinoma	178	3
PRAD	hsa05215	Prostate cancer	Prostate adenocarcinoma	496	51
SKCM	hsa05218	Melanoma	Skin cutaneous melanoma	102	0
STAD	hsa05226	Gastric cancer	Stomach adenocarcinoma	415	35
THCA	hsa05216	Thyroid cancer	Thyroid carcinoma	504	59
UCEC	hsa05213	Endometrial cancer	Uterine corpus endometrial carcinoma	176	23

Abbreviations: BLCA, bladder carcinoma; BRCA, breast cancer; COAD, colon adenocarcinoma; KEGG, Kyoto Encyclopedia of Genes and Genomes;KIRC, kidney renal clear cell carcinoma; KIRP, kidney renal papillary cell carcinoma; LGG, lower grade glioma; LIHC, liver hepatocellular carcinoma; LUAD, lung adenocarcinoma; LUSC, lung squamous cell carcinoma; PAAD, pancreatic adenocarcinoma; PRAD: prostate adenocarcinoma; SKCM, skin cutaneous melanoma; STAD, stomach adenocarcinoma; TCGA: The Cancer Genome Atlas; THCA, thyroid cancer; UCEC, uterine corpus endometrial carcinoma.

To ensure that the log-transformed gene expression profiles are normal or at least close to normal, we calculated Ryan-Joiner (RJ) statistic measures, representing correlations between the expression levels of genes and the corresponding normal distribution scores. The calculation was performed on one gene at a time; effectively, it was testing how well the log-transformed conditional distribution of a gene correlates to a normal distribution. We observed a significant variability in the RJ statistic measures. The correlation coefficient varies from one gene to another. The weakest is between CDK4 and normal with the correlation coefficient 0.956. The strongest is between MAPK3 and normal with JR score 0.999. Statistically speaking, the expression level of CDK4 is considered not normal despite the RJ score 0.956; the distribution is still slightly skewed to the right (some patients have relative high CDK4 levels). Nevertheless, the statistics indicates that normal distribution provides a fairly good approximation to the distribution of gene expression levels.

Given gene expression data $\mathrm{Y}={[y_1,\dots ,y_n]}^{\mathrm{T}}\in {\mathrm{R}}^{n\times p}$ for $n$ samples and $p$ genes, the gene expression profile of each sample, $y_i={[{\mathrm{y}}_i^1,\dots {,\mathrm{y}}_i^p]}^{\mathrm{T}}$, is assumed to be independent and follow a Gaussian distribution $N(\mathit{u},\Sigma )$, where $\mathit{u}$ is the mean and $\Sigma$ is the $p\times p$ covariance matrix. The precision matrix $\mathrm{\Theta }={\sum }^{-1}$ is a positive definite and symmetric matrix and presents a model for an undirected graph $\mathrm{G}=(\mathrm{V},\mathrm{E})$ where V is a set of $p$ vertices corresponding to the $p$ genes, and the edge set $\mathrm{E}=\left\{e_{i,j}\right\}$ describes the conditional dependences among the $p$ genes. $e_{i,j}=1$ indicates that genes $i$ and $j$ are conditionally dependent, whereas $e_{i,j}=0$ states the two genes $i$ and $j$ are conditionally independent of each other. Each entry ${\theta }_{i,j}$ of the precision matrix signifies the strength of the dependence relation. Therefore, learning genetic network is equivalent to estimating the precision matrix $\mathrm{\Theta }$, that is, to maximize the log-likelihood with $L_1$ norm penalty on its precision matrix $\mathrm{\Theta }$:

$$\log \det (\mathrm{\Theta })-\mathrm{trace}\left(\mathrm{S}\mathrm{\Theta }\right)-\rho {\Vert \mathrm{\Theta }\Vert }_1$$ (1)

where S is sample covariance matrix, $\rho$ is non-negative penalty parameter which controls the sparsity of the inverse covariance matrix $\mathrm{\Theta }$ and $\left|\right|\mathrm{\Theta }|{|}_1={\Sigma }_i{\Sigma }_j|{\theta }_{i,j}|$ represents the $L_1-\mathrm{norm}$ of $\mathrm{\Theta }$.^19,20 Clearly, the larger the parameter $\rho$ is, the sparser the estimated $\mathrm{\Theta }$ would be. If $\rho =0$, this problem is reduced to the typically maximum likelihood estimation problem, while when $\rho \to \infty$, $\mathrm{\Theta }=0$ regardless what sample data sets are used in estimation. In this study, the graphical lasso procedure is deployed to estimate the sparse precision matrices corresponding to sparse gene regulatory networks.²⁰ The glasso software version 1.10 was used.²⁷

To apply graphical lasso to infer genetic networks, one important issue is to choose the optimal penalty parameter $\rho$, which controls the sparsity level of the estimated $\mathrm{\Theta }$ and ensures its stability. Any network to be learned from experimental data unavoidably could include some irrelevant and unexpected interactions resulting from the intrinsic “noise” in the experimental data. We expect an estimated network robust with respect to different sample data. Therefore, models with certain stability require $\rho$ to be at a level so that the “noisy” edges in the estimated precision matrix are filtered out. Furthermore, genetic networks are typically considered sparse, and therefore, we expect that the estimated networks to be sparse as well, and the edges represent the true dependences of the genes.^24,28,29 To select an optimal value of the penalty parameter $\rho$, we implemented and tested the subsampling-based approach.³⁰

Results

We inferred 15 cancer networks and 10 normal networks using TCGA RNA-Seq gene expression data sets and GGM with graphical lasso. During the process of penalty parameter selection, a P-value of .05 was used. The typical optimal value of ρ is found to be around 0.03. The edge/node ratio of KEGG networks ranges from 0.8 to 1.2 with an average of 1.01, reflecting the sparsity of these networks. The initial learned GGM networks are much denser despite the application of the graphical lasso. We believe that the edges with extremely low weights are false positive. There are possibly two types of error coming into play during the modeling process: (1) noise in the RNA-Seq data due to variations in patients and experiments and (2) gene expression profiles are not perfect normal (some distributions, such as the one of CDK4, are only approximately normal). As a result, inaccuracies from GGM also contribute to the noise. To reduce the effects of the noise in the data, to strengthen the network stability, and to highlight the most important dependences between genes, we used a threshold of 0.2 to reduce false positives. The estimated network edges with weights below a threshold of 0.2, that is, the corresponding entries in the precision matrix <0.2, were removed. The resulting edge/node ratio is approximately 5.81.

We constructed a map of the gene interactions in 15 types of human cancer and a map of the gene interactions in 10 normal human tissue types. These two maps encapsulating all 25 networks are shown in the Supplemental material Tables S1 and S2. Through comparison and analysis of these derived cancer and normal networks, we identified the cross-cancer gene interactions that were altered in cancerous tissues. The consensus interactions that are unique to cancer networks are presented in Table 2 and Figures 2 and 3. These interactions are shared by at least five cancer networks but absent in all normal networks. The gene interactions that are mostly unique to cancer networks, that is, they appear in at least five cancer networks but also in one normal network, are shown in Table 3 and Figures 4 and 5. Figure 6 integrates the two networks shown in Figures 2 and 4 to illustrate both sets of strong gene interactions presented in cancer.

Table 2.

Cross-cancer gene interactions that are present in cancer but absent in all normal networks.

Consensus gene interactions	Number of shared cancer networks
BAD-MAP2K2	9
CDKN1A-DDB2	9
PIK3CA-PIK3CB	9
MAP2K1-MAPK1	8
PIK3R1-POLK	8
ARAF-E2F3	7
GRB2-PIK3CD	7
POLK-RB1	7
SOS1-SOS2	7
BAD-SOS1	6
GSK3B-PIK3CA	6
HRAS-SOS2	6
KRAS-MAP2K2	6
MAPK1-NRAS	6
AKT2-BAX	5
BAD-KRAS	5
BAD-MAPK3	5
BAK1-CDKN1A	5
E2F1-RB1	5
E2F3-MAPK3	5
GADD45B-MAP2K2	5
GSK3B-PIK3CB	5
HRAS-SOS1	5
MAPK1-MTOR	5
MAPK1-PIK3CA	5
MTOR-PIK3R3	5
PIK3R1-SOS2	5

Figure 2.

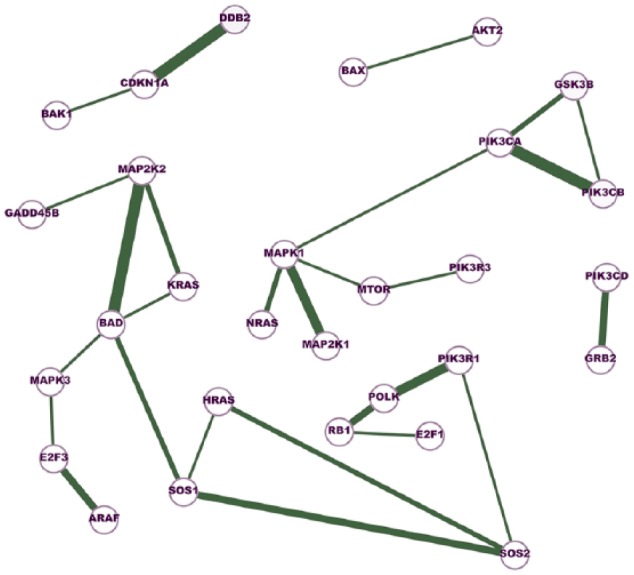
A network of cross-cancer gene interactions that are unique to the inferred cancer networks.

A node in the network represents a gene, and an edge indicates the conditional dependence of the two incident genes. The conditional dependence depicts the interaction of the genes at the expression level. The thickness of an edge represents the degree of consensus of the interaction among the cancer networks. The edges in this network are shared by at least five cancer networks but absent in all normal networks.

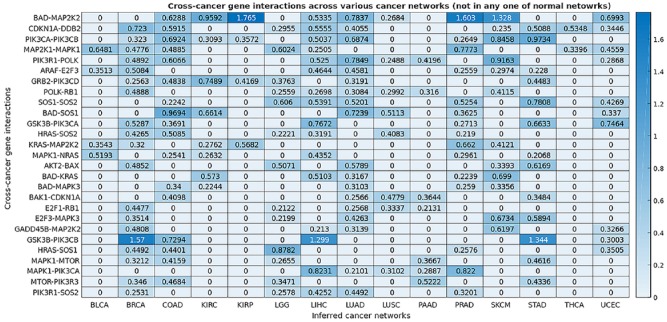
Figure 3.

The map of consensus gene interactions that are appeared in at least 5 of the 15 cancer networks but not present in any normal network.

This map depicts a portion of the precision matrices, indicating the conditional dependence between a pair of genes in a specific cancer. The higher the value in the map is, the stronger the conditional dependence (interaction) of the pair of genes.

Table 3.

Cross-cancer interactions mostly unique to the inferred cancer networks (appear in at least five cancer networks but also in one normal network).

Consensus gene interactions	Number of shared cancer networks
BRAF-PIK3CA	13
BAX-DDB2	9
MAP2K2-PIK3R2	9
BAD-HRAS	8
CDK4-E2F1	7
BAX-MAP2K2	6
BAX-PIK3CA	6
BRAF-HRAS	6
PIK3R1-PIK3R3	6
BAX-CDKN1A	5
HRAS-KRAS	5
HRAS-POLK	5
MAP2K2-PIK3CA	5
PIK3CA-SOS2	5
TGFB1-TGFB3	5

Figure 4.

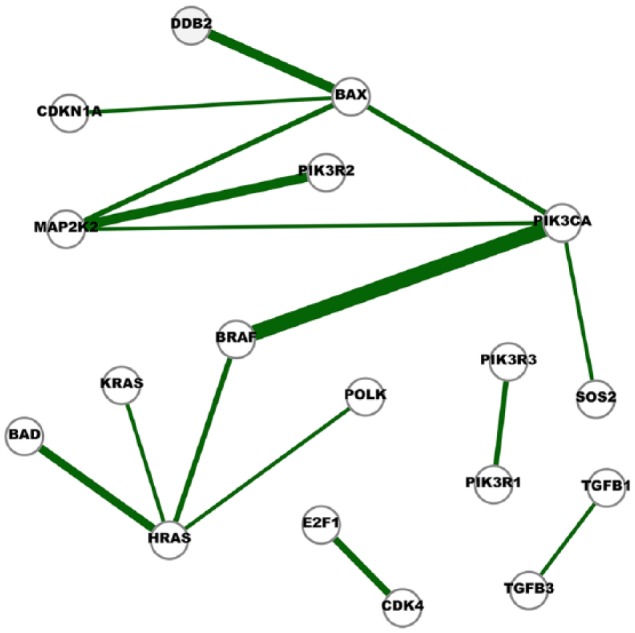
A network of cross-cancer interactions that are mostly unique to the inferred cancer networks.

A node in the network represents a gene and an edge indicates the conditional dependence of the two incident genes. The conditional dependence depicts the interaction of the genes at the expression level. The thickness of an edge represent the degree of consensus of the interaction among the cancer networks. Edges in this network represent the interactions identified in at least five cancer networks but also appeared in one normal network.

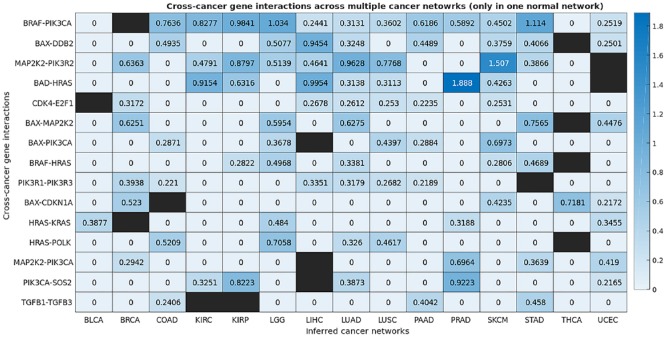
Figure 5.

The map of consensus gene interactions that are appeared in at least 5 of the 15 cancer networks; these interactions are also present in one normal network. The higher the value in the map is, the stronger the conditional dependence (interaction) of the pair of genes.

A black square denotes the interaction is also appeared in the normal network of the corresponding organ.

Figure 6.

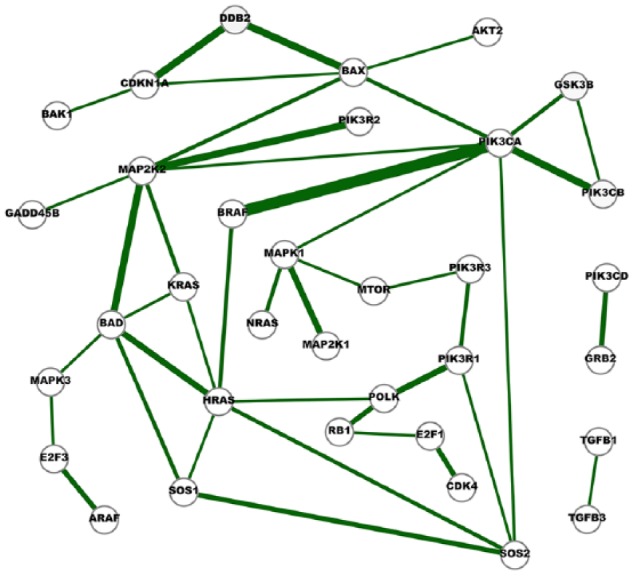
A network of strong cross-cancer interactions.

A node in the network represents a gene and an edge indicates the conditional dependence of the two incident genes. The conditional dependence depicts the interaction of the genes at the expression level. The thickness of an edge represents the degree of consensus of the interaction among the cancer networks. Edges in this network represent the interactions identified in at least five cancer networks, and they are either absent in any normal network or appear in just one normal network.

Discussion

Gene expression is an extremely complicated process during which multiple genes and/or proteins interact in a coordinated way and directly or indirectly control each other’s expression levels. Highlighting the dependences of the coordination helps to elucidate the complicated process. In this study, we identified and analyzed the cross-cancer gene interactions hidden in the gene expression data sets and inferred 15 cancer networks and 10 normal networks using TCGA RNA-Seq gene expression levels and GGM. We focused on the subsets of genes presented in the 13 corresponding KEGG cancer pathways. We uncovered the gene interactions shared among the cancer networks and analyzed these cross-cancer gene interactions and created a map of the altered gene interactions in various types of cancer.

As illustrated in Table 2, Figures 2 and 3, significant numbers of the cross-cancer interactions are closely related to the signaling molecules on the two critical signaling pathways: phosphoinositide 3-kinase (PI3K)/AKT/mTOR pathway and Ras/Raf/MEK/ERK pathway. The PI3K pathway is an intracellular signaling pathway that plays key roles in regulating cell cycle and is linked to many essential cellular processes such as cell proliferation, survival, growth, and motility. The signaling cascade is mediated through serine and/or threonine phosphorylation of a range of downstream molecules. The key proteins involved include PI3K, AKT, GSK3, BAD, BAX, and CDKN1A. It has been widely reported that the PI3K pathway is overactive in many cancers, thus reducing apoptosis and allowing proliferation and uncontrolled cell growth.^31–35 In addition, the alterations of PI3Ks in cancer were detailed along with the therapeutic efficacy of PI3K inhibitors in the cancer treatment.³⁵

Our results show that genes that encode several signaling proteins on the PI3K pathway, AKT2 and BAX, GRB2 and PIK3CD, GSK3B and PIK3CA, GSK3B and PIK3CB, MAPK1 and PIK3CA, MTOR and PIK3R3, PIK3CA and PIK3CB, PIK3R1 and POLK, and PIK3R1 and SOS2, are conditionally dependent on each other at their expression levels in at least five different types of human cancer, and these interactions are unique to cancers and do not appear to be significant in any normal organ tissue (Table 2, Figures 2 and 3). DNA polymerase kappa (POLK) encodes a specialized DNA polymerase that catalyzes translesion DNA synthesis, which allows DNA replication in the presence of DNA damages.³⁶ Although few reports find that POLK is linked to PIK3R1 (a gene that provides instructions for making a regulatory subunit of PI3K), our results reveal that the expression level of POLK is conditionally dependent on that of PIK3R1 in eight different cancers, and the dependence is particularly strong in SKCM (Figure 3). One possible connection between PI3Ks and POLK is through the PI3K downstream transcription factor CREB, which is reported to be a regulator of POLK promoter activity.³⁶ Furthermore, our results indicate that the expression levels of POLK and the well-known tumor suppressor gene RB1 are conditionally linked to seven cancers (Figure 3).

Ras/Raf/MEK/ERK pathway is another key intracellular signaling pathway.^37–42 Dysregulation of this pathway is a common event in cancer as RAS family, small guanosine triphosphatases (GTPases), is often the most frequently mutated oncogene in human cancer.⁴² Our study shows many identified cross-cancer gene interactions that are unique to cancer are linked to this pathway, including ARAF-E2F3, BAD-KRAS, BAD-MAP2K2, BAD-MAPK3, BAD-SOS1, E2F3-MAPK3, GADD45B-MAP2K2, HRAS-SOS1, HRAS-SOS2, KRAS-MAP2K2, MAP2K1-MAPK1, MAPK1-MTOR, MAPK1-NRAS, MAPK1-PIK3CA, and SOS1-SOS2. Ras/Raf/MEK/ERK signaling cascade transmits signals from upstream receptors such as epidermal growth factor receptor (EGFR) to transcription factors such as CREB and E2F3, which in turn regulate gene expression and prevent apoptosis. Key molecules involved in this cascade are GRAB2, SOS, RAS, RAF, MEK, and MAPK. This study reveals how the expression levels of the genes that encode these proteins conditionally depend on each other and on other genes such as BAD, a pro-apoptotic member of the Bcl-2 gene family involved in initiating apoptosis, and E2F3, a transcription factor which is key to cellular proliferation and differentiation.^42–45 Figure 3 shows that the gene expression levels of MAP2K2 is conditionally dependent on the levels of BAD in nine cancer networks, and the conditional dependence is particularly strong in three different cancers, KIRC, KIRP, and prostate adenocarcinoma (PRAD). Transcription factor E2Fs are key regulators of cell cycle progression and share a critical role in tissue homeostasis. Our results reiterate the critical roles MAPK signaling pathway plays in cell proliferation, differentiation, cell movement, and apoptosis.

Furthermore, this study elucidates several cross-talks between the PI3K/AKT/mTOR pathway and Ras/Raf/MEK/ERK pathway, particularly through the gene that encodes BRAF, a proto-oncogene playing major roles in human carcinogenesis,⁴⁶ and the ones that code the downstream kinase mTOR and apoptosis regulator BAX.^47,48

The almost unique consensus network shown in Figures 4 and 5 supports the observations made from Figures 2 and 3. The PI3K-pathway-related interactions presented in Figure 4 include BAX-PIK3CA, BRAF-PIK3CA, MAP2K2-PIK3CA, MAP2K2-PIK3R2, PIK3CA-SOS2, and PIK3R1-PIK3R3, whereas BAX-MAP2K2, BAD-HRAS, BRAF-HRAS, HRAS-KRAS, HRAS-POLK, MAP2K2-PIK3CA, and MAP2K2-PIK3R2 are associated with the MEK/ERK pathway.

Figure 6 integrates the two networks presented in Figures 2 and 4. Six network motifs (small cliques) can be observed in the network, including BAD-HRAS-KRAS, BAD-HRAS-SOS1, BAD-KRAS-MAP2K2, BAX-DDB2-CDKN1A, BAX-MAP2K2-PIK3CA, and GSK3B-PIK3CA-PIK3CB. These six cliques reveal the close dependences among the genes. GSK3B-PIK3CA-PIK3CB is linked with PI3K pathway, BAD-HRAS-SOS1, BAD-KRAS-MAP2K2 and HRAS-SOS1-SOS2, are associated with MEK/ERK pathway, and BAX-MAP2K2-PIK3CA is linked with both pathways. In addition, our study identifies a network motif that is closely linked with cell apoptosis and cell cycle arrest, BAX-CDKN1A-DDB2. It has been reported all three molecules in this clique are regulated by the most well-known tumor suppressor gene p53. The cyclin-dependent kinase inhibitor 1 (p21), encoded by the CDKN1A gene, is a critical player in cell cycle arrests at varies checkpoints after DNA damage.^49–51 The coordination of CDKN1A and DDB2 in the cellular response to ultraviolet (UV) radiation has also been reported.⁵² Our study shows the expression levels of the apoptosis regulator BAX and the two cell cycle arrest regulator CDKN1A and DDB2 are conditionally dependent of each other in cancer.

Conclusions

This study provides rich insights for identifying and analyzing the cross-cancer gene interactions hidden in their expression levels as well as how the interactions are connected in networks. A total of 15 cancer gene interaction networks and 10 normal networks were constructed using TCGA RNA-Seq gene expression data and GGM with graphical lasso. The inferred networks reveal conditional dependences among the genes, and the weights of edges indicate the strength of the dependences. These networks confirm the essential roles played by genes that encode proteins involved in the two key signaling pathway PI3K/AKT/mTOR and Ras/Raf/MEK/ERK in human carcinogenesis. The stable conditional dependences presented in the networks elucidate the expression level interactions among the genes that are implicated in many different human cancers.

The genetic networks constructed in this study are based on RNA-Seq expression data and reveal conditional dependences among the genes at the expression level. We note that these dependences may not indicate the proteins encoded by these genes have direct interactions; in some cases, they belong to different cellular components. In signaling pathways such as PI3K/AKT/mTOR and Ras/Raf/MEK/ERK, the most important event is phosphorylation cascade. One enzyme phosphorylates another may not signify the expression level dependences between the two genes that code the two enzymes. Nevertheless, the expression level dependences of signaling protein-coding genes reveal, to a certain degree, the dynamic nature of phosphorylation cascades because, as concluded by a recent study, on the bulk level and for approximate steady-state conditions, protein levels are largely determined by their transcript concentrations.⁵³ The cross-cancer gene interactions highlighted in the results derived from the expression levels provide another set of knowledge for cancer biologists to propose strong hypotheses so further biological investigations can be conducted effectively.