Mediation analysis for count and zero-inflated count data without sequential ignorability and its application in dental studies

Summary

Mediation analysis seeks to understand the mechanism by which a treatment affects an outcome. Count or zero-inflated count outcomes are common in many studies in which mediation analysis is of interest. For example, in dental studies, outcomes such as the number of decayed, missing and filled teeth are typically zero inflated. Existing mediation analysis approaches for count data often assume sequential ignorability of the mediator. This is often not plausible because the mediator is not randomized so unmeasured confounders are associated with the mediator and the outcome. We develop causal methods based on instrumental variable approaches for mediation analysis for count data possibly with many 0s that do not require the assumption of sequential ignorability. We first define the direct and indirect effect ratios for those data, and then we propose estimating equations and use empirical likelihood to estimate the direct and indirect effects consistently. A sensitivity analysis is proposed for violations of the instrumental variables exclusion restriction assumption. Simulation studies demonstrate that our method works well for different types of outcome under various settings. Our method is applied to a randomized dental caries prevention trial and a study of the effect of a massive flood in Bangladesh on children’s diarrhoea.

1. Introduction

In many studies, the intervention is designed to change intermediate variables under the hypothesis that the change in those intermediate variables will lead to improvement in the final outcomes (MacKinnon and Luecen, 2011). In these studies, in addition to the overall effect of the intervention on the outcome in the end, researchers would like to know whether and how much the intervention affects the outcome through the measured intermediate variables (mediators) as designed (indirect effect) versus ‘direct’ intervention effects on the outcome not through the mediators proposed but involving other unknown pathways. Knowing those effects helps us to understand the working mechanism of an intervention and to tailor specific intervention components for future research and applications in specific populations.

1.1. Detroit Dental Health Project’s motivational interviewing digital video disc study

The Detroit Dental Health Project’s (DDHP’s) motivational interviewing digital video disc (MIDVD) study was a randomized dental trial of a motivational interviewing (MI) intervention to prevent early childhood caries in low income African-American children (0–5 years) in Detroit, Michigan (Ismail et al., 2011). In the study, caregivers in both intervention and control groups watched a 15-min education video on children’s oral health. Then families in the control group DVD were provided with general recommended goals for their children’s oral health. For the intervention group MI+DVD, an MI interviewer reviewed the child’s dental examination with caregivers and discussed caregivers’ personal thoughts and concerns about specific goals for their child’s oral health. Then the interviewer worked with the family to develop their own preventive goals that were printed and placed in a convenient place at home. Families in group MI+DVD also received booster calls within 6 months of the intervention. The study hypothesized that the MI+DVD intervention would change the caregivers’ and children’s oral hygiene behaviours and then the behavioural changes would lead to improved oral health in children. The primary analysis examined the effect of the MI+DVD intervention on children’s cavities, measured as the number of new cavitated and new untreated lesions 2 years later, compared with group DVD (Ismail, 2011). In this paper, we shall conduct a mediation analysis and examine whether or not the intervention did change caregivers’ behaviours regarding their children’s oral health (e.g. parents made sure that their children brushed their teeth at bedtime) as designed and whether or not the behavioural changes had an effect on children’s oral health.

1.2. Literature review and motivation

Standard mediation approaches since 1986 (Baron and Kenny, 1986; Cole and Maxwell, 2003; MacKinnon, 2008), such as regression, path and structural equation models, assume sequential ignorability of the intervention and mediator (effective randomization of the intervention and mediators) to obtain estimates of the direct and mediation effects of the intervention on the outcome. Although the ignorability assumption for the intervention is reasonable when the intervention is randomized, the ignorability assumption for mediators can be questionable because mediators are not randomized by researchers so there may be unmeasured confounders between the mediators and the outcome. Recently developed causal methods (Robins and Greenland, 1992; Pearl, 2001; Rubin, 2004; Ten Have et al., 2007; Albert, 2008; van der Laan and Petersen, 2008; Sobel, 2008; Goetgeluk et al., 2009; VanderWeele and Vansteelandt, 2009, 2010; Elliott et al. ,2010; Imai et al., 2010; Jo et al., 2011; Daniels et al. ,2012; Stayer et al., 2014; Zheng and Zhou, 2015) adopt the potential outcome framework and make different assumptions about the intervention and mediator to estimate the direct and indirect (mediation) effects of the intervention on the outcome. Some of these causal methods have replaced the ignorability assumption of mediators with other assumptions, such as the no-interaction assumption between intervention and mediator.

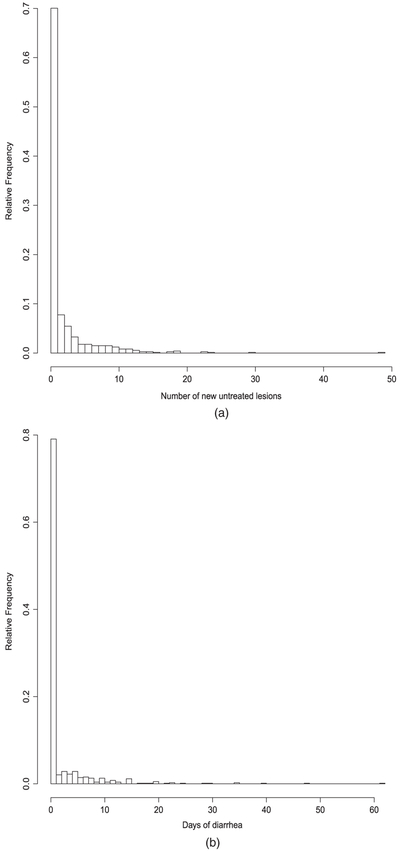
Most standard and causal approaches focus on continuous and/or binary mediators and outcomes. However, the outcome variable in many studies is often a count following a Poisson or negative binomial distribution, or a zero-inflated count that has a higher probability of being 0 than expected under a Poisson or negative binomial distribution. Zero-inflated count outcomes are particularly common in dental caries studies, where the primary outcome of interest is often the number of decayed, missing and filled teeth or surface indices that a subject has. The development of caries is a long-term process during which pathological factors and protective factors work against one another (Featherstone, 2003), so, in a population with a large proportion of low caries risk subjects or young children who have a relatively short time exposure to pathological factors, most subjects do not have any caries and therefore the number of decayed, missing and filled teeth or surface indices are counts with many 0s (Featherstone et al., 2012). Fig. 1(a) shows that the distribution of the number of new untreated lesions has many 0s in the DDHP MIDVD study because the majority of the children did not have any new untreated lesions at the end of the study. Zero-inflated count outcomes are also common in other settings such as the number of days that a child is sick from a cause like diarrhoea or respiratory illness, the number of healthcare visits and the number of days stayed in a hospital (Cameron and Trivedi, 1998).

Fig. 1.

Histograms of outcomes for (a) the dental study and (b) the flood data

Assuming sequential ignorability, Albert and Nelson (2011) discussed a nice generalized mediation approach with application to count dental outcomes, Wang and Albert (2012) provided a mediation formula for the mediation effect estimation in a two-stage model and considered a decomposition of the mediation effect in a three-stage model with application to zero-inflated count outcomes, and Albert (2012) considered an inverse-probability-weighted estimator for the mediation effect on count outcomes. Sequential ignorability is plausible for some studies. However, sequential ignorability may not be plausible for the DDHP MIDVD study, where caregivers’ and children’s oral health behaviours were not randomized or controlled by the investigators but could be affected by factors other than the MI+DVD intervention, such as oral health education that the parents or children received from primary dentists, schools, communities or the Internet. Those factors were not measured in the study and could be confounders of the relationship between the mediator and outcome because of its association with both the mediator (the caregivers’ or children’s oral health behaviour) and their final dental outcomes so sequential ignorability may not hold in this study.

1.3. Our contribution

As discussed in the previous section, the existing mediation methods for zero-inflated count outcomes which rely on sequential ignorability may not work well for the DDHP MIDVD study. Therefore, in this paper, we develop a new mediation analysis method based on the instrumental variable (IV) approach for count and zero-inflated count data when the assumption of sequential ignorability for the mediator might fail. Our new method does not require a parametric distribution assumption on the error of the outcome variable. When confounding is of concern in a study, IV methods are very helpful for obtaining consistent estimates for treatment effects by adjusting for both unmeasured and measured confounders when a valid and strong IV can be found (Angrist et al., 1996). Angrist and Krueger (1991) provided a good review of applications of the IV method. Staiger and Stock (1997) showed that a weak IV will lead to a wide confidence interval. This paper will focus on IVs with reasonable strength, and methods will be developed specifically for weak IVs in future studies. Methods for mediation analysis based on the IV approach have been proposed by investigators (Ten Have et al., 2007; Albert, 2008; Dunn and Bentall, 2007; Small, 2012) using the randomization interacted with baseline covariates as IVs, but those methods focus on linear models for continuous outcomes. When the outcome model is linear, two-stage least squares and two-stage residual inclusion can estimate the direct and indirect effects well when there is a valid IV. We shall show that the two-stage method can give a biased estimate when the mediator is binary and the outcome model is a count or zero-inflated count model. We shall first define the direct and indirect treatment effects in our context and then develop a consistent estimator based on estimating equations and empirical likelihood. We shall use the random assignment interacted with baseline covariates as IVs to account for both measured and unmeasured confounding. Since the randomized treatment itself is not used as the IV, we can estimate the direct and indirect effect of the treatment on the outcome of interest. We also develop a novel method that partially tests the assumption that random assignment interacted with baseline covariates are valid IVs. Although we focus on count and zero-inflated count outcomes in this paper, the method can be generalized to other types of outcome.

1.4. Organization

The paper is organized as follows. In Section 2, we introduce the notation, framework and the direct and indirect treatment effects of interest for count and zero-inflated count data. In Section 3, we introduce the IV and two-stage approaches, and our new method, and provide a sensitivity analysis method. We present simulation studies in Section 4, and, in Section 5, apply our method to the DDHP and another example: a study of the effect of a massive flood in Bangladesh on children’s diarrhoea. In Section 6, we conclude the paper. The proofs and further simulation studies are provided in the on-line supplementary materials.

The data that are analysed in the paper and the programs that were used to analyse them can be obtained from http://wileyonlinelibrary.com/journal/rss-datasets

2. Notation, framework and causal effects of interest

2.1. Notation

We adopt the potential (counterfactual) outcome framework (Neyman, 1990; Rubin, 1974) and use Z_i = z (z = 0 or z = 1) for the randomly assigned treatment for subject i; let $M_i^z$ denote the potential value of a mediator under treatment z; use Y_i(z, m) to denote the potential outcome that subject i would have under the treatment z and mediator m, and Y_i(z, $M_i^z$) for the potential outcome that subject i would have under Z_i = z (where $M_i^z$ would be at its ‘natural’ level under z). We let U_i denote unobserved confounders, X_i denote observed baseline covariates and ${\mathbf{X}}_i^{\text{IV}}$ denote a subset of baseline covariates to construct IVs.

2.2. Direct and indirect effects of interest

For count and zero-inflated count outcomes, we are particularly interested in the controlled and natural direct and indirect ratios for comparing average potential outcomes at different levels of randomization and mediator: controlled effect ratio, direct (z versus z*; m, x, u),

$$\frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z^{\ast },m)\mid \mathbf{x},u\}};$$ (1)

indirect (m versus m*; z, x, u),

$$\frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,m^{\ast })\mid \mathbf{x},u\}};$$ (2)

natural effect ratio, direct (z versus z*; M^z*, x, u),

$$\frac{\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z^{\ast },M^{z^{\ast }})\mid \mathbf{x},u\}};$$ (3)

indirect (M^z versus M^z*; z, x, u),

$$\frac{\mathbb{E}\{Y(z,M^z)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}}.$$ (4)

A ratio of 1 indicates no effect. The controlled direct effect sets the mediator at a fixed value m and the natural direct effect sets the mediator at its ‘natural’ level that would be achieved under treatment assignment z*, M^z* . The natural indirect effect ratio tells us the ratio of average outcomes under treatment z that would be observed if the mediator would change from the value under a treatment z, M^z, to the value under another treatment z*, M^z*. The expectations in expressions (1) and (2) are taken over the conditional distribution of the potential outcome. However, in the natural effect ratio, since the mediator is random, the expectations in expressions (3) and (4) are taken over the conditional joint distribution of the mediator and the potential outcome corresponding to the mediator. We shall discuss below the settings in which the controlled and natural effects are identified and consider models without and with the interaction of the intervention and mediator respectively.

2.3. The model without the intervention-mediator interaction

2.3.1. Model setting

We consider the following generalized linear model for the expected potential outcomes:

$$f[\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}]={\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x}+u,$$ (5)

where f is a link function. For a Poisson or negative binomial count outcome, a log-link function will be used in the model; for a zero-inflated count outcome, we consider a Neyman type A distributed outcome (Dobbie and Welsh, 2001), $y={\Sigma }_{k=1}^N{y}_k$, where

$$\begin{gathered} N\mid \mathbf{x},z,m,u\sim \text{Poisson}\{\text{exp}({\gamma }_0+{\gamma }_{z}z+{\gamma }_{m}m+{\gamma }_{\mathbf{x}}\mathbf{x}+{\gamma }_{u}u)\}, \\ {y}_k\mid \mathbf{x},z,m,u\sim \text{Poisson}\{\text{exp}({\lambda }_0+{\lambda }_{z}z+{\lambda }_{m}m+{\lambda }_{\mathbf{x}}\mathbf{x}+{\lambda }_{u}u)\}. \end{gathered}$$

The Neyman type A distribution is also a special case of expression (5) with

$$\log [\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}]={\gamma }_0+{\lambda }_0+({\gamma }_z+{\lambda }_z)z+({\gamma }_m+{\lambda }_m)m+({\gamma }_{\mathbf{x}}+{\lambda }_{\mathbf{x}})\mathbf{x}+({\gamma }_u+{\lambda }_u)u.$$

Without loss of generality, we shall assume that $\mathbb{E}\{\text{exp}(u)\}=1$ for the count and zero-inflated count with a log-link function.

2.3.2. Controlled effect ratios

Given model (5) with a log-link function, we have

$$\begin{gathered} \frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z^{\ast },m)\mid \mathbf{x},u\}}=\text{exp}\{{\beta }_z(z-z^{\ast })\}, \\ \frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,m^{\ast })\mid \mathbf{x},u\}}=\text{exp}\{{\beta }_m(m-m^{\ast })\}. \end{gathered}$$ (6)

Therefore, estimating the controlled effect ratios is equivalent to estimating β_z and β_m.

2.3.3. Natural effect ratios

For natural effect ratios, model (5) becomes

$$f[\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}]={\beta }_0+{\beta }_{z}z+{\beta }_m{M}^{z^{\ast }}+{\beta }_{\mathbf{x}}\mathbf{x}+u,$$ (7)

and we further consider a model for the mediator:

$$h\{\mathbb{E}(M^{z^{\ast }}\mid \mathbf{x},u)\}={\alpha }_0+{\alpha }_z{z}^{\ast }+{\alpha }_{\mathbf{x}}\mathbf{x}+{\alpha }_{\text{IV}}{z}^{\ast }{\mathbf{x}}^{\text{IV}}+u,$$ (8)

where h is a link function, e.g. the identity and logit functions for continuous and binary mediators respectively. Then the natural indirect effect ratio with a continuous mediator will be

$$\frac{\mathbb{E}\{Y(z,M^z)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}}=\text{exp}\{{\beta }_m{\alpha }_z(z-z^{\ast })+{\beta }_m{\alpha }_{\text{IV}}{\mathbf{x}}^{\text{IV}}(z-z^{\ast })\},$$ (9)

and, with a binary mediator,

$$\frac{\mathbb{E}\{Y(z,M^z)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}}=\frac{P(M^z=1\mid \mathbf{x},u)\text{exp}({\beta }_m)+P(M^z=0\mid \mathbf{x},u)}{P(M^{z^{\ast }}=1\mid \mathbf{x},u)\text{exp}({\beta }_m)+P(M^{z^{\ast }}=0\mid \mathbf{x},u)}.$$ (10)

The natural direct effect ratio for both continuous and binary mediators will be the same as the controlled direct effect ratio:

$$\frac{\mathbb{E}\{Y(z,M^{z^{\ast }})\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z^{\ast },M^{z^{\ast }})\mid \mathbf{x},u\}}=\text{exp}\{{\beta }_z(z-z^{\ast })\}.$$ (11)

The proofs of results (9)–(11) are provided in section 1.1 of the on-line supplementary material. For a continuous mediator, the natural direct and indirect effect ratios (9) and (11) are identifiable given that the parameters β_z, β_m, α_z, and α_IV can be estimated consistently. However, the natural indirect effect ratio for a binary mediator depends on the values of the unmeasured u in equation (10) and is not identifiable without additional assumptions.

2.4. General model with the intervention–mediator interaction

In this section, we shall generalize model (5) to include the intervention–mediator interaction z × m and define the corresponding controlled direct and indirect effect for this generalized model:

$$f[\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}]={\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{zm}z\times m+{\beta }_{\mathbf{x}}\mathbf{x}+u,$$ (12)

where f is a link function. Given model (12) with a log-link function, similarly to expression (6), we can define the controlled effects as

$$\begin{gathered} \frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z^{\ast },m)\mid \mathbf{x},u\}}=\text{exp}\{({\beta }_z+{\beta }_{zm}m)(z-z^{\ast })\}, \\ \frac{\mathbb{E}\{Y(z,m)\mid \mathbf{x},u\}}{\mathbb{E}\{Y(z,m^{\ast })\mid \mathbf{x},u\}}=\text{exp}({\beta }_m+{\beta }_{zm}z)(m-m^{\ast })\}. \end{gathered}$$ (13)

Therefore, estimating the controlled effect ratios is equivalent to estimating β_z, β_m and β_zm. Note that the controlled direct effect depends on the mediator value and the controlled indirect effect depends on the intervention value.

3. The instrumental variable approach

When there is a concern about an unmeasured confounder u, the IV approach is a popular technique for dealing with unmeasured confounding; such unmeasured confounding is not addressed by regular regression and propensity score methods. In the context of mediation analysis, a valid IV is a variable that, given the measured baseline variables,

1. affects the value of the mediator,

2. is independent of the unmeasured confounders and

3. does not have a direct effect on the outcome other than through its effect on the mediator.

Mediation methods based on the IV approach have been proposed by investigators (Ten Have et al., 2007; Albert, 2008; Dunn and Bentall, 2007; Small, 2012) for continuous outcomes, where baseline covariates interacted with random assignment are used as IVs in linear models. In this study, we shall also use baseline covariates interacted with random assignment (Z × X^IV) as IVs, where X^IV is a subset of baseline covariates used to construct the IVs, for mediation analysis; our work is novel in that we consider non-linear models rather than linear models. In the setting of a randomized trial with non-compliance, the randomization Z is often used as an instrument (e.g. Sommer and Zeger (1991) and Greevy et al. (2004)) under the assumption that the randomization has no direct effect on the outcome. In our setting, when Z is randomized we assume that the randomization is complied with but we allow for the randomization itself to have a direct effect. Since the randomization can have a direct effect on the outcome around the mediator (violation of the exclusion restriction (ER)), we cannot use Z as an IV. Instead, we consider Z × X^IV as a possible IV to enable us to estimate consistently both the direct and the indirect effects of the treatment on the outcome of interest discussed in Section 2 without the commonly used sequential ignorability assumption.

We let U* denote the unmeasured confounders and U in expression (5) denote the unmeasured confounders adjusted by the observed baseline covariates U = U* − E(U*\X). We make the following assumptions such that the proposed instruments Z × X^IV are valid IVs.

Assumption 1. The treatment Z is independent of U* given X. This assumption is automatically satisfied if Z is randomized such as in the DDHP MIDVD study and can be satisfied in an observational study if all the baseline confounders are included in X.

Assumption 2. The residual U = U* − E(U*∣X) is homoscedastic, meaning that the distribution of U is the same for different levels of X. If (U*, X) follows a multivariate normal distribution, the assumption automatically holds. Note that this assumption is actually stronger than is necessary to apply our approach. It can be replaced by a weaker homogeneity assumption, i.e. E{exp(U) ∣ X} is the same for all X.

Assumption 3. There is an interaction between randomized treatment Z and baseline covariate(s) X^IV predicting mediator M conditionally on Z and X, i.e. Z × X^IV affects the value of the mediator M. In a real data analysis, this assumptions can be examined by investigating whether the instrument Z × X^IV has a significant effect on the mediator.

Assumption 4. The interaction Z × X^IV affects the outcome only through its effect on the mediator M, conditionally on X and Z. This assumption is often called the ER assumption. One possibility of violating this assumption is that the IV Z × X^IV affects the outcome through other intermediate variables besides the mediator of interest. Although the ER assumption cannot be formally tested, we can partially assess the ER assumption by examining whether the IV has an effect on other known intermediate variables besides the mediator of interest. Additionally a sensitivity analysis can be conducted to see how the results will change if the ER is violated. See Section 3.3 and the on-line supplementary material section 1.5 for more detailed discussion and Section 6 for the real data analysis.

3.1. Two-stage approach

When the outcome y is continuous and an identity link function holds in the outcome model (5), the two-stage least square method provides consistent estimates for the parameters of interest when a valid IV is available. When model (5) involves a non-identity link function, two-stage predictor substitution and two-stage residual inclusion (Nagelkerke et al., 2000; Terza et al., 2008) have been proposed to evaluate the treatment effect with an IV. For the identity link function in model (5), a systematic comparison of two-stage predictor substitution and two-stage residual inclusion (also referred to as the ‘control function’) in general settings has been investigated in Guo and Small (2016). For the logit link function in model (5), Cai et al. (2011) showed that two-stage predictor substitution and two-stage residual inclusion estimators are asymptotically biased for the complier average causal effect when there is unmeasured confounding.

We consider the following true model for the mediator:

$$h[\mathbb{E}\{M\mid z,\mathbf{x},z\times {\mathbf{x}}^{\text{IV}},u\}]={\alpha }_0+{\alpha }_{z}z+{\alpha }_{\text{IV}}z\times {\mathbf{x}}^{\text{IV}}+{\alpha }_{\mathbf{x}}\mathbf{x}+{\alpha }_{u}u,$$ (14)

where h is a link function. When u is not measured, two-stage residual inclusion fits the models with the IV Z × X^IV in two stages: stage I, $h\{\mathbb{E}(M\mid z,\mathbf{x},z\times {\mathbf{x}}^{\text{IV}})\}={\alpha }_0+{\alpha }_{z}z+{\alpha }_{\text{IV}}z\times {\mathbf{x}}^{\text{IV}}+{\alpha }_{\mathbf{x}}\mathbf{x}$, where h is a link function; stage II, $f\{\mathbb{E}(Y\mid m,z,\mathbf{x},\widehat{r})\}={\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x}+{\beta }_r\widehat{r}$, where r̂ is the residual m − m̂ from stage I and f is a link function such as the log-link for count data. The first stage of the two-stage predictor substitution approach is the same as that of two-stage residual inclusion, but, in the second stage, two-stage predictor substitution uses the predicted value m̂ instead of the residual r̂ from the first-stage model so the second-stage model is $f\{\mathbb{E}(Y\mid \widehat{m},z,\mathbf{x})\}={\beta }_0+{\beta }_{z}z+{\beta }_m\widehat{m}+{\beta }_{\mathbf{x}}\mathbf{x}$.

In the examples that are discussed in Section 5, we shall estimate the indirect effect of treatment through a continuous or binary mediator on the count (or zero-inflated count) outcome. Hence, we restrict our attention to the cases with identity or log-link in the outcome model (5) and identity or logit link in the mediator model (14). To simplify the comparison, we also assume that the error follows a normal distribution in the case of the identity link function. Table 1 summarizes the property of two-stage residual inclusion and two-stage predictor substitution estimates under various outcome and mediator models. Specifically, when the identity link function in outcome model (5) holds, both two-stage predictor substitution and two-stage residual inclusion estimators are consistent (Wooldridge, 2010). When the link function in the outcome model (5) and the mediator model (5) is the log-link and identity link respectively, two-stage residual inclusion is consistent whereas two-stage predictor substitution is not guaranteed to be consistent (see Table 8 in the on-line supplementary material); when the link function in model (5) and model (5) is the log-link and logit link respectively, neither the two-stage predictor substitution nor the two-stage residual inclusion estimator is consistent (see Table 7 in the supplementary material). The proof of the property in Table 1 is provided in the supplementary materials. Because two-stage residual inclusion performs better than two-stage predictor substitution, we shall examine and compare the performance of two-stage residual inclusion with the performance of a new approach discussed in Section 3.2 for the mediation analysis in this paper. Simulations in Section 4 show that two-stage residual inclusion can have a large bias when the mediator is binary for a count outcome or the error distribution of the outcome is misspecified.

Table 1.

Two-stage residual inclusion and two-stage predictor substitution estimates under outcome and mediator models with different link functions

	Identity link in outcome model (5)	Log-link in outcome model (5)
Identity link in mediator model (14)	Two-stage predictor substitution and two-stage residual inclusion estimates are consistent	Only two-stage residual inclusion estimate is consistent
Logit link in mediator model (14)	Two-stage predictor substitution and two-stage residual inclusion estimates are consistent	Neither estimate is consistent

Table 8.

Estimated direct and indirect effect rate ratios and bootstrap (CIs) for the flood study

Total effect rate ratio	1.681 (1.141, 2.716)
	EE-EL (90% CI)	Reg (90% CI)
Direct effect rate ratio (controlled = natural)	1.229(0.299, 2.409)	1.611 (1.096, 2.619)
Indirect effect rate ratio
Controlled	0.040 (2.524 × 10−5, 0.822)	0.675 (0.600, 0.915)
Natural	1.685 (1.010, 6.239)	1.061 (1.009, 1.100)

Table 7.

Estimated direct and indirect effect rate ratios and bootstrap CIs for the DDHP MIDVD study

Total effect rate ratio	1.063 (0.829, 1.364)
	EE-EL (90% CI)	Reg (90% CI)
Mediation analysis without z × m interaction
Direct effect rate ratio (controlled = natural)	1.081 (0.770, 1.323)	1.065 (0.820, 1.381)
Indirect effect rate ratio (controlled)	0.595 (0.070, 4.604)	0.973 (0.643, 1.477)
Mediation analysis with z × m interaction
Direct effect rate ratio (controlled = natural)
Did not make sure child brushed at 6 months	1.303 (0.832, 3.565)	1.761 (0.979, 3.004)
Made sure child brushed at 6 months	1.000 (0.667, 1.312)	0.903 (0.685, 1.187)
Indirect effect rate ratio
DVD	0.837 (0.042, 3.142)	1.360 (0.920, 2.115)
MI+DVD	0.643 (0.115, 5.146)	0.697 (0.397, 1.291)

3.2. Estimating equations and empirical likelihood approach

As discussed above, the two-stage residual inclusion estimate may not be consistent for a count outcome with binary mediators. In this section, we consider a different approach to estimate consistently the parameters of interest in non-linear models with unmeasured confounding even when the mediator is binary. Unlike two-stage residual inclusion, this approach does not need to specify the error distribution of the outcome and hence will be robust to the misspecification of the outcome distribution. We let g(w, θ) = (g₁(w, θ),…, g_r (w, θ))^T be estimating functions such that E{g(w, θ)} = 0, where w = (z, x, m, y) and θ = (β₀, β_z, β_m, β_x) are the parameters that are associated with the outcome model. We consider a set of estimating functions (15) to combine information about the parameters and distribution. Under assumptions (1)–(4), we have E{g(w, θ)} = 0. The proof is provided in section 1.2 of the on-line supplementary material. The equations in expression (15) include more estimating equations than parameters and hence are an overdetermined system of estimating equations, where there will not typically be a solution satisfying all the estimating equations in a sample version. Qin and Lawless (1994) proposed to use Owen’s (1988, 1990) empirical likelihood approach when there are more estimating equations than parameters and showed that empirical likelihood provides asymptotically efficient estimates of the parameters (in the sense of van der Vaart (1988) and Bickel et al. (1993)) under the semiparametric model given by the estimating equations

$$\begin{gathered} g_1(w,\theta )=\frac{y}{\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x})}-1, \\ {g}_2(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x})}-1\right\}z, \\ {g}_3(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x})}-1\right\}\mathbf{x}, \\ {g}_4(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x})}-1\right\}{\mathbf{x}}^{\text{IV}}z, \\ {g}_5(w,\theta )=\frac{y}{\text{exp}({\beta }_{m}m)}-\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{\mathbf{x}}\mathbf{x}), \\ {g}_6(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_{m}m)}-\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{\mathbf{x}}\mathbf{x})\right\}z, \\ {g}_7(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_{m}m)}-\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{\mathbf{x}}\mathbf{x})\right\}\mathbf{x}, \\ {g}_8(w,\theta )=\left\{\frac{y}{\text{exp}({\beta }_{m}m)}-\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{\mathbf{x}}\mathbf{x})\right\}{\mathbf{x}}^{\text{IV}}z. \end{gathered}$$ (15)

Following their approach, we let p_i be the probability that data (Z_i, X_i, M_i, Y_i) are observed and maximize ${\Pi }_{i=1}^n{p}_i$, subject to the restrictions

$$\begin{gathered} p_i⩾0, \\ \sum _{i=1}^n{p}_i=1, \\ \sum _{i=1}^n{p}_{i}g(w_i,\theta )=0. \end{gathered}$$

It is equivalent to minimize

$$l_{\mathrm{E}}(\theta )=\sum _{i=1}^n\log \{1+t^{\tau }(\theta )g(w_i,\theta )\},$$ (16)

where l_E(θ) is the profile empirical log-likelihood and t = (t₁,..., t_r)^T are Lagrange multipliers and are determined by

$$\frac{1}{n}\sum _{i=1}^n\frac{g(w_i,\theta )}{1+t^{\mathrm{T}}g(w_i,\theta )}=0.$$

With the estimating equations g₁(w, θ),..., g₈(w, θ) for θ = (β₀, β_z, β_m, β_x)^T, the maximized empirical likelihood estimate will be the solution to the estimating equations ${\Sigma }_{i=1}^n{g}_j(w_i,\theta )=0,j=1,\dots ,8$, that minimize equation (16). Note that θ can be estimated with the first four estimating equations g₁(w, θ),..., g₄(w, θ) but occasionally they lead to extreme solutions where the estimated ${\widehat{\beta }}_0$ is very negative and the estimated ${\widehat{\beta }}_m$ is very positive. Introducing additional information or estimating equations g₅(w, θ),..., g₈(w, θ) that are implied by the model will avoid those extreme solutions. We shall emphasize that g₅(w, θ),..., g₈(w, θ) do not require additional assumptions but just use more information that is implied by the model.

We maximize the empirical likelihood subject to the estimating equations in two steps:

1. fixing θ, we shall minimize equation (16) with respect to t;

2. given t from the first step, minimize equation (16) with respect to θ.

Qin and Lawless (1994) showed that the maximum empirical likelihood estimate for the estimating equations is consistent under some regularization conditions. Proposition 1 provides the theory that this estimator EE-EL is consistent under some mild regularity conditions.

Proposition 1. Under regularity conditions, let $\widehat{\theta }$ denote the minimizer of equation (16); then

$$(\widehat{\theta }-{\theta }_0)\surd n\to N(0,V),V={\left\{\mathbb{E}{\left(\frac{\partial g}{\partial \theta }\right)}^{\mathrm{T}}\mathbb{E}(g{g}^{\mathrm{T}}{)}^{-1}\mathbb{E}\left(\frac{\partial g}{\partial \theta }\right)\right\}}^{-1}.$$

3.3. Testing the exclusion restriction and sensitivity analysis

When assumptions (1)–(4) hold, Z × X^IV is a valid IV. When the IV Z × X^IV actually affects the outcome directly, then the ER assumption (assumption (4)) fails so the estimators will be biased. The violation of the ER assumption means that the IV could have an effect on the outcome through ways other than the mediator of interest. In such cases, the IV could affect the outcome through other intermediate variables besides the mediator of interest. Thus, although the ER assumption cannot be formally tested, we can partially assess the ER assumption by examining whether the IV has an effect on other known intermediate variables besides the mediator of interest. See the on-line supplementary material section 1.5 for details and assumptions underlying this partial test of the ER.

Unfortunately, we cannot test all possible ways in which the ER could be violated. Therefore, we propose a sensitivity analysis to allow Z × X^IV to affect the outcome directly by a specified magnitude and then examine how the results will change. Specifically, we consider

$$g[E\{Y(z,m)\mid z,m,\mathbf{x},u\}]={\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x}+u+\eta z\times {\mathbf{x}}^{\text{IV}},$$ (17)

where η is the sensitivity parameter for the direct effect of the IV on the outcome. When η = 0, the ER assumption holds. When η ≠ 0, the ER assumption fails and Z × X^IV is not a valid IV. Higher values of |η| mean more severe violation of the ER assumption. For a zero-inflated count following a Neyman type A distribution, we have $Y={\Sigma }_{k=1}^N{y}_k$, where

$$\begin{gathered} N\mid \mathbf{x},z,m,u\sim \text{Poisson}\{\text{exp}({\gamma }_0+{\gamma }_{z}z+{\gamma }_{m}m+{\gamma }_{\mathbf{x}}\mathbf{x}+{\gamma }_{u}u+{\eta }_{1}z\times {\mathbf{x}}^{\text{IV}})\}, \\ {y}_k\mid \mathbf{x},z,m,u\sim \text{Poisson}\{\text{exp}({\lambda }_0+{\lambda }_{z}z+{\lambda }_{m}m+{\lambda }_{\mathbf{x}}\mathbf{x}+{\lambda }_{u}u+{\eta }_{2}z\times {\mathbf{x}}^{\text{IV}})\}, \end{gathered}$$

we can represent this model in the form of equation (17) with η = η₁ + η₂. With a log-link function in model (17), we shall adjust the outcome as

$$y^{\text{adj}}=\frac{y}{\text{exp}({\eta }^{\mathrm{T}}{\mathbf{x}}^{\text{IV}}z)}$$

and have a model for the adjusted outcome:

$$\mathbb{E}(y^{\text{adj}}\mid \mathbf{x},z,m,u)=\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m}m+{\beta }_{\mathbf{x}}\mathbf{x}+u).$$

Then we can construct the estimating equations (15) by replacing y with y^adj in equations (15) and (16) and obtain the maximum empirical likelihood estimator. We shall examine how the sensitivity analysis works in the simulation study.

3.4. Multiple mediators and the interaction of intervention and mediator

In addition to settings with one mediator that were discussed above, our method can be applied to settings with multiple conditionally independent mediators, i.e., conditioning on z, x, z × x^IV and u, the mediators are independent. The outcome model (5) is generalized as

$$g[\mathbb{E}(Y(z,\mathbf{m})\mid \mathbf{x},u\}]={\beta }_0+{\beta }_{z}z+{\beta }_{\mathbf{m}}^{\mathrm{T}}\mathbf{m}+{\beta }_{\mathbf{x}}\mathbf{x}+u.$$ (18)

We need at least the same number of IVs as the number of mediators to construct estimating equations and then to use the same approaches discussed above for estimation. Section 3 of the on-line supplementary material discusses a case with two conditionally independent mediators, which can be easily generalized to multiple mediators. Similarly, model (12) with the interaction z × m that was introduced in Section 2.2 can be solved by a modified version of expression (15), where both m and z × m are taken as the endogenous variables. See section 3 of the supplementary material for details.

4. Simulation study

In this section, we shall examine the performance of the methods discussed above in finite samples. We consider outcomes that follow Poisson, negative binomial and Neyman type A distributions with a binary mediator, a normally distributed mediator and multiple mediators respectively. The randomized treatment Z was generated with P(Z_i = 1) = 0.5. We consider one or two (standard normal and binary) covariates, and an unmeasured confounder U with E{exp(U)} = 1. Mediators and outcomes were generated on the basis of models (14) and (5) respectively. In the mediator model (14), α_IV represents the strength of the IV Z × X^IV and α_u represents the strength of endogenous variable U. Table 2 shows the true values of parameters in the outcome models. When there are two mediators, we have two IVs in the models. We consider sample sizes of 500, 1000 and 5000. For each setting, 1000 Monte Carlo replications were performed.

Table 2.

Parameter settings in the simulation studies

Setting	Θ	Value	Θ	Value	Θ	Value	Θ	Value	Θ	Value
A	β0	1	βz	0.5	βm	0.5	βx	0.5		1
B	γ0	0.6	γz	0.25	γm	0.25	γx	0.25	γu	0.5
	λ0	−1	λz	0.25	λm	0.25	λx	0.25	λu	0.5
C	β0	1	βz	0.5	βm1	1	βx1	0.5		1
					βm2	0.5	βx2	0.5
D	γ0	1	γz	0.25	γm1	0.75	γx1	0.5	γu	0.5
					γm2	0.25	γx2	0.5	γu	0.5
	λ0	−0.5	λz	0.25	λm1	0.25	λx1	0.5	λu	0.5
					γm2	0.25	λx2	0.5

4.1. Single binary mediator

We first examine the performance of each approach with a binary mediator, which is generated as

$$m\mid \mathbf{x},z,u\sim \text{Ber}\left\{\frac{\text{exp}(-0.5+0.5z+0.5x+{\alpha }_{\text{IV}}z\times x^{\text{IV}}+0.5u)}{1+\text{exp}(-0.5+0.5z+0.5x+{\alpha }_{\text{IV}}z\times x^{\text{IV}}+0.5u)}\right\},$$ (19)

where we consider two different levels of strength of instruments, α_IV = 1 (denoted as ‘strong’) and α_IV = 0.5 (denoted as ‘weak’). Unless otherwise noted, α_IV is set to 1. The outcome variable is generated with setting A for the Poisson and negative binomial distributions and with setting B in Table 2 for a Neyman type A outcome. There were 21.6% 0s in the generated Poisson outcome, 25.6% 0s in the generated negative binomial outcome and 52.7% 0s in the generated Neyman type A distribution outcome. We considered a standard normal baseline covariate X and the corresponding IV Z × X^IV. We have eight estimating equations in expression (15) for four parameters. Two computational methods are proposed to obtain estimates for the parameters.

1. Estimator EE-EL1: the first four estimating functions g₁,..., g₄ in expression (15) are incorporated in the empirical likelihood for estimates and the next four estimating equations g₅,..., g₈ are used to evaluate the goodness of fit of the estimates.

2. Estimator EE-EL2: all eight estimating functions g₁,..., g₈ in expression (15) are incorporated in the empirical likelihood for estimates.

The comparisons in the on-line supplementary material Table 6 show that both EE-EL1 and EE-EL2 work well. Estimator EE-EL1 is fast in terms of computation whereas EE-EL2 has better performance in terms of median absolute deviation MAD. Simulation studies that are reported in this paper were performed with computationally efficient EE-EL1 whereas real data analyses were conducted with the more stable EE-EL2. Table 3 shows the median and MAD of the estimates from the estimating equations and empirical likelihood (estimator EE-EL), two-stage residual inclusion (estimator 2SRI) and ordinary regression (estimator Reg) for direct and indirect effect parameters (β_z and β_m). The ordinary regression fits a Poisson, negative binomial or zero-inflated Poisson model respectively for the outcome on treatment, mediator and covariates. Estimator 2SRI fits a logistic first-stage model for the binary mediator with the IV Z × X^IV, and then fits a Poisson, negative binomial or zero-inflated Poisson model for the outcome. Estimator EE-EL can be generally used for Poisson and negative binomial outcomes and Neyman type A distributions without specifying the distribution. As shown in Table 3, the ordinary regression estimates Reg are generally biased whereas both 2SRI and EE-EL have reduced bias with the use of the IV. When the mediator is binary, estimator 2SRI has small bias on the direct effect parameter β_z for the Poisson and negative binomial models but can have a bias of greater than 15% for the Neyman type A outcome when there is a large proportion of 0s. For the controlled indirect effect parameter β_m, 2SRI can have a bias of greater than 25% for the Poisson and negative binomial models and a bias of greater than 100% for the Neyman type A model. The estimator EE-EL performed best for all the settings and the small bias diminished with increased sample size and stronger IV.

Table 6.

Participants’ characteristics by intervention assignment

	n (%) or mean ± standard deviation
	Group MI + DVD	Group DVD
Total	370 (50.41%)	364 (49.59%)
Child gender
Male	173 (46.76%)	170 (46.70%)
Female	197 (53.24%)	194 (53.30%)
Child age (years)	4.58 ± 1.63	4.49 ± 1.71
Soda consumption in the past week (days)	2.91 ± 1.81	2.76 ± 1.70
Number of times child brushed	1.66 ± 0.78	1.66 ± 0.95
Child baseline cavities
Decayed, missing and filled teeth index	9.22 ± 10.52	8.83 ± 10.16
Surface index	5.32 ± 8.82	5.01 ± 8.34
Caregiver gender
Male	15 (4.05%)	20 (5.49%)
Female	355 (95.95%)	344 (94.50%)
Caregiver age (years)	31.58 ± 8.78	31.03 ± 9.21
Caregiver highest education level
Less than high school	152 (41.08%)	119 (32.69%)
High school or general educational development examination	27 (7.30%)	32 (8.79%)
Some college or more	191 (51.62%)	213 (58.52%)
Caregiver household income
<$10000	156 (42.16%)	139 (38.19%)
$10000–$19999	105 (28.38%)	97 (26.65%)
$20000–$29999	63 (17.03%)	71 (19.51%)
$30000 or more	46 (12.43%)	57 (15.66%)
Caregivers gave child healthy meals
Baseline	351 (94.86%)	333 (91.48%)
6 months	351 (94.86%)	352 (96.70%)
Caregivers made sure child brushes teeth at bedtime
Baseline	229 (61.89%)	219 (60.16%)
6 months	304 (82.16%)	273 (74.91%)

Table 3.

Estimates for the direct effect parameter (β_z = 0.5) and the indirect effect parameter (β_m = 0.5) with one IV and one binary mediator^†

Outcome distribution	IV	n	Results for direct effect			Results for indirect effect
			EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)
Poisson	Strong	500	0.496(0.126)	0.505(0.150)	0.416(0.117)	0.522(0.691)	0.559(0.722)	0.955(0.102)
Poisson	Strong	1000	0.497(0.094)	0.497(0.111)	0.419(0.080)	0.522(0.489)	0.561(0.495)	0.948(0.082)
Poisson	Strong	5000	0.497(0.039)	0.500(0.047)	0.415(0.034)	0.510(0.225)	0.528(0.224)	0.948(0.036)
Poisson	Weak	500	0.489(0.159)	0.500(0.198)	0.426(0.122)	0.530(1.117)	0.524(1.266)	0.966(0.104)
Poisson	Weak	1000	0.486(0.120)	0.483(0.133)	0.430(0.078)	0.575(0.793)	0.643(0.852)	0.962(0.082)
Poisson	Weak	5000	0.500(0.054)	0.496(0.058)	0.432(0.035)	0.499(0.389)	0.576(0.388)	0.959(0.036)
Negative binomial	Strong	500	0.494(0.164)	0.503(0.155)	0.443(0.127)	0.448(0.820)	0.494(0.736)	0.944(0.131)
Negative binomial	Strong	1000	0.499(0.114)	0.503(0.116)	0.447(0.086)	0.555(0.615)	0.528(0.515)	0.942(0.089)
Negative binomial	Strong	5000	0.498(0.050)	0.499(0.051)	0.442(0.037)	0.486(0.262)	0.502(0.225)	0.945(0.041)
Negative binomial	Weak	500	0.493(0.177)	0.500(0.194)	0.447(0.123)	0.543(1.261)	0.526(1.295)	0.952(0.136)
Negative binomial	Weak	1000	0.489(0.134)	0.493(0.130)	0.439(0.084)	0.525(0.983)	0.515(0.849)	0.955(0.094)
Negative binomial	Weak	5000	0.499(0.068)	0.499(0.060)	0.449(0.039)	0.524(0.468)	0.547(0.395)	0.951(0.038)
Neyman type A	Strong	500	0.465(0.316)	0.413(0.478)	0.386(0.228)	0.589(1.759)	0.841(1.723)	0.988(0.206)
Neyman type A	Strong	1000	0.504(0.209)	0.451(0.395)	0.361(0.174)	0.448(1.256)	0.692(1.365)	0.983(0.157)
Neyman type A	Strong	5000	0.499(0.119)	0.461(0.242)	0.369(0.088)	0.500(0.639)	0.674(0.783)	0.981(0.073)
Neyman type A	Weak	500	0.476(0.293)	0.407(0.581)	0.414(0.239)	0.515(2.261)	1.054(2.896)	1.012(0.211)
Neyman type A	Weak	1000	0.496(0.248)	0.412(0.484)	0.403(0.176)	0.436(1.848)	0.903(2.458)	0.988(0.154)
Neyman type A	Weak	5000	0.499(0.160)	0.448(0.302)	0.400(0.084)	0.500(1.053)	0.766(1.317)	0.982(0.072)

^†sample size; Med, median of 1000 Monte Carlo estimates; MAD, median absolute deviance; EE-EL, estimating equations and empirical likelihood; 2SRI, two-stage residual inclusion; Reg, ordinary regression; strong IV, setting A; weak IV, setting B.

4.2. Single continuous mediator

As we discussed in Section 2.5, the natural indirect effect ratio (9) can be estimated for a continuous mediator. The mediator is generated as m = −0.5 + 0.5z + 0.5x + α_3z × x^IV + 0.5u + v, where v follows a standard normal distribution and the outcome variable is generated with setting A for Poisson and negative binomial distributions and with setting B in Table 2 for Neyman type A outcomes. Table 4 shows the median estimates and MAD for natural direct and indirect effect ratios with a continuous mediator. The ordinary regression estimates are biased whereas both 2SRI and EE-EL are approximately unbiased. The results for controlled direct and indirect effect ratios with a continuous mediator (see the on-line supplementary material Table 2) are similar to the results with a binary mediator in Table 3.

Table 4.

Estimates for the natural indirect rate ratio (9) with one IV and one continuous mediator

Outcome distribution	IV	n	Results for model (9) with x = 1				Results for model (9) with x =-1
			True	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)	True	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)
Poisson	Strong	500	2.117	2.114(0.487)	2.053(0.619)	3.163(0.491)	0.779	0.788(0.082)	0.798(0.098)	0.684(0.081)
Poisson	Strong	1000	2.117	2.088(0.320)	2.100(0.455)	3.169(0.388)	0.779	0.784(0.064)	0.788(0.072)	0.682(0.059)
Poisson	Strong	5000	2.117	2.112(0.152)	2.098(0.219)	3.203(0.184)	0.779	0.779(0.030)	0.781(0.035)	0.678(0.028)
Poisson	Weak	500	1.649	1.644(0.442)	1.635(0.558)	2.247(0.317)	1.000	0.998(0.063)	0.996(0.062)	1.001(0.117)
Poisson	Weak	1000	1.649	1.635(0.305)	1.644(0.417)	2.223(0.214)	1.000	1.001(0.047)	1.000(0.047)	1.003(0.082)
Poisson	Weak	5000	1.649	1.642(0.150)	1.639(0.193)	2.227(0.101)	1.000	1.001(0.023)	1.001(0.022)	1.002(0.037)
Negative binomial	Strong	500	2.117	2.128(0.534)	2.114(0.513)	3.428(0.493)	0.779	0.787(0.093)	0.790(0.089)	0.667(0.088)
Negative binomial	Strong	1000	2.117	2.114(0.379)	2.101(0.357)	3.422(0.343)	0.779	0.781(0.636)	0.787(0.558)	0.667(0.095)
Negative binomial	Strong	5000	2.117	2.115(0.166)	2.096(0.163)	3.421(0.154)	0.779	0.779(0.065)	0.781(0.063)	0.664(0.059)
Negative binomial	Weak	500	1.649	1.661(0.564)	1.650(0.537)	2.376(0.323)	1.000	0.996(0.063)	0.996(0.059)	0.996(0.127)
Negative binomial	Weak	1000	1.649	1.681(0.386)	1.670(0.364)	2.385(0.229)	1.000	1.000(0.051)	1.000(0.050)	1.001(0.095)
Negative binomial	Weak	5000	1.649	1.646(0.156)	1.638(0.158)	2.365(0.103)	1.000	0.999(0.023)	0.999(0.023)	0.999(0.040)
Neyman type A	Strong	500	2.117	2.057(1.256)	2.079(1.064)	3.225(0.787)	0.779	0.788(0.175)	0.796(0.149)	0.684(0.094)
Neyman type A	Strong	1000	2.117	2.141(1.006)	2.075(0.951)	3.247(0.591)	0.779	0.778(0.136)	0.785(0.127)	0.677(0.070)
Neyman type A	Strong	5000	2.117	2.136(0.448)	2.082(0.528)	3.252(0.354)	0.779	0.776(0.055)	0.783(0.071)	0.674(0.035)
Neyman type A	Weak	500	1.649	1.585(1.092)	1.610(1.050)	2.237(0.378)	1.000	0.999(0.084)	0.996(0.069)	0.999(0.119)
Neyman type A	Weak	1000	1.649	1.654(0.889)	1.609(0.799)	2.225(0.280)	1.000	0.998(0.050)	0.997(0.042)	0.998(0.082)
Neyman type A	Weak	5000	1.649	1.627(0.455)	1.631(0.522)	2.233(0.155)	1.000	1.000(0.020)	1.000(0.019)	1.000(0.037)

4.3. Multiple instrumental variables

We also considered settings with more than one IV, e.g.

$$m\mid x,z,u\sim \text{Ber}\left\{\frac{\text{exp}(-0.5+0.5z+0.5x_1+0.5x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}{1+\text{exp}(-0.5+0.5z+0.5x_1+0.5x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}\right\}.$$ (20)

The results (see the on-line supplementary material Table 1) are similar to Table 3. The EE-EL estimator estimates are consistent whereas the 2SRI estimator estimates have large bias in some settings.

4.4. Multiple binary mediators

Considering settings with two independent mediators and two IVs Z × $X_1^{\text{IV}}$ and Z ×$X_2^{\text{IV}}$, mediators m₁ and m₂ are generated independently as

$$m_1\mid x,z,u\sim \text{Ber}\left\{\frac{\text{exp}(-0.5+0.5z+0.5x_1+0.5x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}{1+\text{exp}(-0.5+0.5z+0.5x_1+0.5x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}\right\},$$ (21)

$$m_2\mid x,z,u\sim \text{Ber}\left\{\frac{\text{exp}(1+z-0.5x_1+x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}{1+\text{exp}(1+z-0.5x_1+x_2+z\times x_1^{\text{IV}}+z\times x_2^{\text{IV}}+0.5u)}\right\}.$$ (22)

The outcome variable is generated as

$$\mathbb{E}\{\mathit{Y}(z,m_1,m_2)\mid z,m_1,m_2,x,u\}=\text{exp}({\beta }_0+{\beta }_{z}z+{\beta }_{m,1}{m}_1+{\beta }_{m,2}{m}_2+{\beta }_{x}x+u),$$ (23)

with setting C for Poisson and negative binomial distributions and with setting D in Table 2 for Neyman type A outcome. There were 26.3% 0s in the generated Poisson outcome, 29.8% 0s in the generated negative binomial outcome and 38.6% 0s in the generated Neyman type A distribution outcome. Similarly to Table 3, Table 5 shows that the ordinary regression estimate is heavily biased. 2SRI can reduce the bias in some cases but has large bias in other cases when the sample size is small and/or the percentage of 0s is relatively large. Estimator EE-EL performed best in all the cases and produced consistent estimates with increased sample size.

Table 5.

Estimates for the direct effect parameter (β_z = 0.5) and the indirect effect parameter (β_m1 = 1 and β_m2 = 0.5 ) with two IVs and two binary mediators

Outcome distribution (n)	Results for direct effect			Results for indirect effect 1			Results for indirect effect 2
	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)	EE-EL Med (MAD)	2SRI Med (MAD)	Reg Med (MAD)
Poisson (500)	0.448 (0.218)	0.464 (0.275)	0.319 (0.127)	0.932 (0.911)	1.156 (0.827)	1.425 (0.122)	0.661 (1.127)	0.644 (0.866)	0.911 (0.155)
Poisson (1000)	0.482 (0.162)	0.489 (0.174)	0.319 (0.089)	0.910 (0.703)	1.094 (0.636)	1.417(0.086)	0.527 (0.909)	0.623 (0.687)	0.897 (0.111)
Poisson (5000)	0.490 (0.077)	0.502 (0.085)	0.321 (0.040)	0.990 (0.388)	1.080 (0.298)	1.416 (0.038)	0.521 (0.630)	0.511 (0.294)	0.902 (0.050)
Negative binomial (500)	0.442 (0.248)	0.481 (0.234)	0.342 (0.126)	0.979 (0.964)	1.184 (0.885)	1.432 (0.139)	0.592 (1.185)	0.514 (0.911)	0.950 (0.160)
Negative binomial (1000)	0.470 (0.183)	0.504 (0.153)	0.340 (0.088)	0.910 (0.747)	1.076 (0.585)	1.431 (0.104)	0.579 (0.978)	0.441 (0.636)	0.939 (0.120)
Negative binomial (5000)	0.492 (0.086)	0.508 (0.065)	0.340 (0.040)	0.972 (0.454)	1.088 (0.293)	1.427 (0.041)	0.528 (0.697)	0.437 (0.305)	0.944 (0.052)
Neyman type A (500)	0.423 (0.308)	0.377 (0.495)	0.315 (0.191)	0.925 (1.214)	1.247 (1.362)	1.445 (0.189)	0.653 (1.359)	0.838 (1.411)	0.949 (0.240)
Neyman type A (1000)	0.473 (0.257)	0.440 (0.357)	0.316 (0.132)	0.915 (0.974)	1.185 (1.041)	1.440 (0.126)	0.546 (1.181)	0.616 (0.909)	0.939 (0.165)
Neyman type A (5000)	0.490 (0.119)	0.480 (0.201)	0.311 (0.066)	0.970 (0.541)	1.099 (0.560)	1.436 (0.059)	0.492 (0.801)	0.552 (0.464)	0.917 (0.077)

4.5. Sensitivity analysis method

A sensitivity analysis was examined as discussed in Section 3.3. The sensitivity parameter η represents how much the instruments proposed violate the assumptions that are needed for them to be valid instruments. The on-line supplementary material Table 3 shows that, after we adjust the outcome and use the adjusted outcome in the methods, the results are similar to the results in Table 1 and the EE-EL estimator estimates are approximately unbiased for the direct and indirect effect parameters. Thus, if the amount of violation of the assumptions is correctly specified by η, the sensitivity analysis method provides unbiased estimates of the direct and indirect effect parameters.

4.6. High proportion of 0s and misspecification in outcome distribution

Additional simulation studies were conducted to examine the performance of methods with increased percentage of 0s (50% for Poisson and 55% for negative binomial models), and when the outcome distribution is misspecified in 2SRI. The results with increased percentage of 0s (the on-line supplementary material Table 4) are similar to the results in Table 3. When the outcome distribution is misspecified, 2SRI produced biased estimates whereas EE-EL continues to perform well as it does not rely on a parametric outcome distribution (the supplementary material Table 5).

In summary, the ordinary regression analysis produces biased estimates for the direct and indirect effect parameters when there is unmeasured confounding. Estimators 2SRI and EE-EL reduce bias with the use of IVs. However, 2SRI can have a large bias when the sample size is small or the percentage of 0s is large with a binary mediator or the outcome distribution is misspecified. The EE-EL method generally performs well under various settings and is robust to the misspecification of outcome distribution. The sensitivity analysis that we proposed performs well also.

5. Real data analysis

We shall first present a careful analysis of the dental data, which motivates the development of the method proposed. In addition, we demonstrate how to apply our method to some flood data, where the outcome is also a zero-inflated count variable but the mediator is continuous.

5.1. Dental study

In the DDHP MIDVD trial (Ismail et al., 2011), 790 families (0–5-years-old children and their caregivers) were randomly assigned to one of two education groups (DVD only or MI+DVD), so assumption 1 is satisfied. Both groups of families received a copy of a special 15-min DVD for dental education. Additionally the families in the intervention group MI+DVD met an MI interviewer, developed their own preventive goals and received booster calls within 6 months of the intervention. Table 6 shows that participants’ characteristics were balanced between groups MI+DVD and DVD at baseline; however, caregivers in group MI+DVD were more likely to make sure that their child brushed at bedtime at 6 months compared with group DVD. We would like to assess whether the change in caregivers’ behaviour by MI+DVD intervention led to a change in children’s dental outcome (the number of new untreated lesions at 2 years). Fig. 1(a) shows that more than 60% of children had zero new untreated lesions, so we have a count outcome with many 0s. The mediator is a binary variable whether or not caregivers made sure that their child brushed at bedtime at 6 months.

We constructed IVs with the interactions between intervention and three baseline covariates: the number of times that the child brushed at baseline, whether or not caregivers made sure that their child brushed at bedtime at baseline and whether or not caregivers provided the child healthy meals at baseline. These covariates have been considered as important behavioural variables related to subsequent oral hygiene behaviour and oral health (Featherstone, 2003) and therefore were considered to construct IVs in this study. Thinking that the unmeasured confounder represents the oral health education that caregivers or children received from primary dentists, schools, communities or the Internet, assumption 2 says that the distribution of the oral health education from other sources differs for different levels of baseline covariates by a shift but keeps the same shape. Since the oral health education that caregivers and children received from other sources was not measured in the study, we cannot test this assumption but a shift difference in distribution seems reasonable. A logistic regression was used to model the binary mediator on the treatment and IVs and showed significant effects of IVs (e.g. the increased odds ratio for caregivers making sure that their child brushed at bedtime among children brushing versus not brushing at baseline in group MI+DVD was 2.14 times bigger than than in group DVD), indicating that assumption 3 is satisfied. We also assessed the plausibility of the ER assumption (assumption 4) for the proposed IVs by examining whether the IVs had effects through pathways other than the mediator of our interest as discussed in Section 3.3 and the on-line supplementary material section 1.5. Specifically we examined whether the IVs were associated with other intermediate variables such as whether the caregiver provided the child with non-sugared snacks, whether the caregiver gave the child healthy meals, whether the caregiver checked the child for early non-cavitated demineralized enamel and whether the caregiver made sure that the child saw a dentist at 6 months given the intervention and baseline covariates. None of the IVs were significantly associated with other intermediate variables, indicating no evidence of the violation of the ER assumption of IVs.

Table 7 shows the regular regression estimates and bootstrap confidence intervals (CIs) for the direct and indirect effects of the MI+DVD intervention on children’s dental outcome assuming sequential ignorability. However, these estimates could be biased because the ignorability assumption may not hold for the mediator in this study. Therefore, we used the IV method that is developed in this paper to evaluate the direct and indirect effects. The result shows that the intervention did not have much direct effect on the number of new untreated lesions (controlled direct effect ratio 1.081), and parental behaviour in making sure that their child brushed at bedtime tended to decrease the number of new untreated lesions (controlled indirect effect ratio 0.595) but the effect was not statistically significant with a 90% CI (0.070, 4.604). In addition, we considered model (12) with the intervention–mediator interaction. As shown in Table 7, the indirect effect for the intervention group is 0.643 with a 90% CI (0.015,5.146) and the indirect effect for the control group is 0.837 with a 90% CI (0.042, 3.142), indicating that caregivers making sure that their child brushed at bedtime tended to reduce the number of new untreated lesions in both groups and group MI+DVD tended to have a bigger reduction in cavities but the effects were not significant. There was no significant direct effect of MI+DVD on children’s cavities in both caregivers who made sure that their child brushed at 6 months (1.000; 90% CI (0.667, 1.312)) and caregivers who did not make sure that their child brushed at 6 months (1.303; 90% CI (0.832, 3.565)).

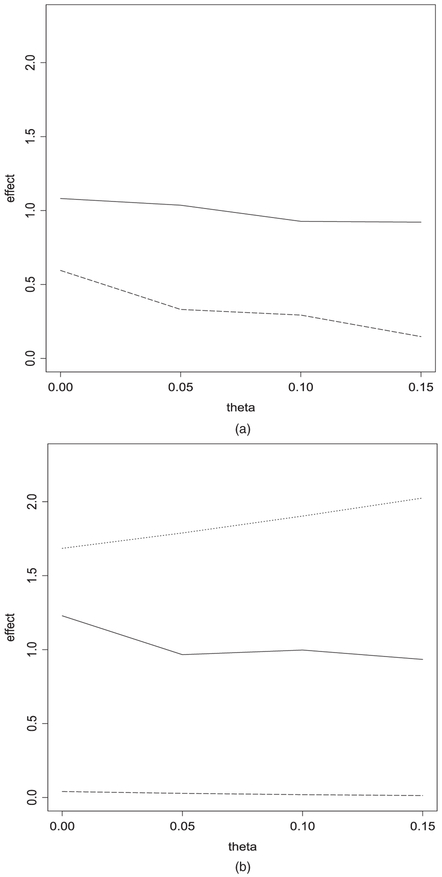
Although we did not find evidence of the ER violation for the IVs in this study, we also conducted a sensitivity analysis to see how the results will change if the ER fails to hold. The sensitivity analysis (Fig. 2) shows that, with increased amount of violation of the ER assumption, i.e. with increased direct effect of the IV (Z × X^IV) on children’s oral health (η increases from 0 to 0.15) not through the mediator (whether or not caregivers made sure their child brushed at bedtime), the MI+DVD intervention tended to reduce children’s number of new untreated lesions at 2 years (the direct effect ratio drops below 1 from 1.081) but the effect was not significant; and caregivers who made sure that their child brushed their teeth at bedtime tended to have a stronger effect in reducing children’s number of new untreated lesions (the controlled indirect effect ratio decreases from 0.595 to 0.147).

Fig. 2.

Sensitivity analysis of the real data: (a) ‘direct’ (——)—the controlled and natural direct effect and ‘indirect’ (– – – )—the controlled indirect effect; (b) ‘direct’ (——)—the controlled and natural direct effect, controlled indirect effect (– – –) and natural indirect effect (· · · ·· ·)

5.2. Flood data analysis

In 1998, two-thirds of Bangladesh suffered from massive floods. del Ninno et al. (2001) conducted a study of the effects of flooding on health outcomes. We shall use our method to see whether a household being severely affected by the flood (treatment) influenced the number of days that a child had diarrhoea in the 3-month period after the flood (outcome) through its effect on the per capita calorie consumption of the household (mediator). The outcome histogram Fig. 1(b) shows that more than 70% children had 0 days of diarrhoea. The continuous mediator allows us to evaluate the natural effects as discussed in Section 2.5.

Although whether a household being severely affected by the flood was not randomized, conditioning on baseline covariates (the amount of farmland available before the flood, sex, age, the size of the household, mother’s education, father’s education, an indicator of missing values for mother’s education and father’s education, mother’s age, father’s age and an indicator of missing values for mother’s age and father’s age), the ignorability of being severely affected by the flood (assumption 1) is reasonable. The interaction of being affected by the flood and a baseline covariate (whether the household has a low or large amount of farmland available) was used as our IV Thinking that the unmeasured confounder represents calorie consumption before the flood, assumption 2 seems reasonable that the distribution of the calorie consumption before the flood differs for different levels of baseline covariates by a shift but keeps the same shape. The significant effect of the IV on the mediator (the per capita calorie consumption of the household) indicates that assumption 3 is satisfied. To assess the plausibility of the ER (assumption 4), we examined whether or not the IV affected children’s number of days of diarrhoea through ways other than the per capita calorie consumption of the household as discussed in Section 3.3. del Ninno et al. (2001) suggested that whether a mother had chronic energy deficiency as a measure of mother’s health could be an alternative pathway. Specifically a mother was classified as having chronic energy deficiency if her body mass index was less than 18.5. Non-significant association of the IV with having chronic energy deficiency (p = 0.1501) given being affected by flood and baseline covariates indicated no evidence of violation of the ER assumption.

Table 8 shows the estimated direct and indirect effects of being affected by the flood on diarrhoea with regressions assuming sequential ignorability. Without the ignorability assumption on the mediator, our IV method was used to estimate the controlled (natural) direct and indirect effect and the bootstrap CIs. It is shown in Table 8 that being affected by the flood tended to increase the number of days of diarrhoea but the effect is not significant (direct effect ratio 1.229; 90% CI (0.300, 2.409)). A larger per capita calorie consumption of a household led to a significant decrease in the number of days that a child had diarrhoea over the 3-month period after the flood (controlled indirect effect ratio 0.040; 90% CI (2.524 × 10⁻⁵, 0.822)); and decreased per capita calorie consumption of a household due to flooding led to a significant increase in the number of days that a child had diarrhoea after the flood (natural indirect effect ratio 1.685; 90% CI (1.010, 6.239)).

We further conducted a sensitivity analysis to see how the results would change with a violation of the ER assumption. Fig. 2 shows that, with increased amount of violation of the ER (increased direct effect of Z × X^IV on children’s diarrhoea), the direct effect of the flood in increasing number of days of diarrhoea (1.229) changed to a small reduction in the number of days of diarrhoea (0.934) with neither significant, higher per capita calorie consumption still had a strong effect in reducing the number of days of diarrhoea (controlled indirect effect ratio from 0.040 to 0.013), and the effect of being affected by the flood on children’s diarrhoea through reduced per capita calorie consumption became more severe.

6. Conclusion

In this paper, we consider mediation analysis for a count or zero-inflated count outcome when there is concern about unmeasured confounding between the mediator and outcome. Direct and indirect effect ratios are defined for the count and zero-inflated count outcomes. Our method uses the interaction of treatment and baseline covariates as IVs, constructs estimating equations and uses the empirical likelihood approach for inference. Our method relaxes the assumption of sequential ignorability with reasonable assumptions and does not rely on the specific distribution assumptions on the error of the outcome.