TREE-BASED REINFORCEMENT LEARNING FOR ESTIMATING OPTIMAL DYNAMIC TREATMENT REGIMES

Abstract

Dynamic treatment regimes (DTRs) are sequences of treatment decision rules, in which treatment may be adapted over time in response to the changing course of an individual. Motivated by the substance use disorder (SUD) study, we propose a tree-based reinforcement learning (T-RL) method to directly estimate optimal DTRs in a multi-stage multi-treatment setting. At each stage, T-RL builds an unsupervised decision tree that directly handles the problem of optimization with multiple treatment comparisons, through a purity measure constructed with augmented inverse probability weighted estimators. For the multiple stages, the algorithm is implemented recursively using backward induction. By combining semiparametric regression with flexible tree-based learning, T-RL is robust, efficient and easy to interpret for the identification of optimal DTRs, as shown in the simulation studies. With the proposed method, we identify dynamic SUD treatment regimes for adolescents.

1. Introduction.

In many areas of clinical practice, it is often necessary to adapt treatment over time, due to significant heterogeneity in how individuals respond to treatment, as well as to account for the progressive (e.g., cyclical) nature of many chronic diseases and conditions. For example, substance use disorder (SUD) often involves a chronic course of repeated cycles of cessation (or significant reductions in use) followed by relapse [Hser et al. (1997), McLellan et al. (2000)]. However, individuals with SUD are vastly heterogeneous in the course of this disorder, as well as in how they respond to different interventions [Murphy et al. (2007)]. Dynamic treatment regimes (DTRs) [Robins (1986, 1997, 2004), Murphy (2003), Chakraborty and Murphy (2014)] are prespecified sequences of treatment decision rules, designed to help guide clinicians in whether or how, including based on which measures, to adapt (and re-adapt) treatment over time in response to the changing course of an individual. A DTR has multiple stages of treatment, and at each stage, information about a patient’s medical history and current disease status can be used to make a treatment recommendation for the next stage. The following is a simple example of a two-stage DTR for adolescents with SUD. First, at treatment program entry, offer adolescents nonresidential (outpatient) treatment for three months, and monitor them for substance use over the course of three months. Second, at the end of three months, if an adolescent has experienced reductions in the frequency of substance use, continue providing outpatient treatment for an additional three months. Otherwise, offer residential (inpatient) treatment for an additional three months. Identification of optimal DTRs offers an effective vehicle for personalized management of diseases, and helps physicians tailor the treatment strategies dynamically and individually based on clinical evidence, thus providing a key foundation for better health care [Wagner et al. (2001)].

Several methods have been developed or modified for the identification of optimal DTRs, which differ in terms of modeling assumptions as well as interpretability, that is, the ease with which it is possible to communicate the decision rules that make up the DTR [Zhang et al. (2015, 2016)]. The interpretability of an estimated optimal DTR is crucial for facilitating applications in medical practice. Commonly used statistical methods include marginal structural models with inverse probability weighting (IPW) [Murphy, van der Laan and Robins (2001), Wang et al. (2012), Hernán, Brumback and Robins (2001)], G-estimation of structural nested mean models [Robins (1994,1997,2004)], targeted maximum likelihood estimators [van der Laan and Rubin (2006)] and likelihood-based approaches [Thall et al. (2007)]. To apply these methods, one needs to specify a series of parametric or semipara-metric conditional models under a prespecified class of DTRs indexed by unknown parameters, and then search for DTRs that optimize the expected outcome. They often result in estimated optimal DTRs that are highly interpretable. However, in some settings, these methods may be too restrictive; for example, when there is a moderate-to-large number of covariates to consider or when there is no specific class of DTRs of particular interest.

To reduce modeling assumptions, more flexible methods have been proposed. In particular, the problem of developing optimal multi-stage decisions has strong resemblance to reinforcement learning (RL) [Chakraborty and Moodie (2013)]. Unlike supervised learning (SL) (e.g., regression and classification), the desired output value (e.g., the true class or the optimal decision), also known as the label, is not observed. The learning agent has to keep interacting with the environment to learn the best decision rule. Such methods include Q-learning [Watkins and Dayan (1992), Sutton and Barto (1998)] and A-learning [Murphy (2003), Schulte et al. (2014)], both of which use backward induction [Bather (2000)] to account for the delayed (or long-term) effects of earlier-stage treatment decisions. Q- and A-learning rely on maximizing or minimizing an objective function to indirectly infer the optimal DTRs and thus emphasize prediction accuracy of the clinical response model instead of directly optimizing the decision rule [Zhao et al. (2012)]. The modeling flexibility and interpretability of Q- and A-learning depend on the method for optimizing the objective function.

There has also been considerable interest in converting the RL problem to a SL problem so as to utilize existing classification methods. These methods are usually flexible with a nonparametric modeling framework but may introduce additional uncertainty due to the conversion. Their interpretability rests on the choice of the classification approach. For example, Zhao et al. (2015) propose outcome weighted learning (OWL) to transform the optimal DTR problem into an either sequential or simultaneous classification problem, and then apply support vector machines (SVM) [Cortes and Vapnik (1995)]. However, it is difficult to interpret the optimal DTRs estimated by SVM. Moreover, OWL is susceptible to trying to retain the actually observed treatments given a positive outcome, and its estimated individualized treatment rule is affected by a simple shift of the outcome [Zhou et al. (2017)]. For observational data, Tao and Wang (2017) propose a robust method for multi-treatment DTRs, adaptive contrast weighted learning (ACWL), which combines doubly robust augmented IPW (AIPW) estimators with classification algorithms. It avoids the challenging multiple treatment comparisons by utilizing adaptive contrasts that indicate the minimum or maximum expected reduction in the outcome given any sub-optimal treatment. In other words, ACWL ignores information on treatments that lead to neither the minimum or maximum expected reduction in the outcome, likely at the cost of efficiency.

Recently, Laber and Zhao (2015) propose a novel tree-based approach, denoted as LZ hereafter, to directly estimating optimal treatment regimes. Typically, a decision tree is a SL method that uses tree-like graphs or models to map observations about an item to conclusions about the item’s target value, for example, the classification and regression tree (CART) algorithm by Breiman et al. (1984). LZ fits the RL task into a decision tree with a purity measure that is unsupervised, and meanwhile maintains the advantages of decision trees, such as simplicity for understanding and interpretation, and capability of handling multiple treatments and various types of outcomes (e.g., continuous or categorical) without distributional assumptions. However, LZ is limited to a single-stage decision problem, and is also susceptible to propensity model misspecification. More recently, Zhang et al. (2015, 2016) and Lakkaraju and Rudin (2017) have applied decision lists to construct interpretable DTRs, which comprise a sequence of “if–then” clauses that map patient covariates to recommended treatments. A decision list can be viewed as a special case of tree-based rules, where the rules are ordered and learned one after another [Rivest (1987)]. These list-based methods are particularly useful when the goal is not only to gain the maximum health benefits but also to minimize the cost of measuring covariates. However, without cost information, a list-based method may be more restrictive than a tree-based method. On the one hand, to ensure parsimony and interpretability, Zhang et al. (2015, 2016) restrict each rule to involve up to two covariates, which may be problematic for more complex treatment regimes. On the other hand, due to the ordered nature of lists, a later rule is built upon all the previous rules and thus errors can accumulate. In contrast, a decision tree does not require the exploration of a full rule at the very beginning of the algorithm, since the rules are learned at the terminal nodes. Instead of being fully dependent on each other, rules from a decision tree are more related only if they share more parent nodes, which allows more freedom for exploration.

In this paper, we develop a tree-based RL (T-RL) method to directly estimate optimal DTRs in a multi-stage multi-treatment setting, which builds upon the strengths of both ACWL and LZ. First of all, through the use of decision trees, our proposed method is interpretable, capable of handling multinomial or ordinal treatments and flexible for modeling various types of outcomes. Second, thanks to the unique purity measures for a series of unsupervised trees at multiple stages, our method directly incorporates multiple treatment comparisons while maintaining the nature of RL. Last but not least, the proposed method has improved estimation robustness by embedding doubly robust AIPW estimators in the decision tree algorithm.

The remainder of this paper is organized as follows. In Section 2, we formalize the problem of estimating the optimal DTR in a multi-stage multi-treatment setting using the counterfactual framework, derive purity measures for decision trees at multiple stages and describe the recursive tree growing process. The performance of our proposed method in various scenarios is evaluated by simulation studies in Section 3. We further illustrate our method in Section 4 using a case study to identify optimal dynamic substance abuse treatment regimes for adolescents. Finally, we conclude with some discussions and suggestions for future research in Section 5.

2. Tree-based reinforcement learning (T-RL).

2.1. Dynamic treatment regimes (DTRs).

Consider a multi-stage decision problem with T decision stages and K_j (K_j ≥ 2) treatment options at the jth (j = 1,…,T) stage. Data could come from either a randomized trial or an observational study. Let A_j denote the multi-categorical treatment indicator with observed value $a_j\in {\mathcal{A}}_j=\{1,\dots ,K_j\}$. In the SUD data, treatment is multi-categorical with options being residential, non-residential or no treatment. Let X_j denote the vector of patient characteristics history just prior to treatment assignment A_j, and X_T+1 denote the entire characteristics history up to the end of stage T. Let R_j be the reward (e.g., reduction in the frequency of substance use) following A_j, which could depend on the covariate history X_j and treatment history A₁,…,A_j, and is also a part of the covariate history X_j+1. We consider the overall outcome of interest as Y = f(R₁,…,R_T), where f(·) is a prespecified function (e.g., sum), and we assume that Y is bounded; higher values of Y are preferable. The observed data are ${\left\{\right(A_{1i},\dots ,A_{\mathit{Ti}},{\mathbf{X}}_{T+1,i}^{⊺}\left)\right\}}_{i=1}^n$, assumed to be independent and identically distributed for n subjects from a population of interest. For brevity, we suppress the subject index i in the following text when no confusion exists.

A DTR is a sequence of individualized treatment rules, g = (g₁,…,g_T), where g_j is a mapping from the domain of covariate and treatment history ${\mathbf{H}}_j={(A_1,\dots ,A_{j-1},{\mathbf{X}}_j^{⊺})}^{⊺}$ to the domain of treatment assignment A_j, and we set A₀ = Ø. To define and identify the optimal DTR, we consider the counterfactual framework for causal inference [Robins (1986)].

At stage T, let Y*(A₁,…,A_T–1, a_T), or Y*(a_T) for brevity, denote the counterfactual outcome for a patient treated with $a_T\in {\mathcal{A}}_T$ conditional on previous treatments (A₁ ,…,A_T–1), and define Y*(g_T) as the counterfactual outcome under regime g_T, that is,

$$Y^{\ast }(g_T)=\sum _{a_T=1}^{K_T}{Y}^{\ast }(a_T)I\{g_T({\mathbf{H}}_T)=a_T\}.$$

The performance of g_T is measured by the counterfactual mean outcome E{Y*(g_T)}, and the optimal regime, $g_T^{\text{opt}}$, satisfies $E\{Y^{\ast }(g_T^{\text{opt}})\}\ge E\{Y^{\ast }(g_T)\}$ for all $g_T\in {\mathcal{G}}_T$, where ${\mathcal{G}}_T$ is the class of all potential regimes. To connect the counterfactual outcomes with the observed data, we make the following three standard assumptions [Murphy, van der Laan and Robins (2001), Robins and Hernán (2009), Orellana, Rotnitzky and Robins (2010)].

Assumption 1 (Consistency). The observed outcome is the same as the counterfactual outcome under the treatment a patient is actually given, that is, $Y={\sum }_{a_T=1}^{K_T}{Y}^{\ast }(a_T)I(A_T=a_T)$, where I(·) is the indicator function that takes the value 1 if · is true and 0 otherwise. It also implies that there is no interference between subjects.

Assumption 2 (No unmeasured confounding). Treatment A_T is randomly assigned with probability possibly dependent on H_T, that is,

$$\{Y^{\ast }(1),\dots ,Y^{\ast }(K_T)\}⫫A_T\mid {\mathbf{H}}_T,$$

where ⫫ denotes statistical independence.

Assumption 3 (Positivity). There exist constants 0 < c₀ < c₁ < 1 such that, with probability 1, the propensity score π_aT(H_T) = Pr(A_T = a_T|H_T) ∈ (c₀, c₁).

Following the derivation in Tao and Wang (2017) under the foregoing three assumptions, we have

$$E\{Y_T^{\ast }(g_T)\}=E_{{\mathbf{H}}_T}\left[\sum _{a_T=1}^{K_T}E(Y\mid A_T=a_T,{\mathbf{H}}_T)I\{g_T({\mathbf{H}}_T)=a_T\}\right],$$

where E_HT(·) denotes expectation with respect to the marginal joint distribution of the observed data H_T. If we denote the conditional mean E(Y|A_T = a_T, H_T) as μ_T,a,T (H_T), we have

$$g_T^{\text{opt}}=\text{arg}\underset{g_T\in {\mathcal{G}}_T}{\text{max}}{E}_{{\mathbf{H}}_T}\left[\sum _{a_T=1}^{K_T}{\mu }_T,a_T({\mathbf{H}}_T)I\{g_T({\mathbf{H}}_T)=a_T\}\right].$$ (2.1)

At stage j, T – 1 ≥ j ≥ 1, $g_j^{\text{opt}}$ can be expressed in terms of the observed data via backward induction [Bather (2000)]. Following Murphy (2005) and Moodie, Chakraborty and Kramer (2012), we define a stage-specific pseudo-outcome PO_j for estimating $g_j^{\text{opt}}$, which is a predicted counterfactual outcome under optimal treatments at all future stages, also known as the value function. Specifically, we have

$${\mathit{PO}}_j=E\{Y^{\ast }(A_1,\dots ,A_j,g_{j+1}^{\text{opt}},\dots ,g_T^{\text{opt}})\},$$

or in a recursive form,

$${\mathit{PO}}_j=E\{{\mathit{PO}}_{j+1}\mid A_{j+1}=g_{j+1}^{\text{opt}}({\mathbf{H}}_{j+1}),{\mathbf{H}}_{j+1}\}$$

and we set PO_T = Y.

For a_j = 1,…,K_j, let μ_j,_aj (H_j) denote the conditional mean E[PO_j|A_j = a_j, H_j], and we have ${\mathit{PO}}_j={\mu }_{j+1,g_{j+1}^{\text{opt}}}({\mathbf{H}}_{j+1})$. Let ${\mathit{PO}}_j^{\ast }(a_j)$ denote the counterfactual pseudo-outcome for a patient with treatment a_j at stage j. For the three assumptions, we have positivity as ${\mathit{PO}}_j={\sum }_{a_j=1}^{K_j}{\mathit{PO}}_j^{\ast }(a_j)I(A_j=a_j)$ , no unmeasured confounding as $\{{\mathit{PO}}_j^{\ast }(1),\dots ,{\mathit{PO}}_j^{\ast }(K_j)\}⫫{\mathbf{H}}_j$ and positivity as π_aj (H_j) = Pr(A_j = a_j∣H_j) bounded away from zero and one. Under these three assumptions, the optimization problem at stage j, among all potential regimes ${\mathcal{G}}_j$, can be written as

$$g_j^{\text{opt}}=\text{arg}\underset{g_j\in {\mathcal{G}}_j}{\text{max}}{E}_{{\mathbf{H}}_j}\left[\sum _{a_j=1}^{K_j}{\mu }_j,a_j({\mathbf{H}}_j)I\{g_j({\mathbf{H}}_j)=a_j\}\right].$$ (2.2)

2.2. Purity measures for decision trees at multiple stages.

We propose to use a tree-based method to solve (2.1) and (2.2). Typically, a CART tree is a binary decision tree constructed by splitting a parent node into two child nodes repeatedly, starting with the root node which contains the entire learning samples. The basic idea of tree growing is to choose a split among all possible splits at each node so that the resulting child nodes are the purest (e.g., having the lowest misclassification rate). Thus the purity or impurity measure is crucial to the tree growing. Traditional classification and regression trees are SL methods, with the goal of inferring a function that describes the relationship between the outcome and covariates. The desired output value, also known as the label, is observed and can be used directly to measure purity. Commonly used impurity measures include Gini index and information index for categorical outcomes, and least squares deviation for continuous outcomes [Breiman et al. (1984)].

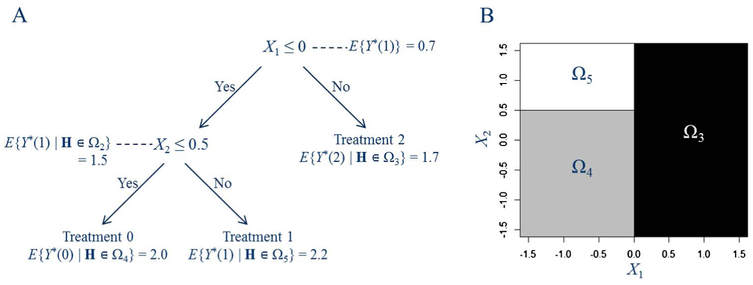
However, the estimation target of a DTR problem, which is the optimal treatment for a patient with characteristics H_j at stage j, that is, $g_j^{\text{opt}}({\mathbf{H}}_j),j=1,\dots ,T$, is not directly observed. Information about $g_j^{\text{opt}}({\mathbf{H}}_j)$ can only be inferred indirectly through the observed treatments and outcomes. Using the causal framework and the foregoing three assumptions, we can pool over all subject-level data to estimate the counterfactual mean outcomes given all possible treatments. With the overall goal of maximizing the counterfactual mean outcome in the entire population of interest, the selected split at each node should also improve the counterfactual mean outcome, which can serve as a measure of purity in DTR trees. Figure 1 illustrates a decision tree for a single-stage (T = 1) optimal treatment rule with $\mathcal{A}=\{0,1,2\}$. Let Ω_m, m = 1, 2,…, denote the nodes which are regions defined by the covariate space following all precedent binary splits, with the root node ${\mathrm{\Omega }}_1={ℝ}^p$ (p is the covariate dimension). We number the rectangular region Ω_m, m ≥ 2, so that its parent node is Ω_⌈m/2⌉, where ⌈·⌈ means taking the smallest integer not less than ·. Figure 1 shows the chosen covariate and best split at each node, as well as the counterfactual mean outcome after assigning a single optimal treatment to that node. The splits are selected to increase the counterfactual mean outcome. At the root node, if we select a single treatment for all subjects, treatment 1 is the most beneficial overall, yielding a counterfactual mean outcome of 0.7. Splitting via X₁ and X₂, the optimal regime g^opt is to assign treatment 2 to region Ω₃ = {X₁ > 0}, treatment 0 to region Ω₄ = {X₁ ≤ 0, X₂ ≤ 0.5}, and treatment 1 to region Ω₅ = {X₁ ≤ 0, X₂ > 0.5}. We can see that this tree is fundamentally different from a CART tree as it does not attempt to describe the relationship between the outcome and covariates or the rule for the assignment of the observed treatments, and instead it describes the rule by which treatments should be assigned to future subjects in order to maximize the purity, which is the counterfactual mean outcome.

Fig. 1.

(A) A decision tree for optimal treatment rules and the expected counterfactual outcome by assigning a single best treatment to each node that represents a subset covariate space. (B) Regions divided by the terminal nodes in the decision tree indicating different optimal treatments.

Laber and Zhao (2015) propose a measure of node purity based on the IPW estimator of the counterfactual mean outcome [Zhang et al. (2012), Zhao et al. (2012)],

$$E\{Y^{\ast }(g)\}=E_{\mathbf{H}}\left[\frac{I(A=g(\mathbf{H}))}{{\pi }_A(\mathbf{H})}Y\right],$$

for a single-stage (T = 1, omitted for brevity) decision problem. Given known propensity score π_A(H), they propose a purity measure ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$ as

$$\underset{a_1,a_2\in \mathcal{A}}{\text{max}}\frac{{\mathbb{P}}_n[\frac{\{Y-\widehat{m}(\mathbf{H})\}I\{A=g_{\omega ,a_1,a_2}(\mathbf{H})\}}{{\pi }_A(\mathbf{H})}I(\mathbf{H}\in \mathrm{\Omega })]}{{\mathbb{P}}_n[\frac{I\{A=g_{\omega ,a_1,a_2}(\mathbf{H})\}}{{\pi }_A(H)}I(\mathbf{H}\in \mathrm{\Omega })]},$$

where ${\mathbb{P}}_n$ is the empirical expectation operator, $\widehat{m}(\mathbf{H})$ is max_a∈A ${\text{max}}_{a\in \mathcal{A}}{\widehat{\mu }}_a(\mathbf{H})$ with μ_a(H) = E(Y∣A = a, H), Ω denotes the node to be split, ω and ω^c is a partition of ω, and for a given partition ω and ω^c, g_ω,a1,a2 denotes the decision rule that assigns treatment a₁ to subjects in ω and treatment a₂ to subjects in ω^c. ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$ is the estimated counterfactual mean outcome for node ω by the best decision rule that assigns a single treatment to all subjects in ω and a second treatment to all subjects in ω^c. However, in an observational study where π_A(H) has to be estimated, ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$ is subject to misspecification of the propensity model. Moreover, as the node size decreases, the IPW-based purity measure will become less stable.

To improve robustness, we propose to use an AIPW estimator for the counterfactual mean outcome as in Tao and Wang (2017). By regarding the K treatment options as K arbitrary missing data patterns [Rotnitzky, Robins and Scharfstein (1998)], the AIPW estimator for E{Y*(a)} is ${\mathbb{P}}_n\{{\widehat{\mu }}_a^{\text{AIPW}}(\mathbf{H})\}$, with

$${\widehat{\mu }}_a^{\text{AIPW}}(\mathbf{H})=\frac{I(A=a)}{{\widehat{\pi }}_a(\mathbf{H})}Y+\left\{1-\frac{I(A=a)}{{\widehat{\pi }}_a(\mathbf{H})}\right\}{\widehat{\mu }}_a(\mathbf{H}).$$ (2.3)

Under the foregoing three assumptions, ${\mathbb{P}}_n\{{\widehat{\mu }}_a^{\text{AIPW}}(\mathbf{H})\}$ is a consistent estimator of E{Y*(a)} if either the propensity model π_a(H) or the conditional mean model μ_a(H) is correctly specified, and thus the method is doubly robust.

In our multi-stage setting, for stage T, given estimated conditional mean ${\widehat{\mu }}_{T,a_T}^{\text{AIPW}}({\mathbf{H}}_T)$ and estimated propensity score ${\widehat{\pi }}_T,A_T({\mathbf{H}}_T)$, the proposed estimator of $E\{Y_T^{\ast }(g_T)\}$ is

$$\begin{array}{cc}\hfill {\mathbb{P}}_n& \left[\sum _{a_T=1}^{K_T}{\widehat{\mu }}_{T,a_T}^{\text{AIPW}}({\mathbf{H}}_T)I\{g_T({\mathbf{H}}_T)=a_T\}\right]\hfill \\ \hfill & ={\mathbb{P}}_n\left[\frac{I(A_T=g_T({\mathbf{H}}_T))}{{\widehat{\pi }}_{T,A_T}({\mathbf{H}}_T)}Y+\left\{1-\frac{I(A_T=g_T({\mathbf{H}}_T))}{{\widehat{\pi }}_T,A_T({\mathbf{H}}_T)}\right\}{\widehat{\mu }}_{T,g_T}({\mathbf{H}}_T)\right],\hfill \end{array}$$

which has the augmented term in addition to the IPW estimator used by Laber and Zhao (2015). Similarly, for stage j (T – 1 ≤ j ≤ 1), the proposed estimator of $E\{{\mathit{PO}}_j^{\ast }(g_j)\}$ is

$${\mathbb{P}}_n\left[\frac{I(A_j=g_j({\mathbf{H}}_j))}{{\widehat{\pi }}_{j,A_j}({\mathbf{H}}_j)}{\widehat{\mathit{PO}}}_j+\left\{1-\frac{I(A_j=g_j({\mathbf{H}}_j))}{{\widehat{\pi }}_{j,A_j}({\mathbf{H}}_j)}\right\}{\widehat{\mu }}_{j,g_j}({\mathbf{H}}_j)\right],$$

where ${\widehat{\pi }}_{j,A_j}({\mathbf{H}}_j)$ is the estimated propensity score, ${\widehat{\mu }}_{j,a_j}({\mathbf{H}}_j)$ is the estimated conditional mean and ${\widehat{\mathit{PO}}}_j={\widehat{\mu }}_{j+1,{\widehat{g}}_{j+1}^{\text{opt}}}({\mathbf{H}}_{j+1})$ is the estimated pseudo-outcome.

Our proposed method maximizes the counterfactual mean outcome through each of the nodes. For a given partition ω and ω^c of node Ω, let g_j,ω,a1,a2 denote the decision rule that assigns treatment a₁ to subjects in ω and treatment a₂ to subjects in ω^c at stage j (T ≤ j ≤ 1), and we define the purity measure ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$ as

$$\underset{a_1,a_2\in {\mathcal{A}}_j}{\text{max}}{\mathbb{P}}_n\left[\sum _{a_j=1}^{K_j}{\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)I\{g_{j,\omega ,a_1,a_2}({\mathbf{H}}_j)=a_j\}I({\mathbf{H}}_j\in \mathrm{\Omega })\right].$$

We can see that ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$ is the estimated counterfactual mean outcome for node Ω and it works as the performance measure for the best decision rule which assigns a single treatment to each of the two arms under the partition ω. Comparing ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$ and ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$ the primary difference is in the underlying estimator for the counterfactual mean outcome. Another difference is that in ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$ one is utilizing all subjects at node Ω with the counterfactual outcomes ${\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)$ calculated using all samples at the root node, while in ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$, one is only using a subset of subjects, depending on compatibility to g_ω,a1,a2 (H_j), which is why there is a denominator in ${\mathcal{P}}^{\text{LZ}}(\mathrm{\Omega },\omega )$ but not in ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$. These differences may lead to better stability for ${\mathcal{P}}_j(\mathrm{\Omega },\omega )$.

2.3. Recursive partitioning.

As we have mentioned, the purity measures for our T-RL are different from the ones in supervised decision trees. However, after defining ${\mathcal{P}}_j(\mathrm{\Omega },\omega ),j=1,\dots ,T$, the recursive partitioning to grow the tree is similar. Each split depends on the value of only one covariate. A nominal covariate with C categories has 2^C–1 – 1 possible splits and an ordinal or continuous covariate with L different values has L – 1 unique splits. Therefore, at a given node Ω, a possible split ω indicates either a subset of categories for a nominal covariate or values no larger than a threshold for an ordinal or continuous covariate. The best split ω^opt is chosen to maximize the improvement in the purity, ${\mathcal{P}}_j(\mathrm{\Omega },\omega )-{\mathcal{P}}_j(\mathrm{\Omega })$, where ${\mathcal{P}}_j(\mathrm{\Omega })$ means to assign a single best treatment to all subjects in Ω without splitting. It is straightforward to see that ${\mathcal{P}}_j(\mathrm{\Omega },\omega )\ge {\mathcal{P}}_j(\mathrm{\Omega })$. In order to control overfitting as well as to make meaningful splitting, a positive constant λ is given to represent a threshold for practical significance and another positive integer n₀ is given as the minimal node size which is dictated by problem-specific considerations. Under these conditions, we first evaluate the following three Stopping Rules for node Ω.

Rule 1. If the node size is less than 2_n0, the node will not be split.

Rule 2. If all possible splits of a node result in a child node with size smaller than n₀, the node will not be split.

Rule 3. If the current tree depth reaches the user-specified maximum depth, the tree growing process will stop.

If none of the foregoing Stopping Rules are met, we compute the best split by

$${\widehat{\omega }}^{\text{opt}}=\text{arg}\underset{\omega }{\text{max}}\left[{\mathcal{P}}_j(\mathrm{\Omega },\omega ):\text{min}\{n{\mathbb{P}}_{n}I({\mathbf{H}}_j\in \omega ),n{\mathbb{P}}_{n}I({\mathbf{H}}_j\in {\omega }^c)\}\ge n_0\right].$$

Before deciding whether or not to split Ω into ω and ω^c, we evaluate the following Stopping Rule 4.

Rule 4. If the maximum purity improvement ${\mathcal{P}}_j(\mathrm{\Omega },{\widehat{\omega }}^{\text{opt}})-{\mathcal{P}}_j(\mathrm{\Omega })$ is less than λ, the node will not be split.

We split Ω into ω and ω^c if none of the four stopping rules apply.

When there is no clear scientific guidance on λ to indicate practical significance, one approach is to choose a relatively small positive value to build a complete tree and then prune the tree back in order to minimize a measure of cost for the tree. Following the CART algorithm, the cost is a measure of the total impurity of the tree with a penalty term on the number of terminal nodes, and the complexity parameter for the penalty term can be tuned by cross-validation (CV) [Breiman et al. (1984)]. Alternatively, we propose to select λ directly by CV, similar to the method by Laber and Zhao (2015). As a direct measure of purity is not available in RL, we again incorporate the idea of maximizing the counterfactual mean outcome and use a 10-fold CV estimator of the counterfactual mean outcome. Theoretically, CV can be conducted at each stage separately and one can use a potentially different λ for each stage. To reduce modeling uncertainty in the pseudo-outcomes and also simplify the process, we carry out CV only at stage T using the overall outcome Y directly. Specifically, we use nine subsamples as training data to estimate the function of μ_τ,aT (·) following (2.3) and $g_T^{\text{opt}}(\cdot )$ using T-RL for a given λ, and then plug in H_T of the remaining subsample to get ${\widehat{\mu }}_{T,a_T}^{\text{AIPW},\text{CV}}({\mathbf{H}}_T)$ and ${\widehat{g}}_T^{\text{opt},\text{CV},\lambda }({\mathbf{H}}_T)$. We repeat the process 10 times with each subsample being the test data once. Then the CV-based counterfactual mean outcome under λ is

$$\widehat{E}\{Y^{\ast }({\widehat{g}}_T^{\text{opt},\text{CV},\lambda })\}={\mathbb{P}}_n\left[\sum _{a_T=1}^{K_T}{\widehat{\mu }}_{T,a_T}^{\text{AIPW},\text{CV}}({\mathbf{H}}_T)I\{{\widehat{g}}_T^{\text{opt},\text{CV},\lambda }({\mathbf{H}}_T)=a_T\}\right],$$

and the best value for λ is $\widehat{\lambda }={\text{arg max}}_{\lambda }\widehat{E}\{Y^{\ast }({\widehat{g}}_T^{\text{opt},\text{CV},\lambda })\}$. As the scale of the outcome affects the scale of ${\mathcal{P}}_j(\mathrm{\Omega },\omega )-{\mathcal{P}}_j(\mathrm{\Omega })$, we search over a sequence of candidate λ’s as a sequence of percentages of ${\mathcal{P}}_T({\mathrm{\Omega }}_1)$, that is, the estimated counterfactual mean outcome under a single best treatment for all subjects (Ω₁ is the root node).

2.4. Implementation of T-RL.

The AIPW estimator ${\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)$, j = 1,…,T, a_j = 1,…, K_j, consists of three parts to be estimated, the pesudo-outcome PO_j, the propensity score π_j,aj (H_j) and the conditional mean model μ_j,aj (H_j).

We start the estimation with stage T and conduct backward induction. At stage T, we use the outcome Y directly, that is, PO_T = Y. For stage j, T – 1 ≥ j ≥ 1, given a cumulative outcome (e.g., the sum of longitudinally observed values or a single continuous final outcome), we use a modified version of pseudo-outcomes to reduce accumulated bias from the conditional mean models [Huang et al. (2015)]. Instead of using only the model-based values under optimal future treatments, that is, ${\mu }_{j+1},g_{j+1}^{\text{opt}}({\mathbf{H}}_{j+1})$, we use the actual observed outcomes plus the expected future loss due to sub-optimal treatments, which means

$${{\mathit{PO}}^{\prime }}_j={{\mathit{PO}}^{\prime }}_{j+1}+{\mu }_{j+1,g_{j+1}^{\text{opt}}}({\mathbf{H}}_{j+1})-{\mu }_{j+1,A_{j+1}}({\mathbf{H}}_{j+1}),$$

where ${\mu }_{j+1},g_{j+1}^{\text{opt}}({\mathbf{H}}_{j+1})-{\mu }_{j+1,a_{j+1}}({\mathbf{H}}_{j+1})$ is the expected loss due to sub-optimal treatments at stage j + 1 for a given patient, which is zero if $g_{j+1}^{\text{opt}}({\mathbf{H}}_{j+1})=A_{j+1}$ and positive otherwise. Given PO′_T = Y, it is easy to see that

$${{\mathit{PO}}^{\prime }}_j=Y+\sum _{t=j+1}^T\{{\mu }_{t,g_t^{\text{opt}}}({\mathbf{H}}_t)-{\mu }_{t,A_t}({\mathbf{H}}_t)\}.$$

This modification leads to more robustness against model misspecification and is less likely to accumulate bias from stage to stage during backward induction [Huang et al. (2015)]. In our simulations, we estimate PO′_j by using random forests-based conditional mean estimates [Breiman (2001)].

The propensity score π_j,aj(H_j) can be estimated via multinomial logistic regression [Menard (2002)]. A working model could include linear main effect terms for all variables in H_j. Summary variables or interaction terms may also be included based on scientific knowledge.

The conditional mean estimate ${\widehat{\mu }}_{j,a_j}({\mathbf{H}}_j)$ in the augmentation term of ${\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)$ can be obtained from a parametric regression model. For continuous outcomes, a simple and oftentimes reasonable example is the parametric linear model with coefficients dependent on treatment:

$$E({{\widehat{\mathit{PO}}}^{\prime }}_j\mid A_j,{\mathbf{H}}_j)=\sum _{a_j=1}^{K_j}({\beta }_{a_j}^{\top }{\mathbf{H}}_j)I(A_j=a_j),$$ (2.4)

where β_a is a parameter vector for H_j under treatment a_j. For binary and count outcomes, one may extend the method by using generalized linear models. For survival outcomes with noninformative censoring, it is possible to use an accelerated failure time model to predict survival time for all patients. Survival outcomes with more complex censoring issues are beyond the scope of the current study.

The T-RL algorithm starting with stage j = T is carried out as follows:

Step 1. Obtain AIPW estimates ${\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)$, a_j = 1,…, K_j, using full data.

Step 2. At root node Ω_j,m, m = 1, set values for λ and n₀.

Step 3. At node Ω_j,m, evaluate the four Stopping Rules. If any of the Stopping Rules is satisfied, assign a single best treatment

$$\text{arg}\underset{a_j\in {\mathcal{A}}_j}{\text{max}}{\mathbb{P}}_n[{\widehat{\mu }}_{j,a_j}^{\text{AIPW}}({\mathbf{H}}_j)I({\mathbf{H}}_j\in {\mathrm{\Omega }}_{j,m})]$$

to all subject in Ω_j,m. Otherwise, split Ω_j,m into child nodes Ω_j,2m and Ω_j,2m+1 by ${\widehat{\omega }}^{\text{opt}}$.

Step 4. Set m = m + 1 and repeat Step 3 until all nodes are terminal.

Step 5. If j > 1, set j = j – 1 and repeat steps 1 to 4. If j = 1, stop.

Similar to the CART algorithm, T-RL is greedy as it chooses splits only at the current node for purity improvement, which may not lead to a global maximum. One way to potentially enhance the performance is lookahead [Murthy and Salzberg (1995)]. We test this in our simulation by fixed-depth lookahead: evaluating the purity improvement after splitting the parent node as well as its two child nodes, comparing the total purity improvement after splitting up to four nodes to the purity improvement without splitting the parent node, and finally deciding whether or not to split the parent node. We denote this method as T-RL-LH.

3. Simulation studies.

We conduct simulation studies to investigate the performance of our proposed method. We set all regression models μ to be misspecified, which is the case for most real data applications, while allowing the specification of the propensity model π be either correct (e.g., randomized trials) or incorrect (e.g., most observational studies). We consider first a single-stage scenario so as to facilitate the comparison with existing methods, particularly Laber and Zhao (2015), and then a multi-stage scenario. For each scenario, we consider sample sizes of either 500 or 1000 for the training datasets and 1000 for the test datasets, and repeat the simulation 500 times. We use the training datasets to estimate the optimal regime and then predict the optimal treatments in the test datasets, where the underlying truth is known. We denote the percentage of subjects correctly classified to their optimal treatments as opt%. We also use the true outcome model and the estimated optimal regime in the test datasets to estimate the counterfactual mean outcome, denoted as $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$. For both scenarios, we generate five baseline covariates X₁,…,X₅ according to N(0, 1), and for Scenario 1, we further consider a setting with additional covariates X₆,…,X₂₀ simulated independently from N(0, 1).

3.1. Scenario 1:

T = 1 and K = 3. In Scenario 1, we consider a single stage with three treatment options and sample size of 500. The treatment A is set to take values in {0, 1,2}, and we generate it from Multinomial (π₀, π₁, π₂), with π₀ = 1/{1 + exp(0.5X₁ + 0.5X₄) + exp(−0.5X₁ + 0.5X₅)}, π₁ = exp(0.5X₁ + 0.5X₄)/{1 + exp(0.5X₁ + 0.5X₄) + exp(−0.5X₁ + 0.5X₅)} and π₂ = 1 – π₀ – π₁. The underlying optimal regime is

$$g^{\text{opt}}(\mathbf{H})=\{\begin{array}{cc}0\hfill & X_1\le 0,X_2\le 0.5,\hfill \\ 2\hfill & X_1>0,X_3\le 0.5,\hfill \\ 1\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

For the outcomes, we first consider equal penalties for sub-optimal treatments through outcome generating model (a), which is

$$Y=1+X_4+X_5+\sum _{a=0}^2[I(A=a)\{2I(g^{\text{opt}}=a)-1\}]+\epsilon .$$

Then we consider varying penalties for sub-optimal treatments through outcome generating model (b), which is

$$\begin{array}{cc}\hfill Y=& 0.79+X_4+X_5+2I(A=0)\{2I(g^{\text{opt}}=0)-1\}\hfill \\ \hfill & +1.5I(A=2)\{2I(g^{\text{opt}}=2)-1\}+\epsilon .\hfill \end{array}$$

In both outcome models, we have ε ~ N(0, 1) and E{Y*(g^opt)} = 2.

In the application of the proposed T-RL algorithm, we consider both a correctly specified model log(π_d/π₀) = β_0d + β_1dX₁ + β_2dX₄ + β_3dX₅, d = 1, 2, and an incorrectly specified one log (π_d/π₀) = β_0d + β_1dX₂ + β_2dX₃. We also apply T-RL-LH to Scenario 1 as mentioned in Section 2.4. For comparison, we use both the linear regression-based and random forests-based conditional mean models to infer the optimal regimes, which we denote as RG and RF, respectively. We also apply the tree-based method LZ by Laber and Zhao (2015). Furthermore, we apply the OWL method by Zhao et al. (2012), and the ACWL algorithm by Tao and Wang (2017), denoted as ACWL-C₁ and ACWL-C₂, where C₁ and C₂ indicate respectively the minimum and maximum expected loss in the outcome given any sub-optimal treatment for each patient. Given outcome model (a), all sub-optimal treatments have the same expected loss in the outcome and we expect ACWL to perform similarly well as T-RL. However, given outcome model (b) when the sub-optimal treatments have different expected losses in the outcome, we expect T-RL to perform better as it incorporates multiple treatment comparison. Both OWL and ACWL are implemented using the R package rpart for classification.

Table 1 summarizes the performances of all methods considered in Scenario 1 with five baseline covariates. We present the percentage of subjects correctly classified to their optimal treatments in the testing datasets, denoted as opt%, and the expected counterfactual outcome obtained using the true outcome model and the estimated optimal regime, denoted as $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$. opt% shows on average how accurately the estimated optimal regime assigns future patients to their true optimal treatments and $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$ shows how much the entire population of interest will benefit from following ${\widehat{g}}^{\text{opt}}$. T-RL-LH has the best performance among all the methods considered, classifying over 93% of subjects to their optimal treatments. However, lookahead has led to significant increase in computational time compared to T-RL, while the improvement is only moderate with ≤ 1% more subjects being correctly classified. T-RL also has an estimated counterfactual mean outcome very close to the true value 2. As expected, ACWL-C₁ and ACWL-C₂ have performances comparable to T-RL under outcome model (a) with equal penalties for treatment misclassification, and the performance discrepancy gets larger under outcome model (b) with varying penalties, due to the approximation by adaptive contrasts C₁ and C₂. Similar results can be found in the Supplementary Table S1. LZ, using an IPW-based decision tree, works well only when the propensity score model is correctly specified and is less efficient than T-RL with larger empirical standard deviations (SDs). In contrast, T-RL-LH, T-RL, ACWL-C₁ and ACWL-C2 are all highly robust to model misclassification, thanks to the combination of doubly robust AIPW estimators and flexible machine learning methods. OWL performs far worse than all other competing methods likely due to the low percentage of truly optimal treatments in the observed treatments, the shift in the outcome, which was intended to ensure positive weights, and its moderate efficiency.

Table 1.

Simulation results for Scenario 1 with a single stage, three treatment options and five baseline covariates (500 replications, n = 500). π is the propensity score model. (a) and (b) indicate equal and varying penalties for treatment misclassification in the generative outcome model. opt% shows the empirical mean and standard deviation (SD) of the percentage of subjects correctly classified to their optimal treatments. $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$ shows the empirical mean and SD of the expected counterfactual outcome obtained using the true outcome model and the estimated optimal regime.

E{Y*gopt)} = 2
π	Method	(a)		(b)
		opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathit{g}}}^{\mathbf{opt}})\}$	opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathit{g}}}^{\mathbf{opt}})\}$
–	RG	74.2 (2.3)	1.49 (0.07)	68.8 (4.0)	1.42 (0.09)
	RF	75.3 (4.5)	1.51 (0.11)	81.1 (4.5)	1.69 (0.10)
Correct	OWL	44.3 (7.6)	0.89 (0.16)	47.1 (8.1)	0.89 (0.21)
	LZ	91.5 (7.5)	1.83 (0.16)	89.4 (9.5)	1.81 (0.18)
	ACWL-C1	93.7 (4.1)	1.87 (0.10)	89.1 (5.3)	1.80 (0.11)
	ACWL-C2	94.7 (3.3)	1.89 (0.09)	87.8 (5.5)	1.79 (0.11)
	T-RL	97.2 (3.3)	1.95 (0.08)	95.1 (5.6)	1.92 (0.11)
	T-RL-LH	97.5 (3.1)	1.96 (0.08)	96.1 (4.0)	1.94 (0.08)
Incorrect	OWL	33.5 (6.0)	0.67 (0.13)	36.7 (5.7)	0.64 (0.19)
	LZ	87.8 (12.0)	1.75 (0.25)	81.8 (14.7)	1.68 (0.27)
	ACWL-C1	92.1 (4.7)	1.84 (0.10)	87.9 (5.6)	1.79 (0.11)
	ACWL-C2	94.7 (3.4)	1.89 (0.09)	86.5 (6.1)	1.78 (0.12)
	T-RL	97.8 (1.8)	1.94 (0.06)	92.9 (7.2)	1.89 (0.13)
	T-RL-LH	98.2(1.6)	1.95 (0.06)	93.7 (6.2)	1.91 (0.10)

RG, linear regression; RF, random forests; OWL, outcome weighted learning; LZ, method by Laber and Zhao (2015); ACWL-C₁ and ACWL-C₂, method by Tao and Wang (2017); T-RL, tree-based reinforcement learning; T-RL-LH, T-RL with one step lookahead.

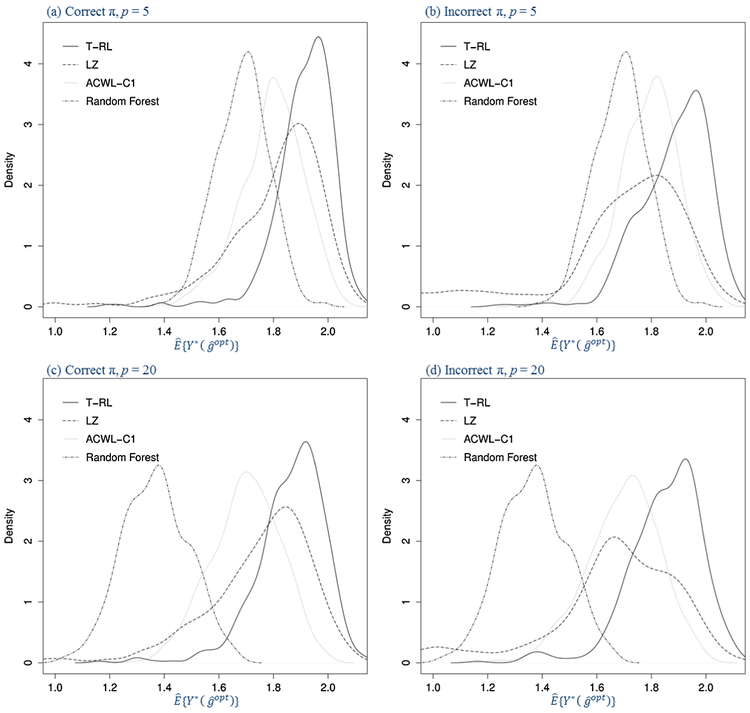
After the inclusion of more noise covariates in Table 2, all methods have worse performances compared to Table 1, with RF suffering the most. T-RL and T-RL-LH have the slightest decreases in opt% and $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$, showing satisfactory stability against noise interference. Thanks to the built-in variable selection feature of decision trees, LZ and ACWL with CART are also relatively stable. Figure 2 shows the density plots for $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$ under outcome model (b), with each panel showing correctly or incorrectly specified propensity model and five or 20 baseline covariates. LZ is the least efficient method with the density plots more spread out. T-RL has the least density in lower values of $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$ and the highest density in higher values.

Table 2.

Simulation results for Scenario 1 with a single stage, three treatment options and twenty baseline covariates (500 replications, n = 500). π is the propensity score model. (a) and (b) indicate equal and varying penalties for treatment misclassification in the generative outcome model. opt% shows the empirical mean and standard deviation (SD) of the percentage of subjects correctly classified to their optimal treatments. $\widehat{E}\{Y^{\ast }({\widehat{g}}^{\text{opt}})\}$ shows the empirical mean and SD of the expected counterfactual outcome obtained using the true outcome model and the estimated optimal regime.

E{Y*gopt)} = 2
π	Method	(a)		(b)
		opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathit{g}}}^{\mathbf{opt}})\}$	opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathit{g}}}^{\mathbf{opt}})\}$
–	RG	66.7 (2.8)	1.34 (0.08)	63.5 (3.4)	1.30 (0.09)
	RF	51.6 (5.7)	1.03 (0.13)	62.7 (5.8)	1.37 (0.12)
Correct	OWL	36.3 (4.2)	0.73 (0.10)	38.4 (5.4)	0.63 (0.17)
	LZ	88.6 (9.4)	1.77 (0.20)	85.5 (0.11)	1.74 (0.21)
	ACWL-C1	89.6 (5.0)	1.79 (0.11)	83.7 (6.0)	1.70 (0.13)
	ACWL-C2	90.7 (4.6)	1.82 (0.11)	82.5 (6.2)	1.70 (0.13)
	T-RL	96.3 (4.1)	1.93 (0.10)	91.9 (6.7)	1.86 (0.13)
	T-RL-LH	96.8 (3.9)	1.94 (0.09)	92.8 (5.4)	1.89 (0.10)
Incorrect	OWL	32.6 (4.0)	0.65 (0.10)	34.5 (4.3)	0.56 (0.15)
	LZ	85.9 (12.6)	1.72 (0.26)	78.4(15.4)	1.62 (0.30)
	ACWL-C1	87.8 (5.5)	1.76 (0.12)	82.6 (6.3)	1.70 (0.13)
	ACWL-C2	90.8 (4.3)	1.82 (0.10)	81.7 (6.3)	1.70 (0.13)
	T-RL	97.4 (2.4)	1.95 (0.07)	90.7 (7.7)	1.85 (0.14)
	T-RL-LH	97.9 (2.0)	1.96 (0.07)	92.0 (6.5)	1.87 (0.11)

RG, linear regression; RF, random forests; OWL, outcome weighted learning; LZ, method b Laber and Zhao (2015); ACWL-C₁ and ACWL-C₂, method by Tao and Wang (2017); T-RL, tree-based reinforcement learning; T-RL-LH, T-RL with one step lookahead.

Fig. 2.

Density plots for the estimated counterfactual mean outcome in Scenario 1 with varying penalties for misclassification in the generative outcome model (500 replications, n = 500). The four panels are under correctly or incorrectly specified propensity model (π) and five or twenty baseline covariates (p).

3.2. Scenario 2:

T = 2 and K₁ = K₂ = 3. In Scenario 2, we generate data under a two-stage DTR with three treatment options at each stage and consider sample sizes of 500 and 1000. The outcome of interest is the sum of the rewards from each stage, that is, Y = R₁ + R₂. Furthermore, we consider both a tree-type underlying optimal DTR and a non-tree-type one.

Treatment variables are set to take values in {0, 1, 2} at each stage. For stage 1, we generate A₁ from the same model as A in Scenario 1, and generate stage 1 reward as

$$R_1=\text{exp}[1.5+0.3X_4-\mid 1.5X_1-2\mid {\{A_1-g_1^{\text{opt}}({\mathbf{H}}_1)\}}^2]+{\epsilon }_1,$$

with tree-type $g_1^{\text{opt}}({\mathbf{H}}_1)=I(X_1>-1)\{I(X_2>-0.5)+I(X_2>0.5)\}$ or non-tree-type $g_1^{\text{opt}}({\mathbf{H}}_1)=I(X_1>-0.5)\{1+I(X_1+X_2>0)\}$, and £₁ ~ N(0, 1).

For stage 2, we have treatment A₂ ~ Multinomial(π₂₀, π₂₁, π₂₂), with π₂₀ = 1/{1 + exp(0.2R₁ – 0.5) + exp(0.5X₂)}, π₂₁ = exp(0.2R₁ – 0.5)/{1 + exp(0.2R₁ – 0.5) + exp(0.5X₂)} and π₂₂ = 1 – π₂₀ – π₂₁. We generate stage 2 reward as

$$R_2=\text{exp}[1.18+0.2X_2-\mid 1.5X_3+2\mid {\{A_2-g_2^{\text{opt}}({\mathbf{H}}_2)\}}^2]+{\epsilon }_2,$$

with tree-type $g_2^{\text{opt}}({\mathbf{H}}_2)=I(X_3>-1)\{I(R_1>0)+I(R_1>2)\}$ or non-tree-type $g_2^{\text{opt}}({\mathbf{H}}_2)=I(X_3>-0.5)\{1+I(X_3+R_1>2)\}$, and £₂ ~ N(0, 1).

We apply the proposed T-RL algorithm with the modified pseudo-outcomes. For comparison, we apply Q-learning which uses the conditional mean models directly to infer the optimal regimes. We apply both the linear regression-based and random forests-based conditional mean models, denoted as Q-RG and Q-RF, respectively. We also apply the backward OWL (BOWL) method by Zhao et al. (2015) and the ACWL algorithm, both of which are implemented using the R package rpart for classification. In this scenario, we attempt to see how sample size and tree- or non-tree-type underlying DTRs affect the performances of various methods.

Results for Scenario 2 are shown in Table 3. ACWL and T-RL both work much better than Q-RG and BOWL in all settings. Q-RF is a competitive method only when the true optimal DTR is of a tree type, but it is consistently inferior to T-RL, likely due to its weakness in emphasizing prediction accuracy of the clinical response model instead of directly optimizing the decision rule. Given a tree-type underlying DTR, T-RL has the best performance among all methods considered, regardless of the specification of the propensity score model. It has average opt% over 90% and $\widehat{E}\{Y^{\ast }({\widehat{\mathbf{g}}}^{\text{opt}})\}$ closest to the truth 8. The results are a bit more complex when the underlying DTR is non-tree-type. The tree-based methods of ACWL with CART and T-RL both have misspecified DTR structures and thus show less satisfactory performances. However, ACWL seems more robust to the DTR misspecification with ACWL-C₂ showing larger opt% and $\widehat{E}\{Y^{\ast }({\widehat{\mathbf{g}}}^{\text{opt}})\}$ in all settings except when sample size is 500 and π is misspecified, in which case T-RL’s stronger robustness to propensity score misspecification dominates. With non-rectangular boundaries in a non-tree-type DTR, a split may not improve the counterfactual mean estimates at the current node but may achieve such a goal in the future nodes. T-RL, with a purity measure based on E{Y*(g)}, will terminate the splitting as soon as the best split of the current node fails to improve the counterfactual mean outcome. In contrast, the misclassification error-based impurity measure in CART may continue the recursive partitioning as the best split may still reduce misclassification error without improving the counterfactual mean outcome at the current node. In other words, T-RL may be more myopic when it comes to non-tree-type DTRs.

Table 3.

Simulation results for Scenario 2 with two stages and three treatment options at each stage (500 replications). π is the propensity score model. opt% shows the empirical mean and standard deviation (SD) of the percentage of subjects correctly classified to their optimal treatments. $\widehat{E}\{Y^{\ast }({\widehat{\mathbf{g}}}^{\text{opt}})\}$ shows the empirical mean and SD of the expected counterfactual outcome obtained using the true outcome model and the estimated optimal DTR.

E{Y*gopt)} = 8
π	Method	Tree-type DTR				Non-tree-type DTR
		n= 500		n= 1000		n= 500		n= 1000
		opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathbf{g}}}^{\mathbf{opt}})\}$	opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathbf{g}}}^{\mathbf{opt}})\}$	opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathbf{g}}}^{\mathbf{opt}})\}$	opt%	$\widehat{\mathit{E}}\{{\mathit{Y}}^{\ast }({\widehat{\mathbf{g}}}^{\mathbf{opt}})\}$
-	Q-RG	54.9 (3.0)	6.24 (0.16)	57.3 (2.5)	6.35 (0.13)	69.2 (4.4)	6.87 (0.17)	72.6 (3.5)	7.01 (0.13)
	Q-RF	84.0 (4.1)	7.53 (0.14)	92.1 (2.5)	7.80 (0.10)	74.4 (2.8)	7.11 (0.14)	77.5 (1.8)	7.25 (0.09)
Correct	BOWL	22.4 (5.1)	4.23 (0.38)	27.9 (5.7)	4.45 (0.43)	25.3 (6.0)	4.53 (0.42)	34.8 (7.0)	4.98 (0.47)
	ACWL-C1	83.6 (5.9)	7.58 (0.18)	92.1 (4.4)	7.82 (0.11)	80.1 (6.1)	7.40 (0.18)	88.3 (3.4)	7.65 (0.11)
	ACWL-C2	81.3 (6.6)	7.53 (0.20)	89.1 (5.7)	7.80 (0.12)	83.3 (5.5)	7.51 (0.16)	89.2 (3.0)	7.68 (0.11)
	T-RL	90.5 (7.0)	7.75 (0.22)	95.7 (3.6)	7.88 (0.11)	82.2 (4.6)	7.45 (0.14)	84.7 (2.9)	7.54 (0.11)
Incorrect	BOWL	16.4 (4.3)	4.20 (0.30)	16.5 (4.9)	4.29 (0.32)	16.3 (4.9)	4.29 (0.34)	17.9 (6.0)	4.56 (0.37)
	ACWL-C1	80.9 (5.9)	7.55 (0.18)	89.1 (4.9)	7.80 (0.11)	73.4 (6.7)	7.30 (0.20)	81.0 (6.3)	7.56 (0.14)
	ACWL-C2	80.4 (6.7)	7.54 (0.19)	86.4 (6.2)	7.76 (0.13)	79.8 (5.9)	7.46 (0.17)	86.3 (4.2)	7.66 (0.11)
	T-RL	90.2 (7.4)	7.74 (0.17)	93.9 (6.0)	7.87 (0.11)	82.2 (6.3)	7.47 (0.15)	84.8 (3.8)	7.55 (0.11)

Q-RG, Q-learning with linear regression; Q-RF, Q-learning with random forests; BOWL, backward outcome weighted learning; ACWL-C₁ and ACWL-C₂, method by Tao and Wang (2017); T-RL, tree-based reinforcement learning.

Additional simulation results can be found in the Supplementary Material A [Tao, Wang and Almirall (2018a)], which leads to similar conclusions for these methods in comparison. In addition, the comparison of T-RL and the list-based method by Zhang et al. (2015) shows slightly better performance for T-RL given no cost information for measuring covariates. To implement the proposed method and the competing methods, the R codes and sample data can be found in the Supplementary Material B [Tao, Wang and Almirall (2018b)].

4. Application to substance abuse disorder data.

We apply T-RL to the data of an observational study, where 2870 adolescents entered community-based substance abuse treatment programs, which are pooled from several adolescent treatment studies funded by the Center for Substance Abuse Treatment (CSAT) of the Substance Abuse and Mental Health Services Administration (SAMHSA). The measurements on individual characteristics and functioning are collected at baseline and at the end of three and six months. We use subscript values t = 0, 1, 2 to denote baseline, month three, and month six respectively.

Substance abuse treatments were given twice, first during months zero ~ three, denoted as A₁ and second during months three ~ six, denoted as A₂. At each stage, subjects were provided with one of the three options: no treatment, non-residential treatment (outpatient only) and residential treatment (i.e., inpatient rehab) [Marlatt and Donovan (2005)], which we denote as 0, 1 and 2, respectively. At stage 1, 93% of the subjects received treatment, either residential (56%), or nonresidential (27%), while at stage 2, only 28% and 13% were treated residentially or non-residentially. We denote the baseline covariate vector for predicting the assignment of A₁ as X₁ and the covariate history just before assigning A₂ as X₁ (X₁ includes X₀). The detailed list of variables used can be found in Almirall et al. (2012). The outcome of interest is the Substance Frequency Scale (SFS) collected during six ~ nine months (mean and SD: 0.09 and 0.13), with higher values indicating increased frequency of substance use in terms of days used, days staying high most of the day, and days causing problems. We take Y = −1 × SFS so that higher values are more desired, making it consistent with our foregoing notation and method derivation. Missing data is imputed using IVEware [Raghunathan, Solenberger and Van Hoewyk (2002)].

We apply the T-RL algorithm to the data described above. Specifically, the covariate and treatment history just prior to stage 2 treatment is ${\mathbf{H}}_2={({\mathbf{X}}_1^{\top },A_1)}^{\top }$ and the number of treatment options at stage 2 is K₂ = 3. We fit a linear regression model for μ_2,A2 (H₂) similar to (2.4) using Y as the outcome; all variables in H₂ are included as interaction terms with A₂. For the propensity score π_2,A2 (H₂), we fit a multinomial logistic regression model including main effects of all variables in H₂. We set the minimal node size to be 50 and maximum tree depth to be 5, and use a 10-fold CV to select λ, the minimum purity improvement for splitting. We repeat a similar procedure for stage 1 except that we have H₁ = X₀, K₁ = 3 and ${\widehat{\mathit{PO}}}_1^{\prime }=Y+{\widehat{\mu }}_{2,{\widehat{g}}_2^{\text{opt}}}({\mathbf{H}}_2)-{\widehat{\mu }}_{2,A_2}({\mathbf{H}}_2)$.

At stage 2, the variables in the estimated optimal regime are yearly substance dependence scale measured at the end of month three [sdsy3, median (range): 3 (0 – 7)], age [median (range): 16 (12 – 25) years], and yearly substance problem scale measured at baseline [spsy0, median (range): 8 (0 – 16)]. At stage 1, the variables in the estimated optimal regime are emotional problem scale measured at baseline [eps7p0, median (range): 0.22 (0 – 1)], drug crime scale measured at baseline [dcs0, median (range): 0 (0 – 5)], and environmental risk scale measured at baseline [ers0, median (range): 35 (0 – 77)]. All these scale variables have higher values indicating more risk or problems. Specifically, the estimated optimal DTR is ${\widehat{\mathbf{g}}}^{\text{opt}}=({\widehat{g}}_1^{\text{opt}},{\widehat{g}}_2^{\text{opt}})$, with

$${\widehat{g}}_1^{\text{opt}}({\mathbf{H}}_1)=\{\begin{array}{cc}\text{no treatment}\hfill & \text{if eps7p0}\le 0.286\&\text{ers}0\le 46,\hfill \\ \text{non-residential}\hfill & \text{if eps7p0}\ge 0.286\&\text{dcs}0\le 2,\hfill \\ \text{residential}\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$

and

$${\widehat{g}}_2^{\text{opt}}({\mathbf{H}}_2)=\{\begin{array}{c}\text{residential}\hfill \\ \text{if sdsy}3>0,\text{or sdsy}3=0\&\text{age}\le 16\&\text{spsy}0>5,\hfill \\ \text{non-residential}\hfill \\ \text{otherwise}.\hfill \end{array}\phantom{\}}$$

According to the estimated optimal DTR, at stage 1, subjects with fewer emotional problems and lower environmental risk do not need to be treated, while those with more emotional problems but lower drug crime scale should be offered outpatient treatment only. At stage 2, all subjects should be treated. Those with higher yearly substance dependence as well as those with no yearly substance dependence but younger age and more yearly substance problems should receive residential treatment, that is, receiving treatment in rehab facilities. In contrast, subjects with older age or fewer yearly substance problems should be provided with outpatient treatment. The majority of subjects at both stages would benefit most from residential treatment. In our data, about 70% of the subjects at stage 1 have the estimated optimal treatment to be residential treatment and the number goes up to 85% at stage 2. Residential treatment is generally more intensive and subjects are in a safe and structured environment, which may explain why subjects with more substance, emotional or environmental problems would benefit more from this type of treatment. Existing studies have found a moderate level of evidence for the effectiveness of residential treatment for substance use disorders [Reif et al. (2014)]. Generally, outpatient programs allow subjects to return to their own environments during treatment. Subjects are encouraged to develop a strong support network of non-using peers and sponsors, and are expected to apply the lessons learned from outpatient treatment programs to their daily experiences [Gifford (2015)]. Nonetheless, subjects may respond sub-optimally to outpatient treatment (relative to residential treatment) if they have a larger network of peers that are using or at risk of using substances. Therefore, it may not be surprising that subjects with a lower environmental risk scale would benefit more from outpatient treatment.

5. Discussion.

We have developed T-RL to identify optimal DTRs in a multistage multi-treatment setting, through a sequence of unsupervised decision trees with backward induction. T-RL enjoys the advantages of typical tree-based methods as being straightforward to understand and interpret, and capable of handling various types of data without distributional assumptions. T-RL can also handle multinomial or ordinal treatments by incorporating multiple treatment comparisons directly in the purity measure for node splitting, and thus works better than ACWL when the underlying optimal DTR is tree-type. Moreover, T-RL maintains the robust and efficient property of ACWL by virtue of the combination of robust semiparametric regression estimators with flexible machine learning methods, which is superior to IPW-based methods such as LZ. However, when the true optimal DTR is non-tree-type, ACWL has slightly more robust performances.

Several improvements and extensions can be explored in future studies. As shown by the simulation, the fixed-depth lookahead is costly and only brings moderate improvement. Alternatively, one can use embedded models to select splitting variables which also enjoys the lookahead feature [Zhu, Zeng and Kosorok (2015)], or consider other variants of lookahead methods [Elomaa and Malinen (2003), Esmeir and Markovitch (2004)]. The method by Zhu, Zeng and Kosorok (2015) enables progressively muting noise variables as one goes further down a tree, which facilitates the modeling in high-dimensional sparse settings, and it also incorporates linear combination splitting rules, which may improve the identification of non-tree-type optimal DTRs. Furthermore, it is of great importance to explore how to handle continuous treatment options in the proposed T-RL framework. One way is to follow LZ to use a kernel smoother in the purity measure, which may suffer from the difficulty in selecting the optimal bandwidth. A simpler approach is to discretize the continuous treatments by certain quantiles and consider it as ordinal treatments, which may improve estimation stability and is also of practical interest as medical practitioners tend to prescribe treatments by several fixed levels instead of a continuous fashion.