Cyclical environments drive variation in life-history strategies: a general theory of cyclical phenology

Abstract

Cycles, such as seasons or tides, characterize many systems in nature. Overwhelming evidence shows that climate change-driven alterations to environmental cycles—such as longer seasons—are associated with phenological shifts around the world, suggesting a deep link between environmental cycles and life cycles. However, general mechanisms of life-history evolution in cyclical environments are still not well understood. Here, I build a demographic framework and ask how life-history strategies optimize fitness when the environment perturbs a structured population cyclically and how strategies should change as cyclicality changes. I show that cycle periodicity alters optimality predictions of classic life-history theory because repeated cycles have rippling selective consequences over time and generations. Notably, fitness landscapes that relate environmental cyclicality and life-history optimality vary dramatically depending on which trade-offs govern a given species. The model tuned with known life-history trade-offs in a marine intertidal copepod Tigriopus californicus successfully predicted the shape of life-history variation across natural populations spanning a gradient of tidal periodicities. This framework shows how environmental cycles can drive life-history variation—without complex assumptions of individual responses to cues such as temperature—thus expanding the range of life-history diversity explained by theory and providing a basis for adaptive phenology.

1. Introduction

Natural populations in all systems must survive environmental fluctuations. Biologists have long known that a particularly common and powerful mode of fluctuations in nature is cyclical, such as seasons. Species around the planet exhibit predictable and sensitive life-history transitions that are tightly associated with seasonal cycles, also referred to as phenology. Environmental cycles in fact occur beyond just the timescale of seasons, such as daily, tidal, lunar, flood, fire, and decadal oscillations, and life histories of species are also often associated with cycles at these timescales [1–6]. Despite the ubiquity of cycles in nature, and clear empirical evidence of the importance of cycles for life histories, we lack a general theory of how life-history evolution is shaped by cycles.

Over the last few decades, perturbations to environmental cycles owing to climate change have driven dramatic life-history changes such as phenological timing in many species [7–15]. In fact, phenological shifts are widely regarded as the most conspicuous and rapid consequence of climate change across marine, freshwater, and terrestrial systems [14]. Notably, different species' phenologies are shifting in different directions, creating phenological mismatches with profound consequences on ecosystem function and health [7,11,16–19]. Disparate case studies of shifts that typically invoke individual-level responses to environmental cues such as temperature may be limited in their potential to explain general evolutionary forces owing to system-specific idiosyncrasies. On the trailing edge of rapidly accumulating empirical evidence of shifts, questions regarding general mechanisms of life-history evolution in cyclical environments have emerged to the forefront of theoretical population biology, biodiversity, and climate change science [20–22].

A first step in understanding the mechanics of life-history evolution in cyclical environments may be to conceptualize cycles as sequential arrivals of harsh conditions whose periodicity is not reciprocally affected by local ecological dynamics. An example is the arrival of winter in seasonal systems. A typical consequence of such cyclical events for a population is heightened mortality as well as some perturbation to population structure (e.g. seedling mortality in plants [23]). This consequence not only reduces population size at a given time but also impacts the long-term trajectory and fitness of the population [24,25]. It follows that, if periodic disturbance is an inherent feature of a habitat, fitness is determined by how well a resident population survives repeated demographic perturbations at regular intervals.

Population ecologists have long been interested in demographic dynamics in variable environments, including cyclically variable environments [22,26–31]. Life-history theorists, on the other hand, have classically focused on how time-invariant (i.e. constant) perturbations on age-, size-, or stage-classes of populations, mediated by trade-offs between biological processes, shape life-history strategies broadly [32–36]. For example, theory predicts that heightened juvenile mortality should induce the evolution of reduced reproductive effort. Such predictions have been widely tested empirically, and their effects are often strong, rapid, and heritable [37–42]. So far, modern models of life-history evolution that do incorporate time-variance in the environment have mainly focused on how optimality predictions are altered by stochasticity (i.e. randomly variable environments), which yield convenient analytical probabilistic conclusions [22,31,43–45]. What is not well understood is how life histories are generally shaped by non-random cycles, despite biological attention to fundamentally cyclical environments such as seasonal systems [22], and the fact that parametric changes to cycles such as season length are repeatedly associated with life-history changes across systems.

Here, I explore the general relationship between periodicity of cycles and evolutionarily optimal life-history strategy. Proximate triggers of phenological expression, such as plastic response to temperature cues, mechanistically vary widely across species and habitats [20]. By taking a demographic life-history theory approach agnostic to system-specific plastic responses, I address the ultimate selective force behind phenological traits and their shifts, given that phenology is fundamentally a study of how life-cycle transitions fit into environmental cycles.

I hypothesize that rates of life-cycle transitions, relative to the periodicity with which environmental cycles incur predictable population perturbations, influence fitness. I test this prediction by calculating which life-history strategy in a population confers maximum fitness in a given periodic regime, and then studying how that optimal life-history changes with changes in periodicity. Further, I hypothesize that fitness, and thus optimal life-history strategies, will be influenced by trade-offs underlying these life-cycle transitions. Thus, I explore how various trade-offs impact the relationship between periodicity and optimality to understand how different species in nature—whose life histories are in reality shaped by different sets of trade-offs—might be differentially affected by the same change in periodic regime.

Next, I test my theoretical predictions in the copepod Tigriopus californicus (Copepoda: Harpacticoida), a crustacean found in rock pools in the supralittoral (upper tidal) zone along the North American Pacific coast. Populations are disturbed periodically by wave-wash at high tide and experience a population decline and heightened juvenile mortality periodically. Periodicity of disturbance varies among populations depending on regional tidal patterns and pool height on the shore. Tigriopus californicus provides an ideal system to study life-history variation in cyclical systems across populations owing to its short generation time and short disturbance cycles, the rare opportunity to sample from homogenized whole populations, and the ease of quick sampling and trait measurements yielding large amounts of within- and across-population data. Across 19 natural populations of T. californicus in two regions of northern Washington I ask: do disturbance cycle periodicity and known trade-offs together predict life-history variation across populations?

2. Material and methods

(a). Model construction

To uncover general predictions of evolutionarily optimal life-history traits in cyclical environments, untied to species-specific idiosyncrasies such as plastic responses to meteorological cues, I describe a hypothetical population in two linked stages of broad applicability: juveniles and reproducing adults. I consider continuous-time demographic dynamics of the stage-structured population and impose stage-specific mortalities at given periodicities (full model description in electronic supplementary material, §S1).

First, I express constant-environment dynamics as a system of ordinary differential equations:

$$\left.\begin{array}{rl}\frac{\mathrm{d}J}{\mathrm{d}t}=& -(\mu +d)J+fA,\\ \mathrm{and}\frac{\mathrm{d}A}{\mathrm{d}t}=& \mu J-\gamma A,\end{array}\right\}$$ 2.1

which can be expressed as matrix M:

$$\mathbf{M}=\left[\begin{array}{cc}-(\mu +d)& f\\ \mu & -\gamma \end{array}\right],$$ 2.2

where J is juveniles, A is adults, μ is the rate at which juveniles mature into reproducing adults, d is background mortality of juveniles, f is the reproductive rate of adults, and γ is background mortality of adults. Then, via eigendecomposition of M, I express the solution at time t as:

$$\left.\begin{array}{rl}J(t)=\hspace{0.17em}& \frac{A(0)v_{(2)1}-J(0)v_{(2)2}}{v_{(2)1}{v}_{(1)2}-\hspace{0.17em}{v}_{(2)2}{v}_{(1)1}}{v}_{(1)1}{e}^{{\lambda }_{1}t}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}\frac{J(0)v_{(1)2}-A(0)v_{(1)1}}{v_{(2)1}{v}_{(1)2}-\hspace{0.17em}{v}_{(2)2}{v}_{(1)1}}{v}_{(2)1}{e}^{{\lambda }_{2}t},\\ \mathrm{and}A(t)=& \hspace{0.17em}\frac{A(0)v_{(2)1}-J(0)v_{(2)2}}{v_{(2)1}{v}_{(1)2}-\hspace{0.17em}{v}_{(2)2}{v}_{(1)1}}{v}_{(1)2}{e}^{{\lambda }_{1}t}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}\frac{J(0)v_{(1)2}-A(0)v_{(1)1}}{v_{(2)1}{v}_{(1)2}-\hspace{0.17em}{v}_{(2)2}{v}_{(1)1}}{v}_{(2)2}{e}^{{\lambda }_{2}t},\end{array}\right\}$$ 2.3

where $v_{(i)j}$ is the jth element of the ith eigenvector corresponding to eigenvalue ${\lambda }_i$ of M. This solution describes simple structured population dynamics in an undisturbed environment, but by eigendecomposing the system I isolate the time parameter t, which will eventually allow me to study demographic dynamics as a direct function of period length between disturbances. To make the solutions explicit with respect to disturbance cycle period T, I let t = T, and at time T, multiply the structure by S_J and S_A to impose juvenile- and adult-specific mortality associated with disturbance. The combined system can be expressed as the matrix P: (electronic supplementary material, equation (S10))

$$\begin{array}{r}\mathbf{P}=\left[\begin{array}{c}{\mathit{S}}_{\mathit{J}}\frac{[({\mathit{v}}_{(1)2}{\mathit{e}}^{{\mathit{\lambda }}_2\mathit{T}}{\mathit{v}}_{(1)2}-{\mathit{v}}_{(1)1}{\mathit{e}}^{{\mathit{\lambda }}_1\mathit{T}}{\mathit{v}}_{(2)2})]}{{\mathit{v}}_{(2)1}{\mathit{v}}_{(1)2}\hspace{0.17em}-\hspace{0.17em}{\mathit{v}}_{(2)2}{\mathit{v}}_{(1)1}}\hspace{0.17em}\hspace{0.17em}{\mathit{S}}_{\mathit{J}}\frac{[({\mathit{v}}_{(1)1}{\mathit{e}}^{{\mathit{\lambda }}_1\mathit{T}}{\mathit{v}}_{(2)1}\hspace{0.17em}-\hspace{0.17em}{\mathit{v}}_{(1)2}{\mathit{e}}^{{\mathit{\lambda }}_2\mathit{T}}{\mathit{v}}_{(1)1})]}{{\mathit{v}}_{(2)1}{\mathit{v}}_{(1)2}\hspace{0.17em}-\hspace{0.17em}{\mathit{v}}_{(2)2}{\mathit{v}}_{(1)1}}\\ {\mathit{S}}_{\mathit{A}}\frac{[({\mathit{v}}_{(2)2}{\mathit{e}}^{{\mathit{\lambda }}_2\mathit{T}}{\mathit{v}}_{(1)2}\hspace{0.17em}-\hspace{0.17em}{\mathit{v}}_{(1)2}{\mathit{e}}^{{\mathit{\lambda }}_1\mathit{T}}{\mathit{v}}_{(2)2})]}{{\mathit{v}}_{(2)1}{\mathit{v}}_{(1)2}-{\mathit{v}}_{(2)2}{\mathit{v}}_{(1)1}}\hspace{0.17em}{\mathit{S}}_{\mathit{A}}\frac{[({\mathit{v}}_{(1)2}{\mathit{e}}^{{\mathit{\lambda }}_1\mathit{T}}{\mathit{v}}_{(2)1}-{\mathit{v}}_{(2)2}{\mathit{e}}^{{\mathit{\lambda }}_2\mathit{T}}{\mathit{v}}_{(1)1})]}{{\mathit{v}}_{(2)1}{\mathit{v}}_{(1)2}\hspace{0.17em}-\hspace{0.17em}{\mathit{v}}_{(2)2}{\mathit{v}}_{(1)1}}\end{array}\right].\end{array}$$ 2.4

Matrix-multiplying initial abundances by P would thus give stage structure after existing in a constant environment for time T and experiencing a disturbance event that incurs stage-specific mortalities. More interestingly, I use this framework to ask: what are the consequences of different combinations of life-history traits on the fitness of a population given that it resides in disturbance regime T?

(b). Fitness

Given the general framework of cyclically perturbed stage-structured population dynamics, I ask how the predicted fitness of the population is influenced by the periodicity of environmental cycles. The dominant eigenvalue (λ) of a population transition matrix is a widely used measure of relative fitness because it represents how well the population will perform in the long run compared to other hypothetical populations with different life-history strategies [25,36]. This metric, related to ‘r' in demography and life-history theory, does not capture consequences of short-term transient dynamics [46,47] but has been useful for drawing broad life-history evolution predictions and conceptualizing relative fitness that match well with empirical observations [24,25,36]. In stochastic environments, fluctuations in instantaneous growth rates may lead λ to give inaccurate evolutionary predictions. In systems that can be modelled by periodic switching between environments, however, eigenvalues and eigenvectors of the matrix that is the product of constituent matrices describing the different environmental states can be used for demographic and life-history analyses in exactly the same way as they are used in time-invariant theory [25,48]. My matrix P is equivalent to periodic models since the system switches between an undisturbed phase and disturbance, and the switching periodicity and population matrix elements do not fluctuate randomly (see electronic supplementary material, figure S1 for simulation results). Thus, here I use the dominant eigenvalue of P (hereafter referred to as λ_P) as the measure of relative fitness to compare the theoretical performance of life-history strategies in a periodically time-variant framework and characterize general selective pressures on life-history strategies as a function of cycle periodicity.

(c). Life-history trade-offs

Life-history evolution is a matter of optimization because limited resources must be allocated into various biological processes such as survival and reproduction involving trade-offs [36,49]. The exact shapes of trade-off functions in organisms are famously difficult to measure, let alone justify in model assumptions [49,50]. Here, I take a conservative approach and assume simple linear trade-offs to investigate general patterns in optimality as a function of the environment without making more complex physiological assumptions. To express a trade-off between any two traits in the construction of a fitness landscape, I computationally set the vector of the range of values of one trait in decreasing order as the other increases, imposing a negative slope between the two traits. When two traits do not trade off, one of the traits remains at the mean of its range as the other varies through its own range. I varied the combinatory inclusions of trade-offs among the four key parameters (μ, maturation rate; f, reproduction rate; d, background juvenile survival, and γ, background adult survival) to create model variants and investigate their relative fit to the data.

(d). Fitness landscapes and optimal life-history strategies

All realizations of P—and thus the construction of fitness landscapes—must be constrained within the space of the interacting life-history parameters, μ, d, f, and γ. Here, I constrained the space with known T. californicus life-history ranges and trade-offs to demonstrate one example of the usage of this framework, but constraints can be set flexibly to represent any given species (see electronic supplementary material, §2.5 for descriptions and citations for parametrization).

Using λ_P, I construct fitness landscapes for μ and f simultaneously for each model. Here, I focus on μ and f because they are life-history traits for which I can collect large amounts of paired data in T. californicus, but it should be noted that fitness landscapes can be created for any life-history trait in the original system of differential equations. For each landscape, I scan across the range of μ or f for a given value of T, while varying all other traits according to trade-off relationships included in the given model. Therefore, I construct a vertical gradient of relative λ_P per T. To construct a landscape, I calculate gradients of relative λ_P across the horizontal axis of T. The optimal trait per T is the trait that maximizes λ_P per T. Finally, to get the curve of optimal trait values across the axis of T, I track values associated with maximum λ_P across T.

(e). Empirical investigation in Tigriopus californicus

Tigriopus californicus is a copepod found widely along the North American Pacific coast (see electronic supplementary material, §2.1 for a detailed description of natural history). Dense populations reside in rock pools above the intertidal zone at varying heights [51–53], which accordingly experience tide cycle disturbance at varying periodicities. When tide levels cyclically reach pool heights and waves wash through pools, T. californicus cling onto the rocky benthos in order to prevent being flushed down to open water or to the lower intertidal zone [53]. If they are washed down, predators that do not occur in T. californicus pools feed on them quickly and re-colonization of T. californicus into the pools appear to be low [53,54]. Despite clinging, tidal disturbance was shown to always decrease population size and, in particular, incur heightened juvenile mortality (electronic supplementary material, figure S4).

I sampled 19 isolated populations across two sites in northern Washington, USA (Neah Bay and Friday Harbor) in order to capture a wide gradient of disturbance periodicities (see electronic supplementary material, §§2.2–2.4 for a detailed description of data collection). I quantified the periodicity of tidal disturbance in each pool via time-series analysis of pool temperature data over four months at 5 min intervals, taking abnormal drops in temperature as signals of wave flush (see electronic supplementary material, §2.2). I siphoned entire isolated populations out of rock pools, and subsampled individuals after homogenizing them, to get representative population samples. I reared 30 mating pairs captured from each population in common garden settings. In these lines, I measured rate of maturity (μ in the model) and rate of reproduction (f in the model) (see electronic supplementary material, §2.4 for a detailed description of trait measurements).

(f). Likelihood and model fitting

I calculated the log-likelihoods of the optimality curves of the two focal life-history traits μ and f produced by each model variant given the variance and covariance of the μ and f data. Each model is a different trade-off model (electronic supplementary material, figure S2 and table S2). Every model has the same number of estimated parameters because they only differ in how the parameters trade off in the construction of the fitness landscapes, which is included computationally by aligning parameter range sequences in reverse order. Therefore, model selection criteria that penalize number of parameters such as Akaike Information Criterion (AIC) were not used. Each model produces optimality curves (dominant eigenvalue of matrix P across the gradient of disturbance period T) of μ and f given trade-off relationships. I searched for the maximum log-likelihood of each model given μ and f data simultaneously within the space of S_A ≥ S_J and compared maximum log-likelihoods of the 13 model variants.

3. Results

(a). Cycle periodicity alters optimal life-history predictions

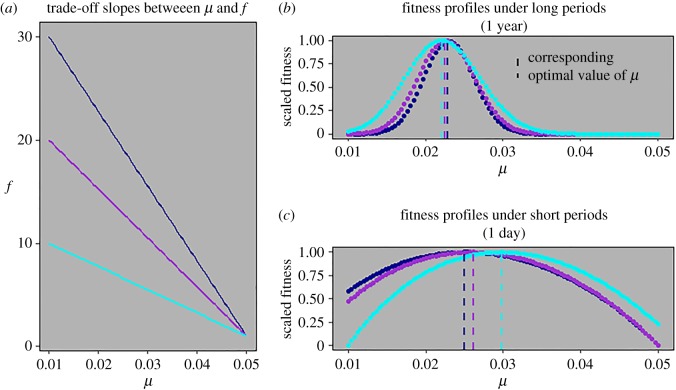
Classic life-history theory balances costs and benefits of key biological investments such as development, reproduction, and survival to predict fitness profiles of life-history traits [36,55,56]. Here, I incorporated these classic balance considerations but imposed cyclical perturbations to population structure and asked if the fitness predictions change as a function of environmental cycle periodicity. Using this framework, I analysed the role of cost (slope of trade-off, figure 1a) on the fitness profile of a life-history trait (maturation rate) in two scenarios: one in which period length is long enough (e.g. to fit more than 10 generations in a period) that the effect of discrete cycles on the evolution of life-history rates should be small (figure 1b), and another in which period length is at a similar timescale to generation time (figure 1c). The former approaches classic formulations of optimal life-history predictions based on trade-offs alone [55]. The latter shows that external periodic perturbations significantly change optimality predictions. In the latter scenario, all trade-off cost assumptions predict higher optimal values of maturation rate compared to the former. The shape of fitness profiles is also flatter in the latter scenario, which may suggest weaker selection or that larger variance of maturation rate can be maintained within a population under shorter disturbance cycles. Lastly, the relationship between trade-off cost and optimality is reversed between the two scenarios: the lowest cost case produces the lowest optimal maturation rate under long periods but the highest optimum under short periods and vice versa. These results show that the periodicity with which harsh environmental conditions arrive and affect survival modifies the expected reproductive value of individuals, and that periodicity significantly alters relative fitness of strategies with which individuals invest biological resources into life-history traits.

Figure 1.

Three hypothetical cost functions between μ—rate at which juveniles mature into reproducing adults—and f—adult fecundity—are analysed while setting linear trade-offs between μ and f, and between those two traits and their respective stage-specific background survival rates (d and γ). Stage-specific survival terms associated with cyclical disturbance are set at S_A = 0.9 and S_J = 0.6. Colours of cost functions in (a) correspond to colours of fitness profiles of μ in (b,c). Dashed lines in (b,c) show peaks of fitness profiles which correspond to optimal values of μ. Periodicity of cyclical perturbation to population structure is set to be much greater than generation time in (b) (T = 365) and at a relevant timescale (<generation time) in (c) (T = 1). Under short periods (c), all cost functions produce higher optimal μ values, wider fitness profiles, and an exactly reversed relationship between cost and optimality compared to long periods (b). (Online version in colour.)

(b). Periodicity and trade-offs interact to produce diverse life histories

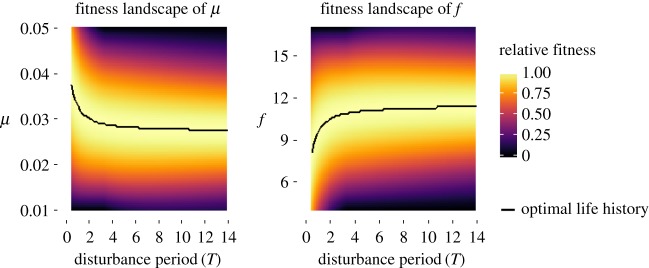
Optimal life history varies nonlinearly as a function of disturbance cycle period, even with assumptions of simple linear trade-offs between traits (figure 2). This nonlinearity implies that changes in the evolutionary optimum of a life-history trait can be of very different magnitudes even with the same magnitude change in periodicity, depending on the initial period length.

Figure 2.

Example fitness landscapes of two focal life-history traits, μ (rate of maturity) and f (reproductive rate), which assumes lower juvenile survival with each disturbance event (S_A = 0.9, S_J = 0.6), and trade-offs between μ and f, between μ and d, and between f and γ. Heat shows normalized fitness of a life-history strategy compared to all other strategies in a disturbance regime (T). Curves track the optimal (maximum fitness) life-history trait across T.

Shapes of optimality curves (optimal traits versus period) can vary dramatically depending on which life-history trade-offs are included (electronic supplementary material, figure S2). For example, when maturation trades off with background juvenile survival and fecundity (electronic supplementary material, figure S2G), optimal maturation rate is expected to decrease and optimal fecundity is expected to increase as period length increases; on the other hand, if maturation trades off with background adult survival and fecundity instead (electronic supplementary material, figure S2I), directions of expected trends in both optimal traits as period length changes are the opposite of the former case. Similarly, when maturation trades off with background adult survival, optimal maturation rate and fecundity are both expected to increase with period length (electronic supplementary material, figure S2C), but both are expected to decline with period length if background juvenile survival trades off with background adult survival (electronic supplementary material, figure S2E). Collectively, this broad range of cases examined demonstrates that the way in which external environmental cycles determine what combination of life-history traits is evolutionarily optimal depends heavily on how traits trade off with one another internally. In the next section, I show that the model that includes known trade-offs in T. californicus has the highest likelihood given T. californicus-specific life-history data; but it is important to note that no one model is necessarily better than another in a general sense because different species in nature will have different levels of complexity and rank order of trade-offs between life-history traits [49,55,57].

(c). Tigriopus trade-offs predict life-history variation across a periodicity gradient

Temperature time-series analyses confirmed that there is a broad range of disturbance cycle periodicities across T. californicus pools across the two regions (electronic supplementary material, §2.1; figure S4A, B, and table S1). These sampled pools provided a gradient of periodic regimes against which I tested optimal life-history predictions. Daily temperature regimes, which may contribute to life-history differences [58,59], were not significantly different among pools of varying periodicity regimes across the two regions (electronic supplementary material, figure S5). Disturbance always caused higher juvenile mortality than adult mortality in subsampled disturbance events, with mean juvenile mortality of 41% and mean adult mortality of 6% (electronic supplementary material, figure S4C).

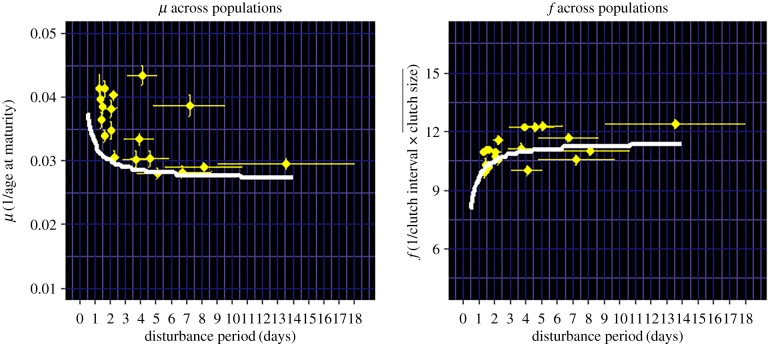
Life-history traits shift as disturbance period changes across T. californicus populations (figure 3), mirroring the shape predicted by the model (figure 2). The best model (likelihood maximizing when μ and f are fit simultaneously, represented by figure 2) was the one that assumed trade-offs between maturation rate and fecundity, between maturation and juvenile survival, and between fecundity and adult survival, consistent with known trade-offs in T. californicus (electronic supplementary material, §2.1). Raw data collected for μ and f per maternal line in my populations also support a general negative relationship between μ and f (electronic supplementary material, figure S6). Finally, model variants with double or tertiary trade-off assumptions generally fit better than ones with only single trade-offs (see electronic supplementary material, figure S2 and table S2 for the full list of models). These comparisons among model variants suggest that multidimensional trade-off relationships—which are typically avoided in empirical measurements or model assumptions of life-history evolution [49,50], but are gaining some attention [60,61]—may actually be important in predicting life-history optimization in cyclical environments because trade-off consequences change as a function of cycle period.

Figure 3.

Mean (±s.e.) values of the two focal life-history traits μ and f across 19 T. californicus populations, against mean (±s.e.) disturbance period determined by time-series analysis of wave disturbance signals in each pool. Curves are optimal life-history functions across periodicity (T) fit simultaneously to μ and f. (Online version in colour.)

4. Discussion

Ecologists have long assumed that environmental cycles are important for life cycle-related traits. But growing knowledge of phenological shifts has generated confusion regarding how environmental cycles shape life-history strategies and thus transition rates of life-cycle phases. A long-accepted tenet in life-history evolution theory is that the mean and variance of population structure perturbations shape life-history variation [24,34,35,39]. Results here show that the temporal nature of such perturbations, such as the period length of environmental cycles, should interact strongly with general life-history trade-off architectures in determining evolutionarily optimal traits. Understanding the interactive link between environmental cycles and life-history optimality may be facilitated by the concept of reproductive value. Reproductive value is the expected contribution of an individual at a particular age or stage to the population through current and future reproduction, determined by biological trade-offs and survival through time [36,62]. Reproductive value is a central evaluation for fitness and evolution because it represents the aggregate consequence of trade-offs among many important life-history traits [63]. Naturally, the realization of current and future reproduction must depend on current and future environmental conditions for survival experienced by individuals. Thus, it can be expected that, in predictably cyclical environments that periodically incur harsh conditions for survival, the period length of cycles will have a tractable influence on which life-history strategy should perform best in the long term. A version of the model tuned with known T. californicus trade-offs successfully predicted the shape of life-history variation across natural periodicity regimes, demonstrating the power of this interactive effect.

A fundamental question in ecology and evolution is why life histories are so diverse in nature. Divergent trends in phenological shifts among species in fact offer a current, global opportunity to study the production of life-history diversity. Here, I show that the interaction between environmental cycles and life-history trade-offs is a simple mechanism that can account for large variations in life histories. First, owing to the nonlinear relationships between cycle period and optimal traits, the same magnitude of period change can induce different magnitudes of life-history evolution between two populations of a species that are in different cyclical regimes (figure 2). Second, different trade-offs produce varying shapes of optimality curves (electronic supplementary material, figure S2), and thus the same change in period can induce an increase, decrease, or no change in a life-history trait for different species in the same system depending on what trade-offs are biologically important for those species. Environmental cycle periodicity is diverse across systems (such as growing season lengths across a latitudinal gradient), and trade-off architectures among populations and species vary widely owing to physiological constraints, environmental conditions, and reaction norms [49]. Combined, cycles and trade-offs can produce a wide array of predicted life-history strategies. Testing this mechanism in species that are controlled by different trade-offs, either across populations in different cyclical regimes or within a single population through time in a habitat undergoing a change in cycle periodicity—for instance, owing to climate change—will provide fruitful avenues for further exploring this perspective.

(a). Stochasticity, evolutionary stable strategy models, and gene flow

Cycles in nature, of course, are not perfectly periodic. The present study focuses on the consideration of period or interval length between autocorrelated events. The mechanistic influence of fundamentally cyclical environments on life-history evolution is noticeably understudied compared to probabilistic expectations in stochastic environments [22], even though regular cycles on various timescales are common in nature. Periodic models can be used to address a real aspect of nature that is difficult or impossible to address explicitly with stochastic models: cyclicality. Here, I take advantage of the fact that periodic models allow the use of matrix properties such as the dominant eigenvalue to infer relative fitness within a fluctuating system [25,48] and analyse conditions for optimization. By doing so, I uncover a novel mechanistic relationship between cyclicality and life-history evolution. However, cyclicality and stochasticity are both important aspects of nature. For instance, stochastic fluctuations in instantaneous population growth rate can significantly modify evolutionary trajectories predicted by time-invariant or periodic theoretical assumptions [46,47,64]. Studying the relative influences of periodicity and stochasticity on optimal strategy, and on how quickly a population evolves to its predicted optimal strategy, are the obvious next steps that will add more richness to the perspective offered here.

Optimality curves in my model framework represent variations in evolutionary stable strategies (ESSs) because I take the long-run growth rate of populations (dominant eigenvalue of P) as the measure of fitness as is commonly done in demography and life-history theory. ESS models are useful for the purpose of predicting general directions of selection over a long term. ESS models take a non-genetic perspective on broad selective forces, although a genetic justification for optimization of a quantitative trait is given by the fact that a mutation can invade the population if it confers a higher r on its carriers [24]. Optimization models and quantitative genetics models are approximately equal for constrained multivariate systems [65]. Nonetheless, results found here are inconclusive with respect to what a population's evolutionary trajectory from one optimum to another should look like in an environment undergoing change in cycle periodicity. Antagonistic selection on correlated traits imposed by different environmental variables associated with seasonal fluctuations, such as photoperiod and temperature, might cause deviations from ESS predictions. Evolutionary trajectories could be altered if bottlenecks are created by a sequence of disturbances and constrain the standing genetic variation subject to selection. In T. californicus, selection on optimal life histories may be obscured if high gene flow among nearby populations exists owing to wave transport. However, colonization rates and genetic exchange have been repeatedly observed to be low in this system [66–68] and demographic dynamics given high mortality rates caused by tidal disturbance likely overwhelm population genetic dynamics on the timescale of tide cycles. In this study, I deliberately chose populations that were deemed to be well isolated given field observations. But the level of gene flow may vary depending on locality owing to habitat characteristics and may contribute to some of the variance within populations and deviations of population means from ESS predictions. Nonetheless, my model fitting results suggest that ESS assumptions predict T. californicus life histories reasonably well given a population's periodic regime.

(b). Trade-off functions

Trade-offs between traits can be nonlinear, and multidimensional architectures of trade-offs can be extremely difficult to measure [49,57,50]. Here, I have taken the conservative approach of assuming linear trade-offs among modelled life-history variables, which biologically equate to strictly substitutable energetic currencies divvied between different traits, to focus on the demonstration that consequent optimality curves across periodicity are nonlinear and that a diverse set of optimality curves can be produced with different trade-offs. The simple linear assumption still performs well, at least with T. californicus life-history data from my sample populations. However, to test this framework further in different species, different functions can and should be used if the relationship between two traits is known to be nonlinear.

(c). Links to evolution of seasonal phenologies

In seasonal environments, cyclical arrival of harsh meteorological conditions (e.g. winter) can incur large demographic perturbations and thus strongly influence population dynamics [69,70]. Here, I show that if periodic arrivals of disturbance incur significant demographic perturbations, individuals and their lineages that have life-history strategies that are non-optimal in the context of their environment's cyclicality will have lower long-term fitness; thus, cyclical perturbations play an important role in driving the evolution of life-history transition rates.

One unresolved paradox in phenology is that various species in the same community (e.g. those in different trophic levels) undergoing the same change in abiotic seasonal cycles often exhibit phenological shifts of vastly different magnitudes or even in opposite directions. Here, my results suggest that an interaction between environmental cycles and general biological trade-off relationships among fitness-related traits might contribute to life history and phenological divergence.

Period is not the only parameter of cycles, however. Particularly for seasons, cycle amplitude may also shape phenologies in important ways and is shifting with climate change in many natural systems (e.g. seasonal CO₂ cycle amplitude [71,72]). Amplitude of seasonal cycles may play two roles for evolution. First, amplitude is associated with intensity of disturbance, which can be explored with survivorship functions in my theoretical framework. If the pattern of stage-specific mortality associated with cyclical disturbance is clear, such as in T. californicus and many seasonal species, then heightened intensity of cyclical disturbance will likely increase strength of selection. Second, amplitude reflects the rate of environmental change within cycle phases. Rate of change may be important for cue-detection and plastic responses. For example, many plants in seasonal environments are well known for tracking growing degree-days as a way of taking cues on the passing of the seasons [73]. In my theoretical framework, cyclical disturbances arrive without warning and simply incur repeated penalties on individuals and cohorts that had non-optimal life-history strategies for the given regime. In reality, there may be a number of continuously changing environmental variables in T. californicus pools such as salinity, and I cannot exclude the possibility that, like plants, birds, or many aquatic invertebrates, T. californicus possess biological mechanisms to use cues from continuously changing parameters to plastically alter their phenotypes. Nonetheless, I was able to predict variation in T. californicus life histories across a periodicity gradient in the environment without accounting for plasticity, suggesting that plastic responses might not have a strong effect on life-history evolution in response to cyclicality. Future phenological work should directly compare the relative roles of demographic influences such as those discussed here and plastic response to cues that can be tracked along continuous cycles.

When considering phenological evolution in cyclical environments, the relative scaling of life cycles and environmental cycles becomes important. For instance, a perennial species must endure multiple seasonal cycle periods per generation. An annual species' generation, on the other hand, fits within a single cycle period. In both cases, consequences of fitness-related phenotypes in one generation carry over to subsequent generations via intergenerational trade-offs in life histories [36], but the trajectory of evolution may differ between the two because of the number of cycle periods a generation experiences. Further, the model framework presented here assumes overlapping generations but many annual organisms have non-overlapping generations and synchronous phenologies. The evolutionary consequences of non-overlapping generations and synchronization in a population in cyclical environments should be explored further.

Phenology is the study of how life cycle schedules are fitted to environmental cycles. A phenological trait is a manifestation of the aggregate life-history strategy of a species [16] and expression timings of traits are ultimately controlled by transition rates between life-history stages [20]. Phenological studies typically measure one representative phenotype such as flowering time in association with proximate drivers such as temperature or precipitation. But phenotypes covary and, therefore, one must consider trade-offs and competing selective forces with a whole-life perspective in order to understand the evolution of cyclical phenological traits. Here, I placed such connections in the general context of environmental cycles, of which the annual seasonal cycle is one example, and tested mechanistic predictions on the relatively short timescale of tide cycles which yielded large amounts of data across many cycle periods and generations quickly. This framework provides a basis for analysing, comparing, and predicting adaptive phenological shifts in changing seasonal environments.

Data accessibility

Data files and scripts are available in the GitHub repository: https://github.com/john-s-park/CyclicalLH.

Competing interests

I declare we have no competing interests.

Funding

This work was supported by University of Chicago Hinds Fund, DOE GAANN and NSF LTREB grant (DEB-1556874).