Effects of nonlinear growth rates of spherical crystals and their withdrawal rate from a crystallizer on the particle-size distribution function

Abstract

In this paper, we show that the nonlinear growth rate of particles in a supersaturated solution or supercooled melt, as well as the rate of removal of crystals from the metastable liquid of a crystallizer, significantly change the size-distribution function of crystals. Taking these rates into account, we present a complete analytical solution of the integro-differential model describing the transient nucleation of solid particles and their evolution in a metastable liquid. The distribution function and metastability degree (supersaturation or supercooling) are found by means of the separation of variables and saddle-point methods. The nonlinear growth rates of crystals in supersaturated solutions and supercooled melts (single-component and binary) are summarized and compared with experimental data.

This article is part of the theme issue ‘Heterogeneous materials: metastable and non-ergodic internal structures’.

1. Introduction

In actual practice, the nucleation and evolution of a polydisperse ensemble of crystals are complicated by their removal from a metastable liquid as well as by the presence of mass sources or heat sinks [1–4]. In addition, the growth rate of crystals in supersaturated solutions and supercooled melts is a nonlinear function of the supersaturation (supercooling) of the metastable liquid [5–11]. Namely, experimental works [5–8] demonstrate that the growth rate V of crystals is close to parabolic with increasing the supersaturation Δ. In other words, the frequently used linear approximation V (τ) = β_*Δ(τ) does not well describe the real experiments (here β_* and τ represent the kinetic coefficient and time). The analytical theory recently developed for supercooled single-component and binary melts [9,10] as well as for supersaturated solutions [11] shows that the crystal growth rate represents the following nonlinear function of metastability degree Δ and time τ

$$V\left(\tau \right)={\beta }_{\ast }\mathrm{\Delta }(\tau )\{\begin{array}{l}(1-{\chi }_1\tau \mathrm{\Delta }(\tau )),\hspace{0.17em}\mathrm{supercooled}\hspace{0.17em}\mathrm{single}\text{-}\mathrm{component}\hspace{0.17em}\mathrm{melts}\hspace{0.17em}[9]\\ (1-{\chi }_2\tau \mathrm{\Delta }(\tau )),\hspace{0.17em}\mathrm{supercooled}\hspace{0.17em}\mathrm{binary}\hspace{0.17em}\mathrm{melts}\hspace{0.17em}[10]\\ (1-{\chi }_3\tau \mathrm{\Delta }(\tau )),\hspace{0.17em}\mathrm{supersaturated}\hspace{0.17em}\mathrm{solutions}\hspace{0.17em}[11]\end{array}$$ 1.1

and

$${\chi }_1=\frac{{\beta }_{\ast }^2{\rho }_{s}L}{{\mathrm{\lambda }}_l},{\chi }_2=\frac{{\beta }_{\ast }^2{\rho }_{s}L}{{\mathrm{\lambda }}_l}(1+\frac{m(1-k)C_0{\mathrm{\lambda }}_l}{D{\rho }_{s}L}),{\chi }_3=\frac{{\beta }_{\ast }^2(k-1)C_p}{D},$$

where λ_l is the thermal conductivity, ρ_s is the density of the solid phase, L is the latent heat of phase transition, m is the liquidus slope, k is the equilibrium partition coefficient, C₀ is the solute concentration far from the growing crystal, D is the diffusion coefficient, and C_p is the concentration at saturation. To find the rate R_g (g/h cm²) of the increase in the mass of growing crystals per unit time per unit area, let us write out the mass of crystals as M = ρ_sNυ, where N is the total number of crystals and υ is the volume of a single particle. Next considering the case of spherical crystals υ = 4πr³/3 one can find the mass growth rate as dM/dτ = 4πρ_sNr²V (τ), where V (τ) is given by expressions (1.1). Now introducing R_g = (4πr²N)⁻¹ dM/dτ = ρ_sV (τ), we come to

$$R_g=\kappa \mathrm{\Delta }(1-{\chi }_3\tau \mathrm{\Delta }),\kappa ={\rho }_s{\beta }_{\ast },$$ 1.2

where the third line of expression (1.1) is taken into account. As the growth rate (1.2) depends on Δ and τ one can use a desupersaturation curve Δ(τ) or its inverse function τ(Δ) to plot the growth rate (1.2) as a function of a single variable V (τ) or V (Δ). Using such a curve experimentally found by Garside et al. [6] (see their fig. 5), we compare in figure 1 the nonlinear growth rates (1.1) and (1.2) with experimental data on the nucleation and evolution of potassium sulfate in a laboratory scale fluidized bed crystallizer.

Figure 1.

Growth rate R_g of potassium sulfate crystals in a fluidized bed crystallizer (symbols designate the experimental data [6] and the solid curve is plotted in accordance with expression (1.2)). Here χ₃ = 0.049 h⁻¹[Δ]⁻¹, κ = 0.082 g/(h cm²[Δ]) and [Δ] denotes the dimension of supersaturation shown on the horizontal axis.

Taking into account the aforesaid, we note that the evolution of a polydisperse ensemble of particles in a metastable liquid should be described by means of an integro-differential model of kinetic and balance equations, which includes the nonlinear growth rates of spherical crystals (1.1). In addition, this model is complicated by the presence of mass sources (heat sinks) and the removal of product crystals in the case of the industrial crystallizer. With that in mind, we develop a new theoretical approach for analytical description of the evolution of a particulate assemblage in a supersaturated solution or a supercooled melt of the industrial crystallizer.

2. The model of nonlinear dynamics of crystals in a crystallizer

Consider the process of evolution of a polydisperse ensemble of particles in the metastable liquid (supersaturated solution or supercooled melt) of a crystallizer. Owing to the mass flux Q_C(τ) introduced from outside (or the heat flux Q_θ(τ) removed from the system) the supersaturation (supercooling) necessary for crystal growth is maintained in the liquid. Taking into account the withdrawal rate of product crystals from the metastable liquid of a crystallizer, let us write down the kinetic equation for the particle-radius distribution function f(r, τ) describing the evolution of a polydisperse assemblage of particles

$$\frac{\mathrm{\partial }f}{\mathrm{\partial }\tau }+V(\tau )\frac{\mathrm{\partial }f}{\mathrm{\partial }r}+h(r)f(r,\tau )=\frac{\mathrm{\partial }}{\mathrm{\partial }r}(D(\tau )\frac{\mathrm{\partial }f}{\mathrm{\partial }r}),r>r_{\ast },\hspace{0.17em}\tau >0,$$ 2.1

where V (τ) = dr/dτ is determined by expression (1.1), r is the radial coordinate, h(r) is the crystal withdrawal rate (h represents the inverse of the mean residence time of particles of radius r in the metastable liquid), r_* is the radius of critical nuclei that are capable to appear in a supersaturated or supercooled system, and D is the coefficient of mutual Brownian diffusion. For the sake of simplicity, we consider the case of constant rate h and D(τ) = d₁V (τ), where d₁ stands for a pertinent factor [4,12–14].

The mass (heat) balance equation for supersaturated (supercooled) liquids reads as

$$\begin{array}{rlr}& \frac{\mathrm{d}C}{\mathrm{d}\tau }=Q_C-4\pi C_p{\int }_{r_{\ast }}^{\mathrm{\infty }}{r}^2(V(\tau )f(r,\tau )-D(\tau )\frac{\mathrm{\partial }f}{\mathrm{\partial }r})\mathrm{d}r,& \tau >0\\ \mathrm{and}& {\rho }_m{C}_m\frac{\mathrm{d}\theta }{\mathrm{d}\tau }=Q_{\theta }+4\pi L_V{\int }_{r_{\ast }}^{\mathrm{\infty }}{r}^2(V(\tau )f(r,\tau )-D(\tau )\frac{\mathrm{\partial }f}{\mathrm{\partial }r})\hspace{0.17em}\mathrm{d}r,& \tau >0,\end{array}\}$$ 2.2

where C is the solute concentration of the supersaturated solution, θ is the temperature of the supercooled melt, ρ_m and C_m are the density and specific heat of the mixture, respectively, and L_V = ρ_sL. Note that the first line of expression (2.2) corresponds to supersaturated solutions, whereas the second line describes a phase transformation in supercooled melts.

The initial distribution function f₀(r) as well as the initial metastability degree Δ₀ = ΔC₀ (Δθ₀) should be known, i.e.

$$f(r,0)=f_0(r),{\mathrm{\Delta }}_0=\{\begin{array}{l}\mathrm{\Delta }{C}_0,\hspace{0.17em}\mathrm{supersaturated}\hspace{0.17em}\mathrm{solutions}\\ \mathrm{\Delta }{\theta }_0,\hspace{0.17em}\mathrm{supercooled}\hspace{0.17em}\mathrm{melts}.\end{array}$$ 2.3

The flux of crystals overcoming the critical nucleation barrier and the distribution function of withdrawn crystals determine the boundary conditions

$$V(\tau )f(r_{\ast },\tau )-D(\tau )\frac{\mathrm{\partial }f}{\mathrm{\partial }r}=I(\mathrm{\Delta }),r=r_{\ast };f(r_p,\tau )=0,r=r_p,$$ 2.4

where I is the rate of nucleation, r_p is the radius of withdrawn crystals (product crystals), and Δ designates the current metastability degree Δ = ΔC = C − C_p or Δ = Δθ = θ_p − θ in cases of supersaturated or supercooled liquids. Here C and θ stand for the current values of solute concentration and temperature, and θ_p represents the phase transition temperature of a supercooled melt.

Our further analysis is devoted to the study of the influence of the nonlinear contribution to the growth rate of individual crystals (which is proportional to τΔ(τ) in (1.1)) on the evolution of a polydisperse ensemble of particles in a metastable liquid of a crystallizer.

3. Analytical solution

For the convenience of further analysis, the mathematical model (2.1)–(2.4) can be rewritten in dimensionless form as (parameter χ plays the role of χ₁, χ₂ or χ₃ introduced in expression (1.1))

$$\begin{array}{rl}& \frac{\mathrm{\partial }F}{\mathrm{\partial }t}+w(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)\frac{\mathrm{\partial }F}{\mathrm{\partial }x}+\gamma F\\ & =u_{0}w(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)\frac{{\mathrm{\partial }}^{2}F}{\mathrm{\partial }{x}^2},t>0,\hspace{0.17em}0<x<x_0,\end{array}$$ 3.1

$$\begin{array}{rl}& \frac{\mathrm{d}w}{\mathrm{d}t}=Q(t)-b_{1}w(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt){\int }_0^{x_0}{(x+s_{\ast })}^2(F-u_0\frac{\mathrm{\partial }F}{\mathrm{\partial }x})\mathrm{d}x,t>0\end{array}$$ 3.2

$$\begin{array}{rl}\mathrm{and}& w=1,F=F_0(x),t=0,F=u_0\frac{\mathrm{\partial }F}{\mathrm{\partial }x}=J(w),\\ & x=0;F=0,x=x_0,\end{array}$$ 3.3

where $J=w^{-1}{(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)}^{-1}\exp (p\varphi (w))$ (p and ϕ(w) are given in §2 in [15] for supersaturated solutions and supercooled melts for the Meirs and Weber–Volmer–Frenkel–Zeldovich kinetics), x and t represent the dimensionless coordinate and time, respectively, F(x, t) and w(t) are the dimensionless distribution function and supersaturation (supercooling), respectively, x₀ is the reduced radius of withdrawn crystals, Q is the dimensionless mass (heat) flux, and all the rest parameters are introduced in [15] (in the case of supercooled liquids the initial supersaturation ΔC₀ should be replaced by the initial supercooling Δθ₀).

To use the method of separation of variables to solve equation (3.1), we make the boundary conditions for the distribution function homogeneous by means of the following substitution:

$$F_1(x,t)=F(x,t)-\frac{J(w(t))(x_0-x)}{x_0+u_0}.$$ 3.4

After that, the problem (3.1), (3.3) takes the form

$$\begin{array}{rl}& \frac{\mathrm{\partial }{F}_1}{\mathrm{\partial }t}+w(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)\frac{\mathrm{\partial }{F}_1}{\mathrm{\partial }x}+\gamma F_1-u_{0}w(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)\frac{{\mathrm{\partial }}^2{F}_1}{\mathrm{\partial }{x}^2}=\nu (x,t),\end{array}$$ 3.5

$$\begin{array}{rl}& F_1=F_0(x)-\frac{x_0-x}{x_0+u_0},t=0;F_1-u_0\frac{\mathrm{\partial }{F}_1}{\mathrm{\partial }x}=0,x=0;F_1=0,x=x_0\end{array}$$ 3.6

$$\begin{array}{rl}\mathrm{and}& \nu (x,t)=\frac{J(w(t))}{x_0+u_0}[w(t)(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)-\gamma (x_0-x)]-\frac{x_0-x}{x_0+u_0}\frac{\mathrm{d}J}{\mathrm{d}t}.\end{array}$$ 3.7

Now representing the reduced distribution function F₁(x, t) as a product of two functions solely dependent on x and t, F₁(x, t) = X(x)T(t), and taking into account that X(0) − u₀X^′(0) = 0 and X(x₀) = 0, we obtain the eigenvalues n_k and eigenfunctions X_k(x) in the form

$$\begin{array}{rl}& X_k(x)=\exp \left(\frac{x}{2u_0}\right)[2n_k{u}_0\cos \left(n_{k}x\right)+\sin \left(n_{k}x\right)],\\ & 2n_k{u}_0\cos \left(n_k{x}_0\right)+\sin \left(n_k{x}_0\right)=0,k=0,1,2\cdots \end{array}\}$$ 3.8

Expanding functions ν(x, t) and F₁(x, 0) in series in the eigenfunctions X_k(x)

$$\nu (x,t)=\sum _{k=0}^{\mathrm{\infty }}{\nu }_k(t)X_k(x),F_1(x,0)=\sum _{k=0}^{\mathrm{\infty }}{F}_{0k}{X}_k(x),$$

and substituting (3.8) into (3.5), we get

$$F_1(x,t)=\sum _{k=0}^{\mathrm{\infty }}[F_{0k}+{\int }_0^t{\nu }_k(t_1)\exp ({\xi }_k(t_1))\hspace{0.17em}\mathrm{d}{t}_1]\exp (-{\xi }_k(t))X_k(x),$$ 3.9

where ν_k(t) and F_0k are determined by expressions (3.9) and (3.10) in [15], and

$${\xi }_k(t)=\frac{S_k(t)}{4u_0},S_k=(1+4u_0^2{n}_k^2){\int }_0^{t}w(t_1)(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)\hspace{0.17em}\mathrm{d}{t}_1+4u_0\gamma t.$$ 3.10

Now taking into account that the derivative S^′(t) > 0 (S(t) reaches a maximum at the upper limit of integration), we estimate the integral contribution in (3.9) on the basis of the saddle-point method for a Laplace-type integral as [16] (u₀≪1)

$${\int }_0^t{\nu }_k(t_1)\exp \left(\frac{S_k(t_1)}{4u_0}\right)\mathrm{d}{t}_1\approx \frac{4u_0{\nu }_k(t)\exp [S_k(t)/(4u_0)]}{S_k^{\mathrm{\prime }}(t)}.$$ 3.11

Combining (3.9) and (3.11), we have

$$F_1\approx \sum _{k=0}^{\mathrm{\infty }}{X}_k(x)[F_{0k}\exp (-{\xi }_k(t))+\frac{4u_0{\nu }_k(t)}{(1+4u_0^2{n}_k^2)U^{\mathrm{\prime }}(t)(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)+4u_0\gamma }],$$ 3.12

where we introduced a new unknown function

$$U(t)={\int }_0^{t}w(t_1)\hspace{0.17em}\mathrm{d}{t}_1.$$ 3.13

Now substituting (3.12) into the mass (heat) balance equation (3.2) and keeping in mind expression (3.4), we arrive at the following Cauchy problem for the determination of the integral function U(t)

$$\begin{array}{rl}& U^{\mathrm{\prime }\mathrm{\prime }}=M_0(U^{\mathrm{\prime }},U,t),\\ & {\tilde{f}}^{\mathrm{\prime }}(t)=U^{\mathrm{\prime }}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}(t)t)\\ \mathrm{and}& U=0,U^{\mathrm{\prime }}=1,\tilde{f}=0,t=0.\end{array}\}$$ 3.14

Here the following notations are introduced

$$\begin{array}{rl}{M}_0(U^{\mathrm{\prime }},U,t)& =\{Q(t)+b_1{(U^{\mathrm{\prime }})}^p\mathit{\Psi }-b_1{U}^{\mathrm{\prime }}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)S_2-b_1{U}^{\mathrm{\prime }}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)4u_0{S}_3\\ & +\hspace{0.17em}{\delta }_1{(U^{\mathrm{\prime }})}^p\}{[1-b_1{U}^{\mathrm{\prime }}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)4u_0{S}_1]}^{-1},\\ \mathit{\Psi }& =\frac{{(x_0+s_{\ast })}^4-4s_{\ast }^3(x_0+s_{\ast })+3s_{\ast }^4}{12(x_0+u_0)},{\delta }_1=\frac{b_1{u}_0[s_{\ast }^3-{(x_0+s_{\ast })}^3]}{3(x_0+u_0)},\\ S_1& =\frac{(p-1){(U^{\mathrm{\prime }})}^{p-2}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)+{(U^{\mathrm{\prime }})}^{p-1}\chi {\tau }_0\mathrm{\Delta }{C}_{0}t}{{(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)}^2}\sum _{k=0}^{\mathrm{\infty }}{\nu }_{k4}\frac{(Z_k-u_0{Y}_k)}{{\mathit{\Phi }}_k\left(U^{\mathrm{\prime }}\right)},\\ S_2& =\sum _{k=0}^{\mathrm{\infty }}{F}_{0k}\exp (-{\xi }_k(t))(Z_k-u_0{Y}_k),{\xi }_k(t)=\gamma t+\frac{(1+4u_0^2{n}_k^2)\tilde{f}(t)}{4u_0},\\ S_3& =\sum _{k=0}^{\mathrm{\infty }}[{(U^{\mathrm{\prime }})}^p{\nu }_{k1}-\frac{{(U^{\mathrm{\prime }})}^{p-1}}{1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t}{\nu }_{k2}-\frac{{(U^{\mathrm{\prime }})}^p}{{(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)}^2}{\nu }_{k3}]\frac{Z_k-u_0{Y}_k}{{\mathit{\Phi }}_k\left(U^{\mathrm{\prime }}\right)},\\ Z_k& ={\int }_0^{x_0}{(x+s_{\ast })}^2{X}_k(x)\hspace{0.17em}\mathrm{d}x,Y_k={\int }_0^{x_0}{(x+s_{\ast })}^2\frac{\mathrm{d}{X}_k(x)}{\mathrm{d}x}\hspace{0.17em}\mathrm{d}x,\\ {\mathit{\Phi }}_k\left(U^{\mathrm{\prime }}\right)& =(1+4u_0^2{n}_k^2)U^{\mathrm{\prime }}(1-\chi {\tau }_0\mathrm{\Delta }{C}_0{U}^{\mathrm{\prime }}t)+4u_0\gamma ,\\ {\nu }_{k1}& =\frac{1}{I_k(x_0+u_0)}{\int }_0^{x_0}{X}_k(x)\exp \left(\frac{-x}{u_0}\right)\mathrm{d}x,\\ {\nu }_{k2}& =\frac{\gamma }{I_k(x_0+u_0)}{\int }_0^{x_0}(x_0-x)X_k(x)\exp \left(\frac{-x}{u_0}\right)\hspace{0.17em}\mathrm{d}x,\\ {\nu }_{k3}& =\frac{1}{I_k(x_0+u_0)}{\int }_0^{x_0}(x_0-x)\chi {\tau }_0\mathrm{\Delta }{C}_0{X}_k(x)\exp \left(\frac{-x}{u_0}\right)\mathrm{d}x,\\ {\nu }_{k4}& =\frac{1}{I_k(x_0+u_0)}{\int }_0^{x_0}(x_0-x)X_k(x)\exp \left(\frac{-x}{u_0}\right)\mathrm{d}x.\end{array}$$

Let us especially note that the solution of the Cauchy problem (3.14) determines the integral function U(t). Then the metastability degree w(t) can be easily found as a derivative of this function, i.e. w(t) = U^′(t). It means that the dimensionless particle size distribution function F(x, t) is also known by means of expressions (3.4) and (3.12) and takes the form

$$\begin{array}{r}F(x,t)=\frac{J(w(t))(x_0-x)}{x_0+u_0}+\sum _{k=0}^{\mathrm{\infty }}{X}_k(x)[F_{0k}\exp (-{\xi }_k(t))+\frac{4u_0{\nu }_k(t)}{(1+4u_0^2{n}_k^2)U^{\mathrm{\prime }}(t)(1-\chi {\tau }_0\mathrm{\Delta }{C}_{0}wt)+4u_0\gamma }].\end{array}$$ 3.15

4. Summary and conclusion

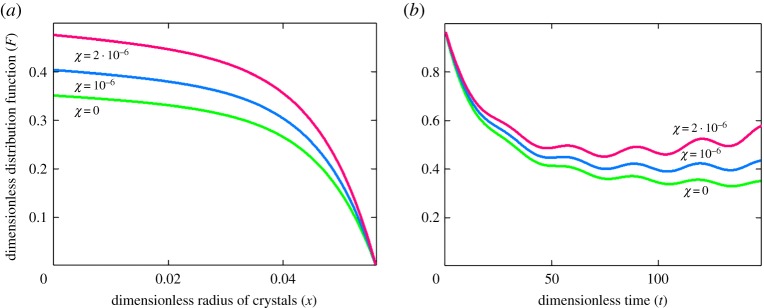
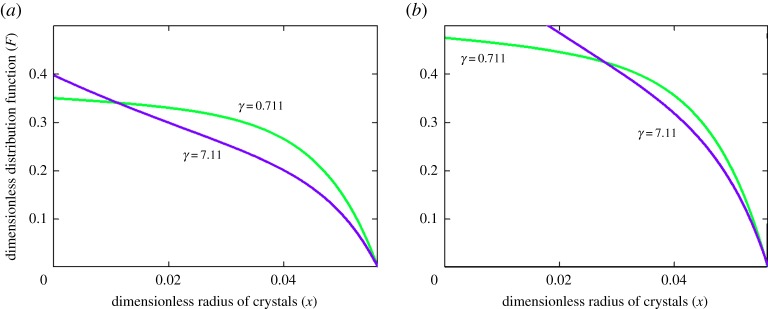
Figures 2–4 illustrate the particle-size distribution function plotted in accordance with the analytical solution (3.15) (physical parameters of the system under consideration are given in [15], Q(t) = A(1 − sin(ωt)/2), A = 0.005, and ω = π/15). The first important conclusion is the fact that the size distribution of crystals strongly depends on the parameter χ (compare curves at different χ in figures 2 and 3a,b). It is easily seen that the nonlinear growth rate of particles in a metastable liquid of crystallizer (expressions (1.1)) substantially changes the particle-size distribution. Our calculations show that the relative error may exceed tens of per cent in the course of time for real metastable liquids. As this takes place, the greatest difference of nonlinear growth law occurs for sufficiently small particles at a fixed time (figures 2a and 3a) and at essentially large times for particles of a given size (figures 2b and 3b). From the physical point of view, the nonlinear growth law (1.1) with non-zero χ means that the growth rates of evolving crystals become lower as compared with the case χ = 0. In other words, we have more crystals in the supercooled (supersaturated) liquid of a crystallizer, which grow longer until they are removed from the system (until they reach a given size x₀).

Figure 2.

Dimensionless distribution function versus dimensionless coordinate x ((a) t = 100) and time t ((b) x = 0.01) for γ = 0.711.

Figure 4.

Dimensionless distribution function versus dimensionless coordinate x at time t = 100 for χ = 0 (a) and χ = 2 · 10⁻⁶ (b).

Figure 3.

Dimensionless distribution function versus dimensionless coordinate x ((a) t = 100) and time t ((b) x = 0.01) for γ = 7.11.

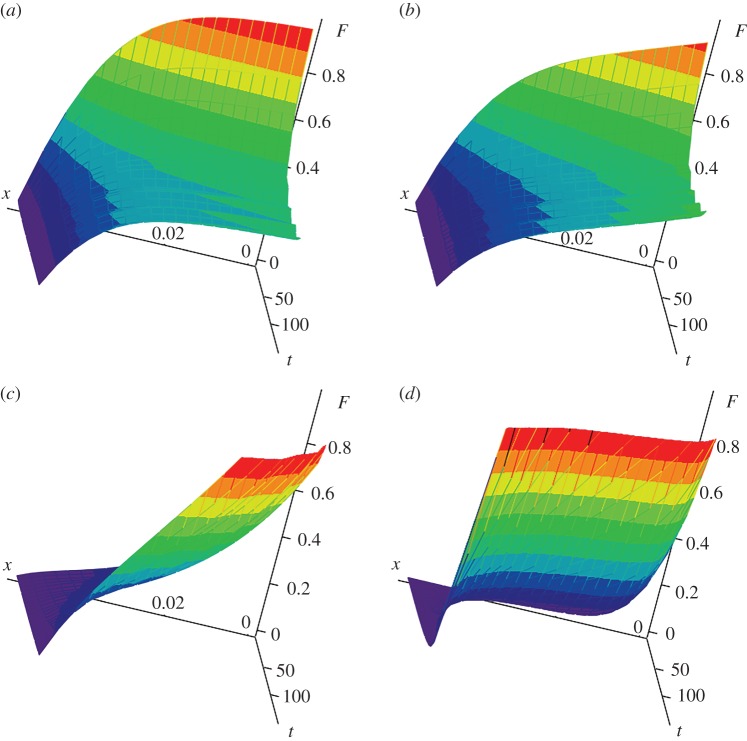
The second important conclusion is the influence of the crystal withdrawal rate h (which is proportional to the parameter γ) on the distribution of growing crystals. Indeed, with an increase in the rate of removal of crystals (γ increases), the number of large particles decreases and the number of small particles increases. Note that this effect takes place in both cases of linear and nonlinear growth rates (figure 4a,b). In other words, with the evolution of a metastable system with the same supercooling (supersaturation), when the number of larger crystals decreases, the number of smaller crystals increases and vice versa. Therefore, the distribution functions shown in figure 4 at various γ have a point of intersection. In addition, the three-dimensional dependencies F of x and t plotted in figure 5 show that the surface of the distribution function is inverted with an increase in the rate of removal of crystals (with increasing γ and h). In this case, the mean residence time of crystals in the metastable liquid of a crystallizer decreases and the surface of the distribution function bends in the direction of smaller times.

Figure 5.

Dimensionless distribution function versus dimensionless coordinate x and time t for χ = 10⁻⁶ and γ = 0.711 (a), γ = 7.11 (b), γ = 71.1 (c) and γ = 711 (d).

In summary, the particle-size distribution function strongly depends on two principal effects influencing the evolution of particulate assemblages in metastable liquids: (i) the nonlinear growth laws of crystals (expressions (1.1)) and (ii) the crystal withdrawal rate from a crystallizer. The theory under consideration, which takes into account these important physical effects should be used for a more precise description of similar phase transition phenomena when the evolution of crystals or other aggregates plays a decisive role. Such processes and phenomena as polymerization and crystallization in continuous apparatuses [17], evolution of protein and insulin crystals [18–20], evolution of aggregates in colloids and magnetic fluids [21–23], crystal growth in mushy layers [24–26], dissolution of dispersed solids, evaporation of a polydisperse mist, combustion of a solid dispersed fuel [27–29] may be mentioned among others.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed equally to the present research article.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Russian Science Foundation (grant no. 18-19-00008).