The evolution of early-life effects on social behaviour—why should social adversity carry over to the future?

Abstract

Numerous studies have shown that social adversity in early life can have long-lasting consequences for social behaviour in adulthood, consequences that may in turn be propagated to future generations. Given these intergenerational effects, it is puzzling why natural selection might favour such sensitivity to an individual’s early social environment. To address this question, we model the evolution of social sensitivity in the development of helping behaviours, showing that natural selection indeed favours individuals whose tendency to help others is dependent on early-life social experience. In organisms with non-overlapping generations, we find that natural selection can favour positive social feedbacks, in which individuals who received more help in early life are also more likely to help others in adulthood, while individuals who received no early-life help develop low tendencies to help others later in life. This positive social sensitivity is favoured because of an intergenerational relatedness feedback: patches with many helpers tend to be more productive, leading to higher relatedness within the local group, which in turn favours higher levels of help in the next generation. In organisms with overlapping generations, this positive feedback is less likely to occur, and those who received more help may instead be less likely to help others (negative social feedback). We conclude that early-life social influences can lead to strong between-individual differences in helping behaviour, which can take different forms dependent on the life history in question.

This article is part of the theme issue ‘Developing differences: early-life effects and evolutionary medicine’.

1. Introduction

In many taxa, the social environment experienced during early life gives rise to predictable between-individual differences in adult social behaviour [1–5]. In many rodents, individuals who have received limited parental care also provide less parental care themselves to their own offspring [6,7]. By contrast, wild mongoose females who received more help from others in early life are more likely to become reproductives rather than helpers themselves [8]. Both examples hint at a form of developmental plasticity, in which social cues early in life lead to irreversible developmental switching [3,5,9], thereby affecting the expression of prosocial behaviour later in life [7,10,11].

The long-term consequences of early-life social adversity, which may even spill over into the next generation, raise the question of why sensitivity to early social experiences has evolved at all: if anything, one might expect that offspring are selectively favoured to buffer the effects of early-life adversity, so that the transmission of adverse social behaviours to future generations is precluded [12]. To understand why developmental plasticity is nonetheless favoured by natural selection, a growing body of theoretical work therefore suggests that early-life effects may be an adaptive response to information about potential future environments (e.g. [13–21], but see [22]), suggesting that social adversity during early life is indicative of future social adversity, thus favouring the development of a less social phenotype. While this explanation is intuitive, a key shortcoming of these models is that they have been exclusively formulated with abiotic environments in mind, whereas in the context of social behaviours, the future is shaped by the actions of individuals themselves. Consequently, these models cannot explain why individuals who have experienced social adversity early in life are selectively favoured to go on and subsequently create a socially adverse environment for their own offspring [3,23].

To understand how early-life social experiences can lead to the intergenerational transmission of socially benign or adverse conditions, we develop an evolutionary model of a developmentally plastic social trait. We focus on the evolution of helping in a patch-structured population, in which individuals make an irreversible decision early in life to develop either as a nonreproductive helper or as a potential reproductive adult; an individual’s strategy determines the probability with which it develops as a helper rather than a breeder (e.g. [24–27]). The exact number of helpers recruited to a patch varies, with the expected number proportional to the average helping tendency expressed by local individuals. In line with the majority of the theoretical literature, helping is assumed to increase the fecundity of the reproductives in the local group [28]. The helping tendency expressed by a newborn can then evolve to become dependent on the number of helpers in the local patch present at the time of birth, reflecting the results of empirical studies in which developmental plasticity is based on the current social structure of the local group (e.g. [4,29,30]). We then study whether social behaviours are indeed likely to become sensitive to social experience in early life, and if so, what form such developmental plasticity takes.

2. The model

We consider a demographically explicit model of a sexually reproducing metapopulation, in which breeders are distributed over infinitely many demes (Wright’s infinite island model [25,31]). Each deme contains n_b adult breeders, who are assumed to reproduce as simultaneous hermaphrodites for the reason of tractability. In addition to breeders, demes can also contain j nonreproductive helping individuals, thereby positively affecting the fecundity of their reproductive patch mates. Throughout the main text, we assume that generations are non-overlapping, while results with overlapping generations are given in §S2.6 of the electronic supplementary material. We assume that individual demes vary in the number 0 ≤ j ≤ n_h,max of helpers that have successfully been recruited (see §2a ‘Life cycle’ below). To assess whether social experiences in early life affect later-life helping, we then ask whether the decision of newborns to become helpers evolves to be dependent (i.e. developmentally plastic helping, [32]) on the number of helpers currently present on the patch. For the sake of comparison, we also study the evolution of unconditional helping, where helping tendencies do not depend on the number of local helpers. Below, we provide a verbal summary of the life cycle, while an extensive description is given in the electronic supplementary material, §S1. See electronic supplementary material, table S1 for an overview of the symbols used in the analytical description of the model below. Finally, we check results using stochastic individual-based simulations in finite populations, which give very similar results (see electronic supplementary material, figure S6).

(a). Life cycle

Consider a focal mutant adult breeder that lives on a patch with n_b − 1 other breeders and j nonreproductive helpers. It randomly chooses a mate from among the n_b breeders in the local patch and subsequently produces a large number f_j offspring. Here, fecundity f_j is an increasing function of the total amount of help received from the j helpers, which we assume to be equally distributed over the n_b breeders present in the patch. A juvenile born from the mutant focal breeder will forego reproduction and develop as a helper with probability $h_{\hspace{0.17em}j}^{●}$, where ^● indicates the helping tendency expressed by the mutant mother (differing slightly from the average helping tendency h_j in the population). As mentioned before, a key assumption of our analysis is that the tendency to develop as a helper can evolve to become dependent on the current number of helpers in the local patch, j (although we also study the evolution of unconditional helping, where the helping tendency is constrained to be independent of the number of local helpers: $h_0=h_1=\dots =h_{n_{h,max}}\equiv h$). Alternatively, with probability $1-h_{\hspace{0.17em}j}^{●}$, a juvenile does not develop as a helper, in which case it either disperses to a randomly chosen remote patch with probability d or remains at the local patch with probability 1 − d.

After juvenile dispersal, all non-helping juveniles, both philopatric and immigrant, then compete for the expected number n_b of vacant breeding positions. The newly established breeders’ fecundity is now affected by a number k of helpers, recruited from the helping juveniles born in the local patch. Specifically, we assume that the number of helpers in each patch is given by a truncated Poisson distribution, where the probability $s_{j\to k}(h_{\hspace{0.17em}j}^{\circ })$ that a local patch that previously contained j helpers now contains k helpers is given by

$$s_{\hspace{0.17em}j\to k}(h_{\hspace{0.17em}j}^{\circ })=\{\begin{array}{cc}\frac{\overline{n}{(h_{\hspace{0.17em}j}^{\circ },j)}^k{\mathrm{e}}^{-\overline{n}(h_{\hspace{0.17em}j}^{\circ },j)}}{k!}& k<n_{\mathrm{h},\max }\\ \sum _{\ell =n_{\mathrm{h},\max }}^{\mathrm{\infty }}\frac{\overline{n}{(h_{\hspace{0.17em}j}^{\circ },j)}^{\ell }{\mathrm{e}}^{-\overline{n}(h_{\hspace{0.17em}j}^{\circ },j)}}{\ell !}& k=n_{\mathrm{h},\max },\end{array}$$ 2.1

where the first line reflects the Poisson probability of recruiting k helpers when ${\overline{n}}_{\mathrm{h}}(h_{\hspace{0.17em}j}^{\circ },j)=n_{\mathrm{b}}{f}_{\hspace{0.17em}j}{h}_{\hspace{0.17em}j}^{\circ }$ is the average number of helping juveniles produced by all adult breeders in the local patch, where $h_{\hspace{0.17em}j}^{\circ }$ is the average helping tendency of all locally born juveniles (including those of the focal mutant mother). The second line reflects the probability that the maximum of k = n_h,max helpers is attained, which occurs when ℓ = n_h,max helpers are sampled, or when more helpers than positions available for them are sampled (i.e. n_h,max < ℓ < ∞), in which case we assume that helpers compete among themselves for the n_h,max available helping positions, with the unsuccessful helpers dying afterwards. After k helpers have been recruited to the local patch, the cycle then repeats.

(b). Fitness

The expected number w_ij of offspring who successfully establish themselves in a patch with i helpers and are born from a mutant adult breeder in a patch with a total number j of helpers is then given by

$$\begin{array}{r}{w}_{ij}=f_{\hspace{0.17em}j}(1-h_{\hspace{0.17em}j}^{●})[\frac{n_{\mathrm{b}}(1-d)s_{\hspace{0.17em}j\to i}(h_{\hspace{0.17em}j}^{\circ })}{C(h_{\hspace{0.17em}j}^{\circ };\mathbf{h},j)}+d\sum _{k=0}^{n_{\mathrm{h},\max }}{u}_k\frac{n_{\mathrm{b}}{s}_{k\to i}(h_k)}{C(h_k;\mathbf{h},k)}],\end{array}$$ 2.2

where f_j reflects the total number of surviving newborns produced by the focal adult breeder, a proportion $1-h_{\hspace{0.17em}j}^{●}$ of which develop as juvenile reproductives (rather than helpers). These juvenile reproductives then go on to compete for any of the n_b available breeding positions in the natal patch with probability 1 − d (first term in square brackets), or in a random, remote patch with probability d (second term in square brackets), where u_k reflects the population-wide frequency of patches currently containing k helpers. Philopatric reproductives compete with a total number $C(h_{\hspace{0.17em}j}^{\circ };\mathbf{h},j)$ of philopatric and immigrant offspring (see electronic supplementary material, equation (S2)), which is a function of (i) the average tendency $h_{\hspace{0.17em}j}^{\circ }$ expressed by any locally born newborn to develop as a helper, (ii) the population-wide tendencies $\mathbf{h}=[h_0,h_1,\dots ,h_{n_{\mathrm{h},\max }}]$ to become helpers in any remote patch and (iii) the current number of helpers j in the local patch. Finally, after successful establishment, the probability that the newly established breeder is accompanied by i helpers in the next generation is then given by $s_{\hspace{0.17em}j\to i}(h_{\hspace{0.17em}j}^{\circ })$ (see equation (2.1)). The expected number of offspring who successfully compete in the remote patch can then be derived in a similar fashion.

(c). Evolutionary dynamics

We use a direct fitness method (also called neighbour-modulated fitness [33,34]) to calculate evolutionary change ${\mathcal{H}}_k$ in the tendency to help when born on a patch containing k helpers. According to a standard result [35–37], ${\mathcal{H}}_k$ is then given by

$${\mathcal{H}}_k={V_k\sum _{i=0}^{n_{\mathrm{h},\max }}\sum _{\hspace{0.17em}j=0}^{n_{\mathrm{h},\max }}{v}_i{u}_{\hspace{0.17em}j}[\frac{\mathrm{\partial }{b}_{ij}}{\mathrm{\partial }{h}_k^{●}}+\frac{\mathrm{\partial }{b}_{ij}}{\mathrm{\partial }{h}_k^{\circ }}{r}_{\mathrm{local},\mathit{j}}]|}_{{\mathbf{h}}^{●}={\mathbf{h}}^{\circ }=\mathbf{h}},$$ 2.3

where V_k is a term that is proportional to the amount of additive genetic variance in the helping tendency h_k. Next, v_i is the individual reproductive value of an adult breeder in a patch with i helpers, while u_j is the stable class frequency of patches containing j helpers. These are obtained from the dominant left and right eigenvectors, respectively, of the resident transition matrix (see electronic supplementary material, equation (S4)). The first partial derivative of the element b_ij of the mutant transition matrix B (see electronic supplementary material, equation (S3)) reflects selection on offspring born from the focal mutant breeder, who express a helping tendency $h_k^{●}$. The second partial derivative reflects selection on all breeders in the mutant’s local patch, whose offspring, on average, express the helping tendency $h_k^{\circ }$. Finally, the relatedness coefficient r_local,j reflects the relatedness between a focal adult breeder and any adult breeding individual (including the focal itself) in the local patch, which currently contains j helpers (see electronic supplementary material, equation (S7)). As we have not been able to find analytical solutions to find the candidate evolutionarily stable helping strategy h_k, we developed an algorithm in C++ (source code available at https://doi.org/10.5281/zenodo.1421729) to numerically find the convergence stable values of the helping tendencies h (see electronic supplementary material). We also ran individual-based simulations to check results (see electronic supplementary material, figure S6), which showed that evolutionary branching of helping tendencies did not occur.

Throughout, we assume that helper-dependent fecundity of a focal breeder in a patch with j helpers is given by the function $f_{\hspace{0.17em}j}=(1/n_{\mathrm{b}})({\varphi }_0+{\varphi }_1{j}^{{\varphi }_2})$, where ϕ₀ is the baseline productivity of a patch without helpers, ϕ₁ is the strength with which productivity increases with increasing helper number and ϕ₂ reflects whether productivity increases in a linear, accelerating or decelerating fashion. We divide by n_b, reflecting the assumption that benefits of helping are equally shared among the local breeders. Electronic supplementary material, figures S2, S3 and S5 show that outcomes are robust to different values of the ϕ_i parameters.

3. Results

(a). Result 1: early-life social experiences strongly affect helping behaviour

To assess how the presence of helpers in early life affects an individual’s tendency to help others, we focus on a scenario where maximally n_h,max = 5 helpers can be recruited to a local patch and where helper number has a linear effect on local productivity. Results are, however, robust to different values of n_h,max (electronic supplementary material, figure S1) or cases where helper numbers increase local productivity in a decelerating fashion (electronic supplementary material, figure S5). We focus on n_b = 2 breeders per patch; higher values of n_b result in lower values of local relatedness, so that helping evolves across a narrower range of parameter space, unless benefits of helping are also larger (see electronic supplementary material, figure S4), in line with standard theory [26,38].

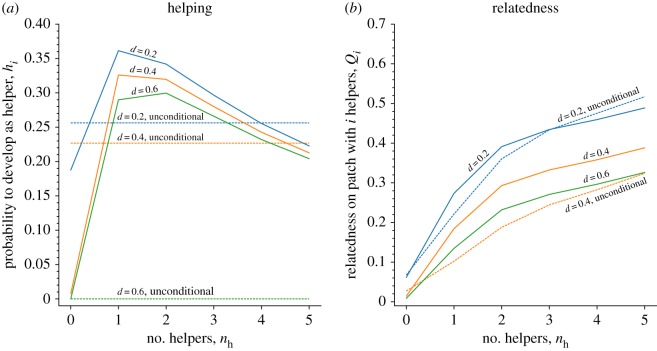
Figure 1a shows that early-life effects on the development of adult helping behaviours are adaptive, as the probability of helping in adulthood is strongly dependent on the amount of help received in early life (as measured by the number of helpers in the local patch). Moreover, we find that those individuals who have experienced an intermediate number of helpers at birth (e.g. n_h = 1, 2, 3) are most likely to develop as helpers themselves in later life, whereas adults who have experienced either a very large amount of help (e.g. n_h = 5), and particularly those who have received no help at all (n_h = 0) are less likely to become helpers themselves. We also find that early-life effects extend the parameter space over which helping evolves (relative to populations that help unconditionally): for example, for high rates of dispersal (d = 0.6), only developmentally plastic helping evolves (compare solid versus dotted green lines in figure 1a). Finally, because of the flexibility of developmentally plastic helping, we find that the population-wide average tendency to help is, in fact, lower for populations with developmental plasticity (see electronic supplementary material, figure S7). This is because developmentally plastic helpers express a low helping tendency in patches with no helpers, whereas unconditionally helping individuals express the same levels of helping everywhere (figure 1a).

Figure 1.

The evolution of developmentally plastic and unconditional helping behaviours in patches that contain 0 ≤ n_h ≤ 5 helpers in early life, for three different values of juvenile dispersal d (a). When helping is developmentally plastic, individuals develop higher levels of help in patches where helpers are present in early life (n_h > 0) relative to patches where help in early life is absent (n_h = 0). (b) The corresponding relatedness coefficients, showing that relatedness is higher in patches with more helpers, as these are more productive (hence making it more likely that philopatric offspring claim breeding spots). Note that when d = 0.6, unconditional helping does not evolve; hence we only have n_h = 0. The corresponding line in (a) is hence only drawn for the purpose of illustration, while we do not depict a corresponding relatedness coefficient for d = 0.6 and unconditional helping. See also electronic supplementary material, figure S1 for n_h,max ∈ {3, 10, 20} and figure S5 when productivity increases in a decelerating (rather than linear) fashion with increasing numbers of helpers. Parameters: n_b = 2, ϕ₀ = 1, ϕ₁ = 5, ϕ₂ = 1, n_h,max = 5. (Online version in colour.)

(i). Local variation in relatedness versus saturation drives plasticity in helping

To understand the evolution of developmental plasticity in helping behaviours, figure 1b depicts the coefficient of consanguinity between two distinct breeders for patches with different numbers of helpers. We find that, once helping evolves, relatedness is highest in those patches that contain the largest numbers of helpers and lowest in patches where helpers are absent. This is because a larger number of helpers increases the fecundity of the local group, so that any vacant breeding spots are more likely to be claimed by locally born juveniles (rather than by remotely born offspring). Consequently, helpers and breeders are more likely to be related in the next generation, thus favouring stronger helping tendencies in patches that currently contain high numbers of helpers.

As relatedness is higher in patches with a large number of helpers, we would thus expect that helping is the highest in patches currently containing the largest numbers of helpers. At the same time, however, high productivities of patches with large numbers of helpers result in a rapid saturation of the available number of helper vacancies, explaining why helping tendencies are only maximized on patches with an intermediate number of helpers (see figure 1a). We therefore conclude that local relatedness (favouring more helping) and saturation of helping positions (favouring less helping) are two opposing forces that determine the shape of the social reaction norm. Indeed, when saturation of helper positions is less important relative to local relatedness (for example, because of a higher total number of helper positions), developmentally plastic helping levels attain higher maximum levels and are maximized for patches with higher numbers of helpers (see electronic supplementary material, figure S1).

(ii). Overlapping generations

When generations are overlapping, we find even stronger differences in helping tendencies between individuals who experienced few versus many helpers during early life (electronic supplementary material, figure S8B–D). However, in sharp contrast to populations with non-overlapping generations (figure 1a; electronic supplementary material, figure S8A), we find a negative relationship, so that individuals who received little help are more likely to help others, while those who received a lot of help are less likely to help others. The reason for this negative relationship between early-life and later-life help is that generational overlap changes the relative importance of local relatedness versus saturation of helping positions: while saturation of helping positions still favours reduced helping tendencies in patches with a higher number of helpers, the effect of local relatedness (which favours higher levels of help with increased helper number) is weakened. Local relatedness is less important because helpers will help their surviving parents (with whom relatedness is always high, regardless of the number of local helpers in the patch). Consequently, the effect of patch saturation prevails when generations overlap, so that individuals help most when having received little help themselves in early life.

(b). Result 2: Helper presence predicts a social future

Our model also allows us to study the longer-term consequences that result from the presence (or absence) of helpers. When helper development depends on the current amount of help received (figure 2), we find that even for relatively high levels of dispersal (i.e. d ≈ 0.6), the current number of helpers is highly predictive of the number of helpers in the future (see also the autocorrelations in figure 3, blue line). For example, patches that currently have no helpers (n_h(t) = 0) are extremely unlikely to recruit any helpers in the future, while patches that currently have the maximum number of helpers (e.g. n_h(t) = 5) are likely to have a large number of helpers again in the future.

Figure 2.

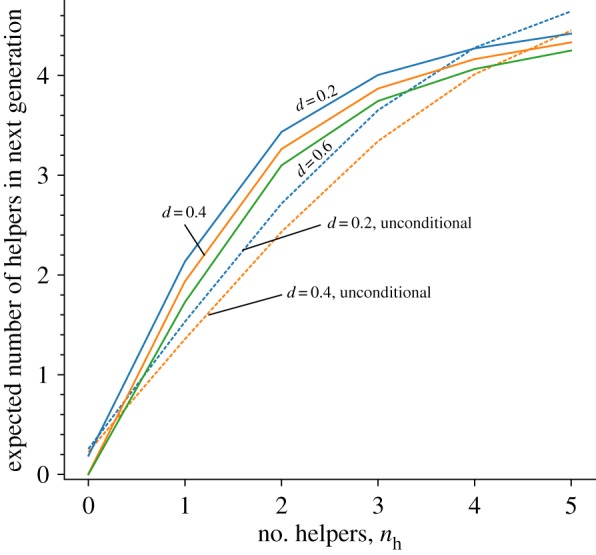
The expected number of helpers recruited in the next timestep increases with the current number of helpers in the local patch. It does so more rapidly in cases where helping is developmentally plastic (solid lines). Note that when d = 0.6, unconditional helping does not evolve; hence the expected number of helpers is always equal to 0. Parameters as in figure 1. (Online version in colour.)

Figure 3.

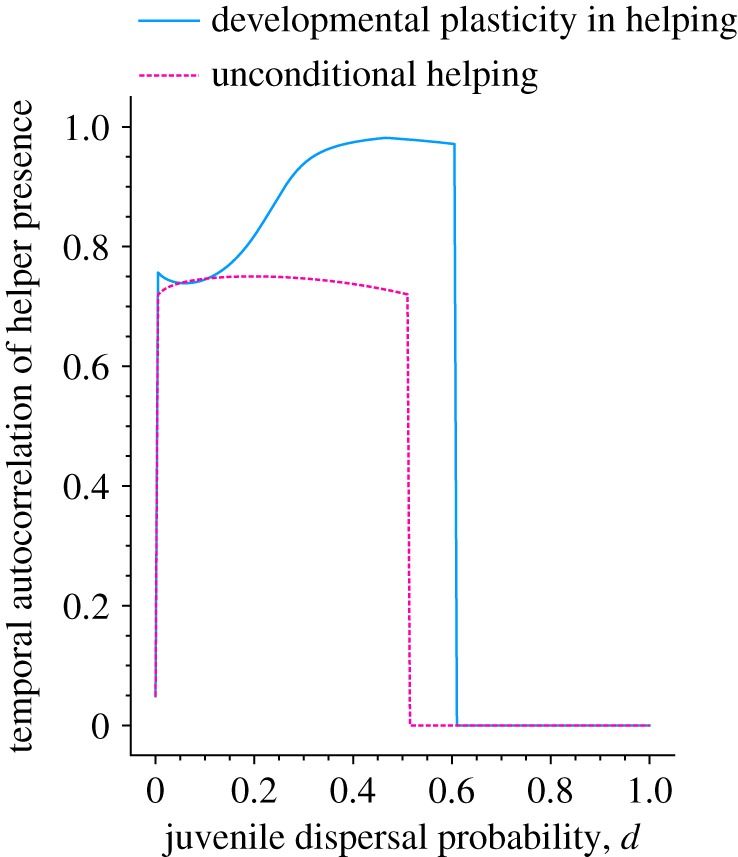
Temporal autocorrelation in patterns of presence versus absence of helpers between parental and offspring generations, for populations in which help is developmentally plastic versus unconditional, while varying the probability of juvenile dispersal d. Parameters as in figure 1. (Online version in colour.)

By contrast, when helping is unconditional, help only evolves when dispersal is more limited (i.e. d < 0.45), but even then the number of helpers experienced in the current generation is a poorer predictor of the amount of help received in the future (see also figure 3). Only in populations where dispersal becomes strongly limited is relatedness high overall, so that helping evolves regardless of the current number of helpers in the local patch. Indeed, when dispersal becomes more strongly limited, the autocorrelations for developmentally plastic and unconditional helping become very similar.

When generations are overlapping, however, the presence of helpers in the current timestep is much less predictive of the number of helpers recruited in the future when compared with unconditional helping (see electronic supplementary material, figure S9). Autocorrelations are lower when generations are overlapping because of the aforementioned negative relationship between helper presence and help in later life (see electronic supplementary material, figure S8).

4. Discussion

Here, we have shown that the social environment experienced in early life can lead to substantial between-individual variation in adult social behaviour. Moreover, we find that this developmental plasticity of social behaviour can take different forms dependent on the life history in question: in taxa with non-overlapping generations, we find that it can lead to positive social sensitivity where greater experience of prosocial behaviour in early life results in a greater tendency to behave prosocially in adulthood, while a reduction in prosocial behaviour is an adaptive response to social adversity in early life. By contrast, the opposite applies when generations are overlapping: here we find a negative social sensitivity, where prosocial behaviour in early life results in a lower tendency to behave prosocially in adulthood, while an increase in prosocial behaviour is an adaptive strategy to social adversity in early life.

Our model predicts a positive relationship between early-life social experience and later-life social behaviour when generations are non-overlapping, because helping promotes local productivity, thereby increasing local relatedness, and greater local relatedness in turn favours more helping. To understand this, focus on a local group with many helpers: this group will produce a large number of offspring, hence increasing the probability that a local breeding spot will be claimed by a locally born (rather than a remotely born) offspring in the next generation. In turn, this results in an increase in local relatedness (see figure 1b), favouring a high tendency to develop as a helper. By contrast, patches that currently contain few helpers are less productive, ultimately resulting in a lower relatedness and a lower tendency to help. Of course, this kind of feedback between sociality and relatedness will only develop when individuals can adjust prosocial behaviour in response to juvenile cues that are predictive of local relatedness experienced as an adult. Our model shows that the experience of being helped in early life can serve as a reliable cue of expected relatedness in this way, thus driving developmental plasticity in later-life social behaviour.

Once positive social sensitivity has evolved, the intergenerational propagation of prosocial behaviour itself amplifies the benefits of helping, because an individual that becomes a helper not only boosts the fecundity of related breeders in the current generation but also increases the tendency to help among progeny that remain on the local patch. Helping, in other words, ends up providing longer-term as well as shorter-term benefits. In a series of seminal models, Lehmann [39,40] has previously shown that persistent benefits, which impact on the fitness of later generations, are particularly favourable for the evolution of helping, because they provide a partial escape from the constraints of local kin competition. These models, however, start from the assumption that the benefits of helping behaviour persist over time, as seems likely to be true for many beneficial modifications of the local environment such as construction or maintenance of a nest or burrow. Our model shows that even if helping has no such physically persistent effects and only boosts the fecundity of breeders in the current generation, it may nevertheless end up yielding longer-term benefits because of the intergenerational propagation of relatedness.

In populations with overlapping generations, however, our model predicts a negative relationship between early-life social experience and later-life social behaviour. Although helping still promotes local productivity and local relatedness, local relatedness itself has a diminished effect on helping. This is because juvenile helpers are now more likely to help their surviving parents, rather than any members of their own generation, with whom relatedness increases with local helper numbers (see figure 1b). Relatedness between a breeding parent and its offspring, however, is roughly constant (0.5) unless inbreeding is very high. Consequently, help experienced during early life is a poor predictor of parent–offspring relatedness and of the advantage of helping. However, the amount of help experienced during early life still predicts local productivity, where higher levels of local productivity imply that available helping positions become quickly saturated. Consequently, as the local number of helpers is now a less important cue of local relatedness than it is for local saturation of helping positions, early-life help now favours a reduced tendency to help with increasing numbers of helpers, in order to avoid saturation of helping positions. Consequently, help received is indicative of both relatedness and local competition for helping positions, with the latter effect prevailing in taxa with overlapping generations, driving a negative feedback.

Previous models of the evolution of early-life effects have focused chiefly on adaptation to fluctuations in the abiotic environment (e.g. [13,15,18,41–44]), with surprisingly little attention given to social sensitivity (as previously noted in [3]). A key prediction of the existing theory is that environmental conditions need to be sufficiently autocorrelated with later-life environmental conditions. However, some studies suggest that autocorrelations from climatic timeseries are, in fact, small and thus cannot readily account for the widespread occurrence of early-life effects (e.g. [22,45]). Our model, however, shows that variation in the social environment can drive the evolution of early-life effects, even in the absence of autocorrelations in the abiotic environment, because social sensitivity itself generates high autocorrelations between parental and offspring social environments (see figure 3). Hence, our study suggests that the social environment may in general play a more important role in the evolution of early-life effects than does the abiotic environment (see also [46,47]).

Our model suggests a number of possible directions for future work: as discussed above, one key prediction is that with non-overlapping generations, increased levels of social behaviour result in increases in relatedness, thus creating a positive feedback loop (unless checked by increased saturation of helping positions). A typical consequence of positive feedback loops is that they often result in alternatively stable states [48]. Indeed, figure 2 suggests that developmental plasticity may well result in a social polymorphism at the patch level, in which some populations may become locked into persistent low prosocial states, whereas others become locked into highly prosocial states. For example, when n_h = 0, the expected number of helpers in the next generation will be again 0 for d = 0.4 or d = 0.6 (see bottom left corner of figure 2), so that the lack of help engenders little help in the future. By contrast, when helpers are present in the local patch (n_h ≥ 1), more helpers are likely to be recruited in the next generation (except when the current number of helpers is already at its maximum), engendering more help in future (figure 2, rightwards). While neither state will persist indefinitely (owing to demographic stochasticity in the recruitment of helpers to a patch), positive transgenerational feedback on social behaviour will tend to maintain these differences between patches for longer than would otherwise be the case. Such persistent polymorphism represents a group-level analogue of the persistent differences in individual behaviour that emerge during early life and are maintained in models of personality evolution [49,50]; one might even speak of the emergence of ‘collective personalities’. However, a complete analysis of these consequences of developmental plasticity in helping is beyond the scope of the current paper and would merit further study.

Next, the current model focused on the evolution of helping behaviours, as this provides a straightforward context for modelling the evolutionary consequences of social adversity. However, it remains to be seen whether these conclusions generalize to other life-history traits as well. In the context of parental care, for example, offspring born from mothers who provide high levels of care are more likely to survive, hence increasing relatedness in the local patch for similar reasons as in the current model. If mating is local, this results in an increase in parent–offspring relatedness, potentially favouring higher levels of parental care. By contrast, a parent who actively harms its offspring (e.g. maternal abuse in macaques [51]) may produce fewer surviving offspring, thus resulting in lower values of parent–offspring relatedness, which in turn may further enhance the evolution of harming. Formal models are therefore necessary to study the role of developmental plasticity in the face of other life-history traits.

Finally, for reasons of tractability, the current study only focused on social traits characterized by plasticity that is irreversible, so that once an individual has committed itself to helping it will do so for the rest of its life. While such social traits may be particularly relevant for some forms of cooperative breeding in insects, many vertebrate societies are characterized by forms of reversible plasticity, in which helpers may become reproductives later in life [3], or reproductives may become helpers (as in the case of grandparental care [52]). However, we would predict that the qualitative features of our predictions may well be robust to the presence of reversible plasticity, with the number of helpers present in early life influencing the total amount of time during an individual’s life that is devoted to help. Overall, our model shows that early-life effects in social contexts can be adaptive but highlights the need for further study to understand their ecological significance.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

B.K. is funded by a Leverhulme Trust Early Career Research Fellowship (ECF 2015-273).