Power and sample size requirements for GEE analyses of cluster randomized crossover trials

Abstract

The cluster randomized crossover design has been proposed to improve efficiency over the traditional parallel cluster randomized design, which often involves a limited number of clusters. In recent years, the cluster randomized crossover design has been increasingly used to evaluate the effectiveness of health care policy or programs, and the interest often lies in quantifying the population-averaged intervention effect. In this paper, we consider the two-treatment two-period crossover design, and develop sample size procedures for continuous and binary outcomes corresponding to a population-averaged model estimated by generalized estimating equations, accounting for both within-period and interperiod correlations. In particular, we show that the required sample size depends on the correlation parameters through an eigenvalue of the within-cluster correlation matrix for continuous outcomes and through two distinct eigenvalues of the correlation matrix for binary outcomes. We demonstrate that the empirical power corresponds well with the predicted power by the proposed formulae for as few as eight clusters, when outcomes are analyzed using the matrix-adjusted estimating equations for the correlation parameters concurrently with a suitable bias-corrected sandwich variance estimator.

1 |. INTRODUCTION

The cluster randomized trials (CRTs) are designed to allocate intact clusters, such as schools, hospitals, or worksites, to intervention and control conditions either because individual randomization is not feasible, or because investigators wish to study the intervention effect at the cluster level.^1,2 Such designs often arise in health care research and have received increasing attention over the past few decades.^3,4 A common practical limitation of CRTs is that only a small number of clusters may be available, thus limiting the study power. To counteract this potential inefficiency, a crossover component can be incorporated into the design by allowing each cluster to receive both intervention and control conditions during consecutive periods in a random order.⁵ This type of design is named the cluster randomized crossover design, or abbreviated as the CRXO design.

To limit the carryover of intervention effect to the next period, a different set of individuals are typically included during each distinct period in each cluster (ie, a cross-sectional design using the terminology of Murray¹) and a washout period may be planned. In many applications from the health services settings, there are naturally different persons presenting for health care in each period,⁶ thereby limiting the potential for carry over effects. In other study designs, different subjects per period are allocated deliberately. For instance, in trials where the units of randomization are classes in a school, each class may be randomly split into two halves, with each half included in a distinct period. It is often assumed in CRXO trials that sets of individuals included in different periods are representative samples of the same population in each cluster. Under this assumption, within-cluster comparisons can inform the intervention effect, eliminates the between-cluster variation, and hence reduces the required sample size.⁷ Additionally, estimating the intervention effect within clusters may also help offset any pre-existing differences among participating clusters; these baseline differences are frequently observed when only a few clusters are allocated to each trial arm.

Because of the cluster-level crossover, two types of correlations are recognized in designing a CRXO trial, the within-period correlation and the interperiod correlation.^8–10 The former describes the similarity between two individual outcomes within the same cluster and from the same period, while the latter measures the similarity between two individual outcomes within the same cluster but from different periods. A graphical explanation of these two correlations and the underlying sources of variability are presented in Arnup et al.¹¹ Based on a multivariate normal model that accounts for both correlations, Giraudeau et al^9,12 derived a sample size formula for continuous outcomes based on cluster-level analysis and balanced cluster-period sizes. For binary outcomes, Forbes et al¹⁰ derived a sample size formula based on the cluster-level risk difference (RD) estimator. In particular, both sample size estimation methods are based on cluster-level analysis, whereas there is scant discussion of sample size estimation appropriate for individual-level analysis, which appears to be more frequently used in CRXO trials according to a recent review by Arnup et al.⁶ The individual-level analysis approaches include the cluster-specific (conditional) model and the population-averaged (marginal) model. An important distinction between these two models is the interpretation of regression parameters, especially for binary outcomes with a canonical logit link. Since the intervention is administered at the cluster level and does not vary within clusters during each period, the marginal model provides a more straightforward population-averaged interpretation.^13–15

To date, there is limited investigation of marginal model inference in CRXO trials. Forbes et al¹⁰ restricted marginal modeling to independence generalized estimating equations (GEE) with the empirical sandwich estimator of Liang and Zeger¹⁶ and showed substantial inefficiency under variable cluster-period sizes. They conjectured that efficiency could be regained by modeling the correlation structure more appropriately. Therefore, in this paper, we first discuss a marginal model fitted with paired estimating equations to analyze a two-treatment two-period CRXO trial, accounting for both within-period and interperiod correlations. In particular, we use GEE to make inference for the marginal mean parameters and adopt the matrix-adjusted estimating equations (MAEE) to estimate the correlation parameters.¹⁷ Matrix-adjusted equation, proposed by Preisser et al¹⁷ for the analysis of pretest posttest CRTs, reduce the finite-sample bias in the correlation estimates obtained from the standard Prentice-type estimating equations.¹⁸ Improved estimation of correlations is vitally important in the analysis of CRXO trials (and CRTs in general) since sample size planning for future trials critically depends on these estimates.¹ Based on the marginal model, we then derive sample size formulae for continuous and binary outcomes, and evaluate their utility using simulations. Finally, since the empirical sandwich variance estimator of GEE tends to underestimate the variability of the intervention effect estimate with a small number of clusters (usually fewer than 30), we consider several popular finite-sample adjustments to the sandwich estimator and inform the choices among these adjustments for practical applications.

The remainder of this article is organized into six sections. In Section 2, we provide details on the GEE analyses of CRXO trials. In Section 3, we derive the sample size formulae appropriate for GEE analyses of continuous and binary outcomes. The simulation study is presented in Section 4, followed by an illustrative example in Section 5. Section 6 discusses possible extensions of the proposed sample size procedures and Section 7 draws conclusions.

2 |. GEE ANALYSES OF CRXO TRIALS

2.1 |. Statistical model

We consider a CRXO trial with n clusters receiving intervention (condition A) and usual care (condition B) during two consecutive periods. We focus on the AB-BA crossover so that nπ clusters (0 < π < 1) receive intervention in the first period, followed by control in the second period (AB sequence), while the remaining n(1 − π) clusters receive control in the first period, and switch to intervention in the second period (BA sequence). We assume randomization is conducted such that the nπ clusters receiving the AB sequence are randomly chosen from the n clusters. Let Y_ijk be the outcome from individual k (k = 1, …, m_ij) in period j (j = 1, 2) and cluster i (i = 1, …, n), where m_ij is the number of individuals observed from the ith cluster in period j (cluster-period size) with cluster size m_i = m_i1 + m_i2. Assuming no carryover effect, we use the following generalized linear model to relate the intervention to the marginal mean outcome μ_ijk as

$$g\left({\mu }_{ijk}\right)={\tau }_j+\delta X_{ij},$$ (1)

where τ_j is the jth period effect, δ is the population-averaged intervention effect, and X_ij = 1 if cluster i receives the intervention in period j and zero otherwise. Note that our choice of marginal mean model (1) follows standard conventions in CRXO analysis that adjust for period effect or time trend.^5,10,19 We further let θ = (τ₁, τ₂, δ)ˊ be the vector of parameters and X_i = (X_i1, X_i2)ˊ be the ith treatment sequence, so that X_i = (1, 0)ˊ for clusters receiving the AB sequence and X_i = (0, 1)ˊ for clusters receiving the BA sequence. Finally, we denote ϕ as the dispersion parameter and h(μ_ijk) as a known variance function of the mean, so var(Y_ijk) = ϕh(μ_ijk).

Aside from the marginal mean structure, two types of correlations should be considered in modeling outcome data from a cross-sectional CRXO trial,^8–10 the within-period correlation, corr(Y_ijk,Y_ijkˊ) = α₀ for k ≠ kˊ and j = 1, 2, and the interperiod correlation, corr(Y_i1k, Y_i2kˊ) = α₁ for all k, kˊ. Similar to the work of Teerenstra et al,²⁰ we define the two-period nested exchangeable correlation structure for cluster i as

$$R_i(\alpha )=\left(1-{\alpha }_0\right)I_{m_i}+\left({\alpha }_0-{\alpha }_1\right){\oplus }_{j=1}^2{J}_{m_{ij}}+{\alpha }_1{J}_{m_i},$$ (2)

where α = (α₀, α₁)ˊ is the vector of correlation parameters, I_u is a u-dimensional identity matrix, $J_s=1_s{1}_s^{\prime }$ is an s by s matrix of ones and “⊕” is a block diagonal operator with nonzero matrices along the diagonal and zero values elsewhere. It is worth noting that valid correlation values are among those such that R_i(α) is positive definite and can be determined analytically by assessing the positivity of eigenvalues of R_i(α). We show in Web Appendix A that R_i(α) has the following three distinct eigenvalues:

$$\begin{gathered} {\lambda }_{i1}=1-{\alpha }_0, \\ {\lambda }_{i2}=1+\left(\frac{m_i}{2}-1\right){\alpha }_0-{\left\{{\left(\frac{m_{i1}-m_{i2}}{2}\right)}^2{\alpha }_0^2+m_{i1}{m}_{i2}{\alpha }_1^2\right\}}^{\frac{1}{2}}, \\ {\lambda }_{i3}=1+\left(\frac{m_i}{2}-1\right){\alpha }_0+{\left\{{\left(\frac{m_{i1}-m_{i2}}{2}\right)}^2{\alpha }_0^2+m_{i1}{m}_{i2}{\alpha }_1^2\right\}}^{\frac{1}{2}}. \end{gathered}$$

Therefore, it follows that the correlation structure is positive definite if and only if −1∕(m_i∕2 − 1) < α₀ < 1 and

$${\alpha }_1^2<\left(\frac{1+\left(m_{i1}-1\right){\alpha }_0}{m_{i1}}\right)\left(\frac{1+\left(m_{i2}-1\right){\alpha }_0}{m_{i2}}\right).$$

Furthermore, since the GEE analysis requires the inverse of the m_i × m_i correlation structure R_i, we derive a closed-form inverse in Web Appendix B as

$$R_i^{-1}(\alpha )=\frac{1}{1-{\alpha }_0}{I}_{m_i}-{\oplus }_{j=1}^2\frac{{\alpha }_0-{\alpha }_1}{{\psi }_{ij}\left(1-{\alpha }_0\right)}{J}_{m_{ij}}-\left({\oplus }_{j=1}^2\frac{{\alpha }_1}{{\psi }_{ij}}{I}_{m_{ij}}\right)J_{m_i}\left({\oplus }_{j=1}^2\frac{1-\left(m_{i1}/{\gamma }_{i1}+m_{i2}/{\gamma }_{i2}\right){\alpha }_1}{{\psi }_{ij}}{I}_{m_{ij}}\right),$$ (3)

where Ψ_ij = 1 + (m_ij − 1)α₀ − m_ijα₁ and γ_ij = Ψ_ij + Ψ_ij(m_i1/Ψ_i1 + m_i2/Ψ_i2)α₁. The significance of the closed-form expression (3) lies in the computational savings arising from not having to numerically invert R_i, a procedure which would otherwise be prohibitive for large cluster sizes that commonly arise in CRXO and other cluster trials.

2.2 |. Estimating equations

We let $Y_i={\left(Y_{i11},Y_{i12},\dots ,Y_{i2m_{i2}}\right)}^{\prime }$ and ${\mu }_i={\left({\mu }_{i11},{\mu }_{i12},\dots ,{\mu }_{i2m_{i2}}\right)}^{\prime }$ be the collection of the m_i outcomes and marginal means from cluster i in both periods. The GEE extend the quasi-likelihood score equations of Wedderburn²¹ to multivariate outcomes and only require the specification of a marginal mean model coupled with a working covariance model.¹⁶ Based on the marginal mean model (1), we define D_i = ∂μ_i∕∂θ′, r_ijk(μ_ijk) = (Y_ijk – μ_ijk)∕h^1/2(μ_ijk), and let the working covariance of Y_i be $V_i=\varphi A_i^{1/2}{\tilde{R}}_i{A}_i^{1/2}$, where A_i is a m_i by m_i diagonal matrix with diagonal elements h(μ_ijk) and ${\tilde{R}}_i$ is the nested exchangeable working correlation. The GEE estimator of θ is the solution to the following θ-estimating equations:

$$\sum _{i=1}^n{D}_i^{\prime }{V}_i^{-1}\left(Y_i-{\mu }_i(\theta )\right)=0.$$ (4)

To estimate the within-period and interperiod correlations, a set of α-estimating equations are required. The standard estimating equations used in Prentice¹⁸ tend to produce biased correlation estimates in finite samples¹⁷; therefore, we adopt the MAEE introduced by Preisser et al,¹⁷ which provide finite-sample bias-correction to the correlation estimates. Since it has been shown that the MAEE can substantially reduce the bias in estimating the correlation parameters with a small number of clusters,¹⁷ we recommend the use of MAEE for the analysis of CRXO trials to improve the reporting of the within-period and the interperiod correlation coefficients, which is critical for future planning of trials. Additionally, Lu et al²² reported that bias correction for α-estimation via MAEE mildly improved the confidence interval coverage of the marginal mean regression parameters based upon the model-based covariance estimator. This result is relevant because the GEE model-based variance estimator has been found to provide better coverage for θ than the empirical sandwich variance estimator in studies with a moderate number of large clusters.²³ Our main focus in this article is the inference for the marginal mean model, and thus, we present the details of MAEE in Web Appendix C.

2.3 |. Bias-corrected covariance estimation

When the number of clusters n is sufficiently large (say, greater than 40), the GEE estimator for the marginal mean model parameters $\widehat{\theta }$ approximately follows a multivariate normal distribution with mean θ and covariance estimated by the model-based estimator ${\mathrm{\Sigma }}_1^{-1}={\left({\sum }_{i=1}^n{D}_i^{\prime }{V}_i^{-1}{D}_i\right)}^{-1}$, or by the sandwich estimator ${\mathrm{\Sigma }}_1^{-1}{\mathrm{\Sigma }}_0{\mathrm{\Sigma }}_1^{-1}$, where

$${\mathrm{\Sigma }}_0=\sum _{i=1}^n{C}_i{D}_i^{\prime }{V}_i^{-1}{B}_i\left(Y_i-{\mu }_i\right){\left(Y_i-{\mu }_i\right)}^{\prime }{B}_i^{\prime }{V}_i^{-1}{D}_i{C}_i,$$ (5)

and both Σ₀ and Σ₁ are evaluated at $\widehat{\theta }$ and $\widehat{\alpha }$. When C_i = I_p and $B_i=I_{m_i}$, Equation (5) is the uncorrected sandwich estimator of Liang and Zeger,¹⁶ which we denote as BC0. BC0 provides valid inference regardless of the correct specification of the working correlation R_i, as long as the number of clusters is sufficiently large, while the consistency of the model-based variance estimator is dictated by the correct specification of the correlation structure. However, the residual vector, $Y_i-{\mu }_i(\widehat{\theta })$, tends to be biased toward zero with a limited number of clusters, and BC0 is likely to underestimate the variance; specific choices of matrices C_i and B_i could provide a partial correction to the finite-sample bias. Denote the cluster leverage²⁴ as $H_i=D_i{\left({\sum }_{i=1}^n{D}_i^{\prime }{V}_i^{-1}{D}_i\right)}^{-1}{D}_i^{\prime }{V}_i^{-1}$. The finite-sample correction of Kauermann and Carroll,²⁵ or BC1, is given by C_i = I_p and $B_i={\left(I_{m_i}-H_i\right)}^{-1/2}$; the finite-sample correction of Mancl and DeRouen,²⁶ or BC2, is given by C_i = I_p and $B_i={\left(I_{m_i}-H_i\right)}^{-1}$. Both BC1 and BC2 estimate cov(Y_i) based on the leverage-adjusted residuals, $B_i(Y_i-{\mu }_i(\widehat{\theta }))$, correcting for the finite-sample bias in the raw residuals in a multiplicative fashion. We also evaluate the finite-sample correction by Fay and Graubard,²⁷ or BC3, given by $C_i=\mathrm{diag}\{{(1-\min \{\zeta ,{[D_i^{\prime }{V}_i^{-1}{D}_i{\mathrm{\Sigma }}_1^{-1}]}_{jj}\})}^{-1/2}\}$ and $B_i=I_{m_i}$, where the bound parameter ζ is a user-defined constant (< 1) with a default value 0.75. In brief, the multiplicative correlation factor C_i is motivated by expanding the estimating function around the truth and assuming the working variance is approximately proportional to the true variance. Because the matrix elements of the cluster leverage are between 0 and 1, we generally have BC0 < BC1 < BC2.¹⁷ Furthermore, Scott et al²⁸ has shown that BC3 tends to be close to BC1, and BC1 can be derived as a modified version of BC3. Bias-corrected covariance estimators for the correlation estimates can be similarly defined. However, since our focus here is the inference for marginal mean parameters, we refer the readers to the work of Preisser et al¹⁷ for a complete discussion on the inference for correlation parameters.

3 |. POWER AND SAMPLE SIZE REQUIREMENTS

Under H₀ : δ = δ₀, the asymptotic variance of $\sqrt{n}(\widehat{\delta }-{\delta }_0)$ is determined by the lower right element of the asymptotic covariance of $\sqrt{n}(\widehat{\theta }-{\theta }_0)$, which we denote for convenience as ${\sigma }_{\delta }^2=n\mathrm{var}(\widehat{\delta })$. By the asymptotic normality of the GEE estimator, we could use the z-test statistic $\sqrt{n}(\widehat{\delta }-{\delta }_0)/{\widehat{\sigma }}_{\delta }$ for sample size determination. A two-sided z-test to detect an effect size δ = δ₀ ≠ 0 with a prescribed type I error rate ε₁ and power 1 − ε₂ requires the number of clusters to satisfy

$$n=\frac{{\left(z_{{\epsilon }_1/2}+z_{{\epsilon }_2}\right)}^2{\sigma }_{\delta }^2}{{\delta }_0^2},$$ (6)

where z_q is the qth quantile of the standard normal distribution. To account for the uncertainty in estimating the asymptotic variance of $\widehat{\delta }$, we could alternatively reference the same statistic to a t-distribution. Specifically, a two-sided t-test to detect the same effect size with a type I error rate ε₁ and power 1 − ε₂ requires the number of clusters to satisfy

$$n=\frac{{\left(t_{{\epsilon }_1/2,n-p}+t_{{\epsilon }_2,n-p}\right)}^2{\sigma }_{\delta }^2}{{\delta }_0^2},$$ (7)

where t_q,u is the qth quantile of the t-distribution with u degrees of freedom. To calculate ${\sigma }_{\delta }^2$, we follow the work of Shih²⁹ and assume the covariance of Y_i to be known as var(Y_i) = V_i. Therefore, ${\sigma }_{\delta }^2$ is the appropriate element of $n{\mathrm{\Sigma }}_1^{-1}$. Because the t-distribution has a heavier tail compared with the standard normal, we would expect that the normality-based test is more likely to result in a liberal test size with the use of an uncorrected sandwich estimator than the t-test. However, a comparison of the two tests may have different implications for the analysis of CRXO trials depending upon the choice of bias-corrected sandwich variance estimators, which are known to provide different degrees of inflation relative to the uncorrected sandwich variance.

To derive the sample size formula, we further assume a balanced design so that m_i = m and m_i1 = m_i2 = m∕2 for all i = 1, …, n. In this case, we know from Web Appendix B that the analytical inverse of the correlation matrix reduces to

$$R_i^{-1}(\alpha )=\frac{1}{1-{\alpha }_0}{I}_m-\frac{{\alpha }_0-{\alpha }_1}{{\lambda }_2\left(1-{\alpha }_0\right)}{I}_2\otimes J_{m/2}-\frac{{\alpha }_1}{{\lambda }_2{\lambda }_3}{J}_m,$$

where ⨂ is the Kronecker product and λ₂ = 1 + (m/2 − 1)α₀ – mα₁/2 = Ψ_ij and λ₃ = 1 + (m/2 − 1)α₀ + mα₁/2 = γ_ij are two distinct eigenvalues of the correlation matrix. Based on this simplification, we present the sample size formulae for continuous and binary outcomes.

3.1 |. Continuous outcomes

Under mean model (1), we can write the design matrix of cluster i as Z_i = [I₂, X_i] ⊗ 1_m/2 such that g(μ_i) = Z_iθ. If Y_ijk is continuous, we can assume g to be the identity link such that model (1) becomes μ_i = Z_iθ. We further have h(μ_ijk) = 1, and therefore, the dispersion parameter ϕ becomes the marginal variance of the outcome σ². Since D_i = Z_i, we can write

$${\mathrm{\Sigma }}_1=\frac{1}{{\sigma }^2}\sum _{i=1}^n{Z}_i^{\prime }{R}_i^{-1}{Z}_i=\frac{1}{{\sigma }^2}\sum _{i=1}^n\left(\begin{array}{cc}M& M{X}_i\\ X_i^{\prime }M& X_i^{\prime }M{X}_i\end{array}\right),$$

where the constant matrix is

$$M=\frac{m}{4{\lambda }_2{\lambda }_3}\left(\begin{array}{cc}{\lambda }_2+{\lambda }_3& {\lambda }_2-{\lambda }_3\\ {\lambda }_2-{\lambda }_3& {\lambda }_2+{\lambda }_3\end{array}\right).$$ (8)

It can be shown by matrix inversion that the bottom-right element of $n{\mathrm{\Sigma }}_1^{-1}$ is

$${\sigma }_{\delta }^2=\frac{{\lambda }_2{\sigma }^2}{m\pi (1-\pi )}.$$ (9)

Inserting (9) into Equation (6), we obtain the required total sample size to achieve a prescribed type I error rate ε₁ and type II error rate ε₂ as

$$n={\left(z_{{\epsilon }_1/2}+z_{{\epsilon }_2}\right)}^2\frac{{\lambda }_2{\sigma }^2}{\pi (1-\pi )m{\delta }_0^2},$$ (10)

Analogously, the required sample size based on a t-test should satisfy

$$n={\left(t_{{\epsilon }_1/2,n-p}+t_{{\epsilon }_2,n-p}\right)}^2\frac{{\lambda }_2{\sigma }^2}{\pi (1-\pi )m{\delta }_0^2}.$$ (11)

Notice that, if the sample size calculation is based on a t-test, Equation (11) should in principle be solved iteratively to obtain the required n. In practice, an approximate approach is to replace the t-percentiles with z-percentiles and multiply the result by factor (n + 1)/(n − 1).³⁰

We recognize that (10) and (11) are the usual sample size formulae for individually randomized control trials with variance inflation factor or design effect, λ₂ = 1 +(m/2 − 1)α₀ – mα₁/2. This design effect suggests that the required number of clusters increases as the within-period correlation α₀ increases and the interperiod correlation α₁ decreases. Furthermore, if we assume an equal number of clusters receiving the AB and BA sequences, namely, π = 1∕2 in Equation (10), the sample size formula is equivalent to that of Giraudeau et al^9,12 based on a multivariate normal model coupled with cluster-level analysis. As noted by Giraudeau et al,^9,12 the design effect λ₂ is equivalent to the inflation factor introduced by Donner et al³¹ for the split-cluster designs with applications in periodontal studies.

We remark that model (1) assumes a period effect τ_j, while the multivariate normal model adopted by Giraudeau et al⁹ did not consider such a period effect. To further explore this discrepancy, we also derive the sample size formula assuming no period effect (setting τ₁ = τ₂) in Web Appendix D. We find that the result is identical to formula (10) when π = 1/2. In other words, the incorporation of period effect makes no difference in sample size calculation under the CRXO design if an equal number of clusters are randomized to receive each treatment sequence. However, in general cases where τ₁ ≠ τ₂, our formula should provide a more accurate characterization of sample size because it is an explicit function of π. On the other hand, the magnitude of period effect does not affect power calculation since formulae (10) and (11) are free of τ_j. In fact, this also explains why formula (10) is consistent with the one given by Cunningham³² for a three-level cluster design with randomization carried out at the second level. Finally, it is immediate from variance expression (9) that, given n and m, the most efficient design is provided by setting π = 1/2 so that an equal proportion of clusters are assigned to each treatment sequence.

3.2 |. Binary outcomes

When Y_ijk is binary, we focus on the logistic model with g specified as the canonical logit function. The marginal mean of cluster i is μ_i = (1 + exp(−Z_iθ))⁻¹, where Z_i is defined in Section 3.1. Following standard conventions, we assume the variance function h(μ_ijk) = μ_ijk(1 − μ_ijk) and no overdispersion, so ϕ = 1. Define P₁ = (1 + exp(−τ₁ − δ₀))⁻¹ and P₂ = (1 + exp(−τ₂))⁻¹ to be the expected prevalence in periods 1 and 2 for clusters receiving the AB sequence. Similarly, we define Q₁ = (1 + exp(−τ₁))⁻¹ and Q₂ = (1 + exp(−τ₂ − δ₀))⁻¹ to be the expected prevalence in periods 1 and 2 for clusters receiving the BA sequence. Using these quantities, a simple way to express the detectable effect size in terms of the log odds ratio (OR) is

$${\delta }_0=\frac{1}{2}\log \left[\frac{P_1/\left(1-P_1\right)}{P_2/\left(1-P_2\right)}\right]-\frac{1}{2}\log \left[\frac{Q_1/\left(1-Q_1\right)}{Q_2/\left(1-Q_2\right)}\right].$$ (12)

We comment here that an equivalent approach to calculate the detectable effect size based on the expected group-by-period prevalence is provided in the work of Rochon³³ using generalized least squares. Next, we define A_i = Ω_i ⨂ I_m/2, where Ω_i = diag{P₁(1 − P₁), P₂(1 − P₂)} for clusters receiving the AB sequence and Ω_i = diag{Q₁(1 − Q₁), Q₂(1 − Q₂)} for clusters receiving the BA sequence. Since D_i = A_iZ_i, we obtain

$${\mathrm{\Sigma }}_1=\sum _{i=1}^n{D}_i^{\prime }{A}_i^{-1/2}{R}_i^{-1}{A}_i^{-1/2}{D}_i=\sum _{i=1}^n\left(\begin{array}{cc}{\mathrm{\Omega }}_i^{1/2}M{\mathrm{\Omega }}_i^{1/2}& {\mathrm{\Omega }}_i^{1/2}M{\mathrm{\Omega }}_i^{1/2}{X}_i\\ X_i^{\prime }{\mathrm{\Omega }}_i^{1/2}M{\mathrm{\Omega }}_i^{1/2}& X_i^{\prime }{\mathrm{\Omega }}_i^{1/2}M{\mathrm{\Omega }}_i^{1/2}{X}_i\end{array}\right)=\frac{nm}{4{\lambda }_2{\lambda }_3}\left(\begin{array}{cc}\mathrm{\Lambda }& \xi \\ {\xi }^{\prime }& \omega \end{array}\right),$$

where the form of matrix M is defined through Equation (8). After some algebraic simplifications, we obtain the bottom right scalar element

$$\omega =\left({\lambda }_2+{\lambda }_3\right)\left[\pi P_1\left(1-P_1\right)+(1-\pi )Q_2\left(1-Q_2\right)\right].$$ (13)

Furthermore, the upper right component vector is

$$\xi =\pi \left(\begin{array}{c}\left({\lambda }_2+{\lambda }_3\right)P_1\left(1-P_1\right)\\ \left({\lambda }_2-{\lambda }_3\right)\sqrt{P_1\left(1-P_1\right)P_2\left(1-P_2\right)}\end{array}\right)+(1-\pi )\left(\begin{array}{c}\left({\lambda }_2-{\lambda }_3\right)\sqrt{Q_1\left(1-Q_1\right)Q_2\left(1-Q_2\right)}\\ \left({\lambda }_2+{\lambda }_3\right)Q_2\left(1-Q_2\right)\end{array}\right),$$ (14)

and the upper left component matrix is

$$\begin{gathered} \mathrm{\Lambda }=\pi (\begin{array}{c}\left({\lambda }_2+{\lambda }_3\right)P_1\left(1-P_1\right)\\ \left({\lambda }_2-{\lambda }_3\right)\sqrt{P_1\left(1-P_1\right)P_2\left(1-P_2\right)}\end{array}\begin{array}{c}\left({\lambda }_2-{\lambda }_3\right)\sqrt{P_1\left(1-P_1\right)P_2\left(1-P_2\right)}\\ \left({\lambda }_2+{\lambda }_3\right)P_2\left(1-P_2\right)\end{array}) \\ +(1-\pi )(\begin{array}{c}\left({\lambda }_2+{\lambda }_3\right)Q_1\left(1-Q_1\right)\\ \left({\lambda }_2-{\lambda }_3\right)\sqrt{Q_1\left(1-Q_1\right)Q_2\left(1-Q_2\right)}\end{array}\begin{array}{c}\left({\lambda }_2-{\lambda }_3\right)\sqrt{Q_1\left(1-Q_1\right)Q_2\left(1-Q_2\right)}\\ \left({\lambda }_2+{\lambda }_3\right)Q_2\left(1-Q_2\right)\end{array}). \end{gathered}$$ (15)

Then, the bottom right element of $n{\mathrm{\Sigma }}_1^{-1}$ is ${\sigma }_{\delta }^2=4{\lambda }_2{\lambda }_3/\left[m\left(\omega -{\xi }^{\prime }{\mathrm{\Lambda }}^{-1}\xi \right)\right]$ by block matrix inversion. Plugging this quantity into Equation (6), we obtain the required sample size based on a z-test

$$n={\left(z_{{\epsilon }_1/2}+Z_{{\epsilon }_2}\right)}^2\frac{4{\lambda }_2{\lambda }_3}{m{\delta }_0^2(\omega -{\xi }^{\prime }{\mathrm{\Lambda }}^{-1}\xi )},$$ (16)

and the required sample size based on a t-test as

$$n={\left(t_{{\epsilon }_1/2,n-p}+t_{{\epsilon }_2,n-p}\right)}^2\frac{4{\lambda }_2{\lambda }_3}{m{\delta }_0^2(\omega -{\xi }^{\prime }{\mathrm{\Lambda }}^{-1}\xi )},$$ (17)

where ω, ξ, and Λ are specified through (13), (14), and (15). Although the aforementioned sample size estimation involves a two-by-two matrix calculation, it can be easily calculated by a closed-form matrix inversion formula or implemented in existing software given prespecified values for the prevalence estimates and the correlations. Unlike the previous formulae for continuous outcomes, the sample size formulae for binary outcomes depend on the two distinct eigenvalues λ₂ and λ₃. The sample size formulae derived for binary outcomes further depend on the magnitude of period effect, as the binomial variance is an explicit function of the marginal mean, and therefore, sensitivity analysis may be warranted to examine how sample size and power would change due to different assumptions of the time trend. Although the impact of the correlation values on the required sample size is challenging to study analytically, we have numerically assessed the value of ${\sigma }_{\delta }^2$ as a function of α₀ and α₁ and illustrated their relationship in Web Appendix E. In general, as the within-period correlation α₀ increases, ${\sigma }_{\delta }^2$ becomes larger and more clusters are required to achieve a fixed power. By contrast, as the interperiod correlation α₁ increases, ${\sigma }_{\delta }^2$ decreases and fewer clusters are required. If no period effect is assumed, namely, τ₁ = τ₂, the sample size formulae reduce to familiar forms and we provide a related discussion in Web Appendix D.

4 |. A SIMULATION STUDY

To evaluate the utility of the proposed power formulae for GEE analyses of CRXO trials, we conduct a small simulation study. Our objective is twofold, ie, to (i) determine the empirical type I error rates for the GEE Wald-tests (a valid test should maintain the nominal type I error rate), and (ii) identify valid tests whose empirical power corresponds well with the power predicted by our sample size formulae. In other words, we use the predicted power as a benchmark value and compare the empirical power estimates of each test with the benchmark. The findings from the simulations could inform practical choices among testing procedures for a trial powered by the proposed formula. Specifically, if a test maintains the nominal type I error rate, and its empirical power is equal to or slightly higher than predicted, then that test is a preferred analysis option for a CRXO trial powered by the proposed formula. On the other hand, if the empirical power of a valid test is lower than predicted, then the proposed sample size formula may be less useful for designing a study that will be analyzed with that test, or equivalently, the test becomes less attractive for a trial powered by our formula.

4.1 |. Simulation design

Correlated continuous outcomes in each cluster are generated from a multivariate normal distribution with mean specified by μ_ijk = τ_j + δX_ij and variance ϕR(α), where R(α) is the nested exchangeable correlation matrix. We set ϕ = 1 so the outcomes have unit marginal variance. For illustration purposes, we let τ₁ = 0 and τ₂ ∈ {−0.1, −0.2} to simulate a gently decreasing period effect. We remark that the conclusions are insensitive to the magnitude of the period effect since the subsequent GEE analyses account for them. We fix the effect size δ/ϕ^1/2 at zero for studying type I error and choose δ/ϕ^1/2 ∈ {−0.2, −0.25, −0.3, −0.4} for studying power. Correlated binary outcomes in each cluster are generated from a binomial model with marginal mean specified by logit(μ_ijk) = τ_j + δX_ij and correlation R(α) using the method of Qaqish³⁴ (see the appendix in the work of Preisser et al³⁵ for an example of the Qaqish method). Baseline prevalence for clusters under the control condition $e^{{\tau }_1}/\left(1+e^{{\tau }_1}\right)$ is set to be 0.3 or 0.5, and a gently decreasing period effect is assumed so that the OR $e^{{\tau }_2}/e^{{\tau }_1}\in \{0.8,0.9\}$. We have also examined scenarios with larger magnitudes of decreasing period effect where more clusters are required to achieve a prespecified power. Since findings are similar and cluster trials typically involve a limited number of clusters, those results are omitted for brevity. The effect size in OR is fixed at 1 for studying type I error and varied from δ ∈ {0.4, 0.5, 0.6} for studying power. For both types of outcomes, we choose α = {α₀, α₁} ∈ {(0.05, 0.025), (0.05, 0.04), (0.07, 0.035), (0.1, 0.05), (0.1, 0.08)} to represent a range of different correlation values. Particularly, the values of α₀ are chosen to reflect commonly reported intraclass correlation coefficients in parallel CRTs,^36,37 and α₁/α₂ ∈ {0.5, 0.8} similar to the work of Forbes et al.¹⁰

Since CRTs usually involve a small number of clusters, we vary the total number of clusters n from 8 to 26. For each value of n, we consider cluster sizes m between 30 to 150 that give predicted power of at least 80% for both tests. For simplicity, we assume a balanced design such that an equal number of clusters are randomized to receive the AB and BA sequences, and further that m/2 individuals are included in each period for each cluster. For each scenario, we generate 1000 data sets and fit GEE for the marginal mean model and MAEE for the nested exchangeable correlation structure (the bias-corrected moment estimator for ϕ in Web Appendix C is used with continuous outcomes and ϕ is set to 1 for binary outcomes). Both the two-sided z-test and the t-test have been considered for testing H₀ : δ = 0, and each test is coupled with five different variance estimators for $\widehat{\delta }$, namely, the model-based variance, BC0, BC1, BC2, and BC3. The convergence rate exceeds 95% for the majority of simulations except for a few cases, and a complete summary of parameter constellation with model convergence is available in Web Tables 1 and 2. We fix the nominal type I error rate at 5%, and consider an empirical type I error rate between 3.6% and 6.4% to be acceptable according to the margin of error under a binomial model with 1000 replications. Since the predicted power for each scenario is at least 80%, we consider an empirical power that differs at most 2.6% from the predicted value to be acceptable.

4.2 |. Results

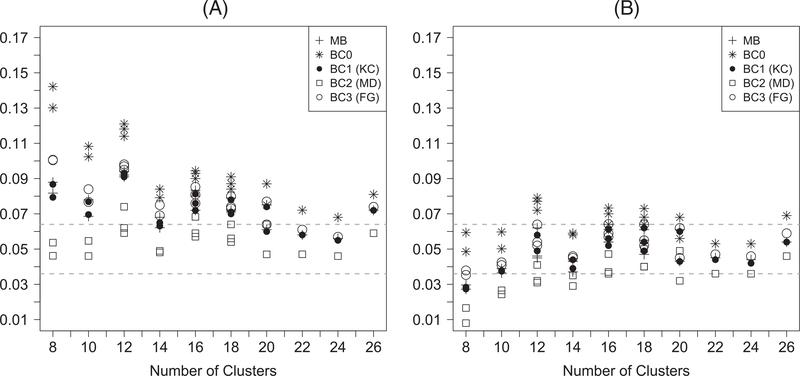
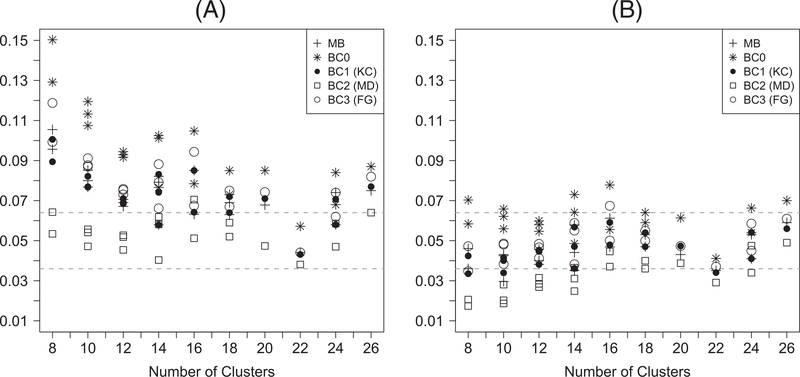
Figure 1 presents the empirical type I error rates of the z-test and the t-test with different variance estimators for continuous outcomes. It is clear that the z-test carries a more liberal size compared with the corresponding t-test. The type I error rate of the z-test is close to nominal with the use of BC2, when there are at least 20 clusters (slightly liberal otherwise), while the z-tests with model-based variance, BC0, BC1, or BC3 tend to carry an inflated test size. Although the t-test with BC0 still tends to be liberal, the t-test maintains the valid type I error rate (occasionally conservative with a small number of clusters) with the use of BC1, BC3, and the model-based variance. Additionally, the use of BC2 with a t-test is often conservative. The simulation results regarding type I error rate for binary outcomes are similar and presented in Figure 2.

FIGURE 1.

Empirical type I error rates for generalized estimating equation–based (A) z-tests and (B) t-tests for continuous outcomes. MB: model-based variance; BC0: uncorrected sandwich variance; BC1: Kauermann-Carroll sandwich variance; BC2: Mancl-DeRouen sandwich variance; BC3: Fay-Graubard sandwich variance. The acceptable bounds are shown with the dashed horizontal lines. For each value of n, there may be multiple points with the same symbol indicating results with different values of m and α₀ and α₁

FIGURE 2.

Empirical type I error rates for generalized estimating equation–based (A) z-tests and (B) t-tests for binary outcomes. MB: model-based variance; BC0: uncorrected sandwich variance; BC1: Kauermann-Carroll sandwich variance; BC2: Mancl-DeRouen sandwich variance; BC3: Fay-Graubard sandwich variance. The acceptable bounds are shown with the dashed horizontal lines. For each value of n, there may be multiple points with the same symbol indicating results with different values of m and α₀ and α₁

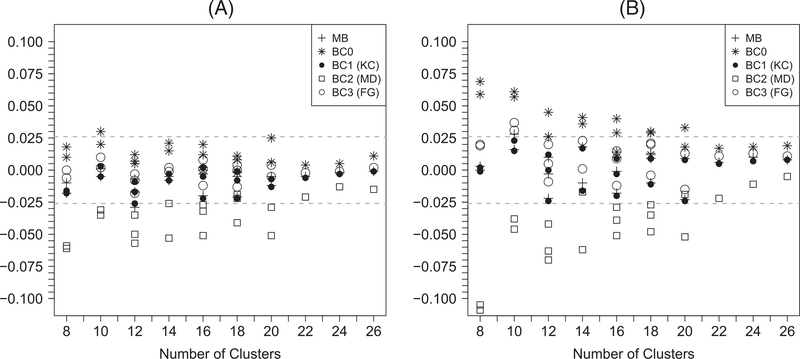
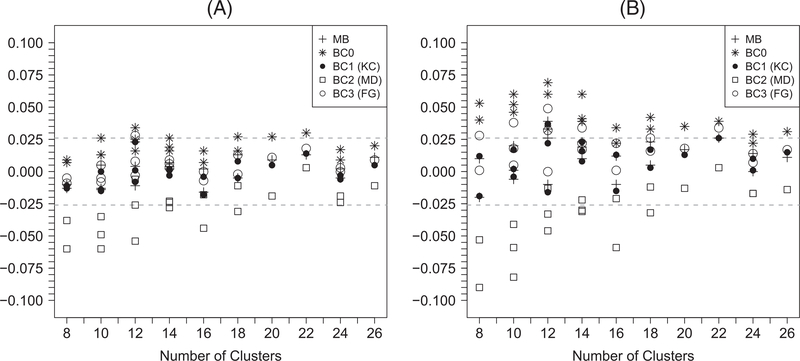
Figure 3 summarizes the difference between empirical and predicted power for each scenario with continuous outcomes (a full tabulation of numeric results are available in Web Table 3). The z-test with BC2 has lower power than predicted when the number of clusters is no greater than 20. Although the z-tests with the rest of variance estimators (model-based variance, BC0, BC1, and BC3) have power close to prediction, caution is needed when interpreting this result since those tests tend to be liberal under the null. On the other hand, the t-tests with model-based variance, BC1, or BC3 have power that corresponds reasonably well with the prediction, while the empirical power of the t-test with BC2 is still lower than predicted when the number of clusters is no greater than 20. Simulation results regarding power for binary outcomes are qualitatively similar and presented in Figure 4 and Web Table 4.

FIGURE 3.

Differences between the empirical power and the predicted power of generalized estimating equation–based (A) z-tests and (B) t-tests for continuous outcomes. MB: model-based variance; BC0: uncorrected sandwich variance; BC1: Kauermann-Carroll sandwich variance; BC2: Mancl-DeRouen sandwich variance; BC3: Fay-Graubard sandwich variance. The acceptable bounds are shown with the dashed horizontal lines. For each value of n, there may be multiple points with the same symbol indicating results with different values of m and α₀ and α₁

FIGURE 4.

Differences between the empirical power and the predicted power of generalized estimating equation–based (A) z-tests and (B) t-tests for binary outcomes. MB: model-based variance; BC0: uncorrected sandwich variance; BC1: Kauermann-Carroll sandwich variance; BC2: Mancl-DeRouen sandwich variance; BC3: Fay-Graubard sandwich variance. The acceptable bounds are shown with the dashed horizontal lines. For each value of n, there may be multiple points with the same symbol indicating results with different values of m and α₀ and α₁

5 |. APPLICATION TO THE TTANGO STUDY

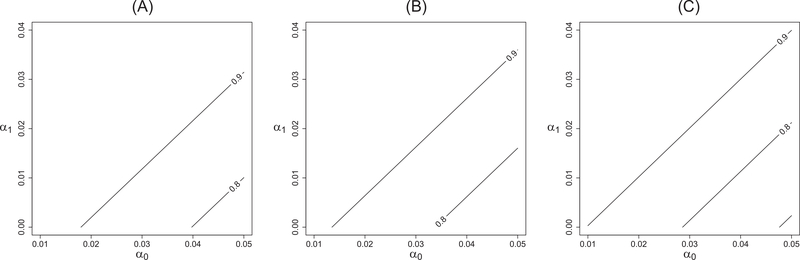
To illustrate our sample size procedure, we consider determing the required number of clusters for the “TEST, TREAT, ANd GO” (TTANGO) trial. The TTANGO study is a CRXO trial evaluating the clinical effectiveness of molecular point-of-care test in reducing rates of repeat positive infections among Aboriginal people with Chlamydia trachomatis (CT) or Neisseria gonorrhea (NG) in Australia.³⁸ Each regional or remote health service that provides primary health care to Aboriginal people is a cluster, which is the unit of randomization. The intervention is the addition of point-of-care testing to the standard diagnostic procedures to reduce CT or NG infection. Each health service will receive one year of intervention and one year of standard care in random order. Specifically, we consider π = 1/2 so that half of the recruited health services will receive the AB sequence and the other half undergo the BA sequence. The binary outcome is whether a patient had a positive retest within three months. Based on the expected number of recruited patients and disease prevalence estimates, we anticipated that 23 patients with CT or NG will be recruited for each health service in each year, and therefore, m = 46. Based on prior studies, it is expected that Q₁ = 30% of patients would have a positive re-test within 3 months during the standard care period. Furthermore, if there is no period effect (τ₁ = τ₂), the positive CT or NG retest rates were expected to reduce to 15%, which suggests a detectable effect size in OR as e^δ ≈ 0.4. The investigators estimated the within-period correlation α₀ to be less than 0.05 and we fixed 0.05 as a conservative value. Although the interperiod correlation α₁ is typically less commonly reported in previous studies, there is prior evidence that α₁ is less than α₀^39,40 and a common choice is α₁ = α₀/2.⁹ Without the period effect, we found that n = 12 health services were required to achieve 80% power with a subsequent analysis using a GEE t-test, which is shown to be valid in Section 4 for this number of clusters. We conducted a sensitivity analysis by varying the plausible values of α₀ and α₁ in Figure 5. A gently increasing or decreasing period effect was assumed in panel (A) and (C) in addition to no period effect in panel (B). The contour plot suggests that n = 12 would provide a reasonably powered trial in most scenarios except when α₀ is close to 0.05 and α₁ is close to zero. Particularly, the decreasing period effect τ₂ < τ₁ represents a more challenging scenario where the test power slightly decreases for a fixed sample size (panel (C)). In the TTANGO trial, the gently decreasing time trend may be considered plausible due to the potentially improved standard care practices over time.

FIGURE 5.

The power contour corresponding to a generalized estimating equation t-test with n = 12 health services and cluster size m = 46 by varying within-period correlation α₀ and interperiod correlation α₁ under (A) a gently increasing period effect, (B) no period effect, and (C) a gently decreasing period effect. All displayed correlation values ensure a positive definite correlation matrix and are hence plausible

6 |. POSSIBLE EXTENSIONS OF SAMPLE SIZE METHODOLOGY

Two extensions of the proposed sample size methodology for CRXO trials are possible, ie, extensions to the use of marginal models with log or identity link and to cohort designs. Although a comprehensive investigation are beyond the scope of this article and is a topic for further research, we provide a brief outline of the extended sample size methodology, and connect with the formulae introduced in Section 3.

6.1 |. Marginal models with alternative link functions

We have assumed g to be the logit link in Section 3.2, based on which the sample size formulae (16) and (17) are established. Based on the logit link, the OR, exp(δ₀), is fairly straightforward to interpret as the effect size, widely used in practice, and has a long history in statistics. However, others may prefer relative risk (RR) or RD as an alternative measure of effect size, for which g is often assumed as the log or identity link, respectively. Given that D_i = ∂μ_i/∂θˊ = diag{μ_i}Z_i for log link and D_i = Z_i for identity link, the values of δ₀, ω, ξ and Λ, in Section 3.2 must be updated. Therefore, the revised sample size formulae share the exact same structures of (16) and (17), with appropriately revised values for δ₀, ω, ξ, and Λ. Additional technical details and the complete forms of the sample size formulae based on RR and RD are included in Web Appendix F. Although the closed-form formulae are available for RR- and RD-based marginal models, the practical application of these models may be less attractive since the estimated marginal probability could exceed its natural bound (below zero or above one) with log or identity link. Furthermore, log-binomial models are also known to exhibit frequent nonconvergence and alternative solutions based on modified Poisson regression have been proposed in the CRT literature.⁴¹

6.2 |. Cohort CRXO designs

The proposed sample size methodology also readily extends to cohort CRXO trials where the same set of individuals from each cluster are followed up in both periods. In that case, we could still describe the marginal mean structure using model (1). However, for the within-cluster association structure, an additional correlation parameter, α₂, is required since repeated measurements are taken from the same individual.⁴² Consequently, the two-period nested exchangeable correlation structure is extended to a two-period block exchangeable correlation structure as in the work of Li et al.⁴³ The derivations provided in Section 3.1 and 3.2 can be repeated with the block exchangeable structure to obtain the revised sample size formulae. We provide additional technical details for such an extension in Web Appendix G. Our main finding is that the revised sample size formulae share the exact same structures with (10), (11), (16), and (17), with λ₂ and λ₃ replaced by the appropriate eigenvalues of the block exchangeable matrix. Despite the possibility of methodological extension to cohort CRXO trials, we caution that additional design considerations must be placed in practice to address the increased likelihood of carryover effect.

7 |. DISCUSSION

Cluster-specific (conditional) and population-averaged (marginal) models are two types of models that have been used in the analysis of CRTs. In this article, we describe the use of a marginal model fitted with GEE to design a CRXO trial, allowing for both within-period and interperiod correlations. The intervention effect estimands are equivalent between a conditional model and a marginal model with continuous outcomes and identity link function. However, with binary outcomes, the estimands may differ between a conditional model and a marginal model for nonlinear link functions, and the one from a marginal model bears a straightforward population-averaged interpretation.¹⁵ Moreover, marginal models are appealing because the within-cluster correlation matrix is specified separately from the marginal mean model in contrast to generalized linear mixed models where the random effects specification impacts both treatment estimand interpretation and the marginal correlation structure of the outcomes that often does not have a closed form.¹⁴

We have provided a novel characterization of the variance inflation factor (design effect) incluster trials with continuous outcomes. We found that an eigenvalue of the two-period nested exchangeable correlation matrix, λ₂, corresponds to the design effect in CRXO trials under the balanced design. We note that this is the same design effect suggested previously for CRXO trials under the mixed-effects modeling framework.^9,32 In fact, our eigenvalue characterization of variance inflation factor is more general and applies to other designs. For instance, the usual design effect 1 + (m − 1)α₀ used for parallel CRTs¹ is the eigenvalue of the exchangeable correlation matrix parameterized by a single intraclass correlation α₀. For a three-level CRT, we could similarly show that the design effect is an eigenvalue of the general nested exchangeable correlation matrix.²⁰ For a cohort stepped wedge CRT, Li et al⁴³ further derived the design effect as a function of the two leading eigenvalues of the block exchangeable correlation matrix involving three correlation parameters.

For continuous outcomes, the design effect λ₂ = 1 + (m/2 − 1)α₀ − mα₁/2 is monotonically increasing in the within-period correlation, α₀, and decreasing in the interperiod correlation, α₁. The same relationship also holds in general for binary outcomes. This suggests that larger values of the within-period correlation will increase the required sample size, while larger values of the interperiod correlation will reduce the required sample size. In planning a CRXO trial, sample size and power calculation should be guided by reasonable estimates of these two correlation parameters. The within-period correlation, α₀, is similar to the conventional intraclass correlation in a parallel cluster randomization trial, whose values may be found in previous trials with a similar endpoint. To date, the interperiod correlation has been reported in only a few studies.^39,40 In the absence of prior estimates, it has been suggested that a practical choice for α₁ is half the within-period correlation α₀.^9,44 Because of the uncertainty in correlation estimates, a sensitivity analysis could be conducted for sample size and power by varying values of α₀ and α₁ within a plausible range. Notably, the combination of (α₀, α₁) is only valid if the resulting correlation matrix is positive definite, as required by the eigenvalue constraints presented in Section 2.1 and Web Appendix A. To aid the planning of future CRXO trials, we strongly advocate reporting the within-period and interperiod correlation estimates in the analysis stage. Furthermore, the MAEE described in Section 2.2 are recommended to reduce the finite-sample bias in estimating the correlations.¹⁷

Although the magnitude of the period effect is ancillary for sample size consideration with continuous outcomes, such an effect should be accounted for in estimating sample size with binary outcomes. In some cases, reasonable estimates of the period effect may be available from previous studies and could be used for planning the CRXO trial. In the absence of such information, we could carry out a sensitivity analysis by varying the period effect assumption. For the TTANGO study, we considered that a gently decreasing period effect was plausible since the standard care practice might improve over time.

We have demonstrated infinite samples that the GEE z-test with the use of BC2 maintains the nominal size and provides adequate power relative to the proposed formula, when the number of clusters is at least 20. In this case, the z-test would be the preferred choice for design and analysis due to its higher power compared with the t-test. Our finding regarding the property of z-test echoes the previous simulation study by Lu et al²² in a parallel design. When the number of clusters was below 20, the t-test with the model-based variance, BC1, or BC3 might be preferred for CRXO trials since they are valid under the null and has power that corresponds well with analytical prediction. Similarly, the t-test with the use of BC1 has also been recommended in the work of Teerenstra et al²⁰ for the analysis of a three-level CRT and the work of Li et al⁴⁵ for the analysis of a parallel cluster trial under constrained randomization. Finally, a keen reviewer also noticed that the empirical type I error rate of the z-test is more sensitive to the choice of variance estimators than that of t-test, while the empirical power of the former is less sensitive to the choice of variance estimators than that of the latter. This indicates the behavior of GEE-based tests could depend on the true effect size, and future research may be carried out to investigate whether such a pattern holds for GEE analyses of other designs.

For the design and analysis of cross-sectional CRXO trials, an implicit assumption often made is that all period-specific sets of individuals are representative of the population of the cluster. In situations where the population of each cluster is identified prerandomization (eg, randomizing classes in a school to arms), splitting the cluster population by randomly assigning its members to periods provides representative samples of the common source population. In other situations where individuals are recruited postrandomization (eg, randomizing hospitals or clinics whose patients are not identified prerandomization), covariate balance between the two sets of samples should be examined in the analysis phase. If there exist prognostic covariates that are unequally distributed between the intervention and control periods (potential confounding), the regression mean model (1) could be extended to adjust for potential confounders. However, a priori knowledge of covariates, and in particular, their joint distribution and effects on outcome are unlikely to be known in most real-world cluster trials. In any case, simulation-based sample size calculation and sensitivity analysis that incorporate individual-level confounding could be informative in the design phase.

One simplification we made in deriving the sample size formulae is the assumption of equal cluster-period size. It has been shown that cluster size imbalance may reduce power in analyzing CRTs and a closed-form relative efficiency formula (of unequal versus equal cluster sizes) is available for use in the design phase.^46,47 However, previous reports exclusively focused on the use of an exchangeable correlation structure in the parallel setting,⁴⁸ and may not be directly generalized to CRXO designs. Therefore, a comprehensive study is warranted to investigate the efficiency property of GEE analyses of CRXO trials coupled with the nested exchangeable correlation structure, perhaps by varying the distribution of the cluster-period sizes (eg, coefficient of variation or the harmonic mean¹⁰), and the values of α₀ and α₁; the findings could help assess the performance of the proposed sample size procedure under imbalanced cluster-period sizes. Additional research is also needed for an relative efficiency formula appropriate for CRXO designs. Another limitation is that we have assumed the nested exchangeable working correlation is the correctly specified within-cluster association structure. However, the GEE estimator is robust to misspecification of the association structure and will remain consistent to the marginal intervention effect estimand. If it is anticipated in the design phase that the working correlation may be mis-specified, one could follow the general idea of Rochon³³ to develop a modified sample size procedure for CRXO trials based on the empirical sandwich variance.