Super-elasticity of three-dimensionally cross-linked graphene materials all the way to deep cryogenic temperatures

Kai Zhao; Tengfei Zhang; Huicong Chang; Yang Yang; Peishuang Xiao; Hongtao Zhang; Chenxi Li; Chandra Sekhar Tiwary; Pulickel M Ajayan; Yongsheng Chen

doi:10.1126/sciadv.aav2589

. 2019 Apr 12;5(4):eaav2589. doi: 10.1126/sciadv.aav2589

Super-elasticity of three-dimensionally cross-linked graphene materials all the way to deep cryogenic temperatures

Kai Zhao ^1,^2,^*, Tengfei Zhang ^1,^2,^*, Huicong Chang ^1,², Yang Yang ^1,², Peishuang Xiao ^1,², Hongtao Zhang ^1,², Chenxi Li ^1,², Chandra Sekhar Tiwary ³, Pulickel M Ajayan ^3,^†, Yongsheng Chen ^1,^2,^†

PMCID: PMC6461457 PMID: 30993202

For the first time, invariant super-elasticity from cryogenic 4 to 1273 K was observed for a bulk 3D cross-linked graphene foam.

Abstract

Until now, materials with high elasticity at deep cryogenic temperatures have not been observed. Previous reports indicated that graphene and carbon nanotube–based porous materials can exhibit reversible mechano-elastic behavior from liquid nitrogen temperature up to nearly a thousand degrees Celsius. Here, we report wide temperature–invariant large-strain super-elastic behavior in three-dimensionally cross-linked graphene materials that persists even to a liquid helium temperature of 4 K, a property not previously observed for any other material. To understand the mechanical properties of these graphene materials, we show by in situ experiments and modeling results that these remarkable properties are the synergetic results of the unique architecture and intrinsic elastic/flexibility properties of individual graphene sheets and the covalent junctions between the sheets that persist even at harsh temperatures. These results suggest possible applications for such materials at extremely low temperature environments such as those in outer space.

INTRODUCTION

Elastic materials, especially those that allow reversible large-strain deformation, can find demand in diverse engineering applications (1–5). However, mechanical properties of almost all existing materials are temperature dependent. In particular, ductility and/or elasticity are generally compromised when considerably lowering the temperature (2, 6). This is because the atomic bonding and/or molecular motion that essentially determine the mechanical properties are inherently thermally activated (2, 7–9). This restricts the range of applications of almost all these materials in variable-temperature conditions, particularly from extremely low to extremely high temperatures. For example, typical elastic polymers have high elasticity in a limited temperature range (e.g., −55° to 300°C for the well-known silicone rubber), above which the material softens and breaks down and below which the material undergoes a glass transition and gradually loses its elasticity (becomes hard and brittle) (10). Conventional inorganic materials, such as metals, ceramics, and their alloys and composites, tolerate only a very small elastic strain [for example, about 0.5% for metals (7) and less than 0.1% for ceramics (7)]. There have been some attempts to create super-elastic alloys (11) and ceramics (12) with reversible phase transformation, rendering a class of elastic materials with improved elastic strain range (generally less than 10% tensile or compressive strain). However, their mechanical properties and elastic strain range remain temperature dependent and typically deteriorate because of atomic diffusion (7, 13). Recently, it has been found that the introduction of structural hierarchy and cellular architecture can improve material utilization with further enlarged elastic strain range and ductility [e.g., polymer foams (2), metallic microlattices (14), and ceramic nanostructures (15)]. However, temperature dependence still exists because the mechanical properties are intrinsically determined by both the solid constituent and their cellular architecture (e.g., polymer foams generally have a glass transition issue) (2). A well-known exception, Elinvar alloys (16), have temperature-independent mechanical properties from a hundred of degree Celsius above zero to tens of degree Celsius below zero. However, its low-temperature limit is far from the desired cryogenic region. Meanwhile, their elastic strain range is quite small (usually <0.2%), and creep is also an issue (17). Thus, it will be unprecedented to have bulk materials exhibiting both large-strain elasticity and temperature-invariant mechanical properties over a wide temperature range, particularly down to the deep cryogenic temperatures.

Carbon nanomaterials, such as carbon nanotube (CNT) and graphene, have been thought as suitable building blocks for making temperature-invariant elastic materials because of their extraordinary mechanical properties, flexibility, and exceptional thermal stability (18–21). However, it has been a great challenge to realize these intrinsic properties in the bulk material scale, because restacking and/or agglomeration of nano-individuals (graphene sheets or nanotubes) severely diminish or weaken most of their intrinsic properties. Previous works have demonstrated compressive elastic three-dimensional (3D) graphene materials that show large and reversible deformation at room temperature (RT) (22–24), in liquid nitrogen (77 K), and in inert atmosphere up to 900°C (25). However, to the best of our knowledge, cryogenic mechanical properties for bulk graphene materials at liquid helium temperature have not been studied yet. This is probably because the experiments at such low temperatures are very challenging and also because no such material with super-elasticity at deep cryogenic temperatures has been reported or predicted before. In addition, we noticed that some intrinsic mechanical properties of the single-layer graphene, including elasticity and other moduli at various temperatures, have been investigated theoretically (26, 27) and experimentally (28, 29). However, studies for these mechanical properties at super-low temperatures (liquid helium temperature) are also rare (30, 31), and there are no reports yet for a material to demonstrate temperature-invariant mechanical properties in a wide temperature range. Inspired by these studies and the unique structure of our 3D cross-linked graphene (3DGraphene) foam (25), together with the intrinsic properties of an individual graphene sheet (26, 27), we wondered whether the super-compressive elasticity and other mechanical properties of graphene foams would be maintained at extreme temperatures, such as at liquid helium temperature, and whether the remarkable mechanical properties of graphene materials could be maintained both at deep cryogenic temperatures and at bulk scales. If cross-linked graphene (foam) structures show repeatable high deformability without fracture at temperature as low as liquid helium, then there would be no parallel to such materials so far. It should also be noted that almost all materials would behave quite differently and, in some cases, might demonstrate unexpected properties at deep cryogenic temperatures, as compared to that at RT or even at liquid nitrogen temperature. For example, the well-known phenomena superconductivity (32) and superfluidity (33) were first discovered until the temperature was down to ~4 K. Therefore, studies for the properties (including mechanics) at such deep cryogenic temperatures should be important, and some unexpected properties might be observed.

In this work, we systematically and quantitatively investigated the mechanical properties of the 3DGraphene foam using a homemade in situ large-strain mechanical analysis system (more details in Supplementary Methods). This system simultaneously realizes real-time recording of the deformations for the materials without resetting the tested sample and breaking the vacuum in a wide temperature range, continuously starting from deep cryogenic temperature at 4 K to a high temperature of 1273 K. We find that even at liquid helium temperature, the 3DGraphene foam, in which randomly oriented graphene sheets are chemically cross-linked through covalent bonds mainly at the edges (Fig. 1A), exhibits the same mechanical properties as those at RT, including nearly fully reversible super-elastic behavior of up to 90% strain, unchanged Young’s modulus, near-zero Poisson’s ratio, and great cycle stability. Furthermore, these mechanical properties are also quantitatively proved to be temperature invariant over a wide temperature range from deep cryogenic temperature (liquid helium, 4 K) to 1273 K. These remarkable and macroscopic temperature-invariant mechanical (super-elastic) properties even down to deep cryogenic temperatures have not been observed/reported for any bulk material before. These unique mechanical behaviors arise from the remarkable temperature-invariant elasticity and flexibility of the individual graphene sheets and covalent junctions between the sheets in the bulk material. The temperature-invariant elasticity and flexibility of graphene is the result of the unique bonding of carbon in the sp²-hybridized planar graphene sheets with soft out-of-plane bending modes and strong in-plane stretching modes with very high energy for defect formation (26, 34). The intrinsic temperature-invariant mechanical properties of graphene, combined with the unique cross-linked structure and high porosity of the 3DGraphene material, makes the bulk material fully elastic and other temperature-invariant mechanical properties down to liquid helium temperature. These results also imply that using the same strategy (cross-linking in the 3D manner) and other 2D structure units as the building blocks, some other unprecedented properties might be achieved for the bulk assembly of recently emerging 2D materials.

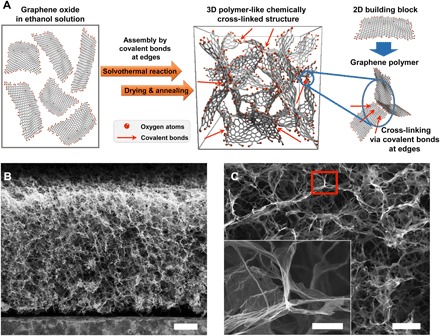
Fig. 1 — (A) Schematic of the formation and structure of the bulk 3DGraphene foam. The spatial density of oxygen atoms mainly at the edges in the schematic was adjusted for clarity but did not represent its actual ratio in the material. (B) Cross-sectional scanning electron microscopy (SEM) image of the 3DGraphene foam (along the axial direction) with a homogeneous and highly porous structure. (C) Magnified SEM of the 3DGraphene foam. Inset: Magnification of the selected area that demonstrates that graphene sheets are chemically cross-linked together at the cell node (with quasi-hexagonal configuration). Scale bars, 200 μm (B), 50 μm (C), and 10 μm [inset of (C)].

RESULTS

Structure of the 3DGraphene foam

The 3DGraphene foam, with an absolute density (ρ_a) of ~1.50 mg cm⁻³, was obtained using a modified method based on our previous work (25) and then cut carefully to regular shapes using laser for accuracy of measurements (fig. S13). It exhibits a porous, open-cell honeycomb structure and graphene only–based interconnected framework, with tens of micrometers of separation between the individual graphene sheets (the cell walls) to form a large void volume (Fig. 1, B and C). As demonstrated in previous works (25, 35), the cell walls were proved to be mostly single-layer (with some minor few layers) graphene sheets, while the graphene cell walls were chemically cross-linked together at the cell node (Fig. 1A and inset of Fig. 1C). As shown in Fig. 1A, in the graphene oxide (GO) suspension, the graphene sheets should be distributed homogeneously at individual sheet state because of its low concentration and strong solvent interaction between GO and the solvent molecules (including the strong H bonding) (25, 36). Then, under solvothermal synthesis conditions, adjacent single-layer graphene sheets were chemically cross-linked with each other mainly at the edges via oxygen-containing groups, such as OH, COOH, and epoxy groups that are mainly located on GO sheet edges, to form a monolithic 3D chemically linked network (25). This structure was essentially homogeneous and isotropic (fig. S14), similar to the theoretically proposed 3D cross-linked graphene monolithic networks (37, 38), resulting in essentially isotropic mechanical properties.

Apparatus for in situ and variable-temperature mechanical measurements

For variable-temperature mechanical measurements from 4 to 1273 K, a homemade mechanical analysis apparatus (fig. S2) that can withstand liquid helium temperatures was used to overcome the temperature limitation of commercial systems. It also simultaneously integrated a cryogenic system (with liquid helium or liquid nitrogen loop filled in the refrigerant pipelines) and a heating system (with electric resistance wire heater) in a homemade extreme temperature–resistant chamber (more details in Supplementary Methods), which could provide a continuously and widely variable temperature environment without moving/resetting the sample or breaking the vacuum. An endoscope was also introduced into the sample chamber to in situ observe and record the sample deformations during the mechanical measurements. To exclude the influence introduced by the interaction between the pore/cell walls (graphene sheets) and the fluid (gases or liquids, as the situations of most previous works) (23, 25) on the mechanical properties, we performed all the tests here for the 3DGraphene material from cryogenic to high temperature in high vacuum (10⁻⁴ Pa). The introduced endoscope, combined with the continuously operable sample chamber under vacuum, makes it possible to in situ observe and record in real time the mechanical properties of the sample, which has not been reported before.

Mechanical properties at deep cryogenic temperatures

The mechanical properties of the 3DGraphene foam were first investigated by a single uniaxial compress-release operation at 4 K using the abovementioned homemade mechanical analysis apparatus (more details in Supplementary Methods). The super-compressive elasticity of the material, which combines both large strain up to 90% and high reversibility, was directly observed at the deep cryogenic temperature of 4 K (Fig. 2A and movie S1). Note that the stress-strain curves at RT (298 K) and deep cryogenic temperature (4 K) almost completely overlap with each other (Fig. 2B). Both the compression plots start from linear elastic behavior and deviate to a deformation with a near-plateau stress and then to a rapid increase of stress up to 90% strain. Upon unloading, the stress dropped sharper than during compression with a slight hysteresis. The responsible mechanisms for the hysteresis could include the intra- and interwall van der Waals adhesion and friction during deformation and de-binding of the cell walls to recover their nearly original configuration upon unloading (4, 39). For our 3DGraphene foam, it is believed that during compression, some local positions of the graphene cell walls would get closer and might have contact with each other and then reversibly separate upon release. Sliding would occur between the graphene cell walls. This is supported by literatures (39) and also the in situ scanning electron microscopy (SEM) observation zoom-in at the cell walls during the compress-release process (Figs. 3 and 5A; figs. S15, S18, and S23; and movies S3 and S4). As schematically shown in fig. S15E, this process would dissipate/consume energy because of van der Waals adhesion and/or mechanical friction between the contacted graphene cell walls. Moreover, if the covalent bond and single-layer graphene behave in fully elastic deformation without internal friction or damping as generally accepted (40, 41), then the unbuckling process would not consume energy. In addition, the cell walls in our 3DGraphene foam consist mainly of single-layer graphene sheets without interlayer shear/friction (42) during unbuckling. This is different from most traditional materials (2, 14), where the internal friction or damping will consume notable energy during the buckling/unbuckling process. The sample showed a high recoverability in such a single uniaxial compress-release operation (~99.4% of its original height at 4 K), and the ~0.6% residual strain is only observed in the first-time measurement and is not accumulated in the subsequent ones (see more details in the cyclical test below). The small (~0.6%) residual strain in the first cycle is mostly because of some tiny imperfections, such as those of surface contact between the sample and the test head, and local imperfections of graphene cell wall that resulted in an irreversible change in the structure at the initial cycling. The remarkable elasticity of the 3DGraphene foam is preserved from RT to deep cryogenic temperature. Stepwise compress-release cycles with increasing maximum strain values (30, 50, 70, and 90% strains) were also carried out along the axial and radial directions of the sample at 4 K. The negligible difference among the results (Fig. 2C) demonstrated both the isotropy and strain independence of the elastic behavior at deep cryogenic temperatures.

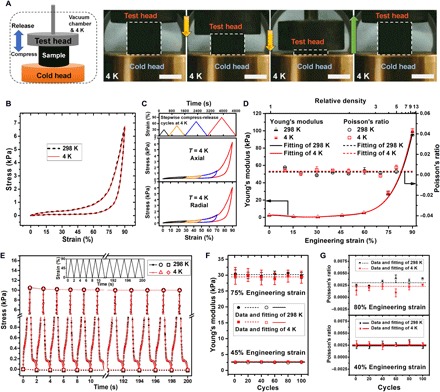
Fig. 2 — (A) Schematic of measurement and optical images demonstrating reversible super-compressive elasticity of the 3DGraphene foam at 4 K. Dotted boxes mark the cylindrical sample with both 15 mm diameter and height; yellow and green arrows indicate the moving directions of the test head. The brightness and contrast of the optical images are enhanced for clarity. Scale bars, 1 cm. (B) The single-cycle stress-strain curve at 4 K is almost completely the same with the curve at RT (both along the axial direction at a rate of 0.1% strain s⁻¹). (C) Strain versus time curve of a stepwise compress-release measurement with increasing maximum strains but a constant rate (0.1 strain s⁻¹) and the corresponding stress-strain curves of such measurements at 4 K along both axial and radial directions. (D) Young’s modulus and Poisson’s ratio plots versus applied engineering strain (and the relative density of the compressed 3DGraphene foam) at 4 and 298 K, showing almost identical Young’s modulus variation trend and constantly near-zero Poisson’s ratio. (E) Stress-time curves of 100 compress-release cycles along the axial direction at 4 and 298 K. Each 2-s cycle was performed between 0 and 90% strain at a rate of 90% strain s⁻¹, as shown in the inset. The stress values at 0 and 90% strains of each cycle were emphasized by labeling symbols, and the dashed and dotted lines correspond to least-squares fittings of stress at 0 and 90% strains of each temperature, respectively. Almost identical and overlapping stress-time curves indicate the great cycle stability of the material maintained even at cryogenic temperature. (F and G) The Young’s moduli (F) and near-zero Poisson’s ratios (G) both remain unchanged during the cycling test at 4 and 298 K, showing the great cycle stability down to deep cryogenic temperatures. Error bars in (D), (F), and (G) represent SDs for repeated measurements.

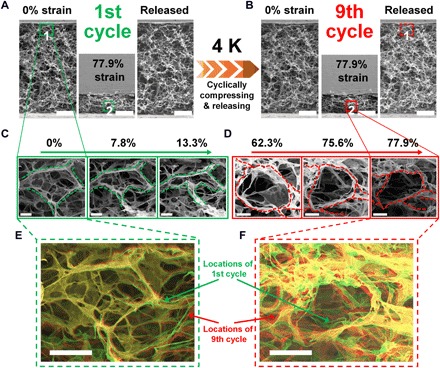
Fig. 3 — (A and B) Totally reversible deformation of the microstructure for the first (A) and ninth (B) compress-release cycles. (C and D) Magnifications of the marked zones with increasing compressive strains, demonstrating deformations of the graphene sheets during compression. (E and F) Overlaps of marked zone 1 with 0% strain in the first and ninth compress-release cycles (E) and of marked zone 2 with 77.9% strains in the first and ninth compress-release cycles (F), and the images of the first and ninth cycles are digitally processed with green and red colors, respectively. Scale bars, 100 μm (A and B), 10 μm (C and D), and 20 μm (E and F).

To precisely obtain the Young’s modulus at specific engineering strains, unloading-reloading cycles with small true strain changes were periodically inserted in a single monotonic compression of the sample (Supplementary Methods and fig. S3). These measurements were carried out at both RT and 4 K, and the statistical results (repeated measurements of five samples and five times for each one) are summarized in Fig. 2D. The Young’s modulus remained almost constant at first and then increased with the engineering strain (also the increasing density of the compressed 3DGraphene foam). This trend was similar to that of the 3DGraphene foam in a fluid environment (air) (25) but, in comparison, exhibited slightly smaller modulus as expected (due to the vacuum condition). The obtained Young’s modulus and its variation with engineering strain at deep cryogenic temperature of 4 K were almost identical with the RT ones (only tiny deviations were observed at large engineering strains) (Fig. 2D), showing that the Young’s moduli of the 3DGraphene foam are also maintained at deep cryogenic temperatures during its compression. Then, the sample was subjected to similar periodically inserted unloading-reloading cycle measurements (Supplementary Methods and fig. S4) to determine the Poisson’s ratios at different engineering strains at both RT and 4 K. The Poisson’s ratios of the material were observed to be always near zero and independent of strain and unaffected by low temperature (Fig. 2D). The isotropy of Young’s moduli and near-zero Poisson’s ratios in compression of the material also remained from RT to cryogenic temperature (figs. S16 and S17).

The cycle stability of the mechanical behavior of the material was studied through cyclical compression and release processes for 100 times. This operation was conducted successively at 298 and 4 K for the same sample, and the stress-time curves are shown in Fig. 2E. For the 100 loading-unloading cycles, each at 4 or 298 K, the almost identical stress versus time curve of every cycle indicates the great cycle stability and also the temperature invariance between RT and 4 K. The stress at 90% strain (larger than what was shown in Fig. 2A because of the much larger strain rate here) for the initial several cycles decreased slightly, which is also caused by the probe head–sample contact issue due to the sample’s surface roughness, but the stress remains almost constant in the subsequent cycles. Moreover, the tiny residual strain in the very initial loading-unloading cycle mentioned above does not accumulate and does not affect the subsequent cycles. The entire plot of the 100 cycles at 4 K almost completely overlaps with that at 298 K, indicating the remarkable elasticity and cycle stability even at 4 K. Furthermore, both the Young’s moduli (Fig. 2F; taking 75 and 45% engineering strains as examples) and Poisson’s ratios (Fig. 2G; taking 80 and 40% engineering strains as examples) remain stable during the 100 cycles at both 4 and 298 K. These values are essentially the same as those at 4 and 298 K, with small statistical errors in the entire cyclical measurement.

Micro–real-time in situ observation of mechanical properties at 4 K

The mechanical behaviors of the macroscopic bulk graphene material at deep cryogenic temperatures prompt us to look directly at the microscopic structure and local graphene building blocks and their behaviors in the compress-release process at 4 K. For this purpose, we used a homemade sample platform with a precise positioner system equipped with heating/cooling head, which was set into a SEM system for the variable-temperature dynamic observation of the global and local deformation without resetting the sample or breaking the vacuum condition (Supplementary Methods). The SEM images (Fig. 3, fig. S18, and movie S3) of the microscopic structure change for the 3DGraphene foam samples during compress-release cycles at cryogenic temperature of 4 K were recorded by such a modified SEM system in the low- temperature mode. Note that the microscopic structure was observed to behave almost completely reversibly during the compress-release cycles, with even large strains of up to 90% (Fig. 3, A and B; fig. S18, A and C; and movie S3). The highly elastic and reversible bending/buckling of the graphene sheets (cell walls) and deformation of the nodes, which dominate the deformation of the microstructure under compressive strain, could also be directly observed (Fig. 3, C and D, and fig. S18, B and D). The highly reversible compressive deformation for the bulk structure and the covalently interconnected individual graphene was further demonstrated by the almost unchanged SEM images before and after the compress-release cycles at 4 K (Fig. 3, E and F).

Temperature-invariant mechanical properties from 4 to 1273 K

The uniaxial and monotonic compress-release measurement was performed on the same sample at 12 different temperatures from 4 to 1273 K (movie S2 demonstrates compress-release cycles at 1273 K, similar to movie S1 for 4 K). The results are presented in a colored 3D surface form, and the stress exhibits no variation with the wide temperature range in both compression (Fig. 4A) and release (Fig. 4B) processes. Similarly, the Young’s moduli and Poisson’s ratios of the 3DGraphene foam during compression were also measured at temperatures of 77, 873, and 1273 K. At each specific strain, very similar Young’s moduli at different temperatures were observed (Fig. 4C and fig. S19). Simultaneously, all Poisson’s ratios measured in a wide strain range between 10 and 80% and temperatures between 77 and 1273 K have almost the same values very close to zero, with only a very small fluctuation in magnitudes of ~10⁻³ (Fig. 4D and fig. S20). Combining these results and those at 4 K (Fig. 2D), the Young’s modulus and near-zero Poisson’s ratio of the material demonstrated a remarkable temperature independence in a wide temperature range from liquid helium temperature to 1273 K. The cycle stability of the 3DGraphene foam’s mechanical properties (including stress-strain behavior, Young’s modulus, and Poisson’s ratio) was also studied successively at 77, 873, and 1273 K by cyclical compression and release, similar to those at 4 K. Negligible degradation of mechanical performance was persistently observed (fig. S21) for the same sample that underwent hundreds of complete cycles with up to 90% strain. The isotropic characteristic for the mechanical properties of the 3DGraphene foam is also temperature independent from 4 to 1273 K (figs. S16, S17, and S22). Furthermore, after high temperature mechanical tests, all the mechanical properties (stress-strain behavior, Young’s modulus, Poisson’s ratio, and cycle stability) at RT and low temperature remained unchanged (fig. S29) for the same sample.

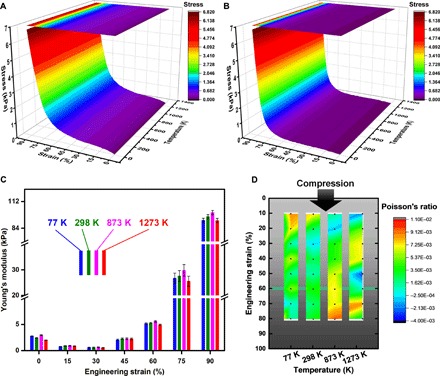
Fig. 4 — (A and B) 3D surface graphs of the stress dependence on strain and temperature in the compression (A) and release (B) processes of the 3DGraphene foam, both exhibiting clear temperature invariance from 4 to 1273 K. (C and D) Grouped column graph (C) of Young’s modulus and intensity map graph of Poisson’s ratios (D) at a series of engineering strains measured at different temperatures, showing excellent temperature invariance of both Young’s modulus and near-zero Poisson’s ratio. Error bars represent SDs for the repeated measurements.

DISCUSSION

Although it has not been experimentally confirmed so far, many theoretical works have proposed that 3D monolithic ordered or random networks could be formed using graphene as the building unit and that they should not only be structurally stable but also exhibit, in principle, graphene intrinsic properties and other unique properties, including mechanical properties, at the macroscopic scale (37, 38, 43, 44). In these theoretically proposed monolithic 3D graphene network models, the graphene units are linked together by sp² and/or sp³ carbon atoms at the junctions. The graphene foam material that was made here constitutes a 3D array of interconnected micrometer-scale units, where graphene sheets are linked mainly at the sheet edges through C─C or C─O bonds (25, 35). It can be seen as one example of such theoretically proposed 3D graphene networks, although it is not an ordered one, which provides a base for theoretical investigation of our material.

Thus, we carried out a theoretical investigation of the macroscopic mechanical properties of the 3DGraphene foam and its underlying mechanisms. Previous theoretical works generally modeled 3D graphene materials with a simple 3D network of graphene sheets without considering the connections, and their mechanical properties were analyzed with the relative density based on the classic theory of cellular materials and continuum mechanics (25, 39). In addition, few reports studied the 3D graphene materials by molecular dynamics simulations (43, 44). However, both of them mostly ignored the real situations of connections between the atomically thin graphene sheets in the bulk material. It would be ideal to build an accurate structural model for our 3DGraphene foam. However, the difficulties related to the high irregularity and randomness of the structure does not make this possible at the current stage (3, 39, 43, 45). However, it is possible to make some reliable estimations based on the basic configuration of the architecture and the cell elements (cell walls and nodes), with a honeycomb-configured cell walls having a commonly used connectivity of three (37, 38) in single nodes (Fig. 1C and fig. S14). This is a reliable assumption for most cellular materials (2). Considering the complexity/disorder of the actual foam structure, we have made some modifications to improve the accuracy of the model (Supplementary Discussion). In situ observations have verified the microscopic structure of the material and elasticity through compress-release cycles at both a cryogenic temperature of 4 K (Figs. 3 and Figs. 5A, figs. S18 and S23, and movie S3) and a high temperature of 1273 K (Fig. 5A, fig. S23, and movie S4). Moreover, the temperature-invariant and reversible deformations of the individual graphene sheets such as bending and buckling under compressive strain of the sample were also directly observed (Figs. 3 and Figs. 5A and figs. S18 and S23) in our experiments. Furthermore, rigorous comparison between the global microstructure and the zoom-in observation at the graphene cell walls and junctions before and after the mechanical tests directly confirmed the structural stability at the microscale (Figs. 3 and Figs. 5A and figs. S18 and S23). On the basis of these results and using a simplified model with periodic honeycomb-like architecture (detailed in Supplementary Discussion), we have carried out the simulation of the elastic behavior for such graphene network considering several compressive deformation modes of the graphene structure, including elastic response of the cross-linked covalent bonds and elastic bending and buckling of the graphene cell wall (3, 39, 43, 46). In addition, our model combined previous theoretical conclusions of intrinsic mechanical properties of graphene and covalent bonds (47, 48), modified continuum mechanics, and cellular structure model (2, 49, 50). Compared with previous reports (25, 39), the graphene cell wall is treated as an atomically thin 2D graphene crystal, while the node is treated as covalent bonds rather than continuum graphene joint. Furthermore, to investigate the temperature dependence of the mechanical properties of the 3DGraphene foam in the compression process, we also introduced the intrinsic temperature dependence/influence of the structural elements (graphene cell wall and covalent bond) and their deformation (such as the dihedral angle torsion and bond angle bending of the covalent bonds that were located and occurred at the nodes and bending/buckling of the graphene cell walls) and corresponding parameters for this simulation into the calculation (Supplementary Discussion). The mechanical modeling and calculation that were carried out in our study began on the basis of structural and molecular mechanics (40). Note that our modeling and calculation started with a theoretical structural model (2, 37) and the intrinsic mechanical properties of covalent bonds (51, 52) and single-layer graphene sheets (53, 54).

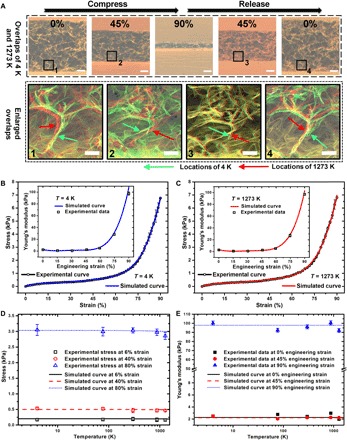
Fig. 5 — (A) Overlays of the in situ SEM images for the full compress-release cycles of the same sample at 4 and 1273 K and enlargements for the labeled areas, showing that the structural stability and the reversible deformations of graphene sheets at microscopic scale are wide temperature independent. Green and red arrows mark the same graphene sheets at 4 and 1273 K. Scale bars, 100 μm (top row) and 25 μm (bottom row). (B and C) The theoretically simulated stress-strain curves agree well with the experimental results for the compression process of the 3DGraphene foam at 4 K (B) and 1273 K (C) and also with the well-matched simulated Young’s modulus–engineering strain curves for 4 K [inset of (B)] and 1273 K [inset of (C)]. (D and E) Theoretically simulated temperature dependence curves of stress (D) and Young’s modulus (E) fit well with the experimental data, suggesting almost negligible temperature influence on the stress-strain behavior and Young’s modulus in the compression process of the 3DGraphene foam down to cryogenic temperatures. All error bars represent SDs for the repeated measurements.

The theoretically simulated results of the material’s mechanical properties in compression agreed well with the experimental results. The obtained simulated stress-strain curves and the Young’s modulus in the compression process at a deep cryogenic temperature of 4 K match well with the experimental mechanical behavior observed, as shown in Fig. 5B (and fig. S27), as well as those at a high temperature of 1273 K (Fig. 5C and fig. S27) and at RT (figs. S26 and S27). The simulated curves of the temperature dependence for the stress (Fig. 5D) and Young’s modulus (Fig. 5E) at different engineering strains also fit well with the experimental results. These results demonstrated that the origins of the temperature-invariant properties of the 3DGraphene foam are the quite small temperature influence on the mechanical properties of the chemically cross-linked nodes (covalent bonds) and the graphene sheets (cell walls) from 4 to 1273 K. The aforementioned simulation results are plotted in Fig. 5E, the insets of Fig. 5 (B and C), and the inset of fig. S26, which all matched well with the experimental results from the Young’s modulus measurement (and experimental results from the normal stress-strain curves). The simulation results not only demonstrated the same origins of the temperature invariance of Young’s modulus down to a deep cryogenic temperature of 4 K but also proved the rationality of both our whole simulation and the approximate method for obtaining Young’s modulus using the normal stress-strain curve.

These results indicate that both the unique architecture and the intrinsic mechanical properties of the graphene building blocks and covalent connections must all be critically important for the observed remarkable temperature-invariant mechanical properties of the graphene bulk material. First, graphene layers as the building blocks for the cell walls are stable over the whole investigated temperature range down to the deep cryogenic region and intrinsically have negligible temperature-dependent elastic and mechanical properties (27, 47, 55). Specifically, the individual single-layer graphene exhibits a small but finite bending stiffness (~k_bT, where k_b is the Boltzmann constant) of 0 to 1600 K by theoretical work (47, 55), and this finally leads to a negligible change in modulus of the 3D graphene structure with high-order approximation (Supplementary Discussion). As a result, the unique atomic structure of graphene endues its temperature-invariant and highly reversible elastic bending/buckling behaviors as the cell walls even at very large bending/buckling without any yield/breakdown at extreme temperatures, which ensures highly reversible (also temperature-invariant) elastic compress/release of the cell/framework. Second, the chemically cross-linked nodes also seem to be stable enough in the entire investigated temperature range, which is partially due to the highly thermal stability of C─O/C─C/C═C bonds (Supplementary Discussion). In addition, on the basis of the literature result (48), its bond length and, consequently, the force constants of elastic torsion and angle bending have negligible changes in the investigated temperature range (Supplementary Discussion). With these results, the cross-linking covalent bonds are intrinsically thermally stable and have temperature-invariant mechanical/elastic properties. Furthermore, the unique highly porous structure that endues the 3DGraphene foam can be seen and treated as a sum of many individual graphene sheets, but without exhibiting the strong coupling properties of the graphene sheets (as is the case for graphite) (35). This unique material structure allows the intrinsic mechanical properties of graphene to be translated into the bulk 3DGraphene foam built from it (even at deep cryogenic temperatures), even with the large number of covalent interconnections between the graphene sheets. In addition, from a structural view, the large void space between the walls offers the compress/release cushion space (Supplementary Discussion) and avoids local stress concentration at weak points (2, 14). Thus, the observations of such excellent temperature-invariant super-elasticity and other mechanical properties even down to liquid helium temperature indicate the high stability of the covalently bonded graphene network (architecture) that was proposed theoretically a long time ago (37, 38). Note that the elastic moduli of most metals and ceramics generally depend on temperature (T) because of anharmonic atomic vibration and thermal expansion/contraction, as T⁴ at sufficiently low temperatures (e.g., far below the Debye temperature), and linearly with T at higher temperatures (56). High elastic materials, such as silicone rubbers and polymeric foams, also have temperature-dependent elasticity (10, 21). Typically, below their glass transition temperatures, they become hardened and even brittle (57). Thus, the temperature-invariant elasticity of our 3DGraphene foam is completely different from conventional materials such as metals, ceramics, and polymers (7). Our results also offer a direct experimental proof that graphene shows negligible temperature dependence for its mechanical properties over the investigated wide temperature range here (26, 27, 47). This could be due to the unique bonding of carbon in the sp²-hybridized planar graphene sheets with soft out-of-plane bending modes and strong in-plane stretching modes with very high energy for defect formation (34). This coupling is crucial for the strong anharmonic behavior of graphene and leads to the unusual temperature independence of the mechanical properties (27). Moreover, it is believed that the overall structure and building blocks (covalently bonded single-layer graphene) are thermally stable within the tested temperature range, without any kinetic phenomena such as temperature-assisted atomic diffusion, mass transport, and phase transition (44). Thus, there are no kinetic phenomena that athermally control the mechanical response of these graphene foams.

Last, it is observed that the Young’s modulus of our material nonlinearly increases from ~0.58 to ~100 kPa with an increasing material density (from ~1.5 to ~15 mg cm⁻³) in this process (fig. S30A). This means that the specific Young’s modulus (the ratio of Young’s modulus to density) of our material is about 0.4 to 6.7 MPa/(g cm⁻³). As an ultralight foam material, the specific Young’s modulus is superior/comparable to other graphene foams, including the experimental results (39) and theoretical simulated results (43) or even those polymer foams (2), nanoporous silica (58), CNT aerogel (21), and ultralight metallic microlattices (14). As indicated above, the superior/compatible specific modulus originated from bending/buckling deformation of the graphene cell wall. It should also be noted that our 3DGraphene foam has a specific stress (the ratio of compressive stress to density) reaching ~0.30 and ~4.50 MPa/(g cm⁻³) at 45 and 90% strain, respectively, and the specific Young’s modulus (the ratio of Young’s modulus to density) is about 1.48 and 6.67 MPa/(g cm⁻³) at 45 and 90% strain, respectively. For the ideal graphene (cell wall) under out-of-plane deformation (bending and buckling) (47), the specific stress is ~0.47 and ~5.70 MPa/(g cm⁻³) at the 45 and 90% vertical deflection ratio, respectively, and the bending stiffness is 16.1 and 7.11 MPa/(g cm⁻³) at the 45 and 90% vertical deflection ratio, respectively. For the ideal graphene under in-plane stress (59), the specific strength is 5.75 × 10⁴ MPa/(g cm⁻³) and the specific Young’s modulus is 48.7 × 10⁴ MPa/(g cm⁻³). These indicate that the specific stress and specific Young’s modulus of our 3DGraphene foam are close to those of the ideal graphene under bending and buckling deformation, although far lower than those of ideal graphene under in-plane stress. With these results, we derived the modulus (E)–density (ρ) relationship of our 3DGraphene foam and compared it with that of other literature reports (fig. S30B). For our 3DGraphene foam, the Young’s modulus (E) depends approximately quadratically on the compressed density (ρ), as E ~ ρ². This scaling law indicates efficient load transfer to graphene cell walls and bending-dominated deformation (2, 14) during reversible buckling, similar to open cell stochastic foams. These results are consistent with the in situ SEM observation zoom-in at the graphene cell wall deformation (Figs. 3 and 5A, figs. S18 and S23, and movies S3 and S4) and support the bending/buckling deformation mechanism (Supplementary Discussion). In contrast, some other low-density foam materials, such as aerogels and CNT foams, exhibit a steeper scaling of E ~ ρ³ (14) because of inefficient load transfer between ligaments. Considering the low-density and random cross-linking nature between the graphene sheets at the edges in this material, the similarity of specific stress and specific Young’s modulus of our material to those of an individual graphene sheet is actually quite unexpected. This is because during compression of the macroscopic sample, the deformations of the graphene cell walls are mainly out-of-plane bending and buckling rather than in-plane compression/tension.

In summary, we have demonstrated highly reversible and robust compressive elasticity in 3DGraphene foam with up to 90% strain at the deep cryogenic temperature of 4 K, a property that has not been observed previously for any bulk material. Other mechanical properties, including the Young’s modulus and near-zero Poisson’s ratio for the graphene-only–based material, are also preserved down to liquid helium temperatures. Furthermore, all of these remarkable mechanical properties were demonstrated across a wide range of temperatures, from 4 to 1273 K, and are thus independent of temperature. These unique behaviors have never been reported for any other material. Temperature-independent reversible deformations of the structure and even building blocks (graphene sheets) were also directly observed at a microscopic scale using a modified temperature invariable in situ SEM. Our simulated mechanical properties and their relationships with temperature matched well with the experimental results, proving that the properties of 3DGraphene foam arise because of both the unique cross-linked graphene network architecture of the material and the temperature-independent mechanical properties of graphene building blocks and their flexible covalent interconnections in the investigated temperature range. The observed mechanical properties of this unique graphene bulk material (and also graphene sheets) at extreme temperatures indicate the potential for applications in outer space and other extremely low-temperature or harsh environments. Last, but maybe more excitingly, if similar bulk materials could be made from other 2D building blocks, using the same assembly strategy, some unexpected and fascinating properties, not only the mechanical aspect, might be discovered.

MATERIALS AND METHODS

Synthesis of 3DGraphene

Commercial materials were used directly for general chemicals unless otherwise indicated. GO was prepared by the oxidation of natural graphite powder using a modified Hummers’ method, as described elsewhere (25). A previously reported solvothermal method (25) was carried out by using GO ethanol solution (0.5 mg ml⁻¹) in a Teflon-lined autoclave at 180°C for 12 hours; then, the ethanol-filled intermediate solid was carefully removed from the autoclave to have a slow exchange of ethanol completely with deionized water. The water-filled intermediate was then freeze-dried. Last, it was annealed at 400°C for an hour in argon atmosphere to obtain the final 3DGraphene foam. The as-prepared 3DGraphene foam sample is shown in fig. S13.

Preparation of 3DGraphene samples

The as-prepared 3DGraphene foam, with a density of ~1.5 mg cm⁻³, was cut using a continuous laser (450 nm and 2 W) into the desired shapes and sizes (cylinder shape or cubic shape with smooth surface for mechanical measurements and thin slides for the micro–real-time in situ SEM observation of mechanical properties). Before mechanical measurements or SEM observation, the samples were thoroughly dried in vacuum at 150°C for more than 2 hours. If using the density of graphite, ρ_g = 2.25 g cm⁻³, as the reference, the relative density of the material (ρ_r = ρ_a/ρ_g) was ~6.67 × 10⁻⁴ and the porosity of the 3DGraphene foam was ~99.93% (1 − ρ_r).

Methods for statistical analysis and error bars

In Figs. 2D and 4C (and Fig. 4D), the Young’s modulus (Poisson’s ratio) at each test temperature was obtained using the above standard measuring method, and this procedure was repeated on five samples (five times for each sample). Then, the average values and SDs of the 25 sets of data were plotted as the Young’s moduli (Poisson’s ratios) and corresponding error bars at this temperature. The error bars in the insets of Fig. 5 (B, C, and E) and figs. S16, S17, S19, and S20 were obtained using the same procedure. The error bars for Young’s modulus data from the standard method in the insets of figs. S26 and S27 were also obtained following this method.

For Fig. 2F (and figs. S21B and S29B), at each test temperature, the sample first completed the above standard process for Young’s modulus measurement (same as fig. S3) and then was compressed-released between 0 and 90% strain at a rate of 90% strain s⁻¹ for 19 cycles. Next, those (1 + 19) measurement cycles were repeated until a total of 100 cycles were completed. The whole process was repeated on five samples. Then, the average values and SDs of the five sets of data were plotted as the Young’s modulus and corresponding error bars at this temperature. The error bars in Fig. 2G (and figs. S21C and S29C) were obtained using a similar procedure except that the standard cycles for Young’s modulus measurement were replaced by standard cycles for Poisson’s ratio measurement.

For Fig. 5 (B to D), at each test temperature, the sample was cyclically compressed between 0 and 90% strain at a rate of 0.1% strain s⁻¹ for five cycles, and this procedure was repeated for five samples. Then, the stress values and SDs were statistically calculated from the 25 cycles.

Because of the isotropy of the 3DGraphene foam, all data and results in the figures and texts were obtained from the axial direction of the samples except those results with specific statements and/or annotations, such as figs. S14, S16, S17, S22, and S24, which show the mechanical properties of the 3DGraphene foam along the different directions.

Supplementary Material

http://advances.sciencemag.org/cgi/content/full/5/4/eaav2589/DC1

supp_5_4_eaav2589__index.html^{(5.3KB, html)}

Download PDF

aav2589_SM.pdf^{(4MB, pdf)}

Movie S1

Download video file^{(8.7MB, mp4)}

Movie S2

Download video file^{(8.7MB, mp4)}

Movie S3

Download video file^{(5.4MB, mp4)}

Movie S4

Download video file^{(5.7MB, mp4)}

Acknowledgments

Funding: We gratefully acknowledge financial support from the Ministry of Science and Technology of China (MoST; 2016YFA0200200), the National Natural Science Foundation of China (NSFC; 51633002, 51472124, and 21421001), Tianjin City (16ZXCLGX00100), and 111 Project (B12015). We also thank the Microscopic Technology & Analysis Center, Institute of Automation, Chinese Academy of Sciences for in situ SEM measurements. Author contributions: Y.C. conceived and directed the study. T.Z. and H.C. synthesized the samples. K.Z. carried out most of the measurements. T.Z., K.Z., Y.C., and P.M.A. analyzed the data and prepared the manuscript. P.X., Y.Y., H.Z., C.L., and C.S.T. participated in characterizations and discussions. All authors participated in the project discussions and production of the final manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/4/eaav2589/DC1

Supplementary Methods

Supplementary Discussion

Fig. S1. The schematic of the sample platform with precise positioner and temperature control in the SEM for in situ and variable-temperature characterization.

Fig. S2. Schematic of the homemade apparatus for mechanical property measurement from 4 to 1273 K.

Fig. S3. Measurements of the Young’s modulus of the 3DGraphene foam at 4 K.

Fig. S4. Measurements of the Poisson’s ratio of the 3DGraphene foam at 4 K.

Fig. S5. The schematic of the nodes under compression.

Fig. S6. The modeling architecture of the plane perpendicular to the compression direction.

Fig. S7. Schematic of the proposed elastic deformation of the 3DGraphene foam under compressive stress.

Fig. S8. The schematic of the periodic honeycomb-like cell architecture for modeling the 3DGraphene foam and enlargement of one unit cell under the applied compressive stress.

Fig. S9. The schematic of a cell node under the applied compressive stress.

Fig. S10. The schematic of elastic bending of the graphene cell wall under the applied compressive stress.

Fig. S11. The schematic of elastic buckling of the graphene cell wall under the applied compressive stress.

Fig. S12. The schematic of deeply elastic bending of the graphene cell wall at large strain of the sample.

Fig. S13. The photograph of the 3DGraphene foam samples.

Fig. S14. Cross-sectional SEM images of the 3DGraphene foam.

Fig. S15. Energy dissipation mechanism.

Fig. S16. Young’s modulus–engineering strain plots along the axial and radial directions at different temperatures.

Fig. S17. Poisson’s ratio at different engineering strain of the 3DGraphene foam along the axial and radial directions at different temperatures.

Fig. S18. In situ SEM observations of the 3DGraphene foam during compress-release cycles at 4 K.

Fig. S19. The Young’s modulus versus applied engineering strain at different temperatures.

Fig. S20. The Poisson’s ratio versus applied engineering strain at different temperatures.

Fig. S21. The cyclic stability at different temperatures.

Fig. S22. The stepwise compress-release cycles with increasing maximum strain along both the axial and radial directions at different temperatures.

Fig. S23. Comparison of the in situ SEM images of the same sample under 0, 45, and 90% strains in the compress process.

Fig. S24. Thermal expansion of the 3DGraphene foam in both axial and radial directions.

Fig. S25. A typical AFM image of GO sheets.

Fig. S26. The simulated stress-strain curve at 298 K.

Fig. S27. The simulated Young’s modulus–engineering strain curves at different temperatures.

Fig. S28. The simulated tangent modulus–strain curves at different temperatures.

Fig. S29. Results of cyclic mechanical test at 1273 K and that of the following test at other temperatures for the same samples.

Fig. S30. The relationship between compressed density and Young’s modulus with strain.

Movie S1. In situ optical observation for compress-release cycles of the 3DGraphene foam at 4 K and corresponding stress-strain transient curves.

Movie S2. In situ optical observation for compress-release cycles of the 3DGraphene foam at 1273 K and corresponding stress-strain transient curves.

Movie S3. In situ SEM observation for compress-release cycles of the 3DGraphene foam at 4 K.

Movie S4. In situ SEM observation for compress-release cycles of the 3DGraphene foam at 1273 K.

References (60–80)

REFERENCES AND NOTES

1.Aliev A. E., Oh J., Kozlov M. E., Kuznetsov A. A., Fang S., Fonseca A. F., Ovalle R., Lima M. D., Haque M. H., Gartstein Y. N., Zhang M., Zakhidov A. A., Baughman R. H., Giant-stroke, superelastic carbon nanotube aerogel muscles. Science 323, 1575–1578 (2009). [DOI] [PubMed] [Google Scholar]
2.L. J. Gibson, M. F. Ashby, Cellular Solids: Structure and Properties (Cambridge Solid State Science Series, Cambridge Univ. Press, ed. 2, 1999). [Google Scholar]
3.Dai Z., Liu L., Qi X., Kuang J., Wei Y., Zhu H., Zhang Z., Three-dimensional sponges with super mechanical stability: Harnessing true elasticity of individual carbon nanotubes in macroscopic architectures. Sci. Rep. 6, 18930 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Zhang Q., Xu X., Lin D., Chen W., Xiong G., Yu Y., Fisher T. S., Li H., Hyperbolically patterned 3D graphene metamaterial with negative Poisson's ratio and superelasticity. Adv. Mater. 28, 2229–2237 (2016). [DOI] [PubMed] [Google Scholar]
5.Qiu L., Huang B., He Z., Wang Y., Tian Z., Liu J. Z., Wang K., Song J., Gengenbach T. R., Li D., Extremely low density and super-compressible graphene cellular materials. Adv. Mater. 29, 1701553 (2017). [DOI] [PubMed] [Google Scholar]
6.D. A. Wigley, Mechanical Properties of Materials at Low Temperatures (Springer Science & Business Media, ed. 1, 2012). [Google Scholar]
7.W. D. Callister Jr., Materials Science and Engineering: An Introduction (Wiley Publishers, ed. 7, 2006). [Google Scholar]
8.Tallon J. L., Wolfenden A., Temperature dependence of the elastic constants of aluminum. J. Phys. Chem. Solids 40, 831–837 (1979). [Google Scholar]
9.Chang Y. A., Himmel L., Temperature dependence of the elastic constants of Cu, Ag, and Au above room temperature. J. Appl. Phys. 37, 3567–3572 (1966). [Google Scholar]
10.Reed R. P., Schramm R. E., Clark A. F., Mechanical, thermal, and electrical properties of selected polymers. Cryogenics 13, 67–82 (1973). [Google Scholar]
11.Gómez-Cortés J. F., Nó M. L., López-Ferreño I., Hernández-Saz J., Molina S. I., Chuvilin A., San Juan J. M., Size effect and scaling power-law for superelasticity in shape-memory alloys at the nanoscale. Nat. Nanotechnol. 12, 790–796 (2017). [DOI] [PubMed] [Google Scholar]
12.Lai A., Du Z., Gan C. L., Schuh C. A., Shape memory and superelastic ceramics at small scales. Science 341, 1505–1508 (2013). [DOI] [PubMed] [Google Scholar]
13.W. F. Smith, J. Hashemi, Foundations of Materials Science and Engineering (McGraw-Hill Companies, ed. 4, 2005). [Google Scholar]
14.Schaedler T. A., Jacobsen A. J., Torrents A., Sorensen A. E., Lian J., Greer J. R., Valdevit L., Carter W. B., Ultralight metallic microlattices. Science 334, 962–965 (2011). [DOI] [PubMed] [Google Scholar]
15.Meza L. R., Das S., Greer J. R., Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 345, 1322–1326 (2014). [DOI] [PubMed] [Google Scholar]
16.Guillaume C. E., The anomaly of the nickel-steels. Proc. Phys. Soc. Lond. 32, 374–404 (1919). [Google Scholar]
17.Cui J., Ren X., Elinvar effect in Co-doped TiNi strain glass alloys. Appl. Phys. Lett. 105, 061904 (2014). [Google Scholar]
18.Ma Y., Chen Y., Three-dimensional graphene networks: Synthesis, properties and applications. Natl. Sci. Rev. 2, 40–53 (2015). [Google Scholar]
19.Kim K. H., Tsui M. N., Islam M. F., Graphene-coated carbon nanotube aerogels remain superelastic while resisting fatigue and creep over −100 to +500 °C. Chem. Mater. 29, 2748–2755 (2017). [Google Scholar]
20.Guo F., Jiang Y., Xu Z., Xiao Y., Fang B., Liu Y., Gao W., Zhao P., Wang H., Gao C., Highly stretchable carbon aerogels. Nat. Commun. 9, 881 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Xu M., Futaba D. N., Yamada T., Yumura M., Hata K., Carbon nanotubes with temperature-invariant viscoelasticity from −196° to 1000°C. Science 330, 1364–1368 (2010). [DOI] [PubMed] [Google Scholar]
22.Xu X., Zhang Q., Yu Y., Chen W., Hu H., Li H., Naturally dried graphene aerogels with superelasticity and tunable Poisson's ratio. Adv. Mater. 28, 9223–9230 (2016). [DOI] [PubMed] [Google Scholar]
23.Sun H., Xu Z., Gao C., Multifunctional, ultra-flyweight, synergistically assembled carbon aerogels. Adv. Mater. 25, 2554–2560 (2013). [DOI] [PubMed] [Google Scholar]
24.Chen Z., Xu C., Ma C., Ren W., Cheng H.-M., Lightweight and flexible graphene foam composites for high-performance electromagnetic interference shielding. Adv. Mater. 25, 1296–1300 (2013). [DOI] [PubMed] [Google Scholar]
25.Wu Y., Yi N., Huang L., Zhang T., Fang S., Chang H., Li N., Oh J., Lee J. A., Kozlov M., Chipara A. C., Terrones H., Xiao P., Long G., Huang Y., Zhang F., Zhang L., Lepró X., Haines C., Lima M. D., Lopez N. P., Rajukumar L. P., Elias A. L., Feng S., Kim S. J., Narayanan N. T., Ajayan P. M., Terrones M., Aliev A., Chu P., Zhang Z., Baughman R. H., Chen Y., Three-dimensionally bonded spongy graphene material with super compressive elasticity and near-zero Poisson's ratio. Nat. Commun. 6, 6141 (2015). [DOI] [PubMed] [Google Scholar]
26.Zakharchenko K. V., Katsnelson M. I., Fasolino A., Finite temperature lattice properties of graphene beyond the quasiharmonic approximation. Phys. Rev. Lett. 102, 046808 (2009). [DOI] [PubMed] [Google Scholar]
27.Huang L. F., Cao T. F., Gong P. L., Zeng Z., Isotope effects on the vibrational, Invar, and Elinvar properties of pristine and hydrogenated graphene. Solid State Commun. 190, 5–9 (2014). [Google Scholar]
28.Jean F., Zhou T., Blanc N., Felici R., Coraux J., Renaud G., Effect of preparation on the commensurabilities and thermal expansion of graphene on Ir(111) between 10 and 1300 K. Phys. Rev. B 88, 165406 (2013). [Google Scholar]
29.Nicholl R. J. T., Conley H. J., Lavrik N. V., Vlassiouk I., Puzyrev Y. S., Sreenivas V. P., Pantelides S. T., Bolotin K. I., The effect of intrinsic crumpling on the mechanics of free-standing graphene. Nat. Commun. 6, 8789 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Liu X., Metcalf T. H., Robinson J. T., Houston B. H., Scarpa F., Shear modulus of monolayer graphene prepared by chemical vapor deposition. Nano Lett. 12, 1013–1017 (2012). [DOI] [PubMed] [Google Scholar]
31.Weber P., Güttinger J., Noury A., Vergara-Cruz J., Bachtold A., Force sensitivity of multilayer graphene optomechanical devices. Nat. Commun. 7, 12496 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Onnes H. K., The resistance of pure mercury at helium temperatures. Commun. Phys. Lab. Univ. Leiden 12, 120 (1911). [Google Scholar]
33.Halperin W. P., Eighty years of superfluidity. Nature 553, 413–414 (2018). [DOI] [PubMed] [Google Scholar]
34.Zhang H., Duan Z., Zhang X., Liu C., Zhang J., Zhao J., Strength and fracture behavior of graphene grain boundaries: Effects of temperature, inflection, and symmetry from molecular dynamics. Phys. Chem. Chem. Phys. 15, 11794–11799 (2013). [DOI] [PubMed] [Google Scholar]
35.Zhang T., Chang H., Wu Y., Xiao P., Yi N., Lu Y., Ma Y., Huang Y., Zhao K., Yan X.-Q., Liu Z.-B., Tian J.-G., Chen Y., Macroscopic and direct light propulsion of bulk graphene material. Nat. Photonics 9, 471–476 (2015). [Google Scholar]
36.Zhang Y., Huang Y., Chen H., Huang Z., Yang Y., Xiao P., Zhou Y., Chen Y., Composition and structure control of ultralight graphene foam for high-performance microwave absorption. Carbon 105, 438–447 (2016). [Google Scholar]
37.Kawai T., Okada S., Miyamoto Y., Oshiyama A., Carbon three-dimensional architecture formed by intersectional collision of graphene patches. Phys. Rev. B 72, 035428 (2005). [Google Scholar]
38.Kuc A., Seifert G., Hexagon-preserving carbon foams: Properties of hypothetical carbon allotropes. Phys. Rev. B 74, 214104 (2006). [Google Scholar]
39.Ni N., Barg S., Garcia-Tunon E., Perez F. M., Miranda M., Lu C., Mattevi C., Saiz E., Understanding mechanical response of elastomeric graphene networks. Sci. Rep. 5, 13712 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Li C., Chou T.-W., A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 40, 2487–2499 (2003). [Google Scholar]
41.Sakhaee-Pour A., Elastic buckling of single-layered graphene sheet. Comput. Mater. Sci. 45, 266–270 (2009). [Google Scholar]
42.Shen Y., Wu H., Interlayer shear effect on multilayer graphene subjected to bending. Appl. Phys. Lett. 100, 101909 (2012). [Google Scholar]
43.Qin Z., Jung G. S., Kang M. J., Buehler M. J., The mechanics and design of a lightweight three-dimensional graphene assembly. Sci. Adv. 3, e1601536 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Xia W., Vargas-Lara F., Keten S., Douglas J. F., Structure and dynamics of a graphene melt. ACS Nano 12, 5427–5435 (2018). [DOI] [PubMed] [Google Scholar]
45.Roberts A. P., Garboczi E. J., Elastic properties of model random three-dimensional open-cell solids. J. Mech. Phys. Solids 50, 33–55 (2002). [Google Scholar]
46.Yashiro K., Ito T., Tomita Y., Molecular dynamics simulation of deformation behavior in amorphous polymer: Nucleation of chain entanglements and network structure under uniaxial tension. Int. J. Mech. Sci. 45, 1863–1876 (2003). [Google Scholar]
47.Liu P., Zhang Y. W., Temperature-dependent bending rigidity of graphene. Appl. Phys. Lett. 94, 231912 (2009). [Google Scholar]
48.Liu T. T., Wang X., Dynamic elastic modulus of single-walled carbon nanotubes in different thermal environments. Phys. Lett. A 365, 144–148 (2007). [Google Scholar]
49.Natsuki T., Endo M., Structural dependence of nonlinear elastic properties for carbon nanotubes using a continuum analysis. Appl. Phys. A 80, 1463–1468 (2005). [Google Scholar]
50.Scarpa F., Adhikari S., Srikantha Phani A., Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology 20, 065709 (2009). [DOI] [PubMed] [Google Scholar]
51.Mayo S. L., Olafson B. D., Goddard Iii W. A., DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 94, 8897–8909 (1990). [Google Scholar]
52.Allinger N. L., Yuh Y. H., Lii J. H., Molecular mechanics. The MM3 force field for hydrocarbons. 1. J. Am. Chem. Soc. 111, 8551–8566 (1989). [Google Scholar]
53.Zhang D.-B., Akatyeva E., Dumitrică T., Bending ultrathin graphene at the margins of continuum mechanics. Phys. Rev. Lett. 106, 255503 (2011). [DOI] [PubMed] [Google Scholar]
54.Pradhan S. C., Buckling of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory. Phys. Lett. A 373, 4182–4188 (2009). [Google Scholar]
55.Fasolino A., Los J. H., Katsnelson M. I., Intrinsic ripples in graphene. Nat. Mater. 6, 858–861 (2007). [DOI] [PubMed] [Google Scholar]
56.Garai J., Laugier A., The temperature dependence of the isothermal bulk modulus at 1bar pressure. J. Appl. Phys. 101, 023514 (2007). [Google Scholar]
57.Park S.-B., Lee C.-S., Choi S.-W., Kim J.-H., Bang C.-S., Lee J.-M., Polymeric foams for cryogenic temperature application: Temperature range for non-recovery and brittle-fracture of microstructure. Compos. Struct. 136, 258–269 (2016). [Google Scholar]
58.Kucheyev S. O., Stadermann M., Shin S. J., Satcher J. H. Jr., Gammon S. A., Letts S. A., van Buuren T., Hamza A. V., Super-compressibility of ultralow-density nanoporous silica. Adv. Mater. 24, 776–780 (2012). [DOI] [PubMed] [Google Scholar]
59.Lee C., Wei X., Kysar J. W., Hone J., Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008). [DOI] [PubMed] [Google Scholar]
60.Li C., Chou T.-W., Elastic moduli of multi-walled carbon nanotubes and the effect of van der Waals forces. Compos. Sci. Technol. 63, 1517–1524 (2003). [Google Scholar]
61.Kirschner K. N., Yongye A. B., Tschampel S. M., González-Outeiriño J., Daniels C. R., Foley B. L., Woods R. J., GLYCAM06: A generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 29, 622–655 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Grandbois M., Beyer M., Rief M., Clausen-Schaumann H., Gaub H. E., How strong is a covalent bond? Science 283, 1727–1730 (1999). [DOI] [PubMed] [Google Scholar]
63.Evans E., Ritchie K., Dynamic strength of molecular adhesion bonds. Biophys. J. 72, 1541–1555 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Beyer M. K., Clausen-Schaumann H., Mechanochemistry: The mechanical activation of covalent bonds. Chem. Rev. 105, 2921–2948 (2005). [DOI] [PubMed] [Google Scholar]
65.Xin G., Yao T., Sun H., Scott S. M., Shao D., Wang G., Lian J., Highly thermally conductive and mechanically strong graphene fibers. Science 349, 1083–1087 (2015). [DOI] [PubMed] [Google Scholar]
66.Senda T., Yamada Y., Morimoto M., Nono N., Sogabe T., Kubo S., Sato S., Analyses of oxidation process for isotropic pitch-based carbon fibers using model compounds. Carbon 142, 311–326 (2019). [Google Scholar]
67.Sudeep P. M., Narayanan T. N., Ganesan A., Shaijumon M. M., Yang H., Ozden S., Patra P. K., Pasquali M., Vajtai R., Ganguli S., Roy A. K., Anantharaman M. R., Ajayan P. M., Covalently interconnected three-dimensional graphene oxide solids. ACS Nano 7, 7034–7040 (2013). [DOI] [PubMed] [Google Scholar]
68.Pathak S., Lim E. J., Abadi P. P. S. S., Graham S., Cola B. A., Greer J. R., Higher recovery and better energy dissipation at faster strain rates in carbon nanotube bundles: An in-situ study. ACS Nano 6, 2189–2197 (2012). [DOI] [PubMed] [Google Scholar]
69.Gibson L. J., Biomechanics of cellular solids. J. Biomech. 38, 377–399 (2005). [DOI] [PubMed] [Google Scholar]
70.Tserpes K. I., Papanikos P., Finite element modeling of single-walled carbon nanotubes. Compos. B Eng. 36, 468–477 (2005). [Google Scholar]
71.Wendel J. A., Goddard W. A. III, The Hessian biased force field for silicon nitride ceramics: Predictions of thermodynamic and mechanical properties for α- and β-Si₃N₄. J. Chem. Phys. 97, 5048–5062 (1992). [Google Scholar]
72.Sakhaee-Pour A., Elastic properties of single-layered graphene sheet. Solid State Commun. 149, 91–95 (2009). [Google Scholar]
73.Wei Y., Wang B., Wu J., Yang R., Dunn M. L., Bending rigidity and Gaussian bending stiffness of single-layered graphene. Nano Lett. 13, 26–30 (2013). [DOI] [PubMed] [Google Scholar]
74.Ferry J. D., Fitzgerald E. R., Grandine L. D. Jr., Williams M. L., Temperature dependence of dynamic properties of elastomers. relaxation distributions. Rubber Chem. Technol. 25, 720–729 (1952). [Google Scholar]
75.Zhao H., Aluru N. R., Temperature and strain-rate dependent fracture strength of graphene. J. Appl. Phys. 108, 064321 (2010). [Google Scholar]
76.Cornell W. D., Cieplak P., Bayly C. I., Gould I. R., Merz K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., Kollman P. A., A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117, 5179–5197 (1995). [Google Scholar]
77.Lii J.-H., Allinger N. L., Molecular mechanics. The MM3 force field for hydrocarbons. 3. The van der Waals' potentials and crystal data for aliphatic and aromatic hydrocarbons. J. Am. Chem. Soc. 111, 8576–8582 (1989). [Google Scholar]
78.Yoon D., Son Y.-W., Cheong H., Negative thermal expansion coefficient of graphene measured by Raman spectroscopy. Nano Lett. 11, 3227–3231 (2011). [DOI] [PubMed] [Google Scholar]
79.Geisinger K. L., Gibbs G. V., Navrotsky A., A molecular orbital study of bond length and angle variations in framework structures. Phys. Chem. Miner. 11, 266–283 (1985). [Google Scholar]
80.Medhekar N. V., Ramasubramaniam A., Ruoff R. S., Shenoy V. B., Hydrogen bond networks in graphene oxide composite paper: Structure and mechanical properties. ACS Nano 4, 2300–2306 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials