Temporal signals underlying a cognitive process in the dorsal premotor cortex

Significance

When trained monkeys discriminate between two sequential vibrotactile stimulus patterns, neurons in the dorsal premotor cortex (DPC) code current and remembered inputs and the commands expressing the decision report. Additionally, responses of these neurons and neurons with no coding responses also reflect the timing of the task sequence. What is the cognitive relevance of these time-dependent signals? We show that time-dependent signals reflected the temporal sequence of the task during both hits and error trials but diminished or disappeared during a nondemanding cognitive task that did not require discrimination for reward. Also, strong links were detected between neuronal population and individual neurons’ time-dependent signals. These time-dependent responses may function as the substrate network dynamics on which task coding components emerge.

Abstract

During discrimination between two sequential vibrotactile stimulus patterns, the primate dorsal premotor cortex (DPC) neurons exhibit a complex repertoire of coding dynamics associated with the working memory, comparison, and decision components of this task. In addition, these neurons and neurons with no coding responses show complex strong fluctuations in their firing rate associated with the temporal sequence of task events. Here, to make sense of this temporal complexity, we extracted the temporal signals that were latent in the population. We found a strong link between the individual and population response, suggesting a common neural substrate. Notably, in contrast to coding dynamics, these time-dependent responses were unaffected during error trials. However, in a nondemanding task in which monkeys did not require discrimination for reward, these time-dependent signals were largely reduced and changed. These results suggest that temporal dynamics in DPC reflect the underlying cognitive processes of this task.

Our ability to anticipate the occurrence of future events is crucial when performing many cognitively demanding behaviors. For example, the benefits of anticipating the arrival of sensory inputs can be decisive in our perceptual behavior (1–3). In this way, neural circuits engaged in cognitive processes of this type would profit from employing temporal signals. Thus, the timing information contained in those signals may then constitute a mechanism to anticipate future task events. In fact, during experiments it is common to find neurons that display noteworthy temporal dependencies in their firing rate (4–9). In particular, a large proportion of the individual neurons from the frontal lobe cortices exhibit intricate time-dependent responses that mesh in myriad ways with stimulus identity and decision outcomes during behavioral tasks (4, 10–12). However, individual neurons must be reflecting a more widespread response across the network; temporal signals that represent anticipation of task events and stimulus identity must be coded at the population level. Recently, these neuronal population signals from the frontal lobe cortex were studied employing methods that reduced the dimensionality of network dynamics (11, 13). These methodological approaches facilitated the recognition of latent population responses during cognitive tasks (14–17). Notably, large differences between the population variance related to purely temporal signals and task parameter coding were observed (11, 13). Markedly, even if the tasks examined were completely different and employed two types of animal models, the temporal signals always captured more than 65% of the total variance. These results indicate that temporal signals occupy a central role during the execution of any behavioral task.

Here, to further investigate the temporal responses in single units and neuronal population, we employed the network activity recorded in dorsal premotor cortex (DPC) during a temporal pattern discrimination task (TPDT) (18, 19). Monkeys were trained to report whether the temporal patterns of two vibrotactile stimuli (P1 and P2) of equal mean frequency were the same or different (Fig. 1A and SI Appendix) by pressing one of two push-buttons (pbs). In two prior works, we studied the coding capacity of DPC single neurons (18) and population responses (19). In the first work, we showed that DPC neurons coded the stimulus patterns as broader categories and signaled them during the working memory, comparison, and decision periods of the TPDT. Furthermore, neurons exhibited mixed selectivity (20) and an extreme heterogeneity in their coding dynamics (21, 22). In our second work, we showed that this heterogeneous population activity can be condensed into two major coding components: one that persistently represented in working memory both the first stimulus identity and the postponed informed choice, and another that transiently coded the initial sensory information and the result of the comparison between the two stimuli. These dynamics, hidden in the neuronal coding heterogeneity, emerged in the DPC population response.

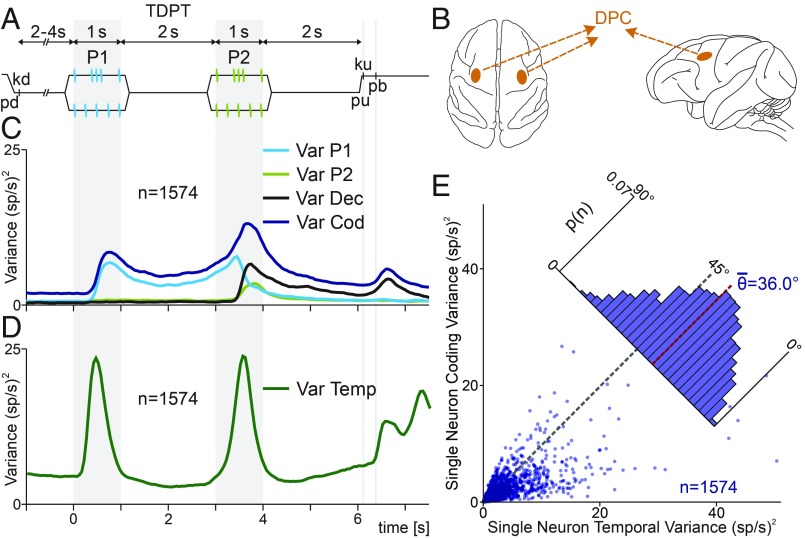
Fig. 1.

Temporal pattern discrimination task (TPDT), single DPC neuron, and population variances. (A) Trial sequence of events. The mechanical probe is lowered (pd), indenting the glabrous skin of one fingertip of the right restrained hand; the monkey places its free hand on an immovable key (kd). After a variable prestimulus period (uniformly distributed from 2 to 4 s), the probe vibrates, generating one of two possible stimulus patterns [P1, either grouped (G) or extended (E); 1 s duration; mean frequency of 5 Hz]; after a first delay (2-s length, from 1 to 3 s) between P1 and P2, the second stimulus is delivered, again either of the two possible patterns (P2, either G or E; 1-s duration; mean frequency of 5 Hz); after a second fixed delay (2-s length, from 4 to 6 s) between P2 and pu, the monkey releases the key (ku) and presses the push-button (pb) to indicate whether P1 and P2 were the same or different (P2 ≠ P1). (B) Top (Left) and lateral (Right) views of the brain. Dark orange spots mark the location of the dorsal premotor cortex (DPC). Single DPC neurons were recorded from both hemispheres, while trained monkeys performed the TPDT. (C) Population instantaneous coding variance (Var_COD, blue, SI Appendix, Eq. S1), P1 variance (Var_P1, cyan trace), P2 variance (Var_P2, light green trace), and decision variance (Var_DEC, black trace). (D) Population instantaneous temporal variance (Var_Temp, green trace). (E) Single-neuron temporal variance (x axis, SI Appendix) is plotted against single-neuron coding variance (y axis, SI Appendix). Each dot corresponds to one neuron (n = 1,574). Diagonal line (45°) indicates equality between both measures. Inset histogram show angular distributions for the population (<θ> = 36.0°). In general, $SNVa{r}_{Temp}^i$ is higher than $SNVa{r}_{Cod}^i$.

An important hypothesis is that the temporal signals should adjust to different cognitive contexts. Here, we tested this conjecture employing single-unit and population methodological approaches. First, focusing on the cognitively demanding TPDT, we compared the variance related to coding against time-dependent variance, using both single DPC neurons and population average. In the two cases, the results were analogous: the proportion of variance related with timing is much higher than that associated with task parameter coding. This means that temporal dynamics is responsible for the large proportion of DPC firing rate fluctuations during the TPDT. In addition, we identified several DPC neurons with pure temporal responses. These responses also proved to be heterogeneous. Furthermore, we focused on the pure temporal signals that emerged from the DPC population. Most of the population variance was captured by these pure temporal components. These signals were engaged during relevant periods of the task: they reflected stimulus arrival and button presses, and had ramping activity during delays.

To further address our hypothesis, we investigated the role of these temporal signals in two different cognitive contexts. First, when the monkeys performed the TPDT and after during a nondemanding variation of the task [light control task (LCT)]. During this control task, no parameter encoding was found in single neurons and population dynamics. Notable, the time-dependent signals observed in the TPDT reduced their intensity or completely vanished during this nondemanding task. Additionally, the temporal variance was diminished in single-unit responses and in their population average. Several temporal neurons reflected this decline in their temporal responses. These results show that pure temporal responses were bound to the cognitive processes of the TPDT. Second, we focused on the relevance of the temporal responses during error trials. Noteworthy, temporal variance remained unaffected in both single neurons and population average during the animals’ hit and error responses. These findings support the idea that the temporal-dependent signals code the temporal sequence of this task. Collectively, our results indicate that time-dependent signals observed in both levels, single units and population dynamics, could be interpreted as a necessary substrate on which the coding responses can develop to reach a decision during the TPDT.

Results

Previously, we identified and classified single neurons associated with relevant task parameter coding during the TPDT (ref. 18 and SI Appendix, Fig. S1 A–L). DPC neurons (Fig. 1B) exhibited a high heterogeneity among their responses during the TPDT. Additionally, several single units coded more than one task parameter throughout the task. This is illustrated in SI Appendix, Fig. S1, where we display 12 DPC neurons that coded different task parameters (P1, decision and class identity). Most of these neurons showed mixed selectivity in their coding responses (18, 20). We then condensed these heterogeneous single-unit responses into two major population signals that built an elegant and compact solution for the task, consistent with the monkeys’ psychophysical performance (19).

Here, to measure the response’s variability associated with task parameters coding, we calculated the population instantaneous coding variance during the TPDT (Var_COD, SI Appendix; Fig. 1C, blue trace). This metric quantified the firing rate fluctuations among classes and neurons at each time point. Clearly, time bins in which more neurons code task parameters usually give rise to higher instantaneous coding variance. Additionally, we calculated the population variance associated with each task parameter: P1 (Var_P1, SI Appendix; Fig. 1C, cyan trace), P2 (Var_P2, SI Appendix; Fig. 1C, light green trace), and decision period (Var_Dec, SI Appendix; Fig. 1C, black trace). In a previous work (18), we quantified the coding dynamic as the percentage of cells that coded each task parameter. Notably, those coding dynamics closely resembled the specific task parameter variances observed here. This means that there was a close relationship between the number of neurons coding a task parameter and the population coding variance associated with it. Notice that before the arrival of P1 (prestimulus period), there is no task parameter to be coded. Thus, one could expect that the population variance associated with each task parameter should be zero. Nevertheless, all of the traces shown in Fig. 1C exhibit a positive value before P1. This nonzero instantaneous variance observed during the prestimulus period could be interpreted as an estimate of the basal variances associated with residual fluctuations. When each type of variance is higher than its basal value, these larger fluctuations must be associated with task parameter coding.

Population and Single-Unit Temporal Variance During the TPDT.

We wondered how much population variance could be associated with temporal dynamics during the TPDT. To quantify this, we calculated the population instantaneous temporal variance with respect to its mean response (Var_Temp, SI Appendix; Fig. 1D). At each time bin, Var_Temp quantifies the quadratic square sum among the neuron’s responses of the difference between their mean firing rates for each time bin [rⁱ(t)] and mean firing rates across the whole task (rⁱ, from −1 to 7.5 s). Whenever the mean population activity departs from its mean value, the temporal variance will increase. Remarkably, the instantaneous temporal population variance was much higher than the coding variance at any time bin (Fig. 1C vs. Fig. 1D). The same effect was observed using the temporal population fluctuation Fluc_Temp computed with respect to the mean basal firing rate (SI Appendix, Fig. S2A and Eq. S6). Hence, most of the population variance in firing rate over the extent of a trial corresponded to variability across the sequential events of the task rather than across classes. Even though Fluc_Temp was highest at stimulus arrival, it exhibited large values during both working memory (from 1 to 3 s) and postponed decision (from 4 to 6 s) delay periods. Additionally, Var_Temp and Fluc_Temp displayed high values after pb presses.

To further study temporal variance, we focused on single-neuron responses. For each unit, we compared the variance associated with parameter coding $\left(SNVa{r}_{COD}^i\right)$ with the temporal variance $\left(SNVa{r}_{Temp}^i\right)$ during the whole task period (from −1 to 7.5 s). On one hand, $SNVa{r}_{COD}^i$ measures the variance of the firing rate among classes from each individual cell (SI Appendix, Eq. S7). On the other hand, $SNVa{r}_{Temp}^i$ computes the average temporal variance for each neuron across the whole task (SI Appendix, Eq. S8). Note, in these single-neuron metrics (Fig. 1E), we averaged across time bins for each unit, whereas in Fig. 1D we averaged across neurons for each time bin. Each point in Fig. 1E represents one neuron response, and the position in the plot was defined by $SNVa{r}_{Temp}^i$ (x axis) and $SNVa{r}_{COD}^i$ (y axis). In concordance with the results observed in Fig. 1D, individual neurons displayed higher values of $SNVa{r}_{Temp}^i$ than $SNVa{r}_{COD}^i$. Hence, the mean value of the angular distributions was <θ> = 36.0° (Fig. 1E, red dotted line), which means that most of the neurons were closer to the temporal than the coding axis. Analogous results were found computing the single-neuron temporal fluctuation ($SNFlu{c}_{Temp}^i$, SI Appendix, Eq. S9) with respect to their mean basal firing rate (from −1 to 0 s, SI Appendix, Fig. S2B). Looking at the distribution shown in Fig. 1E and SI Appendix, Fig. S2B, we can see that there were no neurons with coding variance only. Thus, it is unlikely to find cells with significant task parameter coding and where the firing rate curves cancel out when averaged over trials of different classes.

Temporal Versus Coding Latencies.

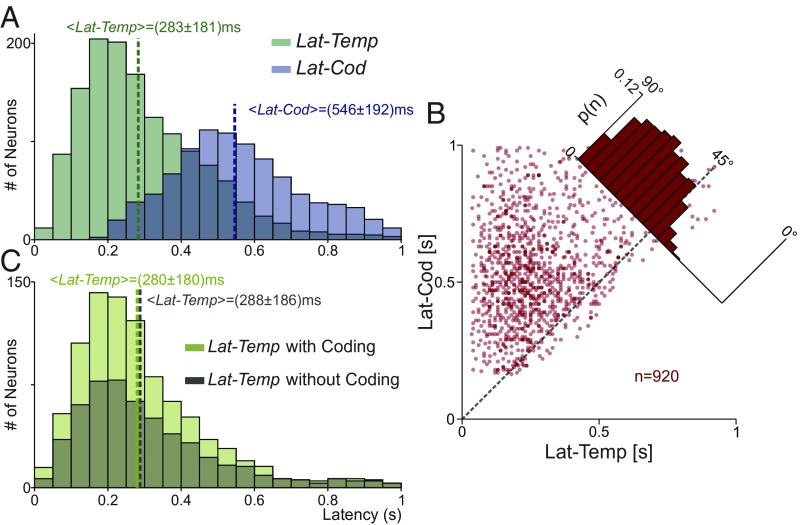
We wondered whether the pure temporal responses increased earlier than the task parameter coding variances. For each neuron, we quantified the time bin at which the temporal and the coding variance increased significantly with respect to its basal value during P1 (from 0 to 1 s). These time bins defined two different latencies: Lat_Temp and Lat_Cod. Fig. 2A shows the latency distributions for Lat_Temp and Lat_Cod. During P1, more neurons displayed a significant increase in the temporal variance (n = 1,436; 91.2%) than in the coding response variance (n = 946; 60.1%). Importantly, the temporal signals emerged before than the coding signals (Fig. 2A, <Lat_Temp> = 283 ± 181 ms vs. <Lat_Cod> = 546 ± 192 ms). Thus, pure temporal responses could act as a precursor for task parameter coding. Previously, similar response and coding latencies were found using a completely different approach (18). In addition, most of the neurons with significant Lat_Cod exhibit significant Lat_Temp (n = 920). For each of these neurons, we plotted Lat_Temp (Fig. 2B, x axis) against Lat_Cod (y axis). In general, the single-neuron temporal responses appeared before the coding signals. This was further documented by dividing the temporal latency (n = 1,436) during P1 into two groups: one with significant coding latency (n = 920) and another without coding (n = 516). Notably, we show that Lat_Temp distributions were statistically the same for these two groups of neurons (Fig. 2C). This means that the temporal signals from single neurons emerged independently of whether the neurons significantly encoded task parameters.

Fig. 2.

Temporal and coding latency variances. (A) Latency distribution for neurons with temporal (green; n = 1,436) or coding (blue; n = 946) variance statistically different from their basal values during P1. In general, pure temporal signal (<Lat_Temp> = 283 ± 181 ms) appeared before coding signals (<Lat_Cod> = 546 ± 192 ms). (B) Neurons with significant latencies of temporal and coding variances (n = 920). Lat_Temp (x axis) is plotted against Lat_Cod (y axis). Each dot corresponds to one neuron. Single-neuron latencies were higher for coding than for temporal variances. (C) Latency distributions of temporal variance for neurons with significant Lat_Temp and Lat_Cod (n = 920; light green) and for neurons with only significant Lat_Temp (n = 516; dark green). Latency distributions are statistically the same in both groups (<Lat_Temp> = 280 ± 180 ms vs. <Lat_Temp> = 288 ± 186 ms). Response temporal latencies were very much alike for neurons with significant temporal and coding responses and for neurons with only significant temporal signals.

Temporal Responses of Single DPC Neurons.

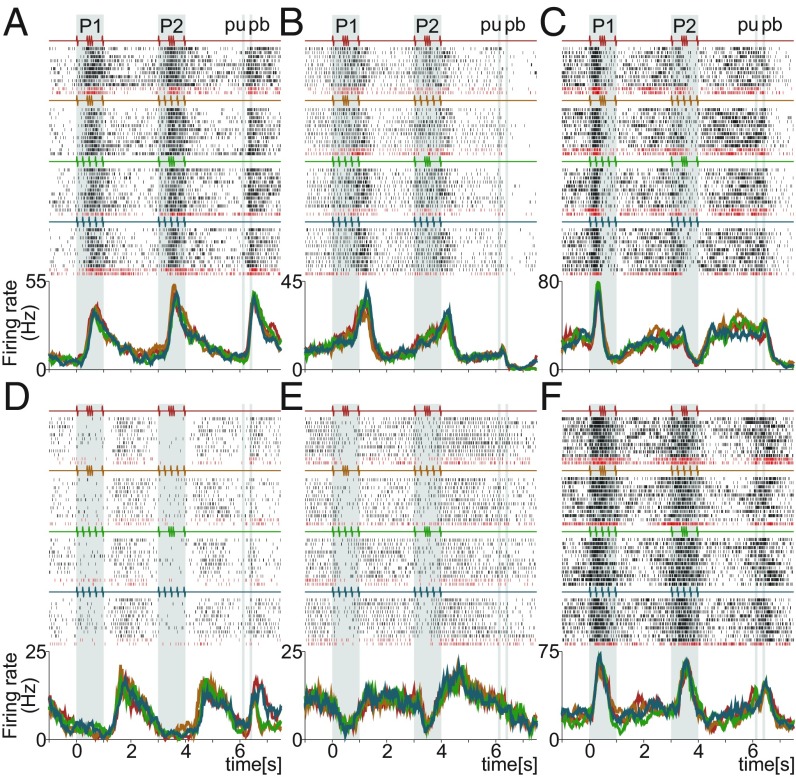
We employed $SNVa{r}_{Temp}^i$ and $SNFlu{c}_{Temp}^i$ to identify neurons with strong temporal signals. Fig. 3 and SI Appendix, Fig. S3 illustrate typical temporal activity of single DPC neurons. Clearly, all of these neurons’ responses are not essentially related with task parameter coding. Most of these neurons do not code any task parameters during the task. These neurons exhibit response dynamics that vary over time, but not in a manner that encodes task variables. Furthermore, DPC neurons exhibited a large repertoire of neuronal responses associated with pure temporal dynamics. Some of these neurons were involved in stimulus arrival with positive (Fig. 3F and SI Appendix, Fig. S3 B, D, and F–H), negative (Fig. 3E and SI Appendix, Fig. S3 C and I), or mixed (Fig. 3C and SI Appendix, Fig. S3A) responses. Another group of neurons was associated with ramping activity during the delay periods (Fig. 3 A, B, and D and SI Appendix, Fig. S3 A, F, G, and I). Finally, another overlapping group of neurons was related to temporal responses after pb (Fig. 3 A, D, and F and SI Appendix, Fig. S3 A, C–E, and G–I). Interestingly, there were neurons that only respond during pb, independently of the decision outcome (SI Appendix, Fig. S3E). Therefore, even for temporal signals, the complexity and diversity of responses was broad. To handle this temporal heterogeneity, we applied dimensional reduction methods of the population activity to reveal temporal latent signals.

Fig. 3.

Single DPC neurons with notable temporal activity during the TPDT. (A–F) Raster plots of six temporal exemplary neurons sorted according to the four possible classes. Each row of ticks is one trial, and each tick is an action potential. Trials were randomly delivered and were sorted by class afterward (only 10 out of 20 trials per class are shown). Correct and incorrect trials are indicated by black and dark red ticks, respectively. Traces below the raster plots are average per-class firing rates [peristimulus time histograms (PSTHs)] for each temporal neuron. Each color refers to one of the four possible classes: G-G (red); G-E (orange); E-G (green); and E-E (blue). Neurons exhibit pure temporal dynamics without coding any task parameter.

Population Principal Components Exhibit Temporal Signals.

Such dimensional reduction was done using a condensed population-level representation of the data, based on the state space of neural responses. The state of the DPC population was represented by a point in a n-dimensional (n = 1,574) space of firing rate responses. Each dimension, at each time point, corresponded to the firing rate of one neuron. The dynamics of the network was described by combining 1,574 firing rates mostly recorded separately (15, 19, 23–25). As neurons’ activity evolves over time, the point moves through the space, forming a trajectory that represents the response of the population.

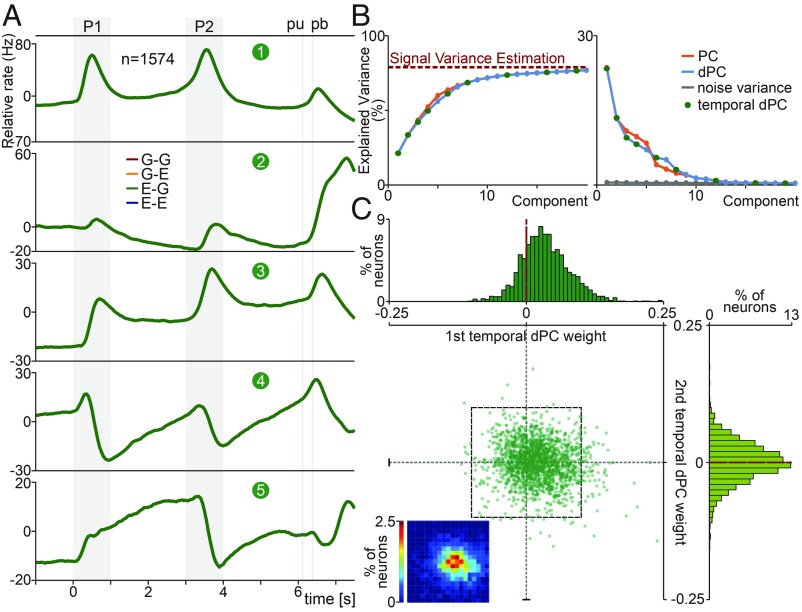
We first employed principal-component analysis (PCA) to identify a lower dimensional subspace underlying the DPC network dynamics (26). The covariance matrix used for PCA was quantified from the whole task (SI Appendix, Eq. S10). Even if PCA could be used to reduce the dimensionality of the dynamics, the new subspace was deficient in highlighting temporal signals or task parameter dynamics (SI Appendix, Fig. S4). Overall, PCA gave a much more complex picture of the population dynamics, dominated by strong temporal signals mixed with parameter coding responses. The first five PCs were ordered by the amount of explained total variance (ETV) (SI Appendix, Eq. S15). For each PC, we displayed the population activity projections sorted by classes. In general, PCs exhibited strong temporal signals that dominate the population dynamics. Notice that the fifth PC displayed a ramping temporal activity during the first (from 1 to 3 s) and second (from 4 to 6 s) delay periods (SI Appendix, Fig. S4). Even though PCA was a fully unsupervised approach, it was possible to recognize almost pure temporal responses such as the fifth PC.

Population Temporal Dynamics.

Then, to focus on the task timing signals from the population activity, we applied demixed PCA (dPCA) (13). Employing dPCA, we were able to extract a low-dimensional subspace more sensitive to the pure temporal responses. Contrary to other approaches, dPCA split the population variability associated with different task parameters employing marginalized matrices. Here, we center our analysis on decomposing the population temporal responses. In a previous study (19), we studied the population components associated with coding task parameters. Fig. 4A displayed the first five temporal dPCs that captured most of the variance during the task. To calculate the temporal dPCs, we applied a temporal marginalization of the population activity. Then, we averaged the responses of all of the trials without considering class identity. The temporal dPCs were optimized to maximize (SI Appendix, Eq. S13) the ETV (SI Appendix). Due to this optimization, the population activity of the four classes overlapped when they were projected onto this axis (Fig. 4A). We selected class E-G (c3, green trace) to be on top of the other four traces.

Fig. 4.

DPC population temporal signals during the TPDT. (A) dPCA was applied to the temporal marginalized covariance matrix obtained from the TPDT. Population activity, sorted by classes, was projected onto the temporal dPCs. Temporal dPCs were ordered according to their explained total variance (ETV). First five temporal dPCs: first ETV, 23.9%; second ETV, 13.5%; third ETV, 9.5%; fourth ETV, 8.25%; fifth ETV, 5.84%. (B) Cumulative sum of explained signal-plus-noise variance (Left, ESNV). The dashed red line shows an estimate of the fraction of task-related variance. ESNV per component (Right). The red traces correspond to PCs; the blue traces are for dPCs. The gray trace represents the percentage of noise variance explained by the dPCs. The green points indicate which dPCs are temporal. (C) Central graph: For each neuron, we use its first and second temporal-dPC weights to plot its location on the plane. Heat-map Inset (Bottom Left) shows the joint weight distribution (20 × 20 grid, 0.01 bin side length, corresponds to black dashed square; color scale goes from 0 to 2.5%). First temporal-dPC weight distribution tends to positive values: µ = 0.028; σ = 0.035 (Top). Second temporal-dPC weights are equally distributed for positive and negative values: µ = 0.0001; σ = 0.029 (Right).

The first temporal dPC displayed an intense response during P1 and P2 periods (Fig. 4A). This component captured 23.9% ETV and represented the most relevant demixed signal. We remark that there was no component with higher variance associated with task parameter coding. This means that the sensory stimulation gave rise to strong temporal dynamics that underlay the coding of the stimulus pattern. Notably, second temporal dPC (Fig. 4A) exhibited a strong temporal response immediately after the pb press. This signal contrasted highly with the first dPC: It was less involved in stimulus presentation and more engaged with a population dynamic after the animals reported their decisions. Although this component was related with the last period of the trial, it explained 13.5% of the total variance. This signal was presumably linked with the strong decision signal that emerged after pb (ref. 18 and Fig. 1C). By construction, this second temporal dPC was orthogonal to the first dPC. This means that the sensory temporal signal (first dPC) was independent of the signal after pb presses (second dPC). The third temporal dPC projections showed a mixed dynamic with sensory and persistent responses (Fig. 4A, 9.5% ETV). It exhibited a stepped change during P1 followed by persistence during the first delay; after that, it showed another stepped response during P2, again followed by persistence during the second delay between P2 and pu. Remarkably, the neural projections onto the fourth temporal dPC presented a temporal pacemaker during both delays (Fig. 4A). This component, which explained 8.25% ETV, begins in each stimulus period with a negative value and reaches peak values during P1, P2, and pb. We notice the resemblance between this component and the fifth PC shown in SI Appendix, Fig. S4. We hypothesize that this pacemaker component could act as an internal time estimator that allows the network to predict the arrival of relevant events during this cognitively demanding task. Last, the fifth temporal dPC showed a ramping temporal activity during the first delay, and with markedly smaller one during the second delay (5.84% ETV).

Task Dimensionality and Temporal Signals.

Subsequently, we studied the dimensionality of the population across the TPDT. We wonder: How many dimensions or components were necessary to explain the network dynamics? Moreover, how many of these relevant dimensions were pure temporal signals? To estimate quantitatively the dimensionality, we used both dPCA and PCA. We constructed a noise population covariance matrix that only included single-trial variability (X_noise; SI Appendix, Eq. S16). Using this noise covariance matrix, we estimated the fraction of the “signal-plus-noise” variance that was related to noise. The percentage of variance that was related with signal and not with noise (1 − Var_Noise) determined the red dashed line in Fig. 4B. In Fig. 4B, Left, we compared the cumulative explained variance for PCs and dPCs. Using both techniques, we obtained analogous results: Few components are necessary to reach the signal variance estimation. In addition, the dimensionality of the population responses estimated with dPCA was equivalent to the one calculated with PCA. Consistently, in Fig. 4B, Right, we showed that there were only few dPCs that captured higher explained signal-plus-noise variance (ESNV) than noise variance (SI Appendix). This means that the inherent population fluctuations (noise) projected onto the dPCs captured significantly less variance, but only compared with the first few components. Keep in mind that there were 1,574 possible dimensions. However, few components are enough to explain the relevant dimensions of the network. We calculated that around 12 dPCs are at least 50% above inherent noise variance. This number estimates the dimensionality of the population responses during the TPDT. In a previous study, this approach was applied to estimate the dimensionality of the dynamic in a frequency discrimination task (11).

Most notably, 7 out of 12 relevant dimensions are pure temporal signals (green dots in Fig. 4B). Then, a large proportion of the dimensions of the network are only related to time. Even more, the first four dimensions, which captured 55.15% ETV (48.1% of ESNV), are temporal signals. These results are strong evidence that temporal signals are a relevant part of the network response and that they might act as a substrate for coding dynamics.

A Common Anatomical Substrate for Temporal Signals.

We speculated on whether there were separate categories of neurons involved in different temporal components. To explore this possibility, we plotted for each neuron their first and second temporal-dPC weights (Fig. 4C). We did not identify evidence for separate clusters of neurons. Even if we showed individual neurons with responses that resembled each of these two components (SI Appendix, Fig. S3 G and F for first dPC, and SI Appendix, Fig. S3E for second dPC), this was not the general trend. Analogous results were observed when we plotted the weights of other temporal dPCs. Thus, although these temporal signals can be read out independently, they were built from the same anatomical substrate. Analogous results were found in previous studies for other types of components and tasks (11, 13, 19, 27).

Additionally, we calculated the distribution of the weights given by this dPCs for each of the 1,574 neurons. Note that the weight distribution for the first temporal dPC (Fig. 4C, Top) exhibited a bias to positive values (µ = 0.028; σ = 0.035). This means that the sensory temporal signals were in general positive (excitatory). Although it was possible to identify negative (inhibitory) temporal sensory neurons (Fig. 3E and SI Appendix, Fig. S3 C and I), they were not as abundant as the positive sensory neurons (Fig. 3F and SI Appendix, Fig. S3 B, D, and F–H). However, the weights given by the second temporal dPCs (Fig. 4C, Right) were equally distributed for both positive and negative values. These results agree with previous studies that found that coding components behave like zero-centered Gaussians distributions (11, 13, 19). Similar distributions were found for higher-order temporal dPCs. Thus, except for the first dPC, the other components exhibited zero-centered weight distributions. Furthermore, the unimodal weight distributions also suggested that there was not a clear division between single neurons that might have participated in temporal signals from those neurons that did not.

Population and Single-Unit Temporal Variances During the LCT.

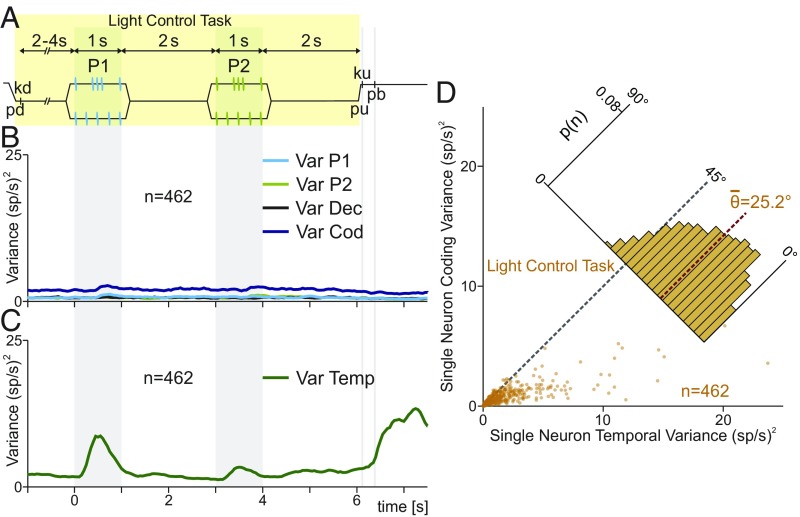
To further quantify whether the DPC temporal signals depended on the animal’s task performance, many of the neurons (n = 462) were also tested in a control variant of the TPDT. In each trial, the monkeys received identical stimuli as in the TPDT, but the correct answer was indicated by a continual visual cue (Fig. 5A). We refer to this task as LCT.

Fig. 5.

Single DPC neuron and population variances during the LTC. (A) During LCT, events proceeded exactly as in Fig. 1A, except that when the probe touched the skin, the correct pb was illuminated. The light was turned off after pu, triggering the pb press. Thus, stimuli and movements were identical to the TPDT, but were cued by visual stimuli. Performance in the LCT was 100% across classes. (B) LCT population instantaneous variances: Var_COD (blue, SI Appendix); Var_P1 (cyan trace), Var_P2 (light green trace), and Var_DEC (black trace). Note the marked differences with Fig. 1. (C) LCT population instantaneous temporal variance (Var_Temp, green trace). (D) Single-neuron temporal variance during LCT (x axis, SI Appendix) is compared against single-neuron coding variance during LCT (y axis). Each dot corresponds to one neuron (n = 462). Inset histogram show angular distributions for the population (<θ> = 25.2°). During the LCT, $SNVa{r}_{Temp}^i$ is much higher than $SNVa{r}_{Cod}^i$.

As before, we calculated the population instantaneous coding variance during the LCT (Var_COD, SI Appendix; Fig. 5B). Analogously, we calculated the population variance associated with each task parameter: P1 (Var_P1; Fig. 5B), P2 (Var_P2), and decision (Var_Dec). Under the LCT, the population coding variance was no longer related to the identity of the stimulus pattern or the decision report (Fig. 5B). Accordingly, the population coding variance stayed constant and equal to its basal value during the whole task. These results agree with the coding dynamics of individual neurons observed before (18). Even though stimuli and final movements were the same as in the TPDT, no coding variance modulation was observed. Thus, the population coding variance increased above its basal state only when the task demanded it.

Again, we wonder how much population variance could be associated with temporal dynamics. We remark that although coding variance was not modulated, the firing rate of the neurons evolved during the LCT. To further show this, we quantified the population instantaneous temporal variance (Var_Temp, SI Appendix, Fig. 5C) during the LCT. In contrast to coding variances, Var_Temp evolved during the LCT. Thus, fluctuations in firing rate are only involved in timing of the task events. However, the values Var_Temp are not as high as during the TPDT (compare Fig. 5C with Fig. 1D). Thus, we could speculate that part of the temporal signals were still present during LCT, but other temporal dynamics diminished or disappeared. In addition, we compared the variance associated with coding $\left(SNVa{r}_{COD}^i\right)$ and temporal $\left(SNVa{r}_{Temp}^i\right)$ for each neuron during the LCT. Each dot in Fig. 5D represents one neuron during LCT ($SNVa{r}_{Temp}^i$, x axis; $SNVa{r}_{COD}^i$, y axis). In concordance, neurons displayed much higher temporal than coding responses. Coding variance remained at small values for all 462 neurons and the angular distribution was biased to small angles (<θ> = 25.2°; Fig. 5D).

Temporal Responses of Single Neurons in the TPDT vs. the LCT.

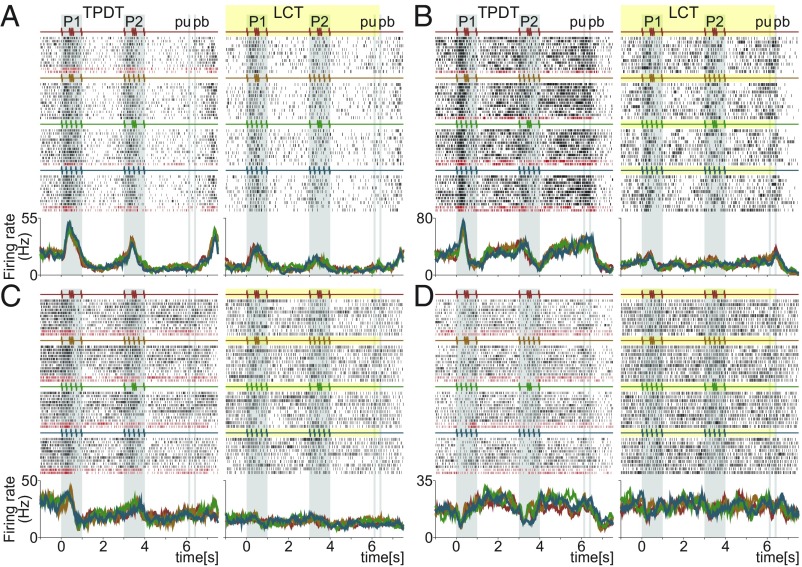
Do the responses of single neurons undergo their own decrease in temporal variability during LCT? To quantify this, we chose neurons with high temporal variance during the TPDT that were also tested in the LCT. In Fig. 6 and SI Appendix, Fig. S5, we show typical DPC temporal activity under both task conditions. In concordance with the differences in Var_Temp between Figs. 1D and 5C, most of the temporal responses declined or vanished during LCT. Notably, even the sensory temporal signal during the stimulus arrival are diminished noticeably during the LCT (Fig. 6 and SI Appendix, Fig. S5 A–C). All ramping activity observed during the TPDT ceased (Fig. 6 A and C and SI Appendix, Fig. S5 A–E). Some of the temporal signals after pb presses remained during both task conditions (SI Appendix, Fig. S5 D–F). In summary, during the LCT, the temporal signals of individual neurons diminished or ceased, while the coding responses disappeared (18).

Fig. 6.

Single DPC neurons with notable temporal activity compared between TPDT and LCT. (A–D) Raster plots of four temporal exemplary neurons tested in both conditions: TPDT (Left) and LCT (Right). Responses are sorted according to the four possible combinations of G and E stimulus patterns delivered during P1 and P2. Correct and incorrect (only in TPDT) trials are indicated by black and dark red ticks, respectively. Traces below the raster plots are average per-class firing rates (PSTHs) for each neuron and condition. Each color refers to one of the four possible stimulus combinations of G and E; the resulting four classes are c1 (G-G, red), c2 (G-E, orange), c3 (E-G, green), and c4 (E-E, blue). Note that these neurons are different from those shown in other figures.

Population PCs During the LCT.

To investigate whether population temporal signals depended on the cognitive context, we implemented the same population analysis to a subgroup of neurons (n = 462) recorded during TPDT and LCT. First, we applied PCA to the population response under each condition (SI Appendix, Fig. S6). We displayed the first five PCs during the TPDT for this subpopulation. We remark that although the number of neurons decreased from 1,574 to 462 (29.3%), the dynamics remained approximately the same (compare SI Appendix, Fig. S4 with SI Appendix, Fig. S6A). This suggests that network dynamics was robust and stable under changes in the number of neurons.

Next, we computed the PCs for the same group of neurons under the LCT (SI Appendix, Fig. S6B). Although the PCs did not show task-related coding, they exhibited prominent temporal responses. Moreover, all of the components appeared to be associated with the stimulus arrivals or the pb presses. Notably, the PCs’ dynamics during delay periods are much weaker than in TPDT. Furthermore, the ramping temporal activity was no longer present under LCT.

Single-Neuron Temporal Variance Compared Between the TPDT and LCT.

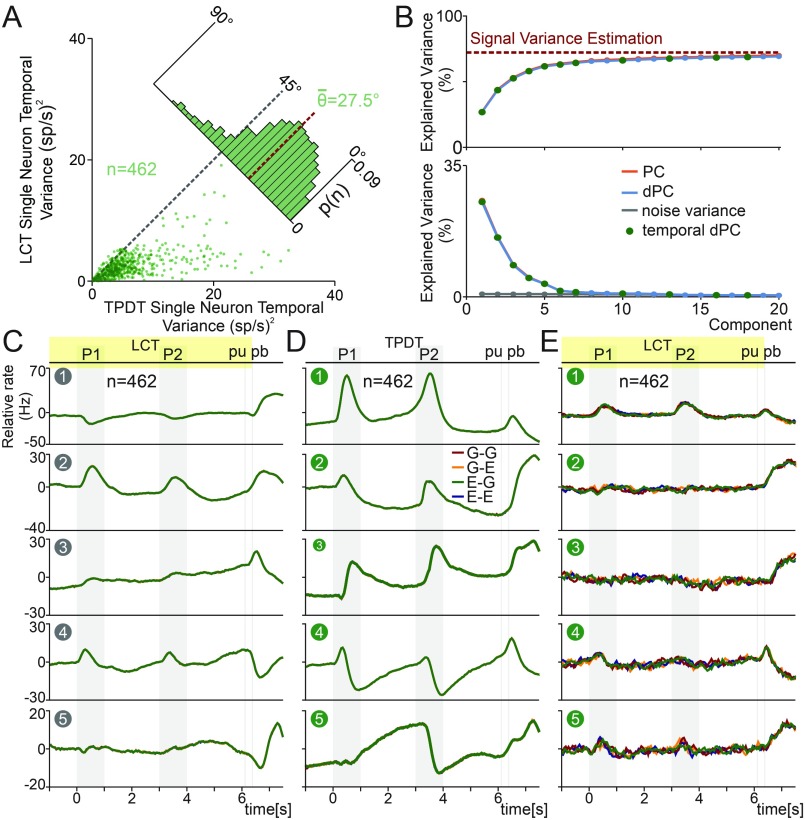
Based on the results shown in the previous three sections, we speculated that single neurons may diminish their temporal variance under a nondemanding cognitive task (LCT). To test this hypothesis, we compared $SNVa{r}_{Temp}^i$ under both task variants. Each point in Fig. 7A was determined by the two values: the TPDT $SNVa{r}_{Temp}^i$ (x axis) and the LCT $SNVa{r}_{Temp}^i$ (y axis). In concordance, cells presented much higher temporal variance under the demanding task (TPDT) than the nondemanding task (LTC). Additionally, the distribution (Fig. 7A) was biased to small angles (<θ> = 27.5°). Similar results were found comparing $SNFlu{c}_{Temp}^i$ for each task condition (SI Appendix, Fig. S7A). This is further evidence that several temporal signals were recruited only when the task was demanding enough.

Fig. 7.

DPC population temporal signals during the LCT. In this figure, we restricted our analysis to the neurons that were recorded during both TPDT and LCT (n = 462). (A) $SNVa{r}_{Temp}^i$ in TPDT (x axis, SI Appendix) is compared with $SNVa{r}_{Temp}^i$ in LCT (y axis). Each dot corresponds to one neuron tested in both conditions (n = 462). Inset histogram show angular distributions for the population (<θ> = 27.5°). $SNVa{r}_{Temp}^i$ is much higher in TPDT than LCT. (B) Cumulative sum of the explained signal-plus-noise variance (ESNV) of the PCs and dPCs during LCT (Top). The dashed red line shows an estimate of the fraction of task-related variance. (Bottom) ESNV of PCs (red) or dPCs (blue). The gray trace represents the percentage of noise variance explained by each dPCs. The green points indicate the temporal dPC. (C–E) Population activity, sorted by class identity, was projected onto each dPC. Components were ordered by their explained total variance (ETV). The same y scale was used among projections to facilitate comparison. (C) First five temporal dPCs optimized for the LCT. First ETV, 30.5%; second ETV, 19.5%; third ETV, 10.6%; fourth ETV, 6.4%; fifth ETV, 4.3%. (D) dPCA was applied to the temporal marginalized covariance matrix obtained from the whole TPDT (n = 462). These signals are similar to those in Fig. 4A. First ETV, 25.1%; second ETV, 14.8%; third ETV, 10.3%; fourth ETV, 9.1%; fifth ETV, 6.4%. (E) LCT activity was projected into exactly the same axes than in D. Since dPCs were optimized for TPDT population activity, projections of LCT activity showed more fluctuations.

Task Dimensionality and Temporal Signals During the LCT.

We applied dPCA to obtain the temporal components optimized for the LCT population. Then, we estimated the dimensionality of the responses during LCT. In Fig. 7B, Top, we displayed the cumulative sum of total variance captured by the dPCs. We computed the fraction of the total population variance associated with the signal variance (red dashed line). Consistently, few components were enough to reach the estimated signal variance. Additionally, the first six components are pure temporal dPCs. In Fig. 7B, Bottom, we estimated ESNV from each LCT component and its fraction associated with noise (gray trace). Notably, only six temporal components were significantly above the noise variance estimate. This means that the dimensionality of the network dynamic diminished from 12 dPCs during the TPDT to 6 dPCs during the LCT. Similar results were found using the same neurons (n = 462) to calculate the dimensionality of the network under both task conditions (SI Appendix, Fig. S6 C and D). This dimensionality reduction was due to two factors: the lack of coding dynamics and the decline of temporal signals during LCT.

In Fig. 7C, we show the temporal dPCs optimized for the LCT activity. Comparing the temporal dPC from TPDT and LCT, the persistent activity and the ramping responses of Figs. 4A and 7D were no longer present in Fig. 7C. This means that temporal signals are not equivalent in LCT and TPDT, except for those related to stimuli or pb presses. Nevertheless, the intensity of the sensory component clearly diminished during the LCT. The most plausible explanation is that as task parameter coding was not necessary during LCT, the temporal responses that supported this coding ceased or disappeared. Note that the first temporal dPC explained 30.5% of the total variance and was mainly associated with the signal after pb presses. Furthermore, the second dPC was involved with stimulus arrival and pb signal (19.5% ETV). Moreover, the absence of coding during LCT, except for the timing of the task events, entailed similar results when we used dPC or PC projections (compare Fig. 7C vs. SI Appendix, Fig. S6B).

Context-Dependent Temporal Signals.

To examine the differences between TPDT and LCT temporal signals, we benefited from the 462 neurons recorded in both task conditions. We calculated the temporal dPCs, now restricted to only those neurons during TPDT. The results were presented in Fig. 7D. Again, as with PCA, the temporal dPCs of this subgroup of neurons (n = 462) matched those of the full population (Fig. 4A). Then, the number of neurons was reduced from 1,574 to 462, and the temporal components remained unaltered. On the other hand, when we used the TPDT temporal dPCs to project the LCT population activity, we observed a pronounced disappearance of most of the temporal signals (Fig. 7E). Thus, the same temporal axes were used to project the TPDT (Fig. 7D) and LCT (Fig. 7E) population activities. This analysis allowed us to compare between task conditions, the temporal signals that remained or disappeared within the components. Consistent with our previous result, the persistent and ramping responses calculated during the TPDT (Fig. 7D) were no longer present in LCT projections (Fig. 7E). However, the temporal responses observed after pb during TPDT, remained unaltered across all LCT projections. This is evidence that pb temporal signals are unconnected to those during the delays. All of these results agree with what was observed across the exemplary neurons (Fig. 6 and SI Appendix, Fig. S5). Collectively, our population findings suggest a close relationship between the temporal dynamics and task execution. These results are strong evidence that some temporal signals were only recruited when parameter coding was needed to solve the TPDT.

Population and Single-Neuron Temporal Variances During Hit and Error Trials.

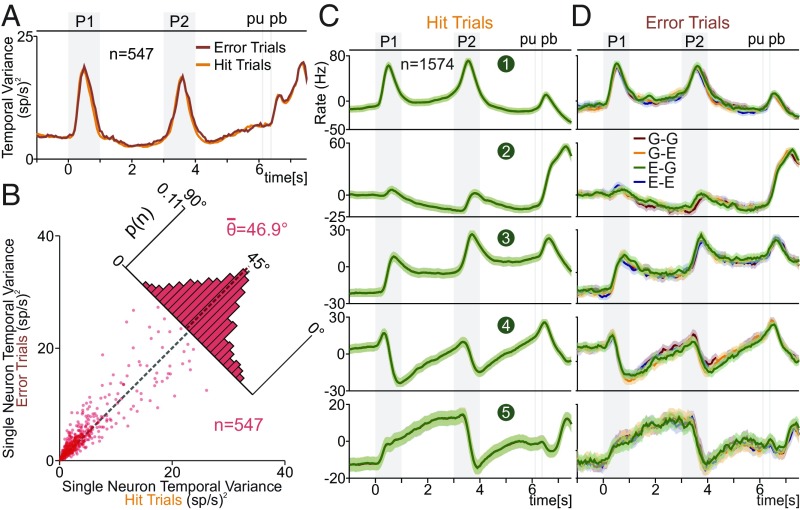
We wanted to determine to what degree the pure temporal signals in the DPC population predicted the monkeys’ performance. We investigated whether the evoked temporal variance was somehow different between correct (hit) vs. incorrect (error) trials during the TPDT. For this, we computed (Var_Temp) during hit and error trials (Fig. 8A). We restricted this analysis to a subgroup of neurons with at least three error trials in each of the four classes (n = 547). Note that during LCT there were no error trials to analyze; the performance was consistently 100%; this reflects that this guided task was not cognitively demanding, which was part of the intended design.

Fig. 8.

DPC temporal signals during hit vs. error trials. (A and B) We restricted our analysis to the neurons (n = 547) with at least three error trials for each class. (A) Var_Temp (SI Appendix) for hit (red) and error (orange) trials. (B) $SNVa{r}_{Temp}^i$ during hit trials (x axis) is compared against $SNVa{r}_{Temp}^i$ during error trials (y axis). Each dot corresponds to one neuron (n = 547). Inset histogram show angular distributions (<θ> = 46.9°). $SNVa{r}_{Temp}^i$ are statistically the same in hit and error trials. (C) Temporal dPCs, calculated with hit trials, were used to repeatedly project the population activity of single hit trials. First five temporal dPCs were ordered according to their ETV. Traces show the average (solid line) and SD (shading) for 1,000 hit trial projections. (D) The same temporal dPCs as for C (calculated with hit trails) were used to project the population activity in single-error trials. The solid lines and shadings were constructed in the same manner, but with error trial population activities.

Notably, (Fig. 8A shows that Var_Temp evolved together during hit and error trials (the same conclusion was obtained employing Fluc_Temp; SI Appendix, Fig. S7B). In other words, at each time point, the quadratic distance between the population mean and the basal firing rate during hit and error trials was approximately the same. This means that it is impossible to use Var_Temp or Fluc_Temp to predict the animals’ choice. This result gave us a first suggestion that temporal responses were the same for error and correct choices. We then evaluated the error effect in temporal variance of single neurons. This was made by measuring the $SNVa{r}_{Temp}^i$ for each cell during hit and error trials. Similar as we have done previously, on Fig. 8B we compared on the same plot the $SNVa{r}_{Temp}^i$ associated with hit (x axis) and error (y axis) trials for each single neuron (n = 547). We found that $SNVa{r}_{Temp}^i$ evoked by the two types of trials were statistically identical (Fig. 8B; <θ> = 46.9 ± 10.1°). The same effect was observed when $SNFlu{c}_{Temp}^i$ is compared in hit vs. error trials (SI Appendix, Fig. S7C). This means that it would also be impossible to differentiate between hit and error trials, based on the temporal variance of single DPC neurons.

Population Temporal Signals During Hit and Error Trials.

Finally, we investigated the relationship between the population temporal signals and monkeys’ behavior. For this purpose, we studied the differences between hit and error trials on the temporal dPCs. We constructed single-trial activity matrices by pseudorandomly selecting trials from all neurons. Then, we plotted the average and SD of repeated projections (1,000) of single-trial activity onto the temporal axis used in Fig. 4A. For error trials, we randomly chose one error trial per iteration for each neuron in each class. Since all neurons (n = 1,574) had at least one error trial per class, we employed the full population for this analysis. The average (solid lines) and SD (shading) of single-hit trial projections are shown in Fig. 8C. Note the similarity between the traces in Figs. 4A and 8C. In addition, the single-trial projection onto each temporal dPC produced small values of SD throughout the task.

Even if it is possible to think that an error in the temporal signal could contribute to an error report, this is not in agreement with our results. Clearly, there was a high correspondence between the temporal signals in error (Fig. 8D) and hit (Fig. 8C) trials. In general, our findings suggest that errors were not associated with the temporal signals. This finding is complemented by previous studies that have shown strong evidence that error trials were associated with task parameter miscoding (18, 28). We remark the notable differences between the temporal signals found in error trials (Fig. 8D) with the LCT temporal components (Fig. 7C). On one hand, a nondemanding task led to a decline in temporal responses (Fig. 7C). On the other hand, during error trials, the temporal signals remained unchanged (Fig. 8D).

Discussion

Previously, we showed that DPC codes the relevant task parameters of the TPDT. Here, we found that although a large percentage of DPC neurons were involved in coding dynamics, the variance related to coding task parameters was small in comparison with the size of temporal variance over time. We observed this by using both single-unit and population-averaged approaches. In both cases, the time-dependent responses showed higher variance than task parameter coding.

Contrary to the neuronal responses recorded in the active task (TPDT), during the control task (LCT), DPC neurons did not code task parameters. Furthermore, the only task-related responses that remained during LCT were some pure temporal fluctuations, but their variance were reduced in comparison with the TPDT. Again, this observation was corroborated using both single-unit and population-averaged approaches. Nevertheless, focusing on the error trials, the total amount of temporal variance was similar to hit trials. Then, fluctuations in firing rate related to time were not affected during the animals’ errors. Thus, it is not possible to predict an error employing neither single neurons nor population temporal variance.

To extend our analyses to the neuronal population level, we employed dimensionality reduction methods (15, 23–25, 29). We found that the population dynamics were robust and stable despite the high variability in the single neuron’s responses. Consistently, a recent study has shown that population responses are unaffected using multiunit threshold crossing activity instead of sorted individual neurons (30). Although PCA served to reduce the dimensionality of the data, most of the components did not reveal a useful representation of the data (13, 14). Consequently, we used dPCA to focalize on the temporal signals of the network responses (13). Thus, we split the whole DPC responses into a more tractable problem. Notable, although temporal dPCs are not linked to task parameter coding, their high explained variance suggested that they constituted a crucial element of task execution. Importantly, these temporal population signals were unaffected during error trials. However, previous studies have shown that coding signals noticeably changed during animals’ errors (18, 19, 28). Combining both results, we hypothesize that errors emerge as task parameter miscoding, but not due to the pure temporal signals. This is further supported by the fact that LCT temporal population signals significantly decreased their intensities or disappeared. These results agree with the decreased in variance measured in single units during the LCT. Thus, a big proportion of the temporal signals appeared only when the animals performed the TPDT. The population signals that remained during LCT were only associated with the stimulus arrival and pb responses. To further understand the role of temporal signals during nondemanding tasks, future studies could employ passive tasks (31–34). Under this condition, stimuli remain the same, but animals are not required to push a button to receive reward. Since there was no decision report and no overt attention is necessary in this context, temporal signals in DPC could cease entirely. In support of this conjecture, other studies have shown that coding dynamics vanish completely in frontal cortices during the passive condition (31, 34).

Several studies have shown that neural activity was often sensitive to the temporal task sequence. In particular, a significant proportion of frontal lobe cortex neurons respond to the amount of time elapsed during the delay period between two events. Cells with these types of responses are generally called ramping neurons (4, 10). Note that it was not necessary for the subject to estimate the duration of the delay period to provide an appropriate answer. If they appear, as they do, it should be because they offer some advantage or alternatively, due to some constraint upon the network dynamics. Here, we showed that these ramping responses are commonly found in DPC neurons during both delays (from 1 to 3 s and from 4 to 6 s). Furthermore, we observed that peacemaker-shaped signals prominently emerged from the population response during the TPDT. Notably, they disappeared during the nondemanding task. This suggests that ramping signals were only generated during the active task. Since the network did not code task parameter during the LCT, it did not need to infer the arrival of the task events. Based on those results, we speculate that as the pacemaker component was no longer necessary, it vanished. Future studies could examine the relevance of this ramping activity during task designs in which each trial consists of delay periods of different durations (6, 35–37). Under duration uncertainty, peacemaker signals could adapt, or become useless to predict the stimulus arrival.

We would like to emphasize that a large proportion of the TPDT network dimensions were only associated with time events. In addition, there was a large disparity between the variance captured by population temporal signals vs. the variance associated with task parameters coding. Furthermore, most of the significant TPDT components were only associated with the temporal sequences of task events: 7 out of 12 relevant dimensions were pure temporal signals. However, during the LCT the dimensionality was even smaller than in the TPDT, and all significant components were associated with the temporal signals. These results are in concordance with a recent theoretical work (38) that showed that network’s dimensionality increases from a simple task to a more complex one. Altogether, this is further evidence that time-dependent signals emerging in relation to different stages in the task constitute an essential element of the network dynamics during cognitive tasks.

A functional distinction between task coding components and time-dependent variations in firing rates has been proposed previously (11, 39). These studies suggested that functional separation appears at the population level, but not at the single neuron’s responses. Our results indicate that temporal readouts arose from diffuse combinations of the single neuron’s responses. The distributions of the weights given to each neuron indicate that they share a common anatomical substrate: the distributions were unimodal and Gaussian-like. Despite this, it was still possible to identify single neurons with temporal dynamics that resembled the population dynamics. This means that although these temporal signals emerge at the population level, there are usually stereotypical neuron responses that mimic these temporal responses. However, we were not able to separate them into different categories or give them labels; neuronal response exists in a continuum. This agrees with the notion that the functional separation does not emerge at the single-neuron level (13, 27).

Another important question regarding time-dependent signals is how they are generated. One possibility is that they are generated by a mechanism independent of the task parameter coding dynamics; a sort of master clock that could allow timing across a variety of contexts (40). However, we are inclined to think that our results point in the direction of a different mechanism that has been already proposed: Neuronal populations can inherently produce temporal signals relevant to the task being performed (41). Many networks models have been put forth to address this issue: Recurrent networks could supply a robust and flexible dynamics to encode the passage of time (42–44).

In previous studies, it was suggested that pure time-dependent signals could adapt much faster than task coding components (5, 10, 11). In other words, temporal signals during delays could readapt in blocks of trials with different durations. This mechanism could increase the flexibility for coding dynamics to solve the same task under different durations (45–47). Although in our experiment we could not test this hypothesis, it is an important question to address in future experiments.

To conclude, we propose that the temporal signals in DPC (or in any other brain areas) could be interpreted as a substrate necessary to supply a framework on which the task parameter coding dynamics can be computed during sequential events required to reach a decision report. Whether these signals are gradually constructed, beginning in sensory areas or whether they arise abruptly in the frontal lobe cortex remain open questions. This yields at least two possibilities: there exist specific brain areas that construct temporal signals such as the ones extracted here, which are broadcast to other regions, or, rather, the capacity to estimate time through these signals is embedded in the circuits across the brain. Further work is needed to answer these possibilities.

Materials and Methods

Monkeys were trained to report whether the temporal structure of two vibrotactile stimuli of equal frequency was the same or different (SI Appendix). Neuronal recordings were obtained in DPC while the monkeys performed the TPDT. Methods for single-unit and population analysis are provided in SI Appendix. Animals were handled in accordance with standards of the National Institutes of Health and Society for Neuroscience. All protocols were approved by the Institutional Animal Care and Use Committee of the Instituto de Fisiología Celular, Universidad Nacional Autónoma de México.