Increasing valence pushes DNA nanostar networks to the isostatic point

Significance

Maxwell (1864) predicted that 3D networks of beams fixed to junctions through freely rotating joints will be rigid only if at least six beams emanate from each junction. This concept is key to macroscopic design of trussed structures, but its relevance to microscopic networks, where thermal fluctuations are large, such as in biomolecular gels, is not as clear. Here, we exploit DNA nanotechnology to create gels of defined connectivity and demonstrate that gel mechanics are controlled by an interplay between entropic effects, network structure, and Maxwell’s rigidity criterion.

Abstract

The classic picture of soft material mechanics is that of rubber elasticity, in which material modulus is related to the entropic elasticity of flexible polymeric linkers. The rubber model, however, largely ignores the role of valence (i.e., the number of network chains emanating from a junction). Recent work predicts that valence, and particularly the Maxwell isostatic point, plays a key role in determining the mechanics of semiflexible polymer networks. Here, we report a series of experiments confirming the prominent role of valence in determining the mechanics of a model system. The system is based on DNA nanostars (DNAns): multiarmed, self-assembled nanostructures that form thermoreversible equilibrium gels through base pair-controlled cross-linking. We measure the linear and nonlinear elastic properties of these gels as a function of DNAns arm number, $f$, and concentration [DNAns]. We find that, as $f$ increases from three to six, the gel’s high-frequency plateau modulus strongly increases, and its dependence on [DNAns] transitions from nonlinear to linear. Additionally, higher-valence gels exhibit less strain hardening, indicating that they have less configurational freedom. Minimal strain hardening and linear dependence of shear modulus on concentration at high $f$ are consistent with predictions for isostatic systems. Evident strain hardening and nonlinear concentration dependence of shear modulus suggest that the low-$f$ networks are subisostatic and have a transient, potentially fractal percolated structure. Overall, our observations indicate that network elasticity is sensitive both to entropic elasticity of network chains and to junction valence, with an apparent isostatic point $5<f_c\le 6$ in agreement with the Maxwell prediction.

Hydrogels are water-laden, cross-linked polymer or colloidal networks that occur naturally in cells and tissues. They have been synthesized and developed for a wide range of applications from hygienic and food products to diagnostic and therapeutic technologies. Much of the utility of hydrogels derives from their viscoelastic nature, which combines the stress-bearing abilities of a solid with the permeability and flow characteristics of a liquid (1). Understanding the microscopic origins of these mechanical properties is an important goal for both directing hydrogel engineering and deciphering their biological designs.

In general, hydrogel mechanics derive from the elastic properties of their constituent polymer/colloidal chains, the stability of cross-links, and the connectivity of the network (2). Network connectivity can be defined in terms of junction multiplicity or valence, $f$ (i.e., the average number of network chains that meet at a node). While connectivity is a potent effector of mechanics in principle (3–5), it is relatively difficult to determine and control in practice (6–9). This is because cross-links are traditionally made by entanglement, by weak bonds (hydrogen bonds, van der Waals forces, hydrophobic or electrostatic interactions), or by chemically reactive side groups, with junctions in which valence is uncontrolled or relatively small (typically $3\le f\le 4$) and is not revealed by either scattering or imaging techniques.

The programmability and thermal reversibility of Watson–Crick base pairing make DNA intriguing as a model material in which to study the effect of network connectivity on hydrogel mechanics. Multiarmed “immobile junctions” were among the first DNA nanostructures to be rationally designed and self-assembled (10). Pioneering work by Luo and coworkers (11) demonstrated the feasibility of producing macroscopic quantities of fully synthetic DNA hydrogels based on three- and four-armed junctions that bind via complementary “sticky ends” and explored their potential for various biotechnological applications (12).

More recently, Sciortino and coworkers (13–18) engineered greater flexibility into the immobile junction design by incorporating unpaired bases at the vertex and sticky ends to create “DNA nanostars” (DNAns) (Fig. 1). They found that tetravalent DNAns transition from a fluid to an equilibrium gel on cooling (16–18), with network dynamics controlled by the sticky-end interaction strength (13, 15, 19). Equilibrium gel formation requires both limited valence ($f<12$) (13, 15, 20–22) and significant flexibility (16, 23) as conferred by the unpaired bases in the DNAns design (Fig. 1A).

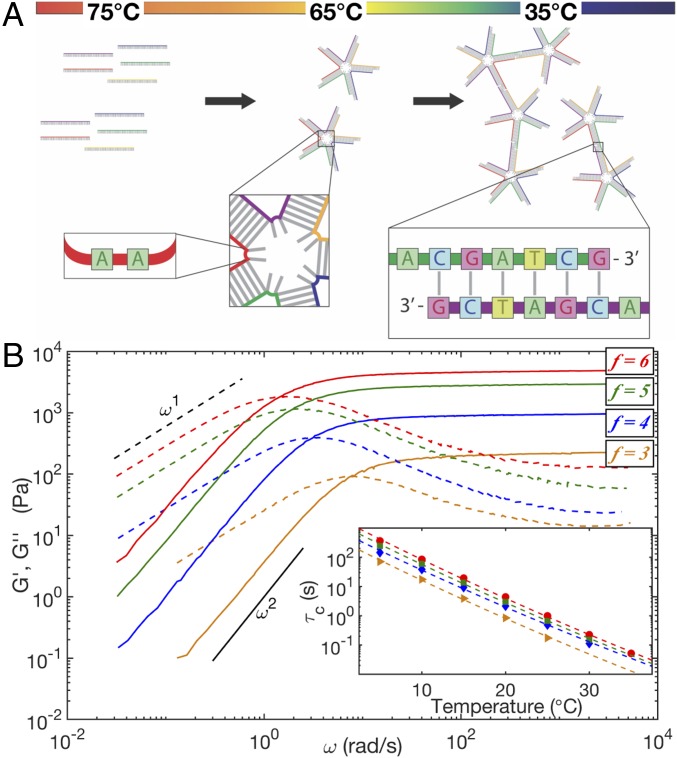
Fig. 1.

(A) A 2D cartoon depicting the formation of a five-arm DNAns network as a function of temperature. Every DNAns has unpaired adenines at the base of each arm to enhance vertex flexibility. Each arm is a 21-bp double helix $\approx 8.5$-nm long that ends in a single-stranded overhang consisting of an unpaired adenine and a 6-nt palindromic sequence, called the sticky end (box on the right). (B) Frequency-dependent mechanical response of DNAns networks at $\gamma =5\%$ and T_ref = 20°C. The storage modulus $G\prime$ (solid lines) and the loss modulus G″ (dashed lines) cross at a frequency, ${\omega }_c$, that is the inverse of the relaxation time, ${\tau }_c$. (Inset) Arrhenius fits to ${\tau }_c\left(T\right)$ have a common slope corresponding to the activation energy for network rearrangement. Orange triangles, blue diamonds, green squares, and red circles correspond to $f=\mathrm{3,4,5},$ and 6 at DNAns concentrations of $\left(500\pm 10\right)$, (490 $\pm$ 10), (490 $\pm$ 20), and $\left(450\pm 30\right)$ $\mathrm{\mu }$M, respectively.

Here, we apply bulk oscillatory rheology to solutions of $f=$ 3-, 4-, 5-, and 6-armed DNAns equilibrium gels over accessible [DNAns] and temperatures to probe the effect of valence on network mechanics and structure. The equilibrium and liquid-like nature of DNAns networks ensures that material handling is easy and that the network’s mechanical and structural properties are history independent. We find that the trends with valence of network stiffness (plateau modulus) and strain hardening are consistent with a network in which mechanics are controlled by a combination of entropic elasticity of network chains and an isostatic critical point occurring at a DNAns valence of $5<f_c\le 6$.

Results

An $f$-armed DNAns consists of $f$ dsDNA arms emanating from a common vertex, each terminating in a palindromic sticky end. On thermal annealing, DNAns first self-assemble from $f$ partially complementary DNA oligomers, and then, at lower temperatures, they bind together via sticky ends to form a network (Fig. 1A).

We used oscillatory rheology to measure the frequency-dependent storage, $G\prime$, and loss, G″, moduli of solutions of DNAns with different arm numbers at various concentrations and temperatures. Then, for each solution, we used time–temperature superposition to shift curves in both frequency and modulus, thus generating master rheological curves that spanned six decades of frequency, $\omega$, at a reference temperature of 20 °C (Fig. 1B and SI Appendix, section S2). At this temperature, a thermodynamic model of sticky-end hybridization predicts $>98\%$ binding (24) (SI Appendix, section S1b).

Frequency sweeps were performed at a constant strain $\gamma =5\%$, well below the onset of nonlinearity (see Fig. 3). For all $f$, repeated measurements of $G\prime$ and G″ were independent of rates of cooling and heating for ≤ 15°C/min (SI Appendix, Fig. S5), confirming that DNAns form thermoreversible equilibrium networks (13).

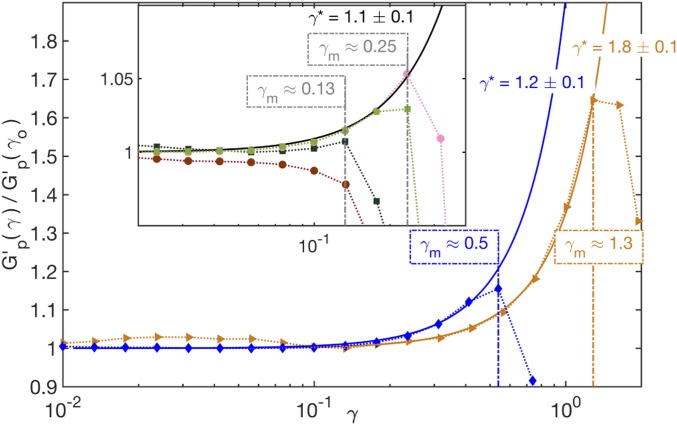
Fig. 3.

Normalized plateau modulus, $G_p^{\prime }\left(\gamma \right)/G_p^{\prime }\left({\gamma }_o\right)$, of DNAns networks as a function of strain, $\gamma$, in the elastic plateau regime ($\omega =63$ rad/s, T = 20°C) for $f=3$ (orange triangles) and 4 (blue diamonds) at [DNAns] of $\left(500\pm 10\right)$ and $\left(490\pm 10\right)$ $\mathrm{\mu }$M, respectively. Solid lines are fits of $\exp \left[{\left(\gamma /\gamma *\right)}^2\right]$ for ($\gamma \le {\gamma }_m$), where ${\gamma }_m$ (vertical dash-dot line) is the strain that maximizes $G_p^{\prime }$ and $\gamma *$ is the characteristic strain scale for stiffening. (Inset) Same plots for $f=5$ at [DNAns] of $\left(300\pm 10\right)$ $\mathrm{\mu }$M (light green) and $\left(550\pm 30\right)$ $\mathrm{\mu }$M (dark green) and for $f=6$ at [DNAns] of $\left(350\pm 20\right)$ $\mathrm{\mu }$M (pink) and $\left(550\pm 30\right)$ $\mathrm{\mu }$M (dark red). The solid black line denotes $\exp \left({\left(\gamma /1.1\right)}^2\right)$, which captures the nonlinear elasticity of the two lower-concentration $f=5$ and $f=6$ networks.

DNAns solutions of every arm number behaved like Maxwellian viscoelastic fluids, with low-frequency liquid behavior (G″ > G′, with $G\prime \hspace{0.17em}\sim \hspace{0.17em}\omega 2$ and G″ ∼ ω) separated by a cross-over frequency ${\omega }_c$ from high-frequency solid-like behavior (G′ > G″, with a plateau modulus $G_p^{\prime }$) (Fig. 1B) (2, 17). While it is possible for such a cross-over to result from solvent drag effects (25–27), we estimate that a drag-induced cross-over would occur at megahertz frequencies, well above our measured values of ${\omega }_c$ (SI Appendix, section S2b). Instead, we note that the characteristic time for network reconfiguration shows an Arrhenius dependence, ${\tau }_c=2\pi /{\omega }_c\propto e^{E_a/RT}$ (Fig. 1B, Inset) with an activation energy $E_a$ that is the same for all $f$ and approximately equal to the enthalpy of hybridization of a single-nanostar overhang sequence (SI Appendix, Fig. S8), consistent with previous dynamic measurements (13, 15, 19). We thus interpret ${\tau }_c$ as corresponding to bond-breaking events, meaning that the high-frequency plateau modulus reflects the stiffness of an instantaneously bonded network.

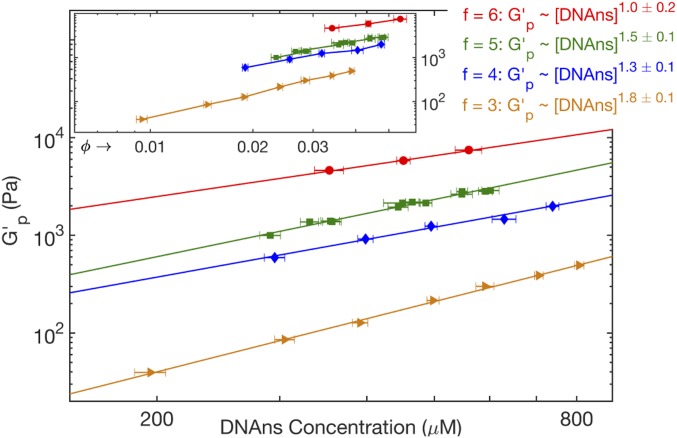
To test how DNAns valence, $f$, affects network stiffness and structure, we measured the plateau modulus, $G_p^{\prime }$, as a function of DNAns concentrations, [DNAns], for $f=\left\{\mathrm{3,4,5,6}\right\}$. $G_p^{\prime }$ increased with $f$ more than might be expected based on density alone (Fig. 2). That is, an $\left(f+1\right)$-armed network was always stiffer than an $f$-armed network with the same volume fraction, $\varphi$, of DNAns arms (Fig. 2, Inset). Furthermore, $G_p^{\prime }$ increased with [DNAns] as a power law, $G_p^{\prime }\sim {\left[\text{DNAns}\right]}^t$, with a best-fit exponent that decreases from $t=1.8\pm 0.1$ for $f=3$ to $t=1.0\pm 0.2$ for $f=6$.

Fig. 2.

Log–log plot of the plateau modulus, $G_p^{\prime }$, as a function of DNAns concentration at T = 20 °C and $\gamma =5\%$ for $f=3$ (orange triangles), 4 (blue diamonds), 5 (green squares), and 6 (red circles). Solid lines show fitted power laws, $G_p^{\prime }\sim \hspace{0.17em}{\left[\mathrm{D}\mathrm{N}\mathrm{A}\mathrm{n}\mathrm{s}\right]}^t$; labels give best-fit exponents with standard fitting error estimates. (Inset) Log–log plot of $G_p^{\prime }$ as a function of DNAns arm volume fraction, $\varphi =f\cdot v\cdot$ [DNAns], where $v=26.7\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$ is the solid cylinder volume equivalent of a DNAns arm. Solid lines connecting the data points are guides for the eye.

We assessed the various networks’ nonlinear elasticity by performing oscillatory stress–strain measurements at a temperature (20°C) and frequency ($\omega \ge 63$ rad/s) corresponding to the elastic plateau regime of all valences. For $\gamma \le 10\%$, all networks exhibited linear elasticity (constant $G\prime$) (Fig. 3). At higher $\gamma$, most networks showed signs of strain hardening as discussed below. Finally, in all cases, the $G\prime \left(\gamma \right)$ curve terminated with a sudden decrease or yielding of the network typically associated with bond breaking (2, 28, 29).

We define the yield strain ${\gamma }_m$ as that which resulted in the largest measured $G\prime$. The $f=3$ and $f=4$ networks were extensible, showing relatively large yield strains of ${\gamma }_m\approx 1.3$ and 0.5, respectively. Accordingly, in those networks, the strain-hardening regime was broad and amenable to analysis: for $\gamma <{\gamma }_m$, the regime was well fit by a relation proposed by Seitz et al. (30), $G\prime \left(\gamma \right)/G\prime \left(\gamma \to 0\right)\sim \exp \left({\left(\gamma /{\gamma }^{*}\right)}^2\right)$, with best-fit values of ${\gamma }^{*}\approx 1.8$ and 1.2 for $f=3$ and $f=4$, respectively (31, 32). ${\gamma }_m$ and ${\gamma }^{*}$ did not vary significantly with [DNAns] (SI Appendix, Fig. S11).

For $f=5$ and $f=6$, relatively small yield strains (${\gamma }_m\approx 0.2$) curtailed the strain-hardening regime, but all $f=5$ curves showed a resolvable strain hardening as did the $f=6$ curve at the lowest [DNAns] (Fig. 3, Inset). These strain-hardening behaviors, while modest, could also be fit to the Seitz expression, with ${\gamma }^{*}\approx 1.1$ for the least concentrated $f=5$ and $f=6$ curve (SI Appendix, Fig. S11A).

Discussion

An Isostatic Picture Explains Plateau Modulus Behavior of DNAns Networks.

The trend of DNAns network stiffness, $G_p^{\prime }$, with DNAns valence, $f$, is qualitatively consistent with the expectation that junctions of greater valence augment network modulus by creating a greater density of stress-bearing chains. The “Phantom network” elastic model (2, 6) quantifies this relation by extending classic rubber elasticity models to account for valence-dependent fixation of the junctions connecting network chains. Specifically, it predicts $G\prime \propto \varphi \cdot \left(f-2\right)/f$. Our data are not consistent with this picture. $G_p^{\prime }$ increases nonlinearly with $\varphi$ for $f=\mathrm{3,4}$, and 5 (Fig. 2). More strikingly, at constant $\varphi$, $G_p^{\prime }$ increases roughly 10-fold from $f=3$ to $f=6$, far exceeding the phantom network model’s prediction of 2-fold stiffening for those valences (Fig. 2, Inset and SI Appendix, Fig. S9).

We instead posit that the variation of DNAns network elasticity with valence is explained by the presence of a Maxwell isostatic point (3, 33) at a critical valence value, $f_c$. The utility of the isostatic point in explaining biomolecular gel mechanics has recently been explored (4, 5, 34–39). The isostatic point occurs when the translational freedom of a junction is exactly constrained by the connections (network chains) emanating from that junction (3–5, 33–37). If each network chain supplies only central forces between the two junctions that it connects (i.e., it acts only by resisting stretching), then $f_c=6$. In practice, real network chains also supply tangential forces due to a combination of nonzero bending stiffness and rotational constraints imposed at the point of fixation to the junction. The effect of nonzero bend stiffness is to decrease $f_c$ below six by an amount dependent on the relative magnitudes of bend and stretch stiffness (4, 37).

Regardless of the precise value of $f_c$, the presence of an isostatic point alters network modulus in a manner consistent with our observations. Networks with $f<f_c$ have underconstrained junctions in which positions are easily perturbed without significant stretching of network chains (4, 33–35, 37). These networks are thus intrinsically floppy, with a low modulus dictated by chain bend behavior. In contrast, $f>f_c$ networks have fixed junctions that can only be moved by stretching network chains (4, 33–35, 37) and are accordingly relatively high-modulus materials. The isostatic model thus predicts a steep increase in modulus as $f$ increases through $f_c$ (4), which is in qualitative agreement with our data (Fig. 2 and SI Appendix, Fig. S9).

Other features of our data also agree with isostatic model predictions. Stretch-dominated, superisostatic ($f>f_c$) networks are expected to have a linear scaling of $G_p^{\prime }$ with $\varphi$ (32, 40–44) as seen at $f=6$ but not at smaller valences (Fig. 2). This implies that the critical valence of our DNAns network is between $5<f_c\le 6$, consistent with the prediction of $f_c=6$ for network chains that have vanishing bending stiffness and little rotational constraint at the junction (4, 34, 37). In the DNAns, we posit that these features are a consequence of the unpaired bases flanking the double-helical arms at the overhang and at the junction, consistent with flexibility seen in simulations of DNAns (18).

It is intriguing that network stiffness is not perfectly monotonic with valence. The $f=3$ and $f=6$ networks show strongly divergent behaviors, demarcating clear end points in the exponent $t$. The $f=4$ and 5 networks both are unambiguously between those end points; however, their trend is not monotonic: $t$ is larger for $f=5$ than for $f=4$. This disagrees with the monotonicity in valence expected from a purely isostatic explanation. We speculate that this is due to a fundamental asymmetry in the $f=5$ nanostars. Electrostatics favor ground states in which the negatively charged DNA arms are equally distant from their nearest neighbors. For $f=4$ and 6, there are well-defined ground-state configurations in which the arms point to the vertices of corresponding platonic solids. However, there is no such configuration available for $f=5$. The resulting frustration could explain the more underconstrained behavior of $f=5$ (i.e., with $t$ values closer to $f=3$ than $f=6$).

Valence Dependence of Strain Hardening Is also Consistent with an Isostatic Picture.

As seen in Fig. 3, the $f=3$ and 4 networks exhibit marked strain-hardening behaviors, with modulus increasing by $\sim$60 and $\sim 15\%$, respectively, before the material yields. Strain hardening of polymeric materials generally occurs when network chains, initially in an unstretched, thermally fluctuating configuration, rigidify under strain as they are straightened to lengths approaching their contour length (2, 30–32, 34, 35). Thus, the strain hardening of the $f=3$ and 4 networks indicates that stress-bearing chains have significant configurational freedom, and therefore, they are underconstrained and subisostatic (34), consistent with the interpretation from the $G_p^{\prime }$ vs. [DNAns] behavior (37, 43).

This interpretation is also supported by the observation that, as with many polymeric and fibrous materials (30–32), DNAns networks strain harden according to $G\prime \sim \exp {\left(\gamma /{\gamma }^{*}\right)}^2$ (Fig. 3). As described by Seitz et al. (30), the fitting parameter ${\gamma }^{*}$ can be related to the network chain’s maximum uniaxial extension ratio, ${\lambda }_{\text{max}}$, which measures the ratio of chain contour length to initial (unstretched) extension (SI Appendix, section S3c and Fig. S13). Fits to our data give ${\lambda }_{\text{max}}\approx 2.3\pm 0.1$ and $1.7\pm 0.1$ for $f=3$ and 4, respectively, indicating that the stress-bearing chains in an $f=3$ network are initially less stretched than those in an $f=4$ network, presumably due to being floppier.

The nonlinear elastic response of the $f=5$ and $f=6$ networks is subtler but still consistent with the isostatic viewpoint (34). For $f=5$, at all concentrations measured, the material hardens before yielding but only by $\sim 2\%$. The curves are again well fit by the Seitz equation (30–32) with ${\lambda }_{\text{max}}=1.9\pm 0.2$, indicating that the network chains are initially more stretched than $f=3$. This is consistent with the $f=5$ network being subisostatic but closer to the critical point than $f=3$.

For $f=6$, a similarly small ($\sim 2\%$) strain hardening is seen at the lowest concentration, but at the other two concentrations, strain hardening is not evident. We interpret the lack of strain hardening as an indication that junctions in those networks lack configurational freedom and consequently, that the networks are isostatic (34, 35).

Analysis of Yield Behavior Measures Cluster Size and Confirms Entropic Origin of Elasticity.

More insight into network structure is enabled by analysis of yield behavior. Yielding occurs at a stress ${\sigma }_y\sim F_c/{\xi }^2$, where $F_c$ is the characteristic bond-breaking force and $\xi$ is the characteristic distance between the first bonds that break (43). Single-molecule manipulation experiments have directly quantified $F_c$ for DNA overhangs loaded in shear, typically finding $F_c\approx$ 50 pN for overhangs of 20–30 bp (45). Thus, for the shorter 6-bp overhang used here, $F_c\approx 10$ pN is a reasonable estimate for a scaling calculation.

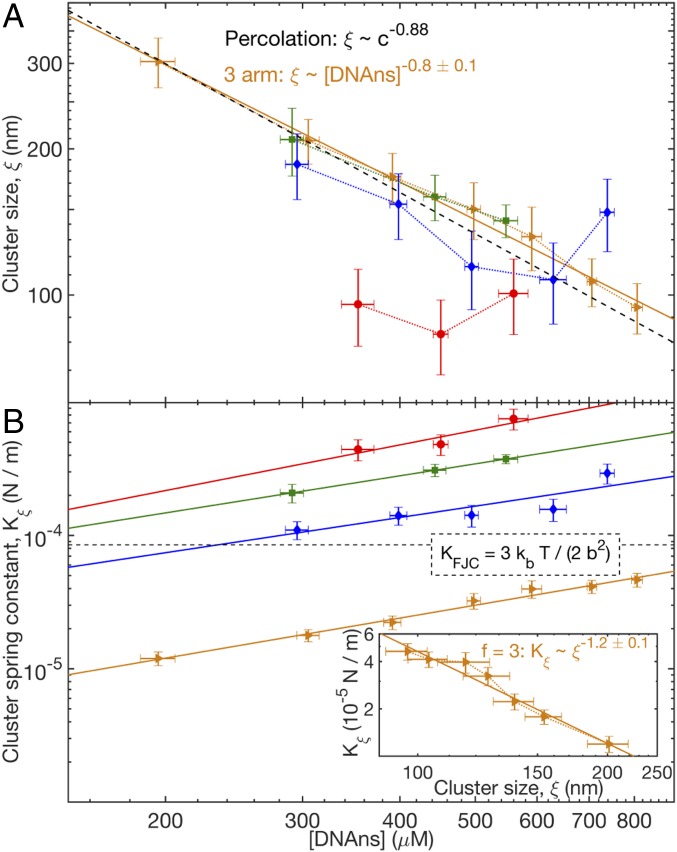
Using this estimate and our measured ${\sigma }_y$, we find that $\xi$ decreases from $\xi \approx 200-300$ nm at the lowest [DNAns] to $\xi \approx 100$ nm at the highest [DNAns] for $f=\mathrm{3,4,5}$ (Fig. 4A). For $f=6$, however, $\xi$ is smaller ($\approx 90\pm 30$ nm) and independent of [DNAns] (Fig. 4A). In all cases, $\xi$ is much larger than the nanostar size ($\approx 15$ nm). It is thus an emergent length scale of the system of roughly 5–20 DNAns in width. We interpret $\xi$ as a measure of cluster size: the characteristic distance between bonds that carry large forces on strain. Within a cluster (i.e., between those vulnerable bonds), the force is dispersed across many DNAns in parallel.

Fig. 4.

Log–log plots of (A) cluster size, $\xi$, and (B) cluster spring constant, $K_{\xi }$, as a function of [DNAns] for $f=3$ (orange triangles), 4 (blue diamonds), 5 (green squares), and 6 (red circles) at a temperature of T = 20°C. In A, the dashed line denotes the predicted scaling relation for 3D percolated clusters with $c$, the particle concentration from refs. 2 and 48. In B, the dashed line denotes the spring constant, $K_{\text{FJC}}$, of an entropic spring composed of two freely jointed (Kuhn) segments of length $b=8.5$ nm (i.e., with length of a DNAns arm), and the solid lines denote the measured power law relation for $K_{\xi }\sim {\left[\text{DNAns}\right]}^r$. (Inset) Log–log plot of $K_{\xi }$ as a function of $\xi$ for $f=3$ at T = 20°C. The solid line denotes the relation $K_{\xi }\sim {\xi }^{-1.2\pm 0.1}$, with SE estimated from fitting.

This interpretation is consistent with simulations that report cluster-like inhomogeneities in equilibrium gels (46). We emphasize that these clusters are different from those found in (nonequilibrium) colloidal gels (47). In DNAns gels, the clusters are transient, enduring only for timescales less than ${\tau }_c$. On longer timescales, the network restructures and behaves as a liquid, with an effectively homogeneous density.

Given $\xi$, we can interpret network modulus in terms of the spring constant per cluster, $K_{\xi }$, which provides a clue to the fundamental origin of elasticity in the system. From $K_{\xi }\approx G_p^{\prime }\cdot \xi$, we find that $K_{\xi }$ increases with valence and concentration (Fig. 4B) (43). To interpret these values, we compare them with the spring constant, $K_{FJC}$, of the fundamental entropic elastic unit in the system: a bonded pair of DNAns arms that connect two junctions. Considering the pair of arms as a two-segment, freely jointed chain with segment (Kuhn) length $b$ equal to the DNAns arm length, the expected spring constant is $K_{\text{FJC}}=3k_{B}T/2b^2\approx 85\hspace{0.17em}\mathrm{\mu }$N/m at T = 20°C, which is in the middle of the estimated $K_{\xi }$ values. This similarity indicates that entropic elasticity arising from DNAns arm configurational freedom controls network modulus. For $f=3$, $K_{\xi }<K_{\text{FJC}}$ as would occur for DNAns loaded in series; this is consistent with the $f=3$ cluster containing a single dominant stress-bearing chain of DNAns. For the higher-valence networks, $K_{\xi }>K_{\text{FJC}}$, likely due to clusters containing more parallelized and interconnected stress-bearing chains.

The entropic origin of network elasticity explains why $G_p^{\prime }$ increases only about 10-fold as $f$ goes from three to six (SI Appendix, Fig. S9). Simulations of networks of nonentropic (athermal) springs predict enormous, multidecade increases in modulus as $f$ increases through the isostatic point (4). The comparatively modest increase that we observe can be attributed to entropic rigidification, which is predicted to mask the modulus increment across the isostatic transition (38, 39).

Origin of Elastic Exponents in Subisostatic Networks.

A potential explanation for the nonlinear power law behaviors of the subisostatic networks can be found by comparing our measured exponents with the results of percolation theory. We focus on the $f=3$ system for which we have the broadest range of [DNAns] and thus, the best estimates. The exponent of $\xi$ vs. DNAns concentration, $-0.8\pm 0.1$, is consistent with the prediction from percolation theory in three dimensions for the scaling of correlation length with bond concentration, $\nu \approx -0.88$ (2). Furthermore, the $f=3$ exponent of $G_p^{\prime }$ vs. [DNAns] $t=1.8\pm 0.1$, which was measured independent of $\xi$, is also consistent with 3D percolation theory predictions of $t\approx 1.9$ (48). Experimentally, similar values of $t$ were measured in gels formed from trivalent gelatin and attributed to percolation behavior (49–51).

Within percolation models, the value of $t$ ultimately derives from fractal exponents describing network structure within clusters. For example, theory predicts that the shortest path through a 3D percolated cluster has a fractal dimension $d_{min}=1.25$ (52). If that shortest path dominates cluster elasticity (consistent with the single-chain interpretation of $K_{\xi }$ for $f=3$) and taking the path to consist of $N$ DNAns in series, we expect that $K_{\xi }\sim 1/N\sim {\xi }^{-d_{min}}$. This is indeed close to the measured scaling of $K_{\xi }\sim {\xi }^{-1.2\pm 0.1}$ (Fig. 4B, Inset). Since $G_p^{\prime }\sim K_{\xi }/\xi$, we see that the measured estimates of $d_{min}\approx 1.2$ and of $\nu \approx -0.8$ give rise to the value $t=-\nu \left(d_{min}+1\right)\approx 1.8$.

Although the correspondence of our concentration-dependent scaling with percolation exponents is intriguing, some caution is warranted. First, our measurements show power law behaviors of $G_p^{\prime }$ and $\xi$ with nonnormalized concentration, while theory (2, 52) and prior experiment (49) observe such behavior only after correcting for a critical concentration; the reason for this discrepancy is unclear. Second, scattering studies can measure the cluster size, $\xi$, directly, and such direct structural evidence is needed to give a percolation interpretation firm support.

Conclusion

Our work highlights the key role of valence in controlling the elasticity of a hydrogel. Notably, for the same density of DNAns arms, a 10-fold gain in stiffness results from using $f=6$ rather than $f=3$ DNAns. At the same time, increasing valence dramatically diminishes network extensibility, because junctions become more constrained as network connectivity increases. Our results are consistent with an isostatic interpretation: there exists a critical connectivity threshold beyond which stress-bearing elements become fully constrained and the network loses configurational freedom, leading to dramatically increased stiffness, reduced yield strain, and a loss of strain hardening.

In this interpretation, the $f=\mathrm{3,4,5}$ networks are subisostatic, with enough configurational freedom at the particle level to exhibit strain-stiffening behavior and a nonlinear dependence of plateau modulus on particle concentration. The rigidity of these floppy networks is attributed to the entropic elasticity of network chains, with another role potentially played by a percolation-like network structure. In contrast, the $f=6$ network is at or above the isostatic threshold, with highly constrained junctions and minimal freedom in the stress-bearing chains. The lack of contortions results in little to no extensibility or strain stiffening. The location of the critical threshold at $f=6$ behavior is consistent with expectations for a network with flexible junctions (4, 38, 39), here insured by the unpaired bases present in the center of the DNAns.

We suggest that the insights gained here regarding the interplay of valence, entropic elasticity, and network structure can be extended to other DNAns-like particles to open avenues for tuning material elasticity.

Materials and Methods

DNAns Design and Oligos.

Each $f$-armed DNAns is formed from $f$ oligos 49 nt in length (SI Appendix, Fig. S1). Each arm consists of a 20-bp dsDNA segment terminating in a 7-nt ssDNA segment with sequence 5′-ACGATCG-3′. The self-complementary subsequence 5′-CGATCG-3′, commonly referred to as a sticky end, mediates binding between any two DNAns arms. Unpaired adenines at the vertex and preceding the sticky end increase the internal conformational freedom of the DNAns and the conformational freedom of the DNAns–DNAns bond, respectively (16, 17, 23).

All oligos were purchased purified with standard desalting from Integrated DNA Technologies (https://www.idtdna.com/pages). Nucleotide sequences for the $f=3$ and $f=4$ DNAns designs were taken from Biffi et al. (13). Additional sequences for $f=5$ and $f=6$ DNAns were designed using NUPACK (24) with the goal of having DNAns form at T = 65°C and bind one another around T = 35°C.

DNAns Solution Preparation.

DNAns solutions were prepared from ssDNA oligo stocks by mixing equal amounts of each of the $f$ oligos. After mixing, the solutions were completely dehydrated in a vacuum concentrator (Savant; Speedvac) with a filter over the sample tube opening to prevent dust from entering the sample. The sample was then rehydrated to the desired DNAns concentration in a buffer solution of 150 mM NaCl, 40 mM Tris, 40 mM acetate, and 1 mM EDTA (pH 8.0). To dissolve the DNA completely, samples were placed in an aluminum heat block at 60°C and mixed vigorously for 15–30 s every 15 min until no visible dehydrated DNA remained. Finally, the solutions were annealed by heating to 90°C for 20 min in the heat block, turning off the power, and allowing the sample to cool to room temperature in the block over $\sim 5$ h. During the entire annealing procedure, a Styrofoam box covered the heat block to insulate the samples from the surrounding environment. After they were annealed, DNAns solutions were stored in a refrigerator (4 °C to 6 °C) and used within 10 d.

DNAns Concentration.

Concentration was determined from A₂₆₀ of solutions that were diluted 100- and 10,000-fold in deionized water (SI Appendix, section S1c). Concentration measurements were made 1 d after annealing and again, immediately after recovery from the rheometer.

The range of DNAns concentrations explored was limited at the high end to $<800\hspace{0.17em}\mathrm{\mu }$M by solubility and at the low end to $>X$ $\mathrm{\mu }$M by phase separation (13, 15, 16, 18, 23). Phase separation was inferred from the onset of erratic variations in rheological data observed at $X<\left\{\mathrm{190,280,280,350}\right\}\hspace{0.17em}\mathrm{\mu }$M for $f=\left\{\mathrm{3,4,5,6}\right\}$, respectively.

Rheology Measurements.

Oscillatory shear measurements were performed in a parallel-plate geometry using a stress-controlled direct-strain rheometer (AR-G2 Rheometer; TA Instruments). Parallel plates were chosen to minimize sample volume (80 $\mathrm{\mu }$L). The bottom plate was a stationary, temperature-controlled stage (±0.020°C). The top plate was a circular steel plate of radius $r=10$ mm that rotated freely via a magnetic bearing.

To load the rheometer, solutions were heated to 60°C—a temperature at which DNAns are stable but do not bind one another, making the solution easy to manipulate. Solution was delivered onto the bottom plate of the rheometer, which was at room temperature, and sandwiched between both plates until the desired gap size, $g=200\hspace{0.17em}\mathrm{\mu }$m, was achieved.

Before any rheological measurements were performed, the solution was quickly annealed a final time while loaded in between the rheometer plates: it was quickly heated at |dT/dt|15°C/min to 60°C, held there for 5 min, and then quickly cooled ($|dT/dt|\le 15°$C/min) to the first measurement temperature. A layer of low-viscosity mineral oil (Fisher Scientific CAS 8012-95-1; Saybolt viscosity = 162) was placed over the exposed sample to prevent solvent evaporation during the experiment.

Two types of oscillatory shear flow measurements were performed: frequency sweeps and strain sweeps. During the frequency sweep, the storage modulus ($G\prime$) and loss modulus (G″) were measured as a function of oscillation frequency (0.63 $<\omega <63$ rad/s) at a single strain ($\gamma =5\%$). During the strain sweep, torsional stress, $\sigma$, was measured as a function of strain $\gamma =\left(r\mathrm{\Delta }\theta /g\right)$, where $\mathrm{\Delta }\theta$ is the angular displacement of the steel plate, at a single frequency. We measured $\sigma$ over the range $1<\gamma <200\%$ at $\omega \ge 63$ rad/s and $T=20°$C (SI Appendix, section S3).