Divergence of the quadrupole-strain susceptibility of the electronic nematic system YbRu₂Ge₂

Significance

A wide range of strongly correlated quantum materials, including some high-temperature superconductors, exhibit “electronic nematic” phases, in which the electronic properties spontaneously break the rotational symmetry of the crystal. However, the role that the corresponding nematic fluctuations play in these complicated systems is unclear, motivating the search for simpler model systems. Here, we identify a particular 4f intermetallic material which exhibits ferroquadrupole order, ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$, as just such a model system. We also provide a robust and accurate method to probe the divergence of an important associated quantity, the quadrupole-strain susceptibility. The temperature dependence of this quantity provides insight into the nature of the interactions that lead to ferroquadrupole order, in this case, magnetoelastic coupling.

Abstract

Ferroquadrupole order associated with local $4f$ atomic orbitals of rare-earth ions is a realization of electronic nematic order. However, there are relatively few examples of intermetallic materials which exhibit continuous ferroquadrupole phase transitions, motivating the search for additional materials that fall into this category. Furthermore, it is not clear a priori whether experimental approaches based on transport measurements which have been successfully used to probe the nematic susceptibility in materials such as the Fe-based superconductors will be as effective in the case of $4f$ intermetallic materials, for which the important electronic degrees of freedom are local rather than itinerant and are consequently less strongly coupled to the charge-carrying quasiparticles near the Fermi energy. In the present work, we demonstrate that the intermetallic compound ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ exhibits a tetragonal-to-orthorhombic phase transition consistent with ferroquadrupole order of the Yb ions and go on to show that elastoresistivity measurements can indeed provide a clear window on the diverging nematic susceptibility in this system. This material provides an arena in which to study the causes and consequences of electronic nematicity.

Electronic nematic order in crystalline solids corresponds to a spontaneously broken discrete rotational symmetry driven by interactions between low-energy electronic degrees of freedom (1). The empirical observation that nematic order occurs in, or near to, superconducting phases in Fe-based materials (2–4) and possibly also cuprates (5–8) motivates a series of fundamental questions about the possible role(s) that nematicity might play in such systems (9–11). Fe-based and cuprate superconductors are complicated materials, with a variety of other intertwined electronic phases, making it highly desirable to identify simpler model systems that exhibit nematic order for which the underlying effective Hamiltonian is better understood. Ferroquadrupole order associated with local $4f$ atomic orbitals of rare-earth ions is a realization of electronic nematic order (12) and in principle can provide just such a model system.

The effective Hamiltonian describing the low-energy properties of rare-earth ions incorporated in crystalline solids is understood in great detail. The $4f$ electronic wavefunctions are spatially localized, and strong spin–orbit coupling yields an electronic multiplet that is described by a total angular momentum number $J$. Due to the local nature of the electrons, the crystal electric field (CEF) from the surrounding ligands acts as a weak perturbation, splitting the degeneracy of the $2J+1$ spherical harmonic basis states. Significantly, the low-energy states of these $4f$ electronic multiplets can exhibit degeneracies or near degeneracies. In these degenerate or near degenerate manifolds, there can exist states with large multipolar moments. Both the coupling of the lattice with quadrupolar degrees of freedom and a $4f-4f$ coupling from the generalization of the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction mediated by conduction electrons can then provide energetically favorable conditions for multipolar instabilities to occur (13). A variety of multipolar behaviors have been observed in such materials. The specific case of ferroquadrupole order, in which each atomic site takes on a quadrupole moment of the same orientation, breaks the rotational symmetry of the point group of the crystal and hence provides an example of a lattice in which sites exhibit collective nematic order.

Several cubic rare-earth intermetallic phases are known to undergo ferroquadrupole order, including $\mathrm{D}\mathrm{y}\mathrm{S}\mathrm{b}$ (14), ${\mathrm{P}\mathrm{r}\mathrm{T}\mathrm{i}}_2{\mathrm{A}\mathrm{l}}_{20}$ (15), and ${\mathrm{P}\mathrm{r}\mathrm{V}}_2{\mathrm{A}\mathrm{l}}_{20}$ (16). However, because of the presence of a cubic invariant in the free energy, such cubic cases cannot undergo a continuous cubic to tetragonal phase transition. In contrast, there are relatively few examples of intermetallic materials which exhibit continuous ferroquadrupole phase transitions, the primary examples being tetragonal-to-orthorhombic phase transitions observed for ${\mathrm{T}\mathrm{m}\mathrm{A}\mathrm{g}}_2$ (17) and ${\mathrm{T}\mathrm{m}\mathrm{A}\mathrm{u}}_2$ (18, 19), motivating the search for additional materials that fall into this category. The present work adds ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ to that list.

${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ has a tetragonal crystal structure at room temperature (space group ${\mathrm{I}}_4$/mmm), belonging to the same ${\mathrm{T}\mathrm{h}\mathrm{C}\mathrm{r}}_2{\mathrm{S}\mathrm{i}}_2$ structure type as the familiar “122” Fe-pnictides such as ${\mathrm{B}\mathrm{a}\mathrm{F}\mathrm{e}}_2{\mathrm{A}\mathrm{s}}_2$. The $4f$ electrons of the trivalent Yb ion form local multiplets with a total angular momentum quantum number J = 7/2. The CEF for the tetragonal point group symmetry results in four Kramers doublets, two with ${\mathrm{\Gamma }}_6$ and two with ${\mathrm{\Gamma }}_7$ character (20) (SI Appendix, section 1). The material displays some weak heavy fermion characteristics (21), but the low-temperature properties can be well understood in terms of these local $4f$ orbitals (20). Analysis of heat capacity, susceptibility, and inelastic neutron-scattering measurements indicate that the CEF ground state is a quasi-quartet comprising states with almost pure $m_j=|\pm 1/2⟩$ (${\mathrm{\Gamma }}_6$) and $m_j|\pm 3/2⟩$ (${\mathrm{\Gamma }}_7$) character, split by approximately 300 K from the other two doublets (20, 21). The material exhibits three continuous phase transitions at low temperature associated with the quasi-quartet: a nonmagnetic phase transition at $T_Q$ = 10.2 K and two magnetic phase transitions [one at $T_{N1}$ = 6.5 K, corresponding to the onset of a collinear amplitude-modulated antiferromagnet state, and a subsequent one at $T_{N2}$ = 5.7 K, the origin of which is currently unknown (21, 22)]. Based on analysis of the multipole moments of the CEF ground state, combined with a mean-field treatment of the effective Hamiltonian for the system, it has been suggested that the origin of the nonmagnetic transition is a ferroquadrupolar ordering of the local $4f$ electrons (ref. 21 and SI Appendix, section 3). However, to date no measurements have confirmed the ferroquadrupolar nature of the phase transition, nor has the quadrupole-strain susceptibility been investigated.

In the present work, we use high-resolution X-ray diffraction to reveal that the nonmagnetic phase transition corresponds to a tetragonal-to-orthorhombic phase transition, consistent with spontaneous ferroquadrupole order with $\mathrm{a}\hspace{0.17em}{\mathrm{B}}_{1g}$ symmetry. We then present elastoresistivity measurements which reveal a divergence of the quadrupole-strain susceptibility (i.e., the nematic susceptibility) in the same (${\mathrm{B}}_{1g}$) symmetry channel, ${\chi }_{B_{1g}}$. Comparison of the divergence of ${\chi }_{B_{1g}}$ and the critical temperature for the ferroquadrupole order $T_Q$ allows evaluation of the Levy criterion (defined below), from which it is inferred that the ferroquadrupole transition in ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ is driven primarily by magnetoelastic coupling. Our measurements establish ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ as a model system to explore electronic nematicity, for example as a possible starting point from which the ferroquadrupole order could be continuously suppressed toward a nematic quantum phase transition.

We start by describing the quadrupole-strain susceptibility (i.e., the nematic susceptibility for the $4f$ quadrupolar system) and its significance for ferroquadrupole order.

A minimal Hamiltonian can be written which describes the quadrupolar behavior of the $4f$ electrons in ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$:

$$H_{eff}=H_{CEF}+\sum _i-\left(B_i{Q}_i{\epsilon }_i+K_i⟨Q_i⟩Q_i\right).$$ [1]

The first term in the sum is the bilinear magnetoelastic quadrupole-strain coupling, and the second term is a mean-field quadrupole interaction term originating from an effective RKKY coupling mediated by the conduction electrons (13). The sum is over the three relevant symmetry channels for the tetragonal system, ${\mathrm{A}}_{1g}$, ${\mathrm{B}}_{1g}$, and ${\mathrm{B}}_{2g}$. $Q_i$ are the quadrupole operators of the $i$th symmetry channel (the well-known Stevens operators) and ${\epsilon }_i$ is the corresponding strain. ${\mathrm{H}}_{CEF}$ describes the crystal electric field from the surrounding Ru and Ge atoms that produces the ground-state quasi-quartet (SI Appendix, section 1). The gap between the ground-state doublet and the first excited doublet has been proposed to be ${\mathrm{\Delta }}_{CE{F}_1}\approx 10\hspace{0.17em}\text{K}$ from entropy considerations (21). The other doublets have been shown to be much higher in energy (${\mathrm{\Delta }}_{CE{F}_2}\approx 300\hspace{0.17em}\text{K}$) and can be ignored for any low-temperature physics.

Strain ${ϵ}_i$, induced by an external stress, admixes and splits the CEF eigenstates (Fig. 1), resulting in an induced quadrupole moment. The associated quadrupole-strain susceptibility ${\chi }_i$ can be defined for each symmetry channel $i$. Considering first the case in which $K_i$ = 0, the quadrupole-strain susceptibility has the form

$${\chi }_i=\frac{{dQ}_i}{d{\epsilon }_i}{|}_{\epsilon \to 0}=\frac{2{⟨q_i⟩}_o^2{B}_i}{{\mathrm{\Delta }}_{CE{F}_1}}\tanh \left(\frac{{\mathrm{\Delta }}_{CE{F}_1}}{2T}\right),$$ [2]

where ${⟨q_i⟩}_o$ is the magnitude of the quadrupole moment (SI Appendix, section 3). In the limit $T>{\mathrm{\Delta }}_{CE{F}_1}$, this reduces to an approximate Curie form ${\chi }_i\sim \frac{{⟨q_i⟩}_o^2{B}_i}{T}$, which becomes exact for ${\mathrm{\Delta }}_{CE{F}_1}=0$.

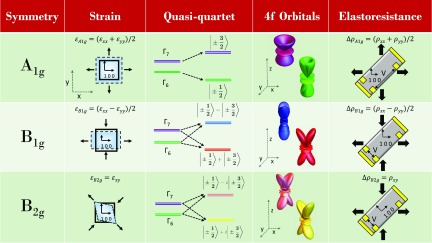
Fig. 1.

Effect of strains of different symmetries on the CEF eigenstates of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ and measurement of the associated elastoresistivity coefficients. Strains corresponding to distinct irreducible representations, induced by external stresses, are indicated by thick black arrows. These strains admix and split the CEF eigenstates; the effect on the low-energy CEF quasi-quartet and the charge density of the ground-state orbitals is illustrated. For simplicity, the ${\mathrm{\Gamma }}_6$ and ${\mathrm{\Gamma }}_7$ eigenstates are illustrated for pure $|\pm 1/2⟩$ and $|\pm 3/2⟩$ character respectively (see main text). Admixture of other ${\mathrm{m}}_J$ states gives the ${\mathrm{\Gamma }}_6$ and ${\mathrm{\Gamma }}_7$ eigenstates a discrete fourfold symmetry, but does not otherwise affect the functional form of the quadrupole-strain susceptibility. The elastoresistance column shows the required orientation of the normal strain (thick black arrows), crystal axes (insets to gray schematic crystals), and voltage contacts (yellow pads, with measured voltages indicated for longitudinal and transverse pairs) for measurement of the associated elastoresistivity coefficients in each symmetry channel.

Adding quadrupole interactions to this model renormalizes the quadrupole-strain susceptibilities. Considering again the limit ${\mathrm{\Delta }}_{CE{F}_1}=0$, this results in a Curie–Weiss functional form:

$${\chi }_i^{\prime }=(\frac{dQ}{dϵ}{)}_i=\frac{{⟨q_i⟩}_o^2{B}_i}{T-{⟨q_i⟩}_o{K}_i}.$$ [3]

Thus, the Weiss temperature of the quadrupole-strain susceptibility in a given symmetry channel is proportional to the strength of the quadrupole–quadrupole interaction term and the saturated quadrupole moment in that channel. If the lattice were infinitely stiff (i.e., strain is treated as a fixed parameter), the system would have a tendency to undergo quadrupolar order at this “bare” critical temperature.

Of course, the lattice is not infinitely stiff, and the magnetoelastic coupling renormalizes the critical temperature. Minimizing the free energy with respect to strain, including the elastic energy terms, the ordering temperature is found to be

$$T_Q={\left(\left(K+\frac{B^2}{C}\right){⟨q⟩}_o\right)}_i=G_i{⟨q_i⟩}_o,$$ [4]

where B and C are the magnetoelastic and elastic constants, respectively, of the ordering symmetry channel i, and G represents the renormalized quadrupolar interaction coefficient.

The relative magnitudes of $\frac{B_i^2}{C_i}$ and $K_i$ dictate whether the nematic phase transition is driven by strain, in the traditional Cooperative Jahn–Teller sense (23), or by electronic quadrupolar fluctuations, as inferred for certain $4f$ ferroquadrupole systems (13, 17, 18) and underdoped 122 Fe-pnictides (4, 24). Thus, a precise measurement that determines the ratio of these two components, known as the Levy criterion, is an essential development to understanding the nature of quadrupolar phase transitions in any given $4f$ system.

While the quadrupole-strain susceptibility is frequently invoked from a theoretical perspective (13), it has rarely been determined experimentally. Simple consideration of thermodynamic relations implies that ${\chi }_i$ can be inferred from softening of the elastic constants, magnetostriction, and measurements of the third-order magnetic susceptibility (13), and all of these approaches have been used previously in other candidate $4f$ systems (19). However, while measurements of the elastic moduli provide a direct perspective on the lattice symmetry modes, a large temperature-dependent background and a strict reliance on a suitable geometry of the sample make it difficult in practice to obtain the temperature dependence of ${\chi }_i$ with quantitative accuracy. Similarly, magnetic measurements face difficulties in obtaining the temperature dependence of ${\chi }_i$, in part because of issues with demagnetization fields and in part because quadrupolar-field susceptibilities must be untangled from the quadrupole-strain susceptibilities to properly infer them. Here, rather than inferring ${\chi }_i$ based on a combination of thermodynamic measurements, we outline how this quantity can be determined via elastoresistance measurements.

Although resistivity is not a thermodynamic measurement, it is a sensitive measure of the electronic scattering rate in a crystal. Considering $4f$ intermetallic systems, the local $4f$ electronic sites serve as strong scatterers of the conduction electrons. Anisotropic scattering from these sites and their associated quadrupolar moments has previously been described for cubic materials (25) but not investigated in the context of quadrupolar phase transitions in tetragonal materials. Under two conditions, which can be readily justified for ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$, we can directly relate a change in the normalized anisotropic resistivity (divided by the isotropic resistivity) to a change in the corresponding quadrupole moment (SI Appendix, section 5 and ref. 26). The first condition is that the resistivity is dominated by scattering of the conduction electrons from the lattice of $4f$ electronic mutliplets. As we demonstrate, this is indeed the case for ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. The second condition is that the induced quadrupole moment is perturbative, which is by definition the case for the technique that we use to determine the elastoresistivity.

When these two conditions are satisfied, an elastoresistivity technique, in which a tunable strain is applied to a material while measuring the induced anisotropic resistivity (illustrated schematically in Fig. 1), provides an ideal method to directly probe the temperature dependence of the material’s quadrupole-strain susceptibility. For example, considering the ${\mathrm{B}}_{1g}$ symmetry channel (Fig. 1, middle row), $\mathrm{a}\hspace{0.17em}{\mathrm{B}}_{1g}$ symmetry strain (caused by some external stresses) induces a finite ${\mathrm{B}}_{1g}$ symmetry change in the resistivity ${\left(\frac{\mathrm{\Delta }\rho }{\rho }\right)}_{{\mathrm{B}}_{1g}}=\frac{\left({\rho }_{xx}-{\rho }_{yy}\right)}{{\rho }_0}$, where ${\rho }_{xx}$ and ${\rho }_{yy}$ are measured in the presence of the strain and ${\rho }_0$ is the unstrained isotropic in-plane resistivity. If the scattering rate $\mathrm{\Gamma }$ is dominated by scattering from the 4f orbitals, and if the effective mass of the conduction electrons is not strongly affected by the induced strain, then

$${\left(\frac{\mathrm{\Delta }\rho }{\rho }\right)}_{B_{1g}}\approx {\left(\frac{{\mathrm{\Gamma }}_{xx}-{\mathrm{\Gamma }}_{yy}}{{\left({\mathrm{\Gamma }}_{xx}\right)}_0+{\left({\mathrm{\Gamma }}_{yy}\right)}_0}\right)}_{4f}\propto ⟨O_2^2⟩.$$ [5]

Taking the appropriate derivatives with respect to strain gives

$$\frac{{\left(\frac{d\rho }{\rho }\right)}_{B_{1g}}}{{d\epsilon }_{B_{1g}}}\propto {\chi }_{B_{1g}}.$$ [6]

Thus, measuring the symmetry decomposed elements of the elastoresistivity tensor provides direct measurements of the corresponding quadrupole-strain susceptibilities. Appropriate orientations of crystal axes, normal strain axes, and contact placement necessary to measure each symmetry channel are illustrated in Fig. 1 and described in greater detail in ref. 27.

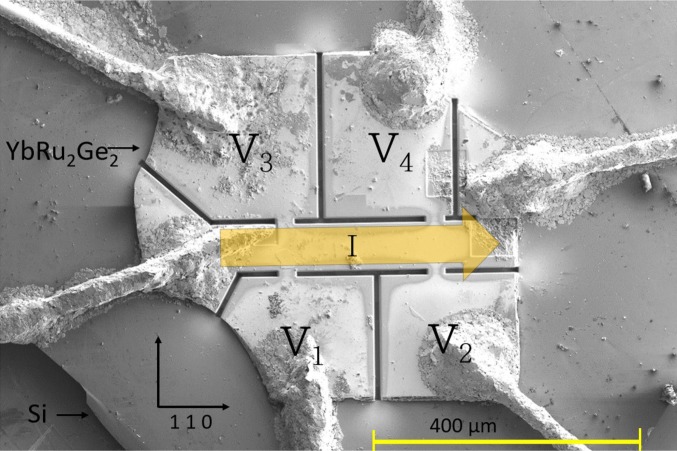
Elastoresistance techniques have previously been used to determine the nematic susceptibility of materials for which the nematicity derives from itinerant electronic states, including Fe-based superconductors (24, 27, 29–31) and ${\mathrm{U}\mathrm{R}\mathrm{u}}_2{\mathrm{S}\mathrm{i}}_2$ (32). Here, we demonstrate that the technique is also appropriate to determine ${\chi }_i$ of materials that undergo ferroquadrupole order of local $4f$ orbitals. Since for such systems ${\chi }_i$ can in principle be large in several symmetry channels $i$, we introduce additional means (described in Materials and Methods) to ensure appropriate symmetry decomposition, using a focused ion beam to prepare the sample for each measurement (Fig. 2).

Fig. 2.

Scanning electron micrograph of a representative microstructured sample used for elastoresistance measurements. The ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ sample is glued to a 50-$\mathrm{\mu }$m-thick Si substrate.The crystal axes (indicated by black arrows) were previously determined by X-ray diffraction and are identified here by the horizontal facets. Line cuts were etched using a focused ion beam to control the current path (indicated by a yellow arrow) and precisely define the voltage contact positions (labeled ${\mathrm{V}}_1$–${\mathrm{V}}_4$). For this particular crystal, four voltage pads allowed four different resistivity measurements. ${\mathrm{V}}_4-{\mathrm{V}}_2$ and ${\mathrm{V}}_3-{\mathrm{V}}_1$ (divided by the current) measured induced ${\mathrm{B}}_{1g}$ resistivity differences $\left({\rho }_{xx}-{\rho }_{yy}\right)/2$ (in the crystal coordinate frame), and ${\mathrm{V}}_3-{\mathrm{V}}_4$ and ${\mathrm{V}}_1-{\mathrm{V}}_2$ measured ${\mathrm{A}}_{1g}$ resistivity values $\left({\rho }_{xx}+{\rho }_{yy}\right)/2$ (27, 28). Two measurements of each symmetry channel were performed to ensure that strain was homogenously transmitted to the sample.

Results

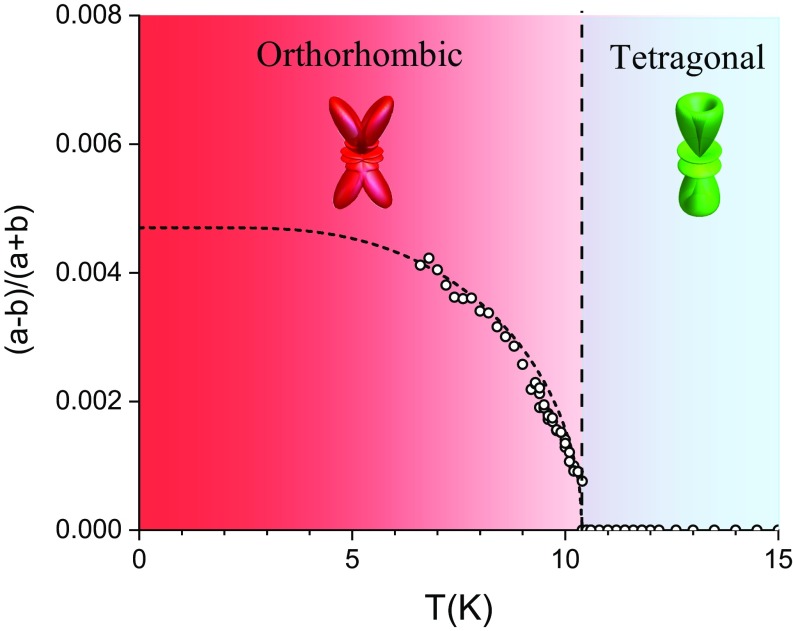
Splitting of the (6 0 0) Bragg peak was observed below 10.2 K along the (1 1 0) and (1 −1 0) directions, with the new peaks indicative of a $B_{1g}$ orthorhombic structural distortion. The temperature dependence of the orthorhombicity parameter of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ is shown in Fig. 3, together with the anticipated temperature dependence of a mean-field Ising order parameter that onsets at 10.2 K (SI Appendix). No evidence for a similar phase transition is found for the nonmagnetic analog ${\mathrm{Y}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ (ref. 33 and Fig. 4, Inset). The data for ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ are consistent with a continuous ferroquadrupole phase transition, as predicted previously based on analysis of the CEF parameters (21). Of the two possibilities (corresponding to either $B_{1g}$ or $B_{2g}$ symmetry), these measurements determine that the ferroquadrupolar state has a $B_{1g}$ symmetry.

Fig. 3.

Orthorhombicity of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. The order parameter of the orthorhombic structural phase transition is plotted against temperature. A mean-field Ising order parameter that becomes finite at 10.2 K is overlaid as a guide to the eye. Insets illustrate the charge density of the $4f$ CEF quasi-quartet ground state of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ in the tetragonal phase (green, with fourfold symmetry) and that in the orthorhombic phase (red, with twofold symmetry). For simplicity, the electron distributions are illustrated assuming the original ${\mathrm{\Gamma }}_6$ and ${\mathrm{\Gamma }}_7$ CEF eigenstates are pure $\left|\pm 1/2\right.⟩$ and $\left|\pm 3/2\right.⟩$ character respectively (see main text). Ferroquadrupole order of the $4f$ orbitals is inferred from the observed orthorhombicity.

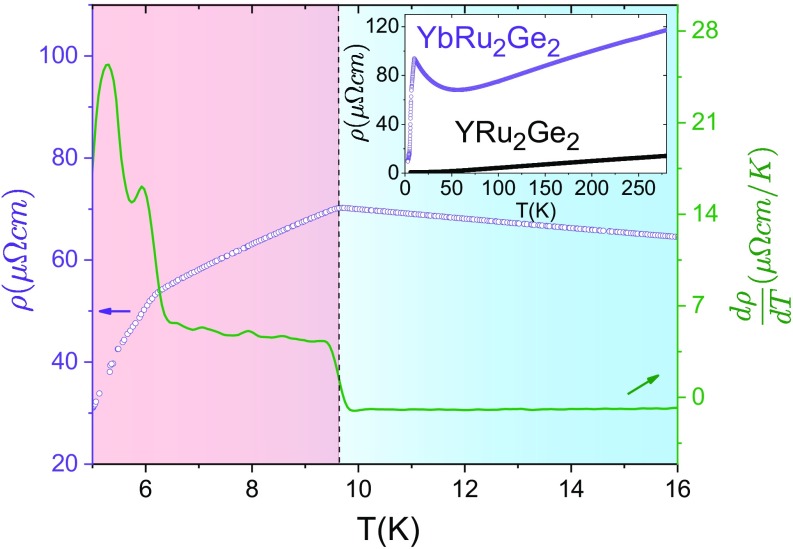
Fig. 4.

Temperature dependence of the resistivity of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. The resistivity (purple data points) and its derivative with respect to temperature (green data points) show clear features at $T_Q$ (marked by a vertical dashed line), as well as $T_{N1}$ and $T_{N2}$. Slight differences in estimates of the critical temperatures relative to values extracted from X-ray diffraction measurements are attributed to differences in sweep rates of the two measurements. Inset shows the resistivity over a larger temperature range, in which a different ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ single crystal is measured. Data are also shown for the nonmagnetic analog, ${\mathrm{Y}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$, for which no phase transitions are observed. Yttrium has an empty $4f$ shell but otherwise the electronic structure of the two materials is anticipated to be very similar, and differences in the resistivity between the two compounds are primarily attributed to $4f$ scattering.

The temperature dependence of the in-plane resistivity of unstrained (i.e., free-standing) ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ is shown in Fig. 4. The data are consistent with previously published measurements, revealing a Kondo-like rise below 50 K and sharp features (seen more clearly in the derivative $\frac{d\rho }{dT}$) signifying the ferroquadrupole and magnetic phase transitions. Similar measurements of the nonmagnetic, iso-structural, iso-electronic analog, ${\mathrm{Y}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$, also shown in Fig. 4, reveal a considerably smaller in-plane resistivity and no signatures of any phase transitions. Since the band structure of the two materials is presumably quite similar, the large difference in the resistivity can be attributed to scattering from the local $4f$ orbitals in ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. Significantly, since the resistivity of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ in the temperature window above $T_Q$ (blue shading in Fig. 4) is dominated by $4f$ scattering, the elastoresistivity (described below) can be directly related to the quadrupole-strain susceptibility in the same symmetry channels, as described previously.

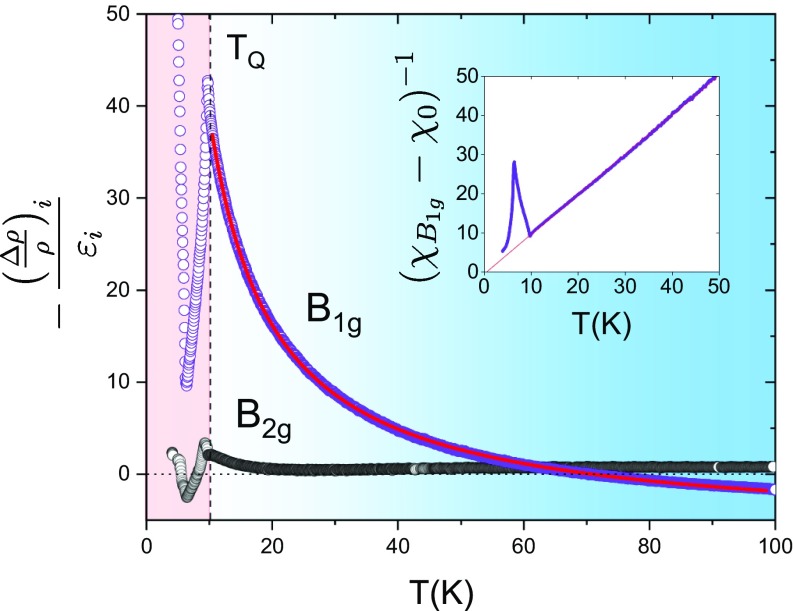
Elastoresistivity measurements were performed for multiple samples. Responses in the ${\mathrm{B}}_{1g}$ and ${\mathrm{B}}_{2g}$ symmetry channels were always found to be linear. Representative data for both of these symmetry channels (taken for samples of equal dimensions) are shown in Fig. 5 as a function of temperature. Elastoresistivity data for the ${\mathrm{A}}_{1g}$ symmetry channel were also recorded during these measurements; while these data do not correspond to a susceptibility of a symmetry-breaking quadrupole order, the measurements are presented in SI Appendix, section 7 for completeness. The response in the ${\mathrm{B}}_{1g}$ channel was found to be considerably larger than that in the ${\mathrm{B}}_{2g}$ channel. If the proportionality constants relating the resistivity anisotropy to the local quadrupole moment (SI Appendix, section 5) are similar for the two symmetry channels, which would be the case for an isotropic Fermi surface but is certainly not guaranteed by symmetry, then the observed large anisotropy in the elastoresistivity would imply that the magnetoelastic coupling coefficient ${\mathrm{B}}_i$ for $i=B_{1g}$ is significantly larger than that for the ${\mathrm{B}}_{2g}$ symmetry channel. This would certainly be consistent with the observed ${\mathrm{B}}_{1g}$ symmetry of the orthorhombic distortion, but needs to be verified by other thermodynamic measurements. The ${\mathrm{B}}_{1g}$ and ${\mathrm{B}}_{2g}$ elastoresistivity coefficients were also measured for ${\mathrm{Y}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. No significant temperature dependence for either channel was found within experimental error, as anticipated given the absence of partially filled $4f$ orbitals in this compound.

Fig. 5.

Temperature dependence of the elastoresistivity of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ in the ${\mathrm{B}}_{1g}$ and ${\mathrm{B}}_{2g}$ symmetry channels. As described in the main text, these quantities (shown by purple and black data points, respectively) are proportional to the quadrupole-strain susceptibility of the same symmetry channels. Inset shows the inverse of the quadrupole-strain susceptibility ${\left(-{\chi }_{B_{1g}}-{\chi }_0\right)}^{-1}$ for the ${\mathrm{B}}_{1g}$ channel, having subtracted a temperature-independent offset ${\chi }_0=4.48$. Red lines in the main plot and Inset show a fit to a Curie–Weiss functional form, with fit parameters described in the main text. The Weiss temperature is found to be 0 K within experimental error. The vertical dashed line indicates $T_Q$, separating tetragonal (blue) from orthorhombic (red) phases.

Since the resistivity of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ in this temperature range is dominated by scattering from $4f$ orbitals (Fig. 4), the temperature dependence of the elastoresistivity provides a good measure of the temperature dependence of the quadrupole-strain susceptibility. Motivated by the previous discussion, we fitted the ${\mathrm{B}}_{1g}$ elastoresistivity to a Curie–Weiss functional form:

$${\chi }_{B_{1g}}^{fit}=-\frac{448.6\pm 1.2}{T-0.11\pm 0.03}+4.48\pm 0.02.$$ [7]

The quality of fit over the full temperature range, right down to ${\mathrm{T}}_Q$ (Fig. 5 and Fig. 5, Inset), indicates that the splitting ${\mathrm{\Delta }}_{CE{F}_1}$ of the quasi-quartet in the tetragonal state is less than $T_Q$ in magnitude, consistent with previous estimates from inelastic neutron scattering (22). Significantly, with reference to Eq. 2, since the Weiss temperature is found to be close to 0 K, it is clear that quadrupolar interactions mediated by the conduction electrons do not play an important role in the eventual ferroquadrupole phase transition. In other words, referring back to Eq. 4 and the Levy criterion, we find that $B_i^2/C_i>>K_i$ for ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ in the ${\mathrm{B}}_{1g}$ symmetry channel and hence deduce that the ferroquadrupole transition must be driven primarily by magnetoelastic coupling in this material.

Summary and Discussion

${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ is a counterpoint to underdoped Fe-based superconductors, such as ${\mathrm{B}\mathrm{a}\mathrm{F}\mathrm{e}}_2{\mathrm{A}\mathrm{s}}_2$, in terms of how the nematic phase transition is driven. Numerous measurements, including elastoresistivity (4, 24, 27, 29–31), elastic moduli (34, 35), Raman scattering (36–38), and NMR (39), have shown that the nematic susceptibility of ${\mathrm{B}\mathrm{a}\mathrm{F}\mathrm{e}}_2{\mathrm{A}\mathrm{s}}_2$ and its analogs follows a Curie–Weiss functional form, with a Weiss temperature that is only slightly lower than the critical temperature for the coupled nematic/structural phase transition. Thus, while nematic–elastic coupling is still a necessary factor in driving the structural phase transition in those materials, the critical temperature is predominantly determined by electronic coupling between the nematic degrees of freedom (13). In contrast, ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ presents a case in which magnetoelastic coupling is the dominant driving force for the phase transition. Even so, the material is clearly nematic: A separate degree of freedom (the local $4f$ quadrupole moment) that couples bilinearly to elastic strain with the same symmetry is evident from the temperature dependence of the quadrupole-strain susceptibility, and its divergence drives a pseudo-proper ferroelastic phase transition. The lattice provides the effective coupling between the local quadrupole moments, but does not itself harbor any tendency toward a structural instability, as demonstrated by the absence of a comparable phase transition in the nonmagnetic analog ${\mathrm{Y}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$.

The significance of the present observation is twofold. First, we have shown that elastoresistance measurements can be used to probe the nematic susceptibility (quadrupole-strain susceptibility) for local $4f$ systems, at least in this specific case of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$. This provides an additional avenue to characterize a critically important characteristic of intermetallic quadrupolar systems. Since the quadrupole-strain susceptibility can, at least in principle, be large in several symmetry channels, we adopted a methodology of microstructuring the crystal using a focused ion beam (FIB) to guarantee symmetry decomposition of the resulting elastoresistivity.

Second, we have established ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ as a model system to explore effects of nematicity in metals. Even though the phase transition is driven by magnetoelastic effects, fluctuations of the local quadrupoles couple directly to ungapped quasiparticles at the Fermi energy. Hence, if the ferroquadrupole order can be suppressed toward zero temperature, and if the phase transition remains continuous, ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ is potentially an ideal system in which to explore the effects of nematic fluctuations on the properties of the metal in the quantum critical regime, including the possibility of emergent electronic phases. Methods of suppressing ferroquadrupole order using doping, magnetic field, or orthogonal antisymmetric strain (12) are readily experimentally accessible.

Materials and Methods

Single crystals of ${\mathrm{Y}\mathrm{b}\mathrm{R}\mathrm{u}}_2{\mathrm{G}\mathrm{e}}_2$ were grown from a high-temperature indium flux, as described elsewhere (40) (SI Appendix, section 9). The resulting crystals could be cleaved to a thickness of 20 $\mathrm{\mu }$m or less and were identified and oriented using single-crystal X-ray diffraction.

Low-temperature, high-resolution, X-ray diffraction measurements were performed on beamline A2 at Cornell High Energy Synchrotron Source (CHESS). The intensity profiles of the (6 0 0) Bragg peak were mapped out in momentum space from 40 K to 6.6 K. The orthorhombicity parameter $\left(a-b\right)/\left(a+b\right)$ was obtained by finding the first moment of the intensity (integrating counts multiplied by position) of line scans of the orthorhombic Bragg peaks (SI Appendix, section 2).

Flat samples were bonded to 50-$\mathrm{\mu }$m-thick Si substrates using Angstrom Bond. Hall bar patterns were then etched into the sample using a focused ion beam (see SI Appendix, section 8 for beam parameters) to precisely define current directions and contact geometry (Fig. 1). The Si substrates were glued onto the side of a piezoelectric stack, and strains experienced by the sample as a consequence of varying the voltage to the stack were estimated via resistive strain gauges, both on the side of the stack and on top of bare Si substrates (24).

Detailed elastoresistivity measurements were taken using an amplitude demodulation technique, following the method described in ref. 31. An ac voltage was applied to the piezoelectric stack, as well as an ac current applied to the sample, and the combination of mechanical and electrical excitations produced voltage signals at the sum and difference of the two frequencies, proportional to the unstrained resistivity of the sample multiplied by its elastoresistivity (31).