A General Unfolding IRT Model for Multiple Response Styles

Abstract

It is commonly known that respondents exhibit different response styles when responding to Likert-type items. For example, some respondents tend to select the extreme categories (e.g., strongly disagree and strongly agree), whereas some tend to select the middle categories (e.g., disagree, neutral, and agree). Furthermore, some respondents tend to disagree with every item (e.g., strongly disagree and disagree), whereas others tend to agree with every item (e.g., agree and strongly agree). In such cases, fitting standard unfolding item response theory (IRT) models that assume no response style will yield a poor fit and biased parameter estimates. Although there have been attempts to develop dominance IRT models to accommodate the various response styles, such models are usually restricted to a specific response style and cannot be used for unfolding data. In this study, a general unfolding IRT model is proposed that can be combined with a softmax function to accommodate various response styles via scoring functions. The parameters of the new model can be estimated using Bayesian Markov chain Monte Carlo algorithms. An empirical data set is used for demonstration purposes, followed by simulation studies to assess the parameter recovery of the new model, as well as the consequences of ignoring the impact of response styles on parameter estimators by fitting standard unfolding IRT models. The results suggest the new model to exhibit good parameter recovery and seriously biased estimates when the response styles are ignored.

Response styles represent the different kinds of cognitive bias that result in responses deviating from individuals’ accurate status, and they are prevalent in responses to the Likert-type items commonly used in the social and human sciences. Several response styles have been posited that are all capable of leading to distorted responses in various ways, including extreme response style (ERS), which involves a tendency to choose the lowest and highest categories; midpoint response style (MRS), which involves a tendency to choose middle categories; acquiescence response style (ARS), which involves a tendency to agree with items; and socially desirable response style (SDRS), which involves a tendency to pretend to look good. The potential of using item response theory (IRT) to deal with the various response styles has been promoted in recent years (Bolt & Adams, 2017; Bolt & Johnson, 2009; Falk & Cai, 2016; Jin & Wang, 2014; Johnson & Bolt, 2010). Most of these response style models were developed for dominance data, in which the probability of endorsement increases monotonically as the latent trait increases. More recently, the substantive response process and the response style process have been disentangled to yield richer information concerning the differing mental processes of respondents (Böckenholt, 2017; Jeon & De Boeck, 2016). An alternative approach models the threshold parameters either by means of random variation across persons or a multiplicative person parameter (Jin & Wang, 2014; Wang, Wilson, & Shih, 2006; Wang & Wu, 2011).

Furthermore, mixture modeling of response styles explores the hidden classes of response styles in a compensatory manner (Wetzel, Carstensen, & Böhnke, 2013). In addition, multidimensional nominal response models have been adopted to distinguish the latent traits involved in response styles from the substantive latent traits (Bolt & Adams, 2017; Bolt & Johnson, 2009; Falk & Cai, 2016; Johnson & Bolt, 2010).

Although different approaches to response styles in relation to dominance data have been developed in recent decades, only a few studies have dealt with response styles in relation to unfolding data (Javaras & Ripley, 2007). In unfolding IRT models, unlike in dominance IRT models, the probability of endorsement increases as the distance between the person location (parameter) and the item location (parameter) decreases. For example, when respondents are asked to indicate their degree of agreement with the statement “I think capital punishment is necessary, but I wish it was not,” they may disagree with the statement for two distinct reasons, namely that capital punishment is necessary, or that capital punishment should be abolished (Andrich, 1988). Only those respondents with a more neutral attitude are likely to offer an endorsement of the statement. To describe such a phenomenon, unfolding models postulate an inverted U-shaped item characteristic curve (ICC) on the relationship between the latent trait and the probability of endorsement.

Unfolding models have attracted significant research interest in relation to the construction and analysis of attitude, personality, job performance, vocational interests, leadership, emotions, and other factors (Cao, Drasgow, & Cho, 2015; Tay & Drasgow, 2012). However, the impacts of the different response styles on unfolding data have been subject to very little investigation in the literature (Javaras & Ripley, 2007; Wang, Liu, & Wu, 2013). It is widely recognized that ignoring response styles results in serious estimation bias in dominance data (Bolt & Adams, 2017; Falk & Cai, 2016), and similar consequences should be expected for unfolding data. In the present study, the authors propose a general unfolding IRT model for multiple response styles, in which one substantive latent trait is assumed to underlie normal responses, whereas one nuisance latent trait (propensity) is assumed to underlie each response style.

The remainder of the study is organized as follows. First, the general unfolding model (GUM) is introduced. Second, the general unfolding model for response styles (GUMRS) in unfolding data is proposed. Third, the new GUMRS and those models previously developed in the literature are discussed and compared. Fourth, the new model is applied to an empirical data set to demonstrate its advantages when accounting for different response styles in unfolding data. Fifth, a series of simulation studies is conducted to evaluate the parameter recovery of the new model, as well as the consequences of ignoring response styles when standard unfolding models are fitted. Finally, conclusions are drawn and suggestions for further studies are offered.

IRT Models for Response Styles

The GUM

In the present study, the GUM for polytomous data (Luo, 2001) is employed as a general framework mainly because of the flexibility of the operational function and intuitive interpretation of the item threshold parameters. The probability function of the polytomous response Zni∈ (0, 1, . . ., C), given person parameter θ_n and item parameter δ_i, is defined as,

$$\mathrm{Pr}(Z_{\mathrm{ni}}=z)=\frac{\underset{k=1}{\overset{C}{\Pi }}{\mathrm{P}}_{\mathrm{nik}}^{U_{\mathrm{zk}}}{\mathrm{Q}}_{\mathrm{nik}}^{1-U_{\mathrm{zk}}}}{\sum _{w=0}^C\underset{k=1}{\overset{C}{\Pi }}{\mathrm{P}}_{\mathrm{nik}}^{U_{\mathrm{wk}}}{\mathrm{Q}}_{\mathrm{nik}}^{1-U_{\mathrm{wk}}}},$$

where C is a positive integer equal to the number of categories minus one, while the dummy variable U_zk = 1 if z≥k, but U_zk = 0 otherwise. In addition, U_wk = 1 if w≥k, although U_wk = 0 otherwise. It is important to note that the conditional parameters are omitted from the probability function for reasons of brevity. P_nik is a probability function defined as,

$${\mathrm{P}}_{\mathrm{nik}}\equiv \mathrm{Pr}(Y_{\mathrm{nik}}=1)=\frac{{\psi }_k\left({\rho }_k\right)}{{\psi }_k\left[{\alpha }_i({\theta }_n-{\delta }_i)\right]+{\psi }_k\left({\rho }_k\right)},$$

and Q_nik = 1 –P_nik, where θ_n is the substantive latent trait (ideal point) of person n, δ_i is the item location, α_i∈ℝ≥ 0 is the slope parameter of item i, ρ_k∈ℝ≥0 is the kth threshold parameter across items because the same scoring rubric is used, and ψ(·) represents an operational function (Wang et al., 2013).

The properties of the operational function ψ(·) are crucial for generating a valid unfolding probability function (Luo, 1998), including (a) nonnegativity: ψ(x) ≧ 0 for any real x; (b) monotonicity in the positive domain: ψ(x) > ψ(y) for any x > y > 0; and (c) symmetry of the function: ψ(x) = ψ(−x) for any real x. Accordingly, the probability function will exhibit a symmetrical ICC. Several operational functions are available (e.g., see Luo, 1998) although the following operational function is used for illustrative purposes in this study (Luo, 2001):

$$\psi \left(x_k\right)=\frac{\cosh \left[(\frac{2C+1}{2}+1-k)x\right]}{\cosh \left[(\frac{2C+1}{2}-k)x\right]}.$$

The operational function enables users to create various ICCs to fit their own unfolding data. The choice of the operational functions can be based on substantive theories and/or model selection criteria (e.g., the deviance information criterion [DIC]). As shown in Equations 58 to 65 in Luo (2001) and Equation 10 in Wang et al. (2013), the GUM subsumes the generalized graded unfolding model (GGUM; Roberts, Donoghue, & Laughlin, 2000) via an appropriate operational function. Wang et al. (2013) used the following operational function:

$${\mathrm{P}}_{\mathrm{nik}}=\frac{{\psi }_k\left({\alpha }_i{\beta }_{\mathrm{ik}}\right)}{{\psi }_k\left[{\alpha }_i({\theta }_n-{\delta }_i)\right]+{\psi }_k\left({\alpha }_i{\beta }_{\mathrm{ik}}\right)},$$

where β_ik is the item threshold for threshold k of item i, α_i is the discrimination for item i, and the others are defined previously. In Equation 2, the authors used a common threshold parameter ρ_k across items. If ρ_ik is used instead of ρ_k in Equation 2, ρ_ik can be partitioned as α_iβ_ik. When Equation 3 is imposed, the GUM becomes the GGUM (Wang et al., 2013). Furthermore, when α_i = 1, the GUM becomes the graded unfolding model (Luo, 2001; Roberts & Laughlin, 1996).

With respective to the interpretation of the threshold parameters ρ_k in the GUM, they are the locations where the ICCs of adjacent categories intersect. However, such interpretation does not exist for the threshold parameters in the GGUM or the graded unfolding model.

We set ρ_ik = ρ_k in this study because of two reasons. First, Likert-type items in an inventory often adopt the same scale (e.g., 5-point disagree–agree scale) so they share the same scoring rubric. Second, as observed by Luo (2000) and this pilot study, constraining a common set of thresholds across items helps stabilize the estimation.

The General Unfolding Model for Response Styles (GUMRS)

The kth threshold parameter ρ_k of the GUM for k = 1, . . ., C represents the location where two adjacent ICCs intersect and the probability is equal to 0.5. That is, ρ_k indicates the location of the intersection between categories k – 1 and k. Assuming that the thresholds vary across respondents (i.e., an individual’s tendency toward the scoring rubric), it is appropriate to extend ρ_k to ρ_nk, which is related to the nth person’s tendency toward the threshold between the adjacent categories (Luo, 1998). However, such an approach can only capture the randomness across individuals, as it does not account for different response styles (Jin & Wang, 2014; Luo, 1998; Wang et al., 2013).

To simultaneously describe multiple response styles, a “softmax” function is proposed and integrated into the GUM. Thus, Equation 1 becomes,

$$\mathrm{Pr}(Z_{\mathrm{ni}}=z)=\frac{{\mathrm{W}}_{\mathrm{niz}}\underset{k=1}{\overset{C}{\Pi }}{\mathrm{P}}_{\mathrm{nik}}^{U_{\mathrm{zk}}}{\mathrm{Q}}_{\mathrm{nik}}^{1-U_{\mathrm{zk}}}}{\sum _{w=0}^C{\mathrm{W}}_{\mathrm{niw}}\underset{k=1}{\overset{C}{\Pi }}{\mathrm{P}}_{\mathrm{nik}}^{U_{\mathrm{wk}}}{\mathrm{Q}}_{\mathrm{nik}}^{1-U_{\mathrm{wk}}}},$$

where W_niz denotes the softmax function, which is defined as,

$$W_{niz}=\frac{\exp \left[{\left({\lambda }_i\circ s_{1+z}\right)}^{\prime }{\gamma }_n\right]}{{\displaystyle \sum _{z=0}^C\exp \left[{\left({\lambda }_i\circ s_{1+z}\right)}^{\prime }{\gamma }_n\right]}},$$

where λ_i is a vector of the slope parameters of size D× 1 for item i, s_1+z is the (1 +z)th column vector of the scoring functions S (D×K), K = 1 +C, ○ denotes the entrywise product, and γ is a vector of the response style latent propensities of size D× 1. Therefore, Equations 2 and 5 together form the new unfolding model for response styles for unfolding data, where P_nik and Q_nik are defined as in Equation 2. λ_i reflects the relationship between the corresponding response style latent propensities, γ_n, and item i. If an element of λ_i is zero, then the corresponding latent propensity does not affect the item response and thus can be ignored. In the GUMRS, we constrained λ_i = λ for all items mainly for estimation stability. If an element of λ = 0, then the corresponding latent propensity does not affect any item response.

It is assumed that γ and θ follow a multivariate normal distribution. The assumption is also made in other studies of multiple response styles (Böckenholt, 2017; Falk & Cai, 2016). Although it is possible that γ and θ may exhibit nonlinear relationship, linear relationship is simpler, easier to understand, and preferred when the model-data fit is acceptable. Besides, nonlinear relationship usually requires more parameters, larger sample sizes, and longer tests, which may not be feasible in practice.

In the GUMRS, γ is specified as a vector of nuisance parameters to account for the randomness of the response styles. The correlation between γ and θ can be estimated under a condition of proper identification (Falk & Cai, 2016; Johnson & Bolt, 2010), which will be explained later. The scoring function S is highly flexible so as to characterize the response styles (Falk & Cai, 2016). Table 1 presents an example of the scoring functions for a 6-point item. For instance, the scoring function, [1 0 0 0 0 1], is used to model the ERS for a 6-point item. The tendency to choose the second, third, and fourth categories is relatively weaker than the tendency to choose the first and last categories, while the first and last categories share the same likelihood of being chosen. λ is very useful for examining the magnitude of response styles, and it can be used to detect whether the corresponding response style trait is significant for dimension d (i.e., H₀: λ_d = 0 for d = 1, . . ., D). The GUMRS is reduced to the traditional GUM when either λ = 0 or γ = 0.

Table 1.

Example of Scoring Functions for 6-Point Likert-Type Items.

Scoring function	Response style latent propensity
[1 0 0 0 0 1]	Extreme response style (ERS)
[0 0 1 1 0 0]	Midpoint response style (MRS)
[2 1 0 0 1 2]	Extreme midpoint response style (EMRS)
[0 0 0 1 2 3]	Acquiescence
[0 0 0 0 1 1]	Acquiescence above agree (AAA)
[0 0 0 0 1a 0]	Socially desirable responding

^aThe fifth category is assumed to be the most socially desirable response.

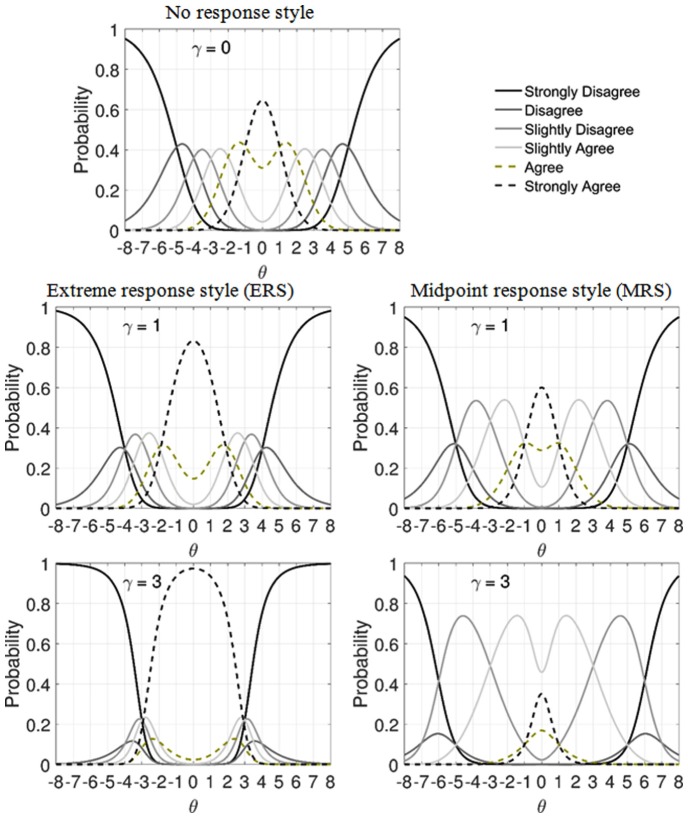
Figure 1 illustrates the ICCs (6-point rubric) of the GUMRS for the ERS (score function: [1 0 0 0 0 1]) and the MRS (score function: [0 0 1 1 0 0]) under different magnitudes of γ, given that λ^ERS = λ^MRS = 1. The upper panel presents the ICC without any response style (i.e., the GUM). The two panels on the left show the ICCs influenced by the ERS with a moderate magnitude (γ = 1) and a strong magnitude (γ = 3). The first and last categories tend to be chosen more frequently when the magnitude of the ERS increases. The two panels on the right show the ICCs influenced by the MRS, wherein the third and fourth categories are more likely to be chosen as the magnitude of the MRS increases.

Figure 1.

ICCs of the GUMRS under the influence of the ERS ([1 0 0 0 0 1]) and the MRS ([0 0 1 1 0 0]), given λ = 1.

Note. The upper panel is the ICC without any response style (γ = 0). The middle panels present the ICCs for the ERS and the MRS with a moderate effect (γ = 1). The lower panel present the ICCS for the ERS and the MRS with a large effect (γ = 3). ρ = [5, 4, 3, 2, 1] and δ = 0. ICC = item characteristic curve; GUMRS = general unfolding model for response styles; ERS = extreme response style; MRS = midpoint response style.

Comparison of the GUMRS With Previous Models

Due to space constraints within this article, the authors only comment on those previous models that are most closely related to the GUMRS. Falk and Cai (2016) proposed a multidimensional nominal response model to simultaneously deal with substantive constructs and multiple response styles. Their model’s probability function is defined as,

$$\mathrm{Pr}\left(Z_{ni}=z\right)=\frac{\exp \left[{\left({\lambda }_i\circ s_{1+z}\right)}^{\prime }{\eta }_n+{\tau }_z\right]}{{\displaystyle \sum _{z=0}^C\exp \left[{\left({\lambda }_i\circ s_{1+z}\right)}^{\prime }{\eta }_n+{\tau }_z\right]}},$$

where η_n is a vector containing the substantive latent trait φ_n (a dominance trait) and the response style latent propensities γ_n for person n, s_1+z is the (1 +z)th column vector of the scoring functions, and τ_z is the intercept parameter of category z. Their model was solely developed for dominance data, whereas the GUMRS is customized for unfolding data. Notably, the scoring function S is applied to the GUMRS to account for multiple response styles in unfolding data.

Luo (1998) extended ρ_k to ρ_nk to relate person n to threshold k and allow for different threshold parameters for different persons, which reflects the variations in the distance judgment between adjacent categories in unfolding data. Thus, Equation 2 becomes,

$${\mathrm{P}}_{\mathrm{nik}}\equiv \mathrm{Pr}(Y_{\mathrm{nik}}=1)=\frac{{\psi }_k\left({\rho }_{\mathrm{nk}}\right)}{{\psi }_k\left[{\alpha }_i({\theta }_n-{\delta }_i)\right]+{\psi }_k\left({\rho }_{\mathrm{nk}}\right)}.$$

Wang et al. (2013) further proposed a random threshold approach by decomposing ρ_nk into ρ_k and a multiplicative parameter exp(κ_nk) for unfolding data, where κ represents the individual’s tendency parameter and exp(·) denotes the exponential function. The corresponding function is,

$${\mathrm{P}}_{\mathrm{nik}}\equiv \mathrm{Pr}(Y_{\mathrm{nik}}=1)=\frac{{\psi }_k\left[{\rho }_k\exp \left({\kappa }_{\mathrm{nk}}\right)\right]}{{\psi }_k\left[{\alpha }_i({\theta }_n-{\delta }_i)\right]+{\psi }_k\left[{\rho }_k\exp \left({\kappa }_{\mathrm{nk}}\right)\right]},$$

where κ_nk is a random threshold parameter for person n at threshold k. Notably, neither Luo (1998) nor Wang et al. (2013) explicitly accounted for multiple response styles.

In contrast to Wang et al. (2013), Jin and Wang (2014) proposed a multiplicative approach to account for the ERS and the MRS using a single dominance trait (φ) for dominance data. The probability function is defined as,

$$\mathrm{Pr}(Z_{\mathrm{ni}}=z)=\frac{\exp \left\{{\upsilon }_i[z({\varphi }_n-{\beta }_i)-{\omega }_n\sum _{k=0}^z{\mathbf{\tau }}_{\mathbf{iz}}]\right\}}{\sum _{w=0}^C\exp \left\{{\upsilon }_i[w({\varphi }_n-{\beta }_i)-{\omega }_n\sum _{k=0}^w{\mathbf{\tau }}_{\mathbf{iz}}]\right\}},$$

where υ_i is the item discrimination for item i, β_i is the item difficulty for item i, and ω_n is a weight parameter of person n on threshold τ_iz, which is posited to follow a log-normal distribution with a mean of zero and a variance of ${\sigma }_{\omega }^2$. When ω > 1, the respondent tends to choose the middle categories, and the higher the value, the higher the tendency. However, when ω < 1, the respondent tends to choose the extreme categories, and the lower the value, the higher the tendency. Hence, the ERS and the MRS are treated as two ends of a continuum. The magnitude of ${\sigma }_{\omega }^2$ depicts the degree of randomness of persons on thresholds. When ${\sigma }_{\omega }^2=0$, Equation 9 is simplified to the general partial credit model (Muraki, 1992). This approach is only applicable for dominance data, and the assumption of a single dimension for both the ERS and the MRS should be empirically tested (Falk & Cai, 2016).

Javaras and Ripley (2007) developed a similar random threshold approach to allow for person-specific variations in unfolding data. Their model is posited as,

$$\mathrm{Pr}(Z_{\mathrm{ni}}=z)=\mathrm{Pr}({\pi }_{n(k-1)}\le Z_{\mathrm{ni}}^{*}\le {\pi }_{\mathrm{nk}}),$$

where $Z_{\mathrm{ni}}^{*}$ is a latent response defined as,

$$Z_{\mathrm{ni}}^{*}={\alpha }_i|{\theta }_n-{\delta }_i|$$

and

$${\pi }_{\mathrm{nk}}={\left({\phi }_n\right)}^{-1}{\pi }_k+{\mu }_n,$$

where ϕ_n is the weight parameter and µ_n is the mean of a threshold parameter π_nk. The model can be made group-specific by adding covariates such as gender or region. Unfortunately, it cannot account for multiple response styles simultaneously.

The multiple decision approach (Böckenholt, 2017; Jeon & De Boeck, 2016) aims to disentangle different response processes. To implement this approach, original data sets should be reformed in different ways according to the pointed response processes. When using this approach, the use of traditional model comparison statistics such as the Akaike information criterion becomes unfeasible (Jeon & De Boeck, 2016), making it difficult to decide which response process is most appropriate. Due to this constraint, the multiple decision approach will not be discussed further in this study.

The constrained dual scaling (CDS) approach (Schoonees, van de Velden, & Groenen, 2015) adopts dual scaling, quadratic monotone spline, and latent class methods to scale persons, items, and classes of persons with different response styles in a nonparametric and exploratory way. Compared with the CDS, the parametric GUMRS is more advantageous for model-data fit assessment, model comparison, prediction of persons’ rating, large number of response styles (possibly larger than four), assessment of differential item functioning, and applications to computerized adaptive/classification testing, among others. The CDS assumes that a person has only one response style, whereas the GUMRS allows users to check whether a person has multiple response styles. In addition, inspecting the slope parameter for a specific response style in the GUMRS reveals whether the corresponding response style exists across persons. On the contrary, the CDS relies on subjective judgment on the scree plot to determine the number of response styles and the meaning of the latent classes.

Of the aforementioned approaches, only Falk and Cai (2016) multidimensional nominal response model, the multiple decision approach, and the GUMRS allow for multiple response styles in a person and correlation between substantive latent traits and response style latent propensities, whereas the other approaches assume one single response style in a person and statistical independence. In practice, it is possible that a person has multiple response styles, so it is too restricted to assume a person has only one response style. How will these response styles be put into operation in a test may depend on test contents and contexts. As demonstrated later in the empirical data analysis, approximately 12% of the respondents exhibited both the ERS and the AAA response style.

Parameter Estimation for the GUMRS

Marginal maximum likelihood estimation is commonly used to estimate parameters in IRT models, especially when the number of dimensions is low (e.g., less than five), as the necessary computation time and computer memory requirement increase exponentially as the number of dimensions increases linearly (Bock & Aitkin, 1981). In recent years, the Bayesian Markov chain Monte Carlo (MCMC) approach has also been widely used for IRT models, although it typically requires heavier computation and Bayesian knowledge (e.g., convergence checking and prior distribution specification). That said, MCMC algorithms are easy to implement, especially for complicated IRT models, including the GUMRS, and they are readily available in open-source software such as the Just Another Gibbs Sampler (JAGS; Plummer, 2003). The effectiveness of the JAGS for unfolding models appears to be satisfactory (Liu & Wang, 2016; Wang et al., 2013; Wang & Wu, 2016). In this study, the authors use the JAGS to estimate the parameters in the GUMRS.

The GUMRS belongs to the class of within-item multidimensional IRT models (Adams, Wilson, & Wang, 1997), whose identification problems require special attention. Falk and Cai (2016) observed that their model, including the scoring functions, could be identified provided that the scoring functions are linearly independent of both each other and the substantive construct. Furthermore, due to the trade-off between α_i and λ_i (i.e., the outcome probability can be the same when α_i increases and λ_i decreases simultaneously, and vice versa), it may be useful to impose an equality constraint on λ_i = λ across items (Johnson & Bolt, 2010). Such a constraint is in line with the common phenomenon whereby response styles are stable across items. All the latent traits are postulated following a multivariate normal distribution with zero means and a covariance matrix where the diagonals are constrained as ones and the off-diagonals are to be estimated.

The settings of the MCMC algorithms are as follows. The prior distributions were set as λ ~ N(0, 10)I(0, ∞), ρ ~ N(0, 10)I(0, ∞), α ~ N(0, 10)I(0, ∞), where the suffix “I(·,·)” of the normal distribution notation N(·,·) specifies the lower and upper bounds of the parameter space. In consideration of the sampling δ, δ_i ~ N(v_i, 2)I(l_i, u_i) was used (Liu & Wang, 2016), where v_i is the starting value generated by the correspondence analysis and standardized with a mean of zero and a standard deviation of one (Polak, Heiser, & de Rooij, 2009), l_i is the lower bound, and u_i is the upper bound, for item i. The sign of item i was assumed to be known in the following simulation study, although the sign should be predetermined by a content expert in a real data analysis (Liu & Wang, 2016). θ and γ_d were assumed to follow a multivariate normal distribution with zero means and a covariance matrix where the diagonals are constrained as ones and the off-diagonals are to be estimated (making it a correlation matrix). For the GUMRS, the JAGS internally chose the slice sampler to draw the MCMC samples. The JAGS code for the GUMRS is provided in the online appendix. Readers can easily modify the code to fit their own data.

Empirical Data Analysis

The censorship data set, which is available on prdlab.gatech.edu/unfolding/data/, was used to demonstrate the GUMRS. Some 223 participants responded to 20 six-point items (1 = strongly disagree, 2 = disagree, 3 = slightly disagree, 4 = slightly agree, 5 = agree, and 6 = strongly agree). Wang et al. (2013) used the same data set to investigate random variations within thresholds, and they found that the variations were larger for polar categories than for middle categories. However, their approach did not account for multiple response styles. Due to the small sample size and moderate test length, a single latent construct together with three response styles (the ERS, the MRS, and AAA) were investigated in this study for illustrative purpose (see Table 1). The three response styles led to eight combinations of models: (a) GUM, (b) GUM-ERS, (c) GUM-MRS, (d) GUM-AAA, (e) GUM-ERS-MRS, (f) GUM-ERS-AAA, (g) GUM-MRS-AAA, and (h) GUM-ERS-MRS-AAA.

The burn-in period featured 10,000 cycles, followed by an additional 40,000 cycles that were thinned by four to obtain the final 10,000 samples. Two MCMC chains were used. Convergence was assessed using the Gelman–Rubin diagnostic statistic (Gelman & Rubin, 1992), where a value less than 1.1 is typically regarded as acceptable as a rule of thumb. After individually fitting the eight models to the censorship data set, the DIC was used to compare the models. A model with a smaller DIC value was preferred. The posterior predictive p (ppp) value with the outfit statistic was used to assess the absolute model-data fit (e.g., van der Linden & Hambleton, 1997).

Preliminary analyses showed that α₂, α₄, α₅, α₁₁, and α₁₇ were not statistically significantly different from zero for all the models (i.e., unrelated to the substantive construct); thus, these five items were removed and the remaining 15 items were reanalyzed.

Results

The Gelman–Rubin diagnostic statistic indicated no convergence problem for any of the models. The DIC indicated that Model 6 had the lowest value (9,799.05), followed by Model 5 (9,866.21), Model 8 (9,875.94), Model 2 (9,960.28), Model 7 (10,031.65), Model 3 (10,135.08), Model 4 (10,177.12), and Model 1 (10,387.08). Model 6 exhibited the best fit among the eight models, which implied significant ERS and AAA. In contrast, the traditional GUM ignored the response styles and thus exhibited the poorest fit. The ppp value for Model 6 was .16, which suggested a reasonably good fit. For illustrative purpose, we also fit the GGUM (Roberts et al., 2000) to the data and its DIC was 10,317.57, which was much larger than that of Model 6.

It was found that ${\hat{\lambda }}_{\mathrm{ERS}}$ = 1.33 with SE = 0.10 and ${\hat{\lambda }}_{\mathrm{AAA}}$ = 0.99 with SE = 0.09 in Model 6. To test whether the corresponding parameters λ_ERS and λ_AAA were zero, we calculated their 95% credible intervals, which were [1.14, 1.55] and [0.82, 1.18], respectively. Because the intervals did not contain zero, it could be claimed that λ_ERS and λ_AAA were not zero, and the ERS and AAA response styles affected the item responses. The estimates of the correlation matrix for the substantive latent trait (Dimension 1), the ERS latent propensity (Dimension 2), and the AAA latent propensity (Dimension 3) are as follows:

$$\mathrm{Cor}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \multicolumn{1}{c}{-.30(.12)}& \hfill 1\hfill & \hfill \hfill \\ \multicolumn{1}{c}{-.57(.11)}& \hfill .22(.15)\hfill & \hfill 1\hfill \end{array}\right],$$

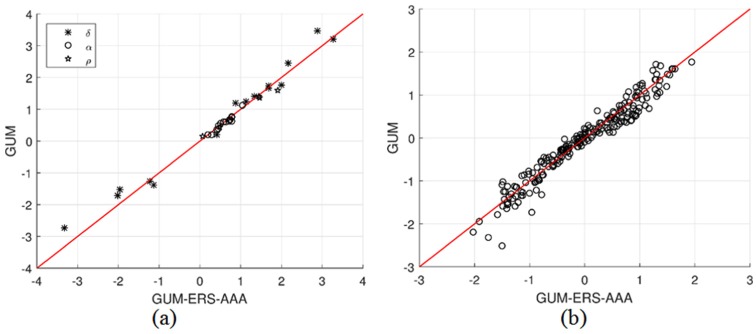
where the substantive latent trait was significantly correlated with both the ERS and AAA latent propensities, although the correlation between the ERS and AAA latent propensities was not significantly different from zero. The results implied that ignoring the correlation between the substantive latent trait and the response style latent propensities might lead to deviating estimates. For illustrative purposes, we compared Model 6 (GUM-ERS-AAA) and Model 1 (GUM) and then plotted the results of the comparison in Figure 2a. It appeared that Model 1 overestimated nine item parameters, but underestimated four item parameters, when compared with Model 6. The standard errors of the item parameter estimates were between 0.14 and 0.73 for $\hat{\delta }$, between 0.05 and 0.18 for $\hat{\mathrm{\alpha }}$, and between 0.08 and 0.14 for $\hat{\rho }$. The range of standard errors for $\hat{\delta }$ was rather wide due to the small sample size.

Figure 2.

Comparison of (a) item estimates and (b) person estimates (expected a posteriori) between the GUM-ERS-AAA and the GUM for the censorship data set.

Note. GUM-ERS-AAA = general unfolding model–extreme response style–acquiescence-above-agree; GUM = general unfolding model.

Figure 2b shows a scatter plot of the person estimates (expected a posteriori) between Model 6 and Model 1. The Pearson correlation coefficient was .97. It was evident that the differences were large in the vicinity of the negative pole, which might result from the mixed effect of the ERS and the AAA on the person estimates.

Table 2 presents three examples of response patterns and person parameter estimates for three persons under the GUM and the GUMRS. For Person 1, there appeared to be no specific response style, so the two response style latent propensities were around 0 under the GUMRS, while the θ (substantive latent trait) estimates were almost identical under the GUM and the GUMRS (−0.56 and −0.55, respectively). For Person 2, 14 out of 15 item responses were either 1 or 6, indicating a very strong ERS. Under the GUMRS, Person 2 had an ERS of 2.69, but an AAA of only 0.30. In addition, the θ estimates were −2.52 and −1.50 under the GUM and GUMRS, respectively, which suggests that when such an ERS was ignored, the θ estimate would be underestimated. For Person 3, 13 out of 15 responses were either 5 or 6, indicating a very strong AAA. Furthermore, only one of the 15 responses was extreme (6), indicating a very weak ERS. Under the GUMRS, Person 3 had an ERS of −1.33 and an AAA of 1.93. The θ estimates were 0.64 and 0.23 under the GUM and the GUMRS, respectively. It appeared that the effects of a weak ERS and a strong AAA canceled out each other out to a certain degree, so ignoring them did not substantially affect the θ estimate under the GUM.

Table 2.

Response Patterns and Person Parameter Estimates of Three Persons Under the GUMRS and the GUM on a 6-Point (1-6) Scale in the Empirical Example.

Person	Response pattern	θGUM	θGUMRS	γ ERS	γ AAA
1	3 2 3 1 5 2 2 5 2 6 4 4 1 4 6	−0.56	−0.55	0.04	0.13
2	6 1 6 1 1 1 1 1 1 4 1 6 1 1 6	−2.52	–1.50	2.69	0.30
3	4 5 5 5 6 5 2 5 5 5 5 5 5 5 5	0.64	0.23	–1.33	1.93

Note. GUMRS = general unfolding model for response styles; GUM = general unfolding model; ERS = extreme response style; AAA = acquiescence-above-agree.

If a respondent had a latent propensity estimate that was statistically larger than 1 SD or smaller than −1 SD, it was declared that the respondent had exhibited the corresponding response style substantially. Overall, approximately 12% of the participants exhibited both ERS and AAA response styles substantially, which supported multiple response styles and the superiority of the GUMRS.

Simulation Studies

The aim of the simulation studies was to investigate the parameter recovery of the GUMRS, as well as the consequences of ignoring the impact of response styles on parameter estimates, by comparing the parameter estimates obtained from the GUMRS with those obtained from the GUM.

Method

A series of simulations were conducted to assess the recovery of the item parameters and the accuracy of the standard error estimators. A single substantive latent trait and two nuisance latent propensities (ERS and AAA) were included in the GUMRS to generate data. A total of 1,000 respondents were drawn from a multivariate normal distribution with zero means and a covariance matrix where the diagonals were constrained as ones and the off-diagonals were to be estimated (i.e., a correlation matrix), with three levels of correlation: 0, .4, and .8. The zero correlation was used as a baseline, in which the response style latent traits could be ignored because they did not provide information about the substantive latent trait. A correlation of .4 indicated a moderate magnitude, while .8 indicated a large magnitude; hence, the response style latent propensities should not be ignored because they provide information about the substantive latent trait (Liu & Wang, 2016). Negative correlations were not considered because reverse biased patterns could be expected. The correlations were set as equal between the latent traits. In addition to the three correlation conditions, the correlation matrix from the previous empirical example under the GUMRS (Equation 14) was also employed. There were 15 six-point items, which was consistent with the previous empirical example and appeared sufficient to demonstrate the consequences of ignoring response styles. The values of α, ρ = [1.91, 1.46, 1.45, 0.48, 0.07], and λ = [1.33, 0.99] were set as the same as those obtained from the previous empirical results of Model 6. To avoid extreme values for the item locations, which may result in large sampling variations, the δ was generated from a uniform distribution between –2 and 2 with an equal step (Liu & Wang, 2016; Wang et al., 2013).

Four data sets, one for each of the three correlations and one for the correlation obtained from the empirical example, were generated according to the GUMRS and then analyzed using the GUM and the GUMRS. The item parameters were fixed, and the latent traits were randomly distributed across 60 replications. Regarding the MCMC algorithms, the burn-in cycles were set at 4,000, followed by an additional 16,000 cycles, which were thinned by four to obtain the final 4,000 samples. Such settings appeared sufficient for unfolding models (Wang et al., 2013). For each replication, the Heidelberger and Welch (1983) convergence diagnostic statistic was used to evaluate the convergence. If the test failed, an additional 4,000 samples were generated until no convergence problem was found.

The overall results were assessed using the bias and root mean square error (RMSE) of an estimator $\hat{\xi }$ computed as $R^{-1}\sum _{r=1}^R({\hat{\xi }}_r-\mathrm{\xi })$ and $\sqrt{R^{-1}\sum _{r=1}^R{({\hat{\xi }}_r-\mathrm{\xi })}^2}$, respectively, where ξ was the true parameter and R = 60. For the standard error estimation, the average of $\mathrm{SE}({\hat{\xi }}_r)$ across the replications was assessed by dividing the empirical standard deviation of the parameter estimator $\mathrm{SD}(\hat{\xi })=\sqrt{\mathrm{RMS}{\mathrm{E}}^2-\mathrm{bia}{\mathrm{s}}^2}$, which is defined as a relative measure (RM): $\mathrm{RM}(\hat{\xi })=[R^{-1}\sum _{r=1}^{R}SE({\hat{\xi }}_r)]\mathrm{SD}(\hat{\xi }{)}^{-1}-1$. The $\mathrm{SE}({\hat{\xi }}_r)$ was estimated using the empirical standard deviation of the MCMC samples. In practice, an RM value of around zero indicates a satisfactory recovery of the standard error estimator.

Results

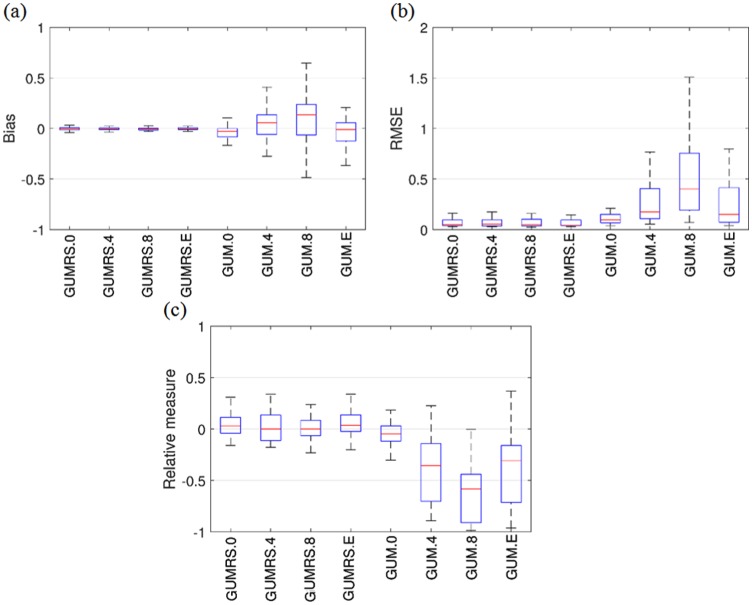
Figure 3a presents a box plot showing the bias values of the item parameter estimators of the GUMRS (i.e., α, δ, ρ, λ, and the correlations were aggregated) and the GUM (i.e., α, δ, and ρ were aggregated) under the three correlation conditions, namely 0, .4, and .8, which are denoted as GUMRS.0, GUMRS.4, and GUMRS.8, respectively, and the correlation obtained from the empirical example, which is denoted as GUMRS.E. The upper and lower quartiles of the bias values were very close to zero for the GUMRS. In contrast, the bias values were rather high for the GUM when the correlation was not zero (see GUM.0, GUM.4, GUM.8, and GUM.E). In addition, the higher the correlation, the more serious the bias values. The RMSE values shown in Figure 3b exhibited similar patterns to those for the bias values in that the RMSE was much lower for the GUMRS than for the GUM, especially when the correlation was as high as .8. Figure 3c shows the RM of the standard error estimators. The quartiles for the GUMRS.0, GUMRS.4, GUMRS.8, and GUMRS.E were within the range of ±.25. In contrast, the RM was much more extreme for the GUM, especially when the correlation was .8. In general, the standard errors were underestimated when the response styles were ignored.

Figure 3.

(a) Bias values, (b) root mean square error of the parameter estimators, and (c) relative measure of the standard error estimators, for 1,000 people and 15 six-point items from the GUMRS and the GUM in the simulation study.

Note. The suffixes “.0,”“.4,”“.8,” and “.E” added to GUMRS and GUM denote the correlations used to generate data from the GUMRS but analyzed with both the GUMRS and the GUM. GUMRS= general unfolding model for response styles; GUM = general unfolding model.

In summary, the GUMRS yielded both good parameter recovery and accurate standard errors. In contrast, when response styles existed but were ignored by fitting the GUM, the parameter recovery was poor and the standard errors were underestimated. The stronger the correlation between the substantive latent trait and the response style latent propensities, the worse the estimation of the parameters and their standard errors. These findings were consistent with those obtained for dominance data (Falk & Cai, 2016; Jin & Wang, 2014; Johnson & Bolt, 2010).

Conclusion

Most previous approaches to response styles were developed for dominance data (Falk & Cai, 2016; Jin & Wang, 2014; Johnson & Bolt, 2010). Although there do exist approaches to response styles in unfolding data, they cannot distinguish between different response styles (Javaras & Ripley, 2007; Luo, 1998; Wang et al., 2013). To meet the demand for IRT models for multiple response styles in unfolding data, the authors developed the GUMRS. The empirical example presented here demonstrates the utility of the GUMRS in accommodating various response styles by forming eight models. Through the model comparison, the statistical significance of the response styles could be tested. The simulation studies demonstrated good parameter recovery for the GUMRS and serious consequences for parameter estimation when the response styles were ignored, especially when the response style latent propensities were highly correlated with the substantive latent trait. These findings are consistent with those found in the literature concerning dominance data (Falk & Cai, 2016; Jin & Wang, 2014; Johnson & Bolt, 2010).

To fit the GUMRS to empirical data, the following steps are recommended. First, examine whether the data conform to the unfolding process. The procedures developed by Tay and Drasgow (2012) and Carter, Dalal, Guan, LoPilato, and Withrow (2017) may be helpful at this stage. Second, determine which types of response styles are involved in the data. In theory, one can include as many scoring functions as possible in the GUMRS; however, a high number of response styles lead to a high dimensionality (the number of dimensions in the GUMRS is one plus the number of response styles), which usually requires a large amount of data (i.e., large sample size and long test) and may result in estimation difficulty. Model compassion statistics, for example, the DIC, can then be applied to compare the models to identify significant response styles. Third, test whether the slope parameter λ for the response styles is significant. If it is statistically significant, which means that the item triggers the corresponding response style, practitioners should review the item content to identify possible reasons for this, rewrite the item, or remove it. Fourth, conduct follow-up interviews with persons who exhibited strong response styles to identify their underlying cognitive bias.

Several issues need further investigation. As the number of response styles employed in the GUMRS increases linearly, the number of combinations of response styles increases dramatically, rendering the MCMC methods very time consuming. Future studies should aim to develop more efficient algorithms for parameter estimation, for instance, the Metropolis–Hastings Robbins–Monro algorithm (Cai, 2010), to replace the MCMC algorithms. Missing data are common, and data may not be missing at random (Liu & Wang, 2016). Hence, the best means of extending the GUMRS to accommodate data that are not missing at random deserves further study.

Model extension is another direction to consider. Sometimes, a test may consist of multiple subtests (or a test battery consists of multiple tests) and each subtest measures a distinct substantive latent trait. Joint analysis of multiple subtests can improve measurement precision because the correlation among latent traits is taken into consideration (Wang, Chen, & Cheng, 2004). The GUMRS can be extended to accommodate multiple subtests. For example, a subscript t for subtest t can be added to Equations 2, 5, and 6 so the item parameters include α_it, δ_it, ρ_kt, and λ_it, and the person parameters include θ_nt and γ_nt. Where appropriate, the constraint γ_nt = γ_n can be set to indicate that each person has a common set of response style propensity parameters across subtests. Furthermore, if the substantive latent traits have a higher order structure, the following linear relationship can be incorporated (Huang & Wang, 2014):

$${\theta }_{\mathrm{nt}}^{(1)}={\beta }_t{\theta }_n^{(2)}+{\epsilon }_{\mathrm{nt}}^{(1)},$$

where ${\theta }_{\mathrm{nt}}^{(1)}$ is the first-order latent trait t for person n, ${\theta }_n^{(2)}$ is the second-order latent trait, ${\epsilon }_{\mathrm{nt}}^{(1)}$ is assumed to be normally distributed with mean zero and independent of other εs and θs, and β_t is the regression weight (factor loading) of the second-order latent trait on the first-order latent trait t. More orders are possible.