Kinetic Pathway of Torsional DNA Buckling

Abstract

In magnetic tweezers experiments, we observe that torsional DNA buckling rates and transition state distances are insensitive to base-pairing defects. This is surprising because defects are expected to kink DNA and lower the energy of a localized loop. Nonetheless, base-pairing defects lead to pinning of buckled structures at the defects, which may be important for DNA repair in vivo. We find that the decrease in entropy from pinning roughly balances the decrease in bending energy, explaining why defects have little effect on buckling rates. Our data are generally consistent with elastic rod theory, which predicts that the transition-state structure for torsional buckling is a localized wave with a specific shape (“soliton”). The transition-state soliton decays to a metastable looped intermediate (“curl”) that is separated from the final, fully-buckled state by a second, low energy, barrier. DNAs with base mismatch defects buckle at lower torque, where elastic rod theory predicts the loop structure is more stable, and manifest an intermediate buckling structure consistent with such a loop. We estimate that, under our high force, high salt experimental conditions, the soliton barrier is approximately 10 k_BT and, to reach this transition state from the unbuckled state, the system torque instantaneously decreases by approximately 1 pN·nm for DNA with or without a small defect.

Graphical Abstract

Introduction

Single-molecule force spectroscopy is a powerful approach to elucidate the free energy landscape associated with folding of proteins and nucleic acids, or the motion of protein domains during enzyme catalysis.¹ Typically the free energy profile represents a projection along the molecular extension or displacement coordinate, which is a natural choice when force is the control parameter and extension measured. Whereas force and extension are common single-molecule force spectroscopy conjugate variables, torque and angular motion are more appropriate for describing the free energy of rotary motors including the FoF1 ATPase,² the bacterial flagellar motor,³ and for the twisting of rotationally constrained polymers such as DNA.⁴ Experiments isolating molecular reactions on both torque and extension axes could provide insight into the thermodynamics and kinetics of physical processes occurring in the cell.

DNA is torsionally stressed during replication and transcription.⁵ Torsionally stressed (supercoiled) DNA buckles, extruding highly bent regions known as plectonemes.⁶ Similar behavior is predicted classically in twisted rods. With torsional stress, plectonemes may form preferentially or accumulate in regions of damaged or mispaired DNA where strong bends are more easily tolerated.⁷ We previously showed that plectonemes in torsionally stressed DNA are pinned at sites of base pairing defects.⁸ This could be biologically relevant as DNA repair enzymes preferentially bind to highly bent regions.⁹ Presentation of damaged DNA in regions of high curvature at the ends of plectonemes could facilitate recognition and repair in vivo.⁸

Methods

Preparation of DNA substrates with and without mismatches and the magnetic tweezers-based measurements of DNA extension as a function of imposed linking number and force are identical to those described.⁸ We provide a condensed version of the procedures here.

DNA preparation -

Mismatches were introduced by ligating oligonucleotides containing specific mismatches into a single stranded DNA gap generated between two nicking sites in the template DNA. A plasmid template was created by inserting the forward sequence GATCGCTGAGGCGCAGCTTCCGACTGCAGCCTGACGCCAGGGCTGAGGT at the BamHI restriction site in plasmid pET-28b. The inserted sequence included a PstI restriction site (CTGCAG) and two BbvCI sites (GCTGAGG). Linear DNA was generated by PCR of the plasmid with forward primer GAACCATCACCCTAATCAAG and reverse primer GAACAACACTCAACCCTATC, which included the 5’ extensions GCTGGGTCTCGCAAC-and GCTGGGTCTCGACCA-, respectively, to introduce non-palendromic Bsal cleavage sites.¹⁰ The purified PCR product was nicked with Nt.BbvCI and cut with Bsal. We then annealed a 10-fold excess of the sequence GGCGCAGCTTCCGACTGCAGCCTGACGCCAGGGCTGA to competitively hybridize with the DNA fragment excised from between the nicking sites by heating to 92°C and slowly cooling to 4°C. This produced DNA with an internal 37 nt gap and unique 4 nt sticky overhangs. We ligated 0.5 kbp handles containing the complementary nt overhangs and functionalized with either multiple biotin or digoxigenin moieties¹⁰ for anchoring the DNA to the streptavidin bead and anti-digoxigenin surface (see below). The following sequences were ligated into the 37 nt gap to introduce a 1, 2, or 4 bp mismatch (underscore).

• n = 1: 5’-TCAGCCCTGGCGTCAGGCAGCAGTCGGAAGCTGCGCC

• n = 2: 5’-TCAGCCCTGGCGTCAGGCACCAGTCGGAAGCTGCGCC

• n = 4: 5’-TCAGCCCTGGCGTCAGGGACGAGTCGGAAGCTGCGCC

Insertion of mismatch sequences destroys the PstI site. Digesting the DNA with PstI therefore eliminated templates that did not contain a mismatch. Intact DNA was prepared similarly but only the BsaI digestion and annealing of the 0.5 kbp labeled handles was performed on the PCR product.

Measuring torsional buckling of single DNA molecules using magnetic tweezers -

DNA molecules 2±0.2 μm in contour length were torsionally constrained between an anti-digoxigenin-coated glass surface and a ~ 1 μm streptavidin-coated paramagnetic bead (Dynal MyOne) using multiple biotin or digoxigenin moieties at either extremity. A magnetic field gradient, controlled by the proximity of permanent magnets, pulled the bead upward and extended the DNA. Rotating the magnets rotated the bead to add turns to the DNA, thereby controlling its topology. Measurements were performed in 10 mM Tris buffer, pH 7.5 with 1 M NaCl and 0.1% Tween-20. Data were collected at 200 Hz. The linking number was incrementally increased by 0.1 turn and 1000 points were measured at each linking number.

Results

Here we focus on the kinetics of buckling events as a function of defect size, using magnetic tweezers to impose torsional stress, hold supercoiling constant, and stretch the DNA at constant force.¹¹ Figure 1a shows a schematic of the experimental setup and data for bead height (DNA extension) as a function of turns applied to the DNA (defined as excess linking number, Lk) for a 6 kbp (2 μm) DNA held under 3.6 pN tension in 1 M NaCl. At a critical link of approximately 25 turns, the bead height suddenly decreases by about 90 nm.^12,13 After this, increasing the number of turns leads to a roughly linear decrease in bead height as the buckled region (plectoneme) increases in length. Near the critical link, the bead height fluctuates between two positions (Figure 1b), corresponding to the DNA fluctuating between unbuckled and buckled states, with the histogram of bead height positions (Figure 1c) showing two peaks. As link increases, the probability of being in the unbuckled state, p_u, decreases. From Boltzmann’s law, p_u is proportional to $e^{-\frac{Gu}{k_{B}T}}$, and the probability of being in the buckled state p_b is proportional to $e^{-\frac{G_b}{k_{B}T}}$, where G_u (G_b) is the free energy of the unbuckled (buckled) state. Defining K = p_b/p_u, ln $\text{ln}K=\frac{G_u-G_b}{k_{B}T}\equiv \frac{G_{u-b}}{k_{B}T}$. DNA in the unbuckled state is often treated as a homogeneous, straight and twisted elastic rod with $G_u=\frac{1}{2}\frac{C{k}_{B}T}{L}{(2\pi \text{Lk})}^2$, where C is the twist persistence length, L is the contour length of the DNA, k_B is the Boltzmann constant, T is temperature, and 2πLk is the angle through which DNA is twisted. When DNA buckles, some of the twist (Tw) gets converted to writhe (Wr, a measure of out-of-plane bending). From a fundamental theorem of topology,¹⁴ Tw = Lk − Wr. The reduction in twist reduces twist energy at a cost of bending energy and work done against the imposed force due to shortening of the DNA (because of curvature). G_b can be written as the sum of bending and translation energy, E_bt, plus twist energy $E_{tw}=\frac{1}{2}\frac{C{k}_{B}T}{L}{(2\pi (\text{Lk}-\text{Wr}))}^2$, minus an entropic contribution since buckling can occur anywhere along the DNA. Defining Lk^† as the link at the midpoint of the buckling transition, where G_u = G_b, allows E_bt and the entropy term to be written in terms of Lk^† and Wr_b, the writhe on buckling. Then ln K simplifies to $\text{ln}K\approx {(2\pi )}^2\frac{C}{L}\left({\text{Lk}}^{†}-\text{Lk}\right){\text{Wr}}_b$.^15,16 This expression is useful as it shows that the derivative of ln K with respect to 2πLk, which is easily computed from the change in probability of being in the buckled state as link is increased, is proportional to the change in torque (due to writhe) on buckling.

Figure 1:

Torsional DNA buckling. a. Extension vs torsion data on a single DNA molecule. Using the magnetic tweezers method,¹¹ the DNA is manipulated by constant upward force and controlled rotation of a tethered magnetic microbead (inset schematic). This permits control over the degree of DNA supercoiling at specific values of excess linking number Lk. Torsional stress causes DNA to buckle at Lk = Lk^†, somewhat past the point Lk* at which the post-buckling slope extrapolates to the top of the curve. The torque at buckling decreases in proportion to the decrease in ${\text{Lk}}_n^{†}-{\text{Lk}}^{*}$ with n mismatches.⁸ b. Extension vs time data for n = 0 mismatches at Lk ≈ Lk^†. The DNA is observed to fluctuate between unbuckled and buckled states. c. Probability distribution. We used the local minimum separating states as a threshold to determine the probabilities of the unbuckled and buckled states (thermodynamics) or the residence times in either state (kinetics). We extracted thermodynamic and kinetic data as a function of Lk by analyzing a previously published data set collected at 5 ms sampling, fixed 3.6 pN force, and 1 M salt on 6 kb DNA molecules with n = 0, 1, 2, or 4 serial mismatches.⁸

Figure 2a shows plots of ln K versus link for DNA with 0, 1, 2 or 4 base-pair mismatches. The midpoint of the buckling transition occurs at ln K = 0, where p_u = p_b. To estimate the buckling link as precisely as possible, we measured it as the distance from a local landmark, the link Lk* at which a straight line through the linear portion of the extension versus link curve intersects the flat portion of the extension versus link curve (see Figure 1a); we assume that Lk* is the same for DNAs with and without base-pair defects. The buckling link decreased with defect size and for DNAs with n = 0, 1, 2 and 4 base-pair defects, Lk^† was closely approximated by 25.4 − 0.17n² (see Fig. 2d of reference 8). Figure 2b shows the torque drops on buckling calculated from the slopes in Figure 2a. Interestingly, the torque drops are similar for intact and mismatch containing DNA molecules.

Figure 2:

Thermodynamic analysis of buckling data on single DNA molecules with n = 0, 1, 2, or 4 mismatches. a. Logarithm of K = p_b/p_u as a function of torsion Lk across the transition between unbuckled (u) and buckled (b) states. Error bars are based on binomial sampling of time spent in unbuckled and buckled states at each point. The transition midpoint occurs at Lk^†, where the buckled and unbuckled states are equally populated and ln K = 0. b. The decrease in torque, $\Delta {\Gamma }_{u-b}=-\frac{k_{B}T}{2\pi }\frac{\partial \text{ln}K}{\partial \text{Lk}}$, between unbuckled and buckled states as a function of mismatch size n is indicated by black circles. Error bars reflect the standard error of weighted fits to the slopes in part a. The sum of the torque drops going from unbuckled to the transition state, and then from the transition state to buckled, calculated from the data in Fig. 3, give the same values, to within error (cyan; see Fig. 3).

The experiments in Figure 2 are effectively equilibrium measurements, but a similar analysis can be applied to the mean times in the unbuckled and buckled states individually, which constitutes a kinetic analysis. The unbuckled and buckled states are separated by a free energy barrier. Let ΔG_s−u (ΔG_s−b) be the free energy difference between the transition state s and the unbuckled (buckled) state. In a simple Kramers model, the mean time in the unbuckled state, τ_u, equals $\frac{1}{k_{att},u}{e}^{\frac{\Delta G_{s-u}}{k_{B}T}}$, where k_att,_u is an attempt rate for going from the unbuckled state to the transition state. If the attempt rate does not depend on Lk, then $-k_{B}T\frac{\partial \text{ln}{\tau }_u}{\partial (2\pi \text{Lk})}=\frac{\partial \Delta G_{s-u}}{\partial (2\pi \text{Lk})}$, which equals the torque drop on going from the unbuckled state to the transition state since the derivative of free energy with respect to 2πLk is torque. Similarly, $k_{B}T\frac{\partial \text{ln}{\tau }_b}{\partial (2\pi \text{Lk})}=\frac{\partial \Delta G_{s-b}}{\partial (2\pi \text{Lk})}$ is the torque drop on going from the transition state to the buckled state. Figure 3a shows plots of the logarithm of mean lifetime in the unbuckled or buckled state as a function of link. Figure 3b shows the torque drops on going from the unbuckled state to the transition state (green) and from the transition state to the buckled state (blue), calculated from the plots in Figure 3a. The torque drops are similar for DNAs with or without defects. The sum of the torque drops going from the unbuckled state to the transition state and then to the buckled state are the same, within measurement error, as the torque drop going from the unbuckled state to the buckled state calculated from equilibrium measurements (cyan versus black dots in Figure 2). For all DNAs, the torque drop going from the transition state to the buckled state is larger than the torque drop going from the unbuckled state to the transition state. The magnitude of the torque drops reported here, and the asymmetry regarding transitions to and from the transition state, are similar to a recent report that measured buckling kinetics of non-defect DNA under a variety of forces and salt conditions.¹⁶ In the latter report, torque drop calculated as 2πΔWrk_BTC/L was about 0.9 pN·nm going from unbuckled to the transition state and 1.6 pN·nm going from the transition to the buckled state for a 7.9 kbp DNA held at 4 pN in 300 mM NaCl.

Figure 3:

Kinetic analysis of buckling data on single DNA molecules with n = 0, 1, 2, or 4 mismatches. a. Mean lifetimes τ_u and τ_b in the unbuckled and buckled states as a function of torsion Lk. Error bars reflect the binomial sampling error in the unbuckled or buckled state lifetime at each point. Mean lifetimes are equal at the buckling transition midpoint Lk^† and insensitive to the number of mismatches. b. Magnitude of kinetic torque changes to the transition state (s) from the unbuckled state (u), $\Delta {\Gamma }_{u-s}=-\frac{k_{B}T}{2\pi }\frac{\partial \text{ln}{\tau }_u}{\partial \text{Lk}}$ (green), and from the buckled state (b), $\Delta {\Gamma }_{s-b}=\frac{k_{B}T}{2\pi }\frac{\partial \text{ln}{\tau }_b}{\partial \text{Lk}}$ (blue). Error bars reflect the standard error of weighted fits to the slopes in part a. The dashed lines indicate mean values at 1.1 ± 0.1 and 1.4 ± 0.1 pN·nm. Note ΔΓ_u−s+ΔΓ_s−b = ΔΓ_u−b (see Fig. 2).

The upper panel in Figure 4 provides a schematic plot of free energy as a function of a reaction coordinate corresponding to decreasing torque. The free energy landscape changes with Lk; this schematic represents the landscape near Lk = Lk^†, where the mean lifetime in the unbuckled state equals the mean lifetime in the buckled state. There is a free energy minimum in the unbuckled state (u), a maximum at a transition state (s), and another minimum in the buckled state (b). The distance between the minimum at u and the transition state is the torque drop on going from unbuckled to the transition state, ΔΓ_u−s, measured from the slope vs Lk of mean lifetime in the unbuckled state (Fig. 3). The distance between the maximum at s and the minimum at b is the torque drop ΔΓ_s−b going from the transition state to the buckled state, measured from the slope vs Lk of mean lifetime in the buckled state. These distances are not equal; the buckled well is broader than the unbuckled well and may include substates (discussed below). From a Kramers model, the rate of going over the barrier from u to b is proportional to the curvature of the well at u times $e^{\Delta G_{s-u}/k_{B}T}$, and analogously for the rate of going from b to u. Since the curvature is inversely related to the width of the well, the barrier height ΔG_s−u must be larger than ΔG_s−b in order for the kinetic rates, and therefore the mean lifetimes, to be equal. The mean lifetimes in the unbuckled state τ_u for each DNA at the link where τ_u = τ_b are plotted in red in Fig. 4b. The mean lifetimes are similar to those obtained in other reports of torsional DNA buckling.^15–17

Figure 4:

Kinetics at the buckling transition midpoint. a. Schematic free-energy profile with decreasing torque as a reaction coordinate. The barrier height ΔG_s−u is the increase in energy from the unbuckled state (u) to the transition state (s) and the ‘distance’ to the barrier is the torque decrease ΔΓ_u−s. We hypothesize that, in further detail, the buckled state may involve substates at distinct torque values for a curl or small plectoneme but in Fig. 3b we measure the change ΔΓ_s−b to a hybrid buckled state (see Fig. 9). b. Equilibrium lifetime vs n mismatches. The experimental points correspond to τ_u = τ_b (open red circles); error bars reflect binomial sampling error in time in the unbuckled state. The theoretical points (blue filled circles) are from Kramers’ formula, with error bars reflecting exponential dependence on E_bt as discussed in text.

We were initially surprised to find that the lifetimes in buckled and unbuckled states were only moderately affected by the presence of base-pair mismatches of increasing size, since defects are expected to change the elastic energy of highly bent states under tension. To understand this observation, we turn to the classical elastic theory of inextensible, cylindrically symmetric rods under tension as a model for DNA.^18–23 This theory predicts that the “saddle point” transition state on the path to buckling is a configuration with a spatially localized region of writhing designated a “soliton.”^18,19 Following Daniels and Sethna,¹⁸ the elastic energy difference between the transition state and the straight, twisted rod just before buckling can be expressed in terms of twist persistence length (C), bend persistence length (A), rod length (L), force (f), and torque (Γ_s) in the soliton:

$$\Delta E_{barrier}=\Delta E_{s-u}=\frac{8k_{B}TA}{l}\text{tanh}\left(\frac{L}{2l}\right)-2\pi {\text{Wr}}_s\left({\Gamma }_s+\frac{\pi k_{B}TC{\text{Wr}}_s}{L}\right)$$ (1)

Here l = (a⁻² – b⁻²)^−1/2 is a characteristic length of the soliton defined in terms of other lengths, $a=\sqrt{k_{B}TA/f}$ and $b=\frac{2k_{B}TA}{{\Gamma }_s}$, and Wr_s is the writhe of the soliton. The first term on the right-hand side of eq. (1) is E_bt, the sum of bending energy and translation work done against the applied force. This can be calculated from the spatial curve of the soliton. For our force and DNA length, l ≈ a ≈ 7 nm << L so $\text{tanh}\left(\frac{L}{2l}\right)\approx 1$ and the first term simplifies to 8k_BTA/l. The second term on the right-hand side is the reduction of torsional energy due to writhe. The writhe of the soliton can be written in terms of Γ_s as ${\text{Wr}}_s=\frac{2}{\pi }\text{arctan}\left[\frac{b}{l\left({\Gamma }_s\right)}\text{tanh}\frac{L}{2l\left({\Gamma }_s\right)}\right]$;¹⁸ this allows the energy barrier to be plotted as a function of Γ_s for a given force and rod length (Fig. 5).

Figure 5:

Barrier height vs transition state torque. The solid curve is the energetic barrier predicted by eq. (1)¹⁸ in the absence of entropy or defects. The dotted curve corrects for entropy using a previous estimate: S/k_B ≈ 5.8 for 740 nm DNA.¹⁸ Assuming entropy scales as the logarithm of DNA length,⁷ this gives S/k_B ≈ 5.8 + ln 2000/740 ≈ 6.8 for our L ≈ 2000 nm DNA. The colored points take ${\text{Lk}}_n^{†}=25.4-0.17n^2$ as the link at buckling for DNA with n mismatches⁸ to estimate torque in the unbuckled state as 2πk_BTC_effLk^†/L; the torque in the transition state is less by amount ΔΓ_u−s (see Fig. 3). Defects eliminate entropy, but rescale bending energy by a factor (1 – ϵ), where ϵ = 0.05 + 0.05n for n = 1,2, or 4 mismatches.⁷ This results in similar barrier heights with or without mismatches. The inset compares free energy barriers for DNAs with defects calculated as above (blue circles), or estimated from the unbuckled lifetimes using Kramers’ theory and γ determined at n = 0, as described in the text (red circles). There are no other adjustable parameters. The reduced χ² = 0.34 over the three mismatched DNAs.

To take temperature into account, we: (i) replace the twist modulus C in eq. (1) with the force-dependent C_eff softened by thermal fluctuations,^{24$C_{\text{eff}}=C\left(1-C/\left(4A\sqrt{AF/\left(k_{B}T\right)}\right)\right)$}, and (ii) add an entropic contribution to convert elastic energy to free energy. The entropy change from buckling is assumed proportional to the logarithm of the DNA length;²³ this allows us to convert the entropy calculated for a 740 nm DNA¹⁸ to the entropy change predicted for our 2000 nm DNA. Fig. 5 shows the barrier height as a function of transition state torque before (solid line) and after (dotted line) taking entropy into account; in Fig. 5 we used k_BT = 4.1 pN·nm, A = 50 nm, C = 95 nm, f = 3.6 pN, and L = 2000 nm.

To estimate the energy barrier for buckling for DNA with no base-pair defects we need to know the torque in the soliton. This is estimated from the torque $\frac{C_{\text{eff}}{k}_{B}T}{L}2\pi {\text{Lk}}_0^{†}$ in the unbuckled state at ${\text{Lk}}_0^{†}=25.4$, less the drop in torque on formation of the soliton, which is 1.2 pN·nm from Figure 3. This gives a transition state torque of 27.7 pN·nm. We estimate uncertainty in torque to be 10% due to uncertainties in C and the value of the link at buckling. Knowing the torque in the soliton, we can calculate the lengths b and l and the bend-plus-translation energy of the soliton: this gives: b = 14.8 ± 1.5 nm, l = 8.8 ± 0.3 nm, and E_bt = 45.5 ± 2.7 k_BT, where uncertainties were estimated from propagation of the error in torque. We estimate the barrier height ΔG_s−u as ΔE_s−u (eq. (1)) less the contribution from entropy. This free-energy barrier is plotted in Fig. 5.

To plot the barrier height ΔG_s−u for DNA with n base-pair mismatches we make three changes. First, since DNA with base-pair mismatches buckles at slightly lower link, we evaluate E_ht at the modified transition state torque Γ_s(n) equal to $\frac{C_{\text{eff}}{k}_{B}T}{L}2\pi {\text{Lk}}_{\text{n}}^{†}$, with ${\text{Lk}}_n^{†}={\text{Lk}}_0^{†}-0.17n^2$ (see above), less the measured drop in torque on going to the transition state shown in Figure 3. Second, we multiply E_bt by a factor 0.95 − 0.05n, since this scaling has been used to model the effect of base-pair mismatches on bending energy of end loops,⁷ and energy minimization leads to bend and translation energies being equal. Third, we do not subtract a correction for entropy because the DNAs with base-pair mismatches buckled only at the defect site. The resulting free-energy barriers ΔG_s−u for DNA with 1, 2 or 4 base mismatches are marked with green, blue and magenta symbols in Figure 5. The barrier heights decrease monotonically with number of base-pair mismatches from n = 1 to n = 4 due to the scaling of E_bt by 0.95 − 0.05n. The reduction in barrier height from changes in bend-translation and twist energies for DNAs with base-pairing defects roughly equals the reduction in barrier height due to entropy for non-defect DNA.

From the barrier height and torque drop one can estimate the “size” of the transition state. We assume for simplicity that the energy landscape consists of upward and downward facing parabolas between the unbuckled and transition states, both with curvature k, with the transition state a distance ΔΓ_u−s from the unbuckled state (Fig. 4). Since the energy at the joining point of the parabolas is $(1/2)k{\left(\Delta {\Gamma }_{u-s}/2\right)}^2=\Delta G_{s-u}/2$, $k=4\Delta G_{s-u}/\Delta {\Gamma }_{u-s}^2$ From Kramers’ theory, the unbuckled lifetime equals $\frac{\gamma }{k}{e}^{\frac{\Delta G_{s-u}}{k_{B}T}}$, where γ is a proportionality factor related to viscous drag. From $\gamma =k{\tau }_u{e}^{-\frac{\Delta G_{s-u}}{k_{B}T}}$, we find γ ~ 10⁻⁴ s/(pN·nm). The uncertainty in γ is dominated by the uncertainty of ±2.7 k_BT in the exponent (see above). This gives a range for γ approximately 15 times larger or smaller. Despite the large range, the magnitude of γ implies a small size for the transition state. To see this, note that γ is a drag coefficient for a reaction coordinate with units of torque. From the Kramers formula, its units are energy · sec/torque². This can be converted to energy · sec/angle², a more conventional drag coefficient for a rotating body, by multiplying by (C/L)². The drag coefficient for a rotating sphere of radius r is 8πηr³, where η is the viscosity of water. This allows one to solve for the radius of a sphere with the same rotational drag as implied by Kramers’ theory for the transition state DNA, placing r in the range of 2 to 12 nm, which is roughly the characteristic size, l = 8.8 ± 0.3 nm, of the transition state soliton.

If we assume the drag factor is unaffected by base-pair mismatches, we can use ${\tau }_u=\frac{\gamma }{k}{e}^{\frac{\Delta G_{s-u}}{k_{B}T}}$ with $k=4\Delta G_{s-u}/\Delta {\Gamma }_{u-s}^2$ to calculate theoretical unbuckled lifetimes for DNAs with defects; these theoretical lifetimes are plotted as blue circles in Figure 4. The decrease in theoretical lifetime with n is mainly due to the scaling of E_bt noted above. However, the uncertainty in theoretical lifetime is large due to the exponential dependence on E_bt. In a similar fashion we calculate a theoretical free energy barrier corresponding to the observed unbuckled lifetimes by solving ${\tau }_u=\frac{\gamma }{k}{e}^{\frac{\Delta G_{s-u}}{k_{B}T}}$ with $k=4\Delta G_{s-u}/\Delta {\Gamma }_{u-s}^2$ for ΔG_s−u. This yields the theoretical free energy barriers plotted in the inset in Fig. 5. Here the uncertainty, estimated as ±2.7 k_BT, is smaller on a relative basis than for τ because it describes uncertainty in an exponent rather than an exponential. We note that these theoretical free energy barriers for DNAs with basepair defects do not depend on assumptions about how bend energy and critical link vary with defect size, yet they are in rough agreement with the estimates using these assumptions and eq. (1).

Eq. (1) for the elastic energy difference between the soliton and the twisted DNA before buckling also sheds light on a recent surprising observation that the equilibrium buckling time for double-stranded RNA is about 100 times larger than for double-stranded DNA, despite only a modest (~20%) increase in its bend persistence length A and no significant difference in its twist persistence length C.¹⁷ The energetic barrier height ΔE_s−u is the difference of two terms, both considerably larger than their difference. For example, for double-stranded DNA under our experimental conditions, the first energy term is ≈ 46 k_BT and the second energy term is ≈ 28 k_BT. The first term is proportional to A/l, and l is roughly proportional to A^0.5, so the first term is about 10% larger for RNA compared to DNA. The second term involves C but not A, so it should be about the same for DNA and RNA. Then ΔE_s−u for our experimental conditions would be about 4.6 k_BT larger for RNA versus DNA. Since τ_u ∝ e^ΔE_s−u, eq. (1) predicts τ_u for RNA should be ~100 times larger than for DNA.

Eq. (1) is derived from a more extensive theory of torsional buckling of elastic rods that predicts configurations besides the soliton that may arise in the course of buckling.^22,23 The theory enables calculation of the energy and extension under force of these structures as a function of link (see below). We observed what may be a post-buckling intermediate structure that is more stable in DNAs with localized defects consisting of a few mispaired bases.

Figure 6, which plots DNA extension versus link for each DNA in the region of buckling, shows that for larger defects (n = 2 and 4 base mismatches) a distinct state with intermediate extension appears at intermediate linking number. We label this state a “curl” because it may correspond to the prediction of a metastable looped structure with that name.²³

Figure 6:

Extension versus change in linking number around the buckling transition for DNA with n = 0, 1, 2, and 4 base mismatches. Each dot reflects data collected over 5 ms. A 1000-point time series was recorded at 200 Hz at each value of Lk, which was increased in increments of 0.1. Neighboring data points were then plotted with a separation of 10⁻⁴ in Lk for visualization. The decrease in extension from the unbuckled state to the curl at the buckling transition midpoint, Lk^†, is well-described by the approximate theoretical formula,²³ $8\sqrt{k_{B}TA/f}$ (≈ 60 nm)for n = 0 mismatches. Note Lk^† shifts leftward according to ${\text{Lk}}_n^{†}-{\text{Lk}}^{*}\approx 3.7-0.17n^2$ for n = 0 to 4 mismatches, indicating a decrease in torque at buckling.⁸ As expected for a kinked curl (arrows), we observe the extension decrease is smaller for mismatches, quantitatively consistent with $(1-ϵ)8\sqrt{k_{B}TA/f}$ using the same ϵ(n) values as in Fig. 5. For n = 1, the buckled state has only some curl character, whereas for n = 4 it is entirely curl.

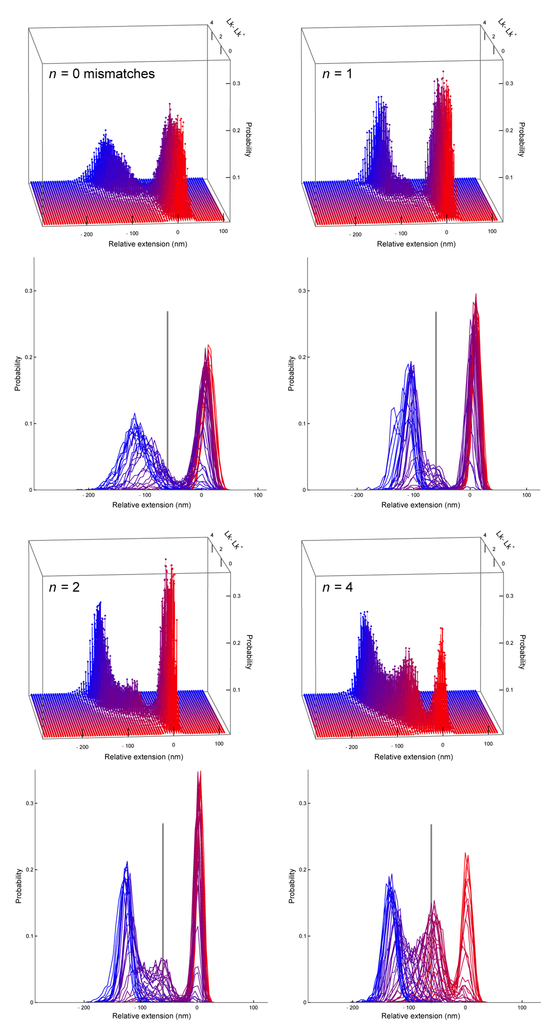
Figure 7 shows in 3-D the probability of a given extension as a function of link, with extension of the unbuckled state set to 0 nm and increasing link color-coded from red to blue. The curl state (appearing at intermediate links, color-coded purple) is barely discernible at n = 1 but increasingly distinct for n = 2 and n = 4. Color-coded slices of the 3-D plots are shown in 2-D as overlaid histograms below each 3-D plot. The extension of the curl state is roughly that predicted by a planar loop model that minimizes bend plus translation energy (black vertical lines in lower panels of Figure 7).^7,23 Figure 8 shows histograms for the average of five slices centered on Lk^† with error bars corresponding to the standard error of the mean of histogram heights for the five slices.

Figure 7:

Probability versus change in extension and change in linking number around the buckling transition for DNA with n = 0,1,2, and 4 base mismatches. The series of colors in the upper 3-D plots correspond to incremental changes of 0.1 in Lk and are matched to the same colors in the corresponding lower 2-D plots. The vertical line in each 2-D plot indicates the position of the curl predicted by theory (see Fig. 8).

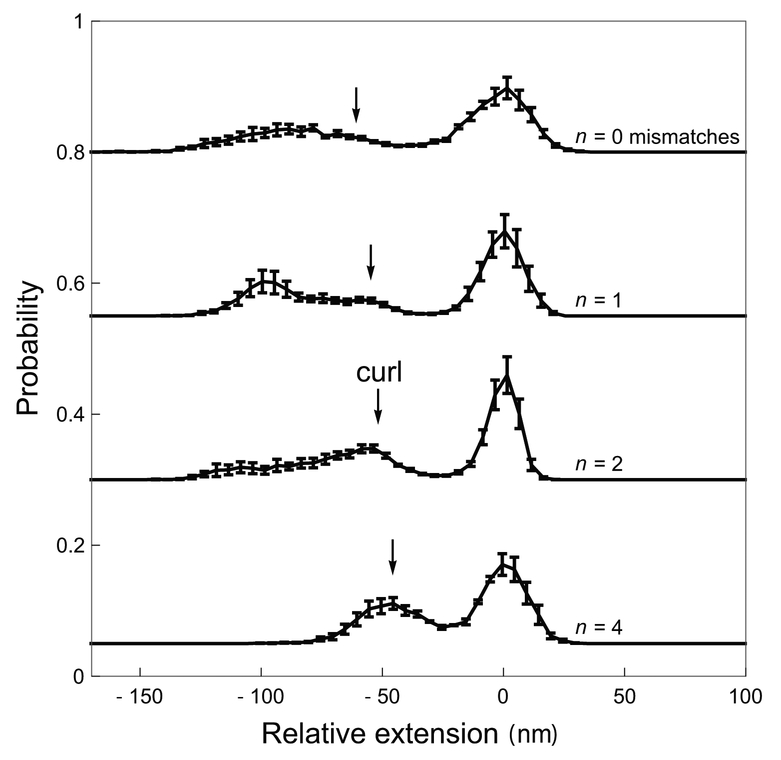
Figure 8:

Extension probabilities for DNA with n = 0, 1, 2, or 4 mismatches showing the development of the curl state at intermediate extension values during buckling as n increases. Error bars indicate the standard error of the mean over five time-series traces recorded near Lk^†. Arrows indicate the expected position of the curl based on the approximate theoretical formula,²³ $8\sqrt{k_{B}TA/f}$ (≈ 60 nm) for n = 0 mismatches, or $(1-ϵ)8\sqrt{k_{B}TA/f}$ for n = 1,2, or 4 using the same ϵ(n) values as in Fig. 5.

Figure 9 provides more detail concerning intermediate structures predicted to occur during the buckling of classical rods. Panel a, which is reproduced with permission from Marko and Neukirch,²³ shows extension as a function of link (upper panel) for three predicted stable configurations (solid lines) and two unstable configurations (dotted lines). The stable configuration (green line) with intermediate extension corresponds to the curl. The saddle-like, unstable state (red dotted line) between the straight, twisted rod (black horizontal line) and the curl is the soliton. The descending solid line is the plectoneme. The lower panel shows the energy of these configurations as a function of link. The energy of the straight-twisted rod rises quadratically with link; the energy of the buckled rod rises linearly with link. The point at which these curves intersect identifies the critical link; at this link, the three stable configurations, and two unstable transition configurations connecting them, all co-exist. Panel b plots the energy versus extension of these configurations at the critical link, with schematics illustrating DNA configurations. The line connecting the points is a guide for the eye. Since the energy barrier between the curl and the fully buckled configuration is small, the curl is unlikely to be detected as a distinct state for a defect-free DNA molecule. However, consistent with our data, this theoretical picture predicts that defects facilitate detection of the curl state by lowering its energy relative to that of fully buckled DNA in a range of linking number slightly below the critical link for buckling of non-defect DNA.

Figure 9:

Theoretical pathway of torsional DNA buckling.^20,22,23 a. Calculated extension and energy vs torsion curves. Buckling occurs at torsion Lk^† (gray vertical line) where energy curves corresponding to unbuckled DNA (lower quadratic curve) and a small plectoneme (linear curve) have the same energy at a crossing point (arrow in inset). DNA extension decreases upon buckling at Lk^†. Starting from the unbuckled state (black) at large extension, the barrier to buckling (red) is a high energy soliton. The buckled state is expected to include both curl (green) and plectoneme (black) structures coexisting at similar energy and separated by a small barrier (blue). b. Schematic buckling pathway derived from the relative extension and energy values in panel a. The unbuckled structure (black point, left) is a straight-twisted rod. The transition state (red point) is a soliton. The buckled state is expected to include a metastable curl (green point) and small plectoneme (black point, right). These structures may be in rapid coexistence because the intervening energy barrier (blue point) associated with initial plectoneme wrapping is low. In the case of defects, the buckled state may take on more curl character because buckling occurs at lower torsion.

Defects lower the energy of highly curved states, but presumably have negligible effect on the energy of the straight, twisted rod. In Figure 9, lowering the buckled state energy line moves the point of intersection with the unbuckled state energy to the left, consistent with our observation that DNA with a defect buckles at a lower link. If the energy of the stable curl intermediate is similarly reduced (as expected), its point of intersection with the unbuckled curve also moves to the left; since the slope of the curl energy is closer to that of fully buckled DNA, its intersection point should move further to the left, raising the possibility that for larger defects, curls and unbuckled DNA might coexist at links lower than required for full buckling. Note that in Figure 9a curls exist at links lower than required for full buckling of DNA.

The schematic of states shown in Figure 9 does not take temperature into account. Presumably, temperature extends the range of link over which curls and fully buckled DNA can exist, although their energies for given linking numbers may be such that their states are infrequently occupied.

The nature of the barrier between the curl and the plectoneme has yet to be elucidated. Note that conversion of a roughly planar curl to a plectoneme involves major reorientation of DNA exiting the curl from roughly vertical in the plane projection shown in Figure 9b to roughly horizontal. We hypothesize that this reorientation increases bending and translation energy more than it reduces twist energy (through increase in writhe), leading to an energy barrier.

We note that the formula for soliton writhe as a function of Γ_s, ${\text{Wr}}_s=\frac{2}{\pi }\text{arctan}\left[\frac{b}{l\left({\Gamma }_s\right)}\text{tanh}\frac{L}{2l\left({\Gamma }_s\right)}\right]$, predicts Wr ≈ 0.7 for Γ_s = 27.7 pN·nm; this is about 60% of the writhe estimated from $\text{Wr}=\Delta {\Gamma }_{u-s}/\frac{2\pi C_{\text{eff}}{k}_{B}T}{L}$ using our empirically measured values of ΔΓ_u−s. This discrepancy is outside of measurement error, and we note that our empirical estimates are comparable to those measured by others.^15,16 The fact that empirical writhe is larger than predicted by elastic rod theory is likely due to thermal effects altering the spatial curve of the DNA. Thermal fluctuations also increase the bend-translation energy compared to the value calculated from the first term in eq. (1). Further work is required to derive a version of eq. (1) that takes thermal effects into account beyond replacing C with C_eff.

Conclusion

We have shown that DNA with base-pair defects buckles at rates comparable to defect-free DNA. To a large extent this can be explained by compensating effects of a reduction in elastic energy required to buckle DNA with a defect (manifest by its buckling at lower torsion) and a decrease in entropy due to buckling localizing to a single site - the site of the defect. This phenomenon may facilitate mutation detection and repair in vivo. More detailed comparison with elastic rod theory shows that defects enable detection of a predicted but previously undetected intermediate curl state.