Abstract
Dynamic nuclear polarization (DNP) can increase nuclear magnetic resonance (NMR) signal strengths by factors of 100 or more at low temperatures. In magnetic resonance imaging (MRI), signal enhancements from DNP potentially lead to enhancements in image resolution. However, the paramagnetic dopants required for DNP also reduce nuclear spin relaxation times, producing signal losses that may cancel the signal enhancements from DNP. Here we investigate the dependence of 1H NMR relaxation times, including T1ρ and T2 under conditions of Lee-Goldburg 1H-H decoupling and pulsed spin locking, on temperature and dopant concentration in frozen solutions that contain the trinitroxide compound DOTOPA. We find that relaxation times become longer at temperatures below 10 K, where DOTOPA electron spins become strongly polarized at equilibrium in a 9.39 T magnetic field. We show that the dependences of relaxation times on temperature and DOTOPA concentration can be reproduced qualitatively (although not quantitatively) by detailed simulations of magnetic field fluctuations due to flip-flop transitions in a system of dipole-coupled electron spin magnetic moments. These results have implications for ongoing attempts to reach submicron resolution in inductively-detected MRI at very low temperatures.
Graphical Abstract
Introduction
Dynamic nuclear polarization (DNP) is a magnetic resonance phenomenon in which excitation of electron spin-flip transitions by microwave radiation leads to enhanced nuclear spin polarizations in a magnetic field. The larger nuclear spin polarizations result in larger nuclear magnetic resonance (NMR) signals, potentially overcoming NMR sensitivity limitations in various circumstances. First predicted by Overhauser1 and demonstrated by Carver and Slichter in alkali metals and liquid ammonia,2 DNP was subsequently extended to a large variety of liquids3–8 and solids.9–16 Recent interest in DNP has been stimulated by the development of the dissolution DNP method for NMR sensitivity enhancement in solution NMR and in vivo NMR by Ardenkjaer-Larsen et al.,17–18 and by the demonstration of large DNP effects at high magnetic fields in frozen solutions of organic and biological molecules by Griffin and colleagues.19–21
Recent applications of DNP have focused on NMR spectroscopy, where NMR signals carry information about molecular and/or chemical structure, dynamics, or other properties, and where DNP allows NMR measurements on smaller sample quantities in shorter times.22–27 As an additional application of DNP, our laboratory is pursuing the use of DNP in magnetic resonance imaging (MRI). Here, DNP can potentially enhance the spatial resolution of MRI, since spatial resolution in MRI is ultimately limited primarily by signal-to-noise. As shown in experiments by Ciobanu et al.28–29 and Weiger et al.,30 inductively-detected 1H MRI of sub-microliter samples near 300 K is limited to isotropic spatial resolution of approximately 3 μm, corresponding to the observation of NMR signals from the 1.8 × 1012 1H nuclei in a 27 μm3 = 27 femtoliter volume element of water. Preliminary experiments in our laboratory31 suggested that isotropic spatial resolution better than 1 μm in 1H MRI may be achievable with low-temperature DNP, where nuclear spin polarizations and NMR signals can be enhanced by factors of 103−104 relative to thermal equilibrium polarizations and signals at 300 K.
Subsequently, we have demonstrated that 1H MRI images with 2.8 μm isotropic resolution can be obtained at temperatures below 30 K without DNP,32 using a radio-frequency (RF) microcoil for excitation and detection of NMR signals, Lee-Goldburg (LG) irradiation33 to attenuate 1H-1H magnetic dipole-dipole couplings during MRI phase encoding, pulsed spin-locking (PSL) to enhance NMR signal detection sensitivity,34–35 and a compact system of magnetic field gradient coils capable of generating gradients in excess of 400 Hz/μm with 20 A gradient current pulses.32,36 In our low-temperature MRI experiments without DNP, we have also used Dy3+ doping to reduce the 1H spin-lattice relaxation time (T1H) of glass-forming glycerol/water mixtures to 0.4 s at 28 K, thereby increasing the rate at which MRI data can be acquired. In experiments at 9.39 T external magnetic field strength (399.2 MHz 1H NMR frequency), an MRI image with a 218 μm × 95 μm × 95 μm field-of-view, 2.8 μm isotropic resolution, and a signal-to-noise ratio of 11 ± 1 was acquired in 208 h.32
All other things being equal, a 100-fold enhancement of NMR signals from DNP (relative to thermal equilibrium signals at 28 K) would be expected to improve the achievable spatial resolution by a factor of (100)1/3 = 4.64. Thus, sub-micron MRI resolution appears to be within reach. Alternatively, an image with 1.0 μm resolution could be obtained in 10 h.
However, all other things are not equal. In particular, paramagnetic dopants for DNP are typically nitroxide-based compounds,37–39 or similar compounds,40–42 which have relatively long electron spin-lattice relaxation times (T1e) compared with Dy3+ and therefore do not produce short T1H values. DNP dopant concentrations must be relatively high (>10 mM electron spin concentrations) to produce large DNP effects. Under these conditions, build-up times for DNP-enhanced nuclear spin polarizations typically exceed 10 s below 30 K.43–45 Moreover, 1H NMR dephasing times during Lee-Goldburg irradiation periods (T2LG) and PSL signal detection periods (T2PSL) are significantly reduced by fluctuating dipolar hyperfine couplings to the DNP dopants, leading to reductions in total NMR signals. These effects on nuclear spin relaxation properties can cancel the NMR signal enhancement produced by DNP, thus preventing improvements in MRI resolution.
Motivated by the considerations described above, we have performed a systematic study of the effects of DNP dopants on various nuclear spin relaxation times, including measurements of the dependences of relaxation times on temperature and dopant concentration. Experimental results are reported below. Importantly, we find that deleterious effects on T2LG and T2PSL from DNP dopants become smaller at temperatures below 10 K, where the thermal energy kBT becomes less than the electron spin-flip energy in a 9.39 T field (where kB is the Boltzmann constant and T is the sample temperature). After presenting the experimental results, we describe a computational model for the temperature- and concentration-dependent nuclear spin relaxation times, in which nuclear spin relaxation is driven by fluctuating local magnetic fields produced by flip-flop transitions among dipole-coupled electron spins. We demonstrate qualitative agreement between experimental and calculated nuclear spin relaxation times, using realistic parameters in numerical calculations based on this model.
Experimental Methods
NMR equipment
1H NMR experiments were performed with a 9.39 T, 89 mm bore magnet and a Tecmag Redstone spectrometer. A variable-temperature NMR probe, based on a Janis Supertran ST-200 continuous flow cryostat (Janis Research LLC), was used as described previously,32 with several modifications. Specifically, to ensure low sample temperatures, the half-wavelength copper coaxial cable between the RF microcoil and the tuning and matching capacitors was replaced with a cryogenic coaxial cable (silver-coated beryllium-copper inner conductor and stainless steel outer conductor) in order to reduce the heat load on the cryostat’s cold finger. In addition, the magnetic field gradient coils were removed, and the sample capillary was moved closer to the cold finger by 2 cm. Each end of the sample capillary (166 μm outer diameter, 100 μm inner diameter) was connected to an adapter (MicroTight P881, IDEX Health & Science, Oak Harbor, WA), allowing us to change samples without making a new RF microcoil (400 μm length, 7.5 turns, wound around and fixed to the capillary with cyanoacrylate glue). The temperature of the cryostat’s cold finger was monitored by a thin film resistance sensor (Cernox CX-1050, Lake Shore Cryotronics, Westerville OH) and was controlled by adjusting the flow of liquid helium and by a temperature controller (CTC 100, Stanford Research System, Sunnyvale CA) that supplied current to the heater in the cryostat. For measurements at 3.3 K, the exhaust outlet of cryostat was connected to the house vacuum. Sample temperatures were confirmed by checking that the 1H NMR spin echo signal amplitude was proportional to the inverse of the set temperature (see Fig. S1 of Supporting Information).
Pulse sequences for relaxation measurements
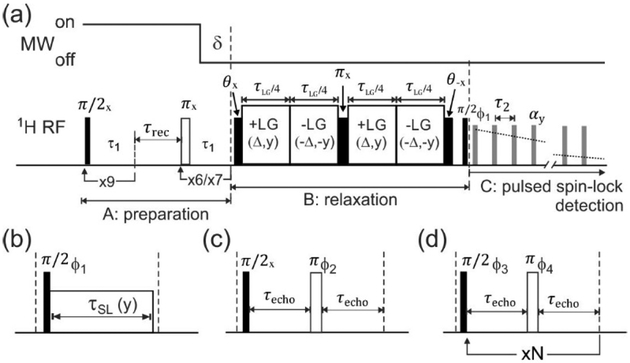
Fig. 1a shows the pulse sequence used to measure values of T2LG, the 1H NMR signal decay time during the Lee-Goldburg irradiation period (block B in Fig. 1a). This pulse sequence is based on the sequence used for solid state MRI,32,36 but does not include magnetic field gradient pulses. In the preparation period (block A), a train of nine π/2 pulses separated by 1.0 τs n periods was used to destroy any pre-existing 1H spin polarization, followed by a period τrec for development of longitudinal 1H spin polarization by recovery toward thermal equilibrium (without microwave irradiation) or toward hyperpolarization induced by DNP (with microwave irradiation). Background signals from outside the RF microcoil were suppressed by application of either six or seven t π pulses (on alternating scans). Signals were measured as a function of the Lee-Goldburg period τLG in block B, which was divided into four periods with alternating phases (±y) and RF frequency offsets (±Δ/2π = ±160 kHz). The RF field amplitude ω1/2π = 226 kHz was adjusted to produce the Lee-Goldburg effective field ωLGl2π = 277 kHz, tilted at the magic angle from z in the rotating frame. Pulses with flip angles θ = θm + π/2 rotated the 1H spin polarization from z to an initial direction perpendicular to the Lee-Goldburg effective field and then back to z. A π pulse in the middle of the πLG period refocused signal dephasing due to static field inhomogeneity. 1H NMR signals were detected in intervals between αy pulses in the pulsed spin-locking period (block C).
Figure 1:
Pulse sequences for measurements of nuclear spin relaxation times. (a) Complete pulse sequence for measurements of T2LG, the 1H NMR dephasing time under Lee-Goldburg irradiation. (b,c,d) Pulse sequence elements for measurements of the 1H T1ρ, Hahn spin echo T2, and Carr-Purcell T2, respectively. These elements substitute for block B in panel a. Definitions of symbols and additional details are given in the main text.
For measurements of T1ρ values, the pulse sequence element in Fig. 1b was substituted in block B of Fig. 1a. 1H NMR signals were measured as a function of the continuous-wave (CW) spin-lock period τSL, during which an on-resonance RF field with phase y and amplitude ω1/2π was applied.
For measurements of Hahn echo T2 values, the pulse sequence element in Fig. 1c was substituted in block B of Fig. 1a. Signals were measured as a function of the variable delay τecho between the π/2 and π pulses. For measurements of Carr-Purcell T2 values, the pulse sequence element in Fig. 1d was substituted in block B of Fig. 1a. Signals were measured as a function of N, the number of π pulses in the Carr-Purcell echo train, with τecho = 30 μs. Phases of these π pulses followed the XY8 pattern ϕ4 = x, y, x, y, y, x, y, x.46
Signal artifacts were minimized by phase cycling, with ϕ1 = x, x, −x, −x in Figs. 1a and 1b, ϕ2 = x, −x, y, −y in Fig. 1c, and ϕ3 = y, y, −y, −y in Fig. 1d. The receiver phase followed the cycle ϕrec = +, −, −, +. In all experiments, the value of τrec was chosen to make the signal-to-noise ratio greater than 30 for the first point in each experimental decay curve.
Signal decay times under pulsed spin-locking (T2PSL) were measured by substituting a single π/2 pulse with phase ϕ1 in block B of Fig. 1a. 1H NMR spectra were obtained from free-induction decays after Hahn spin echoes, without pulsed spin-locking. In certain experiments to examine effects of microwave irradiation on nuclear spin relaxation times, microwaves were switched off at a time δ before the beginning of block B, as shown in Fig. 1a.
Microwave equipment
DNP experiments used a solid-state microwave source (Model VDI-TXS120, Virginia Diodes Inc., Charlottesville, VA) with 30 mW output power at 263.0 GHz. Linearly polarized microwaves from the source were propagated in free space via a quasi-optical microwave system (Thomas Keating Ltd, Billingshurst, UK), transmitted into the NMR magnet through a corrugated waveguide (13 mm inner diameter), passed through a Teflon window in the bottom of the cryostat can, and directed to the sample through a microwave horn and a tapered Teflon rod. To reduce the radiative heat load on the cryostat’s cold finger, the microwave horn within the cryostat was cooled by mounting it on the radiation shield that encloses the cold finger. Contact area between the horn and the Teflon window was minimized, while maintaining concentric alignment with the corrugated waveguide. A TTL signal from the NMR spectrometer, generated by the pulse program, was used to switch off the microwave output in certain experiments.
Data processing and error analysis
For all relaxation measurements, the time-domain 1H NMR signals under pulsed spin-locking were first Fourier-transformed. The zero-frequency amplitude in the Fourier transform was used as the signal intensity at corresponding time points. Subsequent data analyses were performed with Python scripts, using SciPy and NumPy libraries. Each experimental signal decay was fit with either a single-exponential decay function [I(t) = a·exp(−t / b) + c] or a stretched-exponential decay function [I(t) = a·exp[−(t / b)β] + c], providing an analytical function from which the 1/e decay time was taken to represent the nuclear spin relaxation time. In cases where the experimental signals did not decay to 1/e, 50% decay times were used instead. The lower and upper bounds of fit parameters were calculated from the covariance matrix returned from the Levenberg-Marquardt algorithm. Uncertainties in reported relaxation times (error bars in Figs. 3, 4, and 6) were calculated by varying the parameter b between its upper and lower bounds and extracting the corresponding 1/e or 50% decay times. 1H NMR linewidths (full-width-at-half-maximum, FWHM) were determined by fitting the experimental spectra with Lorentzian functions. Uncertainties in linewidths (plus and minus one standard deviation) were calculated from the covariance matrix.
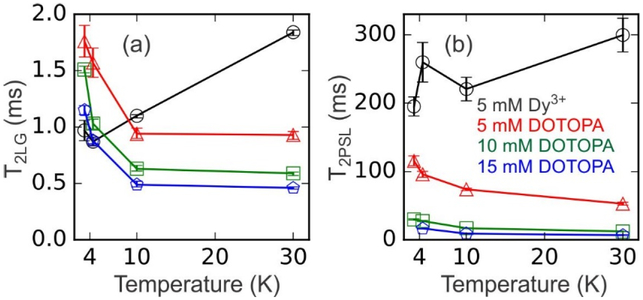
Figure 3:
Experimentally determined temperature dependences of T2LG (a) and T2PSL (b) for samples containing 5 mM Dy3+ (black circles), 5 mM DOTOPA (red triangles), 10 mM DOTOPA (green squares), and 15 mM DOTOPA (blue pentagons). Values of T2LG and T2PSL were obtained from 1H NMR signal decay curves in Figs. S3 and S4. Lines are guides to the eye.
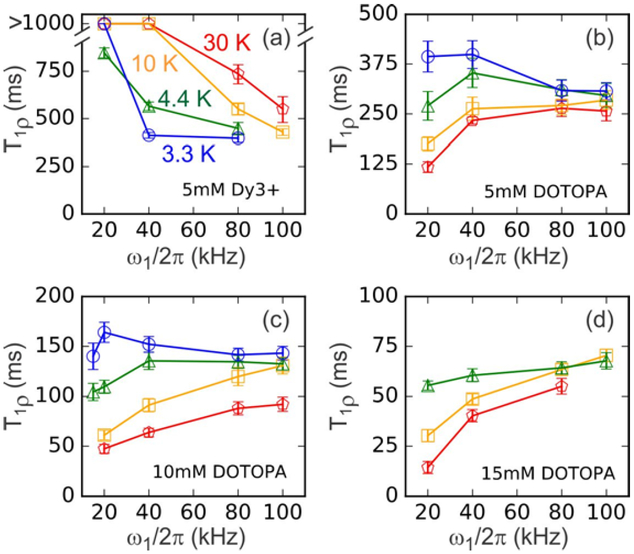
Figure 4:
Experimentally determined values of T1ρ at 30 K (red pentagons), 10 K (orange squares), 4.4 K (green triangles), and 3.3 K (blue circles) for RF spin-locking field amplitudes ω1l2π in the 10–100 kHz range. Data are shown for samples containing 5 mM Dy3+ (a), 5 mM DOTOPA (b), 10 mM DOTOPA (c), and 15 mM DOTOPA (d). Values of T1ρ were obtained from 1H NMR signal decay curves in Fig. S5–S7. Lines are guides to the eye.
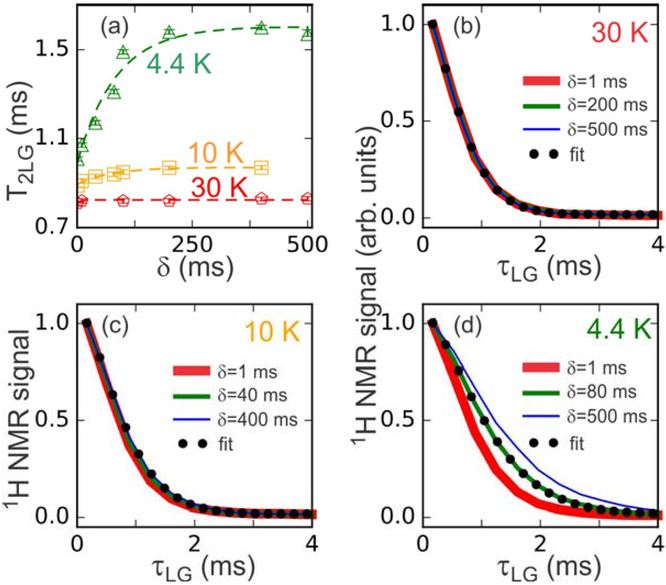
Figure 6:
(a) Dependence of the experimentally determined T2LG value on the delay δ after switching microwaves off (see Fig. 1a) for measurements at 4.4 K (green triangles), 10 K (orange squares), and 30 K (red pentagons). The sample contained 10 mM DOTOPA. Color-coded dashed lines are fits with the functional form T2LG = Ta − Tb exp(−δ / δ0), which yield δ0 = 84 ± 18 ms at 4.4 K, δ0 = 75 ± 15 ms at 10 K, and δ0 = 8 ± 10 ms at 30 K. (b,c,d) Examples of 1H NMR signal decay curves used to determine T2LG values at 30 K, 10 K, and 4.4 K, respectively. Experimental curves (thick red, green, and thin blue lines) are shown for the indicated values of 5 Fits to green lines are shown as black dots.
Samples
Each of the four samples used in experiments described below contained the same mixture of ds-glycerol, D2O (99.9%) and H2O (60:39:1 volume ratios), buffered at pH 3 using formic acid (8.2 μl/ml) and sodium formate (1.12 mg/ml). A proton density of 2.5% for this mixture (relative to a fully protonated sample) was determined by liquid state 1H NMR. A low proton density was used to reduce effects of 1H-1H dipole-dipole couplings on nuclear spin relaxation times. Samples were paramagnetically doped with DyCl3 (5 mM) or with the triradical compound 4-[N,N-di-(2-hydroxy-3-(TEMPO-4′-oxy)-propyl)]-amino-TEMPO (DOTOPA)38,43. DOTOPA concentrations were 5 mM, 10 mM, and 15 mM.
Experimental Results
1H NMR spectra and DNP enhancement
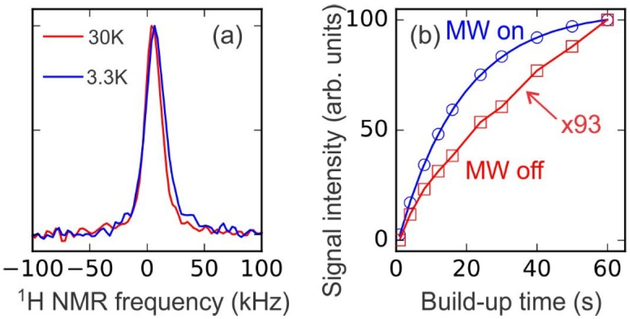
Fig. 2a shows 1H NMR spectra of the sample with 10 mM DOTOPA, obtained without microwave irradiation. Additional 1H NMR spectra are shown in Fig. S2 of Supporting Information, along with the corresponding FWHM linewidth values. Linewidths in these spectra include both inhomogeneous (anisotropic chemical shifts, inhomogeneity of the external magnetic field) and homogeneous (1H-1H dipole-dipole couplings, T2 relaxation) contributions. A small but significant increase in linewidth, from 14 kHz to 17 kHz, is observed as the temperature decreases from 30 K to 3.3 K, attributable to larger static hyperfine fields at the lower temperatures. Fig. 2b shows DNP build-up (with microwave irradiation) and T1H saturation-recovery (without microwave irradiation) curves for this sample at 4.4 K. At 60 s, the 1H NMR signal enhancement factor from DNP is 93. The DNP build-up time (TDNP) determined from a single-exponential fit to the data is 18.36 ± 0.15 s. T1H is greater than TDNP, as expected when electron spins are strongly polarized at low temperatures44–45. Earlier DNP measurements43 on non-deuterated glycerol/water solutions with DOTOPA concentrations in the 20–30 mM range, using the same microwave source, found enhancement factors that increased from 10 to 81 and TDNP values that increased from 1.4 s to 8.2 s as the temperature decreased from 80 K to 7 K.
Figure 2:
(a) 1H NMR spectra of frozen glycerol/water solution with 10 mM DOTOPA at 30 K and 3.3 K. (b) Build-up curves for 1H NMR signal intensities with and without microwave irradiation (blue circles and red squares, respectively) at 4.4 K. Signals without microwave irradiation are scaled up by a factor of 93 relative to signals with microwave irradiation. Fitting the “microwaves on” data with a single-exponential function (blue curve) yields a DNP build-up time of 18.4 ± 0.2 s.
1H T2LG under Lee-Goldburg decoupling
Fig. 3a shows the dependences of 1H T2LG values on temperature for Dy3+−doped and DOTOPA-doped samples. Data were acquired by varying the value of τLG in the pulse sequence in Fig. 1a. T2LG values were obtained by fitting the resulting signal decay curves with stretched-exponential functions (see Fig. S3 of Supporting Information). For DOTOPA-doped samples, T2LG decreases with increasing DOTOPA concentration and increases by roughly a factor of two as the sample temperature decreases from 10 K to 3.3 K.
In contrast, for the Dy3+−doped sample, T2LG decreases with decreasing temperature. This is a clear indication of the qualitative difference between paramagnetic relaxation induced by Dy3+ and paramagnetic relaxation induced by nitroxide-based DNP dopants such as DOTOPA. The larger T2LG values at higher temperatures in the Dy3+−doped sample are attributable to more rapid electron spin-flip transitions at higher temperatures (shorter T1e), which are less efficient for T2LG relaxation. In DOTOPA-doped samples, where T1e is more than 10 ms in the experimentally relevant temperature range (see below), the temperature dependence of T1e does not play a role in the temperature dependence of T2LG.
1H T2PSL under pulsed spin locking
Fig. 3b shows the dependences of 1H T2PSL values on temperature for Dy3+−doped and DOTOPA-doped samples. Data were acquired with the pulse sequence in Fig. 1a, but without the Lee-Goldburg irradiation period. T2PSL values were obtained by fitting the resulting signal decay curves with single-exponential functions (see Fig. S4 of Supporting Information). For DOTOPA-doped samples, T2PSL decreases with increasing DOTOPA concentration and increases by roughly a factor of two as the sample temperature decreases from 30 K to 3.3 K. For the Dy3+−doped sample, T2PSL increases weakly with increasing temperature. The larger values of T2PSL in theDy3+−doped sample are attributable to more rapid electron spin-flip transitions (shorter T1e), which are less efficient for T2PSL relaxation.
1H T1ρ under CW spin locking
Fig. 4 shows the dependence of the 1H T1ρ value on the CW spin-lock field strength (ω1/2π) for samples doped with Dy3+ and DOTOPA at 30 K, 10 K, 4.4 K, and 3.3 K. These data were obtained with the pulse sequence in Fig. 1b, without microwave irradiation. T1ρ values were obtained by fitting the dependences of 1H NMR signals on τSL with stretched-exponential decays. CW spin-lock decay curves for the 5 mM, 10 mM, and 15 mM DOTOPA samples are shown in Figs. S5–S7 of Supporting Information. For DOTOPA-doped samples (Figs. 4b–4d), T1ρ values increase with decreasing temperature and (in most cases) with increasing field strength. With ω1l2π = 20 kHz, T1ρ at 3.3 K is roughly three times greater than at 30 K. T=1ρ also decreases with increasing DOTOPA concentration, being roughly four times greater at [DOTOPA] = 5 mM than at [DOTOPA] = 15 mM.
For the Dy3+−doped sample (Fig. 4a), T1ρ generally increases with increasing temperature, opposite to the behavior of DOTOPA-doped samples. As with the T2LG results discussed above, this difference in temperature-dependence of T1ρ reflects the qualitative difference between paramagnetic relaxation in Dy3+−doped and DOTOPA-doped samples. The larger T1ρ values at higher temperatures in the Dy3+−doped sample are attributable to more rapid electron spin-flip transitions, which are less efficient for T1ρ relaxation.
In addition, for the Dy3+−doped sample, T1ρ decreases with increasing ω1. This is a surprising observation, since one generally expects T1ρ to increase with increasing ω1 [see Eqs. (1) and (3) below]. The reduction in T1ρ from >1 s at ω1/2π ≤ 40 kHz to 550 ms at ω1/2π = 100 kHz may be due to phase noise in the spin-locking field (i.e., small-amplitude fluctuations of the spin-lock field direction in the NMR rotating frame). A decay rate 1/T1ρ ≈ 1.8 s−1 due to phase noise at ω1 / 2π = 100 kHz would explain the data for the Dy3+−doped sample, but would make a minor contribution to data for the DOTOPA-doped samples, for which 1/T1ρ > 3 s−1 due to paramagnetic relaxation. However, phase noise would not explain the reductions in T1ρ with increasing ω1 for the Dy3+−doped sample at temperatures below 30 K. We do not have a comprehensive explanation for the dependences on ω1 in Fig. 4a.
1H T2 in Hahn and Carr-Purcell spin echoes
1H T2 values from Hahn spin echo measurements, obtained with the pulse sequence in Fig. 1c, are roughly 270 μs, 220 μs, 135 μs, and 140 μs for the 5 mM Dy3+, 5 mM DOTOPA, 10 mM DOTOPA, and 15 mM DOTOPA samples, respectively (see Fig. S8 of Supporting Information). T2 values increase somewhat at the lowest temperatures in the 10 mM and 15 mM DOTOPA samples.
1H T2 values from Carr-Purcell echo train measurements, obtained with the pulse sequence in Fig. 1d and with τecho = 30 μs, are roughly 235 μs, 190 μs, 135 μs, and 160 μs for the 5 mM Dy3+, 5 mM DOTOPA, 10 mM DOTOPA, and 15 mM DOTOPA samples, respectively (see Fig. S9 of Supporting Information). Only the 15 mM DOTOPA sample shows a small dependence of T2 on temperature.
We can attribute the temperature-independent T2 value in the Dy3+−doped sample, which corresponds to a homogeneous 1H NMR linewidth of approximately 1.3 kHz, to 1H-1H dipole-dipole couplings. The fact that T2 values are shorter in the 10 mM DOTOPA and 15 mM DOTOPA samples indicates that relatively slow hyperfine field fluctuations in these DOTOPA-doped samples also contribute to T2 The similarity of T2 values from Hahn spin echo and Carr-Purcell echo train measurements indicates that hyperfine field fluctuations on time scales greater than 30 μs do not make a significant contribution to T2 In other words, fluctuations on shorter time scales have sufficient amplitudes to account for the observed T2 values. This inference is consistent with correlation times for hyperfine field fluctuations discussed below.
Effects of microwave irradiation on 1H nuclear spin relaxation times
As described in detail below, the observed dependences of 1H nuclear spin relaxation times (T2LG, T1ρ, and T2PSL) on temperature in DOTOPA-doped samples are due to the temperature dependence of the electron spin polarization at thermal equilibrium. When kBT is large compared with the electron spin-flip energy ħωe, individual electrons have nearly equal probabilities of being in |+〉 or |−〉 spin states. Electron spin flip-flop transitions, which require that coupled electron spins be in opposite states, are then relatively frequent, producing relatively large fluctuations of the local magnetic fields from electron magnetic moments (i.e., hyperfine field fluctuations). Fluctuating local fields then drive nuclear spin relaxation. Conversely, when kBT < ħωe, electron spins become strongly polarized, i.e., the |+〉 state becomes less probable than the |−〉 state. Electron spin flip-flop transitions then become less frequent, fluctuations of local magnetic fields become smaller in amplitude, and nuclear spin relaxation becomes slower.
If this explanation is correct, then it should be possible to increase nuclear spin relaxation rates, at temperatures where electron spins are strongly polarized, by applying microwave radiation that excites electron spin transitions. Excitation of electron spin transitions with microwaves should reduce the electron spin polarization, increase the rate of flip-flop transitions involving coupled pairs of electrons with opposite spin states, and thus increase the amplitude of local magnetic field fluctuations that drive nuclear spin relaxation. At temperatures where electron spins are not strongly polarized, microwave irradiation should have a negligible effect.
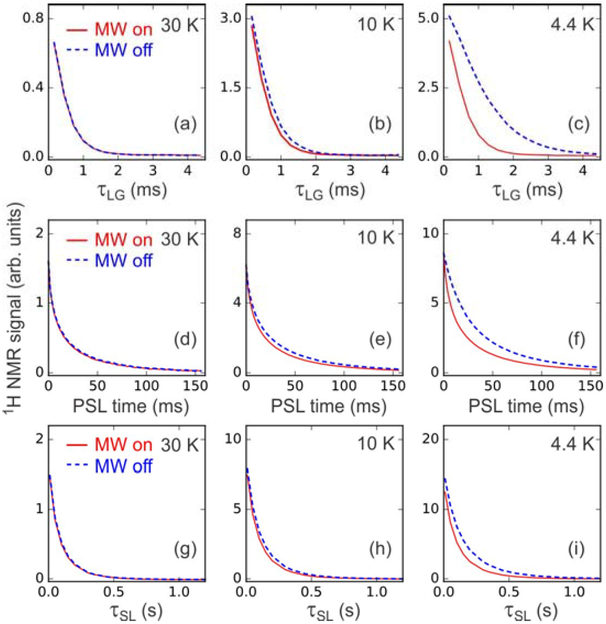
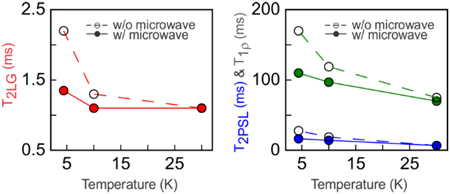
Data in Fig. 5 for the 10 mM DOTOPA sample support this picture. Figs. 5a–c compare T2LG measurements with microwaves on and off. While no difference is observed at 30 K, microwave irradiation reduces T2LG by 15% at 10 K and by a factor of two at 4.4 K. Figs. 5d–f compare T2PSL measurements with microwaves on and off. Figs. 5g–i compared T1ρ measurements with microwaves on and off. While no differences in T2PSL and T1ρ are observed at 30 K, small differences at 10 K and larger differences at 4.4 K (50% reduction in T2PSL, 35% reduction in T1ρ) are observed.
Figure 5:
Experimental 1H NMR signal decay curves for measurements of T2LG (a-c), T2PSL (d-f), and T1ρ (g-i) at temperatures of 30 K (a,d,g), 10 K (b,e,h), and 4.4 K (c,f,i). The sample contained 10 mM DOTOPA. Data were acquired both with (red solid lines) and without (blue dashed lines) microwave irradiation.
Fig. 6 shows the results of T2LG measurements in which microwaves were applied continuously for at least 10 s before each scan, but then switched off at a time δ before the relaxation time period in the pulse sequence (see Fig. 1a). As shown in Fig. 6a, at a sample temperature of 4.4 K, the measured value of T2LG increases from about 1.0 ms to about 1.6 ms as δ increases. Fitting this dependence on δ with a single-exponential function of the form T2LG(δ) = Ta − Tb exp(−δ / δ0) results in δ0 = 84 ± 18 ms. We interpret δ0 as the characteristic time for recovery of the thermal equilibrium electron spin polarization, following reduction in this polarization by microwave irradiation. In other words, δ0 is approximately T1e at 4.4 K. Similarly, at 10 K, we find δ0 = 76 ± 15 ms.
Figs. 6b–6d show examples of T2LG decay curves for several values of δ, from which the T2LG values plotted in Fig. 6a were derived. Similar data for the dependence of T2PSL on δ are shown in Fig. S10 of Supporting Information.
Computational Model
Expressions for nuclear spin relaxation times
A full derivation of expressions for T1ρ and T2LG relaxation times produced by fluctuating local magnetic fields is given in Supporting Information. The final expressions are:
| (1) |
| (2) |
In these expressions, ω0, ω1, Δ, and are the 1H NMR frequency, the RF field strength, the Lee-Goldburg frequency offset and the Lee-Goldburg effective field strength (all in rad/s), and ω = ω0> − Δ. The autocorrelation functions of transverse and longitudinal local magnetic fields are and , respectively. Here γH is the proton gyromagnetic ratio (in rad/s per Gauss) and Bx,y,z is the total fluctuating field at the nucleus from the magnetic moments of surrounding electron spins.
In the simple case when the autocorrelation functions are single-exponential decays [i.e., f(τ) = f0 exp(−τ / τf) and g (τ) = g0 exp(−τ / τg)], Eqs. (1) and (2) become
| (3) |
| (4) |
In our experiments, ω, ω0 >>ω1, ωLG. If ωτf, ω0τf >> 1, which means τf >> 0.4 ns in our experiments, and if τg ~ τf, then terms proportional to f0 are much smaller than terms proportional to g0. If ω1τg,ωLGτg>> 1, which means τg >> 8 μs in our experiments, then T2LG << T1ρ. As discussed below, numerical simulations indicate that the autocorrelation functions are not single-exponential decays. If the autocorrelation functions are multi-exponential decays, T1ρ−1 and T2LG−1 are sums of contributions from each exponentially decaying term, with each contribution having the forms shown in Eqs. (3) and (4).
The equations above apply to NMR T1ρ and T2LG relaxation caused by fluctuating local magnetic fields, regardless of the source of these local fields. The following sections give a method for simulating local field fluctuations that arise from electron-electron flip-flop transitions in a many-electron system. Autocorrelation functions calculated from numerical simulations are then used to evaluate T1ρ and T2LG values.
Expression for electron spin flip-flop rate
If two coupled electron spins i and j in a strong external magnetic field are initially in opposite spin states, it can be shown that the rate of flip-flop transitions (i.e., transitions from the |+−〉 state to the |− +〉 state) can be expressed as
| (5) |
where is the magnetic dipole-dipole coupling strength (Gaussian units), Rij is the inter-spin distance, θij, is the angle between the inter-spin vector and the external field direction, γe is the electron gyromagnetic ratio (in rad/s per Gauss), and Fi(t) and Fj(t) are the free-induction decay signals of the two spins in the absence of the coupling, with Fi(0) = Fj (0) = 1.47 Assuming Fi(t) = exp(−kt2)exp(iωit) and Fj (t) = exp(−kt2)exp(iωit), Eq. (5) becomes
| (6) |
where Δωij is the difference in precession frequencies of the two spins and ωFWHM is their FWHM linewidths (both quantities in rad/s).
Kinetic model for flip-flop transitions in a many-electron system
To estimate 1H NMR relaxation times under different experimental conditions, we calculated the local magnetic field fluctuations arising from electron spin flip-flop events. The calculation was repeated many times with different initial parameters to describe the average behavior of the disordered many-spin system. We now describe the workflow for a single calculation.
First, ND DOTOPA molecules are placed at random positions within a cubic volume, centered at the origin and with dimensions calculated to give the desired DOTOPA concentration. Each molecule is represented by an equilateral triangle with sides equal to 1.3 nm, and the orientation of each molecule is assigned with random Euler angles. Electron spins are located at the vertices of each molecule. Although the positions and orientations of the DOTOPA molecules are generated randomly, positions and orientations that place an electron spin within a minimum radius of the origin (1.5 nm in simulations described below) are rejected, to prevent any single electron spin from making an unrealistically large contribution to the magnetic field at the origin (where the 1H nucleus is located). The precession frequency of each electron spin is set to ωi = Ω(3 cos2 ξi −1) / 3, where ξi is the angle between the direction from the center of its triangle to its vertex and the direction of the external magnetic field (taken to be the z direction). Ω/2π is taken to be 800 MHz, similar to the width of a nitroxide electron spin resonance line in a frozen solution at 9.39 T.
At the beginning of each simulation, each electron spin is randomly assigned a spin state of |+〉 or |−〉, corresponding to spin angular momentum vectors S equal to (0,0, + 1/2) or (0,0, −1/2). The numbers n+ and n− of electrons in the two states are determined by the temperature according to n+/n− = exp(−ħγeB0 / kBT), where B0 is the external magnetic field strength, and kB is the Boltzmann constant. For B0 = 9.39 T, ħγeB0 = kBT when T = 12.6 K. Typical configurations are shown in Fig. 7a. For any configuration, the total magnetic field at the origin produced by the electron spin magnetic moments is
| (7) |
where ri is the position of electron spin i.
Figure 7:
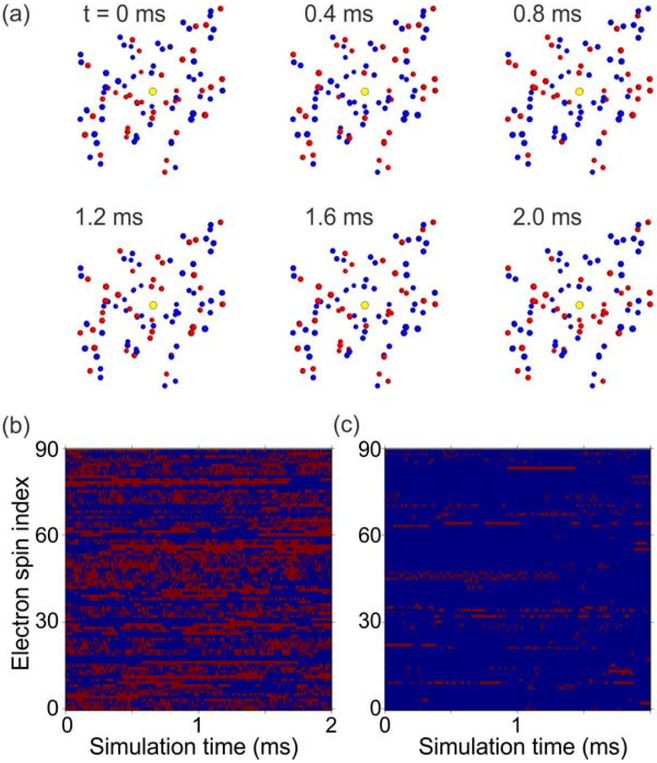
(a) Instantaneous electron spin configurations from numerical simulations of electron spin dynamics in a system of 30 DOTOPA molecules in a cube with 15 mM DOTOPA concentration. The simulation temperature is 30 K. A 9.39 T magnetic field is applied along z. Configurations are shown at the indicated simulation times. Electron spins in the |+〉 and |−〉 states are indicated by red and blue dots, respectively. The yellow disk indicates the position of a single central 1H nucleus, where the total magnetic field from electron spin magnetic moments is evaluated in these simulations. (b,c) Plots of spin states as a function of time for simulations at 30 K and 4.4 K, respectively. Each horizontal line shows the spin state of one electron, using the same color code as in panels a.
Due to flip-flop transitions, the distribution of spin states may change from one time point to the next in a simulation. In each time step, the total probability for electron spin i to undergo a flip-flop transition is given by , where tstep is the length of the time step and kij is defined in Eq. (6). Importantly, kij is zero if spins i and j are in the same state. To determine whether spin i changes its state in this time step, a random number x in the interval [0, 1] is generated. If x <pi, spin i changes its state. To determine the flip-flop transition partner of spin i, flip-flop rates between spin i and all other spins are normalized according to and are used to partition an interval [0, 1] by means of a set of lower bounds and upper bounds υij = λij + kij′. A random number x between [0, 1] is again generated, and if λij < × < υij then spin j also changes its state.
Within each time step, the process described in the previous paragraph is repeated 3ND times, with each electron being selected to be spin i in one repetition. The order of selection of electrons is random in each time step. It should be noted that the distribution of spin states may change in each repetition, which may affect the probabilities pi in subsequent repetitions because kij is non-zero only if spins i and j are have opposite spin states.
After each time step, Eq. (7) is used to calculate the total field at the origin, which is then a function of time B(t). Each configuration (i.e., positions and orientations of DOTOPA molecules and initial spin state assignments) therefore yields time-dependent field components, from which the autocorrelation functions , , and are calculated, according to:
| (8) |
where N is the number of time steps in the simulation. For a given temperature and DOTOPA concentration, autocorrelation functions are averaged over many configurations to produce the final autocorrelation functions, which can then be used to calculate T1ρ and T2LG values according to Eqs. (1) and (2). Although and may be different in a given configuration, by symmetry they must be equal when averaged over configurations. Therefore, these two autocorrelation functions are combined as .
Averaging of autocorrelation functions over configurations with different positions and orientations of the DOTOPA molecules is an approximation that allows us to calculate a single value for each nuclear spin relaxation time. In experiments on frozen solutions, each configuration represents a different structural environment within the sample, with its own relaxation times. Experimental measurements are therefore sums of signals with different relaxation times, and multi-exponential decays are expected. In principle, we could calculate relaxation times for each choice of positions and orientations of the DOTOPA molecules and then simulate the multi-exponential decays. However, this would require longer total simulation times in order to generate adequate autocorrelation functions for each configuration.
Important features of the model described above are: (i) it includes the tri-nitroxide character of DOTOPA explicitly; (ii) it allows calculations to be performed at specified temperatures and dopant concentrations without external assumptions about temperature- and concentration-dependences; (iii) it treats electron spectral diffusion through a flip-flop transition rate that is derived from quantum mechanical time-dependent perturbation theory, rather than treating electron spectral diffusion phenomenologically; (iv) it allows calculations for systems of many electrons over long time periods.
Numerical calculations of correlation functions and nuclear spin relaxation times
Simulations of electron spin dynamics were performed with ND = 30, tstep = 10 ns, and N = 2 × 105 (i.e., 2.0 ms simulation time for each configuration). The value of ωFWHM/2π in Eq. (6) was set to 52 MHz. To match the experiments, DOTOPA concentrations were 5 mM, 10 mM, and 15 mM, corresponding to cubic simulation volumes with sides of 21.5 nm, 17.0 nm, and 14.9 nm. Temperatures were 30 K, 10 K, and 4.4 K, where electron spin polarizations at thermal equilibrium in a 9.39 T field are (n− − n+)/(n− + n+) = 0.21, 0.56, and 0.89, respectively. For each condition, simulations with 300 different configurations were performed. Correlation functions were then calculated according to Eq. (8).
Fig. 7a shows examples of instantaneous configurations from one simulation at 30 K with 15 mM DOTOPA. Under these conditions, most electron spins participate in flip-flop transitions during the simulation. The time dependences of all spin states are shown in Fig. 7b, which is a “spin state trajectory map” that uses a red/blue color code to track states of each spin. In Fig. 7c, the corresponding map from one simulation at 4.4 K illustrates the pronounced effect of temperature. At 4.4 K, most electron do not participate in any flip-flop transitions within the 2 ms simulation period.
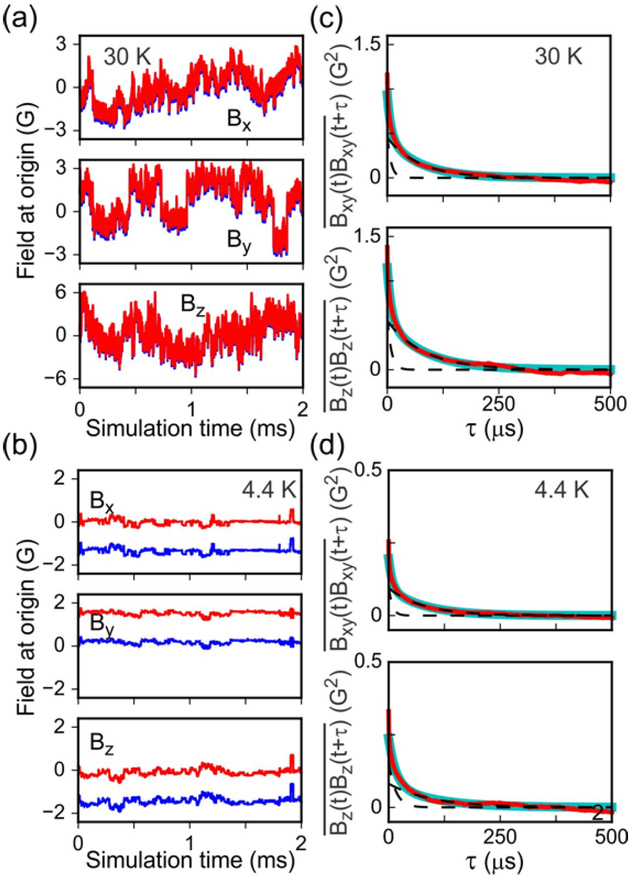
Hyperfine field fluctuations at the origin are plotted in Figs. 8a and 8b, for the same simulations that are depicted in Figs. 7b and 7c. Autocorrelation functions at 30 K and 4.4 K, each calculated from 300 independent simulations with 15 mM DOTOPA, are shown in Figs. 8c and 8d. Autocorrelation functions for all conditions of temperature and DOTOPA concentration are shown in Fig. S11 of Supporting Information. As shown in these figures, the autocorrelation functions can be fit adequately with bi-exponential functions of the form f(τ) = f0a exp(−τ / τfa) + f0b exp(−τ / τfb) + cf and g(τ) = g0a exp(−τ / τga) + g0b exp(‒τ / τgb) + cg up to τ ≈ 500 μs. At larger values of τ, the autocorrelation functions become clearly non-exponential and non-monotonic due to insufficient averaging. Larger values of τ correspond to larger values of n in Eq. (8), which involve averaging of fewer time points.
Figure 8:
(a,b) Time dependences of the magnetic field at the origin (i.e., the position of a 1H nucleus) from simulations at 30 K and 4.4 K shown in Figs. 7b and 7c, respectively. Red and blue lines are field components before and after subtraction of the average values of the field components. (c,d) Autocorrelation functions (left) and at 30 K and 4.4 K, respectively (red lines). Autocorrelation functions are calculated from simulated time-dependent field components as in panels a and b, after subtracting the average values of the field components. Autocorrelation functions are then averaged over 300 independent simulations at each temperature and DOTOPA concentration. Thick cyan lines are bi-exponential fits to the averaged autocorrelation functions. Dashed lines are the two decaying exponential terms.
Best-fit parameters from bi-exponential fits to the calculated autocorrelation functions are listed in Table 1. Using these parameters, values of T2LG and T1ρ can be calculated from Eqs. (3) and (4). The results are given in Table 2. The calculated relaxation times reproduce two important trends in the experimental measurements, namely the reduction in relaxation times with increasing DOTOPA concentration and with increasing temperature. The calculated dependences on DOTOPA concentration are roughly 50% stronger than the experimentally determined dependences in Figs. 3 and 4. The calculated dependences on temperature are much stronger than the experimentally determined dependences. However, calculations and experiments both indicate that the temperature dependences become large only below 10 K. Calculated T1ρ values show a stronger dependence on ω1/2π than the experimental values. These discrepancies are discussed below.
Table 1: Best-fit Parameters from Bi-exponential Fits to Autocorrelation Functions.
Autocorrelation functions for fluctuating hyperfine fields were calculated from simulations of electron spin dynamics at the indicated temperatures and DOTOPA concentrations. Autocorrelation functions and fits are plotted in Fig. S11 of Supporting Information.
| DOTOPA (mM) | Temp (K) | τfa (μs) | τfb (μs) | cf | τga (μs) | τgb (μs) | cg | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 30 | 0.063 | 8.357 | 0.139 | 122.26 | −0.014 | 0.108 | 8.318 | 0.286 | 187.14 | −0.049 |
| 10 | 0.061 | 18.181 | 0.124 | 157.42 | −0.017 | 0.158 | 32.016 | 0.151 | 443.46 | −0.059 | |
| 4.4 | 0.014 | 25.798 | 0.043 | 269.73 | −0.011 | 0.015 | 18.091 | 0.065 | 262.02 | −0.016 | |
| 10 | 30 | 0.275 | 18.597 | 0.342 | 157.14 | −0.048 | 0.388 | 28.765 | 0.358 | 241.00 | −0.083 |
| 10 | 0.225 | 23.123 | 0.156 | 177.53 | −0.029 | 0.343 | 27.541 | 0.196 | 201.98 | −0.041 | |
| 4.4 | 0.084 | 62.732 | 0.032 | 681.49 | −0.02 | 0.088 | 42.296 | 0.031 | 317.31 | −0.012 | |
| 15 | 30 | 0.597 | 15.573 | 0.329 | 160.27 | −0.058 | 0.709 | 14.621 | 0.457 | 170.05 | −0.082 |
| 10 | 0.429 | 16.292 | 0.214 | 182.55 | −0.042 | 0.571 | 12.256 | 0.366 | 159.11 | −0.058 | |
| 4.4 | 0.129 | 22.314 | 0.057 | 290.07 | −0.018 | 0.186 | 21.935 | 0.072 | 370.87 | −0.029 |
Table 2: Calculated 1H NMR Relaxation Times.
Values of T1ρ and T2LG were calculated from simulations of electron spin dynamics at the indicated temperatures and DOTOPA concentrations, using Eqs. (3) and (4) and the best-fit parameters listed in Table 1. For comparison, experimentally-determined values of T1ρ and T2LG are given in parentheses.
| DOTOPA (mM) | T (K) | T1ρ (ms) | T2LG (ms) | ||
|---|---|---|---|---|---|
| ω1/2π = 20 kHz | ω1/2π = 40 kHz | ω1/2π = 80 kHz | |||
| 5 | 30 | 2.7 (120) | 7.3 (230) | 26 (260) | 0.08 (0.9) |
| 10 | 4.4 (180) | 17 (260) | 67 (270) | 0.06 (0.9) | |
| 4.4 | 23 (270) | 84 (350) | 330 (310) | 0.31 (1.6) | |
| 10 | 30 | 1.6 (45) | 6.0 (63) | 24 (88) | 0.04 (0.6) |
| 10 | 1.8 (61) | 6.7 (90) | 26 (120) | 0.09 (0.6) | |
| 4.4 | 10 (110) | 41 (130) | 160 (130) | 0.24 (1.0) | |
| 15 | 30 | 0.58 (15) | 1.8 (39) | 7.0 (55) | 0.05 (0.45) |
| 10 | 0.63 (31) | 2.0 (48) | 7.4 (63) | 0.06 (0.48) | |
| 4.4 | 2.9 (56) | 11 (60) | 41 (64) | 0.14 (0.86) | |
Discussion
Our main conclusion from the experiments presented above is that 1H NMR relaxation times that are important in low-temperature, DNP-enhanced MRI experiments, especially T2LG and T2PSL, become significantly longer at temperatures below 10 K, thereby reducing their negative impact on MRI sensitivity and MRI resolution. With a phase-encoding period of τLG = 700 μs32, the 1.0 ms value of T2LG observed at 4.4 K with 10 mM DOTOPA implies a reduction in MRI signals by a factor of exp(−τLG/T2LG) = 0.50. For a given total image acquisition time and a given signal-to-noise requirement, this translates into an increase in the minimum voxel volume by a factor of 2.00, or a decrease in image resolution by a factor of 2.001/3 = 1.26. The reduction in T2PSL (relative to a Dy3+−doped sample) by a factor of 10 implies a reduction in MRI signal-to-noise by a factor of 101/2 = 3.16, which translates into a decrease in resolution by an additional factor of 3.161/3 = 1.47. Assuming signal enhancement factor of 500 at 4.4 K (with DNP) relative to our earlier MRI experiments at 28 K (without DNP) and a DNP build-up time of TDNP = 18 s (Fig. 2b), to be compared with T1H = 0.4 s in the earlier experiments,32 the net change in image resolution becomes a factor of 1.26 × 1.47 × (18/0.4)1/6 × 500−1/3 = 0.44. It is therefore reasonable to expect an improvement in MRI resolution by a factor of two or more. Additional optimization of the DNP dopant, the microwave irradiation conditions, the RF circuitry in the MRI cryostat, and the spectrometer’s receiver section may lead to further improvements in resolution.
In experiments described above, magnetic field gradient coils for MRI, described in previous publications,32,36 were removed to reduce the thermal load on the cold finger of our cryostat. To make MRI experiments feasible below 10 K, it will be necessary to reduce heat conduction through the wires that carry current pulses to the gradient coils. Modifications of our apparatus for this purpose are currently in progress.
Our simulations of electron spin dynamics lead to temperature-dependent and concentration-dependent T1ρ and T2LG values that reproduce the experimental trends. However, relaxation times from these simulations do not agree quantitatively with experimental measurements. In particular, calculated T1ρ values at 30 K are shorter than experimental values and exhibit a stronger dependence on ω1/2π. These discrepancies indicate that the bi-exponential autocorrelation functions for hyperfine field fluctuations estimated from our simulations (Table 1) are not sufficiently accurate. Using Eqs. (3) and (4), it can be shown that bi-exponential autocorrelation functions are in principle sufficient to account for the experimental data. For example, if , τga = 0.1 μs, , and τgb = 160 μs, one obtains T2LG = 0.59 ms and T1ρ = 42 ms, 69 ms, and 84 ms at ω1/2π = 20 kHz, 40 kHz, and 100 kHz, respectively. These relaxation times are in good agreement with experimental results for the 10 mM DOTOPA sample at 30 K. Thus, it seems that the actual hyperfine field fluctuations have a smaller value for τga (the fast correlation time) and a smaller value for g0b (the slow correlation amplitude), compared with results from our simulations. Further work will be required to identify the source of these differences between experimental observations and numerical simulations.
The simulations also predict larger increases in nuclear spin relaxation times at low temperatures than we observe experimentally. This difference suggests that hyperfine field fluctuations at low temperatures, where electron spins are highly polarized, are larger in real samples than they are in our simulations. Again, the source of this difference may be identified in further work.
Autocorrelation function parameters in Table 1 indicate that the temperature dependences of 1H NMR relaxation times in our experiments on DOTOPA-doped samples are primarily due to reductions in the amplitudes of local magnetic field fluctuations as electron spins become more strongly polarized below 10 K. Effects of electron polarization on NMR relaxation in solids have been discussed more generally by Abragam and Goldman48, although not specifically for T2LG and T1ρ.
In addition to the 1H MRI experiments that are under development in our laboratory, fluctuating hyperfine fields from DNP dopants affect other types of low-temperature NMR experiments. An earlier study by Potapov et al.49 examined effects on 13C T2 relaxation in static samples at 8 K and 16 K. Strong dependences on dopant concentration and on τecho in Carr-Purcell echo train measurements were reported. For DOTOPA concentrations of 6.6–13.3 mM, the experimental data could be fit with a model in which individual electrons undergo spin-flip transitions on the 100–300 μs time scale. Unlike the simulations described above, the electron spin flip rates were not calculated from theoretical expressions such as Eq. (6), but instead were treated as an arbitrary fitting parameter. Since experiments were not performed below 8 K, a significant temperature dependence was not observed by Potapov et al. Based on the 1H NMR measurements described above, one would 13C T2 values to increase significantly below 8 K.
As shown in Figs. 3 and paramagnetic relaxation effects in Dy3+−doped and DOTOPA-doped samples have qualitatively different dependences on temperature. In our Dy3+−doped sample, T2LG, T2PSL, and T1ρ values decrease with decreasing temperature from 30 K to 3.3 K. In our DOTOPA-doped samples, these values increase with decreasing temperature. We attribute these differences in nuclear spin relaxation to differences in the dominant sources of local magnetic field fluctuations from the paramagnetic dopants. Field fluctuations in the Dy3+−doped sample are primarily due to electron spin-lattice relaxation processes that are relatively fast. In particular, the temperature dependence of T1H in a Dy3+−doped glycerol/water solution at 9.39 T shows a minimum at approximately 40 K,32 indicating that T1e ≈ 0.4 ns at 40 K. Thus, at 40 K, the correlation time for local magnetic field fluctuations is short, producing long T2LG, T2PSL, and T1ρ values. As the temperature decreases, T1e becomes longer, producing progressively longer correlation times and consequently shorter T2LG, T2PSL, and T1ρ values (i.e., more efficient transverse nuclear spin relaxation and rotating frame relaxation). In contrast, electron spin-lattice relaxation is relatively slow in DOTOPA-doped samples. As discussed above, data in Fig. 6 indicate T1e > 10 ms below 30 K. Local magnetic field fluctuations are then due to electron spin flip-flop transitions, driven by electron-electron couplings. The amplitude of these fluctuations decreases with decreasing temperature, resulting in progressively longer T2LG, T2PSL, and T1ρ values.
Short T2 and T1ρ values due to fluctuating hyperfine fields from DNP dopants can also limit the effectiveness of various solid state NMR techniques that are used with magic-angle spinning (MAS) in structural studies of biopolymers, including 15N-13C and 13C-13C dipolar recoupling techniques for measuring structurally significant internuclear distances and various techniques for polarization transfers in multidimensional spectroscopy. The severity of these effects may depend on the external magnetic field strength, the MAS frequency, and the nature of the sample50–51, as well as dopant concentration and other factors. Results presented above suggest that T2 and T1ρ can be lengthened by performing MAS DNP experiments at lower temperatures, especially if practical MAS NMR probes that operate below 10 K could be developed.52–55
Conclusion
We have shown experimentally that 1H NMR relaxation times that are important for DNP-enhanced low-temperature MRI experiments, especially T2LG and T2PSL, increase at temperatures below 10 K in frozen solutions that contain nitroxide-based dopants. This result implies that NMR signal enhancements from DNP will not be entirely cancelled by signal losses from NMR relaxation processes, encouraging us to pursue low-temperature DNP as a route to micron-scale MRI. We have also developed a computational model that permits simulations of local magnetic field fluctuations from electron spin flip-flop transitions in many-spin systems. Simulations show that the longer NMR relaxation times at temperatures below 10 K are attributable to reductions in the amplitude of field fluctuations due to high levels of electron spin polarization, which suppress flip-flop transitions.
Supplementary Material
Acknowledgement
This work was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health.
Footnotes
References
- 1.Overhauser AW, Polarization of nuclei in metals. Phys. Rev 1953, 92, 411–415. [Google Scholar]
- 2.Carver TR; Slichter CP, Experimental verification of the Overhauser nuclear polarization effect. Phys. Rev 1956, 102, 975–980. [Google Scholar]
- 3.Dorn HC; Gu J; Bethune DS; Johnson RD; Yannoni CS, The nature of fullerene solution collisional dynamics: A 13C DNP and NMR study of the C60/C6D6/Tempo system. Chem Phys Lett 1993, 203, 549–554. [Google Scholar]
- 4.Denysenkov V; Prandolini MJ; Gafurov M; Sezer D; Endeward B; Prisner TF, Liquid state DNP using a 260 GHz high power gyrotron. Phys Chem Chem Phys 2010, 12, 5786–5790. [DOI] [PubMed] [Google Scholar]
- 5.Turke MT; Tkach I; Reese M; Hofer P; Bennati M, Optimization of dynamic nuclear polarization experiments in aqueous solution at 15 MHz/9.7 GHz: A comparative study with DNP at 140 MHz/94 GHz. Phys Chem Chem Phys 2010, 12, 5893–5901. [DOI] [PubMed] [Google Scholar]
- 6.Griesinger C; Bennati M; Vieth HM; Luchinat C; Parigi G; Hofer P; Engelke F; Glaser SJ; Denysenkov V; Prisner TF, Dynamic nuclear polarization at high magnetic fields in liquids. Prog. Nucl. Magn. Reson. Spectrosc 2012, 64, 4–28. [DOI] [PubMed] [Google Scholar]
- 7.Cheng CY; Varkey J; Ambroso MR; Langen R; Han SI, Hydration dynamics as an intrinsic ruler for refining protein structure at lipid membrane interfaces. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 16838–16843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Barnes R; Sun S; Fichou Y; Dahlquist FW; Heyden M; Han SI, Spatially heterogeneous surface water diffusivity around structured protein surfaces at equilibrium. J. Am. Chem. Soc 2017, 139, 17890–17901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Afeworki M; McKay RA; Schaefer J, Selective observation of the interface of heterogeneous polycarbonate polystyrene blends by dynamic nuclear polarization 13C NMR-spectroscopy. Macromolecules 1992, 25, 4084–4091. [Google Scholar]
- 10.Afeworki M; Vega S; Schaefer J, Direct electron-to-carbon polarization transfer in homogeneously doped polycarbonates. Macromolecules 1992, 25, 4100–4105. [Google Scholar]
- 11.Maresch GG; Kendrick RD; Yannoni CS; Galvin ME, Dynamic nuclear polarization via confined electrons in bulk solids. J Magn Reson 1989, 82, 41–50. [Google Scholar]
- 12.Duijvestijn MJ; Vanderlugt C; Smidt J; Wind RA; Zilm KW; Staplin DC, 13C NMR spectroscopy in diamonds using dynamic nuclear polarization. Chem Phys Lett 1983, 102, 25–28. [Google Scholar]
- 13.Duijvestijn MJ; Manenschijn A; Smidt J; Wind RA, Structural information of undoped trans-polyacetylene obtained by 13C 2D NMR combined with dynamic nuclear polarization. J Magn Reson 1985, 64, 461–469. [Google Scholar]
- 14.Jones RB; Robertson SD; Clague ADH; Wind RA; Duijvestijn MJ; Vanderlugt C; Vriend J; Smidt J, Dynamic nuclear polarization 13C NMR of coal. Fuel 1986, 65, 520–525. [Google Scholar]
- 15.Lock H; Wind RA; Maciel GE; Zumbulyadis N, 29Si dynamic nuclear polarization of dehydrogenated amorphous silicon. Solid State Commun 1987, 64, 41–44. [Google Scholar]
- 16.Wind RA; Lock H; Mehring M, 13C Knight-shift saturation and 1H dynamic nuclear polarization in a polycrystalline sample of the organic conductor (fluoranthenyl)P2F6. Chem Phys Lett 1987, 141, 283–288. [Google Scholar]
- 17.Ardenkjaer-Larsen JH; Fridlund B; Gram A; Hansson G; Hansson L; Lerche MH; Servin R; Thaning M; Golman K, Increase in signal-to-noise ratio of > 10,000 times in liquid state NMR. Proc. Natl. Acad. Sci. U. S. A 2003, 100, 10158–10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ardenkjaer-Larsen JH, On the present and future of dissolution DNP. JM agn Reson 2016, 264, 3–12. [DOI] [PubMed] [Google Scholar]
- 19.Bajaj VS; Farrar CT; Hornstein MK; Mastovsky I; Vieregg J; Bryant J; Elena B; Kreischer KE; Temkin RJ; Griffin RG, Dynamic nuclear polarization at 9 T using a novel 250 GHz gyrotron microwave source. J Magn Reson 2003, 160, 85–90. [DOI] [PubMed] [Google Scholar]
- 20.Becerra LR; Gerfen GJ; Temkin RJ; Singel DJ; Griffin RG, Dynamic nuclear polarization with a cyclotron resonance maser at 5 T. Phys. Rev. Lett 1993, 71, 3561–3564. [DOI] [PubMed] [Google Scholar]
- 21.Hu KN; Yu HH; Swager TM; Griffin RG, Dynamic nuclear polarization with biradicals. J. Am. Chem. Soc 2004, 126, 10844–10845. [DOI] [PubMed] [Google Scholar]
- 22.Lesage A; Lelli M; Gajan D; Caporini MA; Vitzthum V; Mieville P; Alauzun J; Roussey A; Thieuleux C; Mehdi A, et al. , Surface enhanced NMR spectroscopy by dynamic nuclear polarization. J. Am. Chem. Soc 2010, 132, 15459–15461. [DOI] [PubMed] [Google Scholar]
- 23.Gruning WR; Rossini AJ; Zagdoun A; Gajan D; Lesage A; Emsley L; Coperet C, Molecular-level characterization of the structure and the surface chemistry of periodic mesoporous organosilicates using DNP surface enhanced NMR spectroscopy. Phys Chem Chem Phys 2013, 15, 13270–13274. [DOI] [PubMed] [Google Scholar]
- 24.Reggie L; Lopez JJ; Collinson I; Glaubitz C; Lorch M, Dynamic nuclear polarization-enhanced solid-state NMR of a 13C-labeled signal peptide bound to lipid-reconstituted sec translocon. J. Am. Chem. Soc 2011, 133, 19084–19086. [DOI] [PubMed] [Google Scholar]
- 25.Potapov A; Yau WM; Ghirlando R; Thurber KR; Tycko R, Successive stages of amyloid-β self-assembly characterized by solid-state nuclear magnetic resonance with dynamic nuclear polarization. J. Am. Chem. Soc 2015, 137, 8294–8307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Takahashi H; Ayala I; Bardet M; De Paepe G; Simorre JP; Hediger S, Solid-state NMR on bacterial cells: Selective cell wall signal enhancement and resolution improvement using dynamic nuclear polarization. J. Am. Chem. Soc 2013, 135, 5105–5110. [DOI] [PubMed] [Google Scholar]
- 27.Wang T; Park YB; Caporini MA; Rosay M; Zhong LH; Cosgrove DJ; Hong M, Sensitivity-enhanced solid-state NMR detection of expansin’s target in plant cell walls. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 16444–16449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ciobanu L; Seeber DA; Pennington CH, 3D MR microscopy with resolution 3.7 μm by 3.3 μm by 3.3 μm. J Magn Reson 2002, 158, 178–182. [DOI] [PubMed] [Google Scholar]
- 29.Ciobanu L; Pennington CH, 3D micron-scale MRI of single biological cells. Solid State Nucl. Magn. Reson 2004, 25, 138–141. [DOI] [PubMed] [Google Scholar]
- 30.Weiger M; Schmidig D; Denoth S; Massin C; Vincent F; Schenkel M; Fey M, NMR microscopy with isotropic resolution of 3.0 μm using dedicated hardware and optimized methods. Concepts Magn. Reson. Part B 2008, 33B, 84–93. [Google Scholar]
- 31.Thurber KR; Tycko R, Prospects for sub-micron solid state nuclear magnetic resonance imaging with low-temperature dynamic nuclear polarization. Phys Chem Chem Phys 2010, 12, 5779–5785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen HY; Tycko R, Low-temperature magnetic resonance imaging with 2.8 μm isotropic resolution. J Magn Reson 2018, 287, 47–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lee M; Goldburg WI, Nuclear magnetic resonance line narrowing by a rotating RF field. Phys. Rev 1965, 140, 1261–1271. [Google Scholar]
- 34.Ostroff ED; Waugh JS, Multiple spin echoes and spin locking in solids. Phys. Rev. Lett 1966, 16, 1097–1098. [Google Scholar]
- 35.Petkova AT; Tycko R, Sensitivity enhancement in structural measurements by solid state NMR through pulsed spin locking. J Magn Reson 2002, 155, 293–299. [DOI] [PubMed] [Google Scholar]
- 36.Moore E; Tycko R, Micron-scale magnetic resonance imaging of both liquids and solids. J. Magn. Reson 2015, 260, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hu KN; Song C; Yu HH; Swager TM; Griffin RG, High-frequency dynamic nuclear polarization using biradicals: A multifrequency EPR lineshape analysis. J. Chem. Phys 2008, 128. [DOI] [PubMed] [Google Scholar]
- 38.Yau WM; Thurber KR; Tycko R, Synthesis and evaluation of nitroxide-based oligoradicals for low-temperature dynamic nuclear polarization in solid state NMR. J Magn Reson 2014, 244, 98–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zagdoun A; Casano G; Ouari O; Lapadula G; Rossini AJ; Lelli M; Baffert M; Gajan D; Veyre L; Maas WE, et al. , A slowly relaxing rigid biradical for efficient dynamic nuclear polarization surface-enhanced NMR spectroscopy: Expeditious characterization of functional group manipulation in hybrid materials. J. Am. Chem. Soc 2012, 134, 2284–2291. [DOI] [PubMed] [Google Scholar]
- 40.Dane EL; Maly T; Debelouchina GT; Griffin RG; Swager TM, Synthesis of a BDPA-Tempo biradical. Org. Lett 2009, 11, 1871–1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Thurber KR; Le TN; Changcoco V; Brook DJR, Verdazyl-ribose: A new radical for solid-state dynamic nuclear polarization at high magnetic field. J Magn Reson 2018, 289, 122–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mentink-Vigier F; Mathies G; Liu YP; Barra AL; Caporini MA; Lee D; Hediger S; Griffin RG; De Paepe G, Efficient cross-effect dynamic nuclear polarization without depolarization in high-resolution MAS NMR. Chem. Sci 2017, 8, 8150–8163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Thurber KR; Yau WM; Tycko R, Low-temperature dynamic nuclear polarization at 9.4 T with a 30 mW microwave source. J Magn Reson 2010, 204, 303–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shimon D; Hovav Y; Feintuch A; Goldfarb D; Vega S, Dynamic nuclear polarization in the solid state: A transition between the cross effect and the solid effect. Phys Chem Chem Phys 2012, 14, 5729–5743. [DOI] [PubMed] [Google Scholar]
- 45.Siaw TA; Fehr M; Lund A; Latimer A; Walker SA; Edwards DT; Han SI, Effect of electron spin dynamics on solid-state dynamic nuclear polarization performance. Phys Chem Chem Phys 2014, 16, 18694–18706. [DOI] [PubMed] [Google Scholar]
- 46.Gullion T; Baker DB; Conradi MS, New, compensated Carr-Purcell sequences. J Magn Reson 1990, 89, 479–484. [Google Scholar]
- 47.Tycko R; Dabbagh G, A simple theory of 13C nuclear spin diffusion in organic solids. Isr. J. Chem 1992, 32, 179–184. [Google Scholar]
- 48.Abragam A; Goldman M, Principles of dynamic nuclear polarisation. Rep. Prog. Phys 1978, 41, 395–467. [Google Scholar]
- 49.Potapov A; Thurber KR; Yau WM; Tycko R, Dynamic nuclear polarization-enhanced 1H-13C double resonance NMR in static samples below 20 K. J Magn Reson 2012, 221, 32–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jaudzems K; Bertarello A; Chaudhari SR; Pica A; Cala-De Paepe D; Barbet-Massin E; Pell AJ; Akopjana I; Kotelovica S; Gajan D, et al. , Dynamic nuclear polarization-enhanced biomolecular NMR spectroscopy at high magnetic field with fast magic-angle spinning. Angew. Chem.-Int. Edit 2018, 57, 7458–7462. [DOI] [PubMed] [Google Scholar]
- 51.Corzilius B; Andreas LB; Smith AA; Ni QZ; Griffin RG, Paramagnet induced signal quenching in MAS-DNP experiments in frozen homogeneous solutions. J Magn Reson 2014, 240, 113–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sesti EL; Alaniva N; Rand PW; Choi EJ; Albert BJ; Saliba EP; Scott FJ; Barnes AB, Magic angle spinning NMR below 6 K with a computational fluid dynamics analysis of fluid flow and temperature gradients. J Magn Reson 2018, 286, 1–9. [DOI] [PubMed] [Google Scholar]
- 53.Lee D; Bouleau E; Saint-Bonnet P; Hediger S; De Paepe G, Ultra-low temperature MAS-DNP. J Magn Reson 2016, 264, 116–124. [DOI] [PubMed] [Google Scholar]
- 54.Matsuki Y; Nakamura S; Fukui S; Suematsu H; Fujiwara T, Closed-cycle cold helium magic-angle spinning for sensitivity-enhanced multi-dimensional solid-state NMR. J Magn Reson 2015, 259, 76–81. [DOI] [PubMed] [Google Scholar]
- 55.Hackmann A; Seidel H; Kendrick RD; Myhre PC; Yannoni CS, Magic-angle spinning NMR at near-liquid-helium temperatures. J Magn Reson 1988, 79, 148–153. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.