Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Mar 19;123(14):3043–3049. doi: 10.1021/acs.jpcb.9b00982

Molecular Origin of the Elastic State of Aqueous Hyaluronic Acid

Giulia Giubertoni †, Federica Burla †, Cristina Martinez-Torres †, Biplab Dutta †, Galja Pletikapic †, Eddie Pelan ‡, Yves L A Rezus †, Gijsje H Koenderink †,*, Huib J Bakker †,*
PMCID: PMC6466474  PMID: 30888176

Abstract

graphic file with name jp-2019-00982f_0007.jpg

The macroscopic mechanical properties of biological hydrogels are broadly studied and successfully mimicked in synthetic materials, but little is known about the molecular interactions that mediate these properties. Here, we use two-dimensional infrared spectroscopy to study the pH-induced gelation of hyaluronic acid, a ubiquitous biopolymer, which undergoes a transition from a viscous to an elastic state in a narrow pH range around 2.5. We find that the gelation originates from the enhanced formation of strong interchain connections, consisting of a double amide–COOH hydrogen bond and an N–D–COO– hydrogen bond on the adjacent sugars of the hyaluronan disaccharide unit. We confirm the enhanced interchain connectivity in the elastic state by atomic force microscopy imaging.

Introduction

Hydrogels regulate the mechanical properties of cells and tissues and thereby play an important role in many biological and pathophysiological processes, ranging from stem cell differentiation and the degradation of aging cartilage to wound healing.1−6 An important feature of natural hydrogels is their ability to tune their viscoelastic properties in response to environmental stimuli, such as the solution pH, temperature, and salt conditions. Up to now, it has been difficult to connect the macroscopic response of hydrogels to the underlying molecular interactions, e.g., hydrogen-bond and hydrophobic interactions, thus limiting the capability to predict and tune the properties of hydrogels.

One of the few techniques able to track interactions at the molecular scale is two-dimensional infrared spectroscopy (2D-IR).7 2D-IR shares with two-dimensional nuclear magnetic resonance the ability to resolve molecular couplings and dynamics, but 2D-IR can resolve these interactions at a much shorter time scale. Molecular interactions such as hydrogen bonds or electrostatic forces usually change on a time scale of picoseconds, and with 2D-IR, snapshots of these interactions can be taken with femtosecond time resolution.8

Here, we use 2D-IR to identify the molecular interactions that drive the pH-triggered gelation of hyaluronic acid (HA), a natural polyelectrolyte that has received widespread attention, being one of the main components of the extracellular matrix. It is important for cell–cell communication and also plays an important role in many biological processes, such as joint lubrication, skin hydration, and cell migration,9 whereas its dysregulation contributes to cancer development.10 Due to its biocompatibility, hyaluronic acid is also widely used as a scaffold for cell culture and drug delivery.11−15 Hyaluronic acid is a paradigmatic example of a responsive natural hydrogel: it displays a sharp transition in mechanical behavior at pH 2.5, switching from a viscous state to an elastic gel, denoted as the “putty state”.16 The mechanism underlying this remarkable liquid-to-gel transition has been investigated for over almost a century with macroscopic techniques that map the dependence of the viscoelastic properties on pH, temperature, and ionic strength.17−19 Based on these studies, it has been proposed that at pH = 2.5, the net charge of the polyelectrolyte chains may be sufficiently suppressed to enable the formation of interchain hydrogen-bond interactions that would act as crosslinks.20−26 This principle was suggested to be applicable to the wider class of polysaccharides,27 but there has been no direct evidence for this putative pH-triggered hydrogen-bonding mechanism.

Experimental Section

Sample Preparation

The samples were prepared in a glass vial by adding water (or heavy water), NaCl (0.15 M), and HCl (or DCl) to achieve different molarities ranging from 0 to 80 mM of acid. All of these chemicals were provided by Sigma Aldrich. A specific amount of hyaluronic acid sodium salt in powder form from Streptococcus equi bacteria from Sigma Aldrich (1.5−1.8 > 1 MDa), or from Lifecore Biomedical (Mw ∼ 150 kDa), was added to the solution to reach a final concentration ranging from 10 to 20 mg/mL. The samples were left to equilibrate at room temperature for at least 24 h before measuring. Samples were stored for at most 1 week at a temperature of 4 °C, to slow down the hydrolytic degradation process.

Rheology

Rheology measurements were performed with a stress-controlled rheometer (Anton Paar MCR 501), equipped with stainless steel parallel plates with a diameter of 40 mm. The experiments were performed at a gap size of 100 μm and at a temperature of 22 °C set by a Peltier system. Samples left to equilibrate for 1 week to reach homogeneity were loaded on the plate using a spatula. After thermal equilibration, the elastic and viscous shear moduli were probed by performing oscillatory shear measurements at an oscillation frequency of 0.5 Hz and a strain amplitude of 0.5%, which is well within the linear viscoelastic regime for hyaluronan. The reported results are averages of at least three measurements for each pH. For each sample, the pH was measured using a pH meter (Hanna Instruments).

Fourier-Transform Infrared (FTIR)

All linear absorption measurements were performed using a Bruker Vertex 80v FTIR spectrometer, equipped with a liquid-nitrogen-cooled mercury cadmium telluride (MCT) detector. The spectra were recorded under a nitrogen atmosphere at a wavelength resolution of 3 cm–1. For every spectrum, 100 scans were averaged. In all measurements, a standard sample cell with a path length of 100 or 75 μm was used. The reported spectra were corrected for the absorption of the solvent background.

2D-IR

In 2D-IR experiments, we performed one-color experiments by pumping and probing around 1680 cm–1 and two-color experiments by pumping at 1680 cm–1 and probing at 1450 cm–1. The home-built setup that we use has been described before.28 The excitation was performed with a pair of femtosecond mid-infrared pulses. This excitation pulse pair induced transient absorption changes, which were monitored by a probe pulse that was delayed by a time Tw. After transmission through the sample, the probe pulse was sent into an infrared spectrograph and detected with an infrared mercury cadmium telluride (MCT) detector array, thus yielding the transient absorption spectrum as a function of the probe frequency. The dependence of the transient absorption spectrum on the excitation frequency was determined by measuring transient spectra for many different delay times between the two excitation pulses. By Fourier transformation of these spectra, we obtained the dependence of the transient absorption spectrum on the excitation frequency. By plotting the transient absorption spectrum as a function of the excitation and the probing frequency, we obtained a two-dimensional infrared (2D-IR) transient absorption spectrum for each delay time Tw.

Atomic Force Microscopy (AFM) Imaging

For AFM measurements, freshly cleaved mica was briefly rinsed with 0.15 M NaCl before sample deposition. Then, 50 μL of 100 mg/L HA solution were deposited and left to adsorb for 15 min. The mica was then rinsed with ultrapure water and dried at room temperature. Imaging was performed using tapping mode in air with a TAP150 cantilever on a Veeco Dimension 3100 AFM. The scanning rate was set to 0.5 Hz, with a scan resolution of 512 × 512. To retrieve the filament height values, the AFM height images were processed using the open-source software Gwyddion29 to correct for a tilt in the image, and the transversal profiles corresponding to the filament cross section were taken. Using a custom script on MATLAB, each profile was corrected for the background noise, and the values of all local maxima were pooled together to obtain a height distribution for each condition tested.

Results

Rheology and Infrared Spectroscopy

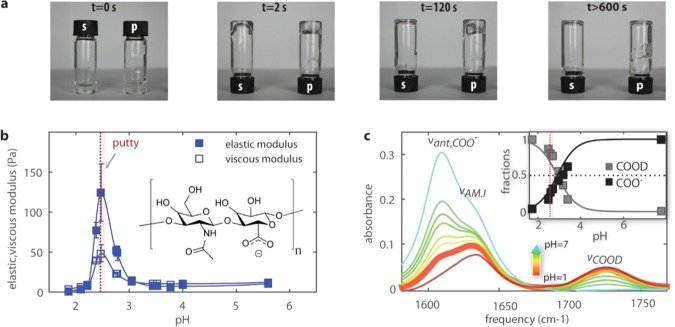
Hyaluronic acid has a relatively simple linear structure and homogeneous composition with repeating disaccharides composed of N-acetyl-glucosamine and glucuronic acid (illustrated in the inset of Figure 1b). The pH-dependent viscoelastic behavior of hyaluronic acid solutions stands out clearly in tube inversion assays, as shown in Figure 1a. Whereas the sample prepared in a solution state (“s”) at pH 1.6 readily flows, the sample prepared in the putty state (“p”) at pH 2.5 only flows on a time scale of minutes. This large difference in time scales originates from a pH-triggered transition in rheological properties from liquid to gel. To study the pH dependence of this transition in quantitative detail, we performed rheological experiments on semidilute solutions of high and low molecular weight hyaluronic acid. We studied solutions in heavy water (D2O), since heavy water is used as a solvent in 2D-IR studies of the amide and carbonyl vibrations. 2D-IR cannot be applied to solutions in H2O, as the amide and carbonyl vibrations of hyaluronic acid absorb in the same infrared frequency region as the bending vibration of H2O (between 1600 and 1700 cm–1). In all experiments, the pD values are converted to pH values30 (see Supporting Information (SI) Appendix). Figure 1b shows that the elastic and the viscous moduli sharply increase in a narrow range around a pH of 2.5, revealing a liquid–gel transition. This transition occurs at a pH value just below the pKa, which is about 2.9.12,18,25 We find a quantitatively similar pH dependence of the viscous and elastic moduli for hyaluronan solutions in H2O (see Supporting Information Appendix, Figure S2), which shows that the isotope composition of the solvent has a negligible effect on the mechanical properties.

Figure 1.

Figure 1

Open in a new tab

Hyaluronic acid solutions undergo a sol–gel transition in a narrow pH range. (a) A tube inversion assay shows that hyaluronic acid solutions prepared at pH 1.6 exhibit viscous flow (s), whereas solutions prepared at pH 2.5 form a viscoelastic gel (p) that flows only on time scales beyond 2 min. (b) The pH dependence of the viscous and elastic modulus of hyaluronic acid in heavy water solutions. We observe a sharp peak in the elastic shear modulus at pH 2.5. The inset shows that hyaluronic acid is a polymer of disaccharides, themselves composed of d-glucuronic acid and N-acetyl-d-glucosamine. (c) Linear infrared spectra for hyaluronic acid solutions in D2O at pH values ranging between 1.6 and 7. The infrared spectrum at pH = 2.5 is represented by the thick solid line. Between 1550 and 1760 cm–1, we observe three bands: the antisymmetric stretching mode of the carboxylate anion group, νant,COO–, at 1607 cm–1, the amide I vibration, νAM.I, at 1633 cm–1, and the carboxylic acid stretching mode, νCOOD, at 1726 cm–1. The inset shows the fractions of COO– and COOD groups determined from the IR spectra as a function of pH. Thick lines represent the expected fractions based on acid–base equilibrium equations (Supporting Information), assuming a pKa = 2.9. We find good agreement between the measured and expected carboxylic and carboxylate fractions, with about 25% deprotonation of the carboxyl groups at pH = 2.5.

We studied the protonation state of hyaluronan as a function of pH with linear IR spectroscopy (Figure 1c). The relative intensities of the carboxylic acid and carboxylate anion bands of hyaluronan directly reflect the protonation state of hyaluronan. The antisymmetric vibration of the carboxylate anion, νant,COO–, absorbs at 1607 cm–1, and the amide I band, νAM.I, absorbs at 1633 cm–1. The C=O vibration of the COOD group, which will be denoted as νCOOD, absorbs around 1726 cm–1. At pH = 2.5, the COO– and COOD groups are present in a ratio of 1:4 (inset in Figure 1c), which corresponds to a pKa of 2.9, as reported in the literature.12

Two-Dimensional Infrared Spectroscopy

We use 2D-IR spectroscopy to study the intermolecular interactions among hyaluronic acid chains that lead to the sol–gel transition. We excite the amide and the carboxyl vibrations with a strong femtosecond infrared pulse pair (∼100 fs, 4 μJ per pulse). This excitation induces transient absorption changes that are probed with a weaker (0.35 μJ) single femtosecond probing pulse that is delayed by a time Tw. The excitation and probe pulses are centered at 1680 cm–1 with a bandwidth of 200 cm–1. The excitation and probe spectra thus have sufficient spectral width to cover the ν = 0 to v = 1 transition (bleach) and the ν = 1 to v = 2 transition (excited state absorption, or esa) of the νant,COO–, νCOOD, and νAM.I vibrations.

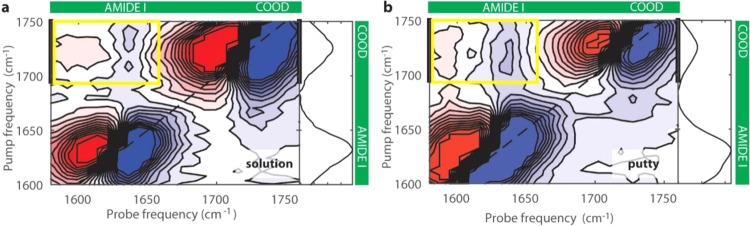
Figure 2a,b compare the 2D-IR spectra measured for the solution (pH = 1.6) and the putty state (pH = 2.5), both for Tw = 1.5 ps. Bleaching (increased transmission) is indicated in blue, whereas increased absorption (esa) is indicated in red. The bleach of the v = 0 to v = 1 transition and the esa of νAM.I are centered at 1639 and 1619 cm–1, respectively, along the probe frequency axis, whereas for νCOOD, these signals are centered at 1731 and 1703 cm–1, respectively (see also Supporting Information Appendix, Table S2). The bleaching and esa of the νant,COO– mode are in the low-frequency wing of the bleaching and esa of the amide I vibration, and lead to an elongation of the bleaching and the induced absorption signals to the lower left corner of the 2D-IR spectrum. We observe additional signals in the off-diagonal regions of the 2D-IR spectrum, indicating that the carboxyl and amide modes are coupled. In the upper pump-frequency region, the cross-peak signal represents the effect of the excitation of the νCOOD vibration on the spectrum of the νAM.I mode. In the lower pump-frequency region, the spectral shape of the carboxylic acid vibration is elongated along the pump axis (Figure S7). This effect reduces the visibility of the upward cross-peak, which represents the effect of the excitation of the νAM.I vibration on the spectrum of the νCOOD vibration. For this reason, we focus our analysis on the downward cross-peak that represents the effect of the excitation of the carboxylic acid vibration on the νAM.I vibration. The excitation of the νCOOD vibration also leads to a cross-peak signal with the amide II mode (νAM.II) at 1490 cm–1. This signal results from the excitation of low-frequency modes following the relaxation of the νCOOD mode. The excitation of these low-frequency modes affects the absorption spectra of both the νCOOD and νAM.II modes (see SI Appendix, Figure S6a,b).

Figure 2.

Figure 2

Open in a new tab

Isotropic two-dimensional infrared spectra of solutions of hyaluronic acid in D2O at a concentration of 20 mg/mL in the spectral region of the carboxylic acid (νCOOD) and the amide I (νAM.I) vibrations. 2D-IR spectra (a) for the solution state (pH = 1.6) and (b) for the putty state (pH = 2.5). The corresponding linear spectra are shown on the right-hand side of the 2D-IR spectra. The spectra were collected at a delay time Tw of 1.5 ps. The cross-peaks are indicated by the yellow rectangles and show the presence of vibrational interactions between νAM.I and νCOOD. The thick black lines represent the integrated pump region used for the fitting. The pump and probe spectra are centered at 1680 cm–1.

To learn more about the mechanism that underlies the cross-peak signals of the amide I modes following excitation of the COOD vibration, we compare the dependence on time delay for the solution and the putty states (Figure 3a). We normalized the transients to the bleaching signal of the carboxylic acid vibration at early time delay (∼0.2 ps). From ∼1.5 ps on, the decay of the transients is quite similar to that of the νCOOD–νAM.II cross-peak, showing a time constant of ∼3 ps. However, the transients of the νCOOD–νAM.I cross-peak signals have their maximum at 0.3–0.5 ps, a much earlier delay time than the one observed for the νCOOD–νAM.II cross-peak (∼1–1.5 ps). In addition, the transients of the νCOOD–νAM.I cross-peak show an additional faster decay component with a time constant of ∼0.6 ps. Interestingly, the transient of the νCOOD–νAM.I cross-peaks has a much higher intensity at early delay times for the putty state than for the solution state. This observation, together with the dynamics observed for the νCOOD–νAM.II cross-peak, indicates that the νCOOD–νAM.I cross-peak signal contains contributions from two distinct mechanisms: (1) energy transfer from the excited COOD vibration to the amide I vibration; (2) anharmonic coupling to low-frequency modes that affect the vibrational spectrum of the amide I mode. The relaxation model corresponding to these two mechanisms is illustrated in Figure 3b.

Figure 3.

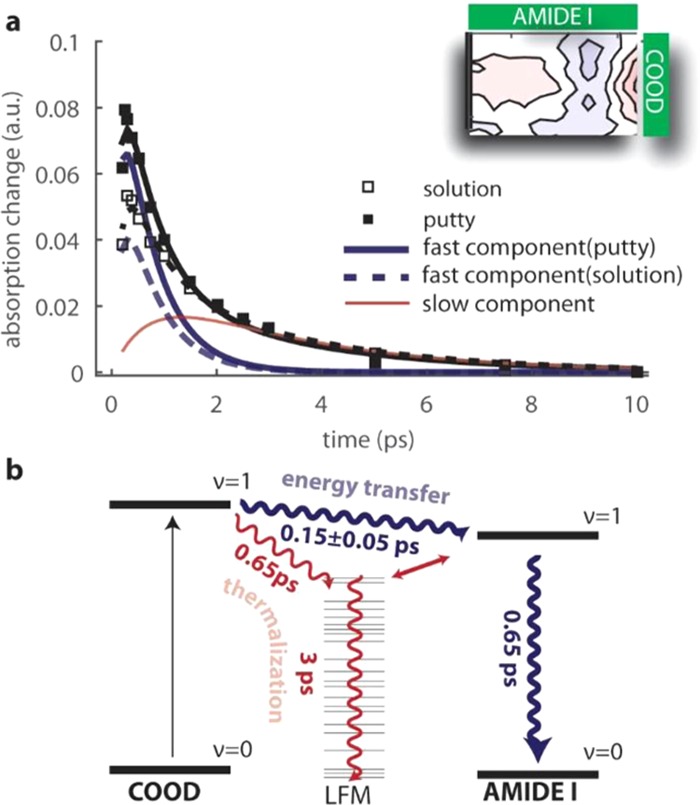
Figure 3

Open in a new tab

a) Decay traces of the cross-peak in the νAM.I vibrational region for hyaluronic acid at a concentration of 20 mg/mL in the solution and putty states. The decay traces are normalized to the carboxylic acid intensity at early time delay. The solid and dashed black lines are fits to the relaxation model (described in the Supporting Information), for the putty and solution states, respectively. The blue lines represent the fast component: thick and dashed lines correspond, respectively, to the putty and solution states. The initial amplitude of the fast component (indicated with cent) is nearly two times larger in the putty state (cent = 0.13 ± 0.01) than in the solution state (cent = 0.077 ± 0.005). The red line represents the contribution of the slow component, whose initial amplitude cth is similar for the putty and solution states (cthputty ≈ cthsol. = 0.024 ± 0.004). Values reported are the mean and standard deviation obtained by averaging over three different independent measurements. (b) Schematic of the relaxation model describing the cross-peak dynamics. Red and blue lines refer, respectively, to the slow component (due to thermalization) and fast component (due to energy transfer) of the cross-peak dynamics. The value shown is the average with standard deviation for six independent measurements.

The cross-peak signal arising from the energy transfer rises with a time constant Tent, representing the time scale of energy transfer from the excited COOD vibration to the accepting amide I vibration, and decays with the vibrational lifetime, T1AM.I, of the amide I vibration. This direct energy transfer does not occur for the amide II mode because there is a rather large energy difference between the νCOOD and νAM.II vibrations. We extract the value of T1AM.I from the diagonal signal of the amide I mode in the 2D-IR spectrum. We find that T1AM.I is comparable to the vibrational lifetime of the COOD vibration: T1AM.I = 0.65 ± 0.1 ps. The time constants of the second mechanism involving anharmonic coupling to low-frequency modes can be extracted from a fit to the transient of the νCOOD–νAM.II cross-peak (SI Appendix, Figure S6b). We thus fit the transients of the νCOOD–νAM.I cross-peak to the following expression containing the lifetimes of the COOD vibration, T1COOD, the amide I vibration, T1AM.I, and the low-frequency-modes, T1LFM

graphic file with name jp-2019-00982f_m001.jpg 1

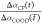Here, Inline graphic is the intensity of the cross-peak normalized to the intensity of the νCOOD vibration at early time delay, t̅ = 200 fs. The parameters canh and cent represent the cross-peak amplitudes associated with the anharmonic coupling and direct energy transfer mechanisms, respectively. Tent, canh, and cent are the only free parameters. As shown in Figure 3a, cent is nearly 2-fold larger for the putty state than for the solution state, whereas canh is comparable for the two states. For the time constant Tent, we obtain a value of 150 ± 50 fs. The energy transfer to the amide I mode constitutes an additional channel for vibrational relaxation of the COOD mode. The fact that we do not observe a significant difference in T1COOD between the putty and the solution state indicates that this energy transfer process occurs only for a minor fraction of the COOD groups. From the values of cent, we estimate this fraction to be 13 ± 2% for the putty state and 7 ± 2% for the solution state. The time constant Tent also does not change upon the formation of the putty state, which shows that the efficiency of the energy transfer remains the same. Hence, upon formation of the putty state only the number of COOD groups showing energy transfer increases.

The ultrafast energy transfer between the C=O vibration of the COOD group and the amide I vibration of the amide group can be well explained from the presence of a hydrogen bond between the COOD and the amide groups.31 To get more information on the nature of this hydrogen bond, we compared the intensity of the νCOOD–νAM.I cross-peak signal for polarizations of the probing pulse parallel and perpendicular to the polarization of the excitation pulse. The ratio of these two signals reveals the relative orientation of the transition dipole moments of the excited and probed vibrations that form the cross-peak signal.32 From the ratio of the signals at Tw between 0.3 and 1 ps (where the energy transfer mechanism is predominant), we find that the angle between the transition dipoles of νCOOD and νAM.I is ∼20° (SI Appendix, Figure S9). As the transition dipole moment of νAM.I is at an angle of 20° relative to the C=O bond of the amide group,33 we conclude that the hydrogen-bond configuration involves a parallel (or anti-parallel) alignment between the C=O groups of the carboxylic acid and amide, forming two closely spaced intermolecular hydrogen bonds between the amide and carboxylic acid groups, i.e., C=O–OD···O=C–ND and −N–D···O=C–OD···O=C–. This geometry, in which the amide and carboxylic acid groups act both as the hydrogen-bond donor and acceptor stabilizing the hydrogen-bonded structure formed by these two molecular groups, constitutes a strong interchain connection. We conclude that the putty state at pH = 2.5 contains a 2-fold higher density of these strong double hydrogen bonds than the solution state at pH = 1.6.

To study the role of the COO– groups in the formation of the putty state, we also measure 2D-IR spectra where we excite and probe the νant,COO– and the νAM.I vibrations. Since the absorption bands of these two vibrations overlap, we subtract the parallel signal from three times the perpendicular signal. In the resulting difference spectrum, the diagonal peaks are strongly suppressed since the corresponding parallel signal is ∼3 times larger than the perpendicular signal. This procedure is thus ideally suited to reveal the presence of cross-peak signals of vibrations that are differently oriented. This strategy has been extensively used in 2D-IR experiments on proteins to resolve vibrational couplings.34Figure 4a reports the resulting difference 2D-IR spectrum at pH = 2.5 (putty state). On the diagonal, we observe some residual signal due to orientational relaxation of the COO– and amide molecular groups.35−37 In addition, we also see clear off-diagonal signals (indicated by the yellow rectangles). In Figure 4b, we plot the transient absorption spectrum at pH = 2.5 (black circles) obtained from Figure 4a by averaging the signals with pump frequencies between 1600 and 1620 cm–1, corresponding to the excitation of the νant,COO– vibration. The resulting spectrum is compared with the transient absorption spectrum at pH = 2.9 that is obtained using the same procedure (SI Appendix, Figure S12). The transient absorption spectrum at pH 2.5 clearly shows an enhanced absorption signal around the amide I vibrational frequency, which implies that the excitation of the νant,COO– vibration yields an enhanced response of the νAM.I vibration at pH = 2.5. This means that in the putty state (pH = 2.5), the interaction between the COO– and amide molecular groups is enhanced. A similar enhancement is observed for the other cross-peak signal, i.e., exciting the amide I vibration and probing the COO– mode (SI Appendix, Figure S11f). Hence, our results show that the formation of single N–D–COO– hydrogen bonds is enhanced in the putty state, in addition to the enhanced presence of double amide–COOH hydrogen bonds in this state.

Figure 4.

Figure 4

Open in a new tab

(a) Difference 2D-IR spectrum for a solution of hyaluronic acid at pH 2.5 at a concentration of 20 mg/mL. The difference 2D-IR spectrum was obtained by subtracting the parallel signal from three times the perpendicular signal. The yellow rectangles indicate the cross-peak signals of the amide I and COO– modes. (b) Transient absorption spectra obtained by averaging over the pump-frequency region between 1600 and 1620 cm–1 at pH 2.5 and 2.9, and normalized with respect to the pure antisymmetric stretching signal of the carboxylate anion group (Figures S10 and S11).

Atomic Force Spectroscopy (AFM)

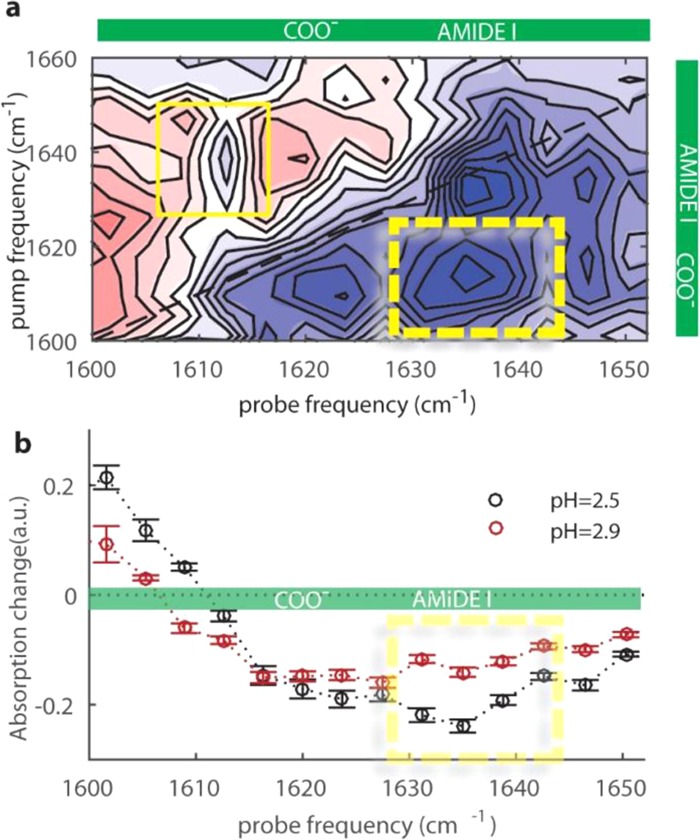
We also perform atomic force microscopy (AFM) imaging of hyaluronic acid solutions at different pH values to investigate to what extent the additional hydrogen bonds in the putty state are formed within or between hyaluronic acid chains (Figure 5a,b). At pH = 7, we mainly observe pearl-necklace conformations: thin chains alternating with thicker globular configurations. The globular portions are likely due to the low affinity for mica.38 At pH = 2.5, the AFM images clearly show a much larger density of thick filaments than at pH = 7, indicative of interchain interactions. To quantify the extent of lateral association of hyaluronan polymers, we measured the heights of the filaments at pH = 7 and 2.5 (Figure 5c). At neutral pH, we find a Gaussian height distribution centered at an average filament height h0 = 0.37 nm. This value is consistent with the expected thickness of a single hyaluronan chain.38 At pH = 2.5, we find a much broader distribution, and h0 = 0.53 nm, meaning that the filaments are thicker. Since the length of the filaments at pH = 2.5 is not changed compared with that at pH = 7, we conclude that this thickening is mainly due to enhanced interchain interactions that laterally associate the strands.

Figure 5.

Figure 5

Open in a new tab

On the top, AFM height images of HA filaments at pH 7 and 2.5, respectively, color coded from 0 nm (dark red) to 1.2 nm (white). The insets show amplitude images of smaller areas of 500 × 500 nm2, indicated by the arrows. Scale bar: 500 nm. On the bottom, filament height distributions with Gaussian fits.

Discussion

The two-dimensional infrared (2D-IR) spectroscopy measurements show that the remarkable pH-triggered gelation of hyaluronic acid at pH 2.5 involves the enhanced formation of double hydrogen bonds between carboxylic acid and amide groups, and of strong single hydrogen bonds between a carboxylate anion (which is a stronger hydrogen-bond acceptor) and amide groups. The enhanced formation of hydrogen bonds is intimately related and even enabled by changes in the structure and electrostatic interactions of the hyaluronan polymer chains.

An important question is why the gelation occurs only in a narrow pH range. In particular, one may wonder why the gelation does not occur for a larger pH range below 2.5, as at lower pH, there will be even more carboxylic acid groups and thus potentially even more strong double hydrogen bonds with the amide groups located on a different chain.

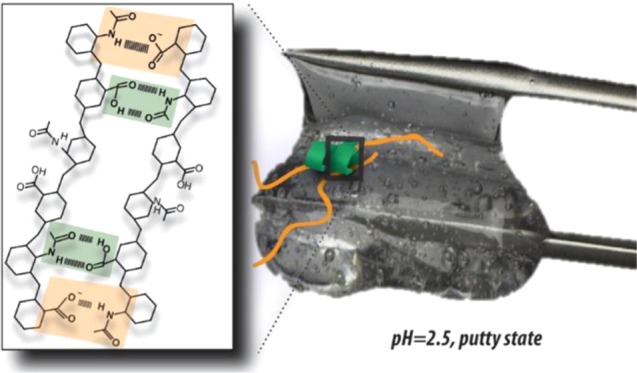
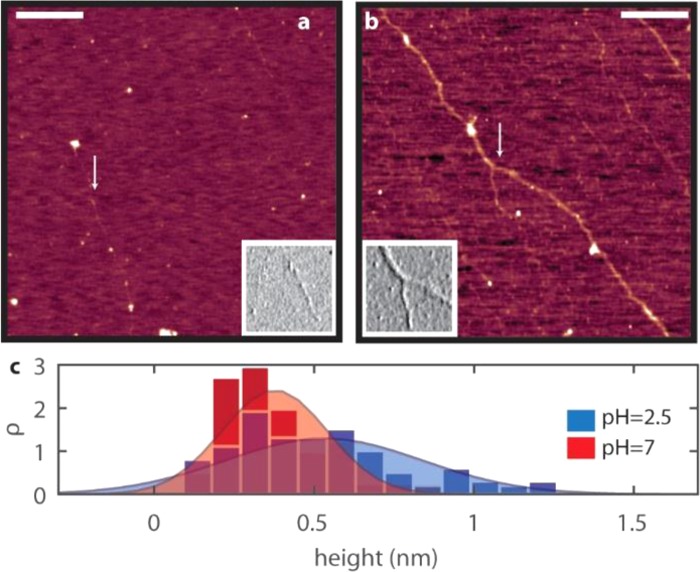
The answer to this question can be found in the special structure of the hyaluronic acid disaccharide unit, which contains a carboxylic acid group and an amide group on neighboring sugar units (see the inset of Figure 1b). The formation of a double amide–carboxylic acid hydrogen-bond structure involves a quite strict local positioning of the hyaluronic acid chains, which prevents the formation of a second double hydrogen-bond structure at the adjacent saccharide units. Hence, the following mechanistic picture arises (Figure 6): at pH = 2.5, the partial deprotonation of the carboxylic acid groups allows for a high probability of forming a strong double amide–COOH hydrogen bond (green box) and an adjacent strong N–D–COO– hydrogen bond (orange box), together forming a very strong interchain connection. In the single N–D–COO– hydrogen bond, the N–D of an amide group acts as the hydrogen bond donor and the COO– anion group as the hydrogen-bond acceptor. For a sufficient length and concentration of the hyaluronic acid chains, this enhanced hydrogen-bond formation will yield a long-range connected network that behaves as an elastic solid, the putty state. This state is not formed at lower pH, because at these pH values, very few carboxylic acid groups are deprotonated and the strong double amide–COOH hydrogen bond can only be combined with a relatively weak single N–D–COOH or single COOH–amide hydrogen bond on the neighboring sugar units, thus forming a weaker interchain connection. As a result, fewer interchain connections are formed (ca. 2-fold less at pH = 1.6), and the overall connectivity is too low to form an elastic gel. Also, at pH values above 2.5, the putty state is not formed because a large fraction of the carboxylic acid groups is deprotonated, which implies that no double amide–COOH hydrogen bonds can be formed. In addition, Coulomb repulsion will prevent the formation of N–D···–O–C hydrogen bonds on neighboring sugar units. As a result, the density of interchain connections is again too low to allow for gel formation.

Figure 6.

Figure 6

Open in a new tab

Schematic images showing the transition from a weakly hydrogen-bonded network of hyaluronan at pH < 2.5 (top left) to a strongly hydrogen-bonded network at pH = 2.5 (right), to isolated single chains at pH > 2.5 (bottom left). At pH = 2.5, the balance between hydrogen-bond and Coulomb repulsion interactions is optimal, and allows the formation of hydrogen bonds between the carboxyl acid and amide groups observed as the fast time component in the cross-peak dynamics in 2D-IR. Green shaded squares indicate the formation of hydrogen bonds between amide and protonated carboxyl groups, whereas orange shaded squares depict the formation of hydrogen bonds between amide and deprotonated carboxyl groups.

Conclusions

In summary, we studied the molecular origin of the putty state of the biologically important polysaccharide hyaluronic acid, which undergoes a sol–gel transformation only in a narrow range around pH = 2.5. Using two-dimensional infrared (2D-IR) spectroscopy, we find that this remarkable transition is accompanied by the enhanced formation of strong interchain connections that consist of a strong double amide–COOH hydrogen bond (green box in Figure 6) and a strong N–D–COO– hydrogen bond (orange box in Figure 6) on the adjacent sugar groups of the hyaluronan disaccharide unit. These strong collective interchain connections can only form when the carboxylic acid groups are partially deprotonated, which explains why the putty state is observed only in a narrow pH range. The enhanced interchain connectivity in the putty state is confirmed by AFM measurements that reveal the association of hyaluronan into thick strands in this state.

This study illustrates that the combination of 2D-IR spectroscopy, AFM, and rheology constitutes a unique tool to identify the molecular mechanisms by which hydrogels respond to environmental stimuli. This combined multiscale approach has great potential to investigate the molecular origin of the biological functionalities of other natural polyelectrolytes and to assist in the rational design of supramolecular biomaterials with life-like functionalities.14

Acknowledgments

This work is part of the industrial partnership programme Hybrid Soft Materials that is carried out under an agreement between Unilever Research and the Netherlands Organisation for Scientific Research (NWO). The authors wish to thank Lukas Helmbrecht for making the photographs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b00982.

  • Data analysis methods; hyaluronic acid gel pictures; rheology experiments in water; linear infrared spectra; anisotropy data; 2D-IR spectra; AFM measurements (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp9b00982_si_001.pdf (1.1MB, pdf)

References

  1. Chaudhuri O.; Gu L.; Klumpers D.; Darnell M.; Bencherif S. A.; Weaver J. C.; Huebsch N.; Lee H.; Lippens E.; Duda G. N.; et al. Hydrogels with Tunable Stress Relaxation Regulate Stem Cell Fate and Activity. Nat. Mater. 2016, 15, 326–334. 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Engler A. J.; Sen S.; Sweeney H. L.; Discher D. E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell 2006, 126, 677–689. 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
  3. Vining K. H.; Mooney D. J. Mechanical Forces Direct Stem Cell Behaviour in Development and Regeneration. Nat. Rev. Mol. Cell Biol. 2017, 728–742. 10.1038/nrm.2017.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lee H.; Gu L.; Mooney D. J.; Levenston M. E.; Chaudhuri O. Mechanical Confinement Regulates Cartilage Matrix Formation by Chondrocytes. Nat. Mater. 2017, 16, 1243–1251. 10.1038/nmat4993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Green J. J.; Elisseeff J. H. Mimicking Biological Functionality with Polymers for Biomedical Applications. Nature 2016, 386–394. 10.1038/nature21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rosales A. M.; Anseth K. S. The Design of Reversible Hydrogels to Capture Extracellular Matrix Dynamics. Nat. Rev. Mater. 2016, 1, 15012. 10.1038/natrevmats.2015.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hamm P.; Zanni M.. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press, 2011. [Google Scholar]
  8. Kolano C.; Helbing J.; Kozinski M.; Sander W.; Hamm P. Watching Hydrogen-Bond Dynamics in a β-Turn by Transient Two-Dimensional Infrared Spectroscopy. Nature 2006, 444, 469–472. 10.1038/nature05352. [DOI] [PubMed] [Google Scholar]
  9. Kogan G.; Šoltés L.; Stern R.; Gemeiner P. Hyaluronic Acid: A Natural Biopolymer with a Broad Range of Biomedical and Industrial Applications. Biotechnol. Lett. 2006, 29, 17–25. 10.1007/s10529-006-9219-z. [DOI] [PubMed] [Google Scholar]
  10. Tian X.; Azpurua J.; Hine C.; Vaidya A.; Myakishev-Rempel M.; Ablaeva J.; Mao Z.; Nevo E.; Gorbunova V.; Seluanov A. High-Molecular-Mass Hyaluronan Mediates the Cancer Resistance of the Naked Mole Rat. Nature 2013, 499, 346–349. 10.1038/nature12234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Singh A.; Corvelli M.; Unterman S. A.; Wepasnick K. A.; McDonnell P.; Elisseeff J. H. Enhanced Lubrication on Tissue and Biomaterial Surfaces through Peptide-Mediated Binding of Hyaluronic Acid. Nat. Mater. 2014, 13, 988–995. 10.1038/nmat4048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kayitmazer A. B.; Koksal A. F.; Kilic Iyilik E. Complex Coacervation of Hyaluronic Acid and Chitosan: Effects of PH, Ionic Strength, Charge Density, Chain Length and the Charge Ratio. Soft Matter 2015, 11, 8605–8612. 10.1039/C5SM01829C. [DOI] [PubMed] [Google Scholar]
  13. Lalevée G.; David L.; Montembault A.; Blanchard K.; Meadows J.; Malaise S.; Crépet A.; Grillo I.; Morfin I.; Delair T.; et al. Highly Stretchable Hydrogels from Complex Coacervation of Natural Polyelectrolytes. Soft Matter 2017, 13, 6594–6605. 10.1039/C7SM01215B. [DOI] [PubMed] [Google Scholar]
  14. Webber M. J.; Appel E. A.; Meijer E. W.; Langer R. Supramolecular Biomaterials. Nat. Mater. 2016, 15, 13–26. 10.1038/nmat4474. [DOI] [PubMed] [Google Scholar]
  15. Rosales A. M.; Vega S. L.; DelRio F. W.; Burdick J. A.; Anseth K. S. Hydrogels with Reversible Mechanics to Probe Dynamic Cell Microenvironments. Angew. Chem., Int. Ed. 2017, 56, 12132–12136. 10.1002/anie.201705684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Balazs E. A.; Cui J. The Story of Hyaluronan Putty. Bioact. Carbohydr. Diet. Fibre 2013, 2, 143–151. 10.1016/j.bcdf.2013.10.004. [DOI] [Google Scholar]
  17. Gibbs D. A.; Merrill E. W.; Smith K. A.; Balazs E. A. Rheology of Hyaluronic Acid. Biopolymers 1968, 6, 777–791. 10.1002/bip.1968.360060603. [DOI] [PubMed] [Google Scholar]
  18. Gatej I.; Popa M.; Rinaudo M. Role of the PH on Hyaluronan Behavior in Aqueous Solution. Biomacromolecules 2005, 6, 61–67. 10.1021/bm040050m. [DOI] [PubMed] [Google Scholar]
  19. Wu S.; Ai L.; Chen J.; Kang J.; Cui S. W. Study of the Mechanism of Formation of Hyaluronan Putty at PH 2.5: Part I. Experimental Measurements. Carbohydr. Polym. 2013, 98, 1677–1682. 10.1016/j.carbpol.2013.05.088. [DOI] [PubMed] [Google Scholar]
  20. Chakrabarti B.; Balazs E. A. Optical Properties of Hyaluronic Acid. Ultraviolet Circular Dichroism and Optical Rotatory Dispersion. J. Mol. Biol. 1973, 78, 135–141. 10.1016/0022-2836(73)90433-6. [DOI] [PubMed] [Google Scholar]
  21. Staskus P. W.; Johnson W. C. Conformational Transition of Hyaluronic Acid in Aqueous-Organic Solvent Monitored by Vacuum Ultraviolet Circular Dichroism. Biochemistry 1988, 27, 1522–1527. 10.1021/bi00405a019. [DOI] [PubMed] [Google Scholar]
  22. Dea I. C.; Moorhouse R.; Rees D. A.; Arnott S.; Guss J. M.; Balazs E. A. Hyaluronic Acid: A Novel, Double Helical Molecule. Science 1973, 179, 560–562. 10.1126/science.179.4073.560. [DOI] [PubMed] [Google Scholar]
  23. Sheehan J. K.; Gardner K. H.; Atkins E. D. T. Hyaluronic Acid: A Double-Helical Structure in the Presence of Potassium at Low PH and Found Also with the Cations Ammonium, Rubidium and Caesium. J. Mol. Biol. 1977, 117, 113–135. 10.1016/0022-2836(77)90027-4. [DOI] [PubMed] [Google Scholar]
  24. Scott J. E.; Heatley F. Biological Properties of Hyaluronan in Aqueous Solution Are Controlled and Sequestered by Reversible Tertiary Structures, Defined by NMR Spectroscopy. Biomacromolecules 2002, 3, 547–553. 10.1021/bm010170j. [DOI] [PubMed] [Google Scholar]
  25. Blundell C. D.; Deangelis P. L.; Almond A. Hyaluronan: The Absence of Amide-Carboxylate Hydrogen Bonds and the Chain Conformation in Aqueous Solution Are Incompatible with Stable Secondary and Tertiary Structure Models. Biochem. J. 2006, 396, 487–498. 10.1042/BJ20060085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gribbon P.; Heng B. C.; Hardigham T. E. The Analysis of Intermolecular Interactions in Concentrated Hyaluronan Solutions Suggest No Evidence for Chain–chain Association. Biochem. J. 2000, 350, 329. 10.1042/bj3500329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mansel B. W.; Chu C. Y.; Leis A.; Hemar Y.; Chen H. L.; Lundin L.; Williams M. A. K. Zooming in: Structural Investigations of Rheologically Characterized Hydrogen-Bonded Low-Methoxyl Pectin Networks. Biomacromolecules 2015, 16, 3209–3216. 10.1021/acs.biomac.5b00870. [DOI] [PubMed] [Google Scholar]
  28. Selig O.; Siffels R.; Rezus Y. L. A. Ultrasensitive Ultrafast Vibrational Spectroscopy Employing the Near Field of Gold Nanoantennas. Phys. Rev. Lett. 2015, 114, 233004 10.1103/PhysRevLett.114.233004. [DOI] [PubMed] [Google Scholar]
  29. Nečas D.; Klapetek P. Gwyddion: An Open-Source Software for SPM Data Analysis. Cent. Eur. J. Phys. 2012, 181–188. 10.2478/s11534-011-0096-2. [DOI] [Google Scholar]
  30. Krȩżel A.; Bal W. A Formula for Correlating PKa Values Determined in D2O and H2O. J. Inorg. Biochem. 2004, 98, 161–166. 10.1016/j.jinorgbio.2003.10.001. [DOI] [PubMed] [Google Scholar]
  31. De Marco L.; Thämer M.; Reppert M.; Tokmakoff A. Direct Observation of Intermolecular Interactions Mediated by Hydrogen Bonding. J. Chem. Phys. 2014, 141, 034502 10.1063/1.4885145. [DOI] [PubMed] [Google Scholar]
  32. Bodis P.; Panman M. R.; Bakker B. H.; Mateo-Alonso A.; Prato M.; Buma W. J.; Brouwer A. M.; Kay E. R.; Leigh D. A.; Woutersen S. Two-Dimensional Vibrational Spectroscopy of Rotaxane-Based Molecular Machines. Acc. Chem. Res. 2009, 42, 1462–1469. 10.1021/ar9000845. [DOI] [PubMed] [Google Scholar]
  33. Krimm S.; Bandekar J.. Vibrational Spectroscopy and Conformation of Peptides, Polypeptides, and Proteins. In Advances in Protein Chemistry; Academic Press, 1986; Vol. 38, pp 181–364. [DOI] [PubMed] [Google Scholar]
  34. Woutersen S.; Hamm P. Isotope-edited two-dimensional vibrational spectroscopy of trialanine in aqueous solution. J. Chem. Phys. 2001, 114, 2727–2737. 10.1063/1.1336807. [DOI] [Google Scholar]
  35. Hamm P.; Lim M.; Hochstrasser R. M. Structure of the Amide I Band of Peptides Measured by Femtosecond Nonlinear-Infrared Spectroscopy. J. Phys. Chem. B 1998, 102, 6123–6138. 10.1021/jp9813286. [DOI] [Google Scholar]
  36. DeCamp M. F.; DeFlores L.; McCracken J. M.; Tokmakoff A.; Kwac K.; Cho M. Amide I Vibrational Dynamics of N-Methylacetamide in Polar Solvents: The Role of Electrostatic Interactions. J. Phys. Chem. B 2005, 109, 11016–11026. 10.1021/jp050257p. [DOI] [PubMed] [Google Scholar]
  37. Cunha A. V.; Salamatova E.; Bloem R.; Roeters S. J.; Woutersen S.; Pshenichnikov M. S.; Jansen T. L. C. Interplay between Hydrogen Bonding and Vibrational Coupling in Liquid N-Methylacetamide. J. Phys. Chem. Lett. 2017, 8, 2438–2444. 10.1021/acs.jpclett.7b00731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Cowman M. K.; Spagnoli C.; Kudasheva D.; Li M.; Dyal A.; Kanai S.; Balazs E. A. Extended, Relaxed, and Condensed Conformations of Hyaluronan Observed by Atomic Force Microscopy. Biophys. J. 2005, 88, 590–602. 10.1529/biophysj.104.049361. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp9b00982_si_001.pdf (1.1MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES