Combinatorial Control through Allostery

Abstract

Many instances of cellular signaling and transcriptional regulation involve switch-like molecular responses to the presence or absence of input ligands. To understand how these responses come about and how they can be harnessed, we develop a statistical mechanical model to characterize the types of Boolean logic that can arise from allosteric molecules following the Monod-Wyman-Changeux (MWC) model. Building upon previous work, we show how an allosteric molecule regulated by two inputs can elicit AND, OR, NAND and NOR responses, but is unable to realize XOR or XNOR gates. Next, we demonstrate the ability of an MWC molecule to perform ratiometric sensing - a response behavior where activity depends monotonically on the ratio of ligand concentrations. We then extend our analysis to more general schemes of combinatorial control involving either additional binding sites for the two ligands or an additional third ligand and show how these additions can cause a switch in the logic behavior of the molecule. Overall, our results demonstrate the wide variety of control schemes that biological systems can implement using simple mechanisms.

Introduction

A hallmark of cellular signaling and regulation is combinatorial control. Disparate examples ranging from metabolic enzymes to actin polymerization to transcriptional regulation involve multiple inputs that often give rise to a much richer response than what could be achieved through a single-input. For example, the bacterial enzyme phosphofructokinase in the glycolysis pathway is allosterically regulated by both ADP and PEP.¹ Whereas PEP serves as an allosteric inhibitor, ADP is both an allosteric activator and a competitive inhibitor depending upon its concentration. This modulation by multiple allosteric ligands gives rise to a complex control of the flux through the glycolytic pathway: increasing ADP concentration first increases the activity of phosphofructokinase (via the allosteric modulation) but ultimately decreases it (from competitive inhibition). Another example is offered by the polymerization of actin at the leading edge of motile cells. In particular, the presence of two ligands, Cdc42 and PIP2, is required to activate the protein N-WASP by binding to it in a way that permits it to then activate the Arp2/3 complex and stimulate actin polymerization.²

In the context of transcriptional regulation, an elegant earlier work explored the conditions under which transcriptional regulatory networks could give rise to the familiar Boolean logic operations, like those shown in Figure 1.³ There it was found that the combined effect of two distinct transcription factors on the transcriptional activity of a given promoter depend upon their respective binding strengths as well as the cooperative interactions between each other and the RNA polymerase. Indeed, by tuning the binding strengths and cooperativity parameters, one could generate a panoply of different logic gates such as the familiar AND, OR, NAND (NOT-AND) and NOR (NOT-OR) gates, known from the world of digital electronics.³

Figure 1. Logic gates as molecular responses.

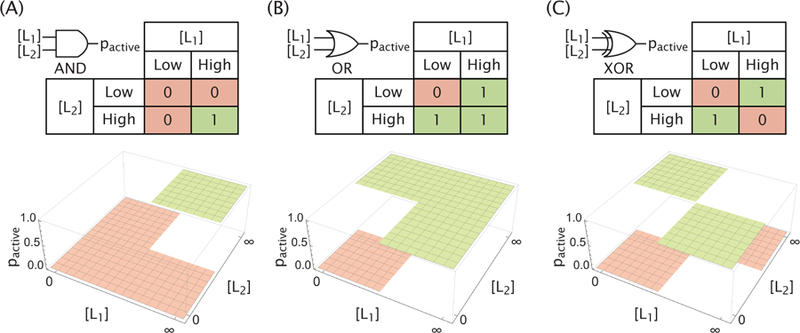
The (A) AND, (B) OR, and (C) XOR gates are represented through their corresponding logic tables as well as target activity profiles regulated by two ligands. The behavior of each gate is measured solely by its activity in the absence and at saturating concentrations of each ligand and not by the character of the active/inactive transition.

Here we explore the diversity of combinatorial responses that can be effected by a single allosteric molecule by asking if such molecules can yield multi-input combinatorial control in the same way that transcriptional networks have already been shown to. Specifically, we build on earlier work that shows that an allosteric molecule described by the Monod-Wyman-Changeux (MWC) model can deliver input-output functions similar to the ideal logic gates described in Figure 1.^4–6 In the MWC model, an allosteric molecule exists in a thermodynamic equilibrium between active and inactive states, with the relative occupancy of each state being modulated by regulatory ligands. ⁷ We use statistical mechanics to characterize the input-output response of such a molecule in the limits where each of the two ligands is either absent or at a saturating concentration and determine the necessary conditions to form the various logic gates, with our original contribution on this point focusing on a systematic exploration of the MWC parameter space for each logic gate.

We then analyze the MWC response modulated by two input ligands but outside of traditional Boolean logic functions. In particular, we show how, by tuning the MWC parameters, the response (probability of the allosteric protein being active) in any three of the four concentration limits can be explicitly controlled, along with the ligand concentrations at which transitions between these limit responses occur. Focusing next on the profile of the response near the transition concentrations, we demonstrate how an MWC molecule can exhibit ratiometric sensing which was observed experimentally in the bone morphogenetic protein (BMP) signaling pathway⁸ as well as in galactose metabolic (GAL) gene induction in yeast.⁹

Additionally, we extend our analysis of logic responses to cases beyond two-ligand control with a single binding site for each ligand. We first discuss the effect of the number of binding sites on the logic response and demonstrate how altering that number, which can occur through evolution or synthetic design, is able to cause a switch in the logic-behavior of an MWC molecule, such as transitioning from AND into OR behavior. Next, we explore the increased diversity of logic responses that can be achieved by three-ligand MWC molecules compared with the two-ligand case and offer an interesting perspective on the role of the third ligand as a regulator that can switch the logic-behavior formed by the other two ligands. We end by a discussion of our theoretical results in the context of a growing body of experimental works on natural and de novo designed molecular logic gates. In total, these results hint at simple mechanisms that biological systems can utilize to refine their combinatorial control.

Results

Logic Response of an Allosteric Protein Modulated by Two Ligands

Consider an MWC molecule, as shown in Figure 2, that fluctuates between active and inactive states (with $\Delta {\text{ε}}_{\text{AI}}$ defined as the free energy difference between the inactive and active states in the absence of ligand). We enumerate the entire set of allowed states of activity and ligand occupancy, along with their corresponding statistical weights. The probability that this protein is active depends on the concentrations of two input molecules, [L₁] and [L₂], and is given by

$${\text{p}}_{\text{active}}\left(\left[{\text{L}}_{\text{1}}\right],\left[{\text{L}}_{\text{2}}\right]\right)=\frac{\left(1+\frac{\left[{\text{L}}_1\right]}{{\text{K}}_{\text{A,1}}}\right)\left(1+\frac{\left[{\text{L}}_2\right]}{{\text{K}}_{\text{A,2}}}\right)}{\left(1+\frac{\left[{\text{L}}_1\right]}{{\text{K}}_{\text{A,1}}}\right)\left(1+\frac{\left[{\text{L}}_2\right]}{{\text{K}}_{\text{A,2}}}\right)+{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\left(1+\frac{\left[{\text{L}}_1\right]}{{\text{K}}_{\text{I,1}}}\right)\left(1+\frac{\left[{\text{L}}_2\right]}{{\text{K}}_{\text{I,2}}}\right)},$$ (1)

where K_A,i and K_I,i are the dissociation constants between the i^th ligand and the active or inactive protein, respectively. We begin with the two-input case such that i = 1 or 2.

Figure 2. States and weights for the allosteric protein.

The two different ligands (blue circle (i = 1) and red triangle (i = 2)) are present at concentrations [L_i] and with a dissociation constant K_A,i in the active state and K_I,i in the inactive state. The energetic difference between the inactive and active states is denoted by $\Delta {\text{ε}}_{\text{AI}}={\text{ε}}_{\text{I}}-{\text{ε}}_{\text{A}}$. Total weights of the active and inactive states are shown below each column and are obtained by summing all the weights in that column.

To determine whether this allosteric protein can serve as a molecular logic gate, we first evaluate the probability that it is active when each ligand is either absent ([L_i] → 0) or at a saturating concentration ([L_i] → ∞). Figure 3A evaluates these limits for eq 1, where we have introduced the parameters ${\text{γ}}_1=\frac{{\text{K}}_{\text{A,1}}}{{\text{K}}_{\text{I,1}}}$ and ${\text{γ}}_2=\frac{{\text{K}}_{\text{A,2}}}{{\text{K}}_{\text{I,2}}}$ to simplify the results.

Figure 3. Logic gate realization of an allosteric protein with two ligands.

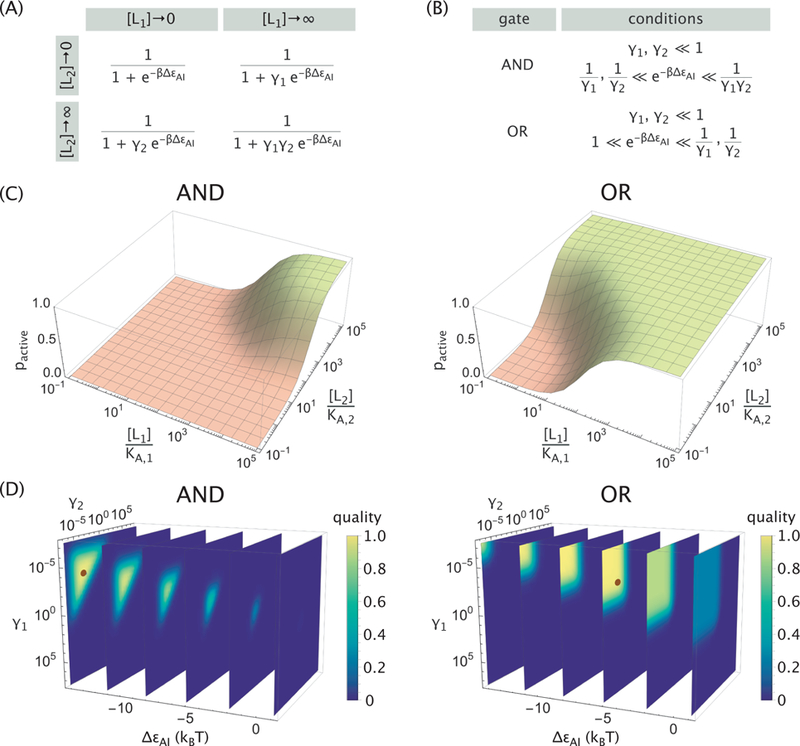
(A) Probability that the protein is active (p_active) in different limits (rows and columns of the matrix) of ligand concentrations, where ${\text{γ}}_i=\frac{{\text{K}}_{\text{A,i}}}{{\text{K}}_{\text{I,i}}}$. (B) Conditions on the parameters that lead to an AND or OR response. (C) Realizations of the AND and OR logic gates. Parameters used were K_A,1 = K_A,2 = 2.5 × 10⁻⁸ M, K_I,1 = K_I,2 = 1.5 × 10⁻⁴ M, and ∆ε_AI = −14.2 k_BT for the AND gate or ∆ε_AI = −5.0 k_BT for the OR gate. (D) Quality of AND (eq 3) and OR (eq 4) gates across parameter space. The brown dots indicate the high quality gates in Panel C.

The probabilities in Figure 3A can be compared to the target functions in Figure 1 to determine the conditions on each parameter that would be required to form a given logic gate. For example, the AND, OR, and XOR gates require that in the absence of either ligand ([L₁] = [L₂] = 0), there should be as little activity as possible, thereby requiring that the active state has a higher (more unfavored) free energy than the inactive state $\left({\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\gg 1\right)$. We note that in the context of transcriptional regulation, this limit of activity in the absence of ligands is called the leakiness, ¹⁰ and it is one of the distinguishing features of the MWC model in comparison with other allosteric models such as the Koshland-Némethy-Filmer (KNF) model that exhibits no leakiness.

For the AND and OR gates, the condition that p_active ≈1 when both ligands are saturating ([L₁], [L₂]→ ∞) requires that ${\text{γ}}_{\text{1}}{\text{γ}}_{\text{2}}{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\ll 1$. The two limits where one ligand is absent while the other ligand is saturating lead to the conditions shown in Figure 3B for the AND and OR gates, with representative response profiles s hown in Figure 3C using parameter values from the single-ligand allosteric nicotinic acetylcholine receptor.¹¹ We relegate the derivations to Appendix A, where we also demonstrate that the XOR gate cannot be realized with the form of p_active in eq 1 unless explicit cooperativity is added to the MWC model. In addition, we show that the NAND, NOR, and XNOR gates can be formed if and only if their complementary AND, OR, and XOR gates can be formed, respectively, by replacing $\Delta {\text{ε}}_{\text{AI}}\to -\Delta {\text{ε}}_{\text{AI}}$ and ${\text{γ}}_{\text{i}}\to \frac{1}{{\text{γ}}_{\text{i}}}$. Finally, Figure 3C demonstrates that the same dissociation constants K_A,i and K_I,i can give rise to either AND or OR behavior by modulating $\Delta {\text{ε}}_{\text{AI}}$, with the transition between these two logic gates occurring at ${\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\approx \frac{1}{{\text{γ}}_{\text{1}}}\approx \frac{1}{{\text{γ}}_{\text{2}}}$ (this corresponds to $\Delta {\text{ε}}_{\text{AI}}\approx -{\text{9k}}_{\text{B}}\text{T}$ for the values of K_A,i and K_I,i in Figure 3).

To explore the gating behavior changes across parameter space, we define a quality metric for how closely p_active matches its target value at different concentration limits for a given idealized logic gate,

$$\text{Q}\left({\text{γ}}_{\text{1}},{\text{γ}}_2,\Delta {\text{ε}}_{\text{AI}}\right)=\prod _{{\lambda }_1=0,\infty }\prod _{{\lambda }_2=0,\infty }\left(1-\left|{\text{p}}_{{\lambda }_1,{\lambda }_2}^{\text{ideal}}-{\text{p}}_{{\lambda }_1,{\lambda }_2}\right|\right),$$ (2)

where ${\text{p}}_{{\lambda }_1,{\lambda }_2}={\text{p}}_{\text{active}}\left(\left[{\text{L}}_{\text{1}}\right]\to {\lambda }_1,\left[{\text{L}}_2\right]\to {\lambda }_2\right)$. A value of 1 (high quality gate) implies a perfect match between the target function and the behavior of the allosteric molecule while a value near 0 (low quality gate) suggests that the response behavior deviates from the target function in at least one limit.

From eq 2, the quality for the AND gate becomes

$${\text{Q}}_{\text{AND}}=\left(1-{\text{p}}_{\text{0,0}}\right)\left(1-{\text{p}}_{\infty ,0}\right)\left(1-{\text{p}}_{\text{0,}\infty }\right){\text{p}}_{\infty \text{,}\infty },$$ (3)

while for the OR gate it takes on the form

$${\text{Q}}_{\text{OR}}=\left(1-{\text{p}}_{\text{0,0}}\right){\text{p}}_{\infty \text{,}0}{\text{p}}_{0\text{,}\infty }{\text{p}}_{\infty \text{,}\infty }.$$ (4)

Figure 3D shows the regions in parameter space where the protein exhibits these gating behaviors (the high quality gates from Figure 3C are denoted by brown dots). More specifically, for a fixed $\Delta {\text{ε}}_{\text{AI}}$, the AND behavior is achieved in a finite triangular region in the γ₁-γ₂ plane which grows larger as $\Delta {\text{ε}}_{\text{AI}}$ decreases. The OR gate, on the other hand, is achieved in an infinite region defined by ${\text{γ}}_{\text{1}},{\text{γ}}_2\lesssim {\text{e}}^{\text{β}\Delta {\text{ε}}_{\text{AI}}}$. In either case, a high quality gate can be obtained only when the base activity is very low $\left(\Delta {\text{ε}}_{\text{AI}}\lesssim 0\right)$ and when both ligands are strong activators $\left({\text{γ}}_{\text{1}},{\text{γ}}_2\ll 1\right)$, in agreement with the derived conditions (Figure 3B). Lastly, we note that the quality metrics for AND/OR and their complementary NAND/NOR gates obey a simple relation, namely, ${\text{Q}}_{\text{AND}/\text{OR}}\left({\text{γ}}_{\text{1}},{\text{γ}}_2,\Delta {\text{ε}}_{\text{AI}}\right)={\text{Q}}_{\text{NAND}/\text{NOR}}\left(\frac{1}{{\text{γ}}_{\text{1}}},\frac{1}{{\text{γ}}_2},-\Delta {\text{ε}}_{\text{AI}}\right)$, which follows from the functional form of eq 2 and the symmetry between the two gates (see Appendix A).

General Two-Ligand MWC Response

We next relax the constraint that p_active must either approach 0 or 1 in the limits of no ligand or saturating ligand and consider the general behavior that can be achieved by an MWC molecule in the four limits shown in Figure 3A. Manipulating the three parameters $\left({\text{γ}}_{\text{1}},{\text{γ}}_2\hspace{0.17em}\text{and}\hspace{0.17em}\Delta {\text{ε}}_{\text{AI}}\right)$ enables us to fix three of the four limits of p_active, and these three choices determine the remaining limit. For example, the parameters in Figure 4A were chosen so that p_0,0 = 0.5 (∆ε_AI = 0), p_0,∞ ≈ 0.9 (γ₂ = 0.1), and p_∞,0 ≈ 0.05 (γ₁ = 20), which fixed p_∞,∞ ≈ 0.3 for the final limit.

Figure 4. General MWC response with two ligands.

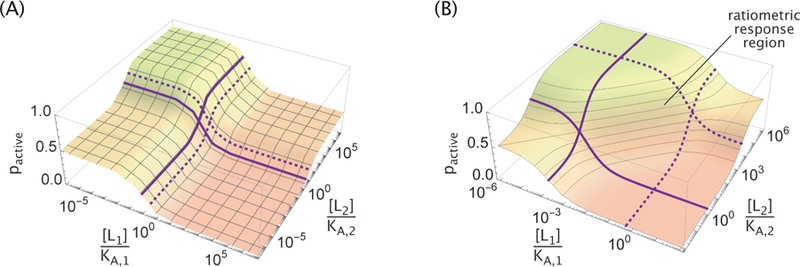
(A) Three of the four limits of ligand concentrations ([L₁], [L₂] → 0 or ∞) can be fixed by the parameters ∆ε_AI, γ₁, and γ₂. Additionally, the midpoint of the [L_i] response when [L_j] → 0 (solid purple curve) or [L_j] → ∞ (dashed purple curve) can be adjusted. (B) Within the region determined by the four midpoints, the MWC response becomes ratiometric⁸ where the concentration ratio of the two ligands determines the activity of the molecule. This is illustrated by the diagonal contour lines of constant p_active in the ratiometric response region.

In addition to the limits of p_active, the locations of the transitions between these limits can be controlled by changing K_A,i and K_I,i while keeping ${\text{γ}}_{\text{i}}=\frac{{\text{K}}_{\text{A,i}}}{{\text{K}}_{\text{I,i}}}$ constant. In Appendix B we generalize previous results for the transition of a single-ligand MWC receptor ¹² to the present case of two ligands. Interestingly, we find that the midpoint ${\left[{\text{L}}_1^{\ast }\right]}_{\left[{\text{L}}_{\text{2}}\right]\hspace{0.17em}\to 0}$ of the response in the absence of [L₂] (solid curve in Figure 4A) is different from the midpoint ${\left[{\text{L}}_1^{\ast }\right]}_{\left[{\text{L}}_{\text{2}}\right]\hspace{0.17em}\to \infty }$ of the response at saturating [L₂] (dashed curve in Figure 4A), with analogous statements holding for the second ligand. More precisely, the two transition points occur at

$${\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to 0}={\text{K}}_{\text{A,i}}\frac{1+{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}}{1+{\text{γ}}_{\text{i}}{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}},$$ (5)

$${\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to \hspace{0.17em}\infty }={\text{K}}_{\text{A,i}}\frac{1+{\text{γ}}_{\text{j}}{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}}{1+{\text{γ}}_1{\text{γ}}_2{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}}.$$ (6)

Notably, the ratio

$$\frac{{\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to \hspace{0.17em}\infty }}{{\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to \hspace{0.17em}0}}=\frac{\left(1+{\text{γ}}_{\text{1}}{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\right)\left(1+{\text{γ}}_2{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\right)}{\left(1+{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\right)\left(1+{\text{γ}}_{\text{1}}{\text{γ}}_2{\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\right)}$$ (7)

is invariant to ligand swapping (i ↔ j); hence, the transition zones, defined as the concentration intervals between solid and dotted curves, have identical sizes for the two ligands, as can be seen in Figure 4.

The MWC response has its steepest slope when the ligand concentration is within the range set by ${\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to \hspace{0.17em}0}$ and ${\left[{\text{L}}_{\text{i}}^{\ast }\right]}_{\left[{\text{L}}_{\text{j}}\right]\hspace{0.17em}\to \hspace{0.17em}\infty }$, and interesting response behaviors can arise when both ligand concentrations fall into this regime. For example, Antebi et al. recently showed that the BMP pathway exhibits ratiometric response where pathway activity depends monotonically on the ratio of the ligand concentrations. ⁸ Similar response functions have also been observed in the GAL pathway in yeast, where gene induction is sensitive to the ratio of galactose and glucose.⁹ Such behavior can be achieved within the highly sensitive region of the MWC model using one repressor ligand (L₁) and one activator ligand (L₂), as shown in Figure 4B. Parameters chosen for demonstration are $\Delta {\text{ε}}_{\text{AI}}=0,{\text{K}}_{\text{A,1}}={\text{K}}_{\text{A,2}}$ and $\frac{{\text{K}}_{\text{I,1}}}{{\text{K}}_{\text{A,1}}}=\frac{{\text{K}}_{\text{A,2}}}{{\text{K}}_{\text{I,2}}}={10}^{-4}$ In this regime, the probability of the protein being active gets reduced

$${\text{p}}_{\text{active}}\left(\left[{\text{L}}_{\text{1}}\right],\left[{\text{L}}_2\right]\right)\approx \frac{\frac{\left[{\text{L}}_{\text{2}}\right]}{{\text{K}}_{\text{A,2}}}}{\frac{\left[{\text{L}}_{\text{2}}\right]}{{\text{K}}_{\text{A,2}}}+\frac{\left[{\text{L}}_1\right]}{{\text{K}}_{\text{I,1}}}},$$ (8)

which clearly depends monotonically on the [L₂]/[L₁] ratio (see Appendix B for details). We note that the region over which the ratiometric behavior is observed can be made arbitrarily large by decreasing the ratios $\frac{{\text{K}}_{\text{I,1}}}{{\text{K}}_{\text{A,1}}}$ and $\frac{{\text{K}}_{\text{A,2}}}{{\text{K}}_{\text{I,2}}}$.

Modulation by Multiple Ligands

A much richer repertoire of signaling responses is available to an MWC protein if we go beyond two ligand inputs with a single binding site for each, as exhibited by phosphofructokinase, for example. Though earlier we mentioned phosphofructokinase in the context of two of its input ligands, in fact, this enzyme has even more inputs than that and thus provides a rich example of multi-ligand combinatorial control. ¹ To start exploring the diversity of these responses, we generalize eq 1 to consider cases with N input ligands, where the i^th ligand has n_i binding sites, concentration [L_i], and dissociation constants K_A,i and K_I,i with the molecule’s active and inactive states, respectively. In general, it is impractical to write the states and weights as we have done in Figure 2, since the total number of possible states, given by $2^{1+{\sum }_{\text{i=1}}^{\text{N}}\hspace{0.17em}{\text{n}}_{\text{i}}}$, grows exponentially with the number of binding sites. However, by analogy with the earlier simple case, the general formula for the probability that the protein is active can be written as

$${\text{P}}_{\text{active}}([{\text{L}}_1],[{\text{L}}_2],\dots ,[{\text{L}}_{\mathrm{N}}]=\frac{{{\prod }_{\text{i}=1}^{\text{N}}\left(1+\frac{[{\text{L}}_{\text{i}}]}{{\text{K}}_{\text{A},\text{i}}}\right)}^{{\text{n}}_{\text{i}}}}{{{\prod }_{\text{i}=1}^{\text{N}}\left(1+\frac{[{\text{L}}_{\text{i}}]}{{\text{K}}_{\text{A},\text{i}}}\right)}^{{\text{n}}_{\text{i}}}+{\text{e}}^{-\mathrm{\beta }\mathrm{\Delta }{\mathrm{\epsilon }}_{\text{A}\mathrm{I}}}{{\prod }_{\text{i}=1}^{\text{N}}\left(1+\frac{[{\text{L}}_{\text{i}}]}{{\text{K}}_{\text{I},\text{i}}}\right)}^{{\text{n}}_{\text{i}}}}.$$ (9)

We first consider an MWC molecule with N = 2 input ligands as in the previous section but with n_i ligand binding sites for ligand i. As derived in Appendix C, the criteria for the AND and OR gates are identical to those for a protein with n_i = 1 binding site per ligand, except that we make the ${\text{γ}}_{\text{i}}\to {\text{γ}}_{\text{i}}^{{\text{n}}_{\text{i}}}$ substitution in the conditions shown in Figure 3B. The protein thus exhibits OR behavior if ${\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\ll \min \left(\frac{1}{{\text{γ}}_1^{{\text{n}}_{\text{1}}}},\frac{1}{{\text{γ}}_2^{{\text{n}}_2}}\right)$ or AND behavior if ${\text{e}}^{-\text{β}\Delta {\text{ε}}_{\text{AI}}}\gg \max \left(\frac{1}{{\text{γ}}_1^{{\text{n}}_{\text{1}}}},\frac{1}{{\text{γ}}_2^{{\text{n}}_2}}\right)$.

Over evolutionary time or through synthetic approaches, the number of binding sites displayed by a single molecule can be tuned, enabling such systems to test a variety of responses with a limited repertoire of regulatory molecules. Since γ₁, γ₂ ≪ 1, increasing the number of binding sites while keeping all other parameters the same can shift a response from AND→OR as shown in Figure 5. The opposite logic switching (OR→AND) is similarly possible by decreasing the number of binding sites, and analogous results can be derived for the complementary NAND and NOR gates (see Appendix C). In the limit where the number of binding sites becomes large (n₁, n₂ ≫ 1), an allosteric molecule’s behavior will necessarily collapse into OR logic provided γ₁, γ₂ < 1, since the presence of either ligand occupying the numerous binding sites has sufficient free energy to overcome the active-inactive free energy difference ∆ε_AI. In addition, having a large number of binding sites makes the p_active response sharper (Figure 5B), as has been seen in the context of chromatin remodeling where 150 bp of DNA “buried” within a nucleosome can be made available for transcription by the binding of multiple transcription factors. ¹³

Figure 5. Increased number of binding sites can switch the logic of an MWC protein from AND into OR.

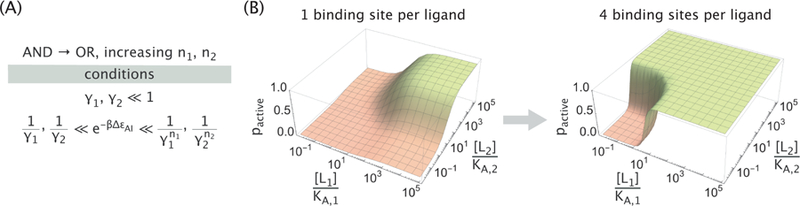
(A) Parameter conditions required for AND → OR switching upon an increase in the number of binding sites. (B) Representative activity plots showing the AND → OR switching. Parameters used were K_A,i = 2.5 × 10⁻⁸ M, K_I,i = 2.5 × 10⁻⁶ M and ∆ε_AI = −7 k_BT.

Next, we examine an alternative possibility of generalizing the MWC response, namely, considering a molecule with N = 3 distinct ligands, each having a single binding site (n_i = 1). The logic response is now described by a 2 × 2 × 2 cube corresponding to the activity at low and saturating concentrations of each of the three ligands (an example realization is shown in Figure 6A). Since each of the 8 cube elements can be either OFF or ON (red and green circles, respectively), the total number of possible responses becomes 2⁸ = 256. This number, however, includes functionally redundant responses, as well as ones that are not admissible in the MWC framework. We therefore eliminate these cases in order to accurately quantify the functional diversity of 3-input MWC proteins.

Figure 6. Third ligand expands the combinatorial diversity of logic responses and enables logic switching.

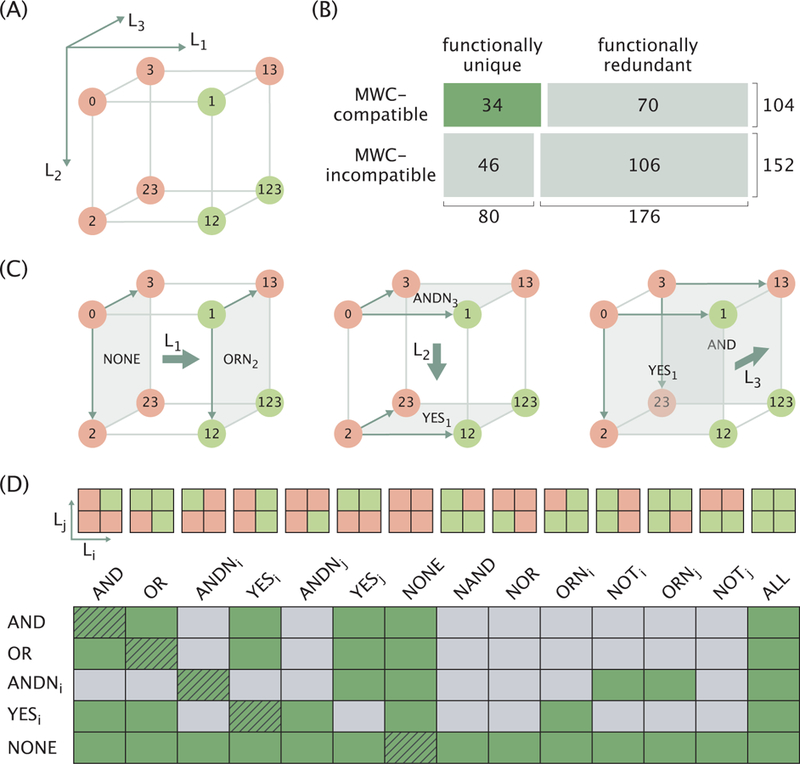
(A) Cubic diagram of a representative molecular logic response. The label “0” stands for the limit when all ligands are at low concentrations. Each digit in the labels of other limits indicates the high concentration of the corresponding ligand (for example, in the “12” limit the ligands 1 and 2 are at high concentrations). Red and green colors indicate the OFF and ON states of the molecule, respectively. (B) Diagram representing the numbers of 3-ligand logic gates categorized by their MWC compatibility and functional uniqueness. The area of each cell is proportional to the number of gates in the corresponding category. (C) Demonstration of different logic transitions induced by a third ligand (thick arrows) on the example of the 3-input gate in Panel A. (D) Table of all possible logic transitions (row → column, green cells) inducible by a third ligand in the MWC framework. Schematics of the 14 MWC-compatible 2-ligand gates corresponding to each column entry are displayed on top (i and j represent different ligands). Results for the transitions between logical complements (NOT row → NOT column) are identical to the results for row → column transitions and are not shown. Trivial transitions between identical gates where the third ligand has no effect are marked with hatching lines.

We consider two responses to be functionally identical if one can be obtained from another by relabeling the ligands, e.g. (1, 2, 3) → (3, 1, 2). Eliminating all redundant responses leaves 80 unique cases out of the 256 possibilities (see Appendix D). In addition, since the molecule’s activity in the eight ligand concentration limits is determined by only four MWC parameters, namely, {∆ε_AI, γ₁, γ₂, γ₃}, we expect the space of possible 3-input gates to be constrained (analogous to XOR/XNOR gates being inaccessible to 2-input MWC proteins). Imposing the constraints leaves 34 functionally unique logic responses that are compatible with the MWC framework (see Figure 6B for the summary statistics and Appendix D for the detailed discussion of how the constraints were imposed).

In addition to expanding the scope of combinatorial control relative to the two-input case, we can think of the role of the third ligand as a regulator whose presence switches the logic performed by the other two ligands. We illustrate this role in Figure 6C by first focusing on the leftmost cubic diagram. The gating behavior on the left face of the cube (in the absence of L₁) exhibits NONE logic while the behavior on the right face of the cube (in the presence of saturating L₁) is the ORN₂ logic (see the schematics at the top of Figure 6D for the definition of all possible gates). In this way, adding L₁ switches the logic of the remaining two ligands from NONE → ORN₂. In a similar vein, adding L₂ changes the logic from ANDN₃ → YES₁, while adding L₃ causes a YES₁ → AND switch.

We repeat the same procedure for all functionally unique 3-ligand MWC gates (see Appendix D) and obtain a table of all possible logic switches that can be induced by a third ligand (green cells in Figure 6D that indicate row → column logic switches). As we can see, a large set of logic switches are feasible, the majority of which (the left half of the table) do not involve a change in the base activity (i.e., activity in the absence of the two ligands). Comparatively fewer transitions that involve flipping of the base activity from OFF to ON are possible (the right half of the table).

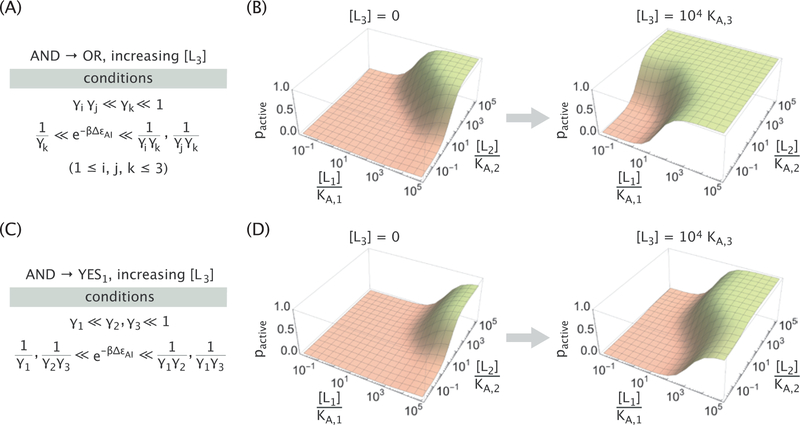
As a demonstration of the regulatory function of the third ligand, we show two examples of logic switching induced by increasing [L₃], namely, AND→OR (Figure 7A,B) and AND→YES₁ (Figure 7C,D), along with the parameter conditions that need to be satisfied to enable such transitions (see Appendix D for derivations). An interesting perspective is to view the L₃ ligand as a modulator of the free energy difference $\Delta {\text{ε}}_{\text{AI}}$. For example, when [L₃] = 0, the protein behaves identically to the N = 2 case given by eq 1; at a saturating concentration of L₃, however, the protein behaves as if it had N = 2 ligands with a modified free energy difference $\Delta {\text{ε}}_{\text{AI}}^{\prime }$ given by

$$\Delta {\text{ε}}_{\text{AI}}^{\prime }=\Delta {\text{ε}}_{\text{AI}}-{\text{k}}_{\text{B}}\text{T}\hspace{0.17em}\text{log}\hspace{0.17em}{\text{γ}}_{\text{3}}.$$ (10)

From this perspective, the third ligand increases the effective free energy difference in the examples shown in Figure 7, since in both cases the γ₃ ≪ 1 condition is satisfied. For the AND→OR transition, the increase in $\Delta {\text{ε}}_{\text{AI}}$ is sufficient to let either of the two ligands activate the molecule (hence, the OR gate). In the AND→YES₁ transition, the change in $\Delta {\text{ε}}_{\text{AI}}$ utilizes the asymmetry between the binding strengths of the two ligands (γ₁ ≪ γ₂) to effectively “silence” the activity of the ligand L₂. We note in passing that such behavior for the N = 3 allosteric molecule is reminiscent of a transistor which can switch an input signal in electronics.

Figure 7. Example logic switches induced by the third ligand.

Parameter conditions and representative activity plots of an allosteric molecule exhibiting AND logic in the absence of the third ligand, while exhibiting OR logic (A,B) or YES₁ logic (C,D) when L₃ is present at a saturating concentration. Parameters used were K_A,i = 2.5 × 10⁻⁸ M and K_I,i = 2.5 × 10⁻⁴ M in Panel B, K_A,i = 2.5 × 10⁻⁸ M, K_I,1 = 2.5 × 10⁻⁴ M and K_I,2/3 = 2.5 × 10⁻⁶ M in panel D, along with ∆ε_AI = −12 k_BT in both panels.

Discussion and Conclusions

Combinatorial control is a ubiquitous strategy employed by cells. Networks of cellular systems of different kinds, such as transcriptional, ^14,15 signaling,¹⁶ or metabolic,¹ integrate information from multiple inputs in order to produce a single output. The statistical mechanical MWC model we employ allows us to systematically explore the combinatorial diversity of output responses available to such networks and determine the conditions that the MWC parameters need to satisfy to realize a particular response.

In this paper, we built on earlier work to show that the response of an allosteric MWC molecule can mimic Boolean logic. Specifically, we demonstrated that a protein that binds to two ligands can exhibit an AND, OR, NAND, or NOR response (also shown by others^4–6), where the former two cases require the protein to be inherently inactive and that both ligands preferentially bind to the active conformation, whereas the latter two cases require the converse conditions. We derived the MWC parameter ranges within which an allosteric protein would exhibit an AND or OR response (Figure 3B), and showed that the corresponding parameter ranges for NAND or NOR responses could be achieved by simply substituting ${\text{γ}}_{\text{i}}\to \frac{1}{{\text{γ}}_{\text{i}}}$ and $\Delta {\text{ε}}_{\text{AI}}\to -\Delta {\text{ε}}_{\text{AI}}$ in the parameter condition equations (Appendix A.3). Since the NAND and NOR gates are known in digital electronics as universal logic gates, all other logic functions can be reproduced by hierarchically layering these gates. In the context of this work, such layering could be implemented if the MWC protein is an enzyme that only catalyzes in the active state so that its output (the amount of product) could serve as an input for the next enzyme, thereby producing more complex logic functions via allostery, though at the cost of noise amplification and response delays.

As in earlier work,^4,5 we showed that the XOR and XNOR responses cannot be achieved within the original MWC framework (eq 1) but are possible when cooperativity between the two ligands is introduced (Appendix A.4). Biological XOR and XNOR behaviors are uncommon in non-transcriptional systems and have also been challenging for synthetic design and optimization.¹⁷ One of the few examples of such systems is a synthetic metallochromic chromophore whose transmittance output level is modulated by Ca²⁺ and H⁺ ions in a XOR-like manner.^18,19

In addition to traditional Boolean logic, we recognized further manifestations of combinatorial control by two-ligand MWC proteins. In particular, we showed that the protein activity in three of the four ligand concentration limits can be set independently by tuning the MWC parameters γ₁, γ₂, and $\Delta {\text{ε}}_{\text{AI}}$, and that the ligand concentrations at which transitions between limit responses take place can be separately controlled by proportionally changing K_A,i and K_I,i, while keeping ${\text{γ}}_{\text{i}}=\frac{{\text{K}}_{\text{A,i}}}{{\text{K}}_{\text{I,i}}}$ constant (eqs 5 and 6). We also showed that when the ranges of ligand concentrations are close to those transition values, then ratiometric sensing observed in the BMP⁸ and GAL pathways,⁹ can be recapitulated through the MWC model (Figure 4B), with larger regions of sensitivity achievable by an appropriate tuning of the parameters. We note that parameter “tuning” can be realized either through evolutionary processes over long time scales or synthetically, using mutagenesis or other approaches.²⁰

Apart from altering the thermodynamic parameters such as the ligand binding affinity or the free energy of active and inactive protein conformations, the number of ligand binding sites of an allosteric molecule can also be changed. This can occur evolutionarily through recombination events, synthetically by engineering combinations of protein domains, ²¹ or through binding of competitive effectors that reduce the effective number of ligand binding sites. We found that these alterations in the number of ligand binding sites are capable of switching the logic behavior between AND ↔ OR or NAND ↔ NOR gates (Figure 5B). Since the MWC model has even been applied in unusual situations such as the packing of DNA into nucleosomes, ^13,22 these results on combinatorial control can also be relevant for eukaryotic transcription. The opening of the nucleosome is itself often subject to combinatorial control because there can be multiple transcription factor binding sites within a given nucleosome, the number of which can also be tuned using synthetic approaches.^23–26

Lastly, we generalized the analysis of logic responses for a molecule whose activity is modulated by three ligands, and identified 34 functionally unique and MWC-compatible gates out of 256 total possibilities. We offered a perspective on the function of any of the three ligands as a “regulator” that can cause a switch in the type of logic performed by the other two ligands and derived the full list of such switches (Figure 6D). Within the MWC model, the role of this regulatory ligand can be viewed as effectively changing the free energy difference ∆ε_AI between the protein’s active and inactive states (Appendix D.2), which, in turn, is akin to the role of methylation ^27,28 or phosphorylation²⁸ in adaptation, but without the covalent linkage. Our in-depth analysis of the logic repertoire available to 3-input MWC molecules can serve as a theoretical framework for designing new allosteric proteins and also for understanding the measured responses of existing systems. Examples of such systems that both act as 3-input AND gates include the GIRK channel, the state of which (open or closed) is regulated by the G protein G_βγ, the lipid PIP₂ and Na⁺ ions,²⁹ or the engineered N-WASP signaling protein which is activated by SH3, Cdc42 and PDZ ligands.³⁰

The exquisite control that arises from the web of interactions underlying biological systems is difficult to understand and replicate. A first step to overcoming this hurdle is to carefully quantify the types of behaviors that can arise from multi-component systems. As our ability to harness and potentially design de novo allosteric systems grows,^21,29–33 we can augment our current level of combinatorial control in biological contexts, such as transcriptional regulation, ^{3,14,15,34,35} to create even richer dynamics.