Dynamic characteristics of GMP reductase complexes revealed by high resolution ³¹P field cycling NMR relaxometry

Abstract

The ability of enzymes to modulate the dynamics of bound substrates and cofactors is a critical feature of catalysis, but the role of dynamics has largely been approached from the perspective of the protein. Here we use an underappreciated NMR technique, subtesla high resolution field cycling ³¹P NMR relaxometry, to interrogate the dynamics of enzyme bound substrates and cofactors in guanosine-5’-monophosphate reductase (GMPR). These experiments reveal distinct binding modes and dynamic profiles associated with the ³¹P nuclei in the Michaelis complexes for the deamination and hydride transfer steps of the catalytic cycle. Importantly, the substrate is constrained and the cofactor is more dynamic in the deamination complex E•GMP•NADP⁺, while the substrate is more dynamic and the cofactor is constrained in the hydride transfer complex E•IMP•NADP⁺. The presence of D₂O perturbed the relaxation of the ³¹P nuclei in E•IMP•NADP⁺, but not in E•GMP•NADP⁺, providing further evidence of distinct binding modes, with different dynamic properties. dIMP and dGMP are poor substrates, and the dynamics of the cofactor complexes of dGMP/dIMP are disregulated relative to GMP/IMP. The substrate 2’-OH interacts with Asp219, and mutation of Asp219 to Ala decreases the value of V_max by a factor of 30. Counterintuitively, loss of Asp219 makes both substrates and cofactors less dynamic. These observations suggest that the interactions between the substrate 2’-OH and Asp219 coordinate the dynamic properties of the Michaelis complexes, and these dynamics are important for progression through the catalytic cycle.

TOC Graphic

INTRODUCTION

Much of the remarkable power and specificity of enzyme catalysis derives from interactions with portions of substrates that are removed from the site of chemical transformation. This phenomenon distinguishes on-enzyme reactions from those in solution. Several general mechanisms can be envisioned to explain how the binding energy of remote interactions is harnessed to promote catalysis. (1) Distal portions of the protein can exert their effects on the ground state by serving as anchors tethering the substrate to the active site, as exemplified by ketosteroid isomerase ¹. Such interactions can enforce productive binding modes that properly position the substrate relative to the catalytic machinery. (2) Distal interactions can induce conformational changes that organize the active site, stabilizing the structure of mobile loops and positioning key catalytic residues. Such conformational changes often create “cages” that envelope the substrate and exclude solvent ². (3) Distal portions of the substrate can stabilize the transition state if their interactions with the protein are optimized in the transition state, as observed in tyrosyl-tRNA synthetase ³. (4) Distal substrate moieties may also contribute to the electrostatic environment of the active site. (5) Lastly, it is not difficult to imagine that distal portions of the substrate could potentially couple motions across the active site.

The ability of enzymes to modulate the dynamics of bound substrates and cofactors is a critical feature of catalysis. Nonetheless, the role of dynamics in enzyme catalysis has largely been approached from the perspective of the protein. Here we use an underappreciated NMR technique, subtesla high resolution field cycling ³¹P NMR relaxometry ^{4, 5,6,7,8, 9,10}, to interrogate the dynamics of enzyme bound substrates and cofactors in guanosine-5’-monophosphate reductase (GMPR). This enzyme presents an excellent system to investigate the dynamics of enzyme-bound ligands because the cofactor has different conformations during the two steps of the catalytic cycle.

GMPR is a triose phosphate isomerase (TIM) barrel protein, the most common enzyme fold, and contains the standard phosphate “gripper” loop found throughout this superfamily ^{11, 12}. The enzyme is a square planar homotetramer with four active sites. The GMP/IMP and nicotinamide binding sites lie within one monomer while the binding site for the adenosine portion of the cofactor is in the adjacent subunit. This enzyme catalyzes two different chemical transformations (Figure 1A) ¹³. The first step is a deamination reaction, where the catalytic residue Cys186 attacks C2 of GMP to create a covalent thioimidate intermediate (E-XMP*) and ammonia (Figure 1A). The cofactor is present for the deamination reaction, but the nicotinamide must be positioned away from GMP to allow deamination to proceed. Then the nicotinamide moves adjacent to C2 of E-XMP* to allow hydride transfer and production of IMP. The x-ray crystal structure of the inactive E•IMP•NADPH complex captures the cofactor in two conformations, an “OUT” conformation believed to be used in the deamination reaction and an “IN” conformation that appears competent for hydride transfer (Figure 1B) ¹³. However, the relevance of these structures to catalysis remains to be established.

Figure 1. The reactions and structure of GMPR.

(A) The GMPR reaction. (B) GMPR active sites with NADPH in the IN and OUT conformations are displayed (PDB entry 2C6Q). Residues in contact with IMP are shown. This figure was produced with UCSF Chimera ¹⁷. (C) The partial reactions catalyzed by GMPR.

Our previously reported field cycling experiments interrogated the NADP⁺ complexes of both GMP and IMP ⁴. These complexes undergo partial reactions that resemble different steps in the full catalytic cycle (Figure 1C) ¹³: (1) E•GMP•NADP⁺ undergoes a partial deamination reaction to form E-XMP*•NH₃•NADP⁺. This partial reaction requires that the cofactor nicotinamide is positioned away from GMP, as observed in the OUT structure. (2) E•IMP•NADP⁺ undergoes a partial hydride transfer reaction to form E-XMP*•NADPH in the absence of ammonia. This reaction requires the nicotinamide to be adjacent to IMP, as observed in the IN structure. The field cycling experiments revealed that the monophosphates of IMP and GMP have distinct binding modes in these cofactor complexes. This finding was not anticipated by the x-ray crystal structures, where the IMP and GMP monophosphate binding sites are virtually identical ^13,14. Contrary to expectations, we could not detect differences in the cofactor binding mode, although different dynamic processes are associated with the cofactor in each complex ⁴. Most intriguingly, the dynamics of the substrate and cofactor are coordinately regulated. In the deamination complex, GMP is relatively constrained while the cofactor is dynamic. In contrast, IMP is dynamic and the cofactor is constrained in the hydride transfer complex. Here we show that the substitution of either the substrate 2’-OH or Asp219 compromises catalysis, and the associated binding modes and dynamic profiles of the ³¹P nuclei are no longer congruous with the requisite chemical transformations.

MATERIALS/EXPERIMENTAL DETAILS

Materials –

NADP⁺ was obtained from Roche Diagnostics. IMP was purchased from MP Biomedicals. GMP, dGMP, dIMP and NADPH were purchased from Sigma. D₂O (99.9%) and deuterated Tris-d₁₁ (98%) were obtained from Cambridge Isotopes.

Overexpression and purification of WT and D219A GMPR –

Expression and purification of recombinant E. coli GMPR was carried out as described previously ⁴. In brief, His-tagged protein was purified using Ni-NTA agarose resin (Molecular Cloning Laboratories, Inc.). Enzyme was dialyzed against 75 mM Tris-HCl, pH 7.8, 100 mM KCl, 1 mM DTT, 0.5 mM EDTA, 5% glycerol and stored at −20 °C. The protein purity was verified by SDS-gel electrophoresis. The protein concentration was determined by A₂₈₀ using the extinction coefficient calculated with ProtParam ¹⁵. Protein was concentrated using Amicon Ultra centrifugal 10K filters for NMR samples.

High-resolution ³¹P field-cycling NMR measurements –

Samples contained 400 μM GMPR and 1.6 mM ligands in 75 mM Tris-HCl, pH 7.8, with 100 mM KCl, 1 mM DTT and 0.5 mM EDTA in 24% D₂O. For D₂O experiments, deuterated Tris-d₁₁ and 100% of D₂O were used. The ³¹P field-cycling spin-lattice relaxation rate (R₁) measurements were taken at 25 °C on a Varian INOVA 500 spectrometer using a standard 10 mm Varian probe in a device that was built to move the sample from the conventional sample probe location at 11.7 T, to a higher position where the magnetic field can be as low as 0.04 T ⁵. A permanent magnet was mounted at the top of the dewar to program fields between 0.003 and 0.04 T. Relaxation experiments were typically 3 to 6 hours long at a given field strength (longer times required at the lowest magnetic fields), each with 5 to 7 programmed delay times, starting at low field and continuing to progressively higher field. Data were analyzed with an exponential function to extract the spin-lattice relaxation rate R₁ = 1/T₁.

³¹P field-cycling NMR data analysis –

Spectra were plotted and intensities were measured by Vnmr 6.1B software. The dependence of R₁ on magnetic field allows the extraction of an effective correlation time (τ) for the ligand bound to GMPR and a dipolar relaxation rate extrapolated for zero field (R₀), as described by the following equation:

$${\text{R}}_{\text{1}}{=[R}_0/2\tau \left]\right\{0{.1J(\tau ,\omega }_{\text{H}}{\text{–ω}}_{\text{P}})+0{.3J(\tau ,\omega }_{\text{P}})+0{.6J(\tau ,\omega }_{\text{H}}{\text{+ω}}_{\text{P}}\text{)}+CSA}$$ [1]

where CSA = C_Lω _P² J(ω_P) + C_H ω_P² H². Here J(τ,ω) is the spectral density function and equal to 2τ/(1+ω_P²τ²), C_L and C_H are low-frequency and high-frequency contributions of the CSA interaction to relaxation, respectively, and ω_H and ω_P are the proton and ³¹P gyromagnetic ratios multiplied by magnetic field, H (in T). The contribution C_Lω _P² J(ω_P) was introduced to account for relaxation occurring in the region from 0.5 to 4 T that could otherwise not be accounted for by dipolar and the CSA detected at high fields ¹⁶. As such it is an empirical ‘correction’. In this work, we ignore CSA except to improve fits of the data. An averaged distance from the nearest protons to the ³¹P is proportional to the sixth root of τ/R₀:

$${\text{r}}_{\text{eff}}{}^{\text{6}}{\text{=(μ}}_{\text{0}}{\text{/4π)}}^{\text{2}}{\text{(h/2π)}}^{\text{2}}{\text{γ}}_{\text{P}}{}^{\text{2}}{\text{γ}}_{\text{H}}{}^{\text{2}}{\text{τ/R}}_{\text{0}}$$ [2]

where h is Planck`s constant and μ₀ is the permeability of free space, and γ_P and γ_H are the gyromagnetic ratios for ³¹P and ¹H, respectively. We define r_eff, as the on-enzyme distance between the ³¹P and nearby protons that are responsible for the dipolar relaxation. It is not normalized to a specific number of protons, since that is not known. However, it does provide a way to compare different substrates and the effect of removing exchangeable protons from the system.

Enzyme Kinetics –

Steady state GMPR analyses were conducted at 25 °C in 75 mM Tris, pH 7.8, 100 mM KCl, 1 mM DTT and 0.5 mM EDTA. Enzyme activity was monitored spectrophotometrically at 340 nm. Initial velocity data were fit to the Michaelis-Menten equation (eq. [3]) where v is the initial velocity, V_m is the maximal velocity, K_m is the Michaelis constant and [S] is the substrate concentration.

$$v=V_m\left[\mathrm{S}\right]/\left(K_m+\left[\mathrm{S}\right]\right)$$ [3]

Pre-steady state kinetics were performed on a stopped-flow spectrophotometer (Applied Photophysics SX.17MV). The reaction was monitored by absorbance at 340 nm at 25 °C. GMPR was mixed with an equal volume of saturating substrates (final concentrations = 10 μM, 500 μM and 500 μM for wildtype GMPR, IMP and NADP⁺, respectively; 10 μM, 500 μM and 500 μM for wildtype GMPR, dIMP and NADP⁺, respectively; 30 μM, 10 mM and 3 mM for D219A mutant, IMP and NADP⁺, respectively). The data were fit to single exponential (Equation 4) for the GMPR+IMP+NADP⁺ and GMPR+dIMP+NADP⁺ reactions.

$${\text{A}}_{\text{t}}{\text{=A}}_{\text{0}}\left(1–\text{exp}\left(-k_{obs}•\text{t}\right)\right)$$ [4]

Here A_t is the absorbance at 340 nm at time t, A₀ is the maximum absorbance, and k_obs is the observed rate constant of the reaction. Data from the D219A+IMP+NADP⁺ reaction were fit to a single exponential plus steady state equation:

$${\text{A}}_{\text{t}}{\text{=A}}_{\text{0}}\left(1–\text{exp}\left(-k_{obs}•\text{t}\right)\right)+Bt+C$$ [5]

where A₀ is the maximum absorbance at 340 nm and k_obs is an observed rate constant of the exponential part, B is the steady state rate constant, and C is the basal absorbance.

RESULTS AND DISCUSSION

Overview of high resolution field cycling.

For a small molecule in solution, the ³¹P spin-lattice relaxation rate (R₁) is dominated by chemical shift anisotropy (CSA) in high magnetic fields. In low magnetic fields, both the CSA and the dipolar contribution to relaxation of the small molecule phosphorus are inefficient, so R₁ is very small. However, if the small molecule is bound to a protein, the longer correlation time of the complex means that the ³¹P nuclei dipolar relaxation by nearby protons is significantly enhanced at low fields ⁷. Under fast exchange conditions, the observed R₁ is then a weighted average of the very small R₁ of the unbound population and the much larger R₁ of the bound population. The effectiveness of dipolar relaxation depends on the number and proximity of nearby protons to the ³¹P nuclei as well as magnetic field strength. In ‘high resolution’ field cycling, samples are excited at high field, shuttled to low field for relaxation, then returned to the high field for detection of the residual magnetization of each nucleus of interest ^{5, 6}. The shuttling preserves the chemical shift differences of phosphorylated molecules allowing spin-lattice relaxation rates to be measured over a wide range of magnetic fields (11.7 to 0.003 T). In this field range both dipolar and CSA mechanisms contribute to the ³¹P R₁ and the dependence of each of these features on magnetic field can be accounted for by equation [1]. The separation of the dipolar R₁ from CSA and its analysis (first term of equation [1]) yields a correlation time (τ) and a relaxation rate extrapolated to zero field (R₀). The sixth root of τ/R₀ is related to the averaged distance between the ³¹P nuclei and the protons that relax it (Equation [2]). A key point in this experiment is that GMPR-bound and free ligands must be in fast exchange to detect the protein-induced relaxation behavior is that for each ³¹P resonance, τ and R₀ characterize substrate and cofactor binding in the Michaelis complex.

Exchangeable protons contribute to relaxation of the substrate monophosphate in the hydride transfer complex.

Significant dipolar relaxation is most likely to arise from interactions between the ³¹P nuclei and nonexchangeable protons attached to carbon atoms, either on the substrate/cofactor or the enzyme. Protons attached to heteroatoms can also contribute to ³¹P relaxation, but these protons must be in slow exchange with solvent. Similarly, solvent protons may also contribute to relaxation if they are in slow exchange with bulk solvent. Inspection of the x-ray crystal structures identified both exchangeable and nonexchangeable protons in close proximity to the ³¹P nuclei of both substrate and cofactors (Figure 2). Therefore, we carried out the field cycling experiments in D₂O instead of H₂O to assess the contribution of exchangeable protons and further assess the relevance of the substrate/cofactor conformations observed in the crystal structures to the conformations in the catalytically competent complexes in solution (Figure 3 and Table 1). At least three independent field cycling experiments were performed for each complex; the individual R₁ values were determined at a minimum of 15 different magnetic fields. If exchangeable protons make a significant contribution to ³¹P relaxation, then R₀ should decrease (if τ is not significantly affected), and the ratio of of τ/R₀ should increase, implying an increase in r_eff.

Figure 2. Candidate proton relaxers.

Hydrogen atoms within 4 Å of the phosphorus atom of IMP (A,B), of the NADPH monophosphate P (C,D) and the NADPH diphosphates P atoms (E,F) in the IN (A,C,E) and OUT (B,D,F) complexes (PDB entry 2C6Q). Protons within 4 Å of the phosphorus are shown as a ball, protons within 3 Å are colored light green. This figure was produced with UCSF Chimera ¹⁷.

Figure 3. Magnetic field dependence of substrate and cofactor ³¹P R₁ in E•GMP•NADP⁺ and E•IMP•NADP⁺ complexes in D₂O.

Samples (E•GMP•NADP⁺ in red and E•IMP•NADP⁺ in blue) are in 75 mM Tris-HCl, pH 7.8, 100 mM KCl, 1 mM DTT and 0.5 mM EDTA: (A) substrate monophosphate, (B) cofactor monophosphate, and (C) cofactor diphosphates. The error bars are the standard error in R₁ from the exponential fit of signal magnitude versus delay time. The data shown are for one of the three independent experiments.

Table 1. Effect of D₂O on ³¹P dipolar relaxation parameters for substrate and cofactor in GMPR ternary complexes extracted from field cycling relaxometry.

Values for τ, R₀ and τ/R₀ are the average and standard deviation from 3 independent experiments.

31P	Complex	Solvent	τ (ns)	R0 (s−1)	τ/R0 × 108 (s2)
IMP	WT•IMP •NADP+	H2O a	55 ± 12	1.9 ± 0.9	3.3 ± 1.1
		D2O	45 ± 1	0.6 ± 0.2	8 ± 3
GMP	WT•GMP •NADP+	H2O a	72 ± 13	0.30 ± 0.02	24 ± 5
		D2O	77 ± 16	0.3 ± 0.1	24 ± 12
NADP+ mono-phosphate	WT•IMP •NADP+	H2O a	103 ± 23	2.9 ± 1.2	3.8 ± 0.9
		D2O	62 ± 3	0.7 ± 0.3	9 ± 4
	WT•GMP •NADP+	H2O a	47 ± 11	0.6 ± 0.1	8.6 ± 2.3
		D2O	55 ± 18	0.4 ± 0.1	13 ± 5
NADP+ diphosphates	WT•IMP •NADP+	H2O a	88 ± 13	1.4 ± 0.3	6.6 ± 1.2
			82 ± 17	1.6 ± 0.3	5.1 ± 0.9
		D2O	70 ± 5	0.6 ± 0.3	12 ± 7
			58 ± 8	0.6 ± 0.3	10 ± 5
	WT•GMP •NADP+	H2O a	44 ± 5	0.5 ± 0.2	9.2 ± 2.4
			45 ± 8	0.5 ± 0.1	9.3 ± 2.5
		D2O	50 ± 9	0.3 ± 0.1	15 ± 5
			50 ± 1	0.3 ± 0.1	15 ± 3

^aValues from ⁴.

For IMP in the E-IMP•NADP⁺ complex in D₂O, the value of R₀ decreased roughly 3-fold. resulting in an approximately 3-fold increase of τ/R₀. Thus, exchangeable protons contribute to the relaxation of the ³¹P of IMP in the hydride transfer complex. Our previous work indicated that the averaged ³¹P-¹H distance (assuming N_H = 1) was 2.9 ± 0.2 Å for the ³¹P of IMP in its NADP⁺ complex ⁴. Inspection of the IN structure identified three nonexchangeable protons and four exchangeable protons within 3 Å of the substrate ³¹P (Figure 2A), so the D₂O effect is consistent with the IMP binding mode observed in the IN structure.

The substrate occupies the same binding site in the OUT crystal structure, again with six protons within 3 Å of the substrate ³¹P, including the same three nonexchangeable protons, and the same backbone amides as in the IN structure (Figure 2B). If the deamination complex adopts the OUT structure, then the relaxation of the ³¹P of GMP should also be perturbed by D₂O. However, the value of τ/R₀ for the GMP ³¹P in the cofactor complex is fairly large in H₂O, making an accurate measurement of the D₂O effect difficult. The errors in determining τ/R₀ in D₂O are large but similar to what is observed in H₂O (Table 1). Nonetheless, a three-fold increase in τ/R₀, as observed for IMP in the complex, is certainly not observed. Thus, predominantly nonexchangeable protons dominate the relaxation of the GMP ³¹P in the ternary complex. The absence of a strong D₂O effect provides further evidence that the monophosphates of the two substrates must have different binding modes in their respective cofactor complexes. Intriguingly, in molecular simulations of the deamination reaction, the substrate monophosphate is displaced from its position in the crystal structure, such that only one nonexchangeable proton, a 5’-H, is within 3 Å of the ³¹P nuclei of GMP (W. Yang, personal communication). This binding mode is more consistent with the observed relaxation.

The D₂O effect on ³¹P relaxation provides evidence for different cofactor conformations in different steps of the catalytic cycle.

Previous field cycling experiments found that the dynamic processes associated with cofactor binding are different in the IMP and GMP complexes ⁴. The cofactor is relatively constrained in the IMP complex, and more dynamic in the GMP complex. However, the values of τ/R₀ for the cofactor ³¹P nuclei were similar in both complexes, so these experiments were unable to corroborate the distinct cofactor conformations expected for each partial reaction and observed in the crystal structures.

We evaluated the effect of D₂O on relaxation of the cofactor ³¹P in the hope of gaining some insight into whether the cofactor binding modes resemble the conformations observed in the IN or OUT crystal structures. The presence of D₂O perturbed the relaxation of all three cofactor ³¹P nuclei in the IMP complex (the values of τ/R₀ increased by approximately a factor of ~2 for all; Table 1), but had a smaller effect on the ³¹P nuclei in the GMP complex. This observation suggests that more exchangeable protons contribute to the relaxation of the cofactor in complex with IMP. Inspection of the environments of the cofactor monophosphate in the IN and OUT structures revealed that the constellation of potential proton relaxers is very similar in both (Figure 2C,D), so the origin of the D₂O effect on this nuclei is not readily apparent. A clear difference is found in the potential proton relaxers in the vicinity of the cofactor diphosphates (Figure 2E,F). While similar numbers of nonexchangeable protons are observed within 4 Å of these nuclei in both the IN and OUT structures (15 and 14, respectively), more exchangeable protons are observed in the IN structure (13) versus the OUT (8). Therefore, we tentatively conclude that the cofactor conformation in the IMP complex resembles the IN structure, and the conformation in the GMP complex resembles the OUT conformation, as originally proposed.

Deoxynucleotides are poor substrates for GMPR.

The crystal structures reveal that the 2’-OH and 3’-OH of both IMP and GMP form hydrogen bonds with Asp219 (Figure 1B; ¹³¹⁴). We assayed the reactions of GMPR with dIMP and dGMP to probe the importance of these interactions for catalysis. As expected, dIMP and dGMP are poor substrates for GMPR (Table 2). The values of K_m increased by factors of 5–6 relative to the ribose substrates, while the values of K_m for the cofactors increased by approximately a factor of 1.6–2. The value of k_cat decreased by a factor of 15 relative to GMP and the value of V_max/[E] for the reverse reaction decreased by a factor of 9 relative to IMP (at fixed [NH₄⁺] = 20 mM; it is not possible to saturate the reaction with respect to NH₄⁺). The rate constant of the partial hydride transfer reaction between dIMP and NADP⁺ is lower by a factor of 7.5 relative to that of IMP (Table 2 and Supporting Figures S1 and S2). The equilibrium constants for the partial reactions estimated from the [NADPH]/[E] are ~0.2 for IMP and ~0.08 for dIMP. The individual rate constants can also be estimated: for IMP, k_f = ~0.07 s⁻¹ and k_r = ~0.4 s⁻¹ while for dIMP, k_f = ~0.006 and k_r = ~0.06 for dIMP. Note that the values of k_r for IMP and dIMP are comparable to the values of k_cat for the reactions of GMP and dGMP, respectively. These observations indicate that hydride transfer is rate-limiting for both ribose and deoxyribose substrates. Note also that these rate constants are slow relative to the time-scale needed for fast exchange on the NMR time scale. This indicates that the E-XMP*•NADPH complex should not contribute to the ³¹P relaxation.

Table 2. Kinetic parameters for WT and D219A GMPR.

Reactions were performed in 75 mM Tris, pH 7.8, 100 mM KCl, 1 mM DTT and 0.5 mM EDTA at 25 °C. NADPH consumption/formation was monitored as described in Methods. Values are the average and standard error of at least two independent experiments. “K_m(S)” denotes the K_m of GMP, dGMP, IMP or dIMP, as appropriate. “k” denotes k_cat for the reaction of dGMP+NADPH, V_m/[E] for the reaction of dIMP+NADP⁺+NH₃ and k_obs for the partial reaction of dIMP+NADP⁺.

Enzyme	Reaction	Km (S) (μM)	Km (cofactor) (μM)	k (s−1)
WT	GMP + NADPH a	3.2 ± 0.5	10.1 ± 0.8	0.35 ± 0.01
	dGMP + NADPH b	15 ± 3	16 ± 4	0.023 ± 0.002
D219A	GMP + NADPH c	380 ± 130	120 ± 20	0.013 ± 0.003
WT	IMP + NADP+ + NH3 d	23 ± 6	50 ± 16	0.018 ± 0.009
	dIMP + NADP+ + NH3 e	140 ± 20	109 ± 28	0.002 ± 0.001
D219A	IMP + NADP+ + NH3 f	1100 ± 240	420 ± 220	(4.0 ± 0.3) x 10−4
WT	IMP + NADP+ g	n.a.	n.a.	0.49 ± 0.01 (16%)
	dIMP + NADP+ g	n.a.	n.a.	0.064 ± 0.001 (10%)
D219A	IMP + NADP+ g	n.a.	n.a.	0.055 ± 0.003 (2.8%)

^aValues from ¹³.

^bReactions performed at saturating concentrations of the fixed substrate dGMP (200 μM) and NADPH (150 μM).

^cReactions performed at saturating concentrations of GMP (2 mM) and NADPH (600 μM).

^dReactions performed at saturating concentrations of IMP (500 μM), NADP⁺ (500 μM) and NH₄⁺ (20 mM).

^eReactions performed at saturating concentrations of the fixed substrate, IMP (1 mM) and NADP⁺ (500 μM).

^fReactions performed at saturating concentrations of the fixed substrate, IMP (10 mM) and NADP⁺ (3 mM).

^gReactions performed at saturating conditions as described above. The percentage of NADPH produced per active site at equilibrium is shown in parentheses; n.a., not applicable

The dynamics of the cofactor complexes of dGMP/dIMP are disregulated relative to GMP/IMP.

The ³¹P relaxation experiments revealed that the dynamic properties of the cofactor complexes with dGMP and dIMP are dramatically different from their ribose counterparts (Figure 4 and Table 3). In the E•GMP•NADP⁺ complex, GMP is constrained and the cofactor is dynamic as reflected in the values of τ extracted with a simple single dipolar component fit ⁴. However, when dGMP was the substrate, the substrate is dynamic and the cofactor is constrained. The value of τ decreased to 36 ns for the ³¹P of dGMP, similar to that observed for the substrate in the hydride transfer complex. The value of τ/R₀ also decreased, indicating that the monophosphate of dGMP is closer to proton relaxers, also as observed for the substrate in the hydride transfer complex. For the cofactor ³¹P nuclei, the values of τ increased to 70–110 ns, similar to the cofactor in the hydride transfer complex. Note that the values of τ/R₀ do not distinguish the conformations of the cofactor in the hydride transfer and deamination complexes, and similar values are observed for the cofactor ³¹P nuclei in E•dGMP•NADP⁺, so no conclusions can be made about the cofactor binding mode. Taken together, the dGMP-cofactor complex is primed for hydride transfer, not deamination.

Figure 4. Magnetic field dependence of deoxy substrate and cofactor ³¹P R₁ in E•dGMP•NADP⁺ and E•dIMP•NADP⁺ complexes.

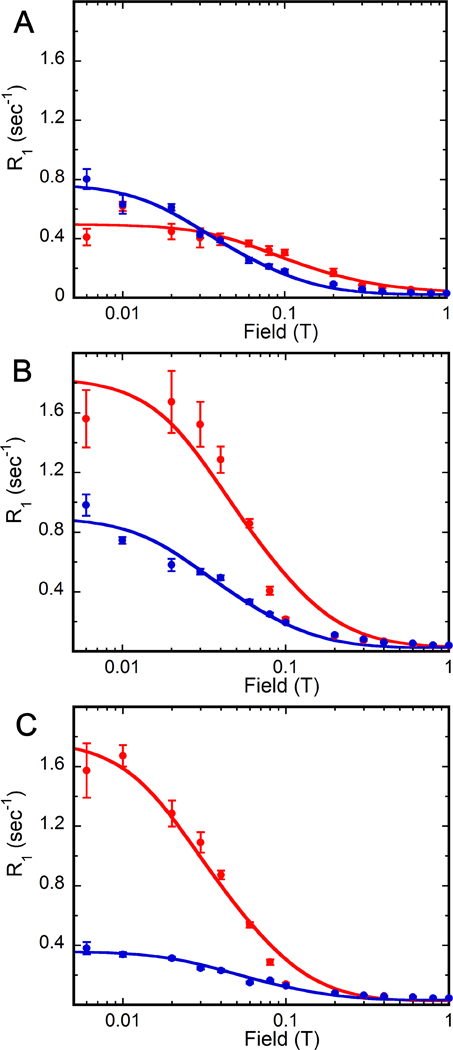
Samples (E•dGMP•NADP⁺ in red and E•dIMP•NADP⁺ in blue) are in 75 mM Tris-HCl, pH 7.8, 100 mM KCl, 1 mM DTT and 0.5 mM EDTA. Data for (A) deoxy substrate monophosphate, (B) cofactor monophosphate and (C) cofactor diphosphates are shown. Error bars are as described in Figure 3.

Table 3.

³¹P dipolar relaxation parameters (from field cycling) for NADP⁺ complexes of GMPR or mutant D219A with GMP, IMP or deoxy-substrates (dGMP and dIMP).

31P	Complex	N a	τ (ns)	R0 (s−1)	τ /R0 × 108(s2)
(d)IMP	WT•dIMP •NADP+	3	75 ± 30	0.8 ± 0.3	10 ± 5
	D219A•IMP •NADP+	2	70 ± 26	1.7 ± 0.3 (4.3 ± 0.7) c	4.1 ± 1.7 (1.6 ± 0.7) c
(d)GMP	WT•dGMP •NADP+	3	43 ± 12	0.4 ± 0.2	11 ± 6
	D219A•GMP •NADP+	4	120 ± 34	3.8 ± 1.2	3.1 ± 1.3
NADP+ mono-phosphate	WT•dIMP •NADP+	3	92 ± 18	0.8 ± 0.2	11 ± 3
	D219A•IMP •NADP+	2	139 ± 9	1.95 ± 0.02 (4.88 ± 0.05) c	7.1 ± 0.5 (2.8 ± 0.2) c
	WT•dGMP •NADP+ b	3	75 ± 8	1.5 ± 0.5	5 ± 2
	D219A•GMP •NADP+ d	4	125 ± 8	2.3 ± 0.3	5.3 ± 0.8
NADP+ diphosphates	WT•dIMP •NADP+	3	61 ± 23	0.3 ± 0.1	18 ± 8
			85 ± 21	0.4 ± 0.1	23 ± 6
	D219A•IMP •NADP+	2	113 ± 6	0.60 ± 0.02 (1.50 ± 0.05) c	18 ± 1 (7.2 ± 0.4) c
			112 ± 4	0.60 ± 0.04 (1.5 ± 0.1) c	18 ± 2 (7.2 ± 0.8) c
	WT•dGMP •NADP+	3	101 ± 27	1.6 ± 0.5	6.3 ± 3
			98 ± 23	1.6 ± 0.4	6.2 ± 3
	D219A•GMP •NADP+ d	4	137 ± 32	0.86 ± 0.15	16 ± 5
			114 ± 13	0.8 ± 0.1	15 ± 3

^aN is the number of independent experiments averaged to obtain the values tabulated.

^cR₀ corrected for the fraction of E•IMP•NADP⁺ compared to total enzyme (0.40).

Similarly, the dynamic characteristics of the dIMP-cofactor complex were very different than those observed with E•IMP•NADP⁺. Whereas IMP is more dynamic than the cofactor, both ligands are relatively constrained in the dIMP complex. The environment of the substrate monophosphate is also different in this complex, with τ/R₀ = 13 × 10⁻⁸ s² for dIMP versus 3.3 × 10⁻⁸ s² for IMP. This value indicates that the dIMP substrate ³¹P nucleus is farther away from proton relaxers, and suggests a conformation/environment similar to in the deamination complex. Larger values of τ/R₀ are also observed for the cofactor ³¹P nuclei, which suggests the presence of an altered cofactor binding mode. Thus, neither the conformation nor the dynamics of the dIMP-cofactor complex appear conducive to hydride transfer.

Asp219 coordinates the dynamics of enzyme bound substrates and cofactors.

Asp219 makes hydrogen bonds with both the 2’-OH and 3’-OH of the ribose substrates, and therefore might be expected to be critical for holding the substrate in position for catalysis (Figure 1B) ¹³. The profound changes in dynamics observed with dGMP and dIMP prompted us to investigate the effects of substituting Asp219 with Ala. Not surprisingly, the mutation of Asp219 to Ala severely diminished enzyme activity. The values of K_m for GMP and NADPH increased by factors of 120 and 12, respectively, while the value of k_cat decreased by a factor of 27 (Table 3). Comparable changes where observed in the reaction of IMP (K_m increased 48-fold), NADP⁺ (K_m increased 8-fold) and NH₄⁺ (V_max/[E] decreased by a factor of 45). D219A also catalyzed the reaction between IMP and NADP⁺ in the absence of NH₄⁺. However, unlike the reaction of the wild-type enzyme, which reached equilibrium within 10 sec (Supporting Figure 1), the progress curve for the D219A reaction displayed a burst of NADPH production followed by a slower phase that could be fit to a steady state rate (Supporting Figure S3). This second phase is faster than the rate of NADPH production observed in longer progress curves (Supporting Figure S3), suggesting that hydride transfer is not rate-limiting for the reaction of D219A. We suggest that the slow production of NADPH may be the result of slow dissociation of NADPH and off-pathway hydrolysis of E-XMP*. Importantly, the rate of the reaction under the conditions of the field cycling experiments is approximately 40% of that observed under saturating substrate conditions, indicating that the fraction of bound enzyme is 0.4 (Supporting Figure 3).

³¹P field cycling experiments revealed that the values of τ are similar (108–143 ns) for all of the substrate and cofactor ³¹P nuclei in both D219A ternary complexes, as would be expected if τ was dominated by rotational relaxation of the enzyme complex (Figure 5 and Table 3; note that the value of τ does not depend on the fraction of substrate bound enzyme – only R₀ is affected). This observation suggests that both substrates and cofactor are constrained within the ternary complexes in the absence of Asp219. Unlike the wild-type enzyme, no difference is observed in the relaxation of GMP and IMP in their respective cofactor complexes with D219A (Figure 5). The values of τ/R₀ for the substrate monophosphates are similar to that observed for IMP in the ternary complex of wild-type enzyme (Table 3; note that the correction of the bound enzyme in the IMP complex has no effect on this conclusion). These observations suggest that GMP can no longer access the distinct binding mode associated with the deamination reaction in D219A and the IMP binding site no longer has the dynamic mode associated with the hydride transfer reaction.

Figure 5. Magnetic field dependence of substrate and cofactor ³¹P R₁ in D219A•GMP•NADP⁺ and D219A•IMP•NADP⁺ complexes.

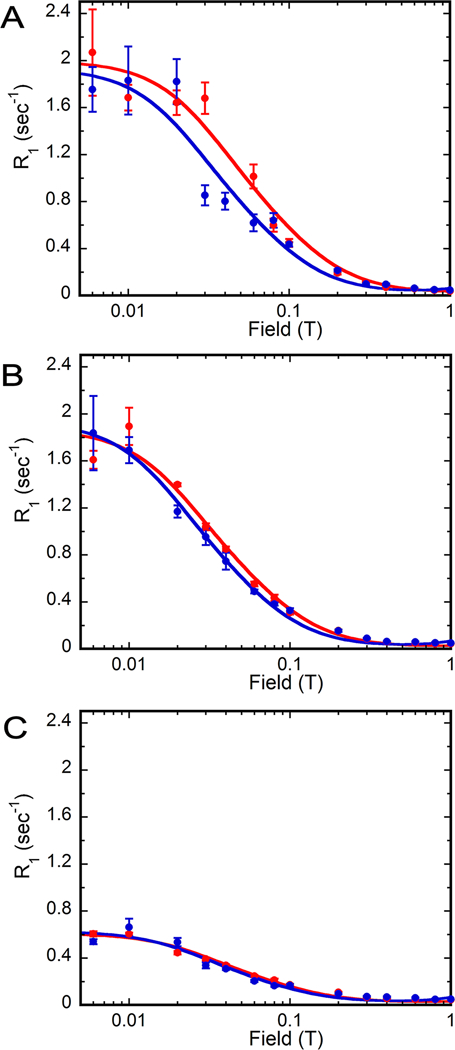
Samples (D219A•GMP•NADP⁺ in red and D219A•IMP•NADP⁺ in blue) are in 75 mM Tris-HCl, pH 7.8, 100 mM KCl, 1 mM DTT and 0.5 mM EDTA: (A) substrate monophosphate, (B) cofactor monophosphate, and (C) cofactor diphosphates. Error bars are described in Figure 3.

While the cofactor was clearly constrained in both substrate complexes with D219A, the effects of this mutation on the cofactor binding modes are difficult to assess. The mutation increases values of τ/R₀ for the cofactor ³¹P nuclei in the GMP complex, perhaps suggesting the presence of a new binding mode. However, the errors for these values overlap with those observed in the wild-type complex. The need to correct for the fraction of bound enzyme further obscures the effects of the mutation on the cofactor conformation in complex with IMP. Therefore, it is possible that D219 also controls cofactor conformation in addition to cofactor dynamics. Interestingly, additional cofactor binding modes are uncovered in molecular simulations (W. Yang, personal communication), so the broad range in τ/R₀ values observed in the field cycling experiment may reflect extensive conformational heterogeneity that is not captured in the x-ray crystal structures.

CONCLUSIONS

Our experiments reveal multiple binding modes for substrates and NADP⁺ in catalytically competent complexes of GMPR. Figure 6 summarizes these findings. Different binding modes are observed for substrates GMP and IMP. This observation contrasts with currently available crystal structures of inactive complexes that observe a single binding mode for both substrates. Moreover, distinct dynamic states are associated with each step in the catalytic cycle. The substrate is constrained and the cofactor is dynamic in the Michaelis complex for the deamination reaction, while the substrate is dynamic and the cofactor is constrained in the Michaelis complex for hydride transfer. A comparatively small structural perturbation, the substitution of H for OH, perturbs these binding modes and dynamic states, with a detrimental effect on catalysis. Lastly, Asp219, rather than simply holding substrates in position for catalysis, plays a critical role in modulating the dynamics of both substrates and cofactor. Thus, these findings provide new insights into how distal portions of the substrate promote catalysis.

Figure 6. Dynamic characteristics of GMPR complexes revealed by high resolution ³¹P field cycling NMR relaxometry.

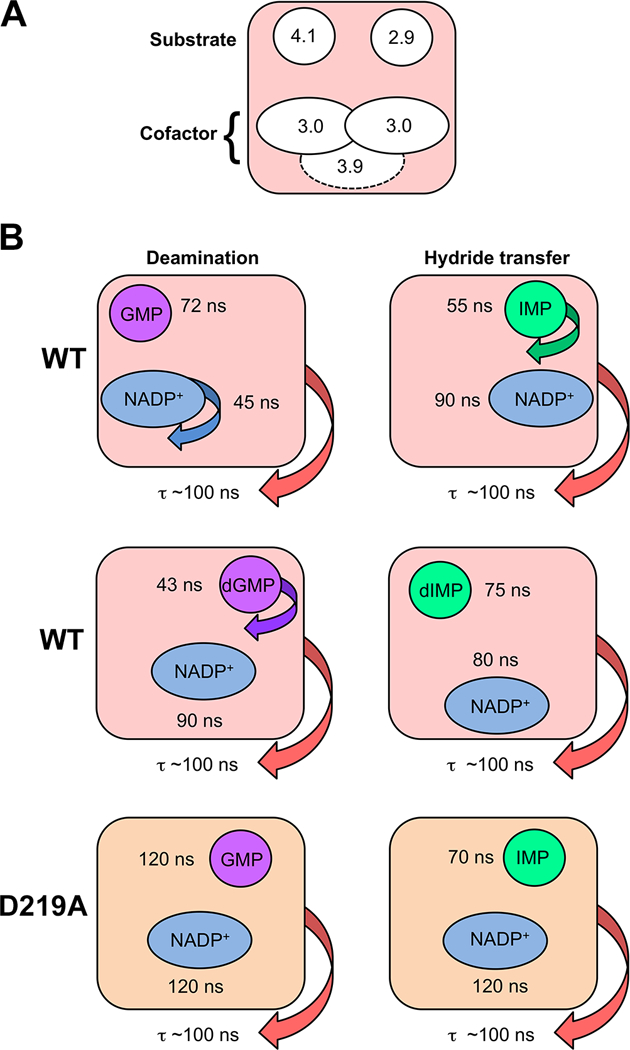
(A) Multiple binding modes for substrate and cofactors. Two distinct binding modes are observed for IMP and GMP in their catalytically active NADP⁺ complexes. The cofactor also has two distinct binding modes in these complexes as shown by the effects of D₂O on relaxation, albeit with similar ³¹P-proton relaxer distances. These binding modes are indicated by the positions of the two ellipses. When the binding mode cannot be distinguished by the values of τ/R₀, the ellipse is positioned in the center. A third conformation, indicated by the dashed ellipse, is observed in the dIMP-cofactor complex. The extrapolated ³¹P-proton relaxer distances are show in Å. (B) Distinct dynamic states are observed in wild-type enzyme and D219A and with ribose and deoxyribose substrates as evidenced by values of τ.