Transport and Loss of Ring Current Electrons Inside Geosynchronous Orbit During the 17 March 2013 Storm

Abstract

Ring current electrons (1–100 keV) have received significant attention in recent decades, but many questions regarding their major transport and loss mechanisms remain open. In this study, we use the four‐dimensional Versatile Electron Radiation Belt code to model the enhancement of phase space density that occurred during the 17 March 2013 storm. Our model includes global convection, radial diffusion, and scattering into the Earth's atmosphere driven by whistler‐mode hiss and chorus waves. We study the sensitivity of the model to the boundary conditions, global electric field, the electric field associated with subauroral polarization streams, electron loss rates, and radial diffusion coefficients. The results of the code are almost insensitive to the model parameters above 4.5 R _E R _E, which indicates that the general dynamics of the electrons between 4.5 R _E and the geostationary orbit can be explained by global convection. We found that the major discrepancies between the model and data can stem from the inaccurate electric field model and uncertainties in lifetimes. We show that additional mechanisms that are responsible for radial transport are required to explain the dynamics of ≥40‐keV electrons, and the inclusion of the radial diffusion rates that are typically assumed in radiation belt studies leads to a better agreement with the data. The overall effect of subauroral polarization streams on the electron phase space density profiles seems to be smaller than the uncertainties in other input parameters. This study is an initial step toward understanding the dynamics of these particles inside the geostationary orbit.

Key Points

• Ring current electron dynamics within geostationary orbit is modeled and the sensitivity of the model to the input parameters is explored

• Global convective electron transport from geostationary orbit to 4.5 R _E can explain Van Allen Probe observations

• Model results below 4.5 R _E are most sensitive to the electric field and electron lifetimes

1. Introduction

The ring current electrons (energies from ∼1 to a few 100 keV) can contribute to surface charging of satellites and may provide from 10% to 25% of the ring current energy during storm times (Frank, 1967; Liu et al., 2005; Zhao et al., 2016). The injections of ∼10‐keV electrons in the inner magnetosphere during enhanced magnetospheric convection excite chorus waves (Hwang et al., 2007; Thorne, 2010), which resonate with relativistic electrons in the radiation belts and provide an effective mechanism of their pitch angle scattering (Albert, 2005; Horne & Thorne, 2003; Shprits et al., 2008; Thorne, 2010) and local acceleration (Horne & Thorne, 1998; Horne et al., 2005; Li et al., 2007; Reeves et al., 2013; Summers et al., 1998). Electrons of 1‐ to 10‐keV energies can be deposited into protective shielding of satellites operating within the ring current region, cause surface charging, and ultimately damage satellite electronics (Baker, 2000; Choi et al., 2011; DeForest, 1972; Ganushkina et al., 2017; Thomsen et al., 2013).

Despite the important role of the ring current electrons, their transport and loss processes within the geosynchronous orbit (GEO) remain poorly understood primarily due to the limited number of measurements. Only several years ago, the Van Allen Probes opened up a whole new opportunity for quantitative tests of models and theory. Reeves et al. (2016) analyzed the Van Allen Probe electron flux measurements and showed the coherence of the particle dynamics across a broad range of energies from a few tens of kiloelectron volts up to megaelectron volts. They found that at any given L shell, the number of enhancement events increases with the decrease in electron energy and the enhancements have an upper energy limit that varies from event to event. Zhao et al. (2016) examined the dynamics of the ring current electrons during storm times in comparison with the ions. Their results indicate that the electrons frequently penetrate deep into the inner magnetosphere and stay in the low‐L region for a long time, while the loss of tens of kiloelectron‐volt protons is much faster at low L shells. They also found that the contribution of the ring current electrons to the Dst index is noticeably smaller than that of the ions. Using the Van Allen Probe observations between December 2012 and September 2013, Turner et al. (2015) found 47 events with signatures of electron injections at L shells ≤ 4, which were limited in energy to ≤250 keV and followed the observations of the injections at higher L shells. They also noted that it is often difficult to distinguish electron injections from the enhanced convection during storms.

It still remains unclear which mechanisms are responsible for the earthward transport of ring current electrons within GEO. It was suggested that the global dawn‐dusk electric field, driven by the dayside reconnection and antisunward magnetic field line convection, together with corotation‐driven radial electric field, defines the electron drift path in the inner magnetosphere (e.g., Axford, 1969; Lyons & Williams, 1984, and references therein). Supporting this theory, Korth et al. (1999) found that lines demarcating enhanced electron flux at GEO match the Alfvén boundaries (the boundaries between open and closed drift trajectories) calculated using the Volland‐Stern global electric field model (Stern, 1975; Volland, 1973). Using polar data, Friedel et al. (2001) showed that electrons are organized by the Alfvén boundaries within GEO, shrinking and allowing deeper access of plasma during storm times.

It was proposed that energetic electrons can be injected in the magnetotail during geomagnetically active times by substorm‐related localized bursty bulk flows (BBFs; Angelopoulos et al., 1992, 1994; Runov et al., 2009, 2011). Gabrielse et al. (2012) showed that the injections are driven by narrow channels of enhanced electric field associated with the BBFs. However, the efficiency of this transport mechanism to inject particles inside GEO still remains uncertain. Dubyagin et al. (2011) found that a significant fraction of flow bursts is unable to penetrate within 9 R _E, and Ohtani et al. (2006) concluded that only a small portion of BBFs can reach geostationary distances. Further studies (Liu et al., 2016; Sergeev et al., 2012) established that many BBFs are not accompanied by particle injections. Liu et al. (2016) showed that only 20 of 71 events of dipolarization fronts detected within GEO between 1 November 2012 and 1 November 2013 were associated with energetic electron injections, typically not propagating closer than ∼6 R _E.

An increase in the large‐scale electric field between L = 3 and L = 6, where L is McIlwain L shell, for moderate to active geomagnetic conditions (Kp > 3) was reported by Rowland and Wygant (1998). They showed that during the strongest geomagnetic activity the enhanced electric field can be observed inside L = 3. Later, their results were confirmed by Califf et al. (2014). The enhancement was attributed to subauroral polarization streams (SAPS; e.g., Foster & Burke, 2002; Foster & Vo, 2002), the northward middle‐latitude ionospheric electric field that arise from the separation between earthward ion and electron plasma sheet boundaries (Southwood & Wolf, 1978) and usually pronounced in the evening sector. Although initial steps were made in order to understand how SAPS affect electrons in the inner magnetosphere (Califf et al., 2017; Lejosne et al., 2018; Su et al., 2016), more comprehensive modeling studies including electron transport and loss processes are required.

Understanding the dynamics of the ring current electron population is a challenging task since the electron distribution significantly depends not only on time and radial coordinate, as it is for the radiation belts, but also on magnetic local time (MLT). Multispacecraft measurements covering different MLT sectors are therefore required to observe the electron population in its global evolution. However, measuring this electron population is complicated by different external effects such as surface charging and contamination by photoelectrons and penetrating radiation (see Denton et al., 2017, and references therein). Numerical modeling helps us gain insight into the dynamics of ring current electrons under the scarcity of satellite measurements.

In recent years, a number of ring current models have been developed (e.g., RCM [Chen et al., 2015; Lemon et al., 2004; Toffoletto et al., 2003], RAM [Jordanova et al., 1996, 2016; Jordanova & Miyoshi, 2005], CIMI [Fok et al., 2014, 2011, 1999], IMPTAM [Ganushkina et al., 2013, 2015, 2014], and HEIDI (Ilie et al., 2012; Liemohn et al., 2001). The models include the ring current electron population and typically take into account the processes, which are important for the electron dynamics, such as global convection, localized particle injections, radial diffusion due to drift resonance with ultralow frequency waves, and local scattering rates of the electrons. All models face similar challenges in describing the dynamics of the electrons. Due to the complexity of the system, it is often difficult to analyze model errors. For instance, the underestimation of observed particle fluxes can be driven by overestimated scattering rates as well as unrealistic transport processes or by the combination of both factors. Such model errors are the main hindrance for understanding which physical processes are responsible for the dynamics of the ring current electrons.

In this study, we use the four‐dimensional Versatile Electron Radiation Belt (VERB‐4D) code (Aseev et al., 2016; Shprits et al., 2015) to understand the mechanisms that control transport and loss of ring current electrons within GEO during the 17 March 2013 storm. By varying different model parameters, we examine the sensitivity of the model and determine the most significant processes that drive the electron transport and loss. To validate the model, we compare simulation results with the Van Allen Probe measurements.

The manuscript is organized as follows. In section 2, we present Van Allen Probe measurements during the 17 March 2013 storm. We describe the modeling approach in section 3. We show simulation results and study the sensitivity of the code in section 4. In section 5, we discuss the results, and the main conclusions of the study are summarized in section 6.

2. Observations of the 17 March 2013 Storm

We use the combined Van Allen Probe Helium, Oxygen, Proton, and Electron (HOPE) mass spectrometer (Funsten et al., 2013) and Magnetic Electron Ion Spectrometer (MagEIS; Blake et al., 2013) Level 3 particle data during the 17 March 2013 geomagnetic storm to calculate electron phase space density (PSD) as a function of the first and second adiabatic invariants μ and K. The HOPE and MagEIS data match up well during the storm (e.g., see supporting information Figure 1 illustrating electron flux spectrum during the storm), and we have not performed an additional intercalibration between the instruments. The apogee of the satellites is located at ∼1 hr MLT, and an inbound satellite pass traverses the postmidnight and prenoon MLT sectors, while an outbound pass crosses postnoon and premidnight sectors. We use T04S (Tsyganenko & Sitnov, 2005) magnetic field model incorporated into the IRBEM library (Boscher et al., 2012) to calculate invariants μ and K from observed local pitch angles and energies. To determine values of μ, we also use magnetic field measurements made by Electric and Magnetic Field Instrument Suite and Integrated Science (Kletzing et al., 2013) aboard the satellite. Since values of μ and K vary along the satellite trajectory, we use bilinear interpolation to calculate PSD for given constant μ and K.

Figures 1a–1c show 5‐min‐averaged electron PSDs, which are obtained from the data for the first adiabatic invariant μ = 0.1,2.3, and 9.9 MeV/G and second invariant K = 0.3 G ^1/2 R _E during the 17 March 2013 storm. The chosen values of the invariants approximately correspond to energies 0.3, 9, and 30 keV at GEO and 1, 30, and 100 keV at L = 4 (see Figure 2 illustrating energy and pitch angle dependence on the L shell). The corresponding pitch angles vary from ∼34° at GEO to 40° at L = 3, which ensures that Van Allen Probe data are available even if the satellite is significantly off the geomagnetic equator, which can happen during active times.

Figure 1.

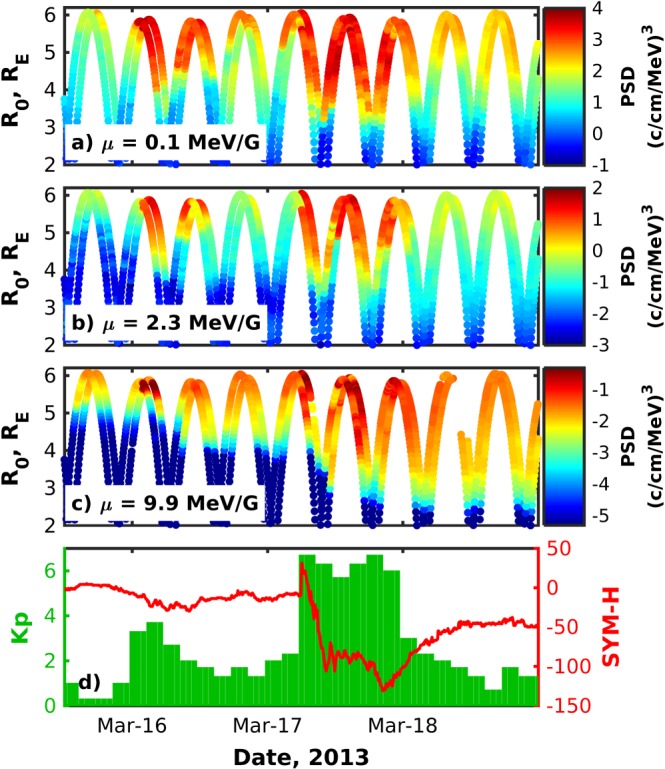
(a–c) Electron PSD derived from the Van Allen Probe observations for μ = 0.1,2.3, and 9.9 MeV/G and K = 0.3 G^1/2 R _E during the 17 March 2013 storm. (d) The K p (green) and S Y M‐H (red) indices. PSD = phase space density.

Figure 2.

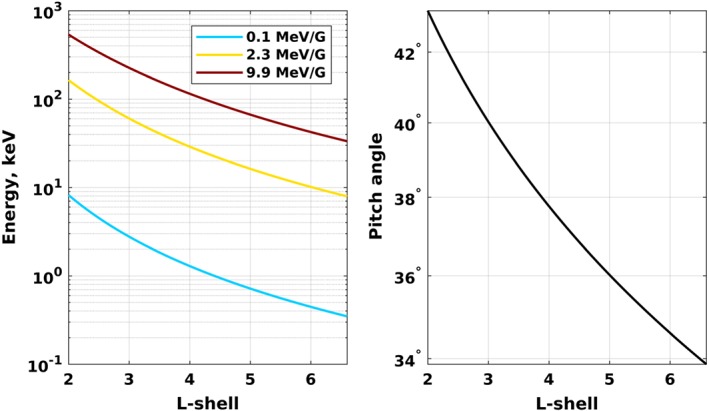
Energies and pitch angles corresponding to different values of the first adiabatic invariant μ. The second invariant K = 0.3 G^1/2 R _E is constant. The energies and pitch angles are calculated using the dipole field.

The geomagnetic storm was driven by a coronal mass ejection that hit the Earth's magnetosphere at 6:00 (see Lyons et al., 2016, for more details). In response to the storm, the Kp index (Figure 1d) showed values above 6− for 18 hr, and SYM‐H index (Figure 1d) reached −130 nT, indicating significant enhancement of the ring current. Ring current electrons were injected down to R ₀ = 2.5–3 R _E, showing the increase in the PSD until the main phase of the storm ended on ∼18 March (see Figures 1a–1c). We note that R ₀ denotes here the distance from the center of the Earth to the point of the minimum magnetic field found along the field line at which the spacecraft resides (for this, we used Olson & Pfitzer, 1977, and IGRF; Thébault et al., 2015, magnetic field models). The recovery phase was characterized by the sharp decrease in 0.1 and 2.3 MeV/G electron PSD and a more gradual decrease in 9.9 MeV/G electron PSD.

Although the storm time dynamics of electrons for considered values of μ and K may look similar, it can be driven by different energy‐dependent mechanisms. Particles with a half‐drift period longer than the main phase of the storm have direct convective access to the ring current region (Lyons & Williams, 1980). The higher‐energy particles have shorter drift periods and more efficiently interact with electric field fluctuations, which lead to the inward displacement driven by radial diffusion (Cornwall, 1968; Lyons & Schulz, 1989). Lyons and Schulz (1989) showed that particles with energies $\succsim$40 keV are closer to diffusive access, while $⪅$40‐keV particles have convective access.

The calculated PSD may depend on the used magnetic field model since the calculation of the invariant K requires an integration along a field line that crosses the spacecraft location. Errors in the field model may lead to the uncertainties in the computed PSD. To study the effects of different magnetic field models, we also calculated PSD, using the Tsyganenko (1989; T89), Tsyganenko (1995; T96), Tsyganenko (2002; T01S), and Tsyganenko and Sitnov (2007; TS07D) models.

Figure 3 shows the calculated PSD profiles as a function of R ₀ for three consecutive Van Allen Probe B passes during the main phase of the storm. For the first satellite pass beginning at 9:00 on 17 March, the magnetic field models have almost no effect on μ = 0.1 and 9.9 MeV/G electron PSD, while a small difference in PSD is observed for 2.3 MeV/G particles between ∼4.6 and 5.3 R _E. For the next pass beginning at 13:30, the PSD profiles, which were calculated using T89, T01S, T04S, and TS07D models slightly differ above ∼4.8 R _E for all values of the first invariant, and the T96 model results in generally lower PSD, which are up to 1 order of magnitude smaller than the profiles calculated using the TS07D model. The PSD values along the following pass at 18:00 show insignificant differences for all profiles. As will be shown later, the differences in the PSD obtained from the Van Allen Probe measurements are much smaller than the uncertainties in the numerical model of the ring current electrons, and the errors that the T04S model introduces can be neglected, given a much larger model uncertainty.

Figure 3.

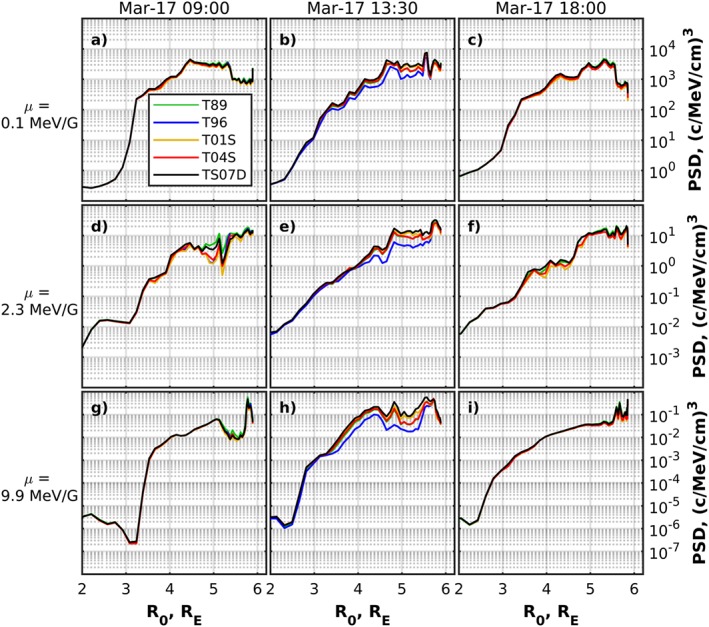
Profiles of electron PSD for K = 0.3 G^1/2 R _E and μ = 0.1 MeV/G (a–c), 2.3 MeV/G (d–f), and 9.9 MeV/G (g–i) calculated using different magnetic field models for three subsequent Van Allen Probe B passes. Columns correspond to the passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). PSD = phase space density.

3. Model Description

We use the VERB‐4D code to model the dynamics of the ring current electrons. The code solves the modified Fokker‐Planck equation with additional advection terms (Aseev et al., 2016; Shprits et al., 2015). It allows simultaneously modeling ring current and radiation belt dynamics by combining electron drift, radial diffusion, pitch angle and energy diffusion, and loss processes that can be parameterized with the lifetime τ (e.g., magnetopause shadowing is accounted by setting up τ to one‐half drift period and loss to the atmosphere is accounted by setting up the lifetimes within the loss cone to one‐fourth bounce time):

$$\begin{array}{ccc}\hfill & \frac{\partial f}{\partial t}=-⟨v_{\phi }⟩\frac{\partial f}{\partial \phi }-⟨v_{R_0}⟩\frac{\partial f}{\partial R_0}+\frac{1}{G}\frac{\partial }{\partial L^{\ast }}G⟨D_{L^{\ast }{L}^{\ast }}⟩\frac{\partial f}{\partial L^{\ast }}+\hfill & \hfill \\ \hfill & +\frac{1}{G}\frac{\partial }{\partial V}G\left(⟨D_{VV}⟩\frac{\partial f}{\partial V}+⟨D_{VK}⟩\frac{\partial f}{\partial K}\right)+\frac{1}{G}\frac{\partial }{\partial K}G\left(⟨D_{KV}⟩\frac{\partial f}{\partial V}+⟨D_{KK}⟩\frac{\partial f}{\partial K}\right)-\frac{f}{\tau },\hfill \end{array}$$ (1)

where f is the PSD; t represents time; φ is MLT, R ₀ is the radial distance to a given point in the geomagnetic equator; V, K, and L ^∗ are modified adiabatic invariants (Subbotin & Shprits, 2012); V = μ·(K + 0.5)²; μ is the first adiabatic invariant; τ is electron lifetime related to scattering into the loss cone and magnetopause shadowing; ⟨v _φ⟩ and $⟨v_{R_0}⟩$ are bounce‐averaged drift velocities; $⟨D_{L^{\ast }{L}^{\ast }}⟩$, ⟨D _VV⟩, ⟨D _VK⟩, ⟨D _KV⟩, and ⟨D _KK⟩ are bounce‐averaged diffusion coefficients; $G=-2\mathrm{\pi }{B}_0{R}_E^2\sqrt{8m_{0}V}/{(K+0.5)}^3/L^{\ast 2}$ is the Jacobian of the coordinate transformation from adiabatic invariants (μ,J,Φ) to (V,K,L ^∗) (Subbotin & Shprits, 2012), B ₀ is the field at the equator at the Earth's surface; and m ₀ is electron rest mass.

The VERB‐4D code has been designed to simplify the implementation of the most important physical processes responsible for the electron dynamics, and it allows us to efficiently perform ensemble simulations or study sensitivity of the code to different input parameters. The numerical schemes implemented in the code have been thoroughly tested (Aseev et al., 2016), and it is guaranteed that the numerical errors do not affect the physical interpretation of the results.

The spatial boundaries are set up at R ₀ = 1 and 6.6 R _E, with 0.5‐hr and 0.2‐R _E grid steps in MLT and radial distance, respectively. To construct a grid in V and K, we create a logarithmic grid in energy and pitch angles limited by 200 eV and 30 keV and 0.7° and 89.3° at GEO with 60 nodes in energy and 61 nodes in pitch angle. Adiabatic invariants are then calculated on this grid, using the dipole field model. We choose these energy limits at GEO to fit in the statistical boundary condition model described below.

To model the enhancement of PSD during the main phase of the storm, we set up initial conditions from Van Allen Probe B inbound pass starting at 20:00 on 16 March and ending at midnight on 17 March. We use PSD derived from HOPE and MagEIS measurements, assume symmetry in MLT, and assign the calculated initial conditions to 20:00 16 March. Boundary conditions in MLT are periodic. At the lower boundary R ₀ = 1 R _E, we assume zero PSD since all particles are lost in the atmosphere. To specify the outer boundary at R ₀ = 6.6 R _E, we use the statistical model of electron fluxes developed by Denton et al. (2016). The model is based on 82 satellite years of observations at GEO made by magnetospheric plasma analyzer instruments onboard Los Alamos National Laboratory satellites. The model provides spin‐averaged electron fluxes as a function of energy, MLT, and the Kp index and covers the energy range from ∼40 eV to 40 keV at GEO. Along with the mean and median values of the fluxes, 5th, 25th, 75th, and 95th percentile limits are also given. To obtain directional flux from the spin‐averaged flux, we assume its sinusoidal dependence on the pitch angle.

We take into account electron scattering driven by hiss and chorus waves by using parameterized electron lifetimes included in the parameter τ instead of local diffusion terms (fourth and fifth terms on the right‐hand side of equation (1)). In this case, boundary conditions in the invariants V and K are not required since there is no feedback from local diffusion terms. We use the MLT‐averaged model of electron lifetimes within the plasmasphere developed by Orlova et al. (2016). Outside the plasmasphere, we utilize the MLT‐dependent scattering rates obtained by Gu et al. (2012). The plasmapause location is calculated using the Carpenter and Anderson (1992) model.

We use the realistic T89 mangetic field model and the Weimer (2005; W05) polar cap potential model to calculate electron E × B and gradient‐curvature drift velocities at the geomagnetic equator. The polar cap potential is mapped along the equipotential dipole field lines down to the geomagnetic equator. At the equator, the electric field is numerically calculated, using a central differencing scheme (we refer to the calculated electric field as W05 electric field model). Compared to the commonly used Kp‐driven Volland‐Stern electric field model, the W05 model is parameterized with solar wind parameters, which ensures more realistic variability of the global electric field, naturally driven by the dayside reconnection. In the current work, we feed 15‐min‐averaged solar wind parameters to the W05 model.

We utilize Kp‐parameterized radial diffusion rates by Brautigam and Albert (2000). We note that similar results are obtained with Ozeke et al. (2014) parameterization. To simultaneously account for the direct convective access and diffusive access of electrons to the ring current region, we smoothly zero out the diffusion rates for electron energies smaller than the threshold of 40 keV proposed by Lyons and Schulz (1989).

4. Results

In this section, we show the results of the VERB‐4D code and compare them with the PSD calculated along the Van Allen Probes trajectories. We present the confidence intervals of the model, which are associated with the uncertainties in the outer boundary conditions. We also study the sensitivity of the results to the input parameters such as convection electric field, electron loss rates, radial diffusion coefficients, and SAPS electric fields.

We start all simulations that are presented in this section at 20:00 on 16 March 2013 with a time step of 15 min. We stop the simulations at 00:00 on 18 March 2013 to model the storm time enhancement of PSD across a given range of energies. We then interpolate the global distribution of PSD provided by the VERB‐4D code along the Van Allen Probe trajectories, using linear interpolation in time, radial distance, and MLT. The target values of μ and K invariants to compare with satellite data were chosen to match the corresponding grid values of the VERB‐4D code.

4.1. Model‐Data Comparison Along the Van Allen Probe Orbits

We use the mean value of the Denton et al. (2015) statistical flux distribution and the W05 electric field to model the storm time dynamics of the ring current electrons. Other input parameters are the same as described in section 3.

Figure 4 shows the comparison between the Van Allen Probe data and the results of the VERB‐4D code for μ = 0.1, 2.3, and 9.9 MeV/G and K = 0.3 G^1/2 R _E electrons. The leftmost orbit along a given inbound or output pass in Figure 4 corresponds to the Van Allen Probe B trajectory since the Van Allen Probe B moves ahead of the Van Allen Probe A for the chosen time interval.

Figure 4.

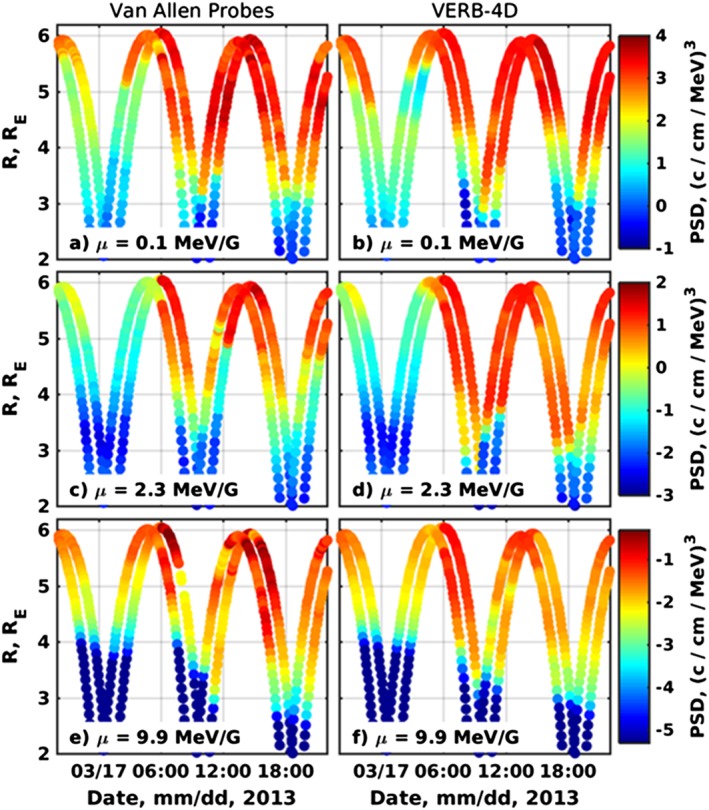
Comparison of the Van Allen Probe PSD (left column) with the VERB‐4D code results (right column) for μ = 0.1, 2.3, and 9.9 MeV/G and K = 0.3 G^1/2 R _E. The figure represents an in situ comparison, made at the location of the spacecraft. The mean boundary flux is used. A leftmost orbit along a given inbound or outbound pass corresponds to the Van Allen Probe B trajcetory. PSD = phase space density; VERB‐4D = four‐dimensional Versatile Electron Radiation Belt.

The storm time dynamics of the 0.1 MeV/G electrons (Figure 4a) is reproduced relatively well by the VERB‐4D code (Figure 4b). The code captures the time and radial extent of the PSD enhancement. The measurements along the pass starting at 6:00 on 17 March 2013, just before the storm onset, show the increase in electron PSD from ∼6 R _E to as low as 3.5–4 R _E, and the code is able to reproduce the increase, predicting the radial extent of the enhancement ∼0.1–0.2 R _E farther away from the Earth than it is seen in the data. In agreement with the data, the model results show the earthward penetration of the electrons along the next satellite pass at ∼9:00 down to 3 R _E for Van Allen Probe B and to 3.5 R _E for the Van Allen Probe A. For the next two passes, the model agrees well with the observations between ∼4 R _E and 6 R _E and generally underestimates PSD between 3 and 4 R _E.

The comparison between the code and the data for μ = 2.3 and 9.9 MeV/G electrons between ∼6:00 and 10:00 reveals an interesting fact that the enhancements in the modeled PSD extend closer to the Earth than the data show, while the code agrees well with the data for μ = 0.1 MeV/G electrons. The increase in 2.3 MeV/G PSD is observed down to ∼4 R _E (Figure 4c), and the code predicts higher PSD between 3 and 4 R _E (Figure 4d). The observed enhancement in 9.9 MeV/G electron PSD extends down to 4.5–5 R _E (Figure 4e) for the same time interval, while the enhancement in the code spreads down to 3.5–4 R _E (Figure 4f). Such a mismatch in the model predictions between 0.1 MeV/G and higher‐energy electrons can be explained by the strong convective electric field or shorter lifetimes of the 0.1 MeV/G electrons, which are implemented in the model.

For the outbound satellite pass between ∼10:00 and 13:00, the code overestimates the observations for μ = 2.3 MeV/G electrons from ∼3.5 to 4.9 R _E, which can be due to the stronger earthward propagation that occurred during the previous pass. We note that the Van Allen Probe A shows the sudden increase in electron PSD at 4.9 R _E occurred at 12:00, as the satellite moves to the apogee. Such an increase cannot be attributed to the energy boundary between HOPE and MagEIS instruments since the boundary is located at ∼3.2 R _E for the given first and second adiabatic invariants. The nature of the increase is not clear since the Van Allen Probe B traversing similar region shows much higher PSD between 4 and 4.9 R _E than the Van Allen Probe A observes. The model overestimates PSD between 3 and 4.5 R _E along the next two satellite passes after 13:00 and agrees better at higher radial distances.

The model results for the μ = 9.9 MeV/G particles matches well the observations between 3 and 4 R _E after 10:00 despite the overestimated PSD at the previous satellite pass. Above 4 R _E, the model generally shows slightly lower PSD values than observed in the data.

The results presented in this section indicate that the model is capable of qualitatively and quantitatively reproducing the dynamics of the ring current electron population above  4.5 R _E. The model can capture the features of the enhancements in that region, although the magnitude of PSD may slightly differ from the observations. The differences between the model and data above 4.5 R _E can be explained by the simplified Kp‐dependent model of the spatial outer boundary conditions. Below 4.5 R _E, the discrepancies between the model and the data are generally higher, which can be indicative of the uncertainties in electric and magnetic fields or in electron lifetimes. In the next sections, we study the discrepancies between the model and the data in more detail by analyzing the sensitivity of the code to the input parameters.

4.2. Sensitivity to the Outer Boundary Conditions

To study the sensitivity of the model to the boundary conditions and provide approximate confidence interval of the model, we perform simulations with 5th, 25th, 75th, and 95th percentiles of statistical distribution of electron flux at GEO (Denton et al., 2015), keeping all other input parameters the same as in section 4.1. Figure 5 presents PSD profiles for μ = 0.1, 2.3, and 9.9 MeV/G and K = 0.3 G^1/2 R _E together with percentile limits for three subsequent Van Allen Probe B passes starting at 9:00 on 17 March. The figure shows that most of the time satellite data are within the percentile limits, generally showing better agreement above R ₀ = 3.5 R _E across all adiabatic invariants. Note that PSD varies by up to 4 orders of magnitude and the model covers rather well this variability within the confidence interval. Below 3.5 R _E, μ = 0.1 MeV/G electron PSD profiles diverge from simulation results, demonstrating deeper earthward displacement by approximately 0.3 R _E for the satellite pass that started at 9:00 (Figure 5a) and lower PSD values for the next pass (Figure 5b), underestimating the inner boundary by approximately 0.3 R _E. The results for 2.3 MeV/G electrons are generally higher than the data for the first two presented satellite passes between 3 and 4 R _E, yet the satellite observations show much better agreement at others radial distances. The values and shapes of PSD profiles for μ = 9.9 MeV/G are very close to the 25th and 75th percentile limits across all radial distances.

Figure 5.

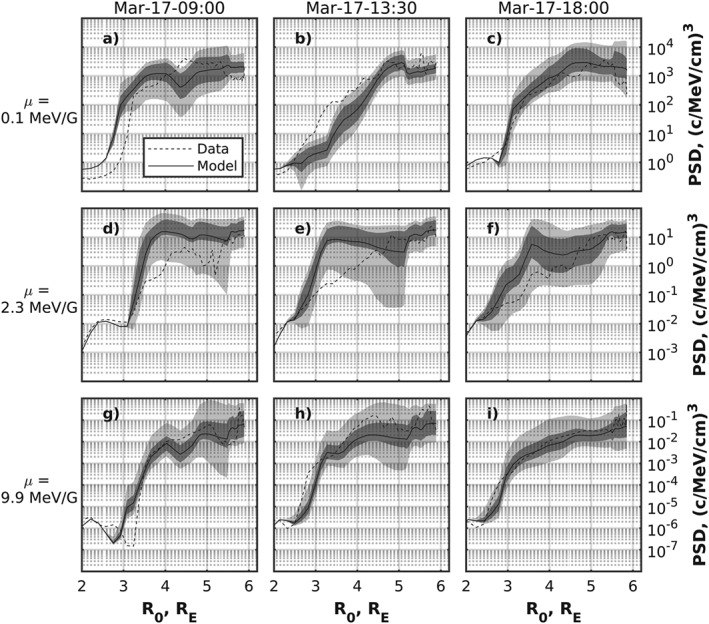
Comparison between Van Allen Probe B data (dashed lines) with the VERB‐4D code results (solid lines) for K = 0.3 G^1/2 R _E and μ = 0.1 MeV/G (a–c), 2.3 MeV/G (d–f), and 9.9 MeV/G (g–i). Columns correspond to satellite passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). The dark gray regions are limited by the 25th and 75th percentiles of the outer radial boundary conditions. The light gray regions are limited by the 5th and 95th percentiles. PSD = phase space density.

Although the magnitude of the modeled PSD depends on the outer boundary conditions that are used in the simulations, the shape of the profiles remains mostly unchanged. This fact does not necessarily imply that the boundary conditions have no effect on the shape of the profiles or the observed smaller‐scale features. Since we use different percentile values of the electron flux at GEO as the boundary conditions, the increase or decrease in the magnitude of the boundary conditions takes place along all MLT sectors at the same time. The percentile values, thus, provide approximate lower and upper limits of the PSD magnitude and do not affect the shape of the profiles.

The fact that the Van Allen Probe observations do not fit in the 5th and 95th percentile limits indicates that the discrepancies between the model and data, which is evident in Figure 5a below 3 R _E and in Figures 5b and 5e between 3 and 4 R _E, are most probably caused by other model parameters such as electric field or electron loss rates.

4.3. Role of the Electric Field Model

The differences between the observed PSD and the results of the VERB‐4D code (e.g., see Figure 4) can partially stem from the inaccuracies of the electric field model. In this section, we study the role of the global electric field in the simulations.

Figure 6 presents the comparison between the local electric field measured by the Van Allen Probe Electric Field and Waves (EFW) instrument (Wygant et al., 2013) and the W05 electric field model interpolated in time and space along the satellite trajectory. The presented electric fields are in a reference frame corotating with the Earth. We use 6‐min moving average of the observed electric fields. We eliminate intervals when spacecraft charging affects the measurements and when the satellites reside in the Earth's shadow and observations are compromised. Figure 6 shows the measured E _y component in the MGSE coordinate system (Wygant et al., 2013) and the E _y component in GSE system obtained from the W05 model. The MGSE system has been developed to isolate the more accurately measured components of the electric field, and the Y‐axis in GSE system is most nearly aligned with the Y‐axis in MGSE system.

Figure 6.

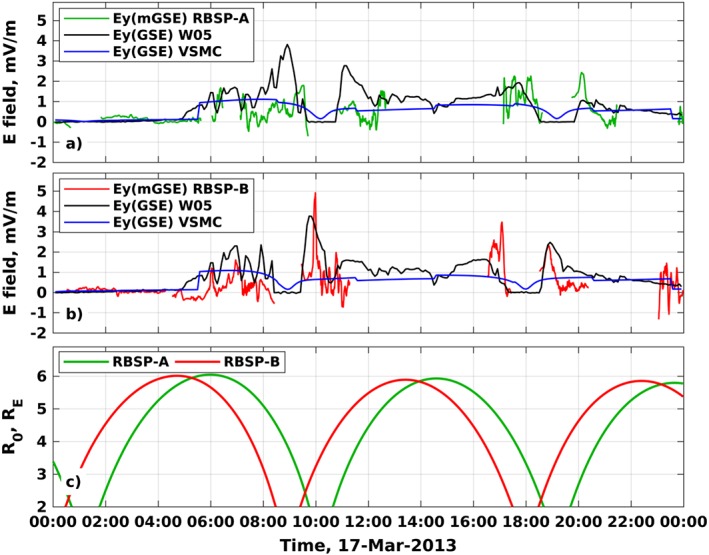
(a, b) Comparison between electric fields measured by the Van Allen Probes A and B (green and red lines), the Weimer (2005) electric field model (black lines), and the VSMC electric field model (blue lines). The electric fields are presented in the reference frame corotating with the Earth. The model electric fields are calculated along the satellite trajectories. (c) The Van Allen Probe R ₀ (the distance from the center of the Earth to the point of the minimum magnetic field along the magnetic field line crossing the spacecraft location). VSMC = Volland, (1973), Stern, (1975), and Maynard and Chen (1975); RBSP = Radiation Belt Storm Probes; GSE = geocentric solar ecliptic; mGSE = modified GSE.

The W05 electric field is similar to the Van Allen Probe observations between ∼6:00 and 8:00 on 17 March 2013, slightly overestimating the measurements. When the Van Allen Probe A moves toward perigee, it observes an increase in the electric field magnitude from 8:00, when the spacecraft is at 5 R _E, to ∼9:30, when the spacecraft resides at 3 R _E. The W05 model also predicts an increase in the electric field, but the model shows a distinct peak at 9:00 (∼ 3.5 R _E) that is ∼3.5 times higher than observed electric field (Figure 6a). The W05 electric field at the next satellite pass also shows a peak at the same location. The Van Allen Probe B shows a similar enhancement at ∼10:00, which is, however, more narrow than the W05 model predicts (see Figure 6b). Overall, the model electric field noticeably overestimates the measurements between 8:00 and 10:00. Such an overestimation can explain the fact that the model results are higher than the data for 2.3 and 9.9 MeV/G particles below 4‐4.5 R _E along the inbound satellite pass beginning at 6:00 (see Figure 4).

To understand how the global electric field can affect simulation results, we perform a simulation, using the Kp‐dependent Volland‐Stern electric field model (Volland, 1973; Stern, 1975; Maynard & Chen, 1975 [VSMC]) and keep all other parameters the same as in section 4.1. The comparison of the VSMC electric field with the EFW measurements is shown in Figure 6. Since the Kp index reaches ∼6 and stays approximately constant for 18 hr, the VSMC model shows almost no variations which are constantly seen in the data. Compared to the W05 model, the E _y component of the VSMC electric field is mostly lower, and the models agree better at higher radial distances.

Figure 7 presents the comparison of the resulting PSD for μ = 0.1, 2.3, 9.9 MeV/G and K = 0.3 G^1/2 R _E electrons interpolated along the Van Allen Probe B trajectory for different electric field models. The electric field models have almost no effect on the profiles of 9.9 MeV/G electrons, due to the gradient and curvature drifts, which are relatively strong for these particles. The magnitude of 0.1 and 2.3 MeV/G electron PSD for W05 and VSMC electric field models are very similar above ∼4.5 R _E. This result is consistent with Figure 6 showing that both electric field models do not differ much at higher radial distances. Below 4.5 R _E, where the VSMC electric field are much smaller than the W05 field, the electron profiles obtained with the VSMC model are significantly lower compared to the profiles obtained with the W05 model. The VSMC electric field model leads to larger differences in 0.1 and 2.3 MeV/G electron PSD profiles and data between ∼2.5 and 4–4.5 R _E. We note a peak in the 0.1 MeV/G profiles that is observed near 3 R _E, which can be formed due to a stronger loss and slow earthward transport from GEO if the VSMC model is used.

Figure 7.

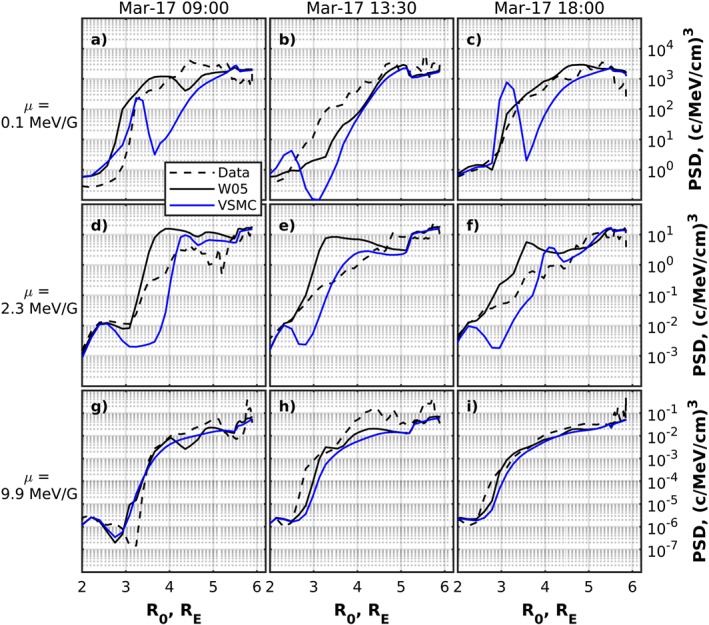
Comparison between the Van Allen Probe B PSD (dashed lines) with the VERB‐4D code results if the W05 electric field model is used (black solid line) and if the Volland, (1973), Stern, (1975), and Maynard and Chen (1975) electric field model is used (blue solid lines) for K = 0.3 G^1/2 R _E and μ = 0.1 MeV/G (a–c), 2.3 MeV/G (d–f), and 9.9 MeV/G (g–i). Columns correspond to satellite passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). PSD = phase space density.

Figures 8 and 9 illustrate the global evolution of the modeled PSD for μ = 2.3 MeV/G and K = 0.3 G^1/2 R _E electrons for different electric field models and several time moments during the main phase of the storm. At 6:00 on 17 March 2013, just before the storm, the PSD obtained with the W05 model show the increase propagating from GEO to ∼5 R _E at the nightside (Figure 8a), while the VSMC model only predicts the increase down to ∼6 R _E (Figure 9a). In general, the W05 model leads to the propagation of the electrons down to 3 R _E at a later time, up to 1 R _E deeper than in the case of the VSMC model. The enhanced PSD obtained with the W05 model fill the region between 3 and 5 R _E in the MLT sector between 21 and 12 hr from 9:00 to 18:00 (Figures 8b–8e). Such an enhancement is also evident in Figure 5 as a peak in 2.3 MeV/G electron PSD profiles computed with the VERB‐4D code. The VSMC model predicts lower PSD in the same region (Figures 9b–9e). Both models give qualitatively and quantitatively similar results above 4.5–5 R _E, in good agreement with the data, as shown in Figure 7. Another region of the difference in the modeled global distributions is around the duskside from 14 to 21 hr MLT. This region contains the stagnation point that separates open and closed drift paths, and the small difference in the electric field model can affect the trapping of particles in the code and potentially lead to the overestimation or underestimation of the measurements. We note that Van Allen Probes do not cross this region during the considered event, and the difference in the dynamics there have to be addressed in future studies.

Figure 8.

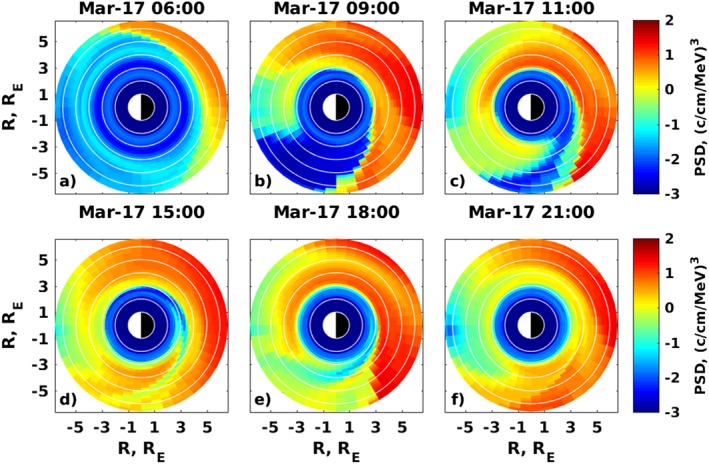
Global PSD distribution of μ = 2.3 MeV/G and K = 0.3 G^1/2 R _E electrons obtained with VERB‐4D code if the Weimer (2005) electric field model is used. PSD = phase space density.

Figure 9.

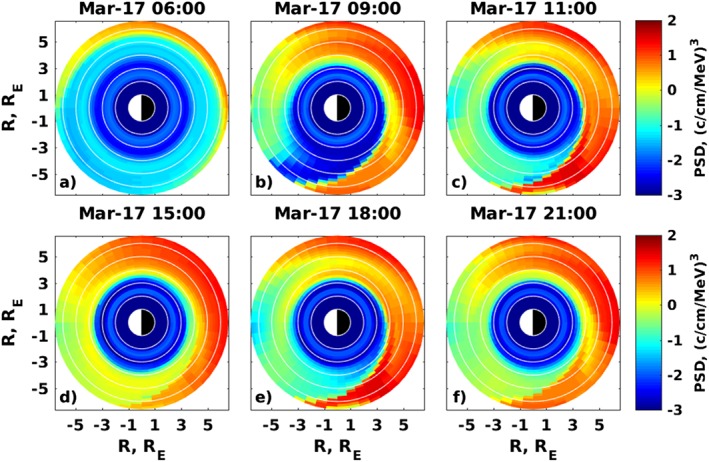
Global PSD distribution of μ = 2.3 MeV/G and K = 0.3 G^1/2 R _E electrons obtained with the VERB‐4D code if the Volland (1973), Stern (1975), and Maynard and Chen (1975) electric field model is used. PSD = phase space density.

4.4. Sensitivity to the Electron Lifetime Model

In this section, we study the sensitivity of the code results to the electron lifetime model. We perform several simulations with the same model parameters as described in section 4.1 and vary the electron lifetimes outside the plasmasphere. We multiply and divide the lifetimes by 2 and 10, and if the lifetimes are lower than the strong diffusion limit predicts, we assume the strong diffusion approximation.

Figure 10 presents the resulting profiles interpolated along the Van Allen Probe B trajectory for different electron lifetimes. The μ = 0.1 MeV/G profiles are the most sensitive to the changes in the lifetimes. The twofold increase or decrease in the lifetimes may lead to the difference in PSD larger than 1 order of magnitude and different shape of the profiles (e.g., Figure 10b). The μ = 2.3 MeV/G profiles are less sensitive to the increase in the electron lifetimes (Figures 10d–10f), while the profiles differ more significantly if the lifetimes are decreased. The twofold decrease in the lifetimes results in similar shape and magnitude of the profiles, while the tenfold decrease leads to unrealistically low model results. The profiles of μ = 9.9 MeV/G particles are not noticeably changed due to the increase and twofold decrease in electron lifetimes, and the tenfold decrease in electron lifetimes produces results much smaller than the data. The model results are generally less sensitive to the electron lifetimes above 4.5 R _E for all μ values, while the difference between the simulations grows with decreasing radial distance.

Figure 10.

Comparison between the Van Allen Probe B PSD (dashed lines) with the VERB‐4D code results for different electron lifetimes outside the plasmasphere (solid lines) for K = 0.3 G^1/2 R _E and μ = 0.1 MeV/G (a–c), 2.3 MeV/G (d–f), and 9.9 MeV/G (g–i). Columns correspond to satellite passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). PSD = phase space density.

4.5. Effects of Radial Diffusion

To demonstrate the role of the radial diffusion, we perform an additional simulation with all input parameters, which have been used in section 4.1 and set up the radial diffusion coefficient $D_{L^{\ast }{L}^{\ast }}$ to 0. Figure 11 shows the comparison between the simulations with and without radial diffusion term for μ = 9.9 MeV/G and K = 0.3 G^1/2 R _E electrons. We note that the diffusion coefficient for 0.1 and 2.3 MeV/G electrons is 0 by the setup of the model, and the results of both simulations are identical for these particle populations. The simulation with radial diffusion term agrees better with the data for all considered satellite passes. The difference between the simulations is most evident along a satellite pass starting at 9:00 (Figure 11). The radial diffusion term results in deeper propagation of the PSD profiles compared to the simulation when radial diffusion is not included in the code. The simulations give almost the same results above 4.5 R _E, and the discrepancies are observed at lower radial distances.

Figure 11.

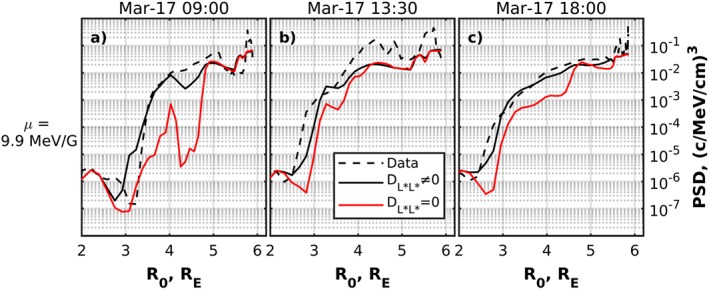
Comparison between the Van Allen Probe B PSD (dashed lines) with the VERB‐4D code results with and without radial diffusion term (black and red solid lines, respectively) for K = 0.3 G^1/2 R _E and μ = 9.9 MeV/G electrons. Columns correspond to satellite passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). PSD = phase space density.

4.6. Effects of SAPS

The SAPS electric field can potentially affect the dynamics of the ring current electrons below ∼4 R _E. To estimate an effect of SAPS, we performed a simulation with the included Kp‐dependent model of SAPS, using the approach developed by Goldstein et al. (2005). Figure 12 presents the results in the same format as Figure 7. The overall effect of SAPS is relatively small for μ = 9.9 MeV/G particles. SAPS lead to the deeper earthward propagation of the 2.3 MeV/G electron PSD profiles than the model without SAPS. The difference between two simulations for 0.1 MeV/G electrons is noticeable between 3 and 4 R _E at 13:30 on 17 March 2013, and results obtained with the SAPS model included diverge strongly from the data along this satellite pass (Figure 12b). The implemented model of SAPS have no effect on the shape of the profiles (except the profiles in Figure 12b), leading to a small earthward shift of the PSD profiles. We note that the Kp‐driven SAPS model creates very slow changes in the electric field, and the effect may be more pronounced with a more variable realistic field.

Figure 12.

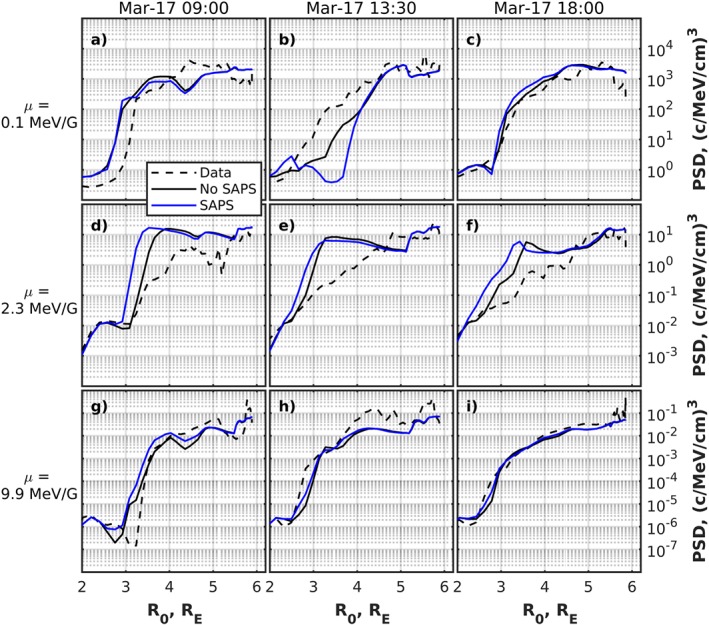
Comparison between Van Allen Probe B data (dashed lines) with the VERB‐4D code results with and without subauroral polarization streams included (blue and black solid lines, respectively) for K = 0.3 G^1/2 R _E and μ = 0.1 MeV/G (a–c), 2.3 MeV/G (d–f), and 9.9 MeV/G (g–i). Columns correspond to satellite passes beginning at 9:00, 13:30, and 18:00 on 17 March (from left to right). PSD = phase space density.

5. Discussion

The comparison between the VERB‐4D code and the Van Allen Probe data demonstrate that the model results are almost insensitive to the input parameters, such as electric field model, electron scattering rates, boundary conditions, radial diffusion, and SAPS model, for μ = 0.1, 2.3, and 9.9 MeV/G and K = 0.3 G^1/2 electrons above ∼4.5 R _E. The observed PSD fit in the approximate confidence intervals associated with the uncertainties in boundary conditions and are almost always within the 25th and 75th percentile limits above 4.5 R _E (see Figure 5). The simulations with the W05 and VSMC electric field models give similar results in that region, with PSD being slightly higher in the case of W05 model (see Figure 7). Between 4.5 R _E and GEO, the code results are almost insensitive to the electron lifetimes, and the SAPS have no effect on the PSD profiles. A good agreement between the model and the observations above 4.5 R _E indicate that realistic boundary conditions that are transported inward by the global‐scale electric and magnetic field can generally explain the PSD enhancement in that region. The use of more accurate boundary conditions from the observations as well as localized electric and magnetic fields may help reproduce smaller‐scale features observed in the data.

The model results differ from the data more noticeably below 4.5 R _E, and the biggest discrepancies are likely explained by the errors in electric field and electron lifetime models. The in situ comparison between the electric field measured by Van Allen Probes and the field computed with the W05 model shows that the model electric field agrees better with the observations at higher radial distances and overestimates the measurements at lower distances down to as low as 3 R _E at the beginning of the storm (see Figure 6). The unrealistically strong electric field at lower radial distances is a possible reason for the overestimation of electron PSD below 4 R _E for 2.3 and 9.9 MeV/G electrons from 8:00 to 10:00 (see Figure 4). The peak in 2.3 MeV/G electron PSD profiles between 3 and 4 R _E (Figures 5d–5f) is not observed in the data and is most probably caused by the uncertainties in W05 electric field model since the VSMC model leads to the less pronounced peak and even underestimation of the measurements at lower radial distances (see Figures 7d–7f). The 0.1 MeV/G electron PSD profiles are the most sensitive to the electron lifetimes, and the simultaneous overestimation of the observed PSD for 2.3 MeV/G electrons and underestimation for 0.1 MeV/G electrons along the Van Allen Probe B trajectory beginning at 13:30 on 17 March 2013 (Figures 5b and 5e) may be caused by the combined effects of uncertainties in the lifetimes and electric field. We note that tenfold decrease in electron lifetimes leads to unrealistic results for all considered adiabatic invariants.

The quantification of the radial diffusion of the ring current electrons needs to be further investigated in future studies. With regard to the 17 March 2013 storm, the global‐scale convection does not reproduce the radial extent of the 9.9 MeV/G profiles below 4–5 R _E, while the inclusion of the radial diffusion term leads to much better agreement with the measurements (see Figure 11). We note here that in general, the radial diffusion is not the only candidate for explaining the dynamics of these particles. For instance, the SAPS electric field can also contribute to their transport. Although the simplest Kp‐dependent model of the SAPS (Goldstein et al., 2005) that we tested in this study produces only a slight earthward shift of the profiles (Figure 12), more realistic models, including self‐consistent treatment of the electric field (Yu et al., 2017), potentially may cause more noticeable effects. The localized particle injections due to penetrating dipolarization fronts can also contribute to the electron radial transport, but their effects are typically observed at higher radial distances.

The use of the local diffusion term and MLT‐dependent chorus wave models can further improve the simulation results. Since most of the chorus wave models have been designed for the radiation belts, they assume that the wave amplitude and normal angle distribution do not vary within rather wide day and night MLT sectors (e.g., Agapitov et al., 2015, 2018; Spasojevic & Shprits, 2013). While such an assumption can be justified in three‐dimensional radiation belt codes, four‐dimensional models of the ring current electrons may require more accurate MLT‐dependent chorus wave parameterizations. We also emphasize the importance of the plasmasphere model that separates hiss and chorus wave‐driven scattering of electrons. Inaccuracy in the demarcation boundary between the regions dominated by different waves and different plasma conditions introduces additional uncertainty in the simulations. More advanced MLT‐dependent models (e.g., derived from neural network‐based model of plasmasphere, e.g., Zhelavskaya et al., 2017) will be included in our future studies.

6. Summary

In this study, we modeled the storm time enhancement of ring current electron PSD during the 17 March 2013 storm for μ = 0.1, 2.3, and 9.9 MeV/G and K = 0.3 G^1/2 R _E electrons, which covers the energies from 1 to 100 keV at L = 4, using the VERB‐4D code. Our model includes magnetospheric convection driven by global magnetic and electric fields, radial diffusion, and electron scattering rates due to interaction with whistler‐mode hiss and chorus waves. We compared the simulation results with the Van Allen Probe data and studied the sensitivity of the model to the input parameters including the global electric field, outer boundary conditions at GEO, electron lifetimes outside of the plasmasphere, radial diffusion, and SAPS. The main conclusions are stated below.

• For the considered event, simulation results are relatively insensitive to all tested input parameters above  4.5 R _E for all considered adiabatic invariants, and the general dynamics of the particles between 4.5 and 6.6 R _E appear to be driven by the transport of the particles from GEO under the action of the global electric and magnetic fields.

• Although the sensitivity of the model to the localized electric fields has not been tested in this study, our results indicate that the discrepancies between the model and data between 4.5 R _E and GEO can be explained by uncertainties in boundary conditions, and additional physical processes, such as the localized fields, may not be needed to reproduce the general evolution of the ring current electrons in that region.

• The main discrepancies between the model and data below 4.5 R _E can be explained by errors in the global electric field and electron lifetimes.

• The global convective transport cannot reproduce the radial extent of the 9.9 MeV/G electron profiles below ∼4.5 R _E, and the inclusion of the radial diffusion term with the diffusion rates by Brautigam and Albert (2000) leads to better agreement with the data.

• The Kp‐driven SAPS model (Goldstein et al., 2005) leads to relatively small changes in the electron profiles, which seem to be less significant than the uncertainties related to lifetimes or electric field.

This study presents the initial step toward understanding the complicated transport and loss processes of low‐energy electrons within GEO. The future extension of this study will include modeling of lower‐energy electrons, improvement of the loss and fields model, and understanding of the contribution of localized electric fields beyond and inside GEO.

Supporting information

Text S1

Aseev, N. A. , Shprits, Y. Y. , Wang, D. , Wygant, J. , Drozdov, A. Y. , Kellerman, A. C. , & Reeves, G. D. (2019). Transport and loss of ring current electrons inside geosynchronous orbit during the 17 March 2013 storm. Journal of Geophysical Research: Space Physics, 124, 915–933. 10.1029/2018JA026031