Reflection phase microscopy using spatio-temporal coherence of light

Abstract

Many disease states are associated with cellular biomechanical changes as markers. Label-free phase microscopes are used to quantify thermally driven interface fluctuations, which allow the deduction of important cellular rheological properties. Here, the spatio-temporal coherence of light was used to implement a high-speed reflection phase microscope with superior depth selectivity and higher phase sensitivity. Nanometric scale motion of cytoplasmic structures can be visualized with fine details and three-dimensional resolution. Specifically, the spontaneous fluctuation occurring on the nuclear membrane of a living cell was observed at video rate. By converting the reflection phase into displacement, the sensitivity in quantifying nuclear membrane fluctuation was found to be about one nanometer. A reflection phase microscope can potentially elucidate biomechanical mechanisms of pathological and physiological processes.

1. INTRODUCTION

Phase measurement based on digital holography has been widely used to investigate the physical properties of translucent specimens in a label-free manner without any exogenous chemical compounds. For instance, phase microscopy has been exploited to obtain biophysical properties of biological specimens, such as dry mass for individual cells [1–4], mechanical properties of red blood cells (RBCs) in various pathophysiological situations [5–9], and scattering or polarization response of tissues [10–12]. However, a single transmission measurement generates only a two-dimensional (2D) project map of the physical properties of interest and cannot provide depth-resolved information, unless multiple acquisitions are used to form a tomographic reconstruction [13–17]. In a reflection configuration, some ofthe limitations ofprojection-based measurement can be readily overcome. For example, the motion of the outermost plasma membrane of a cell can be quantified independently of the unknown cytosolic refractive index distribution [18–22]. Furthermore, the reflection measurement of the interface motion is typically considerably more sensitive than the transmission measurement, since transmission sensitivity is reduced by a factor proportional to the refractive index difference of media, which is typically very small, on both sides of the interface [22]. However, plane wave illumination systems in reflection geometry still lack the depth selectivity needed for many cellular and tissue applications. Light with a broad spectrum can be used to achieve depth selectivity while still using plane waves. Since the axial resolution is determined by the coherence length of light, a suitably broadband light source is necessary to obtain 1–2 μm level axial resolution sufficient to distinguish intracellular structures. Most pulsed lasers, however, due to their relatively limited bandwidth, have a lower resolution than that [20,23–27]. In contrast, thermal light sources have been shown to have sufficient bandwidth to obtain an axial resolution greater than 1 μm, but these sources were subject to a slow acquisition rate due to the inevitably low level of illuminance [19,28–30].

Apart from the use of time gating based on the temporal coherence of light, the depth discrimination generated by the spatial coherence of light has also been employed. Illumination light waves with a short coherence length in a three-dimensional (3D) space have been generated by destroying the spatial mode of lasers with a relatively long coherence length. Reflection phase microscopes have been developed with either a spinning diffuser to produce the time-varying speckle field [31], or a laser transmitted through multimode optical fibers to break its spatial mode [21]. In both methods, the depth-selectivity was determined by the spatial decorrelation ofthe light fields rather than the intrinsic coherence length of the light sources. Although the measurements of topological structures were demonstrated, the achievable depth resolution was not fully realized in living cells due to the reduction of the numerical aperture (NA) caused by the mismatch of the wavefronts in both arms when implementing the interferometry using the off-axis configuration.

Recently, we demonstrated a reflection phase microscope based on the spatial gating produced by the dynamic speckle illumination with a rotating diffuser [22]. In that case, similar to the previous methods, the depth-selectivity was determined by the spatial correlation length of the generated speckle field. However, unlike the former demonstrations, we used the maximum NA of the objective lenses in the interferometric measurements due to the excellent match of the wavefronts by introducing a diffraction grating in the reference beam for the off-axis configuration. We achieved 1-μm axial resolution and successfully distinguished the top and bottom surfaces of the RBCs. However, the axial resolution of our system was determined by the confocal parameter of the objective lenses. Furthermore, due to the loss of light during generation of the speckle field with the use of a rotating diffuser, it was difficult to achieve high-speed measurements for eukaryotic cells with reflectivity considerably lower than that of the RBCs.

Here, we demonstrate a wide-field reflection phase microscope with a superior axial resolution for high-speed quantification of membrane fluctuations in living cells. We use both the spatial and temporal coherence properties of light to achieve improved depth selectivity for better axial discrimination of intracellular structures. A high-power supercontinuum laser was used as the light source, providing a broad spectral bandwidth for improved sectioning while having sufficient power for high-speed measurement. The imperfection of the temporal gating produced by the non-Gaussian shaped spectrum of the supercontinuum laser was refined by the spatial coherence gating generated by the dynamic speckle illumination configuration. Combining these two gating mechanisms eventually led to an improved depth-selectivity of 640 nm beyond the confocal limit set by the NA of the objective lens. With this method, we successfully observed intracellular structures in 3D and measured the dynamic motions of the nuclear membranes of living eukaryotic cells at a speed of 100 frames per second (fps), which was only limited by the acquisition rate of our camera. With the advantage of the superior detection gain of the reflection phase measurement, the nuclear membrane fluctuation was observed with a sensitivity of 1 nm.

2. EXPERIMENTAL SETUP

The experimental setup is schematically presented in Fig. 1(a). The basic configuration is similar to that in our previous demonstration [22], the main difference being the use of a supercontinuum laser (SuperK, NKT Photonics Inc.) in the current demonstration as the light source in the illumination light path. A bandpass filter with a center wavelength λ_c = 800 nm and a bandwidth Δλ = 170 nm was used to define the spectrum of the laser. All optical components were accordingly replaced with those with broadband achromatic coatings. A rotatable polarizer P_α, with a polarizing axis at an angle of α-deg, placed in the beam path defines the polarization state of the input beam and controls the power balance between the two arms of the interferometer in conjunction with a polarizing beam splitter (PBS). Two water immersion objective lenses with the same specifications (1.0 NA, 60, Olympus) were used for the imaging and the reference beams. An off-axis detection configuration is formed by a diffraction grating (G) combined by a 4-f imaging system. In the Fourier plane of the 4-f telescope, two polarizers with orthogonal axes, P₀ and P₉₀, are positioned to separate one beam from the other. For improving the detection efficiency, one modification of the optical configuration was applied to the Fourier plane. Two achromatic quarter-wave plates, each having one retardation axis at ±45 deg, were added immediately behind the polarizers, P₀ and P₉₀. Thus, the perpendicular polarizations of the output beams were set to the circular polarization with the same handedness at the camera plane. This induced the two beams to produce the maximum interference contrast without an additional polarizer with 45-deg axis in front of the camera as a polarization analyzer in the previous setup. Thus, the camera can collect two times the power reflected from a sample. More details on the setup schematics and optics configuration can be found in our previous report [22].

Fig. 1.

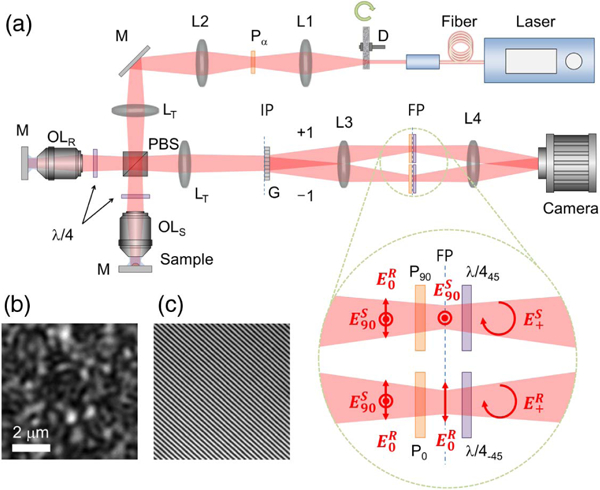
Schematic of the spatio-temporal reflection phase microscope. (a) D: diffuser; L1-L4: lenses; P_α: polarizer with α-deg rotation angle; LT: tube lens; PBS: polarizing beam splitter; λ/4_α: quarter-wave plate with α-deg rotation angle; OL_R and OL_s: objective lenses for the reference arm and the sample arm; G: diffraction grating (the 0th diffraction order is omitted for simplicity); IP: image plane; and FP: Fourier plane;$E_0^R$ : reference beam with s-pol.; $E_{90}^S$ sample beam with p-pol.; $E_{+}^{R,S}$ : reference and sample beams with the same circular-pol. (b) Speckle distribution on the sample arm. (c) Interference fringe pattern on the camera.

Although the supercontinuum laser has a broad spectral bandwidth, a complex speckle pattern is still generated by the diffuser, as shown in Fig. 1(b). This happens because the main scattering source of the diffuser is the surface roughness of the ground glass, which has an average grain size ofsubmicrons, causing single-layer scattering. While the individual beam paths of the various scattered components have large angular diversity, they have similar optical path lengths (OPLs) comparable to the coherence length of the light source, resulting in high-contrast speckle patterns generated at the focal plane of the objective lens. Nonetheless, since a portion of the scattered components can be out of the coherence length of the source, the contrast of the speckle distribution is less than that of a narrowband light source [22,31]. Figure 1(b) shows the representative speckle distribution generated by the supercontinuum laser at the focal plane. The standard deviation of the normalized intensity distribution is 0.46, which is 25% smaller than that obtained in our previous work using a mode-locked Ti: Sapphire laser as the light source. Interestingly, even with this reduced speckle contrast, the interference contrast with the supercontinuum laser is only marginally affected, with only a 7% reduction. This happens because the interference contrast is determined by the relative path length difference in the two interferometric arms, rather than by the coherence property of the single beam.

3. SPATIO-TEMPORAL COHERENCE OF THE LIGHT

Initially, the characteristic for the temporal coherence of the light source was investigated without the speckle illumination configuration using a flat mirror on the sample plane as a test object. The sample mirror was then illuminated with a collimated planar wave from the supercontinuum laser. Using the method described in our previous demonstration [22], the strength of the interference observed from the complex field images of the blank mirror was measured as a function of the axial shifts of the mirror. As presented in Fig. 2(a), the point spread function (PSF) has a multipeak structure, which is composed of three main peaks and several small side lobes, and the temporal coherence survives at more than about 10 μm along the axial direction. From the fit using a multipeak Gaussian distribution, the coherence lengths for the three main peaks were determined and the full width at half maximum (FWHM) l_t for the central main peak was measured as 0.77 ± 0.01 μm. The multipeak nature of the temporal coherence is known to be caused by the spectral complexity of supercontinuum sources [32–35].

Fig. 2.

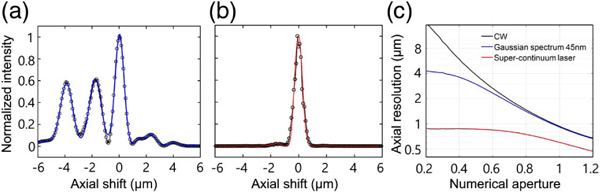
Spatio-temporal coherence of the supercontinuum laser combined with the dynamic speckle illumination. (a) Intact axial response of the supercontinuum laser. The FWHMs of the three mains peaks are 1.06 μm, 1.05 μm, and 0.77 μm (from left to right). (b) Axial response after combination with the dynamic speckle illumination. The FWHM of the peak is 0.64 μm. (c) Axial resolution as a function of numerical aperture, and laser bandwidth, by Eq. (1).

A diffuser is then placed in a conjugate plane, indicated as D in Fig. 1(a), in the input port of the setup and the dynamic speckle illumination configuration is set by spinning the diffuser at the desired rotational speed [22]. Using the diffuser, we found that the axial response of the PSF shows a Gaussian-like single-peak structure, as depicted in Fig. 2(b). The two other main peaks and small side lobes are efficiently suppressed and rejected due to the additional gating provided by the speckle decorrelation around the center of the axial shift. Since the decorrelation length of the generated speckle distribution l_s is 1.03 μm in our setup [22], the combination of the two gating mechanisms produces a well-shaped and single-peak coherence gating.

The analytic expression of the axial response function I (z_s) can be determined from the 3D transfer function of dynamic speckle interference, the details of which are described in [36,37] as

$$I(z_s)\propto {\left|\int \int {\omega }^{2}S\left(\omega \right)P(k_z,\omega )\text{exp}(i{k}_z{z}_s\text{)}d{k}_{z}d\omega \right|}^2,$$ (1)

where z_s is axial shift of the sample mirror, ω is angular frequency, S(ω) is the power spectral density of the laser, k_z is wave vector along the axial direction, and P(k_z, ω) is the 1D aperture function defined as

$$P\left(k_z,\omega \right)=1\text{for}\sqrt{n_0^2{–\text{NA}}^{\text{2}}}<\frac{c{k}_z}{\omega }<n_{\text{0}}.$$ (2)

From Eq. (1), we can calculate the theoretical expectation of axial response, and the result is shown as a red solid line in Fig. 2(b) (see Supplement 1). The resulting FWHM of the peak in Fig. 2(b) was determined as 640 ± 10 nm by a standard Gaussian fit, and agrees well with the theoretical expectation. Considering that the confocal parameter of the objective lens is about 1 μm under our experimental parameters, the combination of temporal coherence gating and spatial coherence gating achieved enhanced depth selectivity by 1.6 times.

We also present the behavior of the axial resolution as a function of the numerical aperture, and the bandwidth of the illumination source with the assumed Gaussian-shaped spectrum in Fig. 2(c). For the limiting case of a low numerical aperture, the axial resolution tends to be determined by the coherence length of the illumination source. On the other hand, for continuous-wave (CW) illumination, the axial resolution is given by the confocal parameter for a given numerical aperture. The combined effect of the two gating mechanisms is clearly shown in the figure. Although the axial response function in Eq. (1) was derived for a dynamic speckle case, we note the results [as seen in Fig. 2(c)] are similar to those presented in [23].

4. DEPTH-RESOLVED IMAGING OF LIVING CELLS

We demonstrated the depth-selective imaging of living cells using our method. Cancer cells (MDA-MB-435S, ATCC) were prepared on a glass slide immersed in a culture medium, which was a mixture offetal bovine serum (FBS) and antibiotics (ABX) at the Roswell Park Memorial Institute (RPMI) as a host solution. We added an anti-reflection coating to the glass slide to reduce the specular reflection of the surface. A Petri dish containing the sample was kept in an incubator for cell stabilization. After a 2–3 h incubation, while the spherical shape of the cells was still retained, the cells were barely attached to the surface of the glass slide. The Petri dish was placed on the sample plane so that the objective lens was immersed by the culture medium. Under this condition, the cells were able to survive for several hours while maintaining their physiological state without temperature and gas controls. However, we performed all the cell experiments within an hour of bringing the samples from the incubator. The same culture medium was introduced for the objective lens in the reference arm for the best match of the OPLs between the two interfero-metric arms. The axial position of the sample was controlled by a high-precision motorized translation stage. In our experiments, the images were acquired typically at 100 fps, which is only limited by the camera acquisition speed used for these experiments. The laser power for the illumination was measured as 0.24 mW at the focal plane of the sample objective lens. Since the exposure time was set as 5 ms at 50% of the maximum laser output power, we can potentially increase the imaging speed by up to 400 fps under our experimental conditions.

Three cells with different heights were captured within the field of view and multiple depth-selective images of the cells were obtained while scanning the sample position along the axial direction from top to bottom, as shown in Figs. 3(a)-3(e). Despite the anti-reflection coating, when the focus was located on the cell-to-glass interface, the glass surface produced a strong reflection signal. This reflected light transmitted the sample twice and then formed a double transmission image. The phase image obtained from this double transmission is depicted in Fig. 3(g). Considering the double transmission geometry, the phase value was divided by 2 to be consistent with a standard transmission phase image. In the transmission image, the cells showed typical smooth boundaries with no particular features.

Fig. 3.

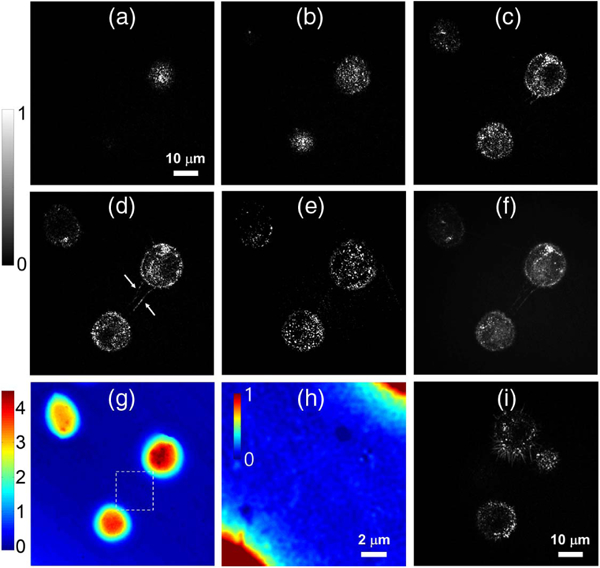
Depth-resolved images of living cells. (a)-(e) Reflectance images taken at different heights of 15 μm, 13 μm, 9 μm, 7 μm, and 4 μm from the bottom surface of the glass slide. (f) The z-stack image of multiple reflection images measured at 50 different depths. (g) Transmission phase image obtained from the double transmission measurement. (h) Zoom-view of the region in the white-box in (g). The measured phase values were divided by two to consider the double transmission in (g) and (h). (i) Another cell cluster showing the vigorous motion of filopodia (see Visualization 2). Color bars: phase in radian.

When the position of the focus was set to be adjacent to the top of the tallest cell [Fig. 3(a)], a membrane associated with the round-shaped cell morphology was observed. If the focus was lowered, the other two cells appeared in the order shown in Figs. 3(b) and 3(c). When the focus was located in the middle of the cells, a relatively strong signal was detected from the cell boundaries, but the signal from the inner regions was weak due to the lack of structures yielding a strong reflection signal. At a height of 7 μm from the bottom surface, several filopodia connecting two of the cells were well observed, as indicated by the arrows in Fig. 3(d). This cell-to-cell connection is not resolved in the transmission image in Fig. 3(g), even after adjusting the color scale in the zoom-view in Fig. 3(h).

After measuring 50 depth-resolved images at different axial positions covering the full height of the tallest cell, a z-stack image was generated by adding all the reflection images, as shown in Fig. 3(f). Strong spotty distributions within the cell bodies originated from the reflection by lipid droplets. Using all the acquired depth-selective images, a 3D map for the cellular structures can be constructed (see Visualization 1).

Next, we brought another cell cluster into the view field and measured the motion of the filopodia [Fig. 3(i)]. The focal plane was placed in the middle of the cells and successive images were acquired for 10 s at 100 fps. After processing all of the images, we took an average every five images to improve the image quality. Visualization 2 shows the time-lapse motion of the cells. The cell in the top of the field of view barely attached to the glass surface; the cell body was thus moving sideways up to a certain distance. We note that the static formation of filopodia has been previously observed using a reflection phase microscope [38]. Unlike this prior work, here we demonstrate the active movement offilopodia that became possible due to the sufficient imaging speed of our setup, although the resultant acquisition speed was reduced to 20 fps after the averaging during the post-processing.

5. OBSERVATION OF DYNAMIC MOTION OF THE NUCLEAR MEMBRANE

In this experiment, we introduced another round cell within the field of view. The axial position of the sample stage was scanned to observe the internal structure of the cell from top to bottom. During the focal scanning, a strong reflection associated with the top membrane was first observed, as shown in Fig. 4(a). Below this surface, the reflection signal reduced due to the lack of structures with high refractive index contrast. Moving the focal plane further, about 4.8 μm below the top surface for this particular cell, another layer with a strong reflection signal was revealed, as shown in Fig. 4(c). It is part of a nucleus of the cell with smooth and round morphology, which is confirmed from the phase distribution of the reflection signal, as shown in Fig. 4(d).

Fig. 4.

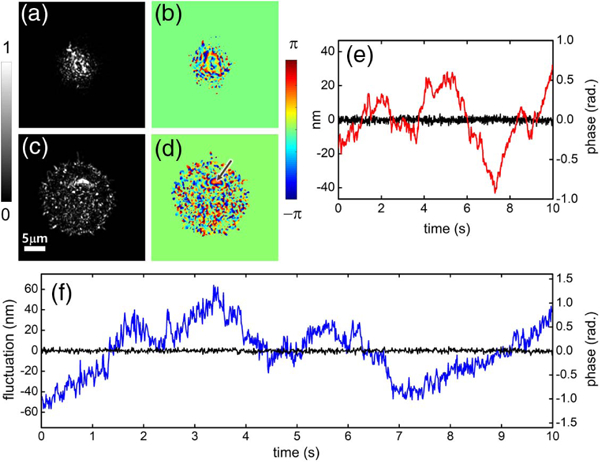
Observation of the nuclear fluctuation. (a) Reflection intensity and (b) corresponding phase image for the top plasma membrane of the cell. (c) Reflection intensity and (d) corresponding phase image for the nuclear membrane of the cell. (e) Background fluctuation before (red line) and after (black line) the phase stabilization. (f) Nuclear membrane motion (blue trace) measured at the point indicated by the arrow in (d). Black trace represents the background fluctuation in the blank region. Color bar in (a) and (c): normalized intensity. (a) and (c) are presented with the same color scale. Color bar in (b) and (d): phase in radians.

Next, we performed time-lapse imaging at 100 fps while retaining the same focus. To reject the phase noise introduced by the unwanted mechanical jitter of the OPLs between the two interfero-metric arms, the sample plane was tilted by about 9 deg with respect to the horizontal plane. A small portion of the glass surface, far from the cell, was revealed in the coherence length, and thus served as a blank reference region (see Supplement 1). From this reference region, the background phase noise could be traced and numerically compensated during post image processing [20]. By this phase stabilization, the background noise was reduced from 332 to 28 mrad, which corresponds to 15.5 nm and 1.3 nm, respectively, in RMS displacement [as shown in Fig. 4(e)]. This enabled measurement of the fine axial motions of the living cells with a sensitivity of about 1 nm.

After the rejection of the mechanical phase noise from all the measured images, we investigated the phase variation of the signal from the nuclear membrane. Visualization 3 shows the time variation of the phase distribution at the focal plane lying on the nuclear membrane. Even after the background phase stabilization, a significant axial motion of the nuclear membrane was observed. The phase variation was converted into a displacement fluctuation using the relation, ${\varphi }_R\approx 2n_{s}k\Delta z_n$, where ${\varphi }_R$ is the reflection phase, $\Delta z_n$ is the axial position of the nuclear membrane, n_s is the refractive index of the cell cytosol, and k is $2\pi /{\lambda }_c$ with the center wavelength of λ_c (see Supplement 1). Since our experiments are based on the reflection measurements, the phase is proportional to n_s rather than the refractive index contrast, as in the case for the transmission measurements. The phase gain in the measurement is then higher by about two orders of magnitude for complex cells than that provided by transmission measurements. Thus, the dynamic motion of the nuclear membrane is clearly resolved from the fluctuation of the phase value even at a point corresponding to the diffraction limited spot in the middle of the nuclear region. We tracked the phase value at the point denoted by the arrow in Fig. 4(d) as a function of time, and the result is presented in Fig. 4(f). The RMS magnitude of the fluctuation of the membrane motion corresponds to 24.6 nm, where n_s = 1.36 was used as the average refractive index of the cell cytosol [14,20]. This is significantly larger than that of the background fluctuations. We also calculated the mean square displacement (MSD) of the phase variation to quantify the fluctuations [1,19,39]. The results are discussed in Supplement 1.

6. CONCLUSION

In conclusion, we have demonstrated highly sensitive reflection phase microscopy using spatio-temporal coherence of light. For the high-speed measurement we employed a high-power supercontinuum laser to obtain a sufficient signal from living cells with a low level of reflectance. Due to the inherent temporal coherence property of the supercontinuum laser, the depth selectivity based on the time gating was significantly degraded, causing the spread of the coherence gating over multiple axial planes. By combining the spatial gating assisted by the dynamic speckle illumination with the coherent characteristics of the supercontinuum laser, we successfully refined the gating characteristics of the light source. Furthermore, both gating mechanisms worked simultaneously to form a single spatio-temporal gating, which provided an improved axial resolution compared to the confocal limit of the objective lens. With this method, the depth-resolved images of living cells were obtained at multiple depths and the 3D reflectance map for the cells was visualized. Furthermore, the dynamic motion of their fine structures, which could not be resolved in a transmission image, were also observed. In particular, the nuclear membrane inside a living cell was distinguished from its plasma membrane, and the spontaneous motion of the nuclear membrane could be observed with 1 nm axial motion sensitivity at the full acquisition rate of our camera.

We believe that this method will facilitate the high-precision and high-speed measurements of cellular morphology and biomechanics in a label-free, noninvasive manner.