Origin of giant negative piezoelectricity in a layered van der Waals ferroelectric

Lattice topology and anisotropic chemical bonds underpin unusual negative longitudinal piezoelectricity in van der Waals solids.

Abstract

Recent research on piezoelectric materials is predominantly devoted to enhancing the piezoelectric coefficient, but overlooks its sign, largely because almost all of them exhibit positive longitudinal piezoelectricity. The only experimentally known exception is ferroelectric polymer poly(vinylidene fluoride) and its copolymers, which condense via weak van der Waals (vdW) interaction and show negative piezoelectricity. Here we report quantitative determination of giant intrinsic negative longitudinal piezoelectricity and electrostriction in another class of vdW solids—two-dimensional (2D) layered ferroelectric CuInP₂S₆. With the help of single crystal x-ray crystallography and density-functional theory calculations, we unravel the atomistic origin of negative piezoelectricity in this system, which arises from the large displacive instability of Cu ions coupled with its reduced lattice dimensionality. Furthermore, the sizable piezoelectric response and negligible substrate clamping effect of the 2D vdW piezoelectric materials warrant their great potential in nanoscale, flexible electromechanical devices.

INTRODUCTION

By definition, the direct piezoelectric effect refers to the generation of electrical polarization by an applied stress, while the converse piezoelectric effect refers to the dimensional change of a material in response to an applied electric field. Since its first observation in 1880 (1), the piezoelectric effect has been the subject of extensive research (2–5), resulting in widespread applications in sonar, ultrasound imaging, piezoelectric motors, sensors, and high voltage sources, etc (6–8).

Although the effect theoretically exists in nearly all materials lacking a center of symmetry (except for the cubic class 432), large piezoelectric coefficients are usually found in ferroelectric materials with spontaneous polarization due to their high susceptibility of lattice distortion under electric field. For example, Pb(Zr_xTi_1−x)O₃ (PZT), a typical ferroelectric material with perovskite structure, has a longitudinal piezoelectric coefficient (d₃₃) of more than 500 pm/V, orders of magnitude larger than that of quartz (2.3 pm/V) (9). Most ferroelectric materials have positive longitudinal piezoelectric coefficients, meaning that the lattice will expand when the applied electric field is along the existing polarization direction (Fig. 1A). From a simple rigid ion model, this originates from the anharmonicity of the bond energy due to the spontaneous ionic displacement (polarization). As a result, the expansion is easier than the compression. Theoretically, negative longitudinal piezoelectricity was predicted in certain compounds (10–12). However, the only experimentally known example is the ferroelectric polymer poly(vinylidene fluoride) (PVDF) and its copolymers, whose lattice contracts when the external field is along the existing polarization direction (Fig. 1B). Although known for decades, the origin of the negative piezoelectric effect of PVDF has been a subject of debate with various models proposed (13–16), most of which attribute the effect to extrinsic factors such as amorphous regions in the sample. PVDF is semicrystalline; however, its crystalline phase consists of one-dimensional (1D) molecular chains with strong internal C─C covalent bonds, packed together by weak van der Waals (vdW) force. In contrast, most conventional ferroelectrics, such as PZT, crystallize with strong ionic/covalent bonds forming continuous 3D networks. It is natural to ask whether the stark differences in terms of atomic packing and bonding energies play a role in their contrasting electromechanical coupling behaviors (Fig. 1C).

Fig. 1. Piezoelectric effect and lattice dimensionality.

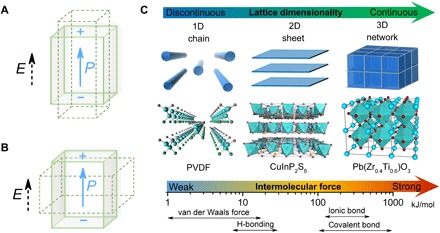
(A and B) Illustrations of negative (A) and positive (B) longitudinal piezoelectric effects, where the lattice contracts or elongates when the electric field is along the direction of the spontaneous polarization. (C) A schematic that outlines the lattice dimensionalities of three representative ferroelectric materials: 1D PVDF, 2D CuInP₂S₆ (CIPS), and 3D Pb(Zr_0.4Ti_0.6)O₃ (PZT). The bottom part shows the energy scales of the inter- and intramolecular bonds. PVDF is known to have a negative piezoelectric coefficient, as schematically shown in (A), while 3D ferroelectrics usually show positive piezoelectric coefficients as illustrated in (B).

An ideal candidate system to look into is a vdW layer ferroelectric, CuInP₂S₆ (CIPS), which has attracted intensive attention recently (17–20). In our previous work, we reported qualitatively that CIPS exhibits negative longitudinal piezoelectricity based on local polarization switching measurements (20). However, local piezoelectric force microscopy (PFM) is notoriously plagued by extrinsic effects such as contact electrostatics (21). Here, by combining quasi-static and dynamic electrostrain measurements and in situ micro–x-ray diffraction (micro-XRD) on parallel plate capacitors, we reveal quantitatively the intrinsic giant negative piezoelectricity and electrostriction in this vdW layered ferroelectric. We find that the generality of the negative piezoelectric effect in PVDF and CIPS stems from their reduced lattice dimensionality associated with highly anisotropic bonding arrangements. In CIPS, the large displacive freedom of the Cu ions coupled with the softness of the vdW interaction results in the large deformation susceptibility of the lattice under electric field.

RESULTS

Quantitative measurements of the piezoelectric and electrostrictive coefficients

For comparison, the converse piezoelectric effects of the three prototypical ferroelectric materials, namely, semicrystalline poly(vinylidene fluoride–trifluoroethylene) (PVDF-TrFE) copolymer thin film, single-crystal CIPS plate, and epitaxial PZT thin film are measured both quasi-statically and dynamically using atomic force microscope (AFM)–based techniques (see Materials and Methods). Parallel plate capacitors are used to eliminate the parasitic effects due to the nonuniform electric field generated by the AFM tip. In the quasi-static measurement, voltage of a triangular waveform is applied to the capacitor with the polarization and the strain hysteresis loops simultaneously recorded. The results are plotted in Fig. 2 (A to F) (also see figs. S1 and S2 for complete voltage and frequency series). The hysteresis loops are divided into four segments, with the voltage sequence indicated by the arrows and numbers, which provide a clear correlation between the polarization and strain evolutions under the electric field. In the PVDF (Fig. 2, A and D) for example, the initial polarization is pointing downward. When the electric field is increased from zero to positive maximum (here, the positive field is defined as pointing upward from bottom electrode toward top electrode), polarization switching occurs at the coercive field (E_c) (segment 1 of Fig. 2A). In the meantime, the strain (positive) increases from zero initially, peaks at the E_c, and suddenly reverses the sign after the polarization switching completes. This means that from the beginning to E_c, the lattice expands when the electric field is against the polarization direction. After ferroelectric switching, the polarization is now aligned with the electric field, resulting in a sudden contraction of the lattice and negative strain. The negative strain reaches its maximum at the highest field and reduces almost linearly to zero following the decrease of the electric field. Meanwhile, the polarization is maintained (segment 2 of Fig. 2A). Segments 3 and 4 reverse this process. The electromechanical response of PVDF observed here is thus consistent with its well-known negative longitudinal piezoelectric effect.

Fig. 2. Piezoelectricity of ferroelectric solids with different lattice dimensionalities.

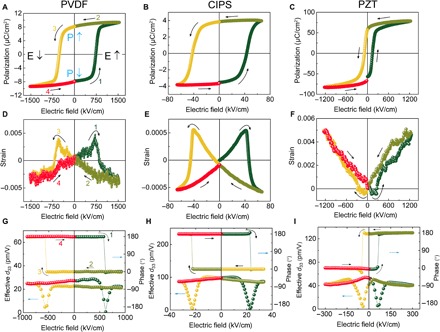
(A to C) Polarization–electric field (P-E) hysteresis loops of PVDF (A), CIPS (B), and PZT (C). (D to F) Corresponding S-E hysteresis loops of PVDF (D), CIPS (E), and PZT (F). (G and H) Hysteresis loops of effective d₃₃ (amplitude) and phase signals obtained by ac piezoresponse measurement for PVDF (G), CIPS (H), and PZT (I). The polarization switching sequence is denoted by the numbers and arrows in (A) and represented using the same color code in all plots.

In comparison, the strain–electric field (S-E) loop of PZT is completely upside down (Fig. 2F). At the initial stage (segment 1 of Fig. 2C), the electric field is against the polarization direction. A negative strain appears when the electric field increases and peaks at E_c. Once polarization switching completes and the electric field is along the polarization direction, its lattice expands with the electric field, which is most prominent at high fields. The behavior is consistent with a positive longitudinal piezoelectric effect, which is commonly observed in oxide ferroelectrics (22).

As for CIPS, its electromechanical behavior appears to be the same as PVDF (Fig. 2, B and E), suggesting that it has a negative longitudinal piezoelectric effect. To corroborate this finding, we also perform dynamic measurements of the piezoelectric effect of all three samples (section S2). In this setup, the polarization is again switched by a slow triangular waveform to obtain the hysteresis loop, which is similar to that in the static measurements. However, instead of recording strain directly, a small ac sinusoidal waveform is superimposed onto the slow triangular waveform, which drives the sample and the AFM tip in contact with the sample surface to oscillate at certain frequency. A lock-in amplifier then picks up the amplitude and phase of the oscillation and forms the d₃₃–electric field loops, as shown in Fig. 2 (G to I). This technique not only allows us to obtain the d₃₃ coefficient directly but also reveals the sign of the piezoelectric effect from the phase signal (fig. S3). Again, PVDF and CIPS behave in the same way that agrees with a negative piezoelectric effect, whereas PZT of positive piezoelectricity shows an opposite phase loop. The obtained d₃₃ values show weak frequency dispersions until the first harmonic of the tip-sample contact resonance at around 1 MHz (fig. S4), thus excluding extrinsic effects arising from flexural vibration modes of either the cantilever or the substrate (23, 24). The zero-field effective d₃₃ of PVDF, CIPS, and PZT obtained from the dynamic measurements are about −25, −95, and 48 pm/V, respectively. These numbers are in good agreements with those deduced from the quasi-static strain measurements (fig. S5) and literature reports for PVDF and PZT with similar compositions and sample forms (14, 16, 25, 26). We also conducted local switching of the ferroelectric polarization using PFM to confirm the correlation between polarization directions and piezoresponse phase signals (fig. S6). As expected, PVDF and CIPS show the same phase contrast, while PZT shows the opposite one.

In situ micro-XRD studies on the lattice deformation under electric field further corroborates the intrinsic negative piezoelectricity of CIPS (section S3 and fig. S7). The calculated d₃₃ from XRD measurements is around −106 ± 10 pm/V, which is in good agreement with the quasi-static and dynamic piezoelectric measurements. The value d₃₃ is much higher than that of PVDF and is among the highest ones in single-phase uniaxial ferroelectrics (27, 28) but with a negative sign.

In phenomenological theory, longitudinal strain, S₃₃, of a ferroelectric crystal developed from its centrosymmetric paraelectric phase can be expressed by a Taylor series expansion of the electric displacement, D₃, with the first nonvanishing term (29)

$$\begin{array}{cc}\hfill {\mathit{S}}_{33}& ={\mathit{Q}}_{33}{\mathit{D}}_3^2={\mathit{Q}}_{33}{({\overrightarrow{\mathit{P}}}_{\mathrm{s}}+{\overrightarrow{\mathit{P}}}_{\mathrm{i}})}^2={\mathit{Q}}_{33}{({\overrightarrow{\mathit{P}}}_{\mathrm{s}}+{\mathrm{\epsilon }}_{33}{\overrightarrow{\mathit{E}}}_3)}^2\hfill \\ & ={\mathit{Q}}_{33}{\overrightarrow{\mathit{P}}}_{\mathrm{s}}^2+2{\mathit{Q}}_{33}{\mathrm{\epsilon }}_{33}{\overrightarrow{\mathit{P}}}_{\mathrm{s}}{\overrightarrow{\mathit{E}}}_3+{\mathit{Q}}_{33}{\mathrm{\epsilon }}_{33}^2{\overrightarrow{\mathit{E}}}_3^2\hfill \end{array}$$ (1)

where Q₃₃ is the longitudinal electrostriction coefficient, ε₃₃ is the dielectric permittivity, ${\vec{\mathit{P}}}_{\mathrm{s}}$ and ${\vec{\mathit{P}}}_{\mathrm{i}}$ are the spontaneous and induced polarizations, respectively. The first term of Eq. 1 is the spontaneous strain developed from the paraelectric-to-ferroelectric phase transition. The second term is the primary electromechanical coupling component, namely, a linear piezoelectric effect with the coefficient d₃₃ defined by 2Q₃₃ε₃₃P_s. The last term is the secondary effect, also known as the quadratic electrostriction effect, which exists in all materials due to the anharmonicity of the chemical bonds (30). The piezoelectricity in ferroelectric crystal can thus be understood as the spontaneous polarization-biased electrostriction. Therefore, the negative piezoelectric coefficient essentially originates from negative electrostriction. To quantitatively assess the longitudinal electrostriction coefficient Q₃₃ for the three samples, based on Eq. 1, we can fit either the data from quasi-static strain measurements using the equation ${\mathit{Q}}_{33}=\frac{{\mathit{S}}_{33}}{{\mathit{D}}_3^2}$ (fig. S8) or those from dynamic measurements by ${\mathit{Q}}_{33}=\frac{{\mathit{d}}_{33}}{2{\mathrm{\epsilon }}_{33}{\mathit{P}}_{\mathrm{s}}}$ (fig. S9 and see section S4 for detailed discussion). Both methods yield similar results. The derived Q₃₃ value of CIPS is around −3.4 m⁴/C², which, to the best of our knowledge, is the largest among inorganic compounds, and even outperforms that of the PVDF (30).

From the first term of Eq. 1, negative Q₃₃ also suggests negative spontaneous strain, which means that when heated through the first-order ferroelectric-paraelectric phase transition point, the lattice parameter along the polar axis should expand because of the sudden drop of the P_s. This behavior was observed in CIPS previously (31), in stark contrast to 3D ferroelectrics, such as PbTiO₃ and BaTiO₃, which typically show contractions of the polar axis and negative thermal expansion across the transition temperatures (section S4 and fig. S10) (32, 33).

Understanding the negative piezoelectricity from lattice dimensionality

Next, we qualitatively explain the anomalous negative piezoelectricity of CIPS by looking into its lattice-dipole relationship in comparison with PVDF and PZT. Different from conventional perovskite oxide 3D ferroelectrics, in which the macroscopic polarization is formed because of the ion off-centering in a continuous lattice with strong covalent/ionic bonds, the dipoles in PVDF and CIPS emerge within isolated layers or chains, which are held together through weak vdW interactions to form “broken” lattices and quantized electric dipoles (Fig. 3, A to C). To illustrate the mechanism, we simplify the ions and bonds using the ball-and-spring model (Fig. 3, D and E) (30, 34, 35). In PZT, when an electric field parallel to the polarization is applied, the positive ions will move along the field direction, and the negative ions move oppositely. However, because of the bond anharmonicity arising from the spontaneous displacement, the expansion is easier than the compression as illustrated by the different ion pair potential profiles (lower part of Fig. 3E), the curvatures of which represent the elastic compliances of the bonds (k₂ > k₁). Therefore, PZT shows positive longitudinal piezoelectricity. In contrast, PVDF and CIPS exhibit strong intramolecular bonds within the chains/sheets and much weaker intermolecular bonds mediated by dipole-dipole interactions (Fig. 3D). The marked difference (≈2 orders of magnitude) between inter- and intramolecular bond energies (Fig. 1C and Table 1) results in highly anisotropic physical properties (36) and underpins the negative piezoelectricity. Under an electric field, because of the softness of the intermolecular bond, the enhanced dipole-dipole interaction will cause the vdW gap to shrink more than the expansion of the intramolecular bond (k₃ >> k₄), if any, leading to the negative longitudinal piezoelectricity. In practice, charge redistributions could take place within the chain/layer in response to the electric field due to the intrinsic spatial confinement effect (37). The electron density redistribution may also cause a change in the intramolecular bond length that also contributes to the negative piezoelectric effect, as demonstrated in crystalline PVDF (15), or, more generally, the dominant negative clamp-ion piezoelectric response (12). However, the simplified rigid-ion model here should capture the key factor for negative piezoelectricity, namely, the markedly anisotropic inter- and intramolecular elastic compliances.

Fig. 3. Simplified rigid ion model for piezoelectricity in polar solids.

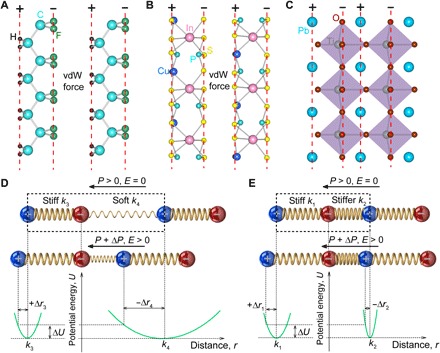
(A to C) Correlations between crystal structures and dipole charges for PVDF (A), CIPS (B), and PZT (C). (D) Negative piezoelectric effect in polar solid with discontinuous (broken) lattice. (E) Positive piezoelectric effect in polar solid with continuous lattice. The unit cell of the lattice is indicated by the dashed box. The polarization and electric field directions are denoted by the arrows. The lower parts show the pair potential energy profiles of the corresponding chemical bonds. The negative ions are taken as a reference point for the relative changes of bond lengths.

Table 1. A list of extracted materials parameters.

P_s, spontaneous polarization; ε₃₃, relative permittivity; d₃₃, longitudinal piezoelectric coefficient; Q₃₃, longitudinal electrostriction coefficient; E_b, intermolecular bond energy; C₃₃, Young’s modulus. The numbers in the parentheses are the intramolecular bond energies.

Material	Ps (μC/cm2)	ε33 (at 10 kHz)	d33 (pm/V) (at 10 kHz)	Q33 (m4/C2)	Eb (kJ/mol)	C33 (GPa)	Coupling factor k33
PVDF-TrFE (70/30)	8	8.2	−25	−2.2	<20 (290–495)	1–3	0.1–0.16
CuInP2S6	4	40	−95	−3.4	<20 (280–440)	20–30	0.71–0.88
Pb(Zr0.4Ti0.6)O3	60	170	50	0.02	370–800	100–150	0.41–0.5

In literature, the “dimensional” model and Maxwell strain have been adopted to explain the negative piezoelectricity and electrostriction in ferroelectric polymers (13, 38). In section S5, we explain in detail the fundamental connection between these two models, both with electrostatic origin. The rigid ion model proposed here is in accordance with them and provides a clearer microscopic picture from the perspective of the lattice dimensionality. The dimensional model assumes a fixed dipole moment M imbedded in an amorphous matrix with the volume V. Since polarization P equals the dipole moment per unit volume, the increase of P under an electric field requires the reduction of V. This is accomplished by the deformation of the amorphous part of semicrystalline PVDF, while in fully crystalline CIPS, the soft vdW gap then plays the role for elastic deformation (fig. S11). The driving force for this deformation is Maxwell stress/strain, which is much larger for the vdW gap due to its small electrical polarizability and elastic modulus. However, although both models qualitatively explain the negative sign, they both strongly underestimate the piezoelectric and electrostriction coefficients of CIPS quantitatively (section S5).

Microscopic origin and computational modeling

To better understand this giant negative piezoelectric effect at atomistic level, we performed single-crystal x-ray crystallography and first-principles calculations based on density functional theory (DFT). The refined crystal structures before and after the electrical poling are overall very similar to each other (fig. S12 and data files S1 and S2). The main difference comes from the Flack parameter, which reflects the amount of the inversion twins (opposite ferroelectric domains) in the crystal. This is consistent with the partial switching of the polarization of the whole crystal (fig. S11). In accordance with the previous report (31), we found highly smeared distribution for Cu atoms. To better account for this anisotropic distribution, we assigned four Cu sites in one of the polarization states (Fig. 4A, polarization downward). The occupancies of the 1 to 4 sites are refined to be about 0.32, 0.37, 0.08, and 0.12, respectively, as reflected by the atomic radii. By doing a fast Fourier transform of the diffraction data, a 2D electron density map of the foremost atomic plane shown in Fig. 4A can be drawn (Fig. 4B). In addition to the strong anisotropic dispersion of Cu atoms along the out-of-plane axis, apparent asymmetry of the intensity distribution can also be found to spread more into the vdW gap. Figure 4E shows the line profile across the electron density of Cu atoms. Apparently, there exists an additional peak besides the thermal dispersion of the main peak, suggesting a possible metastable Cu site inside the vdW gap. The area weight of the Gaussian fit for this interlayer site indicates an occupancy of 0.08.

Fig. 4. Atomistic origin of the giant negative longitudinal piezoelectricity in CIPS.

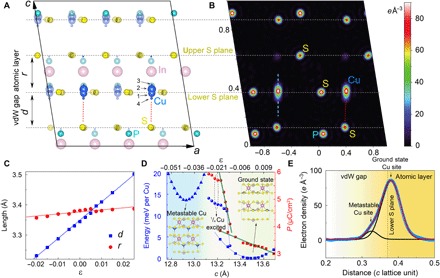
(A) Refined unit cell structure of CIPS viewed along the b axis. The foremost sheet of atoms parallel to (010) plane is highlighted, while the rest are attenuated. The size of the Cu atom indicates its occupancy at the corresponding site. (B) The cross-sectional electron density map of the atomic plane highlighted in (A). The gray dashed lines denote the upper and lower sulfur planes. Red dashed lines indicate the possible interlayer Cu─S bonding across the vdW gap. (C) Calculated changes of the vdW distance d and the layer thickness r of CIPS as a function of strain along c axis. Solid lines are linear fits. (D) Evolution of the free energy E (blue) and the change of ferroelectric polarization P (red) as a function of lattice constant along the c axis under different conditions: triangle, all Cu occupying metastable site; circle, ¼ Cu occupying metastable site; square, all Cu occupying ground-state site. The insets show the corresponding atomic structures. (E) Electron density profile along the blue dashed line shown in (B). The asymmetric distribution of Cu due to the partial occupancy of the metastable site can be fitted by two Gaussian peaks (solid lines).

The optimized lattice constants from our DFT calculations are a = 6.0488 Å, b = 10.4809 Å, and c = 13.4834 Å, which are consistent with the experimental values by extrapolating to 0 K (a ≈ 6.085 Å, b ≈ 10.545 Å, and c ≈ 13.57 Å) (31). Density of states (DOS) calculations show that the bands near the Fermi level are formed by highly hybridized Cu 3d orbitals and S 3p orbitals (fig. S13). The calculated bandgap is about 2.2 eV, slightly smaller than the experimental value (39). The calculated spontaneous polarization is 3.34 μC/cm².

The piezoelectric effect is simulated by tuning the lattice constant along the c axis, while leaving the a/b lattices and atomic positions fully relaxed. The obtained e₃₃ and C₃₃ at 0 K are −0.137 C/m² (green solid line in ground state of Fig. 4D) and 7.5 × 10⁹ N/m², respectively (fig. S14), which leads to a longitudinal piezoelectric coefficient d₃₃ of −18 pC/N. This is, however, much smaller than the experimental value (d₃₃ ≈ −95 pC/N). To better correlate with the experimental results observed at room temperature, we take the partial occupancy of interlayer Cu site into account. First, our structure relaxation confirms the metastable state of the Cu occupying interlayer site, with its energy 14 meV higher than the ground state (Fig. 4D). In this metastable phase, the polarization is greatly enhanced (~12.24 μC/cm²), and the c axis lattice is strongly shrunk with a strain of −0.041. The calculated polarization increases linearly with the occupancy of the interlayer site (fig. S15). Assuming the experimentally observed occupancy (8%), the calculated polarization would be ~4.15 μC/cm², in good agreement with the experimental value, which again justifies the partial occupancy of the interlayer Cu site. To simulate this situation, we consider 25% occupancy of interlayer site (one Cu atom in the unit cell; fig. S15B). As shown in Fig. 4D, with the increase of the c lattice constant, there is a sudden drop of polarization accompanying the transition from the metastable state to the ground state. The approximate e₃₃ for this transition is about −2.72 C/m² (the slope of the green solid line), which converts to d₃₃ ≈ −110 pC/N (the experimental C₃₃ ≈ 25 × 10⁹ N/m² is used). Furthermore, the DFT calculations confirm that the change of the vdW distance d accounts for most of the change in c lattice constant, while the CIPS layer thickness r barely changes (Fig. 4C). As expected, the in-plane lattice constants are relatively unchanged when tuning the out-of-plane lattice constant along the c axis, suggesting an almost zero Poisson’s ratio.

DISCUSSION

The DFT results deliver two important messages. First, the negative piezoelectricity is the intrinsic electromechanical response of CIPS, and the deformation of the vdW gap accounts for the majority of the lattice change due to its soft nature. Second, the large magnitudes of the piezoelectric and electrostrictive coefficients originate from the large displacive instability of the Cu atoms due to the low energy barrier for interlayer site hopping. Since the calculated free energy of the metastable interlayer site (14 meV per Cu atom) can be easily overcome by the room temperature thermal energy (k_BT ≈ 26 meV, where k_B is the Boltzmann constant), the smearing of the Cu electron density is expected to follow the Maxwell-Boltzmann statistics, as evidenced by the fine atomic structure obtained by single-crystal crystallography. Under such a strong thermally excited occupancy dispersion, the first-order–like interlayer-intralayer Cu site transition may also smear into second-order–like, with a flattened energy profile ideal for enhanced piezoelectricity (40). As a result, the experimentally observed d₃₃ at room temperature should lie in between those calculated for the ground state (lower bound) and the excited transition (upper bound), which is the case. The displacive instability of Cu is driven by the pseudo (second-order) Jahn-Teller effect in tetrahedrally coordinated Cu (I) units (41), in which the interlayer sites are stabilized by the enhanced coupling between Cu 4s and S sp orbitals in the adjacent layer (red dashed line in Fig. 4, A and B). The thermally activated hopping motion combined with the softness of the vdW interaction result in giant mechanical deformation under an electric field.

To conclude, we have quantitatively determined the giant negative longitudinal piezoelectricity and electrostriction of vdW layered ferroelectric CIPS. This anomalous electromechanical behavior stems from the large deformation susceptibility of the weak interlayer interaction, mediated by the high displacive instability of Cu ions. The similarity—quantized electric dipoles linked by vdW interaction—between PVDF and CIPS hints on the prevalence of negative piezoelectricity in layered vdW crystals (42). In addition to the interesting physics, from a technological viewpoint, the piezoelectric magnitude of layered CIPS is comparable to those best-performing inorganic ferroelectrics without alloying (28) and has the highest electrostriction coefficient among them. Furthermore, owing to the strong anisotropic chemical bonds, low-dimensional vdW piezoelectrics/ferroelectrics exhibit very small Poisson’s ratio and much lower transverse piezoelectricity than longitudinal one. This intrinsic characteristic implies a much weaker clamping effect of the vdW piezoelectrics/ferroelectrics than their 3D counterparts in thin-film form, as evidenced by the weak thickness-dependent piezoelectric response of CIPS and its better performance compared with thin-film PZT (section S6 and fig. S16). Combining with its superior piezoelectric coefficient and electromechanical coupling factor (Table 1), these unique characteristics of vdW layered ferroelectric CIPS make it highly desirable for nanoscale flexible electromechanical applications and a promising candidate for environmentally friendly piezoelectric devices.

MATERIALS AND METHODS

Sample fabrications

PVDF-TrFE (70/30 mole percent VDF/TrFE copolymer) film with a thickness of around 130 nm was prepared by spin coating on Pt-coated Si substrate (43). The polycrystalline film of the ferroelectric β phase was obtained by annealing at 140°C for 2 hours in air. Single crystals of CIPS were synthesized by chemical vapor transport using stoichiometric elemental precursors (20), with iodine as the transport agent. The precursors were sealed inside a vacuumed quartz ampoule and were then subjected to two-zone horizontal tube furnace for a reaction time of 168 hours under 650° to 750°C. To facilitate the measurements, CIPS crystals with thicknesses ranging from a few to tens of micrometers were solidly glued onto a rigid substrate using conductive silver paste. For the thickness-dependent study, thin flakes of CIPS were prepared by mechanical exfoliation of bulk crystals onto heavily doped Si substrates. Epitaxial PZT thin film with a thickness of around 200 nm was deposited by pulsed laser deposition on SrRuO₃-coated SrTiO₃ single crystal substrate with (100) orientation. To fabricate the capacitors, Au (50 nm)/Ti (5 nm) top electrodes were deposited through a shadow mask by thermal evaporation. The areas of the parallel-plate capacitors range from 0.01 to 0.64 mm².

Ferroelectric, dielectric, and piezoelectric measurements

Polarization–electric field (P-E) hysteresis loops were measured using a commercial ferroelectric tester (Radiant Technologies). Dielectric data were collected using a commercial impedance LCR meter (E4980A, Agilent). S-E hysteresis curves were obtained on a commercial AFM (Asylum Research MFP-3D) in contact mode by maintaining a constant tip height (Z sensor feedback) while monitoring its deflection signal during polarization switching with P-E loops simultaneously recorded. The deflection signal (unit in volts) was converted to actual displacement (unit in meters) using the calibrated inverse optical lever sensitivity (InvOLS; unit in meter per volt). The tip-sample force was carefully chosen so that it is small enough to prevent any indentation damage to the soft samples, while large enough to prevent the tip from leaving the sample surface during thickness contraction. AFM probes with very different spring constants produced comparable results. Dynamic piezoelectric measurements were achieved using standard PFM. An ac voltage (usually V_peak = 1 V) with a frequency of 10 kHz was applied to the conductive tip (large spring constant ~40 N/m to minimize electrostatic contributions) that was in contact with the top electrode and drove the sample surface to vibrate via inverse piezoelectric effect. The amplitude and phase of the vibration were then picked up by a lock-in amplifier. The effective d₃₃ was calculated from the amplitude signal using the conversion factor, InvOLS. To obtain a hysteresis loop, a slow triangular waveform (<0.2 Hz) was applied to the bottom electrode to switch the polarization.

In situ micro-XRD

Electric field–dependent micro-XRD study was conducted on a commercially available x-ray diffractometer with 2D detector (D8 Discover m-HR, Bruker AXS) following previous procedure (44). Point-focused x-rays were converged and monochromated by a 2D layout multilayer x-ray mirror, which reduces the angular spreads of the Cu Kα radiation to δθ = 4 × 10^{− 2} degrees. The x-rays were further focused by the collimator down to 100 μmφ. The sample was then mounted on an open cradle, and the diffracted x-rays were collected by a 2D detector, which has a minimum angular resolution of about 0.034° at a 150-mm sample-to-detector distance. A single-crystal CIPS capacitor with Cr/Au top and bottom electrodes was prepoled into a single-domain state. During the test, a dc electric field in the same direction as the polarization was applied to the capacitor. The lock-coupled (θ-2θ) scan around the (008) Bragg peak was then performed, with a scanning time in the range of a few tens of seconds.

Single-crystal x-ray crystallography

Single-crystal XRD was undertaken using a Bruker SMART APEX-II system. The system uses a Mo-sealed tube source along with a graphite monochromator to produce x-rays of wavelength of 0.71073 Å. Bruker’s SAINT software package was used to collect and integrate x-ray intensity data using a narrow-frame algorithm. Multiscan absorption corrections were applied using SADABS, and the data symmetry was evaluated using XPREP; symmetry equivalent reflections were merged, while Friedal opposites were not merged. The data were solved using SHELXT and refined on F² using SHELXL-97 (45). All electron density maps (observed Fourier maps) were produced using the MAPVIEW module in WinGX (46).

All atoms were refined anisotropically except for the copper atoms, which were treated isotropically to accurately gauge atomic density position along the line of disorder, extending parallel to the c axis from the original copper position at the centre of an S₆ octahedral site. All disordered copper sites were picked out from difference maps, and their occupancy was linked to yield a maximum occupancy of 1. The inversion twin components, which represent the domain fractions of opposite polarization directions, were refined using the Flack parameters (47), before and after electrical poling. The poling was performed using either removable silver paste or amorphous carbon coating as top and bottom electrodes.

Theoretical calculations

The DFT calculation was performed using the Vienna ab initio simulation package with the projector-augmented wave potentials (48–51). In the present study, the Perdew-Burke-Ernzerhof for solids exchange function has been adopted (52). The plane-wave cutoff was 550 eV. Both the lattice constants and atomic positions were fully relaxed until the force on each atom were below 0.01 eV/Å. The Brillouin zone integration was obtained by a 7 × 4 × 3 k-point mesh for the minimum crystalline unit cell. The vdW correction with the DFT-D2 method (53) was taken into account. The standard Berry phase method (54, 55) was adopted to estimate the ferroelectric polarization. Using the optimizated structure, we calculated DOS using the modified Becke-Johnson–type potential of Tran and Blaha (56), which can give more accurate bandgaps for semiconductors and insulators than the standard generalized gradient approximation method, as compared in fig. S13.

The longitudinal piezoelectric coefficients d₃₃ could be estimated using d₃₃ = e₃₃/C₃₃. The elastic constants along the c axis C₃₃ can be obtained from ${\mathit{C}}_{33}=\frac{1}{{\mathit{V}}_0}\frac{{\partial }^2\mathit{U}}{{\partial }^2\mathrm{\epsilon }}$, where V₀ is the unit cell area at the zero strain, U is the energy, and ε denotes the strain. The linear piezoelectric coefficient ${\mathit{e}}_{33}=\frac{\partial \mathit{P}}{\partial \mathrm{\epsilon }}$, where P is the polarization.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/4/eaav3780/DC1

Section S1. Full data series of the P-E and S-E measurements

Section S2. Dynamic piezoelectric measurements

Section S3. Intrinsic piezoelectric response of CIPS by in situ micro-XRD

Section S4. Quantitative determination of the electrostriction coefficient Q₃₃

Section S5. The “dimensional model” and Maxwell strain

Section S6. Thickness-dependent piezoelectric response, clamping effect, and electromechanical coupling factor

Fig. S1. Voltage-dependent P-E and S-E hysteresis curves.

Fig. S2. Frequency-dependent P-E and S-E hysteresis curves.

Fig. S3. Voltage-displacement phase relationship in dynamic piezoelectric measurements.

Fig. S4. Frequency-dependent piezoelectric response.

Fig. S5. Determining the static d₃₃ from S-E curves.

Fig. S6. PFM images with box-in-box patterns written.

Fig. S7. In situ XRD measurements of the CIPS lattice parameter under electric field.

Fig. S8. Quantitative determination of electrostriction coefficient Q₃₃ by linearly fitting the S-P² curves.

Fig. S9. Quantitative determination of electrostriction coefficient Q₃₃ by Q₃₃ = d₃₃/2ε₃₃P_s.

Fig. S10. Lattice anomaly around the ferroelectric-paraelectric phase transition.

Fig. S11. Comparison between the dimensional model and reduced lattice dimensionality induced negative piezoelectricity.

Fig. S12. Switching the polarization of CIPS for single-crystal x-ray crystallography.

Fig. S13. Calculated DOS of CIPS.

Fig. S14. Calculated energy and polarization changes as a function of applied strain.

Fig. S15. Energy and polarization changes as a function of interlayer Cu ratio.

Fig. S16. Dynamic piezoelectric measurements of CIPS flakes with different thicknesses.

Fig. S17. Nanoindentation test of CIPS single crystal.

Data file S1. Crystallographic information file (CIF) of unpoled CIPS crystal.

Data file S2. Crystallographic information file (CIF) of poled CIPS crystal.

References (57–78)