A clustering linear combination approach to jointly analyze multiple phenotypes for GWAS

Abstract

Summary

There is an increasing interest in joint analysis of multiple phenotypes for genome-wide association studies (GWASs) based on the following reasons. First, cohorts usually collect multiple phenotypes and complex diseases are usually measured by multiple correlated intermediate phenotypes. Second, jointly analyzing multiple phenotypes may increase statistical power for detecting genetic variants associated with complex diseases. Third, there is increasing evidence showing that pleiotropy is a widespread phenomenon in complex diseases. In this paper, we develop a clustering linear combination (CLC) method to jointly analyze multiple phenotypes for GWASs. In the CLC method, we first cluster individual statistics into positively correlated clusters and then, combine the individual statistics linearly within each cluster and combine the between-cluster terms in a quadratic form. CLC is not only robust to different signs of the means of individual statistics, but also reduce the degrees of freedom of the test statistic. We also theoretically prove that if we can cluster the individual statistics correctly, CLC is the most powerful test among all tests with certain quadratic forms. Our simulation results show that CLC is either the most powerful test or has similar power to the most powerful test among the tests we compared, and CLC is much more powerful than other tests when effect sizes align with inferred clusters. We also evaluate the performance of CLC through a real case study.

Availability and implementation

R code for implementing our method is available at http://www.math.mtu.edu/∼shuzhang/software.html.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Although the conventional genome-wide association studies (GWASs) focus on a single phenotype, there is an increasing interest in joint analysis of multiple phenotypes because cohorts usually collect multiple phenotypes and jointly analyzing multiple phenotypes may increase statistical power (Solovieff et al., 2013; Stephens, 2013; Yang and Wang, 2012; Zhou and Stephens, 2014). Recently, many statistical methods have been developed for joint analysis of multiple phenotypes. These methods include tests based on combining the univariate analysis results, regression methods and dimension reduction methods. In the tests based on combining the univariate analysis results, one first conducts the univariate tests and then combines the univariate test statistics or combines the P-values of the univariate tests (Kim et al., 2015; Liang et al., 2016; O'Brien, 1984; van der Sluis et al., 2013; Yang et al., 2010, 2016). Regression methods include mixed effect models (Casale et al., 2015; Korte et al., 2012; Zhou and Stephens, 2014), generalized estimating equation (GEE) methods (Zeger and Liang, 1986; Zhang et al., 2014) and reverse regression methods (O'Reilly et al., 2012; Yan et al., 2013). Dimension reduction methods include canonical correlation analysis (CCA) (Tang and Ferreira, 2012), principal components of traits (PCT) (Aschard et al., 2014) and principal components of heritability (PCH) (Klei et al., 2008; Lange et al., 2004; Ott and Rabinowitz, 1999; Wang et al., 2016; Zhou et al., 2015). Although most of aforementioned methods for multiple phenotypes are applicable only to individual-level data, a few methods have been developed for meta-analysis from multiple GWASs (Cichonska et al., 2016; Kim et al., 2015; Kwak and Pan, 2016, 2017; Zhu et al., 2015,b).

Among the methods described above, O’Brien’s method (O'Brien, 1984; Wei and Johnson, 1985) is one of the earliest methods for multiple phenotypes, which can be used to integrate the results from univariate association tests. If the means of individual statistics are homogeneous, O’Brien’s method is the most powerful test among those that linearly combine these statistics. However, if the means of individual statistics are heterogeneous, O’Brien’s method will lose power dramatically, especially, when the means of individual statistics have different signs. To overcome this limitation, one can use the omnibus test with test statistic $T_{omn}=T^T{\Sigma }^{-1}T$, where $T={\left(T_1,\dots ,T_K\right)}^T\sim N\left(0,\Sigma \right)$ under the null hypothesis; $T_k$ is the test statistic to test the association between the genetic variant of interest and the $k^{th}$ phenotype for $k=1,\dots ,K$; and $K$ is the number of phenotypes. Under the null hypothesis, $T_{omn}$ follows a chi-square distribution with $K$ degrees of freedom (df). Yang et al. (2010) also proposed extensions of O’Brien’s method. Our power comparisons show that the omnibus test and Yang et al.’s methods have similar powers over all simulation scenarios (Zhu et al., 2015a). The omnibus test and Yang et al.’s methods may lose power due to the large df.

In this paper, we develop a clustering linear combination (CLC) method. The CLC method is adaptive to the correlation structure of individual statistics by clustering them into clusters of positively correlated individual statistics. Within each cluster, the individual statistics are combined linearly. The between-cluster items are then combined in a quadratic form. Given the number of clusters, CLC follows a chi-square distribution with df equal to the number of clusters. Comparing with O’Brien’s method, CLC improves the robustness to different signs of the means of individual statistics. Comparing with the omnibus test, CLC can reduce df. We also theoretically prove that if we can cluster the individual statistics correctly, CLC is the most powerful test among all tests with certain quadratic forms. We use extensive simulation studies to compare the performance of CLC with that of six existing methods. Our simulation results show that CLC is either the most powerful test or has similar power to the most powerful test among the tests we considered. Furthermore, CLC is much more powerful than other methods when effect sizes align with inferred clusters. We also demonstrate the usefulness of CLC through a real case study.

2 Materials and methods

Let $Y={\left(Y_1,\dots ,Y_K\right)}^T$ denote the random vector of $K$ correlated phenotypes and $X$ denote the random variable of the genotype at the variant of interest. We consider a sample from $\left(X,Y\right)$ with $n$ unrelated individuals. Each individual has genotype at the variant of interest and $K$ correlated quantitative or qualitative phenotypes (1 for cases and 0 for controls for a qualitative phenotype). Let $y_{ik}$ denote the kth phenotype value of the ith individual and $x_i$ denote the genotype of the ith individual at the variant of interest, where $x_i$ is the number of minor alleles that the ith individual carries at the variant. We assume that there are no covariates. If there are covariates, we adjust genotypes and phenotype values for the covariates through linear models.

Consider the generalized linear model (Nelder and Wedderburn, 1972)

$$g(E(y_{ik}|x_i))={\beta }_{0k}+{\beta }_{1k}{x}_i$$ (1)

where $g()$ is a monotone ‘link’ function. Two commonly used models under the generalized linear model framework are (i) the linear model with an identity link for continuous or quantitative phenotypes and (ii) the logistic regression model with a logit link for binary or qualitative phenotypes. Let $T_k$ denote the score test statistic to test the null hypothesis $H_0:{\beta }_{1k}=0$ under the generalized linear model. Under the two commonly used models, $T_k$ is given by (Sha et al., 2011)

$$T_k=U_k/\sqrt{V_k},$$ (2)

where $U_k={\sum }_{i=1}^n{y}_{ik}\left(x_i-\overline{x}\right)$ and $V_k=\frac{1}{n}{\sum }_{i=1}^n{(y_{ik}-{\overline{y}}_k)}^2{\sum }_{i=1}^n{(x_i-\overline{x})}^2$. Since each $T_k$ asymptotically follows a normal distribution with mean ${\beta }_k=E\left(T_k\right)$ and variance 1, let’s assume that $T={\left(T_1,\dots ,T_K\right)}^T$ asymptotically follows a multivariate normal distribution with mean vector $\beta ={\left({\beta }_1,\dots ,{\beta }_K\right)}^T$ and variance matrix $\mathbf{\Sigma }$ (O'Brien, 1984; Yang et al., 2010; Zhu et al., 2015b).

2.1 Estimating $\Sigma$ under the null hypothesis $H_0:{\beta }_{11}=\cdots ={\beta }_{1K}=0$

Let ${\sigma }_k^2=\mathrm{var}\left(Y_k\right)$, then $V_k={\sum }_{i=1}^n{(y_{ik}-{\overline{y}}_k)}^2{\sum }_{i=1}^n{(x_i-\overline{x})}^2/n\to {\sigma }_k^2{\sum }_{i=1}^n{(x_i-\overline{x})}^2$ almost surely and $E\left(T_k\right)\to {\sum }_{i=1}^n{g}^{-1}\left({\beta }_{0k}\right)\left(x_i-\overline{x}\right)/\sqrt{{\sigma }_k^2{\sum }_{i=1}^n{(x_i-\overline{x})}^2}=0$ almost surely. Therefore,$\mathrm{cov}\left(T_k,T_s\right)\to \frac{\sum _{i=1}^n\sum _{j=1}^n\left(x_i-\overline{x}\right)\left(x_j-\overline{x}\right)E\left(\left(y_{ik}-g^{-1}\left({\beta }_{0k}\right)\right)\left(y_{js}-g^{-1}\left({\beta }_{0s}\right)\right)\right)}{{\sigma }_k{\sigma }_s\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}.$ When $i\ne j$, $E\left(\left(y_{ik}-g^{-1}\left({\beta }_{0k}\right)\right)\left(y_{js}-g^{-1}\left({\beta }_{0s}\right)\right)\right)=0$ because the i^th individual and the j^th individual are unrelated. Therefore,

$$\begin{array}{c}\mathrm{cov}\left(T_k,T_s\right)\to \frac{\sum _{i=1}^{n}E\left(\left(y_{ik}-g^{-1}\left({\beta }_{0k}\right)\right)\left(y_{is}-g^{-1}\left({\beta }_{0s}\right)\right)\right){\left(x_i-\overline{x}\right)}^2}{{\sigma }_k{\sigma }_s\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}\\ =\frac{\mathrm{cov}\left(Y_k,Y_s\right)\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}{{\sigma }_k{\sigma }_s\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}=\frac{\mathrm{cov}\left(Y_k,Y_s\right)}{{\sigma }_k{\sigma }_s}=\rho \left(Y_k,Y_s\right),\end{array}$$

where $\rho \left(Y_k,Y_s\right)$ denotes the correlation coefficient between $Y_k$ and $Y_s$. Therefore, $\Sigma \to P\left(Y\right)$ almost surely, where $P\left(Y\right)$ denote the correlation matrix of $Y={\left(Y_1,\dots ,Y_K\right)}^T$. Thus, $\Sigma$ can be estimated by $\widehat{\Sigma }=P^s\left(Y\right)$, where $P^s\left(Y\right)$ is the sample correlation matrix of $Y={\left(Y_1,\dots ,Y_K\right)}^T$. Since $P^s\left(Y\right)$ is a consistent estimator of $P\left(Y\right)$, $P^s\left(Y\right)$ is a consistent estimator of $\Sigma$. Note that under the null hypothesis, the distribution of $T={\left(T_1,\dots ,T_K\right)}^T$ does not depend on the genotypes.

2.2 CLC test statistic

We propose to use the hierarchical clustering method with similarity matrix $\widehat{\Sigma }=P^s\left(Y\right)$ and dissimilarity matrix $1-P^s\left(Y\right)$ to cluster $T_1,\dots ,T_K$. Clustering $T_1,\dots ,T_K$ is equivalent to clustering $K$ phenotypes using the hierarchical clustering method with dissimilarity matrix $1-P^s\left(Y\right)$. To see if hierarchical clustering method with dissimilarity matrix $1-P^s\left(Y\right)$ can cluster phenotypes with different effect sizes, we take the linear model $Y_k={\beta }_{0k}+{\beta }_{1k}X+{\epsilon }_k$ as an example, where we assume that ${\epsilon }_1,\dots ,{\epsilon }_K$ are independent of $X$; correlations between every pair of ${\epsilon }_1,\dots ,{\epsilon }_K$ are all $\rho$ and $\mathrm{var}\left({\epsilon }_k\right)=1$ for $k=1,\dots ,K$; ${\beta }_{11},\dots ,{\beta }_{1K}$ can be divided into two clusters, ${\left({\beta }_{11},\dots ,{\beta }_{1(K/2)}\right)}^T={\left(-\beta ,\dots ,-\beta \right)}^T$ and ${\left({\beta }_{1\left(K/2+1\right)},\dots ,{\beta }_{1K}\right)}^T={\left(\beta ,\dots ,\beta \right)}^T$. Within each cluster, the correlation between $Y_k$ and $Y_l$ is $\left({\beta }^2\mathrm{var}\left(X\right)+\rho \right)/\left({\beta }^2\mathrm{var}\left(X\right)+1\right)$. Between two clusters, the correlation between $Y_k$ and $Y_l$ is $\left(-{\beta }^2\mathrm{var}\left(X\right)+\rho \right)/\left({\beta }^2\mathrm{var}\left(X\right)+1\right)$. We can see that hierarchical clustering method with dissimilarity matrix $1-P^s\left(Y\right)$ can cluster phenotypes with different effect sizes. In the above example, we assume that ${\epsilon }_1,\dots ,{\epsilon }_K$ are exchangeable. If the covariance of ${\epsilon }_1,\dots ,{\epsilon }_K$ has a structure, clustering phenotypic covariance may not successfully cluster genetic covariance. For example, if the covariance of ${\epsilon }_1,\dots ,{\epsilon }_K$ has a structure: $\mathrm{cov}\left({\epsilon }_k,{\epsilon }_l\right)=\rho /2$ if $1\le k,l\le K/2$ and $\mathrm{cov}\left({\epsilon }_k,{\epsilon }_l\right)=\rho$ otherwise. Then the correlation between $Y_k$ and $Y_l$ is $\left({\beta }^2\mathrm{var}\left(X\right)+\rho /2\right)/\left({\beta }^2\mathrm{var}\left(X\right)+1\right)$ if $1\le k,l\le K/2$;$\left({\beta }^2\mathrm{var}\left(X\right)+\rho \right)/\left({\beta }^2\mathrm{var}\left(X\right)+1\right)$ if $K/2+1\le k,l\le K$; and $\left(-{\beta }^2\mathrm{var}\left(X\right)+\rho \right)/\left({\beta }^2\mathrm{var}\left(X\right)+1\right)$ otherwise. It is possible that $-{\beta }^2\mathrm{var}\left(X\right)+\rho \ge {\beta }^2\mathrm{var}\left(X\right)+\rho /2$, that is, the phenotypic correlations between genetic clusters may be greater than the phenotypic correlations within a genetic cluster. Thus, when the covariance of ${\epsilon }_1,\dots ,{\epsilon }_K$ has a structure, clustering phenotypic correlations may not cluster genetic effects.

Suppose that we cluster the phenotypes into $L$ clusters, where $1\le L\le K$. Let $B$ be a $K\times L$ matrix with the (k,l)^th element denoted by $b_{kl}$, where $b_{kl}=1$ if the kth phenotype belongs to the l^th cluster and $b_{kl}=0$ otherwise. Our proposed CLC test statistic with $L$ clusters is given by

$$T_{CLC}^L={\left(WT\right)}^T{\left(W\Sigma W^T\right)}^{-1}\left(WT\right),$$

where $W=B^T{\Sigma }^{-1}$. Under the null hypothesis that none of phenotypes is associated with the variant of interest, $T_{CLC}^L$ follows a chi-square distribution with df $L$ because clustering method only depends on phenotypes not the genotype at the variant of interest.

Note that when $L=1$, $T_{CLC}^L$ is equivalent to O’Brien’s method (O'Brien, 1984); when $L=K$, $T_{CLC}^L$ is equivalent to omnibus test with test statistic $T^T{\Sigma }^{-1}T$; for $1\le L\le K$, $T_{CLC}^L$ for multiple phenotypes and one variant is similar to the multiple linear combination (MLC) regression tests for one phenotype and multiple variants (Yoo et al., 2017).

Let $p_L$ denote the P-value of $T_{CLC}^L$ for $L=1,\dots ,K$. We define the test statistic of CLC as

$$T_{CLC}={\min }_{1\le L\le K}{p}_L.$$ (3)

We use a simulation procedure to evaluate the P-value of $T_{CLC}$. In each simulation, we generate $T$ according to the multivariate normal distribution $N\left(0,\widehat{\Sigma }\right)$. Suppose that we perform the simulation $D$ times. Let $T_{CLC}^{\left(d\right)}$ denote the value of $T_{CLC}$ based on the dth simulated data, where $d=0$ represents the original data. Then, the P-value of $T_{CLC}$ is given by

$$\begin{array}{c}\#\left\{d:T_{CLC}^{\left(d\right)}\le T_{CLC}^{\left(0\right)}\hspace{0.17em}\text{for}\hspace{0.17em}d=0,\dots ,D\right\}/\left(D+1\right)\\ =\left(\#\left\{d:T_{CLC}^{\left(d\right)}\le T_{CLC}^{\left(0\right)}\hspace{0.17em}\text{for}\hspace{0.17em}d=1,\dots ,D\right\}+1\right)/\left(D+1\right).\end{array}$$

The null distributions of $T={\left(T_1,\dots ,T_K\right)}^T$ and thus of $T_{CLC}$ do not depend on the genetic variant being tested. Therefore, the simulation procedure described above to generate an empirical null distribution of $T_{CLC}$ needs to be done only once for a GWAS.

2.3 Theoretical considerations

Theorem. We assume that $T={\left(T_1,\dots ,T_K\right)}^T\sim N\left(\beta ,\Sigma \right)$, where $\beta ={\left({\beta }_1,\dots ,{\beta }_K\right)}^T$. Suppose ${\beta }_1,\dots ,{\beta }_K$ can be divided into $L$ clusters, that is, $\beta ={\left({\theta }_1{1}_{K_1}^T,\dots ,{\theta }_L{1}_{K_L}^T\right)}^T$, $1_s={\left(\underset{s}{\underbrace{1,\dots ,1}}\right)}^T$ and $K_1+\cdots +K_L=K$. If the hierarchical clustering method can correctly cluster $\beta$, $T_{CLC}^L$ is the most powerful test among all tests in the quadratic form ${\left(CT\right)}^T{\left(C\Sigma C^T\right)}^{-1}CT$, where $C$ is an arbitrary $L\times K$ matrix.

Proof. Since $CT\sim N\left(C\beta ,C\Sigma C^T\right)$, ${\left(CT\right)}^T{\left(C\Sigma C^T\right)}^{-1}CT$ follows a chi-square distribution with noncentrality parameter ${\left(C\beta \right)}^T{\left(C\Sigma C^T\right)}^{-1}C\beta$ and df $L$ denoted by ${\chi }^2\left({\left(C\beta \right)}^T{\left(C\Sigma C^T\right)}^{-1}C\beta ,L\right)$. Then, $T_{CLC}^L\sim {\chi }^2\left({\beta }^T{\Sigma }^{-1}B{\left(B^T{\Sigma }^{-1}B\right)}^{-1}{B}^T{\Sigma }^{-1}\beta ,L\right)$. Note that if two noncentral chi-square distributed tests have the same df, the test with larger noncentrality parameter is more powerful than the other one. We only need to prove $\Delta ={\beta }^T{\Sigma }^{-1}B{\left(B^T{\Sigma }^{-1}B\right)}^{-1}{B}^T{\Sigma }^{-1}\beta -{\left(C\beta \right)}^T{\left(C\Sigma C^T\right)}^{-1}C\beta \ge 0$ for an arbitrary $L\times K$ matrix $C$. Note that $\beta =B\theta$, where $\theta ={\left({\theta }_1,\dots ,{\theta }_L\right)}^T$. We have $\Delta ={\theta }^T\left(B^T{\Sigma }^{-1}B-{\left(CB\right)}^T{\left(C\Sigma C^T\right)}^{-1}CB\right)\theta$. Let $d={\Sigma }^{-1/2}B\theta$ be a $K\times 1$ vector and $E=C{\Sigma }^{-1/2}$ be a $L\times K$ matrix. Then, $\Delta =d^T\left(I-E^T{\left(E{E}^T\right)}^{-1}E\right)d\ge 0$ because $I-E^T{\left(E{E}^T\right)}^{-1}E$ is an idempotent and symmetric matrix and therefore is a positive semidefinite matrix.

2.4 Comparison of methods

We compare the performance of the CLC method with those of the O’Brien (O'Brien, 1984), the omnibus test, the Trait-based Association Test that uses Extended Simes procedure (TATES) (van der Sluis et al., 2013), the Tippett’s method (Tippett) (Pesarin and Salmaso, 2010), the Multivariate Analysis of Variance (MANOVA) (Cole et al., 1994), Multiple Trait Mixed Model (MTMM) (Zhou and Stephens, 2014) and the joint model of Multiple Phenotypes (MultiPhen) (O'Reilly et al., 2012). When MTMM is used, we use the software GEMMA provided by Zhou and Stephens (2014) to perform the real data analysis with 7 phenotypes and use GEMMA under the assumption that individuals are unrelated to do simulation studies with 20 phenotypes. This assumption does not reduce the power of MTMM in the simulation studies because we generate phenotypes and genotypes under this assumption in our simulations.

3 Results

3.1 Simulation setup

To evaluate the type I error rate and power of CLC, we generate genotypes according to the minor allele frequency (MAF) and assume Hardy Weinberg equilibrium. We generate $K$ quantitative phenotypes similar to that in Wang et al. (2016). To generate a qualitative disease affection status, we use a liability threshold model based on a quantitative phenotype. A qualitative phenotype is defined to be affected if the corresponding quantitative phenotype is at least one standard deviation larger (smaller) than the phenotypic mean. In the following, we describe how to generate quantitative phenotypes. In details, we generate $K$ quantitative phenotypes by the factor model

$$y=\lambda x+c\mathbf{\gamma }f+\sqrt{1-c^2}\times \epsilon ,$$ (4)

where $y={\left(y_1,\dots ,y_K\right)}^T$; $x$ is the genotype at the variant of interest; $\lambda =\left({\lambda }_1,\dots ,{\lambda }_K\right)$ is the vector of effect sizes of the genetic variant on the $K$ phenotypes; $f={\left(f_1,\dots ,f_R\right)}^T$ is a vector of factors with $R$ elements and $f={\left(f_1,\dots ,f_R\right)}^T\sim MVN\left(0,\Sigma \right)$, $\Sigma =\left(1-\rho \right)I+\rho A$, $A$ is a matrix with elements of 1, $I$ is the identity matrix and $\rho$ is the correlation between factors; $\mathbf{\gamma }$ is a $K$ by $R$ matrix; $c$ is a constant number; and $\epsilon ={\left({\epsilon }_1,\dots ,{\epsilon }_K\right)}^T$ is a vector of residuals, ${\epsilon }_1,\dots ,{\epsilon }_K$ are independent, and ${\epsilon }_k\sim N\left(0,1\right)$ for $k=1,\dots ,K$.

Based on Equation (4), we consider the following four models in which the within-factor correlation is $c^2$ and the between-factor correlation is $\rho c^2$. The phenotypic correlation structures mimic that of UK10K (The UK10K Consortium et al., 2015), that is, the phenotypes are divided into several phenotype blocks (factors) and the within-factor correlation is larger than the between-factor correlation.

Model 1: There is only one factor and genotypes impact on all phenotypes. That is, $R=1$, $\lambda =\beta {\left(1,2,\dots ,K\right)}^T$ and $\mathbf{\gamma }=1K$.

Model 2: There are two factors and genotypes impact on one factor. That is, $R=2$, $\lambda ={\left(0,\dots ,0,\underset{K/2}{\underbrace{\beta ,\dots ,\beta }}\right)}^T$ and $\mathbf{\gamma }=Bdiag\left(D_1,D_2\right)$, where $D_i=1K/2$ for $i=1,2$.

Model 3: There are five factors and genotypes impact on two factors. That is, $R=5$, $\lambda ={\left({\beta }_{11},\dots ,{\beta }_{1k},{\beta }_{21},\dots ,{\beta }_{2k},{\beta }_{31},\dots ,{\beta }_{3k},{\beta }_{41},\dots ,{\beta }_{4k},{\beta }_{51},\dots ,{\beta }_{5k}\right)}^T$ and $\mathbf{\gamma }=Bdiag\left(D_1,D_2,D_3,D_4,D_5\right)$, where $D_i=1K/5$ for $i=1,\dots ,5$; $k=K/5$; ${\beta }_{11}=\cdots ={\beta }_{1k}={\beta }_{21}=\cdots ={\beta }_{2k}={\beta }_{31}=\cdots ={\beta }_{3k}=0$; ${\beta }_{41}=\cdots ={\beta }_{4k}=-\beta$; and $\left({\beta }_{51},\dots ,{\beta }_{5k}\right)=\frac{2\beta }{k+1}\left(1,\dots ,k\right)$.

Model 4: There are five factors and genotypes impact on four factors. That is, $R=5$, $\lambda ={\left({\beta }_{11},\dots ,{\beta }_{1k},{\beta }_{21},\dots ,{\beta }_{2k},{\beta }_{31},\dots ,{\beta }_{3k},{\beta }_{41},\dots ,{\beta }_{4k},{\beta }_{51},\dots ,{\beta }_{5k}\right)}^T$ and $\mathbf{\gamma }=Bdiag\left(D_1,D_2,D_3,D_4,D_5\right)$, where $D_i=1K/5$ for $i=1,\dots ,5$; $k=K/5$; ${\beta }_{11}=\cdots ={\beta }_{1k}=0$; ${\beta }_{21}=\cdots ={\beta }_{2k}=\beta$; ${\beta }_{31}=\cdots ={\beta }_{3k}=-\beta$; $\left({\beta }_{41},\dots ,{\beta }_{4k}\right)=-\frac{2\beta }{k+1}\left(1,\dots ,k\right)$; and $\left({\beta }_{51},\dots ,{\beta }_{5k}\right)=\frac{2\beta }{k+1}\left(1,\dots ,k\right)$.

To evaluate type I error rate of our proposed CLC method, we let $\beta =0$. To evaluate power, we let $\beta >0$. In the simulation studies for evaluation of type I error rate and power, we set MAF = 0.3, the between-factor correlation is 0.15, and the within-factor correlation is 0.25.

3.2 Simulation results

To evaluate type I error of CLC, we consider different types of phenotypes, different number of phenotypes, different sample sizes, different models and different significance levels. In each simulation scenario, the P-values of CLC are estimated by 10 000 simulations and type I error rates are evaluated using 10 000 replicated samples. For 10 000 replicated samples, the 95% confidence intervals (CIs) for type I error rates divided by nominal significance levels 0.01 and 0.001 are (0.80, 1.20) and (0.40, 1.60), respectively. The estimated type I error rates of CLC are summarized in Tables 1 and 2. From these tables, we can see that all of the estimated type I error rates are within the 95% CIs, which indicates that CLC is a valid test. We also evaluate the type I error rates of O’Brien, Omnibus, TATES, MANOVA and MultiPhen by using their analytic P-values (Supplementary Table S1). From Supplementary Table S1, we can see that O’Brien, Omnibus, TATES and MANOVA have correct type I error rates, but MultiPhen has inflated type I error rates when $K=100$.

Table 1.

The estimated type I error rates divided by the nominal significance level of CLC for 20, 40 and 100 quantitative phenotypes under four models

K	Sample	Alpha	Model 1	Model 2	Model 3	Model 4
20	1000	0.01	1.02	0.84	0.85	0.96
		0.001	0.80	0.80	0.70	1.10
	2000	0.01	1.03	0.93	0.96	0.94
		0.001	0.90	0.80	1.20	1.10
40	1000	0.01	1.08	0.82	1.00	1.02
		0.001	1.20	0.70	1.40	1.30
	2000	0.01	0.91	0.91	1.03	0.94
		0.001	1.10	1.50	1.50	0.50
100	1000	0.01	0.95	1.03	0.82	0.89
		0.001	0.65	1.05	0.65	0.95

Note: The P-values of CLC are evaluated by 10 000 simulations and type I error rates are evaluated by 10 000 replicated samples.

Table 2.

The estimated type I error rates divided by the nominal significance level of CLC for 20, 40 and 100 phenotypes with half quantitative phenotypes and half qualitative phenotypes under four models

K	Sample	Alpha	Model 1	Model 2	Model 3	Model 4
20	1000	0.01	1.01	0.83	1.08	1.10
		0.001	1.00	1.20	1.00	1.30
	2000	0.01	1.12	1.01	1.00	1.18
		0.001	0.80	1.50	1.10	1.00
40	1000	0.01	0.88	1.04	0.94	0.97
		0.001	0.80	0.80	1.10	1.20
	2000	0.01	0.87	0.85	1.08	0.98
		0.001	0.80	0.90	0.70	0.80
100	1000	0.01	0.86	1.02	0.93	0.70
		0.001	1.30	0.90	0.70	0.80

Note: The P-values of CLC are evaluated by 10 000 simulations and type I error rates are evaluated by 10 000 replicated samples.

For power comparisons, we consider different types of phenotypes: (i) all phenotypes are quantitative and (ii) phenotypes are half quantitative and half qualitative. In each of the two cases, we consider different numbers of phenotypes and different models. In each of the simulation scenarios, the P-values of CLC are evaluated using 1000 simulations; the P-values of Tippett are evaluated using 1000 permutations; and the P-values of O’Brien, Omnibus test, TATES, MANOVA, MultiPhen and MTMM are evaluated using asymptotic distributions. The power is evaluated using 1000 replicated samples at a significance level of 0.05.

Power comparisons of the seven or eight methods (O’Brien, Omnibus, CLC, TATES, MANOVA, MultiPhen, Tippet and MTMM; we include MTMM only when K = 20 and n = 1000 due to time consuming of MTMM) under four models for different values of the effect size are given in Figures 1 and 2 for 20 and 40 quantitative phenotypes, respectively. These two figures show that (i) when effect sizes of the variant of interest on phenotypes show no groups (Model 1), all seven methods have similar power; (ii) when effect sizes show some groups (Models 2–4), CLC is much more powerful than other methods; (iii) when effect sizes show some groups and have different directions (Models 3-4), MANOVA, MultiPhen, MTMM and Omnibus test are more powerful than TATES and Tippett, and O’Brien has almost no power because the genetic effects have different directions; and (iv) when the effect sizes are in groups and have the same direction in all groups (Model 2), TATES and Tippett are more powerful than MANOVA, MultiPhen and MTMM. We also perform power comparisons for the case of half quantitative and half qualitative phenotypes (Supplementary Figs S1 and S2), for the case of 100 phenotypes (Supplementary Figs S3 and S4), for the case of larger sample size 5000 (Supplementary Figs S5 and S6) and for the case of smaller significance level 10⁻⁴ (Supplementary Fig. S7). The patterns of power comparisons under these scenarios are similar to those of Figures 1 and 2.

Fig. 1.

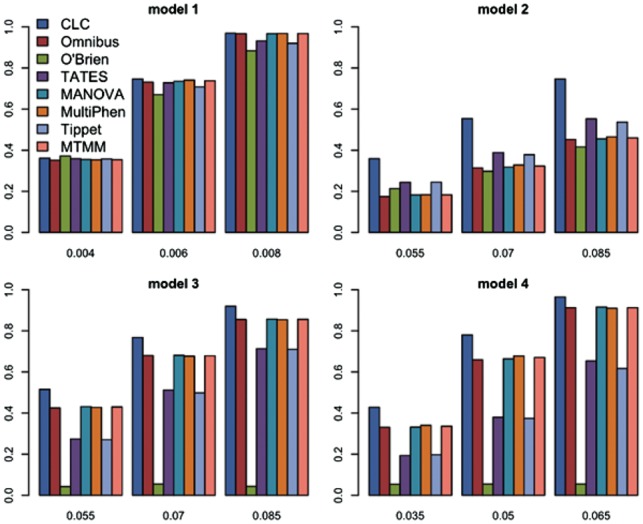
Power comparisons of the eight tests. The powers of O’Brien, Omnibus, CLC, TATES, MANOVA, MultiPhen, Tippet and MTMM as a function of effect size β for 20 quantitative phenotypes. The sample size is 1000. The between-factor correlation is 0.15 and the within-factor correlation is 0.25

Fig. 2.

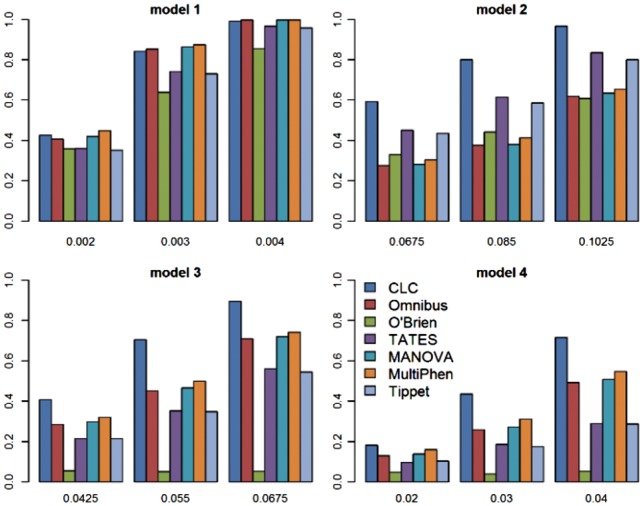
Power comparisons of the seven tests. The powers of O’Brien, Omnibus, CLC, TATES, MANOVA, MultiPhen and Tippet as a function of effect size β for 40 quantitative phenotypes. The sample size is 1000. The between-factor correlation is 0.15 and the within-factor correlation is 0.25

From Figures 1 and 2 and Supplementary Figures S1–S7, we can see that the power of CLC in model 2 is a lot better than that in models 3 and 4 because in models 3 and 4, at least one factor shows no clusters of effect sizes; we can also see that with increasing the number of phenotypes K, the power of CLC (compared with the powers of other methods) in models 2–4 increases because the number of factors is fixed, that is, the df of CLC does not change much comparing to other methods. In summary, CLC is either the most powerful test or has similar power to the most powerful test among the seven or eight tests.

3.3 Application to the COPDGene

The COPDGene Study is a multi-center genetic and epidemiologic investigation to study Chronic Obstructive Pulmonary Disease (COPD) (Regan et al., 2010). This COPDGene dataset has been described in our pervious paper (Liang et al., 2016). Same as Liang et al. (2016), we select seven quantitative COPD-related phenotypes (FEV1, Emphysema, Emphysema Distribution, Gas Trapping, Airway Wall Area, Exacerbation frequency and Six-minute walk distance) and four covariates (BMI, Age, Pack-Years and Sex). In this analysis, a set of 5430 non-Hispanic Whites across 630 860 SNPs is used. The correlation structure of the seven COPD-related phenotypes is given in Supplementary Figure S8. Before analyzing this dataset, we perform the sign alignment of the seven phenotypes (change the signs of six-minute walk distance and FEV1) such that the correlations between the seven phenotypes are all positive. MANOVA, MultiPhen, Tippet, MTMM, TATES and Omnibus are not affected by the sign alignment in phenotypes. CLC is not affected much by the sign alignment. However, O’Brien is affected very much by the sign alignment because O’Brien’s test statistic is a linear combination of the univariate test statistics.

We adopt the commonly used genome-wide significance level $5\times {10}^{-8}$ to identify SNPs significantly associated with the 7 COPD-related phenotypes. There are total 14 SNPs identified by at least one method (Table 3). All of the 14 SNPs had been reported to be associated with COPD by previous studies (Brehm et al., 2011; Cho et al., 2010; Cui et al., 2014; Du et al., 2016; Hancock et al., 2010; Li et al., 2011; Lutz et al., 2015; Pillai et al., 2009; Wilk et al., 2009, 2012; Young et al., 2010; Zhang et al., 2011; Zhu et al., 2014). As shown in Table 3, MultiPhen identified 14 SNPs; Omnibus test, MTMM, CLC and MANOVA identified 13 SNPs; TATES and Tippett identified 9 SNPs; and O’Brien method identified 5 SNPs. We also investigated the 14 significant SNPs and the corresponding adjusted P-values for testing each of the 7 phenotypes individually (Supplementary Table S2). From Supplementary Table S2, we can explain why Tippet and TATES cannot detect some subsets of SNPs because Tippet and TATES mainly depend on the smallest P-value of the seven univariate tests; we can also explain why O’Brien only identified five SNPs because the seven phenotypes have heterogeneous effects. In summary, the number of SNPs identified by CLC is comparable to the largest number of SNPs identified by other tests, which is consistent with our simulation results. Furthermore, since CLC only depends on summary statistics, it can be used in meta-analysis. Among the five methods based on summary statistics (CLC, O’Brien, Omnibus, TATES and Tippett), CLC identified the most gnome-wide significant SNPs.

Table 3.

Significant SNPs and the corresponding P-values in the analysis of COPDGene

Chr	Position	Variant identifier	O’Brien	Omnibus	TATES	Tippett	MANOVA	MultiPhen	CLC	MTMM
4	145431497	rs1512282	$7.69\times {10}^{-9}$	$1.82\times {10}^{-9}$	$5.77\times {10}^{-9}$	$8.00\times {10}^{-9}$	$1.69\times {10}^{-9}$	$1.03\times {10}^{-9}$	${10}^{-9}$	$6.75\times {10}^{-9}$
4	145434744	rs1032297	$3.35\times {10}^{-10}$	$7.73\times {10}^{-14}$	$6.22\times {10}^{-13}$	${10}^{-9}$	$6.52\times {10}^{-14}$	$7.69\times {10}^{-14}$	${10}^{-9}$	$4.58\times {10}^{-12}$
4	145474473	rs1489759	$2.61\times {10}^{-11}$	$1.11\times {10}^{-16}$	$2.52\times {10}^{-16}$	${10}^{-9}$	$1.11\times {10}^{-16}$	$1.22\times {10}^{-16}$	${10}^{-9}$	$1.00\times {10}^{-14}$
4	145485738	rs1980057	$3.04\times {10}^{-11}$	$1.11\times {10}^{-16}$	$9.35\times {10}^{-17}$	${10}^{-9}$	$6.68\times {10}^{-17}$	$8.14\times {10}^{-17}$	${10}^{-9}$	$6.53\times {10}^{-15}$
4	145485915	rs7655625	$3.08\times {10}^{-11}$	$1.11\times {10}^{-16}$	$1.64\times {10}^{-16}$	${10}^{-9}$	$7.12\times {10}^{-17}$	$9.13\times {10}^{-17}$	${10}^{-9}$	$7.81\times {10}^{-15}$
15	78882925	rs16969968	$9.75\times {10}^{-6}$	$1.26\times {10}^{-11}$	$2.98\times {10}^{-8}$	$4.90\times {10}^{-8}$	$1.32\times {10}^{-11}$	$7.84\times {10}^{-12}$	${10}^{-9}$	$8.57\times {10}^{-10}$
15	78894339	rs1051730	$8.99\times {10}^{-6}$	$1.35\times {10}^{-11}$	$2.63\times {10}^{-8}$	$4.20\times {10}^{-8}$	$1.41\times {10}^{-11}$	$8.16\times {10}^{-12}$	${10}^{-9}$	$9.16\times {10}^{-10}$
15	78898723	rs12914385	$6.12\times {10}^{-8}$	$1.66\times {10}^{-12}$	$5.14\times {10}^{-10}$	${10}^{-9}$	$1.76\times {10}^{-12}$	$1.48\times {10}^{-12}$	${10}^{-9}$	$1.66\times {10}^{-10}$
15	78911181	rs8040868	$1.53\times {10}^{-7}$	$2.50\times {10}^{-12}$	$2.40\times {10}^{-9}$	$5.00\times {10}^{-9}$	$2.74\times {10}^{-12}$	$2.59\times {10}^{-12}$	${10}^{-9}$	$2.35\times {10}^{-10}$
15	78878541	rs951266	$1.50\times {10}^{-5}$	$1.69\times {10}^{-11}$	$5.17\times {10}^{-8}$	$8.10\times {10}^{-8}$	$1.77\times {10}^{-11}$	$1.02\times {10}^{-11}$	${10}^{-9}$	$1.15\times {10}^{-9}$
15	78806023	rs8034191	$2.13\times {10}^{-5}$	$1.99\times {10}^{-10}$	$1.02\times {10}^{-7}$	$1.70\times {10}^{-7}$	$2.14\times {10}^{-10}$	$7.74\times {10}^{-11}$	${10}^{-9}$	$1.49\times {10}^{-8}$
15	78851615	rs2036527	$2.65\times {10}^{-5}$	$3.76\times {10}^{-10}$	$1.56\times {10}^{-7}$	$2.41\times {10}^{-7}$	$3.99\times {10}^{-10}$	$1.77\times {10}^{-10}$	$8.33\times {10}^{-10}$	$2.56\times {10}^{-8}$
15	78826180	rs931794	$2.33\times {10}^{-5}$	$2.19\times {10}^{-10}$	$1.18\times {10}^{-7}$	$1.94\times {10}^{-7}$	$2.35\times {10}^{-10}$	$9.09\times {10}^{-11}$	${10}^{-9}$	$1.50\times {10}^{-8}$
15	78740964	rs2568494	$2.38\times {10}^{-3}$	$9.73\times {10}^{-8}$	$2.88\times {10}^{-5}$	$3.42\times {10}^{-5}$	$1.05\times {10}^{-7}$	$4.23\times {10}^{-8}$	$3.98\times {10}^{-7}$	$4.03\times {10}^{-6}$

Note: We changed the signs of six-minute walk distance and FEV1, so that the correlations are all positive. The P-values of CLC are evaluated using 10⁹ simulations. The P-values of Tippett are evaluated using 10⁹ permutations. The P-values of O’Brien, Omnibus, TATES, MANOVA and MultiPhen are evaluated using asymptotic distributions. The graying out P-values indicate the P-values $>\mathrm{ }5\times {10}^{-8}$.

4 Discussion

Based on hierarchical clustering method, we propose the CLC method to test the association between multiple phenotypes and the genetic variant of interest. Extensive simulation studies as well as the real data application show that CLC has correct type I error rates and is either the most powerful test or has similar power to the most powerful test among the seven methods we considered under a variety of simulation scenarios. Furthermore, the real data application demonstrates that the proposed method has great potential in multiple-phenotype GWASs such as COPDGene dataset. CLC has several important advantages. First, it only depends on summary statistics. Second, different types of phenotypes can be easily analyzed together. Third, CLC can test the association between multiple phenotypes and multiple genetic variants as described below. For a set of rare and common variants in a gene or a genomic region, we can combine genotypes of rare and common variants by giving different weights using burden tests (Li and Leal, 2008; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007; Price et al., 2010). Then, we can use CLC to test the association between the combined genotypes and multiple phenotypes. One disadvantage of CLC is that the minimum P-value of CLC with permutation $D$ times is $1/\left(D+1\right)$, therefore, the permutation procedure of CLC could be a potential issue for follow up of highly powered studies.

CLC can be applied to meta-analysis for multiple-phenotype GWASs. Intuitively, it needs individual-level phenotype data or correlation matrix of phenotypes to do clustering for CLC to be applied to meta-analysis. In fact, the correlation matrix can be estimated from the values of summary statistics from independent SNPs in a GWAS (Zhu et al., 2015b). We assume that there are $M$ independent studies and each study has $K$ phenotypes. Denote $T_{1m},\dots ,T_{Km}$ as the summary statistics of the mth study and assume that $T_m={\left(T_{1m},\dots ,T_{Km}\right)}^T\sim N\left(0,{\Sigma }_m\right)$ under the null hypothesis, where ${\mathrm{\Sigma }}_m$ can be estimated from summary statistics $T_m$ from independent SNPs in the $m^{th}$ GWAS study (Zhu et al., 2015a,b). We perform hierarchical clustering method with dissimilarity matrix $1-{\Sigma }_m$ to cluster $T_{1m},\dots ,T_{Km}$. Then, we obtain $T_{CLC}^{(m)}$ as defined in equation (3) for the $m^{th}$ study. We define the CLC test statistic for meta-analysis as $T_{CLC}^{Meta}=-2{\sum }_{m=1}^M\hspace{0.17em}\text{log}\hspace{0.17em}{T}_{CLC}^{(m)}$. CLC can also be applied to phenotype-wide association studies (PheWAS). In PheWAS, the number of phenotypes can be thousands and we can divide phenotypes into many categories. We can apply CLC to each category and combine these CLC statistics by using Fisher’s combination test (Yang et al., 2016) or adaptive Fisher’s combination test (Liang et al., 2016). However, the performance of using CLC to meta-analysis for multiple-phenotype GWASs and PheWAS needs further investigations.

Funding

Research reported in this publication was supported by the National Human Genome Research Institute of the National Institutes of Health (NIH) under Award Number R15HG008209. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This research used data generated by the COPDGene study, which was supported by National Institutes of Health (NIH) grants U01HL089856 and U01HL089897. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung and Blood Institute or the National Institutes of Health. The COPDGene project is also supported by the COPD Foundation through contributions made by an Industry Advisory Board comprised of Pfizer, AstraZeneca, Boehringer Ingelheim, Novartis and Sunovion. Superior, a high-performance computing infrastructure at Michigan Technological University, was used in obtaining results presented in this publication.

Conflict of Interest: none declared.