A roadmap for semi-automatically extracting predictive and clinically meaningful temporal features from medical data for predictive modeling

Abstract

Predictive modeling based on machine learning with medical data has great potential to improve healthcare and reduce costs. However, two hurdles, among others, impede its widespread adoption in hdealthcare. First, medical data are by nature longitudinal. Pre-processing them, particularly for feature engineering, is labor intensive and often takes 50–80% of the model building effort. Predictive temporal features are the basis of building accurate models, but are difficult to identify. This is problematic. Healthcare systems have limited resources for model building, while inaccurate models produce sub-optimal outcomes and are often useless. Second, most machine learning models provide no explanation of their prediction results. However, offering such explanations is essential for a model to be used in usual clinical practice. To address these two hurdles, this paper outlines: 1) a data-driven method for semi-automatically extracting predictive and clinically meaningful temporal features from medical data for predictive modeling; and 2) a method of using these features to automatically explain machine learning prediction results and suggest tailored interventions. This provides a roadmap for future research.

1. Introduction

Machine learning studies computer algorithms that learn from data [1] and has won most data science competitions [2]. Examples of machine learning algorithms include deep neural network (a.k.a. deep learning) [3], support vector machine, random forest, and decision tree. By enabling tasks like identifying high-risk patients for preventive interventions, predictive modeling based on machine learning with medical data holds great potential to improve health-care and lower costs. Trials showed using machine learning helped: 1) reduce patient no-show rate by 19% and boost appointment rescheduling or cancel rate by 17% in outpatients at high risk of no-shows [4]; 2) cut 30-day mortality rate (odds ratio = 0.53) in emergency department patients with community-acquired pneumonia [5]; 3) trim cost by $1500 and ventilator use by 5.2 days per patient at a hospital respiratory care center [6]; 4) boost on- target hemoglobin values by 8.5–17% and reduce hospitalization days by 15%, cardiovascular events by 15%, hemoglobin fluctuation by 13%, expensive darbepoetin consumption by 25%, and blood transfusion events by 40–60% in end-stage renal disease patients on dialysis [7–10]; and 5) cut healthcare cost in Medicare patients’ last half year of life by 4.5% [11].

Despite its potential for many clinical activities, machine learning-based predictive modeling is used by only 15% of hospitals for limited purposes [12]. Two hurdles, among others, impede the widespread adoption of machine learning in healthcare.

1.1. Hurdle 1: predictive temporal features are essential for building accurate predictive models, but are difficult to identify

Most attributes in medical data are longitudinal. It is labor intensive and often takes 50–80% of the model building effort to pre-process medical data, particularly for feature engineering [13–15]. Predictive temporal features are the basis of building accurate predictive models, but are difficult to identify, even with many human resources. This is problematic. Healthcare systems have limited resources for model building, while inaccurate models produce suboptimal outcomes and are often useless.

At present, clinical predictive models are usually created in the following way. Given a modeling task and a long list of attributes in the medical data like those stored in the electronic health record, a clinician uses his/her judgment to choose from the long list a short list of attributes that are potentially relevant to the task. For each longitudinal attribute in the short list, the clinician uses his/her judgment to specify how to aggregate the attribute’s values over time into a temporal feature, e.g., by taking their average or maximum. Then a data scientist uses the features (a.k.a. independent variables) to build a model. If model accuracy is unsatisfactory, which is frequently the case, the process is repeated. From what we have seen at three institutions, it often takes the clinician several months and multiple iterations to finish the manual attribute and feature specification for each modeling task.

Besides being labor intensive, the above model building approach has two other drawbacks. First, many attributes could be useful for the modeling task, but are missing in the short list of attributes chosen by the clinician. Second, many temporal features could have additional predictive power, but are not included in those specified by the clinician [16]. Both drawbacks result from our limited understanding of diseases and lead to degraded model accuracy. Moreover, although the data mining community has done much work on mining and constructing temporal [17,18] and sequence features [19], often many temporal features useful for the modeling task are still waiting to be discovered.

As evidence of all of these issues, Google recently reported using all attributes in the electronic health record and long short-term memory (LSTM) [20,21], a type of deep neural network, to automatically learn temporal features from medical data [22]. For predicting each of three outcomes: in-hospital mortality, unexpected read-missions within 30 days, and long hospital stay, this resulted in a boost of the area under the receiver operating characteristic curve accuracy measure by almost 10% [22]. Several other studies [23–25] also showed that for various clinical prediction tasks and compared to using temporal features specified by experts, using LSTM to automatically learn temporal features from medical data improved prediction accuracy. This is consistent with what has happened in several areas like speech recognition, natural language processing, and video classification, where temporal features automatically learned from data by LSTM outperform those specified by experts or mined by other methods [3]. It is common that many temporal features have additional predictive power, but have not been identified before.

Without prelimiting to a small number of longitudinal attributes and possibly missing many other useful ones, LSTM can examine many attributes and automatically learn temporal features from irregularly sampled medical data of varying lengths in a data-driven way. However, the learned features are suboptimal and unsuitable for direct clinical use. When learning temporal features, the standard LSTM does not restrict the number of longitudinal attributes used in each feature. Consequently, a learned feature often involves lots of attributes, many of which have little or no relationship with each other. This results in three problems.

Problem 1.

The learned features tend to overfit the training data’s peculiarities and become less generalizable, leading to suboptimal model accuracy. As evidence of this, for several modeling tasks engaging longitudinal attributes that can be naturally partitioned into a small number (e.g., three) of modalities at a coarse granularity, researchers have improved LSTM model accuracy using multimodal LSTM [26,27]. A multimodal LSTM network includes several constituent LSTM networks, one per modality. Each feature learned by a constituent network involves only those attributes in the modality linking to the constituent network. Usually, the medical data set contains a lot of longitudinal attributes, many of which could be useful for the modeling task. If we could partition longitudinal attributes meaningfully at a finer granularity and let multimodal LSTM take advantage of this aspect, we would expect the learned features’ quality and consequently model accuracy to improve further. Intuitively, a clinically meaningful temporal feature should typically involve no more than a few attributes.

Problem 2.

Differing healthcare systems collect overlapping yet different attributes. The more attributes a feature involves, the less likely a predictive model built with the feature will be used by other healthcare systems beyond the one that originally developed the model.

Problem 3.

A feature involving many longitudinal attributes is difficult to understand. As reviewed in Section 2, in LSTM, each memory cell vector element depicts some learned feature(s). Karpathy et al. [28] showed that only ~10% of these elements could be interpreted [29]. In clinical practice, clinicians usually refuse to use what they do not understand.

1.2. Hurdle 2: most machine learning models are black boxes, but clinical practice requires transparency of model prediction results

This hurdle is related to Problem 3 mentioned above. Most machine learning models including LSTM provide no explanation of their prediction results. Yet, offering such explanations is essential for a model to be used in usual clinical practice. When lives are at risk, clinicians need to know the reasons to trust a model’s prediction results. Understanding the reasons for poor outcomes can help clinicians select tailored interventions that typically work better than non-specific ones. Explanations for prediction results can provide hints to help discover new knowledge. In addition, if sued for malpractice, clinicians will need to use their understanding of the prediction results to justify their decisions in court.

Previously, for tabular data whose columns have easy-to-understand meanings, we developed a method that can automatically explain any machine learning model’s prediction results with no accuracy loss [30]. This method cannot handle longitudinal data directly. Using the temporal features automatically learned by LSTM, one could convert longitudinal medical data to tabular data and then build machine learning models on the tabular data. But, if the automatically learned features have no easy-to-understand meanings, we still cannot use this method to automatically explain the models prediction results.

1.3. Our contributions

To address the two hurdles, this paper makes two contributions, offering a roadmap for future research.

First, we outline a data-driven method for semi-automatically extracting predictive and clinically meaningful temporal features from medical data for predictive modeling. Using this method can reduce the effort needed to build useable predictive models for the current modeling task. Complementing expert-engineered features, the extracted features can be used to build machine learning, statistical, or rule-based predictive models, improve model accuracy [31] and generalizability, and identify data quality issues. In addition, as shown by Gupta et al. [32], many extracted features reflect general properties of the medical attributes involved in the features, and can be useful for other modeling tasks. Using the extracted features to form a temporal feature library to facilitate feature reuse, we can reduce the effort needed to build predictive models for other modeling tasks.

Second, we outline a method of using the extracted features to automatically explain machine learning prediction results and suggest tailored interventions. This can enable machine learning models to be used in clinical practice, and help transform health-care to be more proactive. At present, healthcare is often reactive. Existing clinical predictive models rarely use trend features [16]. When a health risk is identified, e.g., with existing models, it is often at a relatively late stage of persisting deterioration of health. At that point, resolving it tends to be difficult and costly, and the patient is at increased risk of a poor outcome. Our feature extraction method can find many temporal features reflecting trends. By using these features and our automatic explanation method to identify risky trends early, we can proactively apply preventive interventions to stop further deterioration of health. The automatically generated explanations can help us identify new interventions, warn clinicians of risky patterns, and reduce the time clinicians need to review patient records to find the reasons why a specific patient is at high risk for a poor outcome. The automatically suggested interventions can reduce the likelihood of missing suitable interventions for a patient. All of these factors can help improve outcomes and cut costs.

1.4. Organization of the paper

The rest of the paper is organized as follows. Section 2 reviews the current approach of using LSTM to build predictive models with medical data. Section 3 sketches our data-driven method for semi-automatically extracting predictive and clinically meaningful temporal features from medical data for predictive modeling. Section 4 outlines our method of using the extracted features to automatically explain machine learning prediction results and suggest tailored interventions. Section 5 discusses related work. We conclude in Section 6.

In this paper, we refer to both clinical and administrative data as medical data. We focus on predicting one outcome per data instance (e.g., per patient) rather than per data instance per time step (e.g., per patient per day). When a data instance has one outcome per time step, one way to extract temporal features is to focus on the outcome at the last time step of each data instance.

2. The current approach of using LSTM to build predictive models with medical data

In this section, we review the current standard approach of using LSTM to build predictive models with medical data. In Section 3, we present our temporal feature extraction method based on this approach. Variations of this approach are used in many LSTM-based clinical predictive modeling papers [22–25,33–46]. With proper modifications, our temporal feature extraction method also applies to these variations.

A deep neural network is a neural network with many layers of computation. Ching et al. [47–50] reviewed existing work using deep neural networks on medical data. Deep neural networks have several types, such as recurrent neural network (RNN), convolutional neural network, and deep feedforward neural network. Among them, RNN handles irregularly sampled longitudinal medical data of varying lengths the most naturally. LSTM [20,21] is a specific kind of RNN that uses a gating mechanism to better model long-range dependencies. Much work has been done using LSTM to build predictive models with medical data [22–25,33–46]. Other kinds of RNN like gated recurrent unit have also been used for this purpose [32,51–63]. In this paper, we focus on LSTM having memory cells, from which we extract temporal features.

LSTM processes a sequence of input vectors from the same data instance, one input vector at a time. Each input vector $\stackrel{\rightharpoonup }{x_t}$ is indexed by a time step t. After processing the entire sequence, LSTM obtains results that are used to predict the data instance’s outcome. Often, each data instance refers to a distinct patient. Each input vector includes one patient visit’s information, such as diagnoses and vital signs. The sequence length can vary across data instances. This helps boost model accuracy, as LSTM can use as much of the information of each patient as possible, without having to drop information to make each patient s history be of the same length. This also allows us to make predictions on new patients in a timely manner, without having to wait until each patient accumulates a certain length of history. With a single patient visit’s information available, LSTM can already start to make predictions on the patient.

As shown in Fig. 1, an LSTM network contains a sequence of units, one per time step. In Fig. 1, each rounded rectangle denotes a unit. ⊕ is the element-wise sum. ⊗ is the element-wise multiplication. A unit has a memory cell c_t, a hidden state h_t, an input gate i_t, an output gate o_t, and a forget gate f_t. The memory cell keeps long-term memory and stores summary information from all previous inputs. It is known that LSTM can maintain memory over 1000 time steps [20]. The input gate regulates the input flowing into the memory cell. The forget gate adjusts the forgetting of the memory cell. The output gate controls the output flowing from the memory cell.

Fig. 1.

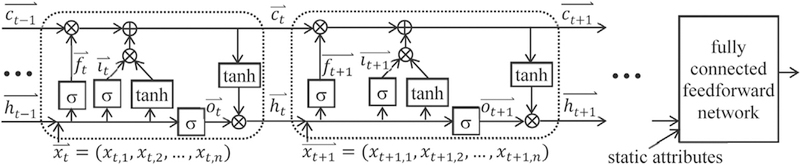
An LSTM network.

For a sequence with m time steps, LSTM works based on the following formulas:

$$\stackrel{\rightharpoonup }{f_t}=\sigma \left(W_f\stackrel{\rightharpoonup }{x_t}+U_f\stackrel{\rightharpoonup }{h_{t-1}}+\stackrel{\rightharpoonup }{b_f}\right)\text{(forget gate)}$$

$$\stackrel{\rightharpoonup }{i_t}=\sigma \left(W_i\stackrel{\rightharpoonup }{x_t}+U_i\stackrel{\rightharpoonup }{h_{t-1}}+\stackrel{\rightharpoonup }{b_i}\right)\text{(input gate)}$$

$$\stackrel{\rightharpoonup }{o_t}=\sigma \left(W_o\stackrel{\rightharpoonup }{x_t}+U_o\stackrel{\rightharpoonup }{h_{t-1}}+\stackrel{\rightharpoonup }{b_o}\right)\text{(output gate)}$$

$$\stackrel{\rightharpoonup }{c_t}=\stackrel{\rightharpoonup }{f_t}\otimes \stackrel{\rightharpoonup }{c_{t-1}}+\stackrel{\rightharpoonup }{i_t}\otimes \mathit{tanh}\left(W_c\stackrel{\rightharpoonup }{x_t}+U_c\stackrel{\rightharpoonup }{h_{t-1}}+\stackrel{\rightharpoonup }{b_c}\right)\text{(memory cell)}$$

$$\stackrel{\rightharpoonup }{h_t}=\stackrel{\rightharpoonup }{o_t}\otimes \mathit{tanh}\left(\stackrel{\rightharpoonup }{c_t}\right)\text{(hidden state)}$$

Here, σ and tanh are the element-wise sigmoid and hyperbolic tangent functions, respectively. $\stackrel{\rightharpoonup }{x_t}=\left(x_{t,1},x_{t,2},\dots ,x_{t,n}\right)$ is the input vector at time step t (1 ≤ t ≤ m). Each $\stackrel{\rightharpoonup }{x_t}$ has the same dimensionality n. $\stackrel{\rightharpoonup }{f_t},$ $\stackrel{\rightharpoonup }{i_t},$ and $\stackrel{\rightharpoonup }{o_t}$ are the forget, input, and output gates’ activation vectors, respectively. $\stackrel{\rightharpoonup }{c_t}$ is the memory cell vector. $\stackrel{\rightharpoonup }{h_t}$ is the hidden state vector. $\stackrel{\rightharpoonup }{b_f},$ $\stackrel{\rightharpoonup }{b_i},$ $\stackrel{\rightharpoonup }{b_{\mathrm{o}}}$ and $\stackrel{\rightharpoonup }{b_c}$ are bias vectors. All vectors except for $\stackrel{\rightharpoonup }{x_t}$ have the same dimensionality. W_f, W_i, W_o, and W_c are the input vector weight matrices. U_f, U_i, U_o, and U_c are the hidden state vector weight matrices. The hidden state vector $\stackrel{\rightharpoonup }{h_m}$ in the last time step summarizes the whole sequence. Along with the sequence, the data instance often contains some static attributes, such as gender and race. We concatenate $\stackrel{\rightharpoonup }{h_m}$ with the static attributes, if any, into a vector. We input the vector to a fully connected feedforward network and compute the data instance’s predicted outcome [26].

The input vector $\stackrel{\rightharpoonup }{x_t}=\left(x_{t,1},x_{t,2},\dots ,x_{t,n}\right)$ contains information of all longitudinal attributes at time step t. We can make $x_{t,i}(1\le i\le n)$ the i-th longitudinal attribute’s value at t. Alternatively, we can embed each categorical attribute value, such as diagnosis or procedure code, into a vector representation and merge all embedded vectors at t into $\stackrel{\rightharpoonup }{x_t}$ [22]. In this case, each embedded x_t,i becomes difficult to interpret.

In LSTM, each element of the memory cell vector $\stackrel{\rightharpoonup }{c_t}$ depicts some learned temporal feature(s). Karpathy et al. [28] showed that only ~10% of these elements could be interpreted [29]. Our goal is to modify LSTM so that it can be used to extract predictive and clinically meaningful temporal features from medical data for predictive modeling.

3. Semi-automatically extracting predictive and clinically meaningful temporal features from medical data

In this section, we sketch our data-driven method for semi-automatically extracting predictive and clinically meaningful temporal features from medical data for predictive modeling. Our method is semi-automatic because its last step requires a human to extract features via visualization. Since temporal feature is one form of phenotype, our method belongs to computational pheno-typing [64–66]. Our method has a different focus than most existing phenotyping algorithms, which use medical data to detect whether a patient has a specific disease.

The standard LSTM imposes no limit on how many input vector elements can link to each memory cell vector element. All input vector elements could be used in each element of the forget and input gates’ activation vectors, and subsequently link to each memory cell vector element. As a result, even if each input vector element links to a distinct longitudinal attribute, no limit is placed on the number of attributes used in each learned temporal feature. A feature involving many attributes is difficult to understand. Our key idea for semi-automatically extracting temporal features from medical data is to restrict the number of longitudinal attributes linking to each memory cell vector element. In this way, more memory cell vector elements will represent clinically meaningful temporal features. The learned features are likely to be predictive, as LSTM frequently produces more accurate clinical predictive models than other machine learning algorithms [22–25].

The rest of Section 3 is organized as follows. Section 3.1 describes how to modify LSTM to limit the number of longitudinal attributes linking to each memory cell vector element. Section 3.2 shows how to visualize the memory cell vector elements in our trained LSTM network to extract predictive and clinically meaningful temporal features. Section 3.3 mentions several ways of using the extracted features and lists our feature extraction method’s advantages. Section 3.4 sketches a method for efficiently automating LSTM model selection. Section 3.5 provides some additional details.

3.1. Multi-component LSTM

To limit the number of longitudinal attributes linking to each memory cell vector element, we use a new type of LSTM termed multi-component LSTM (MCLSTM).

3.1.1. Overview

As shown in Fig. 2, an MCLSTM network contains multiple component LSTM networks. In a given component network and at any time step, each input vector element links to a distinct longitudinal attribute. Each component network uses only a subset of the longitudinal attributes rather than all of them. This is similar to the case of multimodal LSTM [26,27]. Yet, MCLSTM differs from multimodal LSTM in several ways. In multimodal LSTM, all longitudinal attributes are partitioned into a small number of sets, one per modality, based on existing knowledge of the modalities. A set can possibly contain many attributes. Each longitudinal attribute appears in exactly one of the sets. The multimodal LSTM model is trained after attribute partitioning is finalized. In comparison, in MCLSTM, we preselect an integer K that is not necessarily small. All longitudinal attributes are partitioned into K sets, one per component, in a data-driven way when the MCLSTM model is trained. Each set tends to contain one or a few attributes. The same attribute could appear in more than one set. Also, some longitudinal attributes may appear in none of the sets.

Fig. 2.

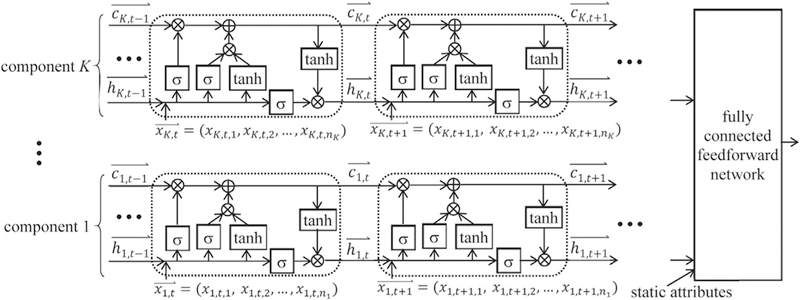
A multi-component LSTM network with K components.

In Fig. 2, n_q denotes the number of longitudinal attributes used in the q-th (1 ≤ q ≤ K) component network. For each element x_q,t,j (1 ≤ j ≤ n_i) of the input vector $\stackrel{\rightharpoonup }{x_{q,t}}$ at time step t, the first, second, and third subscripts indicate the component number, time step, and element number in the component, respectively. For both the memory cell vector $\stackrel{\rightharpoonup }{c_{q,t}}$ and the hidden state vector $\stackrel{\rightharpoonup }{h_{q,t}}$, the first and second subscripts indicate the component number and time step, respectively.

Consider a data instance containing a sequence with m time steps and perhaps some static attributes. The MCLSTM network includes K component networks. We concatenate all K hidden state vectors $\stackrel{\rightharpoonup }{h_{q,m}}$ (1 ≤ q ≤ K) at the last time step, one from each component network, and the static attributes, if any, into a vector $\stackrel{\rightharpoonup }{h_m}$ [26]. We input $\stackrel{\rightharpoonup }{h_m}$ to a fully connected feedforward network to compute the data instance’s predicted outcome.

In MCLSTM, by controlling the number of longitudinal attributes used in each component network, we limit the number of attributes linking to each memory cell vector element, and subsequently the number of attributes involved in each learned temporal feature. This offers several advantages. First, a larger portion of learned features will be understandable and clinically meaningful. Clinicians are more willing to use these features than those they do not understand. Second, the learned features become more generalizable and less likely to overfit the training data’s peculiarities. This helps improve the accuracy of predictive models built using these features [67]. Third, MCLSTM naturally has feature selection capability. Often, some longitudinal attributes appear in none of the component networks, and are regarded as having no predictive power. Only the other longitudinal attributes appearing in the MCLSTM network are deemed relevant and need to be collected for the modeling task. This reduces the number of attributes involved in the predictive model built using the learned features. Such a model is more likely to be used by other healthcare systems beyond the one that originally developed the model, as differing healthcare systems collect overlapping but different attributes.

3.1.2. Setting the network configuration hyper-parameters

Before training an MCLSTM network, we need to set a few hyper-parameters for its configuration. First, we need to select K, the number of component networks in it. Second, for each component network, we need to choose its memory cell vector dimensionality. Recall that except for the input vector, all vectors used in an LSTM unit have the same dimensionality. The memory cell vector is one of them.

We set the network configuration hyper-parameters based on two considerations. First, which component network uses which longitudinal attributes is generally determined in a data-driven way when the MCLSTM network is trained. Ideally, when training is completed, we want to achieve the effect that each component network uses one or a few attributes. That is, every n_q (1 ≤ q ≤ K) is small. Each memory cell vector element of the component network represents some temporal feature(s) involving no more than these attributes. Such a feature is more likely to be understood and clinically meaningful than one involving many attributes. When the medical data set contains lots of longitudinal attributes, many of them could be useful for the modeling task. In this case, we use a large K to allow the useful attributes to appear in the MCLSTM network. Otherwise, when the medical data set contains only a few longitudinal attributes, we use a small K.

Second, for the one or a few longitudinal attributes used in a component network, intuitively no more than a few temporal features using these attributes would be clinically meaningful, predictive, and non-redundant for the modeling task. Hence, the memory cell vectors $\stackrel{\rightharpoonup }{C_{q,t}}$ (1 ≤ q ≤ K) used in each component network should have a low dimensionality. We can use the same low dimensionality for the memory cell vectors in each component network. Alternatively, we can partition all K component networks into multiple groups, and choose a different low dimensionality for the memory cell vectors in each group.

The optimal hyper-parameter values vary by the modeling task and data set. Finding the optimal hyper-parameter values belongs to machine learning model selection, for which much work has been done [68]. We conduct this search by maximizing the MCLSTM network’s prediction accuracy.

3.1.3. Exclusive group Lasso regularization

After setting the network configuration hyper-parameters, the MCLSTM network’s configuration is only partly in place. To complete it, we need to figure out which component network uses which longitudinal attributes. We do this in a data-driven way when the MCLSTM network is trained.

The MCLSTM network contains K component networks. We have n longitudinal attributes. Initially, not knowing which component network will use which attributes, we give all n attributes to each component network. At time step t, all component networks receive the same input vector $\stackrel{\rightharpoonup }{x_t}$ = (x_t,1, x_t,2,…,x_t,n), with x_t,i (1 ≤ i ≤ n) being the i-th longitudinal attribute’s value.

We want the data to tell us which component network should use which longitudinal attributes. The i-th (1 ≤ i ≤ n) longitudinal attribute links to the i-th column of each input vector weight matrix in every component network. An attribute is unused by a component network if and only if all columns of the input vector weight matrices in the component network linking to the attribute are all zeros. After the MCLSTM network is trained, we want to achieve the effect that each component network uses only one or a few attributes. That is, most columns of the input vector weight matrices in the component network are all zeros. Lasso (least absolute shrinkage and selection operator) regularization is widely used to make most weights in a machine learning model zero. Existing Lasso regularization methods cannot achieve our desired effect, as the weights used in the MCLSTM network have a special structure [67]. We design a new Lasso regularization method tailored to this structure to serve our purpose.

Our regularization method performs one type of structured regularization. It is related to, but different from multimodal group regularization, the type of structured regularization conducted in Lenz et al. [67]. Our regularization method is designed for MCLSTM to handle longitudinal data. The goal is to limit the number of longitudinal attributes used in each component network. In comparison, the multimodal group regularization method was developed for a deep feedforward neural network handling static data. There, all attributes are partitioned into a small number of groups, one per modality, based on existing knowledge of the modalities. The goal is to limit the number of modalities that each neuron on the first layer of the network links to. Lenz et al. [67] showed that standard L₁ regularization cannot achieve this goal without degrading the quality of the features learned by the neurons on the first layer. Using multimodal group regularization improved both feature quality and model accuracy.

3.1.3.1. Notations.

Before describing our regularization method’s technical details, we first introduce a few notations. Consider the q-th (1 ≤ q ≤ K) component network. It works based on the following formulas at time step t:

$$\stackrel{\rightharpoonup }{f_{q,t}}=\sigma \left(W_{f,q}\stackrel{\rightharpoonup }{x_t}+U_{f,q}\stackrel{\rightharpoonup }{h_{q,t-1}}+\stackrel{\rightharpoonup }{b_{f,q}}\right)\text{(forget gate)}$$

$$\stackrel{\rightharpoonup }{i_{q,t}}=\sigma \left(W_{i,q}\stackrel{\rightharpoonup }{x_t}+U_{i,q}\stackrel{\rightharpoonup }{h_{q,t-1}}+\stackrel{\rightharpoonup }{b_{i,q}}\right)\text{(input gate)}$$

$$\stackrel{\rightharpoonup }{o_{q,t}}=\sigma \left(W_{o,q}\stackrel{\rightharpoonup }{x_t}+U_{o,q}\stackrel{\rightharpoonup }{h_{q,t-1}}+\stackrel{\rightharpoonup }{b_{o,q}}\right)\text{(output gate)}$$

$$\stackrel{\rightharpoonup }{c_{q,t}}=\stackrel{\rightharpoonup }{f_{q,t}}\otimes \stackrel{\rightharpoonup }{c_{q,t-1}}+\stackrel{\rightharpoonup }{i_{q,t}}\otimes \mathit{tanh}\left(W_{c,q}\stackrel{\rightharpoonup }{x_t}+U_{c,q}\stackrel{\rightharpoonup }{h_{q,t-1}}+\stackrel{\rightharpoonup }{b_{c,q}}\right)\text{(memory cell)}$$

$$\stackrel{\rightharpoonup }{h_{q,t}}=\stackrel{\rightharpoonup }{o_{q,t}}\otimes \mathit{tanh}\left(\stackrel{\rightharpoonup }{c_{q,t}}\right)\text{(hidden state)}$$

Compared to those listed in Section 2, each vector except for the input vector and each weight matrix have an added subscript: q. Let d_q denote the q-th component network’s memory cell vector dimensionality. W_f,q, W_i,q, W_o,q, and W_c,q are the d_q × n input vector weight matrices for the forget gate, input gate, output gate, and memory cell, respectively. W_f,q,s,r, W_i,q,s,r, W_o,q,s,r, and W_c,q,s,r denote the element in the s-th (1 ≤ s ≤ d_q) row and r-th (1 ≤ r ≤ n) column of W_f,q, W_i,q, W_o,q, and W_c,q, respectively. U_f,q, U_i,q, U_o,q, and U_c,q are the d_q × d_q hidden state vector weight matrices for the forget gate, input gate, output gate, and memory cell, respectively. U_f,q,s,r, U_i,q,s,r, U_o,q,s,r, and U_c,_q,_s,_r denote the element in the s-th (1 ≤ s ≤ d_q) row and r-th (1 ≤ r ≤ d_q) column of U_f,q, U_i,q, U_o,q, and U_c,q, respectively.

3.1.4. Basic method

To obtain the desired effect that each component network uses only one or a few longitudinal attributes, our regularization method needs to achieve two goals simultaneously. First, in a component network, the n longitudinal attributes compete with each other. If one attribute is used, the other attributes are less likely to be used. In other words, if an input vector weight matrix element linking to an attribute is non-zero, the regularizer tends to assign zeros to the input vector weight matrix elements linking to the other attributes. Second, in a component network, all input vector weight matrix elements linking to the same attribute tend to be zero (or non-zero) concurrently. Non-zero means the component network uses this attribute.

We borrow ideas from exclusive Lasso [69,70] and group Lasso [71] to reach these two goals. Consider a set of weights w_i,j (1 ≤ i ≤ G, 1 ≤ j ≤ g_i) partitioned into G groups. The i-th group has g_i weights. Exclusive Lasso [69,70] uses the regularizer $\sum _{i=1}^G{(\sum _{j=1}^{g_i}\left|w_{i,j}\right|)}^2$ to make the weights in the same group compete with each other. If one weight in a group is non-zero, the regularizer tends to assign zeros to the other weights in the same group. This can be used to reach our first goal. In comparison, group Lasso [71] uses the regularizer $\sum _{i=1}^G\sqrt{\sum _{j=1}^{g_i}{w}_{i,j}^2}$ to make all weights in the same group tend to be zero (or non-zero) concurrently. This can be used to reach our second goal.

Our regularization method combines exclusive Lasso and group Lasso, and is thus called exclusive group Lasso. In the q-th (1 ≤ q ≤ K) component network, the input vector weight matrix elements linking to the r-th (1 ≤ r ≤ n) longitudinal attribute are W_f,q,s,r, W_i,q,s,r, W_o,q,s,r, and W_c,q,s,r for each s between 1 and d_q. We treat these elements as a group, and use their L₂ norm $R_{q,r}=\sqrt{\sum _{s=1}^{d_q}\left(W_{f,q,s,r}^2+W_{i,q,s,r}^2+W_{o,q,s,r}^2+W_{c,q,s,r}^2\right)}$ to make them tend to be zero (or non-zero) concurrently. If R_q,r = 0, all of them are zero. For each q (1 ≤ q ≤ K), the L₂ norms linking to the n longitudinal attributes are R_q,r for every r between 1 and n. We treat these L₂ norms as a group, and use the regularizer $R_W=\sum _{q=1}^K{[\sum _{r=1}^n{R}_{q,r}]}^2$ to make them compete with each other for being non-zero. Putting everything together, we use the exclusive group Lasso regularizer

$$R_W=\sum _{q=1}^K{\left[\sum _{r=1}^n\sqrt{\sum _{s=1}^{d_q}\left(W_{f,q,s,r}^2+W_{i,q,s,r}^2+W_{o,q,s,r}^2+W_{c,q,s,r}^2\right)}\right]}^2$$

to reach our two goals simultaneously. R_W is a convex function of all input vector weight matrix elements.

For the hidden state vector weight matrices U_{f q}, U_i,q, U_o,q, and U_c,q, we do not need to make most of their elements zero. Instead, we use the L₂ regularizer

$$R_U=\sum _{q=1}^K\sum _{r=1}^{d_q}\sum _{s=1}^{d_q}\left(U_{f,q,s,r}^2+U_{i,q,s,r}^2+U_{\mathrm{o},q,s,r}^2+U_{c,q,s,r}^2\right)$$

for their elements U_f,q,s,r, U_i,q,s,r, U_o,q,s,r, and U_c,q,s,r. Let L denote the loss function measuring the discrepancy between the predicted and actual outcomes of the data instances. R_f denotes the L₂ regularizer for the weights in the fully connected feedforward network used at the end of the MCLSTM network. To train the MCLSTM network, we use a standard subgradient optimization algorithm to minimize the overall loss function L_o = L+λ₁R_W+λ₂R_U+λ₃R_f [3]. λ₁, λ₂, λ₃ are the parameters controlling the importance of the regularizers R_W, R_U, and R_f, respectively.

3.1.5. Extension of the basic method

Sometimes, based on medical intuition, we know which longitudinal attribute by itself or which several longitudinal attributes combined are likely to form predictive and clinically meaningful temporal features, even if we do not know the exact features. In this case, before training the MCLSTM network, for each subset of longitudinal attributes with this property, we specify a separate component network to receive in its input vectors the values of the attributes in this subset rather than all attributes’ values. This can ease model training and help make more learned features represented by the memory cell vector elements clinically meaningful. This also expedites model training by reducing the number of weights that need to be handled.

By default, all component networks in an MCLSTM network use the same set of time steps. Sometimes, all longitudinal attributes fall into several groups, each collected at a distinct frequency. For instance, one group of longitudinal attributes like diagnosis codes is collected per patient visit. Another group of longitudinal attributes, such as air quality measurements and vital signs that a patient self-monitors at home, is collected every day. In this case, for each group of longitudinal attributes, we can specify a different subset of component networks, whose input vectors include only these attributes’ values. Each subset uses a distinct set of time steps based on the frequency at which the corresponding group of longitudinal attributes is collected.

Sometimes, based on medical knowledge or our prior experience with other modeling tasks, we know some temporal features that are clinically meaningful, formed by some of the longitudinal attributes, and likely to be predictive for the current modeling task. In this case, we compute these features, treat them as static attributes used near the end of the MCLSTM network, and can opt to not use the raw longitudinal attributes involved in them when training the network. This can ease model training and help the network form predictive and clinically meaningful temporal features from the other longitudinal attributes.

Section 3.2 outlines our method of visualizing the memory cell vector elements in a trained MCLSTM network to extract predictive and clinically meaningful temporal features. To increase the number of such extracted features, we can iteratively train the MCLSTM network and extract features in multiple rounds. After extracting some features via visualization in one round, we reduce the number of component networks in the MCLSTM network, compute these features, add them to the list of static attributes used near the end of the MCLSTM network, and no longer use the raw longitudinal attributes involved in them when training the MCLSTM network in the next round. This helps the MCLSTM network form predictive and clinically meaningful temporal features from the remaining longitudinal attributes.

Often, the input vector at each time step includes an element showing the elapsed time between the current and previous time steps [33,35,46,51]. For the first time step, the elapsed time is zero. Sometimes, a log transformation is applied to the elapsed time to reduce its skewed distribution [52]. The elapsed time attribute has a different property from the other longitudinal attributes. Intuitively, any other longitudinal attribute tends to be used by one or a few component networks in the MCLSTM network to form temporal features. In comparison, many component networks could use the elapsed time attribute to form temporal features. To reflect this difference, we use the L₂ regularizer rather than the exclusive group Lasso regularizer for the input vector weight matrix elements linking to the elapsed time attribute in each component network.

The above discussion focuses on LSTM with one recurrent layer. Our method also applies to stacked LSTM with multiple recurrent hidden layers stacked on top of each other [72]. Having multiple recurrent hidden layers often helps an RNN learn better features [51]. Fig. 3 illustrates a multi-component stacked LSTM network. It has multiple component networks, each of which is a stacked LSTM network using a subset of longitudinal attributes. In each component network and at each recurrent layer above the first, the input vector at time step t incorporates the hidden state vector elements outputted by the layer below at t. If nothing else is included in the input vector, we use the same method mentioned above to figure out which component network uses which longitudinal attributes. Otherwise, if the input vector at each recurrent layer above the first one at t also includes the input vector elements at the first layer at t, we first use an MCLSTM network with one recurrent layer and the method mentioned above to figure out which component network uses which longitudinal attributes. Then we use this information to form the multi-component stacked LSTM network and train it. In this way, we ensure that in each component network, every recurrent layer links to the same subset of longitudinal attributes.

Fig. 3.

A multi-component stacked LSTM network with K components and two recurrent layers.

In Fig. 3, n_q denotes the number of longitudinal attributes used in the q-th (1 ≤ q ≤ K) component network. For each element x_q,t,j (1 ≤ j ≤ n_i) of the input vector $\stackrel{\rightharpoonup }{x_{q,t}},$ the first, second, and third subscripts indicate the component number, time step, and element number in the component, respectively. For both the memory cell vector $\stackrel{\rightharpoonup }{c_{q,l,t}}$ and the hidden state vector $h_{q,l,t}$, the first, second, and third subscripts indicate the component number, layer number, and time step, respectively.

3.2. Visualizing the memory cell vector elements in a trained MCLSTM network to extract predictive and clinically meaningful temporal features

In LSTM, each memory cell vector element depicts some learned temporal feature(s). After using the training instances to train the MCLSTM network, we visualize its memory cell vector elements to extract clinically meaningful temporal features. These features are likely to be predictive, as LSTM frequently produces more accurate clinical predictive models than other machine learning algorithms [22–25].

We design the visualization method based on three observations. First, LSTM has been shown to use high positive and low negative values of its memory cell vector elements to express information [73]. Second, Kale et al. [31,74–76] showed one can use training instances with the highest activations of a neuron in a deep neural network to identify clinically meaningful features. A memory cell vector element is a neuron. Third, intuitively, an informative sequence of input vectors in a training instance contains one or more segments, each depicting a temporal feature.

Taking these observations as insights, we proceed in four steps to extract zero or more clinically meaningful temporal features from each memory cell vector element at the last time step of the MCLSTM network. In Step 1, we find the top and bottom few training instances with the highest positive and lowest negative values in the memory cell vector element, respectively. These training instances are likely to contain information of useful temporal features. In Step 2, we identify one or more so-called effective segments of the input vector sequence in each of these training instances. Each effective segment tends to reflect a useful temporal feature. In Step 3, we partition all identified effective segments into several clusters. In Step 4, we visualize each cluster of effective segments in a separate figure to extract zero or more clinically meaningful temporal features. By reducing the number of effective segments in each figure and making the effective segments in the same figure more homogeneous, clustering eases visualization and temporal feature extraction. The temporal features extracted from the MCLSTM network include all features extracted from every memory cell vector element at the last time step of the MCLSTM network.

In the rest of Section 3.2, we describe each of the four steps one by one. Our description focuses on a single memory cell vector element at the last time step of the MCLSTM network. For this element, we find the corresponding component network and the longitudinal attributes used in it. Each temporal feature depicted by this element involves no more than these attributes. When mentioning an input vector, we always refer to an input vector of the component network containing only the values of these attributes. The component network usually uses one or a few longitudinal attributes. This is crucial for making our visualization method effective in identifying features describing temporal relationships [77]. Psychology studies have shown that humans can correctly analyze the relationship among up to four attributes [78]. The more complex the relationship among the attributes, the lower the upper limit on the number of attributes [79].

3.2.1. Step 1: finding the top and bottom few training instances with the highest positive and lowest negative values in the memory cell vector element, respectively

We preselect a number N as the maximum number of top/bottom training instances that will be obtained for each memory cell vector element at the last time step of the MCLSTM network. In Step 4, we conduct visualization to extract clinically meaningful temporal features. To avoid cluttering any given figure and creating difficulty with visualization, N should not be too large. To obtain enough signal for identifying clinically meaningful temporal features, N should not be too small. One possible good value of N is 50, as adopted in Che et al. [75].

Consider the given memory cell vector element at the last time step of the MCLSTM network. Let n₊ denote the number of training instances with positive values in the element. n₋ denotes the number of training instances with negative values in the element. We sort all training instances in descending order of the element’s value. Multiple training instances with the same value in the element can be put in any order. We find the top N₊ = min (N, n₊) training instances with the highest positive values in the element [75], and record the lowest one ${\tau }_{+}$ of these values. In addition, we find the bottom N₋ = min (N, n₋) training instances with the lowest negative values in the element [75], and record the highest one ${\tau }_{-}$ of these values. In Step 2, we will use ${\tau }_{+}$ and ${\tau }_{-}$ to identify the effective segments of the input vector sequences in the top N₊ and bottom N₋ training instances, respectively.

Intuitively, the top N₊ training instances include one set of temporal features. The bottom N₋ training instances include another set of temporal features. In Step 4, we will visualize the effective segments of the input vector sequences in the top N₊ and bottom N_- training instances to identify clinically meaningful features in the first and second sets, respectively.

Previously, for image data, researchers have used the activation maximization method to explain the meaning of each neuron in a deep neural network [80]. For each neuron in the network, that method creates a synthetic data instance maximizing the neuron’s output, and uses the data instance to explain the neuron’s meaning. That method does not serve our purpose of extracting temporal features from longitudinal data. For instance, consider a sequence of results of a specific lab test obtained over time. Suppose the actual temporal feature depicted by the memory cell vector element is whether the lab test result is above a fixed threshold value ≥40% of the time. The synthetic data instance maximizing the element’s value is a sequence of lab test results all above the threshold value. From this data instance, we cannot deduce the feature’s property of being ≥40% of the time. In comparison, training instances are real and usually do not push the element to have extreme values. After viewing multiple training instances satisfying this property in various ways, such as one being 40% of the time and another being 50% of the time, we are more likely to identify this property.

3.2.2. Step 2: identifying one or more effective segments of the input vector sequence in each training instance found in Step 1

Consider the given memory cell vector element at the last time step of the MCLSTM network and a training instance found in Step1. The training instance has a sequence of input vectors containing the information of some useful temporal features. Often, the sequence has one or more uninformative segments, which are unrelated to these features and do not contribute to making the element’s value high positive or low negative. Displaying these segments during visualization will clutter the figure and make it harder to identify these features. To address this issue, for each training instance found in Step 1, we identify one or more effective segments of its input vector sequence. Each effective segment tends to reflect a useful temporal feature. During visualization in Step 4, we display only the effective segments rather than the whole input vector sequence.

In the following, we show how to identify the effective segments for a top training instance found in Step 1. The case with identifying the effective segments for a bottom training instance found in Step 1 can be handled similarly.

Recall that in Step 1, we find the top N₊ training instances with the highest positive values in the memory cell vector element at the last time step of the component network, and record the lowest one ${\tau }_{+}$ of these values. As shown in Fig. 4, for each top training instance, the element’s value evolves over time and becomes $\ge {\tau }_{+}$ at the last time step of the training instance’s input vector sequence. ${\tau }_{+}$ can be regarded as a threshold value found in a data-driven way. When the element’s value becomes $\ge {\tau }_{+}$ at a specific time step, it indicates with high likelihood that a useful temporal feature appears there. We use this information to find the effective segment at or around the time step. In Fig. 4, each dashed ellipse denotes an effective segment. The horizontal dotted line depicts ${\tau }_{+}.$

Fig. 4.

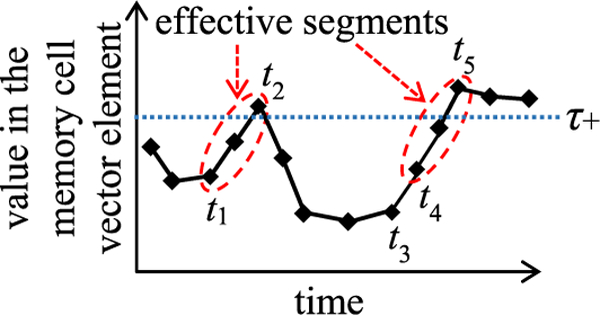
Identifying the effective segments of the input vector sequence in a top training instance.

Consider a given top training instance found in Step 1. We define a segment of its input vector sequence to be effective if the segment satisfies two properties simultaneously.

• 1)Property 1: If we input the segment into the component network, the memory cell vector element at the segment’s last time step will produce a value $\ge {\tau }_{+}.$ Typically, the segment and input vector sequence start at different time steps. If we input the segment vs. the input vector sequence into the component network, we get a different value in the memory cell vector element at the segment’s last time step.
• 2)Property 2: The segment is as short as possible. This eases identifying temporal features via visualization in Step 4. It is easier to recognize a temporal feature from a short segment than from a long segment.

Both properties combined make an effective segment the shortest segment that holds the signal of a useful temporal feature.

The top training instance’s input vector sequence contains one or more effective segments. Each segment is a section of the sequence between a starting time step t_start and an ending time step t_end. We use a sequential search algorithm to find the effective segments one by one. Our high-level idea is to start from the sequence’s last time step and keep going backwards. For each effective segment, we find first its ending and then its starting time step. Then we move on to pinpoint the next effective segment. To make our search algorithm easy to understand, we describe it using the case shown in Fig. 4 as an example.

We start from the last time step of the top training instance’s input vector sequence. Here, the memory cell vector element’s value is $\ge {\tau }_{+}.$ We go backwards, one time step at a time. If the element’s value increases, we go back one more time step. We keep going backwards until the element’s value will decrease if we go back one more time step. This is the first effective segment’s ending time step t_end, at which the element’s value reaches a local maximum $\ge {\tau }_{+}.$ In Fig. 4, t_end is t₅. To avoid violating Property 2, the section between t₅ and the last time step is excluded from the first effective segment. Then we continue to go backwards, one time step at a time. For each time step t that we reach, we check whether the segment between t and t_end satisfies Property 1. If so, this segment also satisfies Property 2 and is the first effective one, with t being its starting time step t_start. Otherwise, if this segment violates Property 1, we keep going backwards until we find a time step, at which Property 1 is satisfied. Such a time step must exist. In the worst case, we reach the first time step of the training instance’s input vector sequence. The segment between the first time step and t_end always satisfies Property 1. In Fig. 4, t_start is t₄. The segment between time steps t₃ and t₅ satisfies Property 1, but not Property 2, and thus is not an effective one.

After finding the first effective segment’s starting time step, we go back one time step to start searching for the second effective segment. In Fig. 4, this refers to starting from time step t₃. We keep going backwards until reaching a time step t’, at which the memory cell vector element’s value is $\ge {\tau }_{+}.$ In Fig. 4, this time step is t₂. If we keep going backwards and still cannot find t’ when reaching the first time step of the training instance’s input vector sequence, the second effective segment does not exist. Otherwise, if we can find t’, we repeat the procedure mentioned in the above paragraph to find first the ending and then the starting time step of the second effective segment. For the same reason explained in the above paragraph, these two time steps must exist. In Fig. 4, the second effective segment is the section between time steps t₁ and t₂. After finding the second effective segment, we move on to pinpoint the third effective segment, and so on. We keep iterating until reaching the first time step of the training instance’s input vector sequence. Our search process ends there.

3.2.3. Step 3: partitioning all identified effective segments into several clusters

Consider the given memory cell vector element at the last time step of the MCLSTM network. In Step 1, we find its top N₊ and bottom N₋ training instances. After identifying all effective segments in these training instances, we partition the segments into multiple clusters to ease visualization in Step 4.

We preselect a number k to set the number of clusters. There are two groups of effective segments, one obtained from the top N₊ training instances and the other from the bottom N₋ training instances. These two groups tend to reflect different temporal features. For either group, we partition the effective segments in it into k clusters, hoping each will reflect a distinct set of temporal features. The memory cell vector element usually depicts no more than a few temporal features. Accordingly, k should be a small number like three. For each group of effective segments, we can test different k values to see which one works the best.

Many clustering algorithms for time series data exist [81]. Each relies on a distance measure for temporal sequences. In the following, we describe our distance measure first, and then present the clustering algorithm used to partition effective segments into clusters.

3.2.3.1. Distance measure for temporal sequences.

We use the multivariate dynamic time warping distance measure, which Kale et al. [82] proposed as an extension of the dynamic time warping technique [83]. Dynamic time warping is widely used for measuring similarity between two temporal sequences, which can be multi-dimensional and have different lengths and sampling intervals. As shown in Fig. 5, dynamic time warping allows time shifting and matches similar shapes even in the presence of a time-phase difference. In Fig. 5, each dash-dotted line links two aligned points, one from each temporal sequence.

Fig. 5.

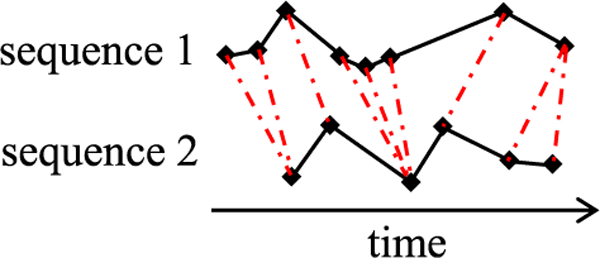
Time alignment of two sequences.

Consider two temporal sequences $Y=\left(\stackrel{\rightharpoonup }{y_1},\stackrel{\rightharpoonup }{y_2},\dots ,\stackrel{\rightharpoonup }{y_{m_1}}\right)\text{and}Z=\left(\stackrel{\rightharpoonup }{z_1},\stackrel{\rightharpoonup }{z_2},\dots ,\stackrel{\rightharpoonup }{z_{m_2}}\right).$ We use a distance measure $d\left(\stackrel{\rightharpoonup }{y_r},\stackrel{\rightharpoonup }{Z_s}\right),$ such as the Euclidean one, between each pair of elements $\stackrel{\rightharpoonup }{y_r}\left(1\le r\le m_1\right)$ and $\stackrel{\rightharpoonup }{Z_S}\left(1\le S\le m_2\right),$, one from each sequence. A warping path $p=\{(r_1,s_1),\left(r_2,s_2\right),\dots ,\left(r_{|p|},S_{|p|}\right)\}$ of length |p| aligns Y and Z via linking $\stackrel{\rightharpoonup }{y_{r_j}}\text{to}\stackrel{\rightharpoonup }{z_{s_j}}(1\le j\le |p|).$ It satisfies two conditions:

• (1)r₁ = s₁ = 1, r_|p| = m₁, and s_|p| = m₂. This condition makes Y’s first element align with Z’s first element, and Y’s last element align with Z’s last element.
• (2)For each j between 1 and $|p|-1,\left(r_{j+1}-r_j,s_{j+1}-s_j\right)$ is (0,1), (1, 0), or (1, 1). Consequently, $r_j\le r_{j+1}\text{and}{s}_j\le s_{j+1}.$ This condition makes each element of Y align with one element of Z, and vice versa. Also, only forward movements along Y and Z are allowed.

The total distance between Y and Z along p is the sum of the distance between each pair of elements aligned via p: $d_p\text{(}Y\text{,}Z)=\sum _{j=1}^{|p|}d\left(\stackrel{\rightharpoonup }{y_{r_j}},\stackrel{\rightharpoonup }{z_{s_j}}\right).$ The dynamic time warping distance between Y and Z is the minimum total distance across all possible warping paths P(Y, Z) between Y and Z: $DTW(Y,Z)=\underset{{}_{p\in P(Y,Z)}}{\min }{d}_p(Y,Z).$

Other things being equal, the dynamic time warping distance increases as temporal sequences become longer. To make the distance comparable across sequences of different lengths, Kale et al. [82] proposed using the multivariate dynamic time warping distance. This distance between sequences Y and Z is computed as their dynamic time warping distance divided by their optimal warping path’s length: MDTW (Y, Z) = DTW (Y, Z)/|p*| = d_p* (Y, Z)/|p*|. Here, |p*| is the length of $p^{*}=\underset{p\in P(Y,Z)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{d}}{d}_p(Y,Z).$

Dynamic time warping is designed for temporal sequences sampled at equidistant points in time [84]. Yet, this is often not the case with medical data. For medical data that violate this property, we can compute the multivariate dynamic time warping distance in one of several ways. One way is to ignore the equidistance constraint and do the computation as presented above. Another way is to use the weighting mechanism in Siirtola et al. [84] to prevent areas of high point density from dominating the distance computation. This mechanism gives smaller and larger weights to points with near and distant neighbors in the temporal sequence, respectively.

Differing longitudinal attributes’ values can be on different orders of magnitude. If this occurs, one attribute could dominate the distance computation for multi-dimensional temporal sequences. This is undesirable. To address this issue, before computing distances, we first normalize each attribute’s values so that the values of different attributes become comparable with each other. More specifically, for each attribute, we compute its mean and standard deviation across all of its values in all training instances. For each value of the attribute, we compute its normalized value by subtracting the mean and then dividing by the standard deviation. During visualization in Step 4, we show the original rather than normalized values to make the presented values easier to understand.

Our distance computation approach considers not only shape, but also amplitude that matters. For instance, for making predictions, a lab test result above its normal range often gives a different signal from one within its normal range. Thus, we do not use the value normalization approach that Paparrizos et al. [85] adopted for computing shape-based distances for temporal sequences. That approach ignores amplitude and computes one mean and one standard deviation per temporal sequence to normalize the values in it.

3.2.3.2. Clustering algorithm.

We use the k-medoids clustering algorithm [86] based on the multivariate dynamic time warping distance measure to partition each group of effective segments into k clusters. A medoid is a representative object of a cluster with the highest average similarity to all objects in the cluster. The k-medoids algorithm is inefficient for clustering many objects [86]. Yet, this is not an issue in our case. For the given memory cell vector element, we find a modest number of top and bottom training instances, and need to cluster only a moderate number of effective segments.

We do not use the k-means clustering algorithm that requires computing the average of multiple objects. For multiple effective segments of different lengths, it is difficult to compute their average properly. Besides the k-medoids algorithm, other clustering algorithms based on dynamic time warping also exist [87] and could be used for our clustering purpose.

3.2.4. Step 4: visualizing each cluster of effective segments in a separate figure to extract zero or more clinically meaningful temporal features

We visualize each cluster of effective segments obtained in Step 3 one by one. For each cluster, we show the effective segments in it in a figure to extract zero or more clinically meaningful temporal features. The figure includes one panel per longitudinal attribute used in the cluster. All panels are aligned by time and stacked on top of each other, as shown in Fig. 6, with each rounded rectangle denoting a panel.

Fig. 6.

Visualizing a cluster of three effective segments involving two longitudinal attributes.

Each panel shows the value sequence of its linked longitudinal attribute in every effective segment in the cluster. An effective segment has one value sequence per longitudinal attribute used in the cluster. If the cluster uses more than one attribute, for each effective segment, we use a dash-dotted polyline to link the first element of each of the segment’s attribute value sequences across all panels. In this way, one can easily know that these sequences belong to the same segment. Each effective segment comes from a training instance. To ease visualization, we use different colors to mark differing training instances in the figure.

Usually, a clinician and a data scientist collaborate to build a clinical predictive model. They view the figure to identify zero or more clinically meaningful temporal features. Each feature involves one or more longitudinal attributes used in the cluster, and is reflected by one or more attribute value sequences in the figure. It is easier to recognize the feature by viewing the sequences than to think of it on one’s own. For each identified feature, the clinician and the data scientist use their domain knowledge to jointly arrive at an exact mathematical definition of an extracted feature. Often, the extracted feature reflects the trend more precisely and performs better than the raw one learned by the MCLSTM network.

Marlin et al. [88] proposed identifying temporal patterns by grouping numeric physiologic time series into clusters. All time series start and end at the same time steps. For every cluster, a distinct panel shows each longitudinal attribute’s mean and standard deviation over time. That approach does not serve our purpose. In our case, each effective segment can start and end at different time steps. Non-numeric attributes like categorical ones can be part of temporal features and need to be shown along with numeric ones. Also, the same feature can appear at different time steps in differing effective segments. If we show each numeric attribute’s mean and standard deviation over time instead of individual effective segments, we are likely to miss such features.

Wanget al. [89] proposed identifying temporal patterns by visualizing multiple patients’ longitudinal medical data in the same figure. The figure includes one panel per patient. All panels are aligned by time and stacked on top of each other. Each panel shows multiple value sequences of a patient, one for each longitudinal attribute. For the same attribute, different patients’ value sequences appear in differing panels. This makes it harder to identify temporal patterns, particularly if the number of patients is not small [90]. In comparison, for the same attribute, our visualization approach puts multiple patients’ value sequences in the same panel.

3.2.4.1. Handling categorical attributes

A neural network takes only numeric inputs. To use LSTM, one converts each categorical longitudinal attribute into one or more numeric attributes using one hot encoding. During visualization, we show the original categorical attribute values instead of the converted numeric ones to make the presentation more succinct and easier to understand. The figure includes a panel for each categorical attribute linking to the cluster of effective segments. In the panel, each distinct value of the attribute appears on a separate row, as illustrated in Fig. 7.

Fig. 7.

Displaying a sequence of values of the visit type attribute.

3.2.4.2. Handling interval attributes

Medical data often include interval attributes, such as the medication use period and hospitalization period. A common way to use interval attributes in LSTM is to convert each interval into two attribute values: its starting time step and its duration. During visualization, we show the original interval instead of the converted attribute values to make the presentation easier to understand. Recall that if the cluster of effective segments uses more than one attribute, for each effective segment, we use a dash-dotted polyline to link the first element of each of the segment’s attribute value sequences across all panels. For each interval attribute used in the segment, the dash-dotted polyline links to the starting point of the first interval in the attribute’s value sequence. To ease visualization, we put the intervals from distinct data instances on different and adjacent horizontal lines, with one line per data instance, as illustrated in Fig. 8.

Fig. 8.

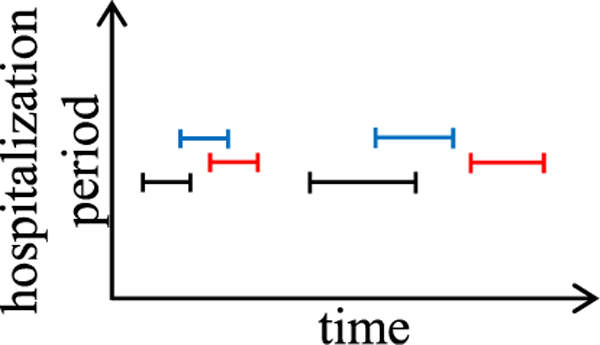
Displaying the interval sequences from three patients’ hospitalization period attribute.

3.2.4.3. Handling missing values

Neural network does not take any missing input value. To use LSTM, one needs to fill in every missing value first. One way to do this is as follows. Consider a value sequence of an attribute. If the value sequence is completely missing, we impute a clinically normal value defined by the clinician [23,31]. Otherwise, for each missing value before the first occurrence or after the last occurrence of a non-missing one, we fill in the missing value with the non-missing one [91]. For each missing value between two non-missing ones, we linearly interpolate them to fill in the missing value. Another way to handle missing values for an attribute is to use a binary indicator for whether a value of it is missing, compute the amount of time since its last observation, and decay its value over time toward its empirical mean value rather than use its last observed value [57,92].

During visualization, no filled-in value is shown. This makes the figure consistent with the raw data to help ensure genuine temporal features are identified.

3.2.4.4. Avoiding using an excessive number of longitudinal attributes

In LSTM, we sometimes embed each categorical attribute value into a vector representation to reduce the input vector dimensionality. This makes model training more efficient and effective [22]. In MCLSTM, no value embedding is used. Instead, each input vector element is a longitudinal attribute’s value. This is essential for making the identified temporal features easy to understand. To make model training efficient and effective, we need to avoid using an excessive number of longitudinal attributes. This requires handling two cases.

First, consider three longitudinal attributes: disease, procedure, and drug. Each attribute is categorical with many possible values. If no value embedding is used, by default the attribute is converted into many numeric attributes, one per possible value, using one hot encoding. This explodes the input vector dimensionality and is undesirable. To address this issue, we can proceed in one or more of the following ways:

• (1)We use grouper models like the Diagnostic Cost Groups (DCG) system to group diseases, procedures, and drugs and reduce the numbers of their possible values [93,94].
• (2)For each of the three attributes, we use a few of its most common values and ignore the others.
• (3)For each of the three attributes, we use a few values of it deemed most relevant to the modeling problem based on medical knowledge, and ignore the others.
• (4)Rajkomar et al. [22] provided a method using LSTM with value embedding and an attribution mechanism to rank categorical attribute values. For each of the three attributes, we use the top few values ranked by this method in MCLSTM and ignore the others.

Second, many lab tests exist. We will have an excessive number of longitudinal attributes, if we use one for each lab test’s values. This is undesirable. To address this issue, we can proceed in one or more of the following ways:

• (1)Pivovarov et al. [95] identified 70 common lab tests of interest to primary care and internal medicine. We use these lab tests and ignore the others.
• (2)We use a few lab tests deemed most relevant to the modeling problem based on medical knowledge, and ignore the others.
• (3)Rajkomar et al. [22] converted numeric attributes to categorical ones via discretization, and provided a method using LSTM with value embedding and an attribution mechanism to compute a weight for each categorical attribute value. For a categorical attribute with multiple possible values, we compute its weight as these values’ maximum weight reflecting its importance. We use the top few lab tests with the highest weights in MCLSTM and ignore the others. This is a form of feature selection for longitudinal attributes.

3.3. Several ways of using the extracted temporal features and our feature extraction method’s advantages

The extracted temporal features are clinically meaningful and tend to be predictive. We combine them with expert-engineered features to build machine learning, statistical, or rule-based predictive models. For machine learning models, this can improve model accuracy [31], as many extracted features reflect trends more precisely and can perform better than the raw ones learned by the MCLSTM network. Also, we can use the method described in Section 4 to automatically explain the models’ prediction results.

Wang et al. [89] showed properly visualizing temporal sequences in medical data could help us spot data quality issues, such as an impossible order of events. When visualizing each cluster of effective segments, we could identify some temporal features that make no sense and reflect the underlying data quality issues. By fixing these issues and enhancing data quality, we can boost model accuracy and improve other applications using the same data set.

Using our feature extraction method can reduce the effort needed to build useable predictive models for the current modeling task. Moreover, Gupta et al. [32] showed that many features an RNN learns from a medical data set reflect general properties of the medical attributes involved in the features, and can be useful for other modeling tasks. Using the features extracted by our method to form a temporal feature library to facilitate feature reuse, we can reduce the effort needed to build predictive models for other modeling tasks.

3.4. Efficiently automating MCLSTM model selection

Each machine learning algorithm has two types of parameters: normal parameters automatically tuned during model training, and hyper-parameters that must be set before model training. Before training a MCLSTM network, we need to set the values of multiple hyper-parameters, such as the number of component networks in it and the learning rate. These values can affect model accuracy greatly, e.g., by two or more times [96]. The optimal hyperparameter value combination is found via an iterative model selection process. In each iteration, we use a combination to train a model. Its accuracy is used to guide the selection of the combination that will be tested in the next iteration.

3.4.1. The need for and the state of the art of automatic machine learning model selection

Machine learning model selection, if done manually, is labor intensive and time-consuming. Frequently, several hundred to several thousand iterations are needed to find a good hyperparameter value combination [96,97]. On a data set of non-trivial size and particularly for deep neural network, testing a combination in one iteration often takes several hours or longer [98]. To cut the human labor needed for model selection, researchers have developed multiple automatic machine learning model selection methods [68]. For certain machine learning algorithms including deep neural network, some of these methods can find better hyper-parameter value combinations than manual search by human experts [68,99].

Recently, Google set up an automatic model selection service called Google Vizier [99]. It has become the de facto model selection engine within Google. Using it to conduct model selection, Google researchers [22] built clinical LSTM models that greatly improved prediction accuracy for three outcomes. The medical data set used there is of moderate size and has 216,221 data instances. As mentioned in the paper posted at https://arxiv.org/pdf/1801.07860v1.pdf, using Google Vizier to perform automatic model selection on the data set consumed >201,000 GPU (graphics processing unit) hours. This is beyond the computational resources available to many healthcare systems and would exceed their budgets quickly. When standard techniques are used, the time needed for automatic model selection usually increases superlinearly with the data set size. On a medical data set larger than the above one, using Google Vizier to perform automatic model selection would consume more computational resources and a higher cost, and quickly reach a point that almost no healthcare system could afford. In fact, this could even become a problem for Google, which has a lot of resources. To run its business, Google regularly needs to build predictive models on large data sets. As mentioned in the Google Vizier paper [99], using Google Vizier to perform automatic model selection on a large data set often takes months or years. As a result, for some mission critical applications, Google has to deploy a model without fully tuning it, and then keep tuning it over several years. Using suboptimal models leads to degraded outcomes. In our case, the situation could become even worse, if we iteratively train the MCLSTM network and extract features in multiple rounds, as each round requires automatic MCLSTM model selection.

3.4.2. Our prior work on efficiently automating machine learning model selection

To expedite automatic machine learning model selection, we recently developed a progressive sampling-based Bayesian optimization method for it. We showed that depending on the data set, our method can speed up the search process by one to two orders of magnitude [97,100,101 ]. Our idea is to conduct progressive sampling [102], filtering, and fine-tuning to quickly shrink the search space. We use a random sample of the data set termed the training sample to train models. We do fast trials on a small training sample to drop unpromising hyper-parameter value combinations early, keeping resources to fine-tune promising ones. We test multiple combinations. For each combination, we test it by training a model using it and the training sample. A combination is promising if the trained model reaches accuracy above an initial threshold. We then raise the threshold, expand the training sample, test and adjust combinations on it, and reduce the search space several times. In the last round, we use the full data set to find a good combination.

For several reasons described below, if we directly apply our progressive sampling-based Bayesian optimization method to automate MCLSTM model selection, we may not obtain the desired search efficiency and search result quality. Instead, for it to better automate MCLSTM model selection, we use four techniques to improve our method. The first technique is specific to deep neural network. The second technique is specific to LSTM. The third and fourth techniques apply to general machine learning algorithms.

3.4.3. Technique 1: performing early stopping when testing a hyperparameter value combination

To train a machine learning model, we often need to process each training instance multiple times. Our progressive sampling-based Bayesian optimization method is designed for the case that satisfies two conditions concurrently. First, it is fast to process a training instance once during model training. This ensures a hyper-parameter value combination can be tested on a small training sample quickly. Second, using a relatively small training sample, we can estimate a combination’s quality with reasonable accuracy. This reduces the likelihood that a high-quality combination is identified as unpromising and dropped at an early stage of the search process.

Neither condition is satisfied on deep neural network. When training a deep neural network, it often takes a non-trivial amount of time to process a training instance once. As a result, quite some time is needed to test a hyper-parameter value combination on even a small training sample. This degrades search efficiency. Moreover, deep neural network is data hungry. To reasonably estimate a combination’s quality for a deep neural network, a large training set is needed. If we start from using a small training sample to identify unpromising combinations, we are likely to drop many high-quality combinations erroneously in the first few rounds of the search process. This can degrade search result quality.

To address these issues, we adopt an early stopping technique for automating deep neural network model selection. Instead of starting from a small training sample, the search process starts from a relatively large training sample. A neural network is trained in epochs. As a model is trained for more epochs, its accuracy generally improves. In the first few rounds of the search process, when testing a hyper-parameter value combination, we train the model for a few rather than for the full number of epochs. In this way, without spending too much time on the test, we can estimate the combination’s quality with reasonable accuracy. This type of early stopping technique has been used previously for expediting automatic machine learning model selection [98,99], but not in combination with progressive sampling.

3.4.4. Technique 2: tuning the learning rate hyper-parameter before tuning the other hyper-parameters in depth

Greff et al. [103] showed that LSTM’s learning rate hyperparameter has a special property. For each data set, there is a large interval, in which the learning rate offers good model accuracy with little variation. The LSTM model can be trained relatively quickly when the learning rate is at the high end of the interval. When searching for a good learning rate, we can start from a high value like one and keep dividing it by ten until model accuracy no longer improves.

Based on this insight, we expedite automatic LSTM model selection by tuning the learning rate before tuning the other hyperparameters in detail. We proceed in four steps. In step one, we use a relatively large training sample to test a few random hyperparameter combinations, and select the one reaching the highest model accuracy. Intuitively, this combination would have reasonable and neither optimal nor terrible performance. In step two, for all hyper-parameters excluding the learning rate, we fix their values according to this combination and use the training sample to tune the learning rate. We start from a high learning rate like one and keep dividing it by ten until model accuracy no longer improves. In step three, we fix the learning rate at the value found in step two, and use our progressive sampling-based Bayesian optimization method to tune all of the other hyper-parameters. In step four, if desired, we perform some final fine-tuning of all hyperparameters simultaneously without significantly changing the value of any of them.

3.4.5. Technique 3: conducting stable Bayesian optimization

Machine learning model selection aims to find an optimal hyper-parameter value combination in the hyper-parameter space. As mentioned in Nguyen et al. [104], when the training or validation set is small, spurious peaks often appear on the performance surface defined over all possible combinations. These peaks are narrow and scattered randomly in low-performance regions. In this case, the search process of automatic machine learning model selection frequently stops at a spurious peak instead of a more stable one. The final model built there has suboptimal accuracy when deployed in the real world.

To prevent the search process from stopping at a spurious peak, Nguyen et al. [104] proposed a stable Bayesian optimization method for automating machine learning model selection.Bayesian optimization uses a regression model to predict a machine learning model’s accuracy based on the hyper-parameter value combination, and an acquisition function to select the combination to test in the next iteration. The regression model is usually a random forest [96] or a Gaussian process [104]. The former has been shown to outperform the latter for making this prediction [105].

The main idea of the stable Bayesian optimization method [104] is to measure a hyper-parameter value combination’s performance stability and include the measure in the acquisition function. The method is designed for the case in which the regression model is a Gaussian process, and each step of the search process uses the whole data set. The technique used in that method does not directly apply to our progressive sampling-based Bayesian optimization method [97], which uses a random forest as the regression model, and a gradually expanded training sample over rounds of the search process.

As our progressive sampling-based Bayesian optimization method starts from a moderate-sized training sample, we could run into spurious peaks in the first few rounds of the search process and get stuck at one of these peaks. To prevent this undesirable situation, we include a performance stability measure for hyperparameter value combinations in the acquisition function.

More specifically, our progressive sampling-based Bayesian optimization method uses a random sample of the data set termed the validation sample to evaluate trained models. For each hyperparameter value combination chosen for testing, our original method [97] uses it to train a model and records the model’s accuracy on the validation sample as its accuracy measure without considering its performance stability. To measure a combination’s performance stability, we partition the validation sample into multiple subsets before the search process starts. For a large data set, we use a validation sample larger than that used in our paper [97] to ensure each subset is of reasonable size. For each combination chosen for testing, we record the trained model’s accuracy on each subset and compute the variance of these accuracies. A large variance indicates the combination has unstable performance. We include this variance as the combination’s performance stability measure in the acquisition function.

In our progressive sampling-based Bayesian optimization method, the training sample expands over rounds. To save time, in each round that is neither the first nor the last one, for each hyper-parameter value combination that looks unpromising in the previous round, we do not use it and the expanded training sample to train a model. Instead, we multiply its accuracy measure from the previous round by a computed factor as its estimated accuracy measure for the current round [97]. Our rationale is that in the search process, which new combinations are chosen for testing in each round tends to be impacted mostly by the promising combinations’ accuracy measures [105]. Using the same rationale, for each unpromising combination, we can handle its performance stability measure over rounds in a similar way.

3.4.6. Technique 4: normalizing the data before starting the search process

Often, we can greatly improve a predictive model’s accuracy by normalizing the data before training the model. To do this, in each round of the search process, we could take a sample of the data set, normalize it, and use it to test and adjust hyper-parameter value combinations. Yet, for each attribute, its mean and standard deviation in the sample are different from those in the whole data set. This will lead to imprecise accuracy estimates of the trained models and subsequently degrade search result quality. To avoid this problem, before the search process starts, we normalize the entire data set that will be used for training and validation in any way. During the search process, we obtain training and validation samples from the normalized data set. Besides boosting search result quality, this also improves search efficiency, as data need to be normalized only once during the search process.

3.5. Additional details

For each longitudinal attribute, one could train an LSTM network using only that attribute without the others, and then extract temporal features from the network’s memory cell vector elements. But, this is unlikely to produce high-quality features. A typical attribute has limited predictive power by itself. An LSTM network built using only this attribute without the others tends to have low prediction accuracy.

Once developed, chronic diseases rarely disappear and usually have a longer lasting impact on future visits than acute diseases. When each input vector includes one patient visit’s information, Bai et al. [46,62] improved LSTM prediction accuracy by learning different time decay factors for differing diseases to reflect this. We can make this more explicit to help LSTM remember long- span history and further boost prediction accuracy. For each common chronic disease, researchers have developed some phenotyping algorithms using medical data to detect whether a patient has this disease [64–66,106,107]. After spotting that a patient has a chronic disease at a specific time step, we add this disease’s diagnosis information into the input vector at each subsequent time step for the patient, regardless of whether this diagnosis is recorded at that time step.

For our temporal feature extraction method to work, we rely on three properties of LSTM. First, LSTM has memory cell vectors, whose elements depict the learned temporal features. Second, the memory cell vector $\stackrel{\rightharpoonup }{c_t}$ at time step t is a function of thejnput vector $\stackrel{\rightharpoonup }{x_t,}\stackrel{\rightharpoonup }{c_{t-1}},$ and the hidden state vector $\stackrel{\rightharpoonup }{h_{t\text{-1}}}$. Third, $\stackrel{\rightharpoonup }{h_t}$ is a function of $\stackrel{\rightharpoonup }{x_t},\stackrel{\rightharpoonup }{c_{t-1}},$ and $\stackrel{\rightharpoonup }{h_{t\text{−1}}}.$ Besides LSTM, several other types of RNN like those given in Zoph et al. [108] also have these three properties. These RNNs can outperform LSTM for certain modeling tasks. We can also apply our method to these RNNs to extract predictive and clinically meaningful temporal features from medical data for predictive modeling.

4. Automatically explaining machine learning prediction results

In this section, we outline a method of using the extracted temporal features to automatically explain machine learning prediction results and to suggest tailored interventions.

Each extracted temporal feature is clinically meaningful and has a precise mathematical definition. Using these temporal features, we convert the longitudinal medical data to an initial table, with one column per temporal feature. Then we add the static attributes to form the final table. Each column of it has an easy-to-understand meaning. Using a supervised machine learning algorithm that can maximize prediction accuracy, we build a predictive model on the final table. Then we use our previously developed method [30] to automatically explain the model’s prediction results and suggest tailored interventions.

4.1. Review of our prior automatic explanation method

For tabular data, our prior method [30] can automatically explain any machine learning model’s prediction results with no accuracy loss. It works in the following way. We use the final table to mine class-based association rules. Each rule contains a feature pattern linking to a value of the outcome variable and is of the form: e₁ AND e₂ AND ... AND e_u → v. The rule suggests that a patient’s outcome variable tends to take value v if the patient satisfies conditions e₁, e₂,..., and e_u. Each condition is on a feature taking a specific value or a value in a given range. An example rule for predicting asthma patient outcome is: the patient’s body mass index kept rising over 12 months AND the patient had an emergency department visit for asthma last year → high risk.

After the association rules are mined, a clinician examines them and drops those that make little or no clinical sense. For each remaining rule with a poor outcome on its right hand side, the clinician pre-compiles zero or more interventions addressing the reason shown by the rule. One such intervention for the example rule mentioned above is to advise the patient to lose weight with a healthy diet and regular exercise. For each patient who is predicted by the machine learning model to have a poor outcome, our method lists zero or more rules. Each rule gives a reason why the patient is predicted to have the poor outcome. Moreover, our method suggests tailored interventions by listing the interventions linking to these rules.

4.2. Shortcomings of our prior automatic explanation method

Our prior automatic explanation method [30] has two shortcomings.

4.2.1. Shortcoming 1: using an association rule mining method suboptimal for imbalanced data

Consider an association rule R with value v on its right hand side. Among all data instances satisfying R’s left hand side, the percentage of data instances whose outcome variables have value v reflects R’s accuracy and is termed R’s confidence. The percentage of data instances satisfying R’s left hand side and whose outcome variables have value v reflects R’s coverage and is termed R’s support. Our prior automatic explanation method uses a standard approach to mine association rules, obtaining rules at a fixed level of minimum confidence (e.g., 50%) and support (e.g., 1%). Yet, this approach is suboptimal on imbalanced data.

Medical data are often imbalanced, with one value of the outcome variable occurring much more frequently than another. In this case, using the same minimum support for different values of the outcome variable is inadequate [109]. If the minimum support is high, we cannot find enough association rules for the rare values. As a result, for many patients whose outcome variables are predicted by the machine learning model to take these values, we cannot explain the model’s prediction results. On the other hand, if the minimum support is too low, the rule mining process will produce too many rules as intermediate results and generate many overfitted rules in the end. The former makes the rule mining process rather slow and the computer easily run out of memory. The latter makes it daunting, if not infeasible, for the clinician to examine the many mined rules.

4.2.2. Shortcoming 2: ignoring those interventions that target the conditions on the mined association rules’ left hand side linking to good outcomes

Our prior automatic explanation method uses only interventions linking to the association rules with poor outcomes on their right hand side. Consider a rule with a good outcome on its right hand side. An intervention helping patients fulfill the conditions on the rule’s left hand side could improve outcomes [53]. Yet, our prior method ignores such interventions and misses the related opportunities for improving outcomes.

4.3. Improving our prior automatic explanation method

We use two techniques to address the two shortcomings mentioned above and to improve our prior automatic explanation method [30].

4.3.1. Technique 1: replacing support by commonality

To address the shortcoming mentioned in Section 4.2.1, we use the approach developed by Paul et al. [109], instead of the standard approach, to mine class-based association rules. There, we replace support by commonality, which is a value-specific support. Consider an association rule R with value v on its right hand side. R’s commonality is defined as the percentage of data instances satisfying R’s left hand side among all data instances whose outcome variables have value v. Intuitively, we want to keep R if the feature pattern on its left hand side is frequent for v, but rare for any other value of the outcome variable. Based on this insight, we mine rules at a fixed level of minimum confidence (e.g., 50%) and commonality (e.g., 10%). If several mined rules have the same left hand side, we keep only the rule with the highest confidence for the value on its right hand side [110].

Compared to using support, using commonality has three advantages. First, the rule mining process produces fewer association rules as intermediate results. This expedites the process, which is important for large data sets. Second, the rule mining process generates fewer overfitted rules in the end. This reduces the time the clinician needs to examine the mined rules. Third, we find more rules for the rare values of the outcome variable. As a result, we can explain the machine learning model’s prediction results for more patients whose outcome variables are predicted by the model to take one of these values.

In clinical applications, the rare values of the outcome variable usually denote poor outcomes and are of more interest to us than frequent values. The mined rules related to the rare values reflect common feature patterns linking to these values. Some patients have these values as their outcomes for uncommon reasons and are covered by none of these rules, no matter how we improve our association rule-based automatic explanation method. Yet, by improving our method, we reduce the number of patients for whom we are unable to explain the machine learning model’s prediction results.

4.3.2. Technique 2: adding interventions that target the conditions on the mined association rules’ left hand side linking to good outcomes

To address the shortcoming mentioned in Section 4.2.2, we add interventions beyond those used in our prior automatic explanation method [30]. For each kept association rule with a good outcome on its right hand side, the clinician pre-compiles zero or more interventions helping patients fulfill some or all of the conditions on its left hand side. For some patients at high risk for poor outcomes, using these interventions could improve outcomes [53]. We consider these interventions when suggesting tailored interventions.

The patients suitable for these interventions are not those satisfying the rule’s left hand side. This is different from the case of the interventions linking to the association rules with poor outcomes on their right hand side. Instead, for each of these interventions, the clinician pre-compiles one or more sets of conditions, under each of which a patient is regarded suitable for the invention. For each patient who is predicted by the machine learning model to have a poor outcome and satisfies one of these sets of conditions, we list the intervention as one of the suggested ones.

4.4. Advantages of and a potential use case for our automatic explanation method for machine learning prediction results on longitudinal medical data

As mentioned in the introduction, our automatic explanation method for machine learning prediction results on longitudinal medical data can enable machine learning models to be used in clinical practice, and help transform healthcare to be more proactive. At present, healthcare is often reactive, resulting in suboptimal outcomes and increased costs. Our feature extraction method can find many temporal features reflecting trends. By using these features and our automatic explanation method to identify risky trends early, we can proactively apply preventive interventions to stop further deterioration of health. The automatically generated explanations can help us identify new interventions, warn clinicians of risky patterns, and reduce the time clinicians need to review patient records to find the reasons why a specific patient is at high risk for a poor outcome. The automatically suggested interventions can reduce the likelihood of missing suitable interventions for a patient. All of these factors can help improve outcomes and cut costs.

Below are several examples of temporal features with potential preventive interventions for asthma patients:

1. Air pollution: Consider the number of days in the past week in which the concentration of a given air pollutant like sulfur dioxide stayed above a fixed level. If either this number or the concentration’s rate of increase exceeds its own specific threshold, the following preventive interventions could be used:

   1. Suggest the patient to stay indoors as much as possible until the pollutant concentration drops below a safe threshold.
   2. Ensure the patient is compliant with his/her current controller therapy like inhaled corticosteroid. If the patient is compliant and symptomatic, consider a temporary increase in controller medication dose during the next two to four weeks.
   3. Ask the patient to increase the dose and/or dosing frequency of quick-relief asthma medication during the next two to four weeks. For example, increase albuterol dose from two to four puffs per dose and/or dosing frequency to four to six doses per day as needed.
2. Pollen count: Consider the number of days in the past week in which a given type of pollen count stayed above a fixed level. If either this number or the pollen count’s rate of increase exceeds its own specific threshold, the following preventive interventions could be used:

   1. Recommend the patient to use allergy medication like antihistamine or nasal steroid spray during the pollen season (February to October depending on the pollen type).
   2. If asthma control worsens during the pollen season despite medication compliance, consider initiating or increasing the dose of the daily controller medication regimen (inhaled corticosteroid).
   3. Consider adding a leukotriene inhibitor to the daily controller medication regimen.
3. Fractional exhaled nitric oxide (FeNO): Rising FeNO levels over time despite treatment may indicate non-compliance with or non-responsiveness to inhaled corticosteroid, or worsening asthma. If this increase occurs, the following preventive interventions could be used:

   1. Assess and address reasons for non-compliance with inhaled corticosteroid.
   2. Adjust the medication type or dose of inhaled corticosteroid.
   3. Perform allergy testing on the patient and prescribe allergy medication as needed.
4. Forced expiratory volume in 1 second (FEV1): Decreasing FEV1 over the past year to below 80% of the predicted normal value or prior personal best may indicate poor asthma control or progressive lung injury from asthma. If this decrease occurs, the following preventive interventions could be used:

   1. Assess the patient for asthma triggers and ensure avoidance of them.
   2. Assess asthma controller medication compliance and dosage. Adjust the medication as indicated.
   3. Assess asthma control and intervene based on the National Heart, Lung and Blood Institute step therapy guidelines.
5. Oral corticosteroid prescription: Increasing frequency of filling oral corticosteroid prescription over the past year indicates poor asthma control. If this increase occurs, the following preventive interventions could be used:

   1. Assess the patient for asthma triggers and ensure the patient avoids them.
   2. Assess asthma controller medication compliance. Prescribe, change, or increase the dose of the medication if indicated.
   3. Prepare a new asthma action plan to intervene more aggressively in the yellow zone [111].
   4. Assess asthma control and intervene based on the National Heart, Lung and Blood Institute step therapy guidelines.
6. Body mass index: The status that a patient’s body mass index keeps rising over 12 months or exceeds 25, the threshold value for overweight, is associated with poorer asthma control. If the patient reaches this status, the following preventive interventions could be used:

   1. Advise the patient to lose weight with a healthy diet and regular exercise. Provide education and information on weight loss to caregivers.
   2. Refer the patient to a dietician and/or a dedicated weight loss clinic.
7. Asthma control test score: The asthma control test score reflects a patient’s asthma control status [112,113 ] and can be assessed every week [114]. A lower score indicates worse asthma control. If over a period of two weeks, the score has trended down but stayed between 15 and 18, the following preventive intervention could be used:

   1. Ensure the patient is compliant with asthma controller medications and avoids asthma triggers. Ask the patient to see his/her care provider for further interventions/ instructions.
      If the score is below 15 at any time, the following preventive intervention could be used:
   2. Besides the actions listed in (a), refer the patient to his/ her personalized asthma action plan for acute interventions including initiating oral corticosteroids.
8. Asthma controller medication compliance: Lack of compliance with daily controller medication can lead to poor asthma control. Yet, medication compliance data are rarely provided to a patient’s care provider. We can track medication compliance data electronically in two ways. First, we track monthly asthma controller medication refills from claims data as a surrogate for medication compliance, as compliance should link to monthly refills. Second, we use the electronic-Asthma Tracker [114,115], an asthma control tracker with a symptom diary tool that also monitors a patient’s daily use of asthma controller medications. When monitoring frequency of monthly refills or daily use of asthma controller medications, the patient’s compliance is expected to be ≥ 80% of prescribed asthma controller medications [116]. If this is not the case, the following preventive intervention could be used:

   1. The care provider assesses over the phone or during clinic visits potential barriers to compliance, and provides education about the importance of achieving and maintaining medication compliance.

The above preventive interventions are useful for asthma care management [117]. Currently, care managers handle most of the care management process and provide limited input on the patient to physicians. Using our automatic explanation method to identify risk trends early and obtain suggestions on potential preventive interventions, care managers can pass this tailored information to physicians for them to act accordingly. This transforms the care management process and makes it more effective via closer collaboration between care managers and physicians.

We can use the final predictive model and automatic explanations to give early warnings for high-risk patients. To measure the number of days of early warning provided by the model, we use an approach illustrated by the following example. Suppose the model predicts an individual patient’s hospitalization in the next 365 days. A patient could be hospitalized more than once during a one-year period. Consider a patient admitted to the hospital on date D. To measure the number of days of early warning the model provides for the patient, we use D-365 as the initial prediction time point and input the patient’s history up to D-365 into the model. If it predicts hospitalization, it warns 365-j₁ days in advance, with D-j₁ being the first day between D-365 and D when the patient was admitted to the hospital. Otherwise, if the model predicts no hospitalization, we move the prediction time point one day forward to D-364 and input the patient’s history up to D-364 into the model. If it predicts hospitalization, it warns 364-j₂ days in advance, with D-j₂ being the first day between D-364 and D when the patient was admitted to the hospital. Otherwise, if the model still predicts no hospitalization, we move the prediction time point another day forward. We keep moving the prediction time point forward until the model predicts hospitalization or we reach D, whichever occurs first. If we reach D, the model warns zero day in advance. For patients ever hospitalized during a certain period, the average number of days of early warning provided by our model reflects how early it gives warnings.

5. Related work

Much related work is mentioned in the previous sections. In this section, we describe some other related work not covered in any of the previous sections.

5.1. Automating feature engineering on tabular data

Several papers have been published on automating feature engineering on tabular data.

As a form of meta-learning, Bilalli et al. [118] used knowledge learned from processing prior data sets to automatically suggest data pre-processing operators for the current data set. That method considers only a few pre-defined operators and cannot handle longitudinal data. In comparison, MCLSTM handles longitudinal data and does not limit the types of temporal features it can learn. Numerous types of clinically meaningful temporal features could be useful for predictive modeling with medical data. The exact forms of many of these types are often unknown beforehand and need to be discovered in a data-driven way.

Khurana [119] automated feature engineering on data stored in a single table, by recursively applying a set of pre-defined transformations on the table’s columns to form new features. That method cannot handle longitudinal data. Often, a feature formed by recursive transformations has no clear medical meaning. It is difficult to use the feature to automatically explain machine learning prediction results. Yet, this function is needed in our case.

Kanter et al. [120–122] described three methods for automating feature engineering on data stored in multiple tables. Each method supports a few predefined aggregate operators like sum and average, and allows them to be applied to temporal data over the same period. Yet, this is insufficient for handling longitudinal medical data. On medical data, many types of temporal features could be useful for predictive modeling. Each feature could be computed on data over a distinct period. For example, one feature is whether a patient’s body mass index kept rising over the past 12 months. Another feature is whether the patient had at least two emergency department visits for asthma in the past six months. Our feature extraction method can obtain features computed on data over different periods.

Lam et al. [123] described a method for automatically learning features from data stored in multiple tables. That method can handle temporal data, if each temporal attribute’s values are stored in a separate table or a separate column of a table linking to the main table via key-foreign key relationships. That method learns temporal features by forming one RNN per temporal attribute. As a result, each learned feature involves only one attribute. Also, the learned features are not guaranteed to be meaningful. In comparison, on medical data, a useful feature could involve more than one longitudinal attribute. Our feature extraction method can find such features and ensures each kept feature is clinically meaningful.

5.2. Temporal and sequential pattern mining

Our temporal feature extraction method is also a pattern mining method, as each temporal feature obtained by it captures a pattern that is temporal and/or sequential. The data mining community has developed many temporal [17,18] and sequential [19] pattern mining techniques, some of which use visualization to facilitate pattern discovery [77,90,124]. Existing techniques [77,124–129] usually handle a single type of attribute. For example, standard sequential pattern mining techniques handle only categorical attributes. This does not serve our feature extraction purpose. In our case, medical data often contain several types of attributes (numeric, categorical, and interval). An extracted temporal feature can involve more than one type of attribute.

Many temporal and sequential pattern mining techniques [125,126,130] ignore pattern interactions and mine each pattern independently of the others. On a data set of non-trivial size, such a technique often finds numerous patterns, many of which are clinically meaningless and highly redundant with each other, e.g., differ by only one item with all other items in the pattern being the same. It is daunting, if not infeasible, for the clinician to examine these patterns and identify the clinically meaningful ones. Without dropping the redundant patterns, using all mined patterns, each as a feature, to build a machine learning predictive model would degrade model accuracy. In comparison, MCLSTM model training considers pattern interactions. Hence, our MCLSTM-based pattern mining method finds mostly non-redundant patterns and avoids the pattern explosion problem. For the clinician and the data scientist involved in the feature extraction process, this greatly reduces the manual examination work needed by them.

Many temporal and sequential pattern mining techniques mine frequent patterns without thinking about building an accurate predictive model [130,131 ]. As a result, many mined patterns have little or no predictive power for the outcome variable. In comparison, our pattern mining method starts from building an MCLSTM predictive model for the outcome variable. The model often has a reasonable accuracy. Thus, the patterns mined by our method tend to have high predictive power for the outcome variable.

Existing temporal and sequential pattern mining techniques either ignore the time gap between consecutive events or require a human expert to specify a threshold, above which the consecutive events in the same sequence are regarded as unrelated to each other [126]. The time gap between consecutive events should be used, as it gives useful information on how closely these events relate to each other. Yet, manually specifying the threshold for the time gap is difficult, particularly because each type of event can have its own optimal threshold that is often unknown beforehand. In comparison, our pattern mining method considers the time gap between consecutive events, requires no manual specification of any threshold for the time gap, and learns which consecutive events in the same sequence relate to each other in a data-driven way.

Some temporal pattern mining techniques use temporal abstraction, which converts a time series of a variable into a sequence of time-interval events [132,133]. Each event denotes a property of the time series. Temporal abstraction requires manual specification of its primitives and thresholds that are often specific to a given disease. This is difficult to do, particularly in a thorough fashion.

Some temporal pattern mining techniques use shapelets [134]. Each shapelet is a univariate time series subsequence that represents a class well in some sense. In comparison, in our case, an extracted temporal feature can involve more than one attribute.

Using shapelets, Ghalwash et al. [135] developed a method to extract multivariate temporal patterns from medical time series. That method assumes time series are evenly spaced, which is often not true in our case. Also, certain temporal patterns can be learned by MCLSTM, but not by that method. One such pattern is that an attribute’s value shows a specific trend, and then after a period of variable length, the attribute’s value shows another specific trend.

Nguyen et al. [136] used a convolutional neural network built on medical data to find sequence patterns of a fixed length. That method handles only categorical attributes and does not fit our case, where temporal patterns can have varying lengths and other types of attributes exist.

Wang et al. [127] used non-negative matrix factorization to mine temporal patterns from medical data. That method handles only binary event attributes, and does not require the mined patterns to correlate with the outcome variable.

Liu et al. [126] used a graph-based method to mine temporal patterns from medical data. That method handles only categorical event attributes.

5.3. Visualizing deep neural networks

Many papers have been published on visualizing deep neural networks [137,138]. Most of these papers focus on convolutional neural network. Only a few of these papers address RNN [138]. Our temporal feature extraction method includes a technique of visualizing MCLSTM.

5.4. Automatically explaining machine learning prediction results

Much work has been done on automatically explaining machine learning prediction results [139,140]. Most of the work focuses on tabular data, images, and texts. To the best of our knowledge, no paper has been published on this paper’s topic of automatically providing rule-based explanations for machine learning prediction results on longitudinal medical data and suggesting tailored interventions [139]. Compared to other forms of explanations for machine learning prediction results used in the literature, rule-based explanations are easier to understand and easier to use for designing tailored interventions. Among the work published on automatically explaining deep neural network’s prediction results [138,141–143], most targets convolutional neural network rather than RNN [141].

5.4.1. Automatically explaining LSTM’s prediction results on genomic and text data

Several papers on automatically explaining LSTM’s prediction results focus on genomic and text data. Unlike a patient’s medical data that have multiple attribute values at each time step, a genomic or text sequence has only one value at every position of the sequence.

For an LSTM network built on genomic data, Lanchantin et al. [144] automatically explained its positive prediction result on a genomic sequence by displaying the sub-sequence of a fixed length that gives the largest score change from negative to positive output score. This approach does not fit our case, where temporal patterns can have varying lengths.

For an LSTM network built on text data, researchers have automatically explained its classification result on a text sequence by showing which words [145], pieces of text [146], or phrases [147] in the sequence are responsible for the classification result. Ming et al. [148] explained the function of each hidden state vector element in the network using the words highly correlated with the element. Strobelt et al. [149] built a tool to visualize the network’s hidden state sequences. For a text sequence, the tool can find other text sequences producing hidden state sequences similar to that produced by this one. In comparison, our feature extraction method uses the memory cell vector elements at the last time step to identify the top and bottom training instances, and visualize their effective segments rather than hidden state sequences.

Besides that done for LSTM on text data, researchers have also done some automatic explanation work for non-LSTM RNN on text data. In particular, Foerster et al. [150] proposed a non-LSTM RNN on text data. That RNN takes a character sequence as its input and computes each input character’s linear contribution to its classification result on the sequence.

5.4.2. Automatically explaining LSTM’s prediction results on medical data

For an LSTM network built on medical data, researchers have automatically explained its prediction result on a patient by highlighting the data elements [22] or medical codes [46] that influence the prediction. Neither of these methods offers rule-based explanations or suggests tailored interventions.

5.5. Other relevant topics

For medical data of a fixed sequence length, Che et al. [151 ] used a gradient boosting tree to mimic an LSTM network built on them and to learn interpretable features. That method neither extracts temporal features nor handles medical data of varying sequence lengths.

To support feature engineering on text data, Brooks et al. [152] built a tool, which visually summarizes misclassified data instances to help find features that can be used to improve model accuracy. Our temporal feature extraction method supports feature engineering on longitudinal medical data.

On non-longitudinal medical data, Ho et al. [153] used tensor factorization to find patterns as features.

Suo et al. [154] used deep neural network to identify non-temporal risk factors. In comparison, many temporal features found by our feature extraction method reflect temporal risk factors.

The usual goal of longitudinal data analysis [155] is to model the expected value of an outcome variable measured repeatedly over time. This is different from our goal of using independent variables measured repeatedly over time to predict an outcome variable that usually has one value per data instance.

6. Conclusions

Identifying predictive and clinically meaningful temporal features is critical for improving the accuracy and transparency of machine learning predictive models on medical data. This paper sketches a method for semi-automatically extracting such features from medical data, and shows how to use these features to automatically explain machine learning prediction results and suggest tailored interventions. This provides a roadmap for future research. Besides being useful for healthcare, our proposed methods can also be used to handle temporal data for non-medical applications.

Below is a list of abbreviations used in the paper

FeNO

fractional exhaled nitric oxide

FEV1

forced expiratory volume in 1 second

GPU

graphics processing unit

Lasso

least absolute shrinkage and selection operator

LSTM

long short-term memory

MCLSTM

multi-component LSTM

RNN

recurrent neural network

Below is a list of symbols used in the paper

⊕

element-wise sum

⊗

element-wise multiplication

λ₁

parameter controlling R_W’s importance

λ₂

parameter controlling R_u’s importance

λ₃

parameter controlling R_f’s importance

σ

element-wise sigmoid function

τ₊

for the top N₊ training instances with the highest positive values in a given memory cell vector element, the lowest one of these values

τ_-

for the bottom N₊ training instances with the lowest negative values in a given memory cell vector element, the highest one of these values

$\stackrel{\rightharpoonup }{b_c}$

the bias vector for the memory cell

$\stackrel{\rightharpoonup }{b_{c,q}}$

the bias vector for the memory cell in the q-th component network

$\stackrel{\rightharpoonup }{b_f}$

the bias vector for the forget gate

$\stackrel{\rightharpoonup }{b_{f,q}}$

the bias vector for the forget gate in the q-th component network

$\stackrel{\rightharpoonup }{b_i}$

the bias vector for the input gate

$\stackrel{\rightharpoonup }{b_{i,q}}$

the bias vector for the input gate in the q-th component network

$\stackrel{\rightharpoonup }{b_o}$

the bias vector for the output gate

$\stackrel{\rightharpoonup }{b_{o,q}}$

the bias vector for the output gate in the q-th component network

$\stackrel{\rightharpoonup }{c_{q,l,t}}$

the memory cell vector on the l-th layer of the q-th component network at time step t

$\stackrel{\rightharpoonup }{c_{q,t}}$

the memory cell vector in the q-th component network at time step t

$c_t$

memory cell at time step t

$\stackrel{\rightharpoonup }{c_t}$

the memory cell vector at time step t

D

date

$d(\stackrel{\rightharpoonup }{y},\stackrel{\rightharpoonup }{z})$

the distance between vectors $\stackrel{\rightharpoonup }{y}\text{and}\stackrel{\rightharpoonup }{z}$

$d_p\text{(}Y\text{,}Z\text{)}$

the total distance between temporal sequences Y and Z along warping path p

d_q

the q-th component network s memory cell vector dimensionality

DTW(Y, Z)

the dynamic time warping distance between temporal sequences Y and Z

e_i

the i-th condition on the left hand side of an, association rule

$\stackrel{\rightharpoonup }{f_{q,t}}$

the forget gate ‘ s activation vector in the q-th component network at time step t

$f_t$

forget gate at time step t

$\stackrel{\rightharpoonup }{f_t}$

the forget gate ‘ s activation vector at time step t

g_i

number of weights in the i-th group

G

number of groups

$\stackrel{\rightharpoonup }{h_{q,l,t}}$

the hidden state vector on the l-th layer of the q-th component network at time step t

$\stackrel{\rightharpoonup }{h_{q,t}}$

the hidden state vector in the q-th component network at time step t

h_t

hidden state at time step t

$\stackrel{\rightharpoonup }{h_t}$

the hidden state vector at time step t

i_q,t

the input gate’s activation vector in the q-th component network at time step t

$i_t$

input gate at time step t

$\stackrel{\rightharpoonup }{i_t}$

the input gate s activation vector at time step t

k

the number of clusters of effective segments that will be created for the top/bottom training instances of a memory cell vector element at the last time step of the MCLSTM network

K

number of component networks

L

the loss function measuring the mismatch between the predicted and actual outcomes of the data instances

L_o

the overall loss function

m, m₁, m₂

number of time steps

MDTW(Y, Z)

the multivariate dynamic time warping distance between temporal sequences Y and Z

n

the input vector’s dimensionality

n₊

the number of training instances with positive values in a given memory cell vector element

n₋

the number of training instances with negative values in a given memory cell vector element

N

the maximum number of top/bottom training instances that will be obtained for each memory cell vector element at the last time step of the MCLSTM network

N₊

the number of identified top training instances with the highest positive values in a given memory cell vector element

N₋

the number of identified bottom training instances with the lowest negative values in a given memory cell vector element

n_q

the number of longitudinal attributes used in the q-th component network

$\stackrel{\rightharpoonup }{o_{q,t}}$

the output gate s activation vector in the q-th component network at time step t

o_t

output gate at time step t

$\stackrel{\rightharpoonup }{o_t}$

the output gate ‘s activation vector at time step t

p, p*

warping path

|p|

warping path p’s length

P(Y, Z)

all possible warping paths between temporal sequences Y and Z

R

association rule

R_f

the L₂ regularizer for the weights in the fully connected feedforward network used at the end of the MCLSTM network

R_q,r

the L₂ norm of the input vector weight matrix elements linking to the r-th longitudinal attribute in the q-th component network

R_U

the L₂ regularizer for the elements of the hidden state vector weight matrices U_f,q, U_i,q, U_o,q, and U_c,q

R_W

the exclusive group Lasso regularizer

$t,t^{\prime },t_1,t_2,t_3,t_4,t_5$

time step

t_end

an effective segment’s ending time step

t_start

an effective segment’s starting time step

tanh

element-wise hyperbolic tangent function

U_c

the hidden state vector weight matrix for the memory cell

U_c,q

the hidden state vector weight matrix for the memory cell in the q-th component network

U_c,q,s,r

the element in the s-th row and r-th column of U_c,q

U_f

the hidden state vector weight matrix for the forget gate

U_f,q

the hidden state vector weight matrix for the forget gate in the q-th component network

U_f,q,s,r

the element in the s-th row and r-th column of U_f,q

U_i

the hidden state vector weight matrix for the input gate

U_i,q

the hidden state vector weight matrix for the input gate in the q-th component network

U_i,q,s,r

the element in the s-th row and r-th column of U_i,q

U_o

the hidden state vector weight matrix for the output gate

U_o,q

the hidden state vector weight matrix for the output gate in the q-th component network

U_o,q,s,r

the element in the s-th row and r-th column of U_o,q

v

value

w_i,j

weight

W_c

the input vector weight matrix for the memory cell

W_c,q

the input vector weight matrix for the memory cell in the q-th component network

W_c,q,s,r

the element in the s-th row and r-th column of W_c,q

W_f

the input vector weight matrix for the forget gate

W_f,q

the input vector weight matrix for the forget gate in the q-th component network

W_f,q,s,r

the element in the s-th row and r-th column of W_f,q

W_i

the input vector weight matrix for the input gate

W_i,q

the input vector weight matrix for the input gate in the q-th component network

W_i,q,s,r

the element in the s-th row and r-th column of W_{i q}

W_o

the input vector weight matrix for the output gate

W_o,q

the input vector weight matrix for the output gate in the q-th component network

W_o,q,s,r

the element in the s-th row and r-th column of W_o,q

$\stackrel{\rightharpoonup }{x_{q,t}}$

the input vector in the q-th component network at time step t

X_q,t,j

the j-th element of the input vector $\stackrel{\rightharpoonup }{x_{q,t}}$

$\stackrel{\rightharpoonup }{x_t}$

the input vector at time step t

x_t,i

the i-th element of the input vector $\stackrel{\rightharpoonup }{x_t}$

Y

temporal sequence

$\stackrel{\rightharpoonup }{y_r}$

the r-th element of temporal sequence Y

Z

temporal sequence

$\stackrel{\rightharpoonup }{z_s}$

the s-th element of temporal sequence Z