Individual Differences in Object Recognition

Abstract

There is substantial evidence for individual differences in personality and cognitive abilities, but we lack clear intuitions about individual differences in visual abilities. Previous work on this topic has typically compared performance with only two categories, each measured with only one task. This approach is insufficient for demonstration of domain–general effects. Most previous work has used familiar object categories, for which experience may vary between participants and categories, thereby reducing correlations that would stem from a common factor. In Study 1, we adopted a latent variable approach to test for the first time whether there is a domain–general Object Recognition Ability, o. We assessed whether shared variance between latent factors representing performance for each of five novel object categories could be accounted for by a single higher–order factor. On average, 89% of the variance of lower–order factors denoting performance on novel object categories could be accounted for by a higher–order factor, providing strong evidence for o. Moreover, o also accounted for a moderate proportion of variance in tests of familiar object recognition. In Study 2, we assessed whether the strong association across categories in object recognition is due to third–variable influences. We find that o has weak to moderate associations with a host of cognitive, perceptual and personality constructs and that a clear majority of the variance in and covariance between performance on different categories is independent of fluid intelligence. This work provides the first demonstration of a reliable, specific and domain–general Object Recognition Ability, and suggest a rich framework for future work in this area.

Individual Differences in Object Recognition

There is substantial evidence for individual differences in personality and cognitive abilities. In the case of personality traits, although test–retest correlations across 1–3 years are in the .2–.5 range during childhood, they are in the .6–.8 range among adults across even longer time spans (e.g., Hampson & Goldberg, 2006; Roberts & DelVecchio, 2000). Cross–situational consistency of behaviors is not as high as we might intuitively believe (e.g., Mischel, 1968; Mischel & Peake, 1982), and r = .30 is the proverbial “personality coefficient” (Mischel, 1968). Nonetheless, personality traits: 1) often account for substantial variance in behaviors, thoughts, and moods averaged across situations, contexts, or measures (e.g., Rushton, Brainerd, & Pressley, 1983); 2) are generally associated with validity coefficients comparable to modal effect sizes found in experimental studies (Meyer, Finn, Eyde, et al. 2001); and 3) predict important life outcomes (e.g., mortality, occupational attainment, vulnerability to psychopathology), with effect sizes comparable to those of SES or cognitive abilities (e.g., Goodwin & Friedman, 2006; Roberts, Kuncel, Shiner, Caspi, & Goldberg, 2007). Similarly, psychometric intelligence is extremely stable over time (e.g., test–retest correlations generally in the .6–.8 range in the time span between childhood and old age, e.g., Deary, Whalley, Lemon, Crawford, & Starr, 2000; Deary, Whiteman, Starr, et al., 2004), and it predicts achievement and other important life outcomes (e.g., health and morbidity) independent of socio–demographic variables (e.g., Deary et al., 2004).

In contrast, we lack clear intuitions about individual differences in visual perception. We have little to no access to the quality of others’ perception and we are very poor at estimating our perceptual abilities, even in a specific domain, relative to other people (Barton et al., 2009; McGugin et al., 2012). Studies of perceptual expertise that reveal variability in ability with specific object categories, such as birds (e.g., Gauthier et al., 2000; Tanaka et al., 2005), fingerprints (Busey & Vanderwolk, 2005), and cars (e.g., Gauthier et al., 2000, 2003) do not address the stability or consistency of individual differences in object recognition performance—is ability in one domain stable over time and related to performance in another domain? Does someone’s ability to recognize birds predict how well they will be able to recognize fingerprints? Surprisingly, despite decades of research on object recognition, there has been almost no work seeking to find evidence of a common “object recognition” ability across domains. Here, we test whether object recognition ability (o) is a valid and reliable construct that can account for performance across categories. The o we are speculating about here would be at least general enough to predict the ability to learn how to discriminate items in any subordinate–level category, such as different dogs, birds or fingerprints¹.

The hypothesis of a general object recognition ability parallels a number of models in the areas of personality, psychometric intelligence, and cognitive abilities. In these areas, hierarchical structures for individual differences have predominated for a number of years (e.g., Guilford, 1967; Markon, Krueger, & Watson, 2005; Reeve & Bonaccio, 2011; Rushton & Irwing, 2011; Spearman, 1927). Such models posit superordinate dimensions or factors (e.g., the general intelligence factor g, negative affectivity in the domain of emotion and temperament) that account for substantial variability in both lower–order factors and observed measures (e.g., Markon et al., 2005; Reeve & Bonaccio, 2011; Zinbarg & Barlow, 1996).

However, a great deal of vision research seems to suggest that visual abilities are more fractionated than common, with the visual system dividing things by the way they look. For instance, neuroimaging studies have identified different brain regions associated with the processing of basic visual properties such as symmetry (e.g., Sasaki et al., 2005), curvature (e.g., Yue et al., 2014), and rectangularity (e.g., Nasr et al., 2014), and with different object categories such as animals, tools (e.g., Chao et al., 2002), houses (e.g., Epstein & Kanwisher, 1998), and faces (e.g., Kanwisher et al., 1997). Measures of connectivity to face selective–areas are found to correlate with face, but not scene, recognition performance (Gomez et al., 2015). Such results raise the possibility that different brain networks support independent recognition abilities for different object categories, such that car recognition ability would not predict ability to match fingerprints or recognize faces.

Starting with the development of the Cambridge Face Memory Test (CFMT; Duchaine & Nakayama, 2006), which captures a wide range of face processing ability with high reliability (e.g., test–retest with 6 months delay =.70, Duchaine & Nakayama, 2006; Cronbach’s alpha = .91, Wilmer et al., 2012), the small body of work that speaks to this question has generally focused on the specificity of face recognition abilities; that is, is face recognitions an independent ability or a special case of a more global ability to learn and/or recognize objects? However, the conclusions that can be drawn from work in this area are limited because 1) the experimental designs typically only include one task (e.g., a single memory test) and two categories (e.g., faces and cars), and 2) only familiar object categories are used, so experience can vary between participants and categories. In what follows, we discuss each of these issues in turn and how they are addressed by the present study.

Importance of Using Multiple Tasks and Categories

Wilmer et al. found only 7% shared variance (r–squared) between the CFMT and performance on a similar task with unfamiliar abstract art (n = 3004, r = .26, Wilmer et al., 2010; n = 1469, r = .26, Wilmer et al., 2012), and studies comparing the CFMT with a similar task using cars have found 8% shared variance (n = 1042, r = .29; Shakeshaft & Plomin, 2015) and 14% (n = 142, r = .37; Dennett et al., 2012). These small but significant relationships are difficult to interpret because performance with different categories was measured using a single task for all categories. Performance with faces, abstract art, and cars could share a small amount of variance either due to the recruitment of a general object recognition system or due to task–specific processes such as working memory or sensitivity to proactive interference, and important to this task. Interpretation is further limited by the fact that only two categories of objects were compared (faces with either abstract art, cars, or houses; see Gauthier & Nelson, 2001).

When studies find only a moderate correlation between a face and a non–face object recognition task, authors often take it as evidence for a face recognition ability that is distinct from an object recognition ability (e.g., Dennett et al., 2012; Shakeshaft & Plomin, 2015; Wilmer et al., 2010). An untested assumption, however, is that abilities to recognize different non–face categories would be more strongly related to one another than each of them would be to face recognition ability. Only a few studies have used several object categories but all with the same task (e.g., Ćepulić et al., 2018). In some of these studies using the VET (McGugin et al., 2012; Van Gulick et al., 2015), the average pairwise correlation between any two non–face categories is no larger (r=.34) than what is typically found between face and non–face object recognition tests (e.g. r=0.37 in Dennett et al, 2012). In other words, when many categories are used, face recognition does not stand out as a particularly distinct ability. Testing with more than two categories shifts the question of whether face recognition ability is distinct to a more general question: given the domain–specificity of performance in high–level vision, is there evidence for a strong domain general object recognition ability, o?

Beyond problems for interpretation, using only two categories each assessed with one task may underestimate true dependence on a common factor. Consider research in the area of personality, where the cross–situational consistency of behavioral measures (particularly when assessed on only one occasion) is typically rather low (e.g., Mischel, 1968; Mischel & Peake, 1982). Importantly, correlations are much higher when behavioral measures are aggregated across a number of situations and correlated with other behavioral aggregates or personality measures (e.g., Jaccard, 1974; Rushton, Brainerd, & Pressley, 1983). Thus, the correlation between one task for cars and one task for faces likely does not provide sufficient aggregation to reveal the influence of a broader construct. Indeed, the few studies that used multiple tasks treated as indicators of a higher–order category–specific latent variable (i.e., factor) found moderate to substantial relationships between distinct face and house perception factors (44–69% shared variance, Hildebrandt et al., 2013; 24% shared variance, Wilhelm et al., 2010). These studies still suffer from the interpretative problems described above, as only two categories were compared. To circumvent these problems, participants in our study completed three tasks of visual object perception and recognition for each of five object categories.

Importance of Controlling for Experience

Although some studies have measured performance for several categories (e.g., Gauthier et al., 2014; McGugin et al., 2012; Van Gulick et al., 2015), most used familiar object categories. This makes it difficult to disentangle variability due to experience from variability in a domain–general ability. Furthermore, differences in experience between categories for the same individual might reduce correlations that would stem from a common factor (Gauthier et al., 2014; Ryan & Gauthier, 2016; Van Gulick et al., 2015). In recent work, object recognition ability was measured with three categories of novel objects (in three groups with ns >325, each tested on two of the three categories, with a single task). The average pairwise correlation (r=.48) was higher than the typical pairwise correlation for familiar object categories, consistent with the idea that differences in experience with familiar objects complicates the measurement of a common visual ability (Richler et al., 2017). To circumvent the problems associated with variability in experience, here we used five categories of novel, unfamiliar objects. Because these novel object categories vary on several perceptual dimensions shown to be associated with unique neural substrates (e.g., animate/inanimate appearance, symmetry, and curvature), their use in the present study will provide a rigorous test of the presence of a common ability.

It is possible, however, that some amount of experience with a category is important for individual differences in ability to be fully reflected in performance. After all, one important component of object recognition is the ability to learn object categories. In other domains, differences among individuals in genetic or other predispositions commonly require the appropriate environmental inputs to be expressed behaviorally (for reviews see Dick, 2011; Manuck & McCaffery, 2014). Therefore, we tested four object categories following a training phase that provided participants with the same amount of controlled experience for each category. We tested performance with the fifth category without any prior training, to assess whether experience affects the expression of a domain–general ability. If so, this design leaves us with four categories to use in the main analyses. We used a training protocol that is relatively short and limits the contribution of non–visual abilities (e.g., it did not require naming). In addition, learning in this task transfers to new exemplars of the category and results in training effects typical of the early stages of perceptual expertise (Bukach et al., 2012).

Latent Variable Modeling Approach

Self–reports of visual abilities are generally poor predictors of performance for most categories (McGugin et al., 2012; Richler et al., 2017; see also Barton et al., 2009). Thus, individual differences in object recognition ability can only be inferred from behavioral measures of task performance. Whatever the nature of the measure, research in the areas of personality and temperament has shown that broad individual differences constructs are optimally assessed using multiple measures (to allow for conclusions that are appropriately generalizable across different measures) and often best modeled as latent variables. Narrowly defined, latent variables are constructs (e.g., ‘object recognition ability’) that are not directly observable. Latent variables are useful whenever unobserved constructs are invoked, for instance in behavioral and social sciences (e.g., Bollen, 2002). The present study adopts a latent variable analytic approach to test the hypothesis that the shared variance in performance across several object categories can be accounted for by a single domain–general visual ability that is modeled as a higher–order latent variable (i.e., factor). This structural representation will be tested using confirmatory factor analysis (CFA, for reviews see Brown, 2015; Tomarken & Waller, 2005). CFA confers several distinct advantages in the present context relative to exploratory factor analysis (EFA) or principal components analysis (PCA). These include the ability to: specify and test the absolute and relative fit of competing models using a variety of indices; specify factor models that posit both lower–order factors that account for correlations among observed indicators and higher–order factors that account for the correlations among lower–order factors; estimate correlations among categories that are free from the attenuating effects of measurement error and category–irrelevant variance, and specify correlated error terms or task–specific method factors that can estimate the contribution of shared methods to correlations among measures (see, e.g., Brown, 2015; Hancock & Mueller, 2006; Tomarken & Waller, 2005).

In our study, participants completed three tasks of visual object perception and recognition for each of five novel object categories (four categories for which they received a fixed amount of training in a simple video game, and one for which they received no training). We then used CFA to estimate the correlations among the different categories in performance. Each category itself was represented as a first–order factor with task scores as observable indicators. Our primary interest was testing a related model that posited an overarching, second–order construct that we denote as ‘o’ representing individual difference in object recognition ability that influences performance on specific object categories. Our goal was to assess the fit of the second–order factor model and estimate the proportion of variance in performance on the lower–order, category–specific factors accounted for by the overarching factor. Finally, via CFA, we assessed the relation between individual differences on the object recognition latent factors and scores on measures of facial recognition and perceptual expertise with familiar objects.

Study 1

Methods

Participants

Two–hundred–and–eighty–five members of the Vanderbilt University Community were recruited for the experiment (123 male, 162 female; mean age = 21.5, age range = 18–38; Caucasian = 170, Asian = 70, African American = 35, Hispanic = 8, Other = 2). There were four at–home sessions of approximately 1.75 hours each, and six lab sessions of one hour each. Participants were compensated $26.25 for each at–home session, and $15.00 for each lab session, for a total of $195.00 for the entire experiment (13 hours). Payment was based on the sessions participants completed, and was not contingent on finishing the experiment. Both the original sample size (285) and the sample size ultimately used for analyses (n=246, see Data Analysis section for elaboration) are very large for studies in the area of perception but on the small side relative to typical confirmatory factor analyses and structural equation models. The target N reflected a tradeoff between practical considerations (i.e., each participant attended 5 laboratory sessions with home sessions intermixed) and the desire to maximize sample size for a statistical procedure that typically requires large sample sizes. In this regard, two considerations are particularly relevant: (1) A priori power analyses indicated excellent power to detect misspecifications under a range of reasonable parameter values with n’s in the range of 250 or so; and, (2) Published simulation studies that mirror various features of the present experiment (e.g., the method of treating missing data, as discussed below) have demonstrated good performance (e.g., empirical Type 1 error rates that correspond to nominal levels) when n’s are in the same range (e.g., Savalei & Falk, 2014).

Stimuli

We used five novel object categories (vertical Ziggerins, asymmetrical Greebles, symmetrical Greebles, horizontal Ziggerins, and Sheinbugs; arbitrary numbers were assigned to categories to simplify data coding and presentation of results, see Figure 1) with 80 exemplars each, and two views per exemplar. Categories were defined by general configuration of parts and color. Thirty exemplars (approximately 1 × 1 degree of visual angle) were used in the training phase, and the remaining 50 exemplars (approximately 2 × 2 degrees of visual angle) were used for testing. A sixth novel object category (YUFOs, Gauthier et al., 2003) was used to practice the training task during an introductory lab session and in the instructions for all test tasks.

Figure 1.

Example stimuli from the five novel object categories used in this study. Numbers were arbitrarily assigned to categories to simplify data coding and presentation of results. Category 0 was the non–exposed category for all participants.

General Procedure

The general procedure is illustrated in Figure 2. First, participants came to the lab for an introductory session in which they completed measures of familiar object recognition (described below), and practiced the training game. At the end of the introductory session (and all subsequent lab sessions), participants scheduled their next lab session and were given a passcode to access the training game that had to be completed at home prior to that date. Participants were told that they should return to the lab within five days of completing the game, and this was taken into consideration during scheduling ². Participants completed the assigned training game for a category at home, and then completed three test tasks (described below) with the same category in the subsequent lab test session (e.g., participants completed the training game with Cat–1 at home, then returned to the lab to complete the test tasks with Cat–1). Home–training and lab–test sessions were repeated until participants completed test sessions for all five categories, with the exception that there was no training session prior to the test session for Cat–0. Category order was randomized for each participant.

Figure 2.

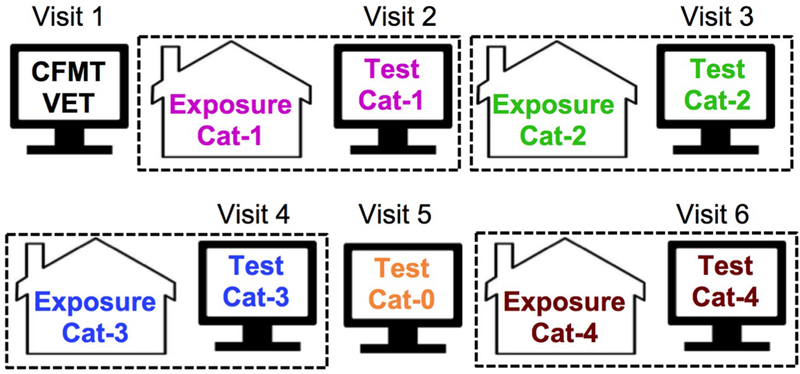
General experiment procedure. Participants completed an introductory lab session on Visit 1, followed by home–training and lab–test sessions for four novel object categories (Cat–1–4), and a lab–test session only for one novel object category (Cat–0). Home sessions and lab visits were grouped for Cat–1–4, such that the home and test sessions for a given category were always consecutive and separated by no more than five days. Category order was randomized.

Training Game

The training game was modeled after the classic arcade game Space Invaders (see Bukach et al., 2012). In each wave, an array of nine objects moved laterally and downward toward participants’ avatar. Objects in the array and the avatar could appear in one of two viewpoints. The arrow keys moved the avatar left and right. Pressing “z” produced a laser that changed the invader’s identity on contact, and pressing “x” produced a laser that eliminated the invader if it matched the identity of the avatar. If an invader with a different identity from the avatar was shot with an “x,” the speed of array movement increased. Importantly, the target invader and avatar could be shown in the same or different viewpoint. Thus, successful task performance required matching on object identity, regardless of viewpoint. Participants had to successfully clear 250 waves (approximately 90 minutes). Because the training game was relatively easy across categories, on average participants initiated 276.41, 259.69, 271.20, and 272.22 waves for categories 1–4, respectively (overall mean = 269.88). A repeated measures linear mixed effects analysis of variance (ANOVA) and subsequent pairwise comparisons indicated that category 2 was associated with fewer waves than the three other categories (category 2 pairwise ps < .025; all other pairwise ps > .20; omnibus test F(3,219) = 7.52, p <.0001). Waves did not have to be completed during a single sitting. Avatar identity and array composition were randomized. During the introductory session participants had to clear 30 waves of YUFOs to familiarize themselves with the task.

Introductory Lab Session

Example trials for the familiar object recognition measures (CFMT and VET) are shown in Figure 3. Task order and trial order within each task were the same for all participants.

Figure 3.

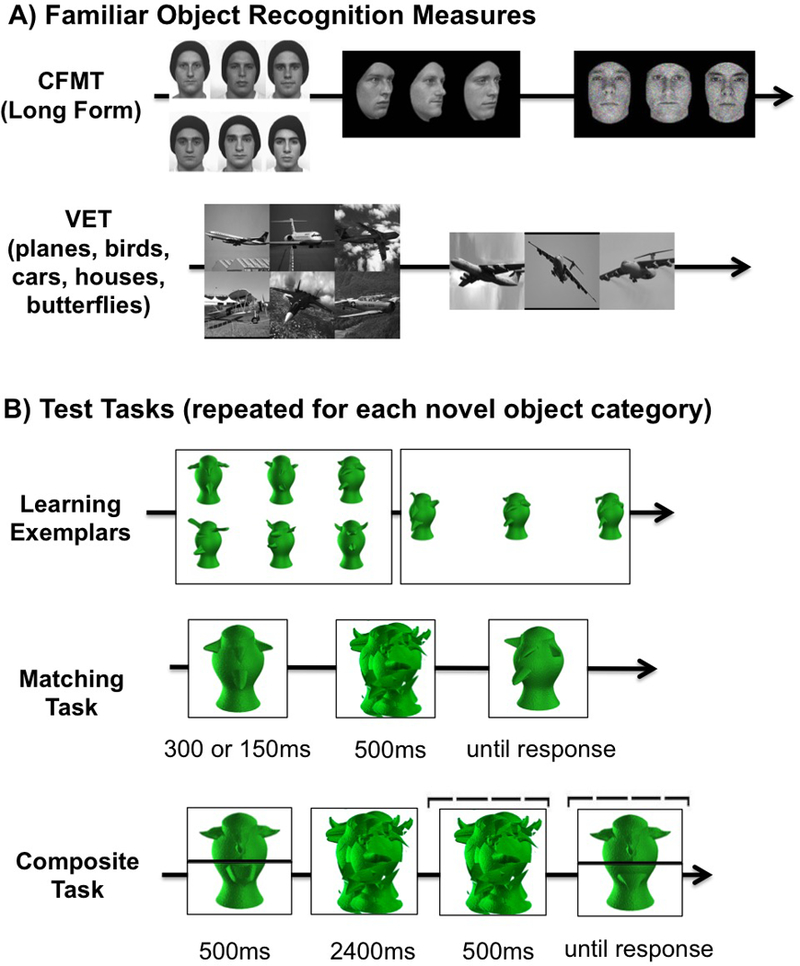
A) Example trials for familiar object recognition measures (CFMT and VET). B) Example trials for each of the three test tasks (Learning Exemplars, Matching Task, Composite Task, denoted by LE, MA and CO in Figure 1).

Cambridge Face Memory Test (CFMT)– Long Form.

In the CFMT (Duchaine & Nakayama, 2006), participants complete an 18–trial introductory learning phase, in which a target is presented in three views, followed by three forced–choice test displays containing the target face and two distractor faces. Then, participants study frontal views of all six target faces together for a total of 20 s, followed by 30 forced–choice test displays. Participants are told to select the face that matches one of the original six target faces. The matching faces vary from the studied versions in terms of lighting condition, pose, or both. Next, participants are given another opportunity to study the six target faces, followed by 24 test displays presented in Gaussian noise. Finally, the last block includes 30 “difficult” test displays where faces are shown as silhouettes, in extreme noise, or with varying expressions. The CFMT is scored as accuracy (percent correct) across all blocks, excluding the introductory learning trials, for a total of 84 trials. Previous work found that the CFMT produces measurements of high reliability in a normal adult population (e.g., test–retest with 6 months delay = .70, Duchaine & Nakayama, 2006; Cronbach’s alpha = .91, Wilmer et al., 2012).

Vanderbilt Expertise Test (VET).

The Vanderbilt Expertise Test (VET; McGugin et al., 2012) is similar in format to the CFMT. Participants study six target exemplars from a category, and are then presented with triplets and asked to indicate by key–press which object is the same identity (but different image) as any of the targets. Five categories were tested in the following order: houses, cars, birds, planes, and butterflies. There were 51 trials for each category. Three trials were catch trials that were not analyzed. Participants were also asked to rate their experience with each of the five categories (“interest in, years exposure to, knowledge of, and familiarity with” from 1 to 9). Accuracy (percent correct) was computed separately for each VET category. Previous work has produced good reliability in measurements with a normal adult population on the various VET subscales (e.g., Cronbach’s alpha = .64–.85 in McGugin et al., 2012; Cronbach’s alpha = .71–.93 in Van Gulick et al., 2015).

Test Sessions

Example test task trials are shown in Figure 3. Test task order was the same for all categories and participants. One trial order was generated for each test task for each category and was the same for all participants.

Learning Exemplars Task.

Thirty–six test objects (6 targets, 30 foils) from each category were used. The Learning Exemplars task was similar in format to the CFMT and VET. Participants studied an array of six target objects (three in view A, three in view B). On the subsequent test trials, three objects were shown in any combination of views A and B, and participants had to indicate by key–press which object matched the identity of any of the targets, regardless of changes in viewpoint. Chance was .33. There were two blocks of 24 trials. In the first block, targets were shown in the same view as during study. In the second block, targets were shown in the unstudied view. In the last six trials of block 1 and the last 12 trials of block 2 objects were presented in visual noise. All targets were shown with an equal frequency for each trial type (e.g., same/different identity x same/different viewpoint), and the same target was never presented on consecutive trials. Performance was scored as accuracy (percent correct) across all 48 trials. Cronbach alphas were .73–.89 (see Table 1). For cross–reference, this task is an earlier version of the Novel Object Memory Test developed later for 3 of the categories (Richler et al., 2017).

Table 1.

Reliability (Cronbach’s α), mean performance measures, and tests of normality for each test task and category (see Figure 2 for number–category mappings).

Category	N	Cronbach’s α	Mean (SD) accuracy (% correct or d’)	Skewness	Kurtosis	Shapiro–Francia Normality Test (V’)
Learning Exemplars
0	225	.84	65.16 (15.04)	−0.44	3.37	2.59*
1	199	.78	49.82 (14.02)	0.17	2.81	1.46
2	208	.89	68.35 (17.69)	−0.58*	3.16	4.45***
3	201	.74	48.05 (12.68)	0.62***	3.58	3.62**
4	212	.73	50.47 (12.36)	0.14	2.68	0.81
Matching Task
0	225	.95	1.62 (.62)	−1.07***	6.49***	10.82***
1	203	.92	1.04 (.50)	−0.79***	5.77***	6.22***
2	212	.96	1.83 (.71)	−1.26***	6.71***	12.10***
3	210	.91	1.03 (.42)	−0.50	4.72	4.86***
4	218	.88	.82 (.40)	−0.55**	3.83**	3.57**
Composite Task
0	225	.91	1.72 (.92)	−0.29	3.38	1.83
1	208	.95	1.25 (.71)	−0.10	3.34*	0.87
2	213	.97	1.69 (.97)	0.17	3.23	1.11
3	208	.95	1.23 (.73)	−0.29	3.03	1.99
4	215	.95	1.12 (.69)	−0.42**	3.56**	2.30*

Note. Accuracy measures are percent correct for Learning Exemplars and d’ for Matching and Composite tasks. Under normality, the expected values of measures of skewness and kurtosis are 0 and 3, respectively. Under normality, when scores are sampled from a normal distribution, the median value of the Shapiro− Francia V’ measure equals 1 (Royston, 1991).

^*p < .05

^**p < .01

^***p < .001

Matching Task.

All 50 test objects from each category were used. On each trial, a study object was presented (300 ms in block 1, 150 ms in block 2), followed by a category–specific random pattern mask (500 ms), then a second object was presented (until response or a maximum of 3 s; time–out trials accounted for less than 1% of the data and were excluded from the analyses). Participants had to indicate by key–press whether the two objects were the same or different identity, regardless of changes in viewpoint or size (on different–size trials the test object was approximately 1.3 × 1.3 degrees of visual angle). There were 45 trials for each combination of correct response, viewpoint (same or different), and size conditions (same or different) for a total of 360 trials. Due to a minor programming error, the number of same and different trials were not evenly divided between blocks (range = 84–96 trials per block). Sensitivity (d’) was calculated separately for each block. Sensitivity was computed using Zhit rate – Zfalse alarm rate, adjusting for hit rates of 1 or false alarm rates of 0 using 1 – 1/(2N) and 1/(2N), respectively where N is the number of same (or different) trials. These scores were correlated (rs = .57–.78, all ps < .001) and were averaged to create a single matching task score for each category with Cronbach alpha .88–.96 (see Table 1).

Composite Task.

Because prior work suggested that using a small number of stimuli improves the reliability of the composite task (Ross et al., 2015), the tops of five objects and the bottoms of a different five objects were used to make composites for each category. These ten objects were not used in the Learning Exemplars task. Trial timing was based on Wong et al. (2009). On each trial, a study composite (top of one object combined with the bottom of another object) was presented (500 ms), followed by a category–specific mask (2900 ms). A cue indicating whether the top or bottom was the target was presented during the last 500 ms of the mask presentation. Then, a test composite was presented with the cue (until response, maximum 3 s; time–out trials accounted for 1% of the data and were excluded from the analyses) and participants had to indicate by key–press whether the cued part was the same or different as the study composite, while ignoring the uncued half. On congruent trials, the cued and uncued parts were associated with the same response (i.e., both parts were the same or both parts were different); on incongruent trials, the cued and uncued parts were associated with different responses (i.e., one part was the same, the other part was different). There were 36 trials for each combination of correct response (same/different), cued part (top/bottom), and congruency (congruent/incongruent) for a total of 288 trials. Sensitivity (d’) was calculated separately for top–congruent, bottom–congruent, top–incongruent, and bottom–incongruent conditions. These scores were correlated (average rs = .41–.60, all ps < .001) and were averaged to create a single composite task score for each category with Cronbach’s alpha .91–.97 (see Table 1). This average composite score indexes overall performance on the task, which is the construct that is most similar to that measured by the other two tasks. It does not reflect congruency (the difference in performance between congruent and incongruent trials), which is an index of holistic processing (Richler & Gauthier, 2014). We did however compute congruency effects for use in an analysis comparing the 4 categories that received pre–training to the 5^th, untrained, category.

Data Analysis

The data and software code for the primary analyses are available in the figshare repository (see supplemental online material). Due to experimenter or computer error, VET data for one or more subscales were missing for five participants and CFMT data were missing from one participant. Thirty–six participants withdrew from the study after the pre–test session (leaving 249 participants from the original 285). CFMT accuracy did not differ between participants who withdrew after the introductory session (M % correct = 61.77, SD = 10.85) and those who completed test sessions for at least one category (M % correct = 63.22, SD = 14.23; t₂₈₂ = 0.59, p = .56, Cohen’s d = .11); however, VET accuracy (aggregated across all categories) was significantly lower for participants who withdrew (M % correct = 63.00, SD = 9.87) vs. those who completed any number of test sessions (M % correct = 66.96, SD = 9.60; t₂₇₈ = 2.30, p = .022, Cohen’s d = .41). Data from three participants were excluded for not completing the exposure game for any category. Thus, data from 246 participants (86% of sample; 105 male, 140 female, 1 not disclosed; mean age = 21.4 years; Caucasian = 144, Asian = 64, African American = 30, Hispanic = 6, Other = 2) are included in the analyses.

Among the 246 participants included in analyses, data for some task–category combinations were not collected due to experimenter or computer error (2.68%) or because participants withdrew from the study after completing at least one test session (n = 30; 8.21% of expected data). Both the intraclass correlation analyses and the confirmatory factor analyses that we report below can accommodate such participants with incomplete data. Of the collected data, 96.95% was included in the analyses. The remaining 3.05% of observations were excluded because of: 1) Failure to finish the exposure game for a given category or excessive delay between home–exposure and lab–test sessions for that category (1.38%); and, 2) Median RTs less than 200 ms for individual Composite and Matching Task categories and median RTs less than 1000 ms for individual Learning Exemplars categories (1.67%).

Intraclass Correlations.

We computed intraclass correlation coefficients (ICCs) on a within–task basis to assess the consistency of individual differences in task performance across categories. ICCs indicate the proportion of the total variability in the data due to consistent differences among people. They are simultaneously a measure of between–subjects variability and within–subjects similarity (for reviews, see, e.g., Shrout & Fleiss, 1979; Strube & Newman, 2007). Here, ICCs assessed the proportion of the total variability in the data due to differences among subjects that are stable across categories.

We computed two different types of ICCs because we think that a case could be made for each. Because we did not equate categories on task difficulty, we calculated the consistency of individual differences (Shrout and Fleiss, 1979). Like a Pearson correlation, it rewards consistency in the relative ranks of a given participant across categories and does not penalize for overall shifts in category means due to variations in task difficulty or other factors that can produce absolute shifts in a participant’s scores across categories. Because categories were made of novel objects, one could argue that the specific categories we used are a random sample from a hypothetical universe of categories. This perspective would favor a second ICC model (categories as random effects) and so we computed a measure of agreement (Shrout and Fleiss, 1979). Within each ICC type, we computed two measures. The first (denoted ICC1 below) indicates the proportion of variance in performance on one category that is due to individual differences and is analogous to a test–retest correlation coefficient. The second (denoted ICC5 below) applied the Spearman–Brown formula to the ICC1 values and assesses the proportion of variance in composite scores averaged across the 5 categories that is due to individual differences.

To estimate ICCs including participants with incomplete data and compute confidence intervals, we adopted a Bayesian analytic approach previously implemented by Tomarken, Han, and Corbett (2015) (cf. Spielhalter, 2001; Turner, Omar, & Thompson, 2001) using SAS PROC MCMC, Version 9.4 of the SAS System for WindowsTM (Copyright © 2002–2014 SAS Institute Inc). We computed medians of the posterior distribution as our ICC estimates and formed 95% Bayesian Highest Posterior Density (HPD) intervals that represent the narrowest intervals with 95% probability (e.g., Christensen, Johnson, Brascum, & Hanson, 2011).

Confirmatory Factor Analyses.

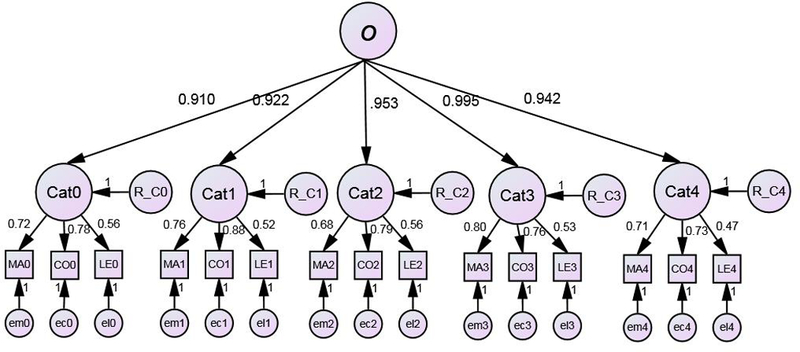
Confirmatory factor analyses were conducted using EQS Version 6.3 (Bentler, 2008). The top panel of Figure 4 depicts the base model that was elaborated in subsequent steps. This model specifies that each of the 15 tasks (Matching (MA), Composite (CO), and Learning Exemplars (LE), for each of the five categories) loads on the factor denoting individual differences in performance on the target category. Rectangles denote observed measures (e.g., MA1) and ovals denote latent variables or, equivalently, factors (e.g., Cat1). The directed arrows from factors to observed measures specifies that a proportion of the variance of each observed task measure is influenced by the latent construct indicating individual differences in ability on a given category. Each directed arrow is associated with a factor–loading coefficient denoting the regression of the observed measure on the latent factor. The double–headed arrows among the category factors specify covariances among the factors. The small circles shown at the bottom of the model (e.g., em0) are residual (i.e., error) terms that denote a combination of reliable influences on observed scores that is specific to that indicator and random measurement error.

Figure 4.

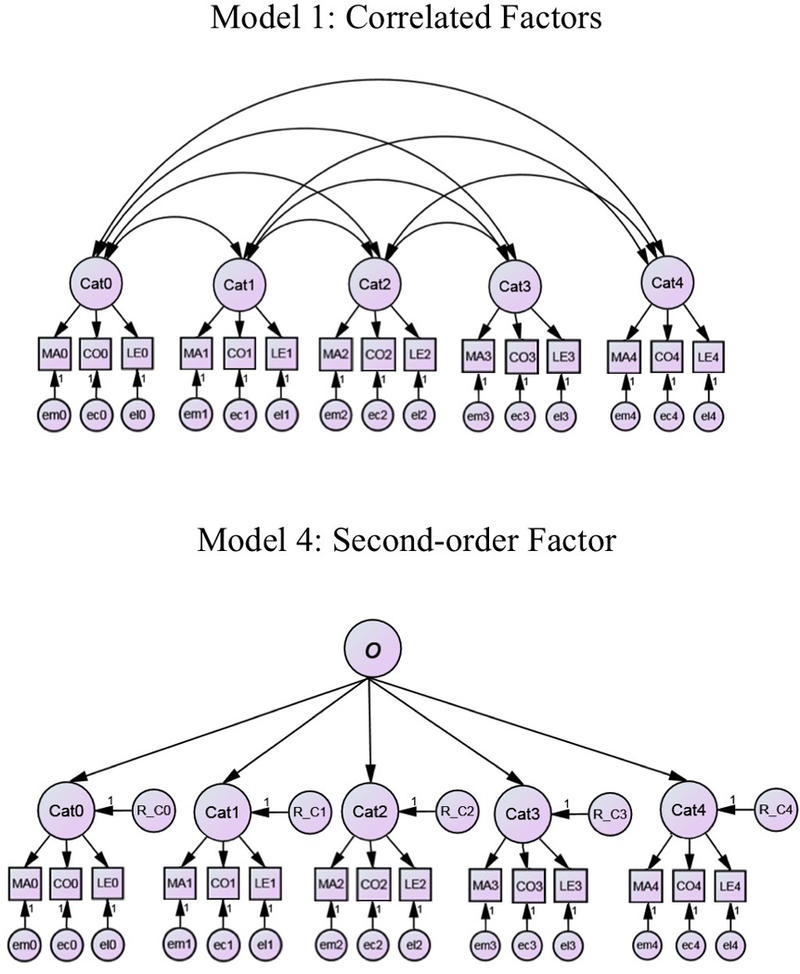
Confirmatory Factor Analysis models for measurement structure of five latent category factors (represented as ovals) each assessed with three measures (indicators) of visual object perception and recognition (represented as rectangles). Both models specify that each of the three tasks assessing performance with a given category loads on the appropriate lower–order category factor. The directed arrows from the factors to each observed measure reflects the specification that a proportion of the variance of each observed task measure (e.g., MA1) is due to the latent construct (e.g., Cat1) of individual differences in ability with a given category. Task–specific correlated errors are not shown for the sake of brevity. Top panel: 1^st–order Correlated Factor Model. Bottom panel: 2^nd–order Factor Model specifying that covariances among category factors are entirely accounted for by one over–arching Object Recognition Ability (o). The R terms (e.g., R_C0) in the 2^nd order model denote the component of the variance of each category factor that is not due to o.

We developed a systematic sequence of models to test both substantive and methodological questions of interest. First, we tested Model 1, depicted in the top panel of Figure 4, that specifies five correlated lower–order category factors. Model 2 assessed whether task–specific influences on the correlations among the observed indicators should be added to the specifications of Model 1. Such influences, often termed “method effects”, could partially account for the inter–correlations among measures of a given task (e.g., MA) assessed across different categories. If so, such effects should be specified and estimated to obtain a better fitting model and less biased estimates of the covariances and correlations among category factors. Although, in theory, the optimal approach would be to specify three method factors, CFA models with a full array of method factors commonly run into failures to converge and inadmissible estimates due to empirical under–identification and other factors (see, e.g., Kenny & Kashy, 1992; Lance, Noble, & Scullen, 2002). We experienced such difficulties when trying to fit models specifying three method factors, one each for the LME, CO, and MA tasks. Instead we estimated task–specific components of variance by specifying covariances among the residual terms (e.g., em0–em4) for a given task. We specified correlated errors among each of the five LME, CO, and MA performance measures, respectively. This correlated uniqueness (CU) (e.g., Lance et al., 2002) approach to modeling method effects is commonly used in confirmatory factor analyses and structural equation modeling (SEM) (Brown, 2015).³ In terms of our sequence of models, we adopted the decision rule that, if, as we expected, the correlated uniqueness model (Model 2) fit better than Model 1 this feature would be included in all subsequent models that we tested. For clarity, Figure 4 omits correlated error terms.

Model 3 built on the best–fitting model from the previous stage and constrained the factor loadings of the three tasks to be equal (i.e., invariant) across the five categories. These constraints were imposed on a within–task cross–category basis (e.g., each of the five MA factor loadings were constrained to be equal). This specification did not reflect a strong prediction of invariance because categories were not equated on task difficulty and other psychometric features. However, this model was of interest because it provided a rather rigorous test of the consistency of individual differences across categories. It additionally allowed us to assess whether the category for which participants received no training (category 0) had a different psychometric structure than the trained categories (1–4).

Model 4 directly tested our prediction that performance across all categories is driven by a higher–order construct that reflects a general visual ability with objects. As shown in the bottom panel of Figure 4, this is a second–order factor model specifying that an over–arching Object Recognition Ability (o) dimension of individual differences influences performance on the lower–order factors. The residual terms (e.g., R_C0) that also influence the lower–order factors represent category–specific influences on individual differences in performance. Model 4 specifies that the higher–order factor is the only determinant of the correlations among the lower–order category factors. It can be shown that this model is a restricted version of the correlated factors model shown in the top panel of Figure 1, such that the relative fit of the two models can be directly compared (see details below). A popular alternative to the second–order factor model is a bifactor model (e.g., Chen, West, & Sousa, 2006; Reise, 2012). The online supplemental discusses bifactor modeling in the present context and why we have chosen to focus on the second–order factor model.

After modeling the internal structure of the performance on the five categories, we addressed the issue of relations to external variables. In model 5, using the best–fitting model from the previous sequence of models 1–4, we examined the correlation between individual differences in performance on the manipulated categories and individual differences in the ability to recognize familiar object categories as assessed by the VET and CFMT. We computed two sets of correlations. The first set is between the observed measures and the latent factor or factors of interest. Using estimated reliabilities, the second set corrected the individual difference measures for measurement error using a latent variable approach in which: 1) Each measure constituted a factor with a single indicator; and, 2) The variances of error terms were fixed at values that yielded the appropriate true score variance estimate for the factor. Random measurement error can attenuate correlations and such reliability corrections are consistent with our emphasis on latent variables.

To estimate all models, we used the robust two–stage estimator (TS) developed by Savalei, Bentler, and colleagues (Savalei & Bentler, 2009; Savalei & Falk, 2014; see also Yuan & Lu, 2008) because of two features of our data: 1) The presence of some missing data; and 2) Non–normality. For the 246 participants included in analyses (i.e., those who completed at least one task for at least one category), 14.94% of the maximal possible number of data points across tasks and categories were missing. In addition, although the most commonly used SEM estimators assume multivariate normality, the set of 15 tasks demonstrated deviations from multivariate normality according to the Doornik–Hansen (2008) test, χ²(30) = 412.42, p < .001 and to Yuan, Lambert, and Fouladi’s (2004) extension to incomplete data structures of Mardia’s (1970) test of multivariate kurtosis, z = 21.78, p < .001. On univariate assessments, the Shapiro–Francia tests of non–normality (Shapiro & Francia, 1972; Royston, 1983) and assessments of skew and kurtosis (D’Agostino, Belanger, & D’Agostino, 1990) indicated significant deviations from normality for all five of the Matching tasks, three of the five Learning Exemplar tasks, and one Composite task (see Table 1). Violations of normality were not extreme but of sufficient magnitude to warrant a robust estimator.

In the first stage of the robust TS algorithm, maximum likelihood (ML) estimates of the vector of means and the covariance matrix of the observed data (including observations with incomplete data) are obtained from a saturated (i.e., unrestricted) model. In the second stage, the specified model is estimated with the covariance matrix generated in the first stage used in place of the observed sample covariance matrix typically used for maximum likelihood (ML) estimation of CFA models. These steps allow for the inclusion of observations with incomplete data. The robust TS estimator uses two additional mechanisms to correct for non–normality: (1) A sandwich–type covariance matrix (Yuan & Lu, 2008) that yields standard errors for parameter estimates that are adjusted for non–normality and for the fact that a two–stage estimation procedure is used; and, (2) The Satorra–Bentler (SB; Satorra & Bentler, 1994) scaled chi–square correction to adjust the overall chi–square test of model fit and fit indices. This correction is used by a variety of SEM estimation methods when data are non–normal and is specifically designed to adjust for non–normal kurtosis. In accord with the statistical theory underlying structural equation modeling (e.g., Cudeck, 1989), all analyses were performed on the covariance matrix estimated in the first–stage and not the correlation matrix. To aid interpretation, however, at several points below we report standardized results (e.g., correlations among factors) calculated either directly (when models allowed fixing factor variances at 1) or from re–scaling of the non–standardized estimates yielded by the TS estimator.⁴

We assessed both the absolute and relative fit of models using several measures. In conventional null hypothesis testing, the hypothesis tested is typically not the researcher’s substantive hypothesis (which is typically aligned with the alternative hypothesis). In contrast, in CFA and structural equation modeling (SEM) in general, the model being directly tested often reflects the researcher’s substantive hypothesis. Thus, non–significant results often favor the researcher’s hypothesis. In terms of absolute fit, although we report the chi–square test of exact fit, it has well–known limitations: 1) There is a strong influence of sample size such that models with only rather trivial misspecifications can be rejected (e.g., Tomarken & Waller, 2003). Although our sample size was on the small side for a SEM analysis, such influence might still have been operative to some extent; 2) It is a measure of model “mis–fit” that favors binary reject/no–reject decisions rather than an evaluation of degree of fit on a more continuous metric; and, 3) It imposes a criterion – that a model fits perfectly – that may be too stringent considering that SEM models have numerous facets and that all models are, at best, approximations (e.g., MacCallum, Browne, & Sugawara, 1996). For this reason, SEM analysts almost always rely on other indices to evaluate model fit. We used the root mean–squared error of approximation (RMSEA; Steiger & Lind, 1980), standardized root mean squared residual (SRMR; Bentler, 1995), and Comparative Fit Index (CFI; Bentler, 1990) to assess model fit. The SRMR is a measure of absolute fit that can be interpreted as the average discrepancy between the correlations among the observed variables and the correlations predicted by the model. Lower values indicate better fit. The RMSEA is an estimate of a parsimony–corrected fit index because it assesses the degree of discrepancy between the observed and model–implied covariances while also penalizing for model complexity (e.g., for equivalent discrepancy it rewards the more parsimonious model that estimates fewer parameters and has more degrees of freedom). Smaller values indicate better fit. The RMSEA is typically treated as the degree to which a model fits approximately in the population, with values < .06 typically taken to indicate close fit (e.g., Hu & Bentler, 1998, 1999). Confidence intervals can also be formed around the estimated RMSEA value in a given sample. We computed the RMSEA estimate and confidence bounds for non–normal data that was developed by Li and Bentler (2006; see Brosseau–Liard, Savalei, & Li, 2012) and that is an option in EQS. The CFI is an index of the incremental or comparative fit of the target model relative to a baseline model of independence in which all the covariances among the observed indicators are fixed at 0. CFI values vary from 0 to 1, with values closer to 1 indicating better fit. Given that the comparison is to the independence model, the CFI often tends to indicate better fit than the other indices. Based on simulations, Hu and Bentler (1998, 1999) recommend the following criteria for adequate fit on these measures: SMSR ≤ .08, RMSEA ≤ .06, and CFI ≥ .95. The RMSEA and CFI were computed using the Satorra–Bentler scaled chi–square values.

A primary focus was the comparison of alternative models, most of which were nested versions of one another. Model A is nested in model B if it is a restricted version of model B; that is, if it is identical to model B except that certain parameters that are freely estimated in B are restricted in A by being fixed at specific values (often 0) or constrained to be equal to other parameters or combinations of parameters. Nested models were compared using the scaled χ² difference test (Satorra & Bentler, 2001) that is appropriate when the Satorra–Bentler (S–B) correction for non–normality is used. We used the version of the scaled difference test developed by Satorra and Bentler (2001) that computes a scaling factor for the test as

$$c_{dif}=\frac{\left[d{f}_{M_0}\times c_{M_0}-d{f}_{M_1}\times c_{M_1}\right]}{d{f}_{M_0}-d{f}_{M_1}},$$

Where $d{f}_{M_0}$ are $d{f}_{M_1}$ the degrees of freedom for the more and less restrictive models, respectively, and $c_{M_0}$ and $c_{M_1}$ are the scaling factors for the two models (equal to the ratio of the uncorrected χ² value for the test of exact fit to the S–B corrected value for each model) (e.g., Bryant & Satorra, 2012). In turn, the scaled difference test is computed as the difference between the uncorrected tests of exact fit divided by c_dif, with degrees of freedom equal to the difference in degrees of freedom between the two models. We used an Excel macro written by Bryant and Satorra (2013) to conduct the S–B difference tests.⁵ If restrictions imposed by Model A do not impair overall model fit relative to Model B, the result would be a non–significant χ² test. Thus, in the context of nested tests, non–significant results often serve to corroborate the researcher’s hypotheses.

In addition, we report values of the Akaike Information Criterion (AIC; Akaike, 1973) and the Bayesian Information Criterion (BIC; Raftery, 1995; Schwarz, 1978) to convey the relative fit of both nested and non–nested models. Both indices penalize for model complexity, operationalized as the number of free parameters estimated by a given model. To compute these indices. we used what is probably the most common approach in SEM analyses, adding to the chi–square test of overall fit a penalty factor that is a function of the number of free parameters estimated by a model (denoted below as k).

We computed these indices using the following formulae:

$$\text{AIC}={\chi }_{SB}^2+2k$$

$$\text{BIC}={\chi }_{SB}^2+k\ln (N)$$

We also present a small–sample corrected version of the BIC (e.g., Enders & Tofigi, 2008), computed as,

$$\text{SBIC}={\chi }_{SB}^2+k\ln \left(\frac{N+2}{24}\right)$$

Lower values of all three indices indicate better fit. The information indices were computed using the Satorra–Bentler scaled chi–square values.

A major focus of our analyses was not simply evaluation of model fit but examining and interpreting parameter estimates of interest (e.g., correlations among factors). Much of the discussion of results below emphasizes model fit not only because it is important in its own right but also because good fit can be considered a necessary condition for examination and evaluation of parameter estimates.

Results

Univariate Descriptive Statistics

Reliability (Cronbach’s alpha), mean performance measures (mean accuracy or d’) and tests of normality (skewness, kurtosis, Shapiro–Francia normality test) for the test tasks and familiar object recognition measures (CFMT and VET) are shown in Tables 1 and 2, respectively. All tasks demonstrated good internal consistency reliability and 10 of the 15 tasks demonstrated statistically significant violations of normality. It is also of interest that average performance on the Learning Exemplar task ranged from .48 to .68 depending on the category. Coupled with the fact that per–subject proportions were calculated across 48 trials, these values indicate that ceiling and floor effects were not significant factors and that transformations of proportions (e.g., computing odds or log odds) were not necessary.

Table 2.

Reliability (Cronbach’s α), mean performance measures, and tests of normality for the CFMT and VET sub−scales.

	N	Cronbach’s α	Mean (SD) Accuracy (% correct)	Skewness	Kurtosis	Shapiro−Francia Normality Test
CFMT (faces)	245	.90	63.27 (14.23)	−0.22	2.07***	3.26*
VET Subscales
Birds	243	.83	68.98 (13.44)	−0.52***	3.44	3.61*
Butterflies	241	.80	60.17 (13.71)	−0.39*	2.82	2.50*
Cars	243	.80	59.60 (14.60)	0.17	3.09	1.11
Houses	243	.83	75.90 (13.10)	−0.33*	2.63	2.05
Planes	242	.77	70.38 (12.02)	−0.40	3.35	3.39**

Note. Under normality, the expected values of measures of skewness and kurtosis are 0 and 3, respectively. Under normality, when scores are sampled from a normal distribution, the median value of the Shapiro−Francia V’ measure equals 1 (Royston, 1991).

^*p < .05

^**p < .01

^***p < .001

Effect of Training

Because we did not equate categories for difficulty, we cannot directly compare mean performance to test for a training effect (in fact, Table 1 suggests that the non–exposed category was generally one of the easier categories). However, the composite task has been used in previous studies to assess training effects, and controls for difficulty differences across categories as it includes its own baseline, allowing a within–category measure of whether training had an influence on performance. Specifically, a difference in performance between congruent and incongruent trials (in either accuracy or RT) is a common marker of face–like expertise (see Richler & Gauthier, 2014), and has been observed following individuation training for novel objects like the ones used here (e.g., Chua et al., 2015; Wong et al., 2009). Indeed, we based the composite task parameters on Wong et al. (2009), who found slower response times on incongruent compared to congruent trials only in participants trained to individuate objects from the tested category.

To test whether a similar effect of training was observed here on the same dependent measures as in Wong et al. (2009), we conducted 2 × 2 repeated measures ANOVAs on sensitivity (d’) and correct RT in the composite task with category (untrained vs. average of trained categories) and congruency (congruent vs. incongruent) as factors. The qualitative effects were the same for both RT and d’ (see Figure 5). There were significant main effects of training (RT: F_1,219 = 9.18 , MSE = 15999.67, p = .003, ηp² = .04; d’: F_1,219 = 81.59 , MSE = .40, p < .001, ηp² = .27) and congruency (RT: F_1,219 = 17.26, MSE = 1561.11, p < .001, ηp² = .07; d’: F_1,219 = 7.06, MSE = .18, p = .008, ηp² = .03). More importantly, the interaction between training and congruency was significant (RT: F_1,219 = 46.34, MSE = 1659.16, p < .001, ηp² = .18; d’: F_1,219 = 8.13, MSE = .16, p = .005, ηp² = .04), such that there was a significant congruency effect for the trained categories (RT: F_1,219 = 99.60, MSE = 978.16, p < .001, ηp² = .31; d’: F_1,219 = 37.20, MSE = .07, p < .001, ηp² = .15), but not the untrained category (RT: F_1,219 = 2.85, MSE = 2242.11, p = .09, ηp² = .01; d’: F_1,219 < .00, MSE = .27, p = .99, ηp² < .00)⁶.

Figure 5.

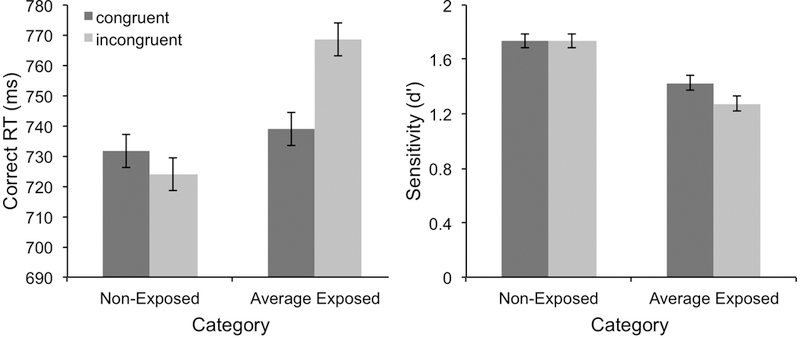
Mean correct RTs (left) and sensitivity (d’; right) for congruent and incongruent composite task trials for the non–exposed category and average of exposed categories. Error bars show 95% confidence intervals for within–subject effects.

We also computed correlations between all categories for each task to determine whether some amount of experience is necessary for individual differences in ability to be reflected in performance. As indicated in Table 3, for each of the three tasks, the means of the correlations between the untrained and trained categories were almost identical to the average of the correlations within trained categories. Thus, although training influenced performance, resulting in effects similar to those seen in previous studies (e.g., Wong et al., 2009) only for trained categories, it does not influence the expression of individual differences. We therefore included the untrained category in the ICC and CFA analyses. As described below, the results of specific CFA analyses also underscore the similarity between the untrained category and the trained ones.

Table 3.

Correlations (Pearson’s r) between all categories for each task. Correlations with the untrained category are highlighted in gray. N per cell ranges from 182 to 207. All correlations are significant at p < .001. (See Figure 2 for number−category mappings).

Category	0	1	2	3	Mean untrained	Mean trained
Learning Exemplars					.50	.49
1	.43
2	.53	.54
3	.52	.52	.56
4	.50	.32	.53	.42
Matching Task					.54	.52
1	.52
2	.S	.45
3	.60	.46	.56
4	.52	.55	.50	.59
Composite Task					.61	.62
1	.64
2	.64	.64
3	.60	.66	.59
4	.60	.61	.61	.59

Note. Correlations were Fisher−transformed before averaging.

Intraclass Correlations

Intraclass correlations and 95% HPD intervals are shown in Table 4. Several patterns are evident. First, the ICC1 values indicate that a significant proportion of the variance in task performance on any single category was attributable to individual differences among participants. Across the three tasks, when consistency of performance was assessed (i.e., category is modeled as a fixed effect), approximately 50–60% of the total variability in the data was due to individual differences. When category was modeled as a random effect and agreement assessed, the proportions of variance were lower, especially for the LE and MA tasks, but by no means trivial. Measurably lower correlations for the agreement measure would be expected in this case because no attempt was made to equate categories on difficulty level. Finally, the ICC5 values indicating the reliability of task performance averaged across categories were quite high and either approached or exceeded the expected range (≥.70) for measures of individual differences in the areas of personality and temperament. This conclusion holds for both measures of consistency and agreement. These results exemplify the beneficial effects of aggregation on reliability and consistency (e.g., Rushton et al., 1983).

Table 4.

Intraclass correlations for each measure.

	ICC1		ICC5
Measure	Consistency	Agreement	Consistency	Agreement
Learning Exemplars	.50 (.44,.55)	.34 (.17,.46)	.83 (.80, .87)	.72 (.52,.82)
Matching Task	.49 (.43,.56)	.31 (.15,.43)	.83 (.79, .86)	.69 (.49,.81)
Composite Task	.62 (.56,.68)	.55 (.40,.65)	.89 (.87, .91)	.86 (.78,.90)

Note: ICC1 estimates both the average correlation in performance among pairs of categories and the proportion of variance in a given category due to between−person differences. ICC5 is the estimated correlation between the aggregate of scores across the five categories and a hypothetical equivalent set of aggregate scores. It estimates the proportion of variance in the average score across categories due to between−person differences. 95% Bayesian highest posterior density (HPD) intervals are shown for each measure. The category factor is modeled as a fixed effect when consistency is assessed and as a random effect when agreement is assessed.

Confirmatory Factor Analysis

Fit statistics for the sequence of CFA models are provided in Table 5. As summarized above, we relied more on other indices than the chi–square test of exact fit. Model 1 specified five correlated category factors, with the relevant LE, MA, and CO task performance measures serving as the observed indicators for each factor. As anticipated, the overall fit of this model was unsatisfactory because it omitted parameters reflecting the correlations within a task (e.g., MA) across categories (see Table 5). For example, the RMSEA was clearly above the range typically recommended for evaluation of fit as adequate. Model 1 also was associated with several inadmissible estimates (e.g., covariances among factors that implied correlations greater than 1) that may also indicate model mis–specification, although other factors (e.g., the generally high correlations among variables) may also have contributed.

Table 5.

Fit statistics for confirmatory factor analyses.

Model	Description	df	Robust χ 2	RMSEA (90% CI)	CFI	SRMR	AIC	BIC	SABIC
1	Correlated Categories (No Task Effects)	80	218.17, p < 001	.116 (.098, .134)	.977	.078	298.17	438.38	311.59
2	Model 1 +Errors Across Tasks	50	73.95, p=.02	.050 (.022, .073)	.996	.030	213.95	459.32	237.43
3	Model 2 +Within−task Invariant Loadings on Category Factors	58	89.56, p=.005	.054 (.030, .074)	.995	.069	213.56	430.89	234.35
4	Model 3+Second−order Category Factor	63	92.01, p=.01	.049 (.025, .070)	.995	.048	206.01	405.82	225.22
5	Model 4 + CFMT and VET measures	147	216.34 P <.001	.050 (.035, .064)	.967	.064	384.34	678.79	412.51

Note: Robust χ2 =Satorra−Bentler robust chi−square test of overall fit generated by the Savalei−Bentler robust two−stage estimator. RMSEA = root mean squared error of approximation. CFI = Comparative Fit Index. SRMR = standardized root mean squared residual. AIC = Akaike Information Criterion. BIC = Bayesian Information Criterion. SABIC = Small− sample corrected Bayesian Information Criterion. Lower scores on the RMSEA, SRMR, AIC, BIC, and SABIC and higher scores on the CFI indicate better fit. Hu and Bentler (1998, 1999) recommended the following criteria for adequate fit on the first three measures: CFI ≥ .95, RMSEA ≤ .06, and SRMR ≤ .08. Because Model 5 includes measures not included in Models 1−4, its values for the AIC, BIC, and SABIC are not directly comparable to those of Models 1−4.

As expected, when correlated errors among the observable task indicators were added in Model 2, the fit was notably improved (nested χ²(30) = 108.61, p < .0001). The values of the RMSEA, CFI, and SMMR all indicate that this model met conventional criteria for adequate fit. Although the AIC and SABIC values for Model 2 were notably lower than the corresponding values for Model 1, somewhat surprisingly the model 2 BIC was higher. This discrepancy is likely due to the fact that the BIC more strongly favors parsimony than the other indices. Nevertheless, the clear weight of the evidence and the plausibility of task–specific shared variance favors Model 2 relative to Model 1.

Using Model 2, we also assessed whether the correlations involving the factor for the untrained category (denoted category 0) were different from the correlations involving only the other four categories. We imposed the linear constraint that the average of the four correlations involving category 0 was equal to the average of the six correlations not involving category 0. That this constraint did not produce a significant impairment in fit relative to Model 2 (S–B nested χ² (1) = 1.51, p = .22) indicates that correlations involving the untrained category were not unique. Similarly there were no differences when the same linear constraint was imposed on factor covariances rather than correlations (S–B nested χ² (1) = 0.80, p = .37).

We also assessed whether correlations within the two relatively visually similar Ziggerin (categories 0 and 3) and the two Greeble (categories 1 and 2) stimulus types were higher than the between–type correlations. We conducted four sets of analyses, each of which compared within–type to across–type correlations. Specifically we tested whether: (1) r₀₃=r₀₁=r₀₂; (2) r₀₃=r₁₃=r₂₃; (3) r₁₂=r₀₁=r₁₃; and, (4) r₁₂=r₀₂=r₂₃. In all four cases, Satorra–Bentler nested chi–square tests indicated that these equality constraints induced no significant impairment in model fit, or even trends, relative to Model 2 (χ² (2) = 3.03, p=.22;χ² (2) = 1.69, p=.44;χ² (2) = 2.58, p=.28; χ² (2) = 1.75, p=.42, respectively). Thus, correlations within a stimulus type were not different from correlations across stimulus types.

Model 3 built upon Model 2 but imposed the restriction of equal factor loadings across categories (e.g., the loadings of MA1–MA5 on their respective category factors were constrained equal). This model also fit adequately (see Table 5). Although the value of the SRMR clearly increased in Model 3 relative to Model 2, it still falls within the conventional range of good fit on this measure. The other 5 indices all adjust for complexity to some degree (i.e., rewarding more parsimonious models) and indicate much smaller differences between the two models (RMSEA, CFI) or favor Model 3 (AIC, BIC, SABIC). A nested chi–square test indicated that the restrictions imposed by Model 3 did not significantly impair fit relative to Model 2, although caution is necessary because the significance level was very close to the rejection threshold (nested χ²(8) = 15.36, p = .052). On balance, we think that these results indicate that the restrictions imposed by Model 3 fit well enough to use it as the starting point for the next steps in the modeling sequence. However, we report below the fit of separate higher–order factor models that include and do not include the restrictions on the loadings. Overall the Model 3 results indicate that the factor structure of the three tasks could be considered reasonably invariant across categories. Such invariance is another indication that that the untrained category (0) did not have a unique structure relative to the other categories.

A notable feature of Model 3 (also characteristic of Model 2) is the magnitude of the association among the category factors. Table 6 shows the correlations among the factors generated by the standardized solution and 95% bias–corrected bootstrap confidence intervals (Williams & MacKinnon, 2008) around these values. As indicated, the correlations among the category factors were quite high, ranging from .82 to .96 (mean r = .895), with even the lower bounds of confidence intervals at very high values (all were greater than .73).

Table 6.

Correlations among the Category Factors (Model 3)

Category	0	1	2	3	4
0	––––––––
1	.82 (.74,.89)	––––––––
2	.87 (.78,.96)	.90 (.81,.98)	–––––––
3	.91 (.81,.98)	.96 (.88,1.00)	.93 (.85,1.00)	–––––––––
4	.92(.84,.99)	.84(.74,.92)	.92(.85,1.00)	.91(.80,.99)	–––––––––

Note: All ps < .001. 95% bias–corrected bootstrap confidence intervals are shown in parentheses. When an upper bound slightly exceeded 1.00,it was fixed at 1.00.

Using Model 3 as a starting point, Model 4 specified the higher–order factor (o) to account for the covariances and correlations among the category factors. This model did not significantly impair fit compared to Model 3 (nested χ²(5) = 2.11, p = .83) and fit well in an absolute sense (see Table 5). Indeed, as indicated by Table 5, the Model 4 values of the fit indices that most explicitly penalize for model complexity were the lowest (RMSEA, AIC, BIC, and SABIC) or essentially tied for the lowest (CFI) among the four models tested. This provides support for our hypothesis that performance across novel object categories can be accounted for by a single overarching Object Recognition Ability factor.

Model 4 is shown in Figure 6 with standardized parameter estimates. The lower–order loadings of the observed measures on factors are generally high, with values for MA, CO and LE ranging, respectively from .68 to .80, .73 to .80, and .47 to .56.⁷ The most notable feature of Model 4 is that the standardized loadings from the higher–order factor (o) to lower–order category factors are quite high (.910–.995; all ps highly significant based on bootstrap assessments), suggesting that the higher–order o factor accounts for on average 89% of the variance in lower–order category factors (% variance = .83, .85,.91,.99, and .89 for categories 0–4). Because of the borderline acceptability of the model imposing invariant factor loadings, we also specified a higher–order factor model in which the lower–order loadings (i.e., of observed indicators on category factors) were not constrained to be equal and compared its fit to model 2 rather than model 3. This model also fit well in an absolute sense (e.g., Satorra–Bentler χ²(55) = 81.10, RMSEA=.050), with no impairment in fit relative to model 2 (nested χ²(5) = 7.16, p

Figure 6.

Higher–order factor model standardized solution (both factors and observed measures standardized). For the sake of clarity, correlated errors among within–task errors are not shown but were specified as part of the model. Factor loadings for a given task are not invariant because invariance was imposed on the non–standardized solution based on covariances instead of correlations.

Correlations Between o and Familiar Object Recognition

Results summarized so far indicate that a single higher–order factor, o, accounts for performance across novel object categories. To test whether o also predicts recognition performance on familiar object categories, we specified a fifth model that examined correlations between o and each familiar object category (faces measured with the CFMT; birds, butterflies, houses, cars, and planes measured with the VET). Table 7 presents correlations when the familiar object measures were corrected for unreliability (using the values of coefficient alpha summarized in Table 2), and uncorrected values. We reliability–corrected the latter by specifying each individual measure as a latent variable and fixing the error variance and factor loading at appropriate values such that the proportion of variance of the observed measure accounted for by the latent factor equaled the reliability of the variable. We then allowed these latent variables to be freely correlated with each other and, most importantly, with o. Other model specifications were identical to that of Model 4. As indicated by Table 5, this model fit well. Because Model 5 introduces several additional variables not included in Models 1–4, its fit indices should not be directly compared to those of the other models. As shown in Table 7, all corrected correlations were statistically significant, with o more highly correlated with performance on birds, butterflies, houses, and planes than faces and cars. The un–corrected correlations shown in the right–hand columns are slightly attenuated but still statistically significant.

Table 7.

Correlations between o and each familiar object category.

Predictor	Reliabilty Corrected		Un–corrected
	r	r2	r	r2
Faces	.28	.08	.26	.07
Birds	.43	.18	.39	.15
Butterflies	.60	.36	.54	.29
Cars	.27	.07	.24	.06
Houses	.47	.22	.42	.17
Planes	.53	.28	.46	.21

Note: All ps <.001

Study 2

In Study 1 we found evidence for o, a higher order factor supporting object recognition performance across different tasks and categories. In Study 2, as an initial effort to establish the divergent validity of o, we explore the extent to which it is related to a battery of cognitive and perceptual constructs, as well as measures of personality. The primary goal is to quantify how much of the individual differences captured in our tasks remain after controlling for such factors. To this end, we measured performance on all three tasks with two of the object categories from Study 1. Although we use a smaller sample in Study 2, we expected to replicate results from Study 1 with moderate to strong relations between categories and object recognition tasks but, at the same time, evidence for discriminant validity.

Prior work with LE tasks with both familiar and novel objects found that performance for each object recognition task was correlated with IQ (r ~ .1–.3) but that virtually none of the shared variance among different categories was explained by IQ (Richler et al., 2017). Here, we also assess IQ, using tests associated with fluid intelligence (gF) and targeting the ability to solve new problems (Engle, Tuholski, Laughlin & Conway, 1999). We expect that despite moderate correlations with some individual object recognition tasks, most of the shared variance between object recognition tasks will not be accounted for by IQ.

Aside from IQ, we selected a variety of tasks from prior individual differences research that could be plausibly expected to account for some of the variance in o (note that our goal was not to decompose o into its constituent parts). We included tasks that tap into different aspects of executive function (Miyake & Friedman, 2012): two Stroop tasks and a shifting task that requires switching between mental sets. We also included a measure of visual short–term memory capacity and a measure of local/global perceptual style. Finally, because our approach requires completion of a large number of tasks (over many sessions in Study 1), we were concerned that more conscientious subjects may have performed better, accounting for some of the shared variance across tasks and categories in Study 1. In Study 2 we gave subjects a personality inventory that includes a measure of conscientiousness. Aside from this self–report measure, the contribution of any aspect of motivation or personality to our object recognition tasks would also be evidenced by strong correlations between object recognition tasks and any of the other performance measures mentioned above.

Methods

Participants

We analyze data for fifty–four participants (13 male, 41 female, 0 not disclosed; mean age = 20.4 years; 50 right–handed). Sixty–six Vanderbilt University Community members were originally recruited (15 male, 51 female, 0 not disclosed; mean age = 20.5 years; 61 right–handed). Four participants only completed the first session and were thus excluded. Additionally, data from 5 participants were excluded because of median RTs less than 200 ms for Composite or Matching Tasks and/or median RTs less than 1000 ms for individual Learning Exemplars categories. Lastly, all data from 3 additional participants were excluded because of too many (>57 out of 144 trials) timed–out trials on the Composite task (on which trials timed out after 3 seconds). Thus, data from 12 total participants were excluded. Power calculations for Pearson correlations indicated that with n=54 we would have 80% power to detect a correlation of .37 or higher and 70% power to detect a correlation of .33 or higher. Note that our primary concern was not so much whether there was any correlation between our object recognition measures and individual difference measures but whether there was a sufficiently large correlation to warrant significant concern that the strong correlations between categories were largely due to associations with individual difference measures.

Of these remaining 54 participants, Fluid IQ data for 3 participants, Stroop data for 1 participant and VSTM data for 1 participant were missing due to computer error, but the rest of their data were analyzed. Finally, due to experimenter error, Stroop data from 4 additional participants were missing after the first session. Thus, these participants completed the Stroop task again at the beginning of the second session.

Test Sessions and Tasks

Participants completed all tasks in two 1.5–hour sessions occurring a maximum of seven days apart and were compensated a total of $45. Because the results of Study 1 suggested that measurement of o was not strongly influenced by whether participants received experience in the Space Invaders Game or not, we did not include a training phase in Study 2. In the first session, participants completed the Stroop tasks, the IPIP, Learning Exemplars–0, Composite–0, Matching Task–0, L–EFT and Number/Letter Shifting Task. In the second session, participants completed the Fluid IQ tasks, the Learning Exemplars–2, Composite–2, Matching–2 and VSTM tasks. Participants completed all tasks in the same order and were allowed to take a break between each task.

Learning Exemplars Task.

This task was identical to that used in Study 1. Here, participants completed the task for categories 0 and 2.

Composite Task.

Participants completed this task as in Study 1, for categories 0 and 2, with the following modifications. Because of the high reliability of this task in Study 1, we shortened the task by using a random selection of only half of the trials (144 instead of 288), with the constraints of keeping the number of trials of each condition type equal (same/different, top/bottom, congruent/incongruent).

Matching Task.

Participants completed this task as in Study 1, for categories 0 and 2, with two modifications. Because reliability of the previous matching tasks was high, to shorten the task we randomly selected half of the original 360 trials to include in this task. Study objects were all presented for 300 ms (instead of both 150 ms and 300 ms in Study 1).

Stroop.

In the first of two blocks, participants reported the color of a word and the word was presented in either a congruent or incongruent color. In a second block, participants reported the quantity of a group of numbers while the numbers themselves were either congruent or incongruent with the quantity (e.g., “4444” is congruent and “33” is incongruent). In each block, trials began with a 500 ms fixation cross followed by a 250 ms inter–stimuli interval and then the stimuli (either words or numbers) presented until a response was made. The Stroop task taps into individual’s selective attention and cognitive flexibility. We calculated a Stroop interference index using the average response time on all correct congruent trials minus that on all correct incongruent trials.

Number/Letter Shifting.

We modified the shifting task from Friedman et al. (2008). Here, we only used the number–letter shifting version of the task (adapted from Rogers and Monsell, 1995). Participants first saw a square appearing above or below a horizontal midline dividing the screen in half for 150 ms. Then a number–letter (5G) or letter–number (A4) pair appeared within the square. When the pair was in the square above the line, participants indicated whether the number was odd or even (2, 4, 6, and 8 for even; 3, 5, 7, and 9 for odd) and when the pair was in the square below the line, participants indicated whether the letter was a consonant or a vowel (G, K, M, and R for consonant; A, E, I, and U for vowel). Participants were instructed to be “as accurate and fast as possible; accuracy is more important.” Two 24–trial practice blocks and 6 warm–up trials at the beginning of each block were not analyzed. Trial order was randomized but constrained such that no more than four switch trials could occur in a row (randomization occurred once and then every subject completed trials in this same randomized order). To prevent item–specific negative priming, trial order was also constrained so that the stimulus on a switch trial was never the same as that on the previous trial. To index shifting ability, we calculated the “switch–cost” (Friedman et al., 2008), which is the difference between the mean reaction times on correct trials in which no switch occurred and mean reaction times on correct trials in which a switch occurred. Individual trials (3.4%) were excluded because reaction times were less than 200 ms or more than 5000 ms.

Leuven Embedded Figures Test (L–EFT).

In the L–EFT, participants have to find a target shape embedded within a larger figure. Participants were shown the target shape and three figures simultaneously and chose which of the three figures contained the target shape. Participants could make a response via button press at any point, but after three seconds, the target shape and three options disappeared. There were two practice trials followed by 64 experimental trials. The L–EFT stimuli were developed specifically to vary in perceptual grouping features like closure, symmetry and complexity so that trial difficulties varied (de–Wit et al., 2017). The test is considered an index of perceptual style (local information processing). We indexed performance using response times for correct answers.

Fluid Intelligence (FIQ).

Following several previous studies (e.g., Redick et al., 2013; Hambrick et al., 2007; Hambrick et al., 2008. Van Gulick et al., 2016), we included three different tasks known to load highly on fluid intelligence (gF) and targeting the ability to solve new problems (Engle, Tuholski, Laughlin & Conway, 1999). There were specific time limits for each block, but no time limits for a response on each trial and within each block, trials were ordered from easiest to most difficult with practice trials preceding every block. In the first task, participants completed as many of 18 trials from the Raven’s Advanced Progressive Matrices (RAPM; Raven, Raven, & Court, 1998) as possible in ten minutes. In the RAPM, a 3 × 3 array of images is presented in which the bottom–right image has been removed. Participants must choose with of eight options is the removed piece based off of patterns within the matrix. This task was followed by a block of Letter Sets (Ekstrom, French, Harman, & Dermen, 1976) in which participants saw five sets of letter strings with all but one of the letter strings following a specific rule. Participants had seven minutes to complete as many of the 30 trials as possible. The final task was number series (Thurstone, 1938), in which each trial presented an array of 5–12 numbers forming some type of pattern. Participants had to choose which of 5 number options would follow the presented array (e.g. if the array was 1 2 3 4 5, the correct response was 6). Participants had five minutes to complete as many of the 15 trials as possible. Fluid intelligence was indexed by the total number of correct responses made for all three tasks given time constraints.

Visual Short–Term Memory Task.

To index visual short–term memory capacity, we used a change detection task in which participants reported if a change occurred between two arrays of colored squares (Xu et al., 2017). Each trial began with a 1,000 ms fixation, followed by an array of colored squared presented for 150 ms. After a 1,000 ms delay period, a probe square appeared at one of the square locations and participants responded if this square was the same or a different color from the original square presented at that location in the array. Here, we only presented arrays of six squares and, based on the results reported in Xu et al., (2017), we used three blocks of 50 trials each with 30 seconds rest in between each block. Trials were randomized across participants. Performance was scored as the total number of correct responses over the 150 trials.

International Personality Item Pool (IPIP).

The IPIP (Goldberg, 1999) requires participants to rate 50 items on a 5–point Likert scale from “Very accurate” to “Very inaccurate.” Subjects completed a paper–version of the questionnaire and were not given any time limit. An average score is computed for each Big–Five personality factors (Extraversion, Agreeableness, Conscientiousness, Emotional Stability, Intellect).

Results

Means and reliability indices for each measure are found in Table 8. The shorter versions of the MA and CO tasks provided measurements that were as reliable as in Study 1. Reliability was above .8 in all cases except the Stroop cost (.50, difference scores often have limited reliability and in the present case it is due to the high correlation between congruent and incongruent RTs, r =.92), and the short versions of each FIQ task (.72–.79), although their combined reliability is .87.

Table 8.

Mean and standard deviations, and reliability (Cronbach’s α for Cat 0 and Cat 2 tasks, Fluid Intelligence and IPIP, average of 10 split–half estimates for other measures).

	N	Mean (SD)	Reliability
Category 0
Learning Exemplars (% correct)	54	66.40 (16.26)	0.87
Matching Task (d’)	54	1.67 (.52)	0.88
Composite Task (d’)	54	1.61 (.73)	0.91
Category 2
Learning Exemplars (% correct)	54	66.44 (17.17)	0.91
Matching Task (d’)	54	1.57 (.67)	0.96
Composite Task (d’)	54	1.59 (.86)	0.95
Stroop Cost (delta RT)	53	80.35 (46.79)	0.50
Shift Cost (delta RT)	54	371.29 (286.79)	0.91
L–EFT (RT)	54	1935.10 (267.45)	0.87
Fluid Intelligence
Ravens (no. correct)	51	11.78 (2.98)	0.72
Letter Sets (no. correct)	51	17.67 (3.72)	0.79
Number Scores (no. correct)	51	10.27 (2.56)	0.72
Visual STM (% correct)	53	68.62 (10.43)	0.88
IPIP
Conscientiousness	54	35.02 (8.28)	0.89
Extraversion	54	30.43 (8.41)	0.90
Emotional Stability	54	29.70 (8.16)	0.90
Agreeableness	54	41.13 (5.67)	0.87
Intellect	54	36.98 (6.29)	0.83

Correlations among Observed Measures

The first two columns of Table 9 present the zero–order Pearson correlations between the cognitive and personality measures and performance on each of the two categories. To form an overall category score for each participant we first standardized each of the three category tasks (CO, MA, and LE) across participants and computed the mean of the three standardized scores for each participant. As expected, the correlation between the Cat0 and Cat2 aggregate scores was very high (r = .71, 95% CI = .54 to .82).

Table 9:

Zero–order, Partial, and Decomposed Correlations for Observed Data

Individual Difference Measure	Cat 0 Pearson r	Cat 2 Pearson r	Cat0/Cat2 Partial r	Component of Cat0/Cat2 r Through Ind. Dif. Path	Component of Cat0/Cat2 r Through Residual Path	Proportion: $\left(\frac{\text{Residual}\hspace{0.33em}\text{Component}}{\text{Cat}0/\text{Cat}2\text{r}\hspace{0.17em}\text{=}\hspace{0.17em}\text{(=}\hspace{0.17em}.71\text{)}}\right)$
Ravens	.41 (.14,.62)	.24 (−.03,.48)	.68 (.47,.81)	.10 (−.02,30)	.60 (.38,.76)	.86 (.59,1.02)
Letter Sets	.32 (.04,55)	.31 (.02,.51)	.67 (.44,.82)	.10 (.01,.26)	.60 (.38,.76)	.86 (.62,.99)
Number Scores	.46 (.21,.64)	.42 (.17,.62)	.63 (.41,.78)	.19 (.04,.39)	.51 (.30,.67)	.72 (.46,.94)
Stroop Cost	−.16 (−.42,.11)	−.19 (−.45,.10)	.69 (.50,.83)	.03 (−.00,.12)	.67 (.46,.81)	.96 (.82,1.00)
Shift Cost	−.37 (−.61,−.13)	−.33 (−.56,−.06)	.67 (.44,.81)	.12 (.01,.29)	.58 (.37,.75)	.82 (.61,.98)
L−EFT	.05 (−.23,.31)	−.00 (−.28,.26)	.71 (.52,.84)	−.00 (−.01,.05)	.71 (.51,.83)	1.00 (.93,1.01)
Visual STM	.23 (−.04,.49)	. 37 (.12,.57)	.69 (.49.83)	.09 (−.00,.24)	.63 (.43,.76)	.88 (.68,1.00)
Conscientiousness	−.26 (−.47,.02)	−.17 (−.40,.10)	.70 (.51,.83)	.04 (−.01,.21)	.67 (.46,.80)	.94 (.71,1.01)
Extraversion	−.00 (−.27,.26)	−.04 (−.30.21)	.71 (.52,.84)	.00 (−.01,.06)	.71 (.52,.83)	1.00 (.92,1.01)
Emotional Stability	−.03 (−.31,.25)	.05 (−.24,.30)	.71 (.52,.84)	−.00 (−.02,.06)	.71 (.51,.83)	1.00 (.91,1.02)
Agreeableness	−.12 (−.34,.16)	−.09 (−.34,.19)	.71 (.51,.84)	.01 (−.00,12)	.70 (.50,.82)	.98 (.84,1.01)
Intellect	−.02 (−.28,.26)	.13 (−.13,.39)	.72 (.52,.84)	−.00 (−.03,.08)	.71 (.52,.83)	1.00 (.89,1.05)

Note. Zero−order correlation between Cat0 and Cat2 = .71. Partial correlations between Cat0 and Cat2 adjust for individual difference measures. Component indices decompose the zero−order correlation between Cat0 and Cat2 into components through the individual difference measure and the residual paths. Bias−corrected and adjusted (BCA) bootstrap confidence intervals are shown in parentheses for zero−order and partial correlations and percentile bootstrap confidence intervals are shown for other indices. Univariate bootstrapping was used to generate samples for zero−order correlations while bivariate bootstrapping was used for other indices. Estimates are bolded when confidence intervals do not include 0. Upper bounds for proportions can exceed 1 due to negative values for the component of the correlation through the individual difference path.

Similar to Study 1, normality assessments indicated that most of the measures had at least some degree of non–normality. Deviations from univariate or bivariate normality can yield confidence intervals for Pearson correlations with inaccurate coverage if conventional Z or t tests are used (e.g., Beasley, DeShea, Toothaker, Mendoza, Bard, & Rogers, 2007; Bishara & Hittner, 2017). For this reason, we computed confidence intervals for correlations using bootstrapping. For each correlation of interest, we used the observed–imposed (OI) univariate sampling bootstrap (e.g., Beasley et al., 2007; Lee & Rodgers, 1988) to generate 1000 samples, after which we computed bias–corrected and accelerated (BCA) confidence intervals (e.g., Efron, 1987; Efron & Tibshirani, 1993, pp. 184–188 and 326–328). Note that 95% confidence intervals that do not include 0 indicate rejection of the two–tailed null hypothesis that the population correlation equals 0. Such cases are indicated in bold in Table 9.

The highest and most consistently statistically significant correlations involved the three FIQ measures (Ravens, Letter Sets, and Number Scores). All three were positively correlated with category performance, with 5 of the 6 confidence intervals having lower bounds greater than zero. The proportions of variance (i.e., r²) in the category measures accounted for by the FIQ measures vary between 5.76% and 21%. The other significant correlations were those between Category 0 and Category 2 scores and the shift cost measure and between Category 2 scores and Visual STM performance. Lower shift costs and better short–term memory performance predicted better category performance, with proportions of variance in the 11–14% range.

Table 9 also presents four additional indices that address a different question: To what degree is the correlation between Cat 0 and Cat 2 accounted for by their associations with the other individual difference measures? First, we computed partial correlations between Category 0 and Category 2 that adjusted for their common association with each of the individual difference measures. These correlations assessed the strength of the association between those components of variance in category performance that were independent of the cognitive measures (i.e., they are identical to zero–order correlations between the Cat0 and Cat2 residuals formed from the regression of each on a given external measure). As the values and BCA confidence intervals shown in Table 9 indicate, partial correlations were quite high (all are > .62), with the great majority very close to the zero–order correlation (r = .71) between the two categories.

We also decomposed the overall correlation between Cat 0 and Cat 2 into two constituent components: The component that can be accounted for by the associations of the two categories with a given individual difference measure and the component that is independent of (i.e., orthogonal to) that measure. The top panel of Figure 7 graphically portrays the logic of the procedure, with Ravens used as the exemplar external measure. The directed arrows from Ravens to the two categories denote the effect of this component of fluid intelligence on individual differences in category performance. The ‘a’ coefficient denotes the effects of Ravens on Cat 0 and the ‘b’ coefficient denotes its effects on Cat 2. It can be easily shown that for a path model of this sort a and b are simply the β coefficients that would be yielded by two simple linear regression analyses regressing Cat 0 on Ravens and Cat 2 on Ravens. D0 and D2 depict the residuals from these two regressions and the double–headed arrow connecting them indicates the covariance between these residuals (analogous to the partial correlations discussed above). Using the tracing rule (Kenny, 1979), it can be shown that the overall covariance between Cat0 and Cat2 can be decomposed into the path through Ravens and the path through the residual terms. For the model depicted,

$${\sigma }_{Cat0,Cat2}=(a)(b){\sigma }_{Ravens}^2+{\sigma }_{d0d2}$$

The first term to the right of the equal sign in formula 1 is the component of the covariance between Cat0 and Cat 2 that is contributed by the Ravens path and the second term is the component of the covariance that is independent of the Ravens path and due to other sources. If all three variables are standardized, then it can be shown that the correlation between Cat 0 and Cat 2 can be analogously decomposed as:

$$r_{Cat0,Cat2}=(r_{Ravens,Cat0})(r_{Ravens,Cat2})+r_{Cat0,Cat2.ravens}\sqrt{1-r_{Ravens,Cat0}^2}\sqrt{1-r_{Ravens,Cat2}^2},$$

where r_{cat0,cat2,ravens} denotes the partial correlation between Cat0 and Cat2 adjusting for Ravens. The first term to the right of the equal sign in formula 2 denotes the correlation component through Ravens and the second denotes the component through the residuals. Because correlations are more readily interpretable than covariances, in Table 9 we present the decomposition of the overall correlation between Cat0 and Cat2 (r =.71) into its two constituent components across each of the external individual difference measures. In addition, we present the proportion of the correlation between these two measures that is due to the residual component. These proportions can be greater than 1 if the pathway through a given individual difference measure produces a predicted negative correlation. Also included are percentile bootstrap confidence intervals for these indices.^8,9

Figure 7.

Top panel: Observed variable model for effects of Ravens on category performance. Bottom panel: Latent variable model assessing the effects of fluid intelligence on category performance.

As shown by Table 9, for each variable the component of the correlation through the residual path (column 6) was notably greater than the component of the correlation through the individual difference measure path (column 5). Only three measures of the individual difference component had confidence intervals that did not encompass 0, while the lower bound for all residual–path measures was notably greater than 0. The lowest proportions of the total correlation through the residual path (column 7) were .72 (number scores) and .82 (shift cost), with the rest of the proportions greater than or equal to .86. As a whole, the results summarized in Table 9 strongly indicate that, considered in isolation, the individual difference measures account for only a small proportion of the association between the categories.

We also conducted a multiple regression analysis that predicted Cat0 and Cat2 from the three FIQ measures, Visual STM, and Shift Cost. We selected these variables because they were significantly correlated with at least one of the two categories (see Table 9). Using MPLUS software (Muthén, L.K. and Muthén, 1998–2017), we estimated a multiple–predictor version of the observed–variable model shown in Table 9 and, in addition, estimated the covariance between the Cat0 and Cat2 residual terms. The proportions of the variance of the category variables accounted for by the set of four predictors were 35% and 31 % respectively. If we apply standard adjusted R square formulae from ordinary least squares regression, these values drop to 28% and 23%, respectively. In addition, the partial correlation between Cat0 and Cat2 was .60 (p < .001) and the set of predictors accounted for 43% of the total correlation between Cat0 and Cat2 with the remaining 57% running through the residual paths. Although these analyses are informative, we should caution that: (1) With six predictors and a sample size = 51 (due to 3 participants with missing observations), there is some potential for bias and overfitting (i.e., reproducibility of the results is an issue); and, (2) These variables were selected post–hoc based on the results of prior analyses of individual external variables. Similar to the issues that arise with stepwise regression, this latter factor might well produce inflated estimates of the effects of the predictors and under–estimate the strength of the alternative, residual path.

Latent Variable Analyses

The correlational results among the observed measures indicate relations between the individual difference measures category performance that, at best (e.g., IQ measures), would be described as medium in strength, with generally small associations evident on the other measures. As noted above, however, measurement error attenuates correlations. Components of variance that are reliable but construct–irrelevant can also attenuate correlations.

These points suggest the advantages of including SEM analyses in Study 2. Unfortunately, CFA and SEM are based on large–sample theory and the available evidence indicates that N=54 is too small, particularly when data are not multivariate normal (e.g., Bentler & Chou, 1987; Boomsma, 1982; Boomsma & Hoogland, 2001). The most common problems are convergence failures (the iterative algorithm does not reach an optimal, final set of parameter estimates) and improper solutions (models with parameter estimates that are outside a permissible range, e.g., negative values of variances, Gagné & Hancock, 2006). Somewhat surprisingly, however, we found that when we ran SEM models that corresponded to the analyses presented in Table 9 but included latent variables for each construct, there were no convergence failures and solutions were proper. Likely, these results are due to the generally high construct reliability (i.e,. quality of measurement) in the models that we specified (e.g., Gagné & Hancock, 2006; Hancock & Mueller, 2001).

Although the results of latent variable SEM analyses should be viewed with caution in the present study, for several reasons we think that it is informative to present two models that focus on the relation between Fluid IQ and category performance: (1) We included three distinct measures of Fluid IQ (Ravens, Letter Sets, and Number Scores) and thus the analyses presented in Table 9 leave particularly unclear the strength of the association between a Fluid IQ latent variable and latent variables that mark the two categories; (2) The Fluid IQ measures had the highest correlations with the category measures when analyses were conducted on observed variables and yet their reliabilities were in the .72 to .79 range. Given that analyses of observed measures alone can attenuate correlations due to measurement error, we used the SEM approach to explore the magnitude of the association between constructs assessed as latent variables; (3) As reported below, the models that we ran assessing relations between FIQ and category performance had good fit; and, (4) Our primary focus was on parameter estimates and small ns tend to have smaller effects on estimation bias than on measures of fit or the magnitude of standard errors (e.g., for a review, see e.g. ,Boomsma & Hoogland, 2001).

Two SEM models were run to generate indices that paralleled those shown in Table 9 for observed variables. The first was a CFA model that simply specified three latent variables (FIQ, Cat0, Cat2, each with three indicators) that were freely correlated with one another. We used the MLR estimator in MPLUS (Muthén, L.K. and Muthén, 1998–2017)^10,11 and formed bias–corrected bootstrap intervals around parameter estimates (Williams & MacKinnon, 2008). This model fit very well (${\chi }_{df=24}^2$ test of exact fit = 25.56, p=.25, RMSEA = .03, CFI=.994, SRMR =.059). Consistent with the results of Study 1, the correlation between the Cat0 and Cat2 factors was .89 (95% bias–corrected bootstrap CI = .70 to 1.00). Both Category factors were significantly correlated with the FIQ factor, (Cat0 r = .57, 95% CI = .23 to .77; Cat2 r =.46, 95% CI = .10 to .67), which accounted for 32% and 21% of the variance of Cat0 and Cat2, respectively.

The second model is shown in the bottom panel of Figure 7. It is analogous to the model shown in the top panel and was designed to decompose the covariance between Cat0 and Cat 2 into paths through FIQ and through the residual terms. It can be shown that this model is an equivalent model (e.g., Tomarken & Waller, 2003) to the factor–analytic FIQ model: Although the specified parameters differ, the overall fit of the two models is identical because they impose the same restrictions on the data. Similar to the computations used for the observed data, we used this model to compute partial correlations between Cat0 and Cat2 and to decompose the correlation between Cat0 and Cat2 into the components due to and independent of FIQ.¹² Despite the non–trivial zero–order correlations between FIQ and the two Category latent factors, the partial correlation between Cat0 and Cat2 was a robust .86 (95% CI = .62 to 1.00). The component of the correlation between Cat0 and Cat2 (r=.89) through the FIQ path was .26 (95% CI =.05 to .54), while the component through the residual was .63 (95% CI = .38 to .85). Thus the overall proportion of the total correlation between Cat0 and Cat2 that was independent of linkages to FIQ was 71% (95% CI = .42 to .94). All told, these results indicate a very strong relation between those components of Cat0 and Cat2 that are independent of FIQ.

We also conducted two–stage least squares estimation (TSLS, Bollen, 1996) because it has been suggested that this limited information estimator might perform better with small sample sizes (although the evidence in support of this point is rather equivocal, e.g., Bollen, Kirby, Curran, Paxton, & Chen, 2007). The results were very similar. For example, while the residual path accounted for 71% of the total correlation between Cat0 and Cat2 when robust ML was used, this path accounted for 72.6% of the correlation when TSLS was used.

The online supplemental material contain additional results for latent variable assessments of the relation between the external individual difference measures and performance on the two categories.

General Discussion

Study 1 offered strong support for the hypothesis that individual differences in object recognition ability can be identified that are consistent across different categories of objects. The intraclass correlation coefficients conducted on a task–per–task basis indicated that performance across categories was rather stable. When consistency was assessed, the ICC1 values indicated that the correlations in performance between any pair of categories ranged from about .50 to .60 depending on the task. When category was treated as a random effect and agreement was assessed, ICC₁’s were lower but still indicated a notable effect of individual differences. Given the well–known importance of aggregation for accurate assessment of individual differences, the ICC₅ values are more critical because they estimate the correlation between the average performance of a given participant across the five categories and a hypothetically equivalent average. Across the two specifications for category (fixed vs. random effects), the ICC5 values ranged from .69 to .89. Thus, between approximately 70% and 90% of the variance in performance averaged across categories reflects individual differences that are stable across categories. Conversely, only a relatively small proportion of the variance of aggregate scores would be deemed due to random error. Using familiar terms derived from the analysis of variance, our findings indicate a strong main effect for persons and a relatively weak person X category interaction.

The confirmatory factor analyses (CFAs) extended the ICC results in several important respects. First, by combining performance across tasks, CFAs allowed for more general conclusions than analyses conducted on a task–by–task basis. In addition, they allowed us to estimate effects due to individual differences in object recognition (i.e., category performance) with the effects of random measurement error and construct–irrelevant variance removed and task–specific components of variance accounted for. Finally, the CFA approach allowed us to assess the overall proportion of variance in lower–order category factors due to the hypothesized object recognition ability o.

The sequence of CFA models offered strong support for our hypotheses. First, as long as task–specific method factors were accounted for, a model (Model 2) that specified correlated category factors fit well according to conventional criteria. A subsequent model (Model 3) that constrained factor loadings to be equal across categories for each task fit adequately – although the value of the nested χ² test indicated some, though non–significant, detriment in fit. This result indicates reasonable consistency of the factor structure of individual differences across categories. This model also indicated very high correlations among category factors, with rs ranging from .82 to .96.

Perhaps most importantly, we found that a model (Model 4) specifying a higher–order object recognition ability (o) fit (see Table 5), with o accounting for a substantial proportion of the variance (on average 89%) of the lower–order factors. Subsequent correlational analyses indicated that o is significantly correlated with individual measures of expertise in the domains of face processing and non–face objects. This result indicates convergent validity.

We found that o correlated more strongly with birds, butterflies, planes and houses than with faces and cars. The first four categories are likely representative of most categories of familiar objects, as previous work with several categories has consistently found faces and cars to be outlier categories (McGugin et al., 2012; Van Gulick et al., 2015, Richler et al., 2017, Ćepulić et al., 2018). Several factors may dampen the correlation between o and performance with familiar objects in this work. First, while we reliability–corrected the expertise measures, we used only a single task for each category. A point that we have emphasized throughout is the importance of aggregation across multiple measures to provide measures that are optimal from a psychometric perspective and thus have a higher ceiling for observable correlations. Second, both variability in experience (Gauthier et al., 2014) and amount of experience (Sunday et al., in press) likely contribute to variability in performance for familiar objects.

At the other end of the spectrum of experience, we assessed whether a small amount of exposure influenced the correlation with o. We used novel objects so that we could eliminate confounds from variability in experience, and we provided all subjects with the same amount (about 90 min) of exposure to objects from each of four of the novel categories, testing them with the fifth category without any prior exposure. Importantly, we found evidence that while short, this exposure was sufficient to increase holistic processing –– a behavioral marker of face perception (see Richler & Gauthier, 2014 for a review) –– for the pre–exposed categories (see also Chua et al., 2015; Wong et al., 2009). However, despite the evidence that on average, experience led performance with novel objects to become more “face–like”, our findings do not indicate that performance with trained objects recruit a different ability. On observed measures, performance on all tasks was equally correlated between the trained and untrained categories. A variant of Model 2 that specified equality constraints indicated that the average correlation involving the untrained category failed to differ from the average correlations among the trained categories. These results converge with a number of studies that suggest holistic processing and part–based processing may be quantitatively, but not qualitatively, different (Sekuler, Gaspar, Gold & Bennett, 2004; Richler, Mack, Palmeri & Gauthier, 2010; Chua et al., 2015) – such that object recognition may rely on o regardless of the processing strategy. In addition, it is worth pointing out that the increase in holistic processing is based on a different dependent variable (the congruency effect) then the average score in the Composite task used in individual differences models. As such they may reflect entirely different mechanisms. Congruency effects in the standard composite task are typically not sufficiently reliable for individual differences analyses (Ross et al., 2015) and while one test of holistic processing for faces was developed for this purpose (Richler et al., 2014), similar tasks do not yet exist for objects.

Taking what we learned from manipulating experience with novel objects and predicting the recognition of familiar categories, our results certainly suggest that experience influences object recognition, but also that o appears relevant to the prediction of performance across a range of objects, novel and familiar, and may help in predicting who can achieve high levels of performance in object recognition when provided with experience.

In Study 2, we found evidence for the specificity of o relative to a variety of constructs. Overall, FIQ measures displayed the strongest correlations with category performance. In the SEM analyses the FIQ latent variable accounted for between 21% and 32% of the variance in the category factors and in the observed–variable analyses, the proportions of variance for individual FIQ measures ranged from .06 to .21. Although these associations are by no means trivial, it is also the case that the clear majority (70 to 80%) of the variance in category performance was independent of FI. Similarly, in the latent–variable analyses, while approximately 30% of the covariance between the two Category factors was due to their common association with FIQ, 70% was independent of FIQ. Further, the Cat0 and Cat2 residual components that were independent of FIQ were very highly correlated. This overall pattern suggests that while individual differences in o are, perhaps not surprisingly, associated with FIQ, the magnitude of the relation is not sufficient to support the argument that FIQ acts as a potent third variable that accounts for the covariation in performance on different categorization tasks. The results of Study 2 also indicate that other individual difference measures assessing a variety of cognitive, perceptual, and personality–motivational constructs tend to have only weak associations with o, with the possible exception of shifting and visual short–term memory, the associations for which are probably best described as moderate. Further, a regression analysis combining all predictors that yielded at least one significant effect in the univariate analyses revealed that approximately 60–70% of the variance of and covariance between the category factors was independent of these predictors. Therefore, while we acknowledge that individual differences in o share some components of variance with these other measures, it is clear there must be other processes and factors implicated in object recognition ability. Put another way, we believe that the results of Study 2 indicate the discriminant validity of the o construct.

We believe that the present work has several strengths. One was the selection of five novel object categories that varied on dimensions (e.g., animate/inanimate appearance, symmetry, and curvature) shown in previous work to engage different neural substrates. We also deliberately had pairs of categories (the two Greeble categories and the two Ziggerin categories) that could have been expected to cluster if visual similarity contributed to individual difference effects. Yet models imposing equality constraints indicated that the within–Greeble and within–Ziggerin correlations were no greater than the across–type correlations. While it is still possible that o is not equally relevant to all kinds of object geometries, we made reasonable efforts to allow evidence for differences due to geometry to emerge and found none. The finding that o also correlates with performance with familiar objects also speaks to its generality over object category.

Cautions and Limitations

Although our findings offered strong support for hypotheses, several cautions and limitations should be noted. First, 36 of the original 285 participants withdrew from Study 1 after the pre–test session. It is conceivable that those who dropped out differed meaningfully from those who stayed in the study, a factor that would somewhat constrain the generalizability of our conclusions. We did find that individuals who withdrew after the introductory session had lower VET accuracy. Although this factor suggests that the sample may have been skewed slightly toward those with better object recognition ability, we were still able to detect strong individual differences in o. People with higher motivation to perform in the first visit may also be more likely to continue or complete the long protocol for reasons unrelated to o (e.g., conscientiousness).

Relatedly, 15% of the possible data points among those continuing in the study beyond the pre–test were missing. Given the time demands on participants, this figure is probably not surprising. We used data–analytic approaches that can incorporate participants with incomplete data and that provide valid inference as long as missing data meet the assumptions of missing completely at random (MCAR) or missing at random (MAR). In future studies – particularly those with similar time demands – it is important to assess as well as possible the reasons for incomplete data and to assess auxiliary variables that predict missingness and can be included in statistical models (e.g.,Yuan & Lu, 2008). That being said, it is important to note that across both the ICC and CFA analyses we found strong effects of individual differences. On that basis, we believe that we would find highly similar effects had there been no missing data.

While our sample size (N = 246) in Study 1 was substantially larger than the typical N’s used in studies in the area of perception, it is on the small side for a typical CFA or SEM study. Although prior simulation studies with conditions that map onto those operative in the present study indicate the likely validity of our results (e.g., Savalei and Falk, 2014), there is still a need for additional research to clarify the precise boundary conditions linked to factors like non–normality, missing data, and sample size and to comparatively evaluate the full range of robust SEM estimators that could potentially be used in such circumstances.

In addition, while our effects were strong (e.g., proportion of variance in lower–order factors accounted for by o) and our final models fit well, there is still clearly room for improvement (e.g., ideally one might like to see RMSEA’s in the .01–.03 range and stronger evidence of factorial invariance than we found). One potential way to optimize fit may be to match psychometrically categories on task difficulty and related factors. This is clearly a goal for future studies.

It is also important to note that the assessment of model fit is a complex task in the context of confirmatory factor analyses or other types of structural equation models (e.g., Tomarken & Waller, 2003). Indeed, it is paradoxically the case that models with better measurement quality (i.e. high proportions of variance of lower–order indicators accounted for by factors) can demonstrate worse fit on some indices than models with poor measurement quality (Hancock & Mueller, 2011; Heene, Hilbert, Draxler et al., 2011). As noted above (see Study 1 Results), the measurement quality in the present study was generally high. Given this consideration, the fact our final models consistently met conventional cutoffs indicates that they strongly fit the observed data.

In addition, the results of any CFA analyses are dependent on the specific array of measures used to assess constructs of interest. The LE, CO, and MA tasks have good reliability, have been used successfully by our laboratory in prior studies, and their correlations with each other suggest that they are valid measures of object recognition. That being said, is important to assess whether our conclusions are generalizable across other potential measures of o. We note that the observed measures of Learning Exemplars had a smaller proportion of variance accounted for by the Category factors (and ultimately o) than the Composite and Matching tasks. This difference may be at least partially due to the fact that the Composite and Matching performance measures were d’ while the Learning Exemplars task used percent correct. Perhaps most important is that the Composite and Matching tasks are more similar to each other by requiring perceptual matching across short delays within a trial, whereas Learning Exemplars requires memory for multiple learned objects across trials. The category factors might have accounted for more variance in Learning Exemplars if we had included another task that was more similar to it. These considerations support the importance of: 1) Accounting for task–specific effects by correlated error terms (as we did) or by other means; and, 2) Creating a wider range of psychometrically adequate tasks to explore object recognition abilities in future studies. Increasing the number of observed measures beyond three per category would have the added benefit of providing a more precise measure of the latent constructs of interest (e.g., Hancock & Mueller, 2001) and more rigorous tests of model fit (Tomarken & Waller, 2003).

Given the markedly high correlations among the category factors, it is reasonable to ask whether they are at least somewhat inflated by shared method variance (i.e., the fact that each of the same three tasks was used across all factors). We addressed this issue by specifying correlated errors among all the indicators of a given task. These terms allowed for an additional pathway by which within–task correlations could be manifest. While this correlated uniqueness approach is the one most commonly used to model method variance in CFA studies, one limitation is that it is not able to model correlated method effects that might occur when two tasks share several features. As noted above, CO and MA share several features that discriminate them from the LE task. As discussed in footnote 3, there is, however, an alternative approach for modeling method effects known as CT–C(M–1) (Eid, 2000; Eid et al., 2003) that involves specification of one less method factor than the total number of possible methods. When we specified a CT–C(M–1) model that included method factors for CO and MA that were allowed to be freely correlated, the loadings of the CO and MA indicators tended to be evenly split between the category and task factors. Even so, the correlations among the category factors were essentially the same as those yielded by the CU approach (mean r for CT–C(M–1) = .882, mean r for CU =.895). Similarly the loadings on o were very comparable across the two approaches. This finding indicates that the high correlations among the category factors that we observed were not inflated by task–specific components of variance.¹³

Our efforts in establishing the discriminant validity of o were limited to cognitive skills, some aspects of visual perception and personality. Future work could explore whether o is related to individual differences in lower level visual abilities that feed all the higher–level functions that are relied upon for object recognition. Although there is agreement that the range of individual differences in such low level visual abilities is larger than was once assumed, there are only a few studies testing large number of participants with a range of basic visual tasks. Some conclude there may be a single visual ability (Halpern et al., 1999) whereas other work suggests at least two factors corresponding to processing of low vs. high spatial frequencies (a magno/parvo distinction, see Ward et al., 2017). In addition, it is important for future studies to use larger sample sizes.\

Summary

In summary, we applied approaches rooted in the rich history of measuring individual differences in areas like personality and intelligence to the study of individual differences in visual abilities. Using confirmatory factor analysis, we showed that a substantial amount of shared variance in performance across five novel object categories could be accounted for by a single higher–order factor. This higher–order factor also predicted performance with several familiar object categories. This is the first demonstration that visual object recognition performance can be accounted for by a domain–general Object Recognition Ability, o. Future research should investigate its relation to various cognitive skills and lower–level abilities, as well as its real–world relevance.