Nanobody-CD16 Catch Bond Reveals NK Cell Mechanosensitivity

Abstract

Antibodies are key tools in biomedical research and medicine. Their binding properties are classically measured in solution and characterized by an affinity. However, in physiological conditions, antibodies can bridge an immune effector cell and an antigen-presenting cell, implying that mechanical forces may apply to the bonds. For example, in antibody-dependent cell cytotoxicity—a major mode of action of therapeutic monoclonal antibodies—the Fab domains bind the antigens on the target cell, whereas the Fc domain binds to the activating receptor CD16 (also known as FcgRIII) of an immune effector cell, in a quasi-bidimensional environment (2D). Therefore, there is a strong need to investigate antigen/antibody binding under force (2D) to better understand and predict antibody activity in vivo. We used two anti-CD16 nanobodies targeting two different epitopes and laminar flow chamber assay to measure the association and dissociation of single bonds formed between microsphere-bound CD16 antigens and surface-bound anti-CD16 nanobodies (or single-domain antibodies), simulating 2D encounters. The two nanobodies exhibit similar 2D association kinetics, characterized by a strong dependence on the molecular encounter duration. However, their 2D dissociation kinetics strongly differ as a function of applied force: one exhibits a slip bond behavior in which off rate increases with force, and the other exhibits a catch-bond behavior in which off rate decreases with force. This is the first time, to our knowledge, that catch-bond behavior was reported for antigen-antibody bond. Quantification of natural killer cells spreading on surfaces coated with the nanobodies provides a comparison between 2D and three-dimensional adhesion in a cellular context, supporting the hypothesis of natural killer cell mechanosensitivity. Our results may also have strong implications for the design of efficient bispecific antibodies for therapeutic applications.

Introduction

Antibodies are major research, diagnostic, and therapeutic tools. These 150 kDa proteins can bind specifically most natural and artificial targets (so-called antigens). In mammals, after contact with a new antigen, highly specific and affine antibody proteins are produced by monoclonal B cells, which are selected in germinal centers in a process called affinity maturation (1, 2). It was recently discovered that selection of high-affinity antibodies occurs when B cells pull actively on their antigens by exerting direct mechanical force on the antibody-antigen bond (3). Indeed, antigen-antibody bonds often act at cell-cell interfaces, for example, between a pathogenic cell and an immune effector cell, including natural killer (NK) cells during antibody-dependent cell cytotoxicity (ADCC) or macrophages during antibody-dependent cell phagocytosis, which leads to the destruction of the pathogenic cell by the immune cell (1). The functional contact established between NK cells or B cells and their target, the so-called immunological synapse, is highly organized by the actomyosin network and the physical forces it produces (4, 5, 6, 7). The quality of the antibody binding is traditionally described by an affinity measured in conditions in which one of the partners (antibody or antigen) is in solution; this parameter might not be completely relevant to describe their behavior when tethered at surfaces and subject to mechanical disruptive forces, further referred to as two-dimensional (2D) environment (8).

The study of protein-protein interactions, like antigen-antibody, have been profoundly renewed by the development of single-molecule manipulation and measurements (9). These techniques allow us to measure interactions between complementary proteins tethered to opposite surfaces that are first put into contact and then separated. They have been successfully used to study 1) the unbinding force of the biotin-streptavidin bond with atomic force microscopy (AFM) (10), 2) anti-immunoglobulin kinetics with the LFC (11), and 3) the biotin-streptavidin energy landscape of dissociation with the biomembrane force probe (12). Bonds behave typically as slip bonds, whose lifetime decreases (off rate increases) with applied force, as predicted by Bell’s law (13). However, catch bonds, whose lifetime increases (on rate decreases) with force, were initially discovered for physiological process such as bacterial adhesion (14) and selectin-mediated interaction between white blood cells and endothelial cells in response to infection (15). This behavior has been identified later in other systems, including adhesion molecules such as cadherins and integrins and in the T-cell receptor (16). However, to our knowledge, no catch bond has been described for antigen-antibody interaction (5).

The laminar flow chamber (LFC) uses hundreds of microspheres conjugated to ligands and convected by a flow above complementary receptors immobilized onto a surface. At low flow velocity and low surface-coated molecule density, it allows efficient ligand-receptor mechanical discrimination at the single-bond level with the advantage of naturally multiplexed measurements (11, 17, 18, 19). Several original features of some antibody-antigen interactions were observed using the LFC in this setting. For example, survival curves exhibited features of bond strengthening over the time after their formation (20); analysis of antibody-antigen association also revealed a nonlinear dependence of bond formation probability as a function of the duration of the molecular encounter between the reactive partners before bond formation, an observation questioning the definition of an association rate between surface-tethered proteins (21, 22, 23). Whether these features are characteristic of many antigen-antibody bonds is important for a fundamental understanding of antigen-antibody interaction as well as for the technical validation of LFC measurements.

Nanobodies (aka single-domain or variable heavy heavy antibodies) are antibody fragments derived from camelidae antibodies devoid of light chain. With a molecular weight of 15 kDa and consisting of a single immunoglobulin domain, they can be used to target hidden epitopes or as elementary bricks to construct multispecific molecules (24). They can also circumvent limitations of conventional antibodies for certain diseases by targeting cryptic conserved epitopes. Very recently, they were used as a library of cell-cell linkers for the engineering of multicellular aggregates (25). Because of their standardized monovalent format, a panel of nanobodies targeting the same antigen constitutes an ideal set to test the questions raised above. We have previously generated a set of nanobodies targeting the low-affinity receptor CD16 (aka FcγReceptor III) expressed on NK cells and macrophages (26). Their on/off kinetics was measured in solution by surface plasmon resonance (SPR) (26). CD16, which binds the Fc fragment of conventional antibodies, is involved in ADCC and antibody-dependent cell phagocytosis and so is naturally subject to disruptive force generated within the immune synapse. Anti-CD16 nanobodies are surrogate Fc fragments that can form stronger bonds than the FcγRIII-Fc fragment interaction and that are dedicated to being coupled to another nanobody with a different specificity in a bispecific construction (27). Such constructions, designed to be insensitive to CD16 polymorphism, were successfully tested to treat HER2-positive breast cancer with low HER2 expression resistant to the therapeutic monoclonal antibody trastuzumab (28). More generally, anti-CD16 nanobodies may serve as universal targeting moiety in various diseases (29), and their kinetic characterization under force would be a valuable information to select the most efficient binders in 2D settings.

In this work, we perform for the first time, to our knowledge, a comparative study of the association and dissociation 2D kinetics of two nanobodies (named C21 and C28) targeting the same human antigen CD16 in the LFC. After determining nanobody densities, ensuring single-bond kinetics measurements, flow velocity was systematically varied. Association probability displays very similar behavior for the two nanobodies as a power law of the molecule interaction duration. The dissociation process shows a strengthening with time for the two nanobodies. However, the dependence of the initial off rate with force strongly differs: one increases when force increases (slip bond), and the other decreases (catch bond). This study identifies, for the first time to our knowledge, a catch-bond behavior for an antibody. We then measured the apparent affinity of the two nanobodies on NK cell surfaces by flow cytometry (three-dimensional (3D)). We also show that NK cell spreading on nanobody-coated surfaces can be equally efficient with a poorly binding antibody in 3D if it displays a 2D catch bound behavior, suggesting that NK cells are applying and sensing forces. This work illustrates how the comparative use of antibodies for which unbinding kinetics are well characterized under force can help in deciphering complex cellular behaviors.

Materials and Methods

Molecules and cells

Nanobodies C21 and C28 were previously generated after immunization of lamas with the recombinant human FcγRIIIB and selected by phage display as described in (26). The GenBank accession numbers are EF5612911 for C21 and EF561292 for C28. Here, C21 and C28, which both exhibit C-terminal c-Myc and six His tags, were produced in Escherichia coli and purified by TALON metal-affinity chromatography as previously described (26) (Fig. S1 A). The transglutaminase-catalyzed biotinylation of the c-Myc tag was performed using the Biotin TGase Protein Labeling kit (Zedira, Darmstadt, Germany) following manufacturer instructions. After 1 h incubation with biotinylation reagents at 22°C, nanobodies were filtered using ZebaTM Spin Desalting Columns (Thermo Fisher Scientific, Villebon-sur-Yvette, France). Biotinylation of nanobodies was assessed by migration on gel using Gel Doc EZ Imager (Bio-Rad, Hercules, CA) for nanobody band visualization and Western blot using anti-His-HRP antibody (clone GG11-8F.3.5.1, Miltenyi Biotec, Paris, France) at 1/5000 and streptavidin HRP at 1/2000 (Thermo Fisher Scientific) (Fig. S1 B). Concentration of nanobodies was determined by measuring amine bonds in protein chains by infrared spectroscopy (Direct Detect Infrared Spectrometer; MilliporeSigma, Burlington, MA).

NK92-CD16 cell line or primary NK cells were used to perform cell spreading experiments on nanobody-coated surfaces. NK92 cells were transfected to express a chimeric molecule containing the extracellular domain of human CD16 (FcγRIIIA-V158) and the transmembrane and intracellular domain of FcERIγ as described by (30). Cells were cultured in RPMI 1640 + 10% fetal bovine serum and Interleukin-2 (Proleukin, Novartis, Bale, Switzerland) at 200 U/ml. Expression levels of CD16 were controlled once per week by flow cytometry using a fluorescent antibody (PE anti-CD16 human, clone 3G8; Biolegend, London, UK). Primary human NK cells from healthy donors were isolated from blood samples provided by the Etablissement Français du Sang (Marseille, France) by negative selection using the MACSxpress whole-blood human NK cell isolation kit (Miltenyi Biotec, Bergisch Gladbach, Germany), according to the manufacturer’s protocol. The purity of NK cells was determined by staining with anti-CD16 PE, anti-CD3 fluorescein isothiocyanate, and anti-CD56 APC antibodies (both Miltenyi Biotec); see flow cytometry protocol in the Supporting Methods. Cells were stored in RPMI 1640 medium complemented with 10% fetal bovine serum at 37°C and used in the following 24 h.

Single-bond kinetic measurements with the LFC

For LFC experiments with microspheres, glass slides were functionalized with biotin-conjugated anti-CD16 nanobodies as described before (18, 23). Briefly, slides were incubated successively with poly-L-lysine, glutaraldehyde, bovine serum albumin (BSA) biotin, glycine, streptavidin (all products from Sigma Aldrich, St. Quentin Fallavier, France), and finally biotinylated anti-CD16 nanobodies at different concentrations. The detailed procedure is described in the Supporting Methods. The nanobody density on the surface at the various incubation concentrations was determined by fluorescence microscopy. For this purpose, surfaces functionalized with nanobodies were further incubated for 30 min with a fluorescently labeled anti-His-phycoerythrin (anti-His-PE, clone GG11-8F.3.5.1, Miltenyi Biotec). The antibody is labeled in average with 1.5 PE group and binds the His tag of the nanobody. The detailed procedure for surface density measurement is described in the Supporting Methods.

For microsphere functionalization with recombinant CD16, 500 μL of microspheres of 4.5 μm diameter functionalized by toluenesulfonyl groups (Dynabeads M-450 Tosylactivated; Thermo Fisher Scientific) was rinsed in borate buffer three times. Then, 200 μL of a solution of 0.5 μg/mL anti-glutation-S-transferase (anti-GST) (Clone P1A12; Biolegend) was added to the microspheres resuspended in 300 μL of borate buffer supplemented with BSA 0.1% and sodium azide 0.1%, and the solution was incubated for 24 h at room temperature. Next, microspheres (40 μL) were rinsed with phosphate-buffered saline (PBS)-BSA 0.2% and incubated with 10 μL of a solution of 0.10 mg/mL of CD16 GST (human FcγIIIA GST tag recombinant protein P01; Abnova, Taipei City, Taiwan) during 30 min with shaking. After this time, microspheres were cleaned with PBS-BSA 0.2% and directly used.

Single-bond measurements were performed using a homemade automated LFC apparatus, composed of three mechanical systems coupled to an imaging system (23). Briefly, a glass slide coated with the nanobodies on the surface formed the bottom of a multichamber device with nine independent chambers used to test several densities of nanobodies on the same sample. The device was connected to one system that injects microspheres, another that controls the flow applied to the microspheres, and the last one, which regulates the temperature inside each chamber. Observation was performed using an inverted microscope equipped with a 20×/0.32 objective (1 pixel = 0.33 μm), and images were recorded at a frame rate of 50 images/s using a camera (IDS, Obersulm, Germany). The temperature was set to 37°C.

Data were analyzed as follows: the velocity of the microspheres was calculated on a time interval of 200 ms. The velocities of the sedimented microspheres (which correspond to the ones at molecular distance of the surface) were distributed around a peak u_p ∼ 0.54aG, where a is the microsphere radius and G the shear rate (22). An interval of velocity was chosen around u_p (Fig. S2 B). The velocity should be within this interval to 1) count the beginning of an arrest and 2) count the traveled distance. On these velocity intervals, arrests of the microspheres were identified on the trajectories and counted (Fig. S2 C). A microsphere was defined as arrested when its displacement δx was lower than 0.33 μm during the defined time interval δt = 200 ms. The true arrest duration d_true was derived from the apparent arrest duration d_app with the correction d_true = d_app + δt − 2δx/u_p (20). To analyze 2D association, the binding linear density (BLD) was defined as the number of arrests divided by the traveled distance (23). To smooth the data, the BLD was first interpolated as a function of the velocity for a given density using a power law function. Then, a series of velocities were chosen, and the interpolated BLD values were used for further analysis (Document S1. Supporting Methods and Figs. S1–S12, Document S2. Article plus Supporting Material D). To analyze 2D dissociation, arrest durations were used to build the survival curves, i.e., the fraction of bonds still existing after time t.

NK cell spreading experiments

For cell spreading experiments, uncoated eight-well μ-Slides (Ibidi, Munich, Germany) composed of eight independent chambers were used. The surface coating with nanobodies was performed with two intermediate layers of BSA-biotin and streptavidin, before the deposition of monobiotinylated nanobodies (see the Supporting Methods for details). Cell spreading was monitored using reflection interference contrast microscopy (RICM), which is sensitive to cell-surface distance (31). Image acquisition starts immediately after deposition of the cells in the devices. To determine the kinetics of spreading of NK92-CD16, several fields were selected and imaged cyclically during 10 min using a motorized stage (Physik Instrumente, Karlsruhe, Germany). Elapsed time between two subsequent images on the same field was typically 20–30 s. After 10 min of cell incubation on the surfaces, ∼20–30 fields were imaged both in transmission and reflection to determine the proportion of spread cells, their spread area, and the tightness of cell-surface contact. Image analysis was performed to detect and measure spread and nonspread cells on the coated nanobody surfaces and to distinguish them automatically from cell fragments (in the case of NK92-CD16) or red blood cells (in the case of cells from donors). For this, images obtained sequentially in transmission and reflection were exploited simultaneously using different homemade procedures. The detailed method is described in Supporting Methods. The kinetics of cell spreading was measured by segmenting cells on RICM sequences as described before (32). The area versus time curves were fitted with a Hill function to extract a typical spreading time.

NK cell laminar flow experiments

Two kinds of experiments with NK92-CD16 cells under laminar shear flow were performed. First, the number and duration of adhesion events of NK92-CD16 cells freely moving in a shear flow on anti-CD16 nanobody-decorated surface was measured. Uncoated μ-Slides IV0.4 (forming six independent channels; Ibidi) were coated with biotinylated anti-CD16 nanobodies as described for spreading experiments. A volume of 200 μL of a suspension of 800,000 cells per mL was injected into the device before each measurement. A second homemade model of automated LFC device controlled a video camera and a syringe pump and successively applied shear stresses of 0.075, 0.3, and 0.6 dyn/cm² while acquiring an independent video for each shear condition. Video analysis of cell trajectories was performed using the same algorithms as for microspheres described above and retrieved arrest lifetimes. Second, deassociation of NK92-CD16 cells was also measured in different conditions. Using the same experimental set-up with a different automaton program, cells were injected in the chamber under a so-called “start flow” of 0.15 dyn/cm² for 20 s. Cells were then allowed to settle for 60 s under a very low shear stress of 0.03 dyn/cm² (so-called “adhesion flow”) that still allowed us to discriminate between adherent and nonadherent cells. Cells were then submitted to a series of higher shear stresses, increasing by steps of 15 s each as follows: 0.2, 0.5, 1, and 2 dyn/cm² (so-called “deadhesion flows”). For the deadhesion analysis, the number of adherent cells (N) was counted at the end of all the periods (N0, NI, NII, NIII, NIV, and NV) (see Fig. S12). The proportion of adhering cells at each period (adhesion and deadhesion) was determined by dividing the number of cells resting at the end of each period by N0 (or the total number of initially adherent cells).

Results

BLD and single-bond assessment in LFC

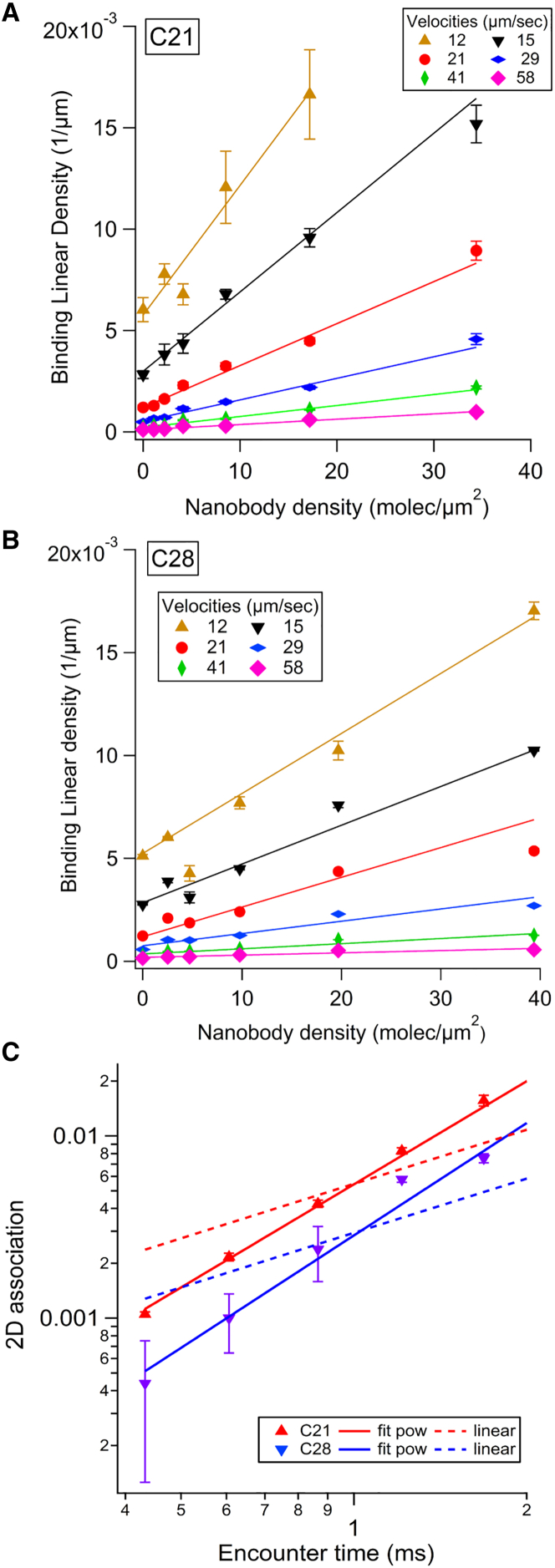
To study the BLD, each nanobody was incubated on the slides with at least six concentrations of each nanobody ranging from 0.004 to 0.125 μg/mL, plus a negative control without nanobody, leading to seven molecular surface densities. For each coated surface, the shear rate in the LFC was set successively to six different values. The BLD was plotted against nanobody surface density for each velocity condition, as shown in Fig. 1 A (nanobody C21) and Fig. 1 B (nanobody C28). For a given velocity and in the range of selected densities, the BLD increases linearly with the molecular density, which indicates measure of single molecular bonds because multiple binding leads to saturation of the BLD. The data were fitted with an affine function, using a weight at each point corresponding to the error bar (most often linearity coefficient R > 0.9). The interaction of the fitting line with the vertical axis represents the fitted nonspecific BLD. It is used to calculate the nonspecific adhesion ratio r, defined as the nonspecific BLD divided by the BLD at a given condition.

Figure 1.

Analysis of 2D association of nanobodies C21 and C28 on recombinant CD16 measured with the LFC. (A and B) BLD plots versus nanobody C21 (A) and nanobody C28 (B) surface density obtained at six velocity peaks u_p of the sedimented microspheres are shown. A linear fit of the data is presented for each u_p. The error bars were defined as BLD divided by the square root of the number of arrests counted for the considered condition. (C) Plot of the 2D association (corresponding to the slope of the BLD versus density linear fit, normalized by the molecular length L = 25 nm (see Fig. S2)) as a function of the encounter time (defined as L/u_p) for C21 and C28 is shown. The error bars were calculated by the variation of the slope when considering the linear fit of BLD versus density line, obtained on a narrower density range (by removing the highest density). Data were fitted to a power law (plain line) or a linear law (dashed line). To see this figure in color, go online.

At a given experimental condition, the survival curve for specific arrests was built by subtracting from the total survival curve a fraction r of arrests distributed according to the nonspecific survival curve, i.e., measured in the absence of nanobody (20). The corrected survival was calculated as ${\mathrm{S}}_{\text{spe}}=({\mathrm{S}}_{\text{total}}-\mathrm{r}\times {\mathrm{S}}_{\text{nonspe}})/(1-\mathrm{r})$. In Fig. S3, the resulting curves are presented for five different velocity intervals and three different incubation concentration of nanobody, corresponding to three molecular surface densities. Each curve represents at least 150 arrests and are restricted to ratio r < 0.65. For a given nanobody and density, the curves superimpose, demonstrating that the dissociation kinetics is independent of the density in this range, ruling out multiple binding, which leads to lower dissociation. Taken together with the linear dependence of BLD on density, this is a strong assessment for single-bond measurements (17, 23).

Molecular association

The 2D association was defined for each velocity as the slope of the BLD versus density line divided by the molecular length L = 25 nm (defined in Fig. S2). The normalization by L accounts dimensionally for the effect of molecular length in estimating the number of molecular encounters. A more precise modeling involves complete Brownian dynamics simulations and the possible rotation of the molecules (22, 23). In Fig. 1 C, the 2D association A_2D is represented for each nanobody as a function of the molecular encounter time t_enc, defined as the ratio of molecular length L and velocity u_p. The 2D association is well described quantitatively by a phenomenological power law: $A_{2\text{D}}\left(t_{\text{enc}}\right)=A_{2D}^{1\text{ms}}\times t_{\text{enc}}^{\alpha }$ with t_enc in ms. Values of the fitting parameters are reported in Table 1. A tentative linear fit (shown as dashed line in Fig. 1 C) emphasizes the finding that the association does not scale linearly with the encounter time. This was already observed in LFC for conventional antibodies (21, 22, 23).

Table 1.

Summary of Time- and Force-Dependent 2D Kinetics Parameters of Bonds Formed between Recombinant CD16 and Anti-CD16 Nanobodies C21 and C28, as Measured by LFC

Nanobody	Association		Dissociation
	2D Association A2D		Initial off rate $k_{\text{off}}^{t0}$		Strengthening a
	$A_{2D}^{1\text{ms}}$ (× 10−3)	α	ko (1/s)	Fk (pN)	ao (1/s)	Fa (pN)
C21	5 ± 0.2	1.88 ± 0.06	1.3 ± 0.1	93 ± 12	2.6 ± 0.1	∞
C28	3 ± 0.02	2.05 ± 0.15	2.6 ± 0.3	−57 ± 9	6.9 ± 1.2	−114 ± 30

Molecular dissociation

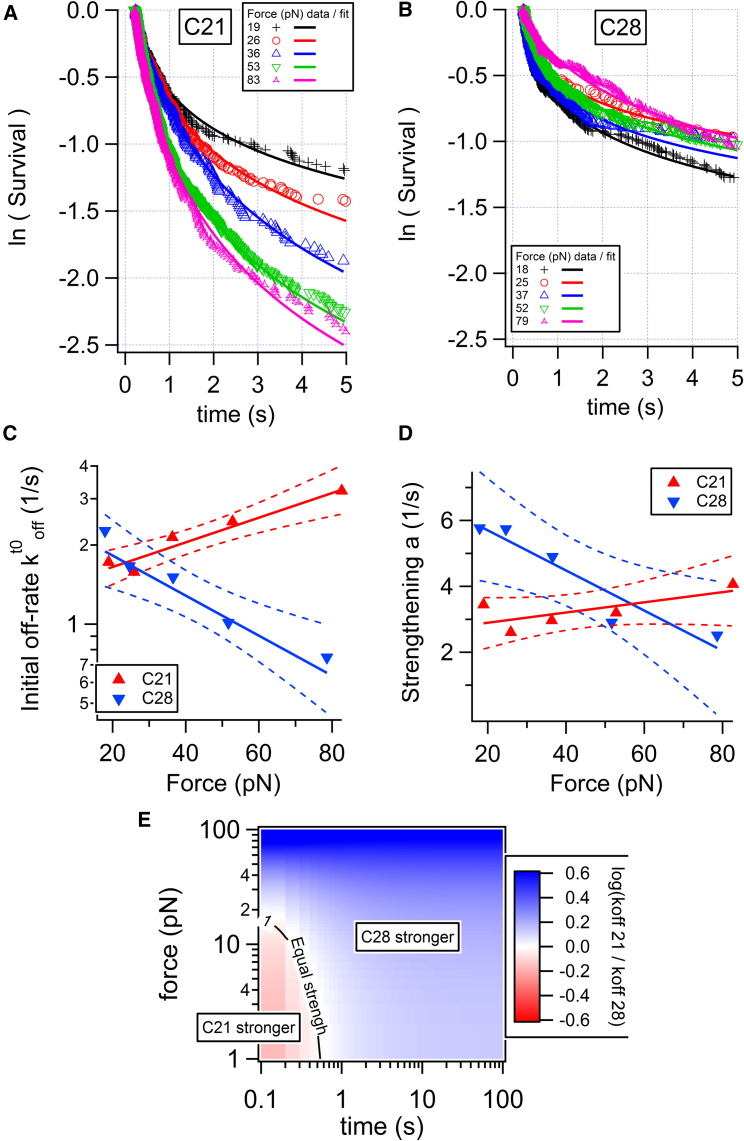
The survival curves displayed in Fig. 2 and Fig. S3 exhibit a nonlinear shape in semi-log representation, indicating the involvement of different timescales in the dissociation process (17, 20). Curves of Fig. 2, A and B were fitted between 0 and 5 s, using the empirical equation

$$S\left(t\right)={\left(1+at\right)}^{-k_{\text{off}}^{t0}/a},$$ (1)

where $k_{\text{off}}^{t0}$ is the initial dissociation rate (in s⁻¹) and a the rate of bond strengthening (in s⁻¹), as applied earlier for conventional antibodies (20). Curves of Fig. 2, A and B also evidence the dependence of the survival on the external force applied to the bond through the flow. The force was proportional to the velocity as F (pN) = 1.25 u_p (μm/s) (17, 20). Therefore, the parameters $k_{\text{off}}^{t0}$ and a are force dependent. The parameter values retrieved from the fits of survival curves obtained at three molecular densities, as well as their average, are displayed as function of the force applied by the flow in Fig. 2, C and D. Nanobody C21 exhibited a clear increase of the initial off rate when force increased, which is characteristic of a slip bond. On the contrary, for C28, the initial off rate decreased when force increased, which is characteristic of a catch bond. Linear correlation test for $\text{ln}\left(k_{\text{off}}^{t0}\right)$ vs. F gives a correlation coefficient R = 0.80 for C21 and R = −0.75 for C28. The confidence interval on the linear regression is shown in Fig. 2, C and D. The strengthening parameter a was roughly independent of force for C21 and decreased with force for C28. $k_{\text{off}}^{t0}$ was fitted with Bell’s equation (13): $k_{\text{off}}^{t0}=k^{\text{o}}\times \text{exp}\left(F/F_{\text{k}}\right)$. k^o represents the off rate at zero force; F_k represents the typical force above which the off rate becomes force dependent. The strengthening parameter a was simply fitted with an affine law a = a^o × (1 + F/F_a). Although this dependence could be justified with some arguments of friction on the energy landscape of the interaction, we use it here simply as a functional dependence to calculate the off rate at any force and time. Values of the fitting parameters for both $k_{\text{off}}^{t0}$ and a are reported in Table 1. These parameters allow us to calculate the dissociation rate for any applied force and maturation time using Eq. 1 (Fig. S4). Interestingly, the ratio of the off rates shows that for durations above 1 s or applied force above 20 pN, C28 was more stable than C21 (Fig. 2 E).

Figure 2.

Analysis of 2D dissociation of nanobodies C21 and C28 from recombinant CD16 measured with the LFC. (A and B) Survival curves for surfaces coated with 125 ng/mL nanobody incubation concentration at various applied forces (in pN) are shown. Each curve was fitted with Eq. 1, where $k_{\text{off}}^{t0}$ is the initial dissociation rate and a is the rate of bond strengthening. (C and D) These rates are represented as a function of the force and fitted with Bell’s law $k_{\text{off}}^{t0}=k^{\text{o}}\times \text{exp}\left(F/F_{\text{k}}\right)$ or an affine law a = a^o × (1 + F/F_a). The solid triangles correspond to the average of $k_{\text{off}}^{t0}$ (C) or a (D) obtained for three different incubation concentrations (31, 62, 125 ng/mL) of nanobody. For each nanobody, linear regression was applied for $\text{ln}\left(k_{\text{off}}^{t0}\right)$ or a vs. force for the set of data corresponding to the entire data set. Regression lines are thick, and 0.95 confidence lines are dashed. (E) The ratio of calculated off rates as a function of applied force and bond lifetime is shown. To see this figure in color, go online.

Cellular binding measured by cytometry

The binding of nanobodies on a cell surface in 3D conditions was measured by flow cytometry. Briefly, NK92-CD16 cells or primary NK cells were incubated with serial dilutions of nanobodies C21 or C28 and further labeled with a fluorescent anti-His antibody. A positive control was performed with a saturating amount of fluorescent anti-CD16 (clone 3G8). Median fluorescent intensities (MFIs) obtained with nanobodies were normalized in each experiment by the MFI of the positive control. The relative binding fractions obtained were pooled between different experiments. The concentration of incubated nanobody giving half of the maximal relative binding represents the apparent affinity c_1/2, a parameter related to the affinity. The complete protocol is detailed in the Supporting Methods.

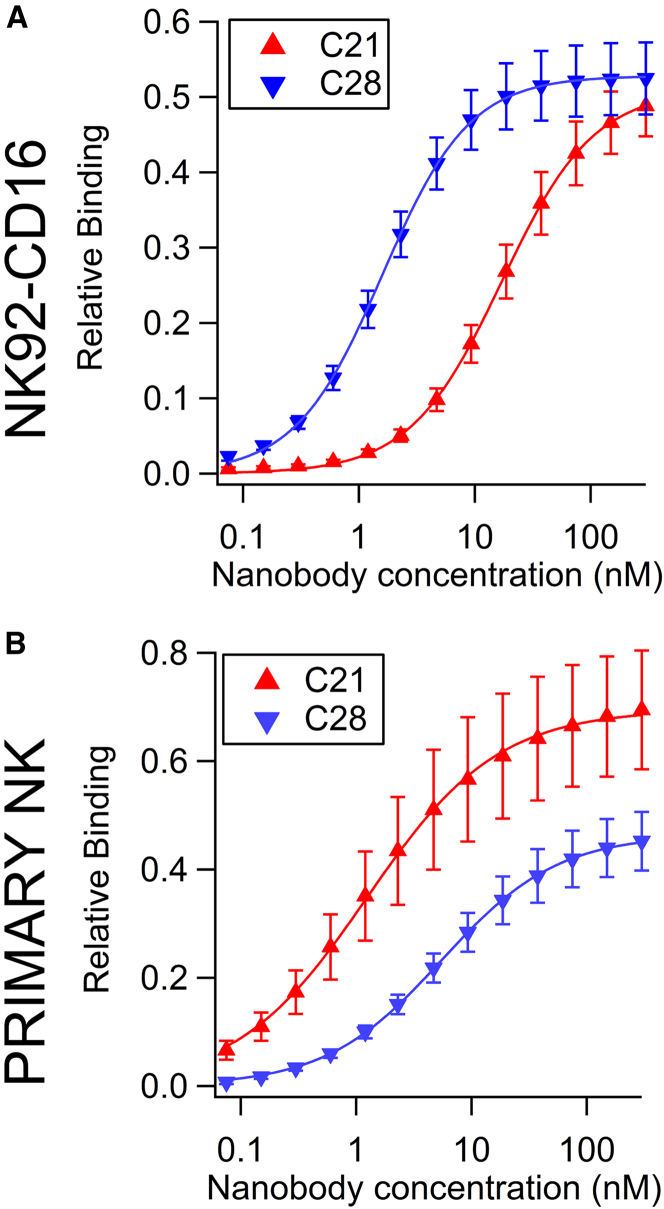
Results for NK92-CD16 are shown on Fig. 3, left. Points represent the relative binding average of six independent experiments and are plotted as a function of the nanobody incubation concentration. Fitting with the Hill equation

$$RB\left(c\right)=\frac{max}{1+{\left(c_{1/2}/c\right)}^{\text{rate}}}$$ (2)

gave an apparent affinity c_1/2 = 27 nM and c_1/2 = 3 nM for C21 and C28, respectively. All fitted parameters are reported in Table 2. This was an unexpected result, in contradiction with the 3D affinity measured with SPR (26). This discrepancy is essentially caused by a reduced affinity of C21 that could result from the chimeric nature of CD16 in transfected NK92. This construct, which consists in the fusion of the extracellular domain of CD16 and the FcRI intracellular γ chain (30), could cause a partial hiding of the C21 epitope.

Figure 3.

Binding of nanobodies to cell surface measured by flow cytometry. NK92-CD16 cells or primary NK cells were incubated with various concentrations of nanobody C21 or C28, and binding was detected using a fluorescent secondary antibody against the His tag. Results are average of six experiments on NK92-CD16 cells (A) and eight experiments (corresponding to eight different donors) on primary NK cells (B). Error bars are mean ± standard error. Before pooling, data were normalized by the values of the positive control obtained with the anti-CD16 monoclonal antibody 3G8. Data were fitted using Eq. 2. To see this figure in color, go online.

Table 2.

Summary of Binding Parameters of Nanobodies on NK Cells Measured by Flow Cytometry Obtained by Fitting Relative Binding RB as a Function of Nanobody Concentration c with a Hill Function

Cell Type	Nanobody	Maximum	Rate	c1/2 (nM)
NK92-CD16	C21	0.51 ± 0.003	1.1 ± 0.02	17 ± 0.3
	C28	0.53 ± 0.002	1.2 ± 0.02	1.6 ± 0.02
Primary NK	C21	0.70 ± 0.005	0.76 ± 0.02	1.2 ± 0.04
	C28	0.46 ± 0.002	0.86 ± 0.01	5.5 ± 0.1

For primary NK cells, the cell selection procedure and raw measurements before normalization are shown for each donor in Fig. S11. The pooled data are represented as normalized MFI versus nanobody concentration on Fig. 3 B. Binding of C21 was higher than that of C28. Fit parameters retrieved with Hill equation gave an apparent affinity c_1/2 = 1 nM and c_1/2 = 7 nM for C21 and C28, respectively. All fitted parameters are reported in Table 2. These results are in line with the 3D affinity measured by SPR (26) as well as previous measurements on Jurkat CD16 cells by Turini et al. (28).

Cellular spreading measured by RICM

To assess the effect of the two different molecular kinetics at the cellular scale, the spreading of NK92-CD16 cells or primary NK cells expressing CD16 on surfaces coated with either C21 or C28 was studied using RICM. The surface density of nanobodies was systematically varied between 1 and 200 molecules/μm², as measured after each experiment, using the procedure described in Fig. S5, A and B. For NK92-CD16 cells, CD16 expression was controlled regularly by flow cytometry (Fig. S5 C). Their spreading capacity was assessed regularly by measuring their spreading area and reflectivity on control surfaces coated with a conventional anti-CD16 antibody (Fig. S5, D and E). For primary NK cells, cellular binding of nanobodies by cytometry was measured for each donor, as well as spreading experiments on nanobodies and positive controls. The fraction of spread cells was measured after 10 min of engagement on the surface by counting the number of cells displaying a contact patch by RICM divided by the number of cells visible by transmission, as described in detail in the Supporting Methods.

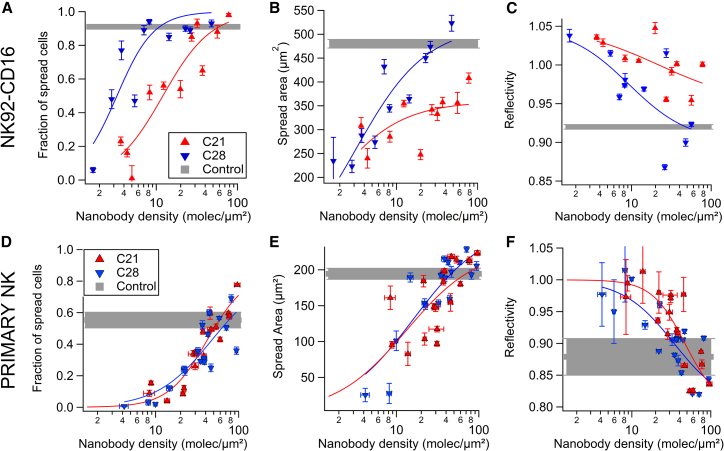
For NK92-CD16 cells, the spread fraction increases with antibody surface density, with the fraction being larger for C28 at most densities (Fig. 4 A). The spread fraction as function of the nanobody molecular density d was fitted with a Hill equation $SF\left(\mathrm{d}\right)=max/(1+{\left({\mathrm{d}}_{1/2}/\mathrm{d}\right)}^{\text{rate}})$. The fitted parameters d_1/2 and rate are reported in Table 3. The value of half density d_1/2 determined for nanobody C28, d_1/2 = 3.3 ± 0.6, was fourfold lower than that determined for nanobody C21, indicating that NK92-CD16 cells spread on lower densities of C28 than C21. The spreading area of cells after 10 min of engagement was also measured as a function of nanobody coverage (Fig. 4 B). A fit with the Hill equation was applied by fixing the rate to 1 and fitting the maximal area, yielding 359 ± 23 and 518 ± 37 μm² for C21 and C28, respectively. Finally, the reflectivity of RICM images was also used to assess the distance between the basal membrane of NK92-CD16 cells and the nanobody-coated surface. Indeed, low gray level can be used as a proxy for short membrane-surface distance (31). This distance decreased with antibody surface density and was smaller for C21 at most of the densities (Fig. 4 C). The kinetics of spreading was also recorded (Fig. S7). There was no significant difference between the duration of spreading on C21 and C28 tested at various surface densities.

Figure 4.

Spreading of NK cells on nanobody-coated surface measured by RICM (A–C: NK92-CD16; D–F: primary NK). (A and D) Plots of the fraction of spread cells in function of nanobody density are shown. (B and E) Plots of the spread area as a function of nanobody density are shown. (C and F) Plots of the reflectivity signal of adhered cells, which provides an estimate of the tightness of cell-surface contact, are shown as a function of nanobody density. In all experiments, controls correspond to cells spread on surfaces coated with the conventional anti-CD16 antibody 3G8 (see Fig. S5). (A–C) Each point represents the pool of four separate experiments with at least 100 cells. (D–F) Each point represents the average of at least 100 cells for one donor at one nanobody density (seven donors in total). All plain lines correspond to fits with a Hill function (see fit function and parameters in Table 3). Error bars are mean ± standard error. To see this figure in color, go online.

Table 3.

Summary of Spreading Parameters of NK Cells on Anti-CD16 Surfaces Measured by RICM

	Cell Type	Nanobody	Maximum	Rate	d1/2 (Molecules/μm2)
Spread fraction	NK92-CD16	C21	1	1.45 ± 0.3	12 ± 2.0
		C28	1	1.9 ± 0.6	3.3 ± 0.6
Spread fraction	Primary NK	C21	0.85	1.9 ± 0.2	42 ± 2
		C28	0.85	1.3 ± 0.3	47 ± 6
Spread area	NK92-CD16	C21	359 ± 23 μm2	1	1.4 ± 0.8
		C28	518 ± 37 μm2	1	3 ± 0.8
Spread area	Primary NK	C21	231 ± 26 μm2	1	13 ± 6
		C28	262 ± 27 μm2	1	16 ± 5

A Hill equation is fitted to the data to describe their dependence on nanobody surface density.

For primary NK cells, spreading was also strongly dependent on antibody surface density. Yet, primary NK cells spread very similarly to C21 and C28 surfaces. Spread fraction, spread area, and reflectivity measured for seven donors are represented as a pool (Fig. 4, D–F) or for individual donors separately (Fig. S11, D–F). All fitted parameters of the Hill functions are reported in Table 3.

Cellular transient adhesion and deadhesion

To quantify further the adhesion of NK92-CD16 cells on nanobody-coated surfaces, we measured cell adhesion in the LFC. Because C21 and C28 survival curves superimposed in all shear rates tested, transient adhesion of NK92-CD16 cells on anti-CD16-coated surfaces does not show any difference between the adhesive capacity of C21 and C28 (Fig. S8). These results show that the difference in off-rate kinetics measured at the molecular scale is not visible at the cellular scale in transient adhesion experiments. It may be hidden by the formation of multiple bonds during the process.

To assess whether the off-rate kinetics plays a role for cells at a longer timescale, in line with the above observations concerning spreading, we let the cells adhere in the flow chamber several seconds before applying a series of flows of increasing shear rates (Fig. S12). Clearly, cells adhering on C28 resist better to the detachment force than cells adhering on C21, indicating that a duration of several seconds of engagement is required to observe the catch-bond effect of C28.

Discussion

The purpose of this study was to dissect the association and dissociation mechanisms between antibody fragments such as nanobodies and their antigen to identify new criteria in the perspective of designing nanobody-based therapeutics. By measuring and comparing the binding of two nanobodies on the same antigen, we have evidenced comparable association and different dependence on the force of the dissociation. The LFC is the method of choice for rapid measurement of both association and dissociation kinetics of ligand-receptor bonds tethered at surfaces. The criteria of single-bond assessment are very stringent, whereas alternative single-bond techniques like AFM often rely only on a maximum of 10% of binding events observed (33). Applied flow limits the encounter duration between receptor on the microsphere and ligand on the underlying surface to the millisecond range. As a consequence, the external part of the energy landscape is probed, as it was shown for the biotin-streptavidin bond (9, 17). Therefore, the results reported here concerning the initial off rate may not be valid for deeper internal parts of the energy landscape. Conversely, the technique allows to precisely control the time of bond formation in the millisecond range. This has two advantages: first, the interaction duration between the reactive partners can be varied and the resulting bond formation measured (23); thus, we were able to show that, as already observed for conventional antibodies, the 2D association varies nonlinearly with the interaction duration (21, 22, 23). Second, bond maturation could be observed and quantified through the strengthening rate a (20). Nanobody-antigen bonds were actually reinforced with time on the second timescale, as previously observed for conventional antibody-antigen bond (20). Interestingly, other immune interactions probed with LFC, like T-cell receptor-peptide major histocompatibility complex (TCR-pMHC), exhibit rather slower strengthening (P. R., unpublished data), suggesting that these observations are not an artifact due to the method. Nevertheless, further efforts should be undertaken to support the concept of bond maturation through new development in the LFC like variable flow, which is currently being tested. Overall, our results emphasize that despite their small size, nanobodies exhibit complex association kinetics with their antigen, consistent with measurements on conventional antibodies.

The aforementioned technical limitations do not affect the comparative study presented here for several reasons. First, the dependence on encounter time of the 2D association is very similar for the two nanobodies, with the exponent differing by less than 10%. This rules out the possibility of an artifactual difference in dissociation caused by significant difference in association. Additionally, it was described that the epitopes recognized by the two nanobodies are different but closely located because both epitopes are shared with monoclonal antibody 7.5.4 (26). Because 2D association depends on the distance between molecules, the similar on rate favors the hypothesis of closely located epitopes with comparable molecular chain length L for the chains obtained with the two nanobodies in our setting (23).

The on/off kinetics of C21 and C28 have been measured previously using SPR with diffusing nanobodies binding CD16 tethered to surfaces (26). The off rate in solution (3D off rate) was found to be 2.8 × 10⁻³ s⁻¹ for C21 and 3.4 × 10⁻³ s⁻¹ for C28. In this study, we find values of k^o, the initial off rate at zero force, ∼1000 larger for both C28 and C21. This discrepancy was already observed in the LFC for kinetics of antibodies but not for TCR-pMHC (11, 19). We attribute this discrepancy to the short encounter duration imposed by the flow, leading to the measurement of dissociation in an early state of the bond (23). This is, however, consistent with the bond strengthening. For example, after 100 s, we predict an off rate at zero force of 5 × 10⁻³ s⁻¹ for C21 and 4 × 10⁻³ s⁻¹ for C28 (Fig. S4, A and B). Previous AFM studies showed a satisfying correlation between the 2D off rate extrapolated at zero force (k^o) and 3D off rate as measured with SPR (34, 35). However, our results show that Bell forces are strongly different: F_k ∼ 90 pN for C21 corresponds to a potential width of 0.04 nm in the energy landscape, likely related to a stiff bond (36). For C28, F_k ∼ −60 pN clearly shows a catch-bond behavior, as based solely on the survival curves. One should, however, consider also the strong reduction of BLD for high velocities (force), which may be the consequence of a selection in measured bonds. Although many instances of catch bonds have been found lately, this is, to our knowledge, the first time it is observed for antibody-antigen bonds. Additionally, because of the short proteins involved here, the observed data may not result from a generic behavior of polymeric linkers, as proposed recently (37). Concerning the association, the values of k_on provided by SPR measurements were 2.9 × 10⁵ M⁻¹ ⋅ s⁻¹ for C21 and 0.4 × 10⁵ M⁻¹ ⋅ s⁻¹ for C28. The conversion of our 2D association into a 3D k_on requires several assumptions on molecular length and flexibility (23). Qualitatively, C21 associates faster than C28 in 2D or 3D.

Our findings are particularly interesting from the perspective of designing bispecific antibodies used in therapeutics (27). For generating nanobody-based bispecific antibodies (bsAbs), the binding properties of those anti-CD16 might be of outmost importance but the basis for choosing the best binder remains elusive. We have previously generated two anti-carcinoembryonic antigen bsAbs using a common anti-carcinoembryonic antigen nanobody and either C21 or C28 (38). Interestingly, although the C21-based bsAb bound more efficiently to CD16-expressing cells by flow cytometry, probably reflecting the difference of dissociation constant K_D, their ability to activate NK cells was very similar, as evidenced by IL2 secretion assays and in vitro ADCC assays. Thus, although the accessibility of the CD16 epitope when displayed on the cell surface might clearly be a relevant consideration, these results suggest that a choice solely based on apparent affinity might be restrictive. C21-based bsAb was the chosen candidate for further resource and time-consuming animal studies (28, 38). However, our 2D measurements indicate here that C28 should exhibit a stronger resistance to force than C21. This is likely to be the case in the NK immune synapse, therefore indicating that C28 may be a better choice. Whether this parameter has an influence in the particular environment of the immune synapse deserved to be further investigated.

The flow cytometry measurements presented in this study reveal an opposite hierarchy of the affinity of anti-CD16 nanobodies, depending on the NK cell type. C28 binds better than C21 on NK92-CD16 (conflicting with 3D affinities (26)), whereas this is reversed on primary NK cells (38). Spreading experiments also display conflicting results depending on the NK cell type. The spreading of NK92-CD16 is largely higher on C28 surfaces, whereas the spreading of primary NK cells is very similar on C21 and C28 surfaces. Taken together, these observations emphasize the complexity of 2D reactions. To rationalize our findings, we propose that the fraction of spread cells results from the product of the 3D affinity of nanobodies for their target as determined by flow cytometry and from the 2D contributions of on rates and off rates (as measured in our experiments with the LFC). At the cell surface interface, the effective 3D concentration can be estimated dimensionally by the nanobody surface density divided by the typical gap size h separating the apical cell membrane from the nanobody-coated surface. For h = 15 nm, corresponding to the gap of immune synapses, a density of 10 molecules/μm² corresponds to an effective concentration of 1000 nmol/L. We thus calculated for each nanobody (C21 or C28) and each effector cell (primary NK or NK92-CD16) the 2D cell binding strength at each nanobody density as the cell spread fraction divided by the 3D relative binding at the corresponding effective concentration. Results are shown in Fig. 5. For both effector cell types, C28 exhibits a superior 2D binding strength than C21, reflecting its superior resistance in the force/timescales involved. Qualitatively, a surface density of nanobody above 1 molecule/μm² gives an effective 3D concentration that saturates the receptors, as measured by cytometry. In the case of NK92-CD16, this implies comparable binding fraction of C21 and C28 (see Fig. 3, left). Spreading is higher on C28 than on C21, reflecting C28’s higher 2D strength. In the case of primary NK cells, an equivalent spreading between the two nanobodies originates from the compensation of a poor 3D binding affinity of C28 by a higher 2D strength.

Figure 5.

2D cell binding strength calculated from cytometry and spreading data for each nanobody and effector cell type (see text for details). To see this figure in color, go online.

In recent years, mechanical forces have been shown to play a central role in the immune system, for example, with mechanotransduction, during cell migration, or immune cell-cell interaction (39). This was especially studied in the case of the recognition of the TCR with the pMHC, which was proposed to function as a catch bond (40, 41). Much less is known about the mechanical response of antibodies and their possible physiological role. The T-cell and NK cell synapses exhibit a strong resemblance, including the role of integrins (42), actin organization and depletion for cytotoxic vesicle release (43), and actin retrograde flow (6). Based on literature and our own experience with T cells (32, 44), we hypothesize that the NK cell synapse is also exerting and sensing force. Our cellular experiments show that NK cells engage an immune synapse on anti-CD16-coated surfaces for sufficiently high densities of antibodies. This does not require additional integrin ligands. It is likely that this process involves the cell pulling on the bond and that C28 offers a better resistance than C21. Using the calculated ratio of the off rates (Fig. 2 E), we speculate that the force may be above 10 pN and the duration of the pulling beyond 1 s. Although much experimental and theoretical work will be required to establish a more quantitative link between the molecular and cellular scale, as attempted recently in the case of the TCR (45) or selectins in biomimetic systems (46), we show here the strong potential to use carefully force-characterized nanobodies as probes for deciphering cell mechanical behavior.

Author Contributions

C.G. carried out all experiments and most of the analysis. P.R. and L.L. designed the research and supervised the experiments and the analysis. P.C., B.K., and D.B. contributed nanobodies and cells. All authors discussed the results. C.G. and L.L. wrote the article.

Editor: Ana-Suncana Smith.