Three-dimensional conditional random field for the dermal–epidermal junction segmentation

Abstract.

The segmentation of the dermal–epidermal junction (DEJ) in in vivo confocal images represents a challenging task due to uncertainty in visual labeling and complex dependencies between skin layers. We propose a method to segment the DEJ surface, which combines random forest classification with spatial regularization based on a three-dimensional conditional random field (CRF) to improve the classification robustness. The CRF regularization introduces spatial constraints consistent with skin anatomy and its biological behavior. We propose to specify the interaction potentials between pixels according to their depth and their relative position to each other to model skin biological properties. The proposed approach adds regularity to the classification by prohibiting inconsistent transitions between skin layers. As a result, it improves the sensitivity and specificity of the classification results.

1. Introduction

In this paper, we address the problem of segmenting the dermal–epidermal junction (DEJ) in in vivo reflectance confocal microscopy (RCM) using a three-dimensional (3-D) conditional random field (CRF) model.

The DEJ is a complex, surface-like, 3-D boundary separating the epidermis from the dermis. Its peaks and valleys, called dermal papillae, are due to projections of the dermis into the epidermis. The DEJ undergoes multiple changes under pathological or aging conditions. Alterations of the epidermal and dermal layers induce a flattening of the DEJ,^1,2 reducing the surface for exchange of water and nutrient from the dermis to the epidermis.

RCM is a powerful tool for noninvasively assessing skin architecture and associated cytology. RCM images provide a representation of the skin at the cellular level, with melanin and keratin working as natural autofluorescent agents.³ Pellacani et al.⁴ have shown that the use of RCM can improve the diagnosis of pathological lesions, while reducing the number of unnecessary excisions. However, the review of confocal images by trained dermatologists requires a lot of time and expertise. Several approaches to automate confocal skin image analysis have been proposed. In this context, they focus on quantifying the epidermal state,⁵ performing computer-aided diagnostic of skin lesions,⁶ or on identifying the layers of human skin.^7–9

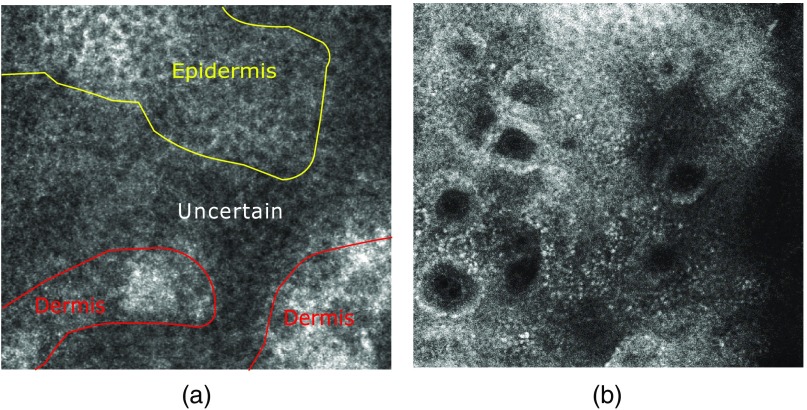
One particularly difficult point is the visualization of the DEJ, which is hard to identify purely by visual means. In fair skin, the DEJ can have multiple patterns. It can appear as an amorphous and low-contrasted structure or as circular rings, which correspond to the two-dimensional vertical view of a dermal papillae (see Fig. 1). Automating the DEJ segmentation makes it easier for clinicians to locate it and opens the way to quantitatively characterize its appearance. It could further improve the diagnosis of pathological lesions and could also result in a better understanding of the skin physiological response toward aging or other environmental conditions.

Fig. 1.

Examples of different DEJ patterns. The circular rings pattern in (a) provides an easy identification of the DEJ compared to the uncertain one in (b). However, the latter one is the most frequent, especially on the cheeks.

1.1. Related Work

As the DEJ appearance varies significantly and its contrast can be low, the precise localization of the DEJ is difficult. Therefore, in practice ground truth annotations often consist of three thick layers: the epidermis (E), an uncertain area containing the DEJ (U), and the dermis (D). There exist different approaches to delineate skin strata in RCM, which can be divided two main groups: on one hand, finding a continuous 3-D boundary between the layers of the skin, which implies a pixel-level classification, and on the other hand, performing an image-level classification to estimate the location of the transitions between layers.

Kurugol et al.⁷ proposed a machine learning-based method using textural features to automatically locate the DEJ location. They reproduce the key aspects of human visual expertise, which relies on texture and contrast differences between layers of the epidermis and dermis, in order to locate the DEJ. They used an LS-SVM method, a variant of support vector machine (SVM), which takes into account the expected similarity between neighboring tiles within images to include spatial relationship between neighbors and to increase robustness. They also propose a second approach, which incorporates a mathematical shape model for the DEJ using a Bayesian model.¹⁰ The DEJ shape is modeled using a marked Poisson process. Their model can account for uncertainty in number, location, shape, and appearance of the dermal papillae. Their main focus is to find the location of the DEJ rather than to study its shape.

Hames et al.⁹ addressed the problem of identifying all of the anatomical strata of human skin using a one-dimensional (1-D) linear chain conditional random field and structured SVMs to model the skin structure. They show an improvement in the classification scores with the use of such a model. However, their 1-D linear chain does not take advantage of the 3-D organization of the skin structure to regularize their output segmentation.

The following methods perform an image-level classification instead of a pixel-level classification.

Somoza et al.¹¹ used an unsupervised clustering method to classify a whole en-face image as a single distinct layer, resulting in a good correlation between human classification and automated assessment. However, the classification assumes that each image contains a single class, and therefore does not allow to capture the complex shape of the DEJ.

Kaur et al.¹² used a hybrid of classical methods in texture recognition and recent deep learning methods, which gives good results on a moderate size database of 15 stacks. They classify each confocal image as one of the skin layers. They introduce a hybrid deep learning approach which uses traditional feature vectors as input to train a deep neural network.

Bozkurt et al.¹³ proposed the use of deep-recurrent conventional neural networks (RNN)^14,15 to delineate the skin strata. The dataset used in this study is composed of 504 RCM stacks. Each confocal image is labeled in one of three classes: epidermis, DEJ, or dermis. They make the assumption that the skin layers are ordered with depth: the epidermis is the top layer of the skin, followed by the DEJ and the dermis. The use of deep RNN on a large dataset allows them to take the sequential dependencies between different images into account. They have trained numerous models with varying networks architectures to overcome the computational memory issues. This approach is potentially more flexible, as it provides the model with the complete RCM stack and allows it to learn what information is useful for slice-wise classification. With partial sequence training, the authors showed no improvement when enlarging the neighborhood of images around the RCM image to be classified. Bozkurt et al.¹⁶ added a soft attention mechanism in order the get information about which images the network pays attention to which making a decision.

Due to the uncertainty in visual labeling and intersubject variability, state-of-the-art methods tend to combine textural information and prior information on the DEJ shape, either by modeling the DEJ shape or by using a regularization of the segmentation through depth. The use of an RNN enables the representation of the dependencies between images.

Most methods focus on the localization of the DEJ in depth, with no consideration toward the characterization of its shape. Our goal is to segment the DEJ shape in order to quantify the modifications it undergoes during aging. In order to do so, we aim to combine textural information and 3-D dependencies between pixels within an RCM stack to perform a pixel-level segmentation.

Graphical models appear to be well-adapted and useful tools toward this purpose.

1.2. Modeling with Conditional Random Fields

Segmenting boundaries of interest in 3-D microscopy images are often challenging due to high intra- and intersubject (or specimen) variability and the complexity of the boundary structures. This task involves predicting a large number of variables (each image pixel is a variable) that depend on each other as well as on other observed variables. In this paper, we address the problem of segmenting the DEJ, a complex 3-D structure, imaged using in vivo RCM.

The way output variables depend on each other can be represented by graphical models, which include various classes of Bayesian networks, factor graphs, Markov random fields, and conditional random fields.

Most works in graphical models have focused on models that explicitly attempt to model a joint probability distribution $p(y|x)$, where $y$ and $x$ are random variables, respectively, ranging over observations and their corresponding label sequences. These models are fully generative, and they identify dependent variables and define the strength of their interactions. The dependencies between features can be quite complex, and the construction of the probability distribution over them can be challenging.

A solution to this problem is the modeling of a conditional distribution. This is the approach taken by CRF.¹⁷ A detailed review can be found in Sutton et al.¹⁸ Conditional random fields are popular techniques for image labeling because of their flexibility in modeling dependencies between neighbors and image features. Linear chain CRFs are the simplest and the most widely used. They have become very popular in natural language processing^19,20 and bioinformatics.²¹ Applications of CRFs have also extended the use of graphical structures in computer vision.^22,23 Medical imaging has been a field of interest in applying CRFs to many segmentation problems such as brain and liver tumor segmentation.^24,25

1.3. Contribution

Our approach consists of designing a 3-D conditional random field, which allows us to provide a spatial regularization on label distribution and to model skin biological properties. Our emphasis lies on exploiting the additional depth and 3-D information of the skin architecture. To our knowledge, this is the first method to include 3-D spatial relationships and to incorporate prior information about the global skin architecture.

We aim to segment the confocal images in three classes: epidermis (E), uncertain (U), and dermis (D). Our approach starts with a random forest (RF) classifier, providing the probabilities of a pixel to belong to one of these three classes, with no assumptions on the dependencies between pixels. The RF output encodes the textural information and gets in the CRF potentials.

The CRF model parameterization is inspired by prior information on the skin structure. The skin architecture is modeled by the conditional relationship between pixels. The relations between pixel neighbors mimic the skin layers behavior in 3-D by imposing a specified potential function according to their depth and their relative position to each other. The CRF potentials are learned from annotated skin RCM data. The CRF model allows us not only to incorporate resemblance between neighbors, but also to specify biological information.

We present several experiments, proving the benefit of the adapted CRF potentials to model the skin properties compared to more standard CRF parameterization strategies and to state-of-the-art methods.

2. Conditional Random Fields

An image $\mathbf{I}$ consists of $M$ pixels $i\in \mathbb{S}=[1,M]$ with observed data ${\mathbf{y}}_i$, i.e., $\mathbf{y}=(y_1,y_2,\dots ,y_M)$. Pixels are organized in layers (en-face images) forming a 3-D structure. We want to assign a discrete label $x_i$ to each pixel $i$ from a given set of classes $\mathcal{C}=\{E,U,D\}$. The classification problem can be formulated as finding the configuration $\widehat{x}$ that maximizes $p(\mathbf{x}|\mathbf{y})$, the posterior probability of the labels given the observations.

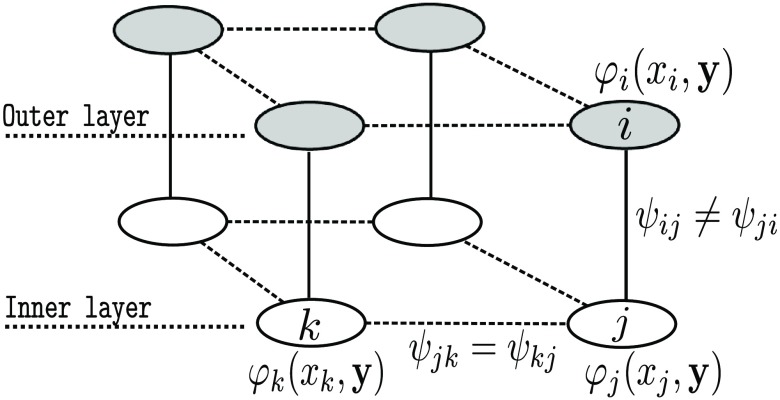
A CRF is a model of $p(\mathbf{x}|\mathbf{y})$ that can be represented with an associated graph $G=(V,\mathbb{E})$, where $V$ is the set of vertices representing the image pixels and $\mathbb{E}$ the set of edges modeling the interaction between neighbors.²⁶ Here $\mathbb{E}$ is the usual 3-D six-connectivity.

We use a model with pairwise interactions defined by

$$p(\mathbf{x}|\mathbf{y})\propto \prod _{i\in \mathbb{S}}{\phi }_i(x_i,\mathbf{y})\times \prod _{(i,j)\in \mathbb{E}}{\psi }_{ij}(x_i,x_j,\mathbf{y}),$$ (1)

where ${\phi }_i(x_i,\mathbf{y})$ is the node potential linking the observations to the class label at pixel $i$, and ${\psi }_{ij}(x_i,x_j,\mathbf{y})$ is the interaction potentials modeling the dependencies between the labels of two neighboring pixels $i$ and $j$.

The CRF model is represented in Fig. 2.

Fig. 2.

Three-dimensional CRF modelization. The set of nodes in gray and in white belong to two different en-face sections. The edge potentials of each en-face sections ${\psi }_{jk}$ [Eq. (3)] are learned at each depth. Edge potentials between en-face sections ${\psi }_{ij}$ [Eq. (3)] impose biological transition constraints.

In this paper, we propose to specify the CRF potentials in order to incorporate biological information. The skin layers are strictly ordered according to their depth. The epidermis is the top skin layer, followed by the uncertain area (containing the DEJ) and then by the dermis. Therefore, a pixel located near the surface will have a higher probability to belong to the epidermis than to the uncertain area or to the dermis. The CRF potentials are defined in order to forbid the incoherent transitions between layers.

The CRF parameters are depth-dependent. We define $\mathbb{D}$ the set of all depths of the image $\mathbf{I}$. For each $d\in \mathbb{D}$, we define:

• •${\mathbb{S}}_d$ is the set of pixels at depth $d$,
• •${\mathbb{E}}_d$ is the set of edges at depth $d$,
• •${\mathbb{E}}_{d\to d\pm 1}$ is the set of edges between depth $d$ and $d+1$, resp. $d-1$.

The notation ${\mathbb{1}}_{x=c}$ represents the indicator function, which takes the values 1 when $x=c$ and 0 otherwise. We denote by $x^{\mathrm{T}}$ the transposed vector of $x$. The operators $\circ$ and $·$ denote, respectively, the Hamadar product (element-wise multiplication) and the dot (or scalar) vector product.

2.1. Node Potential

The node potential is defined as the probability of a label $x_i$ to take a value $c$ given the observed data $\mathbf{y}$, that is:

$${\phi }_i(x_i=c,\mathbf{y})=p[x_i=c|{\mathbf{f}}_i(\mathbf{y})],$$ (2)

with ${\mathbf{f}}_i(\mathbf{y})$ a feature vector computed at pixel $i$ from the observed data.

In our case, each node potential ${\phi }_i(x_i,\mathbf{y})$ is associated with the predicted class probability vector ${\mathbf{f}}_i(\mathbf{y})$ produced by an RF classifier.²⁷ The node potentials ${\phi }_i(x_i,\mathbf{y})$ are linked by the relation

$$\prod _{i\in \mathbb{S}}{\phi }_i(x_i=c,\mathbf{y})=\prod _{d\in \mathbb{D}}\prod _{i\in {\mathbb{S}}_d}{1}_{x_i=c}\circ {\theta }_d·{\mathbf{f}}_i{(\mathbf{y})}^{\mathrm{T}}.$$ (3)

The parameter ${\theta }_d=({\theta }_{\text{epidermis}},{\theta }_{\text{uncertain}},{\theta }_{\text{dermis}})$ balances the bias introduced by labels appearing more often in the training data, i.e., the epidermal and the dermal one.

The feature vector ${\mathbf{f}}_i(\mathbf{y})$ is a $1\times 3$ vector of probability for a pixel to belong to each label. It is produced by an RF classifier²⁷ along with bootstrap aggregating and feature bagging.

Features are computed within a $50\times 50\text{pixel}$ window, which is large enough to include two epidermal cells forming the epidermal honeycomb pattern as their diameter varies from 15 to $35\mu \mathrm{m}$. We use the following well-known textural features inspired by Ref. 7:

• 1.First- and second-order statistics. We calculate statistical metrics mean, variance, skewness, and kurtosis.
• 2.Power spectrum²⁸ of the window.
• 3.Gray level co-occurrence matrix contrast, energy, and homogeneity.²⁹ The features are calculated for four orientations (0 deg, 45 deg, 90 deg, and 135 deg).
• 4.Gabor response filter output.^30,31 We compute a bank of Gabor filters with four levels of frequency and four orientations. As features, the local energy and the mean amplitude of the response are used.

We propose new features to estimate the distance of the current pixel to the DEJ.

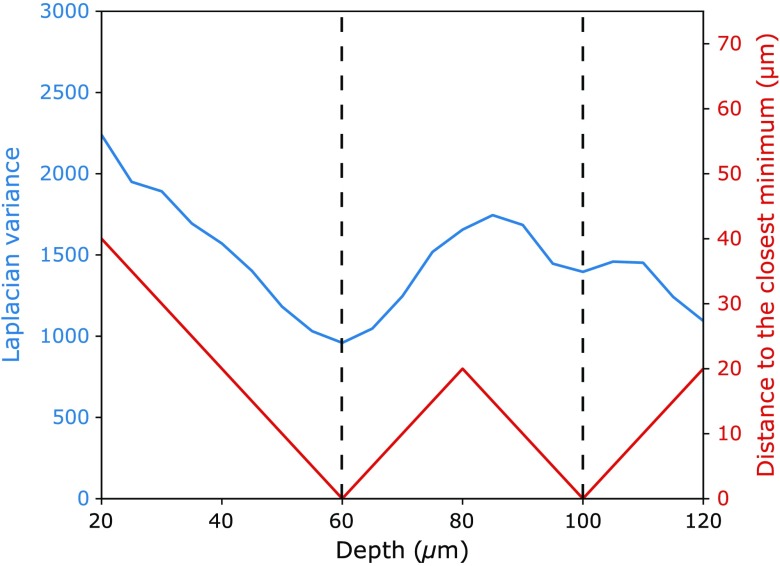
The Laplacian is related to the curvature of intensity changes. In classical edge detection theory,³² the zero-crossings of the Laplacian indicate contour locations. High values in the Laplacian are also associated with rapid intensity changes. The DEJ is an amorphous area compared to the epidermis, which appears as a honeycomb pattern, and to the dermis, which contains collagen fibers. Thus we expect low values in the Laplacian variance³² in confocal sections around the DEJ location. For a pixel $i$ at a given confocal section $p$, we calculate the Laplacian variance for every confocal section at its location.

A feature vector is computed containing the Laplacian variance at pixel $i$ coordinates at all depths. The pixel $i$ is characterized by its distance along the $z$ axis to its closest minimum in the feature vector. We add to the set of features: the Laplacian variance of pixel $i$, its distance to its closest minimum as described above and the features (Laplacian variance and depth) of its closest minimum within the Laplacian feature vector. An example is presented in Fig. 3. The distance to the closest minimum is expressed as the product of the number of confocal images to the closest minimum and the step that has been set for the 3-D acquisition. It is thus expressed in micrometer. For a given acquisition protocol, the distance to the closest minimum should be adjusted by the step parameter.

Fig. 3.

Laplacian variance and distance to the closest minimum for a pixel between 20 and $120\mu \mathrm{m}$. The blue line represents the Laplacian variance at coordinates $(i,j)$ at all depths. The dashed vertical lines mark the position of the minimum of the Laplacian variance. The red line corresponds to the distance to the closest minimum.

These features were chosen for their ability to discriminate texture from blurry patterns, which mostly corresponds to the DEJ pattern. The ringed DEJ pattern can be identified via its strong contrast and specific spatial arrangement. A summary of the proposed features is presented in Table 1.

Table 1.

Set of the 52 features used to produce the node potentials.

Feature type	Number of features	Presumed use
Statistics	4	Low intensity of the blurry DEJ pattern
Power spectrum	1	Low intensity of the blurry DEJ pattern
Gray-level co-occurrence matrix	12	Epidermal pattern and ringed DEJ pattern
Gabor output filter	32	Blurry pattern of the DEJ, epidermal, and dermal contrasted pattern
Laplacian	3	Blurry pattern of the DEJ and its location in depth

2.2. Interaction Potential

The interaction potential describes how likely $x_i$ is to take the value $c$ given the label $c^{\prime }$ of one of its neighboring pixel $j$:

$${\psi }_{ij}(x_i=c,x_j=c^{\prime },\mathbf{y})=p(x_i=c|x_j=c^{\prime }).$$ (4)

Prior information on skin structure is essential to determine efficiently the interaction potentials in our CRF model. The interaction potentials are modeled by a $3\times 3$ matrix representing the transition probabilities between classes.

We define two types of transitions: the transitions within a layer referred to as $H_d$, which are symmetrical and depth-dependent and the transitions interlayers $V{+}_d$ and $V{-}_d$, which are directional and also depth-dependent.

The product of the pairwise interaction potentials ${\psi }_{ij}(x_i,x_j,\mathbf{y})$ is expressed as

$$\begin{gathered} \prod _{(i,j)\in \mathbb{E}}{\psi }_{ij}(x_i=c,x_j=c^{\prime },\mathbf{y})=\prod _{d\in \mathbb{D}}\prod _{(i,j)\in {\mathbb{E}}_d}{\mathbb{1}}_{x_i=c}·H_d·{\mathbb{1}}_{x_j=c^{\prime }}^{\mathrm{T}} \\ \circ \prod _{(i,j)\in {\mathbb{E}}_{d\to d+1}}{\mathbb{1}}_{x_i=c}·V{+}_d·{\mathbb{1}}_{x_j=c^{\prime }}^{\mathrm{T}} \\ \circ \prod _{(i,j)\in {\mathbb{E}}_{d\to d-1}}{\mathbb{1}}_{x_i=c}·V{-}_d·{\mathbb{1}}_{x_j=c^{\prime }}^{\mathrm{T}}. \end{gathered}$$ (5)

2.2.1. Within-layer interaction potential

The within-layer interaction potential $H_d$ models the behavior of the skin at a given depth. We know that several skin layers can coexist in a single en-face section. In an en-face section, edges are modeled symmetrically, i.e., ${\psi }_{ij}={\psi }_{ji}$ (dashed lines in Fig. 2). The within-layer interaction potential $H_d$ is then modeled as a symmetrical matrix, see Table 2.

Table 2.

Horizontal transition matrix with neighboring pixels $i$ and $j$ where $a_d,\dots ,f_d$ are the learned probabilities of transition see Sec. 2.3. The symmetric, nonzero values ensure that transitions in both ways are equally possible.

	${\text{Label}}_i$	${\text{Label}}_j$
		Epidermis	Uncertain	Dermis
$H_d=$	Epidermis	$a_d$	$b_d$	$c_d$
	Uncertain	$b_d$	$d_d$	$e_d$
	Dermis	$c_d$	$e_d$	$f_d$

2.2.2. Interlayer interaction potential

The skin layers follow a specific order from the surface to inner layers: the epidermis is the top skin layer, followed by the uncertain area (containing the DEJ), and then by the dermis. We define an inconsistent transition as a transition not following this specific order. Between en-face sections, only consistent transitions are allowed, the edge potentials thus depend of their direction, i.e., ${\psi }_{ij}\ne {\psi }_{ji}$.

To impose the biological transition order in depth, constraints are added to the transition matrix according to the edge direction. We define in Table 3 $V{+}_d$ as the vertical transition matrix from pixels $i$ to $j$, with $i$ above $j$. The reverse transition matrix $V{-}_d$ from $j$ to $i$ is then defined in Table 4.

Table 3.

Vertical transition matrix with $i$ above $j$ where $m_d,\dots ,s_d$ are the learned probabilities of transition. The null values ensure that inconsistent transitions are impossible.

	$i$	$j$
		Epidermis	Uncertain	Dermis
$V{+}_d=$	Epidermis	$m_d$	$n_d$	$p_d$
	Uncertain	0	$q_d$	$r_d$
	Dermis	0	0	1

Table 4.

Vertical transition matrix with $j$ below $i$ where $m_d,\dots ,s_d$ are the learned probabilities of transition. The null values ensure that inconsistent transitions are impossible.

	$j$	$i$
		Epidermis	Uncertain	Dermis
$V{-}_d=$	Epidermis	1	0	0
	Uncertain	$n_d$	$q_d$	0
	Dermis	$p_d$	$r_d$	$m_d$

2.3. Parameter Optimization

The parameters described above are learned from the ground truth dataset.

Our model can be expressed as

$$\log [p(\mathbf{x}|\mathbf{y})]=\sum _{i\in \mathbb{S}}\log [{\phi }_i(x_i,\mathbf{y})]+\sum _{i,j\in \mathbb{E}}\log [{\psi }_{ij}(x_i,x_j)].$$ (6)

We define ${\mathrm{\Omega }}_d$ the set of parameters at depth $d$ and $\mathrm{\Omega }=\bigcup _{d\in D}{\mathrm{\Omega }}_d$ the set of parameters for all depths. The set of parameters is summarized in Table 5.

Table 5.

Set of parameters of ${\mathrm{\Omega }}_d$ for the CRF model.

Parameter	Form	Number of parameters	Use
${\theta }_d$	$1\times 3$ vector	3	Weight bias vector used to balance the labels occurrences
$H_d$	$3\times 3$ symmetrical matrix	6	Transition matrix between classes at depth $d$
$V{+}_d$	$3\times 3$ upper triangular matrix	5	Transition matrix between classes between $d$ and $d+1$
$V{-}_d$	$3\times 3$ lower triangular matrix	5	Transition matrix between classes between $d$ and $d-1$

Our goal is to find the set of parameters $\overline{\mathrm{\Omega }}$ that maximizes the log-likelihood:

$$\overline{\mathrm{\Omega }}=\underset{\mathrm{\Omega }}{\mathrm{argmax}}\sum _{i\in \mathbb{S}}\log \{p[x_i=c_x|{\mathbf{f}}_i(\mathbf{y})]\},$$ (7)

with $c_x$ is the class of $x$, and $\mathbf{f}({\mathbf{y}}_i)$ is the feature vector.

The parameters ${\theta }_d$, $H_d$, $V{+}_d$, and $V{-}_d$ are depth-dependent. We estimate such transition probabilities from the frequency of co-occurrence of classes ($c$ and $c^{\prime }$) between neighboring pixels $i$ and $j$ in the ground truth images. Co-occurrence frequencies are learned at each depth $d\in \mathbb{D}$ of en-face sections. The value of ${\theta }_d$ is initialized at [0.3 0.3 0.3] for all depths and optimized to increase the model accuracy.

For each depth $d$, we estimate the parameters of ${\mathrm{\Omega }}_d$. The number of parameters $N$ to estimate for $n$ depths is given by the following formula: $N=({\theta }_d\times n)+(H_d\times n)+[V{+}_d\times (n-1)]+[V{-}_d\times (n-1)]$, which leads us to 370 parameters for 20 depths (see Table 5). The parameters in $\mathrm{\Omega }$ are trained using the Powell search method, an iterative optimization algorithm³³ that does not require estimating the gradient of the objective function. We use a loopy belief propagation method to estimate $p(\mathbf{x}|\mathbf{y})$. The computation is done using the library developed in DGM Lib.³⁴

3. Experimentation

3.1. Database

Image acquisition was carried out on the cheek to further assess chronological aging. RCM images were acquired using a near-infrared reflectance confocal laser scanning microscope (Vivascope 1500; Lucid Inc., Rochester, New York).³⁵ On each imaged site, stacks were acquired from the skin surface to the reticular dermis with a step of $5\mu \mathrm{m}$. Our dataset consists of 23 annotated stacks of confocal images acquired from 15 healthy volunteers, with $1.5\pm 0.5$ stacks/subject, with phototypes from I to III,³⁶ i.e., from volunteers whose skin strongly reacts to sun-exposure. As melanin is a strong contrast agent in confocal images, confocal images of fair skin represent the most challenging analysis compared to higher melanin content. The more melanin, the more contrasted skin confocal patterns.

Neither cosmetic products nor skin treatment was allowed on the day of the acquisitions. Appropriate consent was obtained from all subjects before imaging. Visual labeling of the DEJ is not easy to perform even for experts. An expert, whose grading had been previously validated, delineated the stacks in three zones: epidermis (E), uncertain (U), and dermis (D) (see Fig. 1). We segmented confocal images between depths 20 and $120\mu \mathrm{m}$, the images above $20\mu \mathrm{m}$ belonging to the epidermis with high confidence. We used a subject-wise 10-fold cross validation test to evaluate the segmentation results. In order to compare the results, the same subdataset is used for both the training and testing parts for all the experiments. As several stacks acquired from one subject can contribute to the annotation dataset, stacks acquired from the same subject are not considered as independant data. Therefore, a subject-wise cross-validation is conducted, i.e., one subject cannot belong to both the training and testing sets at each fold.

3.2. Feature Evaluation

To evaluate our proposed set of features used for the RF classification, we compare the mean accuracy of our classification results to the state-of-the-art methods. The mean accuracies of the RF classifications are presented in Table 6. Kurugol et al.⁷ achieved 64%, 41%, and 75% of correct classification of tiles for epidermis, transition region, and dermis, respectively. Hames et al.⁹ achieved 82%, 78%, and 88% of correct classification for the epidermis, DEJ, and dermis, respectively. With the proposed set of features, we were able to achieve 90%, 54%, and 75% accuracy, respectively, for the epidermal, uncertain area, and dermal classification. These results suggest that our set of features is relevant to identify the three skin labels according to the visual inspection by experts. However, the result of our initial classification still contains 11% of inconsistent transitions (not following the expected biological order), see Table 10, motivating the introduction of spatial constraints with the CRF regularization.

Table 6.

Results for the unregularized experiments. Mean accuracy of the RF classifications of the three labels. The RF classification provides the node potentials for the CRF model.

	Epidermis	Uncertain	Dermis	Number of RCM stacks
Proposed features	0.90	0.54	0.75	23
Kurugol et al.7	0.64	0.41	0.75	15
Hames et al.9	0.82	0.78	0.88	308

Table 10.

Percentage of inconsistent transitions between the skin layers. Epidermis, E; uncertain, U; and dermis, D.

	U → E	D → U	D → E	Total (%)
RF	0.6	2	3	11
$\mathrm{RF}+{\mathrm{CRF}}_{2\text{-}\mathrm{D}}$	7	3	8	18
$\mathrm{RF}+{\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$	0	4	0	4
$\mathrm{RF}+{\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	0	0	0	0

3.3. CRF Parameters Evaluation

To evaluate the chosen parameters, we compare three cases:

• 1.${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$ is the CRF with only horizontal regularization. Each confocal section is regularized independently using the horizontal transition matrix $H_d$.
• 2.${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$ is the CRF with horizontal regularization $H_d$ and symmetrical vertical regularization, i.e., $V{+}_d=V{-}_d$.
• 3.${\mathrm{CRF}}_{3\mathrm{D}\mathrm{Asym}}$ is the CRF with horizontal regularization $H_d$ and asymmetrical vertical regularization, i.e., $V{+}_d\ne V{-}_d$. This is our proposed model where the skin layers order is imposed.

The global accuracies, presented in Table 7, for the three experiments are comparable. We also achieve a high specificity for the three classes (above 0.90%), see Table 8. The ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ parameterization allows us to increase the sensitivity of the uncertain area classification, compared to ${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$ and ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$, while maintaining the epidermal and dermal sensitivity above 0.90%, see Table 9.

Table 7.

Global accuracy percentage for the three regularization schemes.

	Accuracy
RF	78
$\mathrm{RF}+{\mathrm{CRF}}_{2\text{-}\mathrm{D}}$	85
$\mathrm{RF}+{\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$	85
$\mathrm{RF}+{\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	86

Table 8.

Specificity of the three labeling in the regularized cases.

	Specificity
	Epidermis	Uncertain	Dermis
${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$	0.90	0.89	0.93
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$	0.94	0.92	0.95
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	0.96	0.92	0.95

Table 9.

Sensitivity of the three labeling in the regularized cases.

	Sensitivity
	Epidermis	Uncertain	Dermis
${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$	0.90	0.63	0.83
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$	0.91	0.55	0.90
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	0.90	0.68	0.93

We have defined an inconsistent transition as a transition between skin layers, which does not follow the biological order. The resulting segmentation with ${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$ contains 18% of inconsistent transitions. ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$ still contains 4% of inconsistent transition, whereas ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{ASym}}$ contains none. The inconsistent transitions’ percentages are presented in Table 10.

Examples of resulting segmentations at two following depths are presented in Figs. 4 and 5. A direct classification after features calculation leads to a misclassification and inconsistent transitions between classes. The positive impact of our CRF model is noticeable. Moreover, the computation of the DEJ segmentation only takes a few minutes per stack on a common computer, which enables the use of its use in large-scale analysis and clinical studies.

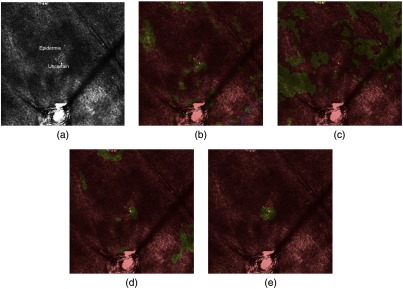
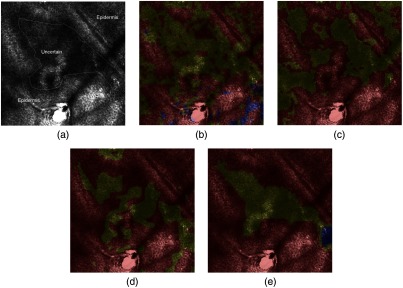
Fig. 4.

Segmentations at depth $d$: epidermis (red), uncertain (yellow), dermis (blue). (a) Annotated image at depth $d$, (b) RF at depth $d$, (c) ${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$ at depth $d$, (d) ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$ at depth $d$, and (e) ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ at depth $d$. The addition of constraints into the CRF model improves the accuracy of the segmentation.

Fig. 5.

Segmentations at depth $d+1$. (a) Annotated image at depth $d+1$, (b) RF at depth $d+1$, (c) ${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$ at depth $d+1$, (d) ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Sym}}$ at depth $d+1$, and (e) ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ at depth $d+1$. Inconsistent transitions exist between depth $d$ and $d+1$. One can notice the misclassification obtained by RF and ${\mathrm{CRF}}_{2\text{-}\mathrm{D}}$. The use of ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ provides a coherent segmentation.

One can notice that the optimization of the parameter set $\mathrm{\Omega }$ improves the sensitivity of the uncertain area classification from 66% to 68% and the epidermal and dermal specificity up to 95%.

3.4. Comparison to State-of-the-Art Methods

We compare our results to the state-of-the-art methods. The results presented below should be considered with caution, because of the differences in labeling and dataset size.

Global accuracy of our model is similar to state-of-the-art methods. The sensitivity and specificity results of the regularized CRF model are presented in Tables 11 and 12. The specificity results obtained by Kurugol et al.⁷ are not available.

Table 11.

Sensitivity results of ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ compared to state-of-the-art methods.

	Sensitivity			Ground truth level	Number of RCM stacks
	Epidermis	Uncertain	Dermis
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	0.90	0.68	0.93	Pixel	23
Kurugol et al.7	0.64	0.41	0.75	Pixel	15
Hames et al.9	0.87	0.79	0.88	Image	308
Bozkurt et al.16	0.94	0.84	0.84	Image	504
Kaur et al.12	0.74	0.51	0.68	Image	15

Table 12.

Specificity results of ${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$ compared to state-of-the-art methods

	Specificity			Ground truth level	Number of RCM stacks
	Epidermis	Uncertain	Dermis
${\mathrm{CRF}}_{3\text{-}\mathrm{D}\mathrm{Asym}}$	0.96	0.92	0.95	Pixel	23
Hames et al.9	0.94	0.87	0.94	Image	308
Bozkurt et al.16	0.96	0.90	0.96	Image	504
Kaur et al.12	0.86	0.75	0.85	Image	15

Deep learning methods by Bozkurt et al.¹⁶ and Kaur et al.¹² seem to also take into account the dependencies between images to perform the classification, the author did not observe any incoherent transitions, but the regression might lack interpretability.

4. Conclusion

We have proposed a method to segment the DEJ in confocal microscopy images. This method combines RF classification with a spatial regularization based on a 3-D CRF. Moreover, the 3-D CRF imposes constraints related to the skin biological properties. The ablation analysis of the model has shown the importance of each of its components—RF, spatial regularization, and biological constraints—in order to achieve the best results. In addition, the results show that the proposed method is competitive compared to state-of-the art methods.

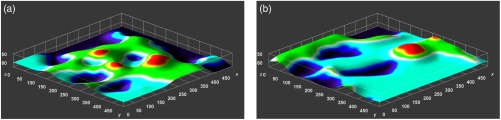
Our DEJ segmentation algorithm has already been used in the context of automatic skin aging characterization from RCM images.³⁷ Indeed, the alteration of the epidermal and dermal layers within skin aging induces a flattening of the DEJ (see Fig. 6) and Longo et al.^38,39 have identified the shape of the peaks and valleys of the DEJ as a skin aging confocal descriptor. We have proposed a characteristic measurement of regularity of the DEJ that can be computed automatically. This measurement, extracted on the DEJ segmented by the method presented in this paper, has a significant positive correlation with the age of the subjects.

Fig. 6.

Visual appearance of the transition from the epidermis to the uncertain area, which corresponds to the epidermal lower boundary. Notice that the aged DEJ (b) appears flatter than the young DEJ (a), as expected. Colors encode the depth.

Biographies

Julie Robic received her PhD in computer vision from the University of Marne-la-Vallée, France, in 2018. She is a project manager in charge of skin image processing for Clarins Laboratories.

Benjamin Perret received his MSc degree in computer science in 2007, and his PhD in image processing in 2010 from the Université de Strasbourg, France. He currently holds a teacher–researcher position at ESIEE Paris, affiliated with the Laboratoire d’Informatique Gaspard Monge of the Université Paris-Est. His current research interests include image processing and image analysis.

Alex Nkengne holds a PhD in medical computer science and has spent the last 14 years as a researcher in the field of skin biophysics and imaging for different companies. He currently leads the Skin Models and Methods Team for Clarins Laboratories.

Michel Couprie received his PhD from the Université Pierre et Marie Curie, Paris, France, in 1988, and the Habilitation à Diriger des Recherches in 2004 from the Université de Marne-la-Vallée, France. Since 1988, he has been working in the Computer Science Department of ESIEE. He is also a member of the Laboratoire d’Informatique Gaspard-Monge of the Université Paris-Est. He has authored/co-authored more than 100 papers in archival journals and conference proceedings as well as book contributions. He supervised or co-supervised nine PhD students who successfully defended their thesis. His current research interests include image analysis and discrete mathematics.

Hugues Talbot received his habilitation degree from the Université Paris-Est in 2013, his PhD from École des Mines de Paris in 1993, and his engineering degree from École Centrale de Paris in 1989. He was a principal research scientist at CSIRO, Sydney, from 1994 to 2004, a professor at ESIEE Paris from 2004 to 2018, and is now a full professor at CentraleSupelec of the University Paris-Saclay. During the period 2015 to 2018, he was the research dean at ESIEE Paris. He is the co-author of 6 books and more than 200 articles in various areas of computer vision, including low-level vision, mathematical morphology, discrete geometry, and combinatorial and continuous optimization.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.