Rapid and Accurate Determination of Nanopore Ionic Current Using a Steric Exclusion Model

Abstract

Nanopore sensing has emerged as a versatile approach to detection and identification of biomolecules. Presently, researchers rely on experience and intuition for choosing or modifying the nanopores to detect a target analyte. The field would greatly bene t from a computational method that could relate the atomic-scale geometry of the nanopores and analytes to the blockade nanopore currents they produce. Existing computational methods are either computationally too expensive to be used routinely in experimental laboratories or not sensitive enough to account for the atomic structure of the pore and the analytes. Here, we demonstrate a robust and inexpensive computational approach—the steric exclusion model (SEM) of nanopore conductance—that is orders of magnitude more efficient than all-atom MD and yet is sensitive enough to account for the atomic structure of the nanopore and the analyte. The method combines the computational efficiency of a finite element solver with the atomic precision of a nanopore conductance map to yield unprecedented speed and accuracy of ionic current prediction. We validate our SEM approach through comparison with the current blockades computed using the all-atom molecular dynamics method for a range of proteins confined to a solid-state nanopore, biological channels embedded in a lipid bilayer membranes and blockade currents produced by DNA homopolymers in MspA. We illustrate potential applications of SEM by computing blockade currents produced by nucleosome proteins in a solid-state nanopore, individual amino acids in MspA and by testing the effect of point mutations on amino acid distinguishability. We expect our SEM approach to become an integral part of future development of the nanopore sensing field.

Graphical Abstract

Measurements of ionic current owing through nanopores in biological or solid-state mem-branes can reveal intricate information about the properties of the nanopores^1,2 but also about the properties of the solutes that can pass through them.^3,4 Indeed, the so-called nanopore sensing approach^5,6 analyzes the changes in the nanopore ionic current to detect the presence of biomolecules within the nanopore and to characterize their properties. To date, the nanopore sensing principle has been applied to study variety of biomolecular sys-tems,^7,8 from ions⁹ to viruses,¹⁰ including determination of the nucleotide sequence of DNA¹¹ and RNA.¹² Tremendous opportunities lie ahead for nanopore sensing in protein character-ization^13–15 and sequencing technologies,^16,17 detection of molecular biomarkers,^18,19 drug design,²⁰ mass spectrometry^21,22 and general purpose analytics.^23,24 Realizing these goals will require development of custom nanopores that produce well-defined current modulations in the presence of target analytes. As experimental modification of nanopore structure remains laborious and expensive, there is considerable interest in characterizing nanopore blockade currents computationally. Successful computational models need, however, to satisfy the conflicting requirements of being both computationally efficient and sensitive to the atomic structure of the analytes.

Over the past twenty years, many theoretical models of ionic current blockades in nanopores have been developed,^25,26 with an overarching goal of relating the experimentally measured blockade currents to the chemical structure of the biomolecules present within the nanopores. Such theoretical models can be associated with one of the following three categories: continuum models relying on the Poisson-Nernst-Planck (PNP) formalism, Brownian dynamics (BD) models that treat solvent implicitly, and explicit solvent all-atom molecular dynamics (MD) simulations. The least computationally intensive is PNP,^27–34 which is a mean-field method that simultaneously solves the Poisson-Boltzmann equation (for ion con-centration and electrical potential) as well as the Nernst-Planck equation (for ion ux). This method does not account for correlated motion between ions, although such correlations can be added by borrowing from density functional theory³⁵ or introduced explicitly.^36,37 Brownian dynamics models^38–43 represent all ions in the system explicitly but describe all other components of the system approximately, most importantly, representing the solvent as a continuum medium. The accuracy of a BD model depends on the level of details the biomolecules and the nanopores are represented in the model. The BD models can attain atomic level precision^41,44,45 when biomolecules are represented using potentials that accurately reproduce the interactions of solvated ions with each other and with solvated biomolecules. The all-atom MD method⁴⁶ represents every atom of the experimental sys-tem explicitly, including water and the membrane containing the nanopore. Although this method offers the highest level of accuracy, it remains computationally demanding which tempers its use for everyday interpretation of nanopore measurements by experimental laboratories.

We have previously shown that a relatively simple theoretical model can account for the complex dependence of ionic current blockade on the type, the orientation and the folding state of a protein.⁴⁷ Brie y, the model assumes that the local conductivity of electrolyte solution near a protein is determined by the bulk electrolyte conductivity and the distance to the nearest protein surface. The nanopore ionic current can thus be obtained by discretizing the nanopore volume and applying the Ohm’s law for resistance elements connected in parallel and in series. Despite its simplicity, the model was shown to reproduce the intricate dependence of ionic current on the type and conformation of a protein observed in explicit solvent all-atom MD simulation. The model, however, implicitly assumes that all resistance elements located within a plane normal to the external electric field are equipotential, a condition that nearly holds for a compact object located in an infinite channel, but fails for realistic pore geometries and complex conformations of the blockade molecules.

Here, we extend our local conductivity model to more complex nanopore geometries by solving the resistance element network numerically. Starting from an all-atom model of a nanopore system, Fig. 1a, we obtain a 3D map of the local conductivity, Fig. 1b, that accounts For fine steric features of the all-atom model, Fig. 1c. Setting the transmembrane potential as a boundary condition for the electric potential, we solve the differential equations using the finite element method to obtain a steady state ionic current. Surprisingly, we find this rather simple model to perform extremely well not only in the case of folded proteins confined to nanopores of simple geometries but also for biological nanopores, reproducing both open pore and blockade currents obtained using the explicit solvent all-atom MD methods. The combination of computational simplicity and sensitivity to atomic-level detail makes our method potentially suitable for everyday use in experimental laboratories for interpretation of the blockade current measurements.

Figure 1:

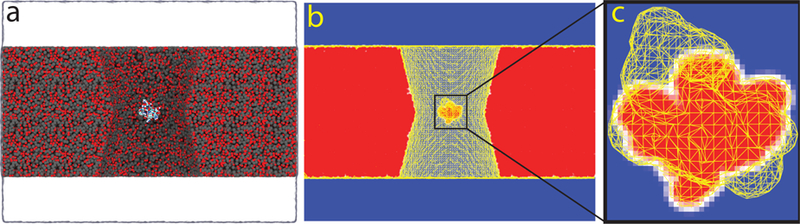
Calculation of nanopore ionic current using the steric exclusion model (SEM). (a) All-atom representation of a solid-state nanopore harboring a protein in its constriction. Silicon and oxygen atoms are represented by gray and red spheres, respectively. Atoms of the proteins are colored according to the atom type: white, red, blue, and cyan indicate hydrogen, oxygen, nitrogen, and carbon atoms, respectively. The electrolyte solution is shown as a semitransparent surface. To reveal the presence of the nanopore, a cut-away view of the membrane is shown. (b) SEM representation of the nanopore system shown in panel a. The image shows a heatmap slice through the 3D map of local conductivity that, along with the boundary conditions, defines the system for ionic current calculations. Blue and red colors indicate regions of the system where local ion conductivity equals the bulk ion conductivity or zero, respectively. A yellow wireframe shows an isosurface of local conductivity value equal 50% of the bulk conductivity. (c) Close up view of the region near the protein. For clarity, the wireframe isosurface near the nanopore walls is not shown.

The rest of the manuscript is organized as follows. In the next section, we describe our steric exclusion model (SEM) of nanopore ionic current. We validate the model through comparison to all-atom MD simulations of ionic current blockade produced by proteins in solid-state nanochannels, open pore currents of biological nanopores and DNA sequence-specific blockades in MspA. We illustrate potential applications of the model by computing ionic current variations produced by translocation of nucleosomal substructures through a solid-state nanopore, translocation of single amino acids through MspA, and point mutations of the biological nanopore structure. We discuss present limitations of the methods and possible future directions for its improvement in the last section of the manuscript.

Results

Steric exclusion model of nanopore ionic current

From the continuity equation in steady state, and Ohm’s law:

$$▽\hspace{0.17em}\cdot \text{J}\left(\text{r}\right)=0,\hspace{1em}\text{J}\left(\text{r}\right)=\sigma \left(\text{r}\right)\text{E}\left(\text{r}\right),\hspace{1em}\text{E}\left(\text{r}\right)=-▽\mathrm{V}\left(\text{r}\right),$$ (1)

where r represents coordinates of a point is 3D space, J(r) is the local current density, σ(r) is the local conductivity, E(r) is the local electric field, and $\varphi \left(\text{r}\right)$ is the local electric potential, the following equation is produced

$$▽\hspace{0.17em}\cdot \hspace{0.17em}\left(\sigma \left(\text{r}\right)▽\text{V}\left(\text{r}\right)\right)=0.$$ (2)

By solving this equation directly under appropriate boundary conditions one can determine a steady-state current through an arbitrary cross section of the system. Thus, finding the ionic current is then reduced to finding the conductivity in the space of interest.

We have previously shown that for a weakly charged protein, the ion conductivity near the protein depends on the distance to a protein surface.⁴⁷ This result was obtained by computing the ion conductivity in concentric shells surrounding a protein from explicit solvent all-atom MD simulation of the protein under external electric field. Within a few angstroms of a protein surface, the ion conductivity is zero because ions are excluded from within the protein surface. As the distance to the protein surface increases, so does the conductivity until reaching the bulk value less than 10 Å away from the surface. In our previous work, we used a hyperbolic tangent function to describe the transition from zero to bulk conductivity values. In our subsequent studies of systems containing lipid membranes (described in detail below), we found that such hyperbolic tangent function does not get sufficiently small at low distances and can produce significant leakage current.

To develop a more accurate description of local conductivity dependence on distance from protein atoms, we simulated four model systems each containing four linear chains of identical atoms (carbon, oxygen, nitrogen or hydrogen) arranged parallel to one another, Fig. 2a. The systems were simulated in explicit solvent under external electric field applied parallel to the linear chains (see Methods for details). The ion concentration and mobility were measured as a function of radial distance from the center of the chains, Fig. 2b. Fig. 2c plots local conductivity—the product of local ion mobility and local ion concentration—as a function of the radial distance normalized by bulk ion conductivity. We find a stepwise linear function of the same slope to closely reproduce the simulated dependence of ion conductivity on radial distance (R) for all four atom-chain systems (see SI Figs. S1 and S2). The x-intercept of the linear part of the function was found to be equal to the atomic radius plus a constant o set of the average value of 1.4 Å. Encouraged by this observation, we describe the linear step function for all other atoms types using the same slope (0.29 Å⁻¹) for the linear part and the x-intercept equal to the atomic radius plus the 1.4 Å offset. Once the linear function reaches 1.0 (σ = σ₀), subsequent σ/σ₀ values are taken to be 1.0.

Figure 2:

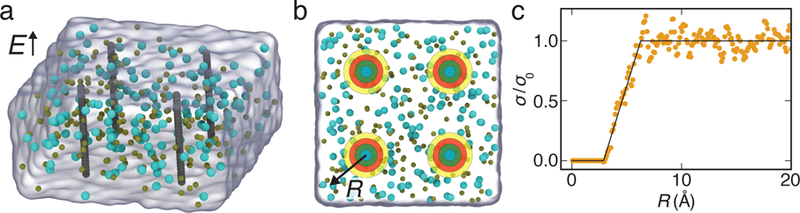
Calibration of local conductivity model. (a) All-atom system used for calibration simulations. Test atoms (gray) are arranged into four linear chains and surrounded by electrolyte solution (gray semitransparent surface); potassium and chloride ions are shown explicitly as tan and cyan spheres, respectively. The chains of test atoms are effectively infinite under periodic boundary conditions. An external electric field of 10 mV/nm is applied parallel to the chains of atoms. The test atoms’ coordinates are harmonically restrained to initial values. (b) Top view of the simulation system. The steady state mobility and concentration of ions are calculated independently for each cylindrical shell (colors) surrounding each chain of test atoms. Conductivity as a function of radius is then calculated as a product of mobility and concentration. (c) Simulated electrolyte conductivity as a function of distance R from the center of the carbon atom, scaled by the bulk conductivity σ₀. SI Figs. S1 and S2 show similar plots for nitrogen, oxygen and hydrogen atoms, as well as the scaled conductivity dependence for individual ion species.

To calculate the ionic current owing through a nanopore at a given voltage bias, the SEM approach takes, as input, the coordinates of all atoms comprising the protein, DNA, lipid and/or inorganic components of the systems, the radii of these atoms, the bulk electrolyte conductivity and the transmembrane bias. The volume occupied by the system is discretized using a 3D grid that, for each grid point, specifies the distance from that grid point to the nearest non-solvent atom. That distance is determined by first finding the distances to the centers of all nearby atoms, subtracting the atomic radii from the respective distances, and then choosing the atom having the smallest grid-to-atom surface distance. Each distance value is then used to compute the local conductivity by multiplying the bulk conductivity value by the value of the stepwise linear function that describes the dependence of the normalized conductivity on the distance to the nearest atom, Fig. 2c. In this work, we used a grid spacing of 1 Å. Using a finer grid would considerably increase the computational cost of the ionic current determination whereas using a coarser grid would wash out the atomic-scale features of the protein surface.

Having obtained a grid of conductance values σ(r), Eq. 2 is solved numerically for the electrical potential, V (r) under the Neumann boundary conditions (∇_nV = 0) at the boundaries of the systems that are normal to the membrane and the Dirichlet boundary conditions (V_top = +V_max, V_bottom = 0 ) at the boundaries of the systems parallel to the membrane, where V is the transmembrane bias. To solve Eq. 2, we use a finite element solver FEn-iCS.^48,49 A regular tetrahedral mesh is created of the same size and resolution as the grid of conductance values. Vertices of the mesh are assigned conductance values from the σ(r) grid. The boundaries of the mesh are flagged to have the above boundary conditions. Eq. 2 is then solved using the Generalized Minimal Residual method (gmres),⁵⁰ with an algebraic multigrid (amg) preconditioner.⁵¹

The nanopore current is obtained by taking the following integral using the integration function of the FEniCS package:

$$∯\widehat{z}\cdot \left(\sigma \left(\text{r}\right)▽\text{V}\left(\text{r}\right)\right)\text{dS},$$ (3)

where the surface of integration is one of the Dirichlet boundaries.

Validation: Blockade currents of proteins confined to a solid-state nanochannel

We begin validation of SEM by applying the model to a collection of protein systems that were previously studied using the all-atom MD method.⁴⁷ Each system contained one of nine different proteins placed at the center of a solid-state nanopore in either folded or unfolded conformation and 2 M KCl solution; several orientations were explored for some of the proteins. The nanopore walls were made from carbon atoms, and the simulation box was periodic so that the nanopore was continuous and in finite along the nanopore axis. Fig. 3a illustrates one such simulation system. Each system was simulated for 150 ns under electric field of 74.7 mV/nm (300 mV over a distance of 40.176 Å) directed along the nanopore axis. All protein atoms were individually harmonically restrained to their initial coordinate using harmonic potentials of 1 kcal/(mol Å) spring constants.

Figure 3:

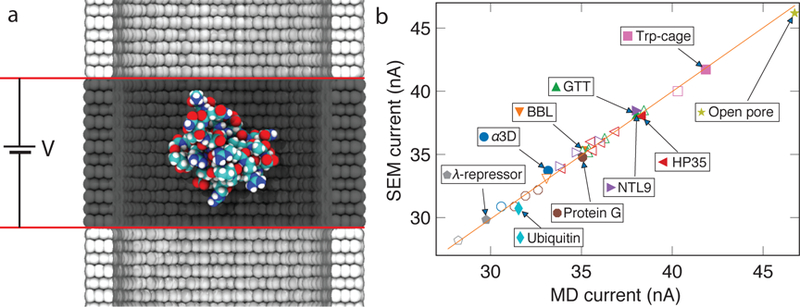
SEM validation against all-atom MD simulations of proteins in an inorganic nanochannel. (a) Schematic of the all-atom MD system. A single proteins (shown as vdW spheres colored according to atom type) is held at the center of a multi-layer graphene nanopore (gray) filled with 2 M KCl electrolyte (not shown). Red lines denote the boundaries of a periodic unit cell. (b) SEM blockade current versus the current measured from explicit solvent MD simulation for 34 protein systems and a system containing no protein (open pore). MD data taken from Ref. 47. Data for proteins of identical amino acid sequences but different folding states and/or orientations are shown using symbols of the same shape and color. Filled/open symbols correspond to folded/unfolded proteins, respectively. The orange line (of slope 1 and intercept of 0) indicates perfect agreement between SEM and all-atom MD data.

The SEM blockade currents were calculated by taking, as input, the coordinates of all atoms comprising the protein and the nanopore components of the MD systems and the system’s dimensions. The entire volume of the system was discretized into a grid using 1 Å cubes, rounding down the system’s dimensions to the nearest integer. Next, we determined the distance from each grid point to the nearest protein or nanopore atom, using, as a measure, the distance between the grid point and the atom’s surface. The distance map was then used to compute the 3D local conductivity map as described in the previous section. The boundary conditions were set to produce a 300 mV drop of electric potential across the simulation unit cell along the nanopore axis, the bias conditions used in the corresponding all-atom MD simulations. The bulk electrolyte conductivity was set to the value obtained from the all-atom MD simulation of 2 M KCl solution. The ionic currents were computed solving Eq. 2 using the FEniCS finite element package and integrating local currents over the periodic boundary of the system. Fig. 3b shows the comparison between the current obtained using SEM and all-atom MD methods. Without any adjustable parameter, the SEM currents matched all-atom MD values for nine different proteins in two folding states and several orientations with a mean squared error of 0.137 nA². The same comparison for the resistors model described in Ref. 47 produced the mean squared error of 0.376 nA². SI Fig. S3 compares the two models to one another. At the time of writing, each finite element-based SEM calculation of the system shown in Fig. 2a took approximately 3.3 s, which is 370 times longer than the calculation based on the resistors model described in Ref. 47. Such an increase in computational complexity pays o in the case of true membrane systems (see next sections), where the equipotential assumption (used Ref. 47) is no longer a good approximation.

Validation: Ion conductance of biological nanopores

Among all nanopore sensors, biological nanopores stand out by their atomically precise, reproducible 3D structures assembled by the robust protein folding process. In this section, we test the ability of SEM to describe the ionic conductance of biological nanopores through comparison with explicit solvent all-atom MD simulations.

Fig. 4a illustrates the nine biological nanopores considered in this work, spanning the ion conductance range from 0.1 to 12 nS. The lowest conductance nanopore OprD (also known as OccD1) was characterized previously by both crystallography and electrophysiology measurements.⁵² Both outer membrane porin OmpF⁵³ and pore-forming toxin α-hemolysin⁵⁴ were studied extensively by crystallography, electrophysiology and an arsenal of computational methods.^38,55,56 The outer membrane protein that imports ferrichrome, FhuA,⁵⁷ was engineered by the Movileanu group to form a robust beta-barrel nanopore.⁵⁸ Another toxin–aerolysin⁵⁹–was recently used to differentiate between different lengths of DNA homopolymers²² and arginine homopeptides.⁶⁰ The four remaining biological nanopores are the viral portal protein G20C modified to insert into lipid bilayer membranes,⁶¹ the alpha pore forming toxin FraC⁶² used extensively for peptide detection,⁶³ a truncated version of the outer membrane porin MspA⁶⁴ used for DNA sequencing¹¹ and single molecule mea-surements,⁶⁵ and another alpha pore forming toxin ClyA⁶⁶ used, among others,⁶⁷ for single molecule enzymology.⁶⁸

Figure 4:

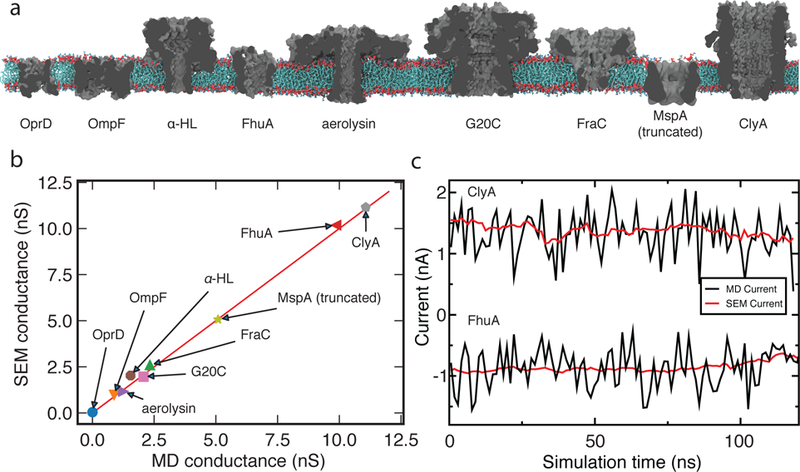
SEM validation against ionic conductance of biological nanopores computed using the all-atom MD method. (a) Biological nanopores used for validation of SEM. Each nanopore is shown as a grey cutaway molecular surfaces, the lipid bilayer is shown in red (head groups) and cyan (lipid tails), water and ions are not shown. SI Table S1 specifies conditions of each MD simulation. (b) Conductance of the biological nanopores calculated using SEM plotted against conductance measured using the all atom MD approach. Each data point represents a trajectory-average ionic current divided by the transmembrane voltage. Red line indicates perfect agreement between the two methods. (c) Ionic current passing through ClyA (at 120 mV, top) and a deletion mutant of FhuA (at –80 mV, bottom) plotted as a function of the MD simulation time. Red and black lines indicate the SEM and MD currents, respectively. The MD current traces show 1.2 ns average of 4.8 ps sampled current for ClyA and 1.2 ns average of 2.4 ps sampled current for FhuA. The SEM current traces show 1.2 ns average of 120 ps sampled current for both ClyA and FhuA.

The all-atom MD simulations of the nine biological nanopore systems were either reported in our previous work (OmpF,⁶⁹ MspA,⁷⁰ α-hemolysin,¹⁹ G20C⁶¹ and FhuA⁷¹), or carried out following the standard MD protocols,⁴⁶ which are also described in SI Methods. Typically, a biological nanopore was placed at the center of a lipid bilayer membrane and solvated in 1 M solution of monovalent electrolyte. After energy minimization and constant pressure equilibration, the nanopores were simulated in a constant volume ensemble under external electric field applied normal to the lipid bilayer membrane. The resulting average ionic current was divided by the voltage to obtain the MD value of the nanopore conductance. Supplementary Table S1 specifies the conditions of each MD simulation.

To compute the ionic conductance of biological nanopores using SEM, we extracted the coordinates of all non-solvent atoms from the respective MD trajectories every 120 ps. Each coordinate frame was used to obtain the minimum distance map at 1 Å resolution, which was then transformed into a 3D conductivity map (see Methods). The SEM current was computed for each coordinate frame using the MD value of the bulk electrolyte conductivity and the voltage drop of the respective all-atom MD simulation. The current values were averaged over the selected frames, the average value was divided by the bias and reported as conductance.

Fig. 4b compares the conductance of the nine biological channels computed using SEM and all-atom MD simulation. The SEM currents are in excellent agreement with the ionic current calculated using explicit solvent MD simulations, taking into account the statistical uncertainty of the latter. In all-atom MD simulations, thermal displacements and counting error dominate the value of nanopore currents at the nanosecond time scale. Being an exact calculation, SEM currents are not susceptive to the above sources of noise. The value of the SEM current can, however, change when it is computed using frames of the MD trajectory, reflecting fluctuation of the nanopore shape. Fig. 4c illustrates the reduction of noise by plotting both MD and SEM currents for the simulation trajectory of ClyA and a deletion mutant of FhuA. Furthermore, the SEM currents reproduce the changes of the open pore current determined by the all-atom MD method, which are related to slow-mode fluctuation of the nanopore structure.

Finally, we applied SEM to an equilibration trajectory of an aquaporin (AQP-1) channel, which is known for its extremely low ion conductivity. The SEM conductance of AQP-1 was less than 1 pS at 1M KCl, suggesting that SEM can also be used in the low conductance regime, where all-atom MD simulations become computationally prohibitive. Thus, SEM can reproduce the conductance of stable biological nanopores obtained using the all-atom MD method with no adjustable parameters and at a tiny fraction (1/10⁵ to 1/10⁶) of the computational cost.

Validation: Blockade currents of DNA homopolymers

Many of the e orts in the nanopore sensing field are directed towards sequencing of DNA, RNA or protein molecules. To test if SEM is capable of capturing essential differences in current blockades produced by DNA molecules of different nucleotide composition, we used SEM to calculate ionic currents owing through a truncated model of MspA containing poly(dA), poly(dC) and poly(dT) homopolymers. Previously, such systems were investigated using the all-atom MD approach,⁷⁰ nding, in general agreement with experiment,⁷² the ionic current to depend on the nucleotide type and the global orientation (3^’ versus 5^’) of the homopolymer.

Fig. 5a shows three systems investigated using the all-atom MD method. In these systems, the DNA homopolymers are threaded through a truncated model of MspA embedded in a patch of a lipid bilayer such that the 5^’ end of each homopolymer is located at the trans side of the membrane. The 3^’ terminal atom of each DNA homopolymer is restrained using a harmonic spring. Subject to a 180 mV transmembrane bias, ions ow through the MspA constriction blocked by DNA. In contrast to the systems considered in the previous two sections, the DNA strand could change its conformation during the simulation, producing considerable temporal variations of the blockade currents, Fig. 5b. We have shown previously that such variations of the blockade current are determined by the number of bulk-like water molecules present in the MspA constriction.⁷⁰

Figure 5:

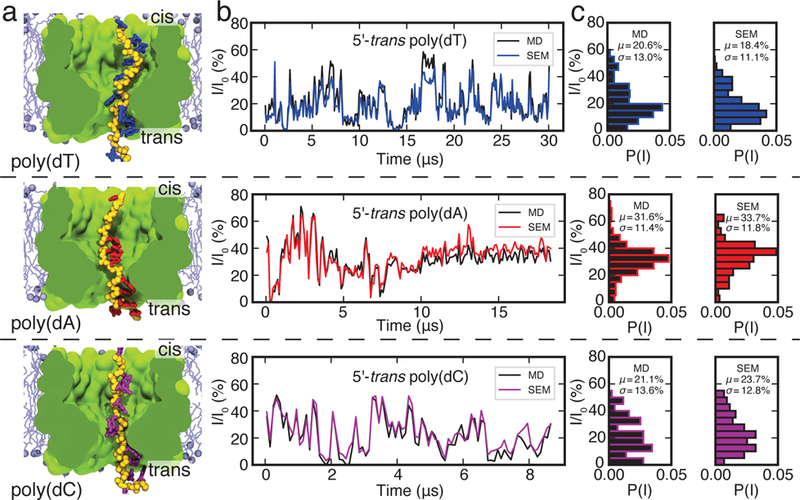
SEM validation against nucleotide-type specific ionic current blockades in MspA. (a) Cut-away view of three all-atom systems containing a strand of poly(dT) (top), poly(dA) (middle) or poly(dC) (bottom) threaded through a truncated MspA pore (green) that is embedded in a lipid bilayer membrane (turquoise) and submerged in 1 M KCl solution (not shown). The 3^’ terminal atom of each DNA strands is restrained to its initial coordinates. Ionic current measured from displacement of ions in explicit solvent MD simulations (black) and computed from the coordinates of DNA and MspA using SEM (colors). For both methods, the transmembrane bias was set to 180 mV, the current was sampled every 100 ps and averaged in 100 ns blocks. (c) Histograms of blockade currents obtained using explicit solvent MD (black) and SEM (colors). SEM calculations were done using simulated bulk conductivity of 1.4 M KCl. Images of the simulated systems and the MD ionic current data are reproduced with permission from Ref. 70.

To test if SEM is capable of reproducing the ionic current blockades obtained by the all-atom method, we took frames from the all-atom MD trajectory of the MspA system recorded every 100 ps and calculated the ionic current for each frame. At the sampling frequency of 100 ps, the instantaneous magnitude of ionic current is determined by thermal fluctuations. Therefore, a meaningful comparison of the two computational approaches requires averaging of the ionic current over many instantaneous configurations of the system. The SEM representation of the truncated MspA system was built using the same approach as described in the previous section. The boundary conditions were set to produce a transmembrane bias of 180 mV, same as the bias applied in the all-atom MD runs. The ionic current values sampled at 100 ps were averaged in 100 ns blocks for both the all-atom MD and SEM calculations.

The ionic current traces obtained using SEM correlate very well with the ionic current trace calculated from the MD, see SI Fig. S4, but are scaled by a small constant factor. Because DNA carries high density of electric charge, the effective ion concentration within the nanopore, and hence the effective conductivity of the electrolyte solution, can differ from the nominal concentration and conductivity of bulk electrolyte. A global t of SEM current traces to all-atom data varying a single parameter—bulk electrolyte conductivity value—yielded an effective conductivity of 23.7 S/m. Using a linear interpolation between simulated ion conductivity of 1 M and 2 M KCl, this ion conductivity corresponds to a solution concentration of 1.4 M KCl electrolyte. Fig. 5b compares the temporal variation of the SEM ionic current traces computed using that effective conductivity value and the results of all-atom MD simulations, whereas Fig. 5c compares the all-point ionic current histograms. The SEM calculations not only correctly reproduce the average blockade current of DNA homopolymers and the shape of the ionic current histograms but also the temporal change of the current, faithfully tracing changes in the conformations of the DNA strands. Similar results were obtained for the 3^’-end-trans systems, SI Fig. S5. The agreement suggests that the blockade ionic current is determined by steric exclusion of ions, confirming an earlier conclusion about the steric nature of sequence-specific blockades in MspA.⁷⁰

Application example: Conductance blockades of nucleosomal sub-structures in solid state nanopores

In addition to considerably reducing the computational cost of obtaining ionic current values from all-atom MD simulations, SEM can be used standalone to compute the ionic current blockades knowing only the pore geometry and the atomic structure of the translocating biomolecule.

In our first application example, we evaluated ionic current blockades produced by the translocation of a nucleosome particle and its substructures through a solid-state nanopore, reproducing the experimental study of Soni and Dekker.⁷³ The atomic structure of a 20 nm diameter nanopore in a 20 nm thick silicon nitride membrane was obtained using the Inorganic Builder⁷⁴ of VMD, Fig. 6a. The computational domain for SEM calculations was defined to be 30×30×30 nm³, matching the lateral dimensions of the solid-state membrane. The volume was discretized into 1 Å cubes to create the conductivity map using the method described above. The boundary conditions were set to a potential drop of 100 mV and the bulk conductivity was set to the experimental value of 10.5 S/m. The open pore current was found to be 13.36 nA at a 100 mV bias.

Figure 6:

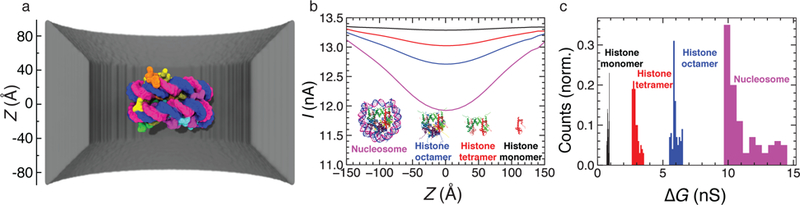
(a) Molecular graphics image of a nucleosome particle (PDB ID:1AOI) at the center of a 20 nm diameter solid-state nanopore. (b) SEM currents computed by placing various nucleosomal substructures along the central axis of the nanopore. The colors of the lines indicate the ionic current traces corresponding go the passage of a complete nucleosome particle (magenta), histone octamer (blue), tetramer (red) and monomer (black). The inset shows to-scale images of the biomolecules. (c) The histogram of the conductance blockade amplitudes corresponding to placement of the four biomolecules at the center of the nanopore in 100 random orientations.

To model a translocation event, a biomolecule of interest (a nucleosome particle, a histone octamer, a histone tetramer or a histone monomer) was placed along the nanopore axis in 10 Å increments spanning the range of ±150 Å from the membrane midplane. For each placement of the biomolecule, the conductance map was recalculated and the ionic current was found as described before. Figure 6b plots the resulting nanopore currents (at 100 mV) as a function of the biomolecule’s z coordinate along the nanopore axis. As the molecules approached the nanopore, the ionic currents gradually decreased reaching a minimum at the pore center and increased again as the molecules were moved away on the other side of the membrane. As expected, the maximum current blockade amplitude increased with the molecular weight of the biomolecules.

To assess the effect of conformational heterogeneity, we placed the four structures at the center of the nanopore, each structure in 100 random orientations. SEM currents were computed for each orientations, following which the conductance blockade amplitude was found by dividing the difference between the open pore and blockade current with the transmembrane voltage. The resulting distributions of the conductance blockade amplitudes are shown in Fig. 6c. It is instructive to compare SEM currents to the experimental values: 8.0±1.4 nS for the nucleosome, 6.0±0.7 nS for the histone octamer, 4.8 ±0.8 nS for the tetramer and 3.4±1.7 nS for the monomer.⁷³ The SEM values are rather close to those measured in experiment. Small discrepancies can be explained by (i) SEM calculations not taking into account the charge of the nucleosomal DNA, which is expected to decrease the blockade by locally increasing the ion concentration;⁷⁵ (ii) the differences in the access resistance conditions⁷⁰ and (iii) the differences in the pore geometry. Note that, unlike the case of infinite DNA, the amplitude of a nanopore blockade produced by a compact object depends on the nanopore geometry.⁷⁶ Overall, SEM provides a good estimate of the conductance blockade values and their variance because of orientational heterogeneity.

Application example: Probing amino acid distinguishability using MspA

Protein sequencing is one of the most transformative potential applications of the nanopore sensing method.^16,17 One of the key challenges is detection of all twenty natural amino acids, which differ from one another just by a handful of atoms. Here we show how SEM can be used to assess distinguishability of the amino acids in biological nanopore MspA.

Using a truncated version of MspA M1-NNN pore, we placed individual amino acids at different locations along the pore axis Fig. 7a. For each position, 500 different conformations of the amino acid were generated by random rotations about the amino acid’s center of mass. The conformations that sterically clashed with the nanopore atoms were removed from further consideration. For each remaining conformation, a conductivity map was obtained at 1 Å resolution using the MD value of 1M KCl bulk conductivity. SEM currents were computed for each conformation and averaged over all sterically allowed configurations at the same location (z coordinate). The currents were normalized by the open pore current to obtain relative residual currents. Figure 7b plots the dependence of the relative residual current on the amino acid location for five representative amino acids. The residual blockade values can be clearly distinguished in the the region immediately above the constriction. Figure 7c plots the average residual current for all twenty amino acids at z = 0 Å, arranged in ascending order. While such SEM calculations do not answer the question of how single amino acid translocation can be realized or how different amino acids can be placed at the same location within MspA, the calculations give a clear idea about the range of the ionic current signal.

Figure 7:

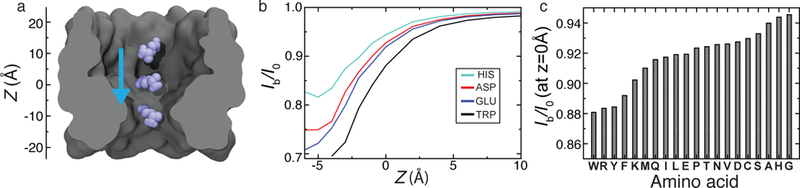
Blockade currents of individual amino acid in MspA. (a) Three representative conformations of a glutamic acid (blue) along the central pore of M1-NNN MspA (grey cutaway molecular surface) embedded in a lipid bilayer (not shown). (b) Relative residual current produced by placing four different amino acids along the central axis of the MspA nanopore. The z axis is defined in panel a. (c) Average relative residual current for all twenty amino acids at z = 0 Å, arranged in ascending order.

Application example: Testing the effect of point mutations

Finally, we show that SEM calculations can be useful for designing better nanopores for sensing specific analytes. In the case of biological nanopores, the nanopore structure can be altered through mutagenesis, which typically involves replacing one or more amino acids. Fig. 8a shows an image of the M1-NNN MspA constriction, highlighting the five residues (N91, N90, N108, I105, and L88) that we selected for mutation. Because of the octameric symmetry of MspA, a point mutation was assumed to take place in all eight MspA monomers. Mutating individual sets of amino acids into tryptophan (W) was found to affect the open pore current, Fig. 8b, but only if the mutated residues were located near the constriction. To investigate the effect of the mutations on the distinguishability of the amino acids, we placed serine and cysteine amino acids at the same (z = 0) location along the pore axis and repeated SEM calculations described in the previous sections. Fig. 8c shows the difference in the residual current computed for the serine and cysteine amino acids, for each of the MspA variants. The L88W mutation was found to increase the current blockade difference by nearly 3 times.

Figure 8:

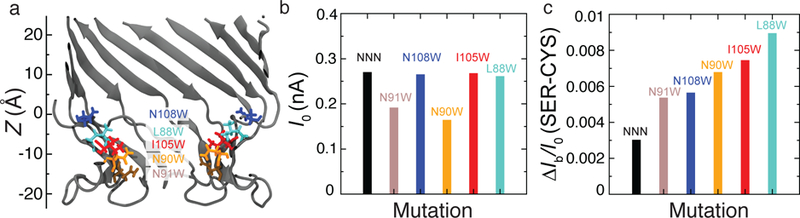
Testing the effect of mutations. (a) The constriction region of M1-NNN MspA (cutaway cartoon representation) along with the cites of point mutations. For clarity, the mutated residues (N91, brown; N90, orange; N108, blue; I105, red; and L88, cyan) are shown only for the two segments nearest to the cutaway plane. (b) Open pore SEM current (at 50 mV) for M1-NNN MspA and its five mutants. Note that the currents are considerably higher than in experiment because of the truncated pore geometry and the access resistance Conditions.⁷⁰ (c) The difference in the blockade currents of serine and cysteine at z = 0 Å for the NNN pore and its five mutants.

Discussion

We have shown that a rather simple model can predict the ionic conductance of diverse nanopore systems to the same accuracy as explicit solvent all-atom MD simulation but at a tiny fraction of the computational cost. We have validated SEM for a solid-state nanopore blocked by 34 proteins different by their 3D structure, folding state and orientation, ten membrane channels embedded in a lipid membrane, and a biological nanopore MspA blocked by DNA homopolymers of different types. The agreement between the two methods is astonishing, given the complex shape of the proteins, biological nanopores and DNA strands, the intricate distribution of charges along the biomolecules and the lack of any solvent-mediated e ects^41,77 in SEM. We attribute the agreement to the high salt condition employed in each of the above systems. Indeed, the Debye screening length at 1M concentration of monovalent salt is comparable to the size of a water molecule and, hence, the charge at the surface of a biomolecule is well screened one water molecule-away from the surface, the distance where electrolyte conductivity starts to become non-zero, Fig. 2c. Similarly, the diffusive fluxes, which are omnipresent and sometimes dominant at low electrolyte conditions, have, in high salt conditions, negligible strength in comparison to deterministic fluxes caused by the applied electric field. Fortunately, most of the nanopore measurements are carried out at high salt conditions to maximize the signal-to-noise ratio, which are exactly the conditions that SEM is expected to perform the best.

There are, of course, numerous limitations to the method. To start, SEM only computes the ionic current for a given configuration of the solute and the analyte. To model a translocation event, one would have to generate a collection of states representative of a typical translocation event using other than SEM methods, which could be as simple as translation of the solute’s coordinates along the pore axis or as complex as an all-atom MD simulation of the translocation event. Even in the latter case, using SEM can be highly beneficial, as it is not susceptible to thermal noise that often dominates ionic currents determined directly by the MD approach. A more subtle issue is the effect of the applied electric field on the conformation and diffusive flux within the nanopore, which are not accounted for in SEM. One prominent manifestation of that is the absence of ionic current recti cation in SEM calculations, which is a common phenomenon in biological ion channels at physiological salt conditions. Finally, SEM does not describe the electro-osmotic ow e ects.

Thus, the current formulation of SEM leaves room for improvement. In the case of DNA systems, it was previously shown that the effect of DNA charge can be accounted for by modifying the shape of the conductivity function.^75,78 Thus, it should be possible to generate the local conductivity map taking into account the surface charge of the biomolecules. Taking into account diffusive fluxes may require replacing the continuity equation with the Smolu-chowski equation. The computational efficiency of SEM can be further improved by using variable-resolution finite element solvers. Overall, we expect our SEM approach to become a go-to method for rapid prototyping of nanopore systems for detection and identification of molecular analytes.

Methods

General MD Methods

All MD simulations were performed using the package NAMD2,⁷⁹ the CHARMM36 force field⁸⁰ and custom NBFIX corrections to non-bonded interactions between ions.⁸¹ RATTLE⁸² and SETTLE⁸³ algorithms were applied to covalent bonds that involved hydrogen in proteins and water molecules, respectively. Periodic boundary conditions were used in all simulations, and the Particle Mesh Ewald (PME)⁸⁴ summation algorithm was used to evaluate long-range electrostatic interactions, with a 1 Å spaced grid. Short-range electrostatics and van-der-Waals interactions were evaluated using a smooth 10–12 Å cutoff. Langevin dynamics were used to maintain a temperature of 293 K unless otherwise specified. Multiple time stepping was used to calculate local interactions every 2 fs, and full electrostatics every 6 fs.

Calibration simulations of local ion conductivity

To determine how local concentration and mobility of ions depend on the distance from the center of carbon, nitrogen, oxygen and hydrogen atoms, we built four simulation systems each containing four chains of the above test atoms arranged parallel to the z axis. Fig. 2a shows the simulation system containing four chains of carbon atoms. The carbon (type CA) atoms were placed 1.418 A apart along the z axis forming, under periodic boundary conditions, an infinite linear chain. The atoms had covalent bonds placed connecting them to their nearest neighbors and were electrically neutral. Harmonic potentials of a 5 kcal/(mol Ų) spring constant restrained the atom to their initial coordinates. Systems containing hydrogen (type HN6), oxygen (type ON1) and nitrogen (type NN1) atoms were prepared in a similar manner. The systems were solvated and ionized to nominal dimensions of 40Å × 40Å × 40Å and 1 M concentration of KCl. The systems were equilibrated at the constant number of particles, pressure and temperature ensemble for 10 ns with a Nosé-Hoover Langevin piston target of 1 atm, oscillation period of 2.4 ps, and decay timescale of 1.2 ps. The pressure control was coupled to the systems dimension within the x–y plain, the system size along the z axis (39.704 Å) was kept constant so that the 27 atoms in each chain were separated by 1.418 Å. This separation distance was used for all atom types studied.

The systems were then simulated in the constant number of particles, volume and temperature ensemble using the average system size observed during the equilibration simulation. An external electric field of 10 mV/nm was applied parallel to the chains of test atoms. Systems containing linear chains of carbon, hydrogen, nitrogen and oxygen atoms were simulated for 462, 234, 180 and 266 ns, respectively.

In order to calculate the concentration of ions, the number of ions in cylindrical shells surrounding the chains of test atoms were counted every timestep, and then averaged over the entire MD trajectory; the first 10 ns were excluded from the analysis. The average number of ions divided by the volume of the cylindrical shell yielded the local concentration of ions. This calculation was done for both ion species.

To find the mobility of the ions as a function of radial distance, the average velocity of ions within each cylindrical shell was calculated for each recorded frame of the simulation. The velocity was calculated using the first-order central difference and z coordinates of the ions from three consecutive frames of an MD trajectory.⁷⁸ An ion velocity was assigned to a particular radial distance bin according to its radial coordinate in the second of the three consecutive trajectory frames. The ion velocities were averaged over the respective MD trajectory. The mobility was calculated by dividing the average ion velocity in each bin by the applied electric field. The conductivity was calculated by multiplying the mobility by the concentration in each bin.⁴⁷