Abstract
Accurate and reliable prediction of clinical progression over time has the potential to improve the outcomes of chronic disease. The classical approach to analyzing longitudinal data is to use (generalized) linear mixed-effect models (GLMM). However, linear parametric models are predicated on assumptions, which are often difficult to verify. In contrast, data-driven machine learning methods can be applied to derive insight from the raw data without a priori assumptions. However, the underlying theory of most machine learning algorithms assume that the data is independent and identically distributed, making them inefficient for longitudinal supervised learning. In this study, we formulate an analytic framework, which integrates the random-effects structure of GLMM into non-linear machine learning models capable of exploiting temporal heterogeneous effects, sparse and varying-length patient characteristics inherent in longitudinal data. We applied the derived mixed-effect machine learning (MEml) framework to predict longitudinal change in glycemic control measured by hemoglobin A1c (HbA1c) among well controlled adults with type 2 diabetes. Results show that MEml is competitive with traditional GLMM, but substantially outperformed standard machine learning models that do not account for random-effects. Specifically, the accuracy of MEml in predicting glycemic change at the 1st, 2nd, 3rd, and 4th clinical visits in advanced was 1.04, 1.08, 1.11, and 1.14 times that of the gradient boosted model respectively, with similar results for the other methods. To further demonstrate the general applicability of MEml, a series of experiments were performed using real publicly available and synthetic data sets for accuracy and robustness. These experiments reinforced the superiority of MEml over the other methods. Overall, results from this study highlight the importance of modeling random-effects in machine learning approaches based on longitudinal data. Our MEml method is highly resistant to correlated data, readily accounts for random-effects, and predicts change of a longitudinal clinical outcome in real-world clinical settings with high accuracy.
Keywords: longitudinal supervised learning, random-effects, machine learning, type 2 diabetes, glycemic control, glycosylated hemoglobin
Graphical Abstract

1. Introduction
Data science has transformed nearly all sectors of the economy, driving rapid innovation, optimization, and growth. For predictive analytics in particular, increasing use of machine learning algorithms has enabled data-driven extraction of information from complex raw data rather than predefined, and often inadequate, a priori assumptions. Despite the potential for data science to improve the efficiencies of healthcare delivery, lower costs of care, and improve patient outcomes, healthcare has lagged behind other fields in adapting and implementing advanced analytic approaches. This is due, in part, to the complexity, heterogeneity, and longitudinal nature of most health-related data; and frequent inadequate quality, availability, and usability of clinical data. In addition, the underlying theory of most machine learning algorithms assume that the training data is independent and identically distributed (i.i.d). However, this assumption is frequently violated in real-world applications, where there are sub-groups of patient observations with multiple distinct repeated measurements exhibiting high degree correlations. Thus, without modifications, most machine learning algorithms are not directly applicable to non i.i.d data.
To overcome this limitation, we developed a novel machine learning framework for the analysis of complex longitudinal data and applied it to a challenging clinical question: which patients with currently controlled and stable type 2 diabetes (T2D) will experience deterioration of glycemic control in the future?
Maintaining glycemic control is important for reducing the risk of diabetes complications and measures of glycemic control (specifically, glycosylated hemoglobin [HbA1c]) are subject to public reporting, pay-for-performance reimbursement, and quality of care benchmarking. For most adults with diabetes, optimal glycemic control is achieved if HbA1c is < 7.0%.[1, 2] Patients with uncontrolled diabetes often receive close monitoring and intervention aimed at improving their glycemic control.[1–3] However, patients with controlled diabetes who are nonetheless at risk for future deterioration would also benefit from early identification and preemptive management.[4, 5] Such efforts have been hindered by the seemingly homogenous difficulty of identifying high-risk individuals, who are usually a minority within a large and patient population.
Our proposed approach combines the structure of GLMM with advanced modeling capabilities of machine learning for efficient estimation of longitudinal outcomes. Specifically, we combine two regression tree methods for longitudinal data: the generalized mixed-effects regression trees (GMERT) structure proposed in [6] and the random-effects expectation maximization (RE-EM) tree structure proposed in [7] to alternatively estimate the fixedand random-effects components of a non-linear mixed-effect model (NLMM). This mixed-effect machine learning (MEml) approach allow us to incorporate random-effects into more accurate, robust and interpretable machine learning models for efficient analysis of longitudinal data.
For the main clinical application problem in this study, we evaluated MEml models by applying it to predict change in HbA1c measured one, two, three, and four encounters in the future using data for patients with controlled T2D from OptumLabs Data Warehouse (OLDW) These models relied on readily available clinical data: baseline patient characteristics (sex, race, comorbidities, geographic region), current HbA1c, and medication use.
To further demonstrate the general applicability of MEml, a series of experiments were performed using two public available longitudinal healthcare data sets and a synthetic clustered data set for accuracy and robustness with respect to correlation introduced by multiple repeated observations. Specifically, we applied MEml to predict: (1) longitudinal enlargement of the liver (hepatomegaly) using the Mayo Clinic primary cirrhosis (PBC) data set [8, 9]; (2) longitudinal increase in left ventricular mass index using the aortic valve replacement surgery data available from the R package joineR [10]; and (3) lung cancer remission using a synthetic three level clustered data.[11].
2. Materials and Methods
2.1. Notations
In longitudinal studies, patients are observed multiple times at varying time intervals, typically with different information about patient characteristics, exposures, and outcomes collected at each time point. For each time t and patient i, we observe a p dimensional vector xit of fixed-effect covariates (e.g. age, gender, race, etc.), a q dimensional vector zit of random-effect covariates (i.e. subject-varying effects), and a response variable yit. The covariates may be constant or varying over time and/or across patients. While this study focuses on binary outcomes, the presented methods can be directly extended to other outcome types.
2.2. Data
2.2.1. Type 2 diabetes data: Source and Study population
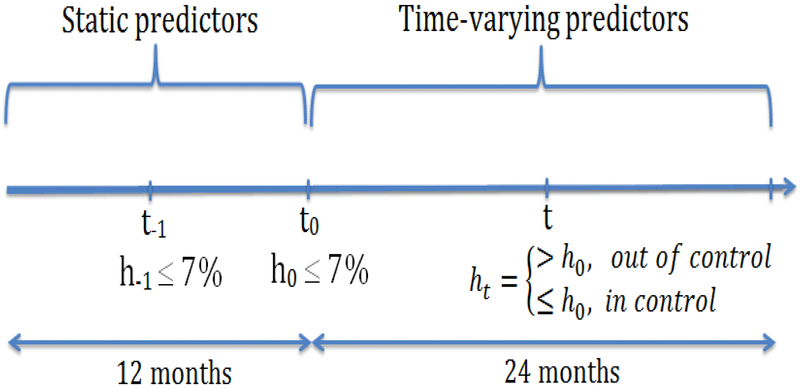
The primary data used to demonstrate the methods developed in this study consist of 27,005 adults, age ≥ 18 years, with stable and controlled T2D included in OLDW between January 1, 2001 and December 31, 2011. OLDW is a large administrative claims database of commercially-insured and Medicare Advantage beneficiaries across the U.S.[12, 13] Stability of diabetes control was ensured by two successive measurements of HbA1c < 7.0%. In Figure 1, h0 is a reference HbA1c value at time t0, where static variables are measured, and the patient is subsequently followed for 24 months. The value h−1 is the HbA1c value not more than 3 months prior to t0 controlling for diabetes stability. To predict glycemic change, patients were required to have ≥ 2 ht values during the 24 months follow-up. Diabetes was defined by Healthcare Effectiveness Data and Information Set criteria [14] ascertained using claims-computable diagnosis codes and pharmacy claims from 12 months preceding t0. To restrict the study to patients at lowest risk of glycemic deterioration, we excluded people using insulin within 12 days prior to t0; or with history of diabetic ketoacidosis (ICD-9-CM 250.1x), hyperglycemic hyperosmolar state (ICD-9-CM 250.2x), diabetic coma (ICD-9-CM 250.3x), severe hypoglycemia (ICD-9-CM 251.x, 250.8x [15]), or poisoning by insulin or anti-diabetic drugs (ICD-9-CM 962.3) within one year of t0.
Figure 1:
Diabetes stability and glycemic control: h0 is the reference HbA1c value at time t0, h−1 is HbA1c value use to control for stability, while ht is the HbA1c value at time t in the 24 months follow up period. For diabetic stability both h−1, h0 ≤ 7% and t0 − t−1 ≤ 3 months
Independent variables
Baseline static patient characteristics used for analysis included sex; race/ethnicity; comorbidities documented within 12 months of t0 and categorized according to the Charlson/Deyo comorbidity measure [16]; geographic region; and h−1. Time varying characteristics included age, diabetes medications use within the follow up period; and all available HbA1c test results (ht) during follow up; and follow up time. HbA1c results were identified using LOINC codes 4548–4, 4549–2, 17856–6, 59261–8, 62388–4 and 4547–6. The time varying diabetes medications were grouped into nine diabetes medication classes (insulins, sulfonylureas, glinides, biguanides, α-glucosidase inhibitors, thiazolidinediones, glucagon-like peptide-1 agonists, amylinomimetics, and dipeptidyl peptidase-4 inhibitors). We included a time varying measure of HbA1c testing frequency during 24-months of follow-up, categorized as: ≤ 2, 3−4, or ≥ 5 tests per year to reflect different intensities of therapeutic monitoring which may influence glycemic control. [17] That is, at each encounter, the number of HbA1c tests performed since baseline is reported. Similarly at each encounter, medication changes in reference to t0 were recorded and classified as: no change, class change, intensification (addition of ≥ 1 drug or insulin), or de-intensification (removal of ≥ 1 drug). The fixed-effect covariates p includes the baseline and time-varying predictors while the random-effect covariates q includes the time varying predictors.
At baseline (t0), the median age was 58 years; 49% were women; and 58% White. h0 was ≤ 5.6% in 10.4% of patients; 5.7–6.4% in 57.1%; and 6.5–6.9% in 32.5%. One-third of the patients were not receiving any glucose lowering medications, while 37.7% received 1 drug, 21.3% received 2 drugs, and 8.2% received ≥ 3 drugs. Table 1 shows a summary of the number of clinical encounters or visits per patient in the data. Full details on cohort construction, variable engineering, and descriptive statistics at t0 can be found in [18].
Table 1:
Clinical visits per patient (Total no of observations = 109,397)
| No of visits | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ≥ 10 |
|---|---|---|---|---|---|---|---|---|---|
| No of patients | 5820 | 6131 | 5584 | 4219 | 2603 | 1545 | 741 | 239 | 126 |
Response variable - glycemic control
For each patient i, the change in HbA1c between a future time point t and the reference t0 was used as a measure of glycemic control status and represented by the binary variable:
| (1) |
We consider time at the granularity of a day, and each day t corresponds to a clinical visit.
2.2.2. Mayo clinic primary biliary cirrhosis data
This publicly available longitudinal data set is from the Mayo Clinic clinical trial in primary biliary cirrhosis (PBC) [8, 9] of the liver conducted between 1974 and 1984. A total of 424 PBC patients referred to Mayo Clinic during that ten-year interval met the well-established clinical, biochemical, serologic, and histologic creteria for PBC and also fulfilled standard eligibility criteria for randomized placebo controlled trial of the drug D-penicillamine. [19] However, only the first 312 patients in the data set participated in the randomized trial. Multiple laboratory measurements were collected for these patients. We imputed missing variables with less than 20% missing values with the missForest [20] package in R.
We used the PBC data to predict longitudinal enlargement of the liver or hepatomegaly. At each longitudinal time point corresponding to a clinical visit, the binary hepatomegaly variable in the data set indicates if the patient has enlarge liver or not.
2.2.3. Aortic valve replacement data
This is a publicly available longitudinal data set (available in the R package joineR [10]) from an observational study on detecting effects of different heart valves implanted in the aortic position. The data consists of longitudinal measurements (three cardiac functions) from patients who underwent aortic valve replacement (AVR) from 1991 to 2001 at the Royal Brompton Hospital, London, United Kingdom. The data was first reported in [21] where the authors used all patients during the 10 years period with at least a year of follow-up with serial echocardiographic measurements and applied a linear mixed-effect model to predict left ventricular mass index (LVMI). Similarly, we predict longitudinal profile laboratory variables. of LVMI categorized as high or normal using several patient baseline characteristics and LVMI is considered increased if LVMI >134 g/m2 in male patients and LVMI >110 g/m2 in female patients, thus values in this range for both sex was considered as the positive class in MEml.
2.2.4. Artificial Data: Hospital, Doctor, Patient data
The Hospital, Doctor, Patient (HDP) [11] dataset is a simulated three-level, hierarchical structured data with patients nested within doctors, and doctors within hospitals. The data is different from the previous three examples of longitudinal data and represents a clustered data structure, i.e there is no time component. The HDP data is generated to mimic a real-world study of a clinical outcome across multiple doctors and hospitals. Several outcomes are generated, however in this study we will consider the problem of predicting whether a patient’s lung cancer goes into remission after treatment or not based on patient, physician, and hospital factors.
The R code for generating the data can be downloaded from [11].Thus, the user can easily modify certain parameters of the data generation process. In addition to the predictors generated in [11], we also generated 9 additional predictors. Specifically, we define nonlinear functions involving the exponential function (x2 + 0.5 exp (−0.5(x − 0.5)2)), the sin function (2 sin(x × y)), and the arctangent function (arctan((x × y − (1/(x × y)))/z) (see Friedman simulations systems for regression modeling [22]), where x, y, z can be any of the variables age, body mass index (BMI), red blood count (RBC), or white blood count (WBC). We then perform a series of experiment where the minimum number of patient per doctor is 2 and the maximum number is taken in {5,10,20,30,40,50,60}. We considered 25 different hospitals with 4 −10 doctors each.
2.3. Generalized Linear Mixed Effects Models
In GLMM [23] random-effects are used to account for the level-wise variabilities in longitudinal data. Specifically, conditional on a vector of subject-specific regression coefficients, the model assumes that the responses yit for a single subject i are independent and follow a distribution from the exponential family with mean and variance specified as:
| (2) |
| (3) |
where is the population fixed-effect parameters; g(·) = h−1(·) is a pre-specified link function; ϕ is a dispersion parameter; and V (·) is a variance function (see [23] for details). The vectors bi are called the random-effects parameters and are assumed to be i.i.d normal random variables. For binary response, g(·) is the logit link function:
| (4) |
where μit = E[yit|bi] is the success probability and Var(yit|bi) = ϕ2μit(1 − μit). Estimation of the parameters (β, bi) in (4) can be done through the penalized quasi-likelihood (PQL) [24]. PQL approximates the data by the mean μit plus an error term εit, and then takes the first order Taylor expansion about the current parameter estimates:
where h′ is the first derivative of h. Using the relationship between the derivative of a function and its inverse and rearranging gives
Letting and , we obtain the linear mixed-effects model (LMM)
| (5) |
with .
2.4. Random-Effects for Machine Learning Models
The GLMM assumes a parametric distribution and imposes restrictive linear relationships between the link function g(·) and the covariates, which can be difficult to verify and often are not applicable to complex clinical settings. Alternatively, advanced non-linear machine learning methods can be applied to extract informative patterns from the data without a priori assumptions. Despite the many advances in machine learning algorithms, most assume that the training data is i.i.d. The underlying theory of Random forest (RF), gradient boosted machine (GBM), support vector machine (SVM), neural networks, and deep learning algorithms all implicitly make the i.i.d assumption. Nevertheless, this where sub-groups assumption is commonly violated in real-world applications, including longitudinal studies of observations exhibit high degree of correlations. Nonetheless, these methods are used for analysis of longitudinal data without accounting for the inherent correlation structure in the data often leading to mediocre performance [6, 7] and potential for misleading inference.
Several techniques have been proposed to extend tree based algorithms to longitudinal data. The earliest approach was done in [25], in which the regression tree split function was modified to accommodate multiple responses. The classification and regression trees (CART) [26] algorithm was extended in [27] for longitudinal data with multiple binary outcomes. The CART algorithm was equally extended in [28] for multivariate outcomes. However, none of these methods allow for modeling time-varying covariates.
More recently, two studies [6] (GMERT) and [7] (RE-EM tree) took the mixed-effects approach and extended the CART algorithm to incorporate random-effects. The basic idea of the approach was to disassociate the fixed-effect component of a LMM from the random-effect and iteratively estimate each component in expectation maximization (EM) [29] manner. Specifically, in [7], the CART algorithm was used to estimate the fixed-effects of a LMM assuming that the random-effects are known, and then estimate the random-effects in the next step assuming the fixed-effects estimated by the CART algorithm in the previous step are correct. Both modifications of the CART algorithm by [6, 7] could naturally accommodate time-varying covariates.
However, both GMERT and RE-EM tree have limitations that make them unsuitable for general longitudinal supervised learning. First, both techniques are based on the CART algorithm which is prone to overfitting and selective bias towards variables with many possible splits. A general framework for mixed-effect machine learning that can deploy advanced learning algorithms such as RF, GBM, SVM, neural networks and deep learning is thus needed. Second, while GMERT can be used to predict binary outcomes, RE-EM tree can only predict continuous outcomes. The proposed MEml framework can be used for different types of outcomes and machine learning algorithms.
We propose a new machine learning framework that combines the GMERT structure for modeling general types of outcomes and the expectation maximization structure of RE-EM tree for estimating the fixed and random-effects components of NLMM.
We note that there are other machine learning approaches for sequential data such as hidden Markov model, [30] and the recent popular recurrent neural network models (RNN). [31] The RNN in particular, is designed to efficiently model sequential data, however, most RNN models are unable to model sparse and irregularly sampled sequential data, [32] which are very common features in longitudinal health care data. Training these models can also be computationally expensive. Thus, we did not consider these approaches as our focus was to develop a simple and interpretable framework for training general machine learning methods on longitudinal and clustered data sets, which we achieved with the MEml framework.
2.5. Formulation of Mixed-Effects Machine Learning
The proposed MEml framework estimates the fixed-effects component (β⊤xit) in (5) using a powerful machine learning algorithm and the random-effects bi using GLMM. Thus equations (4) and (5) can be written as:
| (6) |
| (7) |
where the function f is unknown. We estimate f in equation (7) using 4 tree-based machine learning algorithms: random forest (RF) [33], gradient boosted machine (GBM) [34], model-based recursive partitioning [35], and conditional inference trees [36]. We focus on tree based algorithms for interpretability, however as demonstrated below, any supervised learning algorithm can be used.
RF and GBM are ensemble machine learning methods that construct a committee of models and then combine the predictions. In RF, multiple decision trees are learned on a random sample of observations from the training set and the predictions combined by averaging or majority vote. In contrast, boosting methods iteratively add basis functions (learners) in the ensemble in a greedy fashion such that each additional base-learner further reduces a loss function. In GBM, the new weak base-learner is constructed to be maximally correlated with the negative gradient of the loss function.
RF and GBM have several appealing properties that make them attractive for complex clinical longitudinal data: (i) the methods can easily handle large and high dimensional longitudinal data, (ii) all variables, including those with weak effects, highly correlated and interacting have the potential to contribute to the model fit, (iii) the models easily accommodate complex interactions between variables, (iv) they can perform both simple and complex classification and regression accurately and are less prone to overfitting.
Despite these appealing properties, RF and GBM are not interpretable, i.e. it is difficult to understand how the models make prediction decisions. To overcome this limitation, we apply the inTrees (interpretable trees) [37] algorithm to extract insights from the tree ensembles. Specifically, inTrees consists of algorithms that can extract rules, measure and rank rules, prune irrelevant or redundant rules, find frequent variable interactions, and summarize rules into a simple rule model that can be used for predicting new data without need for the original RF or GBM model.
Model-based recursive partitioning (MOB) is a powerful combination of the recursive partitioning algorithm and classical statistical regression models. The method partitions the feature space into subgroups of observations based on the statistical model and then predicts the response within subgroups. Conditional inference trees (Ctree) is a modification of the CART algorithm to overcome the problems of overfitting and selection bias towards covariates with many possible splits.
Algorithm for Mixed-effect Machine Learning
Tree-base algorithms recursively partition the feature space into disjoint regions such that observations with similar values of the response are grouped in the same region. If is the collection of disjoint regions, the goal of the algorithm is to approximate the unknown functional relationship between the response and the predictors f by a piece-wise constant function that can be written as
| (8) |
where cv is the constant term for the v’th region (e.g., the mean of the response for those observations x ∈ Rv)) and I(·) is the indicator function.
Instead of a single partition, the RF and GBM construct an ensemble of partitions of the feature space. As previously mentioned, the fitted ensemble model is not easy to interpret. To solve this problem and also to facilitate the extension of the RE-EM technique to accommodate RF and GBM, we extracted interpretable and learnable rules from the fitted model using inTrees. The extracted rules equally partition the feature space into disjoint regions , making equation (8) to also apply to RF and GBM.
The proposed MEml follows the EM approach in RE-EM trees with the difference that RE-EM trees estimate a continuous response and is based on alternatively estimating the fixed and random-effects component of a single LMM. In MEml, we can estimate both continuous and binary outcomes, and the EM algorithm is based on alternatively estimating two equations: (6) and (7). Briefly, from equation (7), if the random-effects bi are known, then we can estimate f(xi) using a machine learning model based on the modified response . Assuming that the means μit are also known, we can re-weight each observation in the training set by . This re-weighting scheme can help reduce the variability of the repeated measurements in the machine learning model. On the other hand, from equation (6) if the population-level effects f(xi) were known, then we can estimate the random-effects using traditional GLMM with population-level effects corresponding to f(xi).
This two-step approach for estimating (6) and (7) works well only if the fixed or random-effects are known. However, in practice these values are not known, so we can alternate between estimating the fixed-effects with a machine learning model, and estimating the random-effects with GLMM until convergence. The proposed algorithm for MEml is shown in Algorithm 1.
Note that in estimating equation (6), the fixed-effects component f(xi) estimated in one step can be set as an off-set term in the GLMM model in the next step. Many software packages such as the lme4 package in the R statistical programming environment can readily accommodate an off-set term. This off-set technique allows other general machine learning algorithms such as SVM or neural networks to be used.
2.6. Experimental setup
In this section, we describe the training and validation data structure for the longitudinal data sets (T2D, PBC, and AVS), making predictions, and performance measures. For training and validation on the clustered data (HDP), we randomly split the number of patients for each doctor into equal parts of training and test sets. We trained models on the training set and evaluate on the test set and then repeated the procedure 50 times.

Training and validation data structure for longitudinal data
To predict whether a patient will stay or fall out of glycemic control in the future, we use information in the current and past visits and glycemic control status in the anticipated future visit to construct the training and evaluation data sets. For example, if the goal is to predict the status of the i’th patient at the next visit (t1), we combined information available in the current and past visits and the control status in the next visit yit1 to create the training and validation data i.e. where yit0 and yit1 are computed using equation (1). Thus, in real application, during each visit, a clinician may want to know if at the next, second, third, etc. scheduled visits in advanced, the patient will lose glycemic control or not. So predictor variables available in the current and past visits: are used in the model to predict glycemic change at the future visit: ynext, second, third, etc.
In general, to predict a longitudinal clinical outcome (e.g. glycemic change, hepatomegaly and increase in LVMI) at any future visit λ time units in advance from a reference visit t, the training and evaluation data can be constructed as , such that the independent variables always lag the response by λ time units. Note that is technically not required to include a lag version of the dependent variable as a predictor in the data.Table 2 shows the data structure for λ = 2, which represents two visits in advance.
Table 2:
Lagged training data structure for predicting a longitudinal outcome
| t0 | t1 | t2 | t3 |
|---|---|---|---|
| (X0, Y0), Y2 | (X1, Y1), Y3 | (X2, Y2), Y4 | (X3, Y3), Y5 |
2.6.1. Bootstrap training and validation for longitudinal data
We performed 100 bootstrap resamples from Ditλ, where on each bootstrap iterate, the models are trained on approximately 63% of the data and the left out samples not selected in the bootstrap are used for testing. Simple bootstrap resampling with replacement from Ditλ treats the observations as independent and does not account for the dependence structure in the data, which may lead to invalid inference [38]. In order to preserve the hierarchical structure in the bootstrap resamples, we mimic the data generating mechanism, e.g. by resampling in a nested fashion. In multi-stage bootstrap, we first resample the highest level, then for each sampled unit, we resample the next lower level, and so forth. Each level may be resampled with or without replacement. For the experiments, we implemented the double bootstrap procedure in [38], where we first resample without replacement the individual patients, and then resample with replacement the visit times for each patient.
2.6.2. Prediction
For binary response, the mean μit = E[yit|bi] is the conditional probability of success given the random-effects and covariate values:
For out of sample prediction, we identify two types:
Predictions for new visit times for patients in the training data. If and are new fixed and random-effect covariates for patient i observed at the new visit t, then using the estimated random-effects for the patient and fixed-effects model , the predicted conditional probability is given by
Predictions for new visit times for patients not in the training data. In this case, the random-effects for the new patient is not known, and we simply set in the equation above.
Performance measures
We used the following performance measures to validate the models: balanced accuracy (ACC), area under the ROC curve (AUC), sensitivity (Sens), specificity (Spec), and positive predictive value (PPV). The balanced accuracy is average accuracy on each class and control for any imbalance in the class distributions. [39] We report the average of these measures over the 100 bootstraps (or 50 repeated training and testing) and the 95% confidence intervals in brackets.
3. Results
For experimental evaluation, we compared the performance of MEml models (MErf, MEgbm, MEmob, and MEctree) against GLMM, logistic regression (GLM), GBM and RF in predicting glycemic change using the diabetes data, hepatomegaly using the PBC data, increase in LVMI using the AVS data, and lung cancer remission using the HDP data. We did not train the Model-based recursive partitioning (MOB) and Conditional inference trees (Ctree) models in the bootstrap experiments.
3.1. Predicting future glycemic change
Employing the proposed MEml framework, we learn and validate risk stratification models for identifying patients at risk of future glycemic deterioration at each clinical visit. Specifically, we evaluate how far in advance (e.g. 1st, 2nd, 3rd, and 4th visits) we can correctly identify deteriorating cases. This is an important evaluation criteria for longitudinal supervised learning that is often overlooked, but has crucial implication regarding the utility of the model in clinical practice, where early patient risk stratification can help individualize care and improve health outcomes.
Table 3 presents the performance of MEml models: MErf, MEgbm, MEmod, and MEctree, traditional GLMM; and standard machine learning models without random effects: RF, GBM, and GLM at the 1st, 2nd, 3rd, and 4th visits. Comparable performance can be seen for all MEml models, and GLMM, except for the standard machine learning models. Overall, MEml models predicting future glycemic change at the third and fourth visits are more accurate than the first or second. More generally, as the number of repeated observations used for training increases, models that account for random-effects perform better, whereas those that do not deteriorate. Because we required patients to have at least 2 HbA1c measurements during the 24 months of follow up, to predict future glycemic change using the lagged longitudinal structure described in Table 1 the number of repeated observations used for training is λ + 2. Thus, 3, 4, 5, and 6 repeated observations are used for training models for predicting glycemic change at the 1st, 2nd, 3rd, and 4th visits in advance, respectively. The poor performance of the standard machine learning models as the number of repeated observations increases, reinforces the importance of modeling random-effects in longitudinal supervised learning.
Table 3:
Predicting Change in Glycemic Control using the T2D data set
| Clinical visits in advanced | Model | ACC | AUC | Sens | Spec | PPV |
|---|---|---|---|---|---|---|
| 1 | MErf | 0.73(0.72,0.73) | 0.78(0.76,0.79) | 0.78(0.76,0.80) | 0.66(0.63,0.68) | 0.77(0.75,0.78) |
| MEgbm | 0.73(0.72,0.74) | 0.78(0.76,0.80) | 0.75(0.71,0.78) | 0.70(0.66,0.75) | 0.78(0.76,0.81) | |
| MEmob | 0.73(0.68,0.74) | 0.78(0.71,0.80) | 0.76(0.73,0.78) | 0.67(0.57,0.71) | 0.77(0.71,0.79) | |
| MEctree | 0.72(0.71,0.73) | 0.78(0.76,0.80) | 0.71(0.67,0.77) | 0.73(0.67,0.77) | 0.79(0.76,0.81) | |
| GLMM | 0.73(0.73,0.74) | 0.78(0.76,0.79) | 0.74(0.72,0.77) | 0.72(0.67,0.75) | 0.79(0.76,0.81) | |
| GLM | 0.73(0.72,0.74) | 0.73(0.72,0.74) | 0.75(0.73,0.78) | 0.70(0.65,0.72) | 0.78(0.75,0.79) | |
| GBM | 0.74(0.74,0.74) | 0.75(0.74,0.76) | 0.78(0.76,0.79) | 0.69(0.67,0.71) | 0.78(0.77,0.79) | |
| RF | 0.72(0.71,0.73) | 0.76(0.74,0.77) | 0.74(0.71,0.77) | 0.70(0.66,0.72) | 0.78(0.76,0.79) | |
| 2 | MErf | 0.74(0.73,0.75) | 0.79(0.78,0.81) | 0.77(0.75,0.80) | 0.70(0.66,0.74) | 0.79(0.77,0.81) |
| MEgbm | 0.74(0.73,0.76) | 0.79(0.78,0.81) | 0.77(0.75,0.80) | 0.71(0.68,0.74) | 0.80(0.78,0.81) | |
| MEmob | 0.74(0.73,0.75) | 0.79(0.78,0.81) | 0.76(0.74,0.78) | 0.72(0.71,0.74) | 0.80(0.79,0.81) | |
| MEctree | 0.74(0.73,0.75) | 0.79(0.78,0.81) | 0.75(0.74,0.76) | 0.73(0.70,0.75) | 0.80(0.79,0.81) | |
| GLMM | 0.74(0.73,0.76) | 0.79(0.78,0.81) | 0.74(0.73,0.75) | 0.74(0.73,0.77) | 0.81(0.80,0.82) | |
| GLM | 0.69(0.68,0.71) | 0.71(0.69,0.75) | 0.69(0.67,0.71) | 0.68(0.64,0.71) | 0.76(0.74,0.77) | |
| GBM | 0.73(0.73,0.74) | 0.73(0.72,0.75) | 0.77(0.76,0.78) | 0.68(0.67,0.68) | 0.78(0.77,0.78) | |
| RF | 0.69(0.67,0.71) | 0.75(0.72,0.76) | 0.69(0.66,0.74) | 0.69(0.67,0.71) | 0.77(0.75,0.78) | |
| 3 | MErf | 0.75(0.75,0.76) | 0.79(0.78,0.80) | 0.80(0.79,0.81) | 0.69(0.67,0.71) | 0.79(0.78,0.79) |
| MEgbm | 0.76(0.75,0.76) | 0.79(0.78,0.80) | 0.80(0.79,0.83) | 0.69(0.64,0.71) | 0.79(0.76,0.80) | |
| MEmob | 0.75(0.74,0.75) | 0.79(0.78,0.80) | 0.78(0.77,0.80) | 0.70(0.68,0.72) | 0.79(0.77,0.80) | |
| MEctree | 0.75(0.73,0.76) | 0.78(0.78,0.79) | 0.78(0.71,0.80) | 0.70(0.68,0.75) | 0.79(0.78,0.80) | |
| GLMM | 0.75(0.74,0.76) | 0.78(0.78,0.80) | 0.78(0.76,0.83) | 0.71(0.68,0.71) | 0.79(0.78,0.80) | |
| GLM | 0.66(0.65,0.67) | 0.69(0.69,0.70) | 0.68(0.66,0.70) | 0.64(0.63,0.64) | 0.73(0.73,0.73) | |
| GBM | 0.68(0.67,0.69) | 0.71(0.70,0.72) | 0.70(0.66,0.73) | 0.65(0.62,0.70) | 0.74(0.73,0.76) | |
| RF | 0.69(0.67,0.70) | 0.74(0.73,0.76) | 0.69(0.67,0.70) | 0.69(0.65,0.71) | 0.76(0.74,0.77) | |
| 4 | MErf | 0.78(0.78,0.78) | 0.81(0.81,0.81) | 0.80(0.80,0.80) | 0.75(0.75,0.75) | 0.80(0.80,0.80) |
| MEgbm | 0.78(0.78,0.78) | 0.80(0.80,0.80) | 0.80(0.80,0.80) | 0.75(0.75,0.75) | 0.80(0.80,0.80) | |
| MEmob | 0.78(0.78,0.78) | 0.81(0.81,0.81) | 0.80(0.80,0.80) | 0.75(0.75,0.75) | 0.80(0.80,0.80) | |
| MEctree | 0.78(0.78,0.78) | 0.80(0.80,0.80) | 0.80(0.80,0.80) | 0.75(0.75,0.75) | 0.80(0.80,0.80) | |
| GLMM | 0.79(0.79,0.79) | 0.81(0.81,0.81) | 0.80(0.80,0.80) | 0.76(0.76,0.76) | 0.81(0.81,0.81) | |
| GLM | 0.66(0.66,0.66) | 0.69(0.69,0.69) | 0.66(0.66,0.66) | 0.66(0.66,0.66) | 0.71(0.71,0.71) | |
| GBM | 0.66(0.64,0.67) | 0.70(0.69,0.71) | 0.70(0.63,0.73) | 0.61(0.58,0.66) | 0.69(0.69,0.70) | |
| RF | 0.73(0.71,0.75) | 0.78(0.77,0.78) | 0.74(0.68,0.79) | 0.72(0.66,0.78) | 0.77(0.74,0.80) |
3.2. Predicting future hepatomegaly and increase in LVMI
We used the PBC and AVR data sets to further demonstrate the robustness of MEml models to increasingly correlated data and their predictive superiority compared to the other methods. Table 4 and 5 presents the performance of MEml models in predicting hepatomegaly and increase in LVMI at the 1st, 2nd,…, 7th and 1st, 2nd,…, 4th clinical visits respectively compared to that of GLMM, RF, GBM, and GLM. Specifically, in terms of the AUC, Table 4 shows that the performance of MEml models on the PBC data remains somewhat consistent as the number of repeated observations increases, while the performance of GLMM slowly drop and drops significantly for the non mixed-effect machine learning methods. We find similar results for the AVR data set (Table 5). The AUC’s of MEml models slowly drops to the low .80’s as the number of repeated observations used for training increases, while that for GLMM and the non mixed-effect machine learning approaches significantly deteriorates. An exception was found for the RF model, which appeared to be resistant to increasing correlated data, but was still inferior to MEml.
Table 4:
Predicting Hepatomegaly using the PBC data set
| Clinical visits in advanced | Model | ACC | AUC | Sens | Spec | PPV |
|---|---|---|---|---|---|---|
| 1 | MErf | 0.83(0.78,0.86) | 0.88(0.83,0.91) | 0.86(0.81,0.90) | 0.79(0.72,0.83) | 0.86(0.82,0.90) |
| MEgbm | 0.83(0.77,0.87) | 0.87(0.84,0.90) | 0.88(0.80,0.91) | 0.76(0.67,0.81) | 0.85(0.80,0.89) | |
| MEmob | 0.84(0.81,0.87) | 0.85(0.81,0.91) | 0.86(0.79,0.90) | 0.81(0.77,0.84) | 0.88(0.86,0.90) | |
| MEctree | 0.84(0.78,0.87) | 0.85(0.81,0.89) | 0.86(0.79,0.90) | 0.80(0.63,0.85) | 0.87(0.79,0.91) | |
| GLMM | 0.85(0.82,0.88) | 0.90(0.87,0.92) | 0.86(0.79,0.90) | 0.85(0.79,0.89) | 0.90(0.86,0.93) | |
| GLM | 0.85(0.82,0.88) | 0.90(0.87,0.93) | 0.86(0.80,0.90) | 0.84(0.78,0.88) | 0.89(0.86,0.92) | |
| GBM | 0.85(0.82,0.87) | 0.90(0.87,0.92) | 0.85(0.79,0.90) | 0.86(0.80,0.91) | 0.91(0.87,0.94) | |
| RF | 0.84(0.81,0.87) | 0.90(0.87,0.93) | 0.83(0.78,0.89) | 0.86(0.81,0.92) | 0.90(0.86,0.94) | |
| 2 | MErf | 0.83(0.77,0.87) | 0.87(0.80,0.92) | 0.85(0.76,0.92) | 0.79(0.76,0.86) | 0.85(0.80,0.90) |
| MEgbm | 0.83(0.77,0.88) | 0.87(0.79,0.91) | 0.86(0.78,0.93) | 0.78(0.72,0.85) | 0.84(0.79,0.89) | |
| MEmob | 0.81(0.76,0.88) | 0.86(0.80,0.90) | 0.84(0.77,0.93) | 0.76(0.70,0.82) | 0.83(0.77,0.87) | |
| MEctree | 0.81(0.76,0.86) | 0.85(0.78,0.89) | 0.84(0.74,0.91) | 0.76(0.71,0.82) | 0.83(0.78,0.87) | |
| GLMM | 0.82(0.76,0.86) | 0.86(0.78,0.90) | 0.84(0.74,0.91) | 0.80(0.76,0.85) | 0.85(0.81,0.89) | |
| GLM | 0.78(0.74,0.81) | 0.84(0.77,0.87) | 0.81(0.73,0.87) | 0.74(0.68,0.80) | 0.81(0.74,0.86) | |
| GBM | 0.79(0.74,0.82) | 0.85(0.81,0.88) | 0.80(0.72,0.87) | 0.78(0.71,0.85) | 0.83(0.78,0.87) | |
| RF | 0.81(0.77,0.85) | 0.87(0.81,0.91) | 0.81(0.73,0.90) | 0.81(0.73,0.87) | 0.85(0.78,0.89) | |
| 3 | MErf | 0.83(0.74,0.88) | 0.87(0.79,0.91) | 0.88(0.74,0.94) | 0.78(0.67,0.84) | 0.84(0.75,0.88) |
| MEgbm | 0.83(0.74,0.87) | 0.87(0.79,0.90) | 0.88(0.76,0.94) | 0.77(0.63,0.82) | 0.83(0.74,0.87) | |
| MEmob | 0.82(0.74,0.86) | 0.86(0.80,0.89) | 0.87(0.76,0.93) | 0.75(0.69,0.81) | 0.82(0.77,0.86) | |
| MEctree | 0.82(0.75,0.86) | 0.85(0.80,0.89) | 0.86(0.74,0.92) | 0.77(0.71,0.82) | 0.83(0.79,0.86) | |
| GLMM | 0.82(0.78,0.87) | 0.87(0.82,0.91) | 0.84(0.77,0.91) | 0.80(0.74,0.85) | 0.84(0.79,0.88) | |
| GLM | 0.77(0.72,0.81) | 0.83(0.77,0.86) | 0.78(0.67,0.82) | 0.77(0.70,0.83) | 0.81(0.75,0.86) | |
| GBM | 0.78(0.74,0.82) | 0.84(0.79,0.88) | 0.77(0.70,0.86) | 0.79(0.73,0.89) | 0.82(0.78,0.89) | |
| RF | 0.78(0.73,0.83) | 0.87(0.83,0.90) | 0.76(0.69,0.82) | 0.81(0.70,0.87) | 0.83(0.76,0.88) | |
| 4 | MErf | 0.81(0.64,0.86) | 0.85(0.65,0.89) | 0.83(0.67,0.88) | 0.78(0.55,0.85) | 0.83(0.69,0.89) |
| MEgbm | 0.81(0.65,0.86) | 0.85(0.63,0.89) | 0.84(0.71,0.90) | 0.76(0.53,0.84) | 0.82(0.68,0.88) | |
| MEmob | 0.82(0.75,0.86) | 0.86(0.78,0.90) | 0.84(0.76,0.89) | 0.80(0.71,0.83) | 0.84(0.79,0.87) | |
| MEctree | 0.82(0.65,0.87) | 0.84(0.61,0.89) | 0.84(0.72,0.91) | 0.78(0.55,0.83) | 0.83(0.70,0.87) | |
| GLMM | 0.85(0.79,0.88) | 0.87(0.81,0.90) | 0.86(0.81,0.92) | 0.83(0.76,0.87) | 0.86(0.82,0.89) | |
| GLM | 0.73(0.67,0.79) | 0.78(0.71,0.85) | 0.73(0.66,0.81) | 0.73(0.64,0.83) | 0.78(0.69,0.85) | |
| GBM | 0.73(0.68,0.79) | 0.78(0.72,0.84) | 0.72(0.58,0.84) | 0.74(0.66,0.83) | 0.78(0.72,0.83) | |
| RF | 0.76(0.71,0.81) | 0.80(0.73,0.86) | 0.76(0.69,0.82) | 0.75(0.64,0.83) | 0.79(0.72,0.86) | |
| 5 | MErf | 0.85(0.80,0.89) | 0.88(0.84,0.91) | 0.87(0.78,0.93) | 0.83(0.79,0.90) | 0.87(0.83,0.92) |
| MEgbm | 0.85(0.79,0.88) | 0.89(0.85,0.91) | 0.87(0.76,0.92) | 0.83(0.79,0.89) | 0.87(0.83,0.92) | |
| MEmob | 0.84(0.76,0.89) | 0.87(0.77,0.91) | 0.85(0.74,0.94) | 0.83(0.77,0.88) | 0.86(0.81,0.91) | |
| MEctree | 0.86(0.78,0.90) | 0.88(0.85,0.91) | 0.87(0.78,0.92) | 0.84(0.79,0.89) | 0.87(0.82,0.92) | |
| GLMM | 0.85(0.81,0.90) | 0.86(0.80,0.92) | 0.86(0.79,0.92) | 0.85(0.77,0.91) | 0.88(0.82,0.93) | |
| GLM | 0.67(0.61,0.73) | 0.73(0.62,0.81) | 0.65(0.58,0.78) | 0.70(0.60,0.79) | 0.73(0.66,0.81) | |
| GBM | 0.70(0.64,0.76) | 0.74(0.68,0.81) | 0.67(0.56,0.76) | 0.73(0.61,0.87) | 0.76(0.69,0.85) | |
| RF | 0.74(0.70,0.78) | 0.79(0.76,0.83) | 0.75(0.65,0.83) | 0.74(0.65,0.83) | 0.78(0.72,0.84) | |
| 6 | MErf | 0.82(0.78,0.86) | 0.87(0.82,0.90) | 0.85(0.75,0.92) | 0.80(0.75,0.84) | 0.83(0.78,0.87) |
| MEgbm | 0.83(0.78,0.86) | 0.87(0.82,0.90) | 0.85(0.77,0.91) | 0.80(0.76,0.85) | 0.83(0.79,0.87) | |
| MEmob | 0.82(0.79,0.85) | 0.86(0.82,0.90) | 0.84(0.78,0.92) | 0.79(0.75,0.82) | 0.82(0.79,0.85) | |
| MEctree | 0.82(0.74,0.86) | 0.87(0.81,0.90) | 0.83(0.67,0.92) | 0.80(0.76,0.84) | 0.83(0.78,0.87) | |
| GLMM | 0.83(0.79,0.86) | 0.85(0.80,0.89) | 0.84(0.77,0.89) | 0.82(0.77,0.86) | 0.84(0.81,0.87) | |
| GLM | 0.66(0.57,0.72) | 0.69(0.57,0.78) | 0.62(0.56,0.68) | 0.69(0.57,0.77) | 0.70(0.58,0.79) | |
| GBM | 0.65(0.57,0.72) | 0.68(0.59,0.74) | 0.65(0.52,0.76) | 0.66(0.52,0.83) | 0.68(0.58,0.80) | |
| RF | 0.71(0.63,0.78) | 0.76(0.68,0.82) | 0.71(0.60,0.81) | 0.73(0.61,0.82) | 0.74(0.63,0.84) | |
| 7 | MErf | 0.82(0.80,0.85) | 0.88(0.83,0.92) | 0.84(0.78,0.90) | 0.81(0.76,0.86) | 0.84(0.80,0.90) |
| MEgbm | 0.82(0.78,0.85) | 0.88(0.83,0.91) | 0.83(0.76,0.89) | 0.82(0.77,0.86) | 0.84(0.80,0.89) | |
| MEmob | 0.82(0.77,0.85) | 0.87(0.79,0.91) | 0.82(0.72,0.89) | 0.81(0.75,0.87) | 0.84(0.78,0.89) | |
| MEctree | 0.82(0.80,0.85) | 0.89(0.84,0.92) | 0.83(0.76,0.89) | 0.81(0.77,0.86) | 0.84(0.80,0.89) | |
| GLMM | 0.82(0.71,0.86) | 0.84(0.72,0.88) | 0.85(0.74,0.92) | 0.78(0.63,0.84) | 0.82(0.71,0.88) | |
| GLM | 0.62(0.58,0.70) | 0.61(0.57,0.68) | 0.63(0.49,0.80) | 0.61(0.52,0.74) | 0.66(0.60,0.71) | |
| GBM | 0.65(0.57,0.70) | 0.66(0.57,0.73) | 0.66(0.47,0.80) | 0.63(0.51,0.75) | 0.68(0.62,0.74) | |
| RF | 0.67(0.57,0.72) | 0.70(0.60,0.75) | 0.69(0.57,0.82) | 0.64(0.52,0.78) | 0.70(0.58,0.78) |
Table 5:
Predicting Increase in LVMI using the AVR data set
| Visits in advanced | Classifier | PCC | AUC | Sens | Spec | PPV |
|---|---|---|---|---|---|---|
| 1 | MErf | 0.80(0.77,0.83) | 0.87(0.82,0.91) | 0.79(0.73,0.85) | 0.84(0.75,0.89) | 0.92(0.88,0.94) |
| MEgbm | 0.80(0.76,0.83) | 0.87(0.82,0.91) | 0.77(0.73,0.83) | 0.85(0.69,0.92) | 0.92(0.86,0.96) | |
| MEmob | 0.79(0.74,0.84) | 0.84(0.76,0.90) | 0.78(0.70,0.83) | 0.82(0.76,0.89) | 0.91(0.87,0.94) | |
| MEctree | 0.77(0.66,0.82) | 0.86(0.76,0.90) | 0.74(0.60,0.81) | 0.85(0.77,0.92) | 0.92(0.89,0.96) | |
| GLMM | 0.85(0.78,0.88) | 0.86(0.77,0.89) | 0.86(0.80,0.90) | 0.82(0.73,0.87) | 0.92(0.88,0.95) | |
| GLM | 0.81(0.75,0.85) | 0.82(0.76,0.88) | 0.81(0.72,0.85) | 0.82(0.75,0.88) | 0.91(0.88,0.95) | |
| GBM | 0.84(0.82,0.87) | 0.83(0.79,0.88) | 0.85(0.82,0.89) | 0.81(0.75,0.86) | 0.91(0.89,0.94) | |
| RF | 0.82(0.78,0.86) | 0.85(0.80,0.88) | 0.81(0.76,0.90) | 0.83(0.74,0.91) | 0.92(0.88,0.96) | |
| 2 | MErf | 0.81(0.77,0.86) | 0.86(0.81,0.90) | 0.83(0.77,0.89) | 0.75(0.63,0.85) | 0.89(0.84,0.93) |
| MEgbm | 0.81(0.77,0.84) | 0.86(0.80,0.90) | 0.82(0.75,0.87) | 0.78(0.68,0.86) | 0.90(0.87,0.93) | |
| MEmob | 0.79(0.76,0.83) | 0.83(0.75,0.88) | 0.81(0.78,0.85) | 0.75(0.69,0.78) | 0.88(0.84,0.91) | |
| MEctree | 0.79(0.75,0.84) | 0.85(0.76,0.91) | 0.78(0.73,0.84) | 0.81(0.73,0.89) | 0.91(0.86,0.94) | |
| GLMM | 0.77(0.73,0.82) | 0.79(0.72,0.86) | 0.77(0.69,0.84) | 0.80(0.62,0.87) | 0.90(0.84,0.94) | |
| GLM | 0.80(0.74,0.83) | 0.79(0.75,0.88) | 0.79(0.72,0.85) | 0.81(0.77,0.86) | 0.91(0.88,0.93) | |
| GBM | 0.79(0.76,0.83) | 0.80(0.75,0.83) | 0.80(0.74,0.86) | 0.78(0.69,0.85) | 0.90(0.85,0.93) | |
| RF | 0.81(0.73,0.86) | 0.84(0.80,0.88) | 0.81(0.69,0.89) | 0.80(0.67,0.89) | 0.91(0.86,0.94) | |
| 3 | MErf | 0.78(0.71,0.86) | 0.86(0.81,0.90) | 0.80(0.69,0.91) | 0.74(0.65,0.90) | 0.87(0.82,0.95) |
| MEgbm | 0.80(0.75,0.87) | 0.87(0.83,0.93) | 0.83(0.74,0.93) | 0.75(0.61,0.89) | 0.88(0.80,0.95) | |
| MEmob | 0.64(0.29,0.83) | 0.76(0.57,0.85) | 0.57(0.00,0.90) | 0.80(0.50,1.00) | 0.86(0.70,1.00) | |
| MEctree | 0.79(0.73,0.86) | 0.86(0.83,0.93) | 0.80(0.73,0.87) | 0.79(0.67,0.89) | 0.89(0.83,0.95) | |
| GLMM | 0.76(0.68,0.87) | 0.76(0.68,0.90) | 0.77(0.68,0.92) | 0.74(0.60,0.83) | 0.86(0.80,0.92) | |
| GLM | 0.77(0.73,0.86) | 0.77(0.69,0.88) | 0.77(0.70,0.86) | 0.77(0.70,0.86) | 0.88(0.84,0.92) | |
| GBM | 0.77(0.71,0.84) | 0.78(0.72,0.87) | 0.79(0.72,0.86) | 0.73(0.65,0.84) | 0.86(0.82,0.92) | |
| RF | 0.80(0.73,0.87) | 0.83(0.74,0.91) | 0.81(0.69,0.95) | 0.78(0.70,0.89) | 0.89(0.85,0.95) | |
| 4 | MErf | 0.78(0.70,0.83) | 0.82(0.70,0.90) | 0.82(0.68,0.89) | 0.68(0.56,0.88) | 0.87(0.82,0.95) |
| MEgbm | 0.79(0.72,0.85) | 0.82(0.69,0.87) | 0.81(0.70,0.94) | 0.75(0.63,0.91) | 0.90(0.84,0.96) | |
| MEmob | 0.79(0.77,0.81) | 0.81(0.76,0.87) | 0.81(0.78,0.82) | 0.74(0.64,0.83) | 0.89(0.85,0.94) | |
| MEctree | 0.77(0.72,0.79) | 0.83(0.75,0.86) | 0.78(0.70,0.82) | 0.77(0.57,0.87) | 0.90(0.82,0.94) | |
| GLMM | 0.78(0.73,0.83) | 0.77(0.74,0.80) | 0.77(0.67,0.86) | 0.81(0.71,0.92) | 0.92(0.87,0.96) | |
| GLM | 0.78(0.73,0.83) | 0.77(0.74,0.81) | 0.77(0.67,0.86) | 0.81(0.71,0.92) | 0.92(0.87,0.96) | |
| GBM | 0.79(0.75,0.81) | 0.77(0.70,0.85) | 0.80(0.77,0.85) | 0.75(0.64,0.83) | 0.89(0.84,0.94) | |
| RF | 0.79(0.73,0.88) | 0.82(0.74,0.92) | 0.80(0.73,0.92) | 0.76(0.60,0.91) | 0.90(0.85,0.96) |
3.3. Predicting Lung Cancer Remission using the HDP data set
The performance of MEml shown thus far is based on longitudinal data sets, where repeated measurements from the same patients are observed at different time periods. In clustered data (e.g. clustered randomized clinical trials), groups of patients are nested within larger units such as different treatment arms or providers. To demonstrate the performance of MEml on clustered data, we used the synthetic HDP to predict lung cancer remission, where patients are nested within doctors, and doctors within hospitals. Table 6 shows that the performance of all the models increases with increasing number of patients per doctor. Recalled that the number of patients per doctor ranges in 2–60. Given that the data was generated following a linear model and normally distributed variables, which favors the GLMM model, its performance was consistently better than MEml, while that of MEml was consistently better than the non mixed-effect machine learning models.
Table 6:
Predicting Lung Cancer Remission using the HDP data set
| Maximum no of patients | Model | ACC | AUC | Sens | Spec | PPV |
|---|---|---|---|---|---|---|
| 5 | MErf | 0.81(0.75,0.87) | 0.61(0.50,0.68) | 0.15(0.02,0.33) | 0.93(0.89,0.99) | 0.29(0.11,0.54) |
| 5 | MEgbm | 0.81(0.74,0.87) | 0.72(0.63,0.80) | 0.39(0.25,0.56) | 0.89(0.81,0.96) | 0.40(0.29,0.60) |
| 5 | MEmob | 0.34(0.13,0.79) | 0.68(0.58,0.79) | 0.85(0.39,1.00) | 0.24(0.00,0.85) | 0.20(0.13,0.40) |
| 5 | MEctree | 0.79(0.75,0.84) | 0.70(0.61,0.78) | 0.51(0.37,0.62) | 0.85(0.80,0.90) | 0.38(0.28,0.49) |
| 5 | GLMM | 0.66(0.60,0.73) | 0.69(0.61,0.75) | 0.65(0.53,0.75) | 0.67(0.58,0.75) | 0.26(0.21,0.35) |
| 5 | GLM | 0.63(0.55,0.71) | 0.66(0.57,0.74) | 0.63(0.52,0.75) | 0.63(0.54,0.73) | 0.24(0.18,0.30) |
| 5 | GBM | 0.61(0.49,0.71) | 0.65(0.56,0.71) | 0.64(0.53,0.73) | 0.60(0.46,0.73) | 0.23(0.17,0.31) |
| 5 | RF | 0.63(0.54,0.69) | 0.65(0.58,0.71) | 0.63(0.52,0.73) | 0.63(0.51,0.71) | 0.23(0.18,0.29) |
| 10 | MErf | 0.85(0.80,0.89) | 0.76(0.71,0.84) | 0.30(0.19,0.46) | 0.95(0.90,0.99) | 0.56(0.42,0.74) |
| 10 | MEgbm | 0.82(0.75,0.88) | 0.79(0.73,0.84) | 0.54(0.35,0.68) | 0.87(0.78,0.94) | 0.44(0.34,0.55) |
| 10 | MEmob | 0.72(0.33,0.85) | 0.76(0.69,0.84) | 0.64(0.50,0.96) | 0.73(0.21,0.87) | 0.33(0.19,0.45) |
| 10 | MEctree | 0.75(0.68,0.82) | 0.77(0.69,0.84) | 0.69(0.61,0.77) | 0.76(0.69,0.83) | 0.34(0.26,0.40) |
| 10 | GLMM | 0.73(0.67,0.79) | 0.78(0.72,0.84) | 0.70(0.63,0.79) | 0.73(0.67,0.81) | 0.32(0.26,0.41) |
| 10 | GLM | 0.65(0.56,0.73) | 0.70(0.63,0.77) | 0.67(0.56,0.77) | 0.65(0.54,0.75) | 0.26(0.18,0.32) |
| 10 | GBM | 0.64(0.58,0.70) | 0.69(0.62,0.78) | 0.65(0.58,0.75) | 0.64(0.57,0.71) | 0.25(0.18,0.32) |
| 10 | RF | 0.64(0.57,0.73) | 0.69(0.63,0.76) | 0.64(0.52,0.76) | 0.64(0.56,0.76) | 0.24(0.19,0.31) |
| 20 | MErf | 0.86(0.83,0.89) | 0.81(0.76,0.87) | 0.34(0.20,0.49) | 0.95(0.92,0.98) | 0.58(0.48,0.71) |
| 20 | MEgbm | 0.81(0.77,0.84) | 0.83(0.78,0.88) | 0.64(0.52,0.76) | 0.84(0.80,0.89) | 0.43(0.37,0.49) |
| 20 | MEmob | 0.78(0.66,0.83) | 0.82(0.77,0.87) | 0.70(0.59,0.80) | 0.79(0.64,0.86) | 0.38(0.28,0.46) |
| 20 | MEctree | 0.75(0.70,0.80) | 0.81(0.76,0.86) | 0.74(0.68,0.81) | 0.75(0.70,0.80) | 0.35(0.30,0.41) |
| 20 | GLMM | 0.77(0.72,0.83) | 0.84(0.80,0.89) | 0.77(0.72,0.84) | 0.77(0.71,0.84) | 0.38(0.32,0.45) |
| 20 | GLM | 0.67(0.62,0.72) | 0.72(0.66,0.78) | 0.66(0.57,0.75) | 0.67(0.61,0.74) | 0.27(0.23,0.34) |
| 20 | GBM | 0.68(0.59,0.75) | 0.73(0.65,0.80) | 0.66(0.57,0.74) | 0.68(0.58,0.75) | 0.28(0.22,0.34) |
| 20 | RF | 0.67(0.58,0.73) | 0.72(0.65,0.80) | 0.66(0.60,0.74) | 0.67(0.57,0.74) | 0.27(0.21,0.32) |
| 30 | MErf | 0.87(0.82,0.89) | 0.84(0.78,0.89) | 0.40(0.27,0.52) | 0.95(0.91,0.97) | 0.58(0.41,0.70) |
| 30 | MEgbm | 0.81(0.77,0.86) | 0.85(0.81,0.90) | 0.70(0.55,0.82) | 0.83(0.79,0.91) | 0.43(0.36,0.52) |
| 30 | MEmob | 0.79(0.70,0.84) | 0.84(0.78,0.89) | 0.74(0.67,0.81) | 0.80(0.70,0.86) | 0.40(0.31,0.45) |
| 30 | MEctree | 0.75(0.70,0.79) | 0.83(0.77,0.89) | 0.79(0.72,0.87) | 0.74(0.69,0.79) | 0.35(0.32,0.40) |
| 30 | GLMM | 0.79(0.75,0.84) | 0.86(0.82,0.90) | 0.79(0.73,0.85) | 0.79(0.75,0.86) | 0.40(0.35,0.48) |
| 30 | GLM | 0.68(0.62,0.73) | 0.74(0.66,0.78) | 0.68(0.60,0.73) | 0.68(0.61,0.73) | 0.27(0.20,0.34) |
| 30 | GBM | 0.71(0.65,0.77) | 0.78(0.73,0.84) | 0.71(0.64,0.78) | 0.71(0.64,0.77) | 0.30(0.25,0.36) |
| 30 | RF | 0.69(0.61,0.78) | 0.76(0.69,0.83) | 0.70(0.65,0.75) | 0.69(0.60,0.80) | 0.29(0.22,0.37) |
| 40 | MErf | 0.87(0.83,0.90) | 0.85(0.79,0.91) | 0.40(0.28,0.54) | 0.95(0.92,0.97) | 0.59(0.47,0.68) |
| 40 | MEgbm | 0.82(0.78,0.87) | 0.87(0.82,0.91) | 0.73(0.64,0.80) | 0.83(0.78,0.89) | 0.44(0.37,0.53) |
| 40 | MEmob | 0.79(0.74,0.84) | 0.86(0.81,0.91) | 0.77(0.69,0.86) | 0.79(0.74,0.85) | 0.40(0.33,0.45) |
| 40 | MEctree | 0.74(0.70,0.78) | 0.85(0.79,0.90) | 0.83(0.76,0.90) | 0.72(0.67,0.77) | 0.34(0.31,0.38) |
| 40 | GLMM | 0.80(0.75,0.85) | 0.88(0.84,0.92) | 0.81(0.76,0.87) | 0.80(0.74,0.85) | 0.41(0.34,0.45) |
| 40 | GLM | 0.66(0.62,0.71) | 0.73(0.67,0.78) | 0.70(0.61,0.76) | 0.65(0.61,0.71) | 0.26(0.22,0.32) |
| 40 | GBM | 0.72(0.65,0.78) | 0.79(0.73,0.83) | 0.71(0.64,0.77) | 0.72(0.63,0.79) | 0.31(0.26,0.38) |
| 40 | RF | 0.72(0.64,0.79) | 0.78(0.71,0.85) | 0.70(0.63,0.76) | 0.73(0.64,0.80) | 0.31(0.24,0.36) |
| 50 | MErf | 0.87(0.84,0.90) | 0.86(0.82,0.90) | 0.42(0.32,0.51) | 0.95(0.93,0.97) | 0.61(0.53,0.71) |
| 50 | MEgbm | 0.82(0.78,0.84) | 0.87(0.84,0.91) | 0.76(0.70,0.83) | 0.83(0.79,0.86) | 0.43(0.40,0.48) |
| 50 | MEmob | 0.80(0.77,0.85) | 0.87(0.83,0.90) | 0.77(0.73,0.85) | 0.81(0.77,0.85) | 0.42(0.38,0.47) |
| 50 | MEctree | 0.74(0.70,0.79) | 0.86(0.81,0.90) | 0.83(0.77,0.89) | 0.73(0.68,0.78) | 0.35(0.31,0.39) |
| 50 | GLMM | 0.81(0.77,0.83) | 0.89(0.85,0.91) | 0.81(0.73,0.85) | 0.81(0.77,0.85) | 0.43(0.38,0.48) |
| 50 | GLM | 0.66(0.62,0.72) | 0.73(0.70,0.77) | 0.69(0.64,0.74) | 0.66(0.60,0.72) | 0.26(0.23,0.31) |
| 50 | GBM | 0.73(0.68,0.79) | 0.80(0.75,0.84) | 0.72(0.64,0.77) | 0.73(0.67,0.80) | 0.32(0.29,0.38) |
| 50 | RF | 0.73(0.68,0.79) | 0.79(0.73,0.84) | 0.71(0.63,0.75) | 0.74(0.68,0.81) | 0.32(0.28,0.36) |
| 60 | MErf | 0.86(0.83,0.90) | 0.84(0.80,0.89) | 0.42(0.33,0.51) | 0.95(0.92,0.96) | 0.59(0.52,0.66) |
| 60 | MEgbm | 0.81(0.76,0.85) | 0.86(0.81,0.90) | 0.73(0.66,0.80) | 0.82(0.77,0.87) | 0.43(0.38,0.49) |
| 60 | MEmob | 0.79(0.74,0.83) | 0.86(0.82,0.90) | 0.75(0.69,0.82) | 0.80(0.74,0.83) | 0.41(0.37,0.45) |
| 60 | MEctree | 0.72(0.68,0.76) | 0.84(0.79,0.89) | 0.82(0.76,0.88) | 0.71(0.66,0.75) | 0.34(0.31,0.37) |
| 60 | GLMM | 0.79(0.75,0.83) | 0.87(0.84,0.91) | 0.80(0.75,0.85) | 0.79(0.75,0.83) | 0.41(0.38,0.44) |
| 60 | GLM | 0.66(0.62,0.71) | 0.74(0.70,0.78) | 0.69(0.65,0.73) | 0.66(0.61,0.71) | 0.27(0.23,0.32) |
| 60 | GBM | 0.73(0.69,0.78) | 0.80(0.76,0.84) | 0.72(0.67,0.79) | 0.73(0.67,0.79) | 0.32(0.30,0.37) |
| 60 | RF | 0.73(0.66,0.78) | 0.79(0.74,0.83) | 0.71(0.66,0.76) | 0.73(0.66,0.79) | 0.32(0.27,0.37) |
3.4. Interpretability: Variable Importance and Prediction Rules for T2D data
Of the models examined, MErf and MEgbm are best suited to describe patient characteristics that influence glycemic deterioration, as both methods can produce a variable importance score. This score can aid in hypothesis generation about potential risk factors and interventions, and improve our understanding of model predictions and the disease.
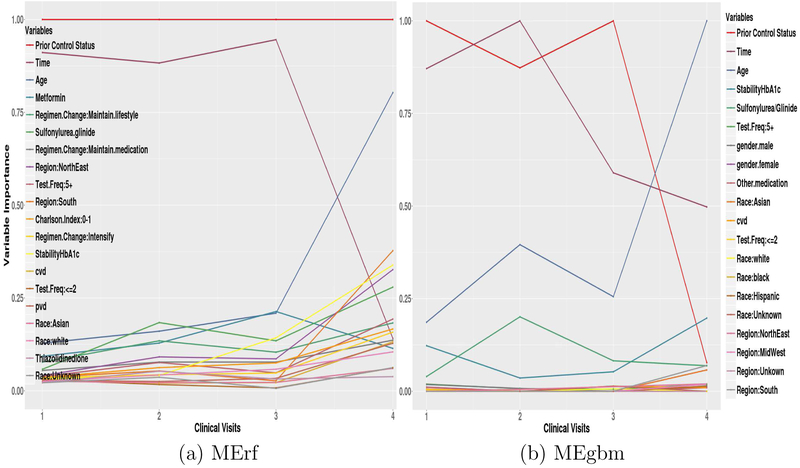
Figures 2 (a) and (b) show the top 20 variable importance (scaled between 0 and 1) plots for MErf and MEgbm at the 1st, 2nd, 3rd, and 4th clinical visits. Significant changes can be seen in the relative importance of some features over time. Prior glycemic control status and follow-up time are the most important features; however, their importance (time for MErf and both for MEgbm) becomes less significant when predicting glycemic control far in the future. Conversely, age (and h−1 or StabilityHbA1c) becomes important in predicting glycemic control only far in advance. For MErf, the importance of metformin decreases slightly while sulfonylurea/glinide drugs become more influential.
Figure 2:
MErf and MEgbm Variable Importance at 1st, 2nd, 3rd, and 4th clinical visits
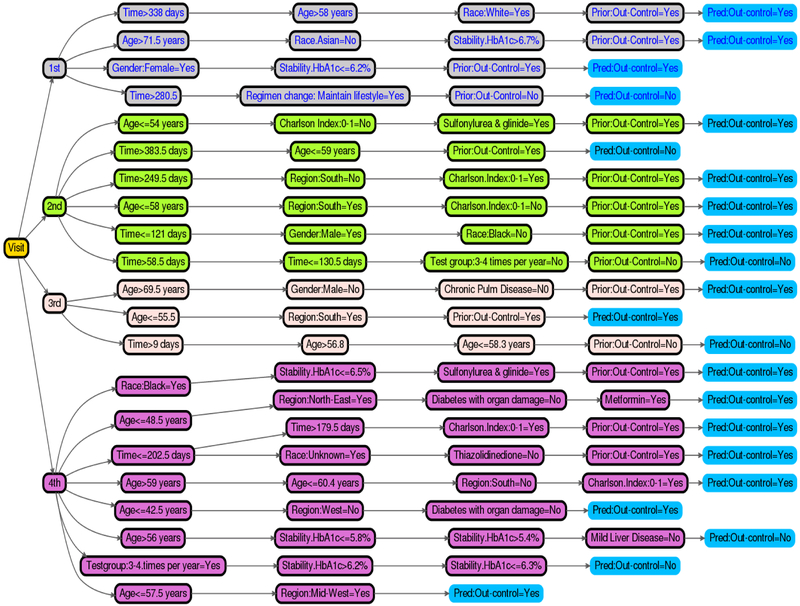
Figure 3 shows a decision tree representation of the top relational rules of the MErf model for the 1st, 2nd, 3rd, and 4th. The rules indicate how frequent the individual trees of MErf combine a set of influential variables to make final predictions of a patients’ future glycemic control status. We selected all rules of length between 2 and 4, with frequency 0.01 and error ≤ 0.35 in predicting glycemic control (shown in the leaves). Thus, instead of relying on the complex MErf model for predictions, this simple and transparent relational rule set can be deployed into practice via a simple clinical web application delivering the same prediction accuracy as the original model, with the additional benefit of conveying relevant clinical information about the model. A similar set of rules can be obtained from the MEgbm model.
Figure 3:
MErf Prediction Rules for the 1st and 2nd visits
4. Conclusion and Discussion
Classical machine learning classification and regression algorithms do not generate high quality models on correlated data. In this study, we developed a methodology for nonlinear longitudinal/clustered data analysis, which is an extension of traditional machine learning methods to longitudinal/clustered data. We formalized the problem of longitudinal/clustered supervised machine learning, as that of learning the two components of a NLMM separately through an iterative expectation maximization-like algorithm, in which we alternatively estimate the fixed-effect component using machine learning methods and the random-effect component using GLMM. This allows the proposed mixed-effect machine learning framework (MEml) to address common real-world data issues like high-dimensionality, non-linearity, variable interactions, and dependencies between variables and observations or groups of observations.
Our MEml framework was successfully applied to the problem of identifying patients with previously controlled T2D who are at increased risk of losing glycemic control in the future. We observed a significant improvement of MEml over classical machine learning methods. In particular, as the number of repeated observations increased, the performance of MEml increased, whereas the performance of classical methods deteriorated. This demonstrates that MEml is able to take advantage of increasing sample sizes and dependencies between the observations to generate more robust and accurate models.
To demonstrate the general applicability of our method, we obtained similar findings on two publicly available longitudinal health care data sets and on an artificially generated clustered data set. In the longitudinal experiments, either the performance of MEml remained consistent or gradually worsened as the correlation in the training data increases compared to the rapid deterioration in performance of the other methods. These results indicates that MEml is resistant to variabilities introduced by correlated data and can predict a clinical outcome with high accuracy using both longitudinal and clustered data.
Another key finding is that while we expected the traditional machine learning methods to perform better in determining a patients’ glycemic control status with more data and as more information about prior status became available, as they do with i.i.d data, this was not observed in our study. This suggests that mere availability of more data does not necessarily translate to better performance when using traditional machine learning methods. This important finding somewhat contradicts the popular view that machine learning models perform better with more data. In fact, our study demonstrates that without taking the i.i.d assumption into account, more data can be detrimental to learning, and researchers should exercise caution when using standard machine learning approaches for longitudinal/clustered supervised learning.
With respect to the main clinical problem addressed in this study, early warning of future glycemic deterioration is important for targeting high-risk patients for monitoring and intervention. The machine learning methods developed in this study can help predict future glycemic change with high accuracy, sensitivity and specificity. Though the proposed MEml did not improve performance over classical GLMM for our main T2D study population, we showed using the three additional data sets that it may be preferred in other studies and health-related research settings as the framework is data-centric, makes fewer assumptions, and effectively identifies temporal heterogeneous and systematic differences in treatment response in large, high dimensional longitudinal datasets.
The developed MEml models are also interpretable, transparent, and easy to deploy in clinical practice. We observed changes in the relative importance of patient characteristics overtime, suggesting that MEml and the introduced lagged training and validation data structure can be used to further investigate temporal effects of risk factors over successive patient visits. By superimposing multiple successive clinical visit times using advanced visualization techniques, we may uncover new insights, shed light on the relationship between risk factors and time, and ultimately improve our understanding of the disease.
By demonstrating the use of MEml methods in deriving knowledge from non i.i.d data and through a series of experiments analyzing the relationships between a longitudinal or clustered outcome and predictors, this study may contribute to facilitate a wider use of machine learning in health care research.
Research highlights.
Integrate random effects into standard machine learning algorithms.
Framework for longitudinal supervised learning with common machine learning models.
Developed interpretable tree based mixed-effect machine learning models.
Method prospectively identifies patients at risk for future glycemic deterioration.
5. Acknowledgements
This work is supported by the Mayo Clinic Robert D. and Patricia E. Kern Center for the Science of Health Care Delivery (Dr. Ngufor, Dr. Shah, and Dr. McCoy) and by the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health under Award Number K23DK114497 (Dr. McCoy). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Garber AJ, Abrahamson MJ, Barzilay JI, Blonde L, Bloomgarden ZT, Bush MA, Dagogo-Jack S, DeFronzo RA, Einhorn D, Fonseca VA, et al. , Consensus statement by the american association of clinical endocrinologists and american college of endocrinology on the comprehensive type 2 diabetes management algorithm–2016 executive summary, Endocrine Practice 22 (1) (2016) 84–113. [DOI] [PubMed] [Google Scholar]
- [2].NICE Type 2 diabetes in adults: management, accessed 05-May-2017 URL https://www.nice.org.uk/guidance/ng28
- [3].Tricco AC, Ivers NM, Grimshaw JM, Moher D, Turner L, Galipeau J, Halperin I, Vachon B, Ramsay T, Manns B, et al. , Effectiveness of quality improvement strategies on the management of diabetes: a systematic review and meta-analysis, The Lancet 379 (9833) (2012) 2252–2261. [DOI] [PubMed] [Google Scholar]
- [4].Turner RC, Cull CA, Frighi V, Holman RR, Group UPDSU, et al. , Glycemic control with diet, sulfonylurea, metformin, or insulin in patients with type 2 diabetes mellitus: progressive requirement for multiple therapies (ukpds 49), Jama 281 (21) (1999) 2005–2012. [DOI] [PubMed] [Google Scholar]
- [5].Best JD, Drury PL, Davis TM, Taskinen M-R, Kesäniemi YA, Scott R, Pardy C, Voysey M, Keech AC, et al. , Glycemic control over 5 years in 4,900 people with type 2 diabetes, Diabetes care 35 (5) (2012) 1165–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Hajjem A, Bellavance F, Larocque D, Generalized mixed effects regression trees, Mixed Effects Trees and Forests for Clustered Data (2010) 34. [Google Scholar]
- [7].Sela RJ, Simono JS, Re-em trees: a data mining approach for longitudinal and clustered data, Machine learning 86 (2) (2012) 169–207. [Google Scholar]
- [8].Therneau TM, Grambsch PM, Modeling survival data: extending the Cox model, Springer Science & Business Media, 2013. [Google Scholar]
- [9].Clinic Mayo, Primary biliary cirrhosis, accessed 05-May-2017 URL http://stat:ethz:ch/R-manual/R-patched/library/survival/html/pbcseq:html
- [10].Asar Ö, Ritchie J, Kalra PA, Diggle PJ, Joint modelling of repeated measurement and time-to-event data: an introductory tutorial, International journal of epidemiology 44 (1) (2015) 334–344. [DOI] [PubMed] [Google Scholar]
- [11].Bruin J, R advanced: simulating the hospital doctor patient dataset, accessed 05-May-2017 (July 2012). URL https://stats:idre:ucla:edu/r/codefragments/mesimulation/
- [12].Wallace PJ, Shah ND, Dennen T, Bleicher PA, Crown WH, Optum labs: building a novel node in the learning health care system, Health A airs 33 (7) (2014) 1187–1194. [DOI] [PubMed] [Google Scholar]
- [13].Optum, Optum research data assets, accessed 05-May-2017 URL https://www:optum:com/content/dam/optum/resources/productSheets/5302_Data_Assets_Chart_Sheet_ISPOR:pdf
- [14].NCQA, National committee for quality assurance (ncqa) healthcare Effectiveness data and information set (hedis) 2013 diabetes mellitus measures, accessed 05-May-2017 URL http://www:ncqa:org/Portals/0/HEDISQM/DM_2013_Measures_9:13:12:pdf
- [15].Ginde AA, Blanc PG, Lieberman RM, Camargo CA, Validation of icd-9-cm coding algorithm for improved identification of hypoglycemia visits, BMC endocrine disorders 8 (1) (2008) 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Deyo RA, Cherkin DC, Ciol MA, Adapting a clinical comorbidity index for use with icd-9-cm administrative databases, Journal of clinical epidemiology 45 (6) (1992) 613–619. [DOI] [PubMed] [Google Scholar]
- [17].McCoy RG, Van Houten HK, Ross JS, Montori VM, Shah ND, Hba1c overtesting and overtreatment among us adults with controlled type 2 diabetes, 2001–13: observational population based study, BMJ 351 (2015) h6138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].McCoy RG, Ngufor C, Van Houten HK, Caffo B, Shah ND, Trajectories of glycemic change in a national cohort of adults with previously controlled type 2 diabetes, Medical care 55 (11) (2017) 956–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].GRAMBSCH PM, DICKSON ER, WIESNER RH, LANGWORTHY A, Application of the mayo primary biliary cirrhosis survival model to mayo liver transplant patients, in: Mayo Clinic Proceedings, Vol. 64, Elsevier, 1989, pp. 699–704. [DOI] [PubMed] [Google Scholar]
- [20].Stekhoven DJ, Bühlmann P, Missforest—non-parametric missing value imputation for mixed-type data, Bioinformatics 28 (1) (2011) 112–118. [DOI] [PubMed] [Google Scholar]
- [21].Lim E, Ali A, Theodorou P, Sousa I, Ashrafian H, Chamageorgakis T, Duncan A, Henein M, Diggle P, Pepper J, Longitudinal study of the profile and predictors of left ventricular mass regression after stentless aortic valve replacement, The Annals of thoracic surgery 85 (6) (2008) 2026–2029. [DOI] [PubMed] [Google Scholar]
- [22].Friedman JH, Multivariate adaptive regression splines, The annals of statistics (1991) 1–67. [Google Scholar]
- [23].Stroup WW, Generalized linear mixed models: modern concepts, methods and applications, CRC press, 2012. [Google Scholar]
- [24].Breslow NE, Clayton DG, Approximate inference in generalized linear mixed models, Journal of the American statistical Association 88 (421) (1993) 9–25. [Google Scholar]
- [25].Segal MR, Tree-structured methods for longitudinal data, Journal of the American Statistical Association 87 (418) (1992) 407–418. [Google Scholar]
- [26].Breiman L, Friedman J, Stone CJ, Olshen RA, Classification and regression trees, CRC press, 1984. [Google Scholar]
- [27].Zhang H, Classification trees for multiple binary responses, Journal of the American Statistical Association 93 (441) (1998) 180–193. [Google Scholar]
- [28].De’Ath G, Multivariate regression trees: a new technique for modeling species–environment relationships, Ecology 83 (4) (2002) 1105–1117. [Google Scholar]
- [29].Dempster AP, Laird NM, Rubin DB, Maximum likelihood from incomplete data via the em algorithm, Journal of the royal statistical society. Series B (methodological) (1977) 1–38. [Google Scholar]
- [30].Kubo Y, Watanabe S, Nakamura A, McDermott E, Kobayashi T, A sequential pattern classifier based on hidden markov kernel machine and its application to phoneme classification, IEEE Journal of Selected Topics in Signal Processing 4 (6) (2010) 974–984. [Google Scholar]
- [31].Graves A, Mohamed A.-r., Hinton G, Speech recognition with deep recurrent neural networks, in: Acoustics, speech and signal processing (icassp), 2013 ieee international conference on, IEEE, 2013, pp. 6645–6649. [Google Scholar]
- [32].Lipton ZC, Kale DC, Elkan C, Wetzel R, Learning to diagnose with lstm recurrent neural networks, arXiv preprint arXiv:1511.03677. [Google Scholar]
- [33].Breiman L, Random forests, Machine learning 45 (1) (2001) 5–32. [Google Scholar]
- [34].Friedman JH, Greedy function approximation: a gradient boosting machine, Annals of statistics (2001) 1189–1232. [Google Scholar]
- [35].Zeileis A, Hothorn T, Hornik K, Model-based recursive partitioning, Journal of Computational and Graphical Statistics 17 (2) (2008) 492–514. [Google Scholar]
- [36].Hothorn T, Hornik K, Zeileis A, Unbiased recursive partitioning: A conditional inference framework, Journal of Computational and Graphical statistics 15 (3) (2006) 651–674. [Google Scholar]
- [37].Deng H, Interpreting tree ensembles with intrees, arXiv preprint arXiv:1408.5456. [Google Scholar]
- [38].Santos LA, Barrios EB, Small sample estimation in dynamic panel data models: A simulation study, Open Journal of Statistics 1 (02) (2011) 58. [Google Scholar]
- [39].Brodersen KH, Ong CS, Stephan KE, Buhmann JM, The balanced accuracy and its posterior distribution, in: Pattern recognition (ICPR), 2010 20th international conference on, IEEE, 2010, pp. 3121–3124. [Google Scholar]