D+: software for high-resolution hierarchical modeling of solution X-ray scattering from complex structures

D+ is a computer program that calculates both monochromatic and anomalous X-ray scattering curves from solutions of complex structures, using a hierarchical reciprocal grid algorithm.

Abstract

This paper presents the computer program D+ (https://scholars.huji.ac.il/uriraviv/book/d-0), where the reciprocal-grid (RG) algorithm is implemented. D+ efficiently computes, at high-resolution, the X-ray scattering curves from complex structures that are isotropically distributed in random orientations in solution. Structures are defined in hierarchical trees in which subunits can be represented by geometric or atomic models. Repeating subunits can be docked into their assembly symmetries, describing their locations and orientations in space. The scattering amplitude of the entire structure can be calculated by computing the amplitudes of the basic subunits on 3D reciprocal-space grids, moving up in the hierarchy, calculating the RGs of the larger structures, and repeating this process for all the leaves and nodes of the tree. For very large structures (containing over 100 protein subunits), a hybrid method can be used to avoid numerical artifacts. In the hybrid method, only grids of smaller subunits are summed and used as subunits in a direct computation of the scattering amplitude. D+ can accurately analyze both small- and wide-angle solution X-ray scattering data. This article describes how D+ applies the RG algorithm, accounts for rotations and translations of subunits, processes atomic models, accounts for the contribution of the solvent as well as the solvation layer of complex structures in a scalable manner, writes and accesses RGs, interpolates between grid points, computes numerical integrals, enables the use of scripts to define complicated structures, applies fitting algorithms, accounts for several coexisting uncorrelated populations, and accelerates computations using GPUs. D+ may also account for different X-ray energies to analyze anomalous solution X-ray scattering data. An accessory tool that can identify repeating subunits in a Protein Data Bank file of a complex structure is provided. The tool can compute the orientation and translation of repeating subunits needed for exploiting the advantages of the RG algorithm in D+. A Python wrapper (https://scholars.huji.ac.il/uriraviv/book/python-api) is also available, enabling more advanced computations and integration of D+ with other computational tools. Finally, a large number of tests are presented. The results of D+ are compared with those of other programs when possible, and the use of D+ to analyze solution scattering data from dynamic microtubule structures with different protofilament number is demonstrated. D+ and its source code are freely available for academic users and developers (https://bitbucket.org/uriraviv/public-dplus/src/master/).

1. Introduction  

Most involved biomolecular complexes (cytoskeleton protein complexes, for example) cannot be crystallized and therefore can only be investigated in their native solution conditions. The challenge of structural biophysics is to determine the high-resolution structure of large self-assembled complexes, made of many subunits, in their biologically relevant solution conditions. Solution small- and wide-angle X-ray scattering (SAXS/WAXS) methods are one of the important label-free and highly sensitive bulk methods for investigating the structure of and interactions between complex molecular constructs (Rädler et al., 1997 ▸; Koltover et al., 1998 ▸; Schilt et al., 2016 ▸; Dvir et al., 2013 ▸, 2014 ▸; Chung et al., 2015 ▸, 2016 ▸; Lotan et al., 2016 ▸; Ojeda-Lopez et al., 2014 ▸; Moshe et al., 2013 ▸; Saper et al., 2012 ▸; Steiner et al., 2012 ▸; Szekely, Schilt et al., 2011 ▸; Szekely, Steiner et al., 2011 ▸; Nadler et al., 2011 ▸; Choi et al., 2009 ▸, 2016 ▸; Wong et al., 2000 ▸; Deek et al., 2013 ▸; Beck et al., 2010 ▸; Kornreich et al., 2016 ▸; Shaharabani et al., 2016 ▸; Ginsburg et al., 2017 ▸; Asor et al., 2017 ▸; Fink et al., 2017 ▸). With modern synchrotron facilities the temporal and spatial resolution of these methods has been greatly improved (Ginsburg et al., 2016 ▸; Kler et al., 2012 ▸).

In solution X-ray scattering experiments, an X-ray beam is focused either on a detector or onto a solution containing structures with random orientations. As the intensities of the scattered photons are recorded rather than their amplitudes, the phase information is lost. Azimuthally integrating the intensities yields 1D curves of the scattered intensity as a function of q, which is the magnitude of the elastic momentum transfer (or scattering) vector, q. 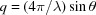, where λ is the X-ray wavelength and θ is half the scattering angle. Owing to the lack of phase and 3D information (resulting from the free rotation of molecules in solution), data analysis is challenging. Problems include addressing the contribution to the scattering signal from individual objects and from their arrangement in space, and accounting for the contribution of the solvating shell and thermal fluctuations, and involve computational and model-fitting aspects [see for example Louzon et al. (2017 ▸)]. Multiple computer programs and algorithms have been developed for analyzing the scattering data from soluble macromolecules or oligomers (Virtanen et al., 2011 ▸; Svergun et al., 1995 ▸; Petoukhov & Svergun, 2005 ▸; Bardhan et al., 2009 ▸; Koutsioubas & Pérez, 2013 ▸; Schneidman-Duhovny et al., 2010 ▸, 2013 ▸, 2016 ▸; Poitevin et al., 2011 ▸; Knight & Hub, 2015 ▸; Franke et al., 2015 ▸; Hura et al., 2009 ▸; Franke & Svergun, 2009 ▸; Spinozzi et al., 2014 ▸; Sarje et al., 2014 ▸; Grant, 2018 ▸; Curtis et al., 2012 ▸; Wright & Perkins, 2015 ▸; Gumerov et al., 2012 ▸; Watson & Curtis, 2013 ▸; Ravikumar et al., 2013 ▸; Petoukhov et al., 2012 ▸; Grudinin et al., 2017 ▸).

The program X+ (https://scholars.huji.ac.il/uriraviv/software/x) was our first attempt to address the challenges when analyzing more complicated and larger self-assembled structures (Székely et al., 2010 ▸; Ben-Nun et al., 2010 ▸, 2016 ▸). Similar types of programs have been developed by others (Pedersen et al., 2013 ▸; Förster et al., 2010 ▸; Ilavsky & Jemian, 2009 ▸). X+ can model multilayer single-geometry-based structures that may also be in space-filling lattices. The geometries include rectangular cuboids, a stack of layered structures, multiple spherical shells, concentric hollow cylindrical or distorted cylindrical structures, and a series of coaxial shifted helical structures. Each layer or subunit has an electron density profile that can be uniform, Gaussian or a sum of hyperbolic tangents (Ben-Nun et al., 2016 ▸). The features of X+ include phase-fitting algorithms to obtain lattice parameters and peak indices, accounting for instrument resolution function and sample polydispersity. The range of models that X+ can compute is limited. Geometrical models may be used to fit low-angle X-ray scattering data (corresponding to relatively low-resolution information in real space). High-quality solution X-ray scattering data at ultra-low to wide angles (Möller et al., 2016 ▸), however, can be obtained using modern synchrotron facilities, high solute concentrations, appropriate background measurement protocols in flow-cell setups (Ginsburg et al., 2016 ▸) and online size exclusion chromatography (Graewert et al., 2015 ▸; Pérez & Koutsioubas, 2015 ▸).

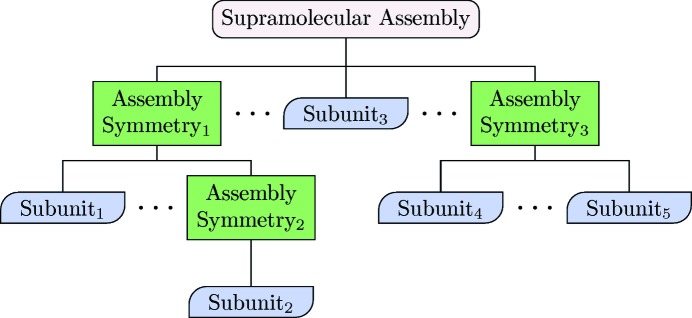
D+ (https://scholars.huji.ac.il/uriraviv/book/d-0) is our new 64 bit computer program, designed to accurately compute the solution X-ray scattering curves from supramolecular structures by docking repeating subunits into their assembly symmetry. Structures can be defined in a hierarchical manner using a data tree structure (Fig. 1 ▸). Subunits may include geometric shapes (like the models of X+) or atomic models when available. Atomic models are presented in Protein Data Bank (PDB; https://www.rcsb.org/) files, containing a list of atoms and the coordinates of their real-space location. The assembly symmetry describes the position and orientation of repeating subunits. The assembly symmetry can be defined in D+ by providing the lattice parameters, position and orientation of each subunit in the graphical user interface (GUI), by uploading a file containing the information, or by writing a script using the Lua (https://www.lua.org/) programming language, which computes these parameters. D+ has a Python application programming interface (API) (https://scholars.huji.ac.il/uriraviv/book/python-api) that can be used to define sophisticated assembly symmetries. Subunits can be added and grouped together at any node in the hierarchical data tree structure to form a new and more involved subunit. At any level of structural complexity, identical copies of any subunit may be shifted and/or rotated in any way. The level of complexity of the elements and the entire structure can be as high as needed. Solvation layers can be computed for any assembly. For each structure or subunit, a finite domain size is directly defined or fitted to data. Advanced features including thermal fluctuations and intermolecular interactions can also be taken into account by using the Python wrapper of D+ or by writing Lua scripts (https://scholars.huji.ac.il/uriraviv/book/examples) inside D+, which can extend, modify or control the arrangements of subunits. The Python API of D+ can also be used to integrate D+ with advanced computations or simulations, as demonstrated by Louzon et al. (2017 ▸).

Figure 1.

Modeling a supramolecular assembly in a hierarchical manner. Each ‘Assembly Symmetry’ may contain multiple children. Children can either be ‘Assembly Symmetries’ or ‘Subunits’. A ‘Subunit’ represents a PDB file or a geometric model. Internal nodes consist of ‘Assembly Symmetries’, whereas each leaf must be a ‘Subunit’. There may be an arbitrary number of hierarchy levels and nodes at each level.

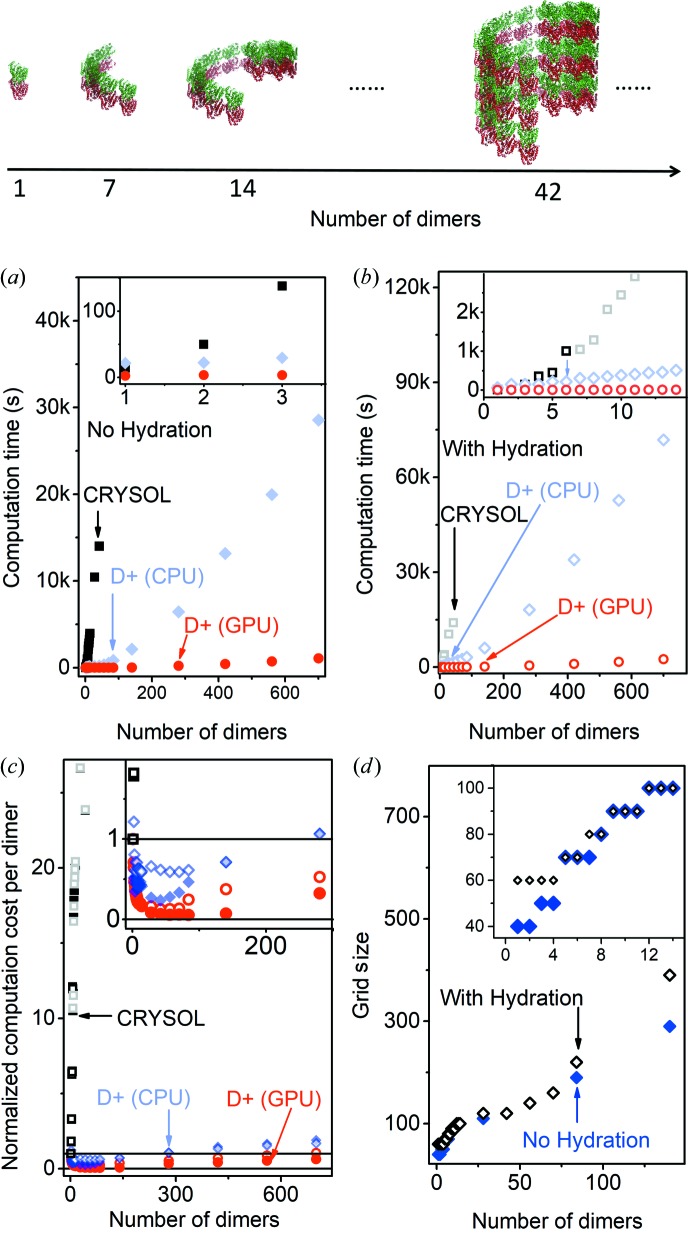
In an earlier publication (Ginsburg et al., 2016 ▸), we described the reciprocal-space grid (RG) hierarchical algorithm for computing solution X-ray scattering intensity curves from complex structures. We then showed results obtained with the algorithm, discussed its limits and presented ways to address them. In particular, we showed that the algorithm is slower than alternative algorithms (Svergun et al., 1995 ▸) for small structures like a soluble protein. The efficiency of the RG algorithm, however, dramatically increases as the number of repeating subunits increases. A fivefold increase in efficiency is obtained above three or four subunits. Above 40 subunits the efficiency increases by a factor of 20. Above about 100 subunits the hybrid method of the RG algorithm is used.

In this paper, we focus on the implementation of the RG algorithm in D+. We describe the 3D spherical grid, its mapping with a single index, how we access the mapped grid and how we interpolate between grid points. The direct and hybrid methods (the latter should be used for very large structures) are explained. We then describe the numerical integration methods used in D+ as well as other algorithms and features that were implemented in the program, including how D+ processes atomic models in vacuum or in solution and accounts for hydrogen atoms and solvation layers of complex structures in a scalable manner, computes numerical integrals, applies fitting algorithms, analyzes anomalous X-ray scattering data, accounts for several coexisting uncorrelated populations of different sizes and/or shapes, and accelerates computations using graphics processing units (GPUs). Finally, we demonstrate how D+ was tested and cross validated, and how solution X-ray scattering data analysis is performed with D+. When possible, we compare D+ with other programs.

2. Applied theory  

The goal of D+ is to evaluate the following solution scattering equations:

Here F is the scattering amplitude, r is the position vector in real space, Δρ(r) is the electron density contrast with respect to the medium as a function of r and r ₀ = 2.82 × 10⁻⁵ Å is the Thomson scattering length, which in D+ is set to 1 unless the anomalous scattering option is used (see Section 5.10). I(q) is the orientation-averaged scattering intensity in solution. Ω_q is the reciprocal-space solid angle. Equation (2) describes structures in solution that are uniformly distributed in all orientations.

The process used by D+ to compute the scattering intensity from a hierarchical assembly (Fig. 1 ▸) is described in our previous paper (Ginsburg et al., 2016 ▸) and can be summarized as follows:

(1) Define a 3D RG, which is essentially a lookup table of the scattering amplitudes at each scattering vector, q.

(2) Compute the amplitude of the lowest node (leaf) for each q point in the grid.

(3) For each level of hierarchy, compute the amplitudes in the grid using the already computed lower level’s amplitudes. Use cubic spline interpolation to compute values between precomputed points on the lower-level grid. Save the new amplitude and discard the old.

(4) Use the highest level’s amplitudes to compute the scattering intensities at each point.

(5) Orientation average the intensity of points on the grid with the same |q|.

In the case of large or elongated assemblies, a hybrid method, which combines direct amplitude computations with RG, should be used. This method can be summarized as follows:

(1) Define an RG and compute the amplitude of the lowest node (leaf) for each q point in the grid.

(2) For each level of hierarchy up to a predetermined level, compute the amplitude using the lower level’s amplitude. For q values between precomputed points, use cubic spline interpolations.

(3) At higher hierarchy levels, grids are no longer computed. Instead, the highest level of computed RG is used as a subunit leaf.

(4) Repeat the last three steps for all the other leaves.

(5) Flatten all the remaining higher-level symmetry nodes by applying them recursively on their subunits until the tree is depth 1 (i.e. root and leaves). For each leaf, the flattening is done by determining the number of identical subunits of the highest level computed, their translations and their rotations. Directly compute the scattering intensity using multiple lookups (depending on the number of subunits) of the scattering amplitude.

(6) Compute the orientation average by repeating the last step for each random orientation of the highest hierarchy (root) level.

In the following we present a rigorous and detailed description of how the RG algorithm is applied in D+.

2.1. Definitions and conventions  

2.1.1. Coordinates  

q is the momentum transfer vector (or the scattering vector), given in reciprocal space by q = (q _x, q _y, q _z) = (q, θ_q, ϕ_q), in Cartesian and spherical coordinates, respectively. The position vector, r, in real space is r = (x, y, z) = (r, θ, ϕ) in the corresponding coordinates.

2.1.2. Rotation convention  

The convention used for rotations is the following Tait–Bryan angles (Goldstein et al., 2001 ▸):

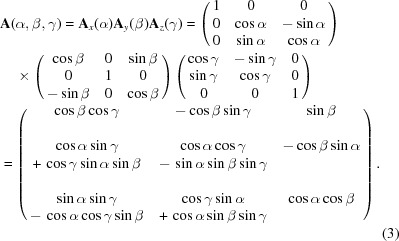The rotation matrix A _i rotates a column vector v by an angle a _i about the i axis, where i ∈ {x, y, z} and a _i ∈ {α, β, γ}. The rotation starts about the z axis, with subsequent rotation about the y axis and finally about the x axis. The rotated vector is then given by Av.

2.2. Rotation and translation in real and reciprocal space  

The RG algorithm is efficient when a structure contains identical objects with different positions and orientations. We therefore need to define the relation between rotation/translation of the objects in real space and the effect of these operations in reciprocal space, in which scattering amplitudes are evaluated. Given an isolated object in real space, r, with an electron density contrast Δρ(r) with respect to its surrounding, its scattering form factor amplitude is given by equation (1). When the object is translated by a vector R and then rotated by a rotation matrix A, its electron density contrast is given by Δρ[A ⁻¹(r − R)] and the form factor of the translated and rotated object is

We define the vector s ≡ A ⁻¹(r − R) and then r = A s + R. As detA = 1, ds = dr. Substituting in gives

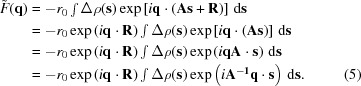The last equation holds because rotating the vector s, given by (A s), or rotating the vector q by the same amount in the opposite direction, given by (A ⁻¹ q), yields the same phase (or scalar product): q · (A s) = A ⁻¹ q · s, as the magnitude of the two new vectors and the angle between them remain unchanged upon rotation (Papoulis, 1968 ▸). Note that because A is a rotation matrix A ⁻¹= A ^T. We therefore get that

D+ uses this relation when objects are translated and rotated.

2.3. Docking  

In real space, the electron density of a complex structure made of K _j,m identical repeats of subunit j, whose orientation is m, is given by

Δρ_ob ^j,m(r) is the subunit electron density contrast, ⊗ is the convolution operation and the collection of delta functions describe the subunit centers of mass, R _j,m,k. In reciprocal q space, this convolution becomes a multiplication of the two contributions. The scattering amplitude, F _j(q), of an object j is given by the Fourier transform of its electron density contrast, Δρ_ob ^j(r), relative to its surroundings. The square of this amplitude, |F _j(q)|², is the form factor of the scattering object. The lattice sum is associated with the relative real-space arrangement of those objects.

If copy k of object j is shifted by R _j,m,k and rotated by a rotation matrix A _j,m with respect to its principal axes, its electron density contrast is given by

and its contribution to the scattering amplitude is given by the Fourier transform of the electron density contrast, which according to equation (6) is

For large assemblies, with repeating subunits (identical or not) that are shifted, rotated and docked onto one another (Fig. 1 ▸), the scattering amplitude is

J is the number of different types of objects, which can be either geometry-based or atom-based models, taken, for example, from PDB files. M _j is the number of instances (rotations and translations) of object type j, given by rotation matrices A _j,m and real-space translation vectors R _j,m. The total number of subunits, n _s, is therefore 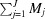. Another way to write equation (10) is

where M ^u _j is the number of unique orientations of an object of type j, given by the rotation matrices A _j,m. K _j,m is the number of real-space translations of object j with orientation A _j,m. Equation (11) is used in the direct and hybrid methods, discussed in Section 3.2.

In Section 3 we describe our implementation of the RG algorithm. Numerical integration methods are explained in Section 4. We then explain how our atomic (Section 5) and geometric (Section 6) models are computed. Ways to account for repeating subunits are explained in Section 7. Uncorrelated mixed structures and key features of D+ are described in Sections 8 and 9, respectively. Accessory tools are presented in Section 10. Validation tests are discussed in Section 11, program modules and workflow are presented in Section 12, and usage examples are given in Section 13.

3. Implementation of the RG algorithm  

3.1. Reciprocal grids  

In our earlier paper (Ginsburg et al., 2016 ▸), we provided a detailed analysis and demonstration of the RG algorithm and its efficiency. We showed that the efficiency considerably increases when the structure contains an increasing number of identical repeats of subunits. The core principle of the RG algorithm is to compute the scattering amplitudes of an object on a 3D grid (or lookup table) containing G _q points in reciprocal q space and to store that computation for later use. When moving up in the hierarchy of the data tree structure (Fig. 1 ▸), the precomputed grid can be used to obtain the scattering amplitudes of the larger structures, containing copies of the smaller object (subunit) at various locations and orientations.

Although the geometry of the RG can be arbitrary (Cartesian, for example), we chose to implement spherical geometry owing to the following distinct advantages. First, as the area of interest is determined by the magnitude of the scattering vector, q, using a Cartesian grid would result in ‘wasted’ corners, which contain about half the grid points [see supporting online materials (SOM) Section 1]. Second, in order for the method to work well on GPUs, we needed a bijective relation between an index m (representing the position in the 1D array onto which the grid is mapped) and the spherical coordinates q, θ_q and ϕ_q. Finally, orientation averaging in reciprocal space becomes simpler as we can fix q and average over θ_q and ϕ_q. To this end, we designed the following spherical-shell-based grid.

The grid origin is stored at m = 0. Surrounding the origin we position N evenly spaced shells, with a spacing of 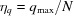, where q _max is the largest q. Note that in the GUI of D+ the parameter Grid Size corresponds to 2N, and hence it should be an even number. Each shell represents the θ_qϕ_q plane of a given radius q. To obtain the bijective relation, D+ uses a modified version of a 3D semi-uniform spherical grid, resulting in a nonuniform grid. In a semi-uniform 3D spherical grid, on the ith shell, at q _i = iη_q, half the circumference is πq _i. Hence, there are

evenly spaced points along the polar axis, θ_q, where . Note that for interpolation reasons (see Section 3.1.3) three additional shells are added to the grid; hence rather than N. The jth polar angle on the ith shell is 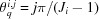, where 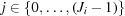. On the jth polar angle of the ith shell, the azimuthal circumference is 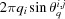; hence there are

evenly spaced points along the azimuthal axis, ϕ_q. The kth azimuthal angle of the jth polar angle on the ith shell is then given by 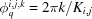, where 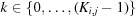. In D+, however, to obtain simple bijective relations, the expressions for J _i and K _i,j were changed to J _i = id _θ + 1 and K _i,j = id _ϕ. We chose d _θ = 3 and d _ϕ = 6 instead of π and 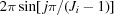, used in the corresponding relations. The grid is nonuniform and the ith shell contains id _ϕ(id _θ + 1) points in its 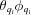plane, which is approximately twice the density in the corresponding semi-uniform 3D spherical grid. The resulting total number of grid points is similar to that of the corresponding 3D Cartesian grid; however, all the grid points are within the sphere (see SOM Section 1).

Within each plane, the values are arranged in a ϕ_q-major storage order (i.e. two neighboring ϕ_q values with the same θ_q will be adjacent in memory, whereas two θ_q values with the same ϕ_q will be separated by d _ϕ i other values). The total number of reciprocal grid points, G ⁱ _q, inside i spheres is therefore

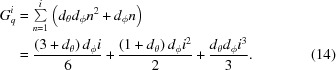With this, we can find the relation between any index m and three indices used to indicate the discrete values of q, θ_q and ϕ_q (i, j and k, respectively). First, note that for all positive i

Hence

unless

in which case

The remainder is

The last two indices are

and

Note that using floating point numbers to compute 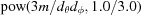to calculate i can be inaccurate. Therefore, a modified stable algorithm is used in D+ for integer values (Warren, 2012 ▸).

Given a point in reciprocal space {q, θ_q, ϕ_q} and the values of q _max and N of the spherical grid, we can find the corresponding point array that is below (or equal to) the given point. Its indices would be

If i = 0 then j = 0 and k = 0. For i > 0,

and

If, however, k = id _ϕ then we reset k = 0. We can then compute the index m. If i = 0, m = 0. For i > 0,

The additions of id _θ + 1 and id _ϕ in the expressions for j and k, respectively, ensure that small negative angles (owing to floating point arithmetic) are accounted for correctly.

3.1.1. Hollow grids  

If the minimal q value, q _min, is not close to the origin (q = 0), a hollow grid that covers the q range of interest, q _range = q _max − q _min, should be used. The spacing between shells is 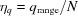, where now N is the number of shells in the hollow grid (N is half the Grid Size). The number of shells in the full grid (from q _min = 0 to q _max) would be

The full and hollow grids may not coincide. To address this situation and to allow interpolations close to q _min and q _max, three shells are added below q _min and above q _max. Hence the modified q _min is q′_min = q _min − 3η_q. Following equations (22), (23) and (24) we get

Because the first point in the grid is {q, θ_q, ϕ_q} = {q′_min, 0, 0}, we get

and

In the full grid, the index of the first point in the hollow grid is then given by equation (25):

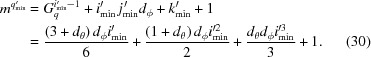The hollow grid is built exactly as the full grid is built, but it contains only the amplitudes that start from 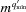. The grid points are located at q _i = iη_q, where , , 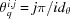where 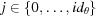, and 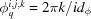, where 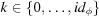. In the hollow grid, the indices, m, of the amplitudes are offset by 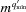with respect to the indices of the same amplitudes in the full grid, given by equation (25):

3.1.2. Grid density  

As explained in our earlier paper (Ginsburg et al., 2016 ▸), to get accurate results, the grid density should be sufficiently high. To find the minimal number of grid points, we need to know the distance L, which is the maximum between the diameter of the sphere that envelopes the structure and the distance of the most distant point in the structure from the origin (0, 0, 0). According to the Nyquist–Shannon sampling rate (Shannon, 1949 ▸; Beaulieu, 2002 ▸), accurate representation using reciprocal grids requires that the grid density satisfies 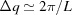(Ginsburg et al., 2016 ▸). The number of grid points, G, is therefore

D+ has a Suggest Parameters tool (https://scholars.huji.ac.il/uriraviv/book/suggests-parameters) that gets q _max and the coordinates of the most distant point in the structure, with respect to the origin (0, 0, 0), and returns the Grid Size parameter (or 2N) required for D+:

where N is the number of shells in the spherical grid. In the current version, q _min is assumed to be zero. Equation (33) returns a multiple of ten.

It is faster to compute the same structure after placing its center of mass at the origin. G will then depend only on the dimension of the object itself rather than the size of the object plus the length of its translation vector [see equation (32)].

3.1.3. Interpolation  

As we often need amplitude values that do not necessarily fall out exactly on a precomputed RG point, we need to interpolate for most values. Cubic spline interpolation is carried out serially, first ϕ_q, then θ_q and finally q (Fig. 2 ▸). As the ϕ_q values are periodic and evenly spaced, all the n derivatives (D _i) for a given q _i and θ^i,j _q can be computed simultaneously by solving (Bartels et al., 1998 ▸)

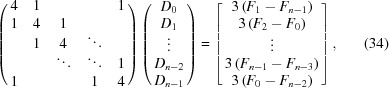where F _i are the amplitudes at each grid point and n = K _i,j. This calculation is done once, upon computation of the RG, and the derivatives are saved for later use. All subsequent (q, θ) cubic splines are calculated on the fly from four evenly spaced q points, two above [, 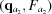] and two below [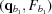, 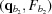] the desired q point (where 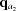is closer to q than 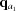and 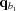is closer to q than 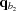). At each interpolation, all the q points differ only in one component, whereas the other two components are fixed. The amplitudes at the four points are calculated using splines from previous interpolations, using the following to calculate the derivatives:

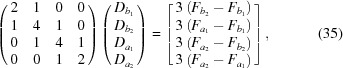which gives

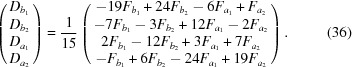The amplitude, F, at q values between points 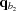and 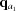is calculated as

where

A crude error estimate of the cubic interpolation is determined by the RG density, ∼η³ _q, which dictates an error of order 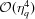(Sonneveld, 1969 ▸).

Figure 2.

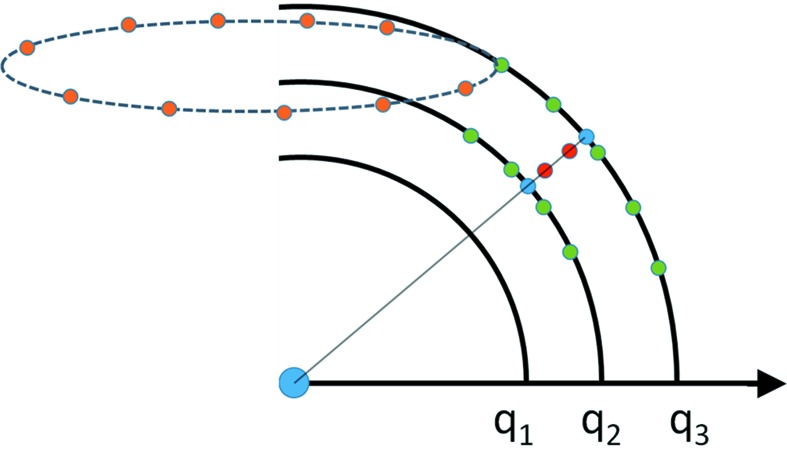
Illustration of the interpolations used in D+. To compute a specific q = (q _i, θⁱ _q, ϕⁱ _q) point (indicated in red), we first interpolate the ϕ_q values in the grid (the orange points show a few grid points), which are periodic (along the broken circle) and evenly spaced. We get the green points that are lying in the (q, θ_q, ϕⁱ _q) plane (solid thick black curves), shown in the figure. We then use the green points to interpolate the θ_q values and obtain the blue points, which are on the (q, θⁱ _q, ϕⁱ _q) line (solid thin line). Finally, we use the blue points to interpolate at the required q values (red points). The interpolation is done simultaneously for all the red points that are located between adjacent blue points.

Three additional shells beyond 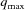are added to the grid, so that interpolations can be performed all the way up to 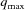. When the required values fall between the first and the second shells, the grid amplitudes that are used for interpolations are taken from the origin (q = 0) and the first, the second and the third shells. When the required values fall between the origin and the first shell, the grid amplitudes that are used for interpolations are taken from the first and second shells, the origin, and the points on the first shell whose azimuthal and polar angles are closest to

and

3.2. The direct and hybrid methods  

For large self-assembled structures the scattering amplitude becomes highly oscillatory in q space. As a result the required RG density (or RG size, G _q) becomes too high (Shannon, 1949 ▸; Beaulieu, 2002 ▸). D+ has two ways to overcome this issue: the direct and hybrid methods. For both methods, the number of computations or lookups can be reduced by identifying identically oriented objects and for each only multiplying by the phase factor associated with its unique position [equation (11)].

3.2.1. The direct method  

In the direct method, no RG is used. Instead, the amplitude is directly computed at each one of the required points in q space. Each geometry or PDB object is identified and all its copies (orientations and locations) in space are collected. The intensity is then computed as

where J is the number of different objects (or the total number of different leaves; see Fig. 1 ▸). M ^u _j is the number of unique rotations A _j,m of object j. K _j,m is the number of copies of object j with orientation m that were translated in real space by vectors R _j,m,k. Orientation averaging is done according to equation (47). The total number of directly calculated subunits is

3.2.2. The hybrid method  

In the hybrid method, RGs are combined with the direct method. All geometries and PDB files (in other words, all the leaves in the hierarchical data tree structure; see Fig. 1 ▸) are calculated to grids. Grids of assembly symmetries are computed up to predetermined nodes in the hierarchical data tree structure (Fig. 1 ▸). Once grids of assembly symmetries are computed, their children are discarded and not used. Assembly symmetries at higher hierarchy levels continue as in the direct method [equation (41)] but use the last computed RG for looking up values once per copy of those structures at each one of the required points in q space.

The evaluation is the same as in the direct method, except that if RGs are computed F _j(A _j,m ⁻¹ q _i) is retrieved from the grid, using interpolations (see Section 3.1.3), and not directly computed. In other words, RGs are computed for all leaves; grids may be calculated for internal nodes and if they are then the node’s leaves are discarded and the internal node is treated as a leaf. The new number of leaves, J, in the data tree structure does not include the discarded grids. The hybrid method can retain near atomic resolution while significantly reducing the computation times. A more comprehensive analysis of the hybrid method is provided in our earlier publication (Ginsburg et al., 2016 ▸). Validation tests of the direct and hybrid methods are shown in SOM Sections 9.1 and 9.2.

4. Numerical integration methods  

To compute the scattering intensity of the assembled structure, the squared norm of the final amplitude (or the amplitude of the root in the data tree structure; Fig. 1 ▸) is calculated. In solution, we have to average over all the orientations of the structure in q space. Hence, the scattering intensity is

where θ_q and ϕ_q are the polar and azimuthal angles in reciprocal space, respectively (see Section 2.1.1). The actual integration is done numerically using one of the methods below.

Some numerical integration methods require generation of random numbers. Pseudo-random numbers were generated by the Mersenne twister algorithm, which has a period of 2¹⁹⁹³⁷ − 1 [instead of 2³² in the rand() function of C++]. Validation tests of the integration methods used in D+ are shown in SOM Sections 9.1 and 9.2.

4.1. Classic Monte Carlo integration  

To compute equation (43), random ϕ_q ⁱ and θ_q ⁱ angles should be generated, from which the vectors q _i = (q, θ_q ⁱ, ϕ_q ⁱ) can be obtained. The orientation average

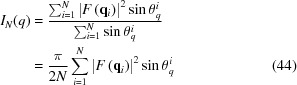needs to be computed until N is large enough, between the limits N _min and N _max, that for each q we get

where ∊ is a small number that defines our error. The value of ∊ is provided by the user (through the Convergence parameter). We chose f = N − pk with k ∈ {1, 2, 3, 4}, where p = 100 for CPU computations and 8192 for GPU computations. In practice, computations are often done up to 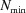, and 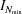is saved. Each time the number of iterations has increased by p from the previously saved curve, another curve is saved to a matrix, which can contain up to four curves. After the first four curves are saved, D+ checks if equation (45) is satisfied. If it is, the computation ends; if not, the number of iterations is increased by an additional p iterations and the last curve is saved. The curves are saved on a first in, first out basis. Each time a new curve is saved, the saved intensity curves are used to check if equation (45) is satisfied.

To uniformly sample the polar and azimuthal angles we use

where u and v are random variates in the [0, 1] range (Weisstein, 2015 ▸). The intensity is then computed by

4.2. VEGAS: an adaptive Monte Carlo integration  

As with numerical integrations in general, integrating the Fourier space intensity does not always result in fast convergence. In some cases (see later), using an adaptive method leads to quicker convergence. To that end, we have included two adaptive integration methods in D+.

Lepage (1978 ▸) introduced an effective method for a biased sampling for the Monte Carlo integration. In this method, the calculation cost grows linearly with the dimension of the integral. The integration domain is divided into bins. After each step of N evaluations, the bins are resized so that the variance within each bin is roughly the same. This method leads to a faster convergence when certain areas of the integration domain fluctuate faster than others. In the case of scattering data, objects that are long in one or two dimensions (and shorter in the remaining dimensions) have this characteristic and therefore the adaptive integration method can be helpful. The VEGAS method is implemented only for the GPU in D+.

4.2.1. Implementation  

We divide the integration space from equation (46) (u and v) into N _b bins, each with a not necessarily equal volume 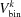. For each bin, the same number of intensity points, ip, are evaluated. The variance in each bin is calculated with the following algorithm.

Per bin, the difference between the ith (unit offset, 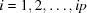) evaluation and the previous mean is

The ith mean is then

and the ith variance is

In the case where there are multiple q values that are calculated simultaneously between two shells (see Section 9.2.3)

where N _q is the number of q points between the shells. The boundaries between the bins are then adjusted such that the variance among the σ² _i values is minimized. Convergence is determined by equation (45).

4.3. Adaptive Gauss–Kronrod  

An alternative integration method that can be used in D+ is the adaptive Gauss–Kronrod quadrature algorithm. The integral is evaluated as a weighted sum at selected points. The Gauss–Kronrod method used is a seven-point Gauss rule with a 15-point Kronrod rule (G ₇, K ₁₅) (Kronrod, 1964 ▸; Laurie, 1997 ▸). The error estimate is given by the relative difference between the two:

Note that the Integration Iterations value in the GUI is in fact the maximum recursion depth and should be of the order of 10 or 15. This method is implemented only for the CPU. It should be used for structures that have between one and three large dimensions.

5. Atomic models  

To calculate the scattering amplitude from a molecule, we take its PDB file representation. Atom identification is based on characters 77, 78 of every ATOM/HETATM entry (PDB v2.0 and greater; Berman et al., 2014 ▸). If an older file format is used, D+ attempts to identify the atom from characters 13, 14 (no charge is assumed in this case; Bernstein et al., 1977 ▸). Other deviations from the standard PDB file format should be amended (or removed from the file) before loading the file into D+. The formal charge is taken from characters 79, 80 (for example, Mg²⁺). The formal charge changes the atomic scattering amplitude and can therefore be important (see Section 5.3). The coordinates of the jth atom are read into r _j and an index that represents the type of atom/ion is saved. There is an index for each of the 209 atoms and ions listed in International Tables for Crystallography (Ibers & Hamilton, 1974 ▸; Marsh & Slagle, 1983 ▸).

5.1. Centering  

As the center of mass of many PDB files is not at the origin, there is an option to find the center of mass and translate the entire object in the opposite direction so that the origin coincides with the center of mass, 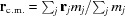, where m _j is the atomic mass of the jth atom. The vector r _c.m. is then subtracted from the coordinates of each atom. Centering of the molecule is enabled by default in D+, but can be disabled before adding a PDB file. Objects that are off-center have an inherent phase in their scattering amplitude. Hence, it is better to compute the same structure after its center of mass is at the origin (see Section 3.1.2).

5.2. Computing the scattering amplitude from solvated atomic models  

The solution scattering amplitude from PDB structures can be computed by using a combination of the following contributions. There are two options to evaluate the scattering amplitude. One option uses dummy atom Gaussian spheres to approximate the volume of solvent excluded by the atoms:

Alternatively, the volume of excluded solvent can be taken into account as a collection of voxels:

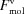is explained in Section 5.3 [equation (56)], 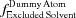in Section 5.5 [equation (63)], 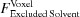in Section 5.8 [equation (68)] and 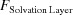in Section 5.9 [equation (70)]. a is equal to 1 unless Solvent Only is indicated in D+, in which case a = 0. If a is set to 0 and, in addition, the mean electron density of the solvent, ρ₀, is set to 0, we get the contribution to the scattering amplitude only from the solvation layer. By loading a PDB file and computing equation (53) using a finite value for ρ_{Solvation Layer} and ρ₀, the solvent contribution to the scattering is computed on the basis of the radii taken from the literature (Fraser et al., 1978 ▸; Slater, 1964 ▸; Svergun et al., 1995 ▸). The volumes of excluded solvent and the solvation layer are then computed on the basis of the chosen radii.

If ρ_{Solvation Layer} is set to 0, when a PDB file is loaded, D+ does not add any solvation layer. If the same PDB file is reloaded and only the contribution from the solvation layer is computed (by setting a = 0, ρ₀ = 0 and ρ_{Solvation Layer} to the mean electron density contrast in the solvation layer, with respect to the bulk solvent), any other method for calculating the solvation layer can be applied, and its contribution can be added to the contributions of the vacuum and dummy atom terms. Splitting the computation in this mode has another advantage. Fitting the value of the solvation layer contrast (ρ_{Solvation Layer} − ρ₀) becomes faster, as it is equivalent to setting ρ_{Solvation Layer} = 1 and fitting the scale factor of the amplitude, and hence does not require a new grid computation for the voxels of the solvation layer. In SOM Section 10, we demonstrate how D+ can be used to compute the contribution to the scattering amplitude from solvation layers of complex structures in a scalable manner. The approach is based on computing the amplitude of the solvated isolated subunits and correcting for spatial overlaps between solvated subunits when they are present in the complex. The corrections are based on the amplitudes from solvated isolated pairs of subunits within the complex and the solvated isolated sub­units. The corrected solvated subunits are then docked into the complex structure. If the same subunit has different solvation overlap corrections then its original assembly symmetry should be divided into smaller assembly symmetries, based on the different solvation overlap corrections. More details and examples are given in SOM Section 10.

5.3. PDB (in vacuo)  

The scattering amplitude of an atom j, in units of −r ₀, is calculated using the five-Gaussian approximation atomic form factor expression (Als-Nielsen & McMorrow, 2011 ▸; Grudinin et al., 2017 ▸)

a _k, b _k and c are the Cromer–Mann coefficients (Ibers & Hamilton, 1974 ▸; Marsh & Slagle, 1983 ▸), given in units of the Thomson scattering length, r ₀ = 2.82 × 10⁻⁵ Å. Note that in D+, however, r ₀ is set to 1.

Given a point in reciprocal space q, and a list of atoms and their coordinates (as in PDB files), the scattering amplitude of the entire molecular structure, containing n atoms, is given by

where r _j is the location in real space of the jth atom.

5.4. Displaced solvent from atomic models  

The displaced solvent contribution may be calculated in multiple ways (Fedorov et al., 1972 ▸; Pavlov & Fedorov, 1983 ▸; Fraser et al., 1978 ▸; Svergun et al., 1995 ▸; Park et al., 2009 ▸; Bardhan et al., 2009 ▸; Poitevin et al., 2011 ▸; Koutsioubas & Pérez, 2013 ▸; Schneidman-Duhovny et al., 2013 ▸; Knight & Hub, 2015 ▸; Grudinin et al., 2017 ▸). One way is to subtract Gaussian dummy atoms localized at the center of each atom (Fraser et al., 1978 ▸; Svergun et al., 1995 ▸; Förster et al., 2008 ▸; Schneidman-Duhovny et al., 2010 ▸, 2013 ▸; Grudinin et al., 2017 ▸); another way is to determine the displaced volume and shape using voxels (Pavlov & Fedorov, 1983 ▸; Bardhan et al., 2009 ▸; Virtanen et al., 2011 ▸). Both methods can be used in D+. Using the Python API of D+ and computer simulations, more accurate methods can be applied [see, for example, Knight & Hub (2015 ▸)].

5.5. Solvent as Gaussian dummy atoms  

The mean atomic volume 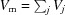and mean atomic radius 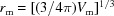are computed on the basis of the list of atoms or atomic groups in the PDB file. 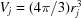is the approximated volume of solvent excluded by the jth atom (or atomic group) and r _j is the published experimental atomic radius of the jth atom (or atomic group) (Fraser et al., 1978 ▸; Svergun et al., 1995 ▸; Grudinin et al., 2017 ▸). When absent, the r _j values were replaced by empirical radii (Slater, 1964 ▸). To match the radii used in CRYSOL (https://www.embl-hamburg.de/biosaxs/crysol.html) (ATSAS 2.8.2; Franke et al., 2017 ▸), we modified the carbon and nitrogen radii to be 1.577 and 0.8414 Å, respectively.

A Gaussian dummy atom is placed at the center of each atom in the PDB file. The electron density of the Gaussian sphere of atom j is

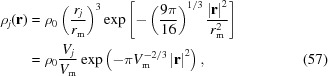where ρ₀ is the mean electron density of the bulk solvent (for example, 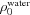= 334 e nm⁻³). The Gaussian electron density profile is normalized so that the total number of excluded electrons, which is given by 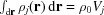, is equivalent to that of a uniform sphere of volume V _j. The reason for using the mean atomic radius, r _m (or the mean atomic volume V _m), in the exponent is to be able to uniformly adjust (and account for) the volume of excluded solvent throughout the entire structure [using equation (60)]. V _m can be slightly varied to better fit experimental data. The scattering amplitude contribution of the Gaussian dummy atom j is then

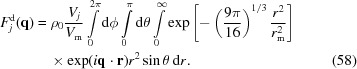The result depends only on the magnitude of the atomic radius (or the atomic volume, V _j), owing to the spherical symmetry of ρ_j(r), and is given by

This expression reproduces the calculations of CRYSOL (ATSAS 2.8.2), which has been extensively used and shown to adequately fit experimental data (Förster et al., 2008 ▸; Schneidman-Duhovny et al., 2010 ▸, 2013 ▸; Svergun et al., 1995 ▸; Grudinin et al., 2017 ▸).

D+ accepts both positive and negative values of bulk solvent electron density, ρ₀. Negative ρ₀ is unphysical. However, when ρ₀ > 0 the contribution of F ^d _j is subtracted from other amplitudes [see equation (61)]. Negative ρ₀ values can only be used to add the contribution of the excluded solvent, F ^d _j [or equation (69)], to other amplitudes. ρ₀ is also subtracted from the electron density of the solvation layer [see equations (53), (54) or (70)]. If there is a solvation layer, negative ρ₀ means that the magnitude of ρ₀ will be added to the electron density of the solvation layer.

To uniformly adjust V _m, each F _j ^d is multiplied by

The default value of c ₁ is 1, corresponding to C ₁(q) = 1. By slightly varying the value of c ₁, the mean volume of solvent excluded by the atoms is adjusted to better fit experimental data, as done in FoXS (Förster et al., 2008 ▸; Schneidman-Duhovny et al., 2010 ▸, 2013 ▸), CRYSOL (Svergun et al., 1995 ▸) or Pepsi-SAXS (Grudinin et al., 2017 ▸). The contribution of atom j to the scattering amplitude in solution is then

The solution scattering amplitude from a molecule, given a list of n atoms whose coordinates are r _i, is

and

5.6. Atomic groups  

The PDB files may contain atomic groups. The type of atomic group is determined by the 14th, 15th and sometimes 16th columns (labeled as CA, CB or CG, for example, corresponding to Cα, Cβ or Cγ) and the 18th to 20th columns that contain the type of amino acid or nucleic acid. This combination determines the type of atomic group (CH, CH₂ or CH₃ in the above example). Other atomic groups are listed in Table 1 of Svergun et al. (1995 ▸). If water molecules are included in a PDB file, D+ will compute their contribution to the scattering curve.

5.7. Implicit and explicit hydrogen atoms  

If hydrogen atoms are included or added to the PDB file (Chen et al., 2010 ▸), D+ will explicitly compute their contribution to the scattering amplitude. The amplitude of the hydrogen atoms is computed on the basis of their position, as listed in the PDB file. In that case, only the contribution from the heavy atom of each atomic group is taken into account (to avoid double counting of hydrogen atoms).

If, however, no hydrogen atoms are included in the PDB file, the contribution of hydrogen atoms will be implicitly taken into account using a five-Gaussian approximation [equation (55)], whose coefficients were obtained as follows. Firstly, the amplitude in vacuum of each type of atomic group was computed by explicitly adding the hydrogen atoms (Chen et al., 2010 ▸) to the heavy atom of the atomic group. The result is a sum of Gaussian functions. Secondly, the coefficients of the five-Gaussian approximation that best fitted each atomic group amplitude were found (see Table 1 ▸), stored and used when needed. Other combinations of coefficients, however, may also fit (Grudinin et al., 2017 ▸).

Table 1. The coefficients for the five-Gaussian approximation for implicit hydrogen atomic groups.

Atomic group	a 1	b 1	a 2	b 2	a 3	b 3	a 4	b 3	c
CH	0.894937	55.7145	0.894429	4.03158	3.78824	24.8323	3.14683 × 10−6	956.628	1.42149
CH2	1.61908	52.1451	2.27205	24.6589	2.1815	24.6587	1.9254 × 10−3	152.165	1.92445
CH3	12.5735	38.7341	−0.456658	−6.28167	5.71547	54.955	−11.711	47.898	2.87762
NH	5.06991 × 10−3	108.256	2.03147	14.6199	1.82122	14.628	2.06506	35.4102	2.07168
NH2	3.00872	28.3717	0.288137	63.9637	3.39248	3.51866	2.03511	28.3675	0.269952
NH3	0.294613	67.4408	6.48379	29.1576	5.67182	0.54735	6.57164	0.547493	−9.02757
OH	−2.73406	22.1288	9.66263 e-3	94.3428	6.64439	13.9044	2.67949	32.7607	2.39981
SH	−127.811	7.19935	62.5514	12.1591	160.747	1.88979	2.34822	55.952	−80.836

Solvent subtraction is done according to equation (59), using the atomic group radii from Table 1 of Svergun et al. (1995 ▸), with the following adjustments to match the radii used in CRYSOL (ATSAS 2.8.2). The atomic group radius, R _AG, was obtained by summing the heavy-atom volume, V _HA, and hydrogen-atom volumes, n _H V _H, where n _H is the number of hydrogen atoms in the atomic group and V _H is the volume of a hydrogen atom. The atomic group volume is therefore V _AG = V _HA + n _H V _H, and its radius is R _AG = (3V _AG/4π )^1/3, in agreement with Svergun et al. (1995 ▸). Fig. S3 and the figures in SOM Section 9.2 show that the results of D+ are in agreement with those of CRYSOL (ATSAS 2.8.2) for atomic models in solution with either implicit or explicit hydrogen atoms.

5.8. Voxelized solvent  

In this method, we equally divide the space occupied by the molecule into voxels of a predetermined size, v (whose default value is v = 0.2 nm, which is smaller than used by Pepsi-SAXS; Grudinin et al., 2017 ▸). For each voxel, we determine whether it contains an atom (or part of one) or not by applying the following algorithm.

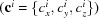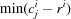(1) Allocate space. The occupied space is defined by going over every atom i, taking its center coordinates , adding and subtracting the atomic radius (r ⁱ) to/from each coordinate, and selecting the minimum and maximum in each of the three dimensions, and 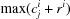, respectively, where j ∈ {x, y, z}. The atomic radii used can be selected (by the user) from the dummy atoms’ (Svergun et al., 1995 ▸), van der Waals (Bondi, 1964 ▸; Mantina et al., 2009 ▸), empirical (Slater, 1964 ▸) or calculated radii (Clementi et al., 1967 ▸). Once the range is determined, it is expanded by 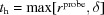, where r ^probe is the Probe Radius and δ is the solvation layer thickness. The minimum and maximum locations are stored as

and

for each j. The space is then allocated, divided into

voxels of volume v ³ and labeled as non-occupied (0 or blue in Fig. 3 ▸).

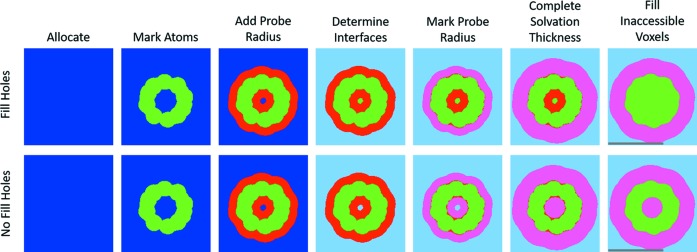
Figure 3.

Stages in determining voxelized solvent and solvation. Here, a slice of C60 is shown as an example of the stages. First the required space is determined, allocated and marked blue (or 0). Second, all voxels within the atomic radius of each atom are marked as excluded volume (green or 1). Third, an additional Probe Radius is added around each atom, marking only blue voxels as red (2). The fourth step is to determine the interfaces between the solvent and the molecule. Depending on how the user chooses to treat ‘trapped’ volume (Fill Holes or not), this is either a trivial swap of blue to light blue (No Fill Holes) or a 3D flood-fill in order to differentiate between inner and outer interfaces. In the case of Fill Holes, the blue voxels that are not changed to light blue are marked as excluded volume (green, 1). The fifth stage marks all red voxels within one Probe Radius of the interface between light blue (3) and red (2) as pink (4). In the sixth stage, the solvation layer thickness is completed from the interface between pink (4) and light blue (3). The final stage marks the remaining red voxels (2) as excluded volume (green, 1). The gray scale bars in the rightmost figures correspond to 1 nm.

(2) Mark all the voxels that contain atoms. For each atom, i, the indices of the lowest neighbor are calculated by 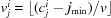for each j. Each voxel within r ⁱ of c _j ⁱ is marked as an atom voxel (1 or green in Fig. 3 ▸).

(3) Mark solvent-accessible layers. Around the lowest neighbor of each atom, v ⁱ _j, each voxel within 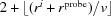voxels for each j is tested. Each voxel within 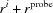of c _j ⁱ is marked as solvation (2 or red in Fig. 3 ▸) if it was previously non-occupied (0 or blue in Fig. 3 ▸). The addition of r ^probe to each atom allows us to simulate a spherical probe that would determine the solvent accessibility as done by Pavlov & Fedorov (1983 ▸).

(4) Outer solvent. If the user selects Fill Holes then any enclosed unoccupied voxels should be marked as excluded volume. To differentiate between the enclosed and outer unoccupied voxels, a 3D queue-based flood-fill algorithm [explained by Heckbert (1990 ▸), for example] labels the outer solvent as 3 (or light blue in Fig. 3 ▸). Any remaining 0 (or blue) voxels will be considered ‘holes’ and marked as 1 (or green in Fig. 3 ▸). If the user did not select Fill Holes then all 0 (or blue) voxels are marked as 3 (or light blue in Fig. 3 ▸).

(5) Mark solvation layer. Find all voxels that are marked as bulk solvent (3 or light blue) and neighbor a voxel marked as solvation (2 or red). All red voxels within 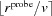voxels of them are marked as 4 (or pink in Fig. 3 ▸).

If 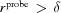then part of the pink (or 4) layer must be marked as light blue (3). Therefore, we find all the voxels that are marked pink (4) and neighbor light blue (3). All pink voxels within 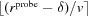voxels of them are marked as light blue (3).

If 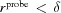then the pink (4) layer must be expanded by the difference. Therefore, we find all the voxels that are marked pink (4) and neighbor light blue (3). All light-blue voxels within 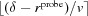voxels of them are marked as pink (4).

To ensure we did not accidentally change a green (or 1) to pink (or 4), we repeat step 2.

(6) Reduce voxels to irregular boxes. To shorten the computation time, when possible, voxels are binned into larger irregular rectangular boxes.

The scattering amplitude of the jth voxel (or box) of dimensions ω_j, τ_j and μ_j, whose center is at r _j ^Voxel, is (Székely et al., 2010 ▸)

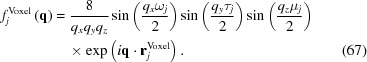The total scattering amplitude of the excluded voxels is then a sum over the green voxels,

and the scattering amplitude of the molecule in the solution is

5.9. Solvation layer  

To determine the scattering amplitude of the solvation layer, we continue and expand upon the method in Section 5.8. The contribution of the solvation layer to the scattering amplitude is computed as the sum over the scattering amplitudes from the collection of voxels composing that layer (pink voxels). The scattering amplitude of the solvation layer voxels is

The scattering amplitude of the solvated molecule is

where 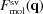may be used instead of .

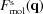By default, D+ sets r ^probe = 0.14 nm, which corresponds to the radius of a water molecule (Richards, 1977 ▸). ρ_{Solvation Layer}, in units of e nm⁻³, is set to 0. When ρ_{Solvation Layer} = 0, D+ ignores the contribution from the solvation layer. Other values should be assigned by the user as relevant. SOM Section 9.3 shows validation tests of the solvation layers of atomic models, by creating atomic models that form hollow or filled spherical structures. The scattering curves from the solvated atomic models were then compared with the scattering curves from the corresponding geometric models to which solvation layers were added. In Figs. 5 and 6 (Section 13.2) and S3, and in SOM Section 10, there are examples in which the contribution of the solvation layer was taken into account.

5.10. Anomalous scattering  

In modern synchrotrons, the energy of the X-ray photons can be selected by a monochromator. If scattering experiments are repeated at multiple wavelengths and the structure contains atoms whose resonant scattering terms, f′ and f′′, respond to the energy scan, additional structural information can be derived. When modeling atomic structures with anomalous scattering, the scattering amplitude from an atom j in units of −r ₀, in vacuum, is given by (Als-Nielsen & McMorrow, 2011 ▸)

Therefore, one needs to provide input in the form of f′_j(λ) and f′′_j(λ) for all the atoms whose resonant scattering terms have a significant contribution to the scattering signal in the relevant X-ray wavelength. In D+, this is done via a text file loaded after loading the PDB file of the atomic structure. D+ uses the input without any sanity checks, so it is the user’s responsibility to ensure that appropriate values are used. In particular, note that in D+ r ₀ is set to 1 when f ⁰ _j(q) is computed. The input is an {f′_j, f′′_j} pair with either a list of the atom indices in the PDB file or an ion type [equation (72) will be applied to all ions of that type]. This type of input may be obtained from X-ray fluorescence spectra and the computer program CHOOCH (Evans & Pettifer, 2001 ▸). See the User’s Manual of D+ (https://scholars.huji.ac.il/uriraviv/book/users-manual) and Usage Examples (https://scholars.huji.ac.il/uriraviv/book/examples) for more details.

The anomalous scattering amplitude in solution from atom j is

and that from a molecule is

5.11. DebyeCalculator  

DebyeCalculator (https://scholars.huji.ac.il/uriraviv/software/debyecalculator) is a separate tool for computing the solution scattering intensity from atomic models using the Debye formula (Debye, 1915 ▸):

The Debye formula applies for spherically symmetric scatterers, which is the case for atoms. f _i ^c(q) and f _k ^c(q) are the atomic form factors in the relevant experimental conditions (vacuum or solution, c ∈ {v, s}) of the ith and kth atoms, respectively, and r _ik is the distance between the atoms i and j. The advantage of the Debye approach is that the orientation average is computed analytically; hence the accuracy is better than that of any of the other methods, which numerically compute the orientation average (Ginsburg et al., 2016 ▸; Svergun et al., 1995 ▸; Watson & Curtis, 2013 ▸; Schneidman-Duhovny et al., 2010 ▸; Grudinin et al., 2017 ▸).

DebyeCalculator is provided with D+ and computes the scattering intensity using equation (75). DebyeCalculator runs on both CPUs and GPUs. The results of DebyeCalculator and D+ are similar when using sufficient integration iterations and grid density in D+. Comparison tests between CRYSOL (Svergun et al., 1995 ▸), DebyeCalculator and D+ are presented in SOM Section 9.2.

6. Geometric form factors  

Leaves in the hierarchical tree structure (Fig. 1 ▸) may also be geometric models. D+ computes the scattering amplitude of uniform rectangular cuboids, multiple uniform spherical shells, concentric uniform or Gaussian hollow cylinders, and helices with a circular cross section (Székely et al., 2010 ▸). Each layer or shape can have uniform electron density contrast with respect to the solvent. In X+ (Ben-Nun et al., 2010 ▸, 2016 ▸), which is a single-geometry software, the form factor of infinite flat slabs or infinitely long cylinders can be computed. In contrast, D+ can add different (geometric or atomic) models to one another. As adding infinite models is unphysical, only models with finite dimensions can be computed in D+. In SOM Section 9.1, the geometric models in D+ are tested and compared with the equivalent models in X+ (Ben-Nun et al., 2010 ▸, 2016 ▸). To cross validate the accuracy of the geometric models of D+, the scattering curves from the geometric models were compared with their corresponding atomic models. The atomic models contained oxygen atoms that were randomly packed into each of the geometric shapes until they filled the shape. The adequate agreement between the models is presented in SOM Section 9.3.

7. Structure factor  

Hierarchical data tree structures often include assembly symmetries, which describe the arrangement in space (shifts and rotations) of identical subunits. The contribution of assembly symmetries to the scattering amplitude (structure factor) may be calculated in the following ways.

7.1. Space-filling symmetry  

If identical subunits are only shifted with respect to one another, as in a finite primitive Bravais lattice, space-filling symmetries can be defined. In three dimensions, space-filling symmetries of subunit j are defined by selecting the xy plane and using the following vectors. A ₁ ^j of length a ^j along the x direction and A ₂ ^j of length b ^j in the same plane. The angle between the two vectors is γ^j. We can then add a third vector A ₃ ^j, defined by its length c ^j and two more angles α^j and β^j, where the former is between the vectors A ₁ ^j and A ₃ ^j, and the latter is between the vectors A ₂ ^j and A ₃ ^j. The angles should satisfy the conditions that the sum of any pair of angles is larger than (or equal to) the third angle and that sinγ^j ≠ 0. D+ checks that both conditions are satisfied. If the sum of two angles equals the third angle, or if sinγ^j = 0, the symmetry is 2D. In this case, the correct usage of D+ is to project the 2D symmetry onto the xy plane. The projection is done by providing the values of a ^j, b ^j and γ^j, setting both α^j and β^j to be 90°, and setting the number of repeating subunits in the third (z) direction to be 1. For 3D space-filling symmetry, the real-space basis vectors are given by

where

and

D+ checks that 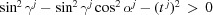. In real space, the unit-cell vectors A _h ^j can then be rotated by a rotation matrix O _j, so that the final unit-cell vectors are a _h ^j = O _j A _h ^j, where h ∈ {1, 2, 3}. If substructure j has a space-filling symmetry with N _h ^j repeating subunits in the 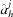directions, the space-filling scattering amplitude, F ^j _sf, is

Here, F _j is the scattering amplitude of repeating subunit j that was rotated by matrix O _j and shifted by a vector T _j. The structure factor, SF^j(q), is given by

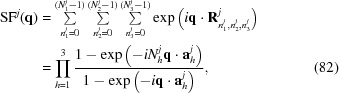where

are the lattice vectors and 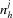are integers.

7.2. Manual and scripted symmetries  

If the orientation 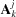and location 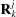of each of n identical subunits of type j are different, D+ enables manual positioning of each repeating subunit. The scattering amplitude, F ^j _man, is then

The positions and orientations can be calculated from a Lua script, taken from a docking list (DOL) file or input manually in the GUI. Each structure-factor contribution may then be recursively used in a hierarchical model (Fig. 1 ▸). Lattice sum validation tests are shown in SOM Sections 9.1 and 9.2. Additional examples can be found in the User’s Manual (https://scholars.huji.ac.il/uriraviv/book/users-manual, Usage Examples (https://scholars.huji.ac.il/uriraviv/book/examples) and Tutorials (https://scholars.huji.ac.il/uriraviv/book/tutorials-d).

8. Mixtures of uncorrelated populations  

The scattering intensity from a mixture of multiple uncorrelated populations is equal to the weighted sum of their intensities, where each weight is the corresponding population molar fraction (Als-Nielsen & McMorrow, 2011 ▸; Spinozzi et al., 2014 ▸):

N _P is the number of populations. S _i ≥ 0 and I _i are the normalized mass fraction and intensity of the ith population, respectively. Equation (85) slightly differs from equation (7) of Konarev et al. (2003 ▸), which uses volume fractions rather than normalized mass fractions.

To simplify this model for optimization, we impose an implicit normalization constraint:

The weighted sum [equation (85)] is then multiplied by the total mass of the measured sample. The motivation behind this modification is twofold:

(1) To disallow physically incoherent S _i weights (for example, negative values).

(2) To simplify the total mass parameter as a scale constant multiplier. This causes the derivatives of I(q) in equation (85) (used when fitting, see Section 9.1) to be faster to compute.

To formulate the new model, we define 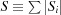and σ_i ≡ |S _i|S ⁻¹. The new model is thus given by

Equation (87) is equivalent to equation (85).

9. Important features  

In our implementation of the above algorithms, D+ employs several computational components. Below, we highlight some of the features that make D+ computationally efficient and versatile.

9.1. Fitting  

Whereas all of the above sections deal with generating a single evaluation given a set of structural parameters, the purpose of this feature is to allow the fitting of a structural model to experimental data. To fit models to data, we incorporated Ceres Solver (Agarwal et al., 2016 ▸) to solve the least-squares problem

where x _i are the model mutable variables. In our case, the sum over i is just a single term (in Ceres Solver terminology, there is only one residual block). f _i(·) is a cost function that computes the residuals of the objective function (and calculates the Jacobian when asked). 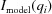Before fitting, the cost function is initialized with the experimental scattering intensity , an object that computes the expected scattering intensity (as explained in the sections above) and a functor that evaluates the residuals. The residuals, f _i, can either be the normal 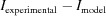, a ratio

where the ± is chosen so that the residual is non-negative, or a logarithmic residual,

ρ_i(·) is a loss function that can be chosen by the user. The complete standard set of loss functions (trivial, Huber, soft L1, Cauchy etc.) from Ceres Solver (http://ceres-solver.org/nnls_modeling.html) is available in the GUI of D+. Cauchy, for example, provides a robust curve fitting as it can deal with outliers in the data. The method with which Ceres Solver tries to minimize ρ_i(·) can also be chosen from several methods including BFGS, LBFGS, Levenberg–Marquardt or Dogleg. When using Levenberg–Marquardt, upper and lower bound constraints for each mutable fitting parameter are also supported by Ceres Solver. To deal with noisy function evaluation (owing to Monte Carlo-based orientation averaging), we use the Ridders adaptive numeric differentiation method in Ceres Solver (Ridders, 1982 ▸).

The variables that control the fitting algorithms are Step Size, which sets a limit on the fraction by which mutable parameters can be changed, Iterations, the maximum number of fitting attempts, Convergence, the cost function cutoff standard, and Der eps, which regulates the value of Step Size on the basis of the change in the value of the cost function. D+ can find the local minimum for a plausible set of initial guess model parameters. Finding the initial guess should be done by several Generate iterations. Alternatively, one can use the Python API of D+ to generate the scattering curves and perform the optimization or fitting using the available fitting algorithms of Python, which may also include global fitting algorithms [see Section 9.3 and the examples in the Python API README file (https://dplus-python-api.readthedocs.io/en/latest/README.html#readme)].

Fitting with certain options (for example, the thickness of a solvation layer, as explained in Sections 5.8 and 5.9) can take a significant amount of time (hours). When this is the case, it is better to use educated guesses. For small solvated structures (like soluble proteins), fitting with CRYSOL or FoXS (https://modbase.compbio.ucsf.edu/foxs/) is faster than with D+ as no grids are computed in those programs. Examples and validation tests of the fitting algorithms are shown in Fig. 5 (Section 13.2) and SOM Section 9.4.

9.2. Parallel computation and optimizations  

Even when using RGs to speed up the computations, the computations are relatively long and can take anywhere from a second or so to several hours. We employed multiple methods to reduce the computation time.

9.2.1. Precalculation  

Often, there are calculations that are repeated many times that can be cached and retrieved from memory, saving computation time. For example, when calculating the scattering amplitudes of a given θ_qϕ_q plane, all the atomic form factors for each ion/atom are exactly the same, with the contribution differing only by the phase. Additionally, if the atoms’ amplitudes are sorted before the computations, the calculation can be done once per ion/atom type, improving some branch prediction or even eliminating it entirely.

When computing the amplitude of assembly symmetries, multiple copies of identically oriented substructures are identified and listed together [equation (11)]. This can significantly reduce the number of lookups to memory during the amplitude computations, speeding them up in an almost linear manner. This is particularly important when using the direct or hybrid methods for orientation averaging, as the number of amplitude evaluations is usually much higher in the simple amplitude computations [equation (41)].

9.2.2. Parallelization  

The computations of the amplitude RGs are ‘embarrassingly parallel’, meaning that for each point on the grid the exact same calculation is performed, differing only in q. Modern GPUs are geared towards quickly computing tasks of this type. Speedups, compared with a regular CPU processor, can be between one and four orders of magnitude. The speedup depends on the choice of hardware, the algorithm and the implementation (Ben-Nun et al., 2015 ▸; Rubin et al., 2015 ▸).

For most of the grid operations (leaf and symmetry amplitude calculation, orientation averaging) a GPU kernel was written using CUDA (https://www.geforce.co.uk/hardware/technology/cuda). The chosen layout of the grid minimizes the number of memory accesses by allowing q to be calculated from a single index (m in Section 3.1). Memory accesses tend to be the bottleneck of GPU kernels and can even make a GPU computation slower than a CPU one. Implementations on the CPU are all parallelized using OpenMP (https://www.openmp.org/).

One of the most commonly calculated functions is 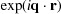. In atomic models, for example, there are many atoms situated at different points in space. By arranging r as an array of structs, this can be vectorized to theoretically achieve up to ×4 to ×8 speedups using streaming SIMD extensions (SSE) or advanced vector extensions (AVX), where SIMD stands for single instruction, multiple data. We used the Eigen (http://eigen.tuxfamily.org/index.php?title=Main_Page) library for the vectorization of the trigonometric functions (Guennebaud et al., 2010 ▸).

9.2.3. Batch integration  

Our RG is arranged in concentric layers. In order to evaluate the amplitude at a point between layers, we first interpolate multiple times in the four layers surrounding that point (two on either side). During the numerical orientation averaging, many points need to be evaluated. In order to minimize the number of accesses to the RG, the final interpolation (along the q direction) is used to evaluate the amplitude at all the desired q values (Fig. 2 ▸). Thus, if there is an experimental measurement at every multiple of 0.0125 nm⁻¹ and the RG is spaced every 0.1 nm⁻¹ then D+ gets the amplitude of eight points at once. The convergence criterion is simply that all of the points are individually converged. This results in an approximately 8× speedup in this example.

9.3. Interfaces  

D+ comes with a full-featured user-friendly GUI for Windows based on the .NET framework. This allows interactive construction of models and helps the user gain understanding of how all parameters affect the structure using visualization as well as the scattering intensity (see Fig. 4 ▸).

Figure 4.

A screenshot of the D+ GUI. The pane positions are all customizable. The user can visualize the structure being modeled alongside its SAXS scattering profile against data.

The actual calculation unit is separate from the GUI and can be compiled on both Windows and Linux. Communication between the GUI and the separated backend is done via JSON (https://www.json.org/) and can be easily set up behind a web server in a scalable manner. In addition to a stand-alone backend, there is a Python wrapper to D+ (https://scholars.huji.ac.il/uriraviv/book/python-api), allowing easy integration into many other models, simulations or advanced tools to perform more involved analyses, including, for example, expressing model parameters by rigorous physically based link functions, accounting for polydispersity in various ways and applying various fitting algorithms (Spinozzi et al., 2014 ▸). The amplitude of the grid can be exported and used in many different ways, for example, by multiplying it externally by any lattice sum or structure factor function, and loading the resulting grid amplitude back into D+ for orientation averaging.

10. Accessory tools  

10.1. PDBUnits  

PDBUnits (https://scholars.huji.ac.il/uriraviv/book/pdbunits) is an accessory software tool for automatically finding the orientation and translations (assembly symmetry) of repeating subunits in a complex supramolecular structure. The input of the tool is (1) the complete structure represented by a PDB file, (2) the structure of a subunit, represented by a smaller PDB file, at a specific orientation (that we shall call the ‘original’ orientation) and (3) the tolerance, given by the maximum root-mean-squared-displacement value within which repeating subunits can be considered similar. The program reads the PDB file of the complete structure and finds all the instances of the subunit. If subunits are split at different locations in a PDB file, the parts should be combined into complete subunits before using the tool. For each instance, the rotation and translation with respect to the original subunit are computed. The tool exports the assembly symmetry of each kind of subunit as a docking list (DOL) text file, which is the required input for D+ in order to compute the entire structure using the RG algorithm (Ginsburg et al., 2016 ▸). More details about the tool are provided in SOM Section 3.

In some cases, before using D+, it is helpful to find the principal axes of an atomic structure (using the algorithm explained in SOM Section 4; Jolliffe, 2002 ▸) in order to align subunits with respect to one another.

10.2. Suggest Parameters  

Suggest Parameters (https://scholars.huji.ac.il/uriraviv/book/suggests-parameters) is a tool that gets as an input 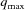and the x, y and z coordinates of the point, P, that is most distant from the origin in the structure for which grids are going to be used. In the current version, 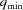is assumed to be zero. If grids are used for the entire structure, P should be the most distant point in the entire structure. However, when the hybrid method is used, P should be the most distant point in the part of the structure for which grids are used.

The tool computes the distance, L, of the most distant point from the origin. It can then compute, using equation (33), the suggested Grid Size for computations that use a grid.

The tool also suggests an integration method and integration parameters, like the number of Integration Iterations that should be used in D+. If the diameter of the sphere that envelopes the structure is larger than L, the x, y and z coordinates should be such that the resulting L will be that diameter. In that case, the integration parameter may not be optimal. The fitting method and fitting parameters are also suggested. In any event, the suggested parameters are only a guide or a first approximation. In practice, higher values might be more appropriate for optimal results.

11. Validation tests  

In our earlier paper (Ginsburg et al., 2016 ▸), several validation tests of the RG algorithm used in D+ and a comparison with other programs, when relevant, were presented. Here we significantly increased the number of tests to cover a much wider range of computational options in D+. SOM Section 9 shows several dozen tests and cross validation tests that D+ successfully passed. Both atomic and geometric models were examined and compared with other programs (Svergun et al., 1995 ▸; Ben-Nun et al., 2010 ▸). Similar structures were computed in several different ways in D+ and compared with one another.

Different combinations of ways for (1) defining assembly symmetry (space-filling, scripted, manual or using a DOL file), (2) computing the scattering amplitude (using grids, or the direct or hybrid methods), (3) performing orientation average integration (Monte Carlo, Vegas Monte Carlo or Gauss–Kronrod), and (4) processing computations though CPU or GPU were compared within D+ and then with the Debye formula (using DebyeCalculator), CRYSOL (ATSAS 2.8.2) or X+ as relevant. D+ returned all the expected results (Svergun et al., 1995 ▸; Ben-Nun et al., 2010 ▸, 2016 ▸). Atomic models were compared with their corresponding geometric models. In particular, the solvation layers of atomic models forming spherical or hollow spherical structures were tested and compared with the equivalent geometric models. The fitting algorithms of D+ were also tested (SOM Section 9.4) and gave adequate results.

12. Program modules and workflow  

Fig. 4 ▸ shows the GUI interface of D+. The main window provides access to basic operations including loading experimental signals and precomputed models, exporting and importing model parameters, amplitudes and graphs, controlling the program layout (or restoring its default layout and/or parameters), launching the accessory tools of D+ (PDBUnits and Suggest Parameters), configuring a server, and getting help.

The workflow in D+ starts by defining the structure by creating the hierarchical tree. The tree contains subunits (the leaves) and assembly symmetries (the nodes), which provide information on how each repeat of a subunit is translated and rotated in space. This stage is done through the Domain View window, containing the list of geometric or atomic Models. Mixtures can also be analyzed by adding Populations in the same window. For any selected subunit Model, its feature parameters are provided through the Parameter Editor. The Symmetry Editor is then used to define the positions and orientations of the subunit repeats.

The next stage includes defining computational parameters in the Preferences pane. The orientation average integration method and convergence criterion are defined, as well as the q range and some of the 3D View graphics parameters. To fit a model to data, the fitting algorithm, the loss and cost functions, and the fitting progress and convergence criteria should be selected in the Fitting Preferences pane. The Controls pane enables one to starts the computation itself and control the 3D View of the computed structure. The results are presented in a separate 2D Graph pane.

More advanced features [see Louzon et al. (2017 ▸) for an example] are accessed through the Script Editor by writing Lua scripts (https://scholars.huji.ac.il/uriraviv/book/examples) or through the Python API (https://scholars.huji.ac.il/uriraviv/book/python-api). More details are provided in the User’s Manual (https://scholars.huji.ac.il/uriraviv/book/users-manual).

13. Usage examples  

Usage examples can be found in our recent publications (Ginsburg et al., 2017 ▸; Louzon et al., 2017 ▸; Asor et al., 2017 ▸, 2019 ▸; Eisenberg et al., 2017 ▸; Shemesh et al., 2018 ▸). To further validate and demonstrate the use of D+, we measured and analyzed the scattering curve from lysozyme and microtubule (MT) structures in solution. Lysozyme is a soluble stable protein that has been well investigated (Levartovsky et al., 2018 ▸) and serves as a validation of atomic models in D+ by comparing the results of D+ with both experimental data and results from other software (Knight & Hub, 2015 ▸; Schneidman-Duhovny et al., 2010 ▸; Svergun et al., 1995 ▸).

MTs are made up of αβ-tubulin heterodimers that dynamically assemble into hollow nanotubes composed of straight protofilaments. Tubulin rings may also form under certain conditions (Díaz et al., 1994 ▸). MT dynamics are facilitated by hydrolysis of guanosine-5′-triphosphate (GTP). Cryo transmission electron microscopy (cryo-TEM) structures of dynamic MTs with 3.5 Å resolution were recently published (Alushin et al., 2014 ▸; Hyman et al., 1995 ▸). In the cryo-TEM studies, the structure of MTs with 14 protofilaments was analyzed. There is, however, a distribution of MT protofilament number that varies with conditions (Raviv et al., 2007 ▸; Andreu et al., 1994 ▸; Pierson et al., 1978 ▸; Wade et al., 1990 ▸; Cueva et al., 2012 ▸; Burton et al., 1975 ▸; Andreu et al., 1992 ▸; Choi et al., 2009 ▸; Chrétien & Wade, 1991 ▸; Ginsberg et al., 2017 ▸).

High-resolution synchrotron X-ray scattering from solutions of dynamic MTs (in the presence of 4 mM GTP and in the absence of stabilizing agents), GMPCPP-stabilized MTs and Taxol-stabilized MTs were measured and analyzed (Ginsburg et al., 2016 ▸, 2017 ▸). D+ was used to compute the expected scattering curves in solution, by docking the atomic model of tubulin dimer (Alushin et al., 2014 ▸) onto a three-start left-handed helical lattice (Mandelkow et al., 1986 ▸) where the atomic dimer model, the pitch (12.195 ± 0.03 nm), the radius (11.940 ± 0.03 nm) and the dimer orientations were derived from PDB ID 3j6f (Alushin et al., 2014 ▸), using algorithms explained by Ginsburg et al. (2016 ▸, 2017 ▸) and in SOM Section 2. In PDB ID 3j6f, the number of protofilaments was fixed at 14. We then extended our earlier analysis (Ginsburg et al., 2016 ▸) and took into account MT structures containing 12, 13, 14 and 15 protofilaments (Ginsburg et al., 2017 ▸; Chrétien & Wade, 1991 ▸). We determined the radii, the pitch and the distribution of protofilament number that best fit the scattering data from a solution containing dynamic MTs. However, the solvation layer was not taken into account. Here we extended the earlier analysis (Ginsburg et al., 2016 ▸, 2017 ▸) by taking into account the solvation layer of the entire MT structure. Initially, the scattering amplitude of the solvated subunits was computed. We then subtracted the scattering amplitude from the various overlap regions of the solvation layers, as explained in SOM Section 10.2. D+ is the only software that can compute the atomic model of long solvated MTs. Hence, in this case, the validation was done by comparison with experimental data. The approach for solvation layer computations was also tested within D+ for the case of atomic spherical and hollow spherical models (in SOM Section 9.3), and for the case of a tubulin ring (SOM Section 10.1) which is sufficiently small that the solvation layer of the entire structure can be computed from a PDB file of the complete tubulin ringv (Shemesh et al., 2018 ▸). The examples discussed in this section and additional examples are available through our web site (https://scholars.huji.ac.il/uriraviv/book/examples) and in our Tutorials (https://scholars.huji.ac.il/uriraviv/book/tutorials-d).

13.1. Materials and methods  

13.1.1. Materials  

Lyophilized powder of lysozyme protein from chicken egg white was purchased from Sigma–Aldrich (catalog No. L6876-1G, Israel). Lysozyme was dissolved in 50 mM sodium acetate buffer that was adjusted to pH 4.5 at a protein concentration of 20 mg ml⁻¹ [for more details see Levartovsky et al. (2018) ▸].

Tubulin was purified from porcine brains by three polymerization/depolymerization cycles. The first cycle was at low salt (Farrell & Wilson, 1984 ▸; Ringel & Horwitz, 1987 ▸) and the other two cycles were performed in a high-molarity buffer (Castoldi & Popov, 2003 ▸). Details of the tubulin purification protocol are provided by Shemesh et al. (2018 ▸).

13.1.2. Methods  

Solution X-ray scattering measurements were performed using an energy of 10 keV at the ID02 beamline (headed by T. Narayanan) of ESRF (Grenoble), at the P12 EMBL BioSAXS beamline (D. Svergun) of PETRA III (DESY, Hamburg) and at the SWING beamline (J. Perez) of the Soleil synchrotron (Gif-sur-Yvette), or with our in-house spectrometer, using an energy of 8 keV. Detailed experimental descriptions of these setups were provided elsewhere (David & Pérez, 2009 ▸; Blanchet et al., 2015 ▸; Van Vaerenbergh et al., 2016 ▸; Nadler et al., 2011 ▸; Louzon et al., 2017 ▸; Fink et al., 2017 ▸). The intensity frames were normalized to the intensity of the transmitted beam, azimuthally averaged (Hammersley, 2016 ▸) and background subtracted as explained below, in SOM Section 5 and in our earlier publications (Ginsburg et al., 2016 ▸, 2017 ▸).

The dynamic MT solution was obtained and measured as explained by Ginsburg et al. (2017 ▸). Briefly, 0.2 mM tubulin in BRB80 buffer [80 mM 1,4-piperazinediethanesulfonic acid, 1 mM MgCl₂, 1 mM ethylene glycol-bis(2-aminoethyl ether)-N,N,N′,N′-tetraacetic acid, adjusted to pH 6.9 with KOH] with 4 mM GTP was incubated at 309 K for 30 min. An aliquot of the resulting dynamic MT solution was measured in a flow cell, with subsequent centrifugation at 20 800 g, at 309 K for 30 min, and an MT pellet was obtained. The supernatant, which contained coexisting small tubulin assemblies, was measured through the same spot in the flow-cell capillary (Fig. S2A). The scattering curve of the supernatant was then subtracted from the scattering intensity of the MT sample (Fig. S2B). The scattering curves from the MT solution and the scattering curve from the supernatant are presented in Fig. S2.

13.1.3. Hardware architecture  

Computations and tests were performed on Windows computers with an Intel Core i5 3470 3.2 GHz CPU and an NVIDIA GeForce GTX Titan GPU card, or Intel Core i5 4590 3.3 GHz CPU and an NVIDIA GeForce GTX Titan Black GPU card. GeForce GTX 1070, GTX 970, NVIDIA TESLA K80 and GTX 960 cards have also passed our tests. The backend was tested via JSON on a Linux computer with an Intel Core i7-5930K 3.5 GHz CPU and a GeForce GTX 980 GPU card as well as on a Tesla P100 card.

13.2. Results and discussion  

Fig. 5 ▸ shows a background-subtracted solution scattering curve from the 20 mg ml⁻¹ lysozyme protein solution. The calculated scattering curves were based on PDB ID 1lyz (Diamond, 1974 ▸), to which hydrogen atoms were added using PyMOL (Schrödinger, 2015 ▸), and computed by D+ and CRYSOL (Svergun et al., 1995 ▸). The two programs can adequately fit the experimental data and agree with each other in most of the q range. Fig. S3 shows a more detailed comparison between the programs, where solvent is always subtracted as dummy atoms [equation (62)]. In Fig. S3A the original PDB structure (1lyz) is used. Hydrogen atoms are then added to the PDB structure (Fig. S3B). Finally, a solvation layer is taken into account, with a thickness of 0.3 nm and an electron density contrast of 30 e nm⁻³ (Fig. S3C). If H atoms are explicitly added, they are taken into account like any of the other heavier atoms. If H atoms are not added, their contribution is implicitly approximated by modifying the relevant heavy-atom volume of excluded solvent to effectively account for the added hydrogen atoms. Solvation layers are computed in each program in a different way. Therefore, the results slightly differed. Fig. 5 ▸, however, shows that after small fitting adjustments both programs can adequately fit the experimental data. The difference between models with implicit and explicit H atoms is negligible. In SOM Section 9.4 similar tests were repeated with ubiqutin (https://www.sasbdb.org/data/SASDAQ2/) and RNase (https://www.sasbdb.org/data/SASDAR2/) proteins; the scattering data are available in the SASBDB database (Valentini et al., 2014 ▸).

Figure 5.

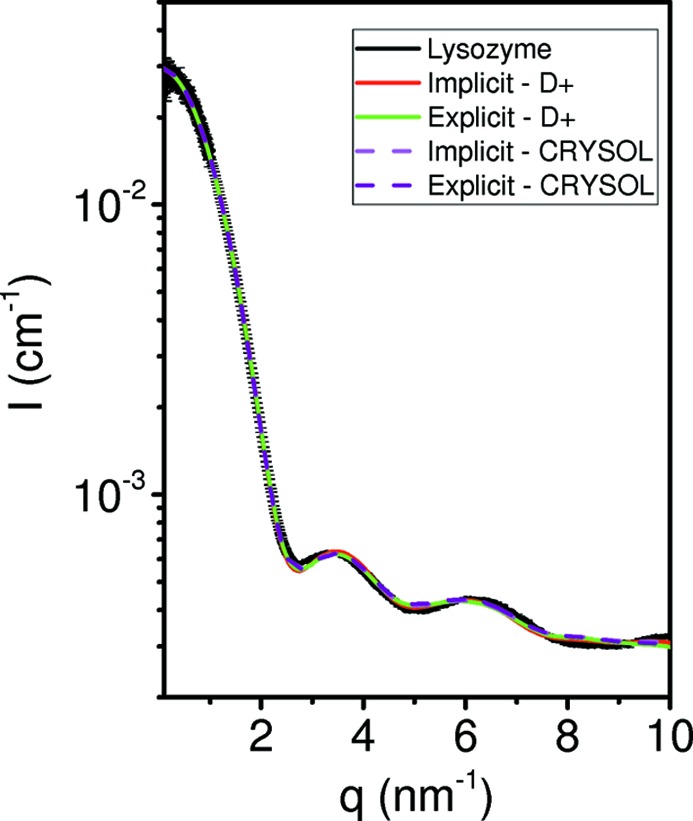
Solution X-ray scattering data and models of lysozyme. Azimuthally integrated background-subtracted scattering intensity as a function of the magnitude of the scattering vector, q, from solutions of 20 mg ml⁻¹ lysozyme in 50 mM sodium acetate buffer, adjusted to pH 4.5, at ambient room temperature. Measurements were performed at the SWING beamline (Soleil synchrotron). The data at q < 1 nm⁻¹ were taken from measurements performed at the P12 EMBL BioSAXS Beamline of PETRA III (DESY, Hamburg), measured under similar solution conditions but at a lysozyme concentration of 2.5 mg ml⁻¹. The solid black curve represents the scattering data. The other curves were based on PDB ID 1lyz. Hydrogen atoms were either implicitly taken into account or explicitly added to the PDB file by PyMol (Schrödinger, 2015 ▸). The broken scattering curves were computed by CRYSOL (ATSAS 2.8.2) (Svergun et al., 1995 ▸), where the maximum order of harmonics was 50 and the order of the Fibonacci grid was 18. The solid curves were computed by D+. In both D+ and CRYSOL the bulk water electron density was set to 334 e nm⁻³ and the contribution of the solvation layer was taken into account. In D+, the grid size was 80, and the orientation average was computed by Monte Carlo integration, using the Mersenne twister algorithm. The solvent Voxel Size was 0.05 nm, the solvent Probe Radius was 0.14 nm and Dummy Atoms were used to account for the volume of excluded solvent [see Section 5.5 and equation (63)]. The fitting algorithm used the normal residuals cost function and the trivial loss function, with 20 iterations, Step Size of 0.01, Convergence Tolerance of 0.01 and Der eps of 0.1 (see Section 9.1). In the implicit model, the solvation layer thickness was 0.2987 nm and its electron density was 337.6 e nm⁻³. The excluded solvent parameter, c ₁, in equation (60) was 1.014, and R ² = 0.998. In the explicit model, c ₁ was 1.012, the solvation layer thickness was 0.301 nm, its electron density was 337.5 e nm⁻³ and R ² = 0.9977. In CRYSOL, in both models, the solvation layer thickness was 0.3 nm and the electron density of the solvation layer was 339 e nm⁻³. In the implicit model χ² = 33.53 and in the explicit model χ² = 35.96. Figs. S38 and S39 in SOM Section 9.4 show two other examples.

Solution X-ray scattering curves from dynamic MTs were measured according to the protocol presented in Section 13.1 and Fig. S2. A more detailed explanation and verification of the protocol is provided in our earlier paper (Ginsburg et al., 2017 ▸). Fig. 6 ▸ presents the background-subtracted scattering data from a dynamic MT solution, which reveals features throughout the measured q range (q _max = 7 nm⁻¹). The computed scattering curves presented in Fig. 6 ▸ are based on atomic MT models, obtained by docking the tubulin dimer structure from PDB ID 3j6f (Alushin et al., 2014 ▸) into the MT three-start left-handed helical lattice. The solvation layer of the tubulin dimer was added to each dimer, and the overlapping solvation layers were subtracted to avoid double counting, as explained in SOM Section 10.2. The thin red curve in Fig. 6 ▸ is based on an MT model with 14 protofilaments, where each protofilament contained 48 tubulin dimers along the long MT axis. To compute the scattering curve from this type of long structure the hybrid method (presented in Section 3.2) is required. No other software can compute this size of atomic model (without the solvation layer and even more so when the solvation layer is added); hence the validation is only against experimental data.

Figure 6.

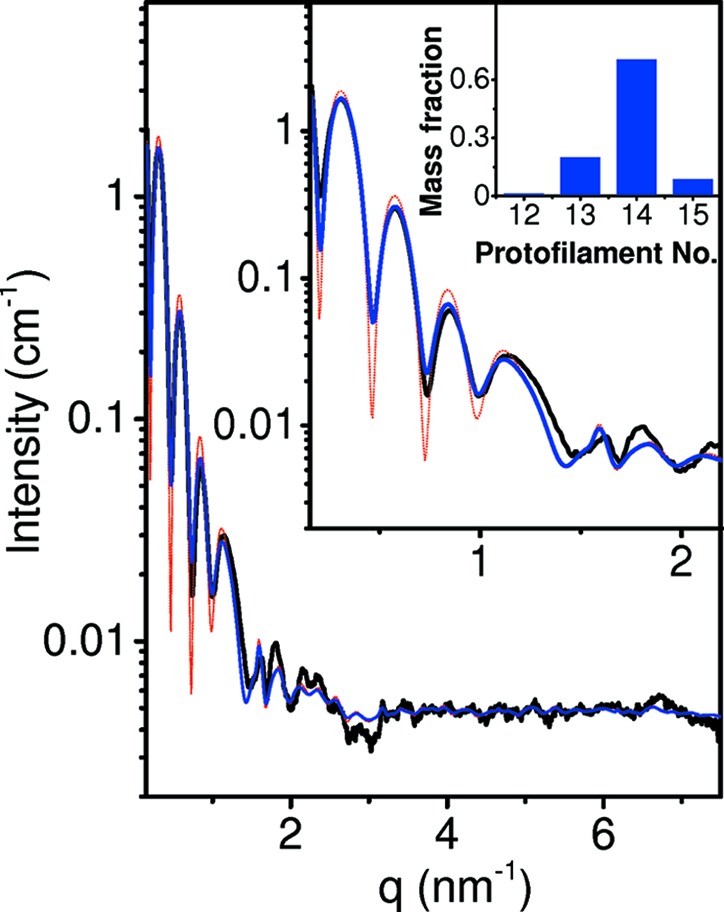
Solution X-ray scattering data and models of dynamic solvated microtubules. Azimuthally integrated background-subtracted scattering intensity (obtained as explained in SOM Section 5 and Fig. S2), as a function of q, from solutions of 0.2 mM tubulin that was polymerized in the presence of 4 mM GTP. The sample was polymerized and measured at 309 K. The black curve represents the scattering data measured at the SWING beamline at the Soleil synchrotron. Similar data were obtained at the ID02 beamline at ESRF. The thin red curve is based on an atomic MT model with 14 protofilaments, each containing 48 tubulin dimers along the long MT axis. The tubulin dimers were arranged in a three-start left-handed helical lattice. The radius and pitch that best fitted the data were 11.9 and 12.214 nm, respectively, in agreement with PDB 3j6f (Alushin et al., 2014 ▸). A solvation layer was added to the entire MT structure, using a Probe Radius of 0.14 nm and the solvation overlap correction method explained in SOM Section 10.2. The shell was 0.28 nm thick and its electron density was 364 e nm⁻³. The thick blue curve is the computed scattering curve, which is based on a fit to a linear combination of similar solvated atomic MT models with radii of 10.2, 11.05, 11.9 and 12.75 nm, corresponding to 12, 13, 14 and 15 protofilaments. The pitch in all the models remained 12.214 nm. A Gaussian resolution function with a full width at half-maximum of 0.01 nm⁻¹ was applied to all individual models forming the blue curve. The larger inset shows the low-q range on an expanded scale. The mass fraction distribution of the population that best fits the data is shown in the smaller inset. Intensity curves were computed on an NVIDIA Titan GPU, using the hybrid method.

The radius and pitch of a single MT helical structure model that best fitted the experimental data were 11.9 and 12.214 nm, respectively, in agreement with PDB 3j6f (Alushin et al., 2014 ▸), which contains nine dimers in a similar symmetry (see Fig. S10 and thin red curve in Fig. 6 ▸).

The thick blue curve in Fig. 6 ▸ is based on a fit to a linear combination of similar atomic MT models with radii of 10.2, 11.05, 11.9 and 12.75 nm, corresponding to 12, 13, 14 and 15 protofilaments, respectively. The pitch in all the models remained 12.214 nm. The mass fraction distribution of the different models, which significantly improved the fit to the data (thin red versus thick blue curve in Fig. 6 ▸), was 20.5 ± 3 and 79.5 ± 3, for MTs with 13 and 14 protofilaments, respectively. This distribution is close to that of an earlier TEM study (Chrétien & Wade, 1991 ▸).

Recently, we have used D+ to analyze various solution X-ray scattering data (Eisenberg et al., 2017 ▸; Asor et al., 2017 ▸, 2019 ▸; Ginsburg et al., 2017 ▸; Chung et al., 2017 ▸; Shemesh et al., 2018 ▸). In particular, we have analyzed solutions of SJW1660 flagellar filaments (Louzon et al., 2017 ▸). The data were fitted to models that took into account the atomic structure of the flagellin subunits. The analysis revealed the exact helical arrangement and the super-helical twist of the flagellin subunits within the filaments. Under osmotic stress, the filaments formed two-dimensional hexagonal bundles. Monte Carlo simulations and D+ were used to determine the fluctuations in the position of the filaments within the bundles, which were consistent with the experimental structure-factor data. The analysis revealed the elastic parameters of the filaments and was validated against osmotic stress data (Louzon et al., 2017 ▸).

14. Performance analysis  

In our earlier paper (Ginsburg et al., 2016 ▸), we compared the accuracy and computation time of DebyeCalculator (see Section 5.11), the golden vector algorithm (Watson & Curtis, 2013 ▸) and CRYSOL (ATSAS 2.8.2) with that of D+. Small (a subunit) and medium-size (ca 100 subunits) atomic models were compared, based on equation (56), which assumes that the electron density (ED) of the surrounding solution is zero (as in a vacuum). CRYSOL was compared with other programs (Virtanen et al., 2011 ▸; Bardhan et al., 2009 ▸; Koutsioubas & Pérez, 2013 ▸; Schneidman-Duhovny et al., 2010 ▸; Poitevin et al., 2011 ▸; Knight & Hub, 2015 ▸; Wright & Perkins, 2015 ▸; Gumerov et al., 2012 ▸; Watson & Curtis, 2013 ▸; Ravikumar et al., 2013 ▸; Schneidman-Duhovny et al., 2016 ▸; Grudinin et al., 2017 ▸) and had accuracy and computation times of the same order of magnitude as the other programs. We therefore consider it sufficient to compare D+ only with CRYSOL. We compared the computation time in solution [equation (62)] and when solvation layers are taken into account [equation (71)]. We created a series of atomic models of tubulin assemblies. Tubulin dimers were gradually added along the three-start left-handed MT lattice, starting from a single dimer (PDB ID 3j6f) and up to 700 dimers (see cartoon in Fig. 7 ▸). Intensity curves were computed in D+ and CRYSOL between q _min = 0 and q _max = 5 nm⁻¹, using a Solvent ED of 334 e nm⁻³ and c ₁ = 1 [equation (60)]. Above 42 dimers, however, CRYSOL could not obtain accurate (relative error of 5% or less) results even when the number of spherical harmonics expansion terms, lm, was set to its maximum value (99).

Figure 7.

Performance analysis of D+ and CRYSOL (ATSAS 2.8.2), using atomic models of tubulin assemblies. The cartoon shows examples of the computed structures. (a) Computation time, C _t, of the atomic models of tubulin assemblies in solution, as a function of the number of tubulin dimers, N _Dimers. Solid black squares correspond to computations done by CRYSOL; the minimum numbers (leading to the shortest computation time) of spherical harmonics expansion terms, lm, used for each N _Dimers are given in Fig. S4. The solid blue diamonds correspond to the upper limit of the computation time of D+ on a single CPU processor. D+ uses all the available CPU processors in parallel, whereas CRYSOL uses a single CPU processor. To properly compare the two programs, we multiplied the actual CPU time of D+ by the number of CPU processors, providing an upper limit on the computation time of D+ using a single CPU processor. The red solid circles correspond to the computation time of D+ on a Titan Black GPU. The optimal computation method was determined in Fig. S5. For large structures (on the right side of the arrows), the hybrid method was used with the following parameters: Grid size: 40 without solvation layers [in (a)] and 60 with solvation layer [in (b)]; Convergence: 10⁻⁴; Integration Iterations: 10⁷; Integration Method: Monte Carlo (Meresenne twister) on a CPU and adaptive (VEGAS) Monte Carlo on a GPU. Smaller structures used grids whose sizes are given in (d). The other parameters were kept the same. (b) C _t as a function of N _Dimers of the same atomic models when the solvation layer of each model was also taken into account. Open symbols match the solid symbols in (a) with similar shapes. The gray open squares correspond to the computation times of CRYSOL. The results of CRYSOL (open gray squares), however, started to be inaccurate, as the structures contained voids in which the solvation layers are not taken into account by CRYSOL. In D+, the computations of the solvation layers were done using the correction method explained in SOM Section 10 and the following parameters: Solvent Probe Radius: 0.14 nm; Solvation Thickness: 0.28 nm; Outer Solvent ED: 364 e nm⁻³. The Fill Holes option was applied, and the Solvent Voxel Size was 0.2 nm (which is smaller than used by other programs; Grudinin et al., 2017 ▸; Svergun et al., 1995 ▸). A much smaller voxel size of 0.05 nm was also tested, and the results are shown in Figs. S6 and S7. (c) The normalized computation time per dimer, given by C _t/N _Dimers C _t ^Dimer, as a function of N _Dimers, where C _t ^Dimer is the computation time of a single tubulin dimer. Solid symbols correspond to the symbols in (a) and open symbols correspond to the symbols in (b). The insets show parts of the graphs on expanded scales. (d) The size of the grids used in the computations in (a) and (b), as a function of the number of dimers. Solid symbols correspond to computations in (a). Open symbols correspond to computations in (b). The effects of larger grid sizes are shown in Figs. S8 and S9.

Fig. 7 ▸(a) shows the computation time, C _t, of the models, in aqueous solution [using equation (62)], as a function of the number of tubulin dimers, N _Dimers. Fig. 7 ▸(b) compares the computation times of the same models, when the solvation layer of each of the structures was also taken into account. The solvation layer was computed for each structure, using equation (71) and the subunit overlap correction methods explained and demonstrated in SOM Section 10.2. D+ could accurately compute all the structures that contained between one and 700 tubulin dimers (larger structures are also possible). In CRYSOL, meaningful results were obtained for up to six dimers (open black symbols). Larger structures (between seven and 42 dimers) contained voids, and hence the results of CRYSOL were inaccurate (these are indicated by open gray symbols).

The results show that, for a single dimer in solution, the algorithm of CRYSOL is faster than that of D+, both with and without solvation layers. As the size of the tubulin assembly increases, the computation time of D+ is significantly shorter with and without solvation layers. We note, however, that fitting to data of a dimer or two dimers, when taking into account the solvation layer, will be slower in D+, as successive evaluations of the hydration layer parameters require computations of new grids, whereas in CRYSOL this is not the case. D+ should be used for larger structures.

Note that the performance of D+ is sublinear in the number of dimers [Fig. 7 ▸(c) ▸] when the number of tubulin dimers is smaller than 300 on a CPU and 700 on a GPU. The computation time per dimer increased for larger structures because in the MT model the structure is long and hence the orientation average started to be longer on the CPU, which uses Monte Carlo integration. The adaptive (VEGAS) Monte Carlo approach used with the GPU helps to reduce the time and keep the performance sublinear in the number of dimers up to 700 dimers. Fig. S5 shows the conditions under which grids were faster than the hybrid method. The hybrid method was used in Fig. 7 ▸ for larger structures. Fig. 7 ▸(d) shows the optimized (minimal) Grid Size as a function of the number of dimers (up to 140 dimers).

Figs. S6 and S7 show the effect of Solvent Voxel Size on the computations times. Figs. S8 and S9 show the effect of Grid Size and the orientation average integration method on the computation times.

15. Conclusions  

In this paper, we introduced our state-of-the-art solution X-ray scattering data analysis software D+. Nearly any complex structure can be modeled in a hierarchical manner and its solution scattering amplitude and intensity curve can be efficiently computed using the reciprocal grid algorithm. 3D grids containing the scattering amplitudes from atomic and/or geometric model subunits are computed and used to calculate the scattering amplitudes from structures containing many subunit repeats. When the scatterers are large, a hybrid method is used, in which grids are computed up to a predetermined point in the hierarchical data tree and used as subunits in direct amplitude computations of the larger structures. D+ can also take into account the X-ray photon energy and thereby be used to compute anomalous X-ray scattering curves from solutions of complex structures at high resolution. D+ has a script editor through which many different kinds of involved models can be defined and computed. The contribution of the solvation layer of complex and large structures can also be taken into account in a scalable manner. The Python wrapper of D+ can be used to compute more advanced models and integrate D+ with various computational tools, modeling or computer simulations and thereby reveal the underlying structural biophysics that leads to the observed scattering data. D+ has been extensively tested and compared with other software and data, and its self-consistency was thoroughly examined (see SOM Section 9). In the future, by applying small adjustments to D+ we shall expand its capabilities to analyze neutron scattering as well as fiber diffraction data. D+ and its source code are freely available at https://scholars.huji.ac.il/uriraviv/book/d-0 for academic users.

Funding Statement

This work was funded by Israel Science Foundation grant 656/16. United States–Israel Binational Science Foundation grant 2016311. Ministry of Science and Technology, Israel grant . Ministry of Economy grant . Hebrew University of Jerusalem grant . Edmond J. Safra Philanthropic Foundation grant . Wolfson Foundation grant . May and Samuel Rudin Family Foundation grant . National Institutes of Health grant R01 AI118933 to Uri Raviv.