Multiparticle adhesive dynamics: Hydrodynamic recruitment of rolling leukocytes

Abstract

The slow rolling motion of leukocytes along the walls of blood vessels mediated by specific receptor-ligand adhesion is important in inflammation and occurs in postcapillary venules over a wide range of wall shear stresses and vessel diameters. The ability of hydrodynamic collisions between cells to induce capture of free-stream leukocytes to a selectin-bearing surface under shear flow was studied experimentally by using a cell-free assay. It was found that carbohydrate-coated spherical beads, representing model leukocytes, tend to attach to the adhesive wall 4–5 cell diameters up- or downstream of a slowly rolling or stationary adhesive bead. A key feature of such “hydrodynamic recruitment” is that only glancing, indirect collisions occurring close to the plane will result in downstream attachment. A direct numerical simulation of cell capture and rolling that includes multiparticle hydrodynamic interactions is shown to reproduce the observed behavior accurately. The theory predicts that hydrodynamic recruitment will occur in the absence of buoyancy effects and over a range of shear rates, suggesting that the mechanism may be important in vivo. This theory is supported by measurements of leukocyte capture in vivo using the hamster cheek pouch model.

The adhesion of cells with surfaces in the microvasculature is important in the inflammatory response (1), lymphocyte homing to lymphatic tissues, and stem cell homing (2). A key step in these adhesive interactions is rolling, in which the adhesion of cells to surfaces slows but does not stop the motion of a cell under hydrodynamic flow. Rolling is caused by the coordinated formation and breakage of receptor-ligand bonds at the front and back of the cell, respectively. Initial adhesive contact in inflammation is mediated by the selectin family of molecules: P- and E-selectin, expressed on the surface of endothelial cells, and L-selectin, which is found at the tips of leukocyte microvilli and their corresponding ligands (3). Rolling leads to firm adhesion and the accumulation of neutrophils at inflammatory sites, the binding of monocytes to atherosclerotic sites (4), and the homing of stem cells to bone marrow (5). Because these physiological phenomena require the accumulation of many cells, a quantitative model of the factors that lead to cell accumulation is needed.

The experimental basis for leukocyte accumulation in vivo has a long history. Addison (6) first observed that 0.5 h after the application of a crystal of salt to the web of a frog's foot, the number of adherent white cells increased considerably and resulted in complete “pavementing” of the vessel wall overnight. Intradermal injection of foreign substances was found to result in leukocyte accumulation near the region of injury in rabbit ear (7) and rat skin (8). Kopaniak et al. (9) quantified the accumulation of neutrophils at the site of intradermal injection of killed Escherichia coli, showing a peak of 7,000 cells per site after 2.5 h and a decrease to zero adhesion after 6 h. Leukocyte accumulation also is associated with ischemia conditions. In a dog model of myocardial ischemia, Engler et al. (10) found via direct histological measurements that leukocytes accumulate early but that the great majority of granulocytes is still intravascular during 1, 3, and 5 h of ischemia. Granger et al. (11) quantified the accumulation of adherent leukocytes during ischemia-reperfusion in cat mesentery. They reported increases of 4 cells per 100-μm vessel length → 18 cells per 100 μm → 28 cells per 100 μm during the transition from control conditions to 60 min of ischemia to 10 min of reperfusion in 30-μm diameter venules. In the acute immune response in hamster cheek pouch, rapid and sustained leukocyte accumulation with minimal extravasation also has been observed (12). Coverage of the microvascular endothelium with adherent leukocytes can occur quite rapidly, within 10 min of exposure of exteriorized rabbit mesentery to zymosan-activated serum (13). In the past decade there has been an explosion of research into the molecular mediators that control leukocyte adhesion and extravasation. Despite this research, the precise physical mechanism by which leukocytes are recruited into adhesive interactions with the vessel wall in these various cases is not well understood.

Recent evidence suggests that the accumulation of leukocytes at inflammatory sites is a collective phenomenon. Walcheck et al. (14) demonstrated that neutrophil-neutrophil interactions cause an enhancement in the accumulation of leukocytes rolling on P-selectin in vitro. Transient tether formation between a rolling cell and one freely suspended in the fluid, mediated by L-selectin, causes free-flowing cells to be captured by the surface and roll adhesively. This capture mechanism tends to align the rolling neutrophils into linear “trains” and is characterized by a time-dependent acceleration of neutrophil accumulation on P-selectin. Alon et al. (15) similarly showed that the L-selectin-mediated recruitment of rolling leukocytes occurs in vitro on inflamed endothelium, purified E-, P-, or L-selectin, VCAM-1, or peripheral node addressin. Specifically, they also demonstrated an enhancement to the rate of leukocyte accumulation due to leukocyte-leukocyte tethering.

Despite the previously cited evidence of leukocyte accumulation in vivo and in vitro, additional evidence from in vivo studies raises questions regarding the precise mechanisms of leukocyte accumulation and leukocyte training. Kunkel et al. (16) studied cell rolling in mouse cremaster muscle stimulated by tumor necrosis factor-α, focusing on identifying the mechanisms of recruitment to clusters of rolling leukocytes. They found that the majority of leukocytes joining a cluster was rolling previously and overtook the slower-moving cluster, whereas only 1.2% of the cells joining the cluster did so directly from the free stream. Their definition of leukocyte-leukocyte interaction used for classification of the observations, a surface-to-surface separation of one-cell diameter, is too small to account for hydrodynamic interactions that are known to persist much farther through the fluid [e.g., these forces attenuate only as 1/r scaled with the radius for spheres under external force (17)]. Finally, Mitchell et al. (18) showed that they could reduce the degree of train formation in vitro greatly by perfusion with whole blood, as opposed to most experiments performed with a dilute suspension of leukocytes in buffer solution.

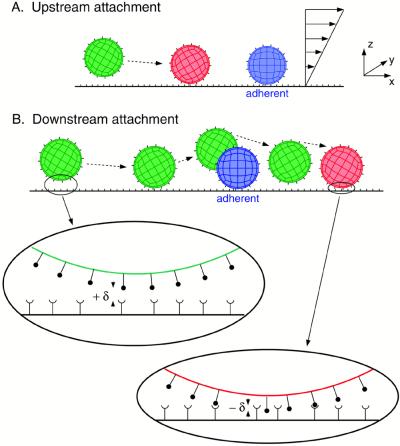
The purpose of this paper is to report on a distinct hydrodynamic mechanism for secondary recruitment of leukocytes that is independent of leukocyte-leukocyte adhesion. Because of hydrodynamic interactions, free-flowing leukocytes approaching an already adherent cell may be deposited and captured by a surface up- or downstream of the adherent cells (Fig. 1). We present detailed measurements of in vitro experiments with carbohydrate-coated spherical beads rolling on P-selectin, which demonstrate that rolling beads can capture incoming beads hydrodynamically. These hydrodynamically induced “secondary attachment” events occur frequently and in a manner that is both regular and predictable by theory. In our analysis we consider only those collisions (where collision is defined as an encounter between a free-stream and bound cell that need not result in molecular contact yet is close enough to significantly alter the trajectory of the free-stream cell) that occur sufficiently far from other beads such that they may be treated as binary interactions. The experimental results are compared with a direct numerical simulation of cell rolling, an extension to the adhesive dynamics algorithm that models each molecular bond as a linear spring with stochastic binding and unbinding based on force-dependent kinetics. We recently have included hydrodynamic interactions between multiple cells in suspension. The model accurately predicts the conditions and cell trajectories that support recruitment observed in vitro and providing insight into the underlying physical mechanisms. Evidence that this mechanism is important in vivo is presented from intravital microscopy of leukocyte recruitment in the hamster cheek pouch.

Figure 1.

Schematic diagram of hydrodynamic recruitment, viewed from the side. A free-stream particle (shown in green) approaches a stationary or slowly rolling particle bound to the surface (shown in blue), close to the wall. The planar boundary is covered with adhesion molecule, and the spherical cells are covered with a specific counterreceptor. Initially, the free-stream (green) cell is too far from the wall to bind with the surface, but as it approaches the bound cell (blue) it is pulled down to a reactive distance from the wall. Binding then can occur (red) before close contact between cells, as shown in A. If binding does not occur upstream of collision, the free-stream cell is lifted off the plane and cannot bind while very close to the bound cell. Downstream of the collision the free-stream cell again is pulled down toward the reactive surface and can attach once the receptors overlap, as indicated in B. Two close-up views of the contact area are provided in which the receptor overlap δ is defined as either positive (no overlap) or negative (finite overlap and possible bond formation). Distances in the x and z directions are exaggerated for visual clarity, and accurate representations of these distances can be found in Figs. 2–4.

Methods

Adhesive Dynamics.

The adhesion between particles and surfaces is modeled using adhesive dynamics (19, 20). The adhesion molecules are modeled as linear springs, and the kinetics of single-bond failure is described by the Bell model (21)

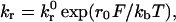1

which relates the rate of dissociation k_r to the magnitude of the force on the bond F. Typical values for the unstressed off-rate k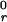 and reactive compliance r₀ are 2 s⁻¹ and 0.4 Å for P-selectin binding with P-selectin ligand-1 (22). The rate of formation directly follows from a Boltzmann distribution for the binding affinity. The solution algorithm is as follows: (i) all unbound molecules in the contact area are tested for formation against the probability P_f = 1 − exp(−k_fΔt); (ii) all the currently bound molecules are tested for breakage against the probability P_r = 1 − exp(−k_rΔt); (iii) the external forces and torques on each cell are summed; (iv) the mobility calculation is performed to determine the rigid body motions of the cells; and (v) cell and bond positions are updated according to the kinematics of cell motion.

Hydrodynamic Interactions.

Unless firmly adhered to a surface, white blood cells can be modeled effectively as rigid spheres, as is evidenced by the good agreement between bead versus cell in vitro experiments (23). Typical values of physical parameters yield Reynolds numbers Re = γ̇a²/ν = O(10⁻³), where γ̇ ≈ 100 s⁻¹ is the shear rate, a = 5 μm is the cell radius, and ν = 1 cS is the kinematic viscosity of the suspending fluid. Thus, inertia can be neglected, and fluid motion is governed by the Stokes equation

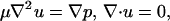2

where u is the velocity, μ is the fluid viscosity, and p is the local pressure. No-slip boundary conditions are enforced at the cell surfaces and at z = 0, the position of the planar wall. We use a technique called the completed double-layer boundary integral equation method (CDL-BIEM), also described by Kim and Karrila (17). Applying the standard boundary element method to the Stokes flow problem produces a Fredholm integral equation of the first kind, which is generally ill-conditioned. By posing the mobility problem in terms of a compact double-layer operator and completing the range with the velocity field resulting from a known distribution of point forces and torques placed inside each cell, one can derive a fixed-point iteration scheme for solving the integral representation of Eq. 2. After reducing the spectral radius of the corresponding discretization, the solution is found to converge rapidly. The presence of a single wall is treated by incorporating the singularity solutions corresponding to a point force near a plane (24). To speed the calculation a coarse discretization is used that does not resolve the cell-cell and cell-plane lubrication forces, which are added from known solutions as “external” forces. As a model of the roughness of the spherical and planar surfaces, it was assumed that both surfaces are covered with small bumps of sufficient coverage to support the particle yet of a dilution that permits the flow disturbance caused by the bumps to be neglected (ɛ_s = 175 nm on the spheres and ɛ_w = 50 nm on the wall). The contact interactions of adhesion and electrostatic repulsion are exerted by the tips of these roughness elements, which in practice comprise a continuous steric layer with thickness equal to the bump height (25). This roughness allows the surfaces to exert contact force on one another despite the fact that mathematically smooth spheres are predicted to remain separated by a lubrication layer of fluid.

Experiments.

Experimental protocol was performed as described by Rodgers et al. (26). SuperAvidin-coated polystyrene microspheres of 5.4-μm radius (Bangs Laboratories, Carmel, IN) were covered with sialyl Lewis^x through a sialyl Lewis^x-PAA-biotin linkage. Sialyl Lewis^x is the functional carbohydrate domain presented by many selectin-binding ligands such as P-selectin ligand-1. The beads then were suspended in a PBS/1% BSA solution. Polystyrene slides were incubated with soluble P-selectin and washed later with PBS and 2% BSA to block nonspecific adhesion. The substrate then was placed in the well of a parallel plate flow chamber. Flow was driven by a syringe pump (Harvard Apparatus), and the system was imaged from below by using an inverted-phase contrast microscope (Nikon). Experiments were recorded with a black and white charge-coupled device camera (Cohu, San Diego) and an SVO-9500MD S-VHS recorder (Sony Medical Systems, Montvale, NJ). Surface coverages were 90 molecules per μm² of sialyl Lewis^x and 180 molecules per μm² of P-selectin, densities that support slow rolling motion at wall shear rates of 40–160 s⁻¹. In each experiment, a dilute suspension (0.1% by volume) of sialyl Lewis^x-coated beads was injected into the flow chamber, where the beads gradually settled, and many started to roll adhesively; others were not adhesive to the surface, and their interaction with already adherent beads could be monitored by using video microscopy.

Results

During an experiment, a dilute collection of adhesively rolling beads (area fraction ≈ 1%) became distributed about the reactive surface in an apparently random configuration. Some of the beads were attached firmly to the substrate, but most were observed to roll at an average velocity of U ≈ 0.015γa. The instantaneous velocity exhibited random fluctuations of order 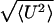/〈U〉 as do rolling leukocytes; this behavior has been described extensively elsewhere (23). Because the rolling beads translate at a much lower velocity than the surrounding fluid, they constantly undergo collisions with unbound beads found on streamlines close to the wall that translate with velocities of O(γ̇a). A small number of such collisions resulted in the free-stream bead attaching to the surface with subsequent rolling of both beads.

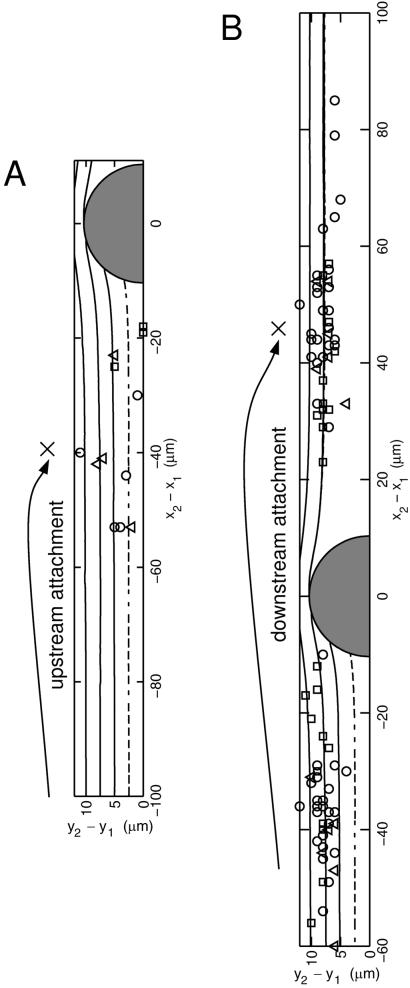
Fig. 2 is a top-view map that shows the type of collisions that resulted in secondary attachment. In Fig. 2A we plot the x-y coordinates of secondary attachment events in which the free-stream bead adhered with the surface before reaching the rolling bead (i.e., upstream of the rolling bead). These data points are compared with collision trajectories computed by using the numerical simulation. Note that these upstream attachment events occurred over the range of Δy displacements and were most common for distances of −53 ≤ Δx ≤ −18 μm. The mechanism for this upstream recruitment of the free-stream bead is discussed below.

Figure 2.

Top view of encounters between a free-stream cell (subscript 2) and an adhesively bound cell (subscript 1). The curves represent trajectories obtained from the simulation, and symbols show coordinates at which secondary recruitment was observed experimentally. Above each plot ↷× shows schematically where cell two binds. Due to symmetry the experimental points have been reflected across the y₂ − y₁ = 0 plane. (A) Upstream attachment. The symbols (□, ○, and ▵) show where a second bead was found to attach to the wall before cell-cell contact is achieved for shear rates γ = 40, 80, and 160 s⁻¹, respectively. (B) Downstream attachment. The symbols at x₂ − x₁ < 0 show the instantaneous cell-cell separations in the x-y plane of free-stream cells that were observed to attach downstream after (near) collision with a bound cell. Simulations predict that the innermost trajectory at Δy₀ = 2.5 μm should not result in downstream attachment.

Fig. 2B presents observations of the more numerous downstream attachment events, at which the free-stream particle underwent near-field hydrodynamic interaction with a rolling sphere before attaching to the surface downstream of collision. The symbols in Fig. 2B located upstream of collision (x₂ − x₁ < 0) show “initial” coordinates of trajectories that went on to result in attachment of the free-stream bead after collision. The symbols located downstream (x₂ − x₁ > 0) show where downstream attachment occurred, and these points were found to be focused around the calculated collision trajectories. Only glancing, i.e., less direct collisions, are found to result in downstream attachment, with only one upstream data point inside of the Δy₀ ≡ (y₂ − y₁)_{t = 0} = 5 μm streamline. This behavior is in direct contrast with upstream attachment, found to occur over the entire range of y as shown in Fig. 2A. The simulation provides detailed information about which incoming free-stream cells are likely to be captured and helps to explain precisely how secondary recruitment occurs.

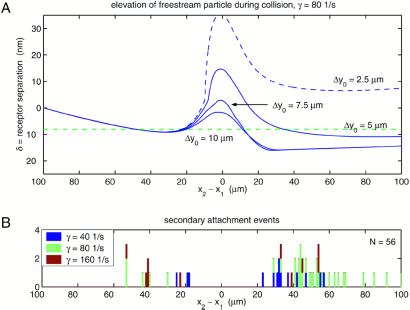
Fig. 3A is a plot of the vertical separation between the free-stream cell and the adhesive lower wall during interaction between particles. Simulations were started with zero initial receptor overlap: z₂(t = 0) = a + ɛ_s + ɛ_w + L_bond = 5.000 + 0.175 + 0.050 + 0.030 = 5.255 μm. This is slightly higher than the height of a stably rolling cell (z₁ = 5.235 μm), which is pulled toward the surface by bonds until the adhesive force directed normal to the plane is balanced by electrostatic repulsion from the plane. This initial separation corresponds to a free-stream velocity of U/γ̇z = 0.664, which is somewhat higher than the experimental free-stream velocity of U/γ̇z = 0.562 ± 0.186 because of simplifications in the simulation: the idealized model of surface roughness, a dilute system of two cells, and a lack of contact friction in the model. Fig. 3A shows how the free-stream cell is lifted slightly off of the plane during approach, a result of the resistance to lateral motion around the rolling cell. For comparison, Fig. 3B shows where attachment was found to occur experimentally. The observations of secondary attachment are grouped at the x position corresponding to the minima in the incoming cell's elevation computed with the simulation. Note that no recruitment was observed while −17 ≤ Δx ≤ 22 μm, i.e., within two cell diameters upstream or downstream of the bound cell. At intermediate distances before Δx < −30 μm and after Δx > 0 collision, however, the free-stream cell is pulled toward the reactive surface by hydrodynamic forces, enhancing the potential for initial bond formation. This vertically directed interaction does not depend on simple gravitational sedimentation (see Fig. 4). Regardless of the precise initial separation of cell two from the surface and the critical distance for adhesive binding, clearly the hydrodynamic interaction between the free and bound cells explains the position of secondary attachment.

Figure 3.

(A) The elevation of a simulated free-stream cell above the reactive surface during collision with an adhesively rolling cell (side view). The four trajectories correspond to different initial displacements in the transverse direction, i.e., Δy₀ → 10 μm is a glancing collision, whereas Δy₀ → 0 is direct. Receptor separation distances ≤0 indicate that ligands on the sphere surface overlap with receptors on the plane and are available for binding. (B) Experimental observations of the location of free-stream bead attachment during binary collisions.

Figure 4.

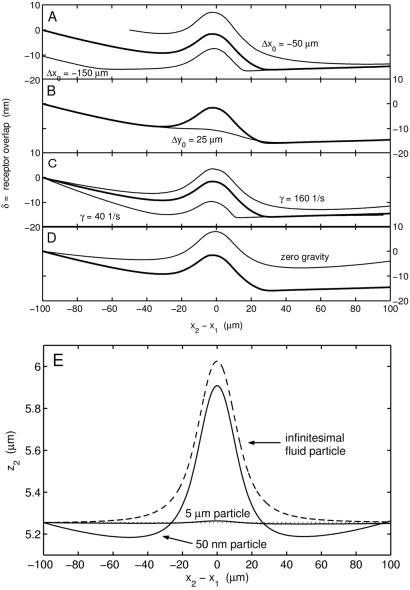
The effect of varying different parameters on the elevation of a simulated free-stream cell above the reactive surface during collision with an adhesively rolling cell (side view). The base case (in bold) is for conditions γ̇ = 80 s⁻¹, Δy₀ = 10 μm, and Δx₀ = 100 μm. (A) Effect of initial separation in the flow direction. (B) Effect of initial separation in the transverse direction. (C) Effect of shear rate. (D) Effect of buoyancy force. Note that the scale for δ is found on alternating sides of the figure. (E) The neutrally buoyant trajectory of D recalculated for either a 50-nm radius sphere or an infinitesimal fluid element. Note also that a finite particle size is necessary for vertical displacement below the initial position.

A series of simulations at different initial separation distances illustrates the mechanics by which cells are captured (Fig. 3A). When Δy₀ ≤ 5.0 μm, the free-stream cell is lifted significantly off of the plane by hydrodynamic interaction with cell one, suggesting that few such cells will be captured. Glancing collisions where Δy₀ ≥ 7.5 μm provide the most favorable conditions for downstream recruitment. These predictions of which trajectories will lead to attachment is in direct agreement with the observed map of attachment events presented in Fig. 2B. Note that the four trajectories shown in Fig. 3A do not diverge significantly from one another until x₂ − x₁ ≈ −20 μm along the collision coordinate, which explains why upstream attachment was observed experimentally to occur over all Δy separations.

The vertical motion of a free-stream cell during collision, which promotes interaction with the reactive surface, occurs over a range of parameters such as initial position, shear rate, and particle density. The effect of initial streamwise position x on receptor overlap (δ) is shown in Fig. 4A. Fig. 4B shows how the vertical displacement during interaction is attenuated when the particles pass by each other with a much larger transverse displacement of five radii. The differences in vertical motion at different shear rates (Fig. 4C) arises from a competition between the time scales of forward convection and sedimentation. In Fig. 4D it can be seen clearly what fraction of the vertical motion is caused by gravity and what fraction is caused by purely hydrodynamic interaction. The two effects are additive, and in the absence of gravity the effect of shear rate on collision trajectories is negligible (data not shown). Because the rolling velocity of cell one is much less than either the free-stream or fluid velocities, the change to these trajectories when cell one is stationary is negligible. Fig. 4E shows the neutrally buoyant trajectory of Fig. 4D, where the free-stream particle has been replaced by either a 50-nm radius particle or an infinitesimal fluid element. This shows how the downward motion of the free-stream particle due to hydrodynamic interaction is caused by the finite size of the second particle and is not reflected in the streamline of flow past a single sphere. Note that because the 50-nm sphere is not within a lubrication distance to the plane it experiences a much greater vertical displacement than the full-sized cell, suggesting that this mechanism may play a role in recruiting smaller blood particles to the surface such as platelets.

Discussion

We have presented experimental and theoretical evidence for a mechanism of recruitment of leukocytes into adhesive contact with a selectin-bearing surface. This mechanism, which we have referred to as “hydrodynamic recruitment” to reflect that it does not rely on any adhesive interaction between leukocytes, occurs over a range of shear rates. Attachment of the free-stream cell can occur both downstream of an adherent cell (after collision) and upstream of an adherent cell (before collision). Attachment can occur a significant distance from the already adherent cell; we observed and calculated a preponderance of capture occurring 40 μm, or four particle diameters, from the adherent cell. This attachment represents a long-range mechanism for capture.

The recruitment demonstrated here is not caused by leukocyte-leukocyte adhesion. With insufficient blocking of nonspecific adhesion by BSA (data not shown), significant bead aggregation can be observed. In such experiments, two colliding spheres will attach to each other on the upstream side of the collision, rotate as a doublet, and result in binding between bead two and the plane directly downstream. This problem has been studied by Whittle et al. (27) in a nonbiological system. Such interactions occurred to a negligible degree in our system, where nonspecific adhesion is minimized as described in Methods.

Our experimental system most closely resembles that of other in vitro studies consisting of two parallel plates with a reactive lower surface (15, 22). The beads sediment to the lower surface because of a slight density difference, (ρ_b − ρ_f)/ρ_f = 0.05, resulting in a locally elevated concentration of beads at the lower wall. This sedimentation promotes cell-wall interactions and cell-cell interactions near the wall in the absence of the non-Newtonian rheology and elevated viscosity that would be associated with a high concentration of beads everywhere in the fluid. In fact, the bulk concentration of beads far from the lower wall is significantly less than the concentration of the initially prepared bead suspension, φ < 0.1% by volume. Although occurring by a different mechanism, the focusing of cells or beads at the lower wall of a flow chamber is analogous to the margination that occurs in vivo. The term margination has been given to the observation that leukocytes tend to collect near the walls of blood vessels and are relatively absent near the centerline. In microcapillaries, Goldsmith and Spain (28) have proposed that leukocytes are marginalized by sudden enlargements of the capillary diameter from 1 to 1.5 times the leukocyte diameter, with groups of red cells previously accumulated behind the leukocyte “plug” moving around one side of the leukocyte while pushing the cell toward the opposing wall. Hence, because of margination leukocyte-leukocyte interactions near the wall are to be expected at a frequency disproportionate to their small numbers in the blood.

The question remains: Is it more appropriate to perform in vitro adhesion experiments in the presence of whole blood rather than dilute suspensions of beads or cells in buffer solution? The margination mechanisms that segregate white cells at the wall and red cells at the vessel centerline in vivo are not present in our flow chamber, which has a much lower surface area/volume ratio than the microvasculature. The in vitro assay is a system that can be controlled easily and as such is useful in identifying subtle mechanisms that may be obscured by the various complexities present in physiological blood flow. Recently we have used in vitro assays and multiparticle adhesive dynamic simulations to probe the leading order effects of cell-cell collisions on the dynamics of selectin-mediated cell rolling as a model of more complex physiological behavior (29). It was found that cell collisions can cause a smoother rolling velocity with fewer pauses by modulating the motion of a rolling cell during the brief forward jumps directly after bond breakage. Further theoretical and experimental work will be necessary to assemble the most important physical mechanisms into a more complete model of blood cell dynamics.

It has been pointed out that gravitational effects are important in vitro but unimportant in vivo (30). This suggests that the hydrodynamic recruitment mechanism described here may be a dominant effect in vivo, where one cannot rely on sedimentation to provide the initial contact necessary for adhesion. Surely leukocyte-erythrocyte collisions are important in certain regions of the circulation, but in other regions of the vasculature a near-wall layer depleted of erythrocytes is well documented (e.g., ref. 31). The collisions examined in this study take place essentially parallel to the wall, requiring a depleted layer little over one-leukocyte diameter in thickness to eliminate leukocyte-erythrocyte collisions during such trajectories. Regions of this size are possible in expansions as suggested by Goldsmith and Spain (28).

The most physiologically realistic experimental system is to visualize the microcirculation directly by using intravital microscopy. Those measurements are being done currently by collaborating laboratories and provide the ultimate test of the relevance of theories developed in idealized representations such as flow chambers. Recent in vivo experiments with the hamster cheek pouch model have found that hydrodynamic recruitment as defined in this paper can account for 42.8% of leukocyte binding events in collecting venules 24–30 μm in diameter compared with 6.6% events mediated by leukocyte-leukocyte adhesion, 22% isolated tethering events, and 28.6% events involving three or more cells (which may also employ the mechanism cited here; I. Sarelius, personal communication). Therefore, the hydrodynamic recruitment described here is a plausible, perhaps predominant mechanism by which leukocytes can accumulate at inflammatory sites. Additional quantitative comparison between our theory and in vivo experimental models is needed to further verify quantitatively that hydrodynamic capture is an important physiological mechanism for capture. Such comparisons must take into account that hydrodynamic interactions can lead to leukocyte capture at separation distances larger than what previous investigators of cell rolling have considered to be possible via direct leukocyte-leukocyte adhesion-mediated capture (16). Therefore, this mechanism may have been overlooked in previous experiments designed to measure mechanisms for secondary recruitment. Also, it is possible that the slight protrusion into the flow field of endothelial nuclei also may act hydrodynamically as a leukocyte nucleation site in vivo in a manner analogous to that of bound leukocytes.

Conclusion

In this paper we have described a computational technique developed to study the adhesive interactions between rigid particles and a planar boundary in a viscous fluid. Application of the multiparticle adhesive dynamics algorithm to the problem of leukocyte adhesion to vessel walls has revealed a mechanism for the capture of free-stream cells once an initial cell has adhered to provide a nucleation site. Predictions of the multiparticle adhesive dynamic simulation were tested with an in vitro assay by using carbohydrate-coated microspheres as synthetic leukocytes. Good agreement was found between the model predictions and experimental observations, most notably a preferred interaction distance of 4–5 cell radii upstream or downstream of the bound cell. The experimental and theoretical techniques described here also may prove useful in technological applications such as the processing of micropatterned surfaces, where the deposition of particles on surfaces at regular intervals is desired.