Abstract
Drug resistance has sharply limited the effectiveness of HIV-1 protease inhibitors in AIDS therapy. It is critically important to understand the basis of this resistance for designing new drugs. We have evaluated the free energy contribution of each residue in the HIV protease in binding to one of its substrates and to the five FDA-approved protease drugs. Analysis of these free energy profiles and the variability at each sequence position suggests: (i) single drug resistance mutations are likely to occur at not well conserved residues if they interact more favorably with drugs than with the substrate; and (ii) resistance-evading drugs should have a free energy profile similar to the substrate and interact most favorably with well conserved residues. We also propose an empirical parameter, called the free energy/variability value, which combines free energy calculation and sequence analysis to suggest possible drug resistance mutations on the protease. The free energy/variability value is defined as the product of one residue's contribution to the binding free energy and the variability of that residue. This parameter can assist in designing resistance-evading drugs for any target.
Keywords: molecular dynamics‖MM/PBSA‖FV value
One of most challenging problems in AIDS therapy is that the HIV virus develops drug-resistant variants rapidly because of the low fidelity of its reverse transcriptase and the high replication rate (1–4). Extensive research in the past decade has been dedicated to designing resistance-evading drugs for the HIV protease, which is critical for the maturation of viral structural (gag) and enzymatic (pol) proteins. The HIV protease is an aspartyl protease and is composed of two symmetric monomers. Many crystal structures of the HIV protease and its complexes with inhibitors have been solved, and extensive clinical resistance data have been accumulated for the five FDA-approved drugs. This information provides the ground for understanding the molecular basis of drug resistance. Here we show that resistance mutations to the five FDA-approved HIV protease drugs occur only at not-well conserved positions, which also interact more favorably with drugs than with the substrate. A combination of conservation analysis and free energy calculations on each protease residue suggests that more potent protease drugs should interact more favorably with well conserved residues, i.e., those catalytically or structurally important residues, especially with Leu-23, Ala-28, Gly-49, Arg-87, and Asp-29. This strategy can be exploited to design resistance-evading drugs for any target. We also propose an empirical parameter, the free energy/variability (FV) value, defined as the product of one residue's contribution to the binding free energy and the variability of that residue, to identify resistance mutations for any HIV protease inhibitors, which can be easily extended to identify critical residues for other protein–protein and protein–ligand interactions.
Methods
(i) Molecular Dynamics (MD) Simulations.
All MD simulations presented in this work were performed by using the amber 5.0 simulation package (5) and the Cornell et al. force field (6) with the TIP3P water model (7). The starting structures of protease–drug complexes are taken from the Protein Data Bank (PDB). The PDB entries are: 1hxb (Saquinavir), 1hpv (Amprenavir), 1hxw (Ritonavir), 1hsg (Indinavir), and 1ohr (Nelfinavir). There are two conformations for Saquinavir in the crystal structure, and the first is used in our simulation. The structure of the substrate (Ace-Ser-Gln-Asn-Tyr-Pro-Ile-Val) was modified from an inhibitor JG365 [Ace-Ser-Leu-Asn-Phe-PSI(CH(OH)-CH2N)-Pro-Ile-Val-OME] complexed with the protease (PDB entry 7hvp) (8). This substrate covers the whole binding site of the protease. The molecules are solvated in an 80 × 80 × 80-Å3 box of water. An appropriate number of counter ions are added to neutralize the system. Particle Mesh Ewald (9) is used to calculate the long-range electrostatic interactions. All structures are minimized first by using the sander module in AMBER5.0. MD simulations are carried out thereafter. The temperature of the system is raised gradually from 50 to 298 K in 50 ps and equilibrated at 298 K for another 120 ps. An additional 120 ps of MD simulation is performed for data collection, and 100 snapshots are saved for the subsequent analysis. The deviations are estimated by the difference between the first and second half of the trajectories. The shake procedure (10) is used to constrain all bonds. The time step of the simulations is 2 fs. A 8.5-Å cutoff is used for the nonbonded interactions. The nonbonded pairs are updated every 15 steps.
(ii) The Molecular Mechanics (MM)/Poisson–Boltzmann Solvation Area (PBSA) Method.
The binding free energy is calculated as (11):
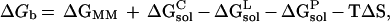 |
1 |
where ΔGb is the binding free energies in
water, ΔGMM is the interaction energy between
the ligand and the protein, ΔG ,
ΔG
,
ΔG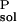 , and ΔG
, and ΔG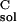 are solvation
free energies for the ligand, protein, and complex, respectively, and
−TΔS is the conformational entropy contribution to the binding.
ΔGMM is calculated from MM interaction
energies:
are solvation
free energies for the ligand, protein, and complex, respectively, and
−TΔS is the conformational entropy contribution to the binding.
ΔGMM is calculated from MM interaction
energies:
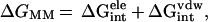 |
2 |
where ΔG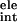 and ΔG
and ΔG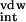 are electrostatic and van der Waals interaction energies between the
ligand and the receptor, which are calculated by using the
carnal and anal modules in the amber
5.0 software suite.
are electrostatic and van der Waals interaction energies between the
ligand and the receptor, which are calculated by using the
carnal and anal modules in the amber
5.0 software suite.
The solvation energy, ΔGsol, is divided into
two parts, the electrostatic contributions, ΔG ,
and all other contributions, ΔG
,
and all other contributions, ΔG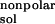 .
.
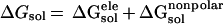 |
3 |
The electrostatic contribution to the solvation free energy,
ΔG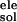 , is calculated by using the delphi
ii software package (12), which solves the PB equations
numerically and calculates the electrostatic energy according to the
electrostatic potential. The grid size used is 0.5 Å. Potentials at
the boundaries of the finite-difference lattice are set to the sum of
the Debye–Huckel potentials. The value of interior dielectric constant
is set to 1. As shown in our previous study (13), after combining all
of the terms, the binding free energy is calculated as:
, is calculated by using the delphi
ii software package (12), which solves the PB equations
numerically and calculates the electrostatic energy according to the
electrostatic potential. The grid size used is 0.5 Å. Potentials at
the boundaries of the finite-difference lattice are set to the sum of
the Debye–Huckel potentials. The value of interior dielectric constant
is set to 1. As shown in our previous study (13), after combining all
of the terms, the binding free energy is calculated as:
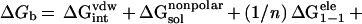 |
4 |
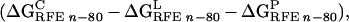 |
where n is the interior dielectric constant, which is 1
in this study. ΔG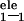 is the molecular mechanics
electrostatic interaction energy between the ligand and the
protein. ΔG
is the molecular mechanics
electrostatic interaction energy between the ligand and the
protein. ΔG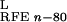 ,
ΔG
,
ΔG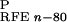 , and
ΔG
, and
ΔG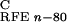 are reaction field energies
obtained from delphi ii for ligand, protein, and complex,
respectively, with interior and exterior dielectric constants set to
n and 80, respectively.
are reaction field energies
obtained from delphi ii for ligand, protein, and complex,
respectively, with interior and exterior dielectric constants set to
n and 80, respectively.
The dielectric constant of water is set to 80. The dielectric boundary is taken as the solvent-accessible surface defined by a 1.4-Å probe sphere. The radii of atoms are taken from the parse parameter set (14). Partial charges are taken from Cornell et al. (6) force field for standard amino acids.
The solvent-accessible surfaces (SAS) are calculated by using the
msms program (15). The nonpolar contribution to the
solvation free energy, ΔG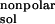 , is calculated
as 0.00542 × SAS + 0.92 kcal/mol (14).
, is calculated
as 0.00542 × SAS + 0.92 kcal/mol (14).
(iii) psi-blast and FV Value.
psi-blast (16) with default parameters (blosum62, Expect = 10, E-value threshold for inclusion in psi-blast iteration = 0.002, Descriptions = 500, Alignments = 500, composition-based statistics) is used to search the swiss-prot database. Multiple sequence alignment is carried out on 80 sequences with scores >64 and E value <1 × 10−10 by using the pileup module in the gcg software package (Ver. 10.1, Genetics Computer Group) with default parameters. These 80 sequences include HIV, simian immunodeficiency virus, and feline immunodeficiency virus proteases.
To identify critical residues for binding, we defined an empirical parameter called the FV value. The FV value is defined as a product of one residue's contribution to binding free energy ΔGres and variability of that residue, Vi. ΔGres is estimated as:
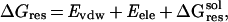 |
5 |
where Evdw and
Eele are van der Waals and
electrostatic interaction energies between the residue and the whole
ligand, respectively. ΔG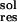 is the contribution of
solvation penalty by that residue. It is calculated as:
is the contribution of
solvation penalty by that residue. It is calculated as:
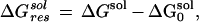 |
6 |
where ΔGsol and ΔG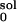 are the solvation energies calculated from Eq. 3 with normal
partial charges and zero charges on that specific residue, respectively
(17).
are the solvation energies calculated from Eq. 3 with normal
partial charges and zero charges on that specific residue, respectively
(17).
The variability Vi is calculated as:
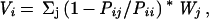 |
7 |
where Wj is the weight of the jth sequence. Wj is calculated for each sequence in the alignment on the basis of sequence identity. If n sequences are >80% identical to each other, each sequence has 1/n weight. Next, the sum of all sequences in the alignment is normalized to 1. This weight prevents overpresenting very similar sequences in the psi-blast search results.
Pij in Eq. 7 represents how likely the amino acid aj in the jth sequence can be mutated to the amino acid ai in the ith sequence and is calculated as:
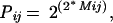 |
8 |
where Mij is the element of blosum62 for ai and aj. blosum62 is chosen to be consistent with the matrix used in psi-blast search. Mij for gap is assigned a penalty score of −4 in the blosum62 matrix.
Results and Discussion
(i) No Single Drug Resistance Mutation Is Observed to Occur at Well Conserved Residues.
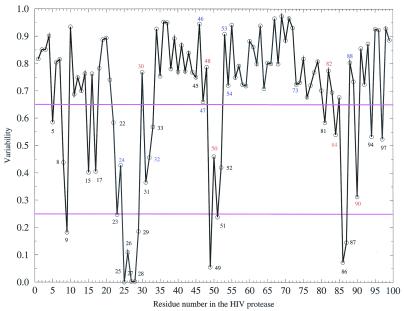
Drug resistance mutants of the HIV protease significantly reduce inhibitor binding without severally deteriorating the protease's own function. Therefore, those catalytically or structurally critical residues, such as the catalytic triad Asp-25, Thr-26, and Gly-27, are not tolerant to any mutations. The variability of each position in the HIV protease is shown in Fig. 1. The variability is calculated on the basis of sequences from different species. Low variability means that the residue in the HIV protease is well conserved across species and may be catalytically or structurally important. From Fig. 1, it is clear that no single drug resistance mutations have ever been observed for positions with variability lower than 0.25 (P9, D25, T26, G27, A28, D29, G49, G51, G86, and R87). These conserved residues are either crucial for catalyzing polypeptide cleavage, e.g., Asp-25, or stabilizing the structure of the protease dimer, e.g., Arg-87, which forms a salt bridge with Asp-29. These residues alone apparently mutate very little or not at all under drug selection pressure. Therefore, single drug resistance mutations can occur only at those not-well conserved residues that are critical for drug binding but are either unimportant or are tolerant of mutations for viral activity.
Figure 1.
Variability at each position of the HIV protease. Single mutations on any red-labeled residues can cause resistance to at least one drug, and residues labeled blue cause resistance when occurring with other mutations, according to the Stanford HIV database (http://hivdb.stanford.edu/hiv/Notes.pl, maintained by Robert Shafer).
(ii) Single Drug-Resistant Mutations Often Occur at Residues That Are Not Well Conserved but Interact More Favorably with Drugs than the Substrate.
To understand the mechanism of drug resistance of the HIV protease, we first identified residues responsible for binding with ligands by calculating the van der Waals interaction energy between each residue in the HIV protease and the substrate; secondly, we evaluated each of these residues' contributions to the binding free energy, ΔGres, and calculated the difference of ΔGres, ΔΔGres, between drugs and the substrate. By analyzing ΔΔGres of each residue and the variability of that sequence position, we found that single drug-resistant mutations often occur at residues that are not well conserved but interact more favorably with drugs than the substrate.
As the first step of our simulation, we modeled the complex of the wild-type HIV protease and one of its gag cleavage sequences, SQNYPIV, on the basis of the complex structure of one linear peptide inhibitor, JG365 (8), because no crystal structure of substrate–protease complex was available, and JG365 is reasonably similar to the substrate. This substrate covers the whole binding site of the protease. We optimized the substrate complex in water by using molecular dynamics until equilibrium was achieved (the rms deviation of all heavy atoms became flat at ≈1.5 Å). We note that Schiffer and coworkers (18) recently have solved a complex structure between an inactive HIV-1 protease (D25N) and a long substrate peptide, KARVLAEAMS, which is different from the substrate we are studying. The structure has been deposited in the PDB database (on hold and PDB entry 1f7a). It would be interesting to compare our modeled structure with this crystal structure after it is released to public access.
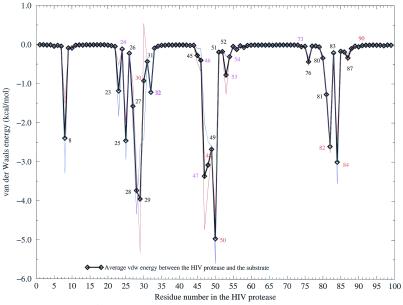
Residues in the HIV protease are considered to be in or close to the binding site if they have a van der Waals interaction energy with the substrate that is more negative than −0.5 kcal/mol (Fig. 2). Residues with the most frequent single drug resistance mutations have relatively more favorable van der Waals energies. The exceptions are L24, G73, and L90, implying that resistances caused by mutations at these three positions might be due to changes of conformation or stability and, therefore, the proteolytic kinetics of the HIV protease. All residues that have van der Waals interaction energies with the substrate more favorable than −0.5 kcal/mol as well as the three known single resistance residues (L24, G73, and L90), which do not have such a favorable van der Waals interaction energy, were evaluated for their contributions to the binding free energy in this study. This set of residues includes all major single drug resistance mutations. We would like to emphasize that in this study, we discuss only single mutations that can cause drug resistance, because (i) the number of combinations of multiple mutations is huge, and (ii) free energy calculations for individual residues are computationally expensive.
Figure 2.
van der Waals interaction energy between each residue in the HIV protease and the substrate. Solid black line, average of two monomers; red and blue lines, monomer.
Before we evaluate ΔGres for each residue, we
estimate the binding free energies of the substrate and the five
FDA-approved drugs, i.e., Ritonavir, Saquinavir, Amprenavir, Indinavir,
and Nelfinavir, by using the MM/PB Solvation Area (PBSA)
method (11) (Table 1). It is obvious that
all inhibitors bind more tightly than the substrate. The substrate is
the largest ligand and thus has the most favorable van der Waals
interactions with the protease. However, it also has the least
favorable electrostatic contribution ΔG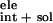 to the binding free energy because of the burial of polar residues Asn,
Tyr, and Pro in the active site. This calculation suggests that
it is important for potent drugs to have optimal electrostatic
interaction with the protease but less desolvation penalty. It is worth
pointing out that the TΔS for substrate or inhibitor binding is not
included in Table 1. Given that our goal is a qualitative comparison of
ΔGbind for substrate and inhibitors, we assume
that the entropies are similar in magnitude for the inhibitors and the
substrate. This assumption seems reasonable, given Kuhn and Kollman's
calculated TΔS for various ligands binding to avidin (19). Also, the
results of Kuhn and Kollman show that the TΔS tends to be larger in
magnitude the larger the ligand; thus, inclusion of this term would
likely increase the relative ΔΔGbind between
substrate and inhibitors, because substrate is the largest ligand.
to the binding free energy because of the burial of polar residues Asn,
Tyr, and Pro in the active site. This calculation suggests that
it is important for potent drugs to have optimal electrostatic
interaction with the protease but less desolvation penalty. It is worth
pointing out that the TΔS for substrate or inhibitor binding is not
included in Table 1. Given that our goal is a qualitative comparison of
ΔGbind for substrate and inhibitors, we assume
that the entropies are similar in magnitude for the inhibitors and the
substrate. This assumption seems reasonable, given Kuhn and Kollman's
calculated TΔS for various ligands binding to avidin (19). Also, the
results of Kuhn and Kollman show that the TΔS tends to be larger in
magnitude the larger the ligand; thus, inclusion of this term would
likely increase the relative ΔΔGbind between
substrate and inhibitors, because substrate is the largest ligand.
Table 1.
Binding free energies of the substrate and five FDA-approved drugs
| Name | Experimental ΔGb*, kcal/mol | ΔG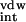 ,
kcal/mol ,
kcal/mol |
ΔG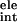 ,
kcal/mol ,
kcal/mol |
ΔGnonpol, kcal/mol | ΔG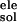 ,
kcal/mol ,
kcal/mol |
ΔG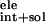 †,
kcal/mol †,
kcal/mol |
ΔGb‡, kcal/mol |
|---|---|---|---|---|---|---|---|
| Substrate | N/A | −88.3 ± 0.1 | −80.6 ± 1.1 | −7.6 ± 0.0 | +161.1 ± 1.4 | +80.6 ± 0.3 | −15.4 ± 0.2 |
| Ritonavir | −14.9 | −80.5 ± 1.0 | −38.4 ± 0.5 | −6.9 ± 0.1 | +100.8 ± 0.6 | +62.4 ± 0.1 | −24.9 ± 1.0 |
| Saquinavir | −14.3 | −67.6 ± 0.3 | −24.6 ± 1.9 | −6.6 ± 0.1 | +72.0 ± 2.0 | +47.4 ± 0.1 | −26.8 ± 0.1 |
| Amprenavir | −13.9 | −62.6 ± 0.5 | −49.6 ± 0.1 | −5.1 ± 0.1 | +96.5 ± 0.8 | +46.9 ± 0.9 | −20.8 ± 0.4 |
| Indinavir | −13.3 | −70.9 ± 1.8 | −31.7 ± 3.8 | −6.3 ± 0.1 | +86.3 ± 3.5 | +54.6 ± 0.3 | −22.6 ± 2.2 |
| Nelfinavir | −13.0 | −65.3 ± 2.3 | −36.8 ± 0.8 | −5.7 ± 0.0 | +82.8 ± 0.8 | +45.9 ± 1.6 | −25.1 ± 0.6 |
Experimental ΔGb(Kis) were measured at pH = 6.5 (25).
ΔG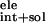 =
ΔG
=
ΔG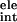 + ΔG
+ ΔG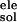 .
.
‡TΔS is not included (see text).
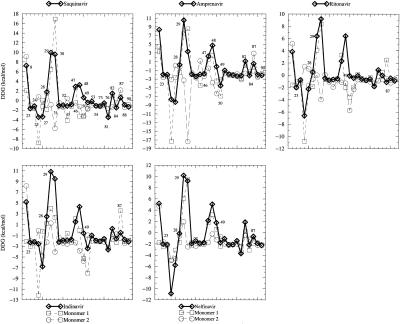
Studying drug resistance requires evaluation of each residue's contribution to the binding, which is an experimentally difficult but computationally feasible task. Here we combine molecular mechanics energies (van der Waals and electrostatic energy) and desolvation penalty (by solving the PB equation) to estimate a single residue's contribution to the binding. ΔΔGress between drugs, and the substrates for selected residues are plotted in Fig. 3. It should be noted that the HIV-1 protease is a dimer. A single mutation of its gene is a double mutation in the protein. Fig. 3 plots ΔΔGress of the double mutations on dimer as well as single mutation on each monomer. According to double mutations, for example, Amprenavir interacts more favorably with residues M46, I50, I84, and L90, but less favorably with residues I47, G48, and V82 than the substrate. This calculation suggests that single mutations on M46, I50, I84, and L90 but not on I47, G48, and V82 may cause resistance to Amprenavir. Experimental measurements show that six of seven (I47, G48, I50, V82, I84, and L90) of our predictions are correct (see below) (Table 2). It is worth noting that M46, I47, G48, and V82 are not conserved with variability higher than 0.65, which suggests that these four residues are either unimportant or tolerant of mutations for viral activity.
Figure 3.
Free energy difference between each residue's contribution to the
binding with drugs and substrate (ΔΔGres =
ΔG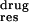 –ΔG
–ΔG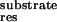 ). All
residue numbers are labeled for Saquinavir, but only a few residues are
labeled for other drugs. Solid black line = dimer; red and blue lines =
monomer.
). All
residue numbers are labeled for Saquinavir, but only a few residues are
labeled for other drugs. Solid black line = dimer; red and blue lines =
monomer.
Table 2.
Predictions of resistant mutations on the basis of FV value calculations
| Residue no. | Experimental
K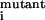 /K /K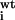
|
FVdouble value | Resistant? Experimental* (Prediction†) | Prediction accuracy | ||||
|---|---|---|---|---|---|---|---|---|
| Saquinavir | ||||||||
| V32 | 1.6–7.3 (V32I) (26) | −0.4 ± 0.3 | N (N) | 75% | ||||
| M46 | 1.0 (M46I) (27) | −0.8 ± 0.2 | N (N) | |||||
| I47 | 1.0 (I47V) (27) | +1.9 ± 0.6 | N (N) | |||||
| G48 | 13.5 (G48V)(28) 163.6 (G48V) (25) | +2.5 ± 1.2 | Y (N) | |||||
| I50 | 21.0 (I50V) (27) | −0.2 ± 0.6 | Y (N) | |||||
| V82 | 0.7–3.7 (V82A/F/I) (26) 3.3–7.3 (V82F/A/I) (29) | +1.1 ± 0.5 | N (N) | |||||
| I84 | 5.8 (I84V) (26) 10.7 (I84V) (29) 12.0 (I84V) (27) | −0.8 ± 0.5 | N (N) | |||||
| L90 | 3.0 (L90M) (28, 30) 20.7 (L90M) (25) | −0.4 ± 0.0 | N (N) | |||||
| Amprenavir | ||||||||
| M46 | 1.0 (M46I) (27) | −1.7 ± 0.2 | N (Y) | 86% | ||||
| I47 | 1.0 (I47V) (27) | +1.5 ± 0.6 | N (N) | |||||
| G48 | 3.5 (G48V) (25) | +3.7 ± 1.1 | N (N) | |||||
| I50 | 83.0 (I50V) (27) | −2.1 ± 0.5 | Y (Y) | |||||
| V82 | 0.4–3.3 (V82A/F/I) (29) | +0.9 ± 0.6 | N (N) | |||||
| I84 | 23.0 (I84V) (27) 2.7 (I84V) (29) | −1.2 ± 0.5 | Y (Y) | |||||
| L90 | 2.7 (L90M) (25) | −0.7 ± 0.0 | N (N) | |||||
| Ritonavir | ||||||||
| M46 | 4.0 (M46I) (27) | −0.5 ± 0.2 | N (N) | 57% | ||||
| I47 | 3.0 (I47V) (27) | +1.5 ± 0.7 | N (N) | |||||
| G48 | 66.7 (G48V) (25) | +5.0 ± 1.0 | Y (N) | |||||
| I50 | 10.0 (I50V) (27) | −0.2 ± 0.5 | N (N) | |||||
| V82 | 0.8–14.7 (V82A/F/I) (29) | +0.7 ± 0.5 | Y (N) | |||||
| I84 | 11.2 (I84V) (29) 20.0 (I84V) (27) | −0.0 ± 0.5 | Y (N) | |||||
| L90 | 6.7 (L90M) (25) | −0.3 ± 0.0 | N (N) | |||||
| Indinavir | ||||||||
| V32 | 8.0 (V32I) (26) | −0.9 ± 0.3 | N (N) | 86% | ||||
| M46 | 4.3 (M46I) (26) | −1.6 ± 0.2 | N (Y) | |||||
| I47 | 3.0 (I47V) (27) | +1.0 ± 0.7 | N (N) | |||||
| G48 | 6.3 (G48V) (25) | +3.4 ± 1.1 | N (N) | |||||
| V82 | 0.6–6.4 (V82A/F/I) (29) 6.9–84.7 (V82A/F/I) (26) | +0.2 ± 0.5 | N (N) | |||||
| I84 | 2.6 (I84V) (29) 10.0 (I84V) (26) | −0.9 ± 0.6 | N (N) | |||||
| L90 | 5.8 (L90M) (25) | −0.7 ± 0.0 | N (N) | |||||
| Nelfinavir | ||||||||
| G48 | 1.0 (G48V) (25) | +4.0 ± 1.0 | N (N) | 75% | ||||
| V82 | 0.8–17.5 (V82F/A/I) (29) | +1.5 ± 0.5 | N (N) | |||||
| I84 | 3.5 (I84V) (29) | −1.2 ± 0.5 | N (Y) | |||||
| L90 | 3.5 (L90M) (25) | −0.7 ± 0.0 | N (N) | |||||
Average prediction accuracy of five drugs is 76%. N, no; Y, yes.
If
K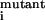 /K
/K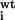 > 10 for single mutation, that residue is considered to be resistant.
> 10 for single mutation, that residue is considered to be resistant.
The criterion used for predicting resistance is FVdouble ≤ −1.0 (in parentheses).
On the basis of the above analysis, we suggest the following mechanism for drug resistance: if a drug's binding with the protease depends on a favorable interaction with a not-well conserved residue, either unimportant or tolerant of mutations for viral activity, more than the substrate, mutation at that residue would not affect the function of the protease but would be able to significantly reduce inhibition of the drug; thus, the mutation causes drug resistance. It is worth pointing out that in vivo formation of heterodimer and multiple mutations could provide the HIV virus with more sophisticated resistance schemes. In principle, our methods can be applied to the study of these situations as well.
(iii) More Favorable Interactions with Well Conserved Leu-23, Ala-28, Gly-49, Arg-87, and, More Importantly, Asp-29 Might Enable the Five FDA-Approved Drugs to Be Nonsensitive to Viral Resistance.
Among residues with <0.25 variability (Fig. 1), it is shown that all drugs interact much more favorably with Asp-25 and Gly-27, slightly more favorably with Leu-23, but slightly less favorably with Ala-28, Gly-49, and Arg-87, and much less favorably with Asp-29 than the substrate (Fig. 3). All these residues are well conserved (Fig. 1) and appear to be catalytically or structurally important; thus, mutations do not tend to occur at these positions.
The above analysis suggests that these five FDA-approved drugs can be altered to become more powerful to combat HIV drug resistance if their interactions with Leu-23, Ala-28, Gly-49, Arg-87, and, more importantly, with Asp-29 are improved. Leu-23 and Ala-28 are hydrophobic and in the center of the binding site. More favorable interactions with them can be achieved by adding some nonpolar groups in the drugs at P1 and P1′. Interactions with Gly-49, Arg-87, and Asp-29 can be improved only if drugs can have more favorable electrostatic interactions with them but less desolvation penalty, which is difficult but not impossible. One speculation is to add some polar or even charged groups at P3 and P3′.
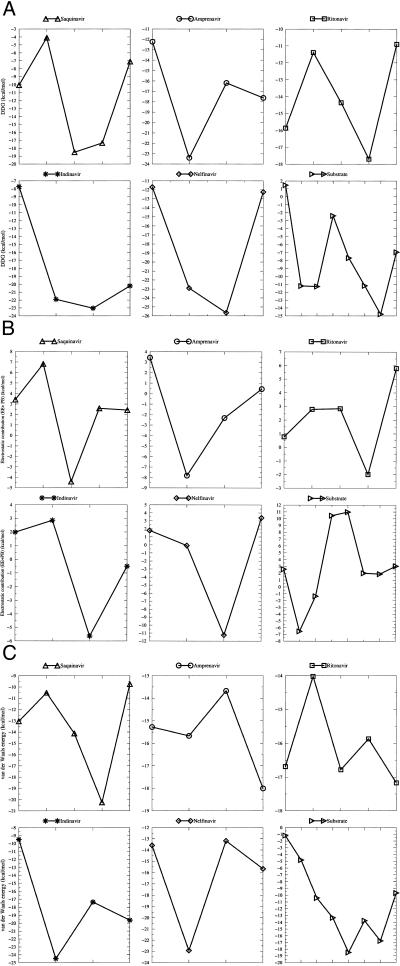
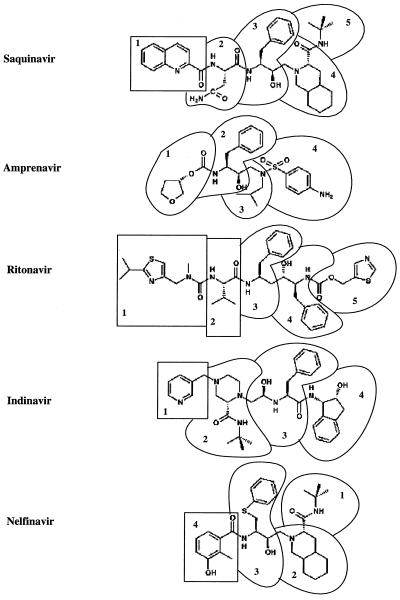
To further illustrate how to improve the five FDA-approved drugs, we calculated the contribution to binding for every residue in each drug (Fig. 5). A residue in a drug is defined on the basis of chemical groups and chosen to be as similar as possible to a natural amino acid (Fig. 4). Investigation of the van der Waals and electrostatic contributions to binding can provide clues to improve these drugs. For example, the third residue of Amprenavir has the least favorable van der Waals energy and the second least free energy contribution, although its electrostatic (PB + Coulomb term) contribution is the second most favorable. This residue is close to Ala-23, which is well conserved. Therefore an additional hydrophobic group, like substituting one of the two methyl groups in the isobutyl by a ethyl group, which makes more favorable interactions with Ala-23, can help Amprenavir to combat viral resistance.
Figure 5.
(A) Free energy, (B) electrostatic contribution (Coulomb + PB), and (C) van der Waals energy of each residue in the drugs and the substrate.
Figure 4.
Definition of residues in the drugs.
(iv) The FV Value Can Identify Drug-Resistant Mutations.
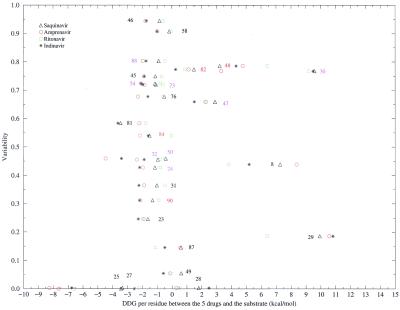
We have plotted ΔΔGres and variability in Fig. 6. Most single drug resistance mutations are in the region of ΔΔGres between 0 and −3.0 kcal/mol. Seven of them have a variability between 0.65 and 0.85.
Figure 6.
Two-dimensional plot of variability at each position and free energy difference between each residue's contribution to the binding with the substrate and drugs.
Encouraged by our successful combination of van der Waals and conservation to suggest critical residues on the Sem-5 SH3 domain (20), we propose an empirical parameter, the FV value, to quantitatively identify drug-resistant mutations (Table 2). The FV value is defined as the product of ΔGres and the variability of that residue. The purpose of defining this parameter is to include free energy and evolution information into one value. A mutation is commonly considered drug resistant if it causes >10-fold change of Ki of drugs. Usually it is assumed that homodimers of the HIV protease are formed, and thus double mutations should be considered. A threshold of −1.0 (= 2 × 1.4 × 0.35) is used for the FV value of double mutations for identifying resistance, which corresponds to 1.4 kcal/mol (10-fold change of Ki) and variability >0.35 (most positions included). The accuracy of identifying resistance mutations by the FV value varies among drugs (see Table 2; also see Table 3, which is published as supporting information on the PNAS web site, www.pnas.org), but average accuracy is 76%, which we think is quite good.
The FV value did not find G48 resistant for Saquinavir and Ritonavir. From previous studies (13, 21, 22), mutating Gly-48 to other hydrophobic residues favors formation of heterodimer of the HIV protease. We can see single G48 interacts more favorably with drugs than with the substrate, which implies that possibly heterodimers of the HIV protease are formed under the selection pressure of Saquinavir and Ritonavir. Another residue on which the FV value is not informative is M46, possibly because M46 is on the surface of the protein and therefore at the boundary of the interior and exterior region when solving the PB equation; thus, more error may be introduced in the PB calculations.
Multiple mutations tend to be found in vivo, but in this study, we compare only residues for which in vitro single mutation experimental data are available. It is obvious that the same analysis can be applied to study multiple mutations.
Conclusion
We have shown here that single drug-resistant mutations can occur only at not-well conserved positions that are critical for drug binding but are either unimportant or tolerant to mutations for viral activity. Therefore, resistance-evading drugs should interact strongly with those conserved residues. We have analyzed the five FDA-approved drugs and suggest that improving interactions between these drugs and residues Leu-23, Ala-28, Gly-49, Arg-87 and, more importantly, with Asp-29 in the protease may possibly enhance their abilities to combat drug resistance. An empirical parameter, the FV value, was exploited to identify drug-resistant mutations and can also be useful in studying other protein–protein or protein–ligand interactions. The FV value is the generalization of the van der Waals conservation value (VC) (20). After this work was finished, it came to our notice that the spirit behind the FV or VC value is consistent with the identification of the common folding nucleus by looking at the number of contacts that certain amino acids make and how conserved they are (23, 24). However, to our knowledge, FV and VC values are the only quantitative parameters to combine energetic and evolutionary information. They thus might be useful for studying protein folding as well.
We have presented only qualitative suggestions for how to improve the five FDA-approved HIV protease drugs rather than detailed calculations, because it makes more sense to do the latter in the context of a program to synthesize and test such molecules. Nonetheless, we feel the approach we have presented to decompose ΔGbind, in terms of either residue or ligand fragment components, is powerful and general. When combined with the residue FV values and the relative ΔGbind of substrate and inhibitors, this approach should be useful both in optimizing ΔGbind and, during such a process of optimization, minimizing viral resistance.
Supplementary Material
Acknowledgments
Soon after this manuscript was submitted, Prof. Peter A. Kollman sadly died of cancer. W.W. truly appreciates completing his Ph.D. thesis with Peter and has learned much from him. Peter was an incredible mentor, and his enthusiasm for science, sense of humor, optimism, and respect for students made doing research in his lab very enjoyable. W.W. also thanks Dr. Junmei Wang for his kind help with profec and Prof. Charles Craik for his comments on the manuscript. This work was supported in part by National Institutes of Health Grant GM-56531 (P. Ortiz de Montellano, Principal Investigator). Part of this investigation was completed by using the facilities in the University of California, San Francisco, Computer Graphics Lab (T. Ferrin, Director) and was supported by Grant RR-1081 from the National Institutes of Health. Supercomputer time at the National Science Foundation centers (National Center for Supercomputing Applications and San Diego Supercomputing Center) is gratefully acknowledged.
Abbreviations
- FV
free energy/variability
- MM
molecular mechanics
- PB
Poisson–Boltzmann
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Wlodawer A, Erickson J W. Annu Rev Biochem. 1993;62:543–585. doi: 10.1146/annurev.bi.62.070193.002551. [DOI] [PubMed] [Google Scholar]
- 2.Erickson J W, Burt S K. Annu Rev Pharmacol Toxicol. 1996;36:545–571. doi: 10.1146/annurev.pa.36.040196.002553. [DOI] [PubMed] [Google Scholar]
- 3.Wlodawer A, Vondrasek J. Annu Rev Biophys Biomol Struct. 1998;27:249–284. doi: 10.1146/annurev.biophys.27.1.249. [DOI] [PubMed] [Google Scholar]
- 4.Erickson J W. Nat Struct Biol. 1995;2:523–529. doi: 10.1038/nsb0795-523. [DOI] [PubMed] [Google Scholar]
- 5.Pearlman D A, Case D A, Caldwell J W, Ross W S, Cheatham T E, Debolt S, Ferguson D, Seibel G, Kollman P A. Comp Phys Commun. 1995;91:1–41. [Google Scholar]
- 6.Cornell W D, Cieplak P, Bayly C I, Gould I R, Merz K M, Ferguson D M, Spellmeyer D C, Fox T, Caldwell J W, Kollman P A. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 7.Jorgensen W L, Chandrasekhar J, Madura J, Impey R W, Klein M L. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 8.Swain A L, Miller M M, Green J, Rich D H, Schneider J, Kent S B H, Wlodawer A. Proc Natl Acad Sci USA. 1990;87:8805–8809. doi: 10.1073/pnas.87.22.8805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Darden T A, York D M, Pedersen L. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 10.Rychaert J P, Ciccotti G, Berendsen H J C. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 11.Kollman P A, Massova I, Reyes C M, Kuhn B, Huo S, Chong L T, Lee M R, Lee T S, Duan Y, Wang W, et al. Acc Chem Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 12.Gilson M K, Sharp K A, Honig B H. J Comput Chem. 1987;9:327–335. [Google Scholar]
- 13.Wang W, Kollman P A. J Mol Bol. 2000;303:567–582. doi: 10.1006/jmbi.2000.4057. [DOI] [PubMed] [Google Scholar]
- 14.Sitkoff D, Sharp K A, Honig B. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 15.Sanner M F, Olson A J, Spehner J C. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 16.Altschul S F, Madden T L, Schaffer A A, Zhang J H, Zhang Z, Miller W, Lipman D J. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chong L T, Duan Y, Wang L, Massova I, Kollman P A. Proc Natl Acad Sci USA. 1999;96:14330–14335. doi: 10.1073/pnas.96.25.14330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Prabu-Jeyabalan M, Nalivaika E, Schiffer C A. J Mol Biol. 2000;301:1207–1220. doi: 10.1006/jmbi.2000.4018. [DOI] [PubMed] [Google Scholar]
- 19.Kuhn B, Kollman P A. J Med Chem. 2000;43:3786–3791. doi: 10.1021/jm000241h. [DOI] [PubMed] [Google Scholar]
- 20.Wang W, Lim W A, Jakalian A, Wang J, Wang J M, Luo R, Bayly C I, Kollman P A. J Am Chem Soc. 2001;123:3986–3994. doi: 10.1021/ja003164o. [DOI] [PubMed] [Google Scholar]
- 21.Babe L M, Pichuantes S, Craik C S. Biochemistry. 1991;30:106–111. doi: 10.1021/bi00215a016. [DOI] [PubMed] [Google Scholar]
- 22.McPhee F, Good A C, Kuntz I D, Craik C S. Proc Natl Acad Sci USA. 1996;93:11477–11481. doi: 10.1073/pnas.93.21.11477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ptitsyn O B. J Mol Biol. 1998;278:655–666. doi: 10.1006/jmbi.1997.1620. [DOI] [PubMed] [Google Scholar]
- 24.Ptitsyn O B, Ting K L H. J Mol Biol. 1999;291:671–682. doi: 10.1006/jmbi.1999.2920. [DOI] [PubMed] [Google Scholar]
- 25.Maschera B, Darby G, Palu G, Wright L L, Tisdale M, Myers R, Blair E D, Furfine E S. J Biol Chem. 1996;271:33231–33235. doi: 10.1074/jbc.271.52.33231. [DOI] [PubMed] [Google Scholar]
- 26.Gulnik S V, Suvorov L I, Liu B S, Yu B, Anderson B, Mitsuya H, Erickson J W. Biochemistry. 1995;34:9282–9287. doi: 10.1021/bi00029a002. [DOI] [PubMed] [Google Scholar]
- 27.Partaledis J A, Yamaguchi K, Tisdale M, Blair E E, Falcione C, Maschera B, Myers R E, Pazhanisamy S, Futer O, Cullinan A B, et al. J Virol. 1995;69:5228–5235. doi: 10.1128/jvi.69.9.5228-5235.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ermolieff J, Lin X L, Tang J. Biochemistry. 1997;36:12364–12370. doi: 10.1021/bi971072e. [DOI] [PubMed] [Google Scholar]
- 29.Klabe R M, Bacheler L T, Ala P J, EricksonViitanen S, Meek J L. Biochemistry. 1998;37:8735–8742. doi: 10.1021/bi972555l. [DOI] [PubMed] [Google Scholar]
- 30.Jacobsen H, Yasargil K, Winslow D L, Craig J C, Krohn A, Duncan I B, Mous J. Virology. 1995;206:527–534. doi: 10.1016/s0042-6822(95)80069-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.